Abstract
Background
Gastric motility and accommodation have a critical role in maintaining normal gastrointestinal homeostasis. Different modalities can be adopted to quantify those processes, that is, scintigraphy to measure emptying time and intragastric Barostat for accommodation assessment. However, magnetic resonance imaging (MRI) can assess the same parameters noninvasively without ionizing radiation. Our study aimed to develop a detailed three‐dimensional (3D) MRI model of the stomach to describe gastric volumes, surface areas, wall tension distribution, and interobserver agreement.
Methods
Twelve healthy volunteers underwent an MRI protocol of six axial T2‐weighted acquisitions. Each dataset was used to construct a 3D model of the stomach: First, the volumes of the whole stomach, gastric liquid, and air were segmented. After landmark placing, a raw 3D model was generated from segmentation data. Subsequently, irregularities were removed, and the model was divided into compartments. Finally, surface area and 3D geometry parameters (inverse curvatures) were extracted. The inverse curvatures were used as a proxy for wall tension distribution without measuring the intragastric pressure.
Key Results
The model was able to describe changes in volume and surface geometry for each compartment with a distinct pattern in response to filling and emptying. The surface tension was distributed nonhomogeneously between compartments and showed dynamical changes at various time points.
Conclusion & Inferences
The presented model offers a detailed tool for evaluating gastric volumes, surface geometry, and wall tension in response to filling and emptying and will provide insights into gastric emptying and accommodation in diseases such as diabetic gastroparesis.
Keywords: abdomen, algorithms, gastric emptying, magnetic resonance imaging, reproducibility
This study presents a three‐dimensional stomach model able to report volume and surface data and describe the distribution of the gastric wall tension, volume, and surface. The method was able to provide insights into both gastric emptying and accommodation in different gastric compartments.
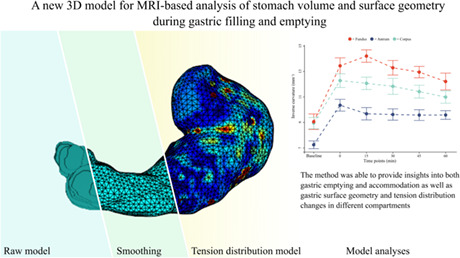
Key Points.
While MRI and ultrasound are getting progressively accepted as methods for evaluating gastric emptying and accommodation, they still do not provide essential insights into those processes.
This study presents a three‐dimensional stomach model able to report volume and surface data and to describe the distribution of the gastric wall tension of gastric compartments by applying the Young–Laplace law.
We observed that volumes and surface geometry showed distinct emptying patterns in each compartment and that the wall geometry distributed nonhomogeneously in the stomach, showing different dynamical changes during the emptying phase. Our observations indicate the fundus as essential in the first phase of digestion, confirming its role as reservoir.
The noninvasive model has the potential to give detailed information about the gastric volumes and surface geometry in response to filling and emptying, with the potential to understand the pathophysiology and improve treatment in patients with gastroparesis.
1. INTRODUCTION
In modern practice, the interest in the function of the stomach has led to an increasing focus on the assessment of gastric emptying, motility, and accommodation, as these processes are closely associated with each other. Various examinations are commonly accepted, such as gamma scintigraphy, 1 , 2 single‐photon emission computed tomography, 3 , 4 breath testing, 5 , 6 intragastric Barostat, 7 ultrasound, 8 , 9 smartpill, 10 and magnetic resonance imaging (MRI). 11 , 12 Some of these methods are limited by invasiveness, the use of radioactive isotopes or the inability to evaluate gastric emptying or anatomy. By contrast, others are time‐consuming and offer only indirect measurements. Gamma scintigraphy is presently accepted as the gold standard in the assessment of gastric emptying as it provides a reliable measure that does not suffer from confounding gastric secretions. 13 Unfortunately, it does not offer a precise evaluation of gastric volumes, the contents' intragastric distribution and wall geometry, resulting in a significant lack of insight into the mechanisms and pathophysiology behind diseases such as gastroparesis. Furthermore, its use is limited due to radiation exposure. The current standard for assessment of accommodation is the intragastric Barostat, an invasive technique not devoid of disadvantages and technical limitations. 7 , 14
Because of these limitations, ultrasound and MRI are becoming progressively more attractive due to their ability to morphologically evaluate gastric emptying and motility, including intragastric volume distribution and geometry, 15 , 16 , 17 without exposing the patient to unnecessary ionizing radiations or invasive procedures. 18 However, ultrasound‐based evaluation methods are prone to be observer‐dependent and unable to visualize gastric air. 19
MRIs, on the contrary, can visualize the entire stomach in one scan session providing three‐dimensional (3D) morphological and functional information through repeated scans. While MRI examinations of the stomach and of the gastric function have been of interest in recent literature, the existing methods still have methodological limitations. For example, the intragastric pressure cannot be directly quantified and, therefore, the absolute wall tension value cannot be measured. Tension data are of utmost importance in the clinical application of these methods, as the gastric wall tension determines the perception of gastric distention. 20 , 21 , 22
We hypothesized that an MRI 3D model would be able to provide essential insights into gastric geometry, motility, and accommodation. Furthermore, we hypothesized that through the application of the Young–Laplace law to the collected geometric data, the model would be able to describe the distribution of the wall tension across different compartments. Therefore, the primary aim of this study was to present a framework for a detailed analysis of gastric volumes, surface areas, and wall tension distribution in response to gastric filling and emptying using T2‐weighted MR images before and after a liquid meal. The secondary aim was to apply the method to 12 healthy subjects, exploring the details of gastric filling and emptying processes. Finally, we aimed to measure the interobserver agreement between two raters to further validate the observations on which our model was built.
2. MATERIALS AND METHODS
2.1. Study subject selection
Data were obtained from 12 healthy subjects, normal‐weighted, without prior history of gastric disorders or other diseases affecting the gastrointestinal (GI) function. None of the subjects was treated with any medication that could affect the GI system. Informed consent was obtained per national and local institutions' ethical standards. The study was approved by the North Denmark Region Committee on Health Research Ethics (N‐20090008).
2.2. Study design
Following a minimum of 6 h of fasting (solids and liquids), a baseline scan (at t:−30 min) was obtained in a transversal plan with the subjects in supine position. Subsequently, subjects were asked to step outside the MRI scanner for 10 min and ingest a liquid meal of lightly heated 250 kcal tomato soup 500 ml “Karolines Køkken” (Arla Foods, Central Denmark Region). Nutritional information per 100 g: fat 3 g, carbohydrates 4.1 g, and proteins 1.1 g. After ingesting the meal, the subjects were scanned at five additional time points (0, 15, 30, 45, and 60 min) with the same sequence as the baseline scan.
2.3. MRI protocol
Magnetic resonance imaging scans were performed using a 1.5 T General Electric model Discovery MR450 (General Electric Medical Systems). Axial steady‐state gradient echo (FIESTA) T2‐weighted image series covering the entire stomach was obtained with an echo time (TE) = 1.5 ms and a repetition time (TR) = 3.5 ms, in‐plane resolution = 0.7422 × 0.7422 mm, flip angle = 45°, slice thickness = 5 mm, 30–35 slices, and no image gap or overlap. Fat signal was not suppressed. Images were obtained in approximately 20 s under a single breath‐hold to minimize respiratory artifacts.
As shown in previous similar studies, 23 , 24 this sequence yielded a high signal of water and high contrast between gastric fluid content, comprehending meal and secretions, and gastric air and between the total gastric content and surrounding body tissues. No contrast‐enhancing agents were deemed necessary to increase the accuracy of the measurement. An example of raw MRI images is shown in Figure 1A.
FIGURE 1.
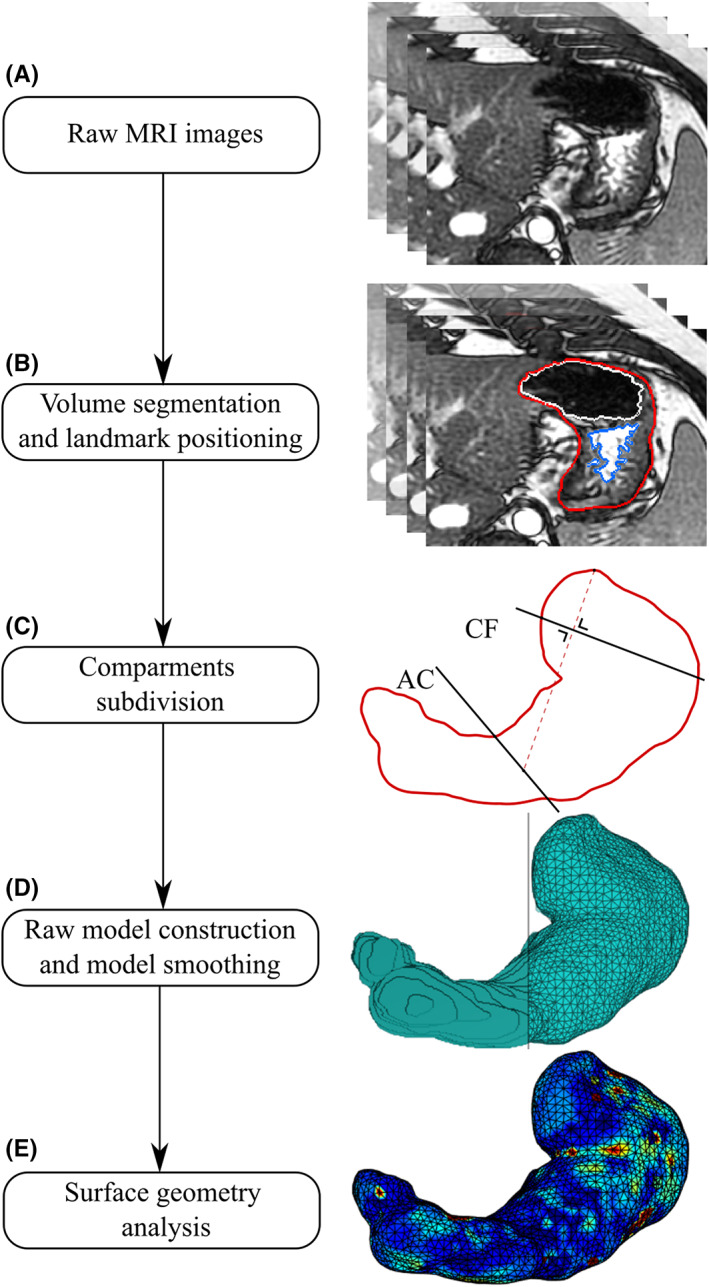
Three‐dimensional model development. First (A), axial T2‐weighted images of the stomach were obtained. Then (B), the volumes of liquid gastric content (blue), air content (white), and total gastric content (red) were segmented. Landmarks at the central part of the cardia, angular incisure, and the topmost part of the stomach were placed in this phase (C). Second, a raw 3‐dimensional model was generated from the segmented total gastric volume images (D). Irregularities were then removed, and the model was divided into compartments. Finally, inverse curvature data could be analyzed on the surface (E).
2.4. Model preparation
2.4.1. Manual segmentation of gastric fluid content, gastric air, and total gastric volume
The segmentation of high‐signal gastric fluid content, low‐signal gastric air, and total gastric volume was manually performed using a segmentation platform implemented in MATLAB (v.R2018b, MathWorks). An example of the segmentation steps is shown in Figure 1B. The total gastric volume was defined by the outer border of the stomach, including the stomach wall. The gastric fluid content volume was defined as the high‐signal volume within the total gastric volume (including areas with low signal caused by residues in the stomach or signal artifacts). By contrast, the gastric air was defined as the low‐signal volume within the total gastric volume. Segmentations were independently performed by two observers (EBM and CS). Firstly, segmentation of gastric fluid content and gastric air was performed. Secondly, an approximation of the total gastric volume boundary was initially drawn automatically using the previously segmented volumes of liquid and gas. An extra pixel layer was added with morphological dilation to encapsulate the stomach wall. Afterward, all slices were manually inspected, and the segmentations were corrected when needed. Then, the boundaries were manually edited to include the gastric wall and gastric areas not included in the other volumes. Segmentations of all three compartments took approximately 2 h per subject's dataset, comprehending all six scans. Only the data generated by the segmentations of the most expert observer (EBM) will be reported, while the second dataset will be used to assess the interobserver variability of our measurements.
2.4.2. Compartments and geometry of the stomach
The stomach volume and surface models were divided into antrum, corpus, and fundus. The antrum was obtained by dividing the stomach with a plane (Antrum‐Corpus plane, AC‐plane) passing the angular incisure and perpendicular to the less curvature in the coronal plane, see Figure 1C. Fundus and corpus were divided by a plane (Corpus‐Fundus plane, CF‐plane) passing the central point of the cardia and perpendicular to the line between the topmost point of the stomach and the middle point of the AC‐plane line in the coronal plane, see Figure 1C. 25 , 26 The angular incisures used to divide the stomach into antrum, corpus, and fundus were defined and independently confirmed by two observers (LD and EBM).
2.4.3. Three‐dimensional volume and surface modeling of the stomach
3D raw stomach volume models were generated from the segmented total gastric volume data, see Figure 1D. The volume of the total stomach model was calculated in ml by multiplying the number of image pixels, pixel size, and slice thickness.
Based on the volume of the 3D stomach model, the first raw surface was computed using the isosurface function in MATLAB with an isovalue of 0. The point cloud obtained from the isosurface was downsampled using a box grid filter in a box size of 5 mm and then presented as the surface of the stomach, represented with triangular facets, see Figure 1D. To remove the high curvature variations while avoiding shrinkage of the original surface, a modified nonshrinking Gaussian smoothing method was used to remove the irregularities of the reconstructed stomach surfaces due to the discretization of the images. 27 The surface area of the entire stomach was then calculated in cm2 by adding up the areas of all triangular facets. 28 The same method was previously applied, for example, in a work of Liao et al. 29 At this step of our pipeline, geometric data were extracted from the model, and inverse curvature data were calculated. For details of surface computations, see Appendix 1: surface smoothing. The processing of geometric data will be discussed in the following sections.
2.5. Data processing
2.5.1. Gastric emptying half‐times
The change in gastric liquid, air, and total gastric volume during the emptying phase was curve‐fitted to a linear‐exponential model (LinExp), 30 allowing to quantify the gastric emptying half‐times as:
| (1) |
This model can handle an initial volume increase (due to gastric secretions) using the coefficient kappa () and the subsequent volume decrease described by the coefficient. 24 The coefficient describes the start volume (t:0 min).
This calculation was performed with the online tool “apps.menne‐biomed.de/gastempt/.” This tool has been previously utilized in other studies. 31 In this work, the fitting method nlme population fit was used.
2.5.2. Wall tension distribution
In this work, the gastric wall tension was not directly measured or estimated. Still, through the following principles and equations, it was possible to describe how the tension was distributed in different compartments (called Wall tension distribution in this work). In medicine, the Young–Laplace Equation (2) has been used to describe multiple phenomena like the formation of diverticula or the expansion of abdominal aorta aneurysms 32 :
| (2) |
where P is defined as , where is the intra‐abdominal pressure and is the intragastric pressure; assuming isotropic tensions, is the tension on the gastric wall, and r 1 and r 2 are the principal radii of curvature.
In differential geometry, the principal curvatures at a given point on a surface are the maximum and minimum values of all the possible curvatures obtained through the section of the surface by planes tangent to the surface containing the normal vector . These two curvatures are denoted k1 and k2 and can be expressed as:
| (3) |
| (4) |
Resolving (4) for the ratio /, (5) is obtained:
| (5) |
Introducing in (5) the mean curvature, an extrinsic measure of curvature defined in fluid mechanics as:
| (6) |
We obtain that:
| (7) |
Furthermore, assuming P o and P i (and therefore ) to be constant (c) within each timepoint, the tension would only be proportional to the inverse mean curvature, allowing us to describe the wall tension distribution in different gastric compartments within the same timepoint, given only geometric data:
| (8) |
and therefore:
| (9) |
To report this distribution, inverse curvature data were normalized to antral values at the same timepoint, as we expected the volumes to be accommodated mainly in the proximal stomach. 26 As the constant c is of unknown value, this method does not allow us to estimate absolute wall tension values. Still, it allows us to evaluate its distribution on the gastric surface. For a visual representation of the forces involved, see Figure 2. and (expressed as mm−1) were calculated from the 3D surface model of the stomach using the algorithm presented by Hartmann et al. 28 See Appendix 1: principal curvatures computation. These analyses were at last applied to the previously generated 3D model. See Figure 3 and Figure 1E.
FIGURE 2.
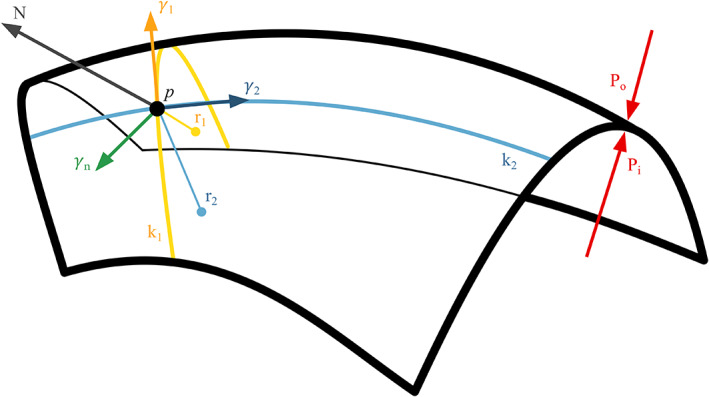
Schematic representation of the physical forces involved in the accommodation process. Po: Abdominal pressure, Pi: Intragastric pressure, k1 and k2 are the principal curvatures with r1 and r2 their relative radii, N is the normal vector perpendicular to the surface, is the tension on the gastric wall.
FIGURE 3.
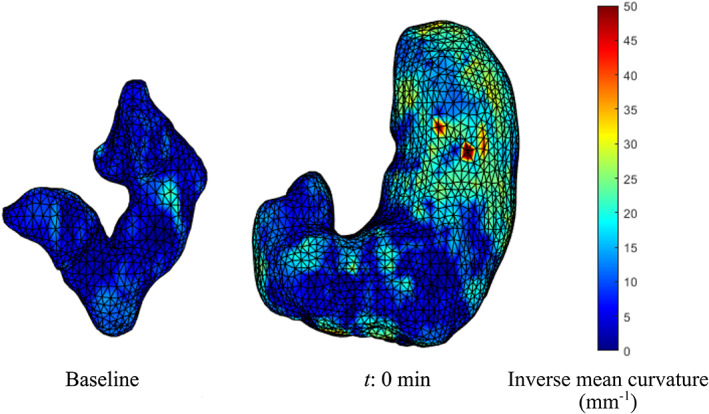
Tension distribution. The image shows an example of an empty stomach at baseline, characterized by lower wall tensions (blue color due to low inverse mean curvature values), compared with an image of a full stomach at t:0 min, characterized by higher tensions, particularly in the fundus (yellow/red colors due to high inverse mean curvature values).
Another important assumption in our model is that the stomach was represented as a thin‐walled membrane. This assumption is based on the premise that to properly apply the Laplace's law on a non‐infinitesimal‐walled structure, the following requirement should be met:
| (8) |
where is the wall thickness, the internal radius, and the intra‐abdominal pressure.
Studies reported mean intra‐abdominal pressures of 1.7 (1.2) cmH20 and mean intragastric pressures of 2.9 (1.7) cmH2O, resulting in = 0.7 in the preswallow resting state. 33 , 34 Resulting in:
| (9) |
This requirement was met in our dataset. Wall thickness data were not reported as outside the scope of this work.
Applying these equations to the geometric data collected allow to describe the distribution of the wall tension in different compartments without measuring or estimating the intragastric pressure.
2.5.3. Data normalization
Volume and surface area data were normalized to their total values to better convey the compartment dynamics during the emptying phase. The inverse curvature data were normalized to antral values at the same timepoint (see Wall tension distribution above).
2.6. Interobserver agreement
As the initial part of this framework is heavily observer‐dependent, interobserver differences in the total gastric volume were explored through Dice similarity coefficients. For validation, intraclass correlation coefficient (ICC) assessments between the two raters (EBM and CS) were performed on the extracted geometric data (inverse curvatures) on which our model was built. The same analyses were performed on the segmental data generated by the model: Dice similarity coefficients were obtained for the compartments' volume, ICC for surfaces area and inverse curvatures. No limit of agreement was established a priori.
2.7. Statistical analysis
Data were analyzed in R (R Core Team, 2021, R Foundation for Statistical Computing) with rstatix package (R package version 0.7.0), and figures were produced using the package ggplot2. 35
After identifying and removing extreme outliers (defined as values above the third quartile +3 interquartile ranges or below the first quartile – 3 interquartile ranges), volume, surface area, and inverse curvature data were inspected for normality through Q‐Q plots and Shapiro–Wilk tests. Due to the relatively small amount of data, extreme outliers were only temporarily removed for the analysis of a single endpoint (segmental volume, surface area, or inverse curvature) and then be reintegrated in the original dataset. Data from outliers were excluded at every timepoint. Correlation tests were then performed with two‐way repeated‐measure analysis of variances (ANOVAs, time and compartment were used as independent variables, dependent variable: volume, surface areas, or inverse curvature, both non‐normalized and normalized), tested for sphericity with Mauchly's test, and corrected with Greenhouse–Geisser and Huynh–Feldt corrections. In the case of positive correlation, post hoc analyses were performed with pairwise t‐tests adjusted with sequential Bonferroni tests (Bonferroni–Holm). A p‐value < 0.05 was considered statistically significant. Data were reported as mean (SD). ICC estimates and their 95% confidence intervals were calculated using R packages blandr and psych. 36 , 37 The model ICC1 (single‐measure, absolute‐agreement, and two‐way mixed effect) was utilized. Data were not transformed for analysis and were visually reported through a Bland–Altman plot.
3. RESULTS
All the recruited subjects fully complied with the study protocol, and a complete dataset was obtained from all 12 subjects (seven males), mean age 27.8 years (range 23–34 years). All the subjects well tolerated the meal.
3.1. Gastric volumes
Volumes of gastric fluid content, gastric air, and the total gastric volume can be seen in Figure 4A.
FIGURE 4.
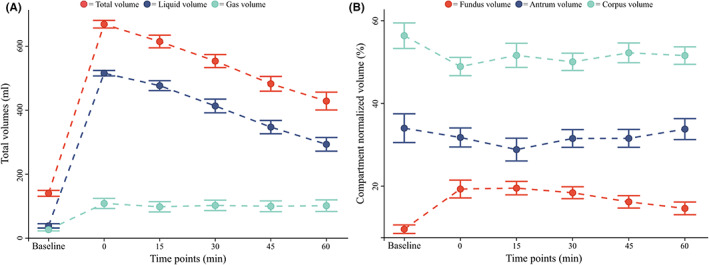
Gastric volume data. (A) total gastric volume (red), total liquid volume (blue), and total gas volume (teal) are shown. (B) Normalized fundus volume (red), normalized corpus volume (teal), and normalized antrum volume (blue) are shown. All data are reported as mean ± 1 standard error (error bars).
The total gastric volume increased from baseline values 140 ± 32 ml to 669 ± 41 ml at t:0 min (p < 0.001) and decreased to 429 ± 97 ml at t:60 min (p < 0.001), remaining however over baseline values (p < 0.001). The initial increase in volume was mostly due to the ingested meal: The liquid volume increased from 39 ± 23 ml at baseline to 516 ± 30 ml at t:0 min (p < 0.001). The liquid volume showed a similar decreasing pattern with a minimal volume of 294 ± 74 ml at t:60 min, never reaching baseline values (p < 0.001).
The gastric gas volume, after a limited initial increase from baseline values of 27 ± 14 ml to 109 ± 55 ml at t:0 min (p < 0.001), remained constant and over baseline values throughout the examination (p < 0.001), with a final volume of 102 ± 63 ml at t:60 min.
All compartments' total volumes (comprehending gastric wall, liquid, and air content) showed a similar dynamic with an initial increase (all p < 0.001) from baseline values to t:0 min and a successive decrease to t:60 min (all p < 0.05). No compartment volume returned to baseline values at t:60 min (all p < 0.05).
Data showed a difference at baseline between the volumes of each compartment with a fundus volume of 13 ± 6 ml, corpus volume of 80 ± 27 ml, and antrum volume of 46 ± 18 ml (all p < 0.001). This observation was confirmed by a two‐way repeated ANOVA that showed an influence of both time and compartment localization on the compartment volumes (all p < 0.001). Normalized data showed that fundus volumes increased from 9.6% ± 3.6% at baseline to 19.3% ± 7.5% at t:0 min and never returned to baseline values throughout the examination, with a volume of 14.6% ± 5.3% at t:60 min. No change from baseline values of corpus (56.4% ± 10.7%) or antrum (64.0% ± 12.0%) was observed (all p > 0.05). The different dynamics can be observed in Figure 4B. One extreme outlier was removed in these analyses (n = 11 records analyzed).
3.2. Assessment of emptying half‐times
The emptying half‐times of the liquid volume showed a mean value of 69 (SD 15) minutes. The emptying half‐times of the total gastric volume showed a mean value of 86 (SD 18) minutes.
3.3. Gastric surfaces
The total gastric surface area increased from 220 ± 27 cm2 at baseline to 536 ± 25 cm2 at t:0 min (p < 0.001) and decreased to 413 ± 54 cm2 at t:60 min. See Figure 5A.
FIGURE 5.
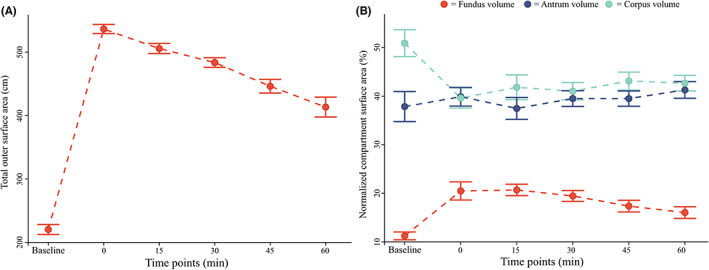
Gastric surface area data. (A) Total gastric surface area is shown. (B) Normalized fundus surface area (red), normalized corpus surface area (teal), and normalized antrum surface area (blue) are shown. All data are reported as mean ± 1 standard error (error bars).
All compartmental surface areas showed a similar dynamic with a starting increase from baseline to t:0 min (all p < 0.001) and a successive decrease toward t:60 min (all p < 0.05).
Fundus surface area was smaller than the other compartmental areas (all p < 0.001), with a baseline value of 25 ± 6 cm2 for fundus, 112 ± 23 cm2 for corpus, and 84 ± 31 cm2 for antrum. This observation was confirmed by a two‐way repeated ANOVA that showed an influence of both time and compartment localization on the compartment surface (all p < 0.001). Normalized data showed that the fundic surface area increased from 11% ± 3% at baseline to 21% ± 4% at t:15 min (p = 0.001), never returning to baseline values throughout the examination. This increment was mirrored by an initial decrease in corpus surface area from 51% ± 10% at baseline to 42% ± 9% at t:15 min (p < 0.001). Corpus surface area never returned to baseline throughout the study. No change was observed in antrum surface area, which remained around baseline (38% ± 11%) during the examination. The different surface area dynamics can be seen in Figure 5B. One extreme outlier was removed in these analyses (n = 11 records analyzed).
3.4. Gastric wall tension distribution
The wall tension distribution was different between compartments (p < 0.001), with mean inverse curvature values in the fundus being higher than those in the corpus (p < 0.001) and corpus values being higher than those in the antrum (p < 0.001) at every timepoint. The dynamical changes in the tension distribution can be seen in Figure 6A for non‐normalized data and Figure 6B for normalized data. Data showed that the corpus tension was 26% ± 26% higher than the antral tension (p = 0.017). At t:0 min, the tension in the fundus increased to values 34% ± 34% higher than those in the antrum (p = 0.018), while corpus tension values still were 21% ± 24% higher than antrum ones (p = 0.026). Fundus tension continued to increase to t:15 min to 51% ± 32% of the antral tension (p < 0.001). From t:15 min, the tension distributed toward the antrum with values in fundus and corpus steadily diminishing throughout the examination to t:60 min.
FIGURE 6.
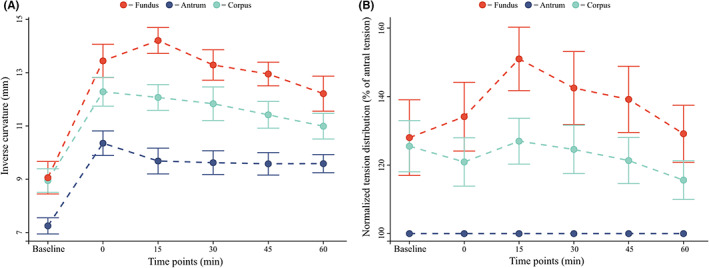
Inverse curvature data. (A) the non‐normalized values of fundus (red), corpus (teal), and antrum mean inverse curvature value (blue) are shown. (B) fundus (red) and corpus (teal) inverse curvatures are shown normalized to antral (blue) values at the same timepoint.
One extreme outlier was removed in these analyses (n = 11 records analyzed). The complete dataset can be found in Appendix 2, Table A3.
3.5. Interobserver agreement
Data showed a median Dice similarity coefficient for total gastric volume of 0.957 (IQR = 0.021) between the two raters.
Dice similarity coefficients for liquid and gas can be seen in Figure 7A. Median values ranged from baseline values: 0.846 (0.047) for total gastric volume, 0.851 (0.101) for liquid volume, and 0.828 (0.020) for gas volume, to 0.965 (0.009) for total gastric volume, 0.975 (0.013) for liquid volume, and 0.902 (0.050) for gas volume at t:0 min. Mean compartmental Dice scores were 0.888 (0.07) for fundus volume, 0.93 (0.03) for corpus volume, and 0.902 (0.05) for antrum.
FIGURE 7.
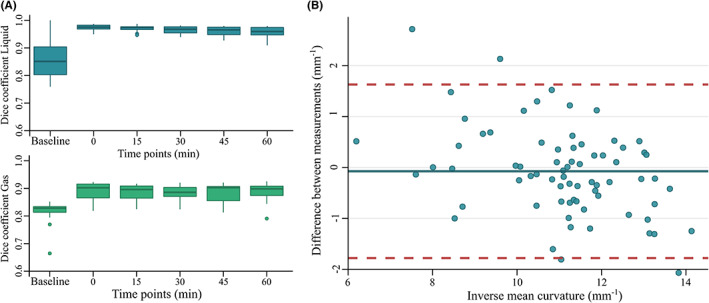
Dice similarity coefficient and intraclass correlation coefficient data. (A) Dice similarity coefficients for the liquid (blue) and gas (green) volumes are shown. (B) Bland–Altman plot for the correlation agreement between the two inverse curvature datasets across every timepoint. Blue dots: Observations, blue line: Bias, red dashed lines: 95% limits of agreement.
Intraclass correlation coefficient validation results can be seen in Figure 7B. The estimated bias was −0.07 mm−1 (−0.28, 0.13), with lower limit of agreement: −1.78 mm−1 (−2.12, −1.43) and upper limit:1.63 mm−1 (1.28, 1.98). The correlation coefficient was 0.87 (lower bound 0.79, upper bound 0.91, p < 0.005). Compartmental ICCs are reported in Appendix 3, Table B1, Figures B1, B2. Outlier distribution is reported in Appendix 3, Table B2.
4. DISCUSSION
The present study presents a 3D MRI‐based model for a detailed geometric assessment of gastric compartment volumes, surface areas, and wall tension distribution using MRI. The most important findings study were as follows: (1) The model was able to describe changes in volume, surface areas, and wall tension distribution in fundus, corpus, and antrum; (2) the changes in the observed gastric variables in response to gastric filling and emptying showed a distinct pattern for each compartment; (3) the wall tension distributed nonhomogeneously between different compartments and showed different dynamical changes during the emptying phase. Furthermore, during gastric filling, we observed that the most significant changes in volume and surface area occurred in the fundus, underlining its role as a reservoir of undigested food. The geometric data on which our model was built also gave us important insights into the dynamics of the emptying process, as, during the first 15 min after meal intake, the normalized fundus tension increased, representing its predominant role in the first phase of the emptying process.
4.1. Gastric volumes and emptying
As expected, the volume of the ingested liquids played a major role in the observed total gastric volume increase, while the gas volume was only accessory and generally constant throughout the examination. Furthermore, we observed that the fundus played a major role in accommodating newly ingested meals, as it was the only compartment to increase its normalized volume and surface area values during the first 15 min. The observed fasting volumes were in line with the literature, 38 , 39 as were the dynamics of the emptying process. 40 The volume and dynamics of total gas content were also in line with findings observed in the literature. 26 With a careful approximation (due to differences in the compartment subdivision of the stomach), it appears that the antral volumes at the start of the filling phase were also in line with the literature. 26
MRI gastric emptying studies have reported emptying half‐times between 64 and 92 minutes in healthy subjects for meals with similar composition. 25 , 41 , 42 Our half‐time measurements of 69 min for liquid and 86 min for the total volume comply with these observations. Direct comparison with previous data is difficult due to differences between study protocols, such as different amounts and kinds of meals, 23 MRI sequences, 25 or different sample sizes or demographics. 30 Moreover, some studies positioned the patients in a right lateral decubitus, which permits an easier outflow through the antrum, 43 and it is not always stated which positions were used between each scan. 44 However, the emptying phase dynamic of the fundus, corpus, and antrum in the present study showed a good agreement with a recent study done by Banerjee et al. 26
4.2. Gastric surface areas analysis
While no standard reference values of surface areas can be found in the literature, the dynamic of our observations is in line with other recent studies. 45 In our work, the fundus appears to sustain the most relevant area increase after meal intake, as it was the only compartment to show an increase in its normalized surface area from baseline to t:0 min.
Previously, we have done geometric surface analyses on 3D imaging data from the stomach, 46 gallbladder, 47 and rectum in humans to investigate the geometry and mechanical change in the models during distension. 48 In our previous surface modeling analysis, we resliced the 3D volume model along the central line of the model to generate the surface, which was very time‐consuming. 48 The method presented in this study has a superior time efficiency compared with the previous modeling analysis as it implemented a surface smoothing which could be performed straightforwardly from the volume model reconstructed from the MR images.
4.3. Gastric tension distribution
In our observations, the gastric tension was distributed unevenly across different compartments, with the highest inverse curvature values in the fundus and the lowest in the antrum. Furthermore, we observed that during the earliest phase of digestion (15 min), the fundus reached tension values up to 51% higher than those observed in the antrum. These observations concords with the reported changes in volume and surface areas elicited in the fundus by the meal, indicating the fundus as the most influential compartment in the first phase of digestion, confirming its role as reservoir. Our data showed wide variations, as observable by relatively high standard deviations. As data were normally distributed and the interobserver variability was excellent (see Interobserver agreement below), these differences can be imputed to significant intersubject variability, which is also often observed in other tracts of the GI system. 10 , 49 , 50
4.4. Interobserver agreement
Our analysis showed an excellent agreement in total gastric volumes between the two observers, defined by an overall Dice similarity coefficient of 0.938. Our observed coefficient is significantly higher than 0.7, defined in the literature as a good overlap. 51 As expected, the lowest scores for both total and compartmental volumes are observed at baseline, where the empty organ is harder to segment due to the low contrast caused by the small volume of intragastric liquids. The highest scores were on the contrary observed at t:0 min, where the organ contrast is at its peak. ICC analysis also showed good reliability, defined as an ICC value between 0.75 and 0.9. 52
4.5. Potential clinical implications
Implementation of analytical tools like the currently described image acquisition and analysis framework in the clinical practice will require optimization of the analysis time, including optimized segmentation and landmark annotation. A more automatic and standardized method will rapidly assess gastric function, emptying, and other motility indexes to evaluate and diagnose motility disturbances. These disturbances range from delayed gastric emptying and gastroparesis to abnormally rapid transit, usually referred to as “dumping syndrome.” 53 , 54 Furthermore, it will give access to the assessment of the gastric accommodation process, which plays an essential role in functional dyspepsia symptoms or in gastroesophageal reflux. 15 These assessments are vital in clinical practice and pharmacological studies. 55 Also, more automatic and standardized methods could be helpful in future research studies, giving them access to fast and straightforward 3D gastric models that could lead to a more robust understanding of the motility and the relative interferences of diseases or potential treatment approaches (drugs, neuromodulation, gastric pacing, and others).
4.6. Study limitations
In the present study, the subjects were placed in supine position after meal intake in the following image acquisitions. This position displaces the gastric content away from the antrum, potentially slowing gastric emptying. 43 A possible improvement could be obtained by oblique positioning in Fowler's position (semi‐ or low‐) as that would offer a more realistic setting for the gastric environment. 56 However, in the majority of similar studies, the study subjects were also placed in supine position as this is easier with standard MRI equipment. 42
An unavoidable issue in the segmentation of gastric volumes is the lack of a precise anatomical boundary between the duodenum and pylorus, making it challenging to outline identical segmented compartments of the stomach during all six scans. Custom boundaries were adopted as previously described, but their overall impact on measurements is still unclear. 57
Due to the lack of a direct measurement of the intragastric pressure, estimating exact absolute wall tension values was not possible in this study. This issue could be overcome by measuring the intragastric pressure before and after food intake. 58 Furthermore, more insights into the stomach's motility could be assessed through cine‐imaging or through thinner slices, which could potentially be implemented in our framework.
5. CONCLUSIONS
As per our aims, the analysis framework presented in this study offered a tool for evaluating gastric volumes, surface areas, and a dynamic estimation of wall tension based on MRI, feasible with only minor preparation. The method was able to provide insights into both gastric accommodation and emptying. Compared with existing gastric emptying studies, our model is improved by estimating the gastric wall tension distribution changes in different stomach compartments and holds promise for future clinical implementations and research.
AUTHOR CONTRIBUTIONS
Davide Bertoli, Esben Bolvig Mark, Jens Brøndum Frøkjær, Donghua Liao, and Asbjørn Mohr Drewes designed the research; Davide Bertoli, Esben Bolvig Mark, and Donghua Liao were involved in data collection; Asbjørn Mohr Drewes, Davide Bertoli, Christina Brock, and Jens Brøndum Frøkjær directed the data interpretation; Davide Bertoli drafted and wrote the manuscript; All the authors revised the final manuscript.
FUNDING INFORMATION
This study is supported by a Novo Nordisk Foundation grant. Grant No. #0052045.
CONFLICT OF INTEREST
No competing interests declared.
ACKNOWLEDGEMENT
We thank Kenneth Krogh Jensen (Aalborg University Hospital) for the assistance in the data collection and the Radiology Research Unit for providing MRI scanner facilities. We thank Christoffer Svinth for the assistance in the data collection.
APPENDIX 1.
SURFACE SMOOTHING
The reconstructed surfaces had some irregularities due to the discretization of the images, which were removed using a modified nonshrinking Gaussian smoothing method. The relation between the position of the vertices before and after N iteration can be expressed as:
| (A1) |
where N was the number of iterations, and are two scale factors, I is the n v n v identity matrix, K = I ‐ W, W is the weight matrix, and n v is the number of the neighborhood of a vertex. In this study, the scale factors and the iteration number ranged from 20 to 50. They were selected according to the criterion that the relative error between the surface area calculated from the smoothed model, and the raw model must be lower than 10%.
PRINCIPAL CURVATURES COMPUTATION
The stomach has a complex 3D geometry but since the surface is smooth and continuous, it can be approximated locally by a quadric surface function as:
| (A2) |
Where ai (i = 1, 2, …, 6) are constants. For each vertex, its 3rd‐folds neighborhood (including vertexes and faces) was first defined. Secondly, the vertex normal was calculated by averaging the faces normals of the neighborhood. The surface area of each face was then weighted by dividing it by the summarized face areas of the neighborhood. The previously defined vertex normal was then utilized to transpose the vertex and its 3rd‐folds neighborhood vertexes within a local coordinate system (o‐xyz). This system was defined with the vertex as the origin point and the vertex normal as the z‐direction of the local coordinate system. The constants a i (i = 1, 2, …, 6) were obtained by least‐squares fitting of the surface function (A2) to the vertex and its 3rd‐folds neighborhood points in the local coordinate system. Hence, the principal curvatures of the vertex can be calculated from the coefficient of the first fundamental form (E, F, and G) and the second fundamental form (L, M, and N) of the differential geometry as:
| (A3) |
| (A4) |
where and are the principal curvatures, and the are Gaussian and Mean curvatures, respectively. KG is a particularly useful curvature parameter that indicates an elliptical surface (KG >0), a parabolic surface (KG = 0), or a hyperbolic surface (KG <0). KM is in inverse proportion to the surface tension according to the Laplace's Law, where denotes the transmural pressure acting on the surface and is the surface tension assumed constant in every direction.
Based on the calculation of fundamental forms of an implicit surface as presented by Hartmann:
The coefficient of the first fundamental form (E, F, and G) are:
| (A5) |
Where F is the surface function in A2, F x , F y, and F z are the first‐order partial derivatives of F.
The coefficient of the second fundamental form (L, M and N) are:
| (A6) |
Where and F xx , F yx = F xy , F yy , F yz = F zy , F zz , and F xz = F zx are the second‐order partial derivatives of the surface function F in A2.
APPENDIX 2.
TABLE A1.
Gastric volume data
| Time | Total gastric volume (ml) | Total liquid volume (ml) | Total gas volume (ml) | Fundus volume (ml) | Corpus volume (ml) | Antrum volume (ml) | Fundus normalized volume (%) | Corpus normalized volume (%) | Antrum normalized volume (%) |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 140 (32) | 39 (23) | 27 (14) | 13 (6) | 80 (27) | 47 (18) | 10 (4) | 56 (11) | 34 (12) |
| 0 | 669 (41) | 516 (30) | 109 (55) | 130 (52) | 327 (51) | 110 (51) | 19 (8) | 49 (8) | 32 (8) |
| 15 | 615 (69) | 477 (54) | 98 (56) | 120 (37) | 316 (59) | 105 (64) | 20 (6) | 52 (10) | 29 (10) |
| 30 | 554 (71) | 414 (74) | 103 (56) | 102 (29) | 276 (49) | 94 (50) | 18 (5) | 50 (7) | 32 (7) |
| 45 | 483 (80) | 347 (72) | 100 (58) | 80 (33) | 250 (48) | 78 (44) | 16 (5) | 52 (8) | 32 (8) |
| 60 | 429 (97) | 294 (74) | 102 (63) | 64 (30) | 219 (45) | 67 (53) | 15 (5) | 52 (7) | 34 (9) |
Note: The table shows total, compartmental, and normalized compartmental volumes. Data are reported as mean (SD). n = 11 records analyzed.
TABLE A2.
Gastric surface area data
| Time | Total gastric surface (cm2) | Fundus surface (cm2) | Corpus surface (cm2) | Antrum surface (cm2) | Fundus normalized surface (%) | Corpus normalized surface (%) | Antrum normalized surface (%) |
|---|---|---|---|---|---|---|---|
| Baseline | 220 (27) | 25 (6) | 112 (23) | 84 (31) | 11 (3) | 51 (10) | 38 (11) |
| 0 | 536 (25) | 110 (36) | 212 (37) | 214 (37) | 21 (7) | 40 (7) | 40 (7) |
| 15 | 506 (28) | 105 (21) | 211 (41) | 190 (44) | 21 (4) | 42 (9) | 38 (8) |
| 30 | 484 (26) | 94 (18) | 198 (30) | 192 (34) | 20 (4) | 41 (6) | 40 (6) |
| 45 | 446 (37) | 78 (21) | 192 (27) | 177 (31) | 17 (4) | 43 (6) | 40 (5) |
| 60 | 413 (54) | 67 (21) | 175 (22) | 172 (40) | 16 (4) | 43 (6) | 41 (6) |
Note: The table shows total, compartmental, and normalized compartmental surface areas. Data are reported as mean (SD). n = 11 records analyzed.
TABLE A3.
Gastric inverse curvature data
| Time | Total inverse curvature (mm−1) | Fundus inverse curvature (mm−1) | Corpus inverse curvature (mm−1) | Antrum inverse curvature (mm−1) | Fundus normalized inverse curvature (%) | Corpus normalized inverse curvature (%) | Antrum normalized inverse curvature (%) |
|---|---|---|---|---|---|---|---|
| Baseline | 8.6 (1.1) | 9.1 (2.1) | 9.0 (1.5) | 7.2 (1.1) | 28.0 (38.2) | 25.5 (25.9) | 1 (0) |
| 0 | 12.0 (0.8) | 13.4 (2.2) | 12.3 (1.9) | 10.4 (1.6) | 34.1 (34.7) | 20.9 (24.4) | 1 (0) |
| 15 | 11.9 (1.0) | 14.2 (1.7) | 12.1 (1.7) | 9.7 (1.7) | 51.0 (32.1) | 27.0 (23.2) | 1 (0) |
| 30 | 11.5 (1.2) | 13.3 (2.0) | 11.8 (2.2) | 9.6 (1.5) | 42.5 (36.9) | 24.6 (24.4) | 1 (0) |
| 45 | 11.2 (0.9) | 13.0 (1.5) | 11.4 (1.7) | 9.6 (1.5) | 39.2 (33.5) | 21.3 (23.3) | 1 (0) |
| 60 | 11.0 (0.9) | 12.2 (2.3) | 11.0 (1.7) | 9.6 (1.2) | 29.1 (28.8) | 15.6 (19.6) | 1 (0) |
Note: The table shows total, compartmental, and normalized compartmental inverse curvature. Normalized data are reported as the increased percentage reported to antral data at the same timepoint. n = 11 records analyzed.
APPENDIX 3.
TABLE B1.
Compartmental’ volume Dice scores
| Time | Compartment | ||
|---|---|---|---|
| Fundus | Corpus | Antrum | |
| Baseline | 0.753 (0.091) | 0.871 (0.055) | 0.791 (0.045) |
| 0 | 0.949 (0.021) | 0.963 (0.014) | 0.941 (0.024) |
| 15 | 0.947(0.045) | 0.963 (0.022) | 0.945 (0.041) |
| 30 | 0.951(0.029) | 0.965 (0.021) | 0.928 (0.035) |
| 45 | 0.926 (0.043) | 0.959 (0.016) | 0.935 (0.042) |
| 60 | 0.949 (0.041) | 0.961 (0.019) | 0.917 (0.037) |
Note: Table shows DICE coefficients in different compartments. Data are reported as median (IQR).
TABLE B2.
Outlier distribution
| Time | Total surface (n) | Total inverse curvature (n) | Total volume (n) | Total Outliers (n) | Total Outliers (%) |
|---|---|---|---|---|---|
| Baseline | 4 | 1 | 1 | 6 | 46 |
| 0 | 0 | 1 | 0 | 1 | 8 |
| 15 | 0 | 0 | 1 | 1 | 8 |
| 30 | 1 | 1 | 1 | 3 | 23 |
| 45 | 0 | 1 | 1 | 2 | 15 |
| 60 | 0 | 0 | 0 | 0 | 0 |
| Total | 5 | 4 | 4 | 13 | 100 |
Note: Table shows the distribution of outliers in total data (total surface, total inverse curvature, and total volume). All 13 total outliers originated from n = 7 different subjects.
FIGURE B1.
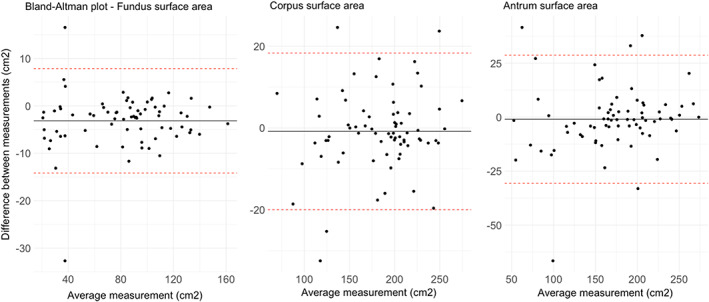
Surface areas ICC. Figure shows Bland–Altman plots for each gastric compartment. Data are reported as cm2. Data show a bias of −3.15 cm2 for fundus data, −0.83 cm2 for corpus, and −0.98 cm2 for antrum.
FIGURE B2.
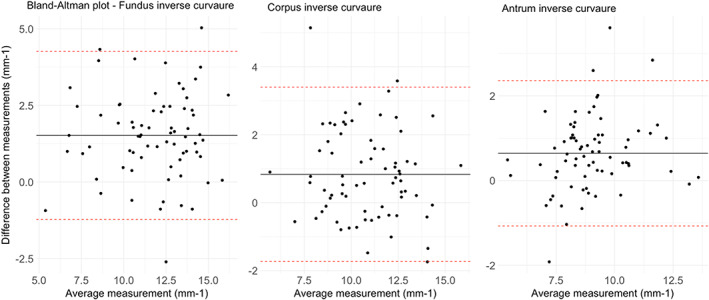
Inverse curvature ICC. Figure shows Bland–Altman plots for each gastric compartment. Data are reported as mm−1. Data show a bias of +1.51 cm2 for fundus data, +0.83 cm2 for corpus, and +0.64 cm2 for antrum.
Bertoli D, Mark EB, Liao D, Brock C, Frøkjær JB, Drewes AM. A novel MRI‐based three‐dimensional model of stomach volume, surface area, and geometry in response to gastric filling and emptying. Neurogastroenterology & Motility. 2023;35:e14497. doi: 10.1111/nmo.14497
REFERENCES
- 1. Solnes LB, Sheikhbahaei S, Ziessman HA. Nuclear scintigraphy in practice: gastrointestinal motility. Am J Roentgenol. 2018;211(2):260‐266. [DOI] [PubMed] [Google Scholar]
- 2. Abell TL, Camilleri M, Donohoe K, et al. Consensus recommendations for gastric emptying scintigraphy: a joint report of the American neurogastroenterology and motility society and the society of nuclear medicine. Am J Gastroenterol. 2008;103(3):753‐763. [DOI] [PubMed] [Google Scholar]
- 3. Henrichon S, Seltzer M, Siegel A. Use of SPECT/CT to confirm inconclusive gastric emptying scintigraphy results. Clin Nucl Med. 2015;40(6):e341‐e342. [DOI] [PubMed] [Google Scholar]
- 4. Simonian HP, Kantor S, Linda CK, et al. Simultaneous assessment of gastric accommodation and emptying of solid and liquid meals. Gastroenterology. 2006;124(4):A53. [Google Scholar]
- 5. Bluemel S, Menne D, Fried M, Schwizer W, Steingoetter A. On the validity of the 13C‐acetate breath test for comparing gastric emptying of different liquid test meals: a validation study using magnetic resonance imaging. Neurogastroenterol Motil. 2015;27(10):1487‐1494. [DOI] [PubMed] [Google Scholar]
- 6. Goetze O, Wieczorek J, Mueller T, Przuntek H, Schmidt WE, Woitalla D. Impaired gastric emptying of a solid test meal in patients with Parkinson's disease using 13 C‐sodium octanoate breath test. Neurosci Lett. 2005;375(3):170‐173. [DOI] [PubMed] [Google Scholar]
- 7. Mundt MW, Samsom M. Fundal dysaccommodation in functional dyspepsia: head‐to‐head comparison between the barostat and three‐dimensional ultrasonographic technique. Gut. 2006;55(12):1725‐1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Okabe T, Terashima H, Sakamoto A. Determinants of liquid gastric emptying: comparisons between milk and isocalorically adjusted clear fluids. Br J Anaesth. 2015;114(1):77‐82. [DOI] [PubMed] [Google Scholar]
- 9. Perlas A, Mitsakakis N, Liu L, et al. Validation of a mathematical model for ultrasound assessment of gastric volume by gastroscopic examination. Anesth Analg. 2013;116(2):357‐363. [DOI] [PubMed] [Google Scholar]
- 10. Farmer AD, Pedersen AG, Brock B, et al. Type 1 diabetic patients with peripheral neuropathy have pan‐enteric prolongation of gastrointestinal transit times and an altered caecal pH profile. Diabetologia. 2017;60(4):709‐718. [DOI] [PubMed] [Google Scholar]
- 11. Bilecen D, Scheffler K, Seifritz E, Bongartz G, Steinbrich W. Hydro‐MRI for the visualization of gastric wall motility using RARE magnetic resonance imaging sequences. Abdom Imaging. 2000;25(1):30‐34. [DOI] [PubMed] [Google Scholar]
- 12. Faas H, Steingoetter A, Feinle C, et al. Effects of meal consistency and ingested fluid volume on the intragastric distribution of a drug model in humans ‐ a magnetic resonance imaging study. Aliment Pharmacol Ther. 2002;16(2):217‐224. [DOI] [PubMed] [Google Scholar]
- 13. Tomita T, Okugawa T, Yamasaki T, et al. Use of scintigraphy to evaluate gastric accommodation and emptying: comparison with barostat. J Gastroenterol Hepatol. 2013;28(1):106‐111. [DOI] [PubMed] [Google Scholar]
- 14. Drewes AM, Gregersen H, Arendt‐Nielsen L. Experimental pain in gastroenterology: a reappraisal of human studies. Scand J Gastroenterol. 2003;38(11):1115‐1130. [DOI] [PubMed] [Google Scholar]
- 15. Buisman WJ, van Herwaarden‐Lindeboom MYA, Mauritz FA, et al. Validation of a novel 3‐dimensional sonographic method for assessing gastric accommodation in healthy adults. J Ultrasound Med. 2016;35(7):1411‐1418. [DOI] [PubMed] [Google Scholar]
- 16. De Zwart IM, De Roos A. MRI for the evaluation of gastric physiology. Eur Radiol. 2010;20(11):2609‐2616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Buisman WJ, Mauritz FA, Westerhuis WE, Gilja OH, van der Zee DC, van Herwaarden‐Lindeboom MYA. Evaluation of gastric volumes: comparison of 3‐D ultrasound and magnetic resonance imaging. Ultrasound Med Biol. 2016;42(7):1423‐1430. [DOI] [PubMed] [Google Scholar]
- 18. Menys A, Keszthelyi D, Fitzke H, et al. A magnetic resonance imaging study of gastric motor function in patients with dyspepsia associated with Ehlers‐Danlos syndrome‐hypermobility type: a feasibility study. Neurogastroenterol Motil. 2017;29(9):1‐9. [DOI] [PubMed] [Google Scholar]
- 19. Holt S, Cervantes J, Wilkinson AA, Kirk Wallace JH. Measurement of gastric emptying rate in humans by real‐time ultrasound. Gastroenterology. 1986;90(4):918‐923. [DOI] [PubMed] [Google Scholar]
- 20. Distrutti E, Azpiroz F, Soldevilla A, Malagelada J. Gastric wall tension determines perception of gastric distention. Gastroenterology. 1999;116(5):1035‐1042. [DOI] [PubMed] [Google Scholar]
- 21. Piessevaux H, Tack J, Wilmer A, Coulie B, Geubel A, Janssens J. Perception of changes in wall tension of the proximal stomach in humans. Gut. 2001;49(2):203‐208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Tack J, Caenepeel P, Corsetti M, Janssens J. Role of tension receptors in dyspeptic patients with hypersensitivity to gastric distention. Gastroenterology. 2004;127(4):1058‐1066. [DOI] [PubMed] [Google Scholar]
- 23. Hoad CL, Parker H, Hudders N, et al. Measurement of gastric meal and secretion volumes using magnetic resonance imaging. Phys Med Biol. 2015;60(3):1367‐1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Fruehauf H, Goetze O, Steingoetter A, et al. Intersubject and intrasubject variability of gastric volumes in response to isocaloric liquid meals in functional dyspepsia and health. Neurogastroenterol Motil. 2007;19(7):553‐561. [DOI] [PubMed] [Google Scholar]
- 25. Min YW, Min BH, Kim S, Choi D, Rhee PL. Effect of DA‐9701 on gastric motor function assessed by magnetic resonance imaging in healthy volunteers: a randomized, double‐blind, placebo‐controlled trial. PLoS One. 2015;10(9):1‐13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Banerjee S, Pal A, Fox M. Volume and position change of the stomach during gastric accommodation and emptying: a detailed three‐dimensional morphological analysis based on MRI. Neurogastroenterol Motil. 2020;32(8):e13865. [DOI] [PubMed] [Google Scholar]
- 27. Taubin G. Curve and surface smoothing without shrinkage. Proceedings of IEEE International Conference on Computer Vision. IEEE Comput. Soc. Press; 1995:852‐857. doi: 10.1109/ICCV.1995.466848 [DOI] [Google Scholar]
- 28. Hartmann E. Blending and implicit with a parametric surface. Comput Aided Geom Des. 1995;12:825‐835. [Google Scholar]
- 29. Liao D, Zhao J, Gregersen H. Three‐dimensional geometry analysis of the stomach in type II diabetic GK rats. Diabetes Res Clin Pract. 2006;71(1):1‐13. [DOI] [PubMed] [Google Scholar]
- 30. Schmitz A, Kellenberger CJ, Liamlahi R, Studhalter M, Weiss M. Gastric emptying after overnight fasting and clear fluid intake: a prospective investigation using serial magnetic resonance imaging in healthy children. Br J Anaesth. 2011;107(3):425‐429. [DOI] [PubMed] [Google Scholar]
- 31. Fruehauf H, Menne D, Kwiatek MA, et al. Inter‐observer reproducibility and analysis of gastric volume measurements and gastric emptying assessed with magnetic resonance imaging. Neurogastroenterol Motil. 2011;23(9):854‐861. [DOI] [PubMed] [Google Scholar]
- 32. Costanzo F, Brasseur JG. The invalidity of the Laplace law for biological vessels and of estimating elastic modulus from total stress vs. strain: a new practical method. Math Med Biol. 2015;32(1):1‐37. [DOI] [PubMed] [Google Scholar]
- 33. Shaw JM, Hamad NM, Coleman TJ, et al. Intra‐abdominal pressures during activity in women using an intra‐vaginal pressure transducer. J Sports Sci. 2014;32(12):1176‐1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. El‐Serag HB, Tran T, Richardson P, Ergun G. Anthropometric correlates of intragastric pressure. Scand J Gastroenterol. 2006;41(8):887‐891. [DOI] [PubMed] [Google Scholar]
- 35. Wickham H. Ggplot2: Elegant Graphics for Data Analysis. Springer‐Verlag; 2016. https://ggplot2.tidyverse.org [Google Scholar]
- 36. Datta D. Blandr: a Bland‐Altman method comparison package for R. 2017.
- 37. Revelle W. Psych: procedures for psychological, psychometric, and personality research. 2022. https://cran.r‐project.org/package=psych
- 38. Chitkara DK, Camilleri M, Zinsmeister AR, et al. Gastric sensory and motor dysfunction in adolescents with functional dyspepsia. J Pediatr. 2005;146(4):500‐505. [DOI] [PubMed] [Google Scholar]
- 39. Grimm M, Koziolek M, Kühn J‐P, Weitschies W. Interindividual and intraindividual variability of fasted state gastric fluid volume and gastric emptying of water. Eur J Pharm Biopharm. 2018;127:309‐317. [DOI] [PubMed] [Google Scholar]
- 40. Khalaf A, Hoad CL, Menys A, et al. MRI assessment of the postprandial gastrointestinal motility and peptide response in healthy humans. Neurogastroenterol Motil. 2018;30(1):1‐9. [DOI] [PubMed] [Google Scholar]
- 41. Marciani L, Hall N, Pritchard SE, et al. Preventing gastric sieving by blending a solid/water meal enhances satiation in healthy humans. J Nutr. 2012;142(7):1253‐1258. [DOI] [PubMed] [Google Scholar]
- 42. Bertoli D, Steinkohl E, Mark EB, Brock C, Drewes AM, Frøkjær JB. Quantification of gastric emptying with magnetic resonance imaging in healthy volunteers: a systematic review. Neurogastroenterol Motil. 2022;e14371. doi: 10.1111/nmo.14371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Boulby P, Gowland P, Adams V, Spiller RC. Use of echo planar imaging to demonstrate the effect of posture on the intragastric distribution and emptying of an oil/water meal. Neurogastroenterol Motil. 1997;9(1):41‐47. [DOI] [PubMed] [Google Scholar]
- 44. Carbonea SF, Tanganelli I, Capodiventoc S, Ricci V, Volterrani L. Magnetic resonance imaging in the evaluation of the gastric emptying and antral motion: feasibility and reproducibility of a fast not invasive technique. Eur J Radiol. 2010;75(2):212‐214. [DOI] [PubMed] [Google Scholar]
- 45. Storlid EL, Hausken T, Lied GA, Gilja OH, Hatlebakk JG. Gastric accommodation in healthy subjects studied by ultrasound, manometry, and impedancemetry. Neurogastroenterol Motil. 2018;30(4):e13249. [DOI] [PubMed] [Google Scholar]
- 46. Liao D, Gregersen H, Hausken T, Gilja OH, Mundt M, Kassab G. Analysis of surface geometry of the human stomach using real‐time 3‐D ultrasonography in vivo. Neurogastroenterol Motil. 2004;16(3):315‐324. [DOI] [PubMed] [Google Scholar]
- 47. Liao D, Duch BU, Stødkilde‐Jørgensen H, Zeng YJ, Gregersen H, Kassab GS. Tension and stress calculations in a 3‐D Fourier model of gall bladder geometry obtained from MR images. Ann Biomed Eng. 2004;32(5):744‐755. [DOI] [PubMed] [Google Scholar]
- 48. Frokjaer JB, Liao D, Bergmann A, et al. Three‐dimensional biomechanical properties of the human rectum evaluated with magnetic resonance imaging. Neurogastroenterol Motil. 2005;17(4):531‐540. [DOI] [PubMed] [Google Scholar]
- 49. Vande VS, Notebaert A, Meersschaut V, Herregods N, Van Winckel M, Van Biervliet S. Colon transit time in healthy children and adolescents. Int J Colorectal Dis. 2013;28(12):1721‐1724. [DOI] [PubMed] [Google Scholar]
- 50. Sugita M, Matsumoto M, Tsukano Y, Fukunaga C, Yamamoto T. Gastric emptying time after breakfast in healthy adult volunteers using ultrasonography. J Anesth. 2019;33(6):697‐700. [DOI] [PubMed] [Google Scholar]
- 51. Zou KH, Warfield SK, Bharatha A, et al. Statistical validation of image segmentation quality based on a spatial overlap index1. Acad Radiol. 2004;11(2):178‐189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Koo TK, Li MY. A guideline of selecting and reporting Intraclass correlation coefficients for reliability research. J Chiropr Med. 2016;15(2):155‐163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Rostas JW, Mai TT, Richards WO. Gastric motility physiology and surgical intervention. Surg Clin North Am. 2011;91(5):983‐999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Freeman R. Diabetic autonomic neuropathy. Handb Clin Neurol. 2014;126:63‐79. doi: 10.1016/B978-0-444-53480-4.00006-0 [DOI] [PubMed] [Google Scholar]
- 55. Van Den Abeele J, Brouwers J, Tack J, Augustijns P. Exploring the link between gastric motility and intragastric drug distribution in man. Eur J Pharm Biopharm. 2017;112:75‐84. [DOI] [PubMed] [Google Scholar]
- 56. Treier R, Steingoetter A, Weishaupt D, et al. Gastric motor function and emptying in the right decubitus and seated body position as assessed by magnetic resonance imaging. J Magn Reson Imaging. 2006;23(3):331‐338. [DOI] [PubMed] [Google Scholar]
- 57. Lu KH, Cao J, Oleson ST, Powley TL, Liu Z. Contrast‐enhanced magnetic resonance imaging of gastric emptying and motility in rats. IEEE Trans Biomed Eng. 2017;64(11):2546‐2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. de Zwart IM, Haans JJL, Verbeek P, Eilers PHC, de Roos A, Masclee AAM. Gastric accommodation and motility are influenced by the barostat device: assessment with magnetic resonance imaging. Am J Physiol Liver Physiol. 2007;292(1):G208‐G214. [DOI] [PubMed] [Google Scholar]


