A novel methodological approach for group classification during fission of a semi‐free‐ranging group of Japanese macaques (Macaca fuscata)

Abstract

The self‐initiated split of a social group, known as fission, is a challenge faced by many group‐living animals. The study of group fission and the social restructuring process in real time provides insights into the mechanism of this biologically important process. Previous studies on fission in Japanese macaques (Macaca fuscata) assigned individuals to newly reorganized groups mainly using behavioral observations and group attendance records based on periods before or after fission itself. Here, we present a novel framework for group classification during the process of fission that uses quantifiable behavioral variables and statistical analyses. The framework was tested on a group fission process at Affenberg Landskron (Austria), a park that housed around 160 semi‐free‐ranging Japanese macaques. The behavioral data were collected for 26 days during fission. We analyzed three behavioral developments recurrent in fissions in Japanese macaques, that is, independence of behavior, participation in group movements, and separation of nomadic ranges. These analyses were combined to assign individuals to different groups. Our study resulted in one main group (N = 33), one subgroup (N = 36) and 56 individuals whose group membership was still undefined. The demographic characteristics of these newly formed groups were comparable with those of fissioned groups in wild populations. Furthermore, we found that these newly forming groups showed early social dynamics of fission five months before group level movements, that is: grouping based on spatial proximity and spatial withdrawal of the subgroup to the periphery. These results underline the validity of our novel framework to study social dynamics in Japanese macaques during the process of fission. It represents an important addition to existing methods, and we recommend testing its scope in other primate societies.

Graphical overview of a novel methodological framework for group classification during fission in Japanese macaques (Macaca fuscata).

Research Highlights

• We studied semi‐free‐ranging Japanese macaques during group fission

• Our applied methodology uses multiple behavioral variables for group classification

• Our framework represents an important addition to existing methods used to study fission

Abbreviations

AIC

Aikake's Information Criterion

AM.

ante meridiem

ANOVA

analysis of variance

ASP

American Society of Primatologists

C‐areas

central areas

df

degrees of freedom

EMM

estimated marginal means

ICC

intraclass correlation coefficient

JH.

J. Herzele

LM

linear model

LMER

linear mixed‐effect model

LSP.

L. S. Pflueger

MSS.

M. S. Stribos

P‐areas

peripheral areas

PM.

post meridiem

PMB.

P. M. Boehm

p‐value (p)

probability value

RH.

R. Hammer

SD

standard deviation

Tukey‐HSD

Tukey Honestly Significant Difference

1. INTRODUCTION

Group living has proven to be beneficial to an individual's fitness in many animal species (Andrews & Belknap, 1986; Harcourt & Waal, 1992; Krause et al., 2002; Morand‐Ferron et al., 2015; Sherman, 1984; Westneat et al., 2000). These benefits include, among others, alloparental care (Hatchwell & Komdeur, 2000) and antipredatory mechanisms (Inman & Krebs, 1987). Group living, however, is also associated with certain costs, the most prominent of which is increased competition over resources (King et al., 2011; Sueur et al., 2011). The balance between benefits and costs of group living can be threatened by external factors, such as ecological or anthropogenic changes in the environment (Bond et al., 2019; Couzin & Laidre, 2009; Lehmann et al., 2006) or a shift in social or demographic features within a group (Bond et al., 2019; Hart & Van Vugt, 2006; Kuester & Paul, 1997; Strier et al., 1993; Sueur et al., 2010), like an increase in group size. These changes may increase intragroup competition to such an extent that a whole faction of the group leaves (Markham & Gesquiere, 2017). Such a group split, also known as fission, is a naturally occurring phenomenon by which animals can avoid increasing intragroup competition (Ramos‐Fernández et al., 2006; Wittemyer et al., 2005). Fissions have been reported in many group‐living primate species (Pan troglodytes, Feldblum et al., 2018; Pan paniscus, Hashimoto et al., 1998; Papio cephalus, Henzi et al., 1997; Brachyteles hypoxanthus, Pavelka, 2011), including macaques (Macaca mulatta, Chepko‐Sade & Sade, 1979). Group‐fission is well‐studied in Japanese macaques (Macaca fuscata), which tend to form big multi‐male‐female groups with a highly despotic social structure (Furuya, 1968; Koyama, 1970; Sugiyama, 1960; Maruhashi, 1982; Yamagiwa, 1985).

Early demographic studies on fissions in free‐ranging Japanese macaques describe three recurrent behavioral developments present during fission. Sugiyama (1960) first described these developments in the wild Takasakiyama group and stated that these occur in different phases. Phase 1—independence of behavior between groups, describes how a faction of the group arrives consistently later at a feeding site or resting place. Phase 2—occurrence of group movements, describes how this faction avoids former group members by moving away in a coordinated cluster without being followed by core group members. Phase 3—separation of nomadic ranges, is indicated by a withdrawal of the faction towards peripheral areas. At the end of the third phase, this faction completely left the home range of the original group to inhabit a new nomadic range. During these developments, Sugiyama (1960) observed that the social contact between this faction and the original group faded gradually, and completely stopped after the third phase.

Sugiyama (1960) included four subsequent phases that further describe the shift in nomadic ranges in which both newly formed groups moved within their habitats depending on seasonal feeding locations. However, only the behavioral developments that occurred in the first three distinct phases, according to Sugiyama (1960), have been observed in other studies (e.g., independence of behavior: Furuya, 1960; independence of behavior and participation in group movements: Koyama, 1970; group movements: Maruhashi, 1982; separation in nomadic ranges and group movements: Yamagiwa, 1985). These studies showed that these behavioral developments may not come in a successive order or may even happen simultaneously (Koyama 1970; Yamagiwa, 1985). This nevertheless underlines that these three behavioral developments are key for dividing a social group into two.

Fission generally results in the formation of a main‐ and a subgroup (Widdig et al., 2006). In most cases, the group that remains in the initial home range is referred to as the main group, while the leaving group is defined as the subgroup. In Japanese macaques, low‐ranking males and females usually transfer to newly formed sub‐groups (Koyama, 1970), resulting in the main group being dominant over the sub‐group (Furuya, 1960; Koyama, 1970; Maruhashi, 1982; Sugiyama, 1960; Yamagiwa, 1985). A suggested reason for this is that low‐ranking individuals face higher chances to increase their social rank position in newly formed groups. Moreover, adolescent males, not yet high in social rank, tend to use fission to move away from their closest female relatives up to about the third degree of maternal consanguinity to avoid inbreeding (Koyama, 1970).

Given the matrilinear and nepotistic nature of Japanese macaque societies, with males being the dispersing sex (Fooden and Aimi 2006), Japanese macaque groups tend to split along matrilines. Hence, matrilines remain fairly intact (Koyama, 1970; Takahata et al., 2002). In addition, no differences were found in group composition (e.g., age or sex ratio) between branched groups (Koyama, 1970).

Studies on the process and consequences of fission create a deeper understanding of a species' behavior, ecological needs, habitat use, and demographics. Such knowledge can be implemented in conservation programs (Bond et al., 2019; Halloway et al., 2020; Ramos et al., 2016; Vink et al., 2020) and any future studies conducted in branched populations. The comparison of behavioral tendencies in the process of fission between captive species and their wild conspecifics helps to improve animal welfare conditions and management strategies of zoos (Amrein et al., 2014; Melfi & Feistner, 2002). However, the empirical study of this event remains challenging. Fission often appears unexpectedly in front of the investigator's eyes, especially when social dynamics are not yet the primary research focus in a specific study group. Up until now, there are no predefined protocols that can be immediately implemented to study the rapidly developing fission. This led studies on fissions in Japanese and other macaques to use different methodologies for studying the same event (e.g., ad libitum observations in Japanese macaques, Furuya, 1960; monthly censuses in Macaca sinica, Dittus, 1988; agent‐based modeling in Macaca tonkeana, Sueur et al., 2010). Moreover, specifically in studies on Japanese macaques, the attribution of individuals to main‐ and sub‐groups has not been based on clear demarcation methods, but instead on sometimes more subjective interpretations of discrete observations. Hence, most previous studies on Japanese macaques have not been conducted with one uniform methodology and were not based on quantifiable data.

Recently, several new methods have been used in the study of group fission in primates, such as social network analyses (Aureli et al., 2012; Larson et al., 2018) and digital modeling (Sueur et al., 2010). Social network analyses are most often based on behavioral variables that are continuously present in a social group such as interindividual distance (Aureli et al., 2012) and affiliative behavior shared between individuals (Larson et al., 2018). Regular scan‐ and focal protocols performed over a long period of time are used to provide insights into the slightest social developments within a society. Such standardized long‐term protocols on all group members, however, are difficult to achieve in big social groups and are therefore often not readily available for many (semi‐) free‐ranging populations. Moreover, fission implies multiple behavioral developments that only occur during fission itself (e.g., group movements). Such fission‐specific developments provide key information that helps us to understand the process of fission better. Nevertheless, these variables have been neglected so far in previous studies of fissions in Japanese macaques. The reason for this might be the occurrence of highly dynamic periods of fission in which all behavioral developments happen simultaneously (see above) (Koyama, 1970; Sugiyama, 1960). In this paper, we refer to such periods as “peak fission.” Peak fission periods require changes in monitoring compared to regular observation methods and it is of special importance to create a rapid assessment of the situation (Koyama, 1970; Sugiyama, 1960). Previously used methodological approaches, such as social network analyses, are limited in this regard since these methods are based on common social variables, lack fission‐specific developments, and compare data before and after a fission has occurred. Hence, previously used methods do not provide insight into these real‐time developments within a population during peak fission.

The present study aims to provide a novel methodological framework that is applicable to study group division during peak fission in Japanese macaques. This framework is based on readily collectible data, provides a rapidly applicable method for group determination instead of a postfission analysis, and incorporates multiple behavioral variables instead of just one. Furthermore, the analyses are based on quantifiable data and clear demarcation values. We studied a semi‐free‐ranging group of Japanese macaques (>160 individuals, Affenberg Landskron, Carinthia, Austria) during a fission event. Our framework was based on the first three behavioral developments observed by Sugiyama (1960) during fission in Japanese macaques, namely (1) independence of behavior, (2) group movements and (3) separation of nomadic ranges. This was achieved by analyzing individual's (i) temporal presence at feeding sites, (ii) participation in group movements, and (iii) area use within the habitat. With these three indicators we were able to assign individuals to branched groups and to investigate the underlying group compositions.

After the group assignment, we analyzed the demographics of each resulting group and compared it with published data on branched free‐ranging populations. Finally, we made use of a second data set covering the five months before the peak fission period (i.e., before group movements started). We analyzed behavioral data of a select group of individuals to assess changing dynamics over time within and between the detected groups with the help of social network analyses. If our group assignment during peak fission proved valid, we would expect a separation of the groups to be detectable before group movements started, that is, via loss of social contact between the factions, change in size of social network, and potential withdrawal of the future subgroup into peripheral areas of the enclosure.

2. METHODS

The present study was of completely noninvasive nature. We declare that the research reported in this manuscript adhered to the legal requirements of Austria and the Affenberg Zoobetriebsgesellschaft mbh. It furthermore adhered to the American Society of Primatologists (ASP) Principles for the Ethical Treatment of Nonhuman Primates (see https://www.asp.org/society/resolutions/EthicalTreatmentOfNonHumanPrimates.cfm).

2.1. Study site

The study was conducted on a semi‐free‐ranging group of Japanese macaques housed at “Affenberg Landskron” zoo (Affenberg Zoobetriebsgesellschaft mbH, Landskron, Carinthia, Austria). The Affenberg‐group originates from a wild group that was translocated from Minoo to Affenberg, Austria in 1996. The demographic development, population dynamics, social characteristics, and reproductive parameters of this group have been extensively documented since their arrival at Affenberg (Pflüger et al., 2021).

The Affenberg‐group is kept in a four‐hectare forested outdoor enclosure, which is open to the public from early April to the beginning of November. During this time, visitors can follow guided tours through one‐third of the enclosure. The remaining areas are only accessible to caretakers and the macaques. Visitors are not allowed to feed, interact with, or touch the macaques.

We demarcated the macaque enclosure area into sub‐sections before this study to note the location of individuals during observations (Figure 1a). These areas are characterized as central‐ (Figure 1.; C‐areas) or peripheral‐areas (Figure 1; P‐areas). C‐areas are relatively open spots in the forest where the visitor pathway is located.

Figure 1.

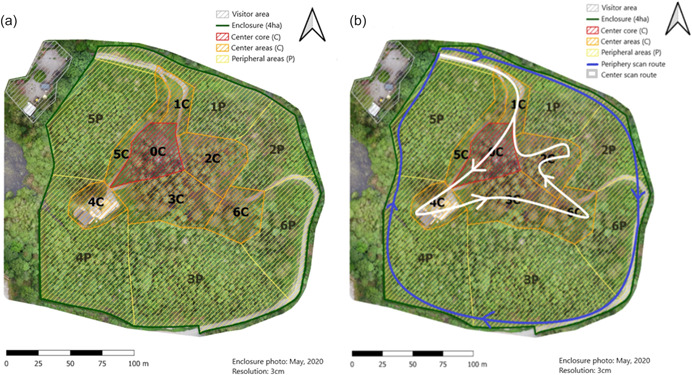
Overview of the Affenberg enclosure. The visitor area (gray) is located next to the four hectare‐sized enclosure. (a) The enclosure is divided into seven central areas (C‐areas) and six peripheral areas (P‐areas). C‐areas are more open and more visible to tourists, provisioned areas and are less vegetated. Provisions were not provided in P‐areas and were only accessible to caretakers and macaques. Vegetation was denser in these areas. (b) Indications of the scan routes through the enclosure. The peripheral route (blue) led along the fence surrounding the enclosure and covered the edges of P‐areas, the center route (white) covered all C‐areas during observations.

During the time of observations, the Affenberg‐group was provisioned daily between 09:00 and 11:00 a.m. with in total ~170 kg of a combination of potatoes, carrots, apples, and wheat grain. During our study period, there were 2 days on which additional food was provided in the afternoon as well (03‐30‐2020 & 04‐03‐2020) since additional fruit deliveries arrived on these days in the afternoon. Food was provided at different feeding spots spread throughout the enclosure to avoid monopolization. Main feeding spots were in the C‐areas (Figure 1a). The most densely vegetated P‐areas were not used as sites for provisioning. Additional information concerning the habitat, provisioning, and management of the Affenberg‐group is described in detail by Pflüger et al. (2021).

2.2. Study population

At the beginning of the present study (10‐03‐2019), the Affenberg‐group consisted of 164 individuals of different sex‐age‐classes following Takahata (1980): 80 sexually mature females (≥3.5 years) of which 11 were adolescent (3.5–4.5 years); 53 sexually mature males (≥4.5 years) of which 20 were adolescent (4.5–9.5 years); and 23 juveniles (>1 year but <3.5/4.5 years) and 8 infants (<1 year) born in 2019. Only data from sexually mature individuals (≥3.5 years for females; ≥4.5 years for males) were used for analyses in the present study. We excluded data on infants and juveniles of both sexes from the analyses of the entire study, because the social tendencies of these age groups are dependent on their mothers (Nishida, 1966; Sugiyama, 1976).

This fission was the first visible separation of the Affenberg‐group since it arrived in Austria. The fission became apparent on 03‐10‐2020 due to atypical group movements (see Section 2.3 Behavioral observations). On that day the group consisted of 159 individuals, including 76 sexually mature females of which 10 were adolescent, and 52 sexually mature males of which 23 were adolescent.

During the period of data collection, five adult females and one adolescent male died. Nevertheless, we kept them in the analyses as a separate group (“deceased”) to analyze the potential effect of their death on group fission and reorganization of other members. None of the immature individuals reached sexual maturity during the study period. One adult male, the former ɑ‐male Pauli, was temporarily removed from the group due to management and health care reasons from 03‐31‐2020 until 04‐11‐2020.

2.3. Methodology of the novel framework

2.3.1. Behavioral observations

We collected data for our framework during peak fission, which covered a period in which group movements occurred and the fission event became apparent at the Affenberg. We noticed the first group movement on 03‐10‐2020. However, due to the beginning of the Covid‐19‐pandemic and associated restrictions by the Affenberg company to enter the park, no researchers were allowed to enter the monkey enclosure until Covid‐19 guidelines were prepared by the management. Researchers were allowed to re‐enter 5 days later, so the first data for our framework was collected on 03‐16‐2020. From this day on, we observed the fission for 26 consecutive days (03‐16‐2020 until 04‐10‐2020). Data collection for the framework ended when group movements stopped and visitor season at the Affenberg park started.

Observations for our framework were conducted by four observers (R. H., M. S. S., J. H., L. S. P.) that were all trained in recognizing the macaques based on facial characteristics. We conducted daily observations between 09:00 a.m. and 06:00 p.m., which consisted of scan sampling, ad libitum sampling, and focal animal sampling (Martin & Bateson, 2007), dependent on the variables of interest (see below).

The variables of interest (hereafter referred to as indicators) used in the framework were based on the three behavioral developments previously described during fissions of Japanese macaques (Sugiyama, 1960; Table 1), namely (1) independence of behavior, (2) participation in group movements, and (3) separation of nomadic ranges.

Table 1.

Variables used as indicators for group division

Fission‐phase	Indicator	Behavioral development	Behavioral measures	Data collection method
1	Independence of behavior	The emergence of independence in behavior characterized by different timings of sleeping and foraging between the splitting factions	Presence at feeding spots	Scan samplinga on feeding spots during provisioning
2	Participation in group movements	A faction displays group movements away from the previous core group	Participation in group movements	Ad libitum a observations of group movements
3	Separation of nomadic ranges	The separation of nomadic ranges between the factions	Area use of the habitat	Scan samplinga throughout the enclosure

Note: Behavioral developments are based on Sugiyama (1960).

^aMartin and Bateson (2007).

Independence of behavior

The increase in independence of behavior during fission becomes most evident during foraging and sleeping (Furuya, 1960; Koyama, 1970; Sugiyama, 1960). In the current study, we only used feeding behavior for this indicator. This was due to limitations in monitoring sleeping sites. Japanese macaques travel to their sleeping spots shortly before and after dusk (Wada et al., 2007). At the study site, the sleeping spots are in high trees (up to 30 m height; Pflüger et al., 2021) with no possibility to identify the macaques individually given the lack of monitoring cameras.

We performed feeding scans up until 30 min after the provisions had been spread in the enclosure (between 10:00–11:00 a.m.; on two days (03‐30‐2020 & 04‐03‐2020), additional feeding scans occurred between 03:00–04:00 p.m.). A feeding spot was characterized by the presence of food and more than one individual feeding on the food provisions. We applied the scan sampling method (Martin & Bateson, 2007) to record which individuals were present at each feeding location at the same time, disregarding their behavior. The identity of the individuals present at the feeding spots at the moment of provisioning and for 30 min afterwards were recorded using a voice recorder (Olympus WS‐510M).

Participation in group movements

Group movements were recognized when single individuals traveled into the outskirts of the enclosure and were subsequently followed by others and thereby forming a moving group. The moving faction was highly clustered, that is: individuals had a high level of proximity (between 1 and 10 m), individuals looked over their shoulders while moving, no moving individuals went completely out of sight from the other moving individuals and all moving individuals had the same approximate speed and direction (as an example of a group movement, see Supporting Information: Video 1).

We considered individuals who moved in the same direction with the same approximate speed and were within a 10‐m distance of other moving individuals as part of the movement. The group movements were highly coordinated. The departure of only a few individuals caused the entire faction to follow. Similarly, when individuals stopped to rest, the others would stop moving as well. Based on these observations, we considered consecutive group movements as separate movements when there was a period of rest of at least 30 min between movements. Such a period of rest began when the first moving individual stopped and was indicated by the absence of large group conflicts and the presence of resting behaviors, such as grooming or lying down.

We recorded each group movement ad libitum whenever it was observed. We used both video (Sony Handycam HDR‐CX130E) and voice (Olympus WS‐510M) recordings to identify and monitor all participants during a group movement. The identity of all individuals that passed by a researcher in movement was voice‐ and video recorded. To ensure that all individuals were correctly identified, the video material was assessed afterwards to confirm the initial identification. The moving group was either observed from three different positions within the group (back, middle and front) to individually identify participants (multiple observers) or, if only one observer was present, this observer would move to the head of the movement and record all individuals as they passed by.

Separation of nomadic ranges

A prerequisite to study the separation of nomadic ranges is to divide the habitat into central‐ and peripheral areas. In the case of Japanese macaques, central areas are preferred areas which most often consist of favored feeding and resting spots, that is, sunny spots with clearings (Hirsch, 2007).

In the present study, we assigned the areas in which most of the group members used to gather throughout the years, such as main feeding spots and preferred resting spots, as central areas. Main feeding spots are those areas where wheat is provided next to fruits and vegetables during feeding times and where additional pieces of fruits and vegetables are offered during guided tours. Preferred resting spots imply open areas or clearings with sunbathing opportunities during winter, which are mostly located in the central areas of the enclosure (Figure 1). Central and peripheral areas were further subdivided into sections depending on the natural borders of the habitat, for example, timberlines, course of the stream, the swamp area.

We used scan sampling (Martin & Bateson, 2007) to record the location of macaques within the entire enclosure by following a predefined pathway which ensured views of each of the different sections (0C‐6C, 0P‐6P, Figure 1b). In the beginning, there was primarily a focus on the C‐areas (0C‐6C, Figure 1b). After 2 weeks, we introduced a standardized scan protocol. We scanned the enclosure twice daily using a voice recorder (Olympus WS‐510M). The scans were performed throughout the day, but not within an hour after the daily provisions were spread (between 09:00 a.m. and 07:00 p.m.), nor within 1 h of the previous scan to avoid dependency in our data. In each scan, an observer walked preset routes through the enclosure (Figure 1b). If two observers worked simultaneously, one followed the peripheral pathway that led through the P‐areas while the other made the center route in which all the C‐areas were observed (Figure 1b). Given the size of the enclosure and accessibility difficulties in certain areas (e.g., swamp area), one scan lasted about 18–25 min. We never recorded an individual twice in the same section. If we saw an individual in another section at a later point in time during one scan, the new location of the individual was recorded again. Hence, one individual could appear repeatedly in one scan but only if it appeared in another section during the same scan. This approach was chosen to prevent double data collection without losing information about the changing of area usage by individuals.

2.3.2. Data processing and analyses

Based on the data collected during peak fission, we calculated individual values for each indicator. These values were the (1) co‐appearance during feeding as a measurement for independence of behavior; (2) percentage of participation in group movements; and (3) overlap in area use as a measurement for separation of nomadic ranges. Using these values, we created three separate group divisions based on strict threshold values before combining the three divisions into a main, sub‐, and undetermined group.

Threshold values

Our framework is based on the reasoning that macaques that want to leave the core group display indicative behaviors. However, even individuals who do not want to leave the group could also show such behaviors due to chance, for example. We, therefore, needed a demarcation method that could separate such random occurrences from those based on active behavioral tendencies. In the current study, we used mean values and standard deviations to differentiate between random occurrences and active behavioral tendencies. Standard deviations show how values are spread throughout the data set (e.g., 68% of data points within a normally distributed data set are located within one standard deviation around the mean [Streiner, 1996]). It can be expected that behavioral frequencies occurring randomly likely cluster around the mean. Behavioral frequencies higher than the mean plus one standard deviation, however, are less likely to occur randomly. Individuals with high frequencies must actively show these behaviors and thus have the motivation to leave the group. The demarcation method in our framework, therefore, consisted of threshold values that were based on the mean value of each indicator plus their standard deviations (see Supporting Information: Text S1 for an extended explanation of the theoretical basis of these threshold values).

We created three different versions of our framework method with varying threshold values (see Supporting Information: Text S1 and Table S1). In this manuscript, we present the first version of our framework that provided the most valid group division. We based this version on findings of earlier studies on fissions in Japanese macaques which have shown that Japanese macaques tend to either commit to a newly forming group from the start or switch group affiliations multiple times during fission (Furuya, 1968; Koyama, 1970; Sugiyama, 1960). We refer to those individuals that commit to one group as core members. To separate the core members from switching members, we applied strict threshold values using the mean value plus two standard deviations for the indicators independence of behavior‐ and separation of nomadic ranges. For the indicator participation in group movements, we expected the strict threshold value would not be applicable, since studies have shown that individuals may hide or rest in between participating in the movements (Furuya, 1968; Koyama, 1970; Sugiyama, 1960), for example, due to exhaustion/injuries. Therefore, we argue that a threshold value of the mean participation plus one standard deviation will be more ecologically relevant as it allows macaques to show other behaviors during group movements. Moreover, group movements were highly clustered, which made it challenging to observe and identify all participants with certainty (See Supporting Information: Video 1). To allow for an accidental inability to identify a moving macaque, we furthermore argue that this adjusted threshold is more applicable.

Co‐appearance during feeding as a measurement for independence of behavior

We calculated the frequency of how often two individuals were simultaneously present at a feeding spot (for location of feeding spots see Figure 1). This was done for every possible dyad within the study population. The resulting numbers were then divided by the total number of feeding scans. We thereby calculated a value of co‐appearance for each possible dyad, a ratio which represents how often two macaques were at the same feeding spot at the same time.

Those dyads that had a co‐appearance value greater than the threshold value were considered as dyads that frequently synchronized their appearance at feeding spots. These synchronized dyads were collectively classified as first feeders, since they co‐appeared within 30 min during and after provisioning. All remaining individuals attended feeding spots after this time frame, which is why they were classified as last feeders. Both synchronized dyads and remaining individuals were illustrated via a network graph in Cytoscape_v3.9.0.

Percentage of participation in group movements

For each individual in the Affenberg‐group, we calculated a percentage of participation in group movements based on the following equation:

$$\%\mathrm{Participation}=\left(\frac{\mathrm{Frequency}\mathrm{of}\mathrm{participation}}{\mathrm{Number}\mathrm{of}\mathrm{movements}\mathrm{able}\mathrm{to}\mathrm{participate}\mathrm{in}}\right)\times 100$$

Instead of using the total number of group movements, we based our calculation on the total number of movements an individual could physically participate in, to control for external restrictions that prevented macaques from participating in movements, such as severe injuries or interventions due to management or health care reasons. The resulting values were used to classify individuals into movers and nonmovers. An individual qualified as a mover if their participation was above the threshold value.

Overlap in area use as a measurement for separation of nomadic ranges

We calculated the frequency of how often two individuals were simultaneously present in a certain section within the enclosure (see Figure 1). We did this for every possible dyad within the study population. The resulting numbers were then divided by the total number of area scans conducted during the study time. We thus calculated a value of overlap in area use for each possible dyad, a ratio which represents how often two macaques were seen at the same time at the same location. Those dyads that had a value of overlap greater than the threshold value were considered as those that frequently come together in certain areas of the enclosure. These values entered a network analysis performed in Cytoscape_v3.9.0 to illustrate the frequency of common area use between individuals by lines connecting them.

The value of overlap in area use was calculated irrespective of the location where the individuals met in the habitat. We can expect, however, that during fission one group withdraws into the peripheral areas while another is dominating the central areas (including the main feeding spots; Sugiyama, 1960; Widdig et al., 2006). To investigate this further we used the emerging network to compare the area use of the individuals involved in each cluster. First, we calculated the frequency of observations in which each individual was found in the central sections of the habitat (0C–6C, Figure 1) and divided this number by the total number of area scans. The resulting ratio represents the amount an individual is present in the center of the habitat. Second, the resulting ratios of each emerging cluster were compared using a Mann–Whitney U‐test. We classified the cluster that was significantly more often observed in the center as the center‐group, while the other cluster was labeled as the peripheral‐group.

Final division

We combined the three indicators used for group division to form the final division of the group into a main, sub‐, and undetermined group. Earlier studies found that those individuals that were present at feeding spots first, did not participate in group movements and spend more time in the central areas of the habitat are part of the main group (Fukuda, 1989; Furuya, 1960, 1968; Koyama, 1970; Maruhashi, 1982; Sugiyama, 1960; Yamagiwa, 1985). In our analyses subjects that were characterized as first feeders, nonmovers, and center‐group members were therefore attributed to the main group. Subsequently, last feeders, nonmovers, and the peripheral‐group members were assigned as subgroup members. Individuals of which the three indicators did not provide a uniform conclusion (e.g., being a non‐mover, center‐group member, but last feeder) were attributed to a third group of undetermined macaques.

2.4. Validity control—Demographics

We assessed how the following characteristics were distributed across the three newly formed groups: age, sex, social rank, and kinship.

We analyzed the differences in age between the groups with a Kruskal–Wallis test and a pairwise Mann–Whitney U‐test with a Bonferroni correction was used as a post hoc analysis. The division of age‐classes across the three groups was analyzed in a Pearson's χ ² test. We applied the same test to analyze the variance in sex across groups.

Additionally, we determined to which group the former high‐ranked individuals were attributed. This analysis was done separately for females and males. The female hierarchy was based on matrilineal rank differences determined shortly before the fission occurred (Pflüger et al., 2021). All females within a matriline received a numerical indicator of their matrilineal rank. The higher the numerical indicator, the higher the rank of the matriline was. We subsequently divided the matrilines according to the group division. The data on female rank was not normally distributed and thus a Kruskal–Wallis test was used to test whether there was a significant difference in rank between the three groups. As post hoc analysis, we used a pairwise Mann–Whitney U‐test with a Bonferroni correction.

The most recent data on male social rank before fission was collected in 2018 (Schmidhuber, unpublished data). Nevertheless, Pflüger et al. (2021) found the male dominance hierarchy in the Affenberg‐group to be very stable concerning high‐ranking positions, and that it followed a gradual succession of alpha‐positions. Adolescent males had to be excluded from this analysis, because males in this age group tend not to have a stable rank position yet (Nishida, 1966; Sugiyama, 1976; Thierry et al., 2004). Furthermore, males that were adolescent in 2018 were also omitted because their position in the dominance hierarchy remained undetermined. This resulted in 33 adult males who entered the rank analysis with a linear rank score (da‐score, cf. Singh et al., 2003). We used this rank score to create a numerical indicator of rank, in which a high value indicated a high rank. The data on male rank adhered to the assumptions of normally distributed data and homoscedasticity of variances, which is why we applied a one‐way ANOVA to test for significant differences in male rank between the groups. This was further analyzed using a post hoc Tukey‐HSD test.

We tested for repeatability between the group division of males and closest female relatives as an indicator of whether males and their closest female relatives were attributed to the same group (Koo & Li, 2016; McGraw & Wong, 1996; Shrout & Fleiss, 1979). To analyze the degree of kinship across the newly formed groups, we assessed the closest living relative of each individual (Table 2). Which individual was regarded as the closest living relative was based on the care providing function during the ontogeny of infants and juveniles in Japanese macaques (MacDonald Pavelka et al., 2002; Nakamichi, Onishi et al., 2010; Nakamichi & Yamada, 2010; Nozaki, 2009; Yamada et al., 2005; 2005). If the mother of a male was still alive, she would be the closest care‐providing relative and therefore included in this analysis. Otherwise, we used the grandmothers, sisters, or aunts, in that order. If there were multiple sisters or aunts possible to be the closest care‐providing relative, the eldest one was chosen since they are more likely to have provided a caring role in ontogeny. Following the same reasoning, an aunt or even grandaunt would be selected over a sister if the sister was younger than the male.

Table 2.

Frequency in variation of relation (and their degree) of closest living female relative of sexually mature males

Relation	Frequency	Degree of consanguinity
Mother	34	1
Sister	7	1 or 2a
Grandmother	5	3
Aunt	6	3
Grandaunt	1	4

^aSince the fathers remained unknown, no difference could be made between sisters of the same father = 1 or sisters with different fathers = 2.

Each male and their closest care‐providing relative was assigned with a numeric indicator of their group affiliation (1: main group; 2: subgroup: 3: undetermined) and subjected to a two‐way intraclass correlation coefficient with the type set to consistency (ICC(3,1)).

The investigation of matriline division was analyzed in a descriptive manner only.

2.5. Validity control—Social dynamics

2.5.1. Behavioral observations

To investigate whether group division was already observable before peak fission, we used data previously collected by Boehm et al. (unpublished data). This study focused on female consort behavior, but additionally collected focal data on 31 females, which entered our analyses. Boehm et al.'s (unpublished data) data collection took place between 10‐03‐2019 and 02‐23‐2020. This period preceding peak fission was observed by one observer (PMB.). The subjects of this study consisted of 31 females who were selected to represent the broad demographics of the population by having an equal spread over age (between 3.5 and 32‐year‐old), rank, and all matrilines.

The 31 female macaques were observed using continuous focal sampling (Martin & Bateson, 2007). One focal observation lasted 20 min. Focal observations included how long the focal animal resided in each area. Furthermore, instantaneous scan sampling (Martin & Bateson, 2007) was added to the focal protocol at the start and every minute mark. In this scan, macaques within body contact, a radius of 1 m, and a radius of 3 m around the focal animal were recorded. At the start and every 5 min macaques within a 5‐m radius were recorded as well. Focal sampling paused whenever the focal animal was out of sight and resumed when this focal animal was found within 3 h. If the focal animal was not found and the total observation was below 15 min, the focal sample was discarded. Focal animals were not observed twice on the same day or twice in 2 consecutive days, which meant that the sampling order of focal animals was semirandom.

From the focal data collected by Boehm et al. (unpublished data), we used the proximity scans to assess changes in social contact (cf. Massen et al., 2010) between the factions and changes in sizes of social networks. Additionally, we used the duration a focal animal was observed in the central or peripheral areas to determine whether the future subgroup withdrew into peripheral areas.

Change in between‐ and within‐group proximity over time

After assigning the 31 focal females to the main‐ and subgroup and undetermined based on our novel framework, we performed a social network analysis using proximity data from the period preceding peak fission. We counted how often a focal animal and another macaque were scanned in proximity (this includes body contact, 1, 3, and 5 m) with each other. This frequency was then divided by the total number of scans performed for this focal animal, resulting in a proximity value. These proximity values were divided into separate groups, depending on the group division of the focal animal and corresponding macaque that was in proximity. This resulted in six between‐group connections based on proximity values (Table 3). The proximity values were divided by month (October–November–December–January–February).

Table 3.

Between‐ and within‐group connections

Code	Connection
Between‐group connections
A	Main group to subgroup
B	Main group to undetermined
C	Subgroup to undetermined
D	Main group to deceased
E	Subgroup to deceased
F	Undetermined to deceased
Within‐group connections
G	Within main group
H	Within subgroup
I	Within undetermined
J	Within deceased

Subsequently, we tested the effect of between‐ and within‐group connection and month on individual proximity values using a linear model (LM) in which “connection” and “month” were used as fixed effects with proximity values as the dependent variable. As a post hoc analysis, we ran two estimated marginal means (EMM) functions. One EMM compared the effects of the different connections on the proximity values with each other, while the other EMM did the same but for months. To test whether the effects of “connection” and “month” were not better explained as random variables, we performed an ANOVA‐based comparison between the LM model and a null model (a linear mixed‐effect model (LMER) interpreting “connection” and “month” as random effects). The model with the lowest Aikake's Information Criterion (AIC) was the most suitable to explain the results.

Finally, we illustrated the proximity data during the entire observation period preceding group movements (not divided by months) as a social network figure in Cytoscape_v3.9.0 (number of connections between individuals within each group) and Microsoft® PowerPoint_v16.60 (thickness of lines connecting the groups represents the product of the µ‐values of connections between two groups and the number of connections).

Changes in number of proximity partners over time

Since future subgroup members are known to form clusters before the new groups fully separate (Suzuki et al., 2022), the number of partners in proximity may reveal an enhanced tolerance to other future subgroup members and thus fission tendencies before peak fission. To investigate this, we analyzed the number of proximity partners per month of all 31 focal females distributed across the future main‐ and subgroup. Using another LM, we tested how the number of proximity partners was affected by group affiliation and month. We performed a subsequent post hoc EMM to test which group affiliation and month explained the observed significant difference. To test if the effect of these variables were not random, we carried out an ANOVA‐based comparison with a null model (an LMER model, interpreting group affiliation and month as random variables).

Withdrawal

To test whether one of the groups retreated more into the peripheral areas during the period preceding peak fission, we analyzed the time spent in central areas for each focal animal. This sum of seconds was divided by the total time of observation for a focal to receive a percentage of time spent in central areas. If a focal was observed in an area that could not be identified as either center or periphery, this time was subtracted from the total observational seconds. The percentage of time spent in central areas was used as a dependent variable in an LM, with “group” and “month” as fixed effects. An EMM function allowed comparison between group and month, and an ANOVA‐based comparison with a LMER null model was carried out to assure “group” and “month” are not better explained as random effects.

2.6. Statistics

All statistical analyses were performed using R (Version 3.5.0; R Core Team, 2022) and alpha was set at 0.05. We created all boxplots and line graphs with StataSE_v17. Network graphs were illustrated in Cytoscape_v3.9.0.

3. RESULTS

3.1. Results of the framework

3.1.1. Independence of behavior

A total of 58 feeding scans were performed and analyzed to determine the independence of behavior. The mean co‐appearance value was 0.0198. The standard deviation within the co‐appearance values was 0.032, making the threshold‐value for this indicator 0.0846. This requirement was met by 582 dyads. A network graph based on the co‐appearance values depicted a clear group formation (Figure 2). This group consists of 59 macaques that were named first feeders and the remaining 66 macaques were referred to as last feeders.

Figure 2.

Individuals who were simultaneously present at feeding spots. Each dot represents an individual (small dots = males; bigger dots = females). Females are labeled according to their matriline (2 = highest ranked matriline; 13 = lowest ranked matriline). Lines between individuals are only represented if their co‐appearance value >mean + 2 SD = 0.0846. A clear group division is visible, in which the connected macaques (N = 59) were most often present together during feeding. This group is referred to as first feeders. The remaining macaques (N = 66), without connections (<mean + 2 SD = 0.0846), are grouped together as last feeders.

3.1.2. Participation in group movements

During the group movement period (03‐10‐2020 until 04‐10‐2021), a total of 25 group movements were observed (1 to 2 movements a day, on 6 days no movement was observed). Within these group movements, there were 118 macaques that participated at least once. The mean percentage (±SD) of participation was 28.64 ± 38.59. The threshold percentage of participation in movements resulted in 67.23% and 38 macaques met this threshold value. These individuals were therefore grouped together as “movers.” The remaining 87 subjects were categorized as “non‐movers.”

3.1.3. Separation of nomadic ranges

A total of 628 independent area scans were performed within the 26 days of observation during the group movements period. The Affenberg‐group had a mean overlap in area use (±SD) of 0.00681 ± 0.00824. The threshold value was therefore 0.0233 and 439 dyads had an equal or higher overlap in area use. These dyads have been visualized in a network graph which shows two groups (Figure 3). Group 1 consisted of 35 macaques and group 2 consisted of 39 macaques.

Figure 3.

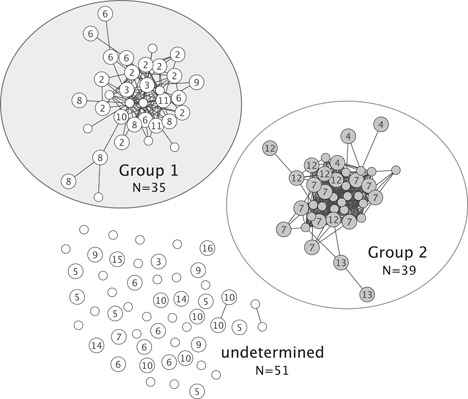
Grouping based on the overlap in area use. Each dot represents an individual (small dots = males; bigger dots = females). Females are labeled according to their matriline (2 = highest ranked matriline; 13 = lowest ranked matriline). Lines between individuals are only represented if the individuals were seen together in the same area groups (>mean + 2 SD = 0.0233). Two clear groups emerged: Group 1 (N = 35) and group 2 (N = 39) consist of macaques that are most often seen together within the same areas. The remaining macaques (undetermined; N = 51) had no overlap in area use with either of the two groups (<mean + 2 SD = 0.0233) and are represented as unconnected dots.

Group 1 was significantly more often seen in the C‐areas than group 2 (Wilcoxon‐signed‐rank test; W = 1331.5; p < 0.001; Figure 4), which is why group 1 was identified as the “central‐ group” and group 2 was named “peripheral‐group.” The remaining 51 macaques that had no connections to these groups (<mean + 2 SD = 0.0233) were defined as “undetermined.”

Figure 4.

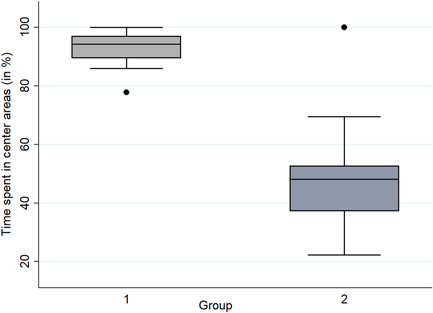
The percentage of scans in which group 1 (N = 35) and group 2 (N = 39) was found in central areas of the enclosure. Group 1 was significantly more often observed in central areas compared to group 2 (Wilcoxon‐signed‐rank test; W = 1331.5; p < 0.001).

3.1.4. Final group division

Combining the three indicators resulted in 33 individuals that were assigned to the “main group.” Slightly more individuals (N = 36) could be assigned as “sub‐group.” The remaining 59 individuals were labeled as “undetermined” (Supporting Information: Table S2).

3.2. Results of the validity controls

3.2.1. Validity control—Demographics

Age and sex

The main‐, subgroup and undetermined macaques displayed no significant variance in the number of females and males (Pearson's χ ² test; X² = 4.772; df = 2; p = 0.092). We found no difference in the age of females between the three groups (Kruskal–Wallis test; χ ² = 2.977; df = 2; p = 0.226; Supporting Information: Table S3). Males, however, did vary in their age between the groups (Kruskal–Wallis test; χ ² = 8.790; df = 2; p = 0.01). Males in the main group were significantly older than the undetermined males (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 0.03; Supporting Information: Table S3). Subgroup males did not differ in age compared to main group males (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 1), nor to males assigned as undetermined (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 0.08). Moreover, there was a difference in the group division of adolescent males: only one adolescent male was part of the main group (8 years), and five adolescent males were part of the sub‐group (mean ± SD = 8.9 ± 1.053 years). The 13 remaining adolescent males (including the youngest, aged 5 years) were part of the undetermined group (mean ± SD = 9.2 ± 3.818 years).

Social rank

The females within the three different groups did vary in their rank (Kruskal–Wallis test; χ² = 13.643; df = 2; p = 0.001). High‐ranked females were more often present in the main group than in the subgroup (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 0.009; Supporting Information: Table S3) and the undetermined‐group (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 0.002; Supporting Information: Table S3). The subgroup and undetermined‐group did not show any differences in the rank of females (pairwise Mann–Whitney U‐test; Bonferroni correction; p = 1).

The rank of males differed between the three groups (One‐way ANOVA; F = 4.231; df = 2; p = 0.024; Supporting Information: Table S3). A post hoc analysis showed that this difference was present between the subgroup and undetermined‐group. The subgroup males had a significantly higher rank (indicated by a higher rank‐score) than the undetermined males (Tukey‐HSD; mean difference = −9.038; p = 0.041, Supporting Information: Table S3). A trend was detected between the main group and the undetermined individuals, with males in the main groups scoring higher in rank than undetermined males (Tukey‐HSD; mean difference = −9.288; p = 0.065, Supporting Information: Table S3).

Male–female kinship division

In total, 51 males and their closest care‐providing female relatives entered our analysis on the degree of kinship across the newly formed groups. We found no significant relationship between the group attribution of the males and their female relatives (ICC; ICC = −0.00859; F = 1.02; p = 0.473). Out of 52 sexually mature males, 18 males were attributed to the same group as their female relatives (35.3%). Out of these, two pairs of males and their closest female relative were found in the main group (male age 11.8 and 13.8 years). The subgroup only had one pair (male age 21.8 years). The majority of males paired with their female relatives in the undetermined group (N = 15 pairings; mean age males ± SD = 9.8 ± 4.9 years). Out of these 15 pairs, 8 involved adolescent males (mean age adolescent males ± SD = 5.9 ± 1.5 years).

Female–female kinship division

The Affenberg‐group had 13 matrilines that consisted of more than one female. Six matrilines remained intact in one of the three groups (Supporting Information: Figure S1). Two of these were fully part of the main group and one was completely attributed to the subgroup. The other three matrilines were part of the undetermined individuals. Seven of the 13 matrilines in the Affenberg‐group were split across two groups. Four matrilines were split up over the main‐ and undetermined‐group, and three matrilines were split up across the subgroup and undetermined individuals. No matriline was separated over the main‐ and subgroup and no matrilines were split up across all three groups.

3.2.2. Validity control—Social dynamics

Out of the 31 focal females, 5 could be attributed to the future main group, 9 to the future subgroup, 13 were undetermined, and 4 females died during the study period. Two focal females died due to illness during the period preceding peak fission. The other two died from injuries sustained during aggressive encounters during peak fission. One adolescent male entered our study as a deceased individual as he was a proximity partner of focal females but died before he could be assigned to any group.

Proximity scans of the females, which could be assigned to different groups, were used to assess whether the divided groups had already stronger social connections within a group compared to between groups during the five months preceding peak fission. A total of 14,642 observation minutes were analyzed. The average minutes of observation per focal was 427 min (range 200−534 min). There were 15,377 proximity scans, with an average of 496 scans per individual (range 204−550). Two females had a reduced number of observation minutes and scans (about 200) since they died in October and December 2019, respectively.

Change in between‐ and within‐group proximity

We found that the connections based on proximity values within a certain group were already stronger than the connection between different groups, either significantly or showing a trend, except for A–I (see Table 4 and Figure 5). No differences were found in the average connections within or between groups. The intergroup connection with the highest number of connections between individuals was between the main group and undetermined macaques, while only very limited proximity dyads were shared between the subgroup and the main group. The subgroup shared the strongest connection with the deceased macaques (Figure 5).

Table 4.

Difference in proximity strength, “within” vs. “between” the different groups

G (within main group)			H (within subgroup)			I (within undetermined)
Estimate	z‐ratio	p Value	Estimate	z‐ratio	p Value	Estimate	z‐ratio	p Value
−2.646	−2.646	0.087	−2.880	−3.153	0.027	−2.433	−2.674	0.105
−1.764	−3.637	0.005	−1.998	−5.287	<0.001	−1.551	−4.167	<0.001
−1.631	−2.750	0.087	−1.865	−3.658	0.005	−1.418	−2.801	0.076

Note: Data was collected from 31 focal females during the period preceding group movements (2019/2020) during the study of Boehm et al. (unpublished data).

Figure 5.

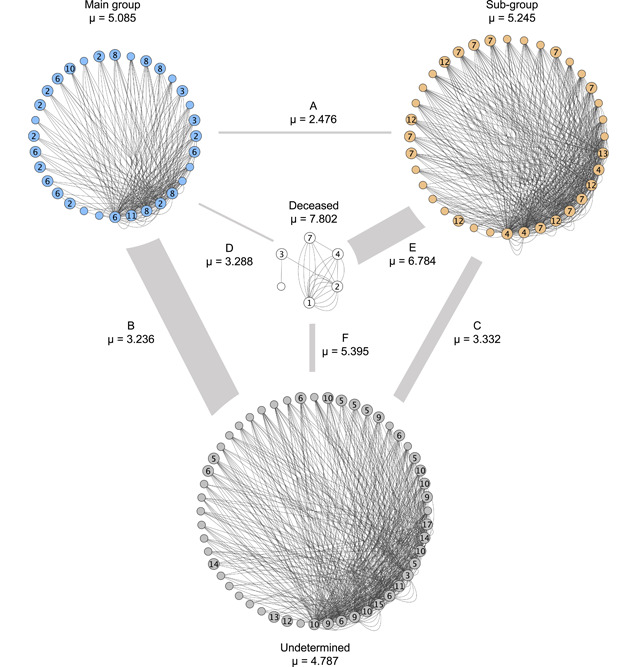
Mean proximity value (μ) within groupings and between groupings based on proximity scans of focal sampling (N = 31) during the period preceding peak fission. Blue dots = main group, orange dots = subgroup, gray dots = undetermined individuals, white dots = deceased individuals. Small dots = males; bigger dots = females. Females are labeled according to their matriline (2 = highest ranked matriline; 13 = lowest ranked matriline). Thickness of gray lines between groups (a–f) depict the product of μ and number of dyads with corresponding connection. Lines connecting group members represent the number of connections (i.e., how often two individuals were seen in proximity).

The effect of these results remained intact after an ANOVA‐based comparison with a null model (X ²(7) = 37.198, p < 0.001).

Changes in number of proximity partners over time

We found no difference in the number of proximity partners between the three groups, neither per month nor over the entire period preceding peak fission. Each group had a higher number of proximity partners in January compared to all other months (January–October: estimate = 10.185, z‐ratio = 6.866, p < 0.001; January–November: estimate = 11.444, z‐ratio = 7.715, p < 0.001; December–January: estimate = −7.852, z‐ratio = −5.293, p < 0.001; February–January: (estimate = −7.556, z‐ratio = −5.093, p < 0.001; Figure 6a). The effect of these results remained intact after an ANOVA‐based comparison with a null‐model X ²(4) = 20.252, p < 0.001).

Figure 6.

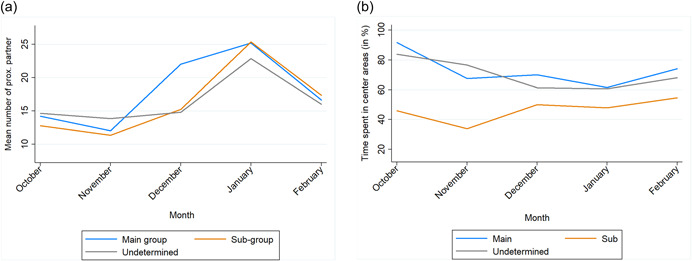
(a) Change in mean number of proximity (prox.) partners over the months (October 2019–February 2020) per group. (b) Change of time spent in the central area (% of observed time) over the months (October 2019–February 2020), per group. Data collected from focal females (N = 31) during the period preceding peak fission.

Withdrawal

In general, we found a significant difference in time spent in the central areas between groups when considering the entire period preceding peak fission. During these five months the females that belong to the main group after fission were already more often observed in the central areas compared to the subgroup (estimate = 26.61, z‐ratio = 5.092, p < 0.001) while the females that would belong to the subgroup were already observed less in the central areas than the undetermined individuals (estimate = −23.77, z‐ratio = −5.850, p < 0.001). The effect of these results remained intact after an ANOVA‐based comparison with a null model (X ²(4) = 23.428, p < 0.001; Supporting Information: Figure S2).

The monthly distribution, however, revealed that these group differences in central‐area use were based on 2 months, October and November, in which the females that later belong to the subgroup had a lower presence in the central area compared to those that would later belong to the main group or be undetermined. (October_sub/main: estimate = 45.93, z‐ratio = 4.438, p < 0.001; October_sub/undeterm.: estimate = −38.11, z‐ratio = −4.736, p < 0.001; ANOVA‐null model comparison (X ²(1) = 10.025, p = 0.002); November_sub/main: estimate = 33.8, z‐ratio = 3.332, p = 0.008; November_sub/undeterm.: estimate = −42.9, z‐ratio = −5.440, p < 0.001; ANOVA‐null model comparison (X ²(1) = 9.790, p = 0.002), Figure 6b).

In December, January, and February, this difference in time spent in the central area between the groups was not found (Figure 6b).

4. DISCUSSION

The present study introduces a novel framework to identify individual group membership during peak fission in semi‐free‐ranging Japanese macaques. To assign individuals to different groups, we analyzed multiple measurable behavioral indicators known to be present during peak fission in this species, namely an increase in independence of behavior, participation in group movements and separation of nomadic ranges. We tested the validity of this group division by (1) comparing the demographics of each resulting group to published data on fissioned Japanese macaque groups and (2) by the use of social network analyses and area usage to uncover separation tendencies of the resulting groups five months before peak fission.

Our framework resulted in two core groups, a main‐ and subgroup, and a rather high number of undetermined individuals. A reason for this could be the strict requirement used by our framework: all three indicators had to provide a unanimous conclusion for a macaque to be attributed to the main‐ or subgroup. Furthermore, our framework was designed to investigate one specific period of fission, that is, peak fission in which different behavioral changes come into play. However, we know that fission was not yet fully completed at the end of our study period, which meant that individuals were still undecided on their group membership. Previous studies on fissions in Japanese macaques have shown that it can take several months and up to 1 year until groups have fully separated (Furuya, 1968; Sugiyama, 1960). In semi‐free‐ranging groups this process may last even longer due to limited space. Even though the Affenberg main group and subgroup began to separate their habitat use, the groups still occupied similar sections of the enclosure during peak fission, although not simultaneously. Free‐ranging populations completely separate their nomadic ranges at the end of the fission process (e.g., Sugiyama, 1960; Yamagiwa, 1985). Closely related Barbary macaques that live in semi‐free‐ranging populations also occupy fully separated habitats after fission when given enough space (Kuester & Paul, 1997). This further shows that fission had not ended yet and indicates that the Japanese macaques at Affenberg might benefit from a future expansion of their habitat for the main‐ and subgroup to enter the final stage of fission.

The detected main‐ and subgroup at the Affenberg already showed demographic characteristics comparable to postfission groups in wild populations, that is, we found no differences in sex and female age (cf. Koyama, 1970), and low‐ranked females moved to the subgroup (cf. Koyama, 1970). However, although we also expected low‐ranking males to move towards the subgroup (Koyama, 1970), we found no pattern in rank of males across the main‐ and subgroup. This is nevertheless in line with the observations of Furuya (1960), who described the absence of male grouping based on social rank. In the Affenberg‐group, the separation of top‐ranking males might be responsible for the lack of differences in male rank between the core groups. The fission event divided top‐ranking males from each other for the first time since Affenberg's existence (Pflüger et al., 2021): the former alpha and gamma males moved to the subgroup while the beta and delta males remained in the main group. While most of the socially mature males decided on one of the two core groups, 68% of the undetermined individuals were adolescent males (also reflected in the lowered mean age of undetermined males compared to the two core groups). The high percentage of adolescent males embedded in the cluster of undetermined individuals may explain why this faction scored lowest in male rank, which is in accordance with the natural demographics of the species, whereby most subadult males stay in the periphery (Koyama, 1970).

Future studies are needed to monitor the reorganizing of male social rank before, during, and after fission. Since the previously stable hierarchical order collapsed, young low‐ranking males, by now most with undetermined group membership, might stand a chance to set foot in the hierarchy during times of social instability.

Another demographic characteristic that deserves further discussion is the division of kin across different groups. We discovered only a few pairs of males and their closest female relatives in the main‐ and subgroup. Males tend to leave their natal group during fission (Koyama, 1970; Sugiyama, 1976). In our study, group membership of the majority of related male/female pairs was undetermined. Most adolescent males were undetermined as well (15 out of 19). Under semi‐free‐ranging conditions, males lack the possibility to entirely move away from their natal groups. During the process of fission, their choice is limited to groups emerging out of their natal group. Adolescent males may particularly struggle in their decision during the process of fission if the affiliation of their female kin is not clearly resolved yet.

A fission event usually does not separate matrilines in wild populations (Fooden and Aimi 2006; Koyama, 1970; Sueur et al., 2010; Takahata et al., 2002). In the Affenberg‐group, those females who were not part of the same group as their matriline were all labeled as undetermined. Undecided females seem to be particularly present in mid‐ to low‐ranking matrilines in which some female relatives were assignable to the main group. Although the social system of Japanese macaques is nepotistic, and kin tends to cooperate more with each other (Sigmundson et al., 2021; Bhattacharjee et al., 2022), dominance competition among female kin exists (Chapais et al., 1994). Individual advantages are given if females form non‐kin alliances with higher‐ranked individuals to outrank higher‐ranked female siblings during conflicts. During the process of fission, females may face a conflict of interest between siding with non‐kin allies and their own kin females (Chapais et al., 1994), at least as long as fission is not fully completed yet.

To validate the results of our framework, we tested our expectation that the future groups would display separation tendencies in the months before the period of peak fission (Sugiyama, 1960). Our social network analyses revealed that macaques belonging to the two future core groups had stronger connections with their future group members than with individuals from other groups. This is in line with the study of Sugiyama (1960) who found that dividing factions slightly reduce proximity before more prominent behavioral changes occur, such as group movements. The lowest between‐group proximities, as well as the amount of intergroup connections was found between the future main group and subgroup. Furthermore, the analyses on area use before peak fission showed that the future subgroup was already less present in the central sections of the enclosure compared to the future main group. These findings support our expectations that the two core groups, detected by our framework, already started to avoid each other five months before peak fission. The social network of the determined core groups did not change in size over time. This is in line with our finding that the proximity values within each group did not change over time either. It therefore seems that the individuals were already connected to core members of their group months before group movements started.

Taken together, these three independent measures revealed that the detected groups already showed segregation from each other and that the subgroup withdrew from the central sections months before peak fission with group movements happened. This, alongside the demographic comparisons with literature, supports the methodology of our framework to be applicable for the assignment of individuals to core groups during peak fission in Japanese macaques. Now that core individuals have been assigned, long‐term monitoring is needed to capture the ongoing fission‐fusion dynamics of the Affenberg group. The applied network analyses and analysis of area use will be applied on a regular basis (during mating and nonmating season; e.g., Yamaguchi & Kazahari, 2022) to uncover future stages of fission in the Affenberg group, which we believe has not yet come to a final end. We are aware that our analyses on the dynamics preceding group movements were solely based on proximity data of a select group of adult females—the only data available to us in this period. Nonetheless, females are known to be the center of societies and highly affect the formation of social connections in macaques (Chaffin et al., 1995; Thierry et al., 2004). The social tendencies of males can be significantly influenced by females, and we therefore consider data on females to be used as a proxy to illustrate fission–fusion dynamics in separating groups.

To conclude, many studies highlight the importance to study fission‐fusion dynamics and the assignment of individual membership for many different primate societies (e.g., Macaca sinica, Dittus, 1988; Macaca cyclopsis, Hsu et al., 2017; Macaca maurus, Okamoto & Matsumura, 2001; Pan troglodytes, Feldblum et al., 2018; Pan paniscus, Hashimoto et al., 1998). We expect our framework to be a helpful addition to previous methodologies as it is the first to consider behavioral changes present during a highly dynamic period of fission (i.e., peak fission). There are key variables common in many fissions in primates, such as the separation of nomadic ranges or desynchronization of behavioral patterns. We call out for future studies to incorporate and test our concept in different primate societies undergoing fission.

AUTHOR CONTRIBUTIONS

Study conception and design: Roy Hammer, Mathieu S. Stribos, and Lena S. Pflüger. Data collection: Roy Hammer, Mathieu S. Stribos, Lena S. Pflüger, Julia Herzele, and Pia M. Böhm. Data analyses and illustrations: Roy Hammer, Mathieu S. Stribos, Lena S. Pflüger, and Katharina E. Pink. Writing, review and editing: Roy Hammer, Mathieu S. Stribos, Lena S. Pflüger, Jorg M. Massen, Michael A. Huffman, and Bernard Wallner. All authors read and approved the final manuscript.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Supporting information

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Supporting information.

Hammer, R. , Stribos, M. S. , Boehm, P. M. , Pink, K. E. , Herzele, J. , Wallner, B. , Huffman, M. A. , Massen, J. J. M. , & Pflüger, L. S. (2023). A novel methodological approach for group classification during fission of a semi‐free‐ranging group of Japanese macaques (Macaca fuscata). American Journal of Primatology, 85, e23463. 10.1002/ajp.23463

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.