Abstract
A North/South difference in crustal thickness is likely at the origin of the Martian dichotomy in topography. Recent crustal thickness maps were obtained by inversion of topography and gravity data seismically anchored at the InSight station. On average, the Martian crust is 51–71 km thick with a southern crust thicker by 18–28 km than the northern one. The origin of this crustal dichotomy is still debated although the hypothesis of a large impact is at present very popular. Here, we propose a new mechanism for the formation of this dichotomy that involves a positive feedback between crustal growth and mantle melting. As the crust is enriched in heat‐producing elements, the lid of a one‐plate planet is hotter and thinner where the crust is thicker, inducing a larger amount of partial melt below the lid and hence a larger rate of melt extraction and crustal growth. We first demonstrate analytically that larger wavelength perturbations, that is, hemispherical perturbations, grow faster because smaller wavelengths are more attenuated by thermal diffusion. We then use a parameterized thermal evolution model with a well‐mixed mantle topped by two different lids characterized by their thermal structures and thicknesses to study the growth of the crust in the two hemispheres. Our results demonstrate that this positive feedback can generate a significant crustal dichotomy.
Keywords: Mars dichotomy, Mars volcanism, crust formation, mantle melting, thermal evolution, InSight
Key Points
On one‐plate planets, regions of thicker crusts are hotter leading to a positive feedback mechanism between crust growth and melt extraction
This mechanism is favored at larger wavelengths because smaller wavelengths are more attenuated by lateral thermal diffusion
This mechanism can explain the hemispheric difference in thickness of the Martian crust
1. Introduction
The Martian surface is characterized by a dichotomy in elevation, crustal thickness and morphology between the northern lowlands and southern highlands (Platz et al., 2013; Watters et al., 2007). The highlands are highly cratered and incised by many old river valleys (Tanaka et al., 2014). The oldest terrains outcrop in the Southern hemisphere (Platz et al., 2013) which also concentrates observations of volcanic constructs and felsic rocks (Carter & Poulet, 2013; Wray et al., 2013). In contrast, the upper portion of the lowlands crust is made of vast and smooth basaltic plains and sedimentary deposits derived from the erosion of the highlands (Platz et al., 2013; Tanaka et al., 2014). The dichotomy is perhaps the most evident feature of the crust (Figure 1). Superposed on the dichotomy boundary is the Tharsis bulge, whose origin may (Andrews‐Hanna et al., 2008), or may not (Neumann et al., 2004), be related to it. Prior to the InSight mission, inversions of gravity and topography data were used to constrain the crustal thickness of Mars and its lateral variations, though these models depended on assumptions such as crustal density and minimum crustal thickness (Neumann et al., 2004; Wieczorek & Zuber, 2004).
Figure 1.
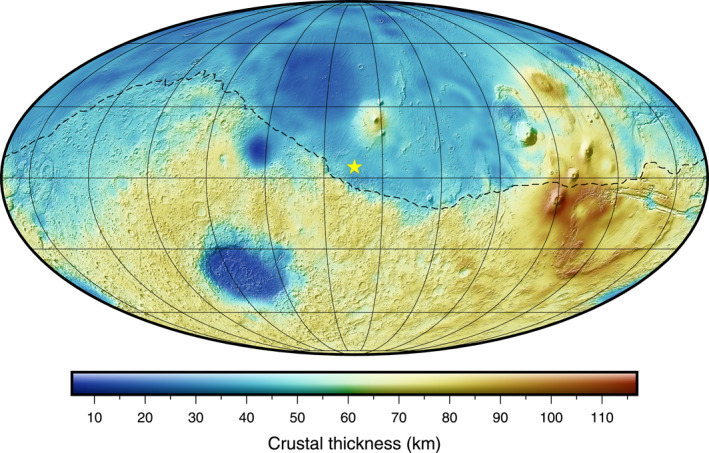
Thickness of the crust of Mars using a crustal density of 2,900 kg m−3. For this model, the mantle density profile is that of Khan et al. (2021) and the crustal thickness at the Insight landing site (yellow star) is 39 km (Knapmeyer‐Endrun et al., 2021). The dashed line represents the dichotomy boundary from Andrews‐Hanna et al. (2008). This map is presented in a Mollweide projection with a central meridian of 136°E longitude.
The NASA InSight (Banerdt et al., 2020) mission has allowed recording for the first time the seismic activity of Mars with the deployment, early 2019, of the seismometer Seismic Experiment for Interior Structure (SEIS) in Elysium Planitia (Lognonné et al., 2020). From P and PP receiver function analyses of teleseismic events recorded by the seismometer, subsurface interfaces, including the crust‐mantle interface or the Mohorovičić discontinuity, commonly referred to as the Moho, have been detected below the station (Durán et al., 2022; Kim et al., 2021; Knapmeyer‐Endrun et al., 2021). This local seismological constraint on the Martian crustal thickness provided a critical anchor point that is necessary for crustal studies that rely on topography and gravity data (Knapmeyer‐Endrun et al., 2021). Following this detection, the Martian crust thickness and its lateral variations have been revealed (Knapmeyer‐Endrun et al., 2021; Wieczorek et al., 2022) (see Section 3.5). A similar procedure was used on the Moon with receiver function and travel‐time data analyses in order to estimate the local crustal thickness beneath the Apollo seismic stations (Lognonné et al., 2003; Vinnik et al., 2001) and to anchor global crustal thickness models based on gravity and topography data (Wieczorek et al., 2013).
The mechanism at the origin of the crustal dichotomy is one of the major debates concerning Mars' evolution (Watters et al., 2007). With an age between 4.5 and 3.7 Gyr, the dichotomy appears to be one of the oldest features of Mars (McGill & Dimitriou, 1990; Solomon et al., 2005). The formation of the dichotomy appears older than the northern lowlands but contemporary to the southern highlands. The younger surface of the northern hemisphere is then probably a late consequence of the dichotomy rather than related to its formation mechanism.
As planetary crusts grow by extraction of buoyant mantle melts, the dichotomy could have originated during crust growth due to laterally variable mantle melt fractions. A degree‐one mantle convection pattern with a hot ascending mantle plume in the South and a cold downwelling in the North can generate such a spatially variable mantle melt fraction. A degree‐one mantle convection may be favored by a radial stratification in viscosity in the mantle (Šrámek & Zhong, 2010; Yoshida & Kageyama, 2006; Zhong & Zuber, 2001). Zhong (2009) linked this degree‐one to the presence of Tharsis. He proposed that melt extraction from the ascending plume and associated stiffening of the lithospheric keel could have generated a lateral viscosity variation that could in turn have triggered a toroidal velocity field inducing plume migration and explaining the location of Tharsis, straddling the dichotomy. In this study, the lithospheric keel was prescribed, extending over one hemisphere. Šrámek and Zhong (2012) lately parameterized partial melting and melt extraction in a 3D convection model to demonstrate that the associated lithosphere stiffening and crustal thickening were large enough to produce the observed dichotomy. The formation of the highlands by migration of the Tharsis plume would require several hundred million years and would imply an age‐distance to Tharsis relationship for the highlands which is not obvious. Recently, Morison et al. (2019) showed that a degree‐one mode of mantle convection could also be generated during magma ocean solidification by melting and freezing at the boundary between the solid cumulates and the liquid; but they did not investigate its consequences on crust formation.
The dichotomy may also result from the reprocessing of the crust after its main extraction phase through one or more impacts, which were frequent in the early times of the Solar System. A large impact in the Northern hemisphere is currently the most popular explanation for the topographic depression in the North (Marinova et al., 2008). This impact could potentially explain the formation of the Martian moons Phobos and Deimos (Marinova et al., 2008) and possibly the cessation of the Martian geodynamo (Roberts & Arkani‐Hamed, 2014). But, while a large impact event may help explain many features of the Martian surface, its real consequences on the structure and evolution of the crust are difficult to quantify and remain partly speculative given the ancient age of this event. The amount of kinetic energy released by a large impact could have significantly raised the mantle temperature (Roberts & Arkani‐Hamed, 2014) inducing such a large amount of melt that the very evidence for an impact basin—that is, the dichotomy—could have been eradicated (Tonks & Melosh, 1993). On another hand, Marinova et al. (2011) used a smoothed particle hydrodynamics (SPH) model to argue that, depending on the impact characteristics, a significant fraction of the melt could have sequestered at depth without contributing to resetting the planetary surface. The size and speed of the impactor would then point to an age of 4.5 Gyr for this impact. An early large impact in the South has also been proposed to explain the larger crustal thickness in this hemisphere (Golabek et al., 2011; Reese et al., 2010).
In one‐plate planets, the convective mantle interior is well characterized by a nearly uniform temperature, where a stagnant lid develops at the top as the cold boundary layer that is too viscous to be advected away (Nataf & Richter, 1982; Solomatov, 1995). The lid base is set by the mantle rheology which mainly depends on its temperature (Davaille & Jaupart, 1993). As a result, in a stagnant lid regime, the thermal structure of the crust largely influences the thickness of the thermal lithosphere and hence the amount of partial melt that is generated in the mantle below (Knapmeyer‐Endrun et al., 2021; Thiriet et al., 2018) because mantle upwellings decompress down to pressures corresponding to the base of the lid. Here, we propose that the Martian dichotomy could have resulted from an instability in crustal growth. Indeed, since the crust is enriched in incompatible heat‐producing elements (HPEs), the lid of a one‐plate planet is thinner where the crust is thicker (Thiriet et al., 2018) and the pressure at its base is lower. Because the solidus temperature decreases more rapidly than the adiabat as pressure decreases, more melt is generated in the mantle below regions of thicker crust. As the melt extraction rate increases with melt fraction (Katz et al., 2022; McKenzie, 1985), there exists a positive feedback between crustal growth and crustal thickness on stagnant lid planets.
Here, we first demonstrate, using a simple analytical model, that larger wavelength perturbations, that is, hemispherical perturbations, grow faster because smaller wavelengths are more attenuated by lateral thermal diffusion. We then develop a bi‐hemispherical parameterized thermal evolution model to show that this positive feedback mechanism can indeed generate a significant dichotomy in crustal thickness from initially small thermal perturbations, and this despite the cooling of the planet. We finally investigate the different types of thermal and crustal extraction histories that are able to reproduce the range of Martian crustal thicknesses as deduced from the InSight mission.
2. Study of the Instability for a Simplified Setup
Before developing a more complex thermal evolution model to study the differential growth of the crust in the Northern and Southern hemispheres of Mars, we first use a simplified toy model along with a linear stability analysis to study the growth of a thermal perturbation as a function of its wavelength. We demonstrate that lateral thermal perturbations of larger wavelengths grow faster because lateral thermal diffusion attenuates more quickly the smaller wavelengths.
Here, we study the thermal evolution of a lid that becomes progressively enriched in HPEs as melts, which concentrate incompatible and HPEs, are extracted from the mantle below and redistributed within this lid. In particular, we follow the temperature at the base of the lid T b (t), assumed to be above the solidus temperature T sol , as well as the instantaneous melt fraction ϕ(t), which is taken to be a linear function of temperature over the melting interval T liq − T sol :
| (1) |
In this simplified model, we assume that, although enriched melts are deposited in the lid, the lid thickness D l = R p − R l remains constant, where R p is the mean planetary radius and R l the radius at the lid base. The volumetric heat production in the lid H(θ, φ, t) evolves with time and is assumed to be radially homogeneous (i.e., the extracted melt is distributed evenly across the lid thickness, and we do not consider a geochemically distinct crust). We finally assume a linear relationship between the melt extraction rate, and hence the enrichment rate of the lid in HPEs , and the melt fraction ϕ at the base of the lid:
| (2) |
where α is the rate of increase in heat production with time of the lid in W m−3 s−1; which could be estimated from α ≈ vH liq/D l , with v a characteristic melt extraction velocity and H liq the melt heat production. The constants and are also positive.
We solve for 3D diffusion of heat in the lid assuming, for this specific toy model, a steady‐state, a constant heat flux from the underlying convective mantle and a constant temperature T(R p ) at the surface:
| (3) |
with k the thermal conductivity. Our background state is such that the zero‐order heat production H 0(t) is laterally constant, and the zero‐order background temperature field T 0(r) is straightforward to obtain from Equation 3 and boundary conditions. We now add small lateral perturbations in heat production and temperature to this background state:
| (4) |
| (5) |
where ϵ ≪ 1, Y lm (θ, φ) are the spherical harmonic functions of degree l and order m, θ the colatitude, φ the longitude, λ(l) the perturbation growth rate and t time.
Injecting Equations 4 and 5 into Equations 3 and 2, we derive the following relations for first‐order perturbations in ϵ:
| (6) |
| (7) |
with the boundary conditions T 1(R p ) = 0 and . This finally gives a general solution for l ≠ 2 and a particular solution for l = 2 (as the denominator of B l and C l is equal to zero in this case, i.e., 6 − l(l + 1) = 0 in Equation 8):
| (8) |
| (9) |
Our solution shows that the growth rate is positive for all wavelengths. This means that perturbations of all wavelengths grow, and no wavelengths are damped (Figure 2). However, since lateral heat diffusion tends to attenuate smaller wavelengths more, the larger the wavelength (the smaller l), the larger the growth rate λ of the perturbation is (Figure 2). Therefore, longer wavelength perturbations grow faster and are favored by this feedback mechanism. The largest growth rate occurs for spherical harmonic degree 1, though the growth rates are not too different for the first few degrees. In order to study if the growth over time of a thermal perturbation is sufficient to induce a significant crustal dichotomy despite planetary cooling, we restrict our study to the case of a hemispherical perturbation (l = 1), which grows the fastest, and construct below a more complex thermal evolution model.
Figure 2.
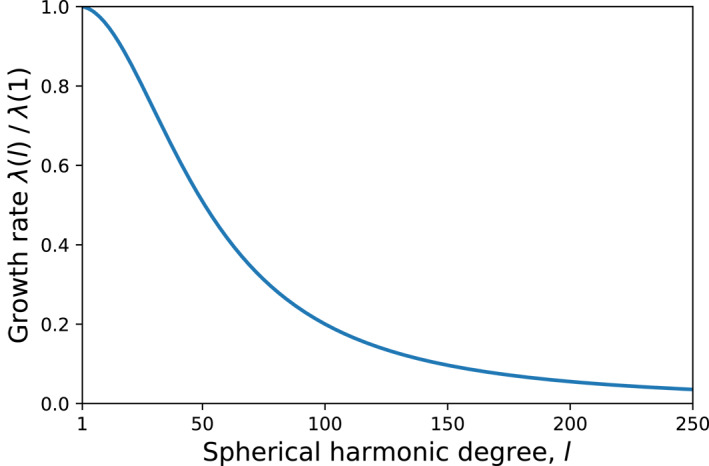
Growth rate λ given by Equations 8 and 9 and normalized by the growth rate for l = 1 as a function of spherical harmonic degree. We use k = 3 W m−1 K−1, R p = 3,390 km, R l = 3,290 km.
3. Model
Although 3‐D convection models can provide a full description of the temperature field over time as well as of the convection pattern (Plesa et al., 2015; Šrámek & Zhong, 2012), they are numerically very time‐consuming and do not yet allow to account for realistic 3‐D segregation of melt from the mantle. Since our goal is to study crust formation by melt extraction, we use a parameterized model for a stagnant lid which considers a well‐mixed convective mantle topped by a conductive lid (here referred to as the lithosphere), where heat is transported by conduction. We assume a well‐mixed mantle characterized by a temperature at its top and an isentropic temperature profile. We neglect the lateral temperature variations that naturally arise in convection flows (Roberts & Zhong, 2006). Following our analytical result (Section 2), we impose a hemispherical perturbation by considering, as in Thiriet et al. (2018), a lid with different characteristics between the two hemispheres, that is, different temperature profiles T(r,t)N/S, lid thicknesses , crust thicknesses and crust enrichments compared to bulk silicate Mars , where the subscripts N/S refer to values for the Northern (N) or Southern hemisphere (S) respectively, (Figure 3).
Figure 3.
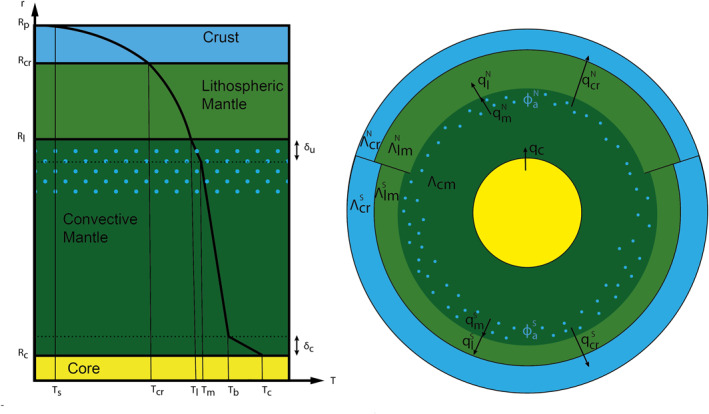
(Left): Parameterized model for one hemisphere with four different layers: the core, the convective mantle, the lithospheric mantle and the crust. A characteristic temperature profile is indicated in black line with the associated temperature at each interface. Blue dots represent melting and dotted lines the thermal boundary layer thicknesses (δ u , δ c ). (Right): bi‐hemispherical parameterized model with five different reservoirs characterized by different heat‐producing element enrichments and enrichment factors Λ: the northern and southern crusts , the northern and southern lithospheric mantles and the convective mantle (Λ cm ).
3.1. Thermal Modeling
3.1.1. Parameterized Convective Heat Flow
The viscosity of planetary mantle rocks is strongly temperature‐dependent and also varies with pressure. Because of the large temperature dependence of the viscosity, a rigid and stagnant lid develops at the top of the convective mantle, where heat is transported by conduction and which encompasses a large range of viscosity variations. We use an Arrhenius law to describe the temperature and pressure dependency of the viscosity:
| (10) |
where T is temperature, P pressure, η 0 is a reference viscosity at the reference temperature T 0 = 1,600 K and pressure P 0 = 3 GPa, R is the gas constant, A the activation energy and V the activation volume. The mantle viscosity may also depend on its water content and melt fraction. However, for simplicity, and as these effects would tend to reinforce the process we explore (see Section 5), we neglect them. The viscosity also depends on the deformation mechanism, which depends on the grain size that is poorly constrained and may vary depending on local conditions. Here, we use a classical activation energy value of 300 kJ mol−1, representative of diffusion creep in a dry peridotite (Karato & Wu, 1993), and V = 3 cm3 to minimize the pressure dependence of the viscosity. We then evaluate how these values affect our results (Section 4.2.2).
We follow the approach of Davaille and Jaupart (1993) and parameterize the heat flow out of the well‐mixed convective mantle as a function of a rheological temperature scale T ν :
| (11) |
where T m is the temperature at the top of the convective mantle and corresponds to the well‐mixed interior temperature. Below the rigid lid, the unstable boundary layer is characterized by a temperature contrast of (Davaille and Jaupart, 1993):
| (12) |
where T l is the temperature at the base of the lid (Figure 3), and a rh a dimensionless coefficient taken equal to 2.54 (Thiriet et al., 2019, Table 1). Following Grott and Breuer (2008) and Thiriet et al. (2018), the mantle is divided into a stagnant lid and a convective mantle characterized by a top and bottom thermal boundary layers which concentrate temperature variations (Figure 3). Because of internal heating and of the temperature and pressure dependence of the viscosity, these two thermal boundary layers are not symmetric and the upper one is considerably thicker. Their average thicknesses are well described by the boundary layer stability analysis as given by Turcotte and Schubert (2002):
| (13) |
where the superscripts u, c stand for the upper and bottom boundary layer respectively, Ra crit is the critical Rayleigh number, the convective height is given by d = R l − R c , with R l the radius at the lid base and R c the core radius (Figure 3). We use β c = 1/3 for the lower boundary layer and β u = 0.335 for the upper one (Thiriet et al., 2019). The Rayleigh number characteristic of the upper/lower boundary layer Ra u/c is given by:
| (14) |
where α is the thermal expansion coefficient, ρ m mantle density, κ m mantle diffusivity, g gravity, ΔT the temperature jump across the boundary layer, η the viscosity. For the lower boundary, we use ΔT c = |T b − T c | with T c the core‐mantle boundary (CMB) temperature and T b the temperature at the top of the lower boundary layer which can be larger than T c early in the planet history; the viscosity η c is estimated at the temperature (T b + T c )/2 and pressure P c characteristic of the CMB. For the upper boundary layer, we use ΔT u = T m − T l and the viscosity η u is estimated at the temperature T m and pressure at the lid base. Since the lid thickness, and hence the radius and pressure at the lid base, may be different in between both hemispheres, the thickness of the upper boundary layer and the Rayleigh number Ra u may also differ between North and South. As in Thiriet et al. (2019), we use a constant critical Rayleigh number for the upper boundary layer and the formulation of Deschamps and Sotin (2001) for the critical Rayleigh number of the lower boundary layer:
| (15) |
where the internal Rayleigh number Ra θ is given by with d θ = R p − R c , η θ estimated at the temperature T m and pressure at the average radius of the lid base and we use ΔT θ = (T m − T surf ) + (T c − T b ). If T c < T b , then we use ΔT θ = (T m − T surf ).
Table 1.
Parameter Values and Description for Our Reference Case
| Parameter | Description | Value | Unit | |
|---|---|---|---|---|
| R p | Planet radius | 3,390 | km | |
| R c | Core radius | 1,825 | km | |
| f | lowlands area fraction | 0.4 | ||
| ρ c | Core density | 6,200 | kg m−3 | |
| ρ p | Primordial mantle density | 3,472 | kg m−3 | |
| ρ cr | Crustal density | 2,900 | kg m−3 | |
| k cr | Crustal thermal conductivity | 3 | W m−1 K−1 | |
| k m | Mantle thermal conductivity | 4 | W m−1 K−1 | |
| C c | Core Heat capacity | 840 | J K−1 kg−1 | |
| C cr | Crust Heat capacity | 1,000 | J K−1 kg−1 | |
| C m | Mantle Heat capacity | 1,142 | J K−1 kg−1 | |
| α m | Thermal expansion coefficient | 2.5 × 10−5 | K−1 | |
| L | Latent Heat of crystallization | 5 × 105 | J kg−1 | |
| D i | Partition coefficient | 0.001–0.01 | ||
| P max | Maximum pressure for Δρ > 0 | 7.4 | GPa | |
| g u | Surface gravity | 3.7 | m s−2 | |
| g c | Core‐Mantle boundary gravity | 3.4 | m s−2 | |
| ϵ c | Ratio of the mean to upper core temperature | 1.1 | ||
| P 0 | Reference pressure | 3 | GPa | |
| T 0 | Reference temperature | 1,600 | K | |
| A | Activation energy | 300 | kJ mol−1 | |
| a rh | Rheological coefficient | 2.54 | ||
| R | Gas constant | 8.314462 | J mol−1 K−1 | |
| η 0 | Reference viscosity | 1020 to 1022 | Pa s | |
| V | Activation volume | 3 × 10−6 | m3 | |
| β u | Upper boundary layer exponent | 0.335 | ||
| β c | Lower boundary layer exponent | 1/3 | ||
|
|
Upper critical Rayleigh number | 450 | ||
| k 0 | Mantle reference permeability | 10−12 to 10−7 | m2 | |
| η l | Melt viscosity | 1 | Pa s | |
| ϕ c | Critical melt fraction | 0.02 | ||
|
|
initial lid thickness | 50 | km | |
|
|
initial crust thickness | 4 | km | |
| T s | Surface Temperature | 200 | K | |
|
|
Initial upper mantle temperature | 1,700 | K | |
|
|
Initial superheating of the core | 100 | K | |
|
|
Initial enrichment of the crust | 10 | ||
|
|
Initial S–N difference in lid thickness | −2 | km |
The parameterized heat flux from the convective mantle into the lid and from the core into the mantle are then respectively given by:
| (16) |
| (17) |
where k m is the mantle conductivity, and δ l , T c , T b , T m , and T l are the same for both hemispheres as the mantle and core are assumed to be well‐mixed, δ u,N/S is hemisphere‐dependent through its dependence on the viscosity at the top of the mantle (V ≠ 0) and on the convective height d N/S. Within the well‐mixed convective part of the mantle, the temperature profile is adiabatic; we use an isentropic formulation (Jaupart et al., 2015) to describe the radial dependence of the temperature and to relate the temperature at the top of the lower boundary T b to the temperature at the top of the well‐mixed convective mantle T m (Grott & Breuer, 2008; Thiriet et al., 2019):
| (18) |
3.1.2. Thermal Evolution
We follow Grott and Breuer (2008); Morschhauser et al. (2011) and Thiriet et al. (2018), and use the conservation of heat in the mantle and core to calculate the evolution of the temperatures at the top of the convective mantle T m and core T c accounting for heat fluxes at the interfaces, as well as, in the mantle case, radioactive heating, latent heat of melting and heat removal by melt extraction. We use a Stefan‐type equation to follow the growth of the lid thickness in each hemisphere from the difference between the convective heat flux and conductive one at the lid base. The temperature profile in each lid T(r,t)N/S is calculated from the time‐dependent heat equation in spherical geometry accounting for different heat sources (radioactive heating as well as sensible and latent heat due to melt intrusion). The details of these equations are given in Appendix A.
3.2. Mantle Melting and Crust Extraction
3.2.1. Mantle Melting
The mantle mineralogy is dominated by solid solutions of olivine and pyroxene with an additional aluminous phase and hence, melting of mantle rocks is temperature, pressure, and composition‐dependent. Here, we use the solidus of Ruedas and Breuer (2017) for a fertile K‐free peridotite that is based on the composition of Wänke and Dreibus (1994). As in Morschhauser et al. (2011) and Thiriet et al. (2018), we also consider the progressive increase in mantle solidus temperature caused by mantle depletion due to crust extraction through an additional term assumed to be linearly proportional to the crustal thickness D cr :
| (19) |
where P is the pressure in GPa (see Table 1 for parameter values). The Martian crust amounts to ∼5%–7% of the volume of the bulk silicate part of the planet (See Section 3.5), which corresponds to a solidus temperature increase of 40–50 K after crust extraction. No experiments have been conducted to determine the Martian liquidus, therefore we follow Breuer and Spohn (2006) and use the liquidus of Takahashi (1990) for a dry terrestrial peridotite: T liq(P) = 2,035 + 57.46P − 3.487P 2 + 0.0769P 3.
For simplicity, the melt fraction is usually considered to be a linear function of temperature over the melting interval, implying constant melt productivity at a given pressure (Morschhauser et al., 2011; Samuel et al., 2019). However, the melt productivity at constant pressure in peridotite has been shown to be highly variable between 0% and 20% melt fraction because it is affected by a phase exhaustion (Hirschmann et al., 1999; Robinson et al., 1998). Near‐solidus productivity is very small and it increases continuously with increasing melt fraction up to clinopyroxene exhaustion (Baker & Stolper, 1994), which occurs around 15%–20% melt in a fertile peridotite. After Cpx exhaustion, melt productivity drops to an almost constant value for melt fractions between ∼20%–30% (Hirschmann et al., 1999). Since we are interested in the mechanism of crust formation by melting and melt extraction from initially fertile material, with melt fraction spanning the range 0%–30%, it is important to account for non‐constant melt productivity.
We consider that clinopyroxene exhaustion occurs at the melt fraction ϕ t = 0.17. For ϕ ≥ ϕ t , the melt fraction is a linear function of temperature over the melting interval ϕ l (T, r) = (T(r) − T sol (r))/(T liq (r) − T sol (r)). Below ϕ t , the melt fraction is taken to vary non‐linearly with temperature and is computed from a degree‐six polynomial written as a function of ϕ l (T, r)/ϕ t . With such a parameterization, melt productivity is indeed low near the solidus but largely increases before clinopyroxene exhaustion to then drop to a constant value (Figure 4). Note that Katz et al. (2003) propose a parametrization of the mantle melt fraction that gives a similar evolution (Figure 4). In the end, the melt fraction is computed from:
| (20) |
where the different coefficients a i of the degree‐6 polynomial are obtained by matching the dry case of Hirschmann et al. (1999), Figure 8, and are given in the caption of Figure 4.
Figure 4.
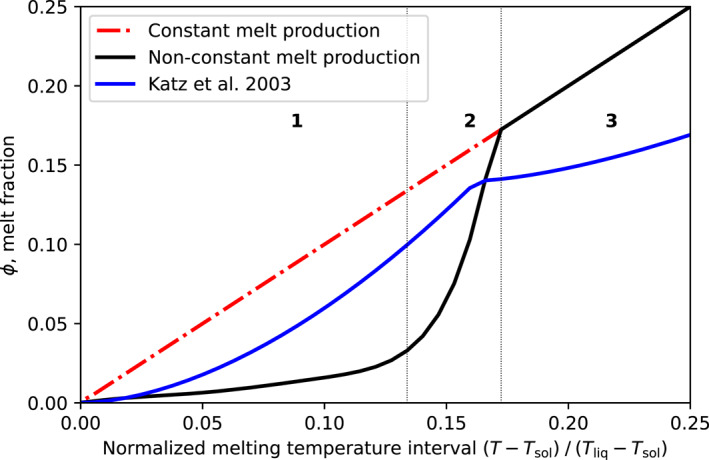
Melt fraction as a function of the temperature difference from the solidus for three different parametrizations: linear (dash‐dotted red line), and non‐linear, from Katz et al. (2003) in blue solid line, or adapted from Hirschmann et al. (1999) (Equation 20) in black solid line. The non‐constant melt production parametrization shows three different phases of melt production: (1) a low productivity near the solidus, (2) an increasingly high productivity below Cpx exhaustion at 17% melt fraction, and (3) a constant melt production after Cpx exhaustion. The coefficient a i of the polynomial are as follows: a 0 = 0, a 1 = 0.035, a 2 = −0.048, a 3 = −0.3305, a 4 = 1.9763, a 5 = −3.3423, a 6 = 1.8814.
Figure 8.
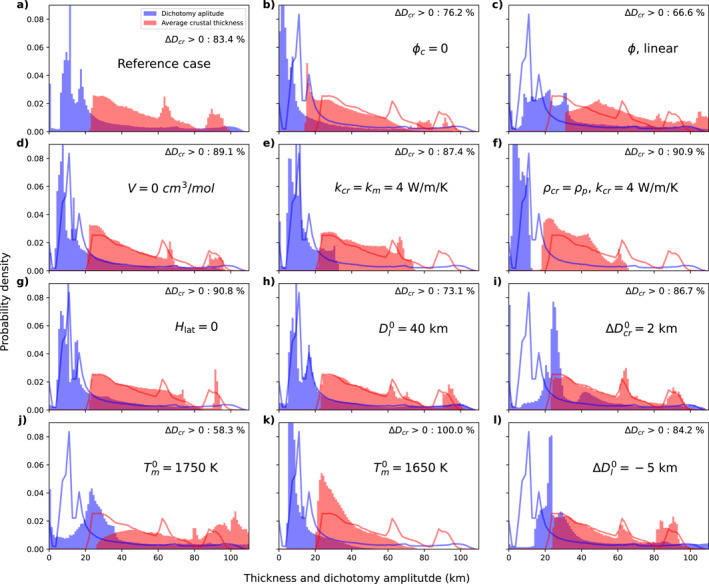
(a) Probability density distribution of the average crustal thickness (red histogram) and of the dichotomy amplitude (blue histogram) obtained for our reference case (Figures 6a–6c). We only consider cases for which the final southern crust is thicker than in the North (i.e., positive dichotomy ΔD cr > 0). The percentage of runs with a present‐day positive dichotomy amplitude is written at the top right of the plot (ΔD cr > 0 = 83.5% for the reference case). The other subplots are the same as (a) but for a change in the value of only one parameter while the curves are the histogram envelopes of the reference case. (b) ϕ c = 0: no critical melt fraction for melt extraction. (c) ϕ = ϕ l linear: constant melt production between solidus and liquidus. (d) V = 0: no pressure dependency for the viscosity. (e) k cr = k m = 4 W m−1 K−1: same thermal conductivity for the crust and the mantle. (f) ρ cr = ρ p , k cr = 4 W m−1 K−1: same density and same thermal conductivity for the crust and the mantle. (g) H lat = 0 in Equation A4: no heat released by magmatism in the crust (h) = 40 km: thinner initial lid (i) km and ΔD l = 0 initial perturbation in crust thickness instead of lid thickness. (j) K: warmer initial mantle temperature. (k) K: colder initial mantle temperature. (l) km, larger amplitude of the perturbation in lid thickness.
The average melt fraction ϕ a over the partially melted volume of the mantle V ϕ is:
| (21) |
However, extraction of the melt is only possible if the melt is interconnected, which occurs if the melt fraction is larger than a critical value ϕ c that is equal to a few percent (Miller et al., 2014) (Table 1). To account for this we define an “effective average melt fraction” (ϕ eff) which is the fraction of interconnected fluid over the partially melted volume of the mantle:
| (22) |
where Φ i (r) N/S = Φ(T,r) N/S if Φ(T,r) N/S ≥ ϕ c , else Φ i (T,r) N/S = 0.
3.2.2. Crust Extraction
Mantle melts are positively buoyant relative to the surrounding mantle rocks and rise through the convective and lithospheric mantle to reach the crust and increase its thickness:
| (23) |
where is the melt output velocity at the lid radius and is the radius where the liquid is injected into the crust. In contrast to Breuer and Spohn (2006), Morschhauser et al. (2011) and Samuel et al. (2019), we do not consider that melt is extracted from the mantle at a rate set by the vigor of convection but at a percolation velocity (Bercovici et al., 2001; McKenzie, 1985; Richter & McKenzie, 1984):
| (24) |
where k ϕ is the permeability of the host rock that is a function of the melt fraction ϕ, η liq the melt viscosity, Δρ = ρ m − ρ liq the density difference between the host rock and the melt. We account for melt compressibility and parameterize the melt density to evolve linearly with pressure in between the crust density at zero pressure and the mantle one at P max = 7.4 GPa (Suzuki & Ohtani, 2003):
| (25) |
which is equivalent to a coefficient of isothermal compressibility of ∼0.02 GPa−1, if Δρ becomes zero or negative, the extraction rate falls to zero.
The host rock permeability k ϕ evolves as (McKenzie, 1985; Richter & McKenzie, 1984):
| (26) |
where k 0 is a reference permeability which may vary over several orders of magnitude, typically between 10−12 and 10−7 m2 depending on the grain size (Miller et al., 2014).
However, the melt extraction rate is limited by the rate of melt supply, which depends on the convection velocity. We thus consider that the melt extraction rate cannot be larger than the characteristic convection velocity, given by the thermal boundary layer theory, times the effective melt fraction (Morschhauser et al., 2011; Samuel et al., 2019):
| (27) |
This limit is however only reached for the highest values of the reference permeability and at large melt fractions. For instance, using Ra = 108, the convection velocity is ∼7 × 10−9 m s−1. To get a similar extraction rate with a melt fraction of 10%, k 0 must be equal to 5 × 10−9 m2, which is large. Thus, in most cases, melt extraction occurs at the Darcy velocity Equation 24. This generally leads to smaller extraction rates compared to previous considerations; it implies that the remaining liquid is entrained by convection with the solid matrix and crystallizes at depth.
As in Morschhauser et al. (2011), we account for the heat flux due to melt extraction at temperature T m from the convective mantle:
| (28) |
with C cr the crust heat capacity. We neglect heat loss during melt ascent in the lid and redistribute the heat as a uniform heat source by volume over the whole crust volume equal to:
| (29) |
where the crust‐mantle boundary is at temperature T cr . Accounting for this heat source has a positive effect on our feedback mechanism since a higher amount of heat deposited in the crust implies a warmer temperature profile and hence a larger amount of melt at depth.
3.3. Heat Production, HPE Distribution and Mass Conservation
Because HPEs are lithophile and incompatible elements, their concentration differs among the different layers of the planet: while the crust, mainly formed by mantle melt extraction, is enriched in HPEs, their concentrations in the core is negligible. Here, we assume that the four major HPEs (40K, 232Th,235U, 238U) are characterized by the same solid‐liquid partition coefficient D i and hence each reservoir j is characterized by a single enrichment factor Λ j :
| (30) |
where [HPE] j is the element concentration in the reservoir j and [HPE]MBS the element concentration in the bulk silicate part of Mars, or primitive mantle (Figure 3). We use the geochemical model of Wänke and Dreibus (1994) for the present‐day HPEs concentration in the bulk silicate Mars.
During melting, HPEs partition in between the melt and residual rock according to their partition coefficient D i :
| (31) |
The convective mantle melt fraction varies only slowly with time, we assume chemical equilibrium; the melt enrichment factor is thus given by:
| (32) |
Melt and HPE extraction deplete the mantle that is assumed to be well‐mixed and homogeneous. However, this is not the case for the lithospheric mantle which is stagnant and grows during crust extraction as the mantle becomes progressively more depleted. We follow the bulk HPE enrichment of the five different reservoirs using mass balance. The mass variation dm in heat producing element in a reservoir j, given by dm = d (ρ j V j Λ j [HPE]MBS), is due to a mass flux from a reservoir k to a reservoir j , expressed as . Accounting for all possible fluxes , we obtain:
| (33a) |
| (33b) |
| (33c) |
where Λ cr is the northern or southern crustal enrichment, Λ lm is the northern or southern lithospheric mantle enrichment and Λ cm the convective mantle enrichment.
The volumetric heat production H j (t) in the reservoir j is given by the sum of the four contributions:
| (34) |
where J i , in W kg−1, is the power produced by the decay of 1 kg of an element i, λ i the decay constant of that element (Ruedas, 2017), ρ j the reservoir density and t is time (with t = 0 at present‐day and negative in the past).
Early in the thermal evolution, the crust extraction rate may be limited by the lid growth rate such that the lid is entirely made of crustal material. If the lid thickness (and hence potentially the crust thickness) decreases, HPEs from the lid and/or crust are recycled back into the mantle. A recent study by Batra and Foley (2021) shows however that a buoyant crust could resist entrainment by the convective mantle, which would then reduce the mantle heat flow and thicken the lid.
Finally, in order to ensure mass conservation of the bulk silicate part of Mars, the mantle density ρ m is taken to increase as the crustal volume V cr increases:
| (35) |
where M p = V p ρ p is the mass of primordial mantle.
3.4. Initial Parameters, Dimensionless Number and Numerical Calculation
3.4.1. Initial State
The initial state is described by a temperature at the top of the mantle , a CMB temperature , a lid thickness , a crustal thickness and associated crustal enrichment . Since our goal is to examine whether this model may be able to produce the dichotomy in crustal thickness, we start with the smallest possible value for the initial crustal thickness in light of our numerical constraints, which is set to km in both the North and South. This represents ∼10% of the minimum final northern crust thickness (Section 3.5). A thicker crust, formed after an initial phase during magma ocean solidification, might have been present initially (Wieczorek et al., 2022). However, the start of our model represents the late, mushy, stage of a magma ocean phase, when the rheological transition to solid‐like convection has been reached. The model thus accounts for the formation of a primary crust by extraction of melts from an enriched mushy mantle (Michaut & Neufeld, 2022). It does not account for the formation of a large initial plagioclase flotation crust as proposed for the Moon; but, given the higher gravity of Mars, this would be less likely. Because the initial crust is so thin, the initial crustal enrichment has a low impact on the subsequent thermal evolution and we use a classical value of , equivalent to 560 ppb of 232Th at present‐day (Knapmeyer‐Endrun et al., 2021; Thiriet et al., 2018).
We use values of and such that the mantle has just reached the rheological transition to solid‐like convection in the mantle, that is, such that the maximum mantle melt fraction Equation 20 is between 0.3 and 0.4 initially (Salvador et al., 2017). (Equation 21) is then less than ∼20%. Following Knapmeyer‐Endrun et al. (2021) and Drilleau et al. (2021), we explore the range 1,650–1,750 K for , and therefore the range 50 ± 10 km for . The core is considered to be superheated by due to core formation and associated dissipation in gravitational potential energy. The initial CMB temperature is thus given by .
We impose an initial small perturbation to the symmetrical base state to trigger the instability. In our reference case, this perturbation is an initial N/S difference in lid thickness of −2 km, (i.e., 4% of the mean lid thickness). We also explore smaller perturbations (down to 2% of the lid thickness) as well as the case of a perturbation in crustal thickness , which is equivalent to a perturbation in total HPE content in the lid (Section 4.2.1). The initial time is equal to −4.5 Gyr. All parameters of the reference case are given in Table 1.
3.4.2. Dimensionless Numbers and Critical Parameters of the Model
In the end, our system is controlled by two main dimensionless numbers. The Rayleigh number Ra determines the vigor of the convection and the cooling rate of the convecting mantle. Since it controls the thickness of the upper thermal boundary layer, Ra also strongly influences the melt fraction; it mostly depends on mantle rock viscosity, and hence on the reference viscosity value η 0. The second dimensionless number, noted Da corresponds to the ratio between a characteristic time for conduction and a characteristic time for crust extraction (τ w = R p η l /k 0Δρg):
| (36) |
The value of Da is mostly determined by that of the reference permeability k 0.
3.4.3. Numerical Resolution
Our physical model is solved numerically. The time‐dependent Equations A1, A3, A5, and 23 form a system of four first‐order differential equations solved using a Runge‐Kutta method of order 4. The diffusion equation in the lid (Equation A4) is solved using a finite volume method in spherical geometry and an implicit Euler scheme in time. Equations 33a–33c are solved explicitly at the end of each time step. We verify that secular cooling corresponds to the balance between surface cooling and heat production to ensure energy conservation and that bulk heat production is conserved as well.
3.5. Present‐Day Crustal Thickness of Mars From Topography and Gravity Data
The Bouguer gravity anomaly can be inverted to provide the relief along the crust‐mantle interface, and hence the crust thickness. These inversions depend upon the crustal density, upper mantle density profile and the local value of the crustal thickness at the InSight landing site (Wieczorek et al., 2022). Using receiver function methods on direct P‐waves of teleseismic events recorded by the InSight seismometer, Knapmeyer‐Endrun et al. (2021) determined two possible crustal structures below the landing site: either the crust is thin and made of 2 layers, or it is thicker and made of 3 layers. The 3‐layer, thicker, crustal model seems more consistent with thermal evolution models (Knapmeyer‐Endrun et al., 2021) as well as PP receiver function analyses (Kim et al., 2021). We thus compare our final crustal thicknesses in the North and South, as well as their differences with that obtained from the inversion of gravity and topography data that considers a thick crustal structure below the InSight landing site as well as the same density for the North and South. We use the dichotomy boundary of Andrews‐Hanna et al. (2008) to calculate the surface average crustal thickness in the North and South. The boundary effectively cuts the Tharsis province in half, with half of Tharsis being located in the northern lowlands, and the other half in the southern highlands. For the sake of consistency, we compare the results of our model with topogravimetric inversions that consider a similar crustal density (ρ cr = 2,900 kg m−3, Table 1). With these considerations, the average northern crustal thickness is between 39.8 and 54.5 km, the average southern crustal thickness is between 57.9 and 82.4 km, and the average amplitude of the N/S dichotomy ranges between 18.1 and 28.0 km. The average thickness of the crust is between 50.7 and 71.2 and corresponds to 5%–7% of the silicate volume.
4. Results
We first describe results corresponding to a reference set of calculations for parameter values (Table 1), varying only the reference permeability (k 0) and the reference viscosity (η 0). We then determine the effects of the other model parameters by comparing to our reference case.
4.1. Reference Simulations
4.1.1. Two Extreme Cases of Evolution
The final range of differences in crustal thickness between the Northern and Southern hemispheres obtained for our set of reference calculations is large, from no crustal dichotomy (dashed lines, Figure 5) to a difference of ∼80 km (solid lines, Figure 5). Generally, melt formation occurs in two phases which could potentially result in two phases of crust extraction depending on the amplitude of melting (Figure 5d). The initial phase of melting occurs within the first ∼100 Myr and mostly depends on the initial conditions and mantle viscosity, with smaller viscosities leading to thinner boundary layers and larger melt fractions. The peak of the second phase of melting occurs between ∼500 Myr and 1 Gyr after the start of the simulation and is due to the temperature increase in the convective mantle (Figure 5a) associated with the combined effect of the blanketing of the lid (Figure 5b), which grows in thickness, and radiogenic decay in the mantle. The amplitude of melting during this second phase mostly depends on model parameters and is not sensitive to initial conditions: it is enhanced if melts and HPEs are preserved in the convective mantle. If, during this second melting phase, the melt fraction exceeds the critical melt fraction, then a late, second phase of crustal extraction can occur, more frequently in regions of thick crusts, such as in the Southern hemisphere—see the increase in crustal growth rate, in the South only, at ∼300 Myr in the LargeDich case on Figure 5c that is associated with the increase in melt fraction in the South at the same time (Figure 5d).
Figure 5.
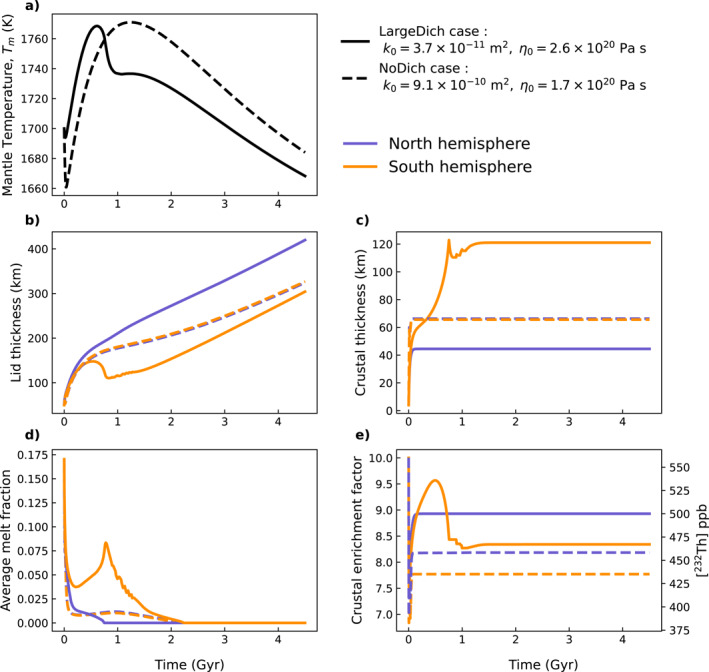
Thermal evolution over 4.5 Gyr for two different calculations. (a) Evolution of the mantle temperature T m , (b) evolution the lid thickness , (c) evolution of the crustal thickness , (d) evolution of the average melt fraction below each lid , (e) evolution of the crustal enrichment factor . Blue lines, evolution for the Northern hemisphere, orange lines, evolution for the Southern hemisphere. Dashed lines, NoDich case with η 0 = 1.6 × 1020 Pa s and k 0 = 9.1 × 10−10 m2, solid lines, LargeDich case: η 0 = 2.6 × 1020 Pa s and k 0 = 3.7 × 10−11 m2.
The case with no significant difference in crustal thickness (NoDich case) is obtained at rather low viscosity η 0 = 1.6 × 1020 Pa s and high permeability of k 0 = 9.1 × 10−10 m2. Initially, in both hemispheres, crust growth is limited by lid growth, resulting in the northern crust being thicker than the southern one because of the imposed initial difference in lid thickness . No second phase of crustal extraction occurs because the melt fraction remains below the critical melt fraction during the second melting phase which peaks at t ∼ 1 Gyr in this case (Figures 5c and 5d) and the difference in crustal thickness remains similar to the imposed initial difference in lid thickness (which is −2 km).
A large dichotomy occurs for a slightly higher viscosity (η 0 = 2.55 × 1020 Pa s) and lower permeability (k 0 = 3.7 × 10−11 m2) and is referred to as the LargeDich case (solid lines on Figure 5). For a higher reference viscosity, the upper thermal boundary is thicker and the initial melt fraction smaller, the lid also grows more quickly on average. This, together with the lower reference permeability, results in a smaller initial crustal extraction phase than in the NoDich case. The lid does not limit crustal growth during the first extraction phase, allowing the initial perturbation to grow. The higher initial melt fraction in the Southern hemisphere, caused by the initial perturbation, results in a larger initial crustal extraction there. The larger crustal growth in the South is then enhanced during the second melting phase associated with the rise in mantle temperature after ∼200 Myr; it implies a larger addition of heat from HPEs and melts which decreases the conductive heat flux at the lid base, compensating for the decrease in the convective heat flux and stopping lid growth in the South (Figure 5d at t ∼ 300 Myr). With continued melt extraction in the South, the crustal temperatures rise further, increasing the melt fraction at the lid base and finally inducing a thinning of the lid at t ∼ 500 Myr. Cooling of the planet by convection manifests in the North, with a large increase in lid thickness, and by an effective cooling of the mantle (Figures 5a and 5b). These two extreme cases do not match InSight constraints on crustal thickness (Section 3.5).
4.1.2. Systematic Exploration of the Effects of η 0, k 0
We now describe a systematic exploration of the effects of the main controlling parameters of our model η 0 and k 0 (Figure 6). Generally, a lower viscosity induces a thinner boundary layer, resulting in a higher melt fraction and crustal extraction rate and hence in a larger crustal thickness (Figures 6a and 6b). A lower reference viscosity η 0 also leads to a higher convective heat flux (Equation 16) which tends to induce colder present‐day mantle temperatures (Figure 6d).
Figure 6.
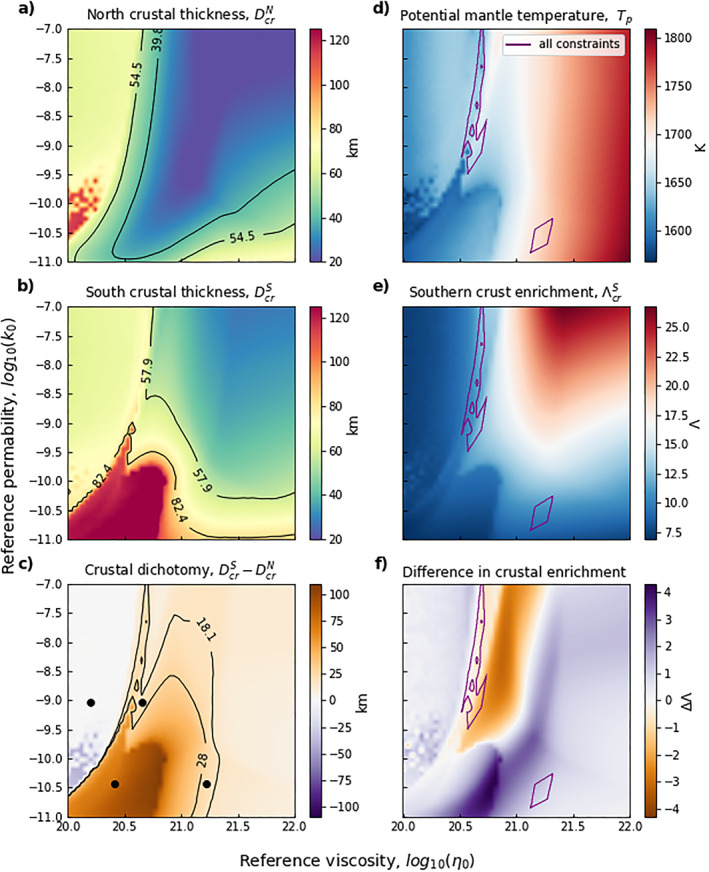
Systematic exploration of (k 0, η 0) for our reference set of parameters (Table 1), with η 0 between 1020 and 1022 Pa s and k 0 between 10−11 and 10−7 m2. (a) Final northern crust thickness, . (b) Final southern crust thickness . (c) Final amplitude of the crustal dichotomy . (d) Present‐day potential mantle temperature . (e) Present‐day bulk southern crust enrichment factor . (f) Present‐day difference in crustal enrichment . The black curves on the left panels delimit the parameter space where each InSight constraint on crust thickness is met (See Section 3.5) and the intersection of these three spaces, that is, the region where all three constraints are met, are represented by the purple curves on the right panels.
The crustal extraction rate increases with the reference permeability (Equation 26). But the largest crustal thicknesses are obtained for low reference permeability values (Figure 6, bottom left of a, b) because melt extraction is an efficient way to cool the convective mantle through the removal of HPEs and sensible heat (, Equation 28). Thus, lower values of k 0 tend to preserve heat and HPEs in the convective mantle, to induce higher mantle temperatures and prolong crustal extraction, resulting in thicker crusts.
For reference viscosity values <1020.6 Pa s (Figure 6c), the thin lid induced by the low reference viscosity initially limits crust growth in both hemispheres. Since we start with a thicker northern lid ( km), this even rapidly leads to a slightly thicker crust in the North as in the NoDich case (Figure 5 dashed‐lines). If the permeability value is sufficiently large (i.e., larger than about ≳10−10.5−10−9.5 m2 depending on η 0), the initially large extraction rates of melts, and associated HPEs and sensible heat, from the convective mantle, strongly limits the duration of crust formation to the very early times, preventing the growth of a dichotomy in crustal thickness as in the NoDich case. However, if the reference permeability is low (k 0 < 10−9.5–10−10 m2), mantle melts and HPEs are retained in the mantle, prolonging mantle cooling. In that case, the retroactive feedback mechanism applies but inversely, the northern crust is thicker, which leads to a reverse dichotomy (the northern crust is thicker than the southern one, Figure 6c).
A larger reference viscosity value leads to a thicker lid and to a lower mantle melt fraction due to the pressure dependence of the solidus. This tends to generate more enriched melts and hence a larger crustal enrichment factor (Figure 6e, for 1020.5 < η 0 < 1021.3 Pa s), in particular for large reference permeability values that strongly limit the duration of crust construction. However, large reference viscosity values also lead to smaller convective heat fluxes, prolonged mantle cooling, higher mantle temperatures and larger melt fractions. This explains the opposite behavior for reference viscosities larger than η 0 > 1021.5 Pa s where the crustal enrichment factor then tends to decrease with increasing value of η 0.
4.1.3. Range of η 0, k 0 Matching InSight Constraints on Crustal Thickness
Two different ranges of values for (k 0, η 0) allow to match all three constraints on crustal thickness: average North and South crustal thicknesses as well as dichotomy amplitude (Section 3.5), each shown as black contours on the left panels of Figure 6. These two ranges (intersection of all black contours) are shown as purple contours on the right panels of Figure 6.
The first region is at rather low viscosity (η 0 ∼ 1020.5 Pa s) and large permeability k 0 > 10−9.5 m2. The simulation EarlyDich (solid lines in Figure 7) well illustrates the type of thermal evolution obtained for these ranges of values. The relatively high permeability induces an early and rapid (<100 Myr) extraction of the crust (Figure 7c) during the initial phase of rapid lid growth (Figure 7b). The early extraction of melt and HPEs causes rapid cooling of the convective mantle (Figure 7a) which induces a rapid decrease in mantle melt fraction, stopping crustal extraction in the North where the crust is thinner and the lid thicker. In the South, the melt fraction becomes significantly larger than in the North very early (because of the positive feedback mechanism and the early crustal extraction); this induces a larger and longer crustal extraction, generating a significant crustal dichotomy very early in Mars' evolution (in less than 100 Myr). The second phase of melting is large enough in the South for the second phase of crustal extraction to occur, which amplifies the crustal dichotomy. This second phase of extraction only occurs for permeability values that are low enough to retain sufficient HPEs in the mantle, that is, k 0 ≲ 10−8.5 m2. In some rare cases, this second phase of extraction occurs in both hemispheres, but it is always more important in the South where the crust is thicker. The rather low viscosity leads to a relatively cold potential temperature at the present‐day (T p ∼ 1675 K, Figure 6d).
Figure 7.
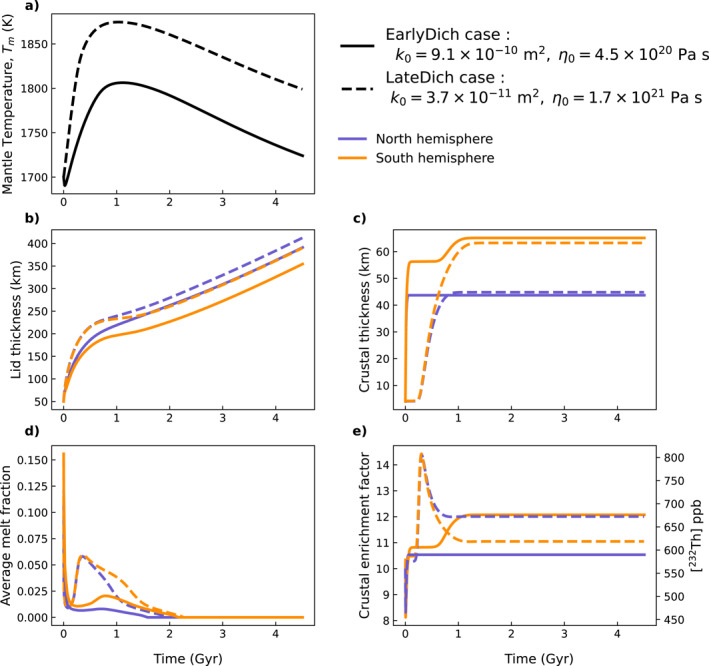
Two types of thermal evolution for Mars matching InSight constraints on crust thickness: Evolution of (a) mantle temperature (b) lid thickness, (c) crustal thickness, (d) average melt fraction and (e) crustal enrichment factor in the North (blue lines) and in the South (orange lines) as a function of time. The evolution in solid lines is for a rather high permeability k 0 = 9.1 × 10−10 m2 and low viscosity η 0 = 4.5 × 1020 Pa s and is associated with an early extraction of the crust (EarlyDich case). The evolution in dashed‐lines is for a lower permeability k 0 = 3.7 × 10−11 m2 and a higher viscosity η 0 = 1.7 × 1021 Pa s and is associated with a late extraction of the crust (LateDich case).
The second region of parameters (k 0, η 0) that allows to match crustal thickness constraints is for a lower permeability of ∼10−10.6 m2 and higher viscosity of 1021.2 Pa s (see case LateDich, dashed lines on Figure 7); it results in a higher present‐day potential temperature (T p ∼ 1750 K Figure 6d). Because of the large viscosity value, the initial melt fraction is low, and the low permeability does not allow for a significant early crustal extraction during the initial phase of rapid lid growth (Figures 7b and 7c); HPEs are thus preserved in the mantle and, together with the smaller convective heat flux caused by the higher viscosity, leading to a significant increase in melt fraction during the heating phase despite the thicker lid (Figure 7d). The melt fraction reaches values larger than ϕ c in both hemispheres, allowing crustal extraction, although at a relatively low rate. This results in a late and prolonged extraction of the crust that occurs over ∼700 Myr, from ∼300 Myr to 1 Gyr (Figure 7c). Here again, the mantle melt fraction remains larger in the South because of the smaller lid growth rate, which results in a significantly larger crust in the Southern hemisphere.
In both cases, the crust is extracted within the first billion years of Mars' evolution, but a significant melt fraction is preserved in the mantle over ∼2 Gyr, that is, up to 1 billion years after crust formation (Figure 7c). The final crustal enrichment is also similar in both cases: between 12 and 15, and corresponds to Thorium concentration in the crust of 672–840 ppb. North/South differences in crustal enrichment factors exist but remain small for both types of solutions (±2, Figure 7e) and have different origins. In the case of an early extraction of the crust (EarlyDich), both crusts become progressively more enriched in HPEs as the melt fraction decreases during extraction (Figures 7c and 7d). The South is then more enriched by Λ S − Λ N = 1.6 which corresponds to a difference in Thorium concentration of 90 ppb, because of its prolonged extraction. In the LateDich case, the South is characterized by higher melt fractions, less concentrated in HPEs (Figures 7d and 7e), which results in the northern crust being slightly more enriched in HPEs (by 60 ppb of Thorium).
4.2. Exploration of the Effects of Other Model Parameters
To well understand the effects of the different parameters on crust and dichotomy formation as well as on the location of the regions matching our crustal constraints in the parameter space (k 0, η 0), we perform a series of calculations centered on our reference case with (k 0, η 0) varying in the same range but changing the value of another single parameter at a time within a given range.
4.2.1. Effects of Different Model Parameters on Crustal Formation
We first characterize the probability density distribution of the average crustal thickness and of the dichotomy amplitude ΔD cr in our reference case (Figure 8a), for the same range of values (k 0, η 0) as for Figure 6. For this reference case (Figure 8a), the dichotomy amplitude is mostly distributed around low values with a peak at ∼12 km. Thinner average crustal thicknesses are more frequent, although two small peaks exist in the distribution around ∼64 and ∼90 km. These two peaks correspond respectively to the NoDich and LargeDich case, the latter giving a very thick southern crust, km.
The absence of a critical melt fraction for melt extraction (i.e., ϕ c = 0, Figure 8b) has a non‐intuitive effect: although the melt volume available for extraction is higher, simulations tend to result in a thinner crust than in the reference case because the absence of critical melt fraction allows the extraction of melts highly enriched in HPEs at low melt fraction. The convective mantle becomes more depleted in these elements, which reduces melting and leads to thinner crusts and smaller dichotomy amplitudes. The classical way to calculate the melt fraction with constant melt productivity, that is, a linear evolution between the solidus and the liquidus (Equation 19), generates higher melt fractions than in our reference case; inducing larger crustal growth rates, crustal thicknesses and dichotomy amplitudes (Figure 8c).
To ensure that the feedback mechanism we propose for the growth of the dichotomy is indeed linked to the enrichment of the crust in HPEs, we perform a series of calculations where we remove different effects that strengthen this feedback. This is the case for the pressure‐dependency of the viscosity which amplifies our positive feedback mechanism by two cumulative effects: (a) a thicker lid grows faster because the convective heat flow at its base (q cm , Equation 16) is reduced (Equation A5) and (b) a thicker boundary layer induces a lower melt fraction. Without this pressure effect (V = 0, Figure 8d), we obtain slightly smaller dichotomy amplitudes, as expected.
A lower thermal conductivity for the crust relative to the mantle also strengthens our feedback mechanism by inducing, in the same way as the crustal enrichment in HPEs, a higher temperature profile for a thicker crust. By imposing the same thermal conductivity for the crust and the mantle (i.e., k cr = k m = 4 W m−1 K−1) the dichotomy amplitude is slightly reduced. The average crustal thickness is also reduced because we chose a larger value for the crust conductivity, favoring planet cooling and reducing melting (D cr ≲ 75 km, Figure 8e).
Another favorable effect is the thickening of the crust itself which reduces the pressure below the crust because of the lower density of the crust compared to the mantle. This also induces a higher melt fraction below a thicker crust. Keeping the same value of the thermal conductivity (as in Figure 8e) and of the density (ρ cr = ρ m = ρ p ) for the crust and mantle, we obtain a significantly lower average crust thickness (D cr ≲ 65 km). This is not only due to the higher pressure and larger surface heat flow (larger k cr ) but also to the higher extraction of energy and HPEs in the melt that both depend on crustal density (Equations (1), (29), (30), (31), (32)). However, although smaller in amplitude, a significant dichotomy is still present (2 ≲ ΔD cr ≲ 15 km, Figure 8f).
The last effect that favors our feedback mechanism is the heating of the crust by magmatism which is more important where the crust thickens more rapidly. Canceling the heating (H lat = 0 in Equation A4, Figure 8g) leads to slightly smaller dichotomy amplitudes and limits the number of cases with very thick crusts.
We also explore the sensitivity of our results to the initial conditions. A warmer initial mantle temperature favors extreme cases of evolution similar to the NoDich and LargeDich cases because of the higher melt fractions (Figure 8j). Inversely, a colder mantle temperature gives less melting, thinner crusts, and smaller dichotomy amplitudes (Figure 8k). The variation of the initial core temperature plays in the same way as the initial mantle temperature, although its effect is less important. A lower initial lid thickness induces a larger initial amount of melt and hence thicker crusts (Figure 8h).
Finally, we investigate the amplitude and the nature of the initial imposed hemispherical perturbation. Imposing an initial difference in crustal thickness ( km, Figure 8i) instead of a difference in lid thickness induces a larger average dichotomy amplitude. As expected, a larger initial perturbation in lid thickness ( km, instead of 2 km, Figure 8l) also generates larger dichotomy amplitudes than for the reference case; however, it is still smaller than in the case of an initial crustal thickness perturbation. It is interesting to note that changing the amplitude of the initial perturbation in lid or crustal thickness has a negligible effect on the distribution of the average crust thickness (Figure 8l).
4.2.2. Effects of Different Model Parameters on the Range of k 0, η 0 Matching Our Constraints
The range of (η 0, k 0) that matches InSight constraints on crustal thickness (purple contours on the right panels of Figure 6) depends on the value of all other model parameters. Here we investigate how these ranges shift in the space (k 0, η 0) following the modification of the value of a single parameter (Figure 9). In most cases, both regions (at either high permeability, low viscosity or at low permeability, high viscosity) are present and their associated thermal histories remain similar to the EarlyDich and LateDich cases (Figure 7).
Figure 9.
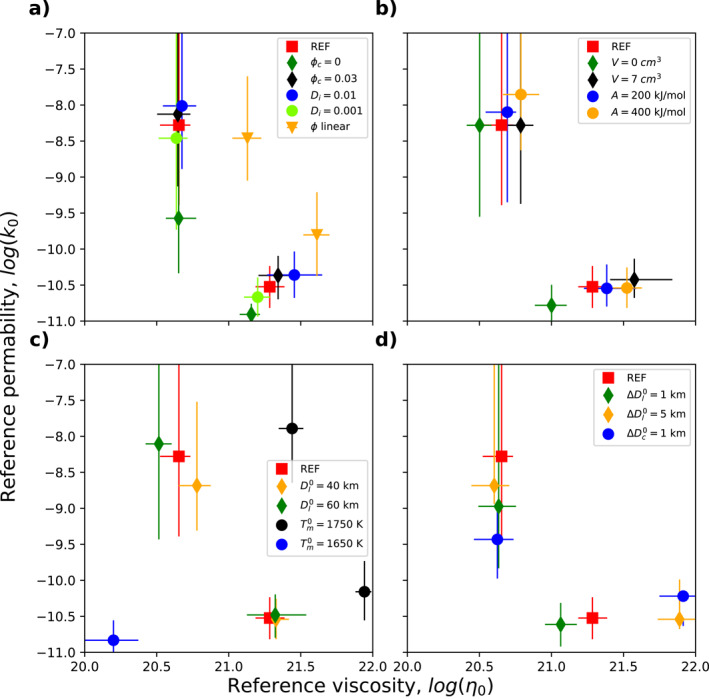
Average position of the region of parameters matching InSight constraints on crustal thickness in the parameter space (k 0, η 0) for different values of the model parameters around our reference case noted “REF” (red square). The value of the parameter that is being changed is indicated in the legend. The ranges are represented by a point, noting the average position, associated with horizontal and vertical bars indicating the minimum and maximum values of the reference viscosity η 0 and permeability k 0 allowing us to match our constraints. (a) Effect of the critical melt fraction ϕ c = 0 (green diamond) and 0.03 (black diamond); effect of the partition coefficient D i = 0.01 (blue circle) and 0.001 (light green circle); effect of considering a constant melt productivity: ϕ linear (yellow triangle). (b) Effect of the activation volume V = 0 cm3 (green diamond) and 7 cm3 (black diamond); Effect of the activation energy A = 200 kJ mol−1 (blue circle) and 400 kJ mol−1 (yellow circle) (c) Effect of the initial lid thickness = 40 km (yellow diamond) and 60 km (green diamond); effect of the initial mantle temperature = 1650 K (black circle) and 1750 K (blue circle). (d) Effect of the initial perturbation in lid thickness = −1 km (green diamond) and −5 km (yellow diamond); effect of an initial perturbation in crust thickness = 1 km (blue circle).
The critical melt fraction ϕ c and the partition coefficient D i do not have a significant effect on the location of the region at low viscosity because the extraction occurs at high melt fractions and far from values of ϕ c (0–0.03) (Figure 9a). However, the permeability must be significantly reduced if ϕ c = 0 for HPEs to be preserved in the mantle to obtain thick enough crusts (Figure 8b). The range at higher viscosity is shifted toward lower viscosity and permeability values as ϕ c and D i are reduced and inversely. For this range, melt extraction occurs at low average melt fractions and the melts are more enriched in HPEs. Hence, as ϕ c and D i are reduced, the range of viscosity and permeability decreases to generate a larger melt fraction and slower extraction rate to preserve HPEs in the mantle and obtain thick enough crusts.
Using a constant melt productivity (i.e., a linear melt fraction ϕ l ) results in higher melt fractions and extraction rates. To mitigate this effect and match InSight constraints, the viscosity range is thus shifted to higher values to generate less melting (Figure 9a).
Crustal extraction occurs at pressures lower than the reference pressure (P 0 = 3 GPa). For pressure ranges characteristic of the top of the convective mantle, where crust extraction occurs, the viscosity is larger if V is larger (Equation 10). Hence, to alleviate this effect, the reference viscosity must be decreased as V increases and inversely (Figure 9b). The effect of the activation energy A is not straightforward as it plays not only on the absolute viscosity value but also on the thickness of the lid through its effect on the basal lid temperature (Equation 12). Larger activation energy results in larger viscosity and hence lower melt fractions, but it also leads to larger T l values and hence thicker and hotter lids, promoting melting at depth. However, the effect of A, when varied within ±100 kJ mol−1 is quite limited (Figure 9b).
A colder initial mantle temperature generates less melt and hence thinner crusts. Within the same range of values for , a single range of parameters matches InSight constraints and is shifted to lower viscosity and permeability values (Figure 9c), toward the region where parameter values favor thicker crusts (see LargeDich case). Inversely, a warmer mantle induces more melt and requires larger viscosity values to form thinner crusts. A change in the initial lid thickness (, Figure 9c) affects only the range at rather low viscosity where the crust and dichotomy form early (case EarlyDich) because it only modifies the initial melt fraction and therefore only plays in the initial phase of crustal extraction.
Varying the initial perturbation in lid thickness does not have much effect on the region at low viscosity (Figure 9d). For the high‐viscosity region, if the perturbation is larger, the viscosity must be increased not to generate a too‐large dichotomy (Figure 6c). The effect of an initial difference of 1 km in crustal thickness is similar to that of a −5 km difference in lid thickness (Figures 8l and 9d) because the perturbation in crustal thickness has a greater impact on dichotomy growth.
5. Discussion
5.1. Positive Feedback Mechanism
The positive feedback between crustal thickness and crustal growth allows forming a significant difference in crustal thickness between the Northern and Southern hemispheres of Mars for a large set of parameters (Figure 6c). This mechanism mainly results from the crustal enrichment in heat sources, which generates higher temperatures and hence more melting where the crust is thicker. The lower thermal conductivity of the crust relative to the mantle and the heat associated with magma intrusions also lead to higher temperatures in regions with thicker crust and help this mechanism (Figure 8). Finally, the pressure dependence of the mantle viscosity creates a positive feedback between the stagnant lid thickness and lid growth through its effect on the convective mantle heat flow, strengthening the mechanism we propose (Figure 8d). Accounting for a dependence of the viscosity on the melt fraction would also play in the same way as the pressure dependence, enhancing this mechanism. Thus, this mechanism should apply not only on Mars but also possibly on other one‐plate planets and should significantly promote crust growth wherever the crust is thicker early in the history of the planet. Through this mechanism, the dichotomy grows within ∼100 Myr to 1.1 Gyr depending on the scenario and initial thermal state of Mars (case EarlyDich vs. LateDich).
5.2. Origin of the Degree‐One Structure
Our linear stability analysis on a simplified setup shows that any thermal perturbation should grow with time and that the longest wavelengths (in particular the degree‐one hemispheric perturbation) will be favored (Section 2). With our numerical calculations, we have shown that the growth of an initially negligible perturbation can be significant even though planetary cooling ultimately stabilizes our feedback mechanism and limits its growth. Lateral variations in temperature and chemical heterogeneities caused by accretion or mantle convection certainly exist early in the history of the planet and can provide initial perturbations of random wavelengths. The fact that the degree‐one perturbation has the largest growth rate (Figure 2) suggests that it could grow the fastest and give rise to the observed dichotomy in crustal thickness through the positive feedback we describe. Therefore, this mechanism alone may explain the difference in crustal thickness between the northern lowlands and southern highlands of Mars.
Convection in a stagnant lid regime typically generates convection patterns and thermal perturbations of shorter wavelengths. Given that the dispersion curve of Figure 2 is rather flat at long wavelengths, it is not totally clear whether mantle convection could impose its pattern and the growth of shorter wavelengths than the degree‐one. Convection simulations in 2‐3D considering two‐phase melt extraction would be necessary to understand its effect on wavelength selection. Lateral melt transport in the lithosphere depends on its stress state (Michaut et al., 2020) and would then constitute another complicating factor.
On another hand, this mechanism might also significantly amplify any other mechanism that could independently generate large wavelength variations in lid or crustal thickness early in Mars history. Several studies have suggested that the dichotomy might originate from a degree‐one mantle convection mode. Zhong and Zuber (2001); Roberts and Zhong (2006) have for instance shown that a degree‐one convection could develop because of viscosity stratification in the Martian mantle. An upper low‐viscosity layer could result from a partially molten layer of several hundreds of km thick with an average melt fraction of ∼0.15 (Mei et al., 2002), which seems possible for early Mars in the frame of our thermal evolution model. The interaction and chemical exchange between a liquid magma ocean and the dense cumulates during magma ocean solidification could also trigger a degree‐one convection mode in the cumulates (Morison et al., 2019). If such a degree‐one indeed occurred during the late phase of magma ocean solidification, it could generate a degree‐one perturbation in temperature and hence in lid thickness that could trigger the feedback mechanism we describe for the formation of the crustal dichotomy.
The most popular explanation for the Martian dichotomy is currently that of a large impact at ∼4.5 Gyr in the northern hemisphere (Marinova et al., 2008). Such a large impact would create a large difference in crustal thickness which would also trigger the mechanism we propose. Since this impact would have occurred at a time when significant melting occurs at depth, it is likely that the feedback mechanism would be strong and lead to very large differences in crustal thickness, potentially too large to match InSight constraints. Indeed, simulations show that initial differences in crustal thickness must be less than a few kilometers in order to fit observations (Figure 9).
5.3. Crust Enrichment in HPE
Our model predicts a crust enrichment factor (Λ cr ) between 10 and 15 depending on the parameters and a possible North/South enrichment difference of ±2. This enrichment corresponds to a crustal Thorium concentration of ≃560–840 ppb and a hemispheric difference of ≃112 ppb. In the case of a rapid crust extraction (EarlyDich), the bulk southern crust is more enriched than the North, and it is the opposite if crustal extraction is longer (case LateDich). The bulk Thorium concentration derived from GRS data is 620 ppb (Taylor et al., 2006) which is consistent with the crustal concentration predicted by our model (Figure 7e). Spatial variations of the Thorium concentration as deduced from GRS data tend to point to a Northern hemisphere slightly more enriched in HPEs than the South, which would be more consistent with our LateDich scenario. However, GRS data may not be representative of the bulk Martian crust and observed spatial variations in Thorium concentration at the surface might as well be linked to surface weathering.
5.4. Melt Extraction and Formation of a Crust of Limited Thickness
Although the Martian crust probably shows a significant difference in crustal thickness in between the North and South, InSight constraints (Wieczorek et al., 2022) suggest that its average bulk crustal thickness is not as large as suggested by some previous studies. Forming a limited amount of crust was rather challenging in previous thermal evolution studies (Drilleau et al., 2021; Knapmeyer‐Endrun et al., 2021; Morschhauser et al., 2011; Samuel et al., 2019). In these studies, in order to limit melting, a significant amount of HPEs had to be extracted from the mantle, pointing toward highly enriched crusts (Λ cr > 15). However, previous studies considered a constant melt production (See Section 3.2.1) and a melt extraction rate parameterized from the convective velocity (Morschhauser et al., 2011; Samuel et al., 2019). Compared to our model, where the melt production is a non‐constant function of temperature below ∼17% melt and where melt extraction mainly occurs at the Darcy velocity (Equation 24), the model of Morschhauser et al. (2011) leads to higher crustal extraction rates and hence thicker crusts for a given viscosity and initial thermal state. Samuel et al. (2019) use the same model as Morschhauser et al. (2011) but with a mantle viscosity decreasing with increasing melt fractions. At a given thermal state and reference viscosity, a higher Rayleigh number is thus obtained, leading to a thinner boundary layer and lid thickness and hence to higher melt fractions and crustal extraction rates. As a result, in order to produce an average crustal thickness of ∼40–70 km, Samuel et al. (2019) point toward higher viscosity values (of order 1022–1023 Pa s) and Morschhauser et al. (2011) to colder initial thermal state ( K) than in our study.
5.5. Crust Construction and Volcanism on Mars
Our two different scenarios allowing to match InSight constraints (LateDich and EarlyDich) point toward different histories of crust construction (Figures 7c and 7d). The LateDich scenario predicts a late and single‐long extraction of melt at a low melt fraction that would therefore be rather uniform chemically. On the contrary, the EarlyDich scenario predicts two different phases of extraction, the first one at a high melt fraction and extraction rate in the early Noachian (<100 Myr) followed by a second one generating a peak in volcanism and crust thickening that would occur at a low melt fraction in the Hesperian (∼3.7 Gyr, Figure 7).
Orbital spectroscopy in the different volcanic provinces suggests a difference in composition, in terms of low‐Calcium and high‐Calcium pyroxene (LCP vs. HCP) content, in between the early Noachian terrains and Hesperian ones (Baratoux et al., 2013). In particular, Noachian terrains show high LCP over HCP ratios (Baratoux et al., 2013; Sautter & Payre, 2021) suggesting partial melt fractions close to pyroxene exhaustion (which occurs at ∼17%, Section 3.2.1). This early volcanism may have taken place during the final, mushy, stage of magma ocean solidification, after the rheological transition to solid‐like convection, where the magma evolves chemically and its buoyancy increases; it would correspond to the extraction of a primary crust from a primitive mantle. On the contrary, the LateDich case does not allow for high melt fractions and early extraction of the crust favorable to LCP‐rich rocks.
A change in the sedimentary record from clay‐dominated sedimentary rocks to sulfate‐dominated rocks is observed at the Hesperian, requiring a large and rapid input of sulfur into the Martian atmosphere (Bibring et al., 2006) which could be explained by a peak in volcanism that is only predicted in the EarlyDich scenario. Hesperian terrains show lower LCP over HCP ratios (Poulet et al., 2009), pointing to lower melting degrees, as expected during the second melt extraction phase in the EarlyDich case. The increase in dichotomy amplitude expected at this peak may also explain the Hesperian tectonic structures present around the dichotomy boundary (McGill & Dimitriou, 1990).
Finally, we note that in all our simulations matching InSight crustal constraints, the most recent phase of melt extraction occurs in the Southern hemisphere where the crust is thicker (Figures 7c and 7d) while observations show that the Northern hemisphere has been resurfaced more recently than the South. None of the other proposed mechanisms for the dichotomy neither explains the relatively young age of the northern hemisphere. Resurfacing of the northern lowlands is in fact not only volcanic in origin as it also comes from the erosion of the highlands and subsequent deposition. The geological map of Tanaka et al. (2014) shows that the lowlands are divided into various units of three different origins: (a) a recent glacial or periglacial origin close to the North Polar Cap, (b) a fluvial, lacustrine or marine origin that could be explained by a circumpolar ocean at the end of the Hesperian, a controversial hypothesis supported by Schmidt et al. (2022), (c) a volcanic origin concentrated around the Elysium and Tharsis formations. These volcanic eruptions are characterized by low LCP over HCP ratios, that is, originate from rather low melting degrees (Farrand et al., 2011; Mangold et al., 2010), and were probably caused by decompression melting in large mantle plumes such as the one giving rise to Tharsis and Elysium. This volcanism cannot be predicted by our simple parameterized model.
5.6. Insight Results on Mantle Structure
Travel‐time inversions for different seismic phases associated with teleseismic events recorded by SEIS on Mars suggest that the thickness of the upper thermal boundary layer (i.e., lid plus mobile thermal boundary layer) is between 400 and 600 km and also predict a rather cold present‐day mantle potential temperature of 1,600–1,700 K (Khan et al., 2021; Stähler et al., 2021). This range of thicknesses is in good agreement with our results: the value of D l + δ u reaches for instance 552 km in the EarlyDich case, where δ u = 133 km at the present‐day, but they do not constrain our thermal evolution any more than the crustal constraints. The rather cold potential temperature is in line with the EarlyDich case (Figure 6d). Drilleau et al. (2022) also used an inversion of the arrival time data with geodynamic constraints and found similar lid thicknesses but with a somewhat warmer potential mantle temperature of 1,830 ± 60 K which is in better agreement with the LateDich scenario. However, the compositional model of Drilleau et al. (2022) is less enriched in HPEs than the one we consider in this study which favors higher initial and hence final temperatures. The detection of the postolivine phase transition at depth provides additional constraints on the thermal state and chemistry of the Martian mantle which also points to a rather cold mantle at the present‐day with T p = 1,605 ± 100 K (Huang et al., 2022). But uncertainties on these values do not allow to further constrain our thermal evolution scenario.
5.7. Interpretation of Bouguer Anomalies in Terms of Crustal Thickness
As the thermal profile in the lithosphere is warmer in the Southern hemisphere, the mantle density should be slightly lower than in the colder Northern hemisphere which should lead to a negative Bouguer gravity anomaly in the South that is not accounted for in topogravimetric inversions. This negative mass anomaly due to the hotter temperature profile in the southern lid leads to an increase in the apparent crustal thickness deduced from these inversions. We estimate the equivalent additional crustal thickness Δh cr by equating the mass anomaly it generates to that due to the hotter temperature profile in the South:
| (37) |
where we use in order to estimate only the effect of the North/South temperature difference in the lid and to avoid any effects due to the convective mantle. Using α = 2 × 10−5 K−1, we obtain Δh cr ∼ 2.24 km in the EarlyDich case. This value is small, although not necessarily negligible, and corresponds to ∼10%–15% of the dichotomy amplitude.
6. Summary
The positive feedback mechanism between crustal growth and mantle melting that we propose, where a thicker crust grows faster, is able to produce the observed dichotomy in crustal thickness between the northern lowlands and southern highlands on Mars without a giant impact or persistent degree‐one mantle convection mode. This mechanism is favored by the higher enrichment of the crust in heat sources compared to the mantle, the lower thermal conductivity of the crust, magma intrusions in the crust, as well as by the pressure‐dependence of the mantle viscosity. Our parameterized, bi‐hemispherical thermal evolution model of Mars includes new features such as a Darcy velocity for mantle melt extraction, non‐constant melt production at low melt fractions and evolving enrichments in HPEs in the crust, lithospheric mantle and convective mantle. Our study points to two different types of thermal evolution that allow fitting InSight constraints on crustal thickness: an early and fast crustal extraction followed by a late phase of crustal extraction in the South or a late and progressive crustal extraction and dichotomy formation. The early scenario appears to fit several observations and constraints, including a widespread peak in volcanism together with a change in the crust composition at the Hesperian and a rather cold mantle potential temperature today.
Acknowledgments
The authors thank Shijie Zhong and Bradford Foley for their helpful comments on the manuscript. The authors acknowledge the French Space Agency CNES and ANR (MAGIS ANR‐19‐CE31‐0008‐08) for funding the InSight Science analysis. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 101001689). CM acknowledges support from the Institut Universitaire de France. PL acknowledges support from IdEx Université Paris Cité (ANR‐18‐IDEX‐0001). This is InSight contribution 305.
Appendix A. Thermal Evolution
As in Grott and Breuer (2008) and Morschhauser et al. (2011), heat conservation in the convective mantle provides an equation for the evolution of the temperature at the top of the convecting mantle T m :
| (A1) |
where ρ m is the mantle density, V cm is the convective mantle volume, ϵ m the ratio between , the mean temperature of the convective mantle, computed at each iteration, and T m , C m the mantle heat capacity, is the convective heat flux in each hemisphere (Section 3.1, Equation 16), the heat flux out of the mantle due to crust extraction (Section 3.2.2, Equation 24), q c the CMB heat flux (Section 3.1, Equation 17), H cm heat production in the convective mantle (See Section 3.3, Equation 34). is the area of the interface between the lid and the convective mantle in each hemisphere and A c is the surface of the CMB as described by Equation A6d. As in Breuer and Spohn (2006), the time‐dependent Stefan number St is defined as the ratio between latent heat released by melting and the sensible heat lost by the convective mantle:
| (A2) |
where is the average melt production over the volume of the convective mantle and V ϕ is the volume of mantle rocks that is above the solidus temperature.
Similarly, heat conservation in the core gives:
| (A3) |
with ρ c the core density, C c the core heat capacity, V c the core volume, ϵ c the ratio between , the mean temperature, and T c .
We solve for the diffusion equation in spherical geometry over the lid thickness to obtain the radial temperature profile in the lid in both hemispheres:
| (A4) |
where H lat (r > R cr , t) is the heat released by cooling and crystallization of melt in the crust (see Section 3.2.2). Downward advection of the crust caused by crustal thickening is neglected (Foley & Smye, 2018).
As the planet cools, the lid thickness grows and its growth rate is determined from a Stefan‐like equation which considers the balance, at the lid base, between the heat flow from the convective mantle and the conductive heat flow (Grott & Breuer, 2008; Morschhauser et al., 2011):
| (A5) |
where is the melt fraction (see Section 3.2.1), L is the latent heat of mantle melting.
The following equations give the volume and basal area of the crust (V cr , A cr ), lithospheric mantle (V lm , A lm ) and convective mantle (V cm , A cm ) as a function of f, the surface fraction of the northern lowlands, taken equal to 0.4 (Andrews‐Hanna et al., 2008):
| (A6a) |
| (A6b) |
| (A6c) |
| (A6d) |
Bonnet Gibet, V. , Michaut, C. , Wieczorek, M. , & Lognonné, P. (2022). A positive feedback between crustal thickness and melt extraction for the origin of the Martian dichotomy. Journal of Geophysical Research: Planets, 127, e2022JE007472. 10.1029/2022JE007472
Data Availability Statement
The figures in the article are made and reproducible from the following available codes and data: Bonnet Gibet (2022).
References
- Andrews‐Hanna, J. C. , Zuber, M. T. , & Banerdt, W. B. (2008). The Borealis basin and the origin of the martian crustal dichotomy. Nature, 453(7199), 1212–1215. 10.1038/nature07011 [DOI] [PubMed] [Google Scholar]
- Baker, M. B. , & Stolper, E. M. (1994). Determining the composition of high‐pressure mantle melts using diamond aggregates. Geochimica et Cosmochimica Acta, 58(13), 2811–2827. 10.1016/0016-7037(94)90116-3 [DOI] [Google Scholar]
- Banerdt, W. B. , Smrekar, S. E. , Banfield, D. , Giardini, D. , Golombek, M. , Johnson, C. L. , et al. (2020). Initial results from the InSight mission on Mars. Nature Geoscience, 13(3), 183–189. 10.1038/s41561-020-0544-y [DOI] [Google Scholar]
- Baratoux, D. , Toplis, M. , Monnereau, M. , & Sautter, V. (2013). The petrological expression of early Mars volcanism. Journal of Geophysical Research: Planets, 118(1), 59–64. 10.1029/2012je004234 [DOI] [Google Scholar]
- Batra, K. , & Foley, B. (2021). Scaling laws for stagnant‐lid convection with a buoyant crust. Geophysical Journal International, 228(1), 631–663. 10.1093/gji/ggab366 [DOI] [Google Scholar]
- Bercovici, D. , Ricard, Y. , & Schubert, G. (2001). A two‐phase model for compaction and damage: 1. General theory. Journal of Geophysical Research, 106(B5), 8887–8906. 10.1029/2000jb900430 [DOI] [Google Scholar]
- Bibring, J.‐P. , Langevin, Y. , Mustard, J. F. , Poulet, F. , Arvidson, R. , Gendrin, A. , et al. (2006). Global mineralogical and aqueous Mars history derived from OMEGA/Mars express data. Science, 312(5772), 400–404. 10.1126/science.1122659 [DOI] [PubMed] [Google Scholar]
- Bonnet Gibet, V. (2022). A positive feedback between crustal thickness and melt extraction for the origin of the Martian dichotomy—Figure software & data. Zenodo. 10.5281/zenodo.7228037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breuer, D. , & Spohn, T. (2006). Viscosity of the Martian mantle and its initial temperature: Constraints from crust formation history and the evolution of the magnetic field. Planetary and Space Science, 54(2), 153–169. 10.1016/j.pss.2005.08.008 [DOI] [Google Scholar]
- Carter, J. , & Poulet, F. (2013). Ancient plutonic processes on Mars inferred from the detection of possible anorthositic terrains. Nature Geoscience, 6(12), 1008–1012. 10.1038/ngeo1995 [DOI] [Google Scholar]
- Davaille, A. , & Jaupart, C. (1993). Transient high‐Rayleigh‐number thermal convection with large viscosity variations. Journal of Fluid Mechanics, 253(1), 141–166. 10.1017/s0022112093001740 [DOI] [Google Scholar]
- Deschamps, F. , & Sotin, C. (2001). Thermal convection in the outer shell of large icy satellites. Journal of Geophysical Research, 106(E3), 5107–5121. 10.1029/2000je001253 [DOI] [Google Scholar]
- Drilleau, M. , Garcia, R. , Samuel, H. , Rivoldini, A. , Wieczorek, M. , Lognonné, P. , et al. (2022). Marsquakes’ location and 1‐D seismic models for Mars from InSight data. Journal of Geophysical Research: Planets, 127(9), e2021JE007067. 10.1029/2021je007067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drilleau, M. , Samuel, H. , Rivoldini, A. , Panning, M. , & Lognonné, P. (2021). Bayesian inversion of the Martian structure using geodynamic constraints. Geophysical Journal International, 226(3), 1615–1644. 10.1093/gji/ggab105 [DOI] [Google Scholar]
- Durán, C. , Khan, A. , Ceylan, S. , Zenhäusern, G. , Stähler, S. , Clinton, J. , & Giardini, D. (2022). Seismology on Mars: An analysis of direct, reflected, and converted seismic body waves with implications for interior structure. Physics of the Earth and Planetary Interiors, 325, 106851. 10.1016/j.pepi.2022.106851 [DOI] [Google Scholar]
- Farrand, W. H. , Lane, M. D. , Edwards, B. R. , & Yingst, R. A. (2011). Spectral evidence of volcanic cryptodomes on the northern plains of Mars. Icarus, 211(1), 139–156. 10.1016/j.icarus.2010.09.006 [DOI] [Google Scholar]
- Foley, B. J. , & Smye, A. J. (2018). Carbon cycling and habitability of earth‐sized stagnant lid planets. Astrobiology, 18(7), 873–896. 10.1089/ast.2017.1695 [DOI] [PubMed] [Google Scholar]
- Golabek, G. J. , Keller, T. , Gerya, T. V. , Zhu, G. , Tackley, P. J. , & Connolly, J. A. (2011). Origin of the Martian dichotomy and Tharsis from a giant impact causing massive magmatism. Icarus, 215(1), 346–357. 10.1016/j.icarus.2011.06.012 [DOI] [Google Scholar]
- Grott, M. , & Breuer, D. (2008). The evolution of the Martian elastic lithosphere and implications for crustal and mantle rheology. Icarus, 193(2), 503–515. 10.1016/j.icarus.2007.08.015 [DOI] [Google Scholar]
- Hirschmann, M. , Asimow, P. D. , Ghiorso, M. , & Stolper, E. (1999). Calculation of peridotite partial melting from thermodynamic models of minerals and melts. III. Controls on isobaric melt production and the effect of water on melt production. Journal of Petrology, 40(5), 831–851. 10.1093/petroj/40.5.831 [DOI] [Google Scholar]
- Huang, Q. , Schmerr, N. C. , King, S. D. , Kim, D. , Rivoldini, A. , Plesa, A.‐C. , et al. (2022). Seismic detection of a deep mantle discontinuity within Mars by InSight. Proceedings of the National Academy of Sciences, 119(42), e2204474119. 10.1073/pnas.2204474119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaupart, C. , Labrosse, S. , Lucazeau, F. , & Mareschal, J.‐C. (2015). Temperatures, heat, and energy in the mantle of the earth. In Schubert G. (Ed.), Treatise on Geophysics (2nd edn, Vol. 7, pp. 223–270). Elsevier. [Google Scholar]
- Karato, S.‐I. , & Wu, P. (1993). Rheology of the upper mantle: A synthesis. Science, 260(5109), 771–778. 10.1126/science.260.5109.771 [DOI] [PubMed] [Google Scholar]
- Katz, R. F. , Rees Jones, D. W. , Rudge, J. F. , & Keller, T. (2022). Physics of melt extraction from the mantle: Speed and style. Annual Review of Earth and Planetary Sciences, 50(1), 507–540. 10.1146/annurev-earth-032320-083704 [DOI] [Google Scholar]
- Katz, R. F. , Spiegelman, M. , & Langmuir, C. H. (2003). A new parameterization of hydrous mantle melting. Geochemistry, Geophysics, Geosystems, 4(9), 1073. 10.1029/2002gc000433 [DOI] [Google Scholar]
- Khan, A. , Ceylan, S. , van Driel, M. , Giardini, D. , Lognonné, P. , Samuel, H. , et al. (2021). Upper mantle structure of Mars from InSight seismic data. Science, 373(6553), 434–438. 10.1126/science.abf2966 [DOI] [PubMed] [Google Scholar]
- Kim, D. , Lekić, V. , Irving, J. C. , Schmerr, N. , Knapmeyer‐Endrun, B. , Joshi, R. , et al. (2021). Improving constraints on planetary interiors with PPS receiver functions. Journal of Geophysical Research: Planets, 126(11), e2021JE006983. 10.1029/2021je006983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapmeyer‐Endrun, B. , Panning, M. P. , Bissig, F. , Joshi, R. , Khan, A. , Kim, D. , et al. (2021). Thickness and structure of the Martian crust from InSight seismic data. Science, 373(6553), 438–443. 10.1126/science.abf8966 [DOI] [PubMed] [Google Scholar]
- Lognonné, P. , Banerdt, W. B. , Pike, W. , Giardini, D. , Christensen, U. , Garcia, R. F. , et al. (2020). Constraints on the shallow elastic and anelastic structure of Mars from InSight seismic data. Nature Geoscience, 13(3), 213–220. [Google Scholar]
- Lognonné, P. , Gagnepain‐Beyneix, J. , & Chenet, H. (2003). A new seismic model of the moon: Implications for structure, thermal evolution and formation of the Moon. Earth and Planetary Science Letters, 211(1–2), 27–44. 10.1016/s0012-821x(03)00172-9 [DOI] [Google Scholar]
- Mangold, N. , Loizeau, D. , Poulet, F. , Ansan, V. , Baratoux, D. , LeMouelic, S. , et al. (2010). Mineralogy of recent volcanic plains in the Tharsis region, Mars, and implications for platy‐ridged flow composition. Earth and Planetary Science Letters, 294(3–4), 440–450. 10.1016/j.epsl.2009.07.036 [DOI] [Google Scholar]
- Marinova, M. M. , Aharonson, O. , & Asphaug, E. (2008). Mega‐impact formation of the Mars hemispheric dichotomy. Nature, 453(7199), 1216–1219. 10.1038/nature07070 [DOI] [PubMed] [Google Scholar]
- Marinova, M. M. , Aharonson, O. , & Asphaug, E. (2011). Geophysical consequences of planetary‐scale impacts into a Mars‐like planet. Icarus, 211(2), 960–985. 10.1016/j.icarus.2010.10.032 [DOI] [Google Scholar]
- McGill, G. E. , & Dimitriou, A. M. (1990). Origin of the Martian global dichotomy by crustal thinning in the late Noachian or early Hesperian. Journal of Geophysical Research, 95(B8), 12595–12605. 10.1029/jb095ib08p12595 [DOI] [Google Scholar]
- McKenzie, D. (1985). The extraction of magma from the crust and mantle. Earth and Planetary Science Letters, 74(1), 81–91. 10.1016/0012-821x(85)90168-2 [DOI] [Google Scholar]
- Mei, S. , Bai, W. , Hiraga, T. , & Kohlstedt, D. (2002). Influence of melt on the creep behavior of olivine–basalt aggregates under hydrous conditions. Earth and Planetary Science Letters, 201(3–4), 491–507. 10.1016/s0012-821x(02)00745-8 [DOI] [Google Scholar]
- Michaut, C. , & Neufeld, J. A. (2022). Formation of the lunar primary crust from a long‐lived slushy magma ocean. Geophysical Research Letters, 49(2), e2021GL095408. 10.1029/2021gl095408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaut, C. , Pinel, V. , & Maccaferri, F. (2020). Magma ascent at floor‐fractured craters diagnoses the lithospheric stress state on the Moon. Earth and Planetary Science Letters, 530, 115889. 10.1016/j.epsl.2019.115889 [DOI] [Google Scholar]
- Miller, K. J. , Zhu, W.‐L. , Montési, L. G. , & Gaetani, G. A. (2014). Experimental quantification of permeability of partially molten mantle rock. Earth and Planetary Science Letters, 388, 273–282. 10.1016/j.epsl.2013.12.003 [DOI] [Google Scholar]
- Morison, A. , Labrosse, S. , Deguen, R. , & Alboussière, T. (2019). Timescale of overturn in a magma ocean cumulate. Earth and Planetary Science Letters, 516, 25–36. 10.1016/j.epsl.2019.03.037 [DOI] [Google Scholar]
- Morschhauser, A. , Grott, M. , & Breuer, D. (2011). Crustal recycling, mantle dehydration, and the thermal evolution of Mars. Icarus, 212(2), 541–558. 10.1016/j.icarus.2010.12.028 [DOI] [Google Scholar]
- Nataf, H. , & Richter, F. (1982). Convection experiments in fluids with highly temperature‐dependent viscosity and the thermal evolution of the planets. Physics of the Earth and Planetary Interiors, 29(3–4), 320–329. 10.1016/0031-9201(82)90020-6 [DOI] [Google Scholar]
- Neumann, G. , Zuber, M. , Wieczorek, M. A. , McGovern, P. , Lemoine, F. G. , & Smith, D. (2004). Crustal structure of Mars from gravity and topography. Journal of Geophysical Research, 109(E8), E08002. 10.1029/2004je002262 [DOI] [Google Scholar]
- Platz, T. , Michael, G. , Tanaka, K. L. , Skinner, J. A. Jr. , & Fortezzo, C. M. (2013). Crater‐based dating of geological units on Mars: Methods and application for the new global geological map. Icarus, 225(1), 806–827. 10.1016/j.icarus.2013.04.021 [DOI] [Google Scholar]
- Plesa, A.‐C. , Tosi, N. , Grott, M. , & Breuer, D. (2015). Thermal evolution and Urey ratio of Mars. Journal of Geophysical Research: Planets, 120(5), 995–1010. 10.1002/2014je004748 [DOI] [Google Scholar]
- Poulet, F. , Mangold, N. , Platevoet, B. , Bardintzeff, J.‐M. , Sautter, V. , Mustard, J. , et al. (2009). Quantitative compositional analysis of Martian mafic regions using the MEx/OMEGA reflectance data: 2. Petrological implications. Icarus, 201(1), 84–101. 10.1016/j.icarus.2008.12.042 [DOI] [Google Scholar]
- Reese, C. , Orth, C. , & Solomatov, V. (2010). Impact origin for the Martian crustal dichotomy: Half emptied or half filled? Journal of Geophysical Research, 115(E5), E05004. 10.1029/2009je003506 [DOI] [Google Scholar]
- Richter, F. M. , & McKenzie, D. (1984). Dynamical models for melt segregation from a deformable matrix. The Journal of Geology, 92(6), 729–740. 10.1086/628908 [DOI] [Google Scholar]
- Roberts, J. H. , & Arkani‐Hamed, J. (2014). Impact heating and coupled core cooling and mantle dynamics on Mars. Journal of Geophysical Research: Planets, 119(4), 729–744. 10.1002/2013je004603 [DOI] [Google Scholar]
- Roberts, J. H. , & Zhong, S. (2006). Degree‐1 convection in the Martian mantle and the origin of the hemispheric dichotomy. Journal of Geophysical Research, 111(E6), E06013. 10.1029/2005je002668 [DOI] [Google Scholar]
- Robinson, J. , Wood, B. , & Blundy, J. (1998). The beginning of melting of fertile and depleted peridotite at 1.5 GPa. Earth and Planetary Science Letters, 155(1–2), 97–111. 10.1016/s0012-821x(97)00162-3 [DOI] [Google Scholar]
- Ruedas, T. (2017). Radioactive heat production of six geologically important nuclides. Geochemistry, Geophysics, Geosystems, 18(9), 3530–3541. 10.1002/2017gc006997 [DOI] [Google Scholar]
- Ruedas, T. , & Breuer, D. (2017). On the relative importance of thermal and chemical buoyancy in regular and impact‐induced melting in a Mars‐like planet. Journal of Geophysical Research: Planets, 122(7), 1554–1579. 10.1002/2016je005221 [DOI] [Google Scholar]
- Salvador, A. , Massol, H. , Davaille, A. , Marcq, E. , Sarda, P. , & Chassefière, E. (2017). The relative influence of H2O and CO2 on the primitive surface conditions and evolution of rocky planets. Journal of Geophysical Research: Planets, 122(7), 1458–1486. 10.1002/2017je005286 [DOI] [Google Scholar]
- Samuel, H. , Lognonné, P. , Panning, M. , & Lainey, V. (2019). The rheology and thermal history of Mars revealed by the orbital evolution of Phobos. Nature, 569(7757), 523–527. 10.1038/s41586-019-1202-7 [DOI] [PubMed] [Google Scholar]
- Sautter, V. , & Payre, V. (2021). Alkali magmatism on Mars: An unexpected diversity. Comptes Rendus Geoscience, 353(S2), 1–30. 10.5802/crgeos.64 [DOI] [Google Scholar]
- Schmidt, F. , Way, M. J. , Costard, F. , Bouley, S. , Séjourné, A. , & Aleinov, I. (2022). Circumpolar ocean stability on Mars 3 Gy ago. Proceedings of the National Academy of Sciences, 119(4), e2112930118. 10.1073/pnas.2112930118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomatov, V. (1995). Scaling of temperature‐and stress‐dependent viscosity convection. Physics of Fluids, 7(2), 266–274. 10.1063/1.868624 [DOI] [Google Scholar]
- Solomon, S. C. , Aharonson, O. , Aurnou, J. M. , Banerdt, W. B. , Carr, M. H. , Dombard, A. J. , et al. (2005). New perspectives on ancient Mars. Science, 307(5713), 1214–1220. 10.1126/science.1101812 [DOI] [PubMed] [Google Scholar]
- Šrámek, O. , & Zhong, S. (2010). Long‐wavelength stagnant lid convection with hemispheric variation in lithospheric thickness: Link between Martian crustal dichotomy and Tharsis? Journal of Geophysical Research, 115(E9), E09010. 10.1029/2010je003597 [DOI] [Google Scholar]
- Šrámek, O. , & Zhong, S. (2012). Martian crustal dichotomy and Tharsis formation by partial melting coupled to early plume migration. Journal of Geophysical Research, 117(E1), E01005. 10.1029/2011je003867 [DOI] [Google Scholar]
- Stähler, S. C. , Khan, A. , Banerdt, W. B. , Lognonné, P. , Giardini, D. , Ceylan, S. , et al. (2021). Seismic detection of the martian core. Science, 373(6553), 443–448. 10.1126/science.abi7730 [DOI] [PubMed] [Google Scholar]
- Suzuki, A. , & Ohtani, E. (2003). Density of peridotite melts at high pressure. Physics and Chemistry of Minerals, 30(8), 449–456. 10.1007/s00269-003-0322-6 [DOI] [Google Scholar]
- Takahashi, E. (1990). Speculations on the Archean mantle: Missing link between komatiite and depleted garnet peridotite. Journal of Geophysical Research, 95(B10), 15941–15954. 10.1029/JB095iB10p15941 [DOI] [Google Scholar]
- Tanaka, K. L. , Robbins, S. , Fortezzo, C. , Skinner, J. Jr. , & Hare, T. M. (2014). The digital global geologic map of Mars: Chronostratigraphic ages, topographic and crater morphologic characteristics, and updated resurfacing history. Planetary and Space Science, 95, 11–24. 10.1016/j.pss.2013.03.006 [DOI] [Google Scholar]
- Taylor, G. J. , Stopar, J. , Boynton, W. V. , Karunatillake, S. , Keller, J. M. , Brückner, J. , et al. (2006). Variations in K/Th on Mars. Journal of Geophysical Research, 111(E3), E03S06. 10.1029/2006je002676 [DOI] [Google Scholar]
- Thiriet, M. , Breuer, D. , Michaut, C. , & Plesa, A.‐C. (2019). Scaling laws of convection for cooling planets in a stagnant lid regime. Physics of the Earth and Planetary Interiors, 286, 138–153. 10.1016/j.pepi.2018.11.003 [DOI] [Google Scholar]
- Thiriet, M. , Michaut, C. , Breuer, D. , & Plesa, A.‐C. (2018). Hemispheric dichotomy in lithosphere thickness on Mars caused by differences in crustal structure and composition. Journal of Geophysical Research: Planets, 123(4), 823–848. 10.1002/2017je005431 [DOI] [Google Scholar]
- Tonks, W. B. , & Melosh, H. J. (1993). Magma ocean formation due to giant impacts. Journal of Geophysical Research, 98(E3), 5319–5333. 10.1029/92je02726 [DOI] [Google Scholar]
- Turcotte, D. L. , & Schubert, G. (2002). Geodynamics. Cambridge university press. [Google Scholar]
- Vinnik, L. , Chenet, H. , Gagnepain‐Beyneix, J. , & Lognonne, P. (2001). First seismic receiver functions on the Moon. Geophysical Research Letters, 28(15), 3031–3034. 10.1029/2001gl012859 [DOI] [Google Scholar]
- Wänke, H. , & Dreibus, G. (1994). Chemistry and accretion history of Mars. Philosophical Transactions of the Royal Society of London Series A: Physical and Engineering Sciences, 349(1690), 285–293. [Google Scholar]
- Watters, T. R. , McGovern, P. J. , & Irwin, R. P. III (2007). Hemispheres apart: The crustal dichotomy on Mars. Annual Review of Earth and Planetary Sciences, 35(1), 621–652. 10.1146/annurev.earth.35.031306.140220 [DOI] [Google Scholar]
- Wieczorek, M. A. , Broquet, A. , McLennan, S. M. , Rivoldini, A. , Golombek, M. , Antonangeli, D. , et al. (2022). InSight constraints on the global character of the martian crust. Journal of Geophysical Research: Planets, 127(5), e2022JE007298. 10.1029/2022je007298 [DOI] [Google Scholar]
- Wieczorek, M. A. , Neumann, G. A. , Nimmo, F. , Kiefer, W. S. , Taylor, G. J. , Melosh, H. J. , et al. (2013). The crust of the Moon as seen by GRAIL. Science, 339(6120), 671–675. 10.1126/science.1231530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieczorek, M. A. , & Zuber, M. T. (2004). Thickness of the martian crust: Improved constraints from geoid‐to‐topography ratios. Journal of Geophysical Research, 109(E1), E01009. 10.1029/2003je002153 [DOI] [Google Scholar]
- Wray, J. J. , Hansen, S. T. , Dufek, J. , Swayze, G. A. , Murchie, S. L. , Seelos, F. P. , et al. (2013). Prolonged magmatic activity on Mars inferred from the detection of felsic rocks. Nature Geoscience, 6(12), 1013–1017. 10.1038/ngeo1994 [DOI] [Google Scholar]
- Yoshida, M. , & Kageyama, A. (2006). Low‐degree mantle convection with strongly temperature‐and depth‐dependent viscosity in a three‐dimensional spherical shell. Journal of Geophysical Research, 111(B3), E003867. 10.1029/2005jb003905 [DOI] [Google Scholar]
- Zhong, S. (2009). Migration of Tharsis volcanism on Mars caused by differential rotation of the lithosphere. Nature Geoscience, 2(1), 19–23. 10.1038/ngeo392 [DOI] [Google Scholar]
- Zhong, S. , & Zuber, M. T. (2001). Degree‐1 mantle convection and the crustal dichotomy on Mars. Earth and Planetary Science Letters, 189(1–2), 75–84. 10.1016/s0012-821x(01)00345-4 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The figures in the article are made and reproducible from the following available codes and data: Bonnet Gibet (2022).


