Abstract
Untangling the relationship between network complexity and ecological stability under climate change is an arduous challenge for theoretical and empirical ecology. Even more so, when considering extreme climatic events. Here, we studied the effects of extreme climatic events (heatwaves) on the complexity of realistic freshwater ecosystems using topological and quantitative trophic network metrics. Next, we linked changes in network complexity with the investigation of four stability components (temporal stability, resistance, resilience, and recovery) of community's functional, compositional, and energy flux stability. We found reduction in topological network complexity to be correlated with reduction of functional and compositional resistance. However, temperature‐driven increase in link‐weighted network complexity increased functional and energy flux recovery and resilience, but at the cost of increased compositional instability. Overall, we propose an overarching approach to elucidate the effects of climate change on multidimensional stability through the lens of network complexity, providing helpful insights for preserving ecosystems stability under climate change.
Keywords: community ecology, disturbance, ecological stability, energy fluxes, heatwave, network analysis, recovery, resilience, stability‐complexity
INTRODUCTION
Species composing ecological communities are interconnected in intricate networks of interactions, which may comprise competition, predation, mutualism, and parasitism (Pilosof et al., 2017; Thomas et al., 2009). Species embedded in an ecological network exchange signals, materials, and energy (Montoya et al., 2006). The way ecological networks are organized (that is, their structure and complexity) depends on the type of interactions linking the nodes of the network, on the strength and allocation of those interactions, and on a wide array of biotic and abiotic factors. The overall structure and complexity of the network determine how an ecosystem functions (Thébault & Fontaine, 2010).
How network complexity influences ecosystem's stability has been hotly debated in ecology over the past half‐century (MacArthur, 1955; May, 1972; McCann et al., 1998, 2000; Montoya et al., 2006; Pimm, 1984). Both theoretical (Allesina & Tang, 2012; Grilli et al., 2016) and empirical (Neutel et al., 2002, 2007) evidence have provided insights on the relationship between stability and network complexity. Yet, how network complexity correlates with stability remains divisive (Landi et al., 2018; MacArthur, 1955; May, 1973; Toju et al., 2017).
Ecological stability is the core notion to understand ecosystem's potential to withstand and/or to recover from perturbations. It underlies our ability to understand today's ecosystem responses to disturbance and to predict future ecosystem dynamics. Ecological stability may be the key to an effective ecosystem management and to the development of meaningful policies against rapid environmental change (Donohue et al., 2016; Kéfi et al., 2019). With the increasing pressure exerted by human activities upon ecosystems, understanding whether and how ecological network properties are related to stability in face of disturbance has become a central matter in ecology (Nagelkerken et al., 2020; Yuan et al., 2021). At the same time, ecological stability has recently emerged as a multidimensional construct (Donohue et al., 2013, 2016). That is, several metrics (including temporal variability, resistance, resilience, and rate of recovery) are needed to fully describe the stability of a system in response to a given disturbance, as no single metric can adequately capture the different response aspects composing stability (Hillebrand et al., 2018; Polazzo & Rico, 2021).
Global climate change is one of the most pervasive anthropogenic disturbances to our planet (IPCC, 2013). Global surface temperature has risen by roughly 1°C since the pre‐industrial era, and it is projected to increase an additional 1.5–4.5°C (depending on the Representative Concentration Pathway scenario) above the reference period's temperature by the end of the century (IPCC, 2021). Owing to its profound implication for species metabolism and ecological dynamics, temperature affects all levels of biological organization (Brown et al., 2004). Increasing temperature is, thus, expected to deeply alter ecological network structure and the nature and intensity of species interactions, influencing the overall stability of ecosystems. Experimental (Nagelkerken et al., 2020), theoretical (Fussmann et al., 2014; Petchey et al., 2010), and mixed approaches (O'Gorman et al., 2019) have investigated the effects of warming on trophic networks structure, interaction strengths, and stability. Results showed that consumers, due to a temperature‐driven increase in metabolism, exert stronger top‐down control on the biomass stocks of lower trophic levels, increasing the overall consumer‐resource biomass ratio (Fussmann et al., 2014; O'Connor et al., 2009; O'Gorman et al., 2019). However, consumers might struggle to meet their rising energy demands under warming (Fussmann et al., 2014; O'Connor et al., 2009). This constrain may lead to shorter and simpler food webs (Fussmann et al., 2014; O'Gorman et al., 2019), reduced energy fluxes efficiency (Barneche et al., 2021), altered distribution of biomass and interaction strengths throughout the food web (Nagelkerken et al., 2020), and potentially to a food web collapse (Ullah et al., 2018).
Most of the experimental and theoretical work done in this area has dealt with the effects of increasing mean temperature on ecological stability and network structure. Yet, climate change is composed of different processes and phenomena (IPCC, 2021), including extreme climatic events, such as heatwaves (HWs; Jentsch et al., 2007). HWs are of particular concern because their magnitude, duration, and frequency are predicted to increase in the future (Meehl & Tebaldi, 2004; Woolway et al., 2021, 2022). Still, how HWs affect trophic networks and ecological stability has received little attention (Polazzo, Roth, et al., 2022). The few empirical evidence of the effects of HWs on multitrophic systems reported that HWs may affect both compositional and functional stability of freshwater communities, particularly in the absence of top predators (Ross et al., 2021).
Here, we used an outdoor pond mesocosm experiment to explore how heatwaves alter network complexity and community stability. Specifically, our main research questions were: (a) whether and how do extreme climatic events impact trophic network complexity; (b) whether and how do extreme climatic events influence multidimensional stability; and (c) whether and how changes in trophic network complexity are related to altered community multidimensional stability. To answer these questions, we recorded the abundance and biomass of all major components of the food web over time (that is, periphyton, phytoplankton, zooplankton, and macroinvertebrates). We then studied the dynamics of trophic network complexity using unweighted/topological metrics (based only on presence/absence of species) and link‐weighted metrics (considering interaction strength). Finally, the relationship between those dynamics with four stability components (temporal variability, resistance, resilience, and recovery) of community's functional, compositional, and energy flux stability were studied. The term “network” is here used for simplicity since our research only focused on trophic interactions, and was hence limited to trophic networks (e.g., food webs).
MATERIALS AND METHODS
Mesocosm experiment
We performed an outdoor mesocosm experiment at the facilities of the IMDEA Water Institute (Alcalá de Henares, Madrid, Spain) between April and August of 2021. The 12 mesocosms used in this study were filled with approximately 40 cm of sediments and 850 L of water from an artificial lagoon. The biological community of the mesocosms was composed of basal species (periphyton and phytoplankton), zooplankton, and macroinvertebrates, and was allowed to establish and homogenize among experimental units for 2 months prior to the start of the experiment.
Eight of the test mesocosms were used to simulate two HW scenarios (n = 4): a long moderate HW and three strong repeated HWs (Figure 1); while four mesocosms were kept at ambient temperature for the whole experimental duration and were used as controls. The long HW lasted for 40 days and was characterized by a temperature increase of +4°C above the control temperature, whereas the reoccurring HWs treatment consisted of three HWs lasting 7 days each and separated one another by 7 days of ambient temperature. In the reoccurring HWs treatment, the temperature was +8°C above the control temperature. During the temperature manipulation phase, the mean recorded temperature in the ambient control treatment was 19.7°C (±3.29°C), in the long HW treatment it was 24.1°C (±3.21°C), and in the reoccurring HWs treatment it was 24.3 (±5.06°C). After the end of the temperature manipulation phase, we monitored the recovery of the systems for 40 days. All temperature manipulations and recordings were carried out using a transportable temperature and heatwave control device (TENTACLE) applicable for aquatic micro‐ and mesocosm experiments (Hermann et al., 2022).
FIGURE 1.
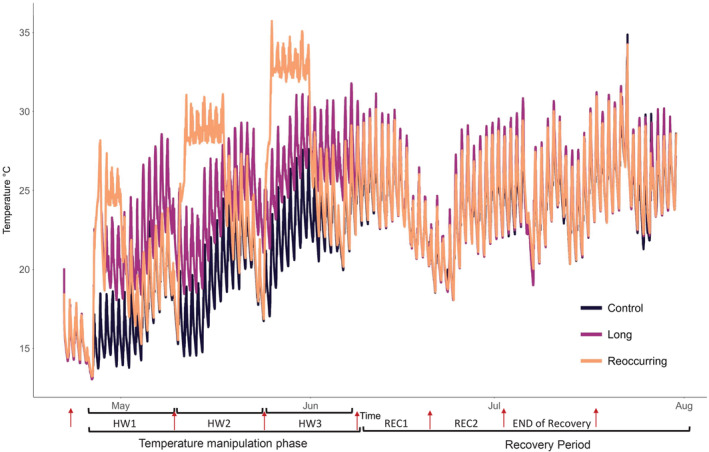
Experimental temperature manipulations and timeline. Measured temperature in the different treatments over the experiment, and different experimental phases. Red arrows indicate biological samplings. HW, heat wave; REC1, Recovery period 1; REC2, Recovery period 2.
Sampling of the freshwater community
The whole community was sampled on days −4, +10, +24, +38, +52, +66, and + 80 relative to the start of the HWs. Samplings of phytoplankton, zooplankton, and macroinvertebrates composing the freshwater community were done following Polazzo et al. (2021). Briefly, the planktonic community was sampled by taking depth‐ integrated water samples with a polyvinyl chloride (PVC) tube (six sub‐samples per mesocosm mixed in a bucket). Next, for phytoplankton samples, 250 ml of this water sample were introduced into glass amber bottles and 10% Lugol's iodine was added for preservation. For zooplankton, 5 L of the collected water sample were passed through a zooplankton net (55 μm) and concentrated to an approximate volume of 100 ml. The concentrated samples were fixed with Lugol's iodine solution and stored in dark conditions at room temperature until identification and counting. In order to sample pelagic and benthic macroinvertebrates individuals, three sampling methods were used. First, a net (mesh size: 0.5 mm) was passed twice through the side of the mesocosms (in both directions) to catch the animals that were swimming or resting on the mesocosm's wall. Second, two pebble baskets positioned over the sediment surface were collected, and third, two traps filled with macrophyte shots (Elodea sp.), Populus sp. leaves and stones were collected from the sediment's surface using a net. The invertebrates sampled from each mesocosm with the three sampling methods were pooled together, identified, and counted. Periphyton colonization in substrates (25 cm2) was measured using transparent polypropylene strips placed in an upright position at 20 cm from the water surface. Strips were taken using a tube of 50 ml filled with water. Samples were stored at 4°C in the dark until they were analyzed, which happened the same day.
Quantification of the biomass
Every basal, zooplankton, and macroinvertebrate node was digitally photographed with scale reference using a camera Samsung 12 mp (4032 × 3024, JPG format), and measured using Image J software (Schneider et al., 2012). The biovolume (μm3/org) of the basal, zooplankton, and macroinvertebrate individuals was calculated using geometric models according to Sun and Liu (2003), Hillebrand et al. (1999), Ruttner‐Kolisko (1977), Alcaraz et al. (2003), and Bernardini et al. (2000). Biovolume was transformed to fresh weight (FW) using the following ratio 1 μg = 106 μm3, assuming specific weight of water = 1. Colonized periphyton was washed and concentrated by centrifugation (Ependorf 5810R at 3500 rpm during 20 min, 4°C). Fresh pellets were weighed using a balance: Denver instrument (precision = 0.005 g). Results were expressed as g/cm2. Finally, fresh biomass of every community (i.e., periphyton, phytoplankton, zooplankton, and macroinvertebrates) was calculated per mesocosm (g/mesocosm).
Trophic network construction
We used publications, personal observations, and the database built by Gray et al. (2015), which represents the largest standardized collection of trophic links for freshwater organisms, to establish the trophic interactions among the species of the experimental mesocosms. The resulting interaction list comprised 1202 possible links and 142 trophic species (91 basal species, 23 zooplankton species, 23 benthic macroinvertebrates and 3 predators). Eighty‐four networks were built (3 treatments including control × 7 sampling days × 4 replicates) considering the biomass for each node.
Unweighted and weighted trophic network properties
Two types of networks were used to characterize the food webs for each mesocosm: topological or unweighted, formed by the presence or absence of nodes and relative interactions, and quantitative or link‐weighted, where interaction strengths were also considered. For the first, we calculated the following unweighted network properties: number of species, number of links (L), link density (L/S, where S is the number of species), connectance (C), generality, vulnerability, number of basal and top species, mean trophic level, maximum trophic level, omnivory, path length, and clustering coefficient. We used the R package multiweb (Saravia, 2022) to obtain these properties. For a complete overview of the calculated network properties and their ecological meaning, please refer to Appendix S1: Table S2.
As for the weighted food webs, we used a bioenergetic modeling approach to estimate interaction strengths (as energy fluxes), which enabled us to calculate three link‐weighted properties: connectance, generality, and vulnerability (Kortsch et al., 2021). We here used the bioenergetic food web model developed by Gauzens et al. (2019) as implemented in the R package fluxweb. Briefly, this approach considers allometric scaling laws to quantify individual metabolic rates that are dependent on body mass and temperature, which together with losses to predation and assimilation efficiencies are used to quantify incoming fluxes (due to consumption) and outcoming fluxes (due to predation) for each species. The main assumption of this approach is the system's equilibrium or steady state (Barnes et al., 2018), implying that the total amount of energy lost by a species, either by predation or physiological processes, is exactly compensated by the metabolized energy it gains from consumption. That is, species loss to predation and metabolism are completely balanced by energetic gains, which are defined as incoming fluxes multiplied by assimilation efficiencies (Jochum et al., 2021).
To calculate the metabolism of each node, species‐specific metabolic rates were derived from body mass metabolic relationships using the allometric equation developed by Brown et al. (2004).
where is the metabolic loss of species i, X 0 is the organism‐specific normalization constant, the body mass of species i (individual/g), is the allometric scaling constant (a = −0.29), E is the activation energy (0.69 eV, Brown et al., 2004), B is the Boltzmann's Constant (8.61 × 10−5 eV/K), T is the temperature (K), and is the biomass of species (g/m3). The X 0 normalization constants are the intercepts of the body mass‐metabolism scaling relationship for invertebrates and vertebrates presented in Brown et al. (2004), which correspond to 15.85 for unicellular organism, 17.17 for invertebrates and 18.47 for vertebrates. Since our study only involved unicellular basal species and invertebrates, we used the normalization constants for these specific classes of organisms.
The metabolic rate increases exponentially with temperature (Brown et al., 2004). Thus, temperature difference between different temperature treatments were accounted for in the bioenergetic model. We did that by using the average temperature recorded in each treatment in the time interval separating one sampling point from another. For the sampling point (e.g., before the beginning of the temperature manipulation), we took the average temperature measured in the 3 weeks before the start of the temperature treatments. Finally, we estimated the different assimilation efficiencies depending on prey type: 0.906 for animal preys (Gauzens et al., 2019) and 0.77 for basal or primary producer preys (Landry et al., 1984). The biomass of each taxon was calculated in grams per m3. As such, the units of the calculated energy flux are joules per m3 per second.
Please note that the calculated energy fluxes are a modeled proxy for energy flow, but that dietary analysis (which was not carried out in this study) would be required to definitively quantify the flow of energy through a network.
Stability properties
We quantified four stability properties: resistance, recovery, resilience, and temporal stability. We calculated the four stability properties for composition, function, and energy flux. Compositional stability was calculated using the Bray–Curtis similarity as a state variable (Donohue et al., 2013; Radchuk et al., 2019), whereas functional stability was based on total biomass (Hillebrand et al., 2018; White et al., 2020). The stability of energy flux was calculated using the total energy flux derived from the bioenergetic model. To account for potential differences in sensitivity to the temperature manipulations of the different organism groups, we calculated the four stability properties separately for three different organism groups: basal (phytoplankton and periphyton), zooplankton and macroinvertebrates.
Resistance is defined as the ability of a system to withstand disturbance (Hillebrand et al., 2018). Hence, resistance was measured as:
where and are the treatment and control values of the variable measured right after the end of the temperature manipulation phase (Figure 1), which corresponded to day 38 relative to the start of the temperature manipulations. Resistance values of 0 reflect maximum resistance (i.e., biomass, energy flux, or Bray–Curtis distances in treatment and control are the same). A negative resistance value means low resistance as compared to the control. Resistance higher than 0 indicates overperformance (increase in biomass or energy flux).
Recovery is here defined as the capacity of a system to return to undisturbed state following a disturbance (Ingrisch & Bahn, 2018). We quantified recovery as:
where and are the treatment and control state variables measured at the end of the recovery period, which corresponded to day 80 relative to the start of the temperature manipulations. The interpretation of the recovery values follows that of resistance.
We defined resilience following the definition of Pimm (1984), also known as engineering resilience. This resilience conception measures the speed of recovery after perturbation, and was quantified for each replicate as the slope of the ln‐response ratio (LRR) of the value in a treatment (T) compared to control (C) over time (Hillebrand et al., 2018):
where = intercept, = time.
We could use linear regression given the ln‐transformation of the response variable, which linearized the trend of the recovery even in the case of an exponential growth after heat stress (Hillebrand et al., 2018). The interpretation of the resilience values depend on the initial response after disturbance. If the resistance is <0, then a positive resilience means recovery over time, whereas a negative value describes a further deviation from the control. If the resistance is >0, then a positive resilience value means lack of resilience, and a negative resilience value means recovery over time.
The temporal stability of each replicate was calculated as the inverse of the coefficient of temporal variation in biomass (functional), Bray–Curtis distances (compositional), or energy flux.
where is the variable coefficient of variation (ratio of the standard deviation to the mean of the variable). Larger values equate to a higher temporal stability. The value was biomass in case of functional recovery, Bray–Curtis distances in case of compositional recovery, and energy flux in case of energy flux recovery.
We quantified the overall functional, compositional, and energy flux stability of each organism group following Pennekamp et al. (2018). This is a more integrative approach which, similarly to ecosystem multifunctionality, integrates variation in multiple stability components into a single measurement. Overall, functional, compositional, and energy flux stability were calculated using the same methodology, which follow the same procedure used to calculate multifunctionality with the averaging method (Maestre et al., 2012):
The function “scale” subtracts the mean and divides by the standard deviation. In this way, all stability components were standardized. Standardization before summing implies that all stability components have the same weight in the overall stability calculation.
Statistical analyses
Analysis of unweighted and link‐weighted network properties was performed using linear regression models, with the reoccurring HWs and long HW as predictors. To check that linear model assumptions were met, we visually examined for the homogeneity of variances and normality using the R function check_model of the R package performance (Lüdecke et al., 2020), and found the resulting models to effectively follow these assumptions. The linear models were constructed using R with the lm function of the package stats (R Core Team, 2021).
Analysis of single stability components and of overall functional, compositional, and energy flux stability was performed using linear mixed‐effects models, with reoccurring HWs (factor, two levels: present/absent) and long HW (factor, two levels: present/absent) as fixed effects. Mesocosm identity and organism group (phytoplankton, zooplankton, and macroinvertebrates) were included as random effects to account for potential idiosyncratic effects of experimental units (mesocosms) and for potential different responses between organism groups, respectively. We used the package nlme for all the linear mixed‐effects model calculations (Pinheiro et al., 2021). Again, the R function check_model of the R package performance was used to visually examine for the homogeneity of variances and normality, finding that models' assumptions were met.
To assess whether communities undergoing different HW treatments were different in the different phases of the experiment, we performed two non‐parametric multivariate analysis of dissimilarity, permutational multivariate analysis of variance (PERMANOVA, function adonis2 of the R package vegan (Oksanen et al., 2022)) and analysis of similarity (ANOSIM, function anosim of the R package vegan (Oksanen et al., 2022)), both with 999 permutations and based on Bray–Curtis distances.
Finally, to analyze the relationship between stability components and between stability components and network properties we calculated Pearson correlation coefficients.
All statistical analyses and trophic networks construction were conducted using the R software (version 4.1.2, R Core Team, 2021).
RESULTS
Before the start of the temperature manipulations, community composition was indistinguishable between control and treatments (PERMANOVA, Long HW: F 1,11 = 1456, p = 0.086; reoccurring HW: F 1,11 = 1.362, p = 0.094), and so was biomass (linear mixed‐effects model, LMM, Long HW: t = −1.017, p = 0.335; reoccurring HW: t = −1.760, p = 0.112) and total energy flux (LMM, Long HW: t = 1.341, p = 0.213; reoccurring HW: t = 0.321, p = 0.755). Consistently, all unweighted and link‐weighted network proprieties were not different between the control and the treatments.
At the end of the temperature manipulation phase (Figure 1), number of species (linear Model, LM, t = −2.282, p = 0.048), number of links (LM, t = −2.49, p = 0.018), number of basal species (LM, t = −2.93, p = 0.016), unweighted generality (LM, t = −2.83, p = 0.019) and link‐weighted vulnerability (LM, t = −3.366, p = 0.008) were significantly decreased by the reoccurring HWs treatments, whereas unweighted mean trophic level was increased (LM, t = −2.801, p = 0.020) (Figure 2c). By contrast, the long HW treatment did not affect any unweighted network property right after the end of the temperature manipulation phase, but it did significantly decline the link‐weighted vulnerability (Figure 2d).
FIGURE 2.
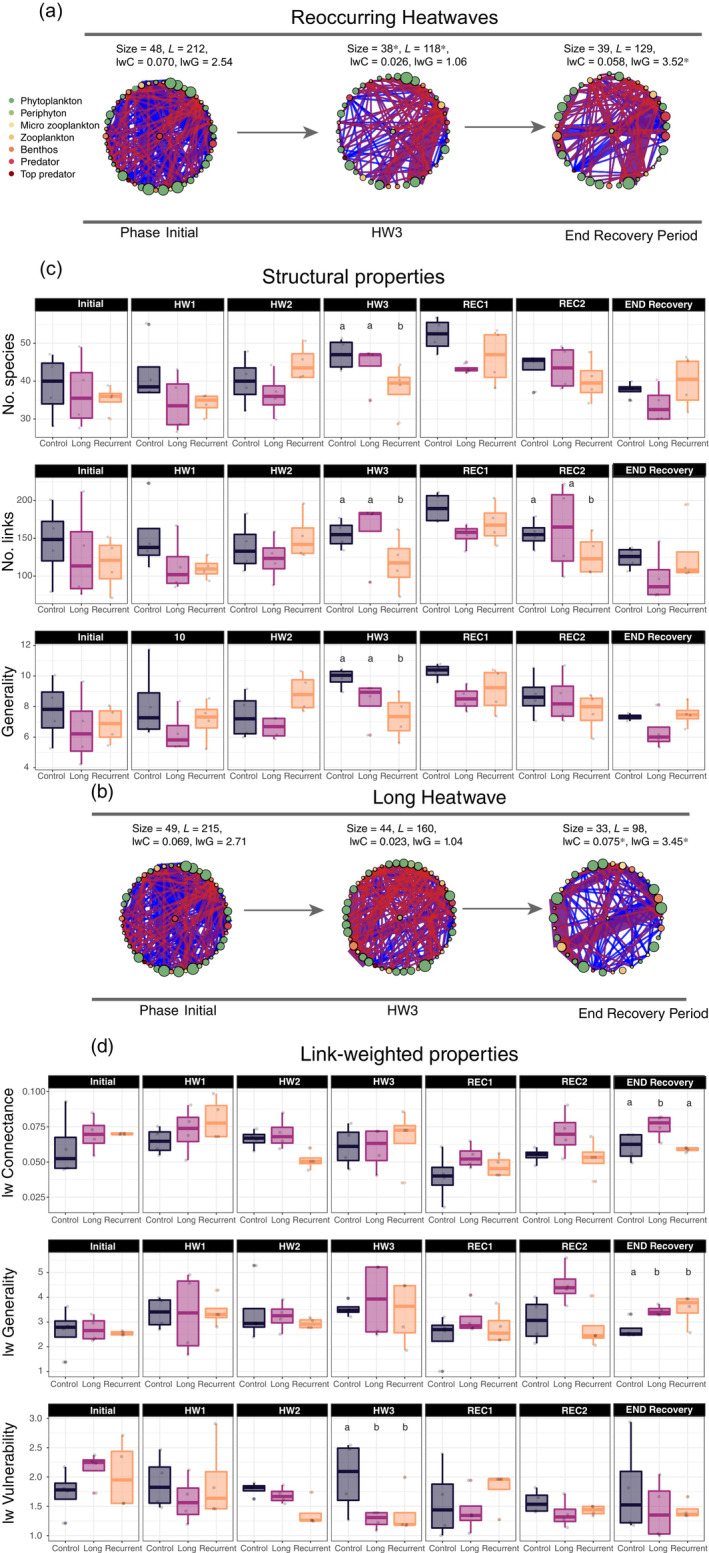
Trophic networks dynamics over time. (a and b) visualization of constructed trophic networks in different experimental phases (initial = before the start of the temperature manipulations, HW3 = end of the temperature manipulation period; end recovery period = last day of the experiment), for (a) the long HW treatment, and for (b) the reoccurring HWs treatment. Red links show fluxes going from primary producers to primary consumers, whereas blue links represent fluxes going from primary consumers to predators. Asterisks indicate significant differences in the metric according to linear regression models. (c and d) box and whisker plots (n = 4, for all measures) showing the (c) unweighted/topological and (d) link‐weighted properties of the networks in the different phases of the experiment. For all box and whisker plots, the center line indicates the median, while the bottom and top hinges of the box correspond to the 25th and 75th percentiles, respectively. Significant (p < 0.05) differences from the control are denoted with superscript letters.
At the end of the recovery period, no significant difference between controls and any of the two treatments was found for any unweighted network property (Figure 2c). Yet, the reoccurring HWs treatment significantly increased link‐weighted generality (LMM, t = 2.518, p = 0.032), while the long HW increased both link‐weighted generality (LMM, t = 2.296, p = 0.047) as well as link‐weighted connectance (LMM, t = 2.625, p = 0.027) (Figure 2d). The reoccurring HWs significantly affected multiple aspects of compositional, functional and energy flux stability (Figure 3). Resistance of function (LMM, t = −2.58, p = 0.015) and of composition (LMM, t = −5.43, p < 0.001) were reduced by the reoccurring HWs (Figure 3a,f). Compositional recovery (LMM, t = −5.00, p < 0.001, Figure 3h) and functional temporal stability (LMM, t = −3.22, p = 0.003, Figure 3d) were also reduced by the reoccurring HWs, whereas the resilience of function (LMM, t = 3.71, p = 0.001, Figure 3b) and recovery of energy flux (LMM, t = 2.80, p = 0.009, Figure 3m) were significantly increased.
FIGURE 3.
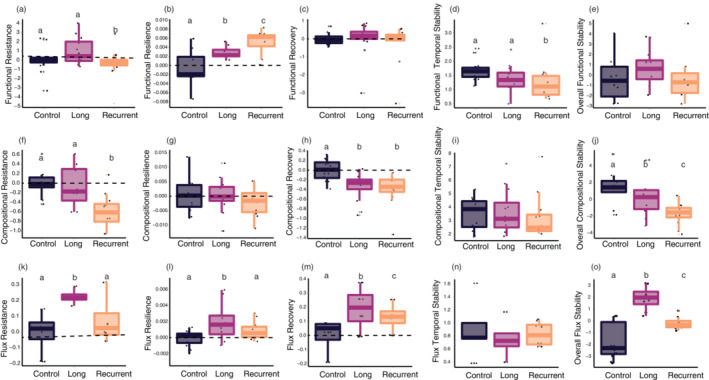
Multidimensional stability response. Effects of experimental temperature manipulation on different stability components of (a–e) functional stability, (f–j) compositional stability, and (k–o) energy fluxes stability. In the box and whisker plots (n = 12, for all measures), the center line indicates the median, while the bottom and top hinges of the box correspond to the 25th and 75th percentiles, respectively. Individual dots show the different stability properties calculated for basal species (n = 4), zooplankton (n = 4), and macroinvertebrates (n = 4). Significant (p < 0.05) differences from the control are denoted with superscript letters.
Although the long HW generally decreased biomass in the temperature manipulation phase (Appendix S1: Figure S1), it only caused a significant increase in functional resilience (LMM, t = 2.75, p = 0.01, Figure 3b). The long HW also reduced compositional recovery (LMM, t = 3.35, p = 0.002, Figure 3h), whereas it increased energy flux resistance (LMM, t = 4.75, p < 0.001, Figure 3k), recovery (LMM, t = 3.77, p = 0.001, Figure 3m), and resilience (LMM, t = 2.96, p = 0.006).
Two additional non‐parametric tests (i.e., PERMANOVA and ANOSIM) confirmed that the reoccurring HWs treatment modified community composition at the end of the temperature manipulation phase, and that both HWs treatments significantly modified community composition by the end of the experiment (Appendix S1: Table S1).
Neither of the HW treatments affected the overall ecosystem functional stability (Figure 3e), whereas both the long HW (LMM, t = −2.91, p = 0.007) and the reoccurring HWs (LMM, t = −5.21, p < 0.001) decreased overall community compositional stability (Figure 3j). Both treatments also significantly increased overall community energy flux stability (long HW, LMM: t = 8.38, p < 0.001; Reoccurring HWs, LMM: t: 3.71, p = 0.001, Figure 3o).
Analyzing the correlations between stability components and the various descriptors of network complexity, we found a positive and significant correlation between functional and compositional resistance (Figure 4a). Both compositional and functional resistance were also positively and significantly correlated to the number of species composing the network, number of links, and unweighted generality (Figure 4a). Functional recovery was positively and significantly correlated with energy flux recovery, and both functional recovery and resilience were positively correlated with link‐weighted connectance and generality (Figure 4b). On the other hand, compositional recovery showed a negative and significant correlation with link‐weighted connectance and generality.
FIGURE 4.
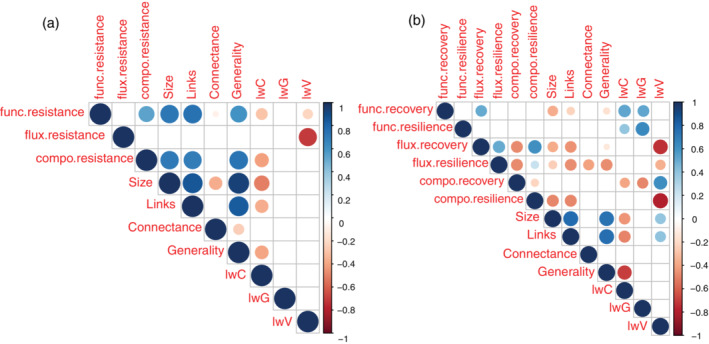
Correlation between stability components and trophic networks properties. (a) Correlation between trophic network structure metrics measured on phase HW3 and the resistance of functional, compositional and energy fluxes stability. (b) Correlation between trophic network structure metrics measured at the end of the recovery phase and the recovery and resilience of functional, compositional and energy fluxes stability. The circle size and color indicate the size and sign of the correlation. Only significant correlations (p of the Pearson's correlation coefficient < 0.05) are shown.
DISCUSSION
Our study shows that repeated extreme climate events may reduce the complexity of the unweighted network structure in the short term. Yet, at least in our simplified freshwater lentic ecosystem, those effects were short‐lived. At the end of the experiment, no single unweighted network property was still affected by the reoccurring HWs, suggesting that the food web's unweighted structure may be regained after extreme climatic events. The initial reduction in unweighted network complexity, though, was positively correlated with decreased functional resistance (Figure 4). Topological network complexity after experimental perturbation was also positively correlated with compositional resistance. That is, compositional and functional resistance were high where topological network complexity remained high. Consistently, in the reoccurring HWs treatment, a decline in unweighted network complexity was reflected by a significant reduction in compositional resistance.
Those results are in line with the body of theoretical and empirical work that has linked reduced network complexity to a decline in ecosystem functioning (Eisenhauer et al., 2019; Morris, 2010; Sebastián‐González et al., 2020; Yuan et al., 2021). Additionally, a recent study has shown that an experimental reduction in unweighted trophic network complexity (removal of high‐level consumers) can significantly reduce both compositional and functional resistance (White et al., 2020). As such, compositional and functional resistance appear to be positively correlated across ecosystem types and despite the nature of disturbance applied (Hillebrand et al., 2018; Polazzo & Rico, 2021; Urrutia‐Cordero et al., 2022; White et al., 2020). On the other hand, we did not find any correlation between trophic network complexity and the resistance of energy flux immediately after the temperature manipulations.
HWs may act essentially as pulse disturbances. A recent synthesis of the effects of pulse disturbance on community multidimensional stability has shown that community's functional responses might be initially severely impacted by pulse perturbation, but function is generally recovered within the experimental time (Hillebrand & Kunze, 2020). Conversely, community multivariate composition appears to recover substantially slower, or to not recover at all, after a pulse perturbation (Hillebrand & Kunze, 2020), suggesting that compositional and functional stability dynamics may follow different pathways (Hillebrand & Kunze, 2020; Ross et al., 2021; White et al., 2020).
In our study, we observed an overall increase in link‐weighted network complexity in both temperature treatments by the end of the experiment (Figure 2). Most of the studies to date have only investigated the effects of chronic warming on topological network properties, and they have found a general reduction in complexity (Fussmann et al., 2014; O'Gorman et al., 2019). Yet, our study aligns with the findings of Kortsch et al. (2021), who found an increase in link‐weighted network complexity over more than three decades in the Baltic Sea, probably related to climate change and to the effect of warming on species metabolism. In our study, this increase in link‐weighted complexity was found to be negatively correlated with compositional recovery (Figure 4). Consistently, both HW treatments significantly reduced compositional recovery, and community composition was significantly modified by both treatments at the end of the experiment. Previous studies have shown that changes in composition may allow a complete functional recovery after pulse disturbance (Hillebrand et al., 2018; Polazzo, Marina, et al., 2022). Complete functional recovery can be achieved because pulse disturbances may select for different compositions which can maintain functional level under disturbance if there is functional redundancy (Yachi & Loreau, 1999). Yet, we also show that the compositional change promoted by both types of heatwaves is associated with an increase in link‐weighted network complexity. Furthermore, the recovery of energy flux (a proxy for interaction strengths) was negatively correlated with compositional recovery (Figure 4). In other words, if total energy flux increase over time, community composition will further depart from control conditions, supporting the hypothesis that changes in interactions strength are linked to compositional divergence (Polazzo, Marina, et al., 2022).
All the different components of the energy flux stability were negatively correlated with link‐weighted vulnerability, which declined in both treatments following an increase in energy flux, although not significantly (Appendix S1: Figure S6). Yet, excluding vulnerability, we found no significant correlations between any other energy flux stability property and link‐weighted connectance and generality. The absence of a significant relationship between these link‐weighted network properties and the stability components of the energy flux suggests that both link‐weighted network complexity and total energy flux might influence the community composition independently. Therefore, the way interaction strength is organized within the network (i.e., link‐weighted network complexity), and the intensity (i.e., total interaction strength) are associated to changes in community composition after pulse disturbance and influence functional levels. The relevance of biotic interactions in determining community structure and functional level under disturbance has been already showed empirically in planktonic communities (Gaedke et al., 2010; Murphy et al., 2020). Our results, align with these previous findings, showing that the reoccurring HW disturbance caused an initial significant decline in functional resistance and modified community composition. Still, this HW‐driven shift in community composition was associated to an increase in link‐weighted generality (Kortsch et al., 2021). Such increase in link‐weighted network complexity consequently increased functional resilience through which functional recovery could be achieved within the experimental time (Polazzo, Marina, et al., 2022).
Finally, our analysis of the overall functional, compositional, and of energy flux stability summarizes our findings obtained when studying the different stability components. It shows that overall functional stability was not affected by either treatment. Still, the retainment of functional stability was linked to a significant reduction of the overall compositional stability in both temperature treatments. This is, even though compositional stability was significantly reduced, functional stability could be maintained. The changes in overall compositional stability were also paired to an increase in overall flux stability. Hence, HWs modify community composition and increase the overall energy flux within the food web, boosted by the temperature‐induced increase in metabolism. This increase in energy flux produces an increase in the trophic network complexity and preserves functional stability (biomass stock).
Our findings have important implications for ecosystem management and for projecting the effects of (future) extreme climatic events and climate change on trophic networks and community stability. First, preserving the topology/structure of the network appears crucial to protect both compositional and functional stability, as reductions in topological complexity were associated with a reduction in functional as well as compositional resistance. The topology of a network is fragile, and can be modified in several ways, for example, by a species loss (and the relative reduction of links and link density), by the introduction of alien species, or by the reduction in connectivity between patches in a landscape. Second, functional recovery and resilience were positively associated to an increase in link‐weighted network complexity, which however, came at the cost of increased compositional dissimilarity (e.g., reduced compositional recovery). Given the different management goals of different stakeholders (e.g., agriculture or aquaculture managers will likely privilege functional stability over compositional stability, whereas managers of natural protected areas might want to maintain compositional stability), tailoring specific protection measures to different objectives does seem a promising way, although needing careful planning. Finally, even though the effects of the reoccurring HWs on compositional and functional stability were somehow stronger compared to the long, moderate heatwave, the latter had a larger effect on the stability of energy flux and network complexity. These observations suggest that constant warming, via its effects on metabolism, causes a larger increase in the individual energetic demand compared to intermittent heat pulses. This higher energetic demand under constant warming is translated into stronger energy flux over time and increased network link‐weighted complexity.
This study shows that all the nuances of climate change are likely to have profound implications for community stability and trophic network complexity. Yet, here we present an overarching approach to investigate the effects of environmental change on multidimensional stability through the lens of trophic network complexity. The results of this study can be used to evaluate policy‐targeted endpoints and provides helpful insights for the preservation of ecosystems stability under global change.
AUTHOR CONTRIBUTIONS
Francesco Polazzo, Markus Hermann, and Andreu Rico designed the study. Francesco Polazzo modeled the unweighted and weighted food web properties. Melina Crettaz‐Minaglia calculated species biomass and built the interactions links together with Francesco Polazzo. Francesco Polazzo performed the statistical analysis and wrote the first manuscript draft. All the authors contributed substantially to the interpretation of the data and to the final written version of the manuscript.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Supporting information
Appendix S1.
ACKNOWLEDGMENTS
This study has been funded by the H2020‐MSCA‐ITN ECORISK2050 project of the European Commission (Grant Agreement no. 813124). A. Rico is supported by the Talented Researcher Support Programme—Plan GenT (CIDEGENT/2020/043) of the Generalitat Valenciana.
Polazzo, Francesco , Hermann Markus, Crettaz‐Minaglia Melina, and Rico Andreu. 2023. “Impacts of Extreme Climatic Events on Trophic Network Complexity and Multidimensional Stability.” Ecology 104(2): e3951. 10.1002/ecy.3951
Handling Editor: Helmut Hillebrand
Funding information European Commission, Grant/Award Numbers: 813124, ECORISK2050, H2020‐MSCA‐ITN; Generalitat Valenciana, Grant/Award Number: CIDEGENT/2020/043
DATA AVAILABILITY STATEMENT
Data (Polazzo, Hermann, et al., 2022) are available in Zenodo at https://doi.org/10.5281/zenodo.7310916.
REFERENCES
- Alcaraz, M. , Saiz E., Calbet A., Trepat I., and Broglio E.. 2003. “Estimating Zooplankton Biomass through Image Analysis.” Marine Biology 143: 307–15. [Google Scholar]
- Allesina, S. , and Tang S.. 2012. “Stability Criteria for Complex Ecosystems.” Nature 483: 205–8. [DOI] [PubMed] [Google Scholar]
- Barneche, D. R. , Hulatt C. J., Dossena M., Padfield D., Woodward G., Trimmer M., and Yvon‐Durocher G.. 2021. “Warming Impairs Trophic Transfer Efficiency in a Long‐Term Field Experiment.” Nature 592: 76–9. [DOI] [PubMed] [Google Scholar]
- Barnes, A. D. , Jochum M., Lefcheck J. S., Eisenhauer N., Scherber C., O'Connor M. I., de Ruiter P., and Brose U.. 2018. “Energy Flux: The Link between Multitrophic Biodiversity and Ecosystem Functioning.” Trends in Ecology & Evolution 33(3): 186–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardini, V. , Solimini A. G., and Carchini G.. 2000. “Application of an Image Analysis System to the Determination of Biomass (Ash Free Dry Weight) of Pond Macroinvertebrates.” Hydrobiologia 439: 179–82. [Google Scholar]
- Brown, J. H. , Gillooly J. F., Allen A. P., Savage V. M., and West G. B.. 2004. “Toward a Metabolic Theory of Ecology.” Ecology 85: 1771–89. [Google Scholar]
- Donohue, I. , Hillebrand H., Montoya J. M., Petchey O. L., Pimm S. L., Fowler M. S., Healy K., et al. 2016. “Navigating the Complexity of Ecological Stability.” Ecology Letters 19: 1172–85. [DOI] [PubMed] [Google Scholar]
- Donohue, I. , Petchey O. L., Montoya J. M., Jackson A. L., Mcnally L., Viana M., Healy K., Lurgi M., O'Connor N. E., and Emmerson M. C.. 2013. “On the Dimensionality of Ecological Stability.” Ecology Letters 16: 421–9. [DOI] [PubMed] [Google Scholar]
- Eisenhauer, N. , Schielzeth H., Barnes A. D., Barry K. E., Bonn A., Brose U., Bruelheide H., et al. 2019. “A Multitrophic Perspective on Biodiversity–Ecosystem Functioning Research.” Advances in Ecological Research 61: 1–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fussmann, K. E. , Schwarzmüller F., Brose U., Jousset A., and Rall B. C.. 2014. “Ecological Stability in Response to Warming.” Nature Climate Change 4(3): 206–10. [Google Scholar]
- Gaedke, U. , Ruhenstroth‐Bauer M., Wiegand I., Tirok K., Aberle N., Breithaupt P., Lengfellner K., Wohlers J., and Sommer U.. 2010. “Biotic Interactions May Overrule Direct Climate Effects on Spring Phytoplankton Dynamics.” Global Change Biology 16: 1122–36. [Google Scholar]
- Gauzens, B. , Barnes A., Giling D. P., Hines J., Jochum M., Lefcheck J. S., Rosenbaum B., Wang S., and Brose U.. 2019. “fluxweb: An R Package to Easily Estimate Energy Fluxes in Food Webs.” Methods in Ecology and Evolution 10: 270–9. [Google Scholar]
- Gray, C. , Ma A., Perkins D., Hudson L., Figueroa D., and Woodward G.. 2015. “Database of Trophic Interactions.” Zenodo. Dataset. 10.5281/zenodo.1375. [DOI]
- Grilli, J. , Rogers T., and Allesina S.. 2016. “Modularity and Stability in Ecological Communities.” Nature Communications 7(1): 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermann, M., R. Jansen, J. van de Glind, E. T. H. M. Peeters, and P. J. Van den Brink. 2022. “A Transportable Temperature and Heatwave Control Device (TENTACLE) for Laboratory and Field Simulations of Different Climate Change Scenarios in Aquatic Micro‐ and Mesocosms.” HardwareX 11: e00307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillebrand, H. , Dürselen C. D., Kirschtel D., Pollingher U., and Zohary T.. 1999. “Biovolume Calculation for Pelagic and Benthic Microalgae.” Journal of Phycology 35: 403–24. [Google Scholar]
- Hillebrand, H. , and Kunze C.. 2020. “Meta‐Analysis on Pulse Disturbances Reveals Differences in Functional and Compositional Recovery across Ecosystems.” Ecology Letters 23: 575–85. [DOI] [PubMed] [Google Scholar]
- Hillebrand, H. , Langenheder S., Lebret K., Lindström E., Östman Ö., and Striebel M.. 2018. “Decomposing Multiple Dimensions of Stability in Global Change Experiments.” Ecology Letters 21: 21–30. [DOI] [PubMed] [Google Scholar]
- Ingrisch, J. , and Bahn M.. 2018. “Towards a Comparable Quantification of Resilience.” Trends in Ecology and Evolution 33: 251–9. [DOI] [PubMed] [Google Scholar]
- IPCC . 2013. “CLIMATE CHANGE 2013 ‐ The Physical Science Basis.” In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change , edited by Stocker T. F., Qin D., G.‐K. Plattner , Tignor M., Allen S. K., Boschung J., Nauels A., Xia Y., Bex V., and P. M. Midgley . Cambridge, UK and New York: Cambridge University Press, 1535 pp.
- IPCC. 2021. “Climate Change 2021: The Physical Science Basis.” In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, edited by Masson‐Delmotte V., Zhai P., Pirani A., Connors S. L., Berger C. Péan, S., Caud N., Chen Y., Goldfarb L., Gomis M. I., Huang M., Leitzell K., E. Lonnoy, Matthews J. B. R., Maycock T. K., Waterfield T., Yelekçi O., Yu R., and Zhou B.. Cambridge, UK and New York: Cambridge University Press. 10.1017/9781009157896. [DOI]
- Jentsch, A. , Kreyling J., and Beierkuhnlein C.. 2007. “A New Generation of Climate‐Change Experiments: Events, Not Trends.” Frontiers in Ecology and the Environment 5(7): 365–74. [Google Scholar]
- Jochum, M. , Barnes A. D., Brose U., Gauzens B., Sünnemann M., Amyntas A., and Eisenhauer N.. 2021. “For flux's Sake: General Considerations for Energy‐Flux Calculations in Ecological Communities.” Ecology and Evolution 11: 12948–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kéfi, S. , Domínguez‐García V., Donohue I., Fontaine C., Thébault E., and Dakos V.. 2019. “Advancing our Understanding of Ecological Stability.” Ecology Letters 22: 1349–56. [DOI] [PubMed] [Google Scholar]
- Kortsch, S. , Frelat R., Pecuchet L., Olivier P., Putnis I., Bonsdorff E., Ojaveer H., et al. 2021. “Disentangling Temporal Food Web Dynamics Facilitates Understanding of Ecosystem Functioning.” Journal of Animal Ecology 90: 1205–16. [DOI] [PubMed] [Google Scholar]
- Landi, P. , Minoarivelo H. O., Brännström Å., Hui C., and Dieckmann U.. 2018. “Complexity and Stability of Ecological Networks: A Review of the Theory.” Population Ecology 60: 319–45. [Google Scholar]
- Landry, M. , Haas L., and Fagerness V.. 1984. “Dynamics of Microbial Plankton Communities: Experiments in Kaneohe Bay Hawaii.” Marine Ecology Progress Series 16: 127–33. [Google Scholar]
- Lüdecke, D. , Makowski D., and Waggoner P.. 2020. “performance: Assessment of Regression Models Performance.” R Package Version 0.4.4. CRAN.R. https://CRAN.R-project.org/package=performance.
- MacArthur, R. 1955. “Fluctuations of Animal Populations and a Measure of Community Stability.” Ecology 36: 533. [Google Scholar]
- Maestre, F. T. , Quero J. L., Gotelli N. J., Escudero A., Ochoa V., Delgado‐Baquerizo M., García‐Gómez M., et al. 2012. “Plant Species Richness and Ecosystem Multifunctionality in Global Drylands.” Science 335: 214–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May, R. M. 1972. “Will a Large Complex System be Stable?” Nature 238: 413–4. [DOI] [PubMed] [Google Scholar]
- May, R. M. 1973. “Stability and Complexity in Model Ecosystems.” Monographs in Population Biology 6: 1–235. [PubMed] [Google Scholar]
- McCann, K. , Hastings A., and Huxel G. R.. 1998. “Weak Trophic Interactions and the Balance of Nature.” Nature 395: 794–8. [Google Scholar]
- McCann, K. S. 2000. “The Diversity–Stability Debate.” Nature 405: 228–33. [DOI] [PubMed] [Google Scholar]
- Meehl, G. A. , and Tebaldi C.. 2004. “More Intense, more Frequent, and longer Lasting Heat Waves in the 21st Century.” Science 305: 994–7. [DOI] [PubMed] [Google Scholar]
- Montoya, J. M. , Pimm S. L., and Solé R. V.. 2006. “Ecological Networks and their Fragility.” Nature 442: 259–64. [DOI] [PubMed] [Google Scholar]
- Morris, R. J. 2010. “Anthropogenic Impacts on Tropical Forest Biodiversity: A Network Structure and Ecosystem Functioning Perspective.” Philosophical Transactions of the Royal Society B: Biological Sciences 365: 3709–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy, G. E. P. , Romanuk T. N., and Worm B.. 2020. “Cascading Effects of Climate Change on Plankton Community Structure.” Ecology and Evolution 10: 2170–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerken, I. , Goldenber S. U., Ferreir C. M., Ullah H., and Conne S. D.. 2020. “Trophic Pyramids Reorganize when Food Web Architecture Fails to Adjust to Ocean Change.” Science 369: 829–32. [DOI] [PubMed] [Google Scholar]
- Neutel, A. M. , Heesterbeek J. A. P., and De Ruiter P. C.. 2002. “Stability in Real Food Webs: Weak Links in Long Loops.” Science 296: 1120–3. [DOI] [PubMed] [Google Scholar]
- Neutel, A. M. , Heesterbeek J. A. P., Van De Koppel J., Hoenderboom G., Vos A., Kaldeway C., Berendse F., and De Ruiter P. C.. 2007. “Reconciling Complexity with Stability in Naturally Assembling Food Webs.” Nature 449: 599–602. [DOI] [PubMed] [Google Scholar]
- O'Connor, M. I. , Piehler M. F., Leech D. M., Anton A., and Bruno J. F.. 2009. “Warming and Resource Availability Shift Food Web Structure and Metabolism.” PLoS Biology 7: e1000178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Gorman, E. J. , Petchey O. L., Faulkner K. J., Gallo B., Gordon T. A. C., Neto‐Cerejeira J., Ólafsson J. S., Pichler D. E., Thompson M. S. A., and Woodward G.. 2019. “A Simple Model Predicts how Warming Simplifies Wild Food Webs.” Nature Climate Change 9: 611–6. [Google Scholar]
- Oksanen, J. , Simpson G., Blanchet F., Kindt R., Legendre P., Minchin P., O'Hara R., et al. 2022. “vegan: Community Ecology Package.” R Package Version 2.6‐4. https://CRAN.R-project.org/package=vegan.
- Pennekamp, F. , Pontarp M., Tabi A., Altermatt F., Alther R., Choffat Y., Fronhofer E. A., et al. 2018. “Biodiversity Increases and Decreases Ecosystem Stability.” Nature 563: 109–12. [DOI] [PubMed] [Google Scholar]
- Petchey, O. L. , Brose U., and Rall B. C.. 2010. “Predicting the Effects of Temperature on Food Web Connectance.” Philosophical Transactions of the Royal Society B: Biological Sciences 365: 2081–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilosof, S. , Porter M. A., Pascual M., and Kéfi S.. 2017. “The Multilayer Nature of Ecological Networks.” Nature Ecology & Evolution 1: 1–9. [DOI] [PubMed] [Google Scholar]
- Pimm, S. L. 1984. “The Complexity and Stability of Ecosystems.” Nature 307: 321–6. [Google Scholar]
- Pinheiro, J. , Bates D., DebRoy S., Sarkar D., and R Core Team . 2021. “nlme: Linear and Nonlinear Mixed Effects Models.” R‐project. https://cran.r-project.org/package=nlme.
- Polazzo, F. , dos Anjos T. B. O., Arenas‐Sánchez A., Romo S., Vighi M., and Rico A.. 2021. “Effect of Multiple Agricultural Stressors on Freshwater Ecosystems: The Role of Community Structure, Trophic Status, and Biodiversity‐Functioning Relationships on Ecosystem Responses.” Science of The Total Environment 807: 151052. [DOI] [PubMed] [Google Scholar]
- Polazzo, F. , Hermann M., Crettaz‐Minaglia M., and Rico A.. 2022. “Data Supporting: Impacts of Extreme Climatic Events on Trophic Network Complexity and Multidimensional Stability.” Zenodo. Dataset. 10.5281/zenodo.7310916. [DOI] [PMC free article] [PubMed]
- Polazzo, F. , Marina T. I., Crettaz‐Minaglia M., and Rico A.. 2022. “Food Web Rewiring Drives Long‐Term Compositional Differences and Late‐Disturbance Interactions at the Community Level.” Proceedings of the National Academy of Sciences of the United States of America 119: e2117364119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polazzo, F. , and Rico A.. 2021. “Effects of Multiple Stressors on the Dimensionality of Ecological Stability.” Ecology Letters 24: 1594–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polazzo, F. , Roth S. K., Hermann M., Mangold‐Döring A., Rico A., Sobek A., Van den Brink P. J., and Jackson M. C.. 2022. “Combined Effects of Heatwaves and Micropollutants on Freshwater Ecosystems: Towards an Integrated Assessment of Extreme Events In Multiple Stressors Research.” Global Change Biology 28: 1248–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. http://www.R-project.org. [Google Scholar]
- Radchuk, V. , De Laender F., Cabral J. S., Boulangeat I., Crawford M., Bohn F., De Raedt J., et al. 2019. “The Dimensionality of Stability Depends on Disturbance Type.” Ecology Letters 22: 674–84. [DOI] [PubMed] [Google Scholar]
- Ross, S. R. P. J. , García Molinos J., Okuda A., Johnstone J., Atsumi K., Futamura R., Williams M. A., et al. 2021. “Predators Mitigate the Destabilising Effects of Heatwaves on Multitrophic Stream Communities.” Global Change Biology 28: 403–16. [DOI] [PubMed] [Google Scholar]
- Ruttner‐Kolisko, A. 1977. “Sugestions for Biomass Calculations of Plankton Rotifers.” Archiv für Hydrobiologie 8: 71–6. [Google Scholar]
- Saravia, L. 2022. “multiweb: Ecological Network Analyses Including Multiplex Networks.” R package version 0.6.10.0000. https://github.com/lsaravia/multiweb.
- Schneider, C. A. , Rasband W. S., and Eliceiri K. W.. 2012. “NIH Image to ImageJ: 25 Years of Image Analysis.” Nature Methods 9: 671–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastián‐González, E. , Morales‐Reyes Z., Botella F., Naves‐Alegre L., Pérez‐García J. M., Mateo‐Tomás P., Olea P. P., et al. 2020. “Network Structure of Vertebrate Scavenger Assemblages at the Global Scale: Drivers and Ecosystem Functioning Implications.” Ecography 43: 1143–55. [Google Scholar]
- Sun, J. , and Liu D.. 2003. “Geometric Models for Calculating Cell Biovolume and Surface Area for Phytoplankton.” Journal of Plankton Research 25: 1331–46. [Google Scholar]
- Thébault, E. , and Fontaine C.. 2010. “Stability of Ecological Communities and the Architecture of Mutualistic and Trophic Networks.” Science 329: 853–6. [DOI] [PubMed] [Google Scholar]
- Thomas, C. I. , José M. M., Jordi B., Nico B., Lee B., Carsten F. D., François E., et al. 2009. “Review: Ecological Networks—beyond Food Webs.” Journal of Animal Ecology 78: 253–69. [DOI] [PubMed] [Google Scholar]
- Toju, H. , Yamamichi M., Guimarães P. R., Olesen J. M., Mougi A., Yoshida T., and Thompson J. N.. 2017. “Species‐Rich Networks and Eco‐Evolutionary Synthesis at the Metacommunity Level.” Nature Ecology & Evolution 1: 24. [DOI] [PubMed] [Google Scholar]
- Ullah, H. , Nagelkerken I., Goldenberg S. U., and Fordham D. A.. 2018. “Climate Change Could Drive Marine Food Web Collapse through Altered Trophic Flows and Cyanobacterial Proliferation.” PLoS Biology 16: 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrutia‐Cordero, P. , Langenheder S., Striebel M., Angeler D. G., Bertilsson S., Eklöv P., Hansson L. A., et al. 2022. “Integrating Multiple Dimensions of Ecological Stability into a Vulnerability Framework.” Journal of Ecology 110: 374–86. [Google Scholar]
- White, L. , O'Connor N. E., Yang Q., Emmerson M. C., and Donohue I.. 2020. “Individual Species Provide Multifaceted Contributions to the Stability of Ecosystems.” Nature Ecology and Evolution 4: 1594–601. [DOI] [PubMed] [Google Scholar]
- Woolway, R. I. , Albergel C., Frölicher T. L., and Perroud M.. 2022. “Severe Lake Heatwaves Attributable to Human‐Induced Global Warming.” Geophysical Research Letters 49: 1–10.35928231 [Google Scholar]
- Woolway, R. I. , Jennings E., Shatwell T., Golub M., Pierson D. C., and Maberly S. C.. 2021. “Lake Heatwaves under Climate Change.” Nature 589: 402–7. [DOI] [PubMed] [Google Scholar]
- Yachi, S. , and Loreau M.. 1999. “Biodiversity and Ecosystem Productivity in a Fluctuating Environment: The Insurance Hypothesis.” Proceedings of the National Academy of Sciences of the United States of America 96: 1463–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan, M. M. , Guo X., Wu L., Zhang Y., Xiao N., Ning D., Shi Z., et al. 2021. “Climate Warming Enhances Microbial Network Complexity and Stability.” Nature Climate Change 11: 343–8. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1.
Data Availability Statement
Data (Polazzo, Hermann, et al., 2022) are available in Zenodo at https://doi.org/10.5281/zenodo.7310916.


