Episodic Plate Tectonics on Europa: Evidence for Widespread Patches of Mobile‐Lid Behavior in the Antijovian Hemisphere

Abstract

A nearly pole‐to‐pole survey near 140°E longitude on Europa revealed many areas that exhibit past lateral surface motions, and these areas were examined to determine whether the motions can be described by systems of rigid plates moving across Europa's surface. Three areas showing plate‐like behavior were examined in detail to determine the sequence of events that deformed the surface. All three areas were reconstructed to reveal the original pre‐plate motion surfaces by performing multi‐stage rotations of plates in spherical coordinates. Several motions observed along single plate boundaries were also noted in previous works, but this work links together isolated observations of lateral offsets into integrated systems of moving plates. Not all of the surveyed surface could be described by systems of rigid plates. There is evidence that the plate motions did not all happen at the same time, and that they are not happening today. We conclude that plate tectonic‐like behavior on Europa occurs episodically, in limited regions, with less than 100 km of lateral motion accommodated along any particular boundary before plate motions cease. Europa may represent a world perched on the theoretical boundary between stagnant and mobile lid convective behavior, or it may represent an additional example of the wide variations in possible planetary convective regimes. Differences in observed strike‐slip sense and plate rotation directions between the northern and southern hemispheres raise the question of whether tidal forces may influence plate motions.

Key Points

• Several regions on Europa can be reconstructed as systems of rigid plates

• Plate motions on Europa are confined to regional patches and limited time periods

• Motions along plate boundaries are limited to less than 100 km and appear to be currently inactive

1. Introduction

The theory of plate tectonics describes how a planet's lithosphere is divided into a global network of multiple rigid blocks (plates) that move relative to each other, accommodating deformation primarily in narrow zones around the edges of the plates. Earth is the only planetary body known to operate under a plate tectonic system. Other terrestrial planets lack fully developed, present day plate tectonics, though Venus may demonstrate localized subduction‐like behavior (Davaille et al., 2017) and Mars may have experienced plate tectonic‐like behavior in its early history (e.g., Nimmo & Stevenson, 2000). Analyses of plate‐like motions on Jupiter's moon Europa have provided insight into the formation and evolution of specific feature types and provided a means of testing processes and assumptions based on terrestrial plate tectonics (Schenk & McKinnon, 1989). The sequential reconstruction of Europa's surface in northern Falga Regio by Kattenhorn and Prockter (2014) raised the possibility of a full plate tectonic system operating on Europa. If true, Europa would be the only known world besides Earth to have plate tectonics. This result is of interest for studies of comparative planetology, and raises questions about how the convective systems on Earth and Europa that underlie their plate tectonic behavior are similar, even though the material differences (silicate vs. ice) are vast. Quantifying the direction, age, and magnitude of plate motion is important for constraining models of Europa's ice shell and for understanding resurfacing mechanisms responsible for Europa's anomalously young surface age (∼40–90 Myr, Bierhaus et al., 2009). Plate motions on Europa also have astrobiological importance, since subsumed surface material could drive the flow of nutrients to Europa's subsurface ocean. In this paper, we describe further observations of apparent plate motions on Europa, highlighting the ways in which the behavior of Europa's plate tectonic system is Earth‐like and the ways in which it is decidedly not.

1.1. Previous Observations of Lateral Motions on Europa

Evidence for lateral motion of Europa's surface ice comes from images obtained by the Voyager missions in 1979 and the Galileo mission in the late 1990s. Images show that most of Europa's surface is covered by ridges and bands (Kattenhorn & Hurford, 2009; Prockter & Patterson, 2009), occasionally interrupted by various forms of chaotic terrain (Collins & Nimmo, 2009). The ridges and bands form a complex, overlapping network of linear tectonic features. In this network, older linear features can be used as “piercing points” when they are crosscut and offset by deformation associated with a younger tectonic feature. Careful attention to the sequence of tectonic events and realignment of piercing points are the keys to reconstructing the history of tectonics on Europa's surface using available imagery.

The first plate‐like reconstruction of Europa's surface was performed by Schenk and McKinnon (1989) in a region of wedge‐shaped bands observed in Voyager images. They showed that offset surface features (or piercing points, as defined above) can be reconstructed by closing a particular set of relatively younger wedge‐shaped bands. Their reconstruction implied 25 km of lateral motion between adjacent blocks of Europa's ice shell due to the opening of the bands, and provided the first hints of mobile lid behavior on Europa.

Pappalardo and Sullivan (1996) used Voyager 2 imagery to reconstruct a single 900‐km‐long band named Thynia Linea. They identified 12 piercing points and showed how the band can be reconstructed with minimal gaps by moving the two edges back together. Because Thynia is so long relative to the radius of Europa, its deformation is best analyzed using a spherical approach. Pappalardo and Sullivan (1996) found that the opening of Thynia can be modeled as a plate‐like motion around a best‐fit rotation pole near the southern end of the band, but that variations in the amount of opening indicate non‐rigid behavior of the plates at the scale of Thynia. Sullivan et al. (1998) reconstructed a small area surrounding Yelland Linea dominated by wedge‐shaped dark bands. They divided the area into 20 plates and found that closing the bands on a flat plane brought the plates back together, with a small gap left in one area where surface material was apparently consumed. Tufts et al. (2000) performed a stepwise reconstruction in the same area around Yelland, showing that the plate motions occurred in a few stages. They also reconstructed the dark band Acacallis Linea (which they call “the sickle”) by pushing the edges back together, showing that pure dilation is a good explanation for the east‐west trending portion of this feature.

Several mapping and reconstruction studies have identified areas of surface convergence, where material has been lost (e.g., Prockter & Pappalardo, 2000; Sarid et al., 2002). Convergence is more challenging to identify than spreading or strike‐slip because the loss of terrain removes pre‐existing ridges, and thus, the information generally used to reconstruct past motions, but it does occur on Europa. For example, a detailed study of rigid plate motions in the Castalia Macula region, which focused on reconstructing strike‐slip offsets using a pole‐of‐rotation approach appropriate for plates moving on a sphere, revealed large‐scale zones of convergence (Patterson et al., 2006). Convergence had been noted in the area in previous work (Sarid et al., 2002). Convergence zones are band‐like in morphology but lack the symmetrical lineations typical of dilational bands and generally do not exhibit mutually parallel sides (Greenberg, 2004; Kattenhorn & Hurford, 2009; Prockter & Patterson, 2009; Sarid et al., 2002).

Kattenhorn and Prockter (2014) took the next step in plate reconstructions by examining a large area of Europa as a system of interacting plate boundaries, and reconstructing surface motions in multiple stages. Taking this approach revealed that large amounts of surface convergence were necessary to explain the motions and rotations in the system of plates, as discussed in more detail below in Section 3.1. The study presented here extends the approach of Kattenhorn and Prockter to include more areas, more plates, and a spherical geometry, as described in Section 2.

1.2. Approach to Using Terrestrial Plate Tectonic Ideas on Europa

Key to reconstructing plate motions on Europa and relating them to the terrestrial plate tectonics paradigm, is the adoption of two central assumptions: plate boundaries are narrow, and plates behave rigidly (i.e., all deformation associated with the motions of a plate is accommodated at the boundaries of the plate; McKenzie & Parker, 1967; Morgan, 1968). Numerous planar reconstructions of Europa's tectonically disrupted surface have been performed implicitly assuming plate rigidity (e.g., Prockter et al., 2002; Sarid et al., 2002; Tufts et al., 1999). Bands and ridges generally delineate plate boundaries in those reconstructions and they are narrow, in a relative sense, with respect to the plates they define. Previous work reconstructing plate motions on Europa using a spherical geometry has indicated that non‐rigid plate behavior could accommodate some inconsistencies associated with specific boundaries or boundary types (Pappalardo & Sullivan, 1996; Patterson et al., 2006). However, more recent work that explicitly tests the assumption of plate rigidity on Europa using the kinematic analysis of triple junctions indicates rigid behavior should be considered the norm, at least for plate boundaries that accommodate extension or strike‐slip motion (Patterson & Head, 2007). The reconstructions presented in this paper are founded on the central assumptions behind plate tectonics, so we must keep these assumptions in mind as we evaluate how well the plate tectonic paradigm serves to describe motions on Europa.

2. General Methodology

There are two approaches that could be used as a basis for plate reconstructions on Europa: an observational fitting method that subjectively balances the geology of the plate boundary material with a visual interpretation of best fit, or a statistical approach that is agnostic about the material of the plate boundaries and tries to optimize the alignment of predefined piercing points. As outlined below, this study adopts an observational approach to plate reconstruction on Europa similar to Kattenhorn and Prockter (2014), with the important addition of performing all plate motions in spherical geometry. In Section 3, we describe the application of this methodology to three areas in the antijovian hemisphere, stretching from 70°N to 70°S near longitude 145°E. For the Castalia area (Section 3.2) we compare our approach for reconstructing plate motions to the statistically‐based inverse modeling approach used by Patterson et al. (2006).

2.1. Image Data

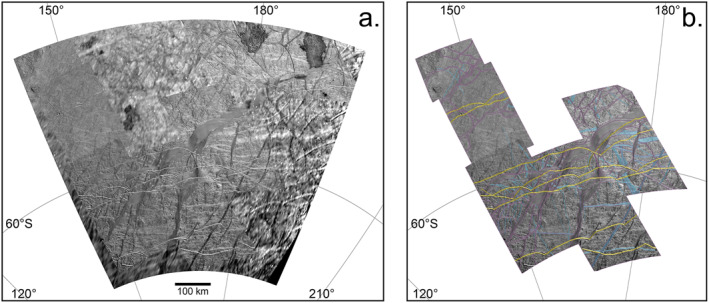
We performed the plate definition, mapping, and reconstructions on an image mosaic (Figure 1) constructed using all of the available contiguous, high incidence angle, regional‐scale imagery on the antijovian hemisphere from the Galileo Solid State Imaging experiment. Input Galileo image sequences important for the plate reconstructions are listed in Table 1. The mosaic was prepared in ISIS3 software, registered to the USGS global image mosaic for Europa for geographic control points, layered to place highest resolution images on top, and resampled to a pixel scale of 165 m. The ISIS‐formatted mosaic can be downloaded from the data repository associated with this article at Collins et al. (2022).

Figure 1.

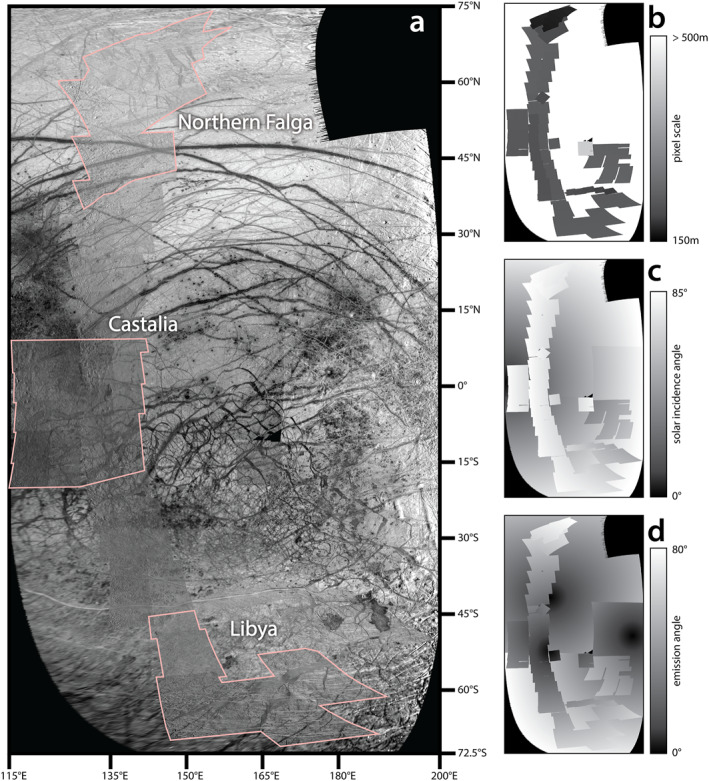
(a) Image mosaic used for this study. The three study areas discussed in Section 3 are highlighted in pink. (b) Pixel scale of input images, on a linear gradient from 150 to 500 m. The area labeled as >500 m is composed of images with pixel scales of approximately 1.5 km (“background images” in Table 1). (c) Solar incidence angle for input images. Note that most of the study areas outlined in (a) are covered by near‐terminator imaging. (d) Emission angle to the spacecraft camera for the input images. Note that the Libya and Northern Falga study areas are only covered by images with oblique viewing angles.

Table 1.

Input Galileo Image Sequences Used for Constructing the High‐Resolution Base Mosaic

Galileo mosaic	Latitude range	Pixel scale (m)	Incidence angle	Emission angle
11ESREGMAP01	20.2°S–9.2°N	219–222	70.8°–85.5°	12.1°–36.6°
15ESREGMAP01	18.4°N–61.3°N	228–235	69.3°–87.6°	19.1°–64.1°
17ESNERTRM01	47.6°S–6.4°N	210–212	76.1°–84.9°	7.8°–41.3°
17ESREGMAP01	70.4°S–20°N	222–228	50.8°–85.6°	0°–68.5°
19ESNORLAT01	49.2°N–84.9°N	202	73.6°–88.6°	53.0°–90°
19ESNORPLN01	57.1°N–76.9°N	166–171	74.4°–85.5°	60.7°–90°
19ESREGMAP01	11.7°N–20.1°N	201–203	73.8°–90°	13.6°–29.7°
Other images in mosaic that are not used in plate reconstructions in this study
C3ESWEDGES01	18.9°S–10.2°S	421	71.8°–81.5°	13.0°–25.9°
14ESWEDGES01	36.7°S–12.5°S	230–238	34.1°–63.5°	24.2°–55.0°
17ESAGENOR01	44.4°S–38.7°S	187–206	50.6°–71.2°	34.2°–51.1°
Background images used in mosaic
G1ESGLOBAL01	50°S–85°N	1,570–1,582	0°–90°	0°–77°
14ESGLOCOL01	82°S–22°N	1,439–1,456	7°–90°	0°–90°

Note. This mosaic has been utilized in the community beyond our plate reconstruction project, and is sometimes referred to in conference abstracts as the “Supermosaic” (Laura & Beyer, 2021).

2.2. Definition of Plates and Plate Boundaries

The first step in each of the study areas is to define the boundaries of the moving plates. Plates represent blocks of crustal material that have translated rigidly across the surface, and we set the criteria for defining a plate according to this principle. For illustration purposes, Figure 2 shows a hypothetical section of Europa's surface that has been deformed by a series of rigid offsets, interpretable as plate motions.

Figure 2.

(a) Sketch of a hypothetical area on Europa with typical cross‐cutting tectonic features, created as an example to illustrate the details of plate definition and reconstruction. See text for discussion of lettered features. (b) Plates that would be defined based on this set of features. During any particular time step, the moving plate consists of one or more of these plates acting together. Only features W, X, and Y offset pre‐existing features, and so they define the edges of the moving plates, colored in purple. Feature Z is ignored for further analysis because it does not offset any features and postdates all plate boundaries.

To begin to define a plate, we find an area in which surface features are continuous. On Europa, the typical continuous surface features are ridges, though in some cases older pits, bands, or background plains textures may show the continuity of terrain. A ridge may curve, change direction, or may be overlapped by a newer ridge or chaos area, but a continuous ridge can always be interpolated along its trend when a newer feature interrupts it. If the interpolated line between the two ends of an interrupted feature is locally parallel to the trend of that feature, we consider the feature to be continuous. In Figure 2a, features Y and Z are both continuous across the entire scene; even though Z cuts across Y, the trend of Y may be followed without interruption where it crosses underneath Z. As an example of a discontinuous feature, feature S in Figure 2a is continuous from the left side until it becomes discontinuous when it meets feature W. Likewise, feature W is continuous from the top and from the bottom until it meets feature X in the center.

Once an area of continuous surface features is identified, we work outward in all directions until we find discontinuities in the surface. Often a more recent tectonic feature such as a ridge or a band will interrupt all of the preexisting features, and will exhibit a discontinuity that offsets all of the preexisting features. Such a feature is a prime candidate for a plate boundary. For example, working from the upper left corner of Figure 2a, features S, T, and U all become discontinuous when they meet features W and X, making W and X candidate plate boundaries. Feature V appears to be continuous under feature X, but this does not necessarily contradict the observations about S, T, and U, depending on the direction of motion; we will return to this point in Section 2.4.

To be flagged as a potential plate boundary, it is not enough just to crosscut a pre‐existing feature, there must be measurable offset. Feature V in Figure 2a crosscuts S and U, but there is no offset so this is not a plate boundary. Similarly, feature Z is the most recent feature, cutting across everything, but the crosscut features are continuous, so it exhibits no offset, so it is not a plate boundary. If we can find a set of candidate plate boundaries that completely surround a given area, we define that area to be a plate. Figure 2b shows the six plates that would be defined in the hypothetical example.

2.3. Time Sequence of Plate Boundaries

Once plate margins and the structures that function as plate boundaries have been identified, the next step is to determine the time sequence of plate boundary structure activity. Plate boundaries at the younger end of the sequence will crosscut and offset plate boundaries at the older end of the sequence. Figure 3a shows an older band crosscut and offset by two parallel younger plate boundaries. Some intersecting plate boundaries are active at the same time, forming triple junctions. Figure 3b shows an example of intersecting spreading bands that appear to have been active at the same time, forming triangular triple junction areas where the bands meet. A potential complication is that some plate boundary structures may be active early in the sequence and then reactivated later in the sequence.

Figure 3.

Time sequence examples for plate boundaries on Europa, initially defined by Sarid et al. (2002) and Patterson et al. (2006). Both examples are located near Castalia Macula, north is up. (a) Two parallel N‐S trending boundaries crosscut an older NE‐SW trending dark band that also forms a plate boundary. Plate motions occurred along the band first, and then along the two N‐S boundaries. (b) A NE‐SW trending dark band in the center of the image merges at either end at triple junctions with adjacent NW‐SE trending dark bands. All the bands form plate boundaries that were active at the same time.

We use the time sequence of plate boundaries to determine the minimum number of time steps necessary for the reconstruction. During each time step, multiple boundaries may be active. Non‐intersecting boundaries may or may not be active in the same time step, boundaries that meet at a triple junction must be active in the same time step, but crosscutting boundaries must be active in separate time steps.

2.4. Sequential Reconstruction Along Plate Boundaries

Reconstruction of plate motions is performed by sequentially undoing the deformation along the plate boundaries, starting with the most recent boundaries and working backward in time to the earliest boundary structures. During each time step, the goal is to bring piercing points (older features seen on either side of the plate boundary) back into alignment. For spreading boundaries or strike‐slip boundaries, this is a fairly straightforward task of moving the plates so as to minimize the distance between all of the matching piercing points. On a strike‐slip boundary, the plates are moved parallel to the boundary until the piercing points are aligned (Figure 4a). On a divergent boundary, the plates are moved so as to move their edges with their piercing points as close together as possible (Figure 4b). For contractional boundaries, it is not possible to minimize the distance between piercing points, since some of the pre‐existing terrain has been destroyed. Instead, the structures that serve as piercing points should be brought into alignment so that linear features can be extrapolated across the gap and meet with their matching features on the other side (Figure 4c). A firm rule is that plates cannot overlap during the course of these sequential motions, because that would indicate that two pieces of existing terrain occupied the same place at the same time; a logical impossibility.

Figure 4.

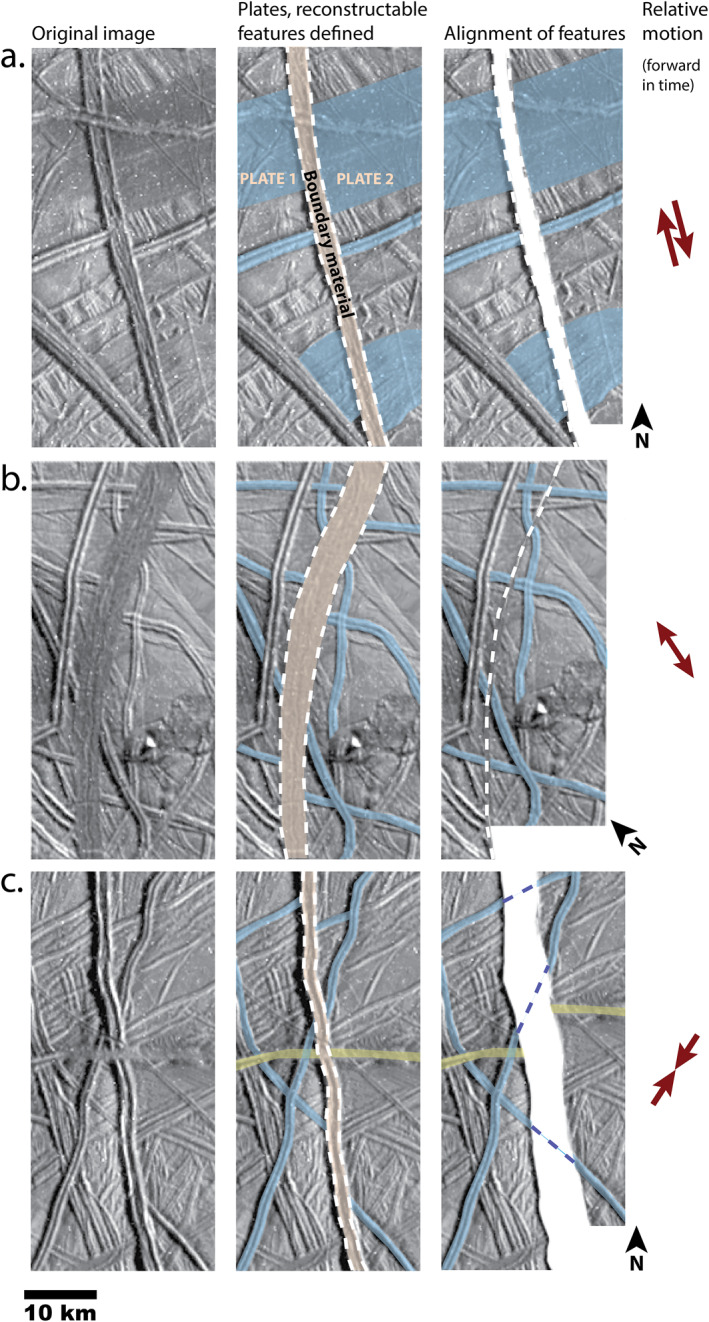
Examples of plate boundaries located near Castalia Macula on Europa, showing three different types of relative motion. The left column shows the original Galileo image. The center column annotates the image with the plate boundary material (brown), prominent reconstructable features (blue), and in the bottom row, a feature postdating the plate boundary that should be ignored (yellow). The right column shows a flat‐plane reconstruction, with associated direction and magnitude of the relative motion of the plates that can be inferred going forward in time. (a) Boundary with right lateral offset. (b) Boundary with divergent offset. In this case the divergence is oblique with a right lateral offset. (c) Boundary with convergent offset. In this case the convergence is oblique with a right lateral offset.

To explain the reconstruction process in a more concrete manner, let us return to the hypothetical Europa surface depicted in Figure 2 Figure 5 shows how this hypothetical surface would be depicted if it were one of the real target areas discussed in Section 3, by defining the major reconstructable features as well as the features to be ignored (Figure 5a). Crosscutting relationships are used to put the plate boundaries into a time sequence (Figure 5b) that will define the number of steps necessary to reconstruct the original surface.

Figure 5.

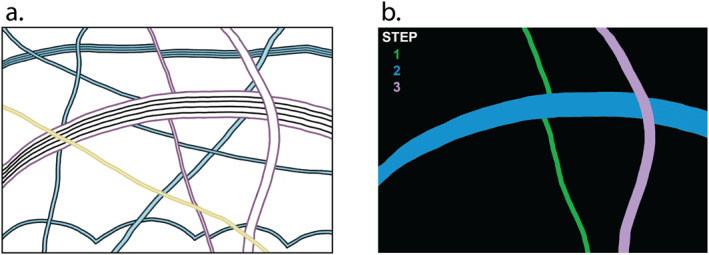
Hypothetical Europa sketch from Figure 2 presented in the same color‐coded scheme as is used to present the areas in Section 3. (a) The surface today, with features to be reconstructed highlighted in blue and features to be ignored (because they post‐date plate motions) highlighted in yellow. Plate boundary edges are highlighted in purple. (b) Time sequence of the plate boundaries. Working backward through the time sequence, the “Step 3” boundary is the last to move, and so is reconstructed first to arrive at the Step 2 reconstruction (Figure 6b), then the “Step 2” boundary is reconstructed (Figure 6c), and finally the “Step 1” boundary brings the plates back to the original reconstructed surface (Figure 6d).

Figure 6 illustrates the steps of the sequential reconstruction for this hypothetical area, showing the appropriate reconstruction for each type of boundary. Figure 6a shows the features and plates defined from the example in Figure 2, note that feature Z has now been removed from consideration because it postdates all plate boundaries and exhibits no offsets of older features. The most recent plate boundary is feature Y, which shows inconsistent amounts of lateral offset of older features. Feature Y offsets features S, U, and X in a right‐lateral sense, but feature T appears to be offset in a left‐lateral sense. Feature S appears to be offset less than U and X. The cycloidal feature R shows no apparent offset, but the cycloidal arc cut by Y appears slightly shorter than the others in the chain. All of these variations in apparent offset can be explained if motion along feature Y is dominated by contraction (e.g., Vetter, 2005; Kattenhorn & Hurford, 2009). Figure 6b shows the realignment of features T, S, X, U, and R if plates 5 and 6 are moved to the right and slightly up relative to all the other plates, and the missing pieces of the older features are interpolated across the zone of contraction. This reconstructive motion of plates 5 and 6 is exactly the reverse of the actual motions those plates took going forward in time. Note that because features S, X, and U trend in very similar directions, there would be considerable uncertainty in the magnitude of contraction if it were not for feature T (trending about 45° CCW of the other features) to provide a hard constraint on the magnitude and direction of plate motion. Working backward through the sequence, the next plate boundary is feature X. Like the previous boundary, the crosscut features show inconsistent apparent offsets: feature V does not show offset, feature T shows apparent left‐lateral offset, and features U and W show different amounts of right‐lateral offset. This can be explained if feature X is dominated by extension. Figure 6c shows precise realignment of the piercing points if plates 2, 4, and 6 are moved up and slightly to the right (again, the reverse of the actual motion forward in time). The oldest plate boundary is feature W, which exhibits consistent amounts of right‐lateral offset of the older features S, U, T, and R. The reconstruction shown in Figure 6d realigns the piercing points through a simple left‐lateral motion along feature W, moving plates 3 through 6 up and slightly to the left. The remaining features in Figure 6d do not show any offsets, and thus represent the original surface before the initiation of plate motion.

Figure 6.

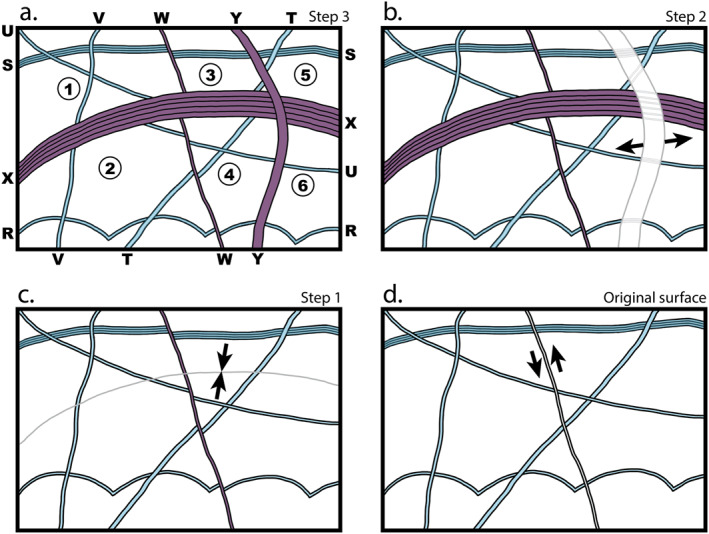
Sequential reconstruction of hypothetical sketch area from Figure 2, illustrating criteria for goodness of fit. (a) Plates defined in Figure 2b, with ignored feature Z removed. This is the final step of the reconstruction sequence, and the other panels go back in time to the original surface. (b) Reconstruction of convergence along feature Y by moving a plate consisting of 5 and 6 to the right; inferred material of older features lost during convergence is shown in gray outlines. (c) Reconstruction of divergence along feature X by moving a plate consisting of 2, 4, and 6 up; complete closure of this boundary brings older features back into alignment. (d) Reconstruction of right‐lateral slip along feature W by moving a plate consisting of 3–6 up; the original surface before plate motion is now reconstructed. Note that the left‐lateral arrows on this panel to reconstruct backward in time are undoing the right‐lateral slip that must have occurred forward in time.

Studies such as Sullivan et al. (1998) and Kattenhorn and Prockter (2014) identified plate boundaries and then sequentially moved the identified plates on the flat plane of a map projected image mosaic to align piercing points and thus reconstruct plate motions through time. Patterson et al. (2006) and Patterson and Ernst (2011) took a more mathematically rigorous approach, using a spherical geometry and testing locations and rotation values of Euler poles between plates to find a statistical best alignment of piercing points on adjacent plates. A strength of that approach is its ability to quantify the goodness of fit for a given two‐plate rotation. However it is not well suited for more complex, multi‐stage reconstructions and does not explicitly prevent plate overlap, as discussed in more detail in Section 3.2.

In this study, we use GPlates software (Müller et al., 2018; Williams et al., 2012) to interactively test plate reconstructions within a spherical coordinate system, and to build a sequence of “good” fit rotations around Euler poles to reconstruct an area of preexisting terrain on Europa that has been broken up by plate motions. While GPlates includes a methodology for quantifying best‐fit poles of rotation based on Hellinger (1981), its application is not straightforward for the work described here because, as will be described in Section 3, Europa's plate systems include numerous small plates and current imaging data limits the number of measurable piercing points per plate. Instead, we rely on the interactive nature of the software to test a variety of potential solutions for a pole of rotation that tightly aligns piercing points on plates without causing overlap violations. Comparisons between the observational fitting method used here and a statistical best fit method are presented in Section 3.2. A good fit is also exemplified by plate boundaries that exhibit similar relative motions for all of the plates moving along that boundary. This is especially important if the boundary appears to be morphologically uniform, as it does not invoke multiple amounts or directions of strain to form the same tectonic feature.

3. Application and Results

We surveyed the entire near‐terminator mosaic of Galileo images on the antijovian hemisphere discussed in Section 2.1, and located several candidate regions for plate reconstructions. Of these, we focused the bulk of our analysis on three target areas: Northern Falga, Castalia, and Libya (Figure 1) because these areas showed the clearest evidence for plate‐like behavior. The setting and reconstruction of each target area is discussed separately in Sections 3.1, 3.2, 3.3, through along with the rationale for where the boundaries of the target areas were set. The time sequence of the reconstructions is presented forward in time ‐ that is, the first step in each reconstruction represents a hypothesized initial configuration of the plates and the last step shows their current positions. All of the GPlates reconstruction files for these three target areas are described in Supporting Information S1 and are available for download from this article's data archive at Collins et al. (2022). In Section 3.4 we discuss preliminary observations of the other areas covered by high resolution imagery that lie between our three target areas. Though some tectonic features in these intermediate areas exhibit lateral motions, we did not perform plate reconstructions in them; see Section 3.4 for details.

3.1. Northern Falga Regio

The Northern Falga target area (Figure 7a) is the northernmost target area in our study region (roughly 40°N to 75°N, see Figure 1), and encompasses the area examined by Kattenhorn and Prockter (2014) (hereafter abbreviated as KP14), plus additional area to the south of their study. The Northern Falga area is relatively free of chaos terrain, and is dominated by fragments of old, low‐albedo, complex ridge structures trending roughly N‐S (some of them highlighted in green in Figure 7b), intermediate age bands trending NE‐SW, and young ridges in a variety of orientations (prominent examples highlighted in yellow in Figure 7). The network of intermediate age bands and associated contemporaneous ridge structures form a network of plate boundaries. Figure 7b shows the mapped plate boundaries as thin purple lines, and subsequent Figures 8, 9, 10 divide the target area along those plate boundaries. We mapped 46 plates of pre‐existing terrain between the plate boundaries. For the purposes of reconstruction, the young ridges are ignored for the remainder of this section, since they postdate plate motions in Northern Falga.

Figure 7.

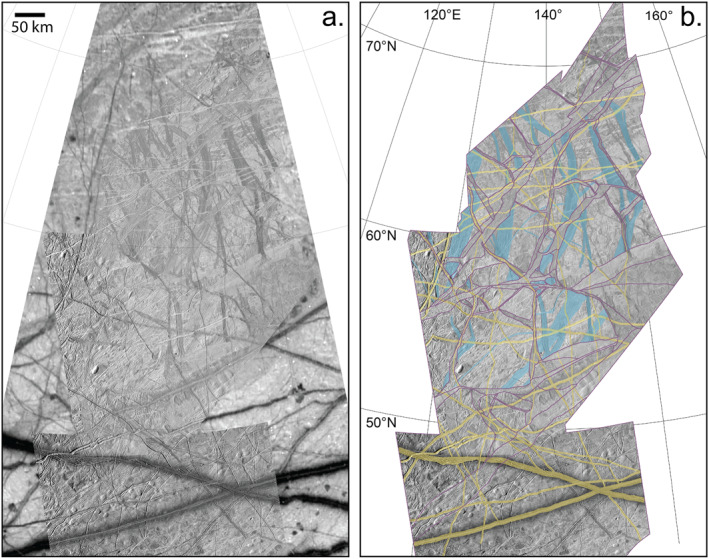
Northern Falga Regio study area. (a) The base mosaic of images from higher‐resolution Galileo observations is shown on top of lower resolution global‐scale images. (b) Only the high‐resolution area is shown, with interpretation of plate boundaries represented as thin purple lines (compare to subsequent figures). The colors in (b) denote prominent features that are younger than the plate boundaries in yellow (which are ignored in the reconstruction process), and prominent features older than the plate boundaries in blue. Images are shown in orthographic projection centered at 60°N, 140°E; north is up. The scale bar is shown in (a), and coordinates for graticules are shown in (b).

Figure 8.

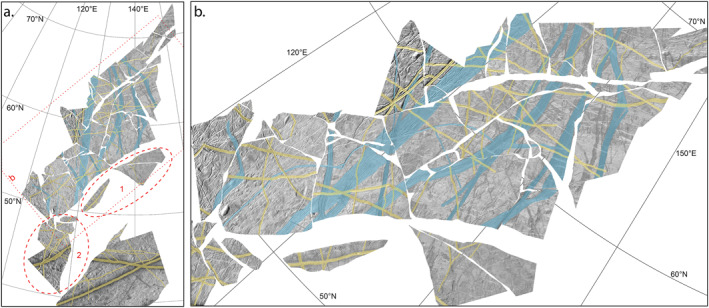
Reconstruction of the Northern Falga area. (a) Reconstruction of original surface before plate motions. The material of the plate boundaries has been removed. The majority of the plates, to the north of the circled areas, reconstruct very well to bring pre‐existing features back into alignment. The plates circled by a thick red dashed line in area 1 share similar morphology but do not match the terrain to the north or south, so their final position and rotation is relatively unconstrained. The plates circled in area 2 have been rotated to align similar background morphology with the plates to the north, but their final position relative to the northern plates is not well constrained. See text for details. The thin dotted red rectangle shows the position of part (b). (b) Obliquely zoomed cut‐out of part (a), showing the details of original features (blue) brought back into alignment through reconstruction.

Figure 9.

Time sequence of final motion along plate boundaries in northern Falga Regio. Mapped material of plate boundaries are colored from oldest to youngest in a green to blue to purple color scale. The “step” scale shows the latest reconstruction step during which the boundaries of that color were still active; refer to Figure 10 for more detail. Note that young plate boundaries may also be active in earlier stages. Map is in orthographic projection centered at 60°N, 140°E.

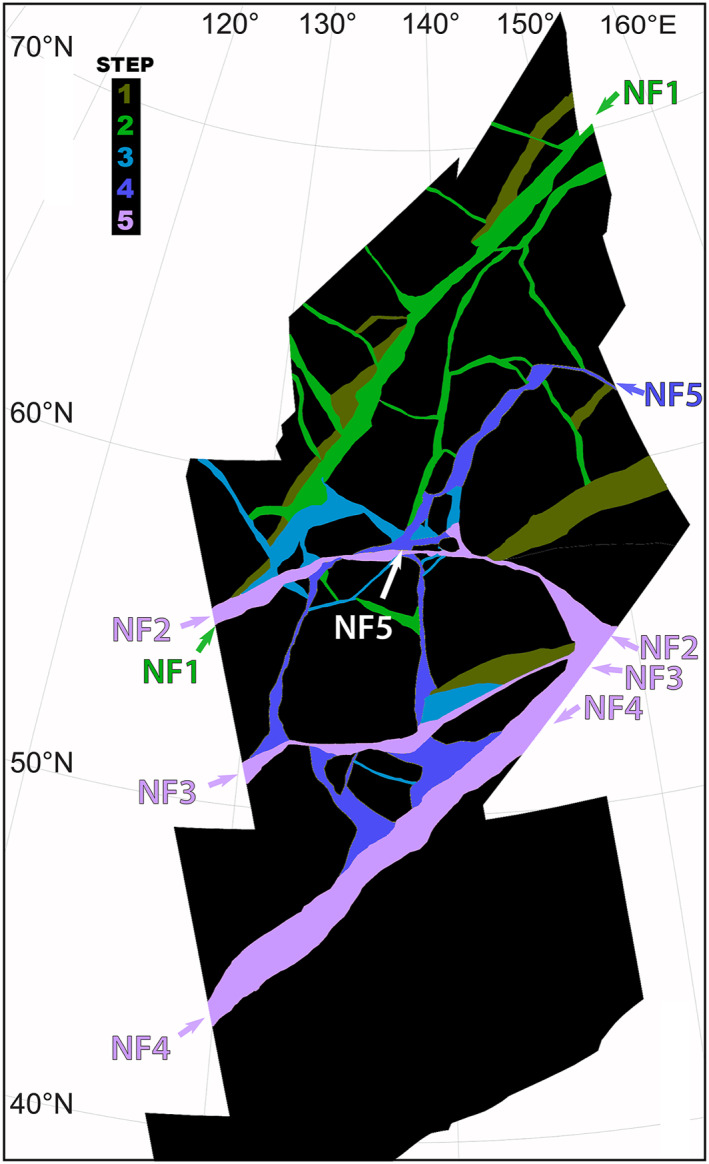
Figure 10.

Steps in reconstructing the original surface to the surface observed today in northern Falga Regio (see also Supporting Information Movie S1). Black polygons are plates, gray polygons are plate boundaries that are no longer active, according to the crosscutting relationships. Arrows show the relative motions necessary to bring the plates to their positions in the next step (cf. Figure 4): red denotes contraction, yellow denotes left‐lateral strike‐slip, and blue denotes extension. Activity generally migrated from north to south over time. Minor extension occurs along several boundaries, mostly early in time. Most of the contraction is along the southern boundary, late in time. Left lateral strike slip in many orientations dominates the reconstruction. Maps are in orthographic projection centered at 60°N, 140°E, and the southernmost plate is held fixed.

The major plate boundaries in this region are visible in Galileo color data as being distinctly whiter than other features. Geissler et al. (1998) examined the colors and cross‐cutting relationships of major tectonic features in this region, based on four‐color imaging at a pixel scale of 1.5 km, and classified them into three categories. The Northern Falga plate boundaries that can be discerned in the Geissler et al. data are contained in the “ancient bands and bright wedges” color category. The data set examined in the Geissler et al. analysis does not reach the other two target areas discussed in Sections 3.2 and 3.3.

The reconstructed original surface shown in Figure 8 is primarily based on the realignment of five N‐S trending complex ridge features, three smaller NW‐SE trending complex ridges and bands, and a prominent cycloidal ridge trending NE‐SW. Three of the N‐S complex ridges and one of the NW‐SE complex ridges are the same as those used by KP14 as the primary basis of their reconstruction.

Examining crosscutting relationships in the plate boundaries, we find that the younger motions are concentrated in the southern portions of the target area, and the oldest plate motions are concentrated in the north (Figure 9). The major plate boundary in the north, labeled NF1 (Northern Falga 1) on Figure 9, is a complex set of ridges. Upon careful examination of boundary NF1, it can be discerned that several “islands” of older ridges (shown in purple) are cross‐cut by a central core of ridges, with several orthogonal branches (shown in blue), and at the southern end this central core is crosscut by younger ridges (shown in green). This sequence of crosscutting ridges internal to boundary NF1 serve as an important guide for the sequential reconstruction of the northern half of this target area. Another important set of boundaries are the youngest features NF2, NF3, and NF4 in Figure 9. The western portions of NF2 and NF3 are often narrow and have a morphology like broken rubble, with subtle strike‐slip indicators pointed out by KP14. The eastern portion of NF3 and all of boundary NF4 are the northern and southern “subsumption zones” identified by KP14. The eastern portion of NF3 appears to have a few generations of crosscutting activity, as shown by the different boundary ages in Figure 9, though the generally smooth morphology of this band makes it difficult to clearly discern all of the crosscutting indicators.

Figure 10 shows the sequence of plate motions derived from our study of northern Falga Regio. An animation of this sequence can be found in Supporting Information Movie S1. The original reconstructed surface shown in Figure 8, which realigns the prominent old bands, is the starting point in Figure 10. Two prominent motions bring the original surface to Step 1. Left lateral motion of ∼20 km along boundary NF1 (Figure 9) opens a releasing bend on its western side, and convergence along boundary NF3 brings unrelated pieces of terrain close together. The uncertainty in the original positions of the plates in area 1 makes it difficult to quantify the partitioning of convergence between NF3 and NF4 in this and later steps.

The transition to Step 2 continues the left lateral motion along boundary NF1 by an additional ∼55 km, but this is accompanied by many more left‐lateral motions in the range of 10–25 km, primarily along faults on the north side of the boundary that are approximately perpendicular to boundary NF1. The combined motion of these intersecting left lateral boundaries accomplished minor clockwise rotations of several small blocks to the north of boundary NF1 and in the southwestern portion of the study area. Boundary NF1 ceases activity at the end of Step 2, and it is worth noting that a previous study of strike‐slip offsets on Europa identified boundary NF1 as the largest measured left lateral offset on Europa (Sarid et al., 2002). A long, narrow band opens during Step 2, parallel to and just south of boundary NF1, accommodating less than 5 km of extension.

The transition to Step 3 is dominated by ∼35 km of left lateral motion along the eastern portion of boundary NF2 and opening along its western portion. This is accompanied by the beginning of clockwise rotations of the blocks sandwiched between boundaries NF2 and NF3. At the same time, 10–15 km of divergent motion opens narrow bands to the north of boundary NF2, and motion begins along boundary NF5.

The transition to Step 4 is dominated by the blocks between boundaries NF2 and NF3 sliding to the east. This motion is accomplished by the western portion of boundary NF2 undergoing ∼30 km of left lateral motion, while the eastern portion of NF2 becomes a convergent zone accommodating this motion. The last clockwise rotations of the small blocks between boundaries NF2 and NF3 occur at this same time, and after this stage the blocks are fused together. The motions also necessitate minor convergence along boundary NF4. Boundary NF5 completes its motion during this stage, with its western portion oriented NE‐SW experiencing <15 km of extension and left lateral slip, while the eastern portion, which bends to the SE, accommodates ∼10 km of convergence while slipping in a left lateral direction. The final transition from Step 4 to today's surface is dominated by convergence of at least 80 km along boundary NF4, and ∼40 km of left lateral motion along boundaries NF2 and NF3.

There are no features that can be aligned with any degree of certainty on either side of boundary NF4. This could be due to large amounts of surface convergence bringing distant surface terrain together, and/or strike‐slip motions moving one of the matching sides outside of the available imaging data. Because of this uncertainty, there is no constraint on the maximum amount of convergence on boundary NF4, nor is there a constraint on strike‐slip motions along boundary NF4. To find the minimum amount of motion accommodated by boundary NF4, the reconstruction presented here assumes no strike‐slip motions along the boundary, and the reconstruction moves the material on either side of the boundary a minimum distance to prevent material overlap during the preceding plate motions. In the reconstruction presented above, the minimum amount of surface convergence accommodated by the widest portion in the center of boundary NF4 is ∼80 km.

The reconstruction presented here is broadly similar to the reconstruction presented in KP14 in that we found abundant left‐lateral motions, and that boundary NF4 accommodated almost 100 km of convergence (>80 km in this work, 99 km in KP14). Several details of the reconstruction are different. One important difference is the recognition that the area north of boundary NF1 and the block between boundaries NF2 and NF3 are composed of several smaller sub‐plates, which causes this block to change shape as the reconstruction progresses. By using a larger number of plates in this reconstruction, we generate a tighter fit of the pre‐existing terrain features than the reconstruction presented in KP14. Another important difference is that we used a mosaic of images covering a larger area than was used in KP14. In particular, our mosaic extends further to the south, and includes more coverage of convergent boundary NF4. This extended coverage shows that a literal interpretation of the reconstruction in KP14 leads to significant overlap of moving plates in the southwestern corner of the study area. Most of this overlap problem is solved through our recognition that the area between boundaries NF2 and NF3 is composed of several blocks that have rotated clockwise through time, and this shape change prevents the plates from overlapping as they would in the KP14 reconstruction. Some of the overlap problem is also solved by recognizing that the convergence along boundary NF4 is non‐uniform; our reconstruction shows twice as much convergence is required at the eastern end of boundary NF4 as there is along the western end of boundary NF4.

Exact measurement of the amount of convergence in boundaries NF3 and NF4 is hampered by the non‐unique solution to the placement of the plates circled in areas 1 and 2 in Figure 8a. The plates in area 1 exhibit no surface features in common with any of the other plates, and so it is impossible to determine their original position with any confidence. This means that the partitioning of strain between boundaries NF3 and NF4 in our reconstruction is uncertain. We took a conservative approach by moving them as little as possible from their final positions, letting these plates “ride along” with their neighboring plates for most of the reconstruction. The plates in area 2 have a surface texture of evenly spaced ridges that is very similar to the plates found immediately to the north on the other side of boundary NF3, with the trend of the ridges in this texture rotated almost 30° CCW. However, the evenly spaced ridges in the background texture allow several piercing point solutions of approximately equal quality, with the area 2 plates possibly sliding 50 km east or west of the reconstructed position shown in Figure 8. The position adopted for the reconstruction has the greatest number of plausible aligned piercing points.

Another unknown quantity is the amount of strike‐slip motion across boundary NF4. Because there are no features in common in the plates across this boundary, we cannot know its exact beginning location. Low resolution images from Galileo (e.g., Geissler et al., 1998) show that this boundary extends for long distances (100s of km) to either side of the target area shown here, but these images are of insufficient quality to identify piercing points outside the target area that could constrain strike‐slip motions. These low resolution images also show that it is not possible to eliminate the convergence seen in this reconstruction by rotation of the southernmost plate, because that would cause areas adjacent to the target area to spatially overlap. For our reconstruction, we adopted the approach of minimizing the amount of total motion of the plate south of boundary NF4, with the understanding that there could be additional strike‐slip motion not shown in the reconstruction.

3.2. Castalia Region

The Castalia region (Figure 11) is near Europa's equator, covering latitudes from 15°N to 16°S, and longitudes from 116°E to 142°E. The eastern and western boundaries of the study area are defined by the extent of Galileo imaging coverage at sufficient resolution. The northern boundary extends just beyond the northernmost plate boundary identified in this area, while the southern boundary is arbitrarily cut off where the pre‐existing plates become very small and difficult to characterize in the Galileo data. The area is named after the prominent dark spot Castalia Macula, which lies near 1.5°S, 134.5°E. Just south of Castalia Macula is a prominent dark band, named Acacallis Linea (also referred to by the unofficial name of Phaidra Linea in previous works), which cuts east‐west across the entire study area, and terminates in a sickle‐shaped curve at its western end (labeled on Figure 12). Another prominent dark band cuts east‐west across the study area between 10° and 11°S, named Arachne Linea (labeled on Figure 12). South of Arachne, in the southeastern corner of the study area, there is a collection of dark band fragments with variable orientations mostly trending NE‐SW. The north‐central portion of the study area is dominated by an irregularly shaped amalgamation of pits, domes, and chaos areas approximately 200–300 km in diameter.

Figure 11.

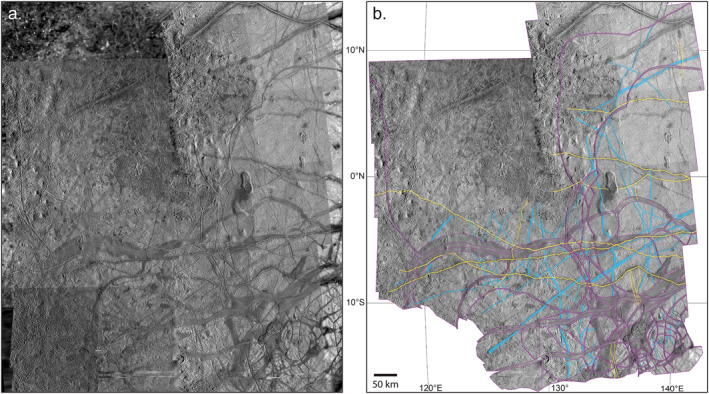
Castalia study area. (a) The base mosaic of images is shown with higher‐resolution Galileo observations on top of lower resolution global‐scale images. (b) Only the high‐resolution area is shown with interpretation of plate boundaries represented as thin purple lines (compare to subsequent figures). The colors in (b) denote prominent features that are younger than the plate boundaries in yellow (which are ignored in the reconstruction process), and prominent features older than the plate boundaries in blue. Images are shown in orthographic projection centered at 0°N, 130°E; north is up. The scale bar and coordinates for graticules are shown in (b).

Figure 12.

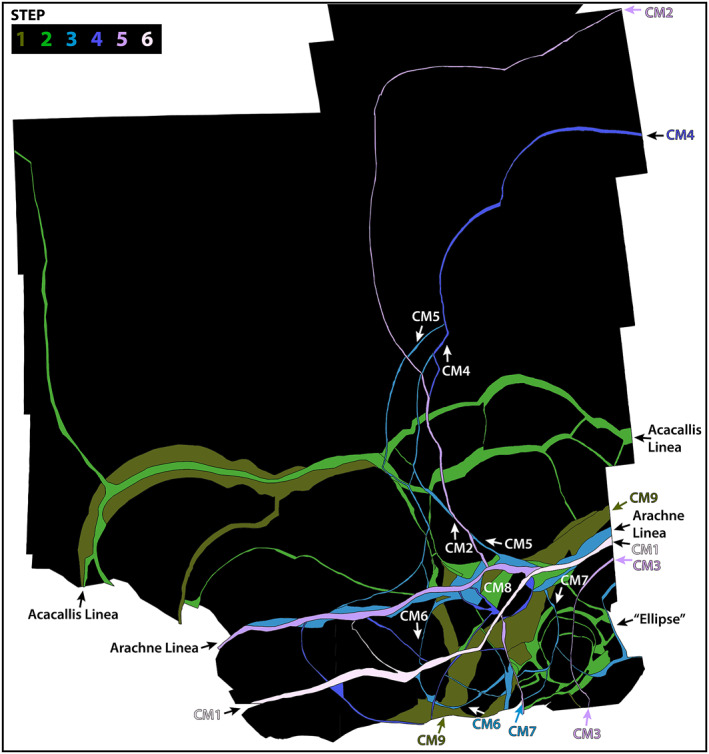
Time sequence of final motion along plate boundaries in the Castalia Macula area. Mapped material of plate boundaries are colored from oldest to youngest in a green to blue to purple color scale. The “step” scale shows the latest reconstruction step during which the boundaries of that color were still active; refer to Figure 14 for the detailed steps. Note that young plate boundaries may also be active in earlier stages. Projection is the same as Figure 11.

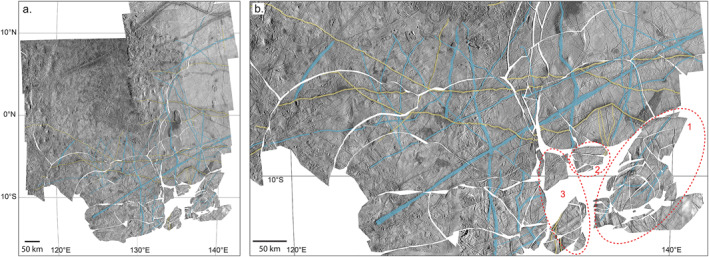
Portions of this region have been examined in previous works. Tufts et al. (2000) reconstructed the westernmost part of Acacallis Linea and the small band that projects from its southern edge, showing that they formed via dilation. Sarid et al. (2002) examined the plate boundaries marked CM4 and CM5 in Figure 12, and showed that a coherent plate 400 km in size had translated laterally by 8 km to form these features. They argued for the existence of a convergent boundary in eastern Arachne Linea to accommodate this motion. Patterson et al. (2006) split the northeastern quadrant of this study area into seven plates and used statistical methods to find the best‐fit poles of rotation to align features that predated the plate boundaries. Melton (2018) performed a detailed plate reconstruction of the southeasternmost corner of the study area, near 15°S, 140°E, highlighting the role of counterclockwise rotations in this area. Patterson and Head (2007) performed kinematic analysis of a triple junction in the westernmost part of Acacallis Linea and demonstrated that the assumption of plate rigidity is valid for the region.

From Arachne Linea to the northern edge of the study area, the identified plate boundaries are composed of bands trending east‐west and ridges or ridge complexes trending north‐south. We mapped 88 plates of pre‐existing terrain between the boundaries. Most of the north‐south trending plate boundaries north of Arachne form a cluster centered around 132°E (features labeled CM2, CM3, and CM4 in Figure 12). South of Arachne and west of 132°E, the pattern of plate boundaries is similar to the northern area, including a prominent east‐west trending band (labeled CM1 in Figure 12). South of Arachne and east of 132°E, the plate boundaries are much more complex and closely spaced. In this southeastern corner of the study area, there are several generations of intersecting bands with different orientations. The largest and most prominent of these band fragments lie along a trend labeled CM9 in Figure 12. One unusual feature centered near 13°S, 139°E is a collection of small plates surrounded by an elliptical set of dark bands (labeled as “Ellipse” in Figure 12). In the southwestern corner of the study area, there is a gap in high‐resolution Galileo imaging, resulting in some ambiguity as to whether the image to the west of the gap has geometric fidelity with the rest of the mosaic, or whether there are plate boundaries hidden in the gap. Because of this ambiguity, we split the plates to the north and south of CM1 along a north‐south line near 129°E, following the center of the gap. In general, the identified plates are smaller in the southern portion of the study area as compared to the northern portion. We did not map plate boundaries in detail beyond the southern boundary of the Castalia study area, but a preliminary examination showed the plates to be yet smaller in that direction.

The time sequence of plate boundary activity is displayed in Figure 12. Crosscutting relationships among the plate boundaries show that motion along the band CM1 is the most recent event. The next most recent event (Step 5) created the central band of Arachne Linea, the ridge complex CM2 branching to the north from central Arachne, and a curved (concave to the east) ridge/band complex running through the middle of the ellipse, labeled CM3. The next event going back in time (Step 4) created the ridge/band complex CM4, as well as several small bands that branch between Arachne Linea and CM1. Boundaries active until Step 3 include the peripheral portions of Arachne, two roughly parallel ridges branching north from Arachne labeled CM5, a “C” shaped set of bands and ridges (concave to the east) labeled CM6, and a curved (concave to the west) ridge/band complex running through the middle of the ellipse labeled CM7. Boundaries active until Step 2 include the two eastern branches of Acacallis Linea, a central band running through western Acacallis, several side branching ridges and small bands running north and south from Acacallis, the network of bands surrounding the ellipse, and an unusual isolated band fragment labeled CM8. The oldest plate boundaries include the outer portions of western Acacallis and a collection of dark band fragments lying along the trend line labeled CM9.

Reconstruction of the original surface (Figure 13) aligns a variety of older ridges and ridge complexes (blue). Prominent reconstructed features include two ridges trending ENE‐WSW across the entire area (Figure 13b) that constrain the motions along CM2, CM4, and CM5, and many north‐south ridges that cross several plates and constrain the motions of CM4, Acacallis, Arachne, and CM1. Four groups of plates in the southeastern corner of the study area (labeled in Figure 13b as 1, 2, and two groups in 3) were not well constrained in their final reconstructed placement.

Figure 13.

Reconstruction of the Castalia area. (a) Reconstruction of original surface before plate motions. The material of the plate boundaries has been removed. Note tight alignment of pre‐existing features marked in blue. Projection is the same as Figure 11. (b) Detail of the southern section of part (a), showing the details of original features (blue) brought back into alignment through reconstruction. Areas circled with dashed red lines indicate groups of plates for which the final placement is uncertain. Each of these groups exhibits an internally consistent reconstruction, but the final placement of each group relative to the surrounding plates is only based on one weakly constrained piercing point. See text for details.

In Group 1, two prominent NE‐SW trending pre‐existing ridges, along with several smaller features, give us high confidence that the plates within this group are properly reconstructed. The only exception is the southeasternmost plate, which does not share prominent reconstructable features with the other plates. Though the reconstruction within Group 1 is convincing, there are no features shared with the plates on the other side of CM9 to the north of Group 1 that provide convincing evidence of where Group 1 connects. We took the approach of moving Group 1 to the north to close band CM9, giving it a slight clockwise rotation to align the pattern of background ridges with the terrain to the north. Its final position in the reconstruction is based on one ridge possibly shared across the boundary, but this fit is not unique and other ridges to the east or west could also fit. We conservatively used the fit for Group 1 that involved the least amount of strike‐slip motion.

The plates in Group 2 are found today to be adjacent to the isolated band fragment CM8. Their position in the reconstruction is based on observations of the stages of motion of the surrounding plates and plate boundary fragments. The justification for the rotation of the plates is based on aligning CM8 with surrounding bands when it opened. The justification for the position of the plates is based on the old boundary material on the northern side of CM8 being very similar in appearance to the old boundary material found where CM5 and CM9 come together. The prominent ridge that gives Group 2 its internal reconstruction consistency may be an extension of a similar ridge found near the southern terminus of CM2. Our hypothesis is that these ridge fragments are pieces of the same feature, and this constrains Group 2 to its final position and orientation. There are other possible ridges that could match if Group 2 experienced significant strike‐slip motion to bring it west from its original position, but our conservative assumption is that Group 2 only rotated and moved south as Arachne opened.

The two groups of plates in Group 3 are the least constrained parts of the reconstruction, and the ones for which we have the least confidence in their original positions. Each cluster of plates in Group 3 is only reconstructed to the rest of the study area with a single ridge.

The first plate motions to break up the reconstructed surface opened two major bands (Figure 14, original surface to Step 1). North‐south extension occurred in western Acacallis Linea and a smaller branch of the band to the south. The amount of extension varies from 43 km in the west to 15 km in the east, as the pole of rotation is located just to the east of Acacallis. Left‐lateral strike‐slip motion through the center of the study area linked extension in Acacallis to extension occurring in eastern Arachne Linea and band CM9. Faults oriented NW‐SE around the “ellipse” began to break up surrounding plates through right‐lateral strike‐slip, including a 20 km offset of the plates at the northern tip of this group.

Figure 14.

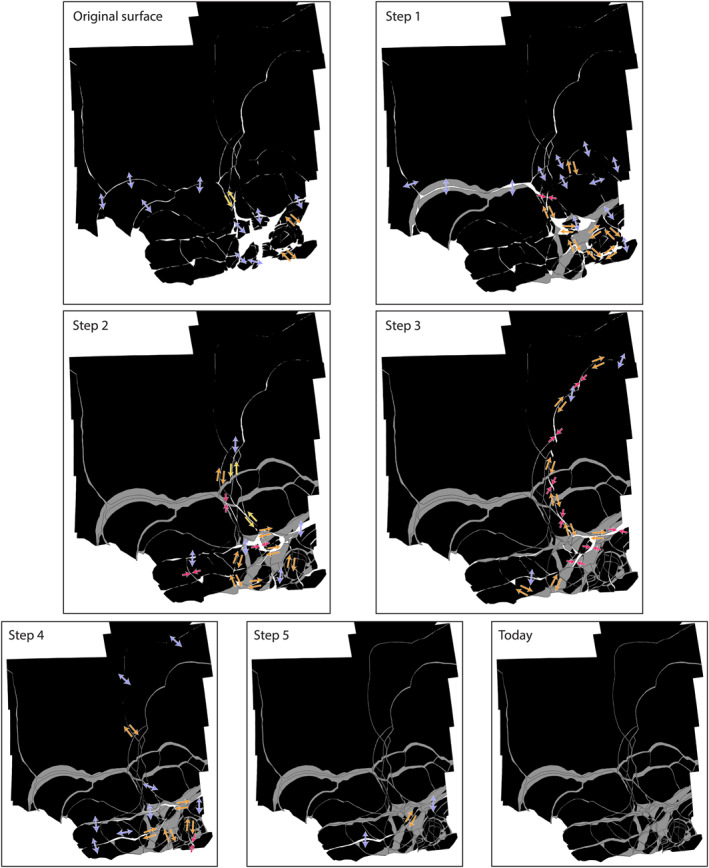
Steps in reconstructing the original surface to the surface observed today in Castalia Macula (see also Supporting Information Movie S2). Black polygons are plates, gray polygons are plate boundaries that are no longer active, according to the crosscutting relationships. Arrows show the relative motions necessary to bring the plates to their positions in the next step (cf. Figure 4): red denotes contraction, blue denotes extension, and yellow and orange denote left‐lateral and right‐lateral strike‐slip, respectively. Early stages are dominated by band extension in the center of the study area, while later stages have minor band extension in the south. Both left‐lateral and right‐lateral strike‐slip motions occur, but right‐lateral motions dominate during most stages. Coupled right‐lateral motions lead to counterclockwise rotations of blocks during several stages. Projection is the same as Figure 11, and the largest plate (the center of the northern section) is held fixed.

The next stage (Figure 14, Step 1 to Step 2) continues north‐south extension through the center of the area, with 5 km of extension continuing in western Acacallis and 20 km of extension distributed among two parallel bands, where eastern Acacallis splits and then rejoins in a triple junction at the eastern edge of the study area. The greater extension in the east is accommodated by right‐lateral strike‐slip through the center of the study area. Minor east‐west contraction of 1–2 km occurs at the northern end of the strike‐slip zone to accommodate the plate motions. In between the two eastern branches of Acacallis, a right‐lateral strike‐slip zone transfers unequal amounts of extension from the southern branch to the northern branch. In the southeast corner of the study area, eastern Arachne and band CM8 undergo north‐south extension, accommodated by right‐lateral strike‐slip motion along a fault branching southward from the center of Arachne, offsetting the two halves of band CM9. The “ellipse” rotates counterclockwise by 29°, accommodated by right‐lateral strike‐slip motions around its entire margin.

Moving from Step 2 to Step 3, the central block trapped between the ridges of CM5 moves south by 1–2 km relative to the surrounding plates. The southern end of CM5 is offset by left‐lateral strike‐slip. The block containing CM8 rotates counterclockwise, as does a large semi‐elliptical block bounded by the curved ridge/band CM6 which exhibits 10 km of right‐lateral motion. The curved ridge CM7 offsets the western part of the “ellipse” via 8 km of right‐lateral motion, opening a small band where CM7 curves at its southern extent. All of Arachne Linea begins minor extension ranging 4–8 km in a north‐south direction, with the exact amount depending on minor strike‐slip offsets in the plates between Arachne and CM1.

The transition from Step 3 to Step 4 is dominated by the small counterclockwise rotation of a large block comprising much of the eastern part of the study area, accommodated by a mixture of extension, right‐lateral strike slip, and contraction along the cycloidal boundary CM4. Oblique convergence and right‐lateral strike‐slip totaling 11 km is taken up in eastern Arachne to accommodate the motion along CM4. Convergence of 5 km occurs along the northern boundary of central CM9 as the southeasternmost group of plates rotates slightly counterclockwise. Right‐lateral motion near the southern boundary of the study area opens a small tear in the center of CM1.

From step 4 to step 5, the boundary CM2 extends by just over 1 km along its northern margin, accommodated by right‐lateral strike‐slip and oblique spreading along the north‐south portion of the boundary. The motion along CM2 appears to be a continuation of the CM4 motion from the previous step, along a slightly different boundary. At its southern end, CM2 merges with the central band of western Arachne, which has extended north‐south by 4 km during this stage. The curved boundary CM3 shifts the eastern portion of the “ellipse” southward by 3 km, opening a band at its northern margin.

The final transition to today's surface is accommodated by motion along CM1, which extends by 3 km in a north‐south direction, exhibiting right‐lateral transtension in its central dogleg portion. An animation of the reconstruction sequence can be found in Supporting Information Movie S2.

Our reconstruction of western Acacallis Linea is very similar to that presented in Tufts et al. (2000), but we recognize two distinct episodes in the opening of the band, as represented by the older outer portion of the band linked with structures to the south, and the smoother, straighter inner portion of the band linked with structures to the northwest and linked with the two branches of Acacallis to the east. Our reconstruction from step 3 to 4 of the motion along the cycloidal boundary CM4 agrees with the rotation found by Sarid et al. (2002) and later works. That study found 8 km of pure convergence along eastern Arachne Linea, while we find 11 km of oblique convergence because we recognize the simultaneous rotation of plates to the south of Arachne. Our reconstruction of the area surrounding the “ellipse” agrees with the work by Melton (2018) in terms of the major motions that occurred, though our work places it into the larger context of extension and right‐lateral motions in the surrounding region.

Patterson et al. (2006) examined the motions along CM2, CM4, and CM5 using a statistical technique to find best‐fit poles of rotation for seven plates. They concluded that some non‐rigid plate behavior present, and that Arachne Linea formed via multiple episodes of extension and strike‐slip motion. A later study using the same technique to examine Acacallis (Patterson & Ernst, 2011) also concluded that non‐rigid plate behavior was present. We tested the statistical pole of rotation technique by using GPlates to recreate the plates mapped in these two studies, and then manually entering their published best‐fit poles of rotation. We found that the statistical fits largely agreed with the plate motions that we found, but they allowed for materials on adjacent plates to pass through each other on the way to their reconstructed destinations. This is clearly nonphysical, and points to the importance of performing and visualizing multi‐stage reconstructions. The other main difference with our work is that we broke the surface down into many more plates. By breaking plates down and accounting for small motions within regions that were considered to be single plates in previous works, we avoid the overlap problem and find that the nonrigidity in the previous works appears best explained by motions in a greater number of smaller plates.

3.3. Libya Linea Region

The Libya Linea target area (Figure 15a) is the southernmost target area in our study region (roughly 45°S to 70°S), and encompasses Libya Linea (LL), Astypalea Linea (AL), and Cyclades Macula, three features that have been previously classified as pull‐apart or smooth bands (Tufts et al., 1999, 2000). Generally, these bands are thought to form via emplacement of material via separation of the satellite's lithosphere (Tufts et al., 1999). LL trends ENE‐WSW, and is non‐uniform in width suggesting multiple types of strain accommodation. LL consists of an intertwining network of bands that are morphologically complex, similar to Arachne Linea (Section 3.2; Sarid et al., 2002), further implying multiple episodes of deformation. AL trends NNE‐SSW and consists of several N‐S trending ridge segments that are aligned in a right‐stepping, en échelon pattern (Kattenhorn, 2004). The ridge segments define the boundaries of at least four rhomboidal pull‐apart features and the orientations of parallel lineations within these pull‐aparts suggest that AL opened at a highly oblique angle. One of these rhomboidal features, Cyclades Macula, includes two sets of unique en echelon features trending NNW where each feature is approximately 10 km in length and spaced 10 km apart from one another. The Libya Linea area is relatively free of chaos terrain.

Figure 15.

Libya Linea study area. (a) The base mosaic of images constructed from higher‐resolution Galileo observations on top of lower resolution global‐scale images. (b) Only the high‐resolution areas shown, with interpretation of plate boundaries as thin purple lines. The colors in (b) denote prominent features that are younger than the plate boundaries in yellow (which are ignored in the reconstruction process), and prominent features older than the plate boundaries in blue. Images are shown in orthographic projection centered at 59°S, 167°E, scale bar is shown in (a), and coordinates for graticules are shown in both.

Figure 15b shows the mapped plate boundaries as thin purple lines, and subsequent figures divide up this image along these boundaries. For the purposes of reconstruction, young cycloidal ridges that overprint LL, AL, and Cyclades Macula (highlighted in yellow in Figure 15b) are ignored for the remainder of this section since they postdate plate motions. Features that are highlighted blue in Figure 15b are older than plate motions in the Libya Linea area and were used to guide our reconstruction. Reconstruction results suggest a series of plate motions that closes AL and Cyclades Macula and partially closes LL and results in a more linear structure than is observed in the present day (Figure 16).

Figure 16.

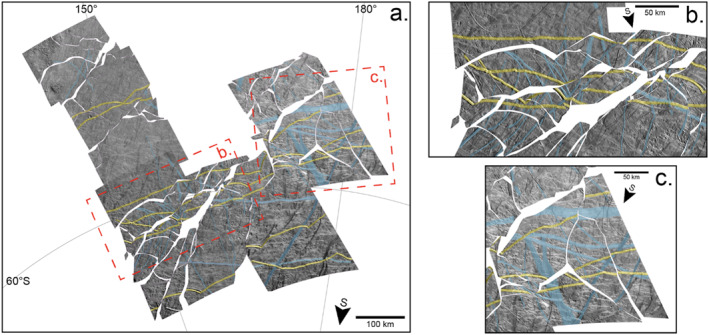
Reconstruction of the Libya Linea area. (a) Reconstruction of original surface before plate motions. The material of the plate boundaries has been removed. The majority of the plates to the northwest of the boxed areas experience minimal plate motions to fit together. Overall, plates rotated counterclockwise to create plate boundaries that form the present day Libya Linea area in Figure 15b. Yellow and blue highlighted features have the same meaning as in Figure 15b. (b) Zoomed in portion of the Libya Linea reconstruction, highlighting the missing terrain that remains after reconstruction of the western portion of Libya Linea and parallel bands to the north, as discussed in the text. (c) Zoomed in image of the eastern portion of Libya Linea and Ancaeus Linea after reconstruction, showing the tight fit of the plates bordering Ancaeus.

To characterize the geologic history of the region that encompasses LL, AL, and Cyclades Macula, we examined crosscutting relationships among ∼70 tectonic features and established a stratigraphic framework (Figure 17). Bands discussed in the subsequent text labeled LA1‐LA5 are annotated in this figure. The stratigraphic framework we developed was then used to define ∼300 plates in the region. Cross‐cutting and offset features associated with the boundaries of the plates were identified and are being used to reconstruct the geologic history of this prominent and complex area of Europa's anti‐Jovian, southern hemisphere.

Figure 17.

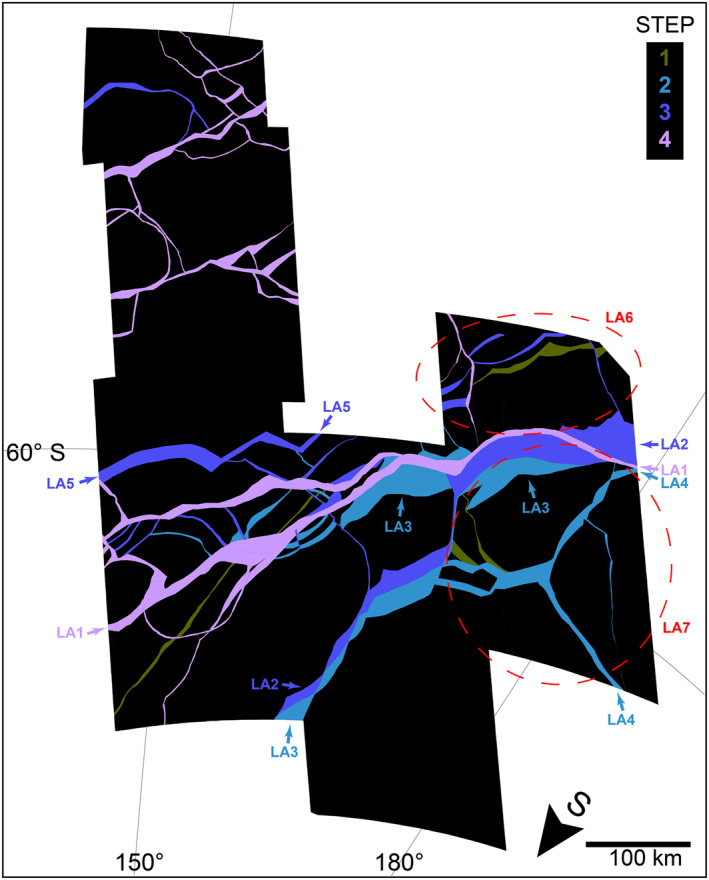
Time sequence of final motion along plate boundaries in the Libya Linea area. Mapped material of plate boundaries are colored from oldest to youngest in a green to blue to purple color scale. The “step” scale shows the latest reconstruction step during which the boundaries of that color were still active; refer to Figure 18 for more detail. Note that young plate boundaries may also be active in earlier stages. Map is in orthographic projection centered at 59°S, 167°E.

An animation of the Libya area reconstruction can be found in Supporting Information Movie S3. The initial stage of plate motion (Step 1, Figure 18) is defined by ∼20 km of right lateral shearing trending NE‐SW and ∼6 km of right lateral transtension trending NNE‐SSW associated with the formation of the first stage of LL. In this first stage, shearing is concentrated along plates southwest of LL and transtension is distributed across the central and northeastern portions of LL. An opposite sense of shearing is observed in the western (right lateral) and eastern portion (left lateral) of LL, although this is likely due to the image gap in the north central portion of the basemap. While plates fit together well in the western portion of LL and in the regions labeled LA6 and LA7 in Figure 17, there are few constraints that tie the western and eastern portion of LL that would allow for a more accurate reconstruction.

Figure 18.

Steps in reconstructing the original surface to the surface observed today in Libya Linea region (see also Supporting Information Movie S3). Black polygons are plates, gray polygons are plate boundaries that are no longer active, according to the crosscutting relationships. Arrows show the relative motions necessary to bring the plates to their positions in the next step (cf. Figure 4): red denotes contraction, yellow denotes left‐lateral strike‐slip, orange denotes right‐lateral strike‐slip, and blue denotes extension. Major activity generally consists of clockwise plate rotations, dilation along LL, AL, and Cyclades Macula, and right‐lateral strike slip motions. Features in the northwestern portion of the study region do not crosscut features closer to LL, AL, and Cyclades Macula thus are stratigraphically unconstrained with the major bands of the region. The motions in the northwestern portion consist of minor dilations, convergence, and right‐lateral strike‐slips. Maps are in orthographic projection centered at 59°S, 167°E, and the plate directly above band LA5 is held fixed.

A second stage of plate motion (Step 2, Figure 18) is defined by ∼20 km of N‐S oriented transtension of LL and Castalia Macula and ∼35 km of right lateral transtension along Astypalea's N‐S oriented en echelon fractures (LA3). During this stage, the opening of Libya, Castalia, and Astypalea are linked through a N‐S trending fracture approximately one km wide. This second stage results in a second phase of Libya opening (LA3), where opening is concentrated in the central and northeastern portions of LA3, and a concurrent first phase of Cyclades and Astypalea open. A sub‐stage of this second stage of plate motions occurs when the formation of Ancaeus Linea ends (LA4). Ancaeus Linea trends NNE‐SSW and resembles AL, albeit on a smaller scale, and dilates by 22 km to the N‐S, accommodated by potential convergence of bands located to the south. After LA4 finishes dilating, the continued opening of Libya, Cyclades, and Astypalea are accommodated by counterclockwise rotation of plates to the south of all LA3.

A third stage of plate motion (Step 3, Figure 18) is defined by ∼6 km of N‐S oriented dilation of band LA5 in Figure 17. The majority of the dilation is concentrated in the western portion of LA5 resulting in a rotation pole located near the eastern extent of the band. During this stage, a counterclockwise rotation of plates between the LA5 and LA2 results in a third phase of LL forming via ∼25 km of N‐S orientated dilation concentrated in the eastern portion of Libya. Along with the formation of the third stage of Libya (LA2), the final phase of Cyclades and Astypalea open (LA2) with the same mechanics as their second opening phase as described in the previous paragraph, including the linkage with Libya along a N‐S oriented, approximately one km wide band. This final opening stage results in an offset of ∼15 km.

The final stage of plate motions (Step 4, Figure 18) are defined by overall slight counterclockwise rotation of plates south of the LA5 resulting in the final opening phase of Libya Linea (LA1) defined by an approximately 10 km wide NE‐SW oriented dilational band and only 2 km of lateral offset. Additional minor clockwise plate rotations along with a combination of convergence, divergence, and shearing concentrated in the northwestern portion of the study site result in the present day terrain (today, Figure 18).

The final reconstruction of the Libya Linea Region results in complete reconstruction of AL, Cyclades, Macula, and Ancaeus Linea. The final reconstruction of LL itself, however, does not result in a perfect fit. In the final reconstruction, there is an approximately ∼50 km wide, ∼1,500 long linear gap spanning 6,000 km² potentially implying that LL is reworked surface material that has taken advantage of a pre‐existing linear weakness in the crust, destroying crustal material that could have been used to aid reconstruction of this region. This hypothesis is further supported by the lack of matchable features on either side of LL, especially in the western portion (see lack of continuous blue shaded features in Figure 16b). Another possibility for this gap in our reconstruction is that we have yet to account for all deformation on either side of LL, thus each side is not in its correct geometrical shape that would allow for a perfect reconstruction.

While LL has not previously been reconstructed, the reconstruction of AL and Cyclades Macula has been investigated by Tufts et al. (1999), Kattenhorn (2004), and Mével and Mercier (2005). Our reconstruction of Astypalaea Linea and Cyclades Macula differ from the reconstructions by Tufts et al. (1999) where they reconstruct Astypalaea and Cyclades under one stage. We find that the two sides of Astypalaea and Cyclades (southern portion of LA2 and LA3 in Figure 17) fit better when considering two stages of opening as seen in Steps 3 and 4 of Figure 18. However, in both our work and Tufts et al. (1999), we both observe that right lateral motions in the same orientation are responsible for the opening of Astypalaea and Cyclades (Kattenhorn, 2004). also reconstructs Astypalaea Linea under one stage of right lateral shearing resulting in dilation along the right stepping en echelon fractures. They also hypothesize that while undergoing right lateral shearing, each individual fault segment developed tail cracks and continued shearing took advantage of those tailcrack to dilate them into the band segments seen today. The resulting reconstruction shows that AL is not a strictly linear band, similar to Agenor Linea or Katreus Linea, but instead has a cycloidal geometry (although this is not to be confused with band dilation along a cycloidal ridge as seen in the Castalia Macula region). Kattenhorn (2004) does not include Cyclades Macula in their reconstruction due to image availability. The most recent reconstruction of Astypalaea Linea by Mével and Mercier (2005) reconstructed AL and portions of Cyclades Macula using several more plates than the two previous studies mentioned. While Tufts et al. (1999) and Kattenhorn (2004) treat Astypalea as a singular plate boundary with one plate on either side, Mével and Mercier (2005) present a reconstruction more similar to what we present here where the surface is broken up beyond two plates which allows for a better fit (see the set of plates labeled LA7 in Figure 17). However, Mével and Mercier (2005) still treat Astypalea and Cyclades as bands that open in one phase and their additional plate boundaries are drawn along nearby ridges and bands that intersect with Astypalea and Cyclades, which differ from where we drew our additional plate boundaries. This is likely because the images they used for their reconstruction were of higher resolution than the images used for our reconstruction. Considering that our reconstruction covered a larger swath of Europa's surface than Mével and Mercier (2005), we aimed to use imagery with a consistent resolution to prevent biases, which resulted in selecting a lower resolution data set that covered a larger area.

3.4. Observations of Other Regions in the Mosaic

Numerous offsets along tectonic features have been observed across Europa, but they are not always part of an organized system of rigid plates. In this section, we share observations about the regions lying between our three study areas. Each of these regions offers insight into the range of tectonic behavior on Europa. The observations in this section complete the nearly pole‐to‐pole survey of high resolution imaging in the region of Europa shown in Figure 1.

To the north of the Castalia Macula study area, plate‐like motions are observed in another region (Figure 19). Because this region is adjacent to Belus Linea, we refer to it below as the Belus region. Relative motions in the Belus region have been noted in previous works, most notably in Sarid et al. (2002) where an asymmetric band was found to accommodate 8 km of contraction. Our initial survey of the Belus region identified dozens of potential plates, but a full multi‐stage reconstruction of this area is challenging due to the density of crosscutting features, and is beyond the scope of our current work. We performed three independent initial surveys of potential plates in the Belus region, and though the surveys differed on the details of where the plate boundaries lie, the agreement on the total area potentially affected by plate‐like motions is outlined by a red dashed line in Figure 19. Also shown in the figure is a ridge outlined in green that crosscuts all of the potential plate boundaries in the Belus region. The green ridge is, in turn, crosscut by another prominent ridge, outlined in blue in Figure 19. The Blue Ridge can be traced across most of the Castalia Macula study area (Section 3.2) where it is crosscut by all ages of plate boundaries in that area. Following the logic of crosscutting relationships, all of the plate boundaries in the Belus region must predate all of the plate boundaries in the Castalia Macula region, with two generations of ridges formed in between. These two neighboring areas thus represent two distinct episodes of plate‐like behavior in Europa's history.

Figure 19.

An area exhibiting plate‐like motions north of Belus Linea is outlined by a red dashed line. The purple lines in the south are plate boundaries CM2 and CM4 from the Castalia Macula reconstruction (see Figure 12). The blue line shows a ridge that is crosscut by CM2 and CM4, and extends all the way south to be crosscut by Acacallis Linea (off the southern edge of this figure). The Blue Ridge crosscuts the green ridge, which crosscuts all of the candidate plate boundaries in the area north of Belus. This shows that all of the plate‐like activity in the area north of Belus is older than the activity in the Castalia Macula study area. Orthographic projection centered at 15°N, 135°E.

South of the Northern Falga study area, there are several linear features that exhibit apparent left‐lateral strike‐slip offsets of 1–3 km (Figure 20). These features can only be traced for a few tens of kilometers before disappearing into the background. No accommodation structures can be found linking these features together to form an organized system of plates. There are three possible explanations for this observation. One explanation is that the offsets and features are too small to be observed given the available images. However, similar scale strike‐slip offsets have been confidently linked to plate boundaries in the other study areas. Another explanation is that these features are too far down in the stratigraphic column, and too many newer features have overprinted the accommodation structures. The final explanation is that this is an area where Europa's surface is truly behaving nonrigidly, and the motions along these segments are being accommodated by distributed deformation in the intervening ice.

Figure 20.

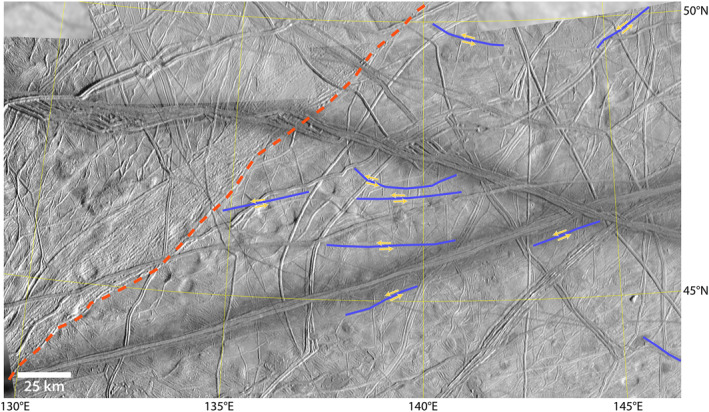
The area to the south of the Northern Falga study area exhibits strike‐slip offsets on disconnected faults but no organized system of plates. The red dashed line shows the southern edge of the subsumption band at the southern margin of the Northern Falga reconstruction. The blue lines denote sections of faults with apparent strike‐slip offsets. Orthographic projection centered at 45°N, 140°E.

In Section 3.2 we noted that plate‐like motions continue to the south of the Castalia Macula area, but the plates become numerous, small, and difficult to confidently reconstruct. Between the Castalia and Libya study areas, specifically within Argadnel Regio, the terrain is generally divided into plates by two sets of orthogonally intersecting bands. These intersecting bands appear to have formed from two separate episodes of diffuse, broad scale lateral shearing that initially formed a set of NW‐SE oriented bands via right‐lateral shearing, and later formed a set of sigmoidal bands oriented NE‐SW via left‐lateral shearing. Two episodes of opposite‐sense shearing may also be observed in Agenor Linea (Hoyer et al., 2014), just to the north of the Libya study area. As the more recent episode of broad scale left‐lateral shearing continued, the plates have rotated counter‐clockwise, similar to plate motions within the southern portion of the Castalia Macula area and observed by Melton (2018) and Detelich and Kattenhorn (2022). The counter‐clockwise rotation of these plates has caused them to disintegrate into circular blocks, similar to what occurs at a much smaller scale in cataclasis, where angular grains in the core of a fault zone will erode into rounded grains as shearing progresses. While the disaggregation between the Castalia Macula and Libya Linea regions appear plate‐like, they are dissimilar from the plates in this study which appear to move independently. Instead, the disaggregation between Castalia Macula and Libya Linea is broadly distributed and appears to be edge driven by east‐west oriented shearing on the northern and southern boundaries of Argadnel Regio and Agenor Linea.

4. Discussion

Before discussing the broader implications of our observations, we offer some observations of the reconstruction process. As discussed in the introduction, many previous works examining lateral motions on Europa have taken the simplified approach of reconstructing features on a flat plane. The reconstructions presented in this work cover regions large enough in latitude and longitude that map projection errors would affect the results if the reconstructions were done in that manner. Present work is limited to areas covered by available high‐resolution Galileo image data, but future reconstructions of an entire plate system on Europa based on expanded imaging data would cover an even larger area. Once more imaging data of Europa is available, future plate reconstructions must be done in a spherical framework.

Many previous works have tended to propose one‐step reconstructions of multi‐plate systems (amounting to a singular rotation). While this is often a necessary simplification when performing an initial survey, the many small motions/accommodations observed in the reconstructions of the Northern Falga, Castalia Macula, and Libya Linea regions make it clear that the kinematic details revealing how strain is accommodated by observed surface features can only be seen by taking a multi‐stage approach. Performing a single step reconstruction on a system of multiple plates and boundaries can also lead to nonsensical behavior, such as plates passing through each other.

Finally, many of the improvements we were able to realize in the reconstructions presented here were only possible by breaking the obvious plates into smaller pieces along less obvious accommodation structures. What may have appeared to be nonrigid behavior in previous reconstructions may instead be an overestimate of the size of the rigid plates. The Northern Falga reconstruction presented in Section 3.1 achieved a tighter fit than Kattenhorn and Prockter (2014) by breaking some large plates into smaller pieces along subtle internal boundaries, thus allowing the plates to change shape as the reconstruction progressed. The Castalia reconstruction also achieved better fits without the overlaps suffered by previous statistical‐based reconstructions in this area (Patterson & Ernst, 2011; Patterson et al., 2006) by considering many smaller plates instead of a few large ones. The drawback of considering many more plates is that it becomes impractical to use a statistical approach when the number of plate pairs to examine is vastly increased.

4.1. Implications for Tectonics on Europa

Based on our observations, we conclude that plate tectonic‐like behavior on Europa is widespread, but it occurs in limited areas, for limited amounts of time, and with limited amounts of motion.

4.1.1. Plate Tectonic‐Like Behavior Is Widespread but Patchy on Europa

We examined a large swath of Europa stretching almost from pole to pole, and found three areas that represent good examples of plate tectonic‐like behavior. The study areas were spread out in latitude, covering the high northern and southern latitudes as well as the equatorial region. As discussed in the introduction, hints of plate tectonic‐like behavior have been found in other regions of Europa (e.g., Greenberg, 2004; Pappalardo & Sullivan, 1996; Sullivan et al., 1998) but lack of wide‐area imaging data at sufficient resolution has thus far hampered a fully global investigation. We are confident based on this work that many more areas with plate‐like motions will be discovered when better imaging data of Europa is available.

However, widespread is not the same as global. There are limits to the extent of plate tectonic‐like behavior in each of the study areas, and some areas do not exhibit organized systems of plates, as far as we can determine. Unlike the Earth, which has a globally integrated system of plates, Europa's plate motions are regionally confined and thus may reflect a more regional or local process.

4.1.2. Plate Tectonic‐Like Behavior Is Episodic and Not Currently Active

In all of the study areas, young ridges and ridge complexes overprint the plate boundaries. The young ridges do not accommodate offsets like those seen in the plate boundaries. Thus, whatever process was driving the plate motions came to an end, and is not actively driving plate motions today in any of the areas studied. The relationship between the Castalia Macula study area and the older Belus area to its north discussed in Section 3.4 demonstrates that the plate tectonic‐like behavior on Europa did not occur all at the same time. Combined with the previous conclusion, we develop the view that plate tectonic‐like behavior on Europa occurs in regional patches and turns on and off at different times in different places.

4.1.3. Upper Limit on the Magnitude of Plate Motions

On the Earth, plate tectonics provides no hard upper limit to the distance of motion that can be accommodated along plate boundaries. It is normal on Earth to see material created at a spreading ridge be later subducted. On Europa, there are no examples of material being formed at a spreading band, traveling to an adjacent convergent margin, and being subsumed. Most of the offsets accommodated along plate boundaries observed in our three study areas were of order 10 km, and no boundaries were observed that accommodated lateral motion of 100 km or more. Together with the observations of the regional, episodic nature of plate tectonic‐like behavior on Europa, this limit on accommodated motion suggests that there is some self‐limiting factor that brings plate motions on Europa to a halt. Is this limitation due to the material of the plates themselves, or due to the driving mechanism behind plate motions?

It is interesting to note that while all of the study areas had convergent plate boundaries accommodating several kilometers of motion, neither the Castalia nor the Libya reconstructions showed the magnitude of convergence (several tens of kilometers) seen at the southern edge of the Northern Falga reconstruction. We can think of three possibilities to explain this. Perhaps the tectonic behavior in the Northern Falga region is special, and it is a unique region of Europa where an unusual amount of convergence happened. Another possibility is related to the gap in boundary materials seen across the reconstructed position of Libya Linea (Section 3.3). If we underestimated the reconstructed distance between the two sides of Libya, there could be additional convergence hidden there. A final possibility for all of the regions is that motions take place in the reconstructions which necessitate convergence somewhere outside the available imaging coverage. Once more imaging coverage is available and such edge effects are accounted for, we will have better constraints on the amount of convergence.

4.2. Missing Information and Future Work

There are two pieces of observational data that would be helpful in making progress on understanding the driving mechanism of plate tectonic‐like behavior on Europa. The first is an inventory of the sizes of rigid plates that are active at any particular time step in the reconstructions. This is not as simple as determining the areas of the mapped plates, because many of the plate motions involve groups of plates and adjacent inactive boundaries moving together. There are also edge effects from the limited imaging coverage that will affect the results of such a study. Nevertheless, a study could be done in the future using the data from our reconstructions to place bounds on the distribution of plate sizes.

The second piece of missing information that would constrain plate dynamics is the velocity of plate motions. Unfortunately we do not currently have a way of determining the absolute ages of individual features on Europa. All we can say is that all of the plate motions happened in a period of time less than the surface age of Europa, which is less than 100 million years (Bierhaus et al., 2009).

Future work stemming from our study could also include an inventory of morphological differences among plate boundaries on Europa, as a function of the type and magnitude of plate motion accommodated by the boundary. The GPlates reconstruction files linked in the open research statement and in Supporting Information S1 for this article can serve as a starting point for such future work. Reconstruction of the Belus region discussed in Section 3.4 is another important area for future work, to compare an earlier episode of plate motions to the later motions in Castalia. In Section 3.1 it was observed that the color maps of Geissler et al. (1998) show the plate boundaries in Northern Falga as being a distinct color unit. Future work is also warranted to characterize the color differences of plate boundaries in the other two target areas, though there is limited color data currently available in those regions.

4.3. Thoughts on Driving Mechanisms for Plate Tectonic‐Like Behavior

As we contemplate the similarities and differences between modern plate tectonics on the Earth and the plate tectonic‐like behavior exhibited by Europa, we should remember several factors affecting tectonic driving mechanisms that are different between the two worlds. For example, temperature‐driven buoyancy changes between the surface and interior of the ice shell are insufficient to drive subduction (Johnson et al., 2017). In addition, Europa's surface is predominantly water ice, and thus will not undergo the eclogitization process that increases the density of subducting slabs on Earth. Though higher density water ice phases exist, the pressure in Europa's water ice layer is never high enough to initiate a change in the solid phase. Compositional changes driven by salt content and porosity, however, may provide the necessary negative buoyancy to aid in shallow subduction (Johnson et al., 2017). Yet, in places where convergence is observed on Europa, there is no strong evidence for the directionality of convergence (i.e., one plate subducting beneath the other), and it is possible that material loss in convergent zones on Europa could be fed from both sides unlike what is observed on modern Earth. In other words, the conditions on Europa differ significantly from the global system of plate tectonics on Earth. While there is evidence and modeling to support the idea that the ice beneath Europa's lithosphere is convecting (e.g., Pappalardo et al., 1998; Pappalardo & Barr, 2004), there is also abundant evidence that tidal forces play a strong role in shaping Europa tectonics (e.g., Kattenhorn & Hurford, 2009). With this in mind, what mechanisms or combination of mechanisms could plausibly drive global or regional plate‐like motions on Europa?

One possibly productive line of reasoning would be to compare Europa plate behavior to early tectonic regimes on the Earth, during the Hadean to Archean when the conditions may not have been favorable for subduction or global plate tectonics. A warmer Hadean/Archean mantle (post Magma Ocean) would hamper the development of plate tectonics in multiple compounding ways. For example, hotter mantle temperatures could increase the buoyancy of the oceanic lithosphere to the extent that it can no longer subduct even with eclogitization (e.g., Davies, 1992). Hotter mantle temperatures also reduce mantle viscosity and, correspondingly, convective stresses (Cooper et al., 2006; Sandu et al., 2011) such that the yield strength of the lithosphere may not be met further inhibiting subduction (Moresi & Solomatov, 1998). Yet, some simulations of early Earth dynamics demonstrate that subduction may still be possible within these limited conditions, but it is weak, intermittent, and likely not long‐lived (van Hunen & Moyen, 2012). In other words, though the early Earth was suboptimal for a global network of well‐developed, long‐lasting subduction zones (a.k.a. plate tectonics), episodic surface removal and compression driven by weak subduction that could mimic characteristics of plate tectonics was still possible, which suggests that this possibility may also exist for the suboptimal conditions for subduction on Europa.

The apparent limits to the magnitude and lateral extent of plate motions on Europa suggests that there may be self‐limiting behavior, either within the plates or the driving mechanism, that inhibits the development of long‐lived plate motions. On Earth, plate motion can become “congested” upon the advent of subducting buoyant material (e.g., Mueller & Phillips, 1991). Moresi et al. (2014) modeled this congestion showing that the motion of the subducting plate stalls during the accretion of buoyant material onto the overriding plate. This stalling then leads to a development of a diffuse plate boundary which remains in operation until the migration of the subduction zone and plate motion resumes. The timing of this process from congestion to re‐establishment of the subduction zone and return to stable plate motion is dependent on the strength of the overriding plate (Moresi et al., 2014). This mechanism could explain how variations in buoyancy driven by composition and/or temperature within the ice could lead to temporary, but repeating bursts of lateral plate motions.

Our observations can help place Europa in a tectonic regime context for compLithgow‐Bertelloni &amp; Richards, 1998arative planetology. However, this exercise must be done with careful attention to the variability in tectonic regimes as well as the non‐unique nature of dynamic systems (Weller & Lenardic, 2012). Stagnant lid and mobile (or “active”) lid regimes are often used to bracket the end members of global tectonic settings delineating between a single lithospheric plate with no discernible lateral motion and multiple plates moving and interacting (e.g., Moresi & Solomatov, 1998). The episodic regime is classically described as a transient state between periods of mobile and stagnant lid tectonics (Moresi & Solomatov, 1998). Yet geodynamic models within parameter sweep investigations of tectonic regimes produce varied behavior beyond those three regimes (e.g., Lenardic, 2018). Several of the non‐end‐member regimes may be applicable to Europa. For example, “sluggish” lid describes behavior that sits between mobile and stagnant lid, where lateral surface motion persists, but at velocities lower than those in the actively convecting region below (Lenardic, 2018). In the sluggish lid regime, which can occur globally or regionally, surface motion is driven by traction forces at the base of the lid (e.g., Phillips, 1990; Lenardic, 2018). Phillips (1990) argued that a tectonic regime driven by traction forces explains large‐scale deformation on Venus. Rozel et al. (2015) demonstrated a ridge‐only regime wherein deformation is centralized around ridge within a more resistant, stagnant lithosphere. While the ridge‐only regime may not be applicable to the observations of deformation and plate motion on Europa, it does highlight the variability of tectonic regimes between mobile and stagnant lid. In addition, the process of transitioning between tectonic regimes, such as from heat‐pipe/stagnant lid to mobile lid introduces short‐lived bursts of lithospheric deformation and motion not solely reflective of a single end‐member regime (e.g., Beall et al., 2018). The observations of plate‐like motions on Europa presented in this study can provide tests for geodynamic studies exploring a wider range of tectonic regimes, as well as the transitions between them.

Another way to view plate motions on Europa is to examine the positions of the Euler poles relative to the plates that they describe. This allows us to observe how much of the motion is poloidal, meaning the poles are far from the plates and all parts of a small plate are moving in roughly the same direction, versus toroidal, meaning the poles are next to the plates and much of the plate motion can be described as spinning in place. In terrestrial plate tectonics, the distribution of poloidal versus toroidal plate motions can have implications for the driving forces of plate motion (Lithgow‐Bertelloni & Richards, 1998) and plate‐mantle coupling (Bercovici & Wessel, 1994). Figure 21 shows plots of the total reconstruction poles calculated by GPlates from the beginning to end of each reconstruction, relative to the fixed plate in each study area. Comparison of the distribution of pole positions to the study area outlines (in which all the plates are located) shows a scatter of distant poles in each study area, with a large number of close‐in poles that are dominantly clockwise in Northern Falga and counter‐clockwise in the other two study areas. While a detailed analysis of pole distributions and their implications is beyond the scope of our current study, Figure 21 points out an interesting avenue for future work.

Figure 21.

Plots of Euler pole postions describing the total motion (beginning to end) of all plates in each study area, relative to the fixed plate in that area. Pink outlines show the locations of the study areas. Orange and blue dots represent poles with clockwise and counter‐clockwise rotations, respectively. Plotted poles are constrained to being within 90° longitude of 140°E (the center of the base mosaic).

The dominance of left lateral displacements and clockwise plate rotations in the northern Falga study area (cf. Figure 10), and right lateral displacements and counterclockwise plate rotations in the other study areas (cf. Figures 14 and 18) may offer a clue to other processes beyond convection for driving Europa plate motions. Over time, fractures on Europa may develop strike‐slip offsets as a result of periodic opening, closing, and shearing stresses caused by tides (e.g., Greenberg et al., 1998; Kattenhorn & Hurford, 2009). Models of tidal deformation predict that tidally‐driven offsets will follow spatial patterns. Specifically, in the far north, most faults will develop left‐lateral offsets while faults in the far south will develop right‐lateral offsets. Between these zones, both left‐lateral and right‐lateral offsets can develop, with the direction of motion determined by the orientation of the fault (Greenberg et al., 1998; Sarid et al., 2002). If Europa's spin pole were precisely perpendicular to its orbit plane (i.e., zero obliquity), the boundaries of the mixed offset zone would be symmetric north and south of the equator and located at the same latitudes at all longitudes. However, there is substantial evidence that Europa's spin pole is slightly titled (<1°), and the direction in which the spin pole is pointing changes over time (Bills et al., 2009; Rhoden et al., 2010). Europa's non‐zero obliquity breaks the symmetry in the tidal stress field, causing the region of mixed right and left lateral offsets to shift off the equator and makes the pattern longitude‐dependent (Rhoden et al., 2012).

Much of the strike‐slip motion we recorded follows the general pattern of mostly left‐lateral offsets in the north, associated with clockwise plate rotation, and mostly right‐lateral offsets in the south, which develop from counter‐clockwise plate rotation. The pattern suggests that tidal stress may play a role in the development of offsets, but how (and whether) tides would drive plate rotations is not yet understood. Furthermore, our results indicate that rigid plate motions occurred in Europa's past, which means that Europa's spin pole likely pointed in a different (and unknown) direction when plates were active. The relationships between offset direction, crack orientation, and location on Europa's surface are sensitive to the spin pole direction. Hence, it is not trivial to link tides with plate motions. An interesting avenue for future study would be to conduct a detailed comparison between the offsets associated with plate rotations and the history of obliquity‐driven tidal stresses to determine the importance of tides relative to other potential drivers of plate motion. A related question is whether tidal stress acts in concert with convective stress to drive plate motions, or whether a shift in convective regime from stagnant to mobile lid behavior simply acts to weaken and detach the stiff surface ice, so that tidal stress can take over to mobilize the plates. Detached plates could be mobilized by edge‐driven tidal shear forces, and perhaps some or all of the extension and contraction observed in these plate systems is passively accommodating these shear motions. Some aspects of plate behavior on Europa may resemble the behavior of terrestrial microplates (see discussion in Melton, 2018 and references therein) where small rigid plates are jostling to accommodate large‐scale regional strain.

5. Conclusion

Surveying a large swath of Europa's surface, at least three regions were found where the tectonic behavior is best described by motions along narrow boundaries in a system of rigid plates—in other words, plate tectonic‐like behavior. Multi‐stage reconstructions of these areas show divergent, strike‐slip, and convergent motions are accommodated along various boundaries, just like the system of plate boundaries on the Earth. However, the plate tectonic‐like behavior on Europa shows clear differences from the current behavior of plate tectonics on Earth. Unlike the Earth, Europa's plate systems are regionally confined and do not appear to be active at the same time. Not all of the surface surveyed was best described by plate tectonic‐like behavior. None of the areas of plate tectonic‐like behavior have been active in the recent past (as defined by when the most recent ridges formed), thus something has caused plate motions to cease.

Our observations lead to a fascinating variety of open questions. What is the role of convection versus tidal forces in driving plate motions on Europa? What do the scale of plates and the magnitude of plate motions tell us about the driving mechanisms for plate motions on Europa? What makes the plate behavior turn on and off, and how long does it last? How much material from Europa's lower crust or ocean is exposed during plate motions, and how much surface material is subsumed into Europa's ice shell? This last question is important for understanding Europa's habitability. When Europa Clipper returns a much more complete high resolution image mosaic of Europa's surface in the early 2030s, we can look forward to performing more detailed and complete reconstructions of plate motions, and perhaps make significant progress on these open questions.

Conflict of Interest

The authors declare no conflicts of interest relevant to this study.

Supporting information

Supporting Information S1

Movie S1

Movie S2

Movie S3

Collins, G. C. , Patterson, G. W. , Detelich, C. E. , Prockter, L. M. , Kattenhorn, S. A. , Cooper, C. M. , et al. (2022). Episodic plate tectonics on Europa: Evidence for widespread patches of mobile‐lid behavior in the antijovian hemisphere. Journal of Geophysical Research: Planets, 127, e2022JE007492. 10.1029/2022JE007492

Data Availability Statement

The Supporting Information S1 for this article contains descriptions and links to all of the GPlates data files used in the reconstructions. All of the data files and the ISIS‐formatted base mosaic can be downloaded from the JHU‐APL data repository for this article at Collins et al. (2022). GPlates software (Müller et al., 2018) is an open source project located at http://gplates.org. The software may be downloaded from the GPlates website at https://www.gplates.org/download or from the project's GitHub page at https://github.com/GPlates. For future compatibility purposes, the GPlates project plans to make older versions of GPlates available on EarthByte at https://www.earthbyte.org/. Mac and Windows installers of GPlates version 2.3, current as of the date of submission of this manuscript and known to work with the archived data files, are included in this article's JHU‐APL data repository in case of future incompatibility Collins et al. (2022).