Abstract
Phagocytosis is the process of engulfment and internalization of comparatively large particles by the cell, that plays a central role in the functioning of our immune system. We study the process of phagocytosis by considering a simplified coarse grained model of a three-dimensional vesicle, having uniform adhesion interaction with a rigid particle, and containing curved membrane-bound protein complexes, or curved membrane nano-domains, redwhich in turn recruit active cytoskeletal forces. Complete engulfment is achieved when the bending energy cost of the vesicle is balanced by the gain in the adhesion energy. The presence of curved (convex) proteins reduces the bending energy cost by self-organizing with higher density at the highly curved leading edge of the engulfing membrane, which forms the circular rim of the phagocytic cup that wraps around the particle. This allows the engulfment to occur at much smaller adhesion strength. When the curved membrane-bound protein complexes locally recruit actin polymerization machinery, which leads to outward forces being exerted on the membrane, we find that engulfment is achieved more quickly and at a lower protein density. We consider spherical as well as non-spherical particles, and find that non-spherical particles are more difficult to engulf in comparison to the spherical particles of the same surface area. For non-spherical particles, the engulfment time crucially depends upon the initial orientation of the particles with respect to the vesicle. Our model offers a mechanism for the spontaneous self-organization of the actin cytoskeleton at the phagocytic cup, in good agreement with recent high-resolution experimental observations.
Phagocytosis, also termed ‘cell eating’1–6, is a cellular process by which cells internalize extracellular particles that are relatively large (0.5 − 20μm). Phagocytosis plays an important role for the immune system, enabling immune cells to destroy foreign elements and clear dead cells and other debris7. This process is also important for diagnostic and therapeutic approaches to cancer, for example, using specialized engulfed particles8,9. Despite its biological importance, it is still not understood how the actin cytoskeleton is coordinated spatio-temporally during the phagocytosis process.
Phagocytosis (and endocytosis) in general requires receptors on the cell membrane that bind to the surface of the target particles10. Binding-driven engulfment, which does not involve the forces of the cytoskeleton, was modelled in10–15, with purely diffusive dynamics of the receptors10,12 as well as with active drift11,14. Engulfment of charged particles was previously modelled, and shown to depend on the lateral segregation of mobile charged membrane components (lipids and proteins), leading to a discontinuous wrapping transition16. The effect of signalling molecules was also considered in11, where using drift and diffusion the model successfully recovered the two stages of the process: an initial slow engulfment followed by fast engulfment of the second half of the spherical object, comparing to experiments of neutrophil phagocytosis of polystyrene beads11. Phagocytosis is, however, an active process which is known to involve the forces of actin polymerization that push the engulfing membrane forward17,18. In subsequent models, detailed description of active forces18–21 and also the bending and elastic energies of the membrane and cortex are considered22–26. The cytoskeletal components of phagocytosis were investigated during engulfment of artificially produced particles14,27–29, or during bacterial engulfment by the immune cell30–32. In14, it was found that the engulfment process either stalls before half engulfment of a spherical object, or leads to complete engulfment. In27,33, the experiment was performed using micro-pipettes to hold both the immune cell and the target particle, allowing the measurement of the cortical tension. Recent experiments provide high-resolution details of the organization of the actin cytoskeleton at the rim of the phagocytic cup34–36, challenging the theoretical modelling of this process.
In reality, however, the shape of the engulfed particles, such as bacteria or viruses, may be highly non-spherical, which motivated several experiments with artificial particles of various geometries28,37–39. In28 it was found that the engulfment time for a non-spherical shapes can be five times larger than for a spherical particle37. In38 it was observed that an oblate spheroid was engulfed more easily compared to spheres, while spheres were easier to engulf compared to prolate spheroid, rod-shaped particles, or needles40. Note that the surface area was not kept constant for the particles with the different geometries. In theoretical studies, several non-spherical shapes were modelled, such as ellipsoids, rod-like particles, and capped cylinder41–43, however, in these studies the effect of active forces have not been considered.
From these studies we know that the phagocytosis process involves highly complex dynamics of cytoskeleton rearrangement, membrane shape deformations and proteins aggregations7. There is at present no complete theoretical understanding of the dynamics of the self-organization of the membrane and actin cytoskeleton, including the active forces it exerts, during the engulfment process. Here, we address this problem, using a coarse-grained theoretical model44–46. In this model, a three-dimensional vesicle that contains curved membrane complexes47–49 which recruit the protrusive forces of the cytoskeleton50, was shown to describe spreading over a flat substrate46. The spreading of the vesicle in this model is driven by the self-organization of the curved proteins in the form of a leading edge aggregate, stabilized by the protrusive forces that describe the actin polymerization pressure. We therefore propose to use this model to describe the dynamics of the spontaneous recruitment of the actin cytoskeleton and the membrane spreading during phagocytosis. This modelling approach can be further motivated by the observations of curved membrane proteins that are also related to actin recruitment at the leading edge of the cell membrane protrusions51–54.
Using this model we aim to expose the role of curved membrane proteins, coupled with adhesion, in self-organizing and regulating the spatio-temporal dynamics of the active cytoskeletal forces, during phagocytosis. This minimal model allows us to explore the basic physical mechanisms during this process, which exist in addition to the more complex biochemical signaling, that plays a role in regulating phagocytosis6,55.
Materials and Methods
Theoretical modelling
We consider a three-dimensional vesicle (Fig. 1), which is described by a closed surface having N vertices, each of them connected to its neighbours with bonds, to form a dynamically triangulated, self-avoiding network, with the topology of a sphere44–46,56,57. For self-avoiding membrane network, the constraint of fixed topology also influences the vesicle shape determination58. The vesicle is kept in contact with a particle, with which the vesicle has an attractive interaction, as shown in Fig. 1. The vesicle energy has four following contributions: The bending energy is given by,
| (1) |
where is the bending rigidity, are the principal curvatures and is the spontaneous curvature. The discrete version of the bending energy is described in SI sec. S-1. The direct binding energy between protein complexes on nearest neighbour nodes is given by,
| (2) |
where, is the Heaviside step function, is the distance between proteins, are the position vectors for proteins, and is the range of attraction, is the strength of attraction. The range of attraction is such that only the proteins that are in the neighbouring vertices can attract each other. The active energy cost for displacing a vertex containing a protein complex is given by,
| (3) |
where, is the magnitude of the active force, representing the protrusive force due to actin polymerization that is acting in the direction of outward normal vector of the local membrane surface (along ) and is the displacement vector of the protein complex. The âĂIJactiveâĂİ forces in our simulations are implemented as external forces that act on specific nodes of the system. This is done by giving a negative energy contribution when the points on which these forces act move in the direction of the force. This means that the work done by these forces effectively enters the energy calculation.
Fig. 1.
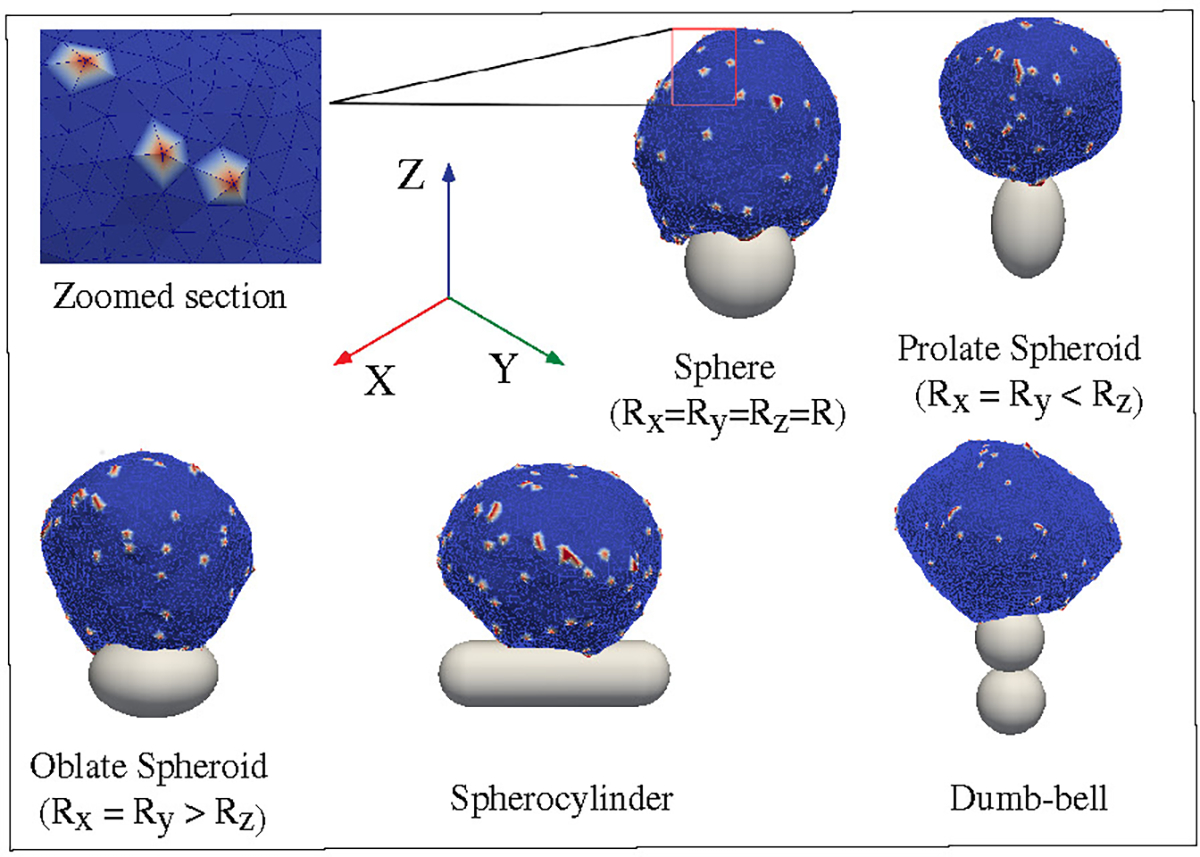
Schematic representation of our model. The vesicle is formed by a closed triangulated surface, having N vertices connected to neighbours by bonds. The red vertices on the surface of the vesicle represent the curved membrane protein complexes, while the blue vertices represent the bare membrane. A zoomed version of a small section of the vesicle surface is shown in the inset. The vesicle is kept in contact with a particle, having attractive interaction between them. We consider spherical as well as non-spherical particles, such as spheroid, spherocylinder, dumb-bell etc.
The above equation indicates that when the proteins are distributed inhomogeneously, there will be a net force on the vesicle in a particular direction46. However, in the present work we only simulate vesicles that are adhered to particles that are fixed in their location, which effectively links our vesicle to the lab frame thereby restoring momentum conservation (fixing the engulfed particle acts as an infinite momentum reservoir).
Finally, the adhesion energy is given by,
| (4) |
where is the adhesion strength, and the sum runs over all the vertices that are adhered to the phagocytic particle45,46,59. By ‘adhered vertices’, we mean all such vertices, whose perpendicular distance from the surface of the particle are less than . We choose to be equal to the length , which is the unit of length in our model, and defines a minimal length allowed for a bond. Here, we assume that the particle is perfectly rigid such that no vertices can penetrate the particle. Note that in our model we measure in energy units, since it is defined as the energy per adhered vertex or node. In the continuum description, however, the adhesion strength is defined in units of energy per area.
We update the vesicle with mainly two moves, (1) vertex movement and (2) Bond flip. In a vertex movement, a vertex is randomly chosen and attempt to move by a random length and direction, with the maximum possible distance restricted by 0.15 . In a bond flip move, a single bond is chosen, which is a common side of two neighbouring triangles, and this bond is cut and reestablished between the other two unconnected vertices45,46,59. While the vertex movement allows the vesicle to change its shape, a bond flip mechanism provides lateral fluidity to the membrane, by allowing vertices (as well as the vertices that are occupied by protein complexes) to diffuse on the membrane surface. This lateral motion allows the protein complexes to move on the membrane surface and aggregate with other protein complexes to form larger aggregates. The maximum bond length is restricted to . The particle is assumed to be static and does not have any independent dynamics. We update the system using Metropolis algorithm, where any movement that increases the energy of the system by an amount occurs with rate exp(−ΔW/kBT), otherwise it occurs with rate unity. Note that our model only captures the wrapping and engulfment events, while the other upcoming processes, such as the membrane fission60, and the movement of the engulfed particle inside the vesicle are not captured in the present model.
The forces exerted at the locations of the curved proteins, are “active” since they give an effective energy (work) term that is unbounded from below (3). This property defines them as out-of-equilibrium, as they can not arise in an energy conserving system. These active forces represent the pushing exerted on the membrane by polymerizing actin filaments61–64, which we do not model explicitly to reduce the complexity of the model65.
Unless specified, we use a vesicle of total number of vertices, (radius ), where is the unit of length in our model, and defines the minimum bond length. The bending rigidity , the protein-protein attraction strength , and is the protein density, with vertices occupied by curved (convex) membrane proteins having spontaneous curvature: . Note that we do not conserve the vesicle volume, although this could be maintained using an osmotic pressure term as the volume constraint45. The membrane area is very well conserved .
Note that our MC simulations do not describe the correct dynamics of the fluid motion around the membrane and the engulfed object. However, it gives the energetically most favorable trajectory that controls the dynamics, without the correct time-scales, which depend on the hydrodynamic dissipation. In addition, the actin filaments that exert the pushing forces at the leading edge of the phagocytic cup, also transmit traction forces to the engulfed particle, which can therefore move and rotate it. These traction forces are not explicitly described, as we maintain the fixed position of the engulfed particle, similar to some experimental set-ups66.
In this numerical study, we chose a fixed vesicle and spherical particle size, for which we have a reasonable balance between accuracy and simulation time. The vesicle radius was chosen to be , while the particle radius was taken to be (smaller and larger particles are explored in the SI sec. S-3, Fig.S1). The mesh size for these dimensions allows us to describe the membrane shapes during the engulfment process with good accuracy, even along the sharp (highly curved) leading edge. The leading edge curvature is determined by the spontaneous curvature of the curved proteins, which we kept from our previous work on vesicle spreading46. We quantified the accuracy by comparing the calculated mean curvature of the membrane with the discrete version, and find that even for spherical vesicles with a radius of , the error is only ~ 10% (Fig.S21). Clearly, membrane features that are on smaller lengthscales than are not captured by this calculation.
Note that our continuum description of the membrane is valid for lengthscales that are larger than that of the membrane width or single-protein size. Our simulations are therefore valid for particles that are larger than this lengthscale. Furthermore, we use the term “curved proteins” to describe any membrane-bound or membrane embedded protein complex, or larger nano-domains, that have the properties of spontaneous curvature and ability to recruit the nucleation of actin polymerization. Let us emphasize that our continuum model of the membrane is not a microscopic model, where each node of the mesh represents a single protein or lipid.
The length scale that we use in our simulation does not necessarily correspond to be a particular length in reality. By signing a different real length to the basic length-scale of the simulation we do not change the resulting dynamics, for the following reason: The dynamics of the engulfment process depends on the energy gain/loss per additional adhered area increment (vertex). The adhesion energy per adhered vertex rescales as , as does the bending energy per vertex (because the total bending energy of a specific shape is scale-invariant, provided we also rescale spontaneous curvature accordingly). The active work is also independent of the absolute scale of , as we define the force exerted by each vertex to be in units of , and therefore its contribution to the total energy increment per unit area, also scales as . The absolute scaling of does not therefore change the qualitative nature of our simulation results: both the adhesion energy and the bending energy per unit area, scale as .
There are important length-scales in this system which we wish to discuss. The first is the lengthscale given by the ratio between the adhesion and bending energy of the adhered membrane. This ratio determines the minimal radius of the spherical particle: , below which the membrane does not lower its energy when adhering and therefore adhesion vanishes completely67. Above the critical radius the engulfment is inhibited by the interplay between the adhesion energy of the adhered membrane and the bending energy of the non-adhered membrane (see SI Fig.S2). The bending energy in this regime depends on the ratio of the vesicle to the particle size67, such that large particles are not engulfed due to the finite size of the vesicle. We demonstrate this using our simulations for the protein-free vesicle in the SI (Fig.S4). This analysis, and the dynamics of the engulfment in this regime, are modified when the vesicle contains curved proteins, as well as active forces, and is the main focus of this work. We leave for future studies the detailed exploration of the effects of some of the parameters of our model, such as C0.
Imaging of Macrophage Phagocytosis
Culturing of RAW264.7 macrophages (ATCC) and generation of murine bone-marrow derived macrophages is described in34. Macrophages were transfected with mEmerald-Lifeact (Addgene, #54148) to label F-actin using the Neon electroporation system, according to manufacturerâĂŹs instructions, and allowed to recover for 24 hr. Flash Red polystyrene beads (Bangs Laboratories Inc., 7 μm diameter) were washed three times in sterile PBS and opsonized overnight at 4°C in 3 mg/mL mouse IgG (Invitrogen). To remove excess antibody, beads were washed three times with PBS and resuspended in sterile PBS. Beads were applied to macrophages, plated on 5 mm round coverslips, in a 37°C-heated, water-coupled bath in imaging medium (FluoroBrite (Thermo Scientific), 0 – 5 % FBS, Pen/Strep) prior to imaging acquisition. Imaging was performed using a lattice light-sheet microscope operated and maintained by the Advanced Imaging Center at the Howard Hughes Medical Institute Janelia Research Campus (Ashburn, VA). 488, 560, or 642 nm diode lasers (MPB Communications) were operated between 40 and 60 mW initial power, with 20 – 50 % acousto-optic tunable filter transmittance. The microscope was equipped with a Special Optics 0.65 NA/3.75 mm water dipping lens, excitation objective, and a Nikon CFI Apo LWD 25 × 1.1 NA water dipping collection objective, which used a 500 mm focal length tube lens. Images were acquired with a Hamamatsu Orca Flash 4.0 V2 sCMOS cameras in custom-written LabView Software. Post-image deskewing and deconvolution was performed using HHMI Janelia custom software and 10 iterations of the Richardson-Lucy algorithm.
Results
We simulate the dynamics of a three-dimensional vesicle, which is described by a closed surface having N vertices, each of them connected to its neighbours with bonds, forming a dynamically triangulated, self-avoiding network, with the topology of a sphere45,46. On this network, we describe a population of curved proteins, that can diffuse in the membrane, and exert active forces. Within our model, the actin polymerization of individual filaments is not explicitly described65, but is mapped to out-of-equilibrium (active) forces that locally push outwards on the membrane. We first study the case where the phagocytic particle is spherical, and then generalize it for non-spherical particles as well.
We chose the surface area of the vesicle to be much larger (at least four times larger) than the particle’s, so that the engulfment is not inhibited by membrane surface area limitation. During phagocytosis the cell is able to increase the local membrane area6, to allow for phagocytosis of larger particles. Note that our vesicle does not represent the entire shape of the cell, and does not include the nucleus and other constraints. Further, we do not explicitly take into account the lateral68 and surface69 membrane tension, but our calculation conserves the membrane area (total area fluctuations of < 1%). In addition, we do not fix the vesicle volume, corresponding to vanishing osmotic pressure gradient across the membrane, as maintained in cells70. This allows our vesicle to undergo both large volume and shape changes during the engulfment process. Introducing a high osmotic pressure inside our simulated vesicle would act to conserve the volume45, and in this way hinder the engulfment process by inhibiting large vesicle shape deformations. The effects of osmotic pressure on the phagocytosis process can be further investigate in the future.
Spherical particles - Passive curved proteins
As a first validation of our model, we simulated the engulfment process of a spherical particle by a protein-free vesicle (see SI secs. S3–S4, Figs.S1–S4; Supplementary Movies–S1,S2). In agreement with previous studies71 we find an optimal size for full engulfment of the particle in this system; very small particles can not be engulfed due to the high bending energy, while very large particles require larger vesicles in order to be fully engulfed. For our further simulations, we choose the particle radius to be (where is the minimal allowed length of an edge on the triangulated surface), which is a suitable size for the parameter ranges we simulate here. The protein-free case can be compared to a simplified analytical model (see SI sec. S4), and used to calibrate the relevant parameter regime. Note that a fully engulfed state in our simulations is when the vesicle encloses the particle, such that only a small hole (of size 1–3 triangles) remains exposed, as shown in Fig. 2d (leftmost image). Since we do not allow for membrane fusion, this hole remains.
Fig. 2.
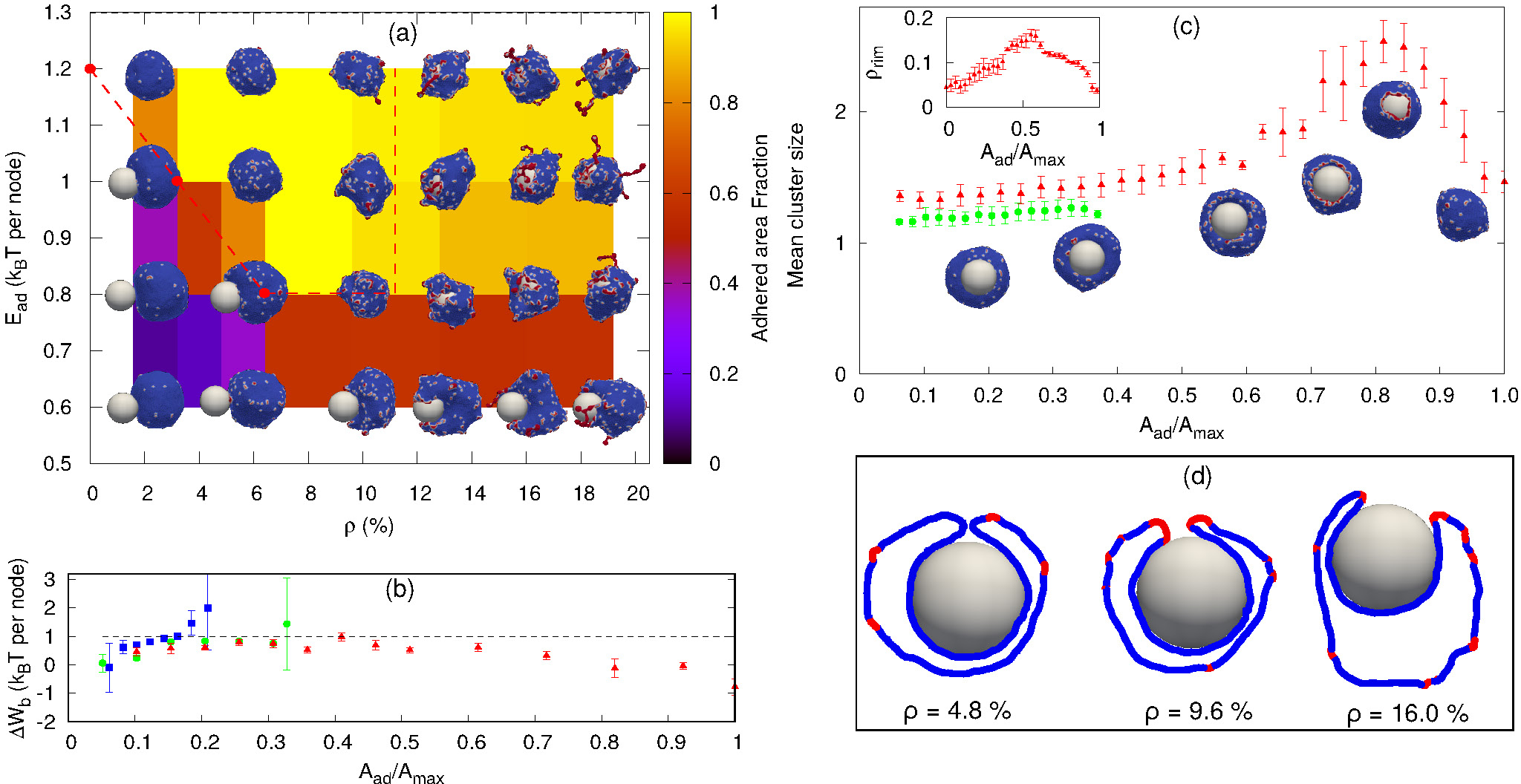
Sphere engulfment by a vesicle with passive proteins. (a) Phase diagram in the Ead − ρ plane, where Ead is the adhesion strength and ρ is the density of curved membrane proteins. Background color is showing the adhered area fraction. The red dashed line is approximately separating the fully engulfed state and the partially engulfed state. The snapshots are shown for Ead = 0.60, 0.80, 1.0, 1.20 (in units of kBT) and ρ = 1.6 %, 4.8 %, 9.6 %, 12.8 %, 16%, 19.2 %. (b) Comparison of adhesion energy gain (dashed horizontal line) and bending energy cost (ΔWb, points) per adhered node (both having units of kBT) as a function of the engulfment fraction, for a fixed adhesion strength Ead = 1.0 kBT and various values of ρ. Blue symbols denote ρ = 0.8%, green circles for ρ = 2.4% and red triangles for ρ = 4.0%. The origin of the large error bars is due to the large fluctuations in the bending energy at the leading edge of the membrane, as well as having a relatively small ensemble of simulations for each case. (c) Mean cluster size (mean number of proteins in a cluster) as a function of the engulfed area fraction, for both partial and complete engulfment cases. The colors codes are same as fig. 2b. Inset shows the increase in the density of curved proteins at the rim of the phagocytic cup during the engulfment process, for ρ = 4.0%. (d) Examples of cross-sections of the vesicle membrane around the particle, at the end of the engulfment process, for different protein densities. We use Ead = 1.0 kBT here. Other parameters are: The total number of vertices (nodes) in the vesicle N = 3127, the radius of the spherical particle R = 10 lmin, the bending rigidity κ = 20 kBT, the protein-protein attraction strength w = 1 kBT, and the spontaneous curvature of curved (convex) membrane proteins .
Next, we consider vesicles with passive (F = 0, where F is the active protrusive force exerted by the proteins), curved proteins. In Fig. 2a, we show the phase diagram in the ρ − Ead plane (where Ead is the adhesion energy per adhered node, and ρ the areal density of the proteins on the vesicle membrane). For small Ead, below ~ 0.60 kBT, we only obtain partial engulfment, with the engulfment area increasing with ρ but not reaching full engulfment. For intermediate Ead (0.80 − 1.0 kBT), there is an incomplete engulfment for small ρ (Movie-S3), but the engulfment is complete for larger ρ (Movie-S4). This is the interesting regime, where engulfment is facilitated by the presence of the curved proteins.
Note that we calculate the adhered fraction of the spherical particle (Aad/Amax), using for Amax the maximum adhered area. This may be larger than the true surface area of the particle, since we defined a finite width of the adhesive interactions, and within this width the adhered membrane may fluctuate, therefore containing a larger membrane area than the area of the rigid bead surface (see for example the cross-sections in Fig. 2d, and for more details see SI, sec. S-2).
Increasing ρ reduces the bending energy cost of the engulfment by the spontaneous aggregation of the curved proteins at the sharp leading edge of the engulfing membrane, and allows the vesicle to adhere more and engulf the particle. This is the same mechanism that allows passive curved proteins to drive vesicle spreading on flat adhesive substrates46.
The engulfment process can be understood by considering the competition between adhesion and bending energy cost of the vesicle as the engulfment proceeds. In Fig. 2b we compare the adhesion energy gain (Ead) and bending energy cost (ΔWb), per additional adhered membrane node, as a function of the adhered fraction of the spherical particle. The bending energy cost increases with adhered fraction, and for small ρ the engulfment process stops where the bending energy cost becomes higher than the adhesion energy gain, per node. In Fig. 2b we show two cases of partial engulfment, for ρ = 0.8 %, 2.4 % (blue and green points), where the bending energy cost becomes larger than the adhesion energy gain, and the system reaches steady-state at Aad/Amax ~0.2, 0.35 respectively. At these low densities the curved proteins fail to form large aggregates at the leading-edge of the engulfing membrane, as shown by the mean cluster size (Fig. 2c), and therefore do not lower the bending energy cost sufficiently (see insets of Fig. 2c for the adhered fractions that are smaller than 0.5).
Complete engulfment is achieved for higher densities, where the adhesion energy gain is larger than the bending energy cost. For ρ = 4.0 % the bending energy cost is always smaller than the adhesion energy gain, and the system proceeds to complete engulfment (red points in Fig. 2b). This is driven by the formation of a large protein cluster along the leading-edge of the engulfing membrane (Fig. 2c and insets for adhered fractions that are larger than 0.5). However, the aggregation at the leading edge is transient, since as the radius of the hole gets too small, the mean curvature of the rim of the hole decreases and is less favorable for the curved proteins (SI sec. S5, Fig. S5), which leads to the dispersal of the curved proteins on the membrane (Fig. 2d, ρ = 4.8%). This is the origin for the appearance of a maximum value of the mean cluster size during complete engulfment (Fig. 2c).
Note that in addition to the adhesion energy gain, there is also the gain in protein-protein binding energy, which further helps drive the membrane over the bending energy barrier, but this is a small contribution due to the small size of the ring-like clusters of proteins (Fig. 2c). Following the completion of the engulfment, this ring-like cluster of curved proteins disperses spontaneously. Since the topology of the membrane is fixed, we do not allow for membrane fusion, and there remains a tiny open membrane neck that connects the engulfed sphere with the space outside the vesicle (Fig. 2d).
For very large ρ (Fig. 2a), however, the wrapping is again incomplete. The large number of curved proteins stabilize the cluster at the membrane rim and prevent the hole from closing up (Movie-S5). In Fig. 2d we show an example of the cross-sectional view of the vesicle at the end of the engulfment process. For high densities (ρ = 9.6% or larger) the protein cluster remains stable at the rim of the phagocytic cup. This cluster maintains the curvature of the rim to fit better the spontaneous curvature of the proteins, and this prevents the rim from shrinking, resulting in incomplete engulfment (SI sec-S6, Fig. S6). Note that at large densities the curved proteins form pearled clusters, that are not directly related to the rim cluster at the edge of the phagocytic cup.
For large Ead(≥ 1.2 kBT), the adhesion interaction between the vesicle and the particle is strong enough to drive complete engulfment even in the absence of curved proteins. The red dashed line in Fig. 2a encloses the region within which we find complete engulfment. The shape of this complete-engulfment transition line can be qualitatively reproduced by a simplified analytical model (SI sec. S7; Figs. S8, S9).
Finally, we also calculated the engulfment time as a function of ρ (see SI sec. S8, Fig. S10), where we find that it is decreasing with increasing ρ. The engulfment time diverges for ρ ~ 2.25 %, below which there is no engulfment (for Ead = 1.0 kBT).
Spherical particles - Active curved proteins
Next, we study the engulfment of a rigid particle by a vesicle containing active curved proteins (Fig. 3). In order to expose most clearly the role of activity during the engulfment process, we start with a low concentration of curved proteins (ρ = 1.6 %), such that their passive effect is weak (Fig. 2a). In Fig. 3a, we show the engulfment phase diagram in the F − Ead plane. We find that the active forces enable full engulfment even at low adhesion strengths, where the passive curved proteins (F = 0) are not sufficient to drive full engulfment. For small Ead, the engulfment is incomplete even for large F, while for intermediate Ead the engulfment becomes complete as F increases (Movie-S6,S7,S8). For large values of Ead, the engulfment is achieved even for the passive system.
Fig. 3.
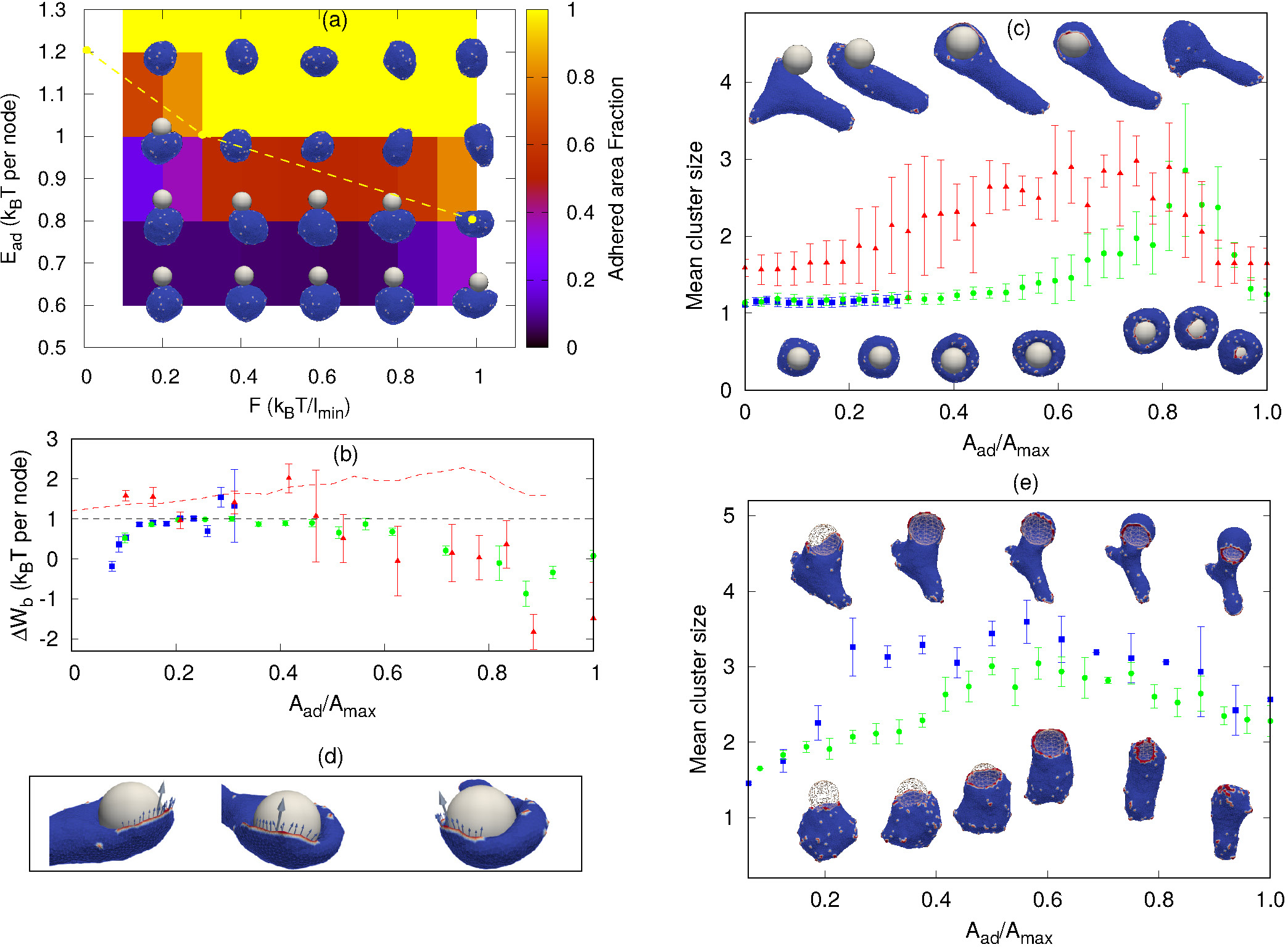
Sphere engulfment by a vesicle with active proteins. (a) Phase diagram in the Ead − F plane for a low concentration of curved proteins ρ = 1.6%, where F represents the protrusive force due to actin polymerization that is coupled with the curved membrane proteins. Background color is showing the adhered area fraction. The dashed yellow line approximately separates the fully engulfed (above the line) from the partially-engulfed states. The snapshots are shown for Ead = 0.60, 0.80, 1.0, 1.20 (in units of kBT) and F = 0.20, 0.40, 0.60, 0.80, 1.0 (in units of kBT/lmin). (b) Comparison of bending energy cost with the adhesion energy gain (both having units of kBT per adhered node) for different values of F. The blue boxes, green circles and the red triangles are for F = 0.1, 0.4 and 2 (in units of kBT/lmin) respectively. The red dashed line is showing the combined effective energy gain per adhered node, including the adhesion and the work done by the active forces (for F = 2 kBT/lmin). (c) The mean cluster size as a function of engulfed area fraction, for the same cases shown in (b) (same color code). Lower snap-shots correspond to F = 0.1, 0.4, and top snap-shots to F = 2. (d) Snap-shots of the vesicle (F = 2 kBT/lmin) indicating the contribution of the active forces to the the engulfment. Arrows show the tangential component of the individual forces (small arrows), and the direction of the total force (large arrow), for proteins that are close to the spherical surface. For (b-d), we use Ead = 1 kBT and ρ = 1.6 %. (e) Mean cluster size for large Ead and ρ. Green circles are for ρ = 6.4%, F = 1.0 kBT/lmin, and blue boxes are for ρ = 4.8 %, F = 2.0 kBT/lmin. We use Ead = 1.5 kBT for both the cases.
As for the passive case, we analyze the engulfment process by plotting the adhesion energy gain and the bending energy cost per adhered node, as a function of Aad/Amax. In Fig. 3b we compare both the case of complete and incomplete engulfment, as the force is increased. As in the passive case, incomplete engulfment occurs when the bending energy cost per node becomes larger than Ead (blue boxes in Fig. 3b). For a higher force (F = 0.40 kBT/lmin), the active force enhances the aggregation of the proteins around the rim and thereby lowers the bending energy cost, resulting in complete engulfment (green circles in Fig. 3b).
Even higher forces (F = 2 kBT/lmin), produce large shape fluctuations of the vesicle, and the bending energy cost increases. However, a complete engulfment is achieved nevertheless (red triangles in Fig. 3b, and top insets in Fig. 3c). In this case, the engulfment is enabled by the active forces that directly push the membrane over the spherical surface, and complete engulfment is achieved even when the bending energy cost per node goes above Ead. In order to extract the contribution due to active forces in this case, we define a region close to the particle (phagocytic cup or rim) and assume that only the forces from these proteins are helping the vesicle to engulf the particle. We then calculate the magnitude of active forces in the tangential direction to the surface of the particle (Fig. 3d). We then divide this total force Ftotal by the length of the leading rim of the membrane, to extract the effective active work done per adhered node (see SI sec. S9, Fig. S11 for details). We add this active work to the adhesion energy gain per adhered node (red dashed line in Fig. 3b), which is shown to be sufficient to offset the bending energy cost per node. The magnitude of total active force (without scaling by rim length) as a function of the adhered fraction, is shown in the SI, Fig. S-11(c). It is clear from Fig.S11(c), that the total active force is very small during the early stages when the curved protein complexes are still dispersed over the membrane surface, so that their active forces are pointing in random directions, before they form the organized aggregate at the leading edge of the phagocytic cup.
Note that in the active case the complete engulfment can proceed at much lower densities of proteins, compared to the passive case, such that there are not necessarily enough of them to complete a ring-like cluster at the leading edge. An arc-like cluster of active proteins, that forms at an earlier stage of the engulfment process (red triangles in Fig. 3c), can be sufficient to drive a flat protrusion that spreads over the spherical particle to complete the engulfment (Fig. 3(c,d)). This is further shown in Fig. 3e, for larger protein densities (Movie-S9,S10). The spherical particle is transparent to ensure the visibility of the protein clusters along the rim of the phagocytic cup. Due to the higher density the rim clusters form at lower adhered fraction (compared to Fig. 3c), but they are still highly fragmented and do not merge to form a complete circular ring until very late stages of the engulfment (Fig. 3e).
Many of the qualitative spatio-temporal features that we found for the curved active proteins in our simulations match very well the recent high-resolution experimental images of the actin organization along the leading edge of the engulfing membrane protrusion during phagocytosis (Fig. 4, Movie-S11,S12)35. In both the experiments and the simulations we find that the actin ring50 is initially discontinuous, and highly fragmented, in the form of dispersed “teeth” and “arcs” along the leading edge. The actin aggregate becomes more cohesive in the final stages of the engulfment, before it disperses after the engulfment is complete (Also see SI sec. S10, Movie-S13). Note that in our model the curved membrane complexes are also the sites of recruitment of actin polymerization, which therefore ends up exerting a protrusive force on the membrane at these sites. We therefore identify the membrane accumulation of the curved proteins in our simulations with the accumulation of cortical actin in the experimental observations.
Fig. 4.
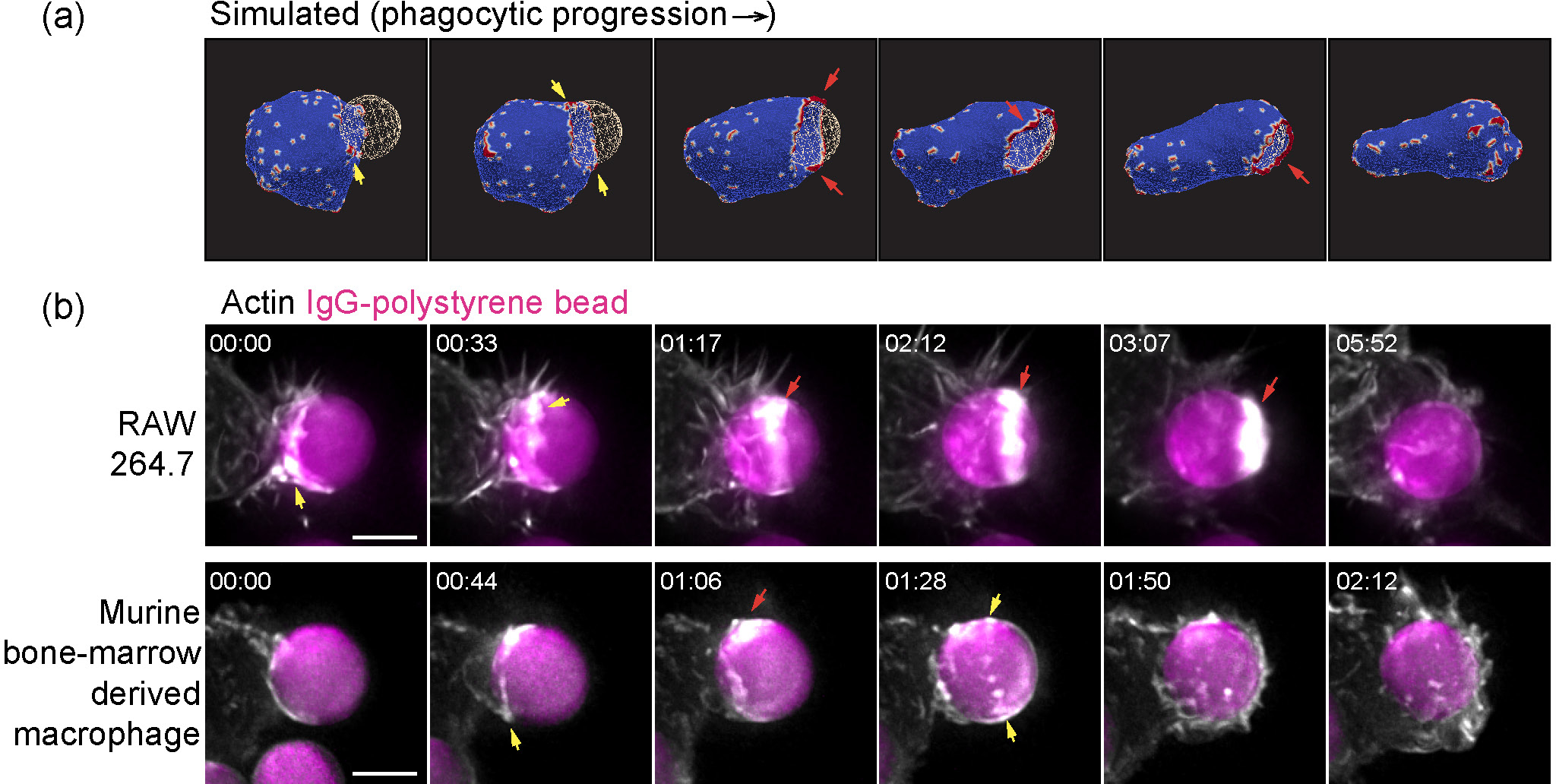
Comparison of the actin organization at the rim of the phagocytic cup, observed in simulations (a) and experiments (b). In both the in vitro experiments and the simulations we find that the actin ring is highly fragmented, in the form of dispersed “teeth” (yellow arrows) or in more continuous “arcs” (red arrows) along the leading edge. “Arcs” often connect to form a complete ring around the leading-edge rim during the final stage of the engulfment process, both in the simulations and the experiments. The actin aggregate becomes more cohesive in the final stages of the engulfment, before it disperses after the engulfment is complete. (a) Snapshots from a simulation, using Ead = 1.50 kBT, ρ = 6.4 % and F = 1.0 kBT/lmin. (b) Time-lapse sequences of maximum intensity projection images illustrating engulfment of Immunoglobulin-G-coated polystyrene beads (7 μm diameter) by (upper) RAW264.7 macrophage-like cell line and by (lower) murine bone-marrow derived macrophages, imaged by lattice-light sheet microscopy. In (b), cells were transfected with mEmerald-Lifeact to label F-actin. Scale bar 5 μm, time is indicated in min:sec.
When comparing to the experiments we have to remember the limitations of our numerical simulation, which can only describe membrane features that are on lengthscales larger than lmin (for a particle of radius 3.5μm, ). However, the main features of the actin organization that we highlight in Fig. 4a, namely the fragmented ring and its continuous closure, are on larger lengthscales and therefore reliably emerge in our simulations. We therefore found this choice of mesh resolution to be sufficient in order to explain the outstanding features of the membrane and actin organization during the engulfment, as observed in the experiments, while maintaining a reasonable computation time. Future studies using a finer mesh may allow to study smaller scale features of this process.
Spherical particles - Engulfment dynamics
The engulfment dynamics for the different systems are shown in Fig. 5a. We note that MC simulations do not provide us with the correct real time dynamics, as the hydrodynamic dissipation processes are not described. Nevertheless, we can obtain the qualitative form of the dynamics, as well as obtain relative engulfment times for comparison between different cases.
Fig. 5.
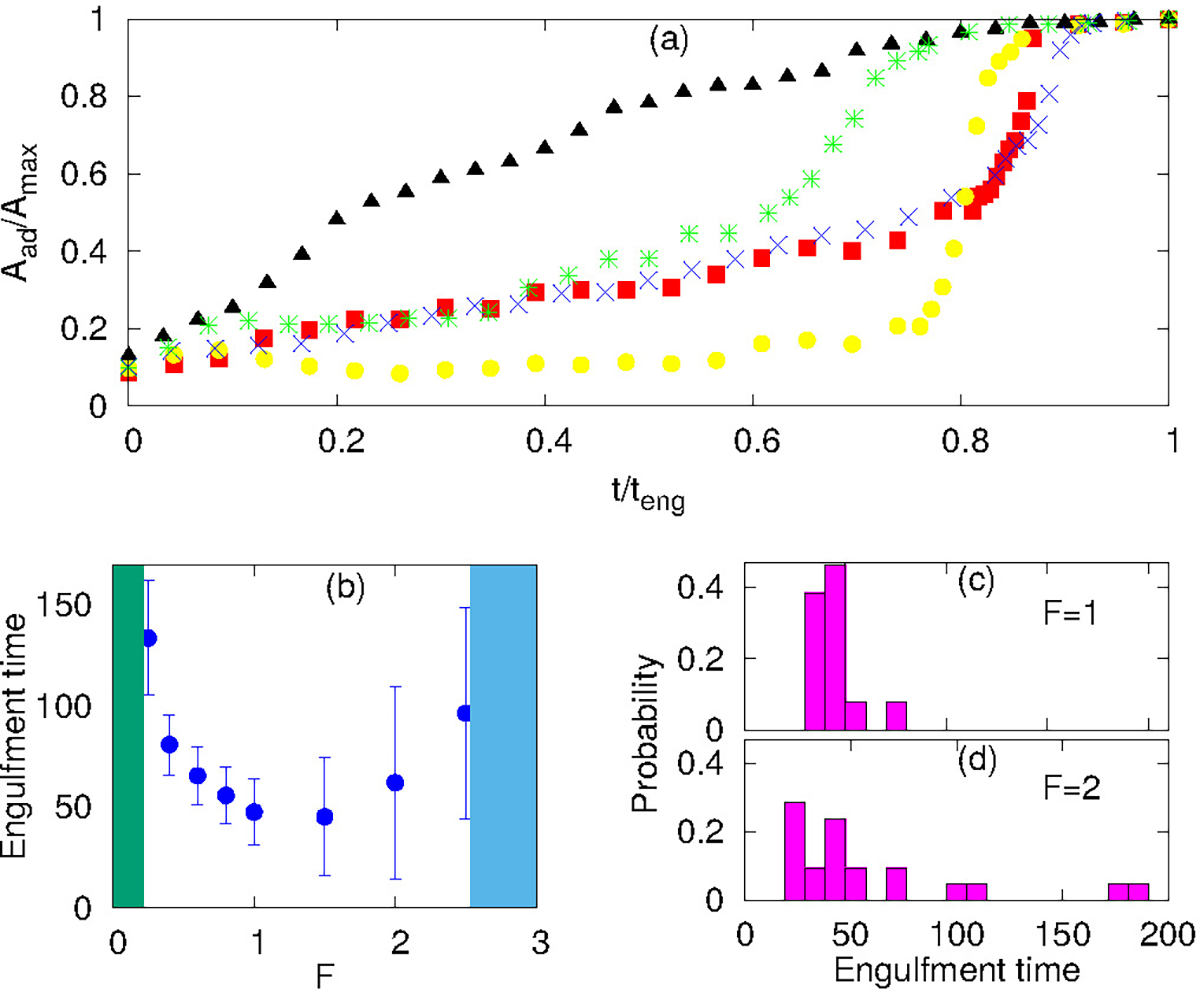
Engulfment dynamics for spherical particles. (a) Different growth behaviour of adhered fraction with time for protein-free, passive and active cases. We scale the area axis by maximum adhered area (Amax) and time axis by the engulfment time (teng). Blue cross symbols are for protein free case with Ead = 1.30 kBT; green star symbols for passive proteins with Ead = 1.0 kBT and ρ = 4.0 %; red boxes for Ead = 1.0 kBT, ρ = 1.6% and F = 0.40 kBT/lmin; yellow circles for Ead = 1.0 kBT, ρ = 1.6% and F = 2.0 kBT/lmin; black triangles for Ead = 1.50 kBT, ρ = 6.4 % and F = 1.0 kBT/lmin. (b) Engulfment time as a function of F, showing the non-monotonic behavior: below and above a critical force (green and blue shaded areas respectively) there is partial engulfment. (c-d) Distributions of the engulfment time for F = 1, 2 kBT/lmin, respectively.
For the protein-free and passive proteins systems, driven by adhesion alone, we find in our simulations the typical “two-stage” behavior: an initial slow growth up to adhered area fraction of ~ 0.5, and then a very fast stage to complete engulfment. A similar behavior is also observed for the active system in the regime of low protein densities. This dynamics was observed experimentally, and for the passive engulfment system was also motivated by theoretical modelling11,16.
However, for the active system at high protein density, where the rim clusters form at an early stage of the engulfment process (Fig. 3e), we find a much more uniform dynamics with steady growth of the adhered fraction (Fig. 5a). This agrees qualitatively with the observations in66, as well as34,35, which indeed correspond to this regime (Figs. 3e,4).
In Fig. 5a the engulfment dynamics are shown as a function of normalized time, so the actual engulfment duration is not presented. The dependence of the mean engulfment time on the active force is found to be non-monotonic (Fig. 5b). Below a critical force, in the regime of low Ead and low ρ, where the passive system does not fully engulf (Fig. 3a), there is no complete engulfment (green shaded area). Above this regime, increasing force induces complete engulfment with faster and more robust engulfment as F increases. The engulfment time distribution in this regime is relatively narrow (Fig. 5c).
However, increasing F beyond some value, which is set by the relation of the adhesion energy and the active work, leads to increasing both the mean value and the variability of the engulfment time. This occurs due to active forces stretching the membrane away from the adhered particle (top insets in Fig. 3c), which gives rise to long “waiting times” during which the engulfment does not progress. Following this “waiting time”, once the protein aggregate forms at the membrane rim (Fig. 3c), the engulfment proceeds rapidly as seen in Fig. 5a (yellow circles). This variability is manifested in the very broad distribution of engulfment times (Fig. 5d).
At even larger forces, the stretching of the membrane sideways by the active forces pulls the membrane away from the adhesive particle and prevents engulfment (blue shaded area in Fig. 5b, and SI sec S11, Fig. S13(a), Movie-S14).
In this regime of large F, if we further increase ρ, we reach the regime where a free vesicle will form a flat pancake-like shape, where all the proteins are aggregated at the rim45. In this regime the vesicle can engulf the particle if this process is faster than the timescale of the formation of the pancake-like shape (SI sec. S11, Fig. S13(b); Movie-S15). For very large forces, we find again a non-engulfed regime (similar to the blue shaded area in Fig. 5b, SI Fig. S13(c), Movie-S16).
Engulfment of non-spherical particles
Immune cells often engulf highly non-spherical objects, such as bacteria. Furthermore, studies with different particle shapes indicated a strong shape-dependence of the engulfment time and success rate12,14,28. We therefore study the engulfment of non-spherical particles by our vesicles that contain passive or active curved proteins.
We first consider spheroids. We keep the surface area constant, i.e. same as for the sphere of radius . We use prolate shapes (Rx = Ry < Rz) and oblate shapes (Rx = Ry > Rz), such that the aspect ratio Rx/Rz < 1 for prolate, and Rx/Rz > 1 for oblate.
In Fig. 6, we show the mean engulfment time for oblate and prolate spheroids, for both the cases when the vesicle is initially in contact from the top (the poles of the shape) or from the side (along the equator), as shown in the insets. For both passive and active curved proteins, we find that the engulfment times increase as the shape deviates from a sphere. This is in agreement with previous experimental observations28, and can be attributed to the higher local curvature on the non-spherical shapes, which increase the bending energy barrier that opposes the progression of the leading edge membrane during their engulfment. Furthermore, we find that the engulfment time increases more rapidly for the oblate shapes, compared to the prolate, for both passive and active, as was observed in experiments28.
Fig. 6.
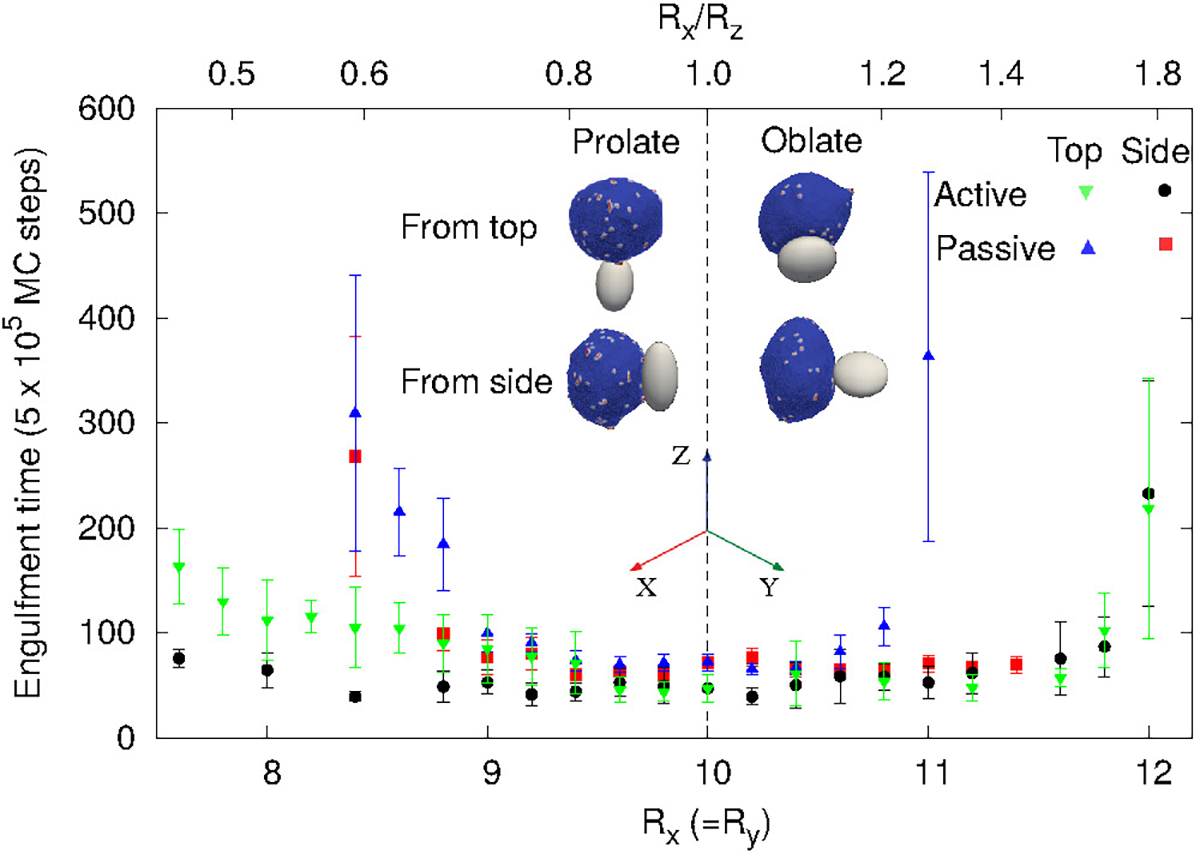
Mean engulfment time for non-spherical particles. The vertical dashed line is separating oblate (right) and prolate (left) shapes. Here, for the passive case, we use: Ead = 1.0 kBT, ρ = 4.8%, and for the active case: Ead = 1.0 kBT, ρ = 1.6%, and F = 1.0 kBT/lmin. The surface area of all the shapes is constant, and equal to that of a sphere of radius 10 lmin. The insets demonstrate the initial conditions of either starting from the top (poles) of the shapes (along their axis of rotational symmetry), or from the side (equator).
For the particles with small aspect ratio (Rx/Rz close to unity), the engulfment time for all the cases are comparable. However, for the particles with large aspect ratios, there are significant differences in the engulfment times, between the passive and active systems. For passive curved proteins (blue triangles and red boxes), we find that the engulfment times increase sharply with the deviation from spherical shape. Furthermore, we find that initialising from the side (red boxes) results in relatively shorter engulfment times, especially for the oblate shapes. For an oblate particle with large aspect ratio (for Rx = Ry > 11 lmin), the particle is engulfed from side, while it is not engulfed from the top (Fig. 6). For prolate shapes with large aspect ratios, however, the engulfment times seem comparable for both initial conditions. The differences between the engulfment dynamics on the oblate and prolate shapes arise from the different local curvatures that the edge membrane encounters during the engulfment: when adhering to the side (rim) of the oblate shape, the leading edge moves mostly on the flat surfaces, which allow the balance of adhesion versus bending to be favorable for smooth progression of the forward motion. When spreading from the top of the prolate shape, the membrane edge encounters the highly bent surface all along the leading edge, and therefore faces a higher bending energy barrier for forward movement of the membrane72. When spreading from the side of the prolate shape, it is similar to the spreading of the vesicle on a cylinder, where one direction has low curvature, and therefore faster engulfment (see these dynamics in terms of the energy of adhesion and bending in Fig. S15).
By comparison, for active curved proteins the engulfment time is lower than for the passive case, even with a lower protein density, and the active curved proteins enable complete engulfment over a larger range of aspect ratios. We also note that for the active curved proteins it is the prolate shape that exhibits a dependence of the engulfment time on the initial conditions, where starting from the side (black circles) leads to faster engulfment. For the oblate shapes, however, the engulfment time is largely independent of the initial conditions, opposite to the behavior of the passive curved proteins.
For a non-spherical particle with high aspect ratio, due to the highly curved poles (in the prolate) or equator (oblate) regions, the engulfment process is slower and the variability in engulfment times increases. The slower engulfment allows the vesicle to reorient on the surface of the particle, driven by both passive energy minimization and active work. We show the details of this reorientation process in the SI sec. S12 (Movie-S17, S18, S19, S20, S21, S22).
When the vesicle is initially at the top of a prolate shape with high aspect ratio, the vesicle takes a longer time to form the initial adhesion since the particle’s surface facing the vesicle has high curvature in all directions. Following this slow initial adhesion time, the vesicle reorients itself always to the side and engulfs the particle, along the easier direction where the long axis of the prolate shape presents a direction of low curvature (Fig. S15e,f). For passive curved proteins, this reorientation process is faster and thereby the engulfment time when started from top or from side are comparable (blue triangles and red boxes in Fig. 6 for Rx/Rz < 1). For active curved proteins, this reorientation process is slower because of large shape fluctuations of the vesicle, and thus the engulfment time when started from the side is smaller than from the top (green inverted-triangles and black circles in Fig. 6 for Rx/Rz < 1).
For the oblate shapes we find a similar reorientation process when the vesicle starts the adhesion from the highly curved sides. In this geometry, the passive vesicle can engulf from side without any reorientation, which is very fast, or it reorients to the top of the oblate shape and ends up with no engulfment. Therefore, when we calculate the engulfment time we only average over those realizations where the particle was engulfed without any reorientation (red boxes for Rx > 11). Otherwise, the mean engulfment time of oblate shapes by passive vesicles diverges for both top and side orientations around aspect ratio ~1.25 (Fig. 6). This value can be explained by the bending energy barrier along the oblate rim, and has local radius of curvature similar to the smallest spherical particle that can still be engulfed (SI sec. S13, Fig. S17).
For the active case, the vesicle reorients in every realization and engulfs from the top. This reorientation process is very fast and the engulfment time is similar for starting either from the side or from the top (green inverted-triangles and black circles in Fig. 6 for Rx/Rz > 1).
We further explore more extreme non-spherical shapes, such as elongated sphero-cylinders and dumb-bell shapes in the SI (Sec. S14, Movie-S23, S24, S25, S26). The elongated particles resemble the shapes of different bacteria or fungi such as E. coli, Bacillus subtilis or budding yeast12,50,73.
Discussion
In this study we demonstrated that curved (convex) membrane-bound protein complexes, or curved membrane nano-domains49, both passive and active, can strongly affect the engulfment process of adhesive and rigid particles by a vesicle. The engulfment process that we calculate, especially using active curved proteins, exhibits many features that are observed during phagocytosis of rigid particles and pathogens by living cells. We therefore propose that our model exposes the physical mechanisms for the self-organization of the membrane and the actin cytoskeleton in the phagocytic cup. These physical mechanisms operate in the cell, in addition to the layers of signaling that allow the cell to optimize the activity of the cytoskeleton near the engulfed surface. However, the curvature-based feedback is shown here to be sufficient to drive the basic underlying dynamics.
We find that the curved proteins spontaneously aggregate around the highly curved rim of the phagocytic cup, and enable the engulfment to proceed efficiently by reducing the bending energy costs. The active forces in our model, which represent the protrusive forces due to the recruited actin polymerization, further facilitate the engulfment, due to several effects that we have identified: the protrusive force at the membrane leading edge promotes the aggregation of the curved proteins (reducing the bending energy cost), as well as directly pushing the membrane over the engulfed particle. However, our model predicts that if the active forces are too large, they induce membrane ruffles that are inefficient for smooth engulfment and may hinder the phagocytosis process.
In addition, the active forces can stretch the membrane to wrap around sharp corners, which enables engulfment of non-spherical particles. Compared to the passive curved proteins, the curved active proteins drive more efficient engulfment at lower adhesion energy, lower curved protein density, and of highly non-spherical particles. For oblate and prolate shapes we recover the experimentally observed increase in engulfment time with the aspect ratio. We expose the mechanisms that allow the active forces to more robustly overcome the local curvature barriers during the engulfment of such non-speherical objects. These results of our model highlight the central role that the recruitment of actin plays during phagocytosis, which is usually abolished by inhibition of actin polymerization (see for example74).
Our model predicts that the actin aggregation at the rim of the phagocytic cup is typically fragmented and does not form a complete circular ring. Nevertheless, it is still highly effective in driving the engulfment. Furthermore, the actin aggregate forms a more cohesive ring in the final stages of the engulfment, before it spontaneously disperses as the engulfment is complete. These features of our model are verified and observed in recent high-resolution imaging of the actin during phagocytosis35 (Fig. 4).
The model we presented currently lacks the contractile forces that arise at the phagocytic cup due to myosin-II activity35. The contractile forces play an important role during the engulfment of soft objects, such as cells75–77, but they are dispensable for the phagocytosis of more rigid particles35,74. Contribution of myosin-II-mediated contractility may be more or less pronounced depending on the particle size and stiffness and, in addition, could influence mechanosensitive signaling within phagocytes rather than directly drive phagocytic cup extension and closure. Our results should therefore be important even without this feature, which we plan to add to our model in the future, especially when modelling the engulfment of flexible particles.
To conclude, we demonstrate that curved membrane proteins can play a key role during phagocytosis. Convex-shaped proteins or a curved complex of proteins, that furthermore recruit actin polymerization, spontaneously aggregate at the leading edge of the membrane, and drive robust engulfment. This is similar to the role of these proteins that was recently found at the leading edge of the lamellipodia, in experiments53,54 and theory46. We also show that concave-shaped proteins can further enhance the engulfment process by reducing the bending energy cost of the membrane that adheres to the particle’s surface78,79 (SI sec. S15, Fig. S20, Movie-S27). Our results should motivate future experimental studies aimed at the identification and characterization of the different curved membrane components that participate in phagocytosis3,52,80.
Supplementary Material
Acknowledgments
We acknowledge useful comments by Orion Weiner. N.S.G. is the incumbent of the Lee and William Abramowitz Professorial Chair of Biophysics, and acknowledges support by the Ben May Center for Theory and Computation, and the Israel Science Foundation (Grant No. 1459/17). This research is made possible in part by the historic generosity of the Harold Perlman Family. A.I. and S.P. were supported by the Slovenian Research Agency (ARRS) through the Grant No. J3-3066 and J2-4447 and Programme No. P2-0232. LLSM imaging was performed at the Advanced Imaging Center (AIC)-Howard Hughes Medical Institute (HHMI) Janelia Research Campus. The AIC is jointly funded by the Gordon and Betty Moore Foundation and the Howard Hughes Medical Institute. MK was supported by the National Institute of General Medical Sciences of the NIH under the Award R01GM138652.
Footnotes
Declaration of Interest
The authors declare no competing interests.
Supplementary Movies
High resolution supplementary movies are also available here.
Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/cXsm00000x/
Additional footnotes to the title and authors can be included e.g. ‘Present address:’ or ‘These authors contributed equally to this work’ as above using the symbols: ‡, §, and ¶. Please place the appropriate symbol next to the author’s name and include a \footnotetext entry in the the correct place in the list.
Notes and references
- 1.Cannon G and Swanson J, Journal of Cell Science, 1992, 101, 907–913. [DOI] [PubMed] [Google Scholar]
- 2.Kumari S, MG S and Mayor S, Cell Research, 2010, 20, 256–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Flannagan RS, Jaumouillé V and Grinstein S, Annual Review of Pathology: Mechanisms of Disease, 2012, 7, 61–98. [DOI] [PubMed] [Google Scholar]
- 4.Ellinger I and Pietschmann P, Wiener Medizinische Wochenschrift, 2016, 166, 193–195. [DOI] [PubMed] [Google Scholar]
- 5.Mylvaganam S, Freeman SA and Grinstein S, Current Biology, 2021, 31, R619–R632. [DOI] [PubMed] [Google Scholar]
- 6.Niedergang F and Chavrier P, Current Opinion in Cell Biology, 2004, 16, 422–428. [DOI] [PubMed] [Google Scholar]
- 7.Richards DM and Endres RG, Reports on Progress in Physics, 2017, 80, 126601. [DOI] [PubMed] [Google Scholar]
- 8.Imani R, Dillert R, Bahnemann DW, Pazoki M, Apih T, Kononenko V, Repar N, Kralj-Iglič V, Boschloo G, Drobne D, Edvinsson T and Iglič A, Small, 2017, 13, 1700349. [DOI] [PubMed] [Google Scholar]
- 9.Xu W and Liu X, Journal of Applied Physics, 2022, 132, 174702. [Google Scholar]
- 10.Gao H, Shi W and Freund LB, Proceedings of the National Academy of Sciences, 2005, 102, 9469–9474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Richards DM and Endres RG, Biophysical journal, 2014, 107, 1542–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Richards DM and Endres RG, Proceedings of the National Academy of Sciences, 2016, 113, 6113–6118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Frey F, Ziebert F and Schwarz US, Phys. Rev. Lett, 2019, 122, 088102. [DOI] [PubMed] [Google Scholar]
- 14.van Zon JS, Tzircotis G, Caron E and Howard M, Molecular Systems Biology, 2009, 5, 298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Khosravanizadeh A, Sens P and Mohammad-Rafiee F, Soft matter, 2019, 15, 7490–7500. [DOI] [PubMed] [Google Scholar]
- 16.FoÅąnarič M, Iglič A, Kroll DM and May S, The Journal of Chemical Physics, 2009, 131, 105103. [Google Scholar]
- 17.Akamatsu M, Vasan R, Serwas D, Ferrin MA, Rangamani P and Drubin DG, eLife, 2020, 9, e49840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Herant M, Heinrich V and Dembo M, Journal of Cell Science, 2006, 119, 1903–1913. [DOI] [PubMed] [Google Scholar]
- 19.Herant M, Lee C-Y, Dembo M and Heinrich V, PLOS Computational Biology, 2011, 7, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Heinrich V, Biophysical journal, 2015, 109, 469–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Francis EA and Heinrich V, PLOS Computational Biology, 2022, 18, 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bahrami AH, Soft Matter, 2013, 9, 8642–8646. [Google Scholar]
- 23.Bahrami AH, Raatz M, Agudo-Canalejo J, Michel R, Curtis EM, Hall CK, Gradzielski M, Lipowsky R and Weikl TR, Advances in Colloid and Interface Science, 2014, 208, 214–224. [DOI] [PubMed] [Google Scholar]
- 24.Dmitrieff S and NÃl’dÃl’lec F, PLOS Computational Biology, 2015, 11, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu J, Kaksonen M, Drubin DG and Oster G, Proceedings of the National Academy of Sciences, 2006, 103, 10277–10282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tollis S, Dart AE, Tzircotis G and Endres RG, BMC Systems Biology, 2010, 4, 149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Herant M, Heinrich V and Dembo M, Journal of Cell Science, 2005, 118, 1789–1797. [DOI] [PubMed] [Google Scholar]
- 28.Champion JA and Mitragotri S, Proceedings of the National Academy of Sciences, 2006, 103, 4930–4934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spanke HT, Style RW, Fran çois Martin C, Feofilova M, Eisentraut M, Kress H, Agudo-Canalejo J and Dufresne ER, Phys. Rev. Lett, 2020, 125, 198102. [DOI] [PubMed] [Google Scholar]
- 30.Eierhoff T, Bastian B, Thuenauer R, Madl J, Audfray A, Aigal S, Juillot S, Rydell GE, Müller S, de Bentzmann S, Imberty A, Fleck C and Römer W, Proceedings of the National Academy of Sciences, 2014, 111, 12895–12900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Patel JC and GalÃąn JE, Current Opinion in Microbiology, 2005, 8, 10–15. [DOI] [PubMed] [Google Scholar]
- 32.Rottner K, Stradal TE and Wehland J, Developmental Cell, 2005, 9, 3–17. [DOI] [PubMed] [Google Scholar]
- 33.Heinrich V and Rawicz W, Langmuir, 2005, 21, 1962–1971. [DOI] [PubMed] [Google Scholar]
- 34.Barger SR, Reilly NS, Shutova MS, Li Q, Maiuri P, Heddleston JM, Mooseker MS, Flavell RA, Svitkina T, Oakes PW et al. , Nature communications, 2019, 10, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vorselen D, Barger SR, Wang Y, Cai W, Theriot JA, Gauthier NC and Krendel M, eLife, 2021, 10, e68627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ostrowski PP, Freeman SA, Fairn G and Grinstein S, Developmental Cell, 2019, 50, 397–410.e3. [DOI] [PubMed] [Google Scholar]
- 37.Paul D, Achouri S, Yoon Y-Z, Herre J, Bryant CE and Cicuta P, Biophysical Journal, 2013, 105, 1143–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sharma G, Valenta DT, Altman Y, Harvey S, Xie H, Mitragotri S and Smith JW, Journal of Controlled Release, 2010, 147, 408–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Doshi N and Mitragotri S, PLOS ONE, 2010, 5, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lu Z, Qiao Y, Zheng XT, Chan-Park MB and Li CM, Med. Chem. Commun, 2010, 1, 84–86. [Google Scholar]
- 41.Dasgupta S, Auth T and Gompper G, Soft Matter, 2013, 9, 5473–5482. [Google Scholar]
- 42.Dasgupta S, Auth T and Gompper G, Nano Letters, 2014, 14, 687–693. [DOI] [PubMed] [Google Scholar]
- 43.VÃącha R, Martinez-Veracoechea FJ and Frenkel D, Nano Letters, 2011, 11, 5391–5395. [DOI] [PubMed] [Google Scholar]
- 44.Ramakrishnan N, Sunil Kumar P and Radhakrishnan R, Physics Reports, 2014, 543, 1–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fošnarič M, Penič S, Iglič A, Kralj-Iglič V, Drab M and Gov NS, Soft Matter, 2019, 15, 5319–5330. [DOI] [PubMed] [Google Scholar]
- 46.Sadhu RK, Penič S, Iglič A and Gov NS, The European Physical Journal Plus, 2021, 136, 495. [Google Scholar]
- 47.Ramakrishnan N, Sunil Kumar P and Ipsen JH, Biophysical Journal, 2013, 104, 1018–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Alimohamadi H and Rangamani P, Biomolecules, 2018, 8, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mesarec L, Drab M, Penič S, Kralj-Iglič V and Iglič A, International journal of molecular sciences, 2021, 22, 2348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Clarke M, Engel U, Giorgione J, Müller-Taubenberger A, Prassler J, Veltman D and Gerisch G, BMC Biology, 2010, 8, 154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chabanon M, Stachowiak JC and Rangamani P, WIREs Systems Biology and Medicine, 2017, 9, e1386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Linkner J, Witte G, Zhao H, Junemann A, Nordholz B, Runge-Wollmann P, Lappalainen P and Faix J, Journal of Cell Science, 2014, 127, 1279–1292. [DOI] [PubMed] [Google Scholar]
- 53.Begemann I, Saha T, Lamparter L, Rathmann I, Grill D, Golbach L, Rasch C, Keller U, Trappmann B, Matis M et al. , Nature Physics, 2019, 15, 848–857. [Google Scholar]
- 54.Pipathsouk A, Brunetti RM, Town JP, Graziano BR, Breuer A, Pellett PA, Marchuk K, Tran N-HT, Krummel MF, Stamou D et al. , Journal of Cell Biology, 2021, 220, e202003086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Masters TA, Pontes B, Viasnoff V, Li Y and Gauthier NC, Proceedings of the National Academy of Sciences, 2013, 110, 11875–11880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Drab M, Sadhu RK, Ravid Y, Iglič A, Kralj-Iglič V and Gov NS, Plasma Membrane Shaping, Academic Press, 2023, pp. 415–429. [Google Scholar]
- 57.Gov NS, Kralj-Iglič V, Sadhu RK, Mesarec L and Iglič A, Plasma Membrane Shaping, Academic Press, 2023, pp. 393–413. [Google Scholar]
- 58.Ramakrishnan N, Ipsen JH and Kumar PBS, Soft Matter, 2012, 8, 3058–3061. [Google Scholar]
- 59.Penič S, Iglič A, Bivas I and Fošnarič M, Soft Matter, 2015, 11, 5004–5009. [DOI] [PubMed] [Google Scholar]
- 60.Gongadze E, Mesarec L, Kralj S, Kralj-Iglič V and Iglič A, Membranes, 2021, 11, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sadhu RK and Chatterjee S, Phys. Rev. E, 2016, 93, 062414. [DOI] [PubMed] [Google Scholar]
- 62.Sadhu RK and Chatterjee S, Phys. Rev. E, 2018, 97, 032408. [DOI] [PubMed] [Google Scholar]
- 63.Sadhu RK and Chatterjee S, The European Physical Journal E, 2019, 42, 15. [DOI] [PubMed] [Google Scholar]
- 64.Sadhu RK and Chatterjee S, Phys. Rev. E, 2019, 100, 020401. [DOI] [PubMed] [Google Scholar]
- 65.Weichsel J and Geissler PL, PLOS Computational Biology, 2016, 12, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zak A, DuprÃl’-Crochet S, Hudik E, Babataheri A, Barakat AI, NÃijsse O and Husson J, Biophysical Journal, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Deserno M, Physical Review E, 2004, 69, 031903. [DOI] [PubMed] [Google Scholar]
- 68.Evans EA and Skalak R, Mechanics and Thermodynamics of Biomembranes, CRC Press, West Palm Beach, United States, 1980. [Google Scholar]
- 69.Ehrig S, Schamberger B, Bidan CM, West A, Jacobi C, Lam K, Kollmannsberger P, Petersen A, Tomancak P, Kommareddy K, Fischer FD, Fratzl P and Dunlop JWC, Science Advances, 2019, 5, eaav9394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sens P and Plastino J, Journal of Physics: Condensed Matter, 2015, 27, 273103. [DOI] [PubMed] [Google Scholar]
- 71.Lipowsky R and DÃűbereiner H-G, Europhysics Letters (EPL), 1998, 43, 219–225. [Google Scholar]
- 72.Khosravanizadeh A, Sens P and Mohammad-Rafiee F, Journal of The Royal Society Interface, 2022, 19, 20220462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Mölller J, Luehmann T, Hall H and Vogel V, Nano letters, 2012, 12, 2901–2905. [DOI] [PubMed] [Google Scholar]
- 74.Prashar A, Bhatia S, Gigliozzi D, Martin T, Duncan C, Guyard C and Terebiznik MR, Journal of Cell Biology, 2013, 203, 1081–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Tsai RK and Discher DE, The Journal of cell biology, 2008, 180, 989–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Araki N, Hatae T, Furukawa A and Swanson JA, Journal of Cell Science, 2003, 116, 247–257. [DOI] [PubMed] [Google Scholar]
- 77.Barger SR, Gauthier NC and Krendel M, Trends in cell biology, 2020, 30, 157–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Sánchez-Barrena MJ, Vallis Y, Clatworthy MR, Doherty GJ, Veprintsev DB, Evans PR and McMahon HT, PLOS ONE, 2012, 7, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Hanawa-Suetsugu K, Itoh Y, Ab Fatah M, Nishimura T, Takemura K, Takeshita K, Kubota S, Miyazaki N, Wan Mohamad Noor WNI, Inaba T, Nguyen NTH, Hamada-Nakahara S, Oono-Yakura K, Tachikawa M, Iwasaki K, Kohda D, Yamamoto M, Kitao A, Shimada A and Suetsugu S, Nature Communications, 2019, 10, 4763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bohdanowicz M and Grinstein S, Physiological reviews, 2013, 93, 69–106. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


