Accelerated epithelial layer healing induced by tactile anisotropy in surface topography

Abstract

Mammalian cells respond to tactile cues from topographic elements presented by the substrate. Among these, anisotropic features distributed in an ordered manner give directionality. In the extracellular matrix, this ordering is embedded in a noisy environment altering the contact guidance effect. To date, it is unclear how cells respond to topographical signals in a noisy environment. Here, using rationally designed substrates, we report morphotaxis, a guidance mechanism enabling fibroblasts and epithelial cells to move along gradients of topographic order distortion. Isolated cells and cell ensembles perform morphotaxis in response to gradients of different strength and directionality, with mature epithelia integrating variations of topographic order over hundreds of micrometers. The level of topographic order controls cell cycle progression, locally delaying or promoting cell proliferation. In mature epithelia, the combination of morphotaxis and noise-dependent distributed proliferation provides a strategy to enhance wound healing as confirmed by a mathematical model capturing key elements of the process.

Gradients of topographic noise induce morphotaxis and affect proliferation improving wound healing of mature epithelia.

INTRODUCTION

Mammalian cells share the ability to sense, integrate, and respond to patterns of biochemical and physical stimuli presented by the extracellular matrix (ECM) (1). The fine control of complex cellular responses, from directional migration to collective tissue morphism (2), is enabled by spatial variations in the intensity of local signals, mapped by cells with tunable resolution over a wide range of length scales, from micrometers to tens of millimeters (3). Mesenchymal cells, including fibroblasts and epithelial cells, interact with the surrounding environment by means of integrin-mediated adhesions (4) and retrieve directional guidance from microscopic gradients of adhesion point density (4), concentration of haptotactic molecules (haptotaxis), variations of substrate stiffness (durotaxis) (5), and density of topographical features (topotaxis) (6). Asymmetric signal distribution is transduced into polarized adhesion reinforcement and actomyosin contractility, which instruct cellular migration along the direction and orientation of the guiding stimulus (4). Similarly, the size (7), geometry (8), orientation, and density (9) of topographic features encode an independent signal guiding the maturation of focal adhesions (FAs) (8), membrane spreading (10), and cell migration (11). Anisotropic matrix components, such as linear fibers and elongated pores, dictate a likewise orientation of the cell cytoskeleton and resulting tractions, yielding directional movement of cells (12).

The response of mammalian cells to topographic order, generally referred to as contact guidance, can be decoupled in vitro using substrates featuring periodic arrays of ridges and grooves or three-dimensional (3D) patterns of topographic elements (13). Planar gratings represent a reference anisotropic signal, which strongly directs migration and polarization (14). This structural remodeling results from the physical interaction between the topographic features and the basal FAs (4, 8, 15). In wound healing, the use of anisotropic geometries results in higher migration speed and directionality (14). In these settings, the mechanical signals are propagated via cell-to-cell junctions from the leader cells, localized at the wound edge, to the followers in the bulk, enhancing monolayer coordination at the mesoscale (14, 16). These emerging collective behaviors (17–19) enable the functional rearrangement of epithelial tissues during organ development and their regeneration in response to wounding (20–22).

Topographic order and anisotropy are frequently observed in the ECM of organs and tissues. In vivo, however, ordered arrays of topographical elements are embedded in a noisy environment, generated by the presence of cellular debris, protein aggregates, and randomly arranged matrix fibers (23).

The concept of topographic noise was introduced by the group of Dalby and Oreffo, with a series of pioneering papers (24, 25) demonstrating how FAs assembly or disassembly is controlled by perfectly ordered or partially disordered nanoscale topographic elements. In this manner, adhesion modulation by the surface geometry instructs the differentiation of mesenchymal stem cells (MSCs). Beyond the result that a specific, rationally developed topography can be used to either differentiate MSCs (24) or preserve them in their uncommitted state (25), these works have established the potential of surface geometry in harnessing complex cellular responses. Along this line of experimental evidence, recent works have shown the possibility to reprogram adult cells through the interaction with gratings, obtained via the lateral compression of the cell nucleus (26). However, the mechanism by which topographic order is read by cells in a noisy environment, such as the ECM, remains to be explored.

In this study, we apply a reductionist model of contact guidance by anisotropic topography, which leverages on a mathematical definition of stochastic noise, to fabricate surface geometries featuring controlled levels of anisotropy. This definition of topographic noise is used to draw a parallelism with what is observed in the ECM in vivo.

On the basis of this model, we introduce engineered substrates featuring anisotropic topographies disturbed by spatial patterns of noise distributed over millimeter distances, yielding gradients with controlled levels of strength and directionality. Using this unique approach, we demonstrate the unexpected tendency of fibroblasts and epithelial cells to establish directional migration along directions of decreasing or increasing topographic noise, a phenomenon distinct from contact guidance, which we name morphotaxis.

While isolated cells only read steep gradients of noise, collective epithelia integrate variations over large millimeter scales, yielding emerging tissue responses, which can guide the healing of large wounds. Together with morphotaxis, the level of topographic noise locally instructs cell proliferation, generating regions of highly proliferating cells, which maintain a sufficient cell density to sustain migration while ensuring confluence. Epithelial collectives can integrate these two signals, to tactically distribute migration and proliferation in the monolayer, yielding improved regenerative efficiency over large distances.

RESULTS

A reductionist model of ECM topographic order and distortion defines gradients of geometrical anisotropy

The ordering and anisotropy of topographic features embedded in the ECM can be appreciated from representative scanning electron microscopy (SEM) images of the human dermis (Fig. 1A). Here, matrix fibers displayed various degrees of alignment along a preferential direction. The intrinsic levels of topographic noise and ordering were described through fast Fourier transform (FFT) and radial projection analyses (Fig. 1B and fig. S1, A and B) (27). The resulting complementary indexes of topographic ordering (I_TO%) and noise (I_TN% = 100 − I_TO%) assume values ranging from 0 to 100%. Specifically, I_TN% values of 0% indicate perfect topographic ordering (corresponding to a parallel array of anisotropic topographic features), while values of 100% indicate a fully random geometry. This analysis confirmed that different regions of the human dermis displayed large ordering variability, within I_TN% ranging from 10 to 80%.

Fig. 1. Biomimetic substrates with controlled topographic noise.

(A) ECM fiber organization in different regions of the human dermis (left, SEM images). The ECM anisotropy is reproduced by rationally designed substrates featuring different levels of topographic noise (right, SEM images). Scale bar, 10 μm. (B) Fast Fourier transform (FFT) analysis of the fiber arrangement (red) and corresponding substrates rendering similar degree of topographic noise (blue). (C) Identification of the two topographical subunits, groove and ridge from the perfectly anisotropic substrate, and insertion of groove defects yielding controllable noise levels. (D) Schematic of the experimental substrates presenting a spatial gradient of topographic noise, from 0% (perfectly anisotropic) to 100% (flat). (E) SEM images of epithelial cells (MDCK) interacting with different regions of topographic noise. Scale bar, 20 μm.

The same values were matched by topographically modified surfaces featuring micrometer-sized geometries. We designed a series of fibronectin-coated polydimethylsiloxane (PDMS) substrates to reproduce topographic noise (Fig. 1C). Gratings with ridge and groove width of 1 μm and groove depth of 1 μm (28) were adopted as a reference for fully ordered topography (i.e., I_TN% = 0%). These geometries reflect the typical size and anisotropy of matrix fibers and maximize directional migration of epithelial cells (14) and fibroblasts (28). In our reductionist model, we adopted perfect gratings as representation of fully anisotropic topography (I_TN% = 0%). The groove and ridge width and the groove depth were chosen to maximize contact guidance (cell and migration alignment to the direction of the gratings), as previously demonstrated by extensive characterization (8, 10, 28, 29). In the generation of anisotropic substrates featuring a specific level of noise (I_TN% from 10 to 100%), the groove design was segmented into a continuous line of empty cubic voxels of 1-μm side length. The filling of one of these voxels generated a bridge between two adjacent ridges. Therefore, the filled groove voxel represents a unit of noise distorting the guidance of gratings. In this theoretical framework, the overall noise level is identified by the density of noise elements, which is expressed as the percentage of filled cubic voxels (i.e., the I_TN%).

In total, 11 regions were created with I_TN% ranging from 0% (perfectly anisotropic gratings) to 100% (a flat substrate) with a 10% step increase (Fig. 1D) (30). Juxtaposing regions with different noise levels, spatial gradients of topographic noise were obtained presenting a stepwise I_TN% increase from 0 to 100% (positive topographic noise gradients, +ΔI_TN%) or decrease from 100 to 0% (negative topographic noise gradients, −ΔI_TN%). The gradient strength, defined as $\frac{\text{Δ}{I}_{\mathrm{TN}\mathrm{\%}}}{\text{Δ}L}$, was modulated controlling the width of the individual regions (table S1). Individual regions with width = 50 μm yielded steep gradients (substrate A), while individual regions with width = 500 μm generated low gradients (substrate B; fig. S1C).

Epithelial cells and fibroblasts were able to adhere and spread on modified substrates featuring various assemblies of topographic noise (Fig. 1E). We used Madin-Darby canine kidney (MDCK) cells and primary human dermal fibroblasts (HDFs) (31) because they represent well-established models for epithelial tissue differentiation and human skin healing (32–35), respectively. MDCK cells expressing the enhanced green fluorescent protein (EGFP)–labeled H2B histones, which localize to the nucleus (MDCK EGFP) (36), were used to track cell migration and division. MDCK cells stably expressing the Fucci two-color cell cycle reporting system (MDCK FUCCI) (37), which is characterized by the nuclear expression of hCdt1-mCherry during the G₁ phase (red fluorescent channel) and hGemAzami Green during the S-G₂-M phases (green fluorescent channel), were instead adopted to assess the duration of individual cell cycle phases.

Topographic noise modulates cell cycle duration

To evaluate the effect of geometrical ordering on cell proliferation, MDCK EGFP and HDF cells were seeded at low density (10,000 cells/cm²) on substrates featuring variable topographic noise with I_TN% values ranging from 0 to 100% (Fig. 2 and fig. S2). The cell cycle duration was directly measured from live cell experiments, which monitored the occurrence and spatial orientation of cell division events. Epithelial cells displayed a bimodal proliferative activity (Fig. 2A). On regions presenting high levels of ordering (I_TN% < 30%), cells divided slowly, with an average doubling time of 24 ± 2 hours. This value sharply dropped to 15 ± 2.5 hours in regions of higher noise (I_TN% > 40%), accounting for a 38% increase in the proliferation rate (Fig. 2B). Similar variations were measured in HDF (fig. S2, A and B). For both MDCK EGFP cells and HDF, a direct correlation was found between the reduced proliferation rate and the increase in the duration of the cell cycle on substrates featuring low levels of topographic noise (I_TN% < 30%) (fig. S2, C and D). In these regions, cell abscission was polarized with a strong angular alignment to the direction of the gratings, as described by the nematic order parameter (NOP; Fig. 2, C and D, and fig. S2, E and F). Specifically, NOP describes the orientational order of a system and assumes values between −1 and 1. In a completely isotropic system, with no preferential direction or orientation, NOP = 0. On the other hand, in an anisotropic system, with a preferential orientation or directionality, |NOP| > 0. A value of 1 identifies perfect ordering of the system along the direction of the external stimulus, and a value of −1 identifies perfect ordering of the system perpendicular to the direction of the external stimulus. In our case, the ridges play the role of the external stimulus that is quantified by I_TN%. This geometrical bias was gradually lost with increasing I_TN% values. At I_TN% > 70%, cell abscission was randomly oriented. A similar result was obtained using HDF cells. In this cell type, abscission alignment fully waned at I_TN% > 50%. Representative examples are provided in fig. S2 (G and H).

Fig. 2. Topographic noise controls cell proliferation via cell signaling.

(A) Duration of the cell cycle in isolated MDCK EGFP cells adhering to experimental substrates with different levels of topographic noise. *P < 0.05 by Mann-Whitney test. n = number of independent experiments, n′ = number of analyzed cells. Error bars correspond to the measured standard deviation of the mean. (B) Normalized proliferation rate of isolated MDCK EGFP cells adhering to substrates featuring different levels of topographic noise. Values are normalized to the I_TN% = 0% region. *P < 0.05; ns, not significant by Mann-Whitney test. n = number of independent experiments, n′ = number of analyzed field of views. Error bars correspond to the measured standard error of the mean. (C) Cartoon introducing the NOP. (D) NOP depicting the cell abscission alignment in isolated MDCK EGFP cells. The corresponding standard deviation (SD) is reported in the graph’s inset. n = number of independent experiments, n′ = number of analyzed cells. (E) Average duration of individual cell cycle phases in isolated MDCK FUCCI cells adhering to experimental substrates with increasing topographic noise and (F) representative fluorescent images of MDCK FUCCI cell cycle reported on regions with various noise level. Scale bar, 50 μm. n = number of independent experiments, n′ = number of analyzed field of views. Error bars correspond to the measured standard error of the mean. (G) Cartoon summarizing the molecular routes linking integrin adhesions to the control of cell cycle progression. (H) Western blot analysis of cell cycle regulator proteins and signaling targets with (I) relative quantification. *P < 0.05 and **P < 0.01, by Mann-Whitney test and two-sample t test. n = number of independent experiments. Error bars correspond to the measured standard deviation of the mean.

We examined what parts of the cell cycle were modulated by the level of topographic ordering. MDCK FUCCI cells were used to measure the average duration of individual cell cycle phases (38) as a function of the local I_TN% value (Fig. 2E). No significant differences were measured in the average span of the M and S phases. On the other hand, for cells interacting with regions of low noise (I_TN% < 30%), the G₂ phase, occurring immediately before cell division, and the G₁ phase were 40 and 30% longer, respectively. A large number of cells lagging in the G₂ phase (Fig. 2F and fig. S2I) were found on regions of low noise (I_TN% ≤ 10%).

Several molecular pathways link the function and maturity of FAs established with the substrate to the progression of the cell cycle (Fig. 2G and fig. S3). FA-mediated signals retrieved by cells from the local substrate constitute an environmental checkpoint, which times the transition through different cell cycle phases. The modulation of distinct signaling pathways includes the activity of extracellular signal–regulated kinase (ERK) (39), the ribosomal S6 kinase (S6K) (40), p38 (41), and AKT (42).

On substrates featuring a low level of topographic noise, I_TN% < 30%, FAs were restricted to the top of the ridges and strongly aligned to them [fig. S3, A to C and F, and (43)]. In the same regions, the geometrical confinement enhanced the adhesion maturation, yielding substantially longer FAs (fig. S3, D and G). On the other hand, no significant effect was measured on the total number of FAs established by individual cells (fig. S3, E and H). Overall, a larger fraction of phosphorylated paxillin was recruited at the adhesion sites, indicating stronger mechanical activity of the FAs on low level of topographic noise [fig. S3, I and J, and (10)]. The corresponding biochemical analysis of the epithelial cell signals controlling proliferation revealed that the phosphorylation of S6K and p38, activator and inhibitor of the G₂-to-M transition (Fig. 2, H and I), respectively, was modulated on substrates featuring I_TN% levels ranging from 0 to 50%. A reduction in the phosphorylation of p38 and a concomitant increase in that of S6K are consistent with the change in the G₂-to-M kinetics. Moreover, a reduction of ERK phosphorylation in regions of noise 20% ≤ I_TN% ≤ 40% was in accordance with the shortening of the G₁ phase. Although with different patterns, a similar regulation occurred also in HDF cells (fig. S2, K to M).

Together, these results demonstrate that high levels of topographic ordering extend the duration of the cell cycle by significantly reducing the proliferation rate of epithelial cells. This effect results from a delay in the progression from the G₂ to M phase and from the G₁ to S phase, which is consistent with a modulation of the related cellular pathways. In addition, topographic ordering efficiently reinforces the FA maturation and alignment and orients cell abscission along the main direction of the gratings in both MDCK cells and HDF, further supporting a direct effect of topographic ordering on cell proliferation.

Topographic noise distorts the contact guidance effect of ordered geometries

To evaluate the effect of noise on contact guidance induced by anisotropic topographies, the alignment of individual cell migration patterns was analyzed. Isolated MDCK EGFP and HDF cells were monitored on substrates featuring low I_TN% gradients of noise (substrate A; table S1 and fig. S4). As expected, a strong alignment of migration along the gratings was evident at I_TN% = 0% (17° ± 1.2° and 10.50° ± 0.6 for HDF and MDCK EGFP, respectively; fig. S4 and movies S1 to S6). The lateral constraint of motion was gradually lost with increasing noise, as migration alignment halved at I_TN% = 40% (32° ± 4.6° and 38.2° ± 1.6 for HDF and MDCK EGFP, respectively).

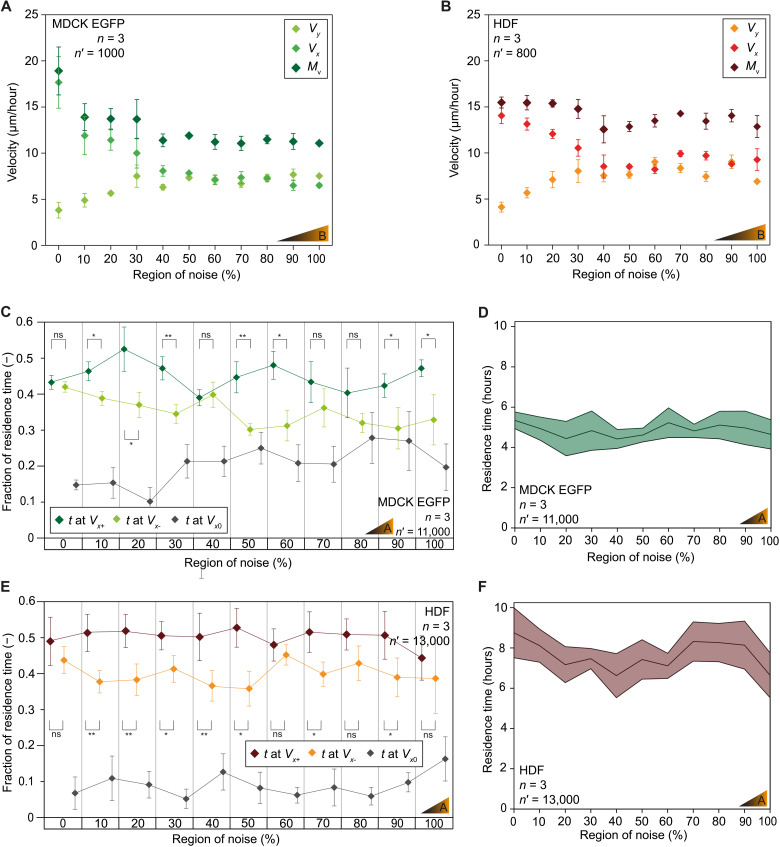
Cell velocity was similarly analyzed as a function of increasing I_TN% on low I_TN% gradients of noise (substrate B; table S1). Specifically, the effect of topographic noise was revealed as the gradual erosion of geometric anisotropy led to the diminishment of contact guidance. On cell migration, this effect was measured by the increase of the migration component along the direction orthogonal to the gratings (the y direction in Fig. 3, A and B) and the corresponding decrease of migration component along the grating’s direction (the x direction in Fig. 3, A and B). The two velocity components (V_x and V_y) became equal in conditions where contact guidance is fully lost.

Fig. 3. Topographic noise controls directional migration and modulates contact guidance.

(A and B) Velocity of directional migration in isolated MDCK cells or HDF adhering to experimental substrates presenting a low gradient of topographic noise (substrate B; table S1). (C and D) Migration persistence and total residence time for isolated MDCK cells in the direction of increasing (t at V_x+) or decreasing topographic noise (t at V_x−) or without migration (t at V_x0). (E and F) Migration persistence and total residence time for isolated HDF on individual regions of topographic noise. n = number of independent experiments, n′ = number of analyzed cells. Error bars correspond to the measured standard error of the mean. *P < 0.05 and **P < 0.01; ns, not significant, by Mann-Whitney test and two-sample t test.

For MDCK EGFP cells, the velocity magnitude (M_v, defined as a scalar value obtained from the square root of the sum of its two vectorial components, V_x and V_y raised to the second power) was higher on regions of low topographic noise (18.9 ± 2.5 μm/hour at I_TN% = 0%) and decreased progressively reaching a plateau at I_TN% ≥ 40% (11 μm/hour; Fig. 3A). Similarly, V_x was elevated at I_TN% < 30% (17.6 ± 2.7 μm/hour on 0%) and decreased thereafter. V_y followed an opposite trend and increased with the level of topographic noise. At I_TN% ≥ 60%, V_x and V_y were equivalent (7 μm/hour).

On the other hand, for HDF cells, the value of M_v remained constant across all the regions of noise (~14 μm/hour; Fig. 3B). Contact guidance was evident at I_TN% < 50%, where V_x was notably higher than V_y (~13 μm/hour). V_x and V_y became equivalent at I_TN% ≥ 50% (7.5 μm/hour) and remained constant in regions of higher topographic noise.

Overall, these results indicate that contact guidance was not impaired until significant levels of noise (I_TN% ≥ 50%) were reached. Isolated cells were able to react to tactile signals and change migration velocity and alignment. Fibroblasts showed a lower ability to detect and respond to directional topographic signals embedded in a noisy environment.

Noise gradients guide the orientation of single-cell migration

We next investigated whether noise gradients affected the direction of individual cell migration. For these experiments, isolated cells were seeded on substrates featuring steep I_TN% gradients of noise (substrate A; table S1 and movies S7 and S8), where individual cells interacted with two or three I_TN% regions simultaneously. Therefore, along their travel path, cells sensed a gradual noise increase or decrease (the ΔI_TN%) of 10 to 20%. In these conditions, cell velocity was similar to the results on low I_TN% gradients of noise (fig. S5, A and B). However, the higher velocity and/or persistence of migration (44) along the direction of increasing (+ΔI_TN%) or decreasing (−ΔI_TN%) topographic noise indicates a response to the tactile stimulus.

First, the two components of migration velocity toward higher (V_x+ in the +ΔI_TN% direction) or lower (V_x− in the −ΔI_TN% direction) I_TN% regions were measured. No significant differences were detected on all analyzed I_TN% noise regions and cell types (fig. S5, C and D). Second, the cell migration persistence was quantified by measuring the fraction of time devoted at migrating in a specific direction (+ΔI_TN% or −ΔI_TN%; Fig. 3, C to F). The migratory paths of MDCK EGFP cells moving toward regions of increasing topographical noise (+ΔI_TN%) lasted on average 20% longer than those moving in the opposite direction (−ΔI_TN%; Fig. 3, C and D). A similar asymmetry was measured in HDF cells (Fig. 3, E and F) with a 20% increase of the migration persistence toward higher topographic noise (+ΔI_TN%). This behavior did not depend on the local I_TN% values.

The migration of isolated cells on perfect gratings (I_TN% = 0%) was characterized by frequent inversions of direction (from +ΔI_TN% to +ΔI_TN% and vice versa; fig. S5, E and F). The increase in migration persistence toward regions of higher topographic noise, induced by the steep I_TN% gradients, implied an overall reduction in the frequency of such switches, leading to a net displacement toward higher I_TN%. As expected, a decrease in the frequency of inversion events was measured for both MDCK EGFP and HDF, reaching a plateau at I_TN% > 50 to 60%.

On the basis of these results, we define the natural tendency of epithelial cells and fibroblasts to move toward regions of the substrate featuring lower geometric ordering (i.e., higher topographic noise), as morphotaxis. Unlike topotaxis, which relies solely on the topological density (6), and contact guidance, which depends on the local levels of topographic anisotropy (Fig. 3, A and B), morphotaxis is defined by the increased persistence of directional migration toward increasing topographic noise. Morphotaxis is instructed by the direction and strength of the topographic noise gradient. It was not detected when isolated cells were seeded on substrates featuring a low I_TN% gradient (substrate B; table S1), confirming that the process requires the physical interaction of cells with two or more regions featuring different levels of topographic order distortion.

Morphotaxis contributes to the collective response of cell monolayers

The effect of topographic noise on cell collectives was investigated by seeding MDCK EGFP and HDF cells at high density on substrates presenting a low I_TN% gradient of noise (substrate B; table S1 and Fig. 4). In this configuration, custom-designed magnetic stencils (fig. S6) were used to locally seed the monolayer. Release of the stencil confinement generated migratory edges moving along the direction of increasing (+ΔI_TN%) or decreasing (−ΔI_TN%) topographic noise.

Fig. 4. Analysis of collective migration.

(A and B) CL in the direction parallel to the topographic noise gradient (CL_x) or orthogonal to it (CL_y) for MDCK EGFP or HDF collectives. Error bars correspond to the measured standard deviation of the mean. (C) Velocity of the front edge for MDCK EGFP cells and HDF collectives on substrates featuring different levels of topographic noise. Error bars correspond to the measured standard error of the mean. (D) ΔM_v/ΔI_TN% of the front edge migrating along the direction of increasing (+Δ_ITN%) or decreasing (−Δ_ITN%) topographic noise in the representative 0% ≤ I_TN% ≤ 40% interval. Experiments performed on substrate B (table S1). Error bars correspond to the measured standard deviation of the mean. (E) Average number of leader cells as a function of the local level of topographic noise. *P < 0.05, **P < 0.01, and ***P < 0.001; ns, not significant, by two-sample t test and Mann-Whitney test. (F to H) Representative inverted fluorescent images of migratory edge depicting the evolution of the wound edge profile, for MDCK EGFP cells seeded on I_TN% = 100, 0, or 50% regions. Scale bar, 200 μm. (I to K) Evolution of the migration velocity for cells at the front edge on the I_TN% = 100, 0, or 50% regions. Results showing one representative experiment of n ≥ 3 and n′ ≥ 2. Error bars correspond to the measured standard deviation of the mean. n = number of independent experiments, n′ = number of analyzed fields of view.

The spatial correlation of cell migration (45), described by the correlation length (CL) in the monolayer, defines collective cell movement. High values of CL are typically observed in mature epithelia featuring strong cell-to-cell junctions (14); on the other hand, fibroblasts did not establish strong lateral contacts and therefore showed only short-range correlation. Cell image velocimetry (CIV) was used to analyze time lapses of monolayer cell migration (16) along the I_TN% gradients (fig. S7). CLs aligned (CL_x) or orthogonal (CL_y) to the noise gradient direction were measured (Fig. 4, A and B). In both cell types, CL_y was low (~75 μm, corresponding to three to four MDCK EGFP cells and to one to two HDF cells, respectively) across the entire substrate. On the other hand, epithelial cells (Fig. 4A), but not fibroblasts (Fig. 4B), displayed high CL_x on regions of low I_TN% gradients (substrate B; table S1). At I_TN% > 40%, CL_x drastically decreased to values comparable to CL_y. These results are visually rendered in fig. S7, showing large clusters of epithelial cells moving coherently as compared to the scattered and individual movements of fibroblast monolayers.

Next, the advancement of the monolayer edge was tracked over time, resolving its velocity along the direction of increasing (+ΔI_TN%) or decreasing (−ΔI_TN%) topographic noise (Fig. 4C and movies S9 to S10). M_v was higher, in both directions, on low-noise regions (I_TN% < 30%) for both cell types. At higher levels of noise (I_TN% > 40%), the monolayer edge velocity was reduced to a minimum (13 ± 0.4 μm/hour and 11.6 ± 0.6 μm/hour for MDCK EGFP and HDF cells, respectively), which was measured at I_TN% = 100%. These results imply that moving along the direction of increasing (+Δ_ITN%) or decreasing (−Δ_ITN%) topographic noise, the front edge either decelerates or accelerates, respectively, when intercepting a threshold region set at 30% > I_TN% > 40%. The absolute values of ΔM_v/ΔI_TN% were substantially higher along the −Δ_ITN% direction (20 and 9% for MDCK EGFP and HDF cells, respectively) than in the opposite one (+Δ_ITN%). Therefore, a morphotactic effect, dependent on the noise gradient directionality, was measured as an increased acceleration toward regions of lower topographic noise (Fig. 4D).

The expansion of epithelial monolayers into an open space is propelled by the formation of leader cells at the cell boundary, which generates migrating fingers along the free-edge perimeter (22). The number and density of leader cells depends on the cell boundary shape and the local substrate properties, ultimately controlling the velocity of monolayer advancement. The formation of leader cells by MDCK EGFP sheets was therefore measured as a function of the local I_TN% (Fig. 4E and fig. S8A). More leader cells emerged on regions of low noise (I_TN% < 20%; average distance between two consecutive leader cells of 182 ± 60 μm). At higher I_TN% values, the average distance between neighboring leader cells was notably higher, 266 ± 61 μm [I_TN% > 20%; (22)].

When crossing the boundary between regions of high and low I_TN% noise (substrate C; table S1), highly migratory MDCK EGFP cells formed a dynamic cluster at the advancing edge (with high M_v and high V_x) that extended for ~500 μm in the monolayer (fig. S8B). These data further demonstrate that spatial variations of topographic noise accelerate the free-edge advancement of confluent monolayers toward regions of higher ordering.

The collective morphotactic effect has a strong impact on epithelial ensembles, supporting the emergence of multiple leader cells along the monolayer edge that enable coordinated directional movements involving multiple rows of follower cells. In addition, epithelial collectives showed increased migration coherence on several noise regions as compared to fibroblasts, suggesting an important contribution of epithelial cell-to-cell junctions.

The collective response to topographic noise gradients requires mature cell-to-cell junctions

To evaluate the contribution of the cell-to-cell junctions in the migratory response of epithelial collectives to substrates featuring different I_TN%, mature MDCK EGFP monolayers were treated with DECMA-1, a blocking antibody that inhibits E-cadherin function and reversibly disassembles lateral contacts (46).

First, the efficiency of the DECMA-1 inhibitor treatment was assessed through the quantitative analysis of its effect on the monolayer connectivity, evaluated by immunostaining of E-cadherin. Specifically, the connectivity index (CI) was measured in the treated and nontreated samples (47). CI values measured in control, mature MDCK EGFP monolayers were ~1, indicating optimal connectivity. Consistently, CI values measured in MDCK EGFP monolayers upon treatment with DECMA-1 were reduced to 0.4 (fig. S9, A and B), indicating the largely compromised integrity of the cell-to-cell junctions.

DECMA-1 treatment induced a macroscopic change in the morphology of the advancing cell front. At high levels of topographic noise (I_TN% = 70% and I_TN% = 100%), the migratory fingers at the cell edge were progressively retracted, leading to the formation of a straight boundary (Fig. 4F and fig. S9, C and E). With unperturbed cell-to-cell junctions, epithelial collectives were instead highly persistent. As the effect of the blocking antibody tapered off after 10 hours due to E-cadherin turnover at the cell-cell contacts (48), the front morphology reorganized and the typical finger-like profile reappeared. The effect of E-cadherin clustering inhibition on substrates featuring high topographic ordering (I_TN% = 0 and 30%) was markedly different (Fig. 4G and fig. S9, F to H). Here, DECMA-1–treated monolayers increased the free-edge perimeter, as compared to the untreated control, through the protrusion of deep migratory fingers (49). An intermediate behavior was seen at I_TN% = 50% (Fig. 4H and fig. S9I).

The velocity of the advancing monolayer (V_x; Fig. 4, I to K, and fig. S9, J and K) was next measured. At high noise levels (I_TN% = 70 and 100%; Fig. 4, I and K), treatment with DECMA-1 considerably hampered the monolayer advancement as compared to the control (~35% reduction). The movement gradually accelerated after 5 hours, reaching values comparable to untreated control. This result is consistent with the concomitant disappearance of migrating fingers (Fig. 4F) on substrates featuring high levels of noise. DECMA-1 treatments did not cause epithelial velocity variations when monolayers migrated on regions of low noise (I_TN% = 10 and 30%; Fig. 4K). In this configuration, the persistence of migrating fingers sustained the advancement at pace comparable to the control.

Overall, these results demonstrate that epithelial adherens junctions (AJs) support collective directional migration on substrates featuring high topographic noise. On the other hand, highly ordered topography ensures a strong contact guidance signal, compensating the loss of cell-to-cell junctions and ensuring efficient advancement of the free edge.

Morphotaxis and distributed cell proliferation contribute to epithelial tissue advancement

The healing of large wounds is accomplished by epithelial monolayers through the execution of two alternative cellular activities. As an immediate response to the contact with a wound, the free edge initiates directional migration, involving leader cells and multiple layers of followers [Fig. 4 and (22)]. This coordinated movement results in the monolayer extension, which is instrumental to rapidly cover the bare substrate, however at the cost of locally reducing the cell density. Replenishment is obtained through proliferation, requiring a temporary halt in the movement of the dividing cells, which do not contribute to migration until abscission is completed (50). The spatial and temporal alternation of migration and proliferation is essential for the efficient reestablishment of a confluent and mature epithelium. Consistently, when cell division was artificially blocked with the drug mitomycin (51), the migration velocity (M_v) of MDCK EGFP monolayers was significantly reduced (from 31.6 ± 5.5 μm/hour to 18.3 ± 3.8 μm/hour), resulting in impaired population of the open space (fig. S10).

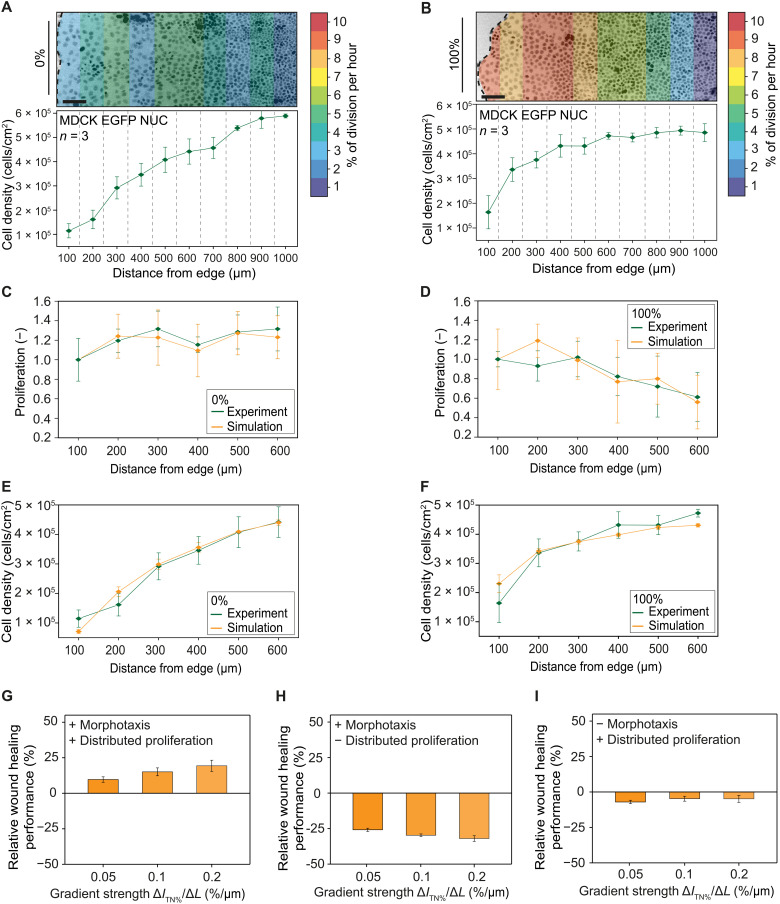
The topographic ordering of the local substrate (i.e., the I_TN%) influences both the proliferation (Fig. 2) and the migration (Figs. 3 and 4) of epithelial cells, suggesting a role in the control of wound healing efficiency. To test this hypothesis, cell proliferation was monitored in advancing epithelial monolayers on substrates presenting high or low I_TN% values (Fig. 5). On substrates featuring high topographic ordering, cell proliferation rate was homogeneously distributed along the entire monolayer, with no detectable variations as a function of the distance from the edge. At the same time, a gradual decrease of the cell density emerged in the advancing cell layer, extending deeply toward the inner regions for 1 mm (I_TN% = 0%; Fig. 5A).

Fig. 5. Collective migration and proliferation and numerical model.

(A and B) Representative inverted fluorescent images of migratory edge, and distribution of cell density and proliferation, as a function of the distance from the monolayer edge, in MDCK EGFP collectives advancing on substates featuring I_TN% = 0% or I_TN% = 100%. (C to F) Comparison between experimental and simulated measurements of cell density and proliferation distribution for MDCK EGFP cells advancing on substrates featuring I_TN% = 0% or I_TN% = 100%. (G) Relative performance of simulated (in silico) epithelial wound healing on substrates featuring gradients of topographic noise with increasing strength (table S2). The histograms report the average relative advantage for monolayers advancing along the negative versus positive direction of the gradient. (H and I) Individual contribution of morphotaxis (H) or distributed proliferation (I) decoupled in simulated epithelial wound healing experiments (in silico) on substrates featuring gradients of topographic noise with increasing strength (table S2). Results are obtained imposing a homogeneous proliferation rate (H) or a homogeneous velocity distribution (I). Error bars correspond to the measured standard deviation of the mean. n = number of independent experiments.

A different picture was obtained upon healing of wounds in the absence of topographical guidance (i.e., on substrates featuring high noise, I_TN% = 100%; Fig. 5B). A 10-fold increase in the cell division rate was measured at the front edge, which gradually decreased over the length of 1000 μm toward the inner regions. The monolayer displayed a limited density decrease in correspondence to the advancing edge. Here, a 30% reduction of cell density was measured in the first 300 μm from the edge.

To decouple the two contributions to wound healing, we developed a model capturing the evolution of epithelia moving on substrates with defined spatial distribution of I_TN% (a full description of the model is available in the Supplementary Materials). The experimental inputs included the initial cell density, the average cell size, and the migration velocity and directionality. The model treated the cells as soft spheres with a constant radius. Each sphere’s motion was determined by the balance of forces, which included the cell’s own motility force, repulsive, and attractive interactions with other cells, and the viscous drag of the surrounding medium. The motility force of each cell was varied by considering the presence of neighboring cells.

In addition, cell proliferation was modeled with a rate dependent on cell type and local environment. Two types of cells were implemented: “Leader” cells had a high maximal motility force, had a low proliferation rate, and were tuning their motility force to cover empty spaces; “follower” cells had a low maximal motility force, had a high proliferation rate, and were tuning their motility force to follow other cells. The simulations closely captured the distribution of proliferation and cell density in the advancing monolayers on high or low I_TN% (Fig. 5, C to F).

To better decouple the effect of morphotaxis (Fig. 4) from that of distributed proliferation (Fig. 2) on wound healing in epithelial monolayers, we run in silico experiments in the frame of the validated model. A net advantage was demonstrated for monolayers advancing along the negative direction of a topographic noise gradient (table S2 and Fig. 5G). The increased performance was dependent on the gradient strength, confirming that morphotaxis represents a collective response to the spatial distribution of topographic regions featuring different levels of order distortion (Fig. 4).

In these settings, we could arbitrarily switch on and off the two components of the cellular response to the spatial I_TN% pattern: the distributed proliferation, with increased cell division rates in regions of high topographic noise (Fig. 5H), and the wound edge acceleration upon movement toward regions of lower topographic noise (Fig. 5I).

The results showed that, when imposing homogeneous proliferation, the performance of wound healing was greatly diminished, losing most of the advantage bestowed by the spatial noise patterning (Fig. 5H). On the other hand, when a constant velocity was set on all subsequent regions of noise, the healing performance reduction was more contained (Fig. 5I) This indicates that morphotaxis and distributed proliferation contribute to support wound healing in epithelial monolayers. In addition, they suggest that the effect of distributed proliferation may be relatively more relevant.

DISCUSSION

The spatial architecture of the ECM can vary greatly over space and time within the same tissue. The human skin is an example of dynamically evolving living material, locally subject to cyclic mechanical strain (52), traumatic events of wounding, healing, and regeneration. For instance, matrix fibers align along the tangential direction of longitudinal wounds following the strain distribution (53). Developing epithelial structures, like 3D acini or cysts, induce fiber bundling and ordering (54) as a result of collective rotation. Similarly, cancerous clusters apply tractions to the surrounding matrix threads as they form aligned beams and channels (55). In all these cases, the generation of topographic order and anisotropy supports the emergence of contact guidance, providing directionality to the migration of individual cells and cell collectives via interaction with the FAs (13, 53). In addition, it implies the existence of transitional regions in which the degree of topographic order varies gradually, yielding spatial gradients of increasing or decreasing contact guidance (Fig. 1).

Topographically engineered substrate surfaces provide minimalistic representations of the ECM topography and elegantly decouple the effect of contact guidance on cell adhesion and migration (56). Here, they were used to reproduce variations of topographic ordering over different length scales (Fig. 1). Individual cells interacting with two or more areas of the substrate featuring different levels of topographic order were exposed to a modulation of the guidance signal at their opposite extremities (Fig. 3). In both epithelial cells and fibroblasts, this unbalance led to a net translocation as a result of the increased persistence of migration paths advancing toward regions of higher disorder (Fig. 3). The polarized cellular movement, sustained by the local variations of contact guidance distortion, was termed morphotaxis.

In mature epithelial collectives, contact guidance increased the spatial correlation of cellular movements (57). In doing so, it promoted the advancement of free edges to cover an open space (Fig. 4). The effect propagated to the millimeter scale in mature epithelia but was negligible in confluent monolayers of fibroblasts, or when cell-to-cell junctions are artificially dismantled (Fig. 4). The establishment of AJs in epithelial monolayers additionally enabled a coordinated response to gradients of topographic noise deployed over several hundreds of micrometers. In this context, the spatial modulation of contact guidance, from the front cells to the monolayer bulk, established collective morphotaxis. The emerging response induced a faster directional movement of the cells at the free edge in the direction of decreasing topographical noise. Notably, in the case of epithelial cell ensembles, morphotaxis promoted migration toward regions of lower disorder, thus in the opposite direction than for individual cells.

The dichotomy between the response of individual cells and cell clusters to an identical migratory gradient or signal has several parallelisms. Endothelial cells migrate when exposed to unidirectional flow (58). However, while individual cells move along the flow direction, the establishment of cell-to-cell junctions enables a collective counterflow movement typical of mature endothelia (59). Isolated cancer seeds move against the increasing signal concentration, while multicellular masses migrate along the opposite direction (60).

In the case of morphotaxis, the origin of the antinomy between disconnected and connected epithelial cells was due to the social interaction established in the latter case. Differently for isolated individual cells, which were free to move in all directions (Fig. 3), the migration polarization of a confluent epithelium was dictated by the global tissue response to the presence of a discontinuity in the monolayer. When exposed to a longitudinal wound, the front of leader cells migrated toward the open space relaying the signal to the inner followers (Fig. 4). A gradual increase of topographic order, added to this innate response, results in confining the cell movement in the direction of healing and thus accelerating the free-edge advancement.

The interaction between topographic features and cell signaling goes beyond the reshaping of the structural and mechanical cellular components necessary for migration (26). Defined levels of topographic noise control the differentiation state of MSCs (24, 61) and the progression of cancer (62). Not surprisingly, topographic ordering impinged on the proliferation rates of epithelial cells and fibroblasts (Fig. 2) through a direct modulation of the checkpoint controlling the access to mitosis. Reading this result in the context of morphotaxis, the efficiency of healing in mature epithelia must be considered.

Full tissue regeneration requires substrate coverage, initially obtained by directional collective migration, and the later reestablishment of full confluence through proliferation (63). Typically, proliferation in the advancing monolayer is promoted by the local decrease in cell density, which is more prominent at the extending front (Fig. 5). However, proliferating cells do not contribute to migration (64), and it is reasonable to assume that the balance and distribution of the two processes strongly influence the overall healing efficiency. The tactical distribution of topographic ordering, yielding gradients of contact guidance and an overlapping signal that locally hinders proliferation, may therefore be sufficient to correctly delineate the two processes contributing to wound healing and thus strongly promote tissue regeneration. The proposed model, capturing the key parameters of morphotaxis and distributed proliferation on topographic noise gradients (Fig. 5), supports the hypothesis that the spatial distribution of a topographic noise gradient can increase the healing efficiency of epithelial collectives, through the synergic contribution of collective morphotaxis and distributed control of cell division.

MATERIALS AND METHODS

Cell culture and treatments

MDCK EGFP cells (65) and HDF cells (66) were cultured in Dulbecco’s modified Eagle’s medium (DMEM)–High Glucose medium (Sigma-Aldrich) supplemented with 10% fetal bovine serum (FBS; Sigma-Aldrich), penicillin-streptomycin (100 U ml⁻¹; LifeScience), and 2 mM l-glutamine (LifeScience) and were maintained at 37°C and 5% CO₂. MDCK FUCCI cells (37) were cultured in DMEM–High Glucose medium (Sigma-Aldrich) supplemented with 10% FBS (Sigma-Aldrich) and penicillin-streptomycin (100 U ml⁻¹; LifeScience) and were maintained at 37°C and 5% CO₂. In the monolayer experiments, a total of 8 × 10⁴ cells/cm² were seeded on coated substrates made of PDMS (Dow Corning, USA). In the single-cell experiments, a total of 10⁴ cells/cm² were seeded on the coated substrates.

Substrate fabrication

Noisy geometries were generated by a custom MATLAB program and transferred on silicon molds using photolithography, as previously reported (29). All the noisy patterns were designed starting from an “unperturbed” microstructured surface with groove depth and width of 1 μm and duty cycle of 2 μm. The groove width is among the key geometrical elements affecting the performance of perfect gratings in inducing contact guidance. Other parameters that can be independently varied are the groove depth and the ridge width. We selected a grating geometry that optimizes contact guidance. The rationale for this choice was to maximize the dynamic ratio of our contact guidance measurements, which is the difference in cell and migration alignment between noisy substrates (I_TN% = 100%) and ordered ones (I_TN% = 0%). This is individuated by gratings featuring groove width and depth of 1 μm and ridge width of 1 μm (10, 14).

Specifically, to obtain the desired effect, the groove shall be sufficiently wide to impede the extension of FAs bridging two adjacent ridges. Only in this condition, the effect of ridge anisotropy can be imposed to the cells. The maximal distance between two points of integrin adhesion that can be bridged into a single FA complex is set at 0.5 μm, as very elegantly demonstrated by the group of J. Spatz (67). Gratings featuring grooves narrower than 0.5 μm would therefore allow the formation of FAs in the direction orthogonal to the gratings, thus diminishing contact guidance (10). On the other hand, when the groove width is sufficient to confine FAs to the ridge top, this value intrinsically defines the spacing between FAs formed at the leading edge of migrating cells. On the basis of all these considerations, the groove width of 1 μm was selected for our experiments.

For similar reasons, the groove depth shall extend beyond the threshold of cell membrane penetration into the groove space. This is necessary to avoid contact with the bottom of the groove and restrict the formation of FAs to the ridge top. We have previously demonstrated that for 1-μm-wide grooves, this value is 0.8 μm. Deeper grooves perfectly separate adjacent ridges. Adhering cells form membrane arcs over these spaces, which are devoid of adhesions (8).

A controlled density of randomly distributed modifications was then intercalated in the ideal layout as previously described (30). As previously reported (14), substrates were cleaned and their hydrophilicity was increased with oxygen plasma treatment (80 W for 60 s, 1 ± 0.2 mbar). The substrates were finally coated with fibronectin (15 μg/ml; Sigma-Aldrich) and mounted at the bottom of hollowed wells.

Magnetic stencil fabrication

Following procedures previously described in (14), Autodesk Inventor Professional was used to design the molds for the fabrication of the magnetic stencils. The Object 500 Connex 3 3D printer was used to print the molds made of Vero White Plus material. Magnetic stencils were made of a PDMS (Dow Corning, USA)–magnetite solution prepared by mixing PDMS at 1:10 ratio and magnetite at 40% (w/v). The PDMS-magnetite solution was poured into the molds upon degassing in a vacuum chamber. After the pouring, the solution was degassed a second time and finally cured for 2 hours at 80°C. The resulting magnetic stencils (MAts) were separated from the mold after the curing process. Before the experiments, MAts were routinely cleaned in 70% ethanol for 10 min and air-dried. The MAts were passivated in a solution of 4% Pluronic F-127 (Sigma-Aldrich) in deionized water for 2 hours, and the final coated MAts were then washed several times with phosphate-buffered saline (PBS) and immediately used.

Magnetic attachment and cell patterning on glass substrates for wound healing experiments

Following procedures previously described in (14), N42 grade magnets (Supermagnete) were placed at the external side of the glass substrates previously glued on the drilled bottoms of a six-well plate. MAts were then carefully placed upon the micropatterned PDMS substrates already glued on the glass substrates. Cells were seeded with a pipette in the space delimited by the MAt and allowed to establish initial adhesion for 1 hour. After 1 hour, the sample was fully covered with fresh medium.

Cells were incubated for 3 hours (MDCK) or 5 hours (HDF) to reach full adhesion to the substrate. To start wound healing experiments, magnets were carefully removed from underneath the glass substrates, allowing MAts to detach and float in the cell culture medium. Cells were rinsed twice with fresh medium before imaging.

Fixation of cells for SEM

As previously reported in (14), samples were washed three times with PBS and incubated for 1 hour with 2.5% glutaraldehyde in 0.15 M sodium cacodylate (pH 7.2) at room temperature (RT). The samples were then washed three times with 0.15 M sodium cacodylate (pH 7.2) and progressively dehydrated in 50, 70, and 100% ethanol. The specimens were stored in 100% ethanol at 4°C, until the critical point dryer procedure (Automegasamdri 915 B, Tousimis). Last, the specimens were sputter-coated with gold/palladium using a BAL-TEC SCD-050 sputter coater and stored at RT until they were imaged with a Zeiss ULTRA 55 SEM.

Fixation of human skin tissues for SEM imaging

Skin samples were incubated overnight in 5 ml of diluted dispase (2.5 ml of dispase: 50 U/ml, Corning; 2.5 ml of Dulbecco’s PBS (DPBS); and 500 μl of gentamicin), after which dermis and epidermis were mechanically separated. The fixation procedure was performed as previously described (14). In detail, dermis samples were washed three times with PBS and incubated for 1 hour with 2.5% glutaraldehyde in 0.15 M sodium cacodylate (pH 7.2) at RT. The samples were then washed three times with 0.15 M sodium cacodylate (pH 7.2) and progressively dehydrated in 50, 70, and 100% ethanol. The specimens were stored in 100% ethanol at 4°C, until the critical point dryer procedure (Automegasamdri 915 B, Tousimis). Last, the specimens were sputter-coated with gold/palladium using a BAL-TEC SCD-050 sputter coater and stored at RT until they were imaged with a Zeiss ULTRA 55 SEM.

Antibodies and drugs

The following primary antibodies were used: monoclonal antibody DECMA-1 (U3254, Sigma-Aldrich), rabbit polyclonal anti–phospho-paxillin [Immunofluorescence (IF): 1:200; 2541S, Cell Signaling Technology], rabbit polyclonal anti-paxillin (IF: 1:200; 2542S, Cell Signaling Technology), p44/42 mitogen-activated protein kinase (MAPK) (ERK1/2) antibody [Western blot (WB): 1:1000; 9102, Cell Signaling Technology], phospho-p44/42 MAPK (ERK1/2) antibody (WB: 1:1000; 9101, Cell Signaling Technology), S6 ribosomal protein (Ser^235/236) antibody (WB: 1:1000; 2317, Cell Signaling Technology), and phospho-S6 ribosomal protein (Ser^235/236) antibody (WB: 1:1000; 2211, Cell Signaling Technology).

Secondary antibodies were chicken anti-rabbit Alexa Fluor 647 (1:400; Thermo Fisher Scientific, A-21443), donkey anti-mouse Alexa Fluor 555 (1:400; Thermo Fisher Scientific, A-32773), anti-rabbit immunoglobulin G (IgG) horseradish peroxidase (HRP)–linked (1:2000; Cell Signaling Technology, 7074), and anti-mouse IgG HRP-linked (1:2000; Cell Signaling Technology, 7076). 4′,6-Diamidino-2-phenylindole (DAPI) was added at 1 μg/ml during a washing step. Mitomycin drug (Sigma-Aldrich, M4287) was used at 25 μg/ml.

Western blotting

Following a protocol previously reported in (68), cells lysates were obtained with modified Laemmli sample buffer [2% SDS, 20% glycerol, and 125 mM tris-HCl (pH 6.8)]. Gels were loaded with the same amount of proteins, subsequently separated by SDS–polyacrylamide gel electrophoresis, and finally transferred to a nitrocellulose membrane (Protran, Whatman). After incubation with primary and HRP-linked secondary antibodies, the targeted bindings were detected with chemiluminescence system (GE HealthCare).

Immunofluorescence

As previously reported (68), cells were fixed for 10 min with 4% paraformaldehyde at RT or with ice-cold methanol at 4°C. Permeabilization was performed with 0.5% Triton X-100 in PBS for 5 min. Cells were blocked for 1 hour at RT in 5% (w/v) bovine serum albumin (Sigma-Aldrich, USA). The samples were incubated with primary antibodies (see the “Antibodies and drugs” section) overnight at 4°C, and then samples were rinsed three times for 5 min with PBS. Secondary antibody was added for 1 hour at RT. Last, the samples were washed three times for 5 min with PBS.

Image acquisition

Following procedures described in (14), live imaging of the migration and proliferation processes was performed using an automated Nikon-Ti spinning disk confocal microscope (Nikon, Japan) equipped with an Andor DU-888 camera (Oxford Instruments, UK) and a pE-100 light-emitting diode (LED) illumination system (CoolLED Ltd., Andover, UK) using a 20× or 10× objective (Plan Fluor, Nikon, Japan). An incubated chamber was used to maintain temperature and CO₂ at 37°C and 5%, respectively (Life Imaging Services, Switzerland). Time-lapse recording was started approximately 1 hour after removing the MAts. The interval between image acquisition was 20 min to 1 hour, and a typical experiment lasted around between 24 to 48 hours. At the end of the experiments, the resulting time lapses for each set position were converted into individual 16-bit images for analysis. Fluorescent z-stacks of the signals emitted by the phospho-paxillin and paxillin at FAs were collected using a Nikon-Ti spinning disk confocal microscope (Nikon, Japan) equipped with an Andor DU-888 camera (Oxford Instruments, UK) and selecting the optical filters based on the respective emission.

E-cadherin inhibition on collectives

Epithelial monolayers of MDCK cells were treated with DECMA-1 (20 μg/ml), and the advancement of the monolayer was monitored and acquired under the microscope for 15 hours.

Image analysis

Wound healing velocity

To correct shifts upon acquisition, image stacks were registered using the “MultiStackReg” tool on ImageJ. To calculate the velocity of wound closure, the “freehand line” tool of ImageJ was used to measure the edge displacement between the different time frames (14).

Cell image velocimetry

Following a protocol previously described (14, 16), the CIV toolbox was used for the analysis of the wound healing experiments. The velocity fields provided by the CIV analysis were used to quantify the mean cell layer speed (mean velocity magnitude), the directed migration (mean velocity projection in the axis aligned perpendicular to the initial wound orientation), and the angular velocity distribution, a measure for the effective migration contribution along 32 equally spaced angular sectors (i.e., with angular bin size of 360°/32). Overlays of phase-contrast images and colored migration direction were exported from the software. The colors indicated different directions of migration. Regions with uniform color indicates a homogeneous migration direction and thus high coherence between cells.

CL measurements

Following a protocol previously described (14), the CIV analysis was performed to obtain the u and v velocity fields corresponding to the direction x (parallel to the wound) and y (perpendicular to the wound edge). To avoid drift-related bias in the analysis, the mean velocity ‹u› and ‹v› were subtracted from the velocity fields u and v: u* = u − ‹u› and v* = v − ‹v›. The CL was calculated to estimate the radius over which cell movements are correlated. The calculation was performed for the x and y components separately. The velocity spatial correlation function is the following: C_vv(r,t) = ‹u*(r₀,t) ⋅ u*(r₀ + r,t)›/[‹u*(r₀,t)²›‹u*(r₀ + r,t)²›]^1/2, where r is the vector of coordinates (x,y) (69, 70). The velocity spatial correlation function was fitted with a decreasing exponential function f(r) = e^−(r/CL) to extract the velocity CL.

Perimeter analysis

The “freehand line” and “measurement” tools of ImageJ were used to measure the wound edge profile as previously described (14). The perimeter ratio was defined as the ratio between the measured edge length P and the fixed length L, corresponding to a straight line encompassing the entire field of view under analysis in the direction orthogonal to the gratings. In the experimental settings adopted to capture the time lapses of wound healing, this length was typically of 1000 μm. On the basis of this definition, Pr = P/L ranges between 1 (the wound edge is perfectly straight and orthogonal to the gratings) and above. Any value higher than 1 indicates that the measured edge is longer, therefore featuring a certain degree of convolution.

Kymographs

The kymographs of the wound healing experiments were obtained following the protocol previously described in (14). In detail, CIV analysis was used to analyze over 32 hours a fixed field of view of the wound healing experiment of 50 μm × 500 μm of size. The u and v velocity fields obtained from the CIV analysis were used to calculate the magnitude of the velocity field (M_v) on MATLAB: M_v = [u(x,y)² + v(x,y)²]^1/2. The M_v field values along the 50-μm dimension were averaged together to get a vector of values per time frame over the 500-μm dimension. The final kymograph shows the evolution of M_v over time.

Angular orientation analysis

The orientation of the migration of cells was performed using the cell tracking software Imaris (Bitplane Scientific Software, Switzerland). In particular, time-lapse videos were uploaded into Imaris and the position of the cells was tracked over time to extract a displacement vector of each cell under analysis. The average alignment between the displacement vector and the direction of the gratings was then calculated to obtain the angular orientation. This analysis was performed for each region of topographic noise. The extent of contact guidance by anisotropic geometries was measured by the average individual cell alignment to the main topographic direction (where 0° indicates perfect alignment, 90° indicates alignment to the orthogonal direction, and 45° indicates random alignment) and/or the corresponding alignment of cell migration. The same definition is applicable to isolated cells and to cell collectives in epithelial monolayers (10, 14).

Single-cell velocity, directional migration, and change direction analysis

As reported in (68), the software Imaris (Bitplane Scientific Software, Switzerland) was used to performed the tracking measurements of the cells migratings on the substrates. Time-lapse videos were uploaded in the software, and the velocity of the cells was obtained by tracking the migration of individual cells between the different time frames taking into consideration the different noise regions.

Directional migration induced by contact guidance was quantified as follows

$${\mathrm{CG}}_{\equiv }=V_{\mathrm{x}}\ast t\mathrm{at}{V}_{\mathrm{x}}/V_{\mathrm{y}}\ast t\mathrm{at}{V}_{\mathrm{y}}$$

where CG_≡ indicates guided migration, which is aligned to the underlying topography (corresponding to the x axis in the video). V_x and V_y are the absolute terms of the velocity components along the two orientations (horizontal and vertical in the images, respectively). t at V_x and t at V_y are the corresponding persistence times (duration of uninterrupted movement along one orientation).

With this, values of CG_≡ above 1 indicate a net movement aligned with the gratings (the x direction), whereas values below 1 indicate directional migration in the orthogonal direction (the y direction). Values close to 1 indicate that the movements along the two directions are of equivalent extent; therefore, no contact guidance is measured.

This definition is substantially different to that of morphotaxis. Starting from the same experimental approach and measures, we only refer to the x component of movement (along which a gradient of topographical noise I_TN% is presented to the cells) and evaluate the extent of movement toward the direction of increasing or decreasing noise. This is formalized as follows

$$\mathrm{MTx}=(V_{\mathrm{x}+}\ast t_{x+})/(V_{\mathrm{x}-}\ast t_{x-})>1$$

where MTx is the morphotaxis. V_x+ is the velocity component along the direction of increasing I_TN%. V_x− is the velocity component along the direction of decreasing I_TN%. t_x+ and t_x− are the corresponding persistence times. Values of MTx above 1 indicate a net displacement along the positive direction of the I_TN% gradient (+ΔI_TN%), values below 1 indicate a net displacement along the opposite direction (−ΔI_TN%), and a value of 1 indicates no net displacement.

Therefore, morphotaxis purely depends on the noise gradient strength and directionality. It does not depend on the local I_TN% value and is not limited to a specific range of topographic noise values. In this, it is substantially separated from contact guidance.

The rate of direction change was calculated (for each cell and as a function of the local I_TN% level) counting the number of shifts in sign of the components of the velocity parallel to the direction of the gratings (V_x+ to V_x− or the opposite). This number was then divided by the elapsed time (30 hours). The direction change rate (number of events per hour) was finally normalized with respect to value measured on perfect gratings (i.e., on the 0% noise region) set as 1 as reference. In this representation, values lower than 1 indicate reduced frequency of inversion (normalized change of direction).

Angle of division analysis

The orientation of cell mitosis was performed using ImageJ. Time-lapse videos were uploaded into the software and rotated to have the topography oriented vertically. With the “Straight” tool, the two nuclei of the divided cell were connected and the angle between the line and the gratings (θ) was shown in the “Results” tab. NOP was calculated in the following way: NOP = 2 × cos²(θ) − 1. In a completely isotropic system, with no preferential direction or orientation, NOP = 0. On the other hand, in an anisotropic system, with a preferential orientation or directionality, |NOP| > 0. For a perfect ordering of the system, NOP = ±1, where +1 represents a perfect alignment in the direction of the ridges and −1 represents a perfect alignment perpendicular to the ridges.

Total and fraction residence time analysis

Tracking measurements were performed using Imaris (Bitplane Scientific Software, Switzerland). Time-lapse videos were uploaded into Imaris, and the velocity V_x values of the cells were obtained by tracking the migration of individual cells over time taking into consideration the different noise regions. The average residence was obtained counting the amount of hours the cells were migrating or stalling on every region of noise. The fraction of residence time analysis was obtained looking at the fraction of time the cells were spending migrating on a specific region of noise toward the higher noise regions (t at V_x+) or toward the lower noise region (t at V_x−) or not migrating at all (t at V_x0).

Leader cell analysis

The number of leader cells at the wound edge for every region of noise was evaluated calculating the average amount of cells at the edge, which were identified by their distinctive morphology, as reported in a previous publication (22). Briefly, the leader cells were located at the tip of migrating finger and displayed an enlarged lamellipodium at the front edge extending in the open space. The relative average distance was obtained dividing the length of the field of view by the number of counted leader cells.

Proliferation analysis and cell cycle phase length analysis

The proliferation analysis was performed using the cell tracking software Imaris (Bitplane Scientific Software, Switzerland). Time-lapse videos were uploaded into Imaris, and the amount of division happening in every region of noise was extracted. The values were then normalized with respect to the 0% noise region. The cell cycle phase length for MDCK FUCCI cells was also performed using the cell tracking software Imaris (Bitplane Scientific Software, Switzerland). In this case, time-lapse videos were uploaded into Imaris comprising all different colored channels associated to the different cell cycle phases. Every single colored channel was analyzed, and the average phase length was obtained for every region of noise. The analysis of the percentage of cells per cell cycle phase was performed by counting the number of cells per field of view in each cell cycle phase and normalizing the calculated values by the total number of cells in the field of view.

Colocalization analysis

The colocalization analysis between paxillin and phospho-paxillin protein was performed using the cell tracking software Imaris (Bitplane Scientific Software, Switzerland). The immunofluorescence images were uploaded into Imaris, and the Pearson’s coefficient, an indicator of colocalization, was computed.

CI DECMA-1 analysis

As previously reported (47), CI was calculated from the average skewness of E-cadherin signal profile along four directions (i.e., +x, −x, +y, and −y). CI values close to 1 indicate a monolayer with preserved cell-to-cell junctions, while values close to zero indicate a diffuse signal in the cytoplasm.

Statistical analysis

To test the normality of the data, the Shapiro-Wilk test was used with a significance level of 0.05. Two-sample t test was conducted for normally distributed data, while Mann-Whitney test was used for nonnormally distributed data. All box plots extend from the 25th to the 75th percentiles, and the line and square in the boxes represent the median and the mean, respectively. Whiskers represent the standard deviation of the mean. n reports the number of independent experiments, while n′ reports the number of total fields of view of the total number of cells analyzed.

Numerical simulation

The numerical simulation was performed on the basis of a particle-based model for cell-cell and cell-substrate interactions (19). Cell motility was incorporated according to the model described in (71). Cells were modeled as circles with uniform and constant diameter, with pairwise interactions, and described by a set of parameters. These parameters are updated during the course of the simulation to account for the current position of the cell on the substrate and its local environment. Cells were allowed to move on a 500-μm-wide and 1000-μm window and were initially “seeded” on a 500-μm-wide and 400- to 450-μm-long surface, with the same initial density obtained from the experiments. A repulsive force was set at the rear end of the window to ensure that no cell was migrating in the backward direction. To remove the influence of the side walls, periodic boundary conditions were implemented in the lower and upper ends of the substrate. Therefore, a cell moving upward to the upper bound of the window would “reappear” on the lower bound. This behavior was also implemented for all interactions, including cell-cell interactions. Cells were considered round, with a radius R₀ = 10 μm. The cell shape was considered fixed, not subjected to any deformations, even when in contact with other cells. Each cell experienced three forces: (i) motility force, (ii) interaction force (attractive or repulsive) from other cells, and (iii) viscous force from the substrate. The velocity of cell i at each time step was determined from the equilibrium of the forces as

$$V_x=\frac{1}{{\mathrm{\eta }}_x}(F_{\mathrm{mot},i}+\sum _{j\ne i}{F}_{\mathrm{cell}j\to \mathrm{cell}i}).\hat{x}$$

$$V_y=\frac{1}{{\mathrm{\eta }}_y}({\mathrm{F}}_{\mathrm{mot},i}+\sum _{j\ne i}{F}_{\mathrm{cell}j\to \mathrm{cell}i}).\hat{y}$$

F_{cell j→cell i} describes the pairwise interaction between neighboring cells. The interaction force is repulsive when the centers of the two cells are closer than a threshold value. It is then attractive until a threshold distance, and becomes zero above this distance. F_mot,i is the force that a cell applies on the substrate to move. It tends to align along the velocity of the cell. $\hat{x}$ is the unit vector in the x direction, and $\hat{y}$ is the unit vector in the y direction. Last, η_x and η_y are the cell-substrate viscosity coefficients in the x and y directions, respectively, as explained in Supplementary Text.

Supplementary Materials

This PDF file includes:

Figs. S1 to S13

Tables S1 to S3

Supplementary Text

Legends for movies S1 to S10

References

Other Supplementary Material for this : manuscript includes the following:

Movies S1 to S10

View/request a protocol for this paper from Bio-protocol.