Size and Proximity of Micro-Scale Hard-Inclusions Increase the Risk of Rupture in Fibroatheroma-like Laboratory Models

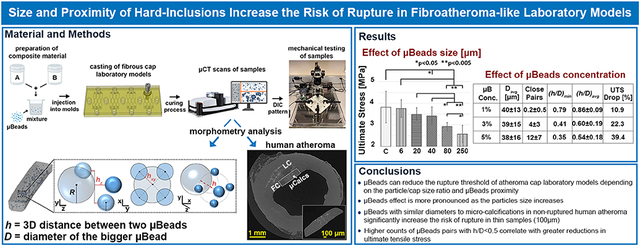
Abstract

Increased mechanical stresses of the fibroatheroma cap tissue is a crucial risk factor on the pathogenesis of asymptomatic coronary artery disease events. Moreover, both numerical and analytical studies have shown that microcalcifications (μCalcs) located in the fibrous cap can multiply the cap tissue stress by a factor of 2-7. This stress amplification depends on the ratio of the gap between particles (h) and their diameter (D) when they are aligned along the tensile axis. However, the synergistic effect of cap stiffness and uCalcs on the ultimate stress and rupture risk of the atheroma cap has not been fully investigated. In this context, we studied the impact of micro-beads (μBeads) of varying diameters and concentration on the rupture of silicone-based laboratory models mimicking human fibroatheroma caps of different stiffness (shear moduli μ_soft=40kPa, μ_stiff=400kPa) and thickness (650μm and 100μm). A total of 145 samples were tested under uniaxial tension up to failure and the true stress and strain response of each model was derived by means of Digital Image Correlation (DIC). Before testing, samples were scanned using high-resolution Micro-CT, to perform morphometry analyses of the embedded micro-beads and determine the number of closely spaced particles (h/D<0.5). The micro-beads structural and spatial features were then compared to the case of 29 non-ruptured human atheroma fibrous caps presenting μCalcs. Samples with and without μBeads exhibited a distinct hyperelastic behavior typical of arterial tissues. Regardless of the sample stiffness, large μBeads (>80μm) significantly reduced the ultimate tensile stress (UTS) of the thick cap models with the effect being more pronounced as the particle diameter increases. Stiff models experienced early rupture in the presence of μBeads with 40μm diameter. Smaller μBeads of 6μm and 20μm didn’t affect the ultimate strength of the thick cap models. However, when 6μm μBeads where introduced in thinner cap models, we observed more than 20% drop in UTS. Increasing the μBeads concentration was also positively correlated with lower stresses at rupture as more clusters formed resulting in lower values of h/D. Morphometry analyses of cap models and human atheroma show that the 6μm μBeads groups present very similar size distributions to μCalcs and that human μCalcs occupy an average volume ratio of 0.79 ± 0.85%. Our results clearly capture the influence of μBeads on the rupture threshold of a vascular tissue mimicking material. This effect appears to be dependent on the μBeads-to-cap thickness size ratio as well as their proximity. These findings support previous numerical and analytical studies suggesting that μCalcs located within the fibroatheroma cap may be responsible for significantly increasing the risk of cap rupture that precedes myocardial infarction and sudden death.

Graphical Abstract

1. Introduction

Cardiovascular disease (CVD) represents the leading cause of death globally and, in the United States alone, coronary artery disease (CAD) is responsible for more than one million acute coronary events annually, comprising both myocardial infarction and sudden coronary death (Bochen Cao, Gretchen A. Stevens, 2020; Roth et al., 2020). The most common underlying cause of acute coronary events is atherosclerosis, which is initiated by cholesterol build-up beneath the arterial endothelium and ultimately evolves into an atherosclerotic plaque, also called atheroma (Burke et al., 1997; Davies, 2000). Approximately half of all cardiovascular deaths associated with acute coronary syndrome occur when the atherosclerotic fibrous cap tissue breaks under the action of high blood pressure (Maseri, Chierchia and Davies, 1986; Virmani et al., 2000).

A crucial factor of plaque rupture risk appears to be the presence of microcalcifications (μCalcs <100μm) in the fibrous cap (Cardoso and Weinbaum, 2018, 2021). These μCalcs are formed by aggregation of calcifying extracellular vesicles (Hutcheson et al., 2016) and have been documented using high-resolution microcomputed tomography (HR-μCT) (Vengrenyuk et al., 2006; Vengrenyuk, Cardoso and Weinbaum, 2008; Maldonado et al., 2012; Kelly-Arnold et al., 2013). Maldonado et al. (Maldonado et al., 2012) even reported one μCalc at the site of rupture of a human coronary atheroma. Evidence from analytical and numerical studies reveals that spherical μCalcs amplify the background stress in the cap by a factor of 2–2.5, resulting in increased tissue rupture risk (Vengrenyuk et al., 2006; Rambhia et al., 2012; Maldonado et al., 2013a; Cardoso et al., 2014; Corti, De Paolis, et al., 2022). This phenomenon originates from the elasticity gradient between the calcified particle and the cap soft tissue, which experiences higher levels of stretches, and thus stresses, at the tensile poles of the μCalc (Cardoso et al., 2014; Barrett et al., 2019). A recent study on the major biomechanical risk factors of atherosclerotic plaque rupture showed that the synergistic effect produced by one spherical μCalc with a diameter of 15μm located within a thin (<50μm) cap is the strongest predictor of plaque rupture (Corti, De Paolis, et al., 2022). In this computational analysis, the presence of a μCalc induced rupture even in 200μm-thick fibrous caps and turned a stable human coronary atheroma into a vulnerable phenotype.

Although a single μCalc represents an alarming indicator of plaque rupture risk, studies have shown that μCalcs can cause up to a 7-fold increase in local tissue stresses when they are closely spaced (Kelly-Arnold et al., 2013; Maldonado et al., 2013a). Maldonado et al. (Maldonado et al., 2013a) demonstrated that the μCalcs-induced stress concentration factor (SCF) is directly associated with the ratio of the gap between two μCalcs and their diameter (h/D). Kelly-Arnold et al. (Kelly-Arnold et al., 2013) further examined this effect in 3D finite element models and reported a linear increase in interfacial stresses when h/D<1 and an exponential increment when h/D<0.5, if the particles were aligned with the tensile axis. The authors estimated a SCF greater than 7 when h/D was below 0.4.

Based on analytical and computational analyses, the impact of μCalcs on plaque vulnerability is evident. However, to the best of our knowledge, there is scarce literature of mechanical tests to assess the role of μCalcs on the Ultimate Tensile Stress (UTS) and rupture of soft tissues. Such work performed directly on human arterial samples would be highly significant, however, it presents important challenges. First, the biomechanics of atheroma is complex and multifactorial. The stress levels and distribution that the fibrous cap experiences vary as a function of the intrinsic properties of the plaque. Major biomechanical factors are the cap thickness (Finet, Ohayon and Rioufol, 2004), the arterial wall material properties (Akyildiz et al., 2015), the morphology of the plaque (Glagov, 1987; Maehara et al., 2002; Ohayon et al., 2008; Cilla, Peña and Martínez, 2012) and the composition of the core underneath the cap (Huang et al., 2001; Finet, Ohayon and Rioufol, 2004; Ohayon et al., 2008). Additionally, blood vessels possess highly heterogeneous tissue compositions with significantly different mechanical behavior depending on their anatomical location, age, sex, and anamnesis of the person (Holzapfel, Sommer and Regitnig, 2004; Holzapfel et al., 2005; Akyildiz, Speelman and Gijsen, 2014; Walsh et al., 2014; Chen and Kassab, 2016; Akyildiz et al., 2018). Lastly, the handling and dissection of samples may easily introduce micro-damage at the cut edges, which could induce early and artificial rupture of the tissue, compromising the reliability of the data. Thus, it becomes arduous to compare the mechanical effect of μCalcs between affected samples and control groups. For these reasons, the use of tissue-mimicking laboratory models is advantageous to isolate and examine the role of μCalcs on the rupture mechanism of the material in a replicable and controllable setting.

The purpose of this study is to provide an accurate characterization of the hyperelastic behavior and rupture threshold of fibrous cap phantoms in the presence of rigid microbeads (μBeads). We investigated the effect of μBeads size with respect to the cap thickness and the particles proximity on the UTS of the material. To this aim, we considered particles of varying diameter and concentration as well as different cap thicknesses and performed uniaxial tensile tests combined with digital image correlation (DIC). An HR-μCT-based morphometry analysis is also presented to compare the structural features and spatial distribution of the μBeads to non-ruptured human coronary atheroma with μCalcs.

2. Material and Methods

2.1. Laboratory models preparation

The laboratory models were designed with an ASTM D412-Type C geometry, the most common testing standard for determining the tensile properties of thermoplastic elastomers, with dimensions scaled down by 80% of the original standard size, to replicate typical sizes of atheroma thick fibrous caps. Each specimen had a gauge region with a length, width, and thickness of 6.6, 1.2 and 0.65 mm respectively. Additionally, we considered the case of a 100μm-thick model to analyze the effect of the group of μBeads with the smallest diameter. Two elastomers of different stiffness were considered as cap tissue mimicking materials to study the role of μBeads diameter, Dowsil EE-3200 (soft model) and Sylgard170 (stiff model) (Dow Corning Corporation). This choice was dictated by the wide variability in the mechanical response of intima tissues reported in the literature (Holzapfel, Sommer and Regitnig, 2004; Walsh et al., 2014). These polymers are supplied as a two-part kits and we used PartA:PartB ratios of 1:1.5 for the soft model and 1:1 for the stiff model, which have been shown to better replicate the typical range of stresses and strains to rupture of carotid and coronary tissues, with shear moduli μ_Dow= 40kPa and μ_S170=400kPa, respectively (Corti, Shameen, et al., 2022b). The elastomer shear modulus was derived by fitting the experimental data of uniaxial tests to the Ogden 3^rd order constitutive model, as described in (Corti, Shameen, et al., 2022b). The Ogden strain energy density function is defined as (Ogden, 1997; Schiavone, Zhao and Abdel-Wahab, 2014):

$$W=\sum _{i=1}^{\mathrm{N}}\frac{2{\mu }_i}{{\alpha }_i^2}({\overline{\lambda }}_1^{{\alpha }_i}+{\overline{\lambda }}_2^{{\alpha }_i}+{\overline{\lambda }}_3^{{\alpha }_i}-3)+\sum _{i=1}^{\mathrm{N}}\frac{1}{D_i}(J^{el}-1{)}^{2i}$$ (1)

where the first term on the right represents the deviatoric part of the model and the second term represents the volumetric part. In the equation, ${\overline{\lambda }}_{\mathrm{i}}$ are the deviatoric principal stretches $\overline{\lambda }\mathrm{i}=J^{-\frac{1}{3}}{\lambda }_i$, where $J$ is the third invariant of the deformation gradient F, $J=det(\mathit{F})={\lambda }_1{\lambda }_2{\lambda }_3$; λ_i are the principal stretches; and ${\alpha }_i$ are power law coefficients that define the slope of the stress-strain curve. Under this form, the shear modulus of the material is given by:

$$\mu =\sum {\mu }_{\mathrm{i}}$$ (2)

From (Corti, Shameen, et al., 2022b), the constitutive coefficients for the soft and stiff models are reported in Table 1.

Table 1.

Constitutive coefficients of the Ogden 3rd order model for the soft and stiff materials.

Model	μ1 (MPa)	μ2	μ3	α1	α2	α3	D1 (MPa−1)	D2,3
Soft	−41.46	21.08	20.42	−0.18	0.24	−0.63	0.78	0
Stiff	−3.15	1.78	1.76	−2.67	0.31	−5.83	0.39	0

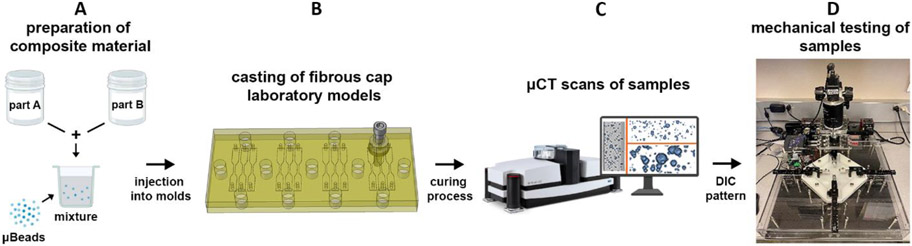
The presence of microcalcifications was mimicked by embedding silica microbeads (Cospheric LLC) into the elastomer matrix after mixing the two polymer parts (Figure 1A), using a dual range semimicro balance (Sartorius AG) to control their concentration. To prepare our samples, the material was thoroughly mixed and degassed for about 30 minutes and injected into a custom-designed molding system consisting of two 0.5in (1.27cm)-thick plates. The bottom plate was carved with a total of 12 sample shapes using a milling machine (Figure 1B). The mixture was cured at 30 °C for 16 hours and then cured again at 50 °C (DowsilEE-3200) or 100 °C (Sylgard170) for 4 hours, as previously indicated (Corti, Shameen, et al., 2022b). After the curing process, models were carefully removed from their cast and visually inspected using a stereomicroscope (SteREO Discovery.V12, Zeiss). We tested different experimental conditions:: (1) elastomers without μBeads (control, n=24; soft models, n=12; and stiff models, n=12); (2) samples with μBeads of varying diameter (D=6, 20, 40, 80, 250μm) at a constant concentration of 1% weight (n=120 total, – 60 soft models, n=12 per diameter group; and 60 stiff models, n=12 per diameter group); (3) models with μBeads of constant diameter (D=40μm) at different concentrations (3% and 5% weight) (n=24 total, n=12 per concentration, stiff models only). For the case of 100μm-thick cap models, two groups of samples were prepared: (1) stiff models without μBeads (n=12); (2) stiff models with 6μm μBeads at 1% concentration (n=12). Before testing, samples were scanned under HR-μCT to perform a morphometric analysis of the μBeads (Figure 1C). Specimens that presented air bubbles or imperfections at the boundaries were discarded. Finally, samples were sprayed with water-based ink to perform digital image correlation (DIC), following the quality guidelines listed by Jones et al. (Jones et al., 2018).

Figure 1.

Illustration of the experimental procedure. (A) Preparation of the elastomer mixture by combining the two Parts and adding μBeads; (B) The material is injected into a custom-designed molding system consisting of two plates that are tightly closed by a set of screws and nuts; (C) Samples are scanned under HR-μCT to visualize the μBeads in the polymer matrix and perform morphometry analyses; (D) Samples are tested using the BiMATs tensile machine detailed in (Corti, Shameen, et al., 2022a).

2.2. Mechanical testing

We tested the samples using a custom-made micro material testing system equipped with real-time control and acquisition software (LabVIEW, v. 2018, National Instruments) (Figure 1D). The machine was equipped with a load cell with a capacity of 10N and sensitivity of 10mN. A detailed, open-source description of our testing system can be found in (Corti, Shameen, et al., 2022a). During the experiments, samples were preconditioned with 10-cycles stretch iterations at 10% strain, followed by one-single pull to rupture. The loading cycle was governed by a ramp waveform under displacement control at a constant strain rate of 1.5mm/s. Throughout the test, the reaction force and displacement were measured by the system and images of the sample were recorded by a FLIR Blackfly S high-resolution camera (Teledyne FLIR) equipped with a Tamron M111FM50 lens (IDS Imaging). The tests data from the tensile machine and the high-resolution images were then used to perform DIC analyses on the samples. This analysis was performed in GOM Correlate software (ZEISS Group, v.2019) which allowed us to obtain the True (Cauchy) stress and strain for each laboratory model. The true stress values were calculated by dividing the tensile load by the instantaneous area, measured from the change in width in the gauge region throughout the test, assuming the material as isotropic. The true strain was determined as the natural logarithm of the ratio of the instantaneous gauge length to the original length.

2.3. Morphometric analysis

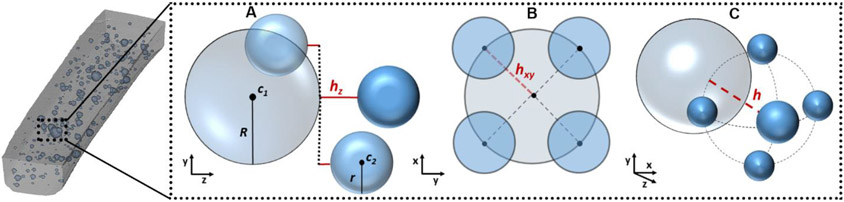
To study the structural parameters (e.g. size distribution, separation between particles) of the μBeads dispersed in the elastomer matrix, we scanned the gauge region of the samples under HR-μCT. The system energy settings were chosen to increase the contrast between the polymer and the microbeads, and the scans contained 1872 2D slices of 4000 by 4000 pixels in-plane matrix, with 4.05μm isotropic voxel resolution and 8-bit gray levels. For the group with 6μm μBeads, the resolution was increased to 2.5μm to better capture the particles size. The cross-section slices acquired from HR-μCT were then reconstructed and corrected from artifacts in NRecon software (v. 1.6.9, SkyScan). The resulting set of images were then imported into CTAn to extract information on the μBeads spatial coordinates and their Sauter mean diameters. These data were analyzed by a custom-made MATLAB script that computes the μBeads diameter distribution, the polymer-to-μBeads volume ratio and the h/D ratio between each pair of close beads. The volume ratio was defined as the volume fraction occupied by the μBeads in the sample and should not be confused by the weight percentage used to control the amount of μBeads introduced in the polymer mixture. To identify closely spaced μBeads, pairs of particles were considered only if they respected the following requirements: (1) the distance between the outer surfaces of the two particles in the tensile direction (hz) is equal or lower than the diameter of the bigger bead (D) (Figure 2A); (2) the Euclidean distance between the centroids of the two particles in the width-thickness plane (hxy) is equal or smaller than the radius of the bigger bead (R) (Figure 2B); (3) the ratio of the Euclidean distance between the outer surfaces of the two particles in the 3D space (h) to the diameter of the larger bead is equal or lower than 1 (Figure 2C). This choice was based on previous work that showed a linear increase in stress concentrations between μCalcs pairs when h/D<1 and an exponential increment when h/D<0.5 (Maldonado et al., 2013b).

Figure 2.

Representation of the conditions inspected by the algorithm to recognize closely spaced μBeads. (A) Drawing of how the distance in the tensile direction is calculated between pairs of μBeads; (B) Drawing of the closed μBeads in the width-thickness plane; (C) Drawing of the Euclidean distance in the 3D space between pairs of μBeads.

2.4. Human atheroma

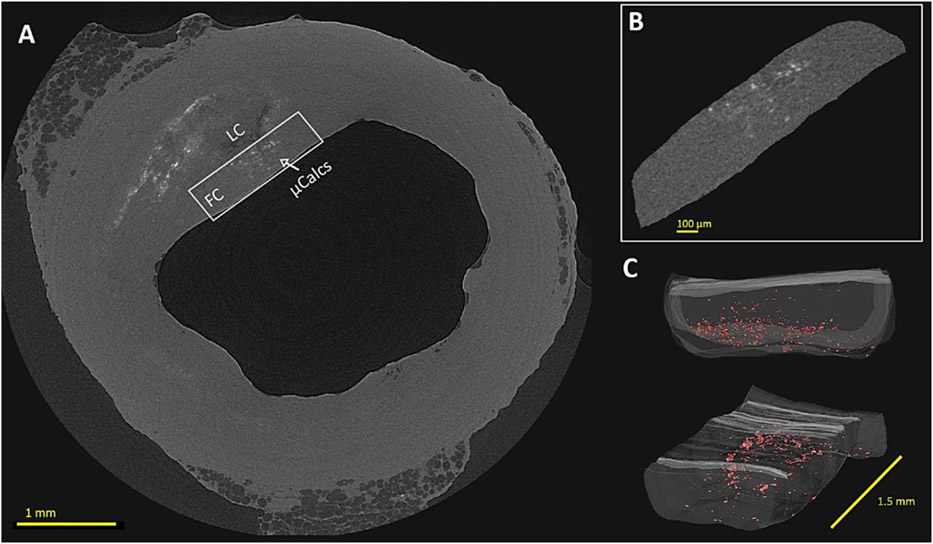
In order to compare the μBeads volume ratio in our laboratory models to human plaques, we extended the morphometric analysis performed by Kelly-Arnold et al. (Kelly-Arnold et al., 2013) in 22 human coronary atheroma presenting μCalcs in the fibrous cap (FC). Samples of the left anterior descending artery (LAD), left circumflex artery (LCX) and right coronary artery (RCA) were dissected from fresh hearts obtained from The National Disease Research Interchange (recovered < 6h post mortem) with myocardial infarction. These specimens were previously scanned with HR-μCT at a resolution of 2.1μm. In the present study, we investigated volumes of interest (VOI) of the fibrous caps with the highest μCalcs content. These regions were selected to include the extent of the FC tissue that covers the lipid core (LC) in the circumferential direction (Figure 3A-B), for a constant length in the longitudinal direction of 1.5 mm (Figure 3C). For each VOI, the μCalcs (calcified tissue) were segmented from the cap (soft tissue) based on a sample-specific grey-level binary threshold in CTAn (v 1.14, SkyScan). Here, the volume of the cap segment and μCalcs as well as the Sauter mean diameter of each μCalc were calculated and exported into a custom-made MATLAB script to derive the cap-to-μCalcs volume ratio and the diameter distribution in the samples. In the analysis, μCalcs with a diameter lower than 5μm were removed from the data set, since they don’t represent a biomechanical risk for cap rupture (Maldonado et al., 2013a).

Figure 3.

Multiscale HR-μCT view of a human coronary atheroma and its cap presenting μCalcs. (A) Cross-sectional view of the whole atheroma sample with cap VOI highlighted; (B) Magnified view of the cap VOI with μCalcs distributed through its thickness; (C) 3D reconstruction of the cap VOI with μCalcs highlighted in red. LC: lipid core; FC: fibrous cap; μCalcs: microcalcifications

2.5. Statistical analysis

Data are reported as meant± SD. Analysis of variance was performed by one-way ANOVA test followed by post-hoc pairwise comparison of the mean strength between the groups. The null hypothesis was rejected if p<0.05.

3. Results

3.1. Effect of μBeads size

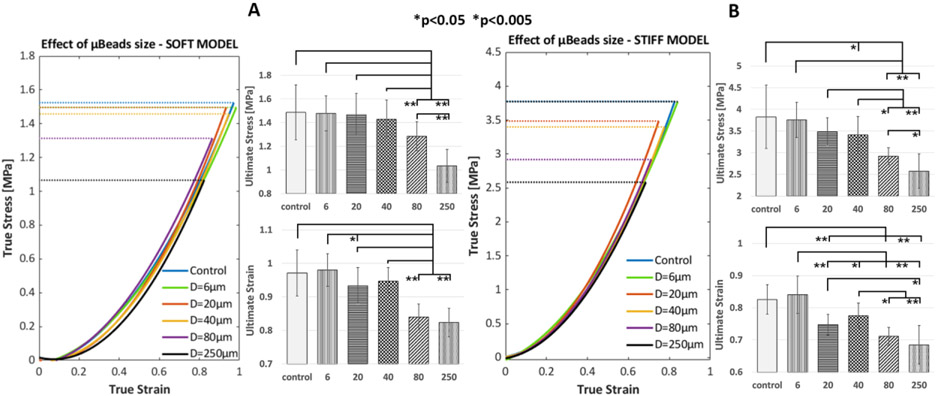
The effect of varying μBeads diameter on the mechanical behavior of soft and stiff fibrous cap laboratory models is shown in Figure 4. Each group exhibits a clear hyperelastic response under tension that is typical of arterial tissues. Regardless of their size, μBeads don’t cause a significant deviation from the True stress-strain curve of the control samples. However, bigger μBeads of 80-250μm decrease substantially the ultimate (at rupture) tensile stress (UTS) of both materials. This phenomenon occurs because the μBeads amplify the local stresses in the tissue at their tensile poles, inducing rupture of the sample at a lower apparent tensile strength.

Figure 4.

Illustration of the effect of μBeads on the rupture threshold of fibrous cap laboratory models of different stiffness and varying μBeads diameters at constant concentration (1 % weight). (Left) True stress vs True strain curves up to rupture and bar plots of ultimate stress and strain of the soft models (DowsilEE-3200, shear modulus μ_Dow= 40kPa); (Right) True stress vs True strain curves up to rupture and bar plots of ultimate stress and strain of the stiff models (Sylgard170, shear modulus μ₁₇₀= 400kPa). Error bars represent standard deviation

In the case of soft models (Figure 4A) smaller particles don’t affect the ultimate tensile stress of the samples, suggesting that the μBeads-induced SCF did not produce early rupture around the particles or that the formed voids at their poles did not grow through the material. Statistical analysis shows significant difference between the strength (i.e. UTS) of samples with large μBeads (80-250μm) and the other groups with smaller μBeads or control. The change in rupture threshold is also significant between the 80 and 250μm groups, with the μBead-to-cap thickness ratio being positively correlated with the drop in ultimate stress and strain (ρ_soft=0.9836, p_soft=0.0025, ρ_stiff=0.9148, p_stiff=0.0295).

In the stiff models, we observed a stronger effect of the particles diameter on the rupture behavior of the material (Figure 4B), as it starts to be apparent at lower μBeads-to-cap thickness ratios. Here, the 20 and 40μm groups already exhibit a certain reduction in UTS compared to control. In particular, samples with 40μm μBeads break at a statistically significant lower stress than controls. Again, large μBeads of 80 and 250μm show the greatest drop in ultimate strength and also significant difference between each other. Notably, the stiff samples with 80μm μBeads experience a greater UTS reduction of 23.7% compared to the 13.6% of the same group in the soft models (Table 2). The 250μm groups show similar values in the stiff and soft models, with a UTS drop of 32.7% and 30.3%, respectively.

Table 2.

Morphometry analysis of soft and stiff fibrous cap models with different μBeads diameter at the same concentration of 1% weight. Values are reported as mean± SD per sample.

Group		Samples	Davg [μm]	Size ratio	Volume ratio [%]	Beads/mm3	# Close Pairs (h/D<1)	(h/D)min	(h/D) avg	UTS Drop [%]
6	Soft	10	5.9± 2	$\frac{1}{110}$	0.25± 0.16	5212± 2996	2± 2	0.61	0.81± 0.14	0.5
	Stiff	11	6.3± 3.6	$\frac{1}{110}$	0.22± 0.12	4061± 1039	3± 3	0.53	0.80± 0.13	1.9
20	Soft	10	18± 0.9	$\frac{1}{30}$	0.29± 0.05	254± 33	1± 1	0.58	0.80± 0.16	3.5
	Stiff	11	20± 0.9	$\frac{1}{30}$	0.33± 0.07	312± 50	2± 1	0.30	0.76± 0.19	8.9
40	Soft	11	43± 13	$\frac{1}{15}$	0.29± 0.04	54± 6	0.1± 0.3	0.95	0.95± 0.0	4.1
	Stiff	10	40± 13	$\frac{1}{15}$	0.34± 0.09	53± 7	0.2± 0.5	0.79	0.86± 0.09	10.9
80	Soft	12	86± 21	$\frac{1}{8}$	0.34± 0.07	9± 2	0.1± 0.3	0.90	0.90± 0.0	13.6
	Stiff	11	81± 27	$\frac{1}{8}$	0.39± 0.07	13± 2	0.3± 0.5	0.92	0.94± 0.03	23.7
250	Soft	11	245± 17	$\frac{1}{3}$	0.39± 0.26	0.5± 0.2	0.09± 0.3	/	/	30.3
	Stiff	10	254± 12	$\frac{1}{3}$	0.36± 0.18	0.4± 0.2	0± 0	/	/	32.7

The morphometry analysis of μBeads in the sample gauge region (Table 2) reveals different μBeads volume ratio depending on their size, with more closely located particles in samples from groups with smaller μBeads diameter. Nevertheless, the average h/D for each case doesn’t reach values that are low enough (h/D<0.5) to significantly increase the stress concentration between pairs of μBeads. Out of the whole set of samples, we found only one pair of μBeads with h/D<0.5 in the 20μm stiff model group. This suggests that the reduction in UTS measured for every group can be assumed as the effect of individual, isolated μBeads, which amplify the stress at their tensile poles by a factor of 2-2.5. Despite the μBeads low volume fraction, our results demonstrate that the localized effect of μBeads can propagate to induce the macroscopic rupture of the sample (Figure 5). Based on previous analytical and numerical analysis, it is known that the damage initiates at the μBead poles in the form of extremely small voids and then explosively grow through the tissue.

Figure 5.

Scanning electron microscopy of the entire cross-section and magnified view of the location of rupture in fibrous cap laboratory models presenting μBeads of 250μm (top) and 80μm (bottom). The sample with bigger μBeads represent a case with a closed pair of particles with h/D<1.

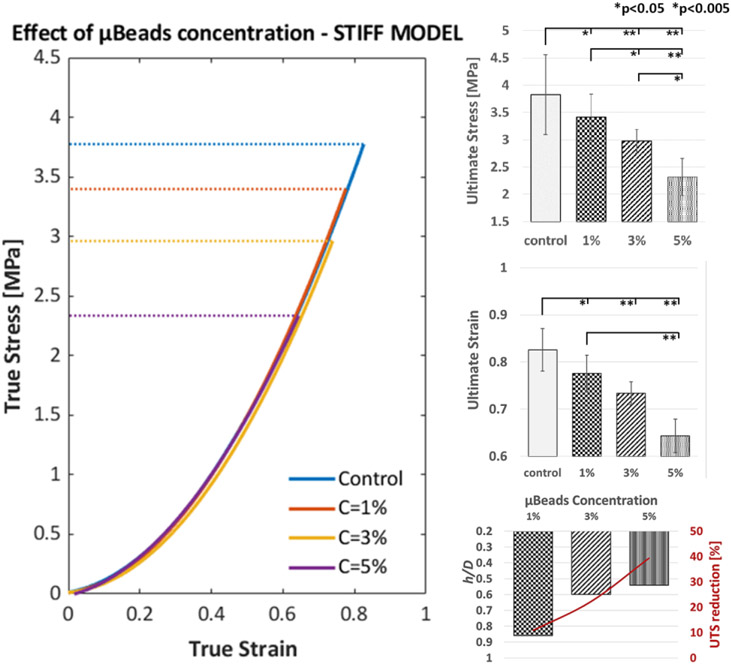
3.2. Effect of μBeads concentration

The influence of μBeads concentration on the material rupture threshold was studied in the stiff models and is illustrated in Figure 6. There is a clear reduction in UTS as more μBeads are introduced in the material. As in the case of varying diameter, the stress-strain response of the samples doesn’t deviate from the control group when μBeads are present.

Figure 6.

Illustration of the effect of concentration and proximity of 40μm μBeads on the rupture threshold of stiff fibrous cap laboratory models. (Left) True stress vs True strain curves up to rupture of the control (no μBeads) group and samples with μBeads at 1%, 3% and 5% weight concentration; (Right) Bar plots of the ultimate tensile stress and strain of each group and the relationship between μBeads concentration, average minimum h/D and UTS reduction. Error bars represent standard deviation.

All the fibrous cap models with μBeads exhibit a statistically significant difference in ultimate tensile stress and strain with the control group as well as among different particles concentrations. The stress at rupture decreases 10.9, 22.3 and 39.4% when the μBeads concentration is 1, 3 and 5% weight, respectively (Table 3).

Table 3.

Morphometric analysis of fibrous cap models with μBeads (D=40μm) at different concentrations of 1, 3 and 5% weight. Values are reported as mean± SD per sample.

Group	Samples	Davg [μm]	Volume ratio [%]	Beads/mm3	# Close Pairs (h/D<1)	(h/D)min	(h/D)avg	UTS Drop [%]
1%	10	40± 13	0.34± 0.09	53± 7	0.2± 0.5	0.79	0.86± 0.09	10.9
3%	9	39± 15	0.73± 0.17	145± 28	4± 3	0.41	0.60± 0.19	22.3
5%	9	38± 16	1.66± 0.54	283± 113	12± 7	0.35	0.54± 0.18	39.4

Based on our analysis, higher μBeads contents are directly proportional to the number of close pairs and inversely proportional to the average and minimum h/D ratio (Table 3 and Figure 6). The 3% group presents μBeads pairs with h/D<1 in every sample, for a total of 38 pairs, of which 4 pairs had an h/D<0.5 in 3 out of 9 samples. As the concentration increases to 5%, we found a total of 107 pairs with h/D<1, where 10 pairs had an h/D<0.5 and were present in 5 of the 9 samples tested. These data picture a direct relationship between the proximity of μBeads and the threshold to rupture of the cap models.

3.3. The case of 100μm-thick FC model and human μCalcs morphometric analysis

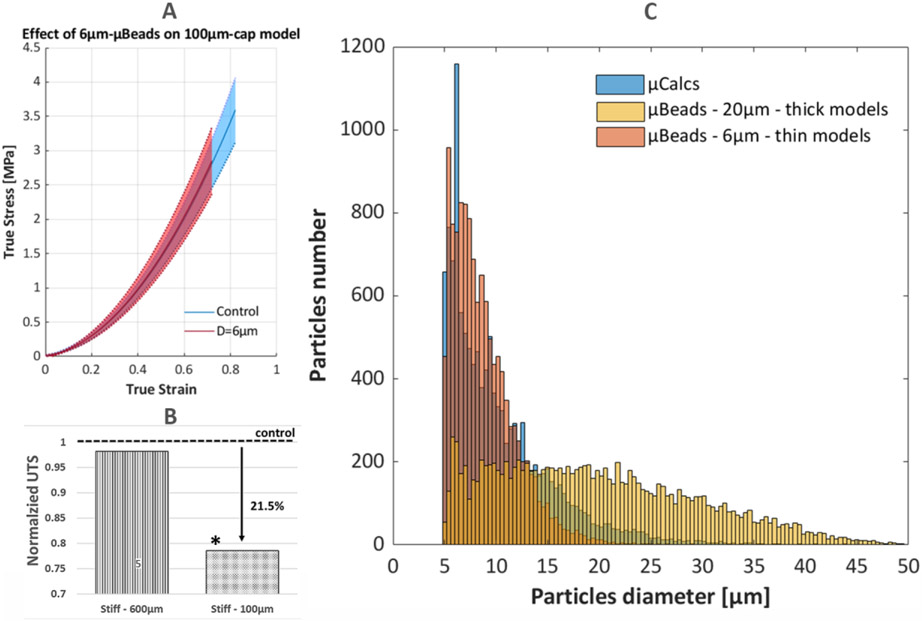
The effect of 6μm μBeads on thin (100μm) cap models is shown on Figure 7A. While these tiny particles don’t influence the UTS of 650μm-thick cap models, their impact becomes evident in thinner samples. This group has now a size ratio of $\frac{1}{15}$ and experiences a 21.5% reduction in UTS when compared to control, which is now a statistically significant change (p=0.0362, Figure 7B). Morphometry analysis of the tested samples (n=8) revealed that there were a total of 1908± 424 μBeads per sample (4048± 1253 μBeads/mm³), with a volume ratio of 0.63± 0.24%. The average number of close μBeads pairs with h/D<1 was 0.4± 0.7, with a total count of 4 pairs in 3 out of 8 samples. There were no instances of h/D<0.5, with the lowest h/D among these μBeads being 0.82, and an average minimum of 0.85± 0.05.

Figure 7.

Illustration of the effect of 6μm μBeads on thin (100μm) cap models. (Top-Left) True stress and strain curves up to rupture of the control (no μBeads) group and samples with 6μm μBeads at 1% weight concentration; (Bottom-Left) Bar plots of the normalized ultimate tensile stress of the thick and thin models

The number of μCalcs, their average diameter and volume ratio for each cap segment are reported in Table 4. Some samples presented more than one lipid core or one cap had more regions with a high count of μCalcs, resulting in a total of 29 cap segments analyzed. The average number of μCalcs found in the human caps was 1154± 1354, with a Sauter mean diameter of 10.82± 5.26μm, where the majority of μCalcs concentrates in the 5-20μm size range.

Table 4.

Morphometric analysis of μCalcs in the fibrous cap VOIs in human coronary atheromas. Values are reported as mean± SD per cap segment.

Human Fibrous Cap	# μCalcs	μCalcs/mm3	Average Diameter [μm]	Volume Ratio %
Segment 1 - RCA	6434	2286	11.84 ± 5.61	1.57
Segment 2 - LAD	2283	244	10.28 ± 7.07	0.53
Segment 3 - RCA	921	336	10.56 ± 5.23	0.27
Segment 4 - RCA	547	712	12.23 ± 6.20	0.44
Segment 5 - LCX	2675	2625	9.70 ± 3.80	0.64
Segment 6 - LAD	1789	1221	11.27 ± 4.79	1.29
Segment 7 - LCX	1634	2093	8.23 ± 2.96	0.30
Segment 8 - LAD	360	1085	10.07 ± 5.18	0.26
Segment 9 - LAD	801	1064	10.58 ± 5.40	0.59
Segment 10 - LAD	549	405	10.37 ± 5.27	0.20
Segment 11 - LAD	816	1525	9.62 ± 3.95	0.45
Segment 12 - LCX	375	766	9.13 ± 3.71	0.20
Segment 13 - LCX	639	798	13.29 ± 7.76	1.19
Segment 14 - LCX	204	332	12.55 ± 8.13	0.34
Segment 15 - RCA	1106	633	10.13 ± 4.75	0.64
Segment 16 – RCA	60	320	12.21 ± 5.44	0.20
Segment 17 – RCA	198	609	11.46 ± 5.65	0.38
Segment 18 - RCA	129	171	13.91 ± 7.74	0.17
Segment 19 - LAD	538	818	12.31 ± 6.02	3.64
Segment 20 - LAD	4106	2708	10.23 ± 4.58	2.15
Segment 21 - RCA	1391	3705	7.92 ± 2.81	1.00
Segment 22 – RCA	629	1395	8.34 ± 2.95	0.20
Segment 23 – LAD	812	2079	9.83 ± 4.24	2.70
Segment 24 - LCX	1438	516	8.29 ± 4.12	0.17
Segment 25 - LCX	1414	431	7.64 ± 2.91	0.51
Segment 26 – LCX	144	155	11.20 ± 5.63	0.06
Segment 27 - RCA	1136	701	11.12 ± 5.57	1.61
Segment 28 - RCA	180	415	15.85 ± 7.20	1.02
Segment 29 - RCA	168	293	13.65 ± 7.98	0.27
Total	1154 ± 1354	1050 ± 906	10.82 ± 5.26	0.79 ± 0.85

The average content of μCalcs per unit volume falls between the 20μm μBeads and the 6μm μBeads at 1% concentration, which represent the groups with the closest size to the human calcifications. The distribution of diameter for μCalcs, 20μm μBeads in thick models and 6μm μBeads in thin models shows that the 6μm μBeads closely replicate the trend in human μCalcs, while 20μm μBeads present a wider range of dimensions, with more frequent instances of larger (>40μm) particles (Figure 7C). The cap-to-μCalcs volume ratio is on average 0.79± 0.85% with a maximum of 3.64% and a minimum of 0.06%, indicating that μCalcs, when present, occupy a minor portion of the cap tissue. These values compare well with the case of 40μm μBeads at 3% concentration in thick samples and the 6μm group in thin samples (vr_40μm,3%=0.73%, vr_6μm=0.63%). The morphometry analysis performed in Kelly-Arnold et al. (Kelly-Arnold et al., 2013) showed similar counts of μCalcs (1564± 2506) when considering the whole extent of the fibrous caps. For the same samples analyzed in this study, the authors reported only 6 pairs of μCalcs with h/D≤0.5 that is the critical value below which the stress concentrations between the two particles increases exponentially.

4. Discussion

In the present study, we examined the tensile behavior until failure of fibrous cap phantoms of different stiffness and thickness in the presence of rigid μBeads with varying diameter and concentration. Mechanical tests were coupled with an HR-μCT-based morphometry analysis of the particles to measure their volume fraction and detect close pairs of μBeads with h/D<1. The data on the laboratory models were also compared to structural and spatial features of μCalcs in human coronary atheroma.

We demonstrated that μBeads can lower the threshold to rupture in laboratory models of thick (650μm) fibrous caps that would be consider as mechanically stable. This effect appears to be size-dependent, as significant reductions in UTS start to be observed at size ratios > $\frac{1}{8}$ and $\frac{1}{15}$ in the soft and stiff models, respectively. Even when μBeads cause a significant change in the rupture threshold of the models, there is no apparent deviation from the macroscopic stress-strain curves of the material and the μBeads occupy a tiny fraction of the whole sample (vr_μBeads<1%). This suggests that the presence of μBeads induces only localized increases in interfacial stresses that can initiate micro-damage at their tensile poles. Under certain circumstances, the tiny voids formed around the μBeads grow through the section of the sample, resulting in early rupture of the material. Morphometry analysis on coronary atheroma showed that the 6μm μBeads present very similar size distributions to human μCalcs. The groups of thick samples with these μBeads didn’t exhibit any variation in their ultimate behavior. Conversely, when the model thickness was decreased to 100μm, the same particles significantly reduced the samples stress and strain at rupture by more than 20%. These observations imply that in the case of spherical particles, the ratio between the cap thickness and the μBeads (or μCalcs) size plays a key role in determining the vulnerability of the material. Other researchers have described this effect when studying polymer composites. Fu et al. (Fu et al., 2008) tested polypropylene with calcium carbonate particles of varying diameter (0.01, 0.08, 1.3 and 58μm, samples thickness not mentioned) under uniaxial loading and reported an inverse correlation between the particles radius and the material strength, for a given volume fraction. The same trend was observed by Lee et al. (Lee, 2016) in silicone KE-12 samples with silica beads (size ratios $\frac{1}{450}$, $\frac{1}{80}$, $\frac{1}{38}$ and $\frac{1}{9}$), for which the tensile strength of the polymer decreased with increasing mean radius. Our morphometry analysis on non-ruptured human coronary atheroma shows that μCalcs that are present in the FC have a small diameter. Thus, it is possible that their sizes relative to the caps thickness were not large enough to initiate rupture or that the background stress was not sufficiently high to exceed the strength of the tissue even when amplified by the μCalc-induced SCF (Corti, De Paolis, et al., 2022). The few instances of large μCalcs in the human caps suggest that these cases are either rare or rather that when they occur, they provoke rupture of the tissue more frequently.

The soft and stiff models display some differences among equivalent groups of μBeads. In DowsilEE-3200, a diameter of 40μm correspond to UTS reductions lower than 4% and are thus negligible to the rupture threshold of the material. However, the same μBeads induce a higher change in ultimate strength of the stiff models, with a drop of 10.9% in UTS. In the context of arterial fibrous caps, μCalcs with the same size ratio may affect the cap UTS to a similar extent, and the cap could reach rupture at blood pressures that wouldn’t be otherwise considered of risk. It is also possible that the cap tissue could behave more like the soft models, where μBeads of $\frac{1}{15}$ size ratio don’t show a significant effect on the threshold for rupture. Since the effect of hard micro-inclusions in a hyperelastic material is associated to the elasticity gradient between the two materials, one would expect a greater impact in the soft models. Cardoso et al. (Cardoso et al., 2014) investigated the effect of the cap material properties on the SCF caused by μCalcs. The authors performed Finite Element Analysis of idealized coronary atheroma presenting μCalcs in their cap and reported a significant reduction in the SCF when the shear modulus of the tissue increased by a factor of 50 and 100. However, the stress amplification at the μCalcs poles decreased only slightly when the shear modulus was 5 times greater. Based on this analysis, we believe the change in SCF in our models to be non-significant, as the two materials possess shear moduli that differ by a factor of 10. Given the extensibility shown by DowsilEE-3200 and its nature as a sealant, the different effect of small μBeads on the two models could originate from a higher bond strength between this material and the particles or a greater tear strength of the soft models compared to Sylgard170. These aspects would preclude a direct comparison on the effect of the matrix stiffness for the same μBead size groups.

Small μBeads may still initiate damage at their poles in the form of microscopic cavities but their surface energy can be far greater than the energy needed for damage growth and would require further tension to expand. This phenomenon was previously documented by Toulemonde et al. (Toulemonde et al., 2017), who tested polyacrylate samples filled with glass beads at a size ratio of $\frac{1}{15}$ and reported numerous micro-cracks around particles at 15% strain, although samples failure occurred at 35% strain, denoting that the presence of cracks does not lead to immediate failure of the specimen. We believe these observations also explain why analytical and numerical studies have reported a SCF of 2-2.5 for isolated μCalcs (Vengrenyuk et al., 2006; Cardoso et al., 2014; Corti, De Paolis, et al., 2022), but our experiments show that this stress increase doesn’t translate into a 1:1 proportional reduction in UTS.

For the case of μCalcs in human fibrous caps, Maldonado et al. (Maldonado et al., 2013a) determined that the preferred mechanism of rupture is cavitation in hyperelastic materials, as opposed to debonding. Under tension, the local pressure in the extracellular matrix of the cap is reduced and dissolved gases come out of solution, forming extremely small voids at the μCalcs poles. However, the interfacial adhesion between μCalcs and the surrounding tissue appears to be complex and may differ depending on the collagen matrix composing the fibrous cap. In atherosclerotic plaques, agglomeration of calcified extracellular vesicles (EVs) has been associated with collagen degradation, as it allows EVs to accumulate and coalesce into microcalcifications (Hutcheson et al., 2016). Therefore, the collagen matrix is a key driver of microcalcifications size and morphology (Zhao et al., 2022). Additionally, a recent study (Gijsen et al., 2021) reported four different collagen fibers distributions surrounding microcalcifications in atherosclerotic carotid atheroma. The authors classified these patterns as attached, pushed-aside, encircling and random. In the case of the ‘attached’ group, the fiber structure was not altered by the presence of the microcalcification and fibers were visible inside the calcified particles. This suggests that this type of calcifications originated from fiber mineralization. Importantly, numerical simulations showed that the four fibers arrangements corresponded to different levels of interfacial stresses, with the pushed-aside group experiencing the highest stresses, followed by the attached fiber pattern group and the encircling pattern exhibiting much lower stresses. These studies highlight the intricate relationship between microcalcifications and the collagen matrix surrounding them, from the early stages of EVs agglomeration to larger calcified particles that can compromise plaque vulnerability. Future work on the bond strength between microcalcifications and the surrounding fibrous tissue will enhance the understanding of their physical interaction and improve numerical simulations and mechanical tests of fibrous cap rupture.

Our results clearly capture the effect of μBeads proximity on the failure threshold of the material. The reduction in ultimate stress and strain of the cap phantoms increases significantly when particles present lower h/D ratios. These experimental results support the numerical simulations in Maldonado et al. (Maldonado et al., 2013a) and Kelly Arnold et al. (Kelly-Arnold et al., 2013), who first described the effect of particles agglomerates on μCalcs-induced SCF. Under constant diameter and particle/sample size ratio, the reduction in ultimate stress rose from 10.9% to almost 40% as approximately 55% of the samples presented close pairs of μBeads with h/D<0.5. Other research groups have reported a similar relationship between particles concentrations and material strength. Zhao et al. (Zhao et al., 2018) studied the effect of higher volume ratios of ceramic, silica and glass microbeads on the rupture properties of polydimethylvinylsiloxane samples under uniaxial tests. They observed a gradual decrease in ultimate tensile strength as the microbeads content increased, regardless of the particles material. Quan et al. (Quan et al., 2021) also tested methyl vinyl samples at different concentration of hollow glass beads with a size ratio of $\frac{1}{50}$ and described a decrease in the tensile fracture energy for higher beads volume ratios. However, these studies didn’t assess the relative spacing between micro-beads and its relationship with particles content. Our results clearly highlight this correlation and the subsequent effect on the ultimate strength of fibrous cap laboratory models. In the set of human atheroma considered in this study, Kelly Arnold et al. (Kelly-Arnold et al., 2013) reported that among the nearly 35,000 μCalcs located in the caps regions, there were only 38 particle pairs with h/D<1 and only six of these pairs had h/D<0.5. Again, these findings may lead to two different conclusions: either closely spaced μCalcs indeed occur seldom, or more of these pairs have not been observed because they highly increase the chance of tissue rupture.

One aspect of this study that could be considered as a limitation is that we characterize the mechanical behavior of fibrous caps laboratory models by means of uniaxial tensile tests, which oversimplify the physiological loadings that vascular tissues experience. Also, the hyperelastic material in our laboratory models is isotropic, while arterial tissues are anisotropic. Vascular layers usually present two distinct distributions of collagen fiber directions, and can be considered as mechanically orthotropic (Ogden, 2009). Healthy arteries show a predominant circumferential alignment of collagen fibers and their load bearing capacity have been demonstrated extensively (Holzapfel et al., 2005; Holzapfel, 2008; Sáez et al., 2016; Akyildiz et al., 2017). In non-atherosclerotic coronary arteries, Holzapfel et al. (Holzapfel et al., 2005) reported different levels of stiffness and UTS values based on the direction of loading, due to the collagen fibers arrangement. Another study (Akyildiz et al., 2017) showed that in the case of atherosclerotic intima, as the plaque progresses into a more advance lesion, the organization of the fiber alignments becomes less structured, due to the various biological processes involved. As a result, the diseased fibrous intima presents a very disorganized fiber alignment and it doesn’t exhibit an apparent predominant fiber orientation. Our laboratory models possess an isotropic behavior which represents a great approximation of the anisotropic response of arterial tissues. However, since the scope of our study is to replicate the fibrous cap tissue which could contain μCalcs, the isotropic nature of the laboratory models appears to better represent the case of an atherosclerotic intima. We believe the analysis of our capmimicking models provide valuable insight on the material tensile response up to failure and they can clearly capture the effect of μBeads on the mechanical rupture risk of the model in a controllable and repeatable manner.

5. Conclusion

We demonstrated that hard micro-inclusions can reduce the rupture threshold of atheroma cap phantoms, depending on the particle/cap size ratio and their proximity. Tiny μBeads of 6μm don’t initiate early rupture when the cap is very thick (>650μm) but they become relevant in thinner (<100μm) models. These results provide supporting evidence that the combination of thin fibrous caps and μCalcs represent a significant high-risk factor for atherosclerotic plaques vulnerability. Additionally, closely spaced μBeads were shown to enhance even further their effect on the material ultimate strength, proving the importance of assessing the potential presence of μCalcs clusters.

Highlights.

• Hard micro-inclusions can reduce the rupture threshold of atheroma cap phantoms when the particle/cap size ratio reaches a critical point.

• The effect of micro-inclusions on the ultimate strength of the cap models is more pronounced as the particles diameter increases.

• Micro-inclusions with similar diameters to micro-calcifications in non-ruptured human atheroma don’t affect the ultimate strength of thick cap models (650μm), but significantly increase the risk of rupture in thinner samples (100μm).

• Instances of closed pairs of particles and their counts correlates to lower ultimate tensile stresses, supporting the notion of higher risk of rupture in the presence of micro-calcifications clusters.