Abstract
Designing a reliable computational methodology to calculate protein:ligand standard binding free energies is extremely challenging. The large change in configurational enthalpy and entropy that accompanies the association of ligand and protein is notoriously difficult to capture in naive brute-force simulations. Addressing this issue, the present protocol rests upon a rigorous statistical mechanical framework for the determination of protein:ligand binding affinities together with the comprehensive Binding Free-Energy Estimator 2 (BFEE2) application software. With the knowledge of the bound state, available from experiments or docking, application of the BFEE2 protocol with a reliable force field supplies in a matter of days standard binding free energies within chemical accuracy, for a broad range of protein:ligand complexes. Limiting undesirable human intervention, BFEE2 assists the end-user in preparing all the necessary input files and performing the post-treatment of the simulations towards the final estimate of the binding affinity.
Introduction
Complete understanding and prediction of the recognition and association of a protein and a ligand is of paramount importance in chemistry and biology, most notably in the field of protein engineering and pharmaceutical sciences. The binding free energy directly mirrors the ability of the ligand to interact with the protein, and is, therefore, regarded as the key quantity in studies of molecular recognition and association phenomena. However, the experimental determination of the binding affinity of any prospective compound is often costly in terms of synthesis time and money. To alleviate this important hurdle in drug design and lead optimization, much attention and effort have been devoted to development of computational methodologies for the accurate estimation of binding free energies in silico1.
The main challenge posed by the estimation of a binding free energy by means of computer simulations is to capture the significant change in configurational enthalpy and entropy corresponding to the conformational, orientational and positional movements of the ligand with respect to the protein in the course of their reversible association2,3. One of the strategies that has proven reliable consists in turning to the combination of molecular dynamics (MD) and advanced-sampling techniques to guarantee the adequate exploration of each relevant degree of freedom1,4,5. Still, the reversible association events of protein:ligand complexes are very difficult to capture in advanced-sampling simulations. A widely adopted strategy to overcome the sampling issue consists in introducing a restraining potential at an intermediate step to control the motion of the ligand relative to the protein binding site during the geometric separation or alchemical decoupling of the partner. This strategy, introduced by Hermans and Shankar6, has been progressively enriched over the years by a number of additional developments and variants7–12. The restraining potential is introduced at one end-point to “confine” the uncoupled ligand within the binding site, and is then “released” at the other end-point, where this step can be carried out analytically6,7,10. Gilson et al. called free-energy calculations in which there is no translational restraint the “double annihilation method” (DAM), and calculations in which there is a translational restraint the “double decoupling method” (DDM)13.
Based on the idea of introducing restraints to confine the ligand with respect to the protein during separation or decoupling of the partner and then estimating the contribution to the binding affinity through post-treatments, since 1996, we have developed a number of numerical schemes14–17, simulation strategies7,18–21, and software22,23 to facilitate in-silico determination of the standard binding free energy. These successive developments are encapsulated in an automated, streamlined, general and accurate methodology23 put forth to calculate the binding affinity of a flexible ligand with respect to a protein, as detailed hereafter.
Development of the protocol
All the algorithms and numerical strategies described below have been automated and implemented in the latest version of the Binding Free Energy Estimator 2 (BFEE2) open-source and user-friendly software23, which can be used in conjunction with the popular visualization platform VMD24.
Except perhaps for the simplest systems, unbiased brute-force MD is largely unable to sample the large conformational, translational, and orientational changes that accompany the reversible association of a drug-like ligand with a protein. To circumvent this problem, we proposed to deliberately control the sampling through the use of configurational restraints and formulate the calculation in terms of geometric or alchemical transformations.18 In 2013, it was shown that both routes lead to equivalent results19. Depending on the particular situation, features of either route may be advantageously exploited and combined for the accurate determination of the standard binding free energy between a drug-like molecule and a protein. Irrespective of the chosen route, restraints may be added and accounted for rigorously, using a set of template-based and generalized collective variables (CVs) describing the slow degrees of freedom of the reversible association (Table 1)10,20.
Table 1 |.
CVs considered in binding free-energy calculations
| CV | Description (the ligand with respect to the protein) | Ligand movement mode |
|---|---|---|
| RMSD | RMSD of ligand heavy atoms with respect to its bound-state conformation | Conformational |
| Θ | Roll angle from the bound-state orientation | Orientational |
| Φ | Pitch angle from the bound-state orientation | Orientational |
| Ψ | Yaw angle from the bound-state orientation | Orientational |
| θ | Polar angle in spherical coordinates | Positional |
| φ | Azimuthal angle in spherical coordinates | Positional |
| r | Center-of-mass distance | Positional |
Geometrical route.
In the geometrical route, restraints are introduced one by one to progressively focus the conformational and orientational movements of the ligand with respect to the protein before their complete separation through a rectilinear pathway. The free energy associated with such a transformation of the object at hand can be expressed in terms of the potential of mean force (PMF). The contributions of the various restraints to the binding free energy are estimated via PMF calculations using WTM-eABF15,16, a variant of the adaptive biasing force (ABF) algorithm (Fig. 1a)25. The theoretical underpinnings of the geometrical route are detailed in refs. 18 and 19.
Fig. 1 |. Illustration of the geometrical and alchemical routes.
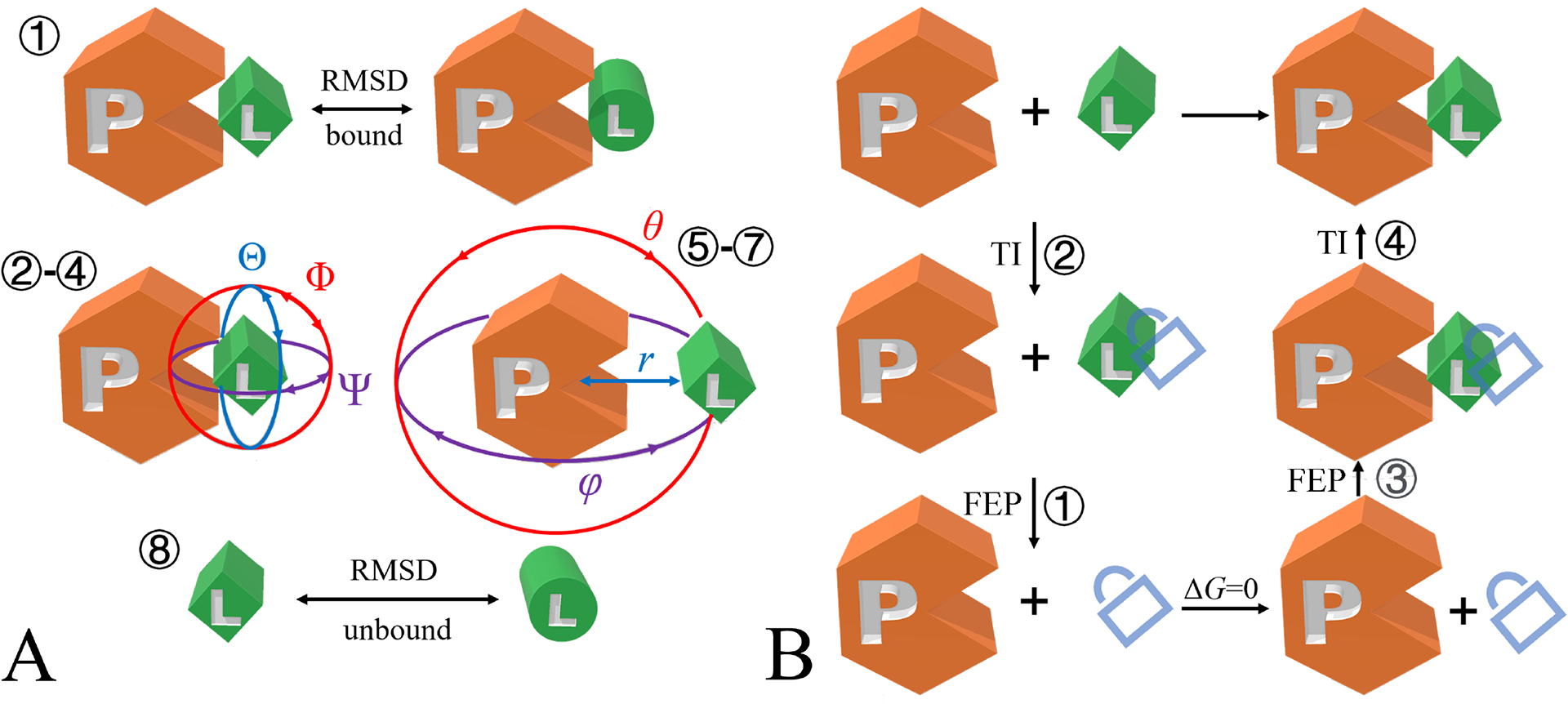
a, geometrical route, b, alchemical route. The numbers indicate the order of free-energy calculations set up using BFEE2. The lock represents the restraints applied to the conformational, orientational and positional degrees of freedom of the ligand with respect to the protein.
Alchemical route.
In the alchemical route, simulations are performed according to the thermodynamic cycle shown in Fig. 1b. The ligand is decoupled reversibly from its environment, i.e., the protein or the bulk, using the so-called alchemical free-energy perturbation (FEP) method, with its position, orientation and conformation restrained to those of the native state26,27. The energetic cost to enforce these restraints is then estimated through thermodynamic integration, zeroing out the associated force constant28,29. To improve the reliability of the free-energy estimates, the simulations are performed bidirectionally for each step depicted in Fig. 1b. The theoretical underpinnings of the alchemical route can be found in ref. 19.
Applications of the methodology
Since the first publication in 1996, our methodology has been applied to many molecular assemblies. For instance, we have accurately evaluated the binding affinity of three flexible decapeptides to the SH3 domain of the Abl kinase19,20. The standard binding free energy of the netropsin-DNA complex, wherein the conformational change of the host molecule is significant, has been determined within chemical accuracy30. We have also employed our methodology blindly in protein engineering and shown that corannulene is more effective than perylene in inhibiting protein activity, which was later confirmed by experiments31. All in all, given the appropriate choice of a route—either geometrical or alchemical, our methodology has proven able to estimate the binding affinity of a large variety of protein:ligand complexes—including, but not limited to rigid and flexible ligands, ligands interred and lying at the surface of the protein, and combination thereof—with suitable accuracy.
Apart from the aforementioned applications, our methodology has been adopted by different research groups32–37. It is noteworthy that an independent benchmarking study has specifically underscored the remarkable reliability of both the geometrical and alchemical routes for the estimation of binding free energies33. Moreover, our methodology has been successfully used in force-field parameterization and validation, which requires very accurate free-energy estimates.38 A selection of success stories of our methodology is given in Table 2.
Table 2 |. Success stories of restraint-based binding free-energy calculations.
Detailed experimental and estimated binding free energies are provided in the Supplementary Information
| Complex | PDB IDa | Error (kcal/mol)b | Remarks | Reference |
|---|---|---|---|---|
| Abl kinase-SH223:p41 | 1BBZ | 0.5c 0.4d |
Large, flexible ligand | 19,20, this work |
| Abl kinase-SH3:p5 | — | 0.1 | Large, flexible ligand | 20 |
| Abl kinase-SH3:p24 | — | 0.3 | Large, flexible ligand | 20 |
| Human p56lck-SH2:pYEEI | 1LKK | ~0.5e | 18 | |
| FKBP12:ligand3 | — | 0.6 | 21 | |
| FKBP12:ligand5 | — | 2.1 | 21 | |
| FKBP12:ligand6 | — | 1.1 | 21 | |
| FKBP12:ligand8 | 1FKG | 0.6 | 21 | |
| FKBP12:ligand9 | 1FKH | 0.5 | 21 | |
| DIAP1-BIR1: Grim peptide | 1SE0 | 0.8 | Large, flexible ligand | 38, this work |
| Trypsin:benzamidine | 3ATL | ~1.1e | Semi-buried ligand | this work |
| HBV Cp:NVR-010–001-E2 | 5E0I | 1.6f | Semi-buried ligand | this work |
| T4 lysozyme L99A:benzene | 4W52 | 0.8 | Buried ligand | 11, this work |
| T4 lysozyme L99A:ethyl benzene | 1NHB | 0.6 | Buried ligand | 11, this work |
| T4 lysozyme L99A:paraxylene | 187L | 0.4 | Buried ligand | 11, this work |
| T4 lysozyme L99A:n-butyl benzene | 186L | 1.0 | Buried ligand | 11, this work |
| human CREBBP-Bromodomain:dihydroquinoxali none | 4NYX | 0.3 | Cation-π interaction dominates | 38 |
| human CREBBP-Bromodomain: isoxazolyl-benzimidazole | 4NR7 | 0.4 | Cation-π interaction dominates | 38 |
| Factor Xa:cation inhibitor | 2JKH | 0.9 | Cation-π interaction dominates | 38 |
| Factor Xa:cation inhibitor | 2Y5H | 1.1 | Cation-π interaction dominates | 38 |
| Factor Xa:cation inhibitor | 2Y5G | 2.1 | Cation-π interaction dominates | 38 |
| Factor Xa:quaternary ammonium | 2BOK | 0.3 | Cation-π interaction dominates | 38 |
| DNA:netropsin | — | 0.5 | Large conformational change of the host | 30 |
| MDM2-p53:NVP-CGM097 | 4ZYF | 0.5 | Semi-buried ligand | this work |
| MUP-I:2-methoxy-3-isopropylpyrazine | 1QY2 | 0.0 | Buried ligand | this work |
| MUP-I:6-hydroxy-6-methyl-3-heptanone | 1I05 | 0.5 | Buried ligand | this work |
| β1-adrenergic receptor:4-methyl-2-(piperazin-1-yl) quinoline | 3ZPR | 1.0 | membrane protein:ligand complex | this work |
| V1-ATPase:ATP (tightly bound) | — | 1.6g | 40 | |
| V1-ATPase:ATP (bound) | — | 1.1g | 40 | |
| V1-ATPase:ATP (empty) | — | 2.0g | 40 | |
| V1-ATPase:ADP+Pi (tightly bound) | — | 2.1g | 40 | |
| V1-ATPase:ADP+Pi (empty) | — | 2.2g | 40 |
”-” means that crystal structure is either not available or not used in the free-energy calculation.
Unsigned errors are provided. If the binding free energy of a complex is recalculated as an example in this study, the error of this calculation is provided.
Alchemical route.
Geometrical route.
Different experimental values are available. The average of them is used to calculate the errors.
Experimental value is not available. Simulation results in Ref. 39 are used as the reference.
The experimental estimates were obtained with F1-ATPase.
Comparison with other methodologies
There is a variety of methodologies designed to estimate the absolute binding free energy of a ligand and a protein. Embodying different schools of thought, they have their own merits and drawbacks, to the extent that there is in general no optimal choice, far superior to the others. Still, selecting the most appropriate methodology to address a specific problem remains of paramount importance.
Free-energy calculations based on an end-point approximation, like molecular mechanics-Poisson-Boltzmann surface area (MM-PBSA)41, only require equilibrium trajectories of the solvated protein:ligand complex and, thus, constitute an attractive option for high-throughput screening. The reliability of MM-PBSA free-energy estimates remains, however, highly uncertain due to the use of an implicit solvent and the inadequacy of the approximation to capture the effects of large conformational changes.
Funnel metadynamics42, as a combination of geometric restraints with the metadynamics technique43, offers a good balance between accuracy and efficiency and is particularly well-suited for the study of rigid ligands lying at the surface of a protein. For flexible or buried ligands—or possibly the combination thereof, one may, however, face convergence issues and difficulty to select an appropriate set of CVs to describe the relative movement of the ligand with respect to the protein. A useful companion guide to funnel metadynamics can be found in ref. 44.
A number of alternate methodologies are inherently similar to the strategy presented in this protocol. For example, DDM13 and the alchemical route can be regarded as variants of each other. Conversely, attach-pull-release37 is akin to the geometrical route, which separates the protein and the ligand by means of a PMF calculation. Confine and release45 uses PMF calculations to account for conformational changes of the protein while performing alchemical FEP to decouple the ligand from the protein. One particular advantage that distinguishes our methodology amid its analogues is the streamlining and automation of the complete free-energy calculation process, from the input generation to the post-treatment, by means of a user-friendly software package, BFEE223.
Standard binding free-energies can be also evaluated through direct simulation of the reversible association using advanced-sampling techniques such as Gaussian accelerated MD46 and replica exchange with solute scaling47. Such approaches do not require a priori knowledge of the native state of a protein:ligand complex and CVs describing the slow degrees of freedom of the reversible association. No simulation strategy relying on spontaneous events, however, can guarantee that the correct binding model can be sampled reversibly within the timescale amenable to MD simulations.
Advantages and limitations of this protocol
Advantages
Theoretically rigorous. Some approaches introduce various approximation to trade accuracy for efficiency, just like MM-PBSA41. We guarantee that our methodology, which builds upon a theoretical framework introduced in 200518, is formally rigorous, to the extent that free-energy calculations following this protocol are expected to converge within force-field accuracy.
Available for a wide range of protein:ligand and host-guest complexes because their nature, namely globular versus membrane protein, buried versus semi-buried ligand and ligand lying at the surface of the protein, rigid versus flexible ligand, is taken into consideration in our methodology and software.
Able to circumvent the difficulty of sampling configurational space. In our methodology, either one-dimensional PMF calculations or alchemical transformations are performed, with a reduced configurational space to sample by virtue of the introduction of geometric restraints. This methodology avoids the dimensionality issue in multidimensional free-energy calculations and obviates the need to capture the large change in protein:ligand configuration by means of advanced-sampling simulations.
Minimal human intervention. Our implementation of the methodology in a user-friendly software, BFEE2, streamlines the overall standard binding free-energy calculation. From the definition of the CVs, the preparation of the different input files, to the post-treatment of the simulations, each step is automated in BFEE2, hence minimizing human intervention. Still, monitoring the trajectories and tuning up the simulation parameters as a function of the protein:ligand complex at hand, e.g., simulation length, is advisable.
Easy assessment of convergence. Convergence of the PMF calculations, or of the alchemical transformations, can be directly assessed through GUI-based tools.
Robustness and reproducibility of results. Since the definition of the CVs (Table 1) and free-energy calculations (Fig. 1) are both standardized19,20, the protocol will yield the same binding affinity for a given protein:ligand complex in replicated simulations.
Limitations
Force-field dependence. The overall accuracy—as opposed to the statistical precision25,48—of binding free-energy calculations rests upon the quality of the force field utilized, as our methodology is based on MD simulations. The end-user is, therefore, strongly suggested to have some level of expertise in the selection and validation of force fields, especially for drug-like molecules. This force-field dependence exists in all MD-based methodologies aimed at estimating binding affinities. To make this protocol self-contained, we explain hereafter how to set up molecular assemblies using the CHARMM49 and Amber50 force fields. It should be made very clear that our method itself is rigorously formulated, independently of the force field, as opposed to approximate schemes like MM/PBSA, and hence, the users can improve the reliability of the standard binding free-energy calculation by turning to a more accurate model (e.g., polarizable force fields such as Drude51 and AMOEBA52) if necessary.
Extremely deeply buried ligands. Our methodology can be employed to determine the binding affinity of ligands buried in a protein. For deeply buried ligands, however, capturing the solvent reorganization, that is water entering and exiting the binding site as the substrate is decoupled reversibly from it, requires extensive simulation times, which might induce convergence issues in the free-energy calculations. In some cases, this issue can be circumvented by treating some water molecules as part of the protein or the ligand. Under the premise that the exchange of water inside and outside the binding site is essential, MD experts may want to turn to advanced-sampling techniques, such as REST247,53 or Monte-Carlo based methods54,55, combined with FEP to address this issue. These approaches are, however, not yet proposed in BFEE2, and the users must modify manually the inputs generated by the software.
Ligands with significant conformational variability between the bound and the unbound state. In many instances, the bound- and unbound-state conformations of the ligand may be different. In the workflow presented below, the RMSD with respect to the bound-state conformation is used as a CV to characterize the conformational change of the ligand. Although this choice is anticipated to be reasonable for most drug-like molecules, the conformation of some ligands, such as those with ribose ring puckering, may not be sensitive to the change of the RMSD with respect to its bound-state conformation. Under such circumstances, the experienced end-user may want to change the default definition of the RMSD to another CV that can characterize the isomerization of the ligand, adapting the relevant configurational files generated by BFEE2. Still, the examples presented below are indicative that the use of the RMSD with respect to the bound-state conformation is sufficient to describe the conformational change of ligands as flexible as a heptapeptide (DIAP1-BIR1:Grim peptide) and proline-rich decapeptides (Abl kinase-SH3:p41/p5/p24).
Computational cost. Our methodology is by and large more expensive than those based on end-point approximations, which is the price to guarantee reliability of the free-energy estimates. Typically, a timescale of a few microseconds, possibly a few hundreds of nanoseconds, is sufficient to determine the binding affinity of a protein:ligand complex with the desired accuracy. In practice, with the development of GPU-based architectures and GPU-accelerated MD engines, microsecond simulations are now routinely performed in the field of drug design. Furthermore, it is worth noting that some of the subprocesses (Fig. 1) in our methodology can be performed in parallel, thereby taking advantage of multi-GPU machines to reduce the total wall-clock time devoted to free-energy calculations. It should be clarified that a priori estimation of the computational time needed to overcome possible bottlenecks, or kinetic traps, such as conformational rearrangements in the binding pocket, is not always possible. Hence, additional computational effort may be sometimes required to guarantee suitable convergence of the simulations.
Other points
Requirement of the native binding motif. It is difficult to ascertain how resilient the methodology is to an assumed initial binding pose. Since the free-energy method rests on configurational sampling, in principle, this procedure by itself has the ability to explore the configurations in the neighborhood of the assumed pose. Simulations may either lead to an improved binding pose or lead to a completely different one. If the assumed initial pose is very inaccurate, the outcome is more uncertain. However, any alternative simulation strategy that does not rely on prior knowledge of the native binding pose implicitly assumes that it has the ability to discover the latter from scratch, which represents a significant computational effort of its own. In practice, we believe that a sufficiently accurate approximation of the native state can be obtained at a reduced computational cost by means of molecular docking when no experimentally determined structure is available.
Overview
In this protocol, we first introduce both the geometrical and alchemical routes for the calculation of the standard binding free energy of a flexible ligand, p41, to the SH3 domain of tyrosine kinase Abl19 using NAMD as our MD engine. To demonstrate the performance of our methodology when applied to different classes of protein:ligand complexes, we provide the following additional examples: (i) DIAP1-BIR1:Grim peptide, illustrating the use of Gromacs as the MD engine (Box 2), (ii) trypsin:benzamidine, the application of the geometrical route to a semi-buried ligand (Box 3), (iii) β1-adrenergic receptor:4-methyl-2-(piperazin-1-yl) quinoline, the study of a membrane protein (Box 4), and (iv) Factor Xa:quaternary ammonium, analyzing the driving force underlying the protein:ligand association (Box 5).
Box 2 |. Use BFEE2 with Gromacs.
Apart from NAMD, BFEE2 supports binding free-energy calculations through the geometrical route using Gromacs60, and is, therefore, compliant with different schools of thought for the determination of protein-ligand binding affinities. Some steps in the preparation of the required input files have to be carried out manually, however, since third-party software, such as VMD and MDAnalysis cannot directly generate files in the desired Gromacs format.
Procedure ● Timing depending on the available computational resources
Compile Gromacs with the Colvars support; see the Supplementary Information for more details.
Open the BFEE2 plug-in. Switch to the “Pre-treatment→Gromacs” tab. Load the topology (TOP) and structure (PDB) files of the solvated complex and ligand, respectively.
Set the temperature of the simulation and define the protein and ligand moieties (following the MDAnalysis syntax).
-
Perform the following simulations sequentially. Each job must be submitted manually only after the previous one is completed.
000_eq/000_eq.mdp 001_RMSD_bound/001_PMF.mdp 002_euler_theta/002_PMF.mdp 003_euler_phi/003_PMF.mdp 004_euler_psi/004_PMF.mdp 005_polar_theta/005_PMF.mdp 006_polar_phi/006_PMF.mdp 007_r/007_Minimize.mdp 007_r/007_Equilibration.mdp 007_r/007_PMF.mdp 008_RMSD_unbound/008_Equilibration.mdp 008_RMSD_unbound/008_PMF.mdp
Note that the definition of centers for the restraints declared in the *.in files must be revised after the PMF calculation over an angle, Euler or spherical-coordinate, is completed. See steps (7–12) of Procedure 1 for the detail of setting the centers keyword and understanding each step. Compilation of the configuration file is required before running a simulation using Gromacs. We have automated the compilation and update of centers by making shell (*.sh) scripts available to the end-user. If a stratification strategy is used, however, the end-user is invited to update the input files manually.
Perform the post-treatment corresponding to steps (15–17) of Procedure 1. Note that the force constants ought to be set to the corresponding values in the *_colvars.dat files, as the unit used internally by Gromacs is different from that used by NAMD.
We have provided examples of input files (PDB ID: 1SE0 and 1BBZ) for Gromacs in the Supplementary Data to be tested by the end-user.
Box 3 |. Handling a semi-buried ligand through BFEE2.
As explained in the main text, the default direction along which the ligand is separated reversibly from the protein is the vector connecting their respective centers of mass. If the ligand is semi-buried, the end-user may want to choose another direction to separate the two partners. We want to emphasize here that this treatment is only useful for the geometrical route—the alchemical route can be adopted without any specific setting, irrespective of the ligand being buried or not.
Procedure ● Timing depending on the available computational resources
Open the structure file of the protein:ligand complex (PDB) with VMD. Observe the structure of the complex and find a possible path along which the barrier of separating the ligand from the protein is minimal. Then, define the path as the line connecting the center of mass of a manually chosen moiety and that of the ligand. This step is critical, and does directly affect the convergence of the binding free-energy calculation.
Follow steps (1–4) of Procedure 1. [AU: Is this correct? If not, please clarify which steps you are referring to here.]
Define the moiety chosen above as the reference by setting “User-defined separation direction→ Reference” (following the MDAnalysis syntax) in the “Advanced settings” menu.
Follow steps (6–12) and (15–17) of Procedure 1.
The end-user is required to monitor the trajectory of the simulation characterizing the separation of the ligand from the protein to ensure that the selected path is appropriate. A suboptimal path may lead to fraying—possibly partial denaturation of the protein in the course of separation. To reduce the trial-and-error overhead, the user can run 007_r/007.1_eq.conf and 007_r/007.2_abf_1.conf and examine the selected path upstream from the formal standard binding free-energy calculation.
Box 4 |. Handling a membrane-protein:ligand complex through BFEE2.
BFEE2 can be used to calculate the standard binding affinity of a ligand towards a membrane protein. If the geometrical route is adopted, the end-user should ascertain that the ligand is appropriately separated from both the protein and its membrane environment by selecting a suitable direction of the translation of the ligand. Should this requirement be overly difficult to satisfy, the alchemical route is preferred. Such is the case of ligand deeply buried in the binding pocket of the membrane protein, e.g., in a G protein-coupled receptor.
Procedure ● Timing depending on the available computational resources
During modeling, ensure that the membrane is perpendicular to the z axis to comply with the flexibleCell option of NAMD.
Select either the geometrical (Procedure 1)or the alchemical (Procedure 2)route. Follow steps (2–4) of the corresponding procedure.
Check “Model→Membrane Protein” in the “Advanced settings” menu. If necessary, define an appropriate separation direction by setting “User-defined separation direction→Reference”,the membrane is perpendicular as detailed in Box 3.
Perform a very long equilibration to ensure proper contact of the lipids with the membrane protein, and proper hydration of the protein’s soluble parts, which can be achieved by manually increasing the simulation time in 000_eq/000_eq.conf and 007_r/007.1_eq.conf (geometrical route) or 000_eq/000.1_eq.conf and 000_eq/000.2_eq_ligandOnly.conf (alchemical route).[AU: Please specify at which step of each corresponding procedure.]
Complete the free-energy calculation by following the remaining steps detailed in Procedure 1 or 2.
We want to emphasize that thorough exploration of the hydration state of the binding site is challenging, as the exchange of water molecules inside and outside the membrane protein is slow. One can equilibrate the membrane protein and its environment without the ligand, allowing water to diffuse inside the protein as a preamble to the PMF calculations—or alchemical transformations, should it prove necessary. During the free-energy calculation, sampling in each window should be sufficient to allow the reversible hydration of the ligand and its binding site to be captured. More elaborate techniques, relying, for instance, on grand-canonical MD, fall beyond the scope of the present contribution54,55,62.
Box 5 |. Analyzing the enthalpic driving force underlying the protein:ligand association.
The pair-interaction calculation feature available in NAMD can be utilized to estimate the interaction energy and forces between any two moieties of the computational assay over an MD trajectory. The enthalpic driving force underlying protein:ligand association can, therefore, be analyzed with exquisite detail in this post-hoc treatment of the trajectory describing the separation of the ligand from the protein. This feature is only available when the geometrical route is followed, as no geometric pathway is determined in the alchemical route.
Procedure ● Timing depending on the available computational resources
Generate all the input files for a binding free-energy calculation following the geometrical route, as documented in Procedure 1.
Reduce the value of dcdFreq in 007_r/abf_*.conf and set colvarsTrajFrequency in colvars_*.in to that of dcdFreq. This step makes NAMD write the trajectory file more frequently than the default, as the trajectory will be used subsequently for analysis purposes. The choice of an appropriate value of dcdFreq is subservient to the available disk space. A dcdFreq of 500 may be acceptable in many cases.
Complete the free-energy calculation following steps XX-YY introduced in Procedure 1[AU: Please specify exact steps here.].
Prepare a PDB file, indicating the interaction of which two moieties will be calculated by setting the beta value of the two moieties as 1 and 2, respectively. If the self-interaction energies of a moiety are required, set the beta value of the moiety as 1.
An example of the configuration file of pair-interaction calculation is provided in the Supplementary Information. Run the pair-interaction calculation just like a standard NAMD job. It ought to be noted that to this date GPU acceleration is not supported for this task. A CPU version of NAMD is required.
The van der Waals and electrostatic interaction energies and forces between the two selected moieties are written for each frame of the trajectory in the NAMD output (log) file. The corresponding value of the CV, i.e., protein:ligand center-of-mass distance, r, for each frame can be found in the output/*.colvars.traj. Hence, the user can calculate the average interaction energy and force between the two selected moieties in each bin. The end-user can then either get the contribution to the PMF of the interaction of the two moieties by integration of the force along the CV, or analyze the pair-interaction energy profile directly. Some smoothing is sometimes necessary to remove the noise in the obtained profiles due to lack of data in the saved trajectories.
Repeat steps (4–6) for any interesting moiety pairs.
An example of the analysis of the enthalpic driving force underlying protein:ligand association is provided in Fig. 11 (PDB ID: 2BOK). In this case, the association of the protein and the ligand, promoted by a cation-π interaction, is hindered by the desolvation of a quaternary ammonium, as the latter is highly hydrophilic. In stark contrast, the protein:water interaction is favorable for association, as the aromatic moieties of the protein are shielded from the solvent. Interestingly enough, when the ligand is very close to the protein, the protein:water interaction becomes unfavorable, as the charged quaternary ammonium perturbs the network of hydrogen bonds formed between the protein and the water. The balance of the aforementioned contributions determines the optimal distance separating the protein from the ligand in the bound state.
Estimating protein:ligand standard binding free energies using our methodology includes four stages, irrespective of the chosen route, namely,
Modeling. This stage consists in preparing the structure and topology files readable by MD engines, which can be carried out by modeling tools such as CHARMM-GUI56 and AmberTools57.
Input files generation. This sub-step consists in preparing all the configurational files for the multistep free-energy calculation, automated in BFEE2.
Simulation. This stage consists in carrying out the different MD simulations. This stage requires human intervention to monitor the convergence of the latter, and, if need be, tune up selected parameters. Molecular visualization software, like VMD24, is required to visualize the trajectory. Part of the convergence analysis is available in the latest version of BFEE2 and in ParseFEP58.
Post-treatment. This stage consists in calculating the binding affinity based on the output files generated in the different MD simulations. Bookkeeping and evaluation of the different configurational integrals are handled by BFEE2.
For first-time users of BFEE2, the additional step of software installation is evidently required, as detailed in the Materials section. After installation, we suggest that the end-user starts learning from the Abl-SH3:p41 illustration to grasp the gist of the methodology, focusing specifically on the “Simulation” stage, which requires the greatest human intervention and expertise. Each example mentioned in this protocol, other than Abl-SH3:p41, highlights a specificity that ought to be paid attention to in practice. We also provide a lookup table to troubleshoot possible issues encountered while applying this protocol.
Expertise needed to complete the protocol
The end-user is expected to know how to run MD simulations using either NAMD59 or Gromacs60. Moreover, some experience of CV-based free-energy calculations using Colvars29 is desirable, though not mandatory. Complete knowledge of the structural detail to define the slow degrees of freedom underlying the reversible association of the protein:ligand complex is in principle not necessary, but the end-user is expected to know the experimental conditions of the three-dimensional structure determination, that is the ionic strength and pH, which are crucial for setting the correct protonation state of the protein and of the ligand and carrying out the simulations with the appropriate salinity.
Experimental design
The workflow of our methodology is shown in Fig. 2 and explained below.
Fig. 2 |. Workflow of our methodology.
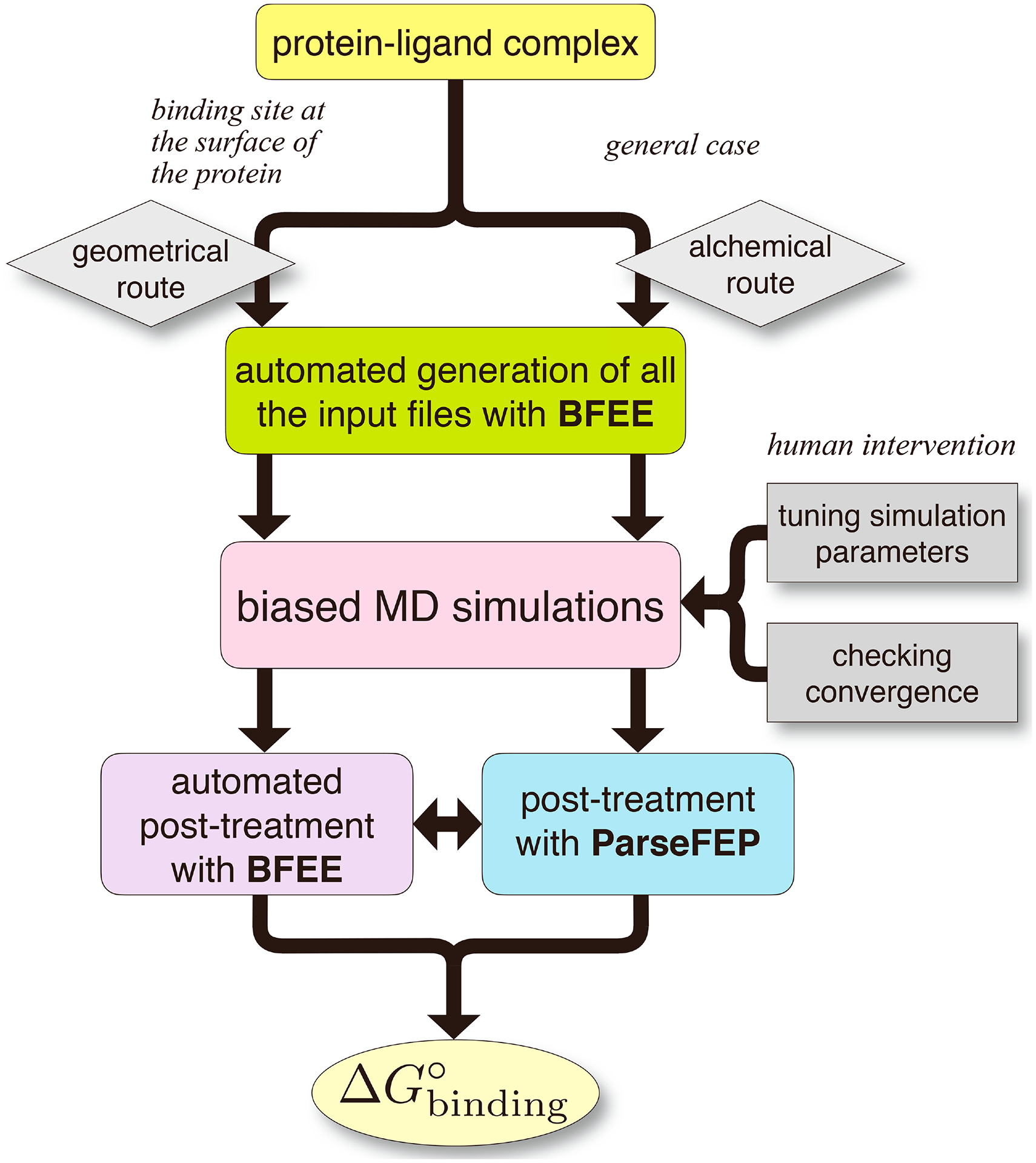
The light-yellow box represents the ‘Modeling’ stage (Procedures 1 and 2, Step 1); the green box, the ‘Input files generation’ stage (Procedure 1, Steps 2–6 and Procedure 2, Steps 1–3); the pink box, the ‘Simulation’ stage (Procedure 1, Steps 7–12 and Procedure 2, Steps 4 and 5); and the purple and cyan boxes, the ‘Post-treatments’ stage (Procedure 1, Steps 13–15 and Procedure 2, Steps 6–8).
Modeling.
The end-user is required to generate structure and topology files readable for MD engines, starting ordinarily from a PDB ID, should there be an experimentally determined three-dimensional structure available, or from a PDB-formatted file obtained using molecular docking. Although we provide an introduction on the use of CHARMM-GUI56, a web-based server, for setting up simulations involving protein:ligand complexes (step 1), discussing the detail of the molecular-modeling stage prefacing the determination of the binding affinity falls beyond the scope of this protocol.
Input-file generation.
In this stage, all the configurational files required for a complete binding free-energy calculation are generated using BFEE2. At this stage, the end-user must determine whether the geometrical or alchemical route will be followed. Whereas the former is only germane to complexes in which the ligand lies at the surface of the protein, the latter is suited to any protein:ligand complex. We provide in this protocol examples for both routes (steps 2–6).
Although the generation of input files is almost completely automated in BFEE2, given that the appropriate route is selected as a function of the nature of the protein:ligand complex at hand, the end-user may find it necessary to tune some parameters, most notably the simulation length and whether or not a stratification strategy25 ought to be used, which requires some prior experience with MD simulations. To give the non-expert an idea of how to tune simulation parameters, we detail the simulation times and stratification strategies for all the examples reported in this protocol and rationalize these settings (Procedure 1 and 2, step 5).
Simulations.
All the simulations are carried out in this stage. It is important that the MD engine, either NAMD or Gromacs, be patched with the latest version of the Colvars module (Materials section). It is noteworthy that the end-user has the burden of assessing convergence of the different free-energy calculations with the help of BFEE2 and any other graphical-interface-based tool like ParseFEP58 (Procedure 1, steps 7–12 and Procedure 2, steps 4 and 5).
Post-treatments.
All the post-treatments—bookkeeping of the free-energy calculations and evaluation of the configurational integrals—can be performed automatically using BFEE2, without any human intervention (Procedure 1, steps 13–15 and Procedure 2, steps 6–8). In addition to the standard binding free-energy calculation, we provide guidelines to analyze the interaction of the partners at play—or moieties thereof—to identify the driving forces that underlie molecular association (Box 6).
Box 6 |. Analyzing alchemical free-energy calculations using ParseFEP.
ParseFEP is a powerful tool for the analysis of FEP calculations. It can be used to improve the reliability of the free-energy estimate and detect possible convergence issues in FEP calculations. The use of ParseFEP as a post-hoc tool is, therefore, highly recommended in the standard binding free-energy calculation that follows an alchemical route. Note that ParseFEP only supports Linux and MacOS operating systems, wherein XMGrace can be installed58.
Procedure ● Timing 20 min
Complete the binding free-energy calculation following the procedure introduced in the main text.
Open ParseFEP through “VMD→Extensions→Analysis→Analyze FEP simulation”.
Load fep_forward.fepout and fep_backward.fepout into ParseFEP. Set parameters, as detailed in https://www.ks.uiuc.edu/Research/vmd/plugins/parsefep/. We suggest using the Bennett-acceptance ratio (BAR) estimator67.
Click “Run FEP parsing” and wait for the computation to complete in the background. The free-energy estimate and statistical error will be displayed in the VMD terminal.
It is noteworthy that ParseFEP will output a series of figures (Fig. 10). For the probability distributions of the perturbation, ΔU, from a bidirectional calculation, the end-user is recommended to ascertain that the forward and the backward simulations sample a similar configurational space, mirroring the microstate-reversibility of the transformation at hand. The end-user can also monitor the evolution of the free-energy estimates in each window to verify the convergence of the bidirectional transformation65.
Materials
Example data
The structure files of the protein:ligand complexes examined in this protocol are accessible in the Protein Data Bank (www.rcsb.org) using a PDB ID or obtained from the Supplementary Data.
Output files from the geometrical and alchemical routes (Supplementary Data).
Hardware and software
In principle, any computer can be used to run the simulations. However, a Linux-based computer with at least one discrete graphics card is recommended for the “Simulation” stage, considering the computational cost and software compatibility. For the other stages, computers running Windows, Linux, or Mac OS are appropriate.
NAMD (www.ks.uiuc.edu/Research/namd) or Gromacs (www.gromacs.org) patched with Colvars (colvars.github.io)
BFEE2 (github.com/fhh2626/BFEE2)
The installation guidelines of these pieces of software are provided in the Supplementary Information.
Procedure 1: The geometric route
CRITICAL We assume here that NAMD is the MD workhorse. The reader is referred to Box 2 to learn the use of Gromacs.
Modeling
-
1
Generate the topology and coordinate files readable by the MD engines. Detail of the procedure using CHARMM-GUI is provided in the Supplementary Information (see also the tutorials for the CHARMM, AmberTools and Gromacs environments).
Input-file generation
-
2Open BFEE by typing
BFEE2Gui.py
in the terminal (Linux and Mac OS environment), or PowerShell (Windows environment). Optionally, one can link BFEE2 with VMD through File→Settings. If BFEE2 is not linked with VMD, some input files, e.g., the structure file of the extended water box, cannot be generated automatically. Under these premises, scripts will be generated automatically and can be run manually within VMD to create all the necessary files for the binding free-energy calculation.? TROUBLESHOOTING
-
3
Set the path to the topology (PSF or PARM) and the structure (PDB or RST) files. If the CHARMM force field is used, the path to the CHARMM force field files (PRM or STR) is also required. For the Abl-SH3:p41 example, the relative paths to the topology and the structure files are workflow/complex.psf and workflow/complex.pdb, respectively. The relative paths to the force-field files are workflow/par_all36m_prot.prm and workflow/toppar_water_ions.prm.
! CAUTION The non-bonded fix (NBFIX) terms of the CHARMM general force field for organic molecules (par_all36_cgenff.prm) rely on the definition of atom types in other force-field files. Either include par_all36m_prot.prm, par_all36_na.prm and par_all36_carb.prm whenever par_all36_cgenff.prm is required, or remove the unnecessary NBFIX terms in par_all36_cgenff.prm manually to satisfy the dependency.
-
4
Set the temperature of the simulation and define the protein and ligand moieties (following the MDAnalysis syntax, as documented in docs.mdanalysis.org/stable/documentation_pages/selections.html). In the Abl-SH3:p41 example, enter 300, segid SH3D and segid PPRO, respectively.
! CAUTION If the CHARMM force field is utilized, it is convenient to make the selection with the keyword segid. Conversely, if the Amber force field is utilized, resid ought to be preferred because Amber PARM files do not have segment information.
-
5Optionally, set the parameters of the “Advanced settings” menu. A short description of these parameters is presented hereafter.
- User-defined Separation direction→Reference. By default, the separation of the ligand from the protein proceeds along the direction of the vector connecting the centers of mass. By defining an additional object as the reference (following the MDAnalysis syntax), the separation is along the direction of the line connecting the centers of mass of the ligand and the reference. This option is useful for handing semi-buried ligands using the geometrical route (see also Box 3).
- User-defined large box. By default, when the CHARMM force field is utilized, BFEE2 automatically expands the TIP3P water box of the molecular assembly to dimensions germane for the separation of the ligand from the protein. If the simulation is to be performed in a non-aqueous environment, if a water model different from the standard TIP3P model is utilized, or if the Amber force field is chosen in lieu of the CHARMM force field, the end-user is mandated to provide the molecular assembly with the relevant solvent box of suitable dimensions.
- Stratification. This option specifies whether the reaction path is decomposed into strata or windows. A value larger than 1 indicates the use of a stratification strategy. For example, for step 2, exploring the Euler angle Θ ranging from −10 to 10 degrees, Stratification set to 2 indicates two separate simulations whereby Θ∈[−10, 0] and Θ∈[0, 10].
- Compatibility→Pinning down the protein. This option ensures that the protein remains at the center of the simulation box through adding restraints. By default, the Euler and spherical-coordinate (polar and azimuthal) angles are defined relying on the “Orientation (quaternion)” CV in the Colvars module. Under these premises, enforcement of roto-translational restraints is required to avoid a net angular acceleration of the protein-ligand complex.
- Compatibility→Use quaternion-based CVs. The default definitions of Euler and spherical-coordinate angles rely on the “Orientation (quaternion)” CV in the Colvars module (supported by NAMD 2.13 and later), requiring pinning down the protein, as discussed above. If this option is unchecked, a new, hard-coded definition of Euler and spherical-coordinate angles is utilized (supported by the git version of NAMD patched with the git version of Colvars), which circumvents the requirement of pinning down the protein, as a torque is added internally to the protein to prevent it from tumbling and drifting. We, nevertheless, recommend that the quaternion-based definition of the angles be utilized, as it has been thoroughly tested, and it is fully compatible with the recent official releases of NAMD.
- Model→Membrane Protein. If this option is checked, BFEE2 will assume that the molecular assembly contains a membrane protein. Semi-isotropic pressure coupling will be adopted, and, for the unbound-state simulations, the ligand will be re-solvated and re-neutralized (see also Box 4). At present, this option is only available when the CHARMM force field is used.
- Parallel runs. We recommend estimating the error associated with a binding free-energy calculation through the geometrical route by running in parallel independent simulations with distinct random-number-generator seeds and computing the standard deviation over the different results obtained. This option determines how many independent simulations are carried out in parallel.
▲ Critical Step Stratification subsumes a set of parameters crucial for the convergence rate of the free-energy calculations at hand. Within the geometric route, the PMF calculations handling the separation of the ligand from the protein may require three to five windows, or strata, whereas those describing the conformational change of the ligand, either in the bound or in the unbound state, may require one to five windows, depending on the flexibility of the substrate. In the Abl-SH3:p41 example, (3, 1, 1, 1, 1, 1, 5, 3) is a good choice for the number of windows for each step of the geometrical route.
-
6
Click on the “Generate Inputs” button and choose the directory where all the input files will be located. Fig. 3 shows the recommended settings for the geometrical route in the case of the Abl-SH3:p41 example.
Fig. 3 |. Settings for the generation of inputs for the Abl-SH3:p41 case example following the geometrical route.
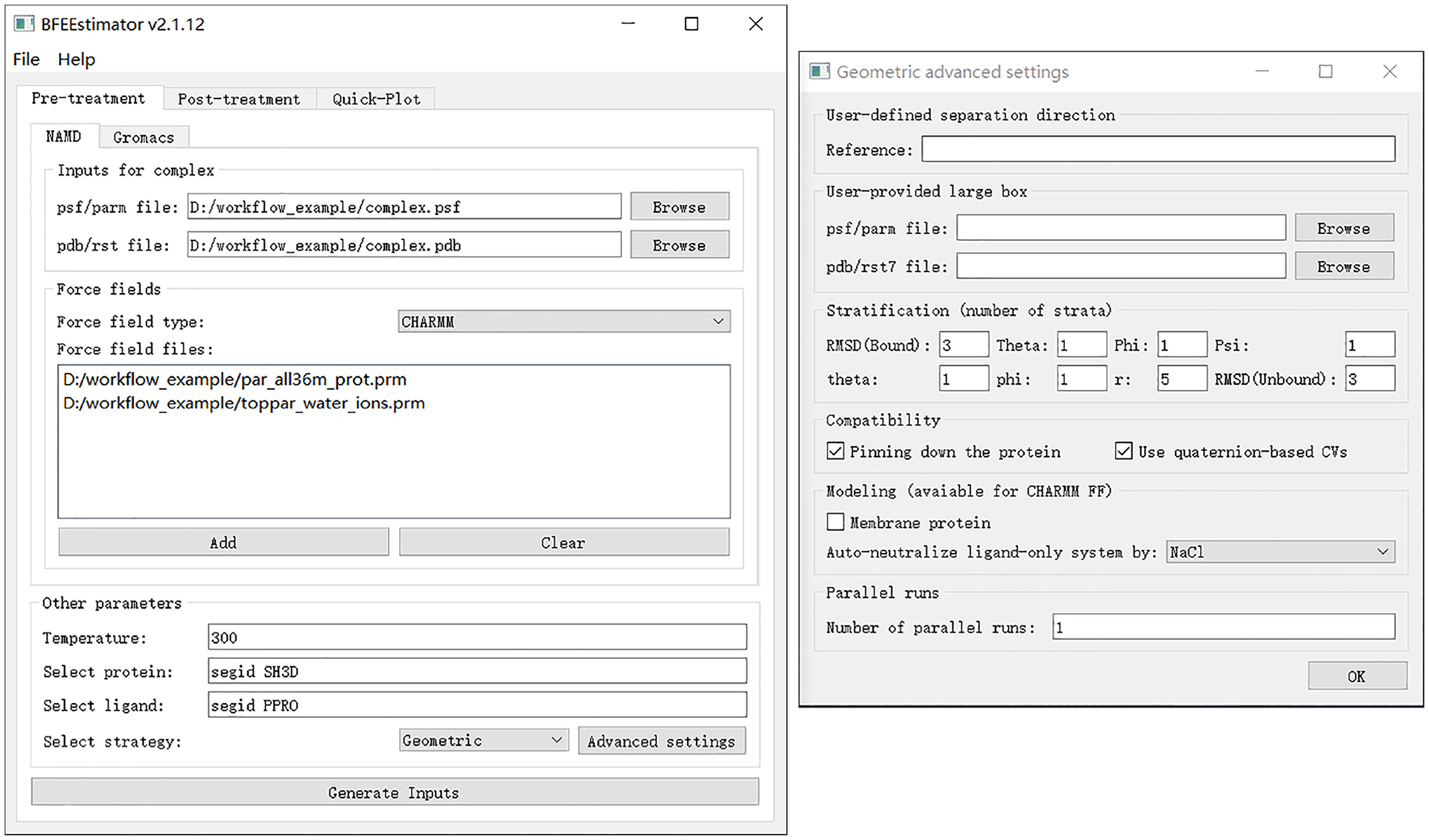
Left, main window of BFEE2; right, advanced settings. Figures 3 and 4 show the BFEE2 interface under Windows 10.
Simulation
-
7Equilibrate the molecular assembly by executing
cd 000_eq namd2 +p8 +idlepoll +devices 0 000_eq.conf > 000_eq.log &
in terminal (Linux and Mac OS) or PowerShell (Windows). +p8 means that eight CPU cores will be used, and +idlepoll +devices 0 indicates that the simulation will be run on GPU 0. The end-user can modify these parameters depending on the available computational resources.? TROUBLESHOOTING
-
8Perform the free-energy calculations dealing with the conformational change of the ligand in the bound state by executing
cd 001_RMSDBound namd2 +p8 +idlepoll +devices 0 001_abf_1.conf > 001_abf_1.log &
If the transformation is stratified, the simulations of the different windows can be performed in parallel. It must be noted, however, that the restart files of window i, which are generated shortly after starting the simulation, are required as the starting point of window i+1. We suggest monitoring the value of the CV in output/001_abf_i.colvars.traj to ensure that it is appropriate for window i+1.
▲ Critical Step The user needs to ascertain that the simulation is suitably converged (Fig. 4). If not, extend the simulation by using, e.g., 001_abf_1.extend.conf, with an appropriate simulation time. We suggest running at least (100, 10, 10, 10, 10, 10, 200, 100) nanoseconds for each step of the Abl-SH3:p41 example. These simulation times are merely indicative, and ought to be adjusted as a function of the nature of the protein:ligand complex.
? TROUBLESHOOTING
-
9Perform the free-energy calculations characterizing the change of Euler angle Θ by executing
cd 002_EulerTheta namd2 +p8 +idlepoll +devices 0 002_abf_1.conf > 002_abf_1.log &
Similar to the previous step, ascertain that the simulation is converged by setting an adequate simulation time. In the geometrical route, the change in the three Euler angles in the PMF calculations does not induce any significant variation of the polar and azimuthal angles, but the opposite is not true. Euler angles must, therefore, be handled prior to the polar and azimuthal angles. There is, however, no particular order for the treatment of the three Euler angles.
? TROUBLESHOOTING
-
10
Let us suppose that the value of Θ corresponding to ΔG=0 is −2° in 002_EulerTheta/output/abf_1.abf1.czar.pmf—or, alternatively, in the file where the different contributions of a stratified free-energy calculation are merged. In the latter case, select the “Merge PMFs” option in the “Quick-plot” tab to see the complete PMF.
Then open 003_EulerPhi/colvars_1.in, and change,harmonic { colvars eulerTheta forceConstant 0.1 centers 0.0 }toharmonic { colvars eulerTheta forceConstant 0.1 centers −2.0 }to guarantee an optimal value for Θ when handing the other CVs.Next, perform the free-energy calculation characterizing the change of Euler angle Φ by executingcd 003_EulerPhi namd2 +p8 +idlepoll +devices 0 003_abf_1.conf > 003_abf_1.log &
? TROUBLESHOOTING
-
11Run the following simulations sequentially, which characterizes, respectively, the changes in Euler angle Ψ and in spherical-coordinate angles θ and φ, the equilibration of the protein:ligand in an extended water box and the separation of the ligand from the protein, namely
004_EulerPsi/004_abf_1.conf 005_PolerTheta/005_abf_1.conf 006_PolerPhi/006_abf_1.conf 007_r/007.1_eq.conf 007_r/007.2_abf_1.conf
! CAUTION Similar to step 10, prior to the simulations, revise the definition of centers for the restraints declared in the *.in files.
? TROUBLESHOOTING
-
12Equilibrate the ligand-only computational assay and perform the PMF calculation describing the conformational change of the substrate in bulk water by running the following simulations sequentially,
008_RMSDUnbound/008.1_eq.conf 008_RMSDUnbound/008.2_abf_1.conf
Then go to step (13).
▲ Critical Step The simulations corresponding to 001_RMSDBound and 008_RMSDUnbound are independent and can, therefore, be performed in parallel, or concurrently, while those corresponding to 002_EulerTheta through 007_r ought to be carried out in a sequential order, due to the need of updating the value of the harmonic-restraint centers.
? TROUBLESHOOTING
Fig. 4 |. Monitoring the convergence of a PMF calculation.
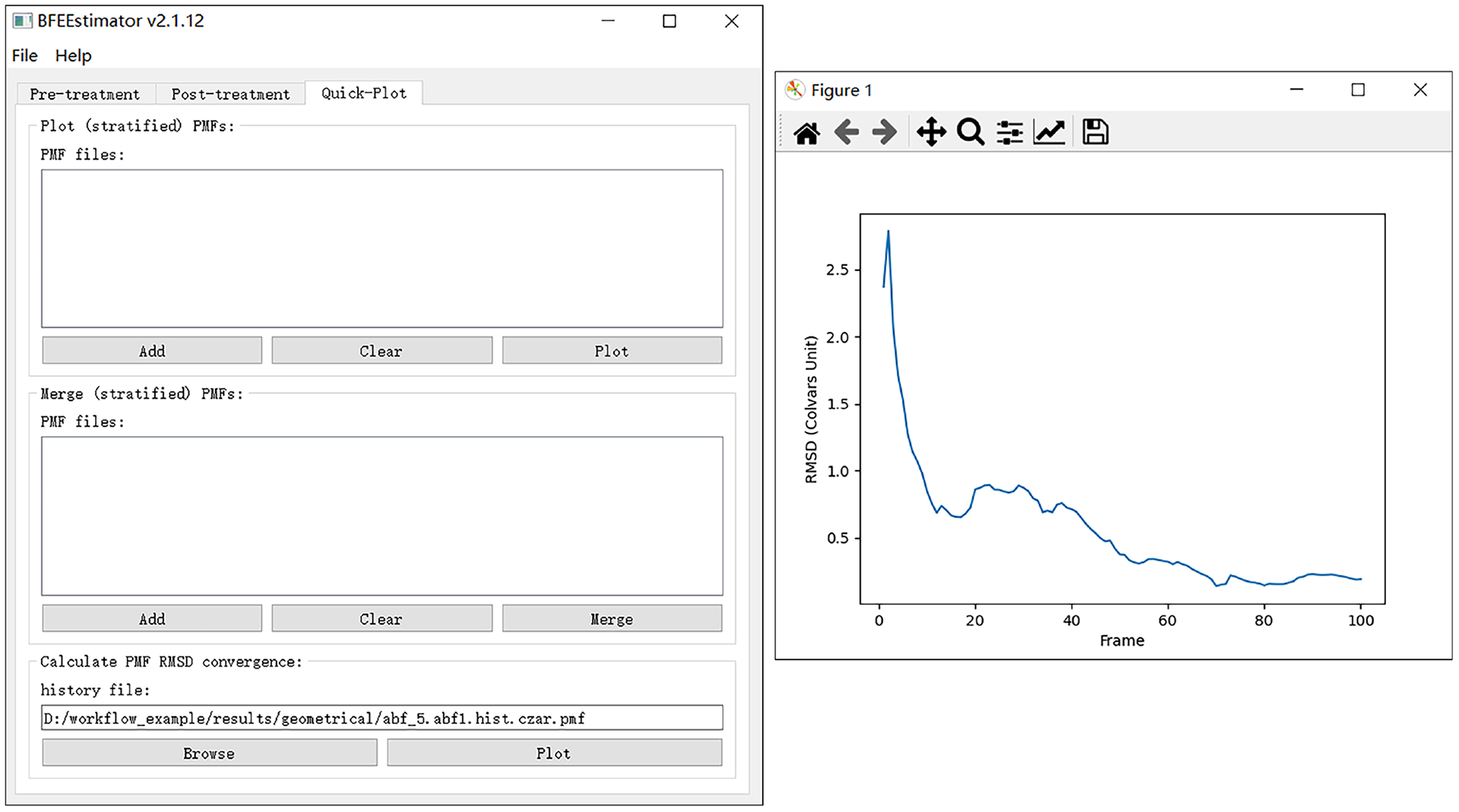
An approximate plateau of the time-evolution of the PMF root-mean-square deviation (RMSD) with respect to its initial value usually is suggestive of a satisfactory convergence. Note that some minor fluctuations of the time-evolution curve are common and can usually be ignored.
Post-treatment
-
13
Open the BFEE2 window and switch to the “Post-treatment→Geometric” tab. Then load the PMF files of each step.
-
14Set the force constants of CVs. The value of these force constants corresponds to, for example, the forceConstant option in the following block.
harmonic { colvars eulerTheta forceConstant 0.1 centers 0.0 }If the forceConstant options in *.in files are not changed manually during the multistep free-energy calculation, the default force constants provided in the “Post-treatment” tab of BFEE2 GUI can be directly adopted.
-
15
Set the temperature of simulations and r* of the integration. The choice of r* should not affect the result of the free-energy calculation, as long as it is sufficiently large (i.e., the PMF curve of 007_r is flat for r > r*). Then click on the “Calculate binding free energy” button. Fig. 5 shows how to do post-treatment of the geometrical route for the Abl-SH3:p41 example.
Fig. 5 |. Settings for the post-treatment of the Abl-SH3:p41 example following the geometrical route.
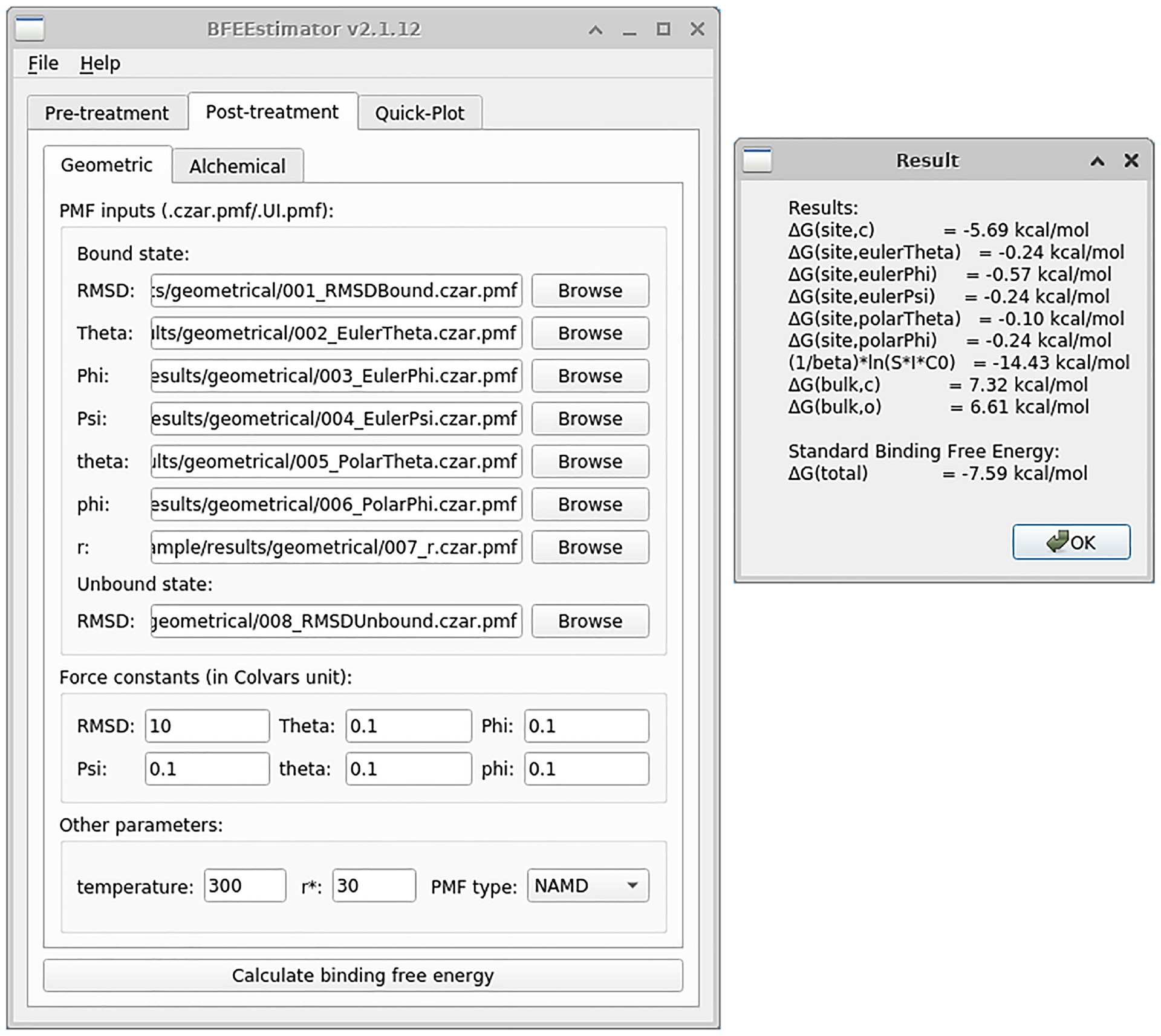
The left panel depicts the main window of BFEE2 and the right one, the results. The contributions from all the steps are supplied, and the standard binding free energy is the sum of them. This figure shows the BFEE2 graphical interface under Ubuntu 20.04.
Procedure 2: The alchemical route
Modeling & Input-file generation
-
1
Perform Step 1–4 from Procedure 1.
-
2Optionally, set the parameters of the “Advanced settings” menu. A short description of these parameters is presented hereafter.
- Stratification. Similar to the corresponding option for the geometrical route.
- Double-wide sampling simulation. If this option is checked, a double-wide sampling simulation in lieu of explicit forward and backward transformations will be performed. The end-user must know how to parse the output files of double-wide simulations.
- Compatibility→Pinning down the protein. Similar to the corresponding option for the geometrical route.
- Compatibility→Use quaternion-based CVs. Similar to the corresponding option for the geometrical route.
- Minimization before sampling. This option allows NAMD to perform an energy minimization prior to an FEP calculation at a given value of the coupling parameter.
- Model→Membrane Protein. Similar to the corresponding option in the geometrical route.
▲ Critical Step Stratification subsumes a set of parameters crucial for the convergence rate of the free-energy calculations at hand. Within the alchemical route, as many as 20 to 400 intermediate states may be required for each transformation, depending on the flexibility—when adding reversibly the relevant geometric restraints, and the size of the ligand—when decoupling it reversibly from its environment. In the Abl-SH3:p41 example, (100, 200, 100, 200) × 2 are good choices for the number of windows for each step of the alchemical route.
-
3
Click on the “Generate Inputs” button and choose the directory where all the input files will be located. Fig. 6 shows the recommended settings for the alchemical route in the case of the Abl-SH3:p41 example.
Fig. 6 |. Settings for the generation of inputs for the Abl-SH3:p41 case example following the alchemical route.
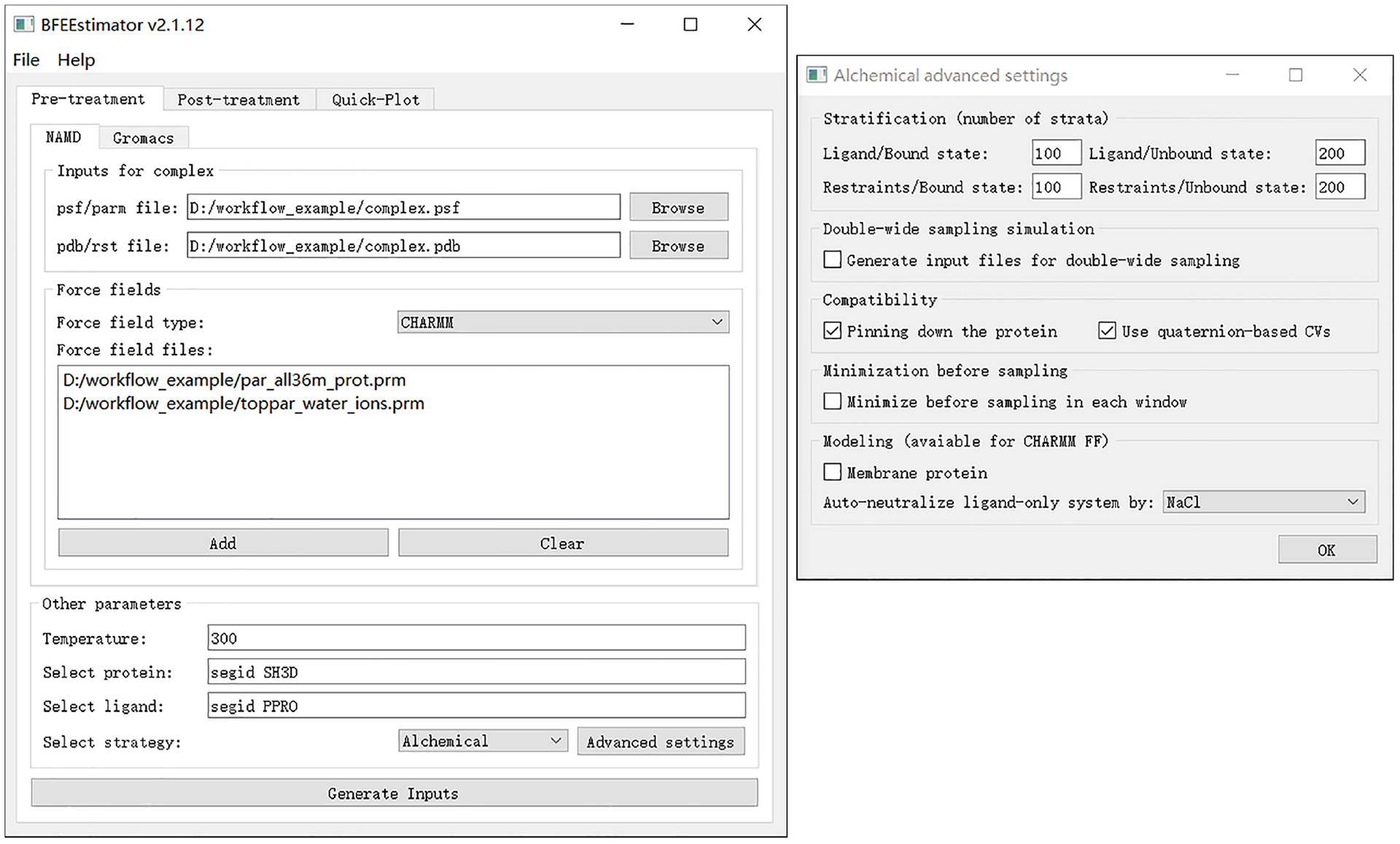
The left panel depicts the main window of BFEE2 and the right one, the advanced settings.
Simulation
-
4Equilibrate the molecular assembly by executing
cd 000_eq namd2 +p8 +idlepoll +devices 0 000.1_eq.conf > 000.1_eq.log & namd2 +p8 +idlepoll +devices 1 000.2_eq_ligandOnly.conf > 000.2_eq_ligandOnly.log &
in terminal (Linux and Mac OS) or PowerShell (Windows). The +p8 means using 8 CPU cores and +idlepoll +devices 0 represents the use of GPU 0. The end-user can adjust these parameters to adapt their own computers.? TROUBLESHOOTING
-
5Run the following simulations,
001_MoleculeBound/001.1_fep_backward.conf 001_MoleculeBound/001.2_fep_forward.conf 002_RestraintBound/002.1_ti_backward.conf 002_RestraintBound/002.2_ti_forward.conf 003_MoleculeUnbound/003.1_fep_backward.conf 003_MoleculeUnbound/003.2_fep_forward.conf 004_RestraintUnbound/004.1_ti_backward.conf 004_RestraintUnbound/004.2_ti_forward.conf
▲ Critical Step These simulations can be carried out in parallel, for as long as the backward alchemical simulations are performed prior to the corresponding forward ones. The end-user should ascertain that the simulation is converged, which is mirrored in a small error between the forward and the backward simulations, as detailed below in the “Post-treatment” section and Box 5. Should the simulation not be converged, one needs to increase either the simulation time or the number of windows—or possibly both, and restart the corresponding simulations. We suggest to run at least (100, 400, 100, 400) × 2 nanoseconds for each step of the Abl-SH3:p41 example, prior to jumping to step 6.
? TROUBLESHOOTING
Post-treatment
-
6
Open the BFEE2 window and switch to the “Post-treatment→Alchemical” tab. Then load the *.fepout or *.log files of each step.
-
7
Similar to the Geometrical route (step 14 of Procedure 1), set force constants of CVs.
-
8Set the centers of restraints and the temperature of the simulations. The centers of restraints correspond to, for example, the centers option in the following block.
harmonic { colvars eulerTheta forceConstant 0.1 centers 0.0 }Then click the “Calculate binding free energy” button. Fig. 7 shows how to perform post-treatment of the Abl-SH3:p41 example for the alchemical route. The errors reflecting the hysteresis between the forward and backward simulations are provided and indicate the convergence of the multistep free-energy calculation. The end-user should extend the simulation time or increase the number of windows—or both, if a significant hysteresis is measured between the forward and backward transformations.
▲ Critical Step The ParseFEP plugin of VMD can be used to improve the reliability of alchemical free-energy calculations. See Box 6 for more details.
Fig. 7 |. Settings for post-treatment of the Abl-SH3:p41 example for the alchemical route.
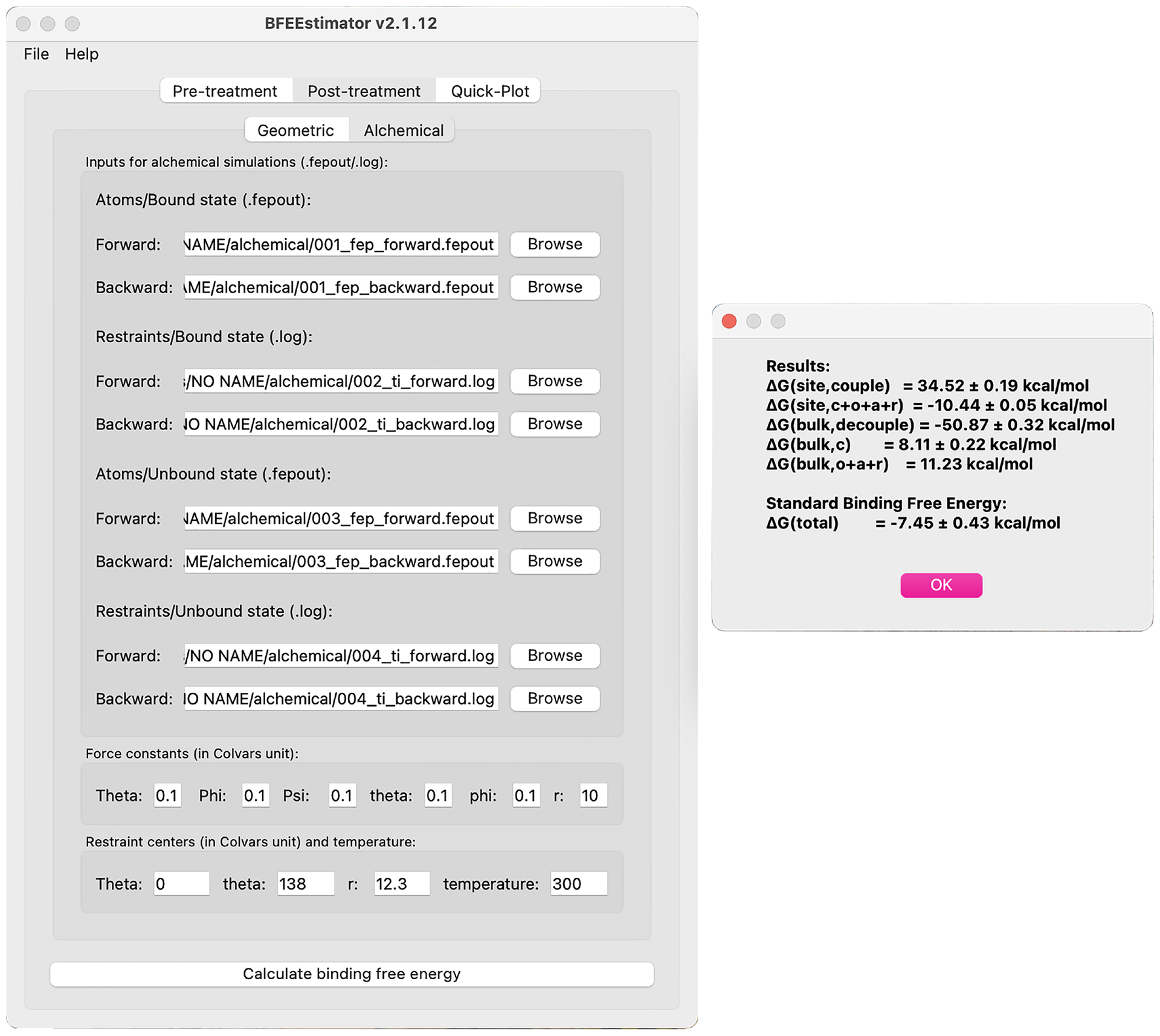
The left panel depicts the main window of BFEE2 and the right one, the results. The contributions of all the steps are provided, and the standard binding free energy is the sum of them. The reported errors show the hysteresis between the forward and backward simulations, which corresponds to an approximate measure of the reliability of the free-energy calculation. This figure shows the BFEE2 graphical interface under Mac OS 11.4.
Troubleshooting
Troubleshooting advice is provided in Table 3. Most of the issues are relevant to the use of NAMD. The end-user, hence, is strongly advised to become familiar with the latter through NAMD User’s Guide and tutorials. We also suggest asking for help experts through the NAMD mailing list (https://www.ks.uiuc.edu/Research/namd/mailing_list/).
Table 3 |.
Troubleshooting table
| Procedure 1 step | Procedure 2 step | Stage | Problem | Possible reason | Solution |
|---|---|---|---|---|---|
| 2 | 2 | Input-file generation | Executing BFEE2 fails with error message “TypeError: ‘Shiboken.ObjectType’ object is not iterable” | Some pip versions of PySide2 are not stable in Windows | Use conda to install BFEE2 |
| 7 | 7 | Simulation | Simulation crashes with error message “FATAL ERROR: DIDN’T FIND vdW PARAMETER FOR ATOM TYPE *****” | Some atom types used in the topology file (PSF) are not found in the provided force field files (PRM) | Determine the necessary force field files and include all of them in the “input generation” step |
| The dependency of NBFIX terms of par all36 cgenff.prm is not satisfied | Either include par all36m_prot.prm, par all36 na.prm and par_all36_carb.prm whenever par all36 cgenff.prm is required, or remove the unnecessary NBFIX terms in par_all36_cgenff.prm manually to satisfy the dependency | ||||
| 7 | 7 | Simulation | Simulation crashes with error message “ERROR: Atoms moving too fast; simulation has become unstable” | The initial structure provided by the user is problematic, e.g., with bad initial contacts of atoms | Check the initial structure before loading it in BFEE2. Re-model the molecular assembly if necessary |
| 7 | 7 | Simulation | Simulation Simulation crashes with error message “ERROR: Periodic cell has become too small for original patch grid” | The initial structure provided by the user is problematic, e.g. with the wrong density of bulk water | Check the initial structure before loading it to BFEE2. Re-model the molecular assembly if necessary |
Timing
Procedure 1: the geometrical route
Step 1, modeling: 10 minutes.
Steps 2–6, generating the required input files: 10 minutes.
Steps 7–12, performing the simulations of the geometrical route and monitoring the convergence: Depends on the available computational resources. As a reference, on a GTX 2070, the simulation speeds for the Abl-SH3:p41 case example are 50 ns/day for the PMF calculation characterizing the separation of the ligand from the protein and 90 ns/day for all other PMF calculations.
Steps 13–15, post-treatments of the geometrical route: 10 minutes.
Procedure 2: the alchemical route
Step 1–6, modeling and generating the required input files: 20 minutes.
Steps 7 and 8, performing the simulations of the alchemical route and monitoring the convergence: Depends on the available computational resources. As a reference, on a GTX 2070, the simulation speeds for the Abl-SH3:p41 case example are 40, 60, 80 and 100 ns/day for the reversible decoupling of the ligand from the protein, adding restraints on the ligand in its bound state, decoupling the ligand from the bulk water, and adding restraints on the ligand in its unbound state, respectively.
Steps 9–11, post-treatments of the alchemical route: 10 minutes.
Boxes
Box 1, analysis of a PMF calculation: 20 minutes.
Boxes 2–4, additional examples of binding free-energy calculations: Depends on the available computational resources.
Box 5, analyzing the enthalpic driving force underlying protein:ligand association: Depends on the available computational resources.
Box 6, analyzing alchemical free-energy calculations using ParseFEP: 20 minutes.
Box 1 |. Analysis of a PMF calculation.
In this box, we show how to check the convergence of a PMF calculation and extend the simulation if convergence is not achieved. We assume that the reader has already completed at least one PMF calculation introduced in the main text.
Procedure ● Timing 10 min
Open the BFEE2 plug-in. Switch to the “Post-treatment → Quick-plot” tab. Load the *_abf_i.abf1.czar.pmf files (if a stratification strategy is used, all the *.pmf files should be loaded) into the “Plot (stratified) PMFs” section and click the “Plot” button to display the PMF.
Convergence of a PMF calculation manifests itself in an approximate plateau of the time-evolution of the PMF RMSD with respect to its initial value (usually a zero vector). To plot this curve, load *_abf_i.abf1.hist.czar.pmf into the “Calculate PMF RMSD convergence” section and click the “Plot” button (See Fig. 4 as an example). If a stratification strategy is used, the convergence of each window should be analyzed independently.
If a stratification strategy is used, we strongly advise checking the continuity of the gradient across adjacent windows. To achieve this, open *_abf_i.abf1.czar.grad and *_abf_(i+1).abf1.czar.grad using a text editor and look at the last value of the gradient in the former and the first value in the latter. One can also plot the gradient curve following the procedure of step (1), loading *_abf_i.abf1.czar.grad instead.
If convergence is not satisfied, use *_abf_i.extend.conf to extend the simulation. By looking at the time-evolution of the PMF RMSD with respect to its initial value, one can estimate the time required to achieve convergence and set an appropriate simulation time in *_abf_i.extend.conf before running the simulation.
It should be noted that in some cases, simply adding simulation time may not guarantee convergence. Instead, the result deteriorates with the increase of simulation time. Under these premises, we suggest to analyzing the trajectory to see whether partial denaturation of the protein has occurred as a result of introducing biasing forces. If so, the end-user may want to improve the initial structure of the simulation, use a stratification strategy, or add apposite restraints to maintain the proper conformation of the protein. Increasing the value of fullSamples in *.in files has also proven to help reduce deleterious nonequilibrium effects through accruing more samples and providing a more accurate estimate of the initial biasing force prior to applying it61.
Anticipated results
The Abl-SH3:p41 case example—Geometrical route.
Eight PMF calculations were performed to estimate the standard binding free energy of the complex (see Fig. 8).
Fig. 8 |. Results of PMF calculations in the geometrical route for the Abl-SH3:p41 example.
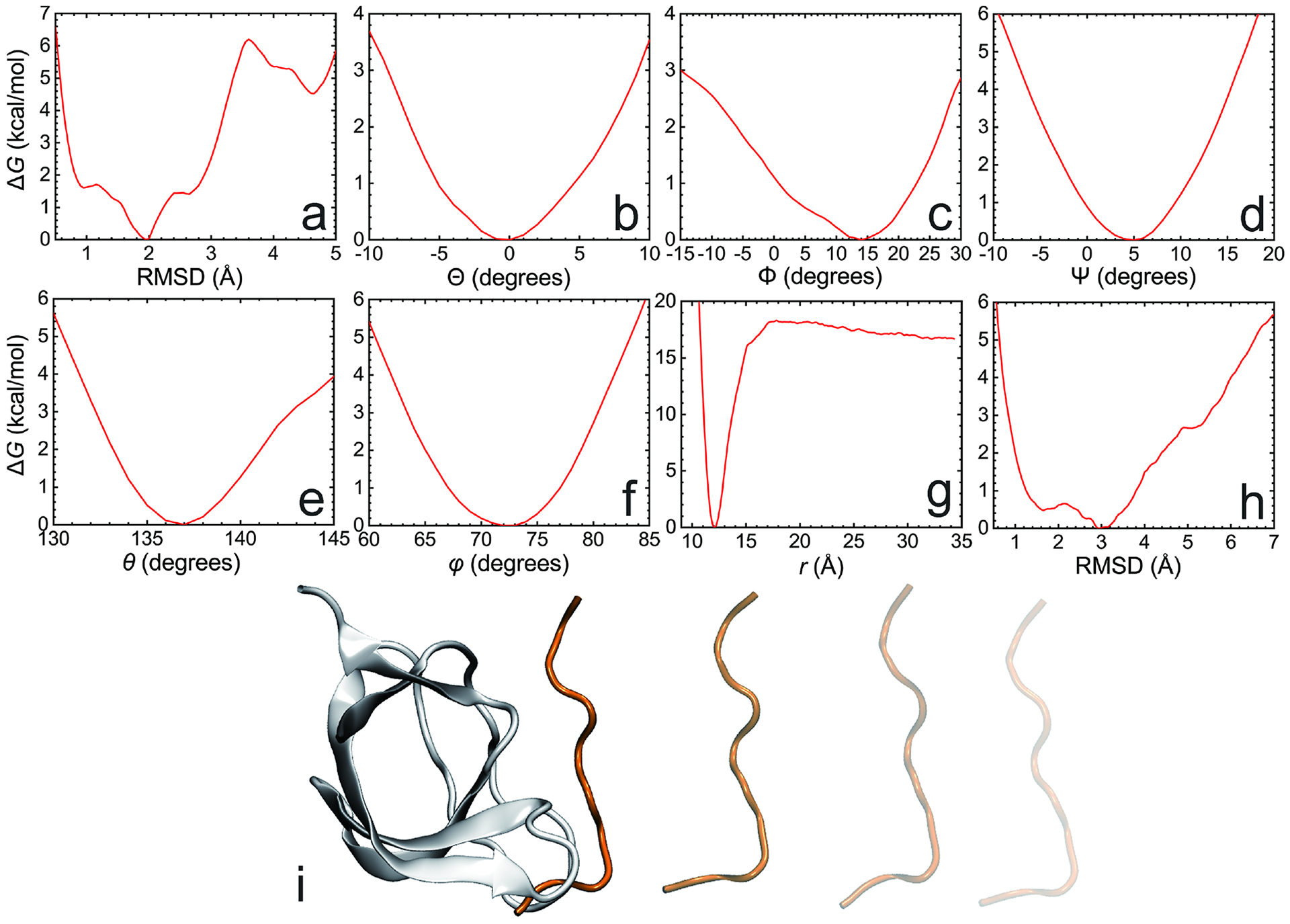
(a-h), the PMF calculations using as the CV the RMSD of the ligand with respect to its native, bound-state conformation (a), the three Euler angles, Θ (b), Φ (c), and Ψ (d), the polar, θ (e), and azimuth, φ (f), angles and the distance between the center of mass of the ligand and that the protein (g), and the RMSD of the ligand in a bulk environment, i.e., in the unbound state, with respect to its native, bound-state conformation (h). The protein:ligand separation follows an unphysical, rectilinear pathway, owing to the restraints acting on all the other CVs, which diminishes the difficulty of capturing the change in configurational entropy as the two partners of the complex associate (i).
It should be noted that for flexible ligands, the thermalized bound-state conformation provided to BFEE2 as the reference may slightly differ between independent runs due to the chaotic nature of MD. This difference might affect the outcome of the PMF calculations, especially those using as a CV the RMSD of the ligand with respect to the reference native conformation. However, the final standard binding free energy is, in principle, not affected by such minute conformational differences between the references provided to BFEE2, assuming that deviation in the protein:ligand structures remain moderate.
The following prerequisites of final PMFs can be used to validate the correctness and convergence of a standard binding free-energy calculation through the geometrical route:
From the simulations using the Euler and spherical-coordinate angles as CVs, the PMFs are generally pseudo-quadratic. If this is not the case, we suggest to extending the range of the CV accordingly.
The simulation describing the reversible separation of the ligand from the protein is the key step of the geometrical route. Starting from the global minimum, the free energy usually increases sharply until a pseudo-plateau is reached. The slight decay in the free energy at large separations stems from the contribution of the geometric entropy, or the Jacobian63, which is evaluated analytically throughout the simulation, and subtracted from the PMF29 by BFEE2. In the Abl-SH3:p41 case example, a pseudo-plateau corresponding to a free energy ranging from 15 to 20 kcal/mol is reasonable.
The final result of the PMF calculations using as a CV the RMSD of the ligand with respect to its native, bound-state conformation may acutely rely on the structure of the reference (bound-state conformation). Generally, the PMF does not necessarily consist of a single well, and is often skewed.
Using the PMFs shown in Fig. 8 (data provided in the Supplementary Data), the estimated standard binding free energy of the Abl-SH3:p41 complex is −7.6 kcal/mol, in excellent agreement with the experimental value, i.e., −7.99 kcal/mol64, as depicted in Fig. 6. If independent simulations are run in parallel to calculate the standard error, the latter should be within 0.5 kcal/mol, considering that combination of our parallel runs in refs. 16, 20 and 22 yields a standard error of 0.2 kcal/mol. As a post-hoc treatment of the free-energy calculation, the driving force underlying protein:ligand association can be studied with exquisite detail using the pair-interaction calculation feature available in NAMD, as described in Box 5.
The Abl-SH3:p41 case example—Alchemical route.
Following Procedure 2, using bidirectional alchemical transformations, the standard binding free energy of the Abl-SH3:p41 complex was estimated to be −7.5 kcal/mol (data provided in the Supplementary Data), with an approximate error of 0.4 kcal/mol based on the hysteresis between the forward and backward transformations.
It is noteworthy that performing bidirectional transformations along the alchemical route is a convenient way to verify thermodynamic micro-reversibility, mirrored in the absence of a hysteresis between the forward and backward simulations, while allowing the corresponding statistical data to be combined to yield a maximum-likelihood estimator of the free energy65. A thorough analysis is observing the free-energy change with respect to λ of the bidirectional simulations, which can be extracted from the FEPOUT or the LOG files by,
grep “#Free energy change for lambda” 001_fep_forward.fepout > 001_lambda_forward.dat
or
grep “dA/dLambda” 002_ti_forward.log > 002_lambda_forward.log
The overlap of the free energy profiles as a function of the coupling parameter, λ, of the forward and backward transformations, is a necessary, albeit not sufficient, condition for convergence of bidirectional simulations65 and, therefore, provides a rough estimate of the reliability of the calculation. In the Abl-SH3:p41 case example, the curves characterizing the forward and backward simulations are very close, suggesting a suitable convergence of our simulations (Fig. 9). A more thoroughe analysis of the convergence, and of the statistical and systematic errors associated to the simulations can be performed using ParseFEP58,65,66. (Box 6 and Fig. 10). If the Bennett acceptance-ratio (BAR) estimator67 implemented in ParseFEP58 is used to improve the precision of free energy calculations, the calculated standard binding free energy of p41 to Abl-SH3 is −7.4 ± 0.3 kcal/mol.
Fig. 9 |. Free-energy changes with respect to λ in the alchemical route.
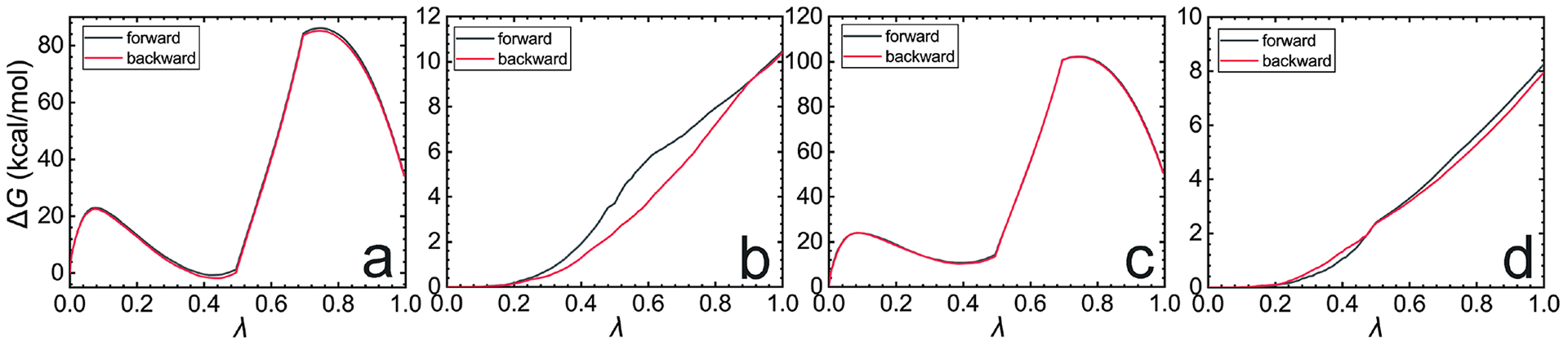
(a-d), free-energy change accounting for reversibly decoupling the ligand from the protein (a), adding restraints on the bound-state ligand (b), decoupling the ligand from the bulk water (c) and adding restraints on the unbound-state ligand (d), respectively.
Fig. 10 |. Example of the outputs of ParseFEP.
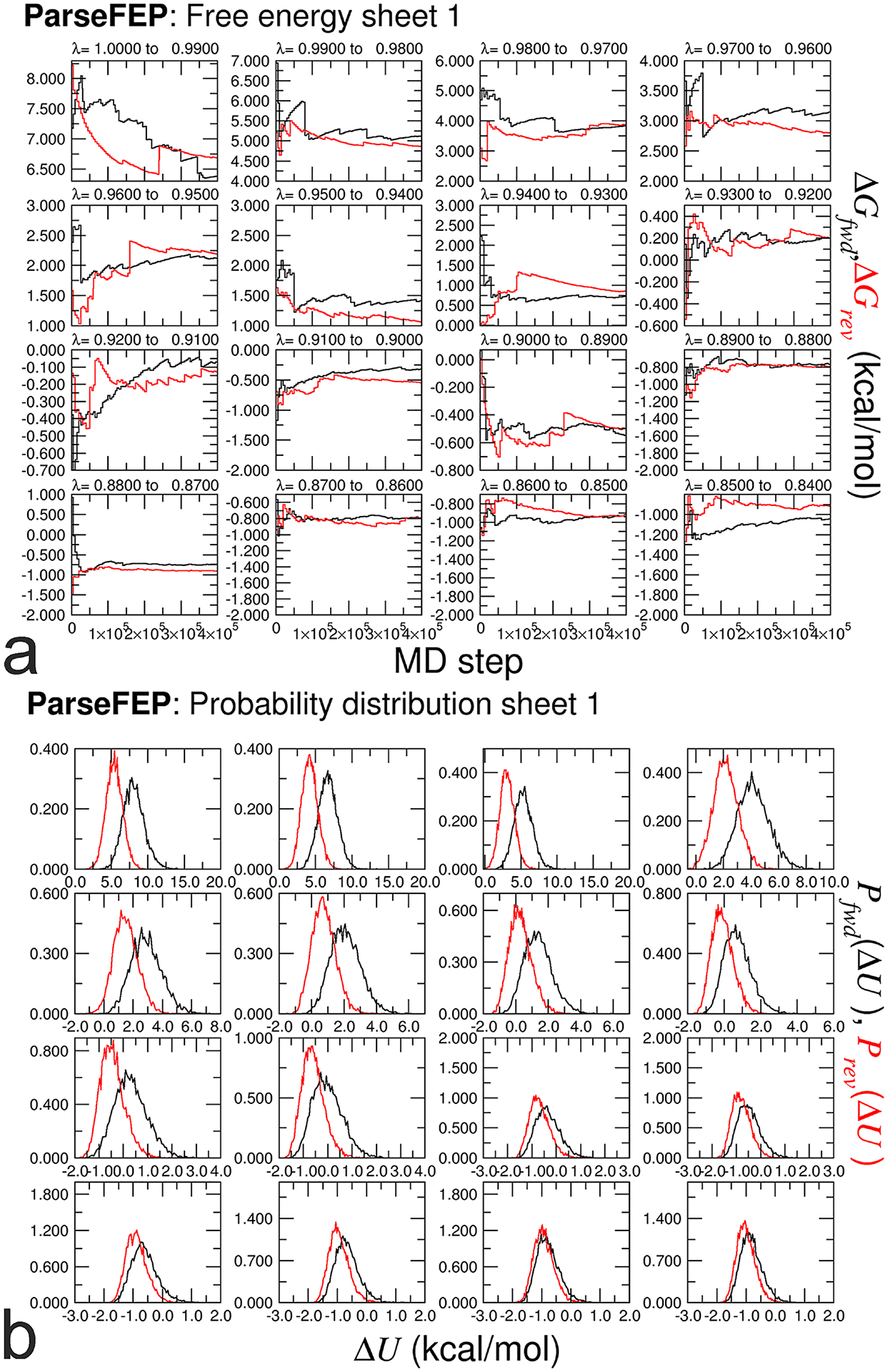
Evolution of the free energy in each window of a stratified, bidirectional calculation (a), and associated probability distributions of the potential-energy difference, ΔU (b). See Box 6 for more details.
Other examples.
Apart from Abl-SH3:p41, we have calculated the standard binding free energies of the following examples to illustrate the use of BFEE2, that is,
DIAP1-BIR1: grim peptide. This example was chosen as an illustration of the use of Gromacs as the MD workhorse. Following the procedure depicted in Box 2, the standard binding free-energy estimate was found to be equal to −8.7 ± 0.7 kcal/mol, in excellent agreement with the experimental value of −9.5 kcal/mol68.
T4 lysozyme L99A:benzene. Since the ligand molecule, benzene, is deeply buried in the protein, the alchemical route was adopted to estimate the binding free energy. In stark contrast with the Abl-SH3:p41 complex, long simulation times are required to decouple reversibly the ligand from its binding site, as capturing the exchange of water molecules between the cavity and the bulk is admittedly slow. The binding free energy estimated in this study, namely, −6.0 ± 1.0 kcal/mol, agrees well with the experimental measurement of −5.2 kcal/mol69.
Trypsin:benzamidine. As benzamidine is semi-buried in the protein, a well-defined pathway is required to separate the former from the latter, should the geometrical route be chosen. Following the guideline provided in Box 3, the computed binding free energy, −7.8 ± 0.6 kcal/mol, only differs slightly from the experimental value (−7.2 to −6.3 kcal/mol)70–72.
Factor Xa:quaternary ammonium. The choice of an appropriate force field is crucial for the estimation of standard binding free energies. The standard CHARMM36m force field49 yields a binding free-energy estimate of −3.7 ± 0.5 kcal/mol, differing significantly from the experimental value, −9.0 kcal/mol73. By grossly ignoring induction phenomena, pairwise additive force fields, like the CHARMM36m force field, are notorious for misrepresenting cation-π interactions,74 which drive association in the factor Xa:quaternary ammonium complex. Switching to a force field germane to cation-π interactions38,75, the computed binding free energy now amounts to −8.7 ± 0.4 kcal/mol, in excellent agreement with the experimental value. This example is also used to illustrate how to analyze the driving force underlying protein:ligand association, as detailed in Box 5.
MUP-I:2-methoxy-3-isopropylpyrazine and MUP-I:6-hydroxy-6-methyl-3-heptanone. Protein:ligand affinity ranking is an important task in pharmaceutical sciences and is usually performed through relative binding free-energy calculations. In this protocol, we show that protein:ligand affinity ranking can be easily achieved through standard binding free-energy calculations. Through the alchemical route, the standard binding free energies of MUP-I:2-methoxy-3-isopropylpyrazine and MUP-I:6-hydroxy-6-methyl-3-heptanone are estimated at −7.8 ± 1.0 and −5.5 ± 0.7 kcal/mol, respectively, in good agreement with the experiment (−7.8 and −6.0 kcal/mol)76,77.
β1-adrenergic receptor:4-methyl-2-(piperazin-1-yl) quinoline. BFEE2 can be used to predict the binding affinity of a ligand to a membrane protein, which has traditionally been seen as a daunting challenge. One of the difficulties is to capture the reversible hydration of the binding site during the PMF calculations or alchemical transformations, as the membrane protein is fully immersed in its lipid environment. Following the procedure of the alchemical route introduced in Box 4, the calculated standard binding free energy of β1-adrenergic receptor:4-methyl-2-(piperazin-1-yl) quinoline of −8.1 ± 1.0 kcal/mol agrees well with the experimental value, namely −9.07 kcal/mol78.
V1-ATPase:nucleotide (ATP or ADP + Pi). One of the most challenging applications of our methodology is the determination of the binding affinity of ATP and ADP + Pi bound towards V1-ATPase in its distinct conformational states, following the alchemical route40. The molecular assemblies at hand, of dimensions on the order of 170 × 170 × 190 Å3, are particularly complex compared with most of the biological objects reported herein. Our results indicate that ATP association in the tight site (−11.6 ± 0.8 kcal/mol) is energetically more favorable than that of ADP + Pi (−8.3 ± 0.9 kcal/mol), and that binding affinities of both of the nucleotides in the empty site are nearly identical (ATP: −4.1 ± 1.1 kcal/mol, ADP: −4.3 ± 0.8 kcal/mol) and less favorable compared with the tight or bound sites. This trend is in good agreement with the experimental measurements carried out on F1-ATPase79.
The pitfalls and caveats of the aforementioned examples are summarized in Table 4. Additional success stories of the methodology are provided in Table 2. To make this protocol completely transparent to the end-user, we provide in the Supplementary Information the detailed description of the complexes, the parameters of the binding free-energy calculation, and the results of the different sub-steps for three practical examples, namely MDM2-p53:NVP-CGM097, MUP-I:2-methoxy-3-isopropylpyrazine, and MUP-I:6-hydroxy-6-methyl-3-heptanone, in addition to the Abl-SH3:p41 case example detailed in the text.
Table 4 |.
Pitfalls and caveats of examples shown in this protocol
| Examples | Pitfalls and caveats | See also |
|---|---|---|
| Abl-SH3:p41 | Captures the conformational change of the flexible ligand. Usually requires a stratification strategy in free-energy calculations. | Main procedure and refs. 19,20 |
| DIAP1-BIR1: grim peptide | - | Box 2 |
| T4 lysozyme L99A:benzene | Buried ligand. Requires long simulation time to capture the water exchange inside and outside the binding cavity. | Refs. 11 |
| Trypsin:benzamidine | Semi-buried ligand. Requires manual definition of the separation direction if the geometrical route is adopted. | Box 3 |
| Factor Xa:quaternary ammonium | Require careful choice of the force field to correctly model cation-π interaction. | Ref. 38 |
| MUP-I:2-methoxy-3-isopropylpyrazine and MUP-I:6-hydroxy-6-methyl-3-heptanone | Bound water in the binding site may drift away during the free energy calculation. Requires definition of additional restraints for these water molecules. | Supplementary Information |
| β1-adrenergic receptor: 4-methyl-2-(piperazin-1-yl) quinoline | Captures the reversible hydration of the binding site for a membrane protein. Requires to equilibrate the membrane protein and its environment without the ligand, allowing water to diffuse inside the protein as a preamble to the free-energy calculations. | Box 4 |
| V1-ATPase:nucleotide (ATP or ADP + Pi) | Practically challenging example. Requires the combination of multiple operation mentioned above. | Ref.40 |
Supplementary Material
Acknowledgements
This study was supported by the National Natural Science Foundation of China (22073050, 22174075 and 22103041), the China Post-doctoral Science Foundation (bs6619012), Frontiers Science Center for New Organic Matter, Nankai University (63181206), the US National Institutes of Health (R01-AI148740), the National Science Foundation (NSF) through Grant No. MCB-1517221, the France and Chicago Collaborating in The Sciences (FACCTS) program, and the Agence Nationale de la Recherche (ProteaseInAction). J.C.G. acknowledges computational resources provided through the Extreme Science and Engineering Discovery Environment (XSEDE; TG-MCB130173). The paper is dedicated to the 100th anniversary of Chemistry at Nankai University.
Related links
Key references using this protocol
Woo, H. et al. Proc. Natl. Acad. Sci. U.S.A. 102, 6825–6830 (2005): https://doi.org/10.1073/pnas.0409005102
Gumbart, J. C. et al. J. Chem. Theory Comput. 9, 794–802 (2013): https://doi.org/10.1021/ct3008099
Fu, H. et al. J. Chem. Theory Comput. 13, 5173–5178 (2017): https://doi.org/10.1021/acs.jctc.7b00791
Fu, H. et al. Acc. Chem. Res. 52, 3254–3264 (2019): https://doi.org/10.1021/acs.accounts.9b00473
Fu, H. et al. J. Chem. Inf. Model. 61, 2116–2123 (2021): https://doi.org/10.1021/acs.jcim.1c00269
Footnotes
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Code availability
The Python package of BFEE2 can be installed through pip (https://pypi.org/project/BFEE2/) and conda (https://anaconda.org/conda-forge/bfee2). The source code of BFEE2 is available on Github (https://github.com/fhh2626/BFEE2)80.
Competing interests
The authors declare no competing interests.
Supplementary information is available for this paper at https://doi.org/xxxxxxxxxxxxxxxxxxxxx.
Data availability
The input and output files of BFEE2 of examples are provided in the Supplementary Data. The data shown in Fig. 8–11 were obtained from new simulations, as a way to verify and guarantee the reproducibility of our protocol, albeit some of the illustrations of the manuscript are taken from previous investigations.
Fig. 11 |. Analysis of the enthalpic driving force of the association of Factor Xa: quaternary ammonium.
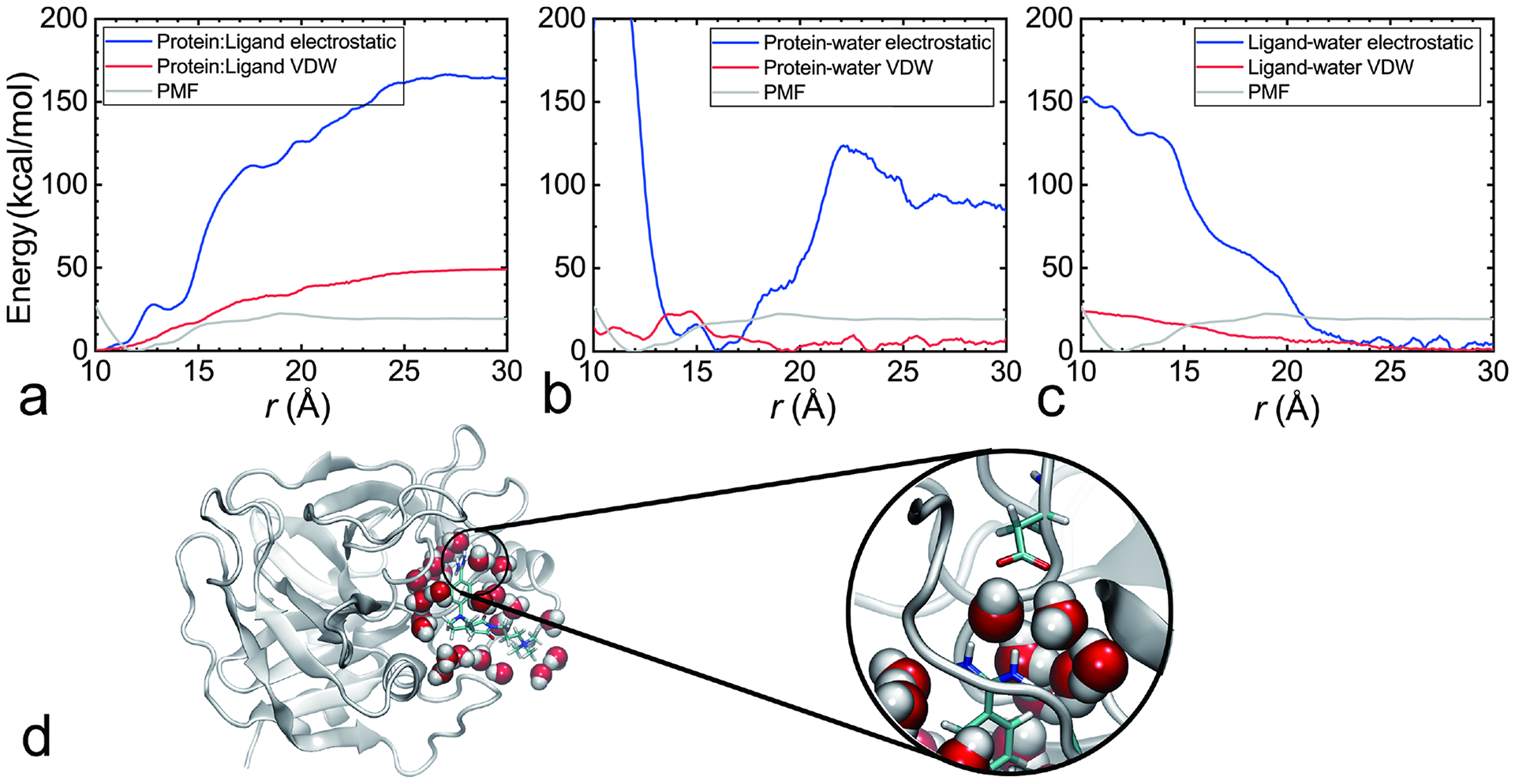
The contributions of protein:ligand (a) protein-water (b) and ligand-water (c) are analyzed. The structure corresponding to the most favorable protein-water interaction (r = 16 Å) is depicted in panel (d). Water-mediated salt bridges are found in this structure.
References
- 1.Limongelli V Ligand binding free energy and kinetics calculation in 2020. WIREs Comput. Mol. Sci 10, e1455 (2020). [Google Scholar]
- 2.Chodera JD & Mobley DL Entropy-enthalpy compensation: Role and ramifications in biomolecular ligand recognition and design. Annu. Rev. Biophys 42, 121–142 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li A & Gilson MK Protein-ligand binding enthalpies from near-millisecond simulations: Analysis of a preorganization paradox. J. Chem. Phys 149, 72311 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.de Ruiter A & Oostenbrink C Advances in the calculation of binding free energies. Curr. Opin. Struct. Biol 61, 207–212 (2020). [DOI] [PubMed] [Google Scholar]
- 5.Chipot C Frontiers in free-energy calculations of biological systems. Wiley Interdiscip. Rev. Comput. Mol. Sci 4, 71–89 (2014). [Google Scholar]
- 6.Hermans J & Shankar S The free energy of xenon binding to myoglobin from molecular dynamics simulation. Isr. J. Chem 27, 225–227 (1986). [Google Scholar]
- 7.Roux B, Nina M, Pomès R & Smith JC Thermodynamic stability of water molecules in the bacteriorhodopsin proton channel: A molecular dynamics free energy perturbation study. Biophys. J 71, 670–681 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hermans J & Wang L Inclusion of loss of translational and rotational freedom in theoretical estimates of free energies of binding. Application to a complex of benzene and mutant T4 lysozyme. J. Am. Chem. Soc 119, 2707–2714 (1997). [Google Scholar]
- 9.Mann G & Hermans J Modeling protein-small molecule interactions: Structure and thermodynamics of noble gases binding in a cavity in mutant phage T4 lysozyme L99A. J. Mol. Biol 302, 979–989 (2000). [DOI] [PubMed] [Google Scholar]
- 10.Boresch S, Tettinger F, Leitgeb M & Karplus M Absolute binding free energies: A quantitative approach for their calculation. J. Phys. Chem. B 107, 9535–9551 (2003). [Google Scholar]
- 11.Deng Y & Roux B Calculation of standard binding free energies: Aromatic molecules in the T4 lysozyme L99A mutant. J. Chem. Theory Comput 2, 1255–1273 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Mobley DL, Chodera JD & Dill KA On the use of orientational restraints and symmetry corrections in alchemical free energy calculations. J. Chem. Phys 125, 84902 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gilson MK, Given JA, Bush BL & McCammon JA The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J 72, 1047–1069 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fu H, Shao X, Chipot C & Cai W Extended adaptive biasing force algorithm. An on-the-fly implementation for accurate free-energy calculations. J. Chem. Theory Comput 12, 3506–3513 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Fu H et al. Zooming across the free-energy landscape: Shaving barriers, and flooding valleys. J. Phys. Chem. Lett 9, 4738–4745 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Fu H, Shao X, Cai W & Chipot C Taming rugged free energy landscapes using an average force. Acc. Chem. Res 52, 3254–3264 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Fu H et al. Finding an optimal pathway on a multidimensional free-energy landscape. J. Chem. Inf. Model 60, 5366–5374 (2020). [DOI] [PubMed] [Google Scholar]
- 18.Woo H-J & Roux B Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci 102, 6825–6830 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gumbart JC, Roux B & Chipot C Standard binding free energies from computer simulations: What is the best strategy? J. Chem. Theory Comput 9, 794–802 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fu H, Cai W, Hénin J, Roux B & Chipot C New coarse variables for the accurate determination of standard binding free energies. J. Chem. Theory Comput 13, 5173–5178 (2017). [DOI] [PubMed] [Google Scholar]
- 21.Wang J, Deng Y & Roux B Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophys. J 91, 2798–2814 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fu H et al. BFEE: A user-friendly graphical interface facilitating absolute binding free-energy calculations. J. Chem. Inf. Model 58, 556–560 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fu H, Chen H, Cai W, Shao X & Chipot C BFEE2: Automated, streamlined, and accurate absolute binding free-energy calculations. J. Chem. Inf. Model 61, 2116–2123 (2021). [DOI] [PubMed] [Google Scholar]
- 24.Humphrey W, Dalke A & Schulten K VMD: Visual molecular dynamics. J. Mol. Graph 14, 33–38 (1996). [DOI] [PubMed] [Google Scholar]
- 25.Comer J et al. The adaptive biasing force method: Everything you always wanted to know but were afraid to ask. J. Phys. Chem. B 119, 1129–1151 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zwanzig RW High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys 22, 1420–1426 (1954). [Google Scholar]
- 27.Chen H et al. Boosting free-energy perturbation calculations with GPU-accelerated namd. J. Chem. Inf. Model 60, 5301–5307 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kirkwood JG Statistical mechanics of fluid mixtures. J. Chem. Phys 3, 300–313 (1935). [Google Scholar]
- 29.Fiorin G, Klein ML & Hénin J Using collective variables to drive molecular dynamics simulations. Mol. Phys 111, 3345–3362 (2013). [Google Scholar]
- 30.Zhang H et al. Accurate estimation of the standard binding free energy of netropsin with DNA. Molecules 23, 228 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Du S et al. Curvature of buckybowl corannulene enhances its binding to proteins. J. Phys. Chem. C 123, 922–930 (2019). [Google Scholar]
- 32.Sun H, Li Y, Tian S, Wang J & Hou T P-loop conformation governed crizotinib resistance in G2032R-mutated ROS1 tyrosine kinase: Clues from free energy landscape. PLOS Comput. Biol 10, e1003729 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Deng N et al. Comparing alchemical and physical pathway methods for computing the absolute binding free energy of charged ligands. Phys. Chem. Chem. Phys 20, 17081–17092 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kuusk A et al. Adoption of a turn conformation drives the binding affinity of p53 C-terminal domain peptides to 14-3-3σ. ACS Chem. Biol 15, 262–271 (2020). [DOI] [PubMed] [Google Scholar]
- 35.Qian Y et al. Absolute free energy of binding calculations for macrophage migration inhibitory factor in complex with a druglike inhibitor. J. Phys. Chem. B 123, 8675–8685 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Comer J et al. Beta-1,3 oligoglucans specifically bind to immune receptor CD28 and may enhance T cell activation. Int. J. Mol. Sci 22, 3124 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Velez-Vega C & Gilson MK Overcoming dissipation in the calculation of standard binding free energies by ligand extraction. J. Comput. Chem 34, 2360–2371 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liu H, Fu H, Chipot C, Shao X & Cai W Accuracy of alternate nonpolarizable force fields for the determination of protein–ligand binding affinities dominated by cation−π interactions. J. Chem. Theory Comput (2021) doi: 10.1021/acs.jctc.1c00219. [DOI] [PubMed] [Google Scholar]
- 39.Liu H, Okazaki S & Shinoda W Heteroaryldihydropyrimidines alter capsid assembly by adjusting the binding affinity and pattern of the hepatitis B virus core protein. J. Chem. Inf. Model 59, 5104–5110 (2019). [DOI] [PubMed] [Google Scholar]
- 40.Singharoy A, Chipot C, Moradi M & Schulten K Chemomechanical coupling in hexameric protein–protein interfaces harnesses energy within V-type atpases. J. Am. Chem. Soc 139, 293–310 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Srinivasan J, Cheatham TE, Cieplak P, Kollman PA & Case DA Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate−DNA helices. J. Am. Chem. Soc 120, 9401–9409 (1998). [Google Scholar]
- 42.Limongelli V, Bonomi M & Parrinello M Funnel metadynamics as accurate binding free-energy method. Proc. Natl. Acad. Sci 110, 6358–6363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Laio A & Parrinello M Escaping free-energy minima. Proc. Natl. Acad. Sci 99, 12562–12566 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Raniolo S & Limongelli V Ligand binding free-energy calculations with funnel metadynamics. Nat. Protoc 15, 2837–2866 (2020). [DOI] [PubMed] [Google Scholar]
- 45.Mobley DL, Chodera JD & Dill KA Confine-and-release method: Obtaining correct binding free energies in the presence of protein conformational change. J. Chem. Theory Comput 3, 1231–1235 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Miao Y, Bhattarai A & Wang J Ligand Gaussian accelerated molecular dynamics (LiGaMD): Characterization of ligand binding thermodynamics and kinetics. J. Chem. Theory Comput 16, 5526–5547 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang L, Friesner RA & Berne BJ Replica exchange with solute scaling: A more efficient version of replica exchange with solute tempering (REST2). J. Phys. Chem. B 115, 9431–9438 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kofke DA & Cummings PT Precision and accuracy of staged free-energy perturbation methods for computing the chemical potential by molecular simulation. Fluid Phase Equilib. 150–151, 41–49 (1998). [Google Scholar]
- 49.Huang J et al. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods 14, 71 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tian C et al. ff19SB: Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J. Chem. Theory Comput 16, 528–552 (2020). [DOI] [PubMed] [Google Scholar]
- 51.Lemkul JA, Huang J, Roux B & MacKerell AD An empirical polarizable force field based on the classical drude oscillator model: Development history and recent applications. Chem. Rev 116, 4983–5013 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ponder JW et al. Current status of the AMOEBA polarizable force field. J. Phys. Chem. B 114, 2549–2564 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jo S & Jiang W A generic implementation of replica exchange with solute tempering (REST2) algorithm in NAMD for complex biophysical simulations. Comput. Phys. Commun 197, 304–311 (2015). [Google Scholar]
- 54.Deng Y & Roux B Computation of binding free energy with molecular dynamics and grand canonical monte carlo simulations. J. Chem. Phys 128, 115103 (2008). [DOI] [PubMed] [Google Scholar]
- 55.Ben-Shalom IY, Lin C, Kurtzman T, Walker RC & Gilson MK Simulating water exchange to buried binding sites. J. Chem. Theory Comput 15, 2684–2691 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jo S, Kim T, Iyer VG & Im W CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem 29, 1859–1865 (2008). [DOI] [PubMed] [Google Scholar]
- 57.Case DA et al. Amber 2020. (2020).
- 58.Liu P, Dehez F, Cai W & Chipot C A toolkit for the analysis of free-energy perturbation calculations. J. Chem. Theory Comput 8, 2606–2616 (2012). [DOI] [PubMed] [Google Scholar]
- 59.Phillips JC et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys 153, 44130 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Abraham MJ et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2, 19–25 (2015). [Google Scholar]
- 61.Miao M et al. Avoiding non-equilibrium effects in adaptive biasing force calculations. Mol. Simul 47, 390–394 (2021). [Google Scholar]
- 62.Samways ML, Bruce Macdonald HE & Essex JW Grand: A python module for grand canonical water sampling in OpenMM. J. Chem. Inf. Model 60, 4436–4441 (2020). [DOI] [PubMed] [Google Scholar]
- 63.Hénin J & Chipot C Overcoming free energy barriers using unconstrained molecular dynamics simulations. J. Chem. Phys 121, 2904–2914 (2004). [DOI] [PubMed] [Google Scholar]
- 64.Pisabarro MT & Serrano L Rational design of specific high-affinity peptide ligands for the Abl-SH3 domain. Biochemistry 35, 10634–10640 (1996). [DOI] [PubMed] [Google Scholar]
- 65.Pohorille A, Jarzynski C & Chipot C Good practices in free-energy calculations. J. Phys. Chem. B 114, 10235–10253 (2010). [DOI] [PubMed] [Google Scholar]
- 66.Hahn AM & Then H Characteristic of Bennett’s acceptance ratio method. Phys. Rev. E 80, 031111 (2009). [DOI] [PubMed] [Google Scholar]
- 67.Bennett CH Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 22, 245–268 (1976). [Google Scholar]
- 68.Brown SP & Muchmore SW Large-scale application of high-throughput molecular mechanics with Poisson−Boltzmann surface area for routine physics-based scoring of protein−ligand complexes. J. Med. Chem 52, 3159–3165 (2009). [DOI] [PubMed] [Google Scholar]
- 69.Morton A & Matthews BW Specificity of ligand binding in a buried nonpolar cavity of T4 lysozyme: linkage of dynamics and structural plasticity. Biochemistry 34, 8576–8588 (1995). [DOI] [PubMed] [Google Scholar]
- 70.Mares-Guia M, Nelson DL & Rogana E Electronic effects in the interaction of para-substituted benzamidines with trypsin: The involvement of the π-electronic density at the central atom of the substituent in binding. J. Am. Chem. Soc 99, 2331–2336 (1977). [DOI] [PubMed] [Google Scholar]
- 71.Katz BA et al. Structural basis for selectivity of a small molecule, S1-binding, submicromolar inhibitor of urokinase-type plasminogen activator. Chem. Biol 7, 299–312 (2000). [DOI] [PubMed] [Google Scholar]
- 72.Schwarzl SM, Tschopp TB, Smith JC & Fischer S Can the calculation of ligand binding free energies be improved with continuum solvent electrostatics and an ideal-gas entropy correction? J. Comput. Chem 23, 1143–1149 (2002). [DOI] [PubMed] [Google Scholar]
- 73.Schärer K et al. Quantification of cation–π interactions in protein–ligand complexes: crystal-structure analysis of Factor Xa bound to a quaternary ammonium ion ligand. Angew. Chemie Int. Ed 44, 4400–4404 (2005). [DOI] [PubMed] [Google Scholar]
- 74.Khan HM, MacKerell AD & Reuter N Cation-π interactions between methylated ammonium groups and tryptophan in the CHARMM36 additive force field. J. Chem. Theory Comput 15, 7–12 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Liu H, Fu H, Shao X, Cai W & Chipot C Accurate description of cation-π interactions in proteins with a nonpolarizable force field at no additional cost. J. Chem. Theory Comput 16, 6397–6407 (2020). [DOI] [PubMed] [Google Scholar]
- 76.Bingham RJ et al. Thermodynamics of binding of 2-methoxy-3-isopropylpyrazine and 2-methoxy-3-isobutylpyrazine to the major urinary protein. J. Am. Chem. Soc 126, 1675–1681 (2004). [DOI] [PubMed] [Google Scholar]
- 77.Timm DE, Baker LJ, Mueller H, Zidek L & Novotny MV Structural basis of pheromone binding to mouse major urinary protein (MUP-I). Protein Sci. 10, 997–1004 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Christopher JA et al. Biophysical fragment screening of the β1-adrenergic receptor: Identification of high affinity arylpiperazine leads using structure-based drug design. J. Med. Chem 56, 3446–3455 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Adachi K, Oiwa K, Yoshida M, Nishizaka T & Kinosita K Controlled rotation of the F1-ATPase reveals differential and continuous binding changes for ATP synthesis. Nat. Commun 3, 1022 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Fu H et al. Determination of protein:ligand standard binding free energies from molecular dynamics simulations. BFEE2: Binding free energy estimator 2. DOI: 10.5281/zenodo.5501842 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The input and output files of BFEE2 of examples are provided in the Supplementary Data. The data shown in Fig. 8–11 were obtained from new simulations, as a way to verify and guarantee the reproducibility of our protocol, albeit some of the illustrations of the manuscript are taken from previous investigations.
Fig. 11 |. Analysis of the enthalpic driving force of the association of Factor Xa: quaternary ammonium.

The contributions of protein:ligand (a) protein-water (b) and ligand-water (c) are analyzed. The structure corresponding to the most favorable protein-water interaction (r = 16 Å) is depicted in panel (d). Water-mediated salt bridges are found in this structure.


