Multi-scale, domain knowledge-guided attention + random forest: a two-stage deep learning-based multi-scale guided attention models to diagnose idiopathic pulmonary fibrosis from computed tomography images

Abstract

Background:

Idiopathic pulmonary fibrosis (IPF) is a progressive, irreversible, and usually fatal lung disease of unknown reasons, generally affecting the elderly population. Early diagnosis of IPF is crucial for triaging patients’ treatment planning into anti-fibrotic treatment or treatments for other causes of pulmonary fibrosis. However, current IPF diagnosis workflow is complicated and time-consuming, which involves collaborative efforts from radiologists, pathologists, and clinicians and it is largely subject to inter-observer variability.

Purpose:

The purpose of this work is to develop a deep learning-based automated system that can diagnose subjects with IPF among subjects with interstitial lung disease (ILD) using an axial chest computed tomography (CT) scan. This work can potentially enable timely diagnosis decisions and reduce inter-observer variability.

Methods:

Our dataset contains CT scans from 349 IPF patients and 529 non-IPF ILD patients. We used 80% of the dataset for training and validation purposes and 20% as the holdout test set. We proposed a two-stage model: at stage one, we built a multi-scale, domain knowledge-guided attention model (MSGA) that encouraged the model to focus on specific areas of interest to enhance model explainability, including both high- and medium-resolution attentions; at stage two, we collected the output from MSGA and constructed a random forest (RF) classifier for patient-level diagnosis, to further boost model accuracy. RF classifier is utilized as a final decision stage since it is interpretable, computationally fast, and can handle correlated variables. Model utility was examined by (1) accuracy, represented by the area under the receiver operating characteristic curve (AUC) with standard deviation (SD), and (2) explainability, illustrated by the visual examination of the estimated attention maps which showed the important areas for model diagnostics.

Results:

During the training and validation stage, we observe that when we provide no guidance from domain knowledge, the IPF diagnosis model reaches acceptable performance (AUC±SD = 0.93±0.07),but lacks explainability; when including only guided high- or medium-resolution attention, the learned attention maps are not satisfactory; when including both high- and medium-resolution attention, under certain hyperparameter settings, the model reaches the highest AUC among all experiments (AUC±SD = 0.99±0.01) and the estimated attention maps concentrate on the regions of interests for this task. Three best-performing hyperparameter selections according to MSGA were applied to the holdout test set and reached comparable model performance to that of the validation set.

Conclusions:

Our results suggest that, for a task with only scan-level labels available, MSGA+RF can utilize the population-level domain knowledge to guide the training of the network, which increases both model accuracy and explainability.

1. INTRODUCTION

Idiopathic pulmonary fibrosis (IPF) is a specific form of chronic, progressive, irreversible, and usually lethal lung disease of unknown causes with an estimated median survival of 3–5 years since the initial diagnosis.¹ In clinical settings, making a correct, rapid, and reliable IPF diagnosis is critical to triage patients’ treatment planning into anti-fibrotic treatment or other causes of pulmonary fibrosis treatment, and even lung transplantation registry.²

According to the official clinical guideline,² computed tomography (CT) has become an integral part of the diagnosis of IPF. Radiological patterns of usual interstitial pneumonia (UIP) are the hallmark of IPF.² Specifically, several CT features are frequently observed in UIP patterns, including honeycombing, subpleural reticulation, and traction bronchiectasis in a lower lobe subpleural distribution.² The diagnosis of IPF involves the collaboration of multi-disciplinary discussion from specialists: clinicians, radiologists, and pathologists.² In more detail, patients suspected to have IPF should undergo an in-depth evaluation of potential causes or associated conditions, such as hypersensitivity pneumonitis, connective tissue disease, etc. If there is no potential cause identified, the chest CT patterns of the patient are evaluated. Despite the existence of these guidelines,² the evaluation of these radiological patterns is a difficult task and needs a multidisciplinary team of experts in interstitial lung disease (ILD) with subject to inter-observer variability.^3,4 The average time from the referral to multidisciplinary diagnosis is a year.

To this end, this research aims to develop a deep learning-based automated diagnosis system to distinguish IPF from non-IPF among subjects with ILD based on chest CT scans. This diagnostic system is a stand-alone system without requiring additional efforts from imaging analysts and radiologists, such as lung segmentation, contouring, or other disease assessment. The clinical meaning of this research area is to (1) reduce inter-observer variability in the IPF diagnosis task, (2) enable timely and reliable IPF diagnosis, and (3) enable early anti-fibrosis treatment which may prolong patients’ survival time in the long term.⁵

Several machine learning and deep learning approaches have been developed to provide diagnostic support for IPF.^6,7 For example, Walsh et al. trained a deep learning-based method to classify fibrotic lung disease into UIP, possible UIP, or inconsistent with UIP based on four CT slice combinations.⁸ Similarly, Christe et al. developed a pipeline for the automatic classification of CT images into several UIP patterns.⁹ The diagnostic pipeline involves lung segmentation and voxel-level tissue characterization. The development and maintenance of these techniques usually involve extensive collaborative efforts from radiologists, imaging analysts, software engineers, data scientists, which are not as desirable taking time and resource considerations into account.¹⁰

Moreover, some work in this area takes several CT slices as training or testing samples^8,11; whereas our work takes 3D CT volumes as input to utilize more information across the lungs.

In recent years, numerous deep learning-based algorithms have achieved great success in various medical imaging tasks, such as segmentation, diagnosis, detection, etc.^12,13 The successful application of deep learning systems in clinical practice relies on these three prerequisites: (1) the availability of well-labeled fine-scale data, which are usually at a pixel, regions of interests (RoI), or image slice level; (2) the extent of explainability on where and how the deep learning-based system makes the decision; and (3) the ability to generalize well to a new dataset.

Attention mechanisms, which originated from natural language processing, have gained substantial interests in research problems that deal with label scarcity, strengthen model generalizability to a new dataset, and encourage long-range dependencies in computer vision.^14–16 Attention mechanisms are one way to explain which region of the image the network’s decision depends on and can enhance the explainability of deep learning-based systems.¹⁷ Attention mechanisms have recently become popular in the medical imaging domain to solve the research question of segmentation^18–20 classification,^21,22 detection,²³ and so on. Notably, attention mechanisms are usually incorporated at multiple resolution scales, to encourage a more effective feature connection.^24,25 In this work, guided attention modules of multiple scales are implemented to encourage the deep learning-based system to focus on the areas of interests, which are lung parenchyma, especially the peripheral lung areas, based on the provided population-level domain knowledge (DK) acquired from prior studies.

The goal of this study is to develop an automated diagnosis system using deep learning that meets explainability and adequate model performance using chest high-resolution CT (HRCT) scans to distinguish IPF from non-IPF among subjects with ILDs.

1 |. MATERIALS AND METHODS

1.1 |. Datasets

Lung CT images in this research were collected from multi-center studies and the UCLA computer vision and imaging biomarkers (CVIB) Laboratory served as the imaging core facility. Only subjects with clinical diagnoses of ILD were included. A total number of 878 volumetric non-contrast HRCT scans were retrospectively collected IPF (N = 349, 39.7%) and non-IPF ILD cohorts (N = 529, 60.3%). In more detail, non-IPF subjects were clinically diagnosed as systemic sclerosis ILD (N = 230), rheumatoid arthritis (RA) ILD (N = 103), myositis ILD (N = 81), hypersensitivity pneumonitis ILD (N = 74), and Sjogren syndrome ILD (N = 41). CT images were collected from May 1997 to May 2018. We applied the stratified random sampling of IPF and non-IPF subjects: the training and validation set (N = 702, 80.0%, IPF% = 39.7%) and the testing set (N = 176, 20.0%, IPF% = 39.8%), as illustrated in Figure 1. As a result, the training, validation, and testing set are composed of CT scans collected from multi-center studies. A five-fold cross-validation was employed to the training and validation with stratification of IPF and non-IPF subjects: four subsets were used to construct the model and one subset was used to evaluate the model performance (shown as “Val” in Figure 1).

FIGURE 1.

The overall separation of the dataset. Val: validation, which is the subset that is used to evaluate the model performance at a specific fold

1.2 |. Image processing

HRCT scans underwent preprocessing (see Supporting information A for details). Each CT scan was standardized to the dimension 256 × 256 × 128, and further resampled a fixed number $\left(M\right)$ of 3D-volumes, with dimension 128 × 128 × 64 to boost sample size and reduce the data dimension. We use subject index $i$ and resample index $j=1,\dots ,M$; for example, $X_{ij}$ is the $j$ th sampled CT volume from subject $i$ (see Supporting information B and Table S1 for the key notations). The total number of resampling $M=20$ was chosen after the evaluation of balance in model performance and computational time (see the details of $M=1,10,20,30$ in Supporting information C.1 and Figure S1).

1.3 |. Elements of two-staged multi-scale guided attention and random forest model

During the model training stage, the input of the system contains three components: $\left\{\left(X_1,\dots ,X_N\right),\left(y_1,\dots \right.\right.,\left.\left.y_N\right),\widetilde{DK}\right\}$ and the expected output contains two parts: $\{\left({\hat{y}}_1,\dots ,{\hat{y}}_N\right),({\hat{\beta }}_{11},\dots ,{\hat{\beta }}_{NM})]$. Specifically, $X_i$ is the patient-level CT scan collected from subject $i;y_i\in \left\{\mathrm{0,1}\right\}$ is the ground truth indicating whether the subject $i$ is clinically diagnosed as IPF $\left(y_i=1\right)$ or non-IPF ILD $\left(y_i=0\right)$, which is used to compute the loss function for model training; $N$ is the number of subjects in the study; $\widetilde{DK}$ is a standardized quantitative measure of population-level DK collected from previous IPF studies, indicating which regions in lung parenchyma are typically prevalent in pulmonary fibrosis. ${\hat{y}}_i$ is the predicted label for scan $i$ and ${\hat{y}}_i\in \left\{\mathrm{0,1}\right\}$. ${\hat{\beta }}_{ij}$ is the estimated attention maps for scan $i$ and sample $j$, highlighting the regions that are closed to $\widetilde{DK}$ image. We implemented two attention multi-scale modules at a high- and medium-resolution level, then ${\hat{\beta }}_{ij}=({\hat{\beta }}_{ij}^h,{\hat{\beta }}_{ij}^m)$, where ${\hat{\beta }}_{ij}^h$ and ${\hat{\beta }}_{ij}^m$ are the estimated attention map at a high- and medium-resolution for a subject’s scan $i$ and sample $j$, respectively. During the model testing stage, only patient-level CT scans $\left(X_i\right)$ are required as model input and model output includes scan-level predictions (IPF vs. non-IPF, ${\hat{y}}_i$,) and estimated attention maps $({\hat{\beta }}_{ij})$.

The dimension of information is: (a) $X_i$ is usually of dimension 512 × 512 × number of CT slices, where 512 is the number of voxels in the $x$-and $y$-dimension for each CT slice; (b) standardized domain knowledge $\widetilde{DK}$ is a multi-dimensional array of dimension 256 × 256 × 128 as an input image. It is down sampled to high- and medium-resolutions, as represented by ${\widetilde{DK}}^h$ and ${\widetilde{DK}}^m$, which are dimension 64 × 64 × 32 and 16 × 16 × 8, respectively (Figure 2); (c) for the estimated attention maps, the dimensions of ${\hat{\beta }}_{ij}^h$ and ${\hat{\beta }}_{ij}^m$ are 64 × 64 × 32 and 16 × 16 × 8, respectively. The image dimension is represented as $H\times W\times D$ throughout this paper, where the depth dimension $D$ is the dimension along the patient’s body from apex to base and height–width $(H--W)$ plane is the axial plane of each CT slice. The dimension of intermediate features generated by 3D-convolutions is $H\times W\times D\times C$, where $C$-dimension is the channel dimension.

FIGURE 2.

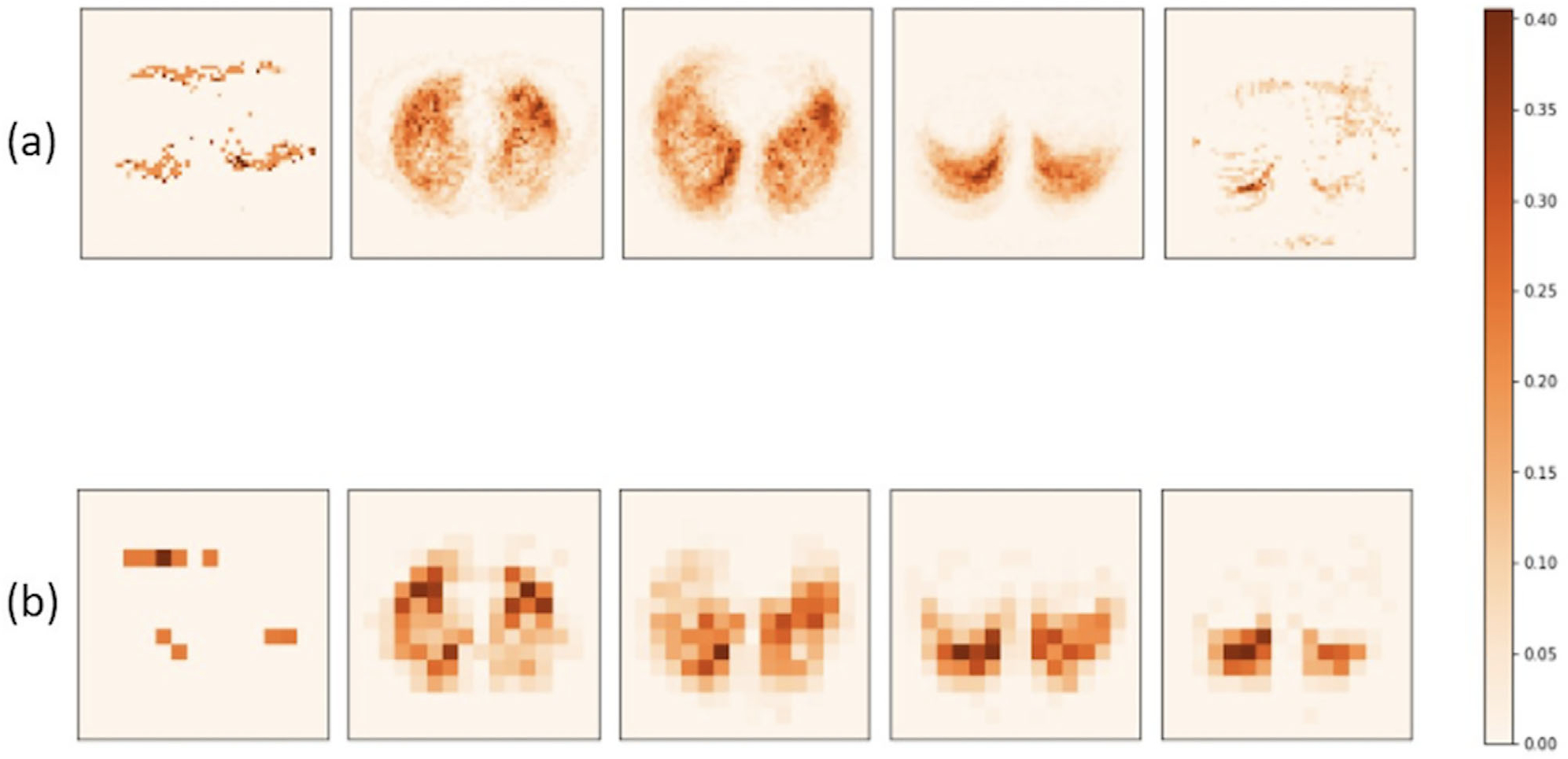
Population-level domain knowledge at high (a) and medium (b) resolutions. Subplots (a) are produced at the 3%, 28%, 53%, 78%, 97% position along the depth D-axis; subplots (b) are produced at the 13%, 38%, 63%, 75%, 88% position along the D-axis

1.4 |. Population-level domain knowledge

1.4.1 |. Explainability

In the past 10 years, quantitative CT imaging biomarkers have been developed and evaluated as clinical studies among patients with ILD.²⁶ These developed measures are spatially traceable and can be used as DK to guide the training of IPF diagnosis model.

Quantitative lung fibrosis (QLF) is a well-developed automated algorithm to classify CT voxels into different types, including normal, lung fibrosis, ground glass opacity, honeycombing etc.²⁷ In this study, QLF score is used to provide a DK map, which is defined as a marginal probability map that serves as a general guidance on where disease patterns usually locate, especially for IPF subjects. Therefore, DK is calculated before the training of the IPF diagnosis models and is not dependent on the training and testing procedure of the IPF diagnosis model.

DK is acquired as follows: (1) Voxel-level prediction: using the QLF algorithm to predict the CT scans from the 102 eligible IPF subjects on a voxel-level. We define ${\mathrm{D}\mathrm{K}}_v^t=1$ or 0 indicating if the scan for subject $t$ at voxel location $v$ is predicted as lung fibrosis; (2) Population-level sum and standardization: after acquiring the voxel-level prediction for all 102 subjects, we sum over all subjects for each voxel location by ${\mathrm{D}\mathrm{K}}_v={\sum }_{t=1}^T{\mathrm{D}\mathrm{K}}_v^t$, and then standardize to a scale of [0, 1]: ${\widetilde{DK}}_v=\frac{{\mathrm{D}\mathrm{K}}_v}{{\mathrm{m}\mathrm{a}\mathrm{x}}_v{\mathrm{D}\mathrm{K}}_v}$. By definition, $\widetilde{\mathrm{D}\mathrm{K}}$ ranges from 0 to 1.

Domain knowledge $\left(\widetilde{\mathrm{D}\mathrm{K}}\right)$ is later downsampled to two resolution scales: 64 × 64 × 32 and 16 × 16 × 8, as shown in Figure 2. A 3D representation of the DK map is provided in Supporting information D and Figure S2. Higher intensity values (more orange) in Figure 2 represent a greater value of ${\widetilde{\mathrm{D}\mathrm{K}}}_v$, which concentrates on the Rol for this IPF diagnosis task. Lung areas, especially peripheral lungs, are highlighted in Figure 2, which agrees with IPF-related CT features. In the future sections, we will discuss how DK is incorporated as an integral part of the loss function during training to encourage the model to focus on IPF disease patterns.

1.5 |. Attention gates

We provide a schematic of the proposed guided attention gates in Figure 3. The attention gates take intermediate feature maps $x$, and population-level domain knowledge $\widetilde{\mathrm{D}\mathrm{K}}$ as input and produce two outputs: (1) a feature map $A\left(x\right)$ with the same dimension as the input $\left(x\right)$, and (2) an estimated attention map $\hat{\beta }\mid x$. For simplicity, $\hat{\beta }\mid x$ is represented as $\hat{\beta }$ throughout the paper. Theoretically, attention gates can be incorporated in any layer of any existing $\mathrm{C}\mathrm{N}\mathrm{N}$ architecture. In this work, we focus on the attention gates that are suitable for 3D-CNN architectures, which generate intermediate feature maps of four dimensions, including height, width, depth, and channel.

FIGURE 3.

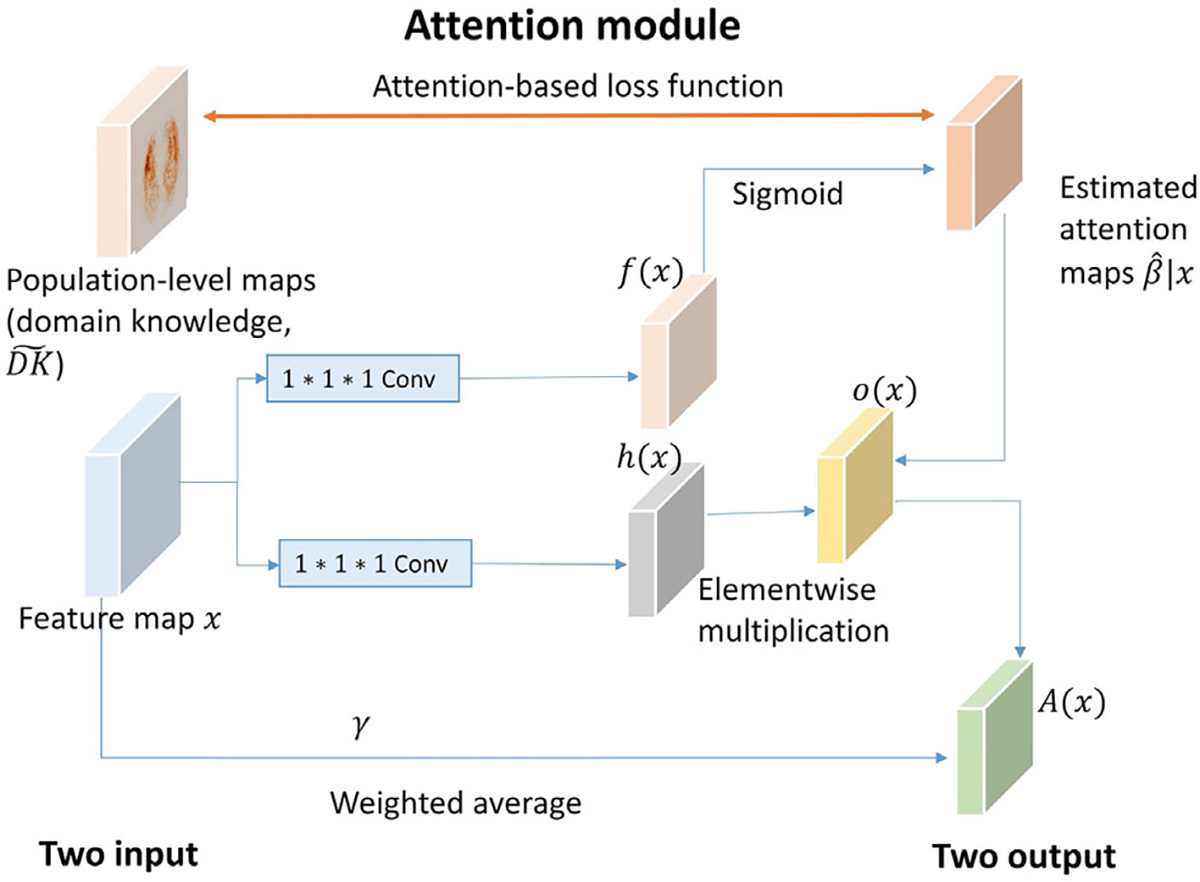
Attention gate (AG) modules

Suppose the attention gates are implemented at the $I^{\text{th}}$ layer and takes the intermediate feature maps $x^l$ that are generated at the previous layer, that is, $(l-1{)}^{\text{th}}$ layer, as input. For 3D-CNN architectures, $x^l$ is a four-dimensional tensor with $x^l\in {\mathbb{R}}^{H^l\times W^l\times D^l\times C^l}$, where $H^l,W^l,D^l,C^l$ are the height, weight, depth, the number of channels at the $l^{\text{th}}$ layer, respectively. For simplicity, we omit the subject index $i$ and sample index $j$ throughout this section $E$. The intermediate feature maps $x^l$ are first transformed into two feature spaces $f(x{)}^l$ and $h(x{)}^l$ using 1 × 1 × 1 convolutions: $f(x{)}^l=x^l\times W_f^l,h(x{)}^l=x^l\times W_{h^{\mathrm{\text{'}}}}^l$ where $W_f^l\in {\mathbb{R}}^{C^l},f(x{)}^l\in {\mathbb{R}}^{H^l\times W^l\times D^l},W_h^l\in {\mathbb{R}}^{C\times C^l},h(x{)}^l\in {\mathrm{R}}^{H^l+W^l\times D^l\times C^l}$

A sigmoid function is applied to the feature space $f(x{)}^l$ to calculate the attention scores (i.e., estimated attention maps) at layer $/$ at a three-dimensional voxel location $v=(v^{H^l},v^{W^l},v^{D^l}),{\hat{\beta }}_v^l$, where ${\hat{\beta }}_v^l=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(-f(x{)}_v^l)}$. Here, ${\hat{\beta }}_v^l$ is a scalar, and $v^{H^l}\in {\mathbb{R}}^{H^l},v^{W^l}\in {\mathbb{R}}^{W^l},v^{D^l}\in {\mathbb{R}}^{D^l}$. The dimension of ${\hat{\beta }}^l$ is decided by the choice of layers $l$, where the attention module is implemented in. In our example, let the model layers where the attention modules are incorporated be $l=h$ and $l=m$, which represent the high and medium attention, respectively. Based on our design, $\beta$ h is a three-dimensional tensor with ${\beta }^h\in {\mathbb{R}}^{H^h\times W^h\times D^h}={\mathbb{R}}^{\text{64}\times \text{64}\times \text{32}}$ and ${\beta }^m\in {\mathbb{R}}^{H^m\times W^m}\times D^m={\mathbb{R}}^{16\times 16\times 8}$.

We further calculate the element-wise multiplication of $h(x{)}^l$ and the estimated attention maps ${\hat{\beta }}^l$ across each channel: $o(x{)}_c^l={\hat{\beta }}^l\odot h(x{)}_c^l$, where $o(x{)}_c^l$ is the cth channel of the intermediate feature maps $o(x{)}^l,o(x{)}_c^l\in {\mathbb{R}}^{H^l\times W^l\times D^l};h(x{)}_c^l$ is the cth channel of $h(x{)}^l,h(x{)}_c^l\in {\mathbb{R}}^{H^l\times W^l\times D^l}$, and $\mathrm{\Theta }$ is the elementwise multiplication operation.

The final output of the attention gate $(A(x{)}^l)$ is a weighted average of the input intermediate feature maps $x$ and $o(x):A(x{)}^l={\gamma }^l\times o(x{)}^l+\left(1-{\gamma }^l\right)\times x^l$, where ${\gamma }^l$ is a trainable scalar parameter initialized at zero.

1.6 |. Multi-scale guided-attention model

1.6.1 |. Loss function

We use the voxel-wise mean absolute error as the attention-based loss to measure the similarity between the estimated map of each sample $({\hat{\beta }}_{ij}^l)$ with the provided population-level maps $({\widetilde{DK}}^l):L_{ij}^l=\mathrm{a}\mathrm{v}\mathrm{g}(|{\hat{\beta }}_{ij}^l-{\widetilde{DK}}^l|)$ where ${\hat{\beta }}_{ij}^l$ is the estimated attention maps for subject $i$ and sample $j$ at layer $l,{\widetilde{\mathrm{D}\mathrm{K}}}^l$ is the rescaled domain knowledge map at layer $I$ that has the same dimension as ${\hat{\beta }}_{ij}^l$, and $\mathrm{a}\mathrm{v}\mathrm{g}(x)$ is the grand average of all elements from a tensor $x$.

During training, the attention-based loss function is calculated by averaging all the samples: $L^l=\frac{{\sum }_{i=1}^N{\mathrm{\Sigma }}_{j=1}^M{L}_{ij}^l}{NM}$. In this work, we introduced two attention modules at high- and medium-resolution scales; therefore, attention-based loss $\left(L^l\right)$ is incorporated into the overall loss function under two forms: $L^h$ and $L^m$, where $h$ and $m$ represent high and medium.

1.6.2 |. Explainability

The overall schematic diagram of MSGA is provided in Figure 4b. 3D-residual blocks are used as building blocks for our model, which is shown as RB1, RB2, and RB3 in Figure 4b). Detailed implementations of 3D-residual blocks, including layer name, hyperparameters, and output size, are provided in Supporting information E and Table S2. For each scan $i$, we first produce $M$ number of 3D samples for each scan, indexed by $j=1,\dots ,M$. During the model training procedure, the system includes three types of input: the processed CT scans $\left(X_i\right)$, the population-level domain knowledge maps at two resolution scales (${\widetilde{\mathrm{D}\mathrm{K}}}^h$ and ${\widetilde{\mathrm{D}\mathrm{K}}}^m$), and the patient-level clinical ground truth $\left(y_i\right)$. MSGA takes each sample as a training or testing unit and produces three types of output for each input sample: the sample-level predicted score of being IPF $\left({\hat{p}}_{ij}\right)$ the learned attention map at different resolution scales (${\hat{\beta }}_{ij}^h$ and ${\hat{\beta }}_{ij}^m$) and the estimated attention-based loss values at two resolution scales $\left(L_{ij}^h\right.$ and $L_{ij}^m$). The attention gates are incorporated into the training of the IPF diagnosis model in an end-to-end manner, at two resolution scales, shown as AG1 and AG2.

FIGURE 4.

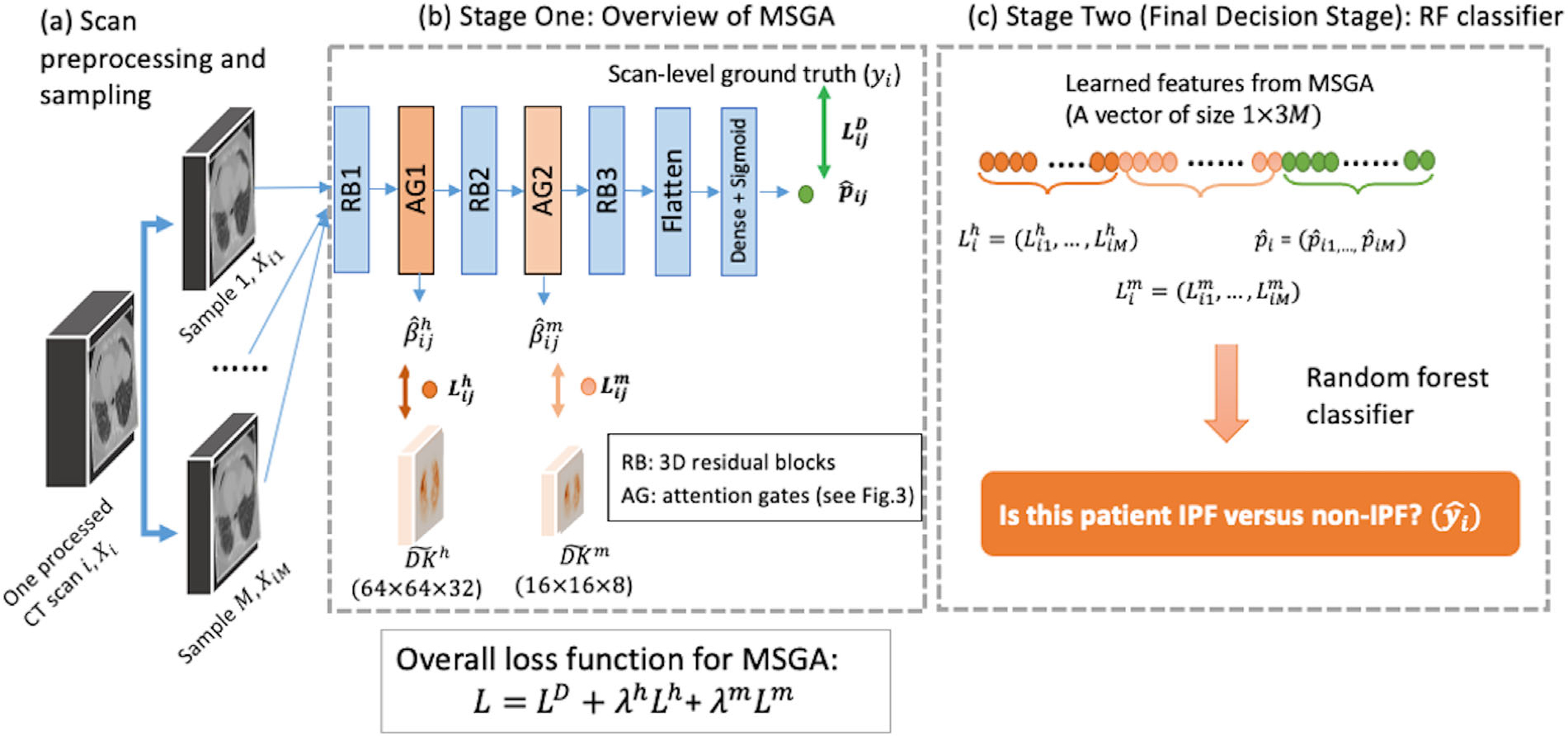
Schematic of the overall system. First, a total number of Msamples are generated from one processed computed tomography (CT) scan $\mathbf{i},{\mathbf{X}}_{\mathbf{i}}$. The samples are presented as ${\mathbf{X}}_{\mathbf{i}\mathbf{j}}$, where $\mathbf{j}=1,\dots ,\mathbf{M}$. Multi-scale, domain knowledge-guided attention (MSGA) takes each function at a high- $\left({\mathbf{L}}_{\mathbf{i}\mathbf{j}}^{\mathbf{h}}\right)$ and medium- $\left({\mathbf{L}}_{\mathbf{i}\mathbf{j}}^{\mathbf{m}}\right)$, and the estimated attention maps at a high- $({\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}}_{\mathbf{i}\mathbf{j}}^{\mathbf{h}})$ and medium- $({\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}}_{\mathbf{i}\mathbf{j}}^{\mathbf{m}})$ resolutions. The overall loss function for MSGA is a weighted average of three loss function components: overall IPF diagnosis loss (${\mathbf{L}}^{\mathbf{D}}$), attention-based loss at a high- (${\mathbf{L}}^{\mathbf{h}}$) and medium- $\left({\mathbf{L}}^{\mathbf{m}}\right)$ resolution. At the final decision stage, random forest (RF) takes the output from MSGA from all M samples and produces a patient-level diagnosis. RB: 3D residual blocks; AG: attention gates (see Figure 3 for the details)

Binary cross-entropy loss is used for the IPF diagnosis task:

$$L^D=-\frac{1}{NM}{\sum }_{i=1}^N{\sum }_{j=1}^M\left[y_i\mathrm{l}\mathrm{o}\mathrm{g}\left({\hat{p}}_{ij}\right)+\left(1-y_i\right)\mathrm{l}\mathrm{o}\mathrm{g}\left(1-{\hat{p}}_{ij}\right)\right]$$

where $y_i=0,1$ if the subject $i$ is clinically diagnosed as non-IPF or IPF, respectively, and ${\hat{p}}_{\tilde{i}}$ is the predicted probability of subject $i$, sample $j$ being IPF at the last layer of MSGA.

The overall loss function of the system is composed of a weighted average of two attention-based losses and one diagnosis-based loss:

$$L=L^D+{\lambda }^h{L}^h+{\lambda }^m{L}^m,$$

where $L^D$ is the binary cross-entropy for IPF diagnosis, $L^h$ is the attention-based loss at a high resolution, $L^m$ is the attention-based loss at a medium resolution. ${\lambda }^h$ and ${\lambda }^m$ are the relative task importance for the high- and medium-resolution attention models, respectively, with ${\lambda }^h\ge 0$ and ${\lambda }^m\ge 0$. We note that when setting ${\lambda }^h=0$ and ${\lambda }^m=0$, this represents a scenario where both attention modules are unguided with population-level maps (see Figure 5 for IPF and Figure S3 for non-IPF examples of the estimated AG1 and AG2).

FIGURE 5.

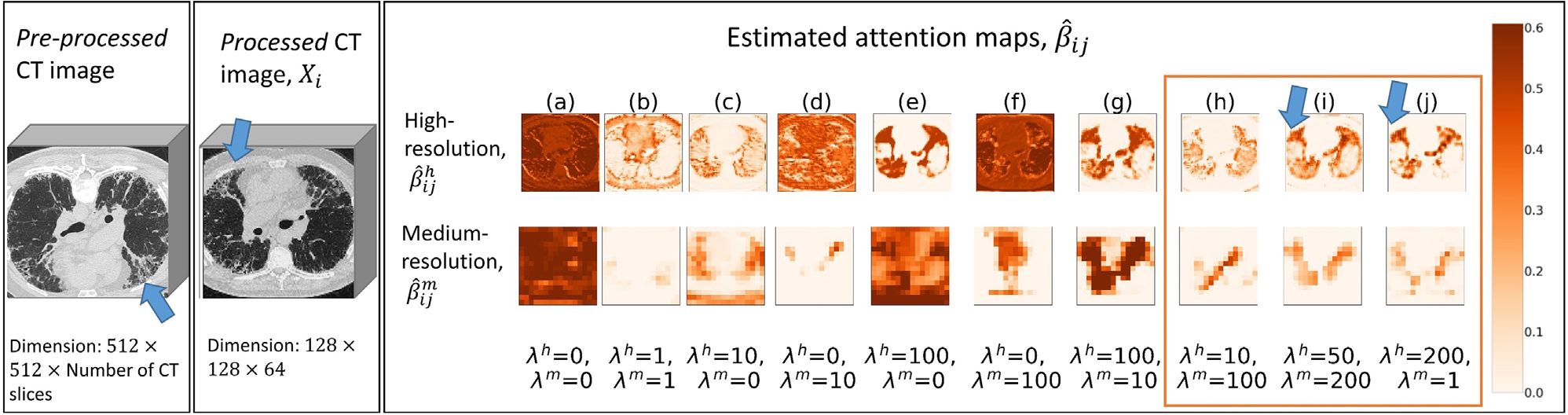
Estimated attention map for an idiopathic pulmonary fibrosis (IPF) subject with 10 different hyperparameters. One representative computed tomography (CT) slice (slice number = 153; in total 309 slices for this scan) of the pre-processed image is provided. One processed CT image is plotted at D = 33 out of 64. The estimated attention maps for high- and medium-resolutions are plotted at D = 17 out of 32 and D = 5 out of 8, respectively. Key CT features of usual interstitial pneumonia (UIP) are highlighted as arrows. Three top performing combinations based on multi-scale, domain knowledge-guided attention (MSGA) are highlighted as an orange rectangle. The models that used this scan as validation samples were selected for plotting. For all ten hyperparameter collections (𝝀^h and 𝝀^m), both MSGA and MSGA+RF successfully classify this scan as IPF (true positives)

1.6.3 |. Evaluation of explainability

We provide both qualitative and quantitative methods to examine the extent of explainability in this research. Qualitatively, the scan-level estimated attention maps at both high- and medium-resolution can be viewed to see if highlighted areas correspond to disease-specific regions (Figure S4). This method can shed some light on what specific regions are critical for this IPF diagnosis task.

From a quantitative perspective, previous research has shown that histogram analysis of the segmented lung areas is associated with the disease progression of IPF subjects.²⁸ Specifically, a low kurtosis of lung regions is found to be associated with a higher risk of mortality. In this study, we use kurtosis from the estimated attention maps as an explainability index to identify patients with IPF from other causes of pulmonary fibrosis. More technical details are provided in the Supporting information G and Table S3.

1.7 |. Random forest classifier

1.7.1 |. Enhanced improvement

Random forest (RF) is a popular supervised machine learning approach, where the model output is decided based on majority voting of multiple decision trees.²⁹ For a classification task, such as patient-level IPF diagnosis, RF outputs the mode of the classes (IPF vs. non-IPF) predicted by individual decision trees. It has been widely used in medical fields due to its high accuracies, robustness to outliers, explainable nature, and a possibility of parallel processing.³⁰ RF is chosen as the final stage classifier for this research since (1) it is easy to implement and computationally fast; (2) it can handle correlated variables, for example, in our case, the estimated attention loss from M samples; and (3) it is a relatively interpretable algorithm where the variable importance can be used to empirically understand the model decision process.

The intuition of adding RF in the final decision stage is that the high magnitude of attention-based loss ($L_i^h$ and $L_i^m$) in the training model can also play a role in the feedback loop of improving the classification of IPF and non-IPF, where the hyperparameters are not close to optimal (Figure S5 for the variable importance in RF). We provide a figure (Figure S6), which shows the distribution of the estimated attention loss values is visually different for IPF and non-IPF subjects. The estimated attention-based loss depicts how each processed CT scan differs from the population-level IPF information. Therefore, we utilize the information of difference of the processed CT scan from the population-level IPF information (i.e., $L_i^h$, and $L_i^m$) as well as the predicted probability (i.e., ${\hat{p}}_i$) for IPF diagnosis.

For each CT scan $i$, we leverage these three types of information acquired from all samples, including the estimated high- $\left(L_i^h=\left(L_{i1}^h,\dots ,L_{iM}^h\right)\right)$ and medium- $\left(L_i^m=\right.\left.\left(L_{i1}^m,\dots ,L_{iM}^m\right)\right)$ resolution attention loss and the predicted probability of being $\mathrm{I}\mathrm{P}\mathrm{F}\left({\hat{p}}_i=\left({\hat{p}}_{i1},\dots ,{\hat{p}}_{MM}\right)\right)$, to build an RF model that classifies whether a given CT scan is from an IPF subject or a non-IPF ILD subject. For each scan, the designed MSGA produces a vector of size $1\times M$ for $L_i^h,L_i^m,{\hat{p}}_{\text{in}}$, respectively, representing the estimated high-, medium attention-based loss function and the predicted IPF score from the $M$ samples. This is later combined into a vector of size $1\times 3M$, in our case, $1\times 60$, as the input for the RF model, as shown in Figure 4c).

After the training process of the MSGA is completed, we continue to build an RF-based classifier for each hyperparameter selection (${\lambda }^h$ and ${\lambda }^m$) and for each fold. At each fold, we construct an RF using training samples only. For simplicity, we fix the hyperparameters during the training of RF for each model: RF classifier was consistently configured to use 90 decision trees with a maximum depth of 4.

1.8 |. Overall proposed method: multi-scale, domain knowledge-guided attention +random forest

We propose a two-stage model for scan-level IPF diagnosis.

1.8.1 |. Stage one (multi-scale, domain knowledge-guided attention)

For each CT scan $i$, MSGA provides (1) two estimated attention maps at high- and medium- resolutions and (2) three outputs, including the loss function for high- $\left(L_i^h\right)$ and medium- $\left(L_i^m\right)$ attention gates, and the binary cross-entropy loss for IPF diagnosis $\left(L_i^D\right)$. The training process of stage one is end-to-end. For each hyperparameter selection, we constructed five MSGA models, leaving one fold of data as the validation set as a time.

1.8.2 |. Stage two (random forest)

For each CT scan, RF takes the features produced by MSGA as input and produces the final probability of being IPF for each scan. We then built an RF model for each MSGA model using the training cases in that fold only. The mean and standard deviations (SDs) across five folds for both MSGA and MSGA+RF were reported as validation set performance. Based on the validation set performance, we further selected the best performing hyperparameter combination as our final model to apply to the test set. Test set performance was reported as the mean and SD across five-fold models.

1.9 |. Model implementation details

For model training, we used Adam optimizer with an initial learning rate of 10⁻⁴, followed by an exponential decay after 20 epochs of decay rate 0.05. The batch size was set to be 5 and the model trained after 200 epochs was saved for evaluation. The hardware of Tesla V100-SXM2–32GB and GeForce RTX 2080 Ti and Keras framework were used.³¹ Sensitivity analysis of epoch numbers is included in Supporting information C.

2 |. RESULTS

2.1 |. Model results: multi-scale, domain knowledge-guided attention (validation set performance)

We report the performance of MSGA from two perspectives of accuracy and explainability. Accuracy was assessed by the area under the curve (AUC) from an ROC analysis. The other assessment is done to visually examine explainability, which is characterized by reviewing the estimated attention maps.

2.1.1 |. Multi-scale, domain knowledge-guided attention model accuracy: idiopathic pulmonary fibrosis diagnosis

Regarding the sample-level IPF diagnosis, Table 1 summarizes the AUC values of MSGA with mean and SD across folds under the validation set, with different selections of hyperparameters (${\lambda }^h$ and ${\lambda }^m$). Both ${\lambda }^h$ and ${\lambda }^m$ are selected from a range of values: 0, 1, 10, 50, 100, 200. This range of hyperparameter searching was selected by examining the empirical values of each loss function component. Also, similar work which optimizes a multi-objective loss function utilizes hyperparameters within this range.^17,21

TABLE 1.

Area under curve (AUC) mean and standard deviation values of multi-scale, domain knowledge-guided attention (MSGA) performance on validation set for various λ^h and λ^m (task importance) parameters

		λm
		0	1	10	50	100	200
λh	200	0.87 (0.14)	0.98 (0.02)	0.88 (0.21)	0.89 (0.18)	0.87 (0.21)	0.97 (0.02)
	100	0.85 (0.20)	0.96 (0.04)	0.86 (0.20)	0.90 (0.10)	0.84 (0.21)	0.97 (0.03)
	50	0.83 (0.20)	0.88 (0.09)	0.89 (0.22)	0.84 (0.22)	0.97 (0.01)	0.98 (0.02)
	10	0.87 (0.21)	0.92 (0.09)	0.84 (0.17)	0.85 (0.21)	0.99 (0.01)	0.81 (0.23)
	1	0.87 (0.18)	0.84 (0.21)	0.95 (0.07)	0.89 (0.08)	0.89 (0.12)	0.76 (0.23)
	0	0.93 (0.07)	0.93 (0.07)	0.93 (0.09)	0.86 (0.15)	0.94 (0.04)	0.85 (0.21)

Note: λ^h and λ^m are the relative task importance parameters in the overall loss function, representing high- and medium-resolution attentions, respectively. Three top performing combinations (λ^h = 200 and λ^m = 1; λ^h = 50 and λ^m = 200; λ^h = 10 and λ^m = 100) are in bold font.

As shown in Table 1, without including guided attention by attention-based loss function (${\lambda }^h=0$ and ${\lambda }^m=$ $0$), the IPF diagnosis model reached an AUC $(\pm \mathrm{S}\mathrm{D})$ of $0.93(\pm 0.07$). In most cases (9 out of 10 hyperparameter combinations), only incorporating guided high- $\left({\lambda }^h>0\right.$ and $\left.{\lambda }^m=0\right)$ or medium-resolution attention $\left({\lambda }^h=0\right.$ and ${\lambda }^m>0$) decreased the performance of IPF diagnosis, compared to without guided attention in the loss function (${\lambda }^h=0$ and ${\lambda }^m=0$). Under one hyperparameter setting $\left({\lambda }^h=0\right.$ and $\left.{\lambda }^m=100\right)$, the average AUC across five folds is 0.94, which is slightly higher than that of the unguided model (average AUC$=0.93$).

Our proposal, which included both high- and medium-resolution attentions, was able to reach the highest AUC (± SD) value of $0.99(\pm 0.01)$ for all of the experiments, under certain hyperparameter selections (${\lambda }^h=10$ and ${\lambda }^m=100$). Three top performing hyperparameter combinations are (1) ${\lambda }^h=200$ and ${\lambda }^m=1;$ (2) ${\lambda }^h=50$ and ${\lambda }^m=200;$ (3) ${\lambda }^h=10$ and ${\lambda }^m=100$. Notably, model performance is sensitive to the selection of relative task importance. For example, under certain hyperparameter combinations, that is, ${\lambda }^h=1$ and ${\lambda }^m=200$, the AUC (± SD) decreased to $0.76(\pm 0.23)$.

2.1.2 |. Model explainability: estimated attention maps

We explored the model explainability by plotting the estimated attention maps at both high- and medium-resolutions $({\hat{\beta }}_{ij}^h,{\hat{\beta }}_{ij}^m)$ using one randomly sampled IPF as an example, shown in Figure 5. We also provided one non-IPF ILD subject in Supporting information F and Figure S3. We note that without guided attention models (Figure 5, column a), the observed attention maps are uninformative and lack explainability.

When we provide guidance from population-level DK in constructing the overall loss function, the estimated attention maps begin to focus on the lung parenchyma. Specifically, when the relative task importance is low (column b), the attention maps begin to concentrate on the lungs, but it is not clear. When we add solely the high-resolution guided attention in the loss function (Figure 5, columns c and e), visual examinations indicate that high-resolution attention maps can characterize the lungs, while the medium-resolution attention maps are less informative. On the other hand, when only medium-resolution guidance is added (Figure 5, columns d and f), both high- and medium-resolution attention maps do not concentrate on the lung parenchyma.

Finally, when we provide guidance on both high- and medium-resolution attentions with considerable relative task importance (Figure 5, columns g, h, i, and j), the estimated attention maps become instructive, focus on the lung parenchyma, and suppress irrelevant background areas. Under certain hyperparameter collection (columns h, i, and j), both the estimated attention map and a high- and medium-resolution can focus on peripheral lungs, which are the key regions for making a correct IPF diagnosis. These highlighted areas are critical for this task of IPF diagnosis and are incorporated into the training of deep learning systems.

2.2 |. Model results: multi-scale, domain knowledge-guided attention +random forest (validation set performance)

Table 2 summarizes the model performance using MSGA+RF with mean and SE across five folds under the validation set, under different selections of hyperparameters $\left({\lambda }^h\right.$ and $\left.{\lambda }^m\right)$. Top three hyperparameter selections based on MSGA remained one of the best performing hyperparameter groups for MSGA+RF (average $UC\ge 0.98$); therefore, these three models were selected as best performing models and were used as the final models for this task (see Table S4 for the each fold).

TABLE 2.

Area under curve (AUC) mean and standard deviation values of multi-scale, domain knowledge-guided attention + random forest (MSGA+RF performance on validation set for various λ^h and λ^m (task importance) parameters

		λm
		0	1	10	50	100	200
λh	200	0.95 (0.04)	0.98 (0.01)	0.99 (0.01)	0.97 (0.01)	0.97 (0.04)	0.98 (0.02)
	100	0.97 (0.03)	0.98 (0.02)	0.97 (0.03)	0.95 (0.06)	0.96 (0.04)	0.97 (0.02)
	50	0.97 (0.03)	0.96 (0.03)	0.97 (0.03)	0.94 (0.05)	0.97 (0.02)	0.98 (0.02)
	10	0.95 (0.06)	0.98 (0.02)	0.97 (0.03)	0.95 (0.05)	0.99 (0)	0.96 (0.02)
	1	0.99 (0.02)	0.98 (0.02)	0.97 (0.05)	0.94 (0.05)	0.97 (0.03)	0.92 (0.08)
	0	0.97 (0.03)	0.98 (0.01)	0.99 (0.01)	0.94 (0.04)	0.95 (0.03)	0.95 (0.06)

Note: λ^h and λ^m are the relative task importance parameters in the overall loss function, representing high- and medium-resolution attentions, respectively. Three top performing combinations based on MSGA (λ^h = 200 and λ^m = 1; λ^h = 50 and λ^m = 200; = 10 and = 100) are in bold font.

We also calculated and plotted the variable importance for the constructed RF using the normalized total reduction of Gini impurity brought by each feature (as shown in Supporting information H). Variable importance plots show that when MSGA can perform well (Figure S5a), RF mostly leveraged information from the predicted probability of IPF generated in the last layer of MSGA for the final classification; when MSGA performs unsatisfactorily (Figure S5c), attention-based loss values play a role in the final classification of MSGA+RF and boosted the model performance.

2.3 |. Test set performance

Based on the validation set performance and the estimated attention maps, we applied the three best performing models to the holdout test set $(N=176)$. The three best performing models (i.e., (1) ${\lambda }^h=$200 and ${\lambda }^m=1$; (2) ${\lambda }^h=50$ and ${\lambda }^m=200$; (3) ${\lambda }^h=$10 and ${\lambda }^m=100$) had the AUC (± SD) values 0.987 (±0.007), 0.975 (±0.011), and 0.980 (±0.018), respectively.

3 |. DISCUSSIONS AND CONCLUSIONS

We presented a two-stage model for automated IPF diagnosis among subjects with ILD based on chest HRCT images. The model combines an MSGA, for explainability and an RF model for enhancing accuracy in the final decision. MSGA+RF is well-suited for other weakly supervised tasks in medical imaging domains, where population-level DK is available. Several advantages can be addressed using MSGA+RF.First,population-level DK from the prior studies was utilized, which may overcome the black-box approaches of deep learning and the time and expert-dependent labeling of machine learning. Guided with population-level DK at various resolution scales, we can accomplish satisfactory model performance only using the clinical information of IPF diagnosis in subjects with ILD.

Second, using attention models at various resolution scales increase model explainability, which is a crucial step for transparency in AI for medical applications. Over the past decade, there have been extensive discussions regarding enhancing the explainability of deep learning-based systems, especially in clinical settings.³² Building explainable deep learning models can increase trust in models and it is a critical step for model diagnostics. Saliency maps,³³ and class activation mapping³⁴ are effective post hoc methods for visualizing deep learning models; attention mechanisms, on the other hand, can encourage the network to focus on specific areas of interest (in our case, lung parenchyma) in a trainable and end-to-end manner. Furthermore, using attention models at different resolution scales can effectively capture more useful information for this diagnosis task and improve model performance. For example, low-resolution attention gates can focus more on the overall disease distribution, whereas high-resolution attention gates are able to capture more detailed disease characteristics. Previous research also found that combining multi-scale features can improve model performance.^20,35

The third advantage is in accuracy. To boost model performance, traditional machine learning models tend to increase model accuracy by adding model features in a classifier.³⁶ We borrowed a similar idea here by adding RF classifiers using the feature sets learned from the estimated loss function of learning from MSGA, as the final decision stage. This is necessary since we note that results on the validation set are sensitive to the selection of relative task importance (i.e., λ^h and λ^m). For example, in Table 1, 36 hyperparameter combinations,7 out of 36 combinations have a mean AUC less than 0.85 using stratified five-fold cross-validation on the validation sets. However, after adding the RF classifier, as results shown in Table 2, all 36 combinations have a mean AUC greater than 0.92. Therefore, in our example, having a two-stage model increases the model’s robustness against changes regarding relative task importance. Overall, RF can boost the performance of the worst-performing models, but it does not aid the best-performing models. The ceiling effect may be one reason since the three best-performing models have achieved an AUC of greater than 0.98 without RF, leaving limited room for improvement.

Based on our understanding, it is infeasible to compare our results with other literature since little research has been concentrated on developing automated software for a scan-level IPF diagnosis. On a similar note, Walsh et al. developed an algorithm to classify several CT slices into different UIP patterns and reported an accuracy of 76.4% on the test set.⁸ Christe et al. built an automated UIP classification model that includes lung segmentation, tissue characterization, and quantification. This algorithm can perform on par with radiologists with a reported accuracy of 81%.⁹ The novelty of this study is to utilize the DK and multi-scale attention gated model. The DK of the expected spatial location in ILD patterns in the lung serves as indirect lung segmentation. Multi-scale attention models increase the explainability of this model, increase model performance, and lead to reliable measurements.

Most of the criticism in deep learning models is that model accuracy does not guarantee satisfactory model explainability on the validation set in deep learning. To overcome this issue, we designed a two-stage model that combines explainability achieved by a deep learning approach, MSGA, and accuracy by a machine learning technique, RF. Strengthened by the combined benefit of a transparent model decision process and boosted diagnostic performance, the proposed method serves as an important step for clinical applications.

Certain limitations exist in this work: (1) the current MSGA setup requires population-level DK acquired from prior studies; (2) only volumetric CT scans with consistent slice spacing were included in the training and testing sets, which limited the applicability of this trained model to other non-volumetric CT scans; (3) the selections of relative task importance requires extensive computational time and resources in hyperparameter selections. (4) It is worth investigating the model performance when applying to datasets from different institutions, which may contain CT scans collected from different non-IPF disease types, disease severity, and various CT imaging protocols. Although some research works demonstrated the superior generalizability of attention models to unseen datasets,¹⁶ the evaluation of our proposed model to independent datasets is underway and is out of the scope of this paper.

In this paper, we have developed an automated IPF diagnosis using CT images and demonstrated a promising method of attention maps for both enhancing explainability and increasing performance. Future work includes examining the trained MSGA+RF on independent cohort and prospective studies.

DATA AVAILABILITY STATEMENT

Raw data were generated from UCLA. Derived data from HRCT images supporting the findings of this study are available from the corresponding author GK on reasonable request.