Abstract
The impact of COVID-19 on stock market dynamics and other macroeconomic indicators has been extensively researched. However, the question of how it affects corporate vulnerability has received less attention. This article aims to fill this gap by examining the implications of COVID-19 on corporate vulnerability in the United States (US) and China, using daily data from January 2020 to December 2021. The empirical results of cointegration analysis demonstrate that COVID-19 considerably worsen corporate vulnerabilities in the long-term in the US and in the short-term in China. Additionally, non-linear results demonstrate long-run asymmetries in the US and short-run asymmetries in China, confirming the accuracy of error prediction and suggesting that US corporations are more exposed to COVID-19-induced risks. The channels through which COVID-19 may affect corporate vulnerability include changes in consumer behavior and demand, disruptions in supply chains, financial stress, government policies and regulations, and changes in the competitive landscape. This study sheds light on the effects of the COVID-19 pandemic on corporate vulnerability in the US and China, revealing regulatory implications that may necessitate greater government involvement, managerial implications that emphasize risk management and contingency planning, and social implications that highlight the importance of prioritizing stakeholder welfare and embracing digital transformation.
Keywords: COVID-19, Corporate vulnerability, Nonlinear ARDL, Machine learning, US, China, Dynamically Simulated ARDL
1. Introduction
Historically, it is evident that global financial markets and the corporate world in general, are greatly affected by global crises, whether they are financial, global pandemics, or geopolitical in character. Recent events such as COVID-19 and the Russian invasion of Ukraine have devastated the global economy and corporate world. According to Alshater, Alqaralleh, and El Khoury (2023) the most recent pandemic saw an increase in the total volatility spillover, which is driven primarily by short-term events. Investment returns are favorably guided by government action in response to COVID-19, as shown by Guven, Cetinguc, Guloglu, and Calisir (2022). However, daily increases in fatalities and new cases also have an unsettling impact on the value of stocks.
During the COVID–19 pandemic, financial contagion is spread in part through the media. In March and April, there is a strong link between the media and ESG indices, and during the pandemic, the US is experiencing more shocks than it is delivering (Akhtaruzzaman, Boubaker, & Umar, 2022). Where there are extreme negative bank returns, jumps in volatility are very important. During COVID-19, this effect is stronger than it was during the global financial crises (Batten, Choudhury, Kinateder, & Wagner, 2022). Gold, U.S., UK, and German sovereign bonds constitute a safe option for investors, especially during times of extreme volatility when widespread panic prevails (Kinateder, Campbell, & Choudhury, 2021). Stock returns decline as the number of proven COVID-19 cases rises, although this negative effect is mitigated for larger, lower-debt, more diversified, and more democratically-run firms (Hoang, Nguyen, & Nguyen, 2022). The authors claim that the connection between stock returns and COVID-19 is strongly moderated by national cultural practices and traditions.
Societies that are more collectivistic and cooperative, less tolerant of uncertainty, and more long-term oriented can mitigate the detrimental effects of COVID-19. The detrimental impact of the pandemic on stock market performance varies widely across industries, and fearful investors may compound this by selling their shares at a loss (Liu, Dai, Huynh, Zhang, & Zhang, 2022). Globally, Asian markets took a relatively larger loss (Pandey & Kumari, 2021). Weber and Huynh (2022) identify a number of firm characteristics that are associated with a higher probability of pandemic response, including some that are typically associated with a diminished ability to respond to market conditions, such as state ownership. Pandey, Kumari, and Tiwari (2022) suggest policymakers boost share prices during crises with corporate announcements. Investors will benefit from a deeper understanding of the stock market and should make wise decisions before reacting to corporate actions during a pandemic or emergency. Investors focus on portfolio risk-return parameters, while policymakers focus on share prices.
Despite many nations’ governments introducing substantial countermeasures such as severe lockdowns to contain the spread of the coronavirus, the subsequent economic problems triggered continue to affect people, businesses, and economies to this day. This humanitarian crisis poses many economic and financial challenges for each nation depending on the nature and circumstances involved. According to the World Health Organization (WHO, 2022)1 in the US, from 3 January 2020 to 8:36pm CEST, 14 April 2022, there have been 79,716,960 confirmed cases of COVID-19 with 979,321 deaths, reported to WHO, while by 7 April 2022, a total of 549,330,665 vaccine doses have been administered. Similarly, in China,2 for the same period, there have been 954,346 confirmed cases of COVID-19 with 14,440 deaths, reported to WHO, and by 7 April 2022, a total of 3,293,526,192 vaccine doses have been administered.
Developing economies encountered serious implications in terms of unprecedented capital outflows, tighter financing conditions, rising unemployment and collapse of business systems, and currencies under pressure. According to S&P Global rating research, comprehensive COVID-19 control measures are leading the world into its deepest recession since the Great Depression, at a rate of deterioration which this time is much faster than any previous crisis. Declining cash flow and poor economic conditions, combined with the effects of oil prices, are affecting creditworthiness and may lead to more businesses defaulting3 (S&P, 2020). From a financial institution's perspective, the circumstances that caused the COVID-19 crisis have specific implications for the management and mitigation of credit risk. O’Donnell, Shannon, and Sheehan (2021) caution that the closure of borders and traditional commerce due to the COVID-19 pandemic is expected to have a lasting financial impact. They further recommend that the governments, regulators, and relevant stakeholders should consider the spatiotemporal nature of COVID-19 (potential future waves) to mimic further extreme societal disruptions. Clearly, an unfamiliar financial environment (emerged due to COVID-19) has encountered the existing financial system to monitor and evaluate credit risk with limited visibility and access to reliable data (Albulescu, 2021; O'Donnell et al., 2021). Albulescu (2021) finds that the prolongation of the coronavirus pandemic is an important source of financial volatility, challenging the risk management activity.
Ftiti, Ben Ameur, and Louhichi (2021) employ data from the Shanghai stock market to examine the effects of the pandemic on stock returns. They used the number of daily cases and fatalities to assess the pandemic's severity, finding that COVID-19 shocks increase illiquidity and volatility by increasing investor pessimism. The impact of the pandemic on three key economic indicators in China was studied by Louhichi, Ftiti, and Ameur (2021), who document that the pandemic co-moves with the indicators only in the short-term. They believe that the effect is more lasting in other nations analysed, and the indicators are more sensitive to the number of deaths than the number of cases. Louhichi et al. (2021) claim that the pandemic affects currency and financial markets on distinct timescales.
During the COVID–19 period, Akhtaruzzaman, Boubaker, and Sensoy (2021) investigated how financial contagion occurs between China and G7 countries, and discover that financial and non-financial listed enterprises in these nations experience large increases in conditional correlations between stock returns. The authors find that during the COVID-19 crisis, these correlations increased significantly for financial firms, revealing their role in financial contagion transmission. They also show that optimal hedge ratios rise dramatically during COVID-19, implying increasing hedging costs. Another study (Akhtaruzzaman, Boubaker, Chiah, & Zhong, 2021) investigates the global financial and non-financial industries’ vulnerability to COVID–19 pandemic-triggered oil price risk. The empirical results suggest that positive oil price risk shocks help oil supplier companies, but positive oil price shocks hurt oil user and finance industries. Akhtaruzzaman, Boubaker, Chiah, and Zhong (2021) find that financial and non-financial industries appear to be less vulnerable to the COVID–19 pandemic, which has implications for managing energy risk during a pandemic.
The recent inspired work conducted by Goodell (2020) has highlighted the enormous economic and social impact of COVID-19 on financial markets and institutions, either directly or indirectly (based on the literature). Goodell indicates avenues for future research that are empirically tested by many researchers by linking the impact of COVID-19 on financial markets, among others. For example, Baker et al. (2020) and O'Donnell et al. (2021) believe that no previous infectious disease outbreak has affected the stock market as much as COVID-19 has. Among many others, Al-Awadhi, Alsaifi, Al-Awadhi, and Alhammadi (2020), Albulescu (2021), Okorie and Lin (2021) and O'Donnell et al. (2021), argue that the daily growth in the total number of confirmed cases and total number of deaths caused by COVID-19 are causing significant damage to stock market returns. The effects of COVID-19 were so strong that even relatively safer products and/or goods/services suffered when the pandemic entered the US.
There is a significant body of literature exploring the adverse impact of COVID-19 on stock market returns and volatility. However, the effects of the pandemic on corporate vulnerability have received less attention and remain an intriguing and unanswered question. Given the significant damage caused to the economies of the United States and China as a result of the pandemic (Akhtaruzzaman et al., 2022), this study aims to investigate the response of the corporate vulnerability index (CVI) to COVID-19, including growth in cases and deaths, as well as cumulative growth. It is worth noting that the US is an advanced economy, and therefore, it is possible that the identified relationship between COVID-19 and CVI might differ in an emerging economy. Thus, to provide a comparative picture, we have included China in our estimation as an emerging economy as it is already a large one with potential comparability with the United States. Through this study, we seek to contribute to the literature by shedding light on the impact of COVID-19 on corporate vulnerability in two significant economies, one developed and the other emerging. Our findings may provide valuable insights for policymakers, investors, and other stakeholders seeking to mitigate the adverse effects of the pandemic on the corporate sector.
Based on the empirical analysis, the co-integration relationship between COVID-19 and CVI_EW in the case of the US is supported by the significant t-statistics value (T_BDM), as well as the significant F-statistics value (F_PSS). However, in the case of China, weak cointegration exists only at a 10% significance level, and therefore, the co-integration relationship between COVID-19 and CVI_EW is not fully supported. Importantly, the empirical findings of classical and advanced econometrics (ARDL, Nonlinear ARDL, and Dynamically Simulated ARDL) and deep machine learning (RF, KNN, and CNN) differ in both economies. It is evident that CVI is more pronounced in the US due to COVID-19, and a weak association is witnessed in the Chinese economy.
The findings are important for policymakers and other stakeholders on account of using the machine learning to predict the relationship between underlying variables in corporate finance and the financial market literature. It is contended that the co-usage of the latest algorithms such as KNN, CNN, and others with the latest econometric estimators in financial economics problem-solving and optimization may encourage better decision-making with policy implications at the micro and macro levels. Given these motivations, this paper is a timely contribution to the examination of corporate vulnerability in the US and China by employing a novel dynamic ARDL. Overall, the pandemic has created a challenging environment for businesses and corporations, and many are still navigating the ongoing outcomes.
The rest of the paper is organized as follows. In the subsequent section the issue of demand and supply dynamics of CVI under COVID-19 is presented. In section 3, a comparative account of research model is provided. In section 4, the dynamics of machine learning approaches are discussed while section 5 contains information about the research model, and it explains about the key components of the model. Section 6 presents empirical results along with a discussion on interpreting the important outcomes. The final section contains some concluding remarks.
2. Demand and supply dynamics of CVI under COVID-19
The spread of COVID-19 elevated corporate vulnerabilities worldwide, and CVI is mainly induced by supply and demand shocks resulting from public health measures, as well as changes in preferences resulting from infection avoidance (Del Rio-Chanona, Mealy, Pichler, Lafond, & Farmer, 2020). The need for supply chains to be resilient and risk management policies functioning well is more obvious than ever as firms attempt to improve their operations and market viability. At the industrial level supply shocks are more likely to constrain output in sectors like manufacturing, mining, and services by supply-side reductions as a result of non-essential industries closing and employees being unable to work at home (Del Rio-Chanona et al., 2020). Some scholars have estimated the supply shock from labor supply, for example Dingel and Neiman (2020) and Koren and Pető (2020). In the meantime this may vary depending upon the nature of the industry, either essential or non-essential.
Conversely, demand shocks are more likely to constrain output in sectors like transportation by demand-side changes as a result of people's immediate response to the pandemic, such as reduced demand for goods or services that are likely to put people at risk of infection = , e.g. tourism (Del Rio-Chanona et al., 2020). According to Guerrieri, Lorenzoni, Straub, and Werning (2020), in a two-sector new Keynesian model with limited substitution in consumption, asymmetric labor supply shocks can lead to larger demand reductions than the initial shock. According to their model, sectoral heterogeneity is required for bigger supply shock impacts. Large supply and demand shocks are present in the entertainment, restaurant, and tourism industries, however, high-wage occupations are more immune to supply- and demand-side shocks at the occupation level, yet low-wage occupations are substantially more vulnerable (Del Rio-Chanona et al., 2020; Ftiti, Ben Ameur, & Louhichi, 2021). A reduction in demand greater than a drop in supply is possible if long-term labor supply restrictions cause a drop in investment, and consumption preferences changes due to reasons such as infection risk, fewer positive externalities in social consumption, and explicit government guidelines (Del Rio-Chanona et al., 2020).
Summing up this section, the COVID-19 pandemic has affected corporate vulnerability in a variety of ways. First, many businesses have been forced to close or scale back operations due to government-mandated lockdowns, resulting in a loss of revenue and making it difficult for them to meet financial obligations. Second, the pandemic has caused disruptions to global supply chains, making it difficult for companies to access the materials and goods they need to operate. Third, the shift to remote work has made it harder for companies to maintain productivity and collaboration, which can lead to increased costs and reduced efficiency. Fourth, the pandemic has accelerated the shift to online commerce, putting pressure on brick-and-mortar businesses to adapt to the digital landscape, which can be a costly transition. Fifth, companies have also seen increased costs due to additional sanitation measures, and other expenses related to the pandemic. Sixth and lastly, the pandemic has caused a reduction in consumer demand, further exacerbating the financial difficulties encountered by businesses.
3. Which cointegration method and why?
We frequently meet scenarios in time series analysis where we want to model one non-stationary time series as a linear combination of other non-stationary time series. There are various approaches for determining the long-term associations between two or more sets of variables. These long-run estimations are typically known as “cointegration”, a concept which has garnered substantial attention in the last two decades among research scholars to estimate the relationship among non-stationary variables. Among them, for example, the conventional Engle-Granger Two-Step technique begins by constructing residuals based on the static regression, which are then tested for the presence of unit-roots. It checks for stationarity units in time series using the Augmented Dickey-Fuller Test or other tests. The Engle-Granger approach will reveal the residuals' stationarity if the time series is cointegrated. The Engle-Granger approach has the drawback of showing more than two cointegrating associations if there are more than two variables. Another drawback is that the model is based on a single equation.
The Johansen approach partially addresses the disadvantages of the Engle-Granger approach, by testing cointegrating correlations between different non-stationary time series data. The Johansen approach, unlike the Engle-Granger test, allows for more than one cointegrating association. However, a small sample size would produce unrealizable results due to the condition of asymptotic properties (large sample size). Another shortcoming is that it is sometimes not applicable in a situation when underlying time series variables are departing from the condition of first order of integration I(1). To overcome the specific flaws with the Johansen approach, Pesaran, Shin, and Smith (2001) introduced the linear autoregressive distributed lag (ARDL) because it is flexible to mixed integration order, and it can be applied to series with a non-identical order of integration, i.e., I(0) and I(I), (not I(2) and it is found efficient in case of small sample size. The major drawback of classical ARDL is its inapplicability in each situation where nonlinearities may exist.
According to Ftiti, Ben Ameur, and Louhichi (2021), the best model for predicting future volatility for both crisis and non-crisis periods is a heterogeneous autoregressive model that contains both positive and negative leaps. According to the authors, only the negative leap component is statistically significant during the crisis, however the extended heterogeneous autoregressive model includes positive and negative dimensions, making it the best compared to the other models. Such potential nonlinear relationships may be calculated using extended asymmetric modelling (Non-linear Autoregressive Distributed Lag – NARDL) of Shin, Yu, and Greenwood-Nimmo (2014), which establishes the non-linearity and examines the short- and long-run dynamics between variables. Although it requires the similar integration order of ARDL, it establishes the existence of nonlinear co-integration between variables, which linear models typically ignore. Shin et al. (2014) use positive and negative partial sum decompositions of the explanatory variables to introduce short- and long-run nonlinearities. Generated here are two separate series (positive and negative) from the core explanatory variable.
Thus, the asymmetric impact may be estimated but this approach overlooks the simulation features while estimating the short- and long-run asymmetries. The package is given by Jordan and Philips (2018), known as the DYS-ARDL approach, and it takes into account the simulation mechanism and liberty to use positive and negative shocks in an explanatory variable. Furthermore it captures the impact in a variable of interest. According to recent literature (M. A. Khan, Ahmed, Olah, & Popp, 2020; M. I. Khan, Teng, & Khan, 2020; M. K. Khan, Teng, Khan, & Khan, 2019), this novel approach is capable of predicting the actual positive and negative changes in the explanatory variable and its subsequent impact on the dependent variable. Moreover, it can stimulate, estimate, and automatically predict, and graph said changes. The authors also believe that classical ARDL can only estimate the long-term and short-term relationships of the variables.
Contemplating the limitations associated with traditional estimators, this study uses NARDL by Shin et al. (2014), and Jordan and Philips' (2018) inspired development of the DYS-ARDL estimator to examine the relationship between COVID-19 and corporate vulnerabilities in the US and China. While each technique has distinct characteristics depending on the situation in which they are deployed, it is worthwhile to contribute to the corporate and behavioral finance literature by experimentally examining the cointegration relationship between US and Chinese corporate vulnerabilities under COVID-19 conditions, coupled with deep machine learning approaches. The next section discusses various deep machine learning approaches and respective implications.
4. Machine learning approaches
The use of modern machine learning (ML) algorithms for credit default prediction improves predictive performance, but it also introduces new model risks, particularly regarding the supervisory validation process. The confusion about how managers might evaluate these risks is frequently mentioned in recent industry surveys as a potential barrier to innovation. In this paper, we suggest a fresh framework to measure model risk adjustments and evaluate the effectiveness of various ML approaches. Traditional time series forecasting techniques involve statistical techniques like ARIMA models or exponential smoothing (Hyndman & Athanasopoulos, 2018). In recent decades, however, time series forecasting is now possible utilizing artificial intelligence methods. Although the most popular machine learning method for time series forecasting is artificial neural networks (Zhang, Patuwo, & Hu, 1998), other methods, including Gaussian Processes (Andrawis, Atiya, & El-Shishiny, 2011) or KNN (Martínez, Frías, Pérez, & Rivera, 2019), have been employed. When compared to traditional statistical models, computational intelligence techniques exhibit certain noteworthy characteristics, such as nonlinearity, absence of an underlying model, or non-parametricity. Excellent packages for time series forecasting statistics are available in R. For instance, the prediction package offers implementations of the Theta method (Hyndman & Khandakar, 2008), exponential smoothing, ARIMA, and other fundamental methods that can be used as benchmark methods, including the random walk approach.
4.1. Random forest
The random forest (RF) approach introduced by Breiman (2001), has been very effective as a multipurpose classification and regression technique. The method has demonstrated good performance in situations where the number of variables is significantly greater than the number of observations. It combines a number of randomized decision trees and averages their predictions. Additionally, it can be quickly modified to fit a variety of ad hoc learning tasks and returns measurements of variable importance. It is versatile enough to be applied to large-scale problems.
The RF methodology has been successfully applied to a number of real-world issues, including air quality prediction in a data science hackathon (http://www.kaggle.com/c/dsg-hackathon), ecology (Désir, Bernard, Petitjean, & Heutte, 2013), and 3D object recognition and bioinformatics (Howard & Bowles). It has been asserted that ensembles of decision trees, also known as “random forests,” have been the most successful general-purpose algorithm in modern times. H. Varian, the chief economist at Google, supports the use of random forests in econometrics (Varian, 2014).
4.2. K-nearest neighbors
An approach to data classification known as the k-nearest-neighbor algorithm, which is commonly abbreviated as KNN, determines how likely it is for a data point to be a member of one group or the other depending on which group the data points that are closest to it belong to in the classification. Despite the fact that R offers a wide range of computational intelligence regression methodologies, including the caret package (Kuhn, 2008), these approaches cannot be used to predict time series data. However, a few innovative packages are addressing this gap. Users can predict time series using artificial neural networks by using tools like the NNFOR package (Kourentzes, 2017) or the NNETAR function from the forecast package, for instance. A very popular approach for both classification and regression is KNN. This algorithm simply keeps a list of examples. Each regression example has a specific value that is a numeric vector of features that describe the example. According to a distance metric like the Euclidean distance, KNN discovers its k closest matches to a new example, which are referred to as nearest neighbors, and forecasts the value of the new example as an accumulation of the target values connected to its nearest neighbors. In this article, we develop the TSFKNN R package for KNN regression-based univariate time series forecasting.
4.3. Convolutional neural networks
Deep learning convolutional neural networks (CNN) are employed to automatically learn information and discriminative features from raw data in order to solve the issue of poor classification accuracy caused by high segmentation error (Bengio, Courville, & Vincent, 2013). Regarding the Visual Recognition Challenge in 2012, CNN obtained some intriguing results (Krizhevsky, Sutskever, & Hinton, 2012). CNN are utilized in this work to extract features. For comparison, the effectiveness of several classifiers is evaluated. A CNN is a deep learning model that consists of sub-sampling layers, additional convolutional layers, non-linear and pooling layers, and fully connected layers as the final levels. The sub-sampling layers are convolution, non-linear, and pooling layers. The data used in this work is a zero-centred normalized dataset put into the convolutional layer. Subtracting the mean activity throughout the dataset produces the result (Krizhevsky et al., 2012).
The pooling layers pool operates by summing the responses of the features in each incoming local rectangular patch to down-sample the feature maps. Calculating the maximum activations is how this is accomplished. Max-pooling is the term for this phenomenon. Features become impervious to minute changes in the data as a result. Two neurons at the final fully connected layer compute the classification probability for each class using softmax regression. Convolutional and pooling layers produce feature maps with smaller dimensions than the input. Several fully connected layers receive feature maps produced at CONV and pool. Initial fully connected layers produce the feature vector which becomes more abstract in deeper fully connected layers.
When the size of the training set is small and insufficient for the network, transfer learning is the deep learning method and it shows the most promise. Smaller datasets cause over-fitting in CNN. To begin learning a new task, one can employ a pre-trained CNN. CNNs are feed-forward networks because the input they receive at intermediate layers consists of features created at lower layers. For multi-class classification, softmax regression, an extended variant of logistic regression, is utilized. The softmax layer of a convolutional neural network employs a loss function, or cross-entropy, known as a softmax activation function. A non-linear version of logistic regression is offered by softmax (Chen, Deng, & Du) which is CNN's Softmax layer.
In summary, RF, KNN, and CNN are very suitable to use alongside econometrics as they provide a more complete and accurate analysis of economic data. These machine learning algorithms can help to: firstly, identify complex patterns and relationships in the data that might be missed by traditional econometric methods; and secondly, make more accurate predictions about economic outcomes. In this study, we employed various econometric approaches, namely ARDL, Non-linear ARDL, and Dynamically Simulated ARDL to analyse the cointegration of variables. We incorporated deep machine learning algorithms such as RF, KNN, and CNN to measure the accuracy of error prediction. This enabled us to explore the complex and non-linear relationships between variables that might not be easily captured using traditional econometric methods. By utilizing both econometric and machine learning approaches, we aimed to provide a more comprehensive analysis of the data and obtain more accurate predictions about economic outcomes.
5. The models, variables, and the data
The dependent variable is the Corporate Vulnerability Index (CVI) which is sourced from the Credit Research Initiative (CRI, 2020), which is governed by the Asian Institute of Digital Finance at the National University of Singapore. Two measures of CVI are utilized in this study: 1) value weighted index (CVI_VW); and 2) equally weighted index (CVI_EW). The CVI is updated daily and it measures the creditworthiness of a selected region, economy, or portfolio of interest. The CVI_EW measure is an average value of the probability of default, which accounts for the number of firms at risk in a group. On the other hand, the CVI_VW aggregates the individual probabilities of default with reference to the market capitalization of each firm as a weight. A high score indicates that firms constituting the index are more exposed to default risk.
Fig. 1 graphically illustrates the CVI_EW index for the US, and China from January 1, 2020, to December 31, 2021. A surge clearly shows that the period after mid-February to the first week of March marked the climax of CVI_EW, which slightly declined by the end of March, followed by a sharp fall by the end of April. Interestingly, this was the same period when COVID-19 struck the US economy with full intensity. This fact motivated us to empirically examine the relationship between CVI and COVID-19. The CVI_VW curve continues to fluctuate until the first week of June and becomes relatively stable until the end of August and onward. Conversely, the curve shows an upward movement for China in second half of 2021.
Fig. 1.
Historical pattern of Ln_CVI_EW for the US and China. Source: Credit Research Initiative (CRI, 2021).
The independent variable is COVID-19, which is represented by: 1) case growth, 2) death growth (Al-Awadhi et al., 2020; Ashraf, 2020), 3) cumulative cases growth, and 4) cumulative deaths growth. The data on 1–4 are accessed from the World Health Organization's website (https://covid19.who.int/info), which ranges from 21/01/2020 (the first case reported) to 31/12/2021, for the US, and from 04/01/2020 (first case reported) to 31/12/2021, for China. We also included the economic policy uncertainty index (EPU) as the potential control variable considering its expected micro and macro implications. The data for US and China EPU originated from the economic policy uncertainty website, which is referred to above. This newspaper-based index is updated on a daily basis, and data is publicly available at http://www.policyuncertainty.com/(see Baker, Bloom, Davis, & Kost, 2019 for more details about the process and constituents of this index). The CVI and EPU are transformed into a natural logarithm for convenient interpretation.
5.1. The models
The Capital Asset Pricing Model (CAPM) and Arbitrage Pricing Theory (APT) remain the prominent theoretical models often used to validate the effects of shocks and other risks on stock market returns. The latter particularly assumes that asset return is generated with the following linear equation:
| (1) |
Where the return on assets , the unconditional expected return is denoted by , is a vector of different risk factors, stands for a vector measuring influence that each risk factor has on the return on asset and error term for the residual effect of the returns. However, in the context of this study, we isolate the risk-free return from stock market return to consider risk premium a component that is probably translated by risk factor such as COVID-19 shocks. Risk-free portion of stock return is assumed to be least influenced by risk factors, thus, risk premium is replaced with corporate vulnerability index. Subsequently, we present a modified version of the above APT as follows:
| (2) |
Where is defined as corporate vulnerability index while denotes COVID-19, which indicates expected risk from changes in cases growth and death growth. Meanwhile COVID-19 changes may be expected to have different effects on CVI of US and China (for aggregate vulnerability), depending on the anticipated effect of shock on either the demand or supply4 of future cash flow of the potential company or country (Ftiti et al., 2021, Ftiti et al., 2021; Huang, An, Gao, & Sun, 2017). This may partly explain why positive/negative changes in COVID-19 cases and death growth introduce different effects on CVI (see, for example Bjørnland, 2009; Hooker, 2002; Jiménez-Rodriguez, 2007). Recent studies have shown that the effect of COVID-19 shock on stock market could be asymmetric (Akhtaruzzaman, Boubaker, Lucey, & Sensoy, 2021). Hence, we partition COVID-19 shock in Eq. (2) into positive and negative COVID-19 shocks, and the revised equation is written as:
| (3) |
Where denotes the positive and negative COVID-19 shocks, respectively.5
The preliminary step to test the relationship between the dependent variable (CVI_VW) and respective regressors is to satisfy the stationarity condition of the individual series, especially the dependent variables which must be integrated at the first difference, I(1). Likewise, all the independent variables must not be stationary at the second difference, I(2). To determine the integration order, this study uses the Augmented Dickey-Fuller (ADF) test. The next step is to determine the optimal lag length to be included for estimation, for which the study uses the Akaike information criterion (AIC), Schwarz information criterion (SC), and Hannan-Quinn information criterion (HQ). All these criteria show that 8 lags are appropriate.
Motivated by a recent study (M. A. Khan, Teng, & Khan, 2020) on US policy uncertainty and stock market, the authors of this research argue that dynamic ARDL simulation carries unique features in capturing the effect of positive/negative shocks in explanatory variable on dependent variable. Thus, this study uses the Pesaran and Shin ARDL Bounds test to initially determine the existence of a cointegration relationship between COVID-19 and CVI in the US and China. It further substantiates the estimation with Nimo and Shin Nonlinear setting, and dynamic ARDL simulations estimator (Jordan & Philips, 2018), which can be expressed in the following standard form:
| (4) |
Where the change in the dependent variable (y) is a function of intercept (), and all the independent variables at time at levels to the maximum of and lags in respective first difference along with error term at time . The study uses Pesaran et al.’s (2001) ARDL bounds testing approach for a level relationship using Kwiatkowski-Phillips-Schmidt-Shin (2018) critical values as a benchmark. The null hypothesis for no level relationship obtained by joint F-statistics derived from the estimation is rejected against the critical bounds, when estimated F-statistics is greater than the upper bound [I(1)]. Drawing on the empirical specification illustrated in Eq. (4), the error correction transformations of the ARDL bounds estimators are estimated using the following formula:
| (5) |
In Eq (5) CVI is corporate vulnerability index, CASES_G denotes growth in COVID-19 number of cases, EPU represents economic policy uncertainty, stands for ECT, capture short-run coefficient, and indicates a long-run coefficient for each of the regressors, respectively. Referring to the estimation process, CASES_G is replaced by DEATH_G, CUM_CASES_G, and CUM_DEATH_G, respectively, in various models.
5.2. Machine learning model approaches
In this paper, a comprehensive analysis of three different ML approaches is employed which include Random Forest (RF), K-Nearest Neighbor (K-NN) and Convolutional Neural Network (CNN) to predict the accuracy of error in the estimation of COVID-19 and CVI. We determine how well these approaches predict and confirm the accuracy of error rate under various criteria to compare their performance. Once the ARDL model specifies the significant coefficients of the independent and dependent variables the ML models access the error rate and accuracy of these models. We utilize the KNN (Martínez et al., 2019), RF (Biau & Scornet, 2016) and CNN (Bengio et al., 2013; Krizhevsky et al., 2012) time series models to predict COVID-19. We use 20% testing and 80% training parts, respectively, to overcome the overfitting problem. We use different packages for RF, KNN and CNN in R.
5.2.1 Forecast Evaluation Criterions
In this study, two datasets of COVID-19 (US and China) are used for evaluation. Due to the continuous nature of the response variable in this study, the predicting abilities of several machine learning algorithms are assessed using four distinct criteria: Mean square error (MSE), mean absolute error (MAE), root mean square error (RMSE), and mean absolute error (MAPE) which are all presented in Table 1 . Here, Yt and t stand for the observed and predicted values, respectively, while n denotes the total number of predictions made on the training and testing parts, respectively.
Table 1.
Forecasting evaluation measurement tools.
| Criterion | Formula |
|---|---|
| Mean square error (MSE) | |
| Mean absolute error (MAE) | |
| Root mean square error (RMSE) | |
| Mean absolute percentage error (MAPE) |
Table 1 The machine learning forecasting evaluation measurement tools, and respective formula for these tools, namely MSE, MAE, RMSE, and MAPE.
6. Empirical results
The descriptive properties of the data are reported in Table 2 , and unit root results are shown in Table 3 . The reported results of ADF in Table 3 reveal that both measures of CVI are stationary at the first difference in the US and China while the rest of the indicators are showing integration order of I(0). Meanwhile none of the underlying variables is integrated at the second difference, I(2). Namely, CVI_EW, CVI_VW and, EPU, are not stationary at level, while they become stationary when converted to first difference. CASES_G and DEATHS_G, CUM_CASES_G, and CUM_DEATH_G are found to be stationary at level. The mixed integration order satisfies the pre-condition for estimating the ARDL model.
Table 2.
Descriptive statistics.
| Variable | Obs | Mean | Std.Dev. | Min | Max |
|---|---|---|---|---|---|
| US | |||||
| LN_CVIEW | 729 | 2.2 | .237 | 1.637 | 2.66 |
| LN_CVIVW | 729 | 3.966 | .456 | 3.231 | 5.327 |
| CASES_G | 683 | .02 | .308 | −1.897 | 2.092 |
| CUMCASES_G | 711 | .025 | .069 | 0 | .693 |
| DEATH_G | 667 | .009 | .395 | −1.723 | 2.136 |
| CUM_DEATH_G | 671 | .02 | .077 | 0 | 1.386 |
| EPU | 729 | 5.237 | .645 | 3.027 | 6.758 |
| China | |||||
| LN_CVIEW | 729 | 3.464 | .238 | 3.081 | 3.924 |
| LN_CVIVW | 729 | 4.504 | .089 | 4.303 | 4.687 |
| CASES_G | 712 | .002 | .532 | −3.153 | 2.639 |
| CUMCASES_G | 727 | .016 | .12 | 0 | 2.42 |
| DEATH_G | 239 | −.002 | .906 | −4.63 | 4.317 |
| CUM_DEATH_G | 719 | .012 | .068 | 0 | 1.041 |
| EPU | 729 | 5.941 | .14 | 5.38 | 6.495 |
Table 3.
Unit-root testing.
| Variable | ADF |
ADF |
||
|---|---|---|---|---|
| Level |
1st difference |
Level |
1st difference |
|
| US | China | |||
| LN_CVI_VW | −0.943 | −15.051*** | −2.864 | −15.561*** |
| LN_CVI_EW | −2.925 | −15.242*** | −1.550 | −15.677*** |
| CASES_G | −0.943*** | – | −20.938*** | – |
| DEATHS_G | −20.643*** | – | −12.294*** | – |
| CUMCASES_G | −6.879*** | – | −12.371*** | – |
| CUMDEATHS_G | −6.606*** | – | −5.122*** | – |
| EPU | −6.034*** | – | −3.488** | – |
***p < 0.01, **p < 0.05, *p < 0.1.
Table 2 The descriptive properties of the underlying variables used in this study for the US and China, respectively. CVI_EW: Equally weighted CVI, CVI_VW: Value weighted CVI, CASES_G: COVID-19 cases growth, DEATHS_G: COVID-19 death growth, CUMCASES_G: COVID-19 cumulative cases growth, CUMDEATHS_G: COVID-19 cumulative death growth, EPU: Economic policy uncertainty. CVI_EW, CVI_VW, and EPU are expressed in natural logarithm.
Table 3 The unit root test results Augmented Dickey-Fuller (ADF) test for the variables in both countries. The ADF results confirm that except for LN_CVI_VW, and LN_CVI_EW, all the variables are stationary at level, while these two variables are stationary art first difference.
Table 4 below reports the Pesaran, Shin, and Smith bounds test which reveals the existence of a cointegration relationship between CVI_EW, CVI_VW, and COVID-19 indicators along with control. In four estimated models CVI_EW and CVI_VW function as a dependent variable, respectively, while COVID-19 dimensions such as growth in cases, deaths, cumulative cases, and cumulative death are the independent variables (one by one in each model). The absolute F-statistics are significant at the 10% level in the US and this corresponds to models 1 and 4, while it is significant at 1% in model 3. The decision is based on Kripfganz and Schneider's (2018) critical values. However, for China we do find that across all models, the computed F-statistics value is insignificant at all confidence intervals. The evidence of a long-run cointegration relationship between the underlying variables in the US motivates the analysis to be extended further to test for the existence of possible non-linearities (asymmetries), in both the short- and long-term.
Table 4.
ARDL Bounds test.
| Estimated model | Variable | US |
China |
||
|---|---|---|---|---|---|
| LN_CVI_EW | LN_CVI_EW | LN_CVI_EW | LN_CVI_EW | ||
| 1. | CASES_G | 3.955* | 2.814* | 1.232 | 1.193 |
| 2. | DEATH_G | 2.644 | 2.479 | 0.100 | 0.464 |
| 3. | CUM_CASES_G | 8.793*** | 8.029*** | 0.078 | 1.339 |
| 4. | CUM_DEATH_G | 4.365* | 4.817** | 0.339 | 1.714 |
Table 4 The Pesaran, Shin, and Smith bounds test of cointegration relationship between CVI_EW, CVI_VW, and COVID-19 for US, and China, respectively. The results confirm the presence of cointegration in the US but it is missing for China. The results concerning LN_CVI_VW are consistent but not reported for brevity.
6.1. Nonlinear ARDL results
The cadre of development for the US and China significantly differs, and the findings with response to ARDL affirm the same in Table 4. We proceed further and estimated the asymmetric relationship between COVID-19 indicators and CVI, and found the consistency in reported results in Table 5 with that of in Table 4. Literature shows that during COVID-19 the markets are more sensitive to bad news rather than positive news (see Ftiti, Louhichi, & Ben Ameur, 2021). Thus, aligned with Ameur et al. (2021), we utilize a Shin et al. (2014) nonlinear autoregressive distributed lag (NARDL) framework because it takes into account asymmetry and nonlinearity in both the long- and short-term scenarios. To estimate NARDL in a comparison of the US and China we analysed the Shin et al. (2014) model. In this section we also test the cumulative effect of CASES_G, and DEATH_G on CVI_EW of both economies. The results are documented in Table 5.
Table 5.
Comparative asymmetric analysis results.
| VARIABLES | USA |
China |
||||||
|---|---|---|---|---|---|---|---|---|
| CVIEW: CASES_G |
CVIEW: CUMCASES_G |
CVIEW: DEATH_G |
CVIEW: CUMDEATH_G |
CVIEW: CASES_G |
CVIEW: CUMCASES_G |
CVIEW: DEATH_G |
CVIEW: CUMDEATH_G |
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| ECT(-1) | −0.048*** | −0.048*** | −0.078*** | −0.054*** | −0.005 | −0.006* | −0.019 | −0.006* |
| (-4.26) | (-4.08) | (-5.50) | (-3.87) | (-1.60) | (-1.81) | (-1.22) | (-1.79) | |
| CASES_G + | 0.002 | −0.004 | ||||||
| −0.25 | (-1.60) | |||||||
| CASES_G - | 0.001 | −0.004 | ||||||
| −0.13 | (-1.60) | |||||||
| CUMCASES_G + | 0.078*** | 0.016 | ||||||
| −3.02 | −1.35 | |||||||
| CUMCASES_G - | 0.060** | 0.015 | ||||||
| −2.3 | −1.35 | |||||||
| DEATHS_G + | 0.002 | −0.001 | ||||||
| −0.24 | (-0.99) | |||||||
| DEATHS_G - | 0.001 | −0.001 | ||||||
| −0.1 | (-1.09) | |||||||
| CUMDEATHS_G + | −0.129** | 0.009 | ||||||
| (-2.54) | −0.49 | |||||||
| CUMDEATHS_G - | −0.068* | 0.009 | ||||||
| (-1.75) | −0.53 | |||||||
| EPU+ | −0.005 | 0.000 | −0.005 | 0.000 | 0.000 | −0.001 | 0.009 | −0.002 |
| (-1.11) | (-0.07) | (-1.36) | −0.04 | −0.06 | (-0.26) | −0.45 | (-0.32) | |
| EPU- | −0.004 | 0.000 | −0.004 | 0.000 | −0.003 | −0.005 | 0.001 | −0.005 |
| (-0.95) | −0.01 | (-1.08) | −0.09 | (-0.46) | (-0.99) | −0.08 | (-1.05) | |
| (-1.67) | (-1.34) | (-1.43) | (-2.20) | −0.86 | −0.84 | −0.03 | −0.96 | |
| ΔCASES_G + | −0.003 | 0.012 | 0.003 | −0.161*** | −0.002 | 0.000 | 0.001 | 0.000 |
| (-0.57) | −0.29 | −0.61 | (-3.72) | (-1.55) | −0.03 | −0.67 | (-0.02) | |
| ΔCASES_G j + | 0.000 | 0.063 | 0.001 | 0.360** | 0.000 | −0.037 | −0.002 | −0.029 |
| −0.05 | −0.99 | −0.22 | −2.4 | −0.13 | (-1.42) | (-1.37) | (-1.16) | |
| ΔCASES_G - | 0.002 | 0.086 | −0.001 | 0.417** | 0.000 | −0.022 | −0.003 | −0.033 |
| −0.26 | −1.34 | (-0.26) | −2.3 | (-0.27) | (-0.79) | (-1.42) | (-1.55) | |
| ΔCASES_G j - | 0.006 | 0.027 | −0.002 | −0.065* | 0.001 | −0.006 | 0.000 | −0.004 |
| −1.17 | −0.68 | (-0.32) | (-1.71) | −0.98 | (-1.16) | −0.33 | (-0.34) | |
| Constant | 0.132*** | 0.059*** | 0.210*** | 0.310*** | 0.015 | 0.015 | 0.047 | 0.018 |
| −4.78 | −3.06 | −5.54 | −5.6 | −1.41 | −1.03 | −1.14 | −1.32 | |
| Observations | 676 | 709 | 665 | 669 | 710 | 725 | 185 | 717 |
| R-squared | 0.051 | 0.055 | 0.061 | 0.076 | 0.022 | 0.02 | 0.029 | 0.022 |
| F statistics | 2.56 | 2.910 | 0.7069 | 3.84 | 1.12 | 1.040 | 0.400 | 1.11 |
| TBDM | −4.259*** | −4.078*** | −5.500*** | −3.866*** | −1.603 | −1.808 | −1.215 | −1.792 |
| FPSS | 5.030*** | 5.674*** | 6.782*** | 7.321*** | 1.294 | 1.595 | 0.360 | 1.308 |
| Long run asymmetries | ||||||||
| CASES_G | 5.516** | 17.77*** | 5.516** | 5.084** | 0.002581 | 0.04226 | 0.7622 | 0.009505 |
| P-value | 0.019 | 0.000 | 0.019 | 0.024 | 0.959 | 0.837 | 0.384 | 0.922 |
| Short run asymmetries | ||||||||
| CASES_G | 0.5865 | 0.2025 | 0.5865 | 4.744** | 3.257** | 0.295 | 0.2792 | 0.05999 |
| P-value | 0.444 | 0.653 | 0.444 | 0.03 | 0.072 | 0.587 | 0.598 | 0.807 |
***p < 0.01, **p < 0.05, *p < 0.1.
The empirical results calculated by t-statistics value, developed by Banerjee, Dolado, and Mestre (1998), and the F-statistics value from () (Shin et al., 2014) are significant. In fact they support the co-integration relationship between COVID-19 and CVI_EW in the US but not China (weak cointegrating exists only at the 10% significance level). Our findings are consistent with the literature, for example Louhichi et al. (2021), show that the impact of the pandemic's evolution on the main economic indicators in China exhibits a different pattern from France, Italy, and the USA. The impact of the COVID-19 pandemic on three key economic indicators in China was studied by Louhichi et al. (2021), who document that the pandemic co-moves with the indicators only in the short-term.
After estimating the Nonlinear ARDL, we estimate the Dynamic ARDL simulation approach. One of the unique features of the Dynamic ARDL simulation approach is the automatic prediction of estimated values and generation of the graph, which helps us to understand the response of the dependent variable to positive and negative shocks at a given rate. Impulse response function is exhibited from Fig. 2, Fig. 3, Fig. 4, Fig. 5 . Fig. 2 graphically illustrates the CVI_VW response to 5% ± change in COVID-19 cases growth in the US. Average predicted values are denoted by dots, while dark blue to light blue lines indicate the confidence interval of 90%, 95%, and 99%. The left-hand side in Fig. 2 shows that in the short-term CVI negative response changes to a 5% positive shock/change in cases growth scenario and in the long-term they move in the same direction. The right-hand side depicts the CVI reaction of 5% negative shock/change in cases growth.
Fig. 2.
Graphical illustration of the CVI_VW response to 5% ± change in COVID-19 cases growth in the US. Average predicted values are denoted by dots, while dark blue to light blue lines indicate the confidence intervals of 90%, 95%, and 99%. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Fig. 3.
Graphic illustration of the CVI_EW response to 5% ± change in COVID-19 cases growth in the US. Average predicted values are denoted by dots, while dark blue to light blue lines indicate the confidence intervals of 90%, 95%, and 99%. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Fig. 4.
Graphical illustration of the CVI_VW response to 5% ± change in COVID-19 cases growth in China. Average predicted values are denoted by dots, while dark blue to light blue lines indicate the confidence intervals of 90%, 95%, and 99%. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Fig. 5.
Graphical illustration of the CVI_EW response to 5% ± change in COVID-19 Deaths growth in China. Average predicted values are denoted by dots, while dark blue to light blue lines indicate the confidence intervals of 90%, 95%, and 99%. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Interestingly, both in the short- and long-run the decline in cases growth also curtails the CVI, which is a useful input for policy matters. Similarly, Fig. 3 exhibits the CVI_EW response to 5% ± change in COVID-19 cases growth in the US, where the scenario is not much different. A 5% positive change in cases growth increases the CVI both in the short- and long-run, while a negative change with the same momentum slightly induces the CVI in the short-run but reduces it in the long-run. This implies that COVID-19 induced risk has made US corporations more vulnerable both in the short- and long-term. Such a susceptible situation caused by COVID-19 has put credit pressure on corporate capital structure, forcing it to be debt-centric due to a probable surge in the cost of financing, stock price volatility, and resultant concentrated trading. We also tested the implications of 1%, and 10% positive/negative shocks on CVI and found very consistent prospects which are not reported.
The graphical illustrations in Fig. 4, Fig. 5 appear to be a puzzle regarding China. The depiction is very different to the picture of the US. On average the CVI_VW response to 5% ± change in COVID-19 cases growth in China reveals a similar pattern, while it conversely reacts to the changes in COVID-19 cases growth. As the simulated shock of 5% ± is artificial, we may argue that actual results show short-term asymmetries only in the short run in the Chinese context (as reported in Table 4), so owing to the econometric rule of thumb we do not focus on insignificant results. One more potential reason behind the unusual pattern revealed in reference Fig. 4, Fig. 5 may be referred to in the literature. For example Louhichi et al. (2021), show that the impact of COVID-19 on the main economic indicators in China exhibits a different pattern from developed economies, namely France, Italy, and the USA.
6.2. Machine learning results
We evaluate models to compare their performance using various accuracy metrics including MSE, MAE, RMSE and MAPE. These metrics provide different perspectives to access prediction models. The training sample is used to estimate the parameters for specific model architecture. The testing set then serves to select the best model among all models considered here. Table 6 summarizes RF, KNN and CNN forecasting accuracy measures for the training dataset of CASES_G of COVID-19 on ln_CVI_EW for the US and China. The reported results strongly suggest that the MAPE yields the most accurate error prediction across all the algorithms used.
Table 6.
Predicting accuracy measures of all models of training data.
| Error Measurement Tools | |||||
|---|---|---|---|---|---|
| Method | Country | MSE | MAE | RMSE | MAPE |
| RF | China | 3.241074 | 1.298987 | 1.800298 | 0.01446721 |
| USA | 13.68807 | 2.152615 | 3.699739 | 0.03806436 | |
| KNN | China | 2.584853 | 1.164732 | 1.607748 | 0.01284716 |
| USA | 27.36907 | 3.388844 | 5.231545 | 0.05585816 | |
| CNN | China | 36.59196 | 4.633266 | 6.049129 | 0.05170903 |
| USA | 25.03099 | 3.537157 | 5.003098 | 0.05602282 | |
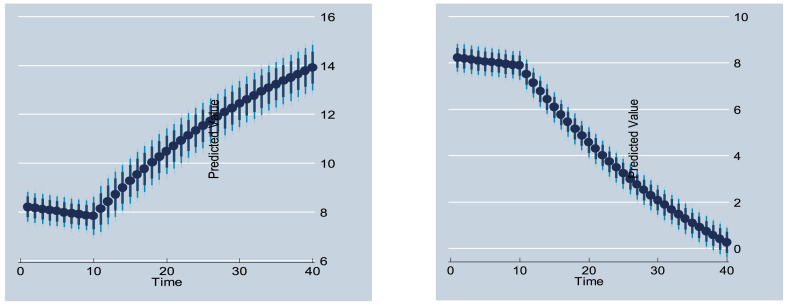
Fig. 6 depicts the original and forecast values of RF model for CASES_G of COVID-19 on ln_CVI_EW of US and China using training set. From plot (a) it is observed that the in case of the US RF model forecast values are very close to the original values and it also follow the same trend. Similarly, in plot (b) in the case of China the forecast values are not closer to the original on some points. It is inferred that the drawn prediction indicated that COVID-19 induced risk has made US corporations more vulnerable.
Fig. 6.
The error accuracy prediction of CASES_G of COVID-19 on ln-CVI_EW in the US and China using the RF model.
Fig. 7 plots the original and forecast values using the KNN model for CASES_G of COVID-19 on ln_CVI_EW in the US and China. From plot (a) it is observed that the KKN model predicted values are very close to the original values and also follows the same trend, with the subsequent line fluctuating near 170. As well, the forecast trend gradually declines over time in case of the US. Similarly, in plot (b) in the case of China the forecast values are not closer to the original on some points, meaning that COVID-19 induced risk has not affected the Chinese corporations whereas the US corporations are comparatively vulnerable.
Fig. 7.
Plots error accuracy prediction of CASES_G of COVID-19 on ln-CVI_EW in the US and China using the KNN model.
Fig. 8 illustrates the original and forecast values of CNN model for CASES_G of COVID-19 on ln_CVI_EW for the US and China. From plot (a) it is evident that the CNN model in the US context predicted values are not very closer initially to the original values and for some point in the middle era. However, overall trend shows that both curves comove and the rest of the prediction follows the original pattern to some extent and then intensively to the original data. Conversely, the prediction for the Chinese economy is not much different to the findings shown by RF and KNN. Plot (b) for China shows the divergence of forecast values and original values. This indicated that COVID-19 induced risk is prominently translated in the US corporations (as measure by ln_CVI_EW) while Chinese corporations are not influenced.
Fig. 8.
The error accuracy prediction of the CNN model for CASES_G of COVID-19 on ln_CVI_EW for the US and China.
7. Concluding remarks
This article explores the impact of the recent COVID-19 pandemic on corporate vulnerability in the US and China using econometric and machine learning approaches. Employed here are cointegration methods such as ARDL, Non-linear ARDL, and Dynamically Simulated ARDL, as well as deep machine learning methods, namely RF, KNN, and CNN, to predict error accurately. The findings indicate that COVID-19 has had an unprecedented impact, significantly worsening corporate vulnerabilities in the long-term in the United States and in the short-term in China. Non-linear ARDL reveals long-run asymmetries in the United States, while short-run asymmetries exist in China. These results confirm the accuracy of error prediction and suggest that US corporations face COVID-19-induced risk. Importantly, the results remain robust across alternative cointegration measures and machine learning approaches, with relatively accurate error prediction using mean absolute percentage error criteria. These results are relevant for policymakers and stakeholders, highlighting the importance of utilizing the most recent algorithms in financial economics problem-solving and optimization, together with econometric estimators, to support informed decision-making and policy implications.
7.1 Beyond the debate
While this study sheds light on the impact of COVID-19 on corporate vulnerability in the US and China, it is important to acknowledge the need for further discussion on the significant impact of the Russia-Ukraine conflict on capital markets (Abbassi, Kumari, & Pandey, 2022). Boubaker, Goodell, Pandey, and Kumari (2022), The conflict has generated negative anomalous returns in Russian invaded areas due to exposure to risk and reliance on trade, resulting in vulnerability to geopolitical concerns and trade reliance. The effect of border tension heterogeneously affects the stock market, while posing an overall negative effect, leading to increased risk and volatility resulting in higher returns during the post-event window (Kumari, Pandey, Kumar, & Xu, 2022) (Hassan, Boubaker, Kumari, & Pandey, 2022). However, in the case of an unexpected war's commencement, hostilities can cause stock prices to fall (Brune, Hens, Rieger, & Wang, 2015). Likewise, the global currency values fell as a result of the conflict between Russia and Ukraine; nevertheless, a regional breakdown reveals that although European currency values fell, Asian currency values rose (Chortane & Pandey, 2022). As a result of Russia's invasion of Ukraine, some investors' priorities may have shifted, and due to their increasing importance in ensuring a sustainable future, investors now favor the energy and aerospace & defence industries (Singh, Patel, & Singh, 2022).
Similarly, Sun and Zhang (2022) show that volatility on stock markets around the world ever since the Russia-Ukraine war broke out has magnified and abnormal returns for listed firms have been seen to be heterogeneous around the time the war broke out. According to Tosun and Eshraghi (2022), the war, as evidenced by the fact that a portfolio of remainders firms in Russia underperforms the leavers and the market benchmark, equity markets appear to be highly sensitive to corporate decisions during times of political conflict. The equity markets appear to be highly sensitive to corporate decisions during times of political conflict, as evidenced by increased trading volume and selling pressure on remainders. Therefore, further exploration of how corporate vulnerability is triggered by the Russia-Ukraine conflict is warranted.
CRediT authorship contribution statement
Muhammad Asif Khan: Conceptualization, Methodology, Software, Writing – original draft. Juan E.Trinidad Segovia: Writing – original draft, preparation, Writing – review & editing, Supervision. M.Ishaq Bhatti: Visualization, Investigation, Validation, Writing – review & editing. Asif Kabir: Data curation, Writing – original draft, Writing – review & editing.
Declaration of competing interest
This manuscript has been completed and agreed upon by all the authors, and they declare no conflict of interest. The manuscript does not involve animal/human for which ethical approval or informed consent is needed. The used in the study may be made available on reasonable request to the corresponding author.
Footnotes
Demand and supply dynamics are discussed under mechanisms through which CVI is translated.
Shown by COVID-19 cases growth, death growth, and cumulative growth for each country during the study period.
Data availability
Data will be made available on request.
References
- Abbassi W., Kumari V., Pandey D.K. What makes firms vulnerable to the Russia–Ukraine crisis? The Journal of Risk Finance. 2022 doi: 10.1108/JRF-05-2022-0108. [DOI] [Google Scholar]
- Akhtaruzzaman M., Boubaker S., Chiah M., Zhong A. COVID−19 and oil price risk exposure. Finance Research Letters. 2021;42 doi: 10.1016/j.frl.2020.101882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhtaruzzaman M., Boubaker S., Lucey B.M., Sensoy A. Is gold a hedge or a safe-haven asset in the COVID–19 crisis? Economic Modelling. 2021;102 doi: 10.1016/j.econmod.2021.105588. [DOI] [Google Scholar]
- Akhtaruzzaman M., Boubaker S., Sensoy A. Financial contagion during COVID–19 crisis. Finance Research Letters. 2021;38 doi: 10.1016/j.frl.2020.101604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhtaruzzaman M., Boubaker S., Umar Z. COVID–19 media coverage and ESG leader indices. Finance Research Letters. 2022;45 doi: 10.1016/j.frl.2021.102170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Awadhi A.M., Alsaifi K., Al-Awadhi A., Alhammadi S. Death and contagious infectious diseases: Impact of the COVID-19 virus on stock market returns. Journal of Behavioral and Experimental Finance. 2020;27 doi: 10.1016/j.jbef.2020.100326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albulescu C.T. COVID-19 and the United States financial markets' volatility. Finance Research Letters. 2021;38 doi: 10.1016/j.frl.2020.101699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alshater M.M., Alqaralleh H., El Khoury R. Dynamic asymmetric connectedness in technological sectors. The Journal of Economic Asymmetries. 2023;27 doi: 10.1016/j.jeca.2022.e00287. [DOI] [Google Scholar]
- Ameur H.B., Ftiti Z., Louhichi W. Revisiting the relationship between spot and futures markets: Evidence from commodity markets and NARDL framework. Annals of Operations Research. 2021;313:171–189. doi: 10.1007/s10479-021-04172-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrawis R.R., Atiya A.F., El-Shishiny H. Forecast combinations of computational intelligence and linear models for the NN5 time series forecasting competition. International Journal of Forecasting. 2011;27(3):672–688. [Google Scholar]
- Ashraf B.N. Stock markets' reaction to COVID-19: Cases or fatalities? Research in International Business and Finance. 2020;54 doi: 10.1016/j.ribaf.2020.101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K.J. National Bureau of Economic Research; 2019. Policy news and stock market volatility. Working Paper 25720. [DOI] [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K., Sammon M., Viratyosin T. The unprecedented stock market reaction to COVID-19. The Review of Asset Pricing Studies. 2020;10(4):742–758. doi: 10.1093/rapstu/raaa008. [DOI] [Google Scholar]
- Banerjee A., Dolado J., Mestre R. Error‐correction mechanism tests for cointegration in a single‐equation framework. Journal of Time Series Analysis. 1998;19(3):267–283. [Google Scholar]
- Batten J.A., Choudhury T., Kinateder H., Wagner N.F. Volatility impacts on the European banking sector: GFC and COVID-19. Annals of Operations Research. 2022 doi: 10.1007/s10479-022-04523-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengio Y., Courville A., Vincent P. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- Biau G., Scornet E. A random forest guided tour. Test. 2016;25(2):197–227. [Google Scholar]
- Bjørnland H.C. Oil price shocks and stock market booms in an oil exporting country. Scottish Journal of Political Economy. 2009;56(2):232–254. [Google Scholar]
- Boubaker S., Goodell J.W., Pandey D.K., Kumari V. Heterogeneous impacts of wars on global equity markets: Evidence from the invasion of Ukraine. Finance Research Letters. 2022;48 doi: 10.1016/j.frl.2022.102934. [DOI] [Google Scholar]
- Breiman L. Random forests. Machine Learning. 2001;45(1):5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Brune A., Hens T., Rieger M.O., Wang M. The war puzzle: Contradictory effects of international conflicts on stock markets. International Review of Economics. 2015;62(1):1–21. doi: 10.1007/s12232-014-0215-7. [DOI] [Google Scholar]
- Chen B., Deng W., Du J. Noisy softmax: Improving the generalization ability of dcnn via postponing the early softmax saturation. 2017. https://arxiv.org/abs/1708.03769 arXiv.
- Chortane S.G., Pandey D.K. Does the Russia-Ukraine war lead to currency asymmetries? A US dollar tale. The Journal of Economic Asymmetries. 2022;26 doi: 10.1016/j.jeca.2022.e00265. [DOI] [Google Scholar]
- Del Rio-Chanona R.M., Mealy P., Pichler A., Lafond F., Farmer J.D. Supply and demand shocks in the COVID-19 pandemic: An industry and occupation perspective. Oxford Review of Economic Policy. 2020;36(Supplement_1):S94–S137. doi: 10.1093/oxrep/graa033. [DOI] [Google Scholar]
- Désir C., Bernard S., Petitjean C., Heutte L. One class random forests. Pattern Recognition. 2013;46(12):3490–3506. [Google Scholar]
- Dingel J.I., Neiman B. How many jobs can be done at home? Journal of Public Economics. 2020;189 doi: 10.1016/j.jpubeco.2020.104235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ftiti Z., Ben Ameur H., Louhichi W. Does non-fundamental news related to COVID-19 matter for stock returns? Evidence from Shanghai stock market. Economic Modelling. 2021;99 doi: 10.1016/j.econmod.2021.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ftiti Z., Louhichi W., Ben Ameur H. Cryptocurrency volatility forecasting: What can we learn from the first wave of the COVID-19 outbreak? Annals of Operations Research. 2021 doi: 10.1007/s10479-021-04116-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodell J.W. COVID-19 and finance: Agendas for future research. Finance Research Letters. 2020;35 doi: 10.1016/j.frl.2020.101512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerrieri V., Lorenzoni G., Straub L., Werning I. Macroeconomic implications of COVID-19: Can negative supply shocks cause demand shortages? The American Economic Review. 2020;112(5):1437–1474. [Google Scholar]
- Guven M., Cetinguc B., Guloglu B., Calisir F. The effects of daily growth in COVID-19 deaths, cases, and governments' response policies on stock markets of emerging economies. Research in International Business and Finance. 2022;61 doi: 10.1016/j.ribaf.2022.101659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassan M.K., Boubaker S., Kumari V., Pandey D.K. Border disputes and heterogeneous sectoral returns: An event study approach. Finance Research Letters. 2022;50 doi: 10.1016/j.frl.2022.103277. [DOI] [Google Scholar]
- Hoang H.V., Nguyen C., Nguyen D.K. Corporate immunity, national culture and stock returns: Startups amid the COVID-19 pandemic. International Review of Financial Analysis. 2022;79 doi: 10.1016/j.irfa.2021.101975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooker M.A. Are oil shocks inflationary? Asymmetric and nonlinear specifications versus changes in regime. Journal of Money, Credit, and Banking. 2002;34(2):540–561. [Google Scholar]
- Howard J., Bowles M. Strata Conference Presentation; New York: 2012. The two most important algorithms in predictive modeling today. February 28. [Google Scholar]
- Huang S., An H., Gao X., Sun X. Do oil price asymmetric effects on the stock market persist in multiple time horizons? Applied Energy. 2017;185:1799–1808. [Google Scholar]
- Hyndman R.J., Athanasopoulos G. OTexts; 2018. Forecasting: Principles and practice. [Google Scholar]
- Hyndman R.J., Khandakar Y. Automatic time series forecasting: The forecast package for R. Journal of Statistical Software. 2008;27:1–22. [Google Scholar]
- Jiménez-Rodriguez R. Banco de España Research Paper No. WP-0731; 2007. The industrial impact of oil price shocks: Evidence from the industries of six OECD countries. [Google Scholar]
- Jordan S., Philips A.Q. Cointegration testing and dynamic simulations of autoregressive distributed lag models. STATA Journal. 2018;18(4):902–923. doi: 10.1177/1536867X1801800409. [DOI] [Google Scholar]
- Khan M.A., Ahmed M., Olah J., Popp J. US policy uncertainty and stock market nexus revisited through dynamic ARDL simulation and threshold modelling. Mathematics. 2020;8(11):2073. [Google Scholar]
- Khan M.I., Teng J.Z., Khan M.K. The impact of macroeconomic and financial development on carbon dioxide emissions in Pakistan: Evidence with a novel dynamic simulated ARDL approach. Environmental Science and Pollution Research. 2020;27(31):39560–39571. doi: 10.1007/s11356-020-09304-z. [DOI] [PubMed] [Google Scholar]
- Khan M.K., Teng J.-Z., Khan M.I., Khan M.O. Impact of globalization, economic factors and energy consumption on CO2 emissions in Pakistan. Science of the Total Environment. 2019;688:424–436. doi: 10.1016/j.scitotenv.2019.06.065. [DOI] [PubMed] [Google Scholar]
- Kinateder H., Campbell R., Choudhury T. Safe haven in GFC versus COVID-19: 100 turbulent days in the financial markets. Finance Research Letters. 2021;43 doi: 10.1016/j.frl.2021.101951. [DOI] [Google Scholar]
- Koren M., Pető R. Business disruptions from social distancing. PLoS One. 2020;15(9) doi: 10.1371/journal.pone.0239113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kourentzes N. Nnfor: Time series forecasting with neural networks. R package version 0.9. 2017;2:229. https://CRAN.R-project.org/package=nnfor [Google Scholar]
- Krizhevsky A., Sutskever I., Hinton G.E. In: Advances in neural information processing systems: Proceedings of the First 12 Conferences. Jordan M.I., et al., editors. MIT Press; Cambridge, Mass: 2012. Imagenet classification with deep convolutional neural networks. [Google Scholar]
- Kuhn M. Building predictive models in R using the caret package. Journal of Statistical Software. 2008;28:1–26. [Google Scholar]
- Kumari V., Pandey D.K., Kumar S., Xu E. What do border disputes cost? Evidence from an emerging market. International Journal of Emerging Markets. 2022 doi: 10.1108/IJOEM-06-2022-0918. ahead-of-print(ahead-of-print) [DOI] [Google Scholar]
- Liu Z., Dai P.-F., Huynh T.L.D., Zhang T., Zhang G. Industries' heterogeneous reactions during the COVID-19 outbreak: Evidence from Chinese stock markets. Journal of International Financial Management & Accounting. 2022 doi: 10.1111/jifm.12166. [DOI] [Google Scholar]
- Louhichi W., Ftiti Z., Ameur H.B. Measuring the global economic impact of the coronavirus outbreak: Evidence from the main cluster countries. Technological Forecasting and Social Change. 2021;167 doi: 10.1016/j.techfore.2021.120732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez F., Frías M.P., Pérez M.D., Rivera A.J. A methodology for applying k-nearest neighbor to time series forecasting. Artificial Intelligence Review. 2019;52(3):2019–2037. [Google Scholar]
- O'Donnell N., Shannon D., Sheehan B. Immune or at-risk? Stock markets and the significance of the COVID-19 pandemic. Journal of Behavioral and Experimental Finance. 2021;30 doi: 10.1016/j.jbef.2021.100477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okorie D.I., Lin B. Stock markets and the COVID-19 fractal contagion effects. Finance Research Letters. 2021;38 doi: 10.1016/j.frl.2020.101640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandey D.K., Kumari V. Event study on the reaction of the developed and emerging stock markets to the 2019-nCoV outbreak. International Review of Economics & Finance. 2021;71:467–483. doi: 10.1016/j.iref.2020.09.014. [DOI] [Google Scholar]
- Pandey D.K., Kumari V., Tiwari B.K. Impacts of corporate announcements on stock returns during the global pandemic: Evidence from the Indian stock market. Asian Journal of Accounting Research. 2022;7(2):208–226. doi: 10.1108/AJAR-06-2021-0097. [DOI] [Google Scholar]
- Pesaran M.H., Shin Y., Smith R.J. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics. 2001;16(3):289–326. [Google Scholar]
- S&P . S&P Global Ratings, March 17. 2020; 2020. COVID-19 credit update: The sudden economic stop will bring intense credit pressure.https://nuscri.org/en/visited [Google Scholar]
- Shin Y., Yu B., Greenwood-Nimmo M. In: Festschrift in honor of peter schmidt: Economic methods and applications. Sickles R., et al., editors. Springer; New York: 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework; pp. 281–314. [Google Scholar]
- Singh A., Patel R., Singh H. Recalibration of priorities: Investor preference and Russia-Ukraine conflict. Finance Research Letters. 2022;50 doi: 10.1016/j.frl.2022.103294. [DOI] [Google Scholar]
- Sun M., Zhang C. Comprehensive analysis of global stock market reactions to the Russia-Ukraine war. Applied Economics Letters. 2022:1–8. doi: 10.1080/13504851.2022.2103077. [DOI] [Google Scholar]
- Tosun O.K., Eshraghi A. Corporate decisions in times of war: Evidence from the Russia-Ukraine conflict. Finance Research Letters. 2022;48 doi: 10.1016/j.frl.2022.102920. [DOI] [Google Scholar]
- Varian H.R. Big data: New tricks for econometrics. The Journal of Economic Perspectives. 2014;28(2):3–28. [Google Scholar]
- Weber B.S., Huynh T.L.D. COVID-19 challenges and firm responses: Analysis of a city-wide census in a developing country. Managerial and Decision Economics. 2022;43(6):2184–2195. doi: 10.1002/mde.3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Who . World Health Organization; 2022. WHO coronavirus disease (COVID-19) dashboard.https://covid19.who.int/ visited. [Google Scholar]
- Zhang G., Patuwo B.E., Hu M.Y. Forecasting with artificial neural networks:: The state of the art. International Journal of Forecasting. 1998;14(1):35–62. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.