Pattern dynamics and stochasticity of the brain rhythms

Significance

Waveforms are commonly described in terms of their instantaneous properties, which are agnostic of protracted behaviors, or their time-averaged characteristics, which highlight mean trends. The actual shapes and patterns of waves over finite timescales thus remain unexplored. We propose an approach that allows quantifying waveforms as single entities and attributing precise meaning to intuitive notions of waves’ “regularity,” “typicality,” or “orderliness.” Thus, it becomes possible to distinguish statistically mundane patterns from deviant ones and to capture transitions between pattern types. We use these instruments to demonstrate that patterns of hippocampal rhythms in mice are dynamically coupled to motor activity in both behavioral and spatial contexts, which offers a fresh perspective on hippocampal circuit dynamics and functionality.

Abstract

Our current understanding of brain rhythms is based on quantifying their instantaneous or time-averaged characteristics. What remains unexplored is the actual structure of the waves—their shapes and patterns over finite timescales. Here, we study brain wave patterning in different physiological contexts using two independent approaches: The first is based on quantifying stochasticity relative to the underlying mean behavior, and the second assesses “orderliness” of the waves’ features. The corresponding measures capture the waves’ characteristics and abnormal behaviors, such as atypical periodicity or excessive clustering, and demonstrate coupling between the patterns’ dynamics and the animal’s location, speed, and acceleration. Specifically, we studied patterns of θ, γ, and ripple waves recorded in mice hippocampi and observed speed-modulated changes of the wave’s cadence, an antiphase relationship between orderliness and acceleration, as well as spatial selectiveness of patterns. Taken together, our results offer a complementary—mesoscale—perspective on brain wave structure, dynamics, and functionality.

Oscillations of the extracellular fields—the brain waves—are produced by synchronized activity of large neuronal ensembles (1). These waves are key sources of neurophysiological information about brain activity at various spatiotemporal scales: spiking of individual neurons, synchronized circuit-level computations, high-level cognitive processes, etc. Common approaches to studying brain waves can be broadly divided in two categories. The first is based on correlating instantaneous phases, amplitudes, and frequencies with parameters of cognitive, behavioral, or neuronal processes. For example, instantaneous phases of the θ-wave (4 to 12 Hz) modulate neuronal spikings (2, 3), while the γ-waves’ (30 to 80 Hz) amplitudes and frequencies link the synaptic and circuit dynamics (4–8). The second category of analyses is based on quantifying the brain waves’ time-averaged characteristics, e.g., establishing dependencies between the mean θ-frequency and the animal’s speed (9, 10) or acceleration (11), linking rising mean θ- and γ-power to heightened attention states (12–14), and so forth.

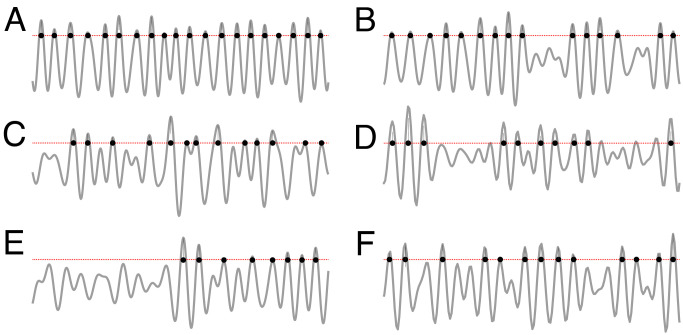
However, little work has been done to examine the waves’ overall structure, e.g., the temporal arrangement of peaks and troughs or sequences of sharp wave ripples or spindles generated over finite periods. Yet, the physiological relevance of a brain wave’s shape, or morphology^* (15), is well-recognized: Rigidly periodic or excessively irregular rhythms that contravene a certain “natural” level of statistical variability are suggestive of circuit pathologies (16–25) or may indicate external driving (26, 27). For example, the nearly periodic sequences of peaks shown on Fig. 1 A and B are common for θ-waves but are perhaps too regular for the γ-waves. Conversely, the intermittent patterns on Fig. 1 C and D are unlikely to appear among θ-waves but may occur among γ-waves or ripples. The series of clumping peaks shown on Fig. 1 D and E are usual for ripples and may highlight underlying neuronal events. On the other hand, the waveform on Fig. 1F may represent an episode of θ-arhythmicity or mundane temporal disorder of higher-frequency waves.

Fig. 1.

Waveform morphologies. (A and B) Waves exhibiting nearly periodic sequences of peaks are commonly found among θ-oscillations (4 to 12 Hz), but rarely among high frequency waves. The intermittent patterns shown on panels (C) or (D) may be exhibited by γ-waves (30 to 80 Hz), but for the θ-waves, they would be atypical. The temporal clustering shown on panels (D) and (E) are all in all ordinary for γ- or ripples (150 to 250 Hz) but too irregular for the θ-waves. F-pattern could potentially be a θ-wave, a γ-wave, or a ripple. Shown are the peaks exceeding 1/2 of standard deviation from the mean (dashed red line), to exclude the spurious low-amplitude peaks. In actuality, panels A and B are experimental θ-waveforms recorded from the mouse hippocampal CA1 (45, 46), panels C and D are the recorded γ-waves, and panels E and F show ripples.

It remains unclear, however, how to characterize these patterns impartially and quantify the intuitive notions of “regularity,” “typicality,” “orderliness,” etc. Furthermore, since all brain waves exhibit a certain level of erraticness, it is unclear how justified the experiential, visceral classifications of the waveforms as “mundane” or “irregular” are. For example, might the patterns assessed as “not-θ” on Fig. 1 actually be short-time fluctuations of otherwise regular θ-waves? Would that be a structural peculiarity or an impossibility?

In the following, we address these questions by studying patterns of waves recorded in the CA1 region of mouse hippocampus, using two independent mathematical frameworks, two cognate quantifications, which allow understanding the brain rhythms’ structure at intermediate timescales and linking the wave patterns to the animal’s behavior.

1. Approach

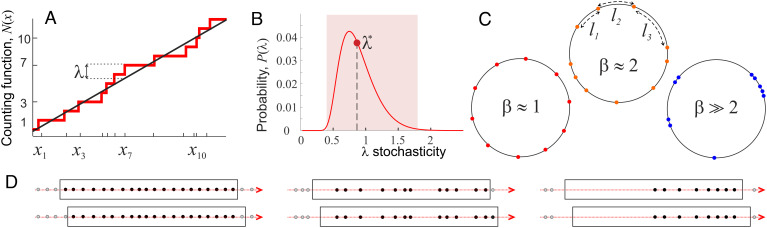
1. Kolmogorov stochasticity, λ, describes deviation of an ordered sequence, X, from the overall trend—in the following, X will refer to the series of the brain waves’ peaks, whose trend is defined by the expected mean rate of the peaks’ appearance. A remarkable observation made in ref. 28 is that the λ-values are universally distributed. As it turns out, deviations, λ(X), that are too high or too low are rare: sequences with λ(X)≤0.4 or λ(X)≥1.8 appear with probability less than 0.3%, Fig. 2 A and B, (29–34). In other words, typical patterns are consistent with the underlying mean behavior and produce a limited range of λ-values, with mean λ^* ≈ 0.87. Thus, the λ-score can serve as a universal measure of stochasticity and be used for identifying statistical biases (or lack of thereof) in various patterns (35–40).

Fig. 2.

Stochasticity parameters. (A) The elements of an ordered sequence X = {x₁, x₂, …, x_n} following a linear trend $\overline{N}(x)=\overline{f}x+b$ (solid black line). The sequence’s maximal deviation from the mean, λ(X), exhibits statistical universality and can hence impartially characterize the stochasticity of the individual data sequence X (Section 3). (B) The probability distribution of λ-scores is unimodal, with mean λ^* ≈ 0.87 (red dot). About 99.7% of all sequences produce λ-scores in the interval 0.4 ≤ λ(X)≤1.8 (pink stripe); these sequences are typical and consistent with the underlying mean behavior. In contrast, sequences with smaller or larger λ-scores are statistically uncommon. (C) A sequence X arranged on a circle of length L produces a set of n arcs. The normalized quadratic sum of the arc lengths is small for orderly sequences, β ≈ 1 (Left), as high as β ≈ n for the “clustering” sequences (Right), and intermediate, β ≈ 2 (Middle), for generic sequences. (D) Top row: the “beads” of peaks illustrated on Fig. 1A, C, and E. The black boxes represent time windows with widths scaled proportionally to the periods of θ-waves, γ-waves and ripples. The gray dots represent the upcoming and the past peaks. Bottom row: time windows slide to the right (red arrows), causing pattern changes.

2. Arnold stochasticity, β, is alternative measure that quantifies whether the elements of a pattern (e.g., the aforementioned peaks) “repel” or “attract” each other. Repelling elements seek to maximize separations and hence produce orderly, more equispaced arrangements, for which β-stochasticity score is close to its minimum, β(X)≈1. On the other hand, attracting entities tend to cluster together, yielding patterns with higher stochasticity—their β(X) can be as high as there are components in the sequence. Since both attraction and repulsion (any interaction, for that matter) contravene randomness, β-scores of sequences with independent elements are neither small nor large. As shown in ref. 41–44, β-scores of the sequences with independent elements are universally close to β^* ≈ 2 (Fig. 2 C and Methods). Thus, the β-score can be used to characterize orderliness of brain rhythms, complementing the λ-score.

3. Time-dependence. The recurrent nature of brain rhythms suggests a dynamic view on pattern stochasticity. Given a time window, L, containing a sequence of events, X_t, such as θ-peaks or ripples, evaluate their scores λ(X_t) and β(X_t), then shift the window over a time step Δt, evaluate the next set λ(X_{t + Δt}) and β(X_{t + Δt}), and so on. The consecutive wave segments, obtained by small window shifts, X_t, X_{t + Δt}, X_{t + 2Δt}, …, differ only slightly from one another. Correspondingly, their stochasticity scores produce semicontinuous time dependencies λ(t) and β(t), which describe the dynamics of the waveforms over the signal’s entire span (Fig. 2D).

For a visualization, one can imagine the elements of a given sample sequence, X_{t + kΔt}, as “beads” scattered over a necklace of length L. As the sliding window shifts forward in time, new beads may appear toward the front, as the beads in the back of the window disappear, while a majority of the beads retain their relative positions. The corresponding λ- and β-values will then produce semicontinuous dependencies λ(t) and β(t) that quantify the “necklace dynamics”—gradual pattern changes in time, with β describing the orderliness of the beads’ distribution and λ measuring statistical typicality of the beads’ ongoing arrangement (Fig. 2D).

As an illustration of the methods, consider simulated data series with random spacings between the adjacent values—intervals drawn from the familiar exponential, uniform, and Poisson distributions, with sample patterns containing about 25 consecutive elements. As shown on Fig. 3 A and C, the λ(t)-dependence of the exponential sequences remains, for the most part, constrained within the “typicality band” (pink stripe on Figs. 2B and 3A), while the uniformly distributed patterns are more variable, and the Poisson patterns follow the mean most closely. The β-scores of exponentially and uniformly distributed patterns are overall mundane, while the Poisson patterns exhibit periodic-like orderliness.

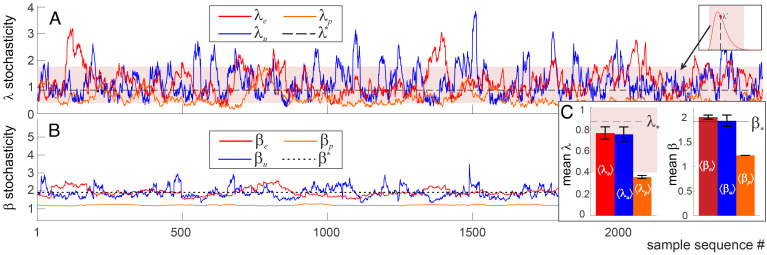
Fig. 3.

Pattern dynamics for three kinds of random sequences in which the intervals between consecutive points are distributed 1) exponentially with the rate ν = 2; 2) uniformly with constant density ρ = 1; or 3) with Poisson rate μ = 5. Sample intervals are selected proportionally to the distribution scales (L_u = 25ρ, L_e = 25ν, and L_p = 25μ, so that each sample sequence contains about n = 25 elements) and are shifted by a single data point at a time. (A) The Kolmogorov parameter of the exponential sequence (red trace, λ_e), uniform sequence (blue trace, λ_u), and Poisson sequence (orange trace, λ_p) remains mostly within the “pink zone” of stochastic typicality (pink stripe is the same as on Fig. 2B, but stretched horizontally—note the illustration in the right corner). λ_u is the most volatile and often escapes the expected range, whereas λ_p is more compliant, lingering below the expected mean λ_p ≲ λ^* ≈ 0.87 (black dashed line). (B) The corresponding Arnold stochasticity parameters show similar behavior: β_u = 1.93 ± 0.2 fluctuates around the expected mean β^*(25) = 1.92 (black dotted line). The exponential sequence has smaller β-variations and a slightly higher mean, β_e = 2 ± 0.04. The Poisson sequence is the least stochastic (nearly periodic), with β_p = 1.22 ± 0.004, due to statistical suppression of small and large gaps. (C) The mean stochasticity scores, ⟨λ⟩ and ⟨β⟩ computed for about 10⁴ random patterns of each type. For sample patterns, (SI Appendix, Fig. 1A).

The mean λ- and β-scores in the uniform and exponential sequences are close to the universal means, λ^* and β^*, which shows that, on average, they are statistically unbiased. In contrast, the Poisson-distributed patterns are atypically orderly, due to statistically suppressed small and large gaps between neighboring elements (Fig. 3B). Also, note that the fluctuations of stochasticity scores—the rises and drops of λ(t) and β(t) on Fig. 3—are chancy, since random sequences vary sporadically from instantiation to instantiation. In contrast, brain wave patterns carry physiological information, and therefore, the dynamics of their stochasticity is coupled with behavior and with physiological states, as discussed below.

2. Results

A. Stochasticity in Time.

We analyzed Local Field Potentials (LFP) recorded in the hippocampal CA1 area of wild-type male mice for experimental details see refs. 45 and 46 and studied patterns of their θ-waves, γ-waves, and ripples (47). The recurring nature of brain rhythms implies that their key features distribute uniformly over sufficiently long periods. The expected mean used for evaluating the Kolmogorov λ-parameter is hence linear,

$$\begin{array}{c}\hfill \overline{N}(t)=\overline{f}t+b,\end{array}$$ [1]

with the specific coefficients $\overline{f}$ (the mean frequency) and b obtained via linear regression. The lengths of the sample sequences were selected to highlight a particular wave’s structure and functions, as described below.

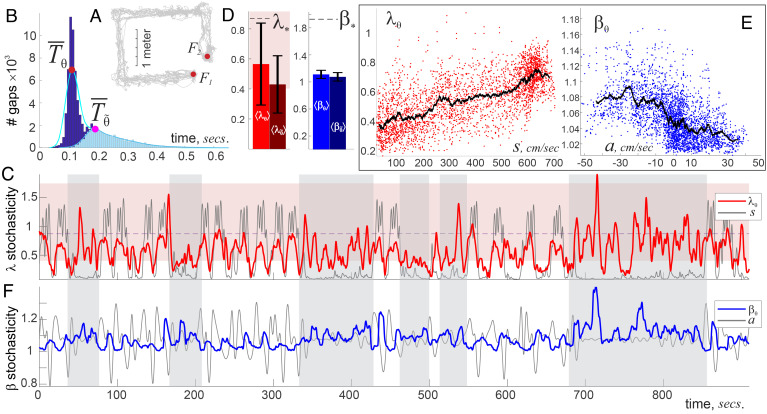
1. θ-Waves 4 to 12 Hz, (48, 49) are known to correlate with the animal’s motion state, which suggests that the sample sequences should be selected at a behavioral scale (9–11). In the analyzed experiments (45, 46), the mice shuttled between two food wells on a U-shaped track, spending about 22 secs per lap (average for 5 mice, for both inbound and outbound runs) and consumed food reward over 17 s (Fig. 4A). On the other hand, the intervals between successive θ-peaks distribute around the characteristic θ-period, ${\overline{T}}_{\theta }\approx 1/{\overline{f}}_{\theta }\approx 110$ msecs, which defines the timescale of oscillatory dynamics (Fig. 4B). To accommodate both timescales, we used time intervals required to complete 1/6^th of the run between the food wells, L_θ ≈ 3.6 s, containing about 20 to 30 peaks—large enough to produce stable λ- and β-scores (50–52), but short enough to capture the ongoing dynamics of θ-patterns.

Fig. 4.

θ-wave’s stochasticity. (A) The animal’s lapses (trajectory shown by gray line) between food wells, F₁ and F₂, take on average 22 s. (B) A histogram of intervals between subsequent θ-peaks concentrates around the characteristic θ-period, ${\overline{T}}_{\theta }\approx 110$ ms: gaps shorter than ${\overline{T}}_{\theta }/2$ or wider than $2{\overline{T}}_{\theta }$ are rare. θ-amplitude, $\tilde{\theta }$, oscillates with $T_{\tilde{\theta }}\approx 180$ ms period. (C) The dynamics of λ_θ(t) (red trace) correlate with the speed profile (gray line) when the mouse moves methodically. The λ_θ(t)-stochasticity remains mostly within the “typical” range (pink stripe in the background), falling below it as the mouse slows down. For rapid moves there is a clear similarity between the λ_θ-score and the speed, e.g., their peaks and troughs roughly match. When the mouse meanders (vertical gray stripes), the coupling between speed and λ_θ-stochasticity is lost. (D) Due to quasiperiodicity of the θ-wave and of its envelope, $\tilde{\theta }$, the average scores ⟨λ_θ⟩, $⟨{\tilde{\lambda }}_{\theta }⟩$, ⟨β_θ⟩, and $⟨{\tilde{\beta }}_{\theta }⟩$ are significantly lower than the impartial means λ^* and β^*, with small deviations (data for 5 mice). (E) Locally averaged ${\widehat{\lambda }}_{\theta }$-score grows with speed, whereas ${\widehat{\beta }}_{\theta }$ tends to drop down with acceleration. (F) The Arnold score β_θ(t) (blue trace) remains close to β_min = 1, affirming θ-wave’s quasiperiodicity. Note the antiphasic relationship between the β_θ-stochasticity and the acceleration a(t) (the latter graph is shifted upward to match the mean level ⟨β_θ⟩): θ-periodicity loosens as the animal slows down (β_θ-splashes correlate with animal’s deceleration) and sharpens as he speeds up.

Fast moves. As mentioned above, the experimental design enforces recurrent behavior, in which speed goes up and down repeatedly as the animal moves between the food wells. When the mouse moves methodically (lap time less than 25 s), λ_θ rises and falls along with the speed with surprising persistence (Fig. 4C and SI Appendix, Fig. 1B). Yet, the θ-patterns appearing in this process are stochastically generic—the entire sequence of λ_θ-values remains mostly within the “domain of stochastic typicality” (pink stripe on Figs. 4 C and D and 2B), below the universal mean λ^*. However, the patterns become overtly structured as the animal slows down: the Kolmogorov scores then drop below λ_θ ≈ 0.1, exhibiting uncommon compliance of the θ-wave with the mean behavior. Such values of λ_θ can occur by chance with vanishingly small probability Φ(0.1)< 10⁻¹⁷ (Section 3), which, together with small β_θ ≈ 1, show that limited motor driving confines θ-wave to a simple, nearly harmonic oscillation with a base frequency ${\overline{f}}_{\theta }\approx 9$ Hz.

Increasing speed drives θ-patterns farther from the mean: the faster the mouse moves, the higher the λ_θ. To quantify the uncanny similarity of the stochasticity to the speed profile, we used the Dynamic Time Warping (DTW) approach. This technique uses a series of local stretches to match two functions—in this case, λ_θ(t) and s(t)—so that the net stretch can be interpreted as a measure of separation, or distance^† between functions in “feature space” (54, 55). In our case, the DTW-distance between the speed and the λ_θ(t)-score during active moves is small, D(λ_θ, s) = 19.6%, indicating that θ-patterns are strongly coupled to the animals’ motor mobility (SI Appendix, Fig. 2).

Note that DTW-affinity between λ_θ(t) and speed does not necessarily imply a direct functional dependence. Indeed, plotting points with coordinates (s, λ_θ) yields scattered clouds, suggesting a broad trend, rather than a strict relationship (Fig. 4E). However, if the λ-scores and the speeds are locally averaged, i.e., if each individual s- and λ-value is replaced by the mean of itself and its adjacents, then the pairs of such local means$({\widehat{s}}_i,{\widehat{\lambda }}_i)$ reveal the underlying dependence: Increasing speed of the animal entails higher variability of the θ-patterns.

In the meantime, the Arnold stochasticity score, β_θ(t), is closely correlated with the mouse’s acceleration, a(t). As shown on Fig. 4F, the β_θ-score rises as the mouse decelerates (θ-wave clumps) and falls when he accelerates (θ-wave becomes more orderly), producing a curious antiphasic β_θ−a relationship, which is also captured by the local averages $({\widehat{a}}_i,{\widehat{\beta }}_i)$ (Fig. 4E). The distance between β_θ(t) and −a(t) (the minus sign accounts for the antiphase) is D(β_θ, −a) = 33.6%, which means that speed influences the θ-wave’s statistical typicality more than acceleration impacts its orderliness.

Slow moves. When the mouse meanders and slows down (lapse time over 25 s), θ-patterns change: the λ_θ-score increases in magnitude and uncouples from speed (DTW distance is twice that of the fast moves case, D(λ_θ, s) = 38.8%), suggesting that, without active motor driving, θ-rhythmicity is less controlled by the mean oscillatory rate, i.e., is more randomized. The Arnold parameter β_θ also slightly increases, D(β_θ, −a) = 36.1%, indicating concomitant θ-disorder.

Overall, the Kolmogorov scores of θ-patterns are low, with mean ⟨λ_θ⟩ = 0.54 ± 0.12, indicating that, on average, θ-cycles closely follow the prescribed trend [1]. The low mean Arnold score ⟨β_θ⟩ = 1.1 ± 0.03 ≈ β^min also points at a near-periodic behavior of the θ-wave (Fig. 4C). One may wonder, therefore, whether such structural rigidity should be viewed as a mere background that modulates the “true” θ-stochasticity—the deviations of the θ-wave from periodicity. In other words, one can view the times of the θ-peaks’ occurrences, t_{θ, k}, as a periodic series disturbed by arrhythmic inputs, $t_{\theta ,k}=k{\overline{T}}_{\theta }+{\xi }_{\theta ,k}$, and inquire about the stochasticity of the latter. Expectedly, the “bare noise” patterns are more variegated: the λ_ξ-scores cover the full range of stochastic typicality, reflecting generic nature of the θ-flickery (SI Appendix, Fig. 3A). The orderliness, β_ξ(t), also grows significantly above the impartial mean β^* ≈ 2, exposing cluttering of the θ-fluctuations (SI Appendix, Fig. 3B). What is surprising however, it is that the ξ_θ-patterns show no coupling to the speed, acceleration, or the physiological state, in contrast to the original θ-wave. This observation is essential: It demonstrates that the semiperiodicity of the θ-waveforms is, in fact, instrumental for linking θ-patterns to movement activity.

The overall conclusion is that, during active behavior, θ-waveforms are strongly controlled by the mouse’s moves. Highly ordered, nearly periodic θ-peaks appear when the animal starts running, i.e., the θ-frequency range narrows, while deviating from the expected value. Decreasing speed stirs up the θ-patterns; the disorder grows and reaches its maximum when the animal moves slowest and begins to accelerate. During periods of inactivity, the coupling between θ-patterns and speed is weakened but then reinforced again as the mouse reengages into the task.

We emphasize that these dependencies should not be viewed as naive manifestations of known couplings between the waves’ instantaneous or time-averaged parameters and the animals’ activity (10, 11). Indeed, the momentary frequencies or amplitudes are agnostic of the wave’s protracted behaviors and alter many times over the span of each extended peak series (56, 57). In contrast, the stochasticity scores describe the waveform as a single entity, without averaging, i.e., sensitive to the individual elements and features.

To further illustrate this point, we evaluated cross-correlation R between the λ_θ-score and the animal’s speed during the active moving periods, which show that the similarity is highest when speed just barely lags behind λ_θ, on average by δt_θ ≈ 0.6 s (R_θ = 0.6 ± 0.02). Getting ahead of the upcoming discussions, the highest correlation with the λ_γ (stochasticity of the γ-wave) is also achieved when the speed lags by about δt_γ = 0.45 s (R_γ = 0.51 ± 0.15). In contrast, the strongest correlation with λ_re (stochasticity of the ripple waves, R_re = 0.69 ± 0.03) may occur for leading speeds. The β_θ-score shows similar range of maximal correlations with acceleration (R_* ≈ 0.5), but with a wider spread of time shifts (0 ≲ δt_* ≲ 1.5 s), also with positive or negative lags. A similar variety of lagging and leading correlations are observed between the stochasticity scores and the waves’ amplitudes and frequencies. Taken together, these observations suggest that the waveforms are neither spontaneous field deflections nor immediate reactions to ongoing idiothetic inputs but rather integrative processes that unfold at the behavioral timescale. The λ- and β-scores describe these waveforms integrally and put each pattern, as a whole, into a statistical perspective. It hence becomes possible to approach the questions addressed in the Introduction: identify typical and atypical wave patterns, quantify levels of their orderliness, detect deviations from natural behavior, and so forth.

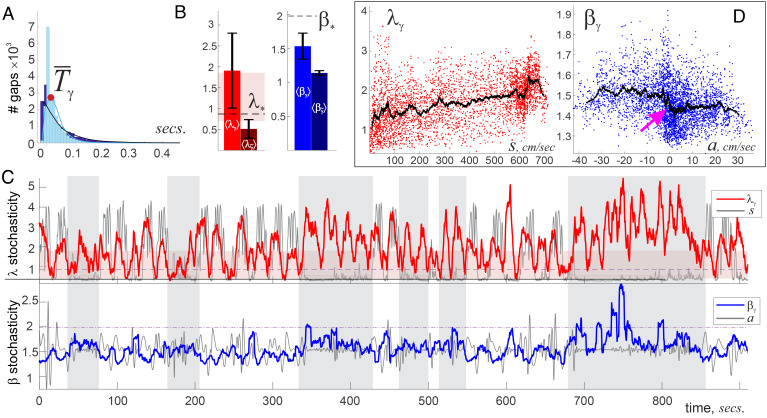
2. γ-waves 30 to 80 Hz, (6) exhibit a wider variety of patterns than θ-waves. The interpeak intervals between consecutive γ-peaks, T_γ, are nearly exponentially distributed, which implies that both smaller and wider γ-intervals are statistically more common, leading to higher pattern variability (Fig. 5A).

Fig. 5.

γ-wave stochasticity. (A) A histogram of γ-interpeak intervals exhibits an exponential-like distribution with mean characteristic γ-period, ${\overline{T}}_{\gamma }=18.6\pm 1.9$ ms, about six times smaller than ${\overline{T}}_{\theta }$. (B) The average scores ⟨β_γ⟩ and ⟨λ_γ⟩ are higher than for the θ-wave, indicating that γ-patterns are more diverse than θ-patterns. (C) The dynamics of the λ_γ-score (Top panel) correlate with changes in the speed when the animal moves actively. Note that λ_γ often exceeds the upper bound of the “pink stripe,” i.e., γ-waves often produce statistically uncommon patterns, especially during rapid moves. The β_γ-score (Bottom panel) correlates with the animal’s acceleration, which is lost when lap times increase (gray stripes). (D) Locally averaged λ-score, ${\widehat{\lambda }}_{\gamma }$, grows with speed, while ${\widehat{\beta }}_{\gamma }$ switches from higher to lower value with increasing acceleration (pink arrow).

Fast moves. For consistency, the sample sequences, X_γ, were drawn from the same time windows, L_γ = L_θ ≈ 3.6 s, which contained, on average, about 100 elements that yield a mean Kolmogorov score ⟨λ_γ⟩ = 1.84 ± 1.03—more than twice higher than the impartial mean λ^* and three times above the ⟨λ_θ⟩ score. Such means can occur randomly with probability 1 − Φ(1.84)≲2 ⋅ 10⁻³, which suggests that generic γ-patterns are statistically atypical and may hence reflect organized network dynamics, rather than random extracellular field fluctuations (Fig. 5B). The average Arnold parameter also grows compared to the θ-case, but remains lower than the impartial mean, ⟨β_γ⟩ = 1.61 ± 0.53 < β^*, implying that, although γ-waves are more disordered than the θ-waves, they remain overall oscillatory.

On average (for all five mice), the λ_γ-score escapes the domain of “stochastic typicality” approximately half of time through transitions that closely follow speed dynamics. A wider γ-diversity (larger range of λ_γ-values) is accompanied by a weaker coupling to speed: The average DTW distance to the latter, D(λ_γ, s)≈23.4%, is slightly bigger than in the case of λ_θ dynamics, which illustrates that γ-patterns are less sensitive to speed than θ-patterns (Fig. 5C).

From a structural perspective, the γ-wave becomes closer to periodic when the animal is actively moving: during these periods, β_γ-score reduces close to minimum, β_γ ≈ 1, and the Kolmogorov score grows to the improbable λ_γ ≈ 3.5 (cumulative probability of that is Φ(3.5)≲10⁻¹⁰). In contrast, the lowest deviations of γ-patterns from the mean (λ_γ ≳ 0.2), accompanied by high β_γ-scores, happen as the mice slow down, implying that circuit activity is least structured during these periods (Fig. 5 C and D). The relation between γ-orderliness, β_γ(t), and acceleration is similar to the one observed in the θ-waves: Acceleration induces stricter γ-rhythmicity and deceleration randomizes γ-patterns, with about the same overall DTW distance, D(β_γ, −a)≈34.4%.

During slower movements, the γ-dynamics change qualitatively: the magnitudes of both λ_γ(t) and β_γ(t) grow higher, indicating that decoupling from motor activity enforces statistically atypical γ-rhythmicity in the hippocampal network, as in the θ-waves. In particular, the uncommonly high β_γ-scores point at frequent γ-bursting during quiescence.

Once again, we emphasize that these results do not represent known correlations between instantaneous or time-averaged γ-characteristics and motion parameters (58, 59) but reflect the dynamics of γ-waves at pattern-changing timescale. Note in this connection that the amplitude of γ-waves, (γ-envelope, $\tilde{\gamma }$), has low stochasticity scores, comparable to the ones produced by the Poisson process, $⟨{\beta }_{\tilde{\gamma }}⟩=1.15\pm 0.08$ and $⟨{\lambda }_{\tilde{\gamma }}⟩=0.52\pm 0.26$ (Figs. 3 and 5B). In other words, instantaneous amplitudes and frequencies exhibit restrained, quasiperiodic behavior, and yet allow a rich morphological variety of the underlying γ-oscillations.

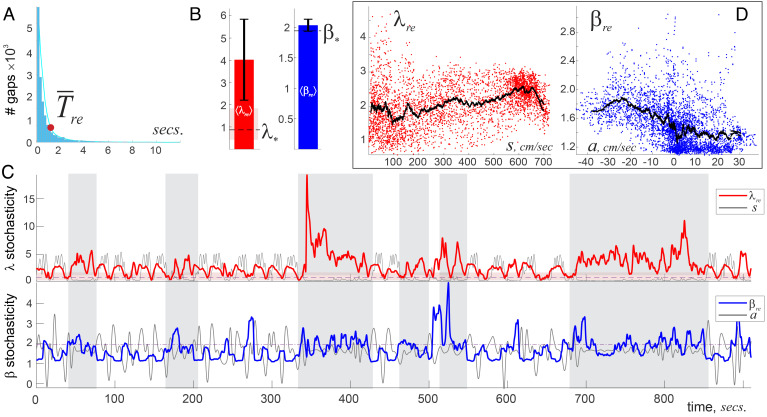
3. Ripple events (RE) High-amplitude (over 2.5 standard deviations above the mean) splashes of high-frequency waves 150 to 250 Hz (47), exhibit the richest pattern dynamics.

During fast moves, RE appears at an exponential rate ${\overline{T}}_{\mathit{re}}\approx 0.5$ s. Approximately, 20–30 RE occur in each 3.6-s window, which is comparable with the number of θ-peaks over the same period, but RE have significantly higher λ-scores, ⟨λ_re⟩ = 2.40 ± 1.57 (Fig. 6 A and B). The low probability of these patterns (1 − Φ(2.4)≈10⁻⁴) and the relatively high mean β-score, ⟨β_re⟩ = 1.71 ± 0.64, indicate that RE tends to exhibit clustering that reflect time-specific, targeted circuit activity.

Fig. 6.

Ripple Events’ stochasticity. (A) A histogram of intervals between RE is nearly exponential. (B) The averages ⟨λ_re⟩ and ⟨β_re⟩ are high, indicating both frequent deviation of RE from the mean and higher temporal clustering than for the θ- and γ-patterns. (C) The animal’s speed (gray line, Top panel) correlates with the Kolmogorov parameter λ_re during fast exploratory laps. During inactivity (vertical gray stripes), the λ_re-stochasticity uncouples from speed, exhibiting high spikes that mark strong “fibrillation” of RE patterns and may reflect awake replay activity. The antiphasic relationship between the animal’s acceleration a(t) (gray line, Bottom panel) and Arnold score β_re(t) shows that RE tends to cluster when as the animal decelerates, while acceleration enforces periodicity. During slower moves (gray stripes), the relationship between speed, acceleration, and stochasticity is washed out and stochastically improbable patterns dominate. (D) Locally averaged ${\widehat{\lambda }}_{\mathit{re}}$ grows with speed and ${\widehat{\beta }}_{\mathit{re}}$ drops with acceleration.

Interestingly, RE-patterns also correlate with the animal’s speed profile about as much as γ-patterns, D(λ_re, s)≈23.8% (60). The β_re(t)-dependence displays the familiar antiphasic relationship with the animal’s acceleration—RE tends to cluster more when the animal slows down (Fig. 6 C and D). However, orderliness of RE is driven by acceleration even stronger than orderliness of γ-patterns: the range of β_re-scores is twice as wide as the range of β_γ-scores (broader pattern variety), with a similar DTW distance D(β_re, −a)≈39.7%.

During quiescent periods, RE are known to mark instances of endogenous network activity—sequential reactivations of hippocampal neurons that represent previous or future behavioral experiences—awake replays and preplays (60–66) no sleep periods involved, Section 3 and (45, 46). As shown on Fig. 6C, these RE patterns are highly uncommon: the extremely high λ_re-scores and above-average β_re-values indicate statistically improbable, clustered RE sequences.

Overall, the temporal clumping comes forth as a characteristic feature of the RE, suggesting that these phenomena are manifestations of fast network dynamics that brusquely “ripple” the extracellular field, unlike the rhythmic θ and γ undulations (47).

Note that although stochasticity scores of different waves exhibit similar qualitative behaviors, e.g., all λs grow with speed and all βs increase with acceleration, they remain largely independent from each other, e.g., λ_θ is independent from λ_γ, β_γ does not depend on β_re, etc. (SI Appendix, Fig. 4). In other words, the results illustrated on Figs. 4, 5, and 6, are not redundant—they each provide a standalone description of the oscillatory dynamics in the corresponding frequency band.

B. Stochasticity in Space.

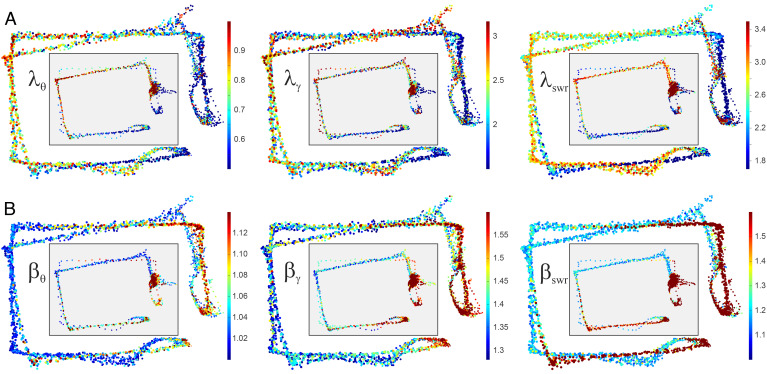
Distributing the λ- and β-scores along the animal’s trajectory yields spatial maps of stochasticity for each brain rhythm and reveals a curious spatial organization of LFP patterns with similar morphology. As shown on Fig. 7, higher λ-values for all waves are attracted to segments where the mouse is actively running with maximal speed, furthest away from the food wells. Patterns that are close to the expected average (low-λ) concentrate in the vicinity of food wells where the animal moves slowly. These regions also tend to host high β-scores that appear as the animal slows down to eat, as well as the lowest βs, which appear as the animal accelerates away (65). In other words, the LFP waves become more “trendy” and, at the same time, more structured (either more periodic or more clustered) over the behaviorally important places (e.g., food wells) that require higher cognitive activity. On the other hand, the outer parts of the track, where the brain waves are less controlled by the mean and remain moderately disordered, are marked by irregular patterns.

Fig. 7.

Spatial stochasticity maps were obtained by plotting λ and β parameters along the trajectory. Note that the inbound and the outbound trajectories are slightly different, leading to two seemingly displaced tracks in each plot. (A) The λ-maps show that θ-wave, γ-wave, and RE generally follow the mean trend near the food wells (with scattered wisps of high stochasticity) and deviate from the mean over the areas most distant from the food wells. The smaller maps in the gray boxes represent slow lapses: the overall layout of high-λ and low-λ fields is same as during the fast moves, which suggests spatiality of λ-stochasticity. (B) The behavior of β_θ is opposite: the “uneventful,” distant run segments attract nearly periodic behavior, while the food wells attract time-clumping wave patterns. Note that, at the food wells, the waves exhibit highly improbable (high-λ), disordered (high-β) patterns.

Intriguingly, the same map structure is reproduced during slow lapses, when the motor control of the patterns weakens, suggesting that speed and acceleration are not the only determinants of the LFP patterns. As shown on Fig. 7, even when the mouse dawdles, the waves tend to deviate from the mean around the outer corners and follow the mean in the vicinity of the food wells. Similarly, the patterns start clumping as the mouse approaches the food wells and distribute more evenly as he moves away.

These results suggest that spatial context may, by itself, influence hippocampal brain rhythm structure, in a way that is reminiscent of the place-specific activity of spatially tuned neurons in sectioned environments, e.g., place cells (67) or parietal neurons (68), which highlight geometrically similar domains (see also linearized maps, SI Appendix, Fig. 5). Specifically, the “bursting fields” (high-β) and “domains of regularity” (small λ) surround food wells; the “quasiperiodicity fields” (small βs) as well as “wobbling fields” (large λs) stretch over the outer segments, notably corners (Fig. 7). Physiologically, spatiality of stochasticity may reflect a coupling between the hippocampal place-specific spiking activity and extracellular field oscillations.

3. Discussion

Recorded LFP signals are superpositions of locally induced extracellular fields and inputs transmitted from anatomically remote networks. The undulatory appearance of the LFP is often interpreted as a sign of structural regularity^‡, but the dynamics of these rhythms is actually highly complex. Understanding the balance between deterministic and stochastic perspectives on LFPs pose significant conceptual challenges, as it happened previously in other disciplines (70).

Structurally, LFP rhythms may be described through discrete sequences of wave features (heights of peaks, specific phases, interpeak intervals, etc.) or viewed as transient series—bursts—of events, as in the case of REs (71). It is well-recognized that such sequences are hard to forecast, e.g., a recent discussion of a possible role of bursts in brain waves’ genesis posits: “An important feature that sets the burst scenario apart is the lack of continuous phase-progression between successive time points—and therefore the ability to predict the future phase of the signal—at least beyond the borders of individual bursts” (71). In other words, the nonlinearity of LFP dynamics, as well as its transience and sporadic external driving, result in effective stochasticity of LFP patterns—an observation that opens a new round of inquiries (71, 72). For example, how exactly should one interpret the “unpredictability” of a temporal sequence? Does it mean that its pattern cannot be resolved by a particular physiological mechanism or that it is unpredictable in principle, “genuinely random,” as, e.g., a gambling sequence? What is the difference between the two? Are the actual network computations based on “overcoming randomness” and somehow deriving the upcoming phases or amplitudes from the preceding ones or may there be alternative ways of extracting information? Does the result depend on the “degree of randomness” and if so, how to distinguish between “more random” and “less random” patterns? These questions are not technical, pertaining to a specific mechanism, nor specifically physiological; rather, these are fundamental problems that transcend the field of neuroscience. Historically, similar questions have motivated mathematical definitions of randomness that are still debated to this day (73–75).

The approach suggested by Kolmogorov in 1933 the year when brain waves were discovered (76) is based on the statistical universality of deviations from the expected behavior (28, 29). From Kolmogorov’s perspective, randomness is contextual: if a sequence X deviates from an expected mean behavior within bounds established by the distribution [3], then X is effectively random. In other words, an individual sequence may be viewed as random if it could be randomly drawn from a large pool of similarly trending sequences, with sufficiently high probability. This view permits an important conceptual relativism: Even if a sequence is produced by a specific mechanism or algorithm, it can still be viewed as random as long as its λ-score is “typical” according to the statistics [3]. For example, it can be argued that geometric sequences are typically more random than arithmetic ones, although both are defined by explicit formulae (30–34). By analogy, individual brain rhythms may be generated by specific synchronization mechanisms at a precise timescale, and yet they may be empirically classified and quantified as stochastic.

A practical advantage of Kolmogorov’s approach is that mean trends, such as [1], can often be reliably established, interpreted, and then used for putting the stochasticity of the underlying sample patterns into a statistical perspective. Correspondingly, assessments based on λ-scores were previously applied in a variety of disciplines from genetics (35–37) to astronomy (38) and from economics (39) to number theory (30–34, 40–44, 77). Some work has also been done in brain wave analyses, e.g., for testing normality of electroencephalograms’ long-term statistics (78–81). Arnold β-score provides an independent assessment of orderliness (whether elements of an arrangement tend to attract, repel, or be independent of each other) and it has not been, to our knowledge, previously used in applications.

Importantly, Kolmogorov and Arnold scores are impartial and independent from physiological specifics or contexts, thus providing self-contained semantics for describing the LFP data and a novel venue for analyzing the underlying neuronal mechanisms. It becomes possible to distinguish “statistically mundane” LFP patterns from exceptional ones and to capture the transitions between them, as well as to link pattern dynamics to changes in the underlying network’s dynamics. For example, since θ-bursts are physiologically linked to long-term synaptic potentiation (82, 83), θ-patterns with high β-scores may serve as markers of plasticity processes taking place in the hippocampal network at specific times and places (84–86). Furthermore, high-β_θ regions near food wells indicate that reward proximity may also trigger hippocampal plasticity and, since hippocampal neurons’ spiking is coupled to θ-cycles (2), have a particular effect on memory processing. On the other hand, low-β_θ indicates limit cycles in the network’s phase space that uphold simple periodicity. γ-bursts (high β_γ) mark heightened attention and learning periods (5, 87). In our observations, they appear during the mouse’s approach to the reward locations and disappear as it ventures away from them. Clustering ripples during quiescence reflect dense replay activity (61, 62), indicative of periods of memory encoding, retrieval, and network restructurings (63, 88).

Overall, the proposed approach allows studying brain rhythms from a new perspective that complements existing methodology, which may lead to a deeper understanding of the synchronized neuronal dynamics and its physiological functions.

Materials and Methods

Experimental Procedures.

The LFP data used in this study were previously analyzed via the conventional Fourier transformation method and published in refs. 45 and 46. Data were recorded from the CA1 pyramidal cell layer of hippocampus. The animals were trained in a familiar room to run back and forth on about ∼2-m long rectangular track (Fig. 4B) for food reward. The daily recording procedure consisted of two sessions on the track, lasting about 15 min each, followed by one to two 15-min break in the sleeping box. The recording was repeated 3–10 d. The LFP data were sampled at 2 kHz rate. Two color diodes (red, green) were mounted over the animal’s head to track its positions, sampled at 33 Hz with a resolution approximately 0.2 cm. Further details on surgery, tetrode recordings, and other procedures can be found in (45, 46).

Computational Algorithms.

The following outline of mathematical methods is based on refs. 28–34, 41–44

1. Kolmogorov score. Let X = x₁ ≤ x₂ ≤ … ≤ x_n, be an ordered sequence and let N(X, L) be the number of elements smaller than L,

$$\begin{array}{c}\hfill N(X,L)=\{\text{number of}0\le x_k<L\}.\end{array}$$

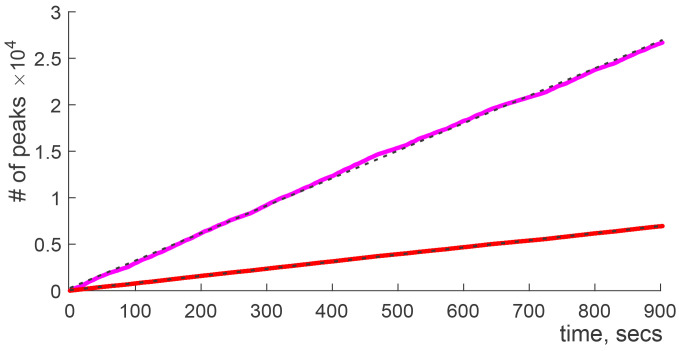
Let $\overline{N}(X,L)$ be the expected number of elements that interval; in case of the brain rhythms, this number will grow proportionally to the length of the interval, with the slope defined by the rhythm’s frequency (Fig. 8).

Fig. 8.

Counting functions for θ-peaks (N_θ, red) and γ-peaks (N_γ, magenta) evaluated for one entire running session, for one mouse. The black lines show the estimated (95% prediction interval) linear trends.

The closer X follows the prescribed behavior, the smaller the normalized deviation^§

$$\begin{array}{c}\lambda (X)=\underset{L}{\sup }|N(X,L)-\overline{N}(X,L)|/\sqrt{n}.\end{array}$$ [2]

A remarkable observation made in ref. 28 is that the cumulative probability of having λ(X) smaller than a given λ converges to the function

$$\begin{array}{c}\text{Φ}(\lambda )={\displaystyle \sum _{k=-\infty }^{\infty }{(-1)}^k{e}^{-2k^2{\lambda }^2}},\end{array}$$ [3]

that starts at Φ(0) = 0 and grows to Φ(∞) = 1. The derivative of the cumulative density [3] defines the probability distribution for λ, P(λ)=∂_λΦ(λ) illustrated on Fig. 2B Even though the range of P(λ) includes arbitrarily small or large λs, the shape of the distribution implies that excessively high or low λ-values are rare, e.g., sequences with λ(X)≤0.4 or λ(X)≥1.8 appear with probability less than 0.3%, Φ(0.4)≈0.003, and Φ(1.8)≈0.997. Since these statistics are universal, i.e., apply to any sequence X, the λ-score can serve as a universal measure of “stochastic typicality” of a pattern (29–34). This is akin to the familiar use of normally distributed z-scores: “typical” zs (99.7% of them) lay in the range −3 ≤ z ≤ 3, while small (z < −3) or large (z > 3) scores appear with probability 0.3%. Just as the z-scores are used to detect outliers in a normal distribution, λ-scores measure typicality of patterns: if a pattern X deviates from the expected mean within limits established by the “hump” of the P(λ)-distribution (pink stripe on Fig. 2B), then X is typical. If, however, these limits are surpassed, then the pattern is “atypical,” “uncommon,” “not chancy,” and may be viewed as a sign of a severe trend violation, or a “trend change.”

2. Corrections to Kolmogorov score up to the order n^−3/2,

$$\begin{array}{c}\hfill \lambda (X)\to \lambda (X)\left(1+\frac{1}{4n}\right)+\frac{1}{6n}-\frac{1}{4n^{3/2}},\end{array}$$ [4]

allow increasing the accuracy of the finite-sample estimates to over 0.01% for sequences containing as little as 10 to 20 elements (50–52). In this study, all λ-evaluations are based on the expression [4] and use data sequences that contain more than 25 elements.

3. Mean Kolmogorov stochasticity score. The mean λ can then be computed as

$$\begin{array}{c}\hfill {\lambda }^{\ast }={\int }_0^{\infty }\lambda P(\lambda )d\lambda ={\int }_0^{\infty }\mathrm{\Phi }(\lambda )d\lambda ,\end{array}$$

where we used integration by parts and the fact that the distribution P(λ) starts at 0, P(0) = 0, and approaches 0 at infinity, P(∞) = 0 (Fig. 2B). Integrating the Gaussian terms in expansion [3] yields Mercator series

$$\begin{array}{c}{\lambda }^{\ast }=\sqrt{\frac{\pi }{2}}{\displaystyle \sum _{k=1}^{\infty }{(-1)}^{k+1}\frac{1}{k}=\sqrt{\frac{\pi }{2}}\ln 2\approx 0.8687}.\end{array}$$

4. Φ(λ) estimates. For small λs, the Kolmogorov Φ-function [3] can be approximated by

$$\begin{array}{c}\hfill \mathrm{\Phi }(\lambda )\approx \frac{\sqrt{2\pi }}{\lambda }{e}^{-{\pi }^2/8{\lambda }^2},\end{array}$$ [5]

and for large λs, it is approximated by the two lowest-order terms in [3], Φ(λ)≈1 − 2e^−2λ2 (28, 29). These formulae allow quick evaluations of the λ-scores’ cumulative probabilities outside of the “stochastic typicality band,” λ < 0.4 or λ > 1.8.

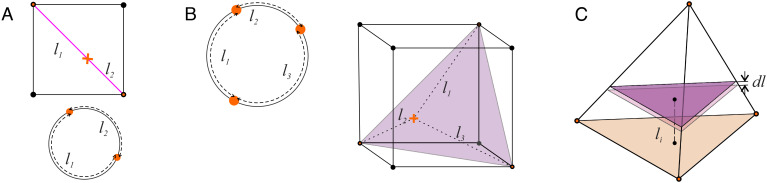
5. Arnold score. Let us arrange the points of the sequence X on a circle of length L and consider the arcs between pairs of consecutive elements, x_i and x_{i + 1} (Fig. 2C). If the lengths of these arcs are l₁, l₂, …, l_n, then the sum

$$\begin{array}{c}\hfill B=l_1^2+l_2^2+\dots +l_n^2,\end{array}$$ [6]

grows monotonically from its smallest value B_min = n(L/n)² = L²/n, produced when the points x_k lay equidistantly from each other, to its largest value, B_max = L², attained when all elements share the same location, with the mean B^* = B_min2n/(n + 1)≈2B_min (41–44).

Intuitively, orderly arrangements appear if the elements “repel” each other, “clumping” is a sign of attraction, while independent elements are placed randomly. Hence, the ratio β = B/B_min can be used to capture the orderliness of patterns:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\beta (X)\approx 1,\hfill & \text{indicates atypically ordered, nearly equidistant sequences;}\hfill \\ \beta (X)\approx {\beta }^{\ast }\approx 2\hfill & \text{marks statistically typical, commonly scattered sequences;}\hfill \\ \beta (X)\gg {\beta }^{\ast }\hfill & \text{corresponds to clustering sequences.}\hfill \end{array}\right.\end{array}$$ [7]

6. The length L of the circle accommodating a random sample sequence X in Arnold’s method was selected so that the distance between the end points, x₀ and x_n, became equal to the mean arc length between the remaining pairs of neighboring points,

$$l_n={|x_n-x_0|}_{modL}=\frac{1}{n-1}\sum _{i=1}^{n-1}{l}_i.$$

7. Mean Arnold stochasticity score. A short derivation of β^* is provided below for completeness, following the exposition given in ref. 44.

• The n arcs lengths l₁, l₂, …, l_n produced by n points, X = {x₁, x₂, …, x_n}, can be viewed as the “coordinates” of X in a n-dimensional sequence space. If these coordinates could vary independently on a circle of length L, then the sequences would be in one-to-one correspondence with the points of a n-dimensional hypercube with the side L. However, since the sum of l_is must remain fixed,

  $$\begin{array}{c}\hfill l_1+l_2+...+l_n=L,\end{array}$$ [8]

  the admissible l-values occupy a hyperplane that cuts between the vertices (0, 0, …, 0) and (L, L, …, L). For example, two values l₁ and l₂ = L − l₁ define a point on the diagonal of a L-square (Fig. 9A), three values define points of a “diagonal” equilateral triangle in the L-cube (Fig. 9B), four values represent points of a regular tetrahedron (Fig. 9C), and so forth. A generic n-sequence is hence represented by a point in a polytope spanned by n vertices in (n − 1)-dimensional Euclidean space—a (n − 1)-simplex, σ^{(n − 1)} (89).

• The defining property of a simplex is that any subcollection of its vertices spans a subsimplex: a tetrahedron, σ⁽³⁾, is spanned by four vertices, any three of which span a triangle σ⁽²⁾—a “face” of σ⁽³⁾; any two vertices span an edge, σ⁽¹⁾, between them, etc. (89). Correspondingly, a generic section of the σ^{(n − 1)}-simplex by a hyperplane is also a σ^{(n − 2)}-simplex (Fig. 9C).

• Averaging the sum [6] requires evaluating the mean of each l_i²,

  $$\begin{array}{c}\hfill ⟨l_i^2⟩=\frac{1}{V_{n-1}}{\int }_{{\sigma }^{(n-1)}}{l}_i^{2}dV,\end{array}$$ [9]

  for i = 1, 2, …, n. Here, V_{n − 1} refers to the volume of σ^{(n − 1)} and “dV” refers to the volume of a thin layer positioned at a distance l_i away from the ith face (Fig. 9C). By the defining property of simplexes mentioned above, the base of this layer is a (n − 2)-simplex specified by the equation

  $${\displaystyle \sum _{j\ne i}^n{l}_j=L-l_i,}$$

  which implies that the sides of this base have length L − l_i just as the sides of σ^{(n − 1)} defined by [8] have length L. The volume of the thin layer is dV = C(L − l_i)^{n − 2}dl_i, so that

  $$\begin{array}{c}\hfill ⟨l_i^2⟩=\frac{C}{V_{n-1}}{\int }_0^L{l}_i^2{(L-l_i)}^{n-2}d{l}_i=\frac{C{L}^{n+1}}{V_{n-1}}{\int }_0^1{u}^2{(1-u)}^{n-2}du,\end{array}$$

  where u = l_i/L. Using the variable v = 1 − u, the latter integral yields:

  $$\begin{array}{c}\hfill ⟨l_i^2⟩=\frac{C{L}^{n+1}}{V_{n-1}}{\int }_0^1{(1-v)}^2{v}^{n-2}dv=C\left(\frac{1}{n-1}-\frac{2}{n}+\frac{1}{n+1}\right).\end{array}$$

  The volume of the σ^{(n − 1)}-simplex is

  $$\begin{array}{c}\hfill V_{n-1}={\int }_0^{L}dV=\frac{C{L}^{n-1}}{n-1};\end{array}$$

  hence the sum [6] divided by B_min = L²/n yields

  $$\begin{array}{c}\hfill ⟨{\beta }_n⟩=n^2\left(1-2\frac{n-1}{n}+\frac{n-1}{n+1}\right)=2\frac{n}{n+1}\approx {\beta }^{\ast }=2.\end{array}$$ [10]

Fig. 9.

Averaging over a simplex. (A) If two coordinates l₁ and l₂ of a two-element sequence could independently vary between 0 and L, then the pair (l₁, l₂) would cover a 2D square. However, if the elements (x₁, x₂) remain on a circle (orange dots below) then the Eq. 8 restricts (l₁, l₂)-values to the cube’s diagonal (orange cross on the Top panel), i.e., to a 1-dimensional simplex. (B) A configuration of three points on a circle corresponds to a point on the diagonal section of a L-cube. (C) Tetrahedron—a section of a 4D cube—is the highest dimensional (3D) depictable simplex σ⁽³⁾, which is used to schematically represent n-dimensional simplexes, σ⁽ⁿ⁾. Averaging over l_i² in [9] involves integrating over it the (n − 1)-dimensional layers of σ⁽ⁿ⁾.

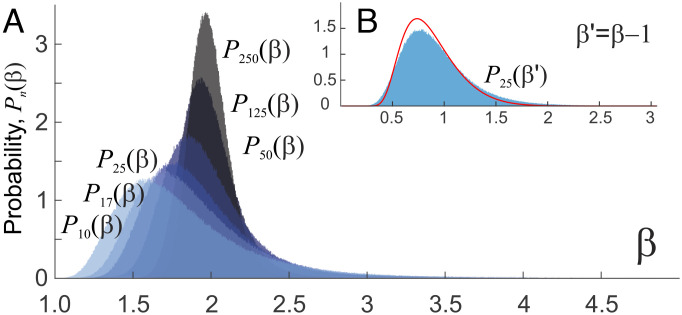
8. Probability distributions of β-values form a family parameterized by the number of elements in the sequence. As shown on Fig. 10, these distributions have a well-defined peak at ${\beta }_n\approx 2\frac{n}{n+1}$ (see below) and rapidly decay as β approaches 1 or for β > 3.5, which illustrates that typical β-values, for all n, remain near the impartial mean β^* ≈ 2.

Fig. 10.

β-distributions. (A) Histograms of β-values obtained for 10⁶ sequences containing n = 17, 25, 50, 125, and 250 elements peak in a vicinity of the impartial mean β^* and rapidly decay for β ≲ 1.2 and β ≳ 3.5. (B) The distribution of β′=β − 1 for sequences containing about n = 25 points is close to the universal Kolmogorov distribution P(λ) (red line, Fig. 2A).

9. The sliding window algorithm can be implemented in two ways:

• using a fixed window that may capture different numbers of events at each step, i.e., L_t = L, but n_t and n_{t + 1} may differ;

• using a fixed number of events per window, i.e., n_t = n, but L_t and L_{t + 1} may differ.

In both cases, the mean window width $\overline{L}$ is proportional to the mean separation between nearest events,

$$\begin{array}{c}\hfill \overline{l}\equiv ⟨l_i⟩=⟨x_{i+1}-x_i⟩,\end{array}$$ [11]

and the mean number $\overline{n}$ of the data points in the sample sequence, $\overline{L}=\overline{l}\overline{n}$. The resulting estimates for λ(t) and β(t) are nearly identical and, for qualitative assessments, can be used interchangeably.

10. Local averaging. To build the dependencies between local averages, we ordered the values assumed by the independent variable, e.g., the speeds, from smallest to largest,

$$\{s_1,s_2,\dots \}\to \{s_1^{\prime }\le s_2^{\prime }\le \dots \},$$

subdivided the resulting sequence into consecutive groups containing 100 elements and averaged each set,

$${\widehat{s}}_i=\frac{1}{100}{\displaystyle \sum _{k=-50}^{50}{s}_{i+k}^{\prime }}.$$

Since each s_ik is associated with a particular moment of time t_ik, we computed the averages of the corresponding dependent variable, e.g., λ_ik,

$${\widehat{\lambda }}_i=\frac{1}{100}{\displaystyle \sum _{k=1}^{100}{\lambda }_{i_k}}.$$

Similarly, ordering the β-scores and evaluating their local means produces the ${\widehat{\beta }}_i$-values, along with the means of their λ_ik-counterparts that occur at the corresponding moments t_ik.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Previously published data were used for this work (45). Data files uploaded, sharing URL: https://datadryad.org/stash/share/zchXWoaNFMQhI1b2Qlt3mGgpr3Da09cHJse5ACYwhcU (90).