Abstract
Background
Time‐resolved 4D cone beam–computed tomography (4D‐CBCT) allows a daily assessment of patient anatomy and respiratory motion. However, 4D‐CBCTs suffer from imaging artifacts that affect the CT number accuracy and prevent accurate proton dose calculations. Deep learning can be used to correct CT numbers and generate synthetic CTs (sCTs) that can enable CBCT‐based proton dose calculations.
Purpose
In this work, sparse view 4D‐CBCTs were converted into 4D‐sCT utilizing a deep convolutional neural network (DCNN). 4D‐sCTs were evaluated in terms of image quality and dosimetric accuracy to determine if accurate proton dose calculations for adaptive proton therapy workflows of lung cancer patients are feasible.
Methods
A dataset of 45 thoracic cancer patients was utilized to train and evaluate a DCNN to generate 4D‐sCTs, based on sparse view 4D‐CBCTs reconstructed from projections acquired with a 3D acquisition protocol. Mean absolute error (MAE) and mean error were used as metrics to evaluate the image quality of single phases and average 4D‐sCTs against 4D‐CTs acquired on the same day. The dosimetric accuracy was checked globally (gamma analysis) and locally for target volumes and organs‐at‐risk (OARs) (lung, heart, and esophagus). Furthermore, 4D‐sCTs were also compared to 3D‐sCTs. To evaluate CT number accuracy, proton radiography simulations in 4D‐sCT and 4D‐CTs were compared in terms of range errors. The clinical suitability of 4D‐sCTs was demonstrated by performing a 4D dose reconstruction using patient specific treatment delivery log files and breathing signals.
Results
4D‐sCTs resulted in average MAEs of 48.1 ± 6.5 HU (single phase) and 37.7 ± 6.2 HU (average). The global dosimetric evaluation showed gamma pass ratios of 92.3% ± 3.2% (single phase) and 94.4% ± 2.1% (average). The clinical target volume showed high agreement in D 98 between 4D‐CT and 4D‐sCT, with differences below 2.4% for all patients. Larger dose differences were observed in mean doses of OARs (up to 8.4%). The comparison with 3D‐sCTs showed no substantial image quality and dosimetric differences for the 4D‐sCT average. Individual 4D‐sCT phases showed slightly lower dosimetric accuracy. The range error evaluation revealed that lung tissues cause range errors about three times higher than the other tissues.
Conclusion
In this study, we have investigated the accuracy of deep learning–based 4D‐sCTs for daily dose calculations in adaptive proton therapy. Despite image quality differences between 4D‐sCTs and 3D‐sCTs, comparable dosimetric accuracy was observed globally and locally. Further improvement of 3D and 4D lung sCTs could be achieved by increasing CT number accuracy in lung tissues.
Keywords: 4D imaging, adaptive proton therapy, deep learning, synthetic CT
1. INTRODUCTION
The intent of adaptive radiation therapy (ART) is to ensure accurate dose delivery throughout the treatment course by closely monitoring patient's anatomy and restoring dose conformity by adapting the treatment in accordance with anatomical changes. 1 , 2 , 3 , 4 To detect anatomical changes, frequent volumetric imaging is essential for any ART workflow. Cone beam–computed tomography (CBCT) is routinely used for daily patient position verification in photon and proton radiotherapy. CBCTs are considered valuable for ART, given that they provide a daily representation of the patient anatomy in the actual treatment position. 5 However, due to imaging artifacts such as scatter, beam hardening, or a smaller field of view (FOV), CBCT image quality is inferior to diagnostic CT image quality. 6 Although this is acceptable for patient alignment, it affects the dose calculation accuracy and thereby the suitability for ART, especially in proton therapy. Hence, within ART workflows, a correction of CBCTs is required before CBCT‐based dose calculations can be performed. 7
In proton therapy, the characteristic dose falloff after the dose maximum (Bragg peak) and the associated sensitivity to density changes along the beam path leads to even higher demands on the CT number accuracy than conventional photon dose calculations. 8 Various CBCT correction approaches have been previously investigated for photon and proton dose calculations, including methods based on histogram matching, 9 deformable image registration (DIR), 10 , 11 , 12 projection‐based corrections, 13 , 14 , 15 and Monte Carlo simulations. 16 , 17 Recently, the focus shifted towards deep learning–based correction methods. 18 These approaches utilize deep convolutional neural networks (DCNNs) for image‐to‐image translation and learn a correction of CBCT artifacts from assumingly artifact‐free diagnostic CT images. The corrected images, also referred to as synthetic CTs (sCT), have shown promising results for dose calculations in various anatomical regions, such as brain, 19 head and neck, 20 , 21 , 22 lung, 23 and prostate. 24 , 25
Previous studies on deep learning–based sCTs focused on 3D‐imaging, neglecting any internal motion of the patient (e.g., respiratory and cardiac). In the thorax and abdomen, respiratory motion affects the position of target volumes and healthy tissues and may have a severe impact on the dose distribution and treatment quality. In clinical practice, the quasiperiodic breathing motion, in combination with the high sensitivity of proton beams to density changes, motivates the routine use of time‐resolved 4D imaging during treatment planning and treatment verification. Patient alignment CBCTs can also be acquired with dedicated 4D‐CBCT acquisition protocols and reconstruction algorithms. Although 4D‐CBCTs are more commonly used in the photon radiotherapy field, they are slowly being adopted in particle therapy. 26 4D‐CBCT acquisitions with an image quality comparable to that of 3D‐CBCTs require more projection data, resulting in higher imaging dose and longer acquisition times, and are not yet commonly used in proton therapy. To overcome these limitations and still achieve acceptable image quality, advanced reconstruction algorithms have been developed to reconstruct 4D‐CBCTs from sparse‐view acquisitions (a limited number of projections) originally used for 3D‐CBCTs. 27 , 28
Previous studies already investigated non–deep learning strategies to correct 4D‐CBCTs and enable dose calculations for proton therapy. Niepel et al. and Bondesson et al. investigated a DIR–based method, 29 , 30 whereas Schmitz et al. extended a previously investigated projection‐ and prior‐based scatter correction algorithm to a 4D scenario. 31 All three studies utilized an ex vivo porcine lung phantom to validate their CBCT correction strategies and showed the general feasibility of 4D‐CBCT‐based proton dose calculations. However, none of these approaches used actual patient 4D‐CBCT data. Madesta et al. presented a self‐contained deep learning method to improve 4D‐CBCT image quality. 32 This method showed considerable improvements in image quality, but it was not evaluated in the context of photon or proton dose calculations.
Daily time–resolved 4D imaging can reduce the impact of breathing motion–induced uncertainties, which impact the quality of proton therapy treatments in the thorax. The purpose of this study was to investigate the ability of a DCNN to generate 4D‐sCTs from sparse view 4D‐CBCTs and to evaluate the suitability of 4D‐sCTs for proton dose calculations in adaptive proton therapy workflows.
2. MATERIALS AND METHODS
2.1. Patient datasets
A dataset of 45 thoracic cancer patients, treated at the University Medical Center Groningen, was used to train and evaluate a DCNN for 4D‐sCT generation. Patients were aged between 18 and 83 years (mean age: 61.3 years). For each patient, a 4D‐CT, raw CBCT projections, structure sets, treatment plans, breathing signals, and treatment delivery log files were retrospectively collected. All patients were treated with pencil beam scanning intensity‐modulated proton therapy (PBS‐IMPT) using three beam angles. Patients breathing rates varied from 13.4 to 24.5 breathing cycles/min in the testing set and from 11.4 to 26.4 cycles/min in the training set. The Supporting Information contain a table showing breathing rates for each patient (Table S2 and Figure S2).
2.2. Imaging data
2.2.1. CBCT reconstruction
To reconstruct 4D‐CBCTs, raw CBCT projections from a single fraction were collected for each patient. CBCT projections were acquired using the gantry‐mounted CBCT scanner of an IBA Proteus Plus proton therapy system (IBA, Belgium), with a resolution of 1440 × 1440 pixels, a pixel size of 0.3 × 0.3 mm, a full 360‐degree arc, a detector offset to enlarge the axial‐FOV (500 mm), a tube voltage of 110 kVp, a tube current of 320 mA, and an exposure time of 12.5 ms. Each acquisition consisted of 472 projections, with an angular spacing of 0.8 degrees and a total acquisition time of ∼70 s. Two different FOV settings in cranio‐caudal (CC) direction were used: (1) long scan: All 1440 pixels rows were irradiated, (2) short scan: Only the central 720 rows were irradiated. Short scans were chosen for imaging dose reduction in patients that did not require the full FOV for pretreatment position verification.
CBCT projections were reconstructed into 4D‐CBCTs with six breathing phases using the iterative MA‐ROOSTER reconstruction algorithm. 28 The algorithm performs spatial and temporal regularization utilizing a‐priori information from a planning 4D‐CT scan. Similar reconstruction parameters as the ones used by den Otter et al. and Mory et al. were chosen for the reconstruction of 4D‐CBCTs, except for the number of breathing phases. 26 , 28 To have a uniform FOV in CC direction, CBCTs for all patients were reconstructed with a reduced FOV using only the central 720 pixels in CC direction. Reconstruction was performed using the MA‐ROOSTER implementation of the open‐source reconstruction toolkit RTK (www.openrtk.org). 33 Preprocessing of projections, and motion estimation, using a diffeomorphic morphons algorithm, was performed using the 4D‐CBCT‐reconstruction workflow of the open‐source MATLAB toolbox open‐REGGUI (www.openreggui.org).
2.2.2. 4D‐CTs
In this study, 4D‐CTs were used for two purposes. First, for the reconstruction of 4D‐CBCTs using the MA‐ROOSTER algorithm. Deformable vector fields were generated between each breathing phase and a reference phase (50% phases, maximum exhale) of the planning 4D‐CT. Second, follow‐up 4D‐CTs, acquired on the same day as the CBCT projections, were used as ground‐truth images to evaluate the quality of 4D‐sCTs.
Planning 4D‐CT images were acquired 1–2 week before start of treatment, using a Siemens SOMATOM Definition AS scanner (Siemens Healthineers, Germany), whereas verification CT scans were acquired on a Siemens SOMATOM Confidence scanner, directly at the proton therapy center. Both planning and follow‐up 4D‐CTs were acquired with a tube voltage of 120 kVp, a variable tube current, a pixel size of 1.0 × 1.0 mm2, an axial resolution of 512 × 512 pixels, and a slice thickness of 2 mm. All 4D‐CTs were reconstructed with 10 breathing phases.
To reduce the impact of anatomical and positional differences on the sCT evaluation, a phase‐by‐phase DIR between 4D‐CBCT and the ground‐truth 4D‐CT was performed. 4D‐CTs were reconstructed into 10 breathing phases, whereas 4D‐CBCTs only into 6. Therefore, to generate a six‐phase ground‐truth image, the closest 4D‐CT phase was chosen and registered to the respective 4D‐CBCT phase (e.g., 4D‐CBCT 17% phase to 4D‐CT 20% phase). A diffeomorphic morphons algorithm, implemented in open‐REGGUI and extensively investigated for deformable registration of CBCT and CT images, 11 , 12 , 34 was used for the DIR. For simplicity, we will still refer to the deformed 4D‐CT as just 4D‐CT in the following sections.
2.3. Synthetic CTs
To generate sCTs, a U‐net‐like DCNN architecture, originally proposed by Spadea et al., 35 was utilized. This network architecture was already thoroughly investigated for image synthesis in the context of MR‐ and CBCT‐based proton dose calculations for brain, 35 head‐and‐neck, 20 , 21 and thoracic 23 cancer patients. A figure depicting the neural network architecture is presented in Figure S1. A special feature of the DCNN proposed by Spadea et al. is that separate networks are trained with axial, coronal, and sagittal slices. Each individual sCT is then combined into a final sCT by averaging voxel values from the three anatomical views. For more details on the network architecture, the reader is referred to previous work by Spadea et al. 35
Our dataset was randomly split into a training (27 patients), validation (3 patients), and testing set (15 patients). Training of the DCNN was performed with pairs of 0%‐phase images of 4D‐CBCT and 4D‐CT. To generate a full 4D‐sCT during inference, the networks, trained exclusively with 0%‐phase images, were applied to all other 4D‐CBCT phases. Similarly to previous studies, a batch size of 1 was used, and training was stopped when no decrease in training loss was observed for five consecutive epochs. Training and inference were performed on an NVIDIA GTX 1080 TI graphical processing unit (GPU) with 11 GB of VRAM.
2.4. Comparison with 3D‐sCTs
For comparison purposes, 3D‐sCTs, based on the clinically used 3D‐CBCTs, were generated for all patients. These 3D‐CBCTs were reconstructed from the same set of projections as 4D‐CBCTs, but with the clinically used reconstruction algorithm and settings of the clinically used IBA Adapt Insight software (IBA, Belgium). The reconstructed 3D‐CBCTs were converted into 3D‐sCTs with a previously trained network. A full description of this DCNN for 3D lung sCTs is provided by Thummerer et al. 23 A figure depicting the entire workflow for 4D and 3D evaluation of sCTs is presented in Figure S3.
2.5. Image evaluation
Image quality of sCTs was evaluated against ground‐truth 4D‐CTs for a variety of scenarios: (1) for the two extreme 4D‐sCT phases (0% maximum inhale, called “4D‐sCT‐0%” and 50% maximum exhale, called “4D‐sCT‐50%”); (2) for a “4D‐CT‐average” obtained by averaging voxel values of the six breathing phases; and (3) for the 3D‐sCT. For the single‐phase 4D‐sCTs, the respective 4D‐CT phases were used as a ground‐truth image. For the 4D‐sCT‐average, an average 4D‐CT was generated in the same way the 4D‐sCT‐average was created and used as reference. For the 3D‐sCT, the average projection of a same‐day verification 4D‐CT was deformed to the 3D‐CBCT and used as ground truth. Detailed image quality results for the other breathing phases (17%‐, 33%‐, 67%‐, and 83%‐phase) are presented in Figure S4 and Table S5.
Image similarity between sCTs and the reference CTs was quantified via mean absolute error (MAE), mean error (ME), peak signal‐to‐noise ratio (PSNR), structural similarity (SSIM), and the dice similarity coefficient (DSC). These metrics are defined in the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
where and are the respective HU values of the i‐th voxel of sCT and CT, is the total number of voxels within the patient outline, Q stands for the highest observed HU value of sCT and rCT, and for the average pixel values of sCT and rCT, and for the variances of sCT and rCT, for the covariance between sCT and rCT, and L for the dynamic range of sCT and rCT. MAE and ME were only calculated for voxels within the patient volume, PSNR and SSIM for the entire image. Air and bone regions were approximately segmented using a simple thresholding technique (air <400 HU, bone >300 HU) to calculate the DSC between these regions on sCTs and rCTs. Finally, an MAE spectrum was obtained by grouping voxels into bins of 20 HU and calculating MAE for each bin. This allows one to quantify the MAE of various tissues across a HU range (−1000 to 500 HU).
2.6. Proton radiography simulations
To assess the difference between 4D‐CTs and 4D‐sCTs in terms of proton range, we performed proton radiography (PR) simulations using the PR module of the open‐source toolkit openREGGUI. It features a direct ray‐tracing algorithm to simulate PR acquisitions with a multilayered ionization chamber. 36 All PRs were simulated with a gantry angle of 0 degrees (anterior–posterior direction), an energy of 210 MeV, and a spacing between individual pencil beams of 1 mm in left–right and 2 mm in CC direction (similar to the 4D‐CT grid). Range errors between PRs were calculated according to previous studies. 37 , 38 , 39
Range error maps were computed for 4D‐sCT‐50%, 4D‐sCT‐average, and the 3D‐sCT. The range error maps were analyzed by calculating mean and standard deviation for range probes within the patient outline and reported for each patient individually. Range probes were divided into two groups: range probes traversing lung tissue and range probes not traversing lung tissue. This allowed one to isolate the contribution of lung tissue in terms of HU accuracy and to perform a comparison to the remaining tissues. The lung area was selected by first generating a lung segmentation on the 4D‐CT (using a threshold of −600 HU) and then projecting the 3D lung segmentation along the beam direction (0 degrees). This resulted in a 2D mask that could be applied to the range error maps.
2.7. Dosimetric evaluation
To quantify dosimetric differences between 4D‐CT and 4D‐sCT, clinically used PBS‐IMPT treatment plans were recalculated on 4D‐sCT‐0%, 4D‐sCT‐50%, 4D‐sCT‐average, and 3D‐sCT. Dose calculations were performed using the Monte Carlo dose engine of RayStation 10B (RaySearch, Sweden), with a statistical uncertainty setting of 1% and a dose grid of 3 × 3 × 3 mm3. The resulting dose distributions were evaluated globally by performing gamma analysis using a 3%/3‐mm criterion and a 10% dose threshold. Local dose differences were investigated for the clinical target volume (CTV) D 98 and organs‐at‐risk (OARs) (D mean of lung, heart, and esophagus). Structures were transferred from the planning CT to the corresponding ground‐truth image using the DIR feature of RayStation.
To showcase a real 4D use case of 4D‐sCTs, a log‐file‐based 4D dose reconstruction was performed for each patient using treatment delivery log files and patient‐specific breathing signals acquired during treatment using a pressure belt system (ANZAI, Japan). For 10 patients, breathing signals were not available retrospectively. In those cases, instead of recorded pressure belt signals, an artificial breathing signal with a cycle duration of 4.5 s was used.
The 4D dose reconstruction was done according to the procedure described by Meijers et al. 40 Six subplans corresponding to each breathing phase were generated based on treatment delivery log files, breathing signals, and the treatment plan. Each subplan contained only spots delivered in the corresponding breathing phase. For each subplan, dose was calculated on the respective 4D‐sCT and 4D‐CT phase. Afterward, the subplan doses were warped and accumulated onto a reference phase (50% phase) using the RayStation treatment planning system. The resulting accumulated dose distributions were evaluated similarly to the other dose distributions (gamma analysis, local dose differences CTV, lung, heart, and esophagus).
2.8. Normal tissue complication probability (NTCP)
Normal tissue complication probability (NTCP) models predict the risk to develop specific radiotherapy‐induced side effects. In the Netherlands, NTCP models are used to determine which patients benefit most from proton radiotherapy. In the Dutch national indication protocol for proton therapy, 41 NTCP models for radiation pneumonitis (RP), 42 acute esophageal toxicity (AET), 43 and 2‐year mortality 44 are included. Clinical parameters (e.g., age, smoking status, and tumor location) and mean dose parameters for OARs (heart, lungs, and esophagus) are used as inputs for NTCP models. In this study, we used clinically employed NTCP models to translate dosimetric differences into more clinically relevant parameters by calculating the NTCP difference between 4D‐CTs and 4D‐sCTs.
3. RESULTS
3.1. Image quality
Figure 1 presents axial slices of CBCTs (4D‐CBCT‐0%, 3D‐CBCT), sCTs (4D‐sCT‐0%, 4D‐sCT‐average, and 3D‐sCT), and ground‐truth CT images (4D‐CT‐0%, 4D‐CT‐average, and 3D‐CT) of patient 2. A visual inspection of Figure 1 clearly shows a lower image quality of 4D‐CBCTs with respect to 3D‐CBCTs. However, after converting CBCTs into sCTs, this image quality difference is substantially reduced. 4D‐sCTs, especially single‐phase images, show less details and more artifacts in soft tissues and lung than 3D‐sCTs, as shown in Figure 2 with HU difference maps between sCTs and ground‐truth CTs.
FIGURE 1.

Overview of axial slices from cone beam–computed tomographies (CBCTs) (4D‐0%, 3D), synthetic computed tomographies (sCTs) (4D‐0%, 4D‐average, 3D) generated using a deep convolutional neural network compared to the CTs (4D‐0%, 4D‐average, and 3D) for patient 2
FIGURE 2.
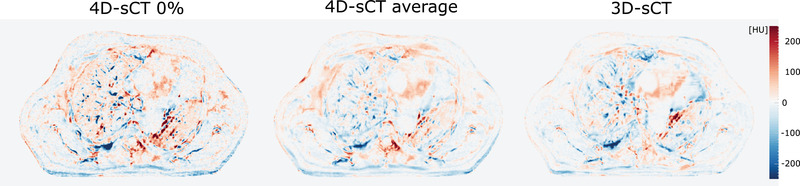
Difference maps for 0% 4D‐synthetic computed tomography (sCT), 4D‐sCT average, and the 3D‐sCT of patient 2
Image similarity differences were globally quantified via MAE, ME, PSNR, and SSIM. On average, the lowest MAE was observed for the 3D‐sCT and 4D‐sCT‐average, with MAEs of 37.2 ± 7.7 and 37.7 ± 6.2 HU. 4D‐sCT‐0% and 4D‐sCT‐50% resulted in a higher MAE of 47.5 ± 6.1 and 48.1 ± 6.5 HU. The remaining breathing phases showed a variation of less than 1 HU, ranging from 47.9 ± 6.3 to 48.6 ± 6.6 HU. Average MEs were −3.0 ± 7.2 HU for 4D‐sCT‐average, 0.1 ± 7.4 HU for 4D‐sCT‐0%, −4.5 ± 7.1 HU for 4D‐sCT‐50%, and −3.1 ± 7.8 HU for the 3D‐sCT.
Figure 3 shows bar charts of MAE and ME for 4D‐sCT‐0%, 4D‐sCT‐50%, 4D‐sCT‐ave, and the 3D‐sCT. Similar to MAE, the highest PSNR values were observed for the 3D‐sCT (45.4 ± 1.9 dB) and 4D‐sCT‐average (45.4 ± 1.9 dB). The 0% and 50% phase resulted in lower PSNR of 43.3 ± 1.5 and 43.3 ± 1.4 dB, respectively. The remaining breathing phases showed almost no differences with PSNR ranging from 43.1 to 43.3 dB. High uniformity was observed for individual breathing phases, with all phase images resulting in an SSIM value of 0.93 ± 0.02. The 4D‐sCT‐average and 3D‐sCT resulted in slightly higher SSIM of 0.94 ± 0.02 and 0.95 ± 0.02, respectively. For bone and air regions, DSC was used to assess the similarity between sCTs and reference CTs. For the air region, almost no difference was observed between individual phase images, average sCT, and the 3D‐sCT. 3D‐sCT, 4D‐sCT‐average, and 4D‐sCT‐00% resulted in a DSC of 0.98 ± 0.01. 4D‐sCT‐50% and all other 4D‐phases showed a DSC of 0.97. Significantly, lower DSC‐values were observed for bones with values of 0.66 ± 0.08 for the 3D‐sCT, 0.65 ± 0.06 for the 4D‐sCT‐average, 0.60 ± 0.07 for 4D‐sCT‐00%, and 4D‐sCT‐50%. The remaining breathing phases showed values between 0.60 and 0.61. Additional charts for PSNR, SSIM, and DSC and results for all breathing phases are presented in Figure S4 and Table S5.
FIGURE 3.

(a) Mean absolute error for 0% (blue) and 50% (orange) 4D‐synthetic computed tomography (sCT) phases, 4D‐sCT average (green), and the 3D‐sCT (red). The dashed lines indicate mean values of the entire dataset. (b) Mean error for 0% and 50% 4D‐sCT phases, 4D‐sCT average, and the 3D‐sCT
In Figure 4, the MAE spectrum and an average HU histogram are presented. As expected, the spectrum confirms the higher MAE of the single‐phase 4D‐sCT when compared to 4D‐sCT‐average and 3D‐sCT. All sCT‐types show the lowest MAE in soft tissues between −150 and 50 HU. This is also the HU region with the most voxels. The MAE‐spectrum also confirms the larger error for bone structures observed with the DSC. 3D‐sCT shows a peak for very low HUs, whereas 4D‐sCTs do not show this behavior. However, this appears in an HU region with very low number of voxels and, therefore, has only a negligible impact on the overall MAE of 3D‐sCTs.
FIGURE 4.

Average mean absolute error spectrum for 4D‐synthetic computed tomography (sCT)‐50% (orange), 4D‐sCT average (green), and the 3D‐sCT (red). The corresponding error regions represent the standard deviation of the dataset. The dashed black line shows an average image histogram.
Figure 5 presents HU‐profiles of patient 2 for 4D‐sCT 0%, 4D‐sCT‐average, and the 3D‐sCT compared to HU‐profiles of the respective reference images. Figure 5a shows a profile in anterior–posterior direction, whereas the profile in Figure 5b is going from right to left. Both profiles were chosen to intersect the CTV. High agreement between sCT and CT profiles were observed. In general, synthetic CT profiles are smoother than reference CT profiles. Tissue boundaries (e.g., soft tissue—lung or soft tissue—bone), however, are well represented on the sCTs and differences between profiles are primarily seen within tissues and not at interfaces.
FIGURE 5.

Comparison of∖ profiles of 4D‐synthetic computed tomography (sCT) 0%, average 4D‐sCT, and 3D‐sCT to their reference images along the red line indicated on CT scan. The clinical target volume (CTV) is shown in yellow on the CT scan: (a) right‐to‐left direction, (b) anterior‐to‐posterior direction.
3.2. Proton radiography simulations
Figure 6 presents range error maps of patient 2 for 4D‐sCT‐50%, 4D‐sCT‐average, and the 3D‐sCT, overlayed with patient surface and lung contours. Figure 6d shows a water equivalent thickness map of the same patient. For all sCT types, the largest range errors could be observed for range probes traversing lung tissue, whereas the surrounding soft tissues and bones show lower range errors.
FIGURE 6.

Range error maps of 4D‐synthetic computed tomography (sCT) 50% (a), 4D‐sCT average (b), and the 3D‐sCT (c) for patient 2, accompanied by a water‐equivalent thickness map of this patient (d). The green contour shows the patient outline, the orange contour the lung region.
This is consistent throughout the dataset, as shown in Figure 7, where the mean and standard deviation of range errors for each patient are depicted, for either the entire patient (Figure 7a), only lung tissues (Figure 7b), or for everything besides lung tissues (Figure 7c). This confirms the visual observation of a systematically higher range error in lung tissues compared to surrounding tissues.
FIGURE 7.
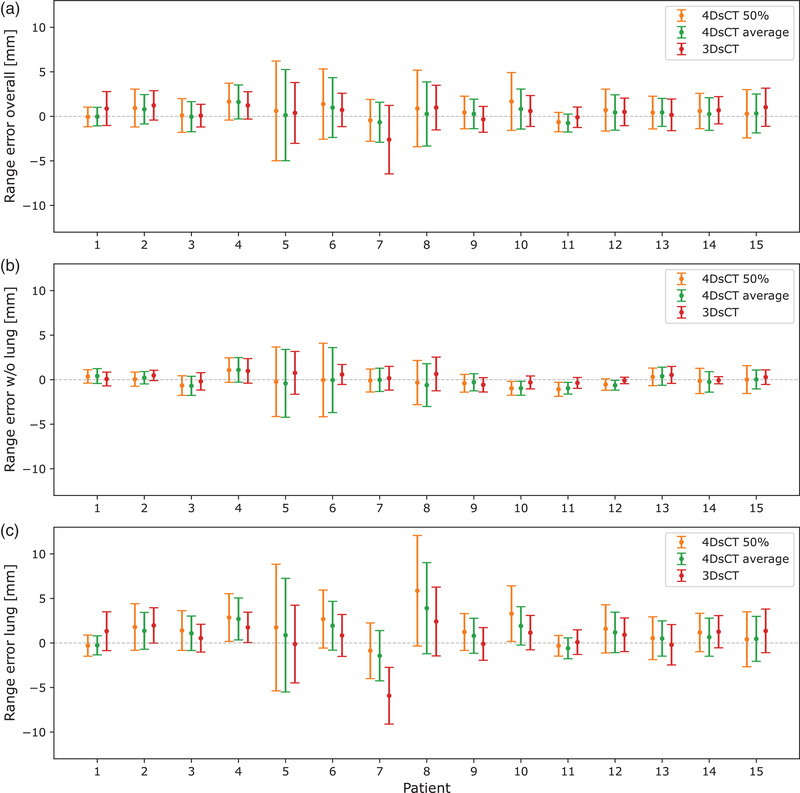
Results from the range error evaluation for (a) the entire patient, (b) all tissues except lung tissues, and (c) only lung tissues. Error bars extend to one standard deviation.
To quantify the range error for the entire dataset, we calculated mean absolute range errors (MARE). On average, the 3D‐sCT resulted in the lowest overall (for the entire patient) MARE of 1.5 ± 0.6 mm. 4D‐sCT‐average and 4D‐sCT‐50% showed a slightly higher MARE of 1.6 ± 0.5 and 1.8 ± 0.6 mm, respectively. When only range probes traversing lung tissue were considered, the average MARE increased for all sCT‐types: for the 3D‐sCT to 2.2 ± 1.2 mm, for 4D‐sCT‐average to 2.3 ± 1.1 mm, and for 4D‐sCT‐50% to 2.8 ± 1.4 mm. The opposite effect was observed when excluding range probes that went through the lungs. MARE decreased to 0.7 ± 0.3 mm for 3D‐sCT, to 0.9 ± 0.3 for 4D‐sCT‐average, and to 1.0 ± 0.3 for 4D‐sCT‐50%.
3.3. Dosimetric evaluation
Results from the global dosimetric evaluation using gamma analysis are shown in Figure 8. The clear differences in image quality were not similarly observable in the dose calculation accuracy. Average 3%/3‐mm gamma pass ratios did not show large differences between the various sCT types and ranged from 92.3 ± 3.2% of 4D‐sCT‐50% to 94.4 ± 2.1% of 4D‐sCT‐average. 4D‐sCT‐0% and the 3D‐sCT resulted in average pass ratios of 93.2 ± 2.1% and 93.7 ± 2.1%, respectively.
FIGURE 8.
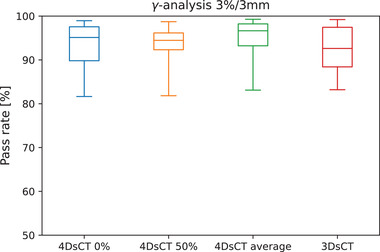
Results from the gamma analysis using a 3%/3‐mm criterion and a dose threshold of 10%. Whiskers extend to the min/max observed values.
Figure 9 shows boxplots for local dose differences in the CTV and selected OARs (lung, heart, and esophagus). Excellent agreement was found for CTV and lung doses, with differences below 2.4% for all patients and sCT types. Larger dose differences were observed for heart and esophagus. Due to their smaller size and location in close proximity to steep dose gradients near the target volume, these OARs are more sensitive to dose shifts. For all sCT types, the highest dose differences were observed in the heart (sCT‐3D: 8.4%, sCT‐4D‐ave: 4.6%, sCT‐4D‐0%: 6.7%, and sCT‐4D‐50%: 8.0%). No systematic differences in OAR doses were found among sCT‐4D‐0%, sCT‐4D‐50%, sCT‐4D‐ave, and the 3D‐sCT
FIGURE 9.
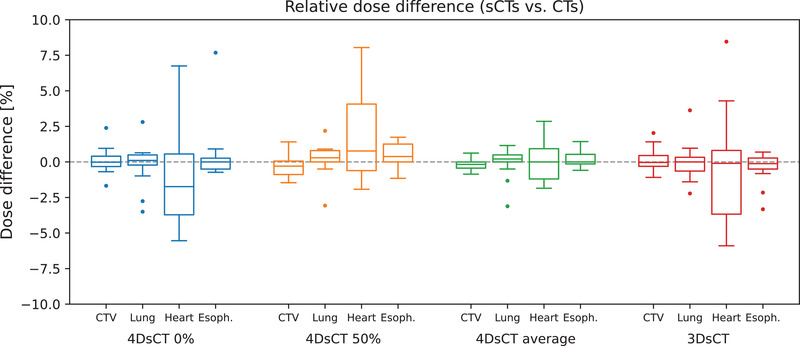
Relative dose differences for clinical target volume (CTV), lung, heart, and esophagus calculated for 4D‐synthetic computed tomography (sCT)‐0%, 4D‐sCT‐50%, 4D‐sCT‐average, and the 3D‐sCT. Whiskers extend to the last value within the interquartile range. Outliers are visualized by a dot.
3.4. 4D dose accumulation
A comparison between 4D accumulated doses based on 4D‐sCT and 4D‐CT resulted in an average gamma pass ratio of 93.7 ± 4.9%. This is similar to average pass ratios of 3D‐sCT (93.7%) and 4D‐sCT‐average (94.4%). In target volumes and OARs, similar dose differences as in the other sCT types were observed. The heart showed the largest mean dose difference with up to 4.5%. For esophagus, lung (both mean dose), and CTV (D 98), maximum dose differences did not exceed 1.4%, 2.3%, and 2.4%, respectively. Figure 10 shows the reconstructed doses of 4D‐sCT and 4D‐CT for each breathing phase together with the accumulated dose. Due to averaging effects, the accumulated dose shows noticeably lower dose differences than the individual breathing phases. Table 1 presents mean 3%/3‐mm and 2%/2‐mm gamma pass ratios for subplan doses of each breathing phase.
FIGURE 10.
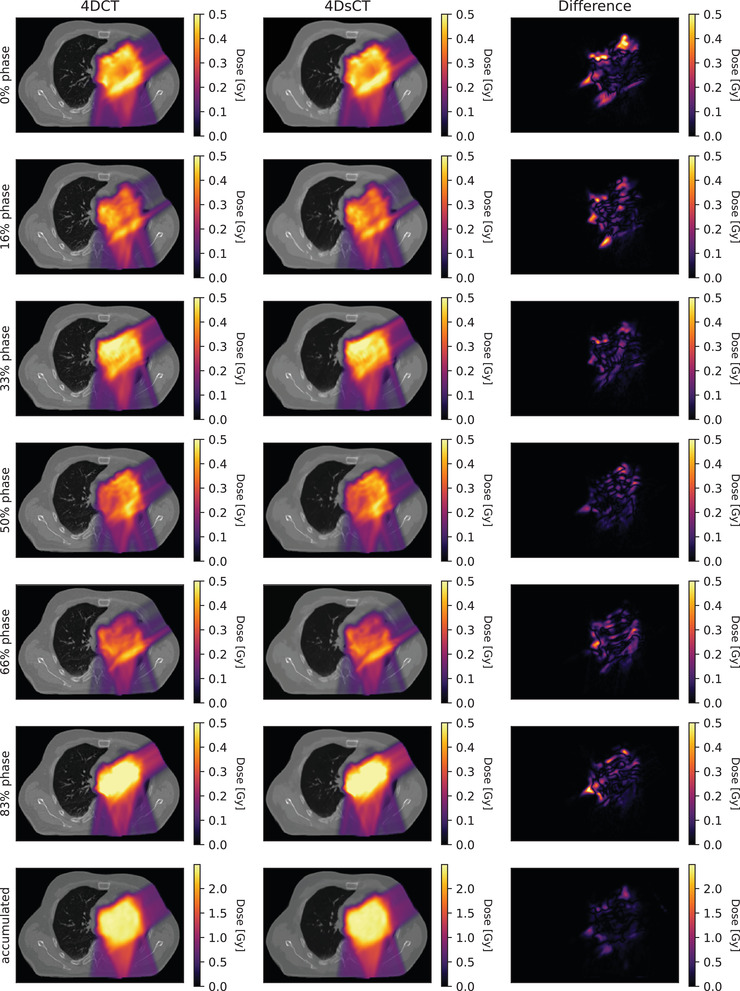
Rows 1–6 show dose distributions for individual breathing phases (calculated with the corresponding subplans used in the dose accumulation) and the difference between 4D‐computed tomography (CT) and 4D‐synthetic computed tomography (sCT) doses. Row 7 presents the accumulated dose and dose difference. Results are shown for patient 2.
TABLE 1.
Mean gamma pass ratios for subplan doses of each breathing phases using a 3%/3‐mm and 2%/2‐mm criterion
| Gamma | 0% phase | 16% phase | 33% phase | 50% phase | 66% phase | 83% phase |
|---|---|---|---|---|---|---|
| 3%/3 mm | 93.9 ± 3.6 | 92.9 ± 3.6 | 94.0 ± 3.7 | 93.0 ± 4.3 | 93.6 ± 4.4 | 94.0 ± 3.5 |
| 2%/2 mma | 88.9 ± 4.7 | 87.5 ± 4.7 | 89.0 ± 4.8 | 87.5 ± 5.5 | 88.3 ± 5.5% | 88.9 ± 4.8% |
3.5. Normal tissue complication probabilities (NTCP)
OAR doses were used in combination with clinical features to calculate NTCP for grade ≥2 RP, grade ≥2 AET, and 2‐year mortality. Results for each model and sCT type are presented in Figure 11. As expected from the relatively low‐dose differences observed in OARs, NTCP values showed high agreement between sCTs and ground‐truth CTs. Median values for all sCT types and toxicities were close to zero. Maximum differences did not exceed ±1.7%. No substantial differences were observed between the various sCT types.
FIGURE 11.

Normal tissue complication probability (NTCP) differences between synthetic computed tomographies (sCTs) and CTs for 2‐year mortality (2yM), grade ≥2 acute esophageal toxicity (AET), and grade ≥2 radiation pneumonitis (RP). Whiskers extend to the last value within the interquartile range. Outliers are visualized by a dot.
4. DISCUSSION
In this study, we investigated the use of a DCNN to correct sparse view 4D‐CBCTs and generate 4D‐sCTs to enable accurate daily proton dose calculations. Furthermore, a comparison against 3D‐sCTs was performed to assess the impact of a 4D‐CBCT reconstruction using the same set of projections as for the 3D‐CBCTs.
Visually, 4D‐CBCTs showed considerably lower image quality than 3D‐CBCTs. This difference can be attributed to the low number of projections available for a single phase of the 4D‐CBCT (∼1/6 of the total number of projections). The low number of projections causes additional sparse view artifacts and leads to the further decreased image quality of 4D‐CBCTs. Our study used a retrospective dataset; hence, we were limited to the clinically used acquisition protocol, which is currently optimized for 3D‐CBCTs. An advanced iterative 4D reconstruction, in the form of the MA‐ROOSTER algorithm, was used to optimize the 4D‐CBCT image quality. Furthermore, 4D‐CBCTs were only reconstructed with six phases, whereas for the reference 4D‐CTs 10 breathing phases were available. The reconstruction with less phases is a tradeoff between temporal resolution of 4D‐CBCTs and a higher image quality of each individual phase image. Because we utilized DIR to deform reference CT images to the CBCTs, the mismatch in breathing phases had a negligible influence on the results.
In the future, better image quality and/or a larger number of breathing phases could be achieved by using dedicated 4D‐CBCT acquisitions protocols, containing significantly higher number of projections. However, this comes at the cost of an increase in imaging dose and acquisition time, which lengthens the time a patient stays in the treatment room and might be counterproductive for efficient online adaptive proton therapy workflows.
During sCT generation, the DCNN was able to mostly compensate for the large image quality differences between 3D‐ and 4D‐CBCTs. Although individual 4D‐sCT phases resulted in a 10‐HU higher MAE than 3D‐sCTs (47 vs. 37 HU), 4D‐sCT‐average had a similar MAE as the 3D‐sCT. This outcome suggests that averaging six low‐quality single‐phase images results in a similar MAE as a 3D‐sCT based on a high‐quality 3D‐CBCT.
The evaluation of proton dose calculations on the various synthetic CT types showed small differences between 3D and 4D images. 3D‐sCT and 4D‐sCT‐average resulted in the highest pass ratios (94.4% and 93.7%). Single‐phase 4D‐sCTs showed a marginal difference of 1.4% lower average pass ratio with respect to 3D‐sCTs, a trend that was also observed in local dose differences and NTCP differences, however, at a lower magnitude. Highest agreement was observed for CTV and lung structures. The dosimetric results show a comparable performance of 4D‐sCTs with respect to 3D‐sCTs, suggesting the potential suitability of sparse view 4D‐CBCT‐based sCTs for proton dose calculations in adaptive proton therapy workflows.
The clinical suitability of 4D‐sCTs was demonstrated by performing 4D dose reconstructions using treatment log files and breathing signals. Good agreement was found between doses calculated on 4D‐CT and 4D‐sCT for single breathing phases and the accumulated dose. For the accumulated doses, an average pass ratio of 94.2% was measured. For comparison, the phantom‐based proton dose calculation study by Schmitz et al. 31 resulted in higher 3%/3‐mm gamma pass ratios between 97.3% and 99.7%. Niepel et al. reported 3%/3‐mm pass ratios >95% for a dual beam plan. 29 Bondesson et al. performed a 4D dose accumulation similar to this study and reported gamma pass ratios of 96.7%. However, all the previous studies utilized a porcine lung phantom to mimic lung tissue properties, and no dosimetric results of actual patients were reported yet. Further studies with actual patient data are required to compare these non–deep learning methods to our proposed deep learning approach.
PR simulations were used to visualize and quantify range errors of sCTs. The higher HU accuracy of 3D‐sCT and 4D‐sCT‐average was reflected in slightly lower range errors compared to single‐phase 4D‐sCTs. PR simulations also revealed that the main error contribution in thoracic sCTs stems from lung tissue. Range probes through lung tissue showed range errors roughly three times higher than range probes not crossing the lungs. This was consistent throughout all 3D‐ and 4D‐sCTs. In clinical practice, the impact of range errors is mitigated by using multiple beam directions from target‐specific angles. There are multiple causes that could lead to increased range errors in lung tissue: First, the low‐density lung tissue shows low HU accuracy because it is heavily affected by streaking and scattering artifacts in CBCTs. For 4D‐CBCTs, this effect is amplified due to the low number of projections used for reconstruction. Second, we observed substantial density variations of lung tissues between different patients. Such density variations might be represented on a diagnostic CT scan, but this may not be the case for CBCTs or sCTs, due to the previously mentioned shortcomings of CBCTs. Third, these large variations in lung density and the disparity between CTs and CBCTs hinder the mapping of lung HUs between CBCT and CT performed by the DCNN. A visualization of differences in lung tissues of CBCTs, CTs, and sCTs, as observed in our dataset, is presented in Figure S6. The presented results confirm our previous conclusion 23 that the lung region is the most challenging part for the deep learning–based sCT generation. The large influence of lung tissues on sCT HU accuracy suggests that a further improvement of sCTs should focus on this area. Advances of imaging hardware and software of proton therapy CBCT systems might be necessary to improve the accuracy in the representation of lung tissues of sCTs. Besides directly improving CBCTs, utilizing and developing more advanced neural network architectures might further improve image quality. The network architecture used in this study was similar to previous 3D‐studies and not adapted to 4D input data. The DCNN was solely trained with 0% phase images for two reasons: First, the difference between individual phase images of a single patient is much smaller than the difference between patients. Second, for the number of patients we wanted to include in the training set the limited amount of memory of the GPU used in this study (Nvidia GTX 1080 TI) did not allow us to utilize all breathing phases at the same time. Our results showed that training our type of neural network on a single phase does not have a negative impact on other phases. However, with a more sophisticated network architecture, the relation between individual breathing phases or between 3D and 4D images could potentially be exploited and further improve the image quality of 4D‐sCTs.
No real ground‐truth images were available for this study because 4D‐CBCT and 4D‐CT were acquired in two different sessions. To overcome this limitation, DIR was used to generate reference images by registering individual phases of the same‐day 4D‐CT and 4D‐CBCT. Our results, therefore, depend on the accuracy of the DIR itself. A quantification of DIR accuracy is very challenging, 45 , 46 and in this work, we relied on visual inspection of deformation results. Furthermore, DIR was also used during 4D‐CBCT reconstruction, dose accumulation, and to transfer structures from the planning CT to sCTs, which makes this study quite dependent on DIR accuracy.
Our previous study about thoracic 3D‐sCTs proposed a patient‐specific correction method to increase sCT accuracy in lungs. 23 This method showed promising results but relies on computationally expensive DIR of diagnostic CTs. For 4D‐sCTs, this would lead to a substantial prolongation of the sCT conversion because it has to be performed individually for each breathing phase. Therefore, this patient‐specific correction was considered to be unsuitable for (online) adaptive proton therapy workflows and was not investigated in this study.
Deep learning–based sCT generation has shown to be sufficiently fast for online adaptive proton therapy. Conversion times as fast as a few seconds have been reported in literature. 24 , 47 , 48 The DCNN method presented in this work requires about 2–3 min to generate a full resolution 3D‐sCT or single 4D‐sCT phase image (using an NVIDIA GTX 1080Ti GPU). However, with further software and hardware optimizations, a substantial conversion time reduction could be achieved. The 4D‐sCT generation can also be parallelized because each phase is independent from the other phases. Therefore, if enough computing hardware is available, 4D‐sCT generation should not be more time‐consuming than 3D‐sCT generation. What currently requires significantly more time is the reconstruction of 4D‐CBCTs using the MA‐ROOSTER registration algorithm. Reconstructing a six‐phase 4D‐CBCT required on average 45 min. To reconstruct 4D‐CBCTs with optimal image quality and clinically feasible characteristics (e.g., reconstruction duration), further investigation into (alternative) 4D reconstruction algorithms (e.g., MA‐ROOSTER, 4D‐FDK, and MC‐FDK) and their impact on proton dose calculation accuracy is required. Vendor‐side implementation of various reconstruction algorithms in clinically used systems is desirable for clinical implementation in online adaptive proton therapy workflows.
The standard deviations of the image similarity metrics (e.g., 7.7 HU for MAE of 4D‐sCT‐average), dosimetric metrics (e.g., 2.1% for gamma pass ratio of 4D‐sCT‐average), and the variability in the magnitude of range errors (e.g., 0.6 mm for 4D‐sCT‐average) indicate that sCT quality varies across patients. Quality control workflows for sCTs need to be developed to ensure reliable sCT quality, to identify potential outliers, and to enable the clinical translation of sCTs. The lack of ground‐truth images for daily CBCT‐based sCTs complicates efforts to introduce such quality control tools. Recently, Seller Oria et al. demonstrated the use of in vivo PR acquisitions as a quality control tool for sCTs in head‐and‐neck cancer patients. 49 A similar approach could be taken for lung cancer patients, but as respiratory motion would have to be considered, the PR image interpretation would be more challenging. An option for automated quality control of synthetic sCTs would be to use uncertainty measures directly linked to deep neural networks. 50 , 51
5. CONCLUSION
In this study, we have shown the ability of a DCNN to generate 4D‐sCTs based on 4D‐CBCTs reconstructed from a sparse view projection set. Despite image quality differences between 4D‐ and 3D‐sCTs, comparable dosimetric accuracy and NTCP accuracy was observed. For further improvement of 3D and 4D lung sCTs, the HU accuracy in lung tissues should be targeted. This study evaluated the image quality and dosimetric accuracy in reference to same day CT images. Further studies are required to study the role of 4D‐CBCT‐based sCTs in clinical adaptive proton therapy workflows and the criteria to determine the clinical suitability of 4D‐sCTs on a patient‐specific basis.
CONFLICT OF INTEREST
Langendijk JA is a consultant for International Scientific Advisory Committees of IBA and RaySearch.
The Department of Radiation Oncology, University Medical Centre Groningen, has active research agreements with IBA, RaySearch, Siemens, Elekta, Leonie and Mirada.
Supporting information
Supporting Information
ACKNOWLEDGMENT
This study was financially supported by a grant from the Dutch Cancer Society (KWF research project 11518).
Thummerer A, Seller Oria C, Zaffino P, et al. Deep learning–based 4D‐synthetic CTs from sparse‐view CBCTs for dose calculations in adaptive proton therapy. Med Phys. 2022;49:6824–6839. 10.1002/mp.15930
Maria Francesca Spadea and Stefan Both contributed equally to this work.
REFERENCES
- 1. Lim‐Reinders S, Keller BM, Al‐Ward S, Sahgal A, Kim A. Online adaptive radiation therapy. Int J Radiat Oncol Biol Phys. 2017;99(4):994‐1003. 10.1016/j.ijrobp.2017.04.023 [DOI] [PubMed] [Google Scholar]
- 2. Sonke JJ, Aznar M, Rasch C. Adaptive radiotherapy for anatomical changes. Semin Radiat Oncol. 2019;29(3):245‐257. 10.1016/j.semradonc.2019.02.007 [DOI] [PubMed] [Google Scholar]
- 3. Albertini F, Matter M, Nenoff L, Zhang Y, Lomax A. Online daily adaptive proton therapy. Br J Radiol. July 2019;93:20190594. 10.1259/bjr.20190594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Paganetti H, Botas P, Sharp GC, Winey B. Adaptive proton therapy. Phys Med Biol. 2021;66(22):10. 10.1088/1361-6560/ac344f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Landry G, Hua CH. Current state and future applications of radiological image guidance for particle therapy. Med Phys. 2018;45(11):e1086‐e1095. 10.1002/MP.12744 [DOI] [PubMed] [Google Scholar]
- 6. Schulze R, Heil U, Groß D, et al. Artefacts in CBCT: a review. Dentomaxillofac Radiol. 2011;40(5):265‐273. 10.1259/DMFR/30642039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Giacometti V, Hounsell AH, McGarry CK. A review of dose calculation approaches with cone beam CT in photon and proton therapy. Physica Med. 2020;76:243‐276. 10.1016/J.EJMP.2020.06.017 [DOI] [PubMed] [Google Scholar]
- 8. Newhauser WD, Zhang R. The physics of proton therapy. Phys Med Biol. 2015;60(8):R155‐R209. 10.1088/0031-9155/60/8/r155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Arai K, Kadoya N, Kato T, et al. Feasibility of CBCT‐based proton dose calculation using a histogram‐matching algorithm in proton beam therapy. Physica Med. 2017;33:68‐76. 10.1016/j.ejmp.2016.12.006 [DOI] [PubMed] [Google Scholar]
- 10. Landry G, Nijhuis R, Dedes G, et al. Investigating CT to CBCT image registration for head and neck proton therapy as a tool for daily dose recalculation. Med Phys. 2015;42(3):1354‐1366. 10.1118/1.4908223 [DOI] [PubMed] [Google Scholar]
- 11. Kurz C, Kamp F, Park YK, et al. Investigating deformable image registration and scatter correction for CBCT‐based dose calculation in adaptive IMPT. Med Phys. 2016;43(10):5635‐5646. 10.1118/1.4962933 [DOI] [PubMed] [Google Scholar]
- 12. Veiga C, Janssens G, Teng CL, et al. First clinical investigation of cone beam computed tomography and deformable registration for adaptive proton therapy for lung cancer. Int J Radiat Oncol Biol Phys. 2016;95(1):549‐559. 10.1016/j.ijrobp.2016.01.055 [DOI] [PubMed] [Google Scholar]
- 13. Park YK, Sharp GC, Phillips J, Winey BA. Proton dose calculation on scatter‐corrected CBCT image: feasibility study for adaptive proton therapy. Med Phys. 2015;42(8):4449‐4459. 10.1118/1.4923179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hansen DC, Sørensen TS. Fast 4D cone‐beam CT from 60 s acquisitions. Phys Imaging Radiat Oncol. 2018;5:69‐75. 10.1016/j.phro.2018.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Andersen AG, Park YK, Elstrøm UV, et al. Evaluation of an a priori scatter correction algorithm for cone‐beam computed tomography based range and dose calculations in proton therapy. Phys Imaging Radiat Oncol. 2020;16:89‐94. 10.1016/J.PHRO.2020.09.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Thing RS, Bernchou U, Hansen O, Brink C. Accuracy of dose calculation based on artefact corrected cone beam CT images of lung cancer patients. Phys Imaging Radiat Oncol. 2017;1:6‐11. 10.1016/j.phro.2016.11.001 [DOI] [Google Scholar]
- 17. Thing RS, Bernchou U, Mainegra‐Hing E, Brink C. Patient‐specific scatter correction in clinical cone beam computed tomography imaging made possible by the combination of Monte Carlo simulations and a ray tracing algorithm. Acta Oncol (Madr). 2013;52(7):1477‐1483. 10.3109/0284186x.2013.813641 [DOI] [PubMed] [Google Scholar]
- 18. Spadea MF, Maspero M, Zaffino P, Seco J. Deep learning‐based synthetic‐CT generation in radiotherapy and PET: A review. Med. Phys. 2021;48:6537‐6566. 10.1002/mp.15150 [DOI] [PubMed] [Google Scholar]
- 19. Harms J, Lei Y, Wang T, et al. Paired cycle‐GAN‐based image correction for quantitative cone‐beam computed tomography. Med Phys. 2019;46(9):3998‐4009. 10.1002/mp.13656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Thummerer A, Zaffino P, Meijers A, et al. Comparison of CBCT based synthetic CT methods suitable for proton dose calculations in adaptive proton therapy. Phys Med Biol. 2020;65(9):95002. 10.1088/1361-6560/ab7d54 [DOI] [PubMed] [Google Scholar]
- 21. Thummerer A, de Jong BA, Zaffino P, et al. Comparison of the suitability of CBCT‐ and MR‐based synthetic CTs for daily adaptive proton therapy in head and neck patients. Phys Med Biol. 2020;65(23):235036. 10.1088/1361-6560/abb1d6 [DOI] [PubMed] [Google Scholar]
- 22. Liang X, Chen L, Nguyen D, et al. Generating synthesized computed tomography (CT) from cone‐beam computed tomography (CBCT) using CycleGAN for adaptive radiation therapy. Phys Med Biol. 2019;64(12):125002. 10.1088/1361-6560/ab22f9 [DOI] [PubMed] [Google Scholar]
- 23. Thummerer A, Seller Oria C, Zaffino P, et al. Clinical suitability of deep learning based synthetic CTs for adaptive proton therapy of lung cancer. Med Phys. 2021;48(12):7673‐7684. 10.1002/MP.15333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Landry G, Hansen D, Kamp F, et al. Comparing Unet training with three different datasets to correct CBCT images for prostate radiotherapy dose calculations. Phys Med Biol. 2019;64(3):35011. 10.1088/1361-6560/aaf496 [DOI] [PubMed] [Google Scholar]
- 25. Kurz C, Maspero M, Savenije MHF, et al. CBCT correction using a cycle‐consistent generative adversarial network and unpaired training to enable photon and proton dose calculation. Phys Med Biol. 2019;64(22):225004. 10.1088/1361-6560/AB4D8C [DOI] [PubMed] [Google Scholar]
- 26. den Otter LA, Chen K, Janssens G, et al. Technical note: 4D cone‐beam CT reconstruction from sparse‐view CBCT data for daily motion assessment in pencil beam scanned proton therapy (PBS‐PT). Med Phys. 2020;47(12):6381‐6387. 10.1002/MP.14521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Shieh CC, Gonzalez Y, Li B, et al. SPARE: sparse‐view reconstruction challenge for 4D cone‐beam CT from a 1‐min scan. Med Phys. 2019;46(9):3799‐3811. 10.1002/MP.13687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Mory C, Janssens G, Rit S. Motion‐aware temporal regularization for improved 4D cone‐beam computed tomography. Phys Med Biol. 2016;61(18):6856‐6877. 10.1088/0031-9155/61/18/6856 [DOI] [PubMed] [Google Scholar]
- 29. Niepel K, Kamp F, Kurz C, et al. Feasibility of 4DCBCT‐based proton dose calculation: an ex vivo porcine lung phantom study. Z Med Phys. 2019;29:249‐261. 10.1016/j.zemedi.2018.10.005 [DOI] [PubMed] [Google Scholar]
- 30. Bondesson D, Meijers A, Janssens G, et al. Anthropomorphic lung phantom based validation of in‐room proton therapy 4D‐CBCT image correction for dose calculation. Z Med Phys. 2022;32(1):74‐84. 10.1016/J.ZEMEDI.2020.09.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Schmitz H, Rabe M, Janssens G, et al. Validation of proton dose calculation on scatter corrected 4D cone beam computed tomography using a porcine lung phantom. Phys Med Biol. 2021;66(17):175022. 10.1088/1361-6560/ac16e9 [DOI] [PubMed] [Google Scholar]
- 32. Madesta F, Sentker T, Gauer T, Werner R. Self‐contained deep learning‐based boosting of 4D cone‐beam CT reconstruction. Med Phys. 2020;47(11):5619‐5631. 10.1002/MP.14441 [DOI] [PubMed] [Google Scholar]
- 33. Rit S, Vila Oliva M, Brousmiche S, Labarbe R, Sarrut D, Sharp GC. The Reconstruction Toolkit (RTK), an open‐source cone‐beam CT reconstruction toolkit based on the Insight Toolkit (ITK). J Phys Conf Ser. 2014;489(1):012079. 10.1088/1742-6596/489/1/012079 [DOI] [Google Scholar]
- 34. Veiga C, Alshaikhi J, Amos R, et al. Cone‐beam computed tomography and deformable registration‐based “dose of the day” calculations for adaptive proton therapy. Int J Part Ther. 2015;2(2):404‐414. 10.14338/IJPT-14-00024.1 [DOI] [Google Scholar]
- 35. Spadea MF, Pileggi G, Zaffino P, et al. Deep convolution neural network (DCNN) multiplane approach to synthetic CT generation from MR images—application in brain proton therapy. Int J Radiat Oncol Biol Phys. 2019;105(3):495‐503. 10.1016/j.ijrobp.2019.06.2535 [DOI] [PubMed] [Google Scholar]
- 36. Farace P, Righetto R, Meijers A. Pencil beam proton radiography using a multilayer ionization chamber. Phys Med Biol. 2016;61(11):4078‐4087. 10.1088/0031-9155/61/11/4078 [DOI] [PubMed] [Google Scholar]
- 37. Farace P, Righetto R, Deffet S, Meijers A. Vander Stappen F. Technical note: a direct ray‐tracing method to compute integral depth dose in pencil beam proton radiography with a multilayer ionization chamber. Med Phys. 2016;43(12):6405‐6412. 10.1118/1.4966703 [DOI] [PubMed] [Google Scholar]
- 38. Meijers A, Seller Oria C, Free J, Langendijk JA, Knopf AC, Both S. Technical Note: first report on an in vivo range probing quality control procedure for scanned proton beam therapy in head and neck cancer patients. Med Phys. 2021;48(3):1372‐1380. 10.1002/mp.14713 [DOI] [PubMed] [Google Scholar]
- 39. Oria CS, Marmitt GG, Both S, Langendijk JA, Knopf AC, Meijers A. Classification of various sources of error in range assessment using proton radiography and neural networks in head and neck cancer patients. Phys Med Biol. 2020;65(23):235009. 10.1088/1361-6560/ABC09C [DOI] [PubMed] [Google Scholar]
- 40. Meijers A, Jakobi A, Stützer K, et al. Log file based dose reconstruction and accumulation for 4D adaptive pencil beam scanned proton therapy in a clinical treatment planning system: implementation and proof‐of‐concept. Med Phys. 2019;46(3):1140‐1149. 10.1002/mp.13371. Published online 2019. [DOI] [PubMed] [Google Scholar]
- 41. Nederlandse Vereiniging voor Radiotherapie en Oncologie. Rapporten. https://nvro.nl/images/documenten/rapporten/LIPP_longen_final_01122019.pdf. Accessed August 23, 2022.
- 42. Appelt AL, Vogelius IR, Farr KP, Khalil AA, Bentzen SM. Towards individualized dose constraints: adjusting the QUANTEC radiation pneumonitis model for clinical risk factors. Acta Oncol (Madr). 2014;53(5):605‐612. 10.3109/0284186X.2013.820341 [DOI] [PubMed] [Google Scholar]
- 43. Dankers FJWM, Wijsman R, Troost EGC, et al. External validation of an NTCP model for acute esophageal toxicity in locally advanced NSCLC patients treated with intensity‐modulated (chemo‐)radiotherapy. Radiother Oncol. 2018;129(2):249‐256. 10.1016/j.radonc.2018.07.021 [DOI] [PubMed] [Google Scholar]
- 44. Defraene G, Dankers FJWM, Price G, et al. Multifactorial risk factors for mortality after chemotherapy and radiotherapy for non‐small cell lung cancer. Radiother Oncol. 2020;152:117‐125. 10.1016/j.radonc.2019.09.005 [DOI] [PubMed] [Google Scholar]
- 45. Nenoff L, Ribeiro CO, Matter M, et al. Deformable image registration uncertainty for inter‐fractional dose accumulation of lung cancer proton therapy. Radiother Oncol. 2020;147:178‐185. 10.1016/J.RADONC.2020.04.046 [DOI] [PubMed] [Google Scholar]
- 46. Amstutz F, Nenoff L, Albertini F, et al. An approach for estimating dosimetric uncertainties in deformable dose accumulation in pencil beam scanning proton therapy for lung cancer. Phys Med Biol. 2021;66(10):105007. 10.1088/1361-6560/ABF8F5 [DOI] [PubMed] [Google Scholar]
- 47. Kida S, Nakamoto T, Nakano M, et al. Cone beam computed tomography image quality improvement using a deep convolutional neural network. Cureus. 2018;10(4):e2548. 10.7759/cureus.2548. Published online 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Maspero M, Houweling AC, Savenije MH, et al. A single neural network for cone‐beam computed tomography‐based radiotherapy of head‐and‐neck, lung and breast cancer. Phys Imaging Radiat Oncol. 2020;14:24‐31. 10.1016/j.phro.2020.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Seller Oria C, Thummerer A, Free J, et al. Range probing as a quality control tool for CBCT‐based synthetic CTs: in vivo application for head and neck cancer patients. Med Phys. 2021;48(8):4498‐4505. 10.1002/mp.15020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Maspero M, Bentvelzen LG, Savenije MHF, et al. Deep learning‐based synthetic CT generation for paediatric brain MR‐only photon and proton radiotherapy. Radiother Oncol. 2020;153:197‐204. 10.1016/j.radonc.2020.09.029 [DOI] [PubMed] [Google Scholar]
- 51. van Harten LD, Wolterink JM, Verhoeff JJC, Išgum I. Automatic online quality control of synthetic CTs. Proc. SPIE 11313, Medical Imaging 2020: Image Processing. 2020:11313. 10.1117/12.2549286 [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


