The future is 2D: spectral‐temporal fitting of dynamic MRS data provides exponential gains in precision over conventional approaches

Abstract

Purpose

Many MRS paradigms produce 2D spectral‐temporal datasets, including diffusion‐weighted, functional, and hyperpolarized and enriched (carbon‐13, deuterium) experiments. Conventionally, temporal parameters—such as T₂, T₁, or diffusion constants—are assessed by first fitting each spectrum independently and subsequently fitting a temporal model (1D fitting). We investigated whether simultaneously fitting the entire dataset using a single spectral‐temporal model (2D fitting) would improve the precision of the relevant temporal parameter.

Methods

We derived a Cramer Rao lower bound for the temporal parameters for both 1D and 2D approaches for 2 experiments: a multi‐echo experiment designed to estimate metabolite T₂s, and a functional MRS experiment designed to estimate fractional change ($\delta$) in metabolite concentrations. We investigated the dependence of the relative standard deviation (SD) of T₂ in multi‐echo and $\delta$ in functional MRS.

Results

When peaks were spectrally distant, 2D fitting improved precision by approximately 20% relative to 1D fitting, regardless of the experiment and other parameter values. These gains increased exponentially as peaks drew closer. Dependence on temporal model parameters was weak to negligible.

Conclusion

Our results strongly support a 2D approach to MRS fitting where applicable, and particularly in nuclei such as hydrogen and deuterium, which exhibit substantial spectral overlap.

Short abstract

Click here for author‐reader discussions

1. INTRODUCTION

Dynamic MRS refers to an experiment in which a series of 1D spectra are acquired sequentially, often while varying a sequence parameter or administering an external time‐dependent stimulus or manipulation. This encompasses a wide range of experimental designs, including observation of the dynamic incorporation of carbon‐13 and deuterium–labeled metabolites following the injection of a labeled compound ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ ; functional MRS designed to detect endogenous metabolic changes in glutamate, GABA, and lactate in response to an external visual, motor, or cognitive manipulation ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ ; multiparametric MR spectroscopic experiments aimed at simultaneously and efficiently quantifying multiple spin parameters ²¹ , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ ; diffusion MRS whereby the diffusion‐weighting gradients are varied to quantify the diffusion coefficient of different metabolites ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² ; and even simple relaxometry, where, for example, T₂ might be measured by measuring spectral data at different TEs (MTE). ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹

The analysis of the 2D spectral‐temporal data sets produced by dynamic MRS experiments is conventionally done piecewise in two stages. First, each spectrum is fit using a linear combination of basis functions ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ to extract the temporal dependence of each metabolite's amplitudes. Then, the time‐series for each metabolite's amplitude is fit to the dynamic model, which describes the temporal behavior to extract the relevant temporal constants, such as T₁ or T₂, diffusion coefficients, or metabolite kinetics, depending on the experiment in question. We will refer to this approach as piecewise, or 1D. Recently, it has been suggested that multiple spectra comprising a dynamic data set should be analyzed and fitted in tandem rather than sequentially using a model that combines the spectral and temporal degrees of freedom. ⁴² , ⁴⁹ , ⁵⁰ , ⁵¹ Such an approach utilizes the temporal correlations inherent in the data to benefit the spectral estimations of metabolite amplitudes, and—in principle—should provide more precise and accurate estimates of the temporal constants. We will refer to such approaches as dynamic, or 2D. The two approaches are contrasted schematically in Figure 1.

FIGURE 1.

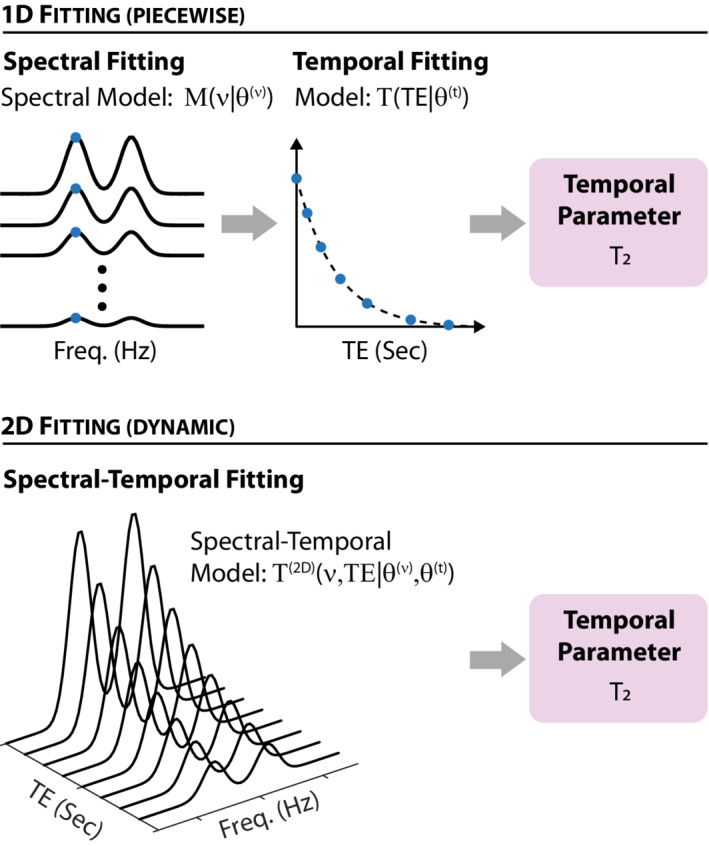
A schematic overview of 1D (piecewise) versus 2D (dynamic) fitting schemes for a fictitious multi‐echo MRS experiment designed to estimate the T₂. (Top) In 1D fitting, data is initially fit to a spectral model to extract the relevant spectral parameters, ${\theta }^{(\nu )}$, such as the area (or amplitude) of each spectral peak or metabolite basis function. These are then fit to the relevant temporal model to extract the relevant temporal parameters, ${\theta }^{(t)},$ which for a multi‐echo experiment include T₂. (Bottom) In 2D fitting, the entire spectral‐temporal dataset is fit simultaneously to a spectral‐temporal model. Such fitting simultaneously furnishes all spectral and temporal parameters—for example, T₂ for a multi‐echo experiment

In the current work, we set out to investigate the theoretical gains in precision offered by 2D fitting of dynamic MRS data relative to the more conventional 1D approach. Rather than quantifying the exact improvements, which would invariably depend on the specific details of the temporal and spectral models, we instead asked ourselves two questions: First, is 2D fitting indeed uniformly superior to 1D fitting? And, if so, which specific spectral or temporal features—or combination thereof—yielded the most substantial gains? To answer these, we assumed a simple spectral model consisting of two Gaussian peaks, and investigated two temporal models: an MTE relaxometry experiment designed to estimate T₂ (which, formally, is equivalent to a diffusion‐weighted experiment designed to estimate the apparent diffusion coefficient), and a functional MRS (fMRS) experiment in which one of the peaks changes in response to an external stimulus, whereas the other remains unchanged. For each model (MTE, fMRS) and each approach (1D, 2D), we calculated the Cramer Rao lower bound (CRLB), ⁵² , ⁵³ a theoretical estimate on the variance of the relevant dynamical parameter—T₂ (MTE) and fractional metabolite change (fMRS)—and explored the relative gain in precision offered by 2D fitting.

2. METHODS

2.1. Models

Our spectral model $ℳ\left(\nu |{\theta }^{(\nu )}\right)$ consisted of the sum of two Gaussian lineshapes, each with a respective amplitude (A), center ($\mu$), and linewidth ($\mathrm{\Delta }$):

$$ℳ\left(\nu |{\theta }^{(\nu )}\right)=G\left(\nu |A_1,{\mu }_1,{\mathrm{\Delta }}_1\right)+G\left(\nu |A_2,{\mu }_2,{\mathrm{\Delta }}_2\right),$$ (1)

with ${\theta }^{(\nu )}=\left.\left(A_1,{\mu }_1,{\mathrm{\Delta }}_1,A_2,{\mu }_2,{\mathrm{\Delta }}_2\right..\right)$, and

$$G(\nu |A,\mu ,\mathrm{\Delta })=A·\exp \left(-\frac{{(\nu -\mu )}^2}{2{\mathrm{\Delta }}^2}\right).$$ (2)

In this notation, $\nu$ is the independent frequency variable, whereas A, $\mu$, and $\mathrm{\Delta }$ are the model parameters (Figure 2A).

FIGURE 2.

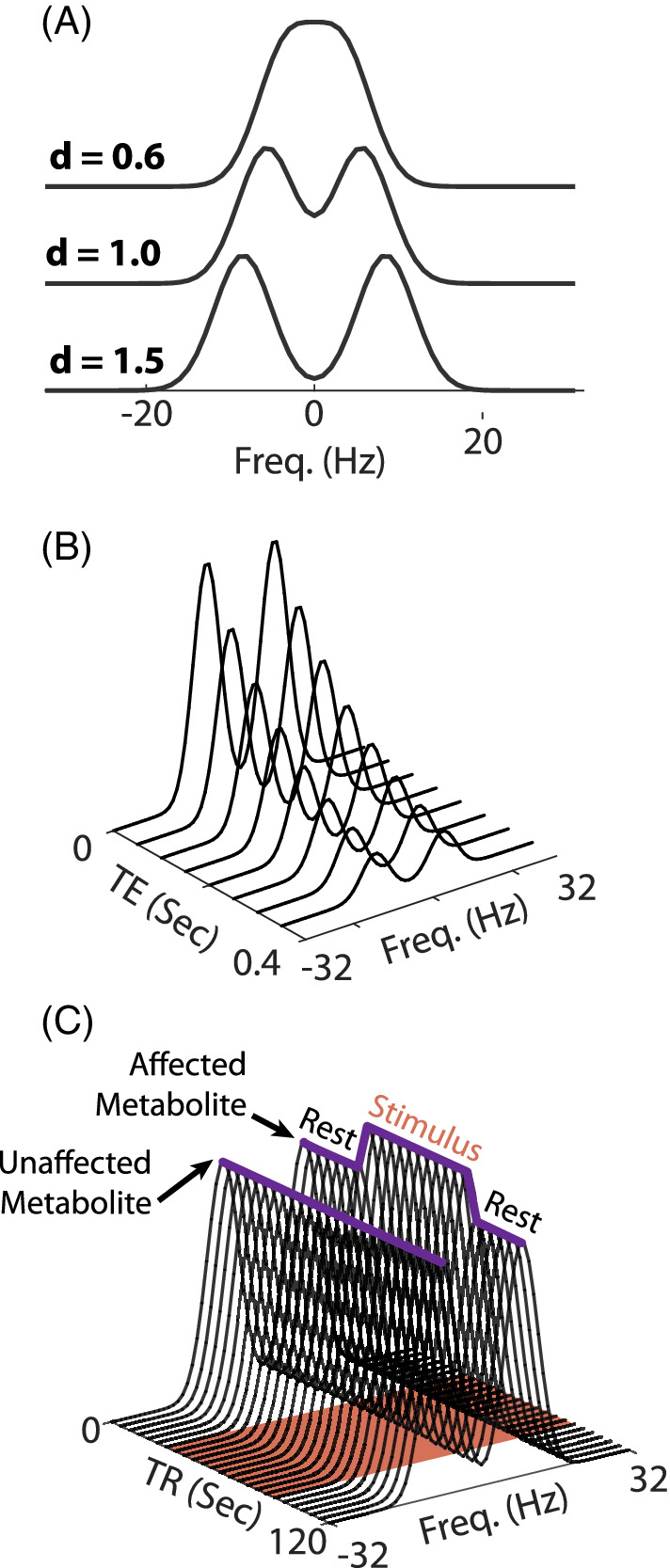
An illustration of the spectral and temporal models under investigation, without any added noise. (A) The spectral model, which consists of two Gaussians, for several values of the distance parameter d (Equation (5)). Additional parameters: unit amplitudes, FWHM of 8 Hz, SW = 64 Hz, 64 sampled points. (B) MTE temporal‐spectral data with equal amplitudes, FWHM = 8 Hz, d = 1.5, $T_{2,\mathrm{A}}=T_{2,\mathrm{B}}=200$ ms, $\mathrm{TE}=0,0.05,\dots 0.35$ s. (C) fMRS temporal‐spectral data with FWHM = 8 Hz, d = 1.5, equal amplitudes, ${\delta }_{\mathrm{A}}=0$, ${\delta }_{\mathrm{B}}$= 0.2, $k_{\mathrm{A}}=k_{\mathrm{B}}=2$ s, pulse TR = 2 s. The red‐shaded patch indicates the presence of the external stimulus between 30 and 90 s. The two purple solid curves trace the maxima of the 2 peaks as a function of time, showing their temporal dynamics: 1 peak remains unaffected by the stimulus $\left({\delta }_{\mathrm{A}}=0\right)$, whereas the other increases and then returns to baseline $\left({\delta }_{\mathrm{B}}=0.2\right)$ fMRS, functional MRS; MTE, multi‐echo.

We considered two temporal models. The first temporal model is that of a MTE experiment (Figure 2B) in which the signal decays exponentially with a time constant T ₂ as a function of the TE:

$$T_{\mathrm{MTE}}\left(\mathrm{TE}|{\theta }^{(t)}\right)=T_{\mathrm{MTE}}\left(\mathrm{TE}|s_0,T_2\right)=s_0·\exp \left(-\frac{\mathrm{TE}}{T_2}\right),$$ (3)

with ${\theta }^{(t)}=\left(s_0,T_2\right)$ the vector of temporal constants. We note that an MTE experiment is formally equivalent to a simple diffusion‐weighted experiment in which peak amplitudes decay exponentially with a time constant given by the apparent diffusion coefficient D as a function of the b value, which is altered by changing the diffusion‐encoding gradient amplitudes (so ${\theta }^{(t)}=\left(s_0,D\right)$). The full 2D dynamic model for each peak consisted of the outer product of the spectral and temporal models, with 1 minor modification. The amplitude parameter $s_0$ in the temporal model was set to unity, given that the spectral amplitudes $A_1$, $A_2$ can be used to adjust the overall amplitude of each peak:

$$\begin{array}{l}{T}_{\mathrm{MTE}}^{(2\mathrm{D})}(\nu ,\mathrm{TE}|\theta )\\ =T_{\mathrm{MTE}}^{(2\mathrm{D})}\left(\nu ,\mathrm{TE}|A_1,{\mu }_1,{\mathrm{\Delta }}_1,T_{2,\mathrm{A}},A_2,{\mu }_2,{\mathrm{\Delta }}_2,T_{2,\mathrm{B}}\right)\\ =G\left(\nu |A_1,{\mu }_1,{\mathrm{\Delta }}_1\right)·T_{\mathrm{MTE}}\left(\mathrm{TE}|1,T_{2,\mathrm{A}}\right)+G\left(\nu |A_2,{\mu }_2,{\mathrm{\Delta }}_2\right)\\ ·T_{\mathrm{MTE}}\left(\mathrm{TE}|1,T_{2,\mathrm{B}.}\right).\end{array}$$

The second temporal model is that of an fMRS experiment using a single‐condition block design (Figure 2C). Such a design is described the convolution of a boxcar function H(t) of unit amplitude between some initial ($t_{\mathrm{i}}$) and final ($t_{\mathrm{f}}$) times—representing the external stimulus, such as a visual checkerboard pattern—and a point spread function (PSF), which we have taken to be Gaussian with a width $\sigma$: $\mathrm{PSF}(t|\delta ,k)=G\left(t|\sqrt{\frac{2}{\pi k^2}}\delta ,3k,k\right)$. This ensures that the fractional change in the metabolite's amplitude will be given by $\delta$. The shift $3k$ ensures causality, effectively zeroing out the temporal dynamics prior to the administration of the stimulus. Thus,

$$\begin{array}{c}{T}_{\text{fMRS}}\left(t|{\theta }^{(t)}\right)=T_{\text{fMRS}}\left(t|s_0,\delta ,k\right)\\ =s_0(1+(\mathit{PSF}\otimes H)(t))\\ =s_0\left(1+\frac{\delta }{2}\left.\left[\mathrm{erf}\left(\frac{t_{\mathrm{f}}-t}{\sqrt{2k^2}}\right)-\mathrm{erf}\left(\frac{t_{\mathrm{i}}-t}{\sqrt{2k^2}}\right)\right.\right]\right)\end{array},$$

whereas the full 2D spectral‐temporal model is:

$$\begin{array}{c}{T}_{\text{fMRS}}^{(2\mathrm{D})}(\nu ,t|\theta )\\ =T_{\text{fMRS}}^{(2\mathrm{D})}\left(\nu ,t|A_1,{\mu }_1,{\mathrm{\Delta }}_1,{\delta }_{\mathrm{A}},k_{\mathrm{A}},A_2,{\mu }_2,{\mathrm{\Delta }}_2,{\delta }_{\mathrm{B}},k_{\mathrm{B}}\right)\\ =G\left(\nu |A_1,{\mu }_1,{\mathrm{\Delta }}_1\right)·T_{\text{fMRS}}\left(t|1,{\delta }_{\mathrm{A}},k_{\mathrm{A}}\right)+G\left(\nu |A_2,{\mu }_2,{\mathrm{\Delta }}_2\right)·\\ T_{\text{fMRS}}\left(t|1,{\delta }_{\mathrm{B}},k_{\mathrm{B}}\right).\end{array}$$

This temporal model can also be used to describe the incorporation of a labeled nucleus—such as deuterium or carbon‐13—in the observable peaks as it undergoes different metabolic cycles within the tissue.

2.2. Cramer Rao lower bounds (CRLBs)

For all models, we assume the acquired data contains additive, normally distributed noise with zero mean. Under this simplification, the Fisher information matrix for a model with $\eta =\left({\eta }_1(\theta ),{\eta }_2(\theta ),\dots ,{\eta }_N(\theta )\right)$ measurements, which depend on M parameters $\theta =\left({\theta }_1,{\theta }_2,\dots ,{\theta }_M\right)$, has matrix elements given by:

$$F_{\mathrm{mn}}=\frac{\partial {\eta }^T}{\partial {\theta }_m}{\sum }^{-1}\frac{\partial \eta }{\partial {\theta }_n}+\frac{1}{2}\text{trace}\left({\sum }^{-1}\frac{\partial \sum }{\partial {\theta }_m}{\sum }^{-1}\frac{\partial \sum }{\partial {\theta }_n}\right),$$ (4)

where $\sum$ is the $N\times N$ covariance matrix of the N measurements.

For the full 2D models, the covariance matrix is diagonal and proportional to the identity, $\sum ={\sigma }_n^{2}I$, with the noise's variance being ${\sigma }_n^2$. The means are all independent, drawn from the same distribution, and given by the relevant model expression; for example, for MTE MRS, ${\eta }_j\sim N\left(T_{\mathrm{MTE}}^{(2\mathrm{D})}(\nu ,t|\theta ),{\sigma }^2\right)$. This implies the derivatives of the covariance matrix are all zero, and the second term in Equation (4) can be omitted. The $M\times M$ CRLB matrix is derived by inverting the $M\times M$ Fisher information matrix and equals to covariance matrix of the parameters in $\theta$. The square root of its diagonal provides the lower bound on the standard deviation (SD) of each parameter in $\theta$, including the relevant temporal constant (e.g., T _2,A and T _2,B for MTE MRS). Note that if $N^{(\nu )}$ points are sampled along the spectral dimension and $N^{(t)}$ spectra are acquired along the temporal dimension, then the number of independent measurements is $N=N^{(\nu )}{N}^{(t)}$.

For piecewise 1D fitting approaches, the analysis is slightly more involved: First, the 1D spectral model (Equation (1)) is fitted, and then the amplitude of each peak is fit to the corresponding 1D temporal model to extract the relevant temporal constant. Consequently, Equation (4) is first computed and inverted to calculate the $6\times 6$ covariance matrix of the 6 spectral parameters in ${\theta }^{(\nu )}$ (${\sigma }_n$ is assumed the same as for the full 2D model). The $2\times 2$ covariance submatrix for the two amplitudes $A_1,A_2$ is then extracted for each 1D spectrum, and $N^{(t)}$ such covariance matrices are then chained together along the diagonal to produce a $2N^{(t)}\times 2N^{(t)}$ covariance matrix $\sum$ for the temporal model; the block diagonal form reflects the statistical dependence of the two spectral amplitudes, which becomes nonnegligible once the peaks overlap. The expression for the mean, ${\eta }_k\left({\theta }^{(t)}\right)$, is given by the corresponding expression for the 1D temporal model (e.g., Equation (3) for MTE MRS). Calculating and inverting Equation (4) produces the covariance matrix of the temporal parameters, and the square root of its diagonal yields the SDs of each of the temporal constants. The MATLAB code for carrying out the calculations of the CRLB is provided as Supporting Information.

2.3. Spectral parameters

Because spectral lines tend to have very similar linewidths, we set the widths of our Gaussian lines to be identical throughout: ${\mathrm{\Delta }}_1={\mathrm{\Delta }}_2\equiv \mathrm{\Delta }=2.355·\text{FWHM}$. Typical spectral lineshapes are approximately 5–10 Hz, and we set FWHM = 8 Hz. For all simulations, we defined a distance parameter,

$$d\equiv \frac{{\mu }_2-{\mu }_1}{\sqrt{2}·\text{FWHM}},$$ (5)

which quantified the closeness of the two Gaussian peaks. $d\gg 1$ implies little to no overlap, whereas $d\sim 1$ and lower signifies significant overlap.

Because the CRLB matrices are always proportional to ${\sigma }_n^2$, the variance of the noise in the spectra, and because we were only interested in relative SDs between the two approaches, the absolute value of ${\sigma }_n$ was irrelevant and set to unity. The spectral range was set to $[-32,32]$ Hz and sampled at a spectral resolution of 1 Hz, equivalent to a typical FID acquisition time of 1 s, with $N^{(\nu )}=64$.

2.4. Temporal parameters: MTE

For MTE MRS, we investigated the relative SD of the two decay constants $T_{2,\mathrm{A}}$ and $T_{2,\mathrm{B}}$ between the two fitting approaches as a function of d. First, we considered 3 cases of equal $T_2$s: $T_{2,\mathrm{A}}=T_{2,\mathrm{B}}=50,100,$ and 200 ms. We also calculated the effect of unequal $T_2$s by fixing $T_{2,\mathrm{A}}=100\mathrm{ms}$ and varying $T_{2,\mathrm{B}}$ between 30 and 300 ms for two values of d: d = 0.7 and d = 1.4. For all cases, the following TEs were sampled: $\mathrm{TE}=0,50,100,\dots ,350$ ms; This resulted in a 2D dataset with $N^{(\nu )}\times N^{(t)}=64\times 8=512$ data points.

2.5. Temporal parameters: fMRS

For fMRS, we investigated the relative SD of the fractional change during activation, $\delta$, between the two fitting approaches. We assumed a 2 min experiment with TR = 2 s and a 60 s boxcar stimulus administered between 30 and 90 s. Only 1 of the peaks was assumed to change, whereas the other remained static (${\delta }_{\mathrm{B}}\ne 0,{\delta }_{\mathrm{A}}=0$). We plotted the SD of the fractional change $\delta$ for each of the two peaks as a function of d for both the fast (k = 2 s) and slow (k = 15 s) metabolite dynamics, for ${\delta }_{\mathrm{B}}=0.05,0.1,$ and 0.2. We then explored the effect of the activation timescale, k, for two spectral peak distances, $d=0.8,1.5$, assuming ${\delta }_{\mathrm{B}}=0.1$. For each case, the resulting 2D dataset consisted of $N^{(\nu )}\times N^{(t)}=64\times 60=3840$ data points.

3. RESULTS

3.1. Multi‐echo (MTE) MRS

The relative gains in precision of T₂ offered by 2D fitting are summarized in Figure 3. Figure 3A shows that the relative SD is independent of T₂ as long as $T_{2,\mathrm{B}}=T_{2,\mathrm{A}}$. When the peaks have little to no spectral overlap ($d\sim 1$ and above), this relative gain is 20%. This increases exponentially as the peaks begin to overlap ($d\to 0$), indicating that 2D fitting could be a powerful tool in resolving the overlap of metabolites in crowded spectra. Figure 3B shows that some variation ($\pm 20\%$) in the gain is to be expected when $T_{2,\mathrm{B}}\ne T_{2,\mathrm{A}}$ and the peaks overlap spectrally (d = 0.7), with the optimal performance being observed for $T_{2,\mathrm{B}}=T_{2,\mathrm{A}}$. No variation is observed when the peaks do not overlap (d = 1.5). Finally, Figure 3C —plotted for quality assurance—confirms that the spectral peak amplitudes have no effect on the relative performance because the CRLB matrix is proportional to the SNR for both 1D and 2D fittings, and this dependence cancels out once the 1D/2D ratio is formed.

FIGURE 3.

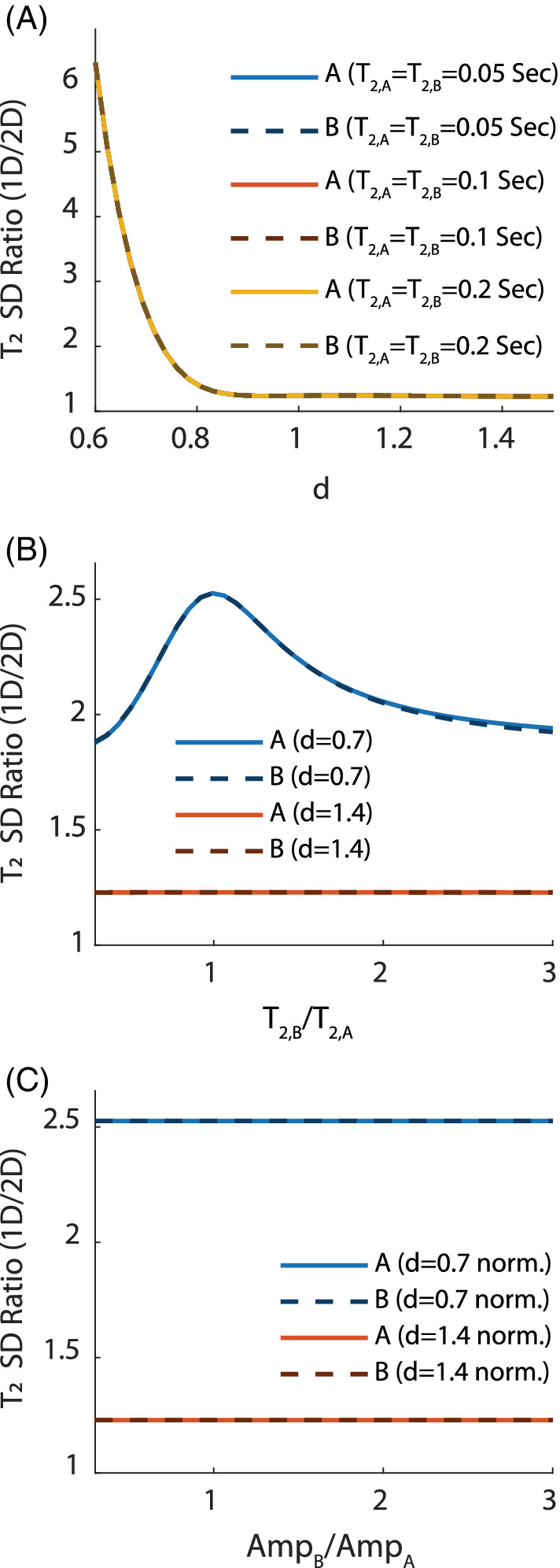
Results: Relative (1D/2D) SD of T₂ in an MTE experiment. Solid lines are for peak A, whereas dashed lines are for peak B. Unless otherwise stated, $\mathrm{TE}=0,0.05,\dots ,0.35$ s, Spectral Width = 64 Hz, $N^{(\nu )}=64$ spectral points, FWHM = 8 Hz, and amplitudes are kept equal. (A) Relative SD as a function of the distance d between the spectral peaks for several values of T ₂, which were kept equal between the two peaks. All curves match almost perfectly, indicating that the relative performance is independent of the absolute value of T ₂ so long as $T_{2,\mathrm{A}}=T_{2,\mathrm{B}}$. This also indicates performance of 2D fitting becomes exponentially better as the peaks begin to spectrally overlap. (B) Relative SD for two distances (d = 0.7, 1.4) while varying the ratio $T_{2,\mathrm{B}}/T_{2,\mathrm{A}}$ (fixing $T_{2,\mathrm{A}}=0.1$ s). When the peaks are far apart, the relative performance is independent of the absolute value of T ₂ (in accordance with (A)). When overlap occurs, 2D fitting provides the best relative performance when the relaxation times are equal. (C) The relative SD is a function of the ratio of amplitudes of the two peaks (fixing A ₁ = 1) for two different spectral distances (d = 0.7, 1.4), keeping the amplitude of the first peak fixed at unity. This “sanity check” confirms that, as expected, the performance is independent of the SNR because the SD of the noise cancels out once the ratio of the CRLBs (1D/2D) is taken. For all plots, as $d\gg 1$, the relative performance of 2D fitting remains fixed at approximately 1.2 (see Discussion section for an explanation of this)CRLBs, Cramer Rao lower bounds.

3.2. Functional MRS (fMRS)

The relative gains in precision of $\delta$, the fractional change in metabolite concentration, offered by 2D fitting are summarized in Figure 4. The overall behavior of the relative SD is highly similar between fMRS and MTE MRS: when the peaks do not overlap, the relative gain in precision for 2D fitting is approximately 20%, regardless of all other model parameters; this gain grows exponentially as $d\to 0$. This is confirmed for both fast (Figure 4A) and slow (Figure 4B) temporal dynamics. Figure 4C shows the ratio of dynamical time constants $k_{\mathrm{B}}/k_{\mathrm{A}}$ has a negligible (<5%) effect on the relative SD whether or not the peaks overlap spectrally.

FIGURE 4.

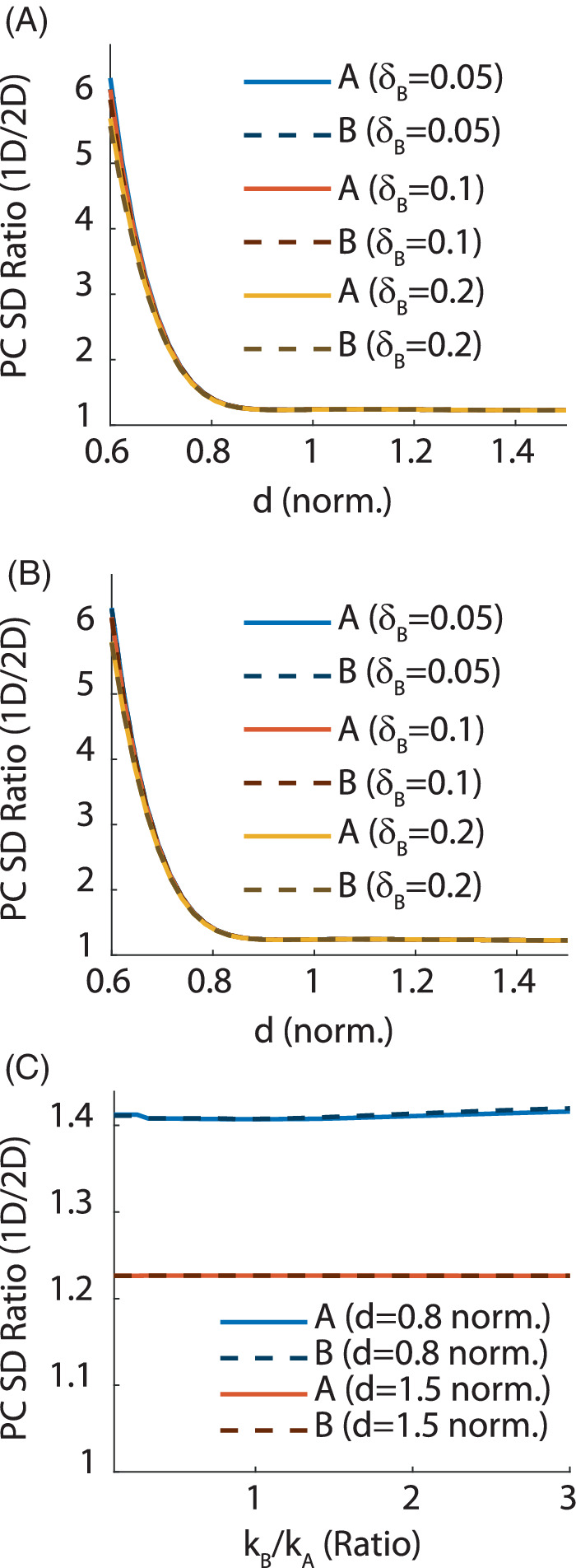
Results: Relative (1D/2D) SD of the fractional change in metabolite concentrations $\delta$ in an fMRS experiment. Solid lines are for peak A, whereas dashed lines are for peak B. Unless otherwise stated, TR = 2 s, TA = 2 min, and stimulus was administered between 30 and 90 s. Spectral parameters were Spectral Width = 64 Hz, $N^{(\nu )}=64$ spectral points, FWHM = 8 Hz, and equal amplitudes. (A) Relative SD as a function of the spectral distance d between the peaks for several values of ${\delta }_{\mathrm{B}}$ (keeping ${\delta }_{\mathrm{A}}=0$) and fast temporal dynamics ($k_{\mathrm{A}}=k_{\mathrm{B}}=2$ s). All curves match almost perfectly, indicating that the relative performance is independent of the fractional change. As with the MTE model, this indicates performance of 2D fitting becomes exponentially better as the peaks begin to overlap spectrally. (B) The same as (a) but for slow temporal dynamics ($k_{\mathrm{A}}=k_{\mathrm{B}}=15$ s). This indicates the temporal dynamics has virtually no effect on the ability to quantify metabolite changes when $k_{\mathrm{A}}=k_{\mathrm{B}}$. (C) Relative SD as a function of the ratio $k_{\mathrm{B}}/k_{\mathrm{A}}$, keeping $k_{\mathrm{A}}$ fixed at 5 s and varying $k_{\mathrm{B}}$, for two values of the spectral distance (d = 0.8, 1.5). This indicates that the ratio of temporal constants has non‐zero but negligible (<5%) effect on quantification precision, even when the peaks overlap. Much like for the MTE plots (Figure 3), the relative gain in precision for 2D fitting remains fixed at approximately 1.2 as $d$ increases

4. DISCUSSION

In the Introduction, we have laid out two questions that we are now poised to answer: Is 2D fitting always superior to 1D fitting? And when does it achieve its biggest gains? First, our results confirm that 2D fitting is indeed uniformly superior to 1D fitting. For all parameter combinations considered and for all models, the ratio of SDs between 2D and 1D approaches exceed $\approx 1.2$. The lower bound was attained for both models once the peaks did not overlap spectrally ($d\gg 1$), regardless of the value of all other parameters. This can be explained by noting that all 2D models fit 1 parameter fewer than their 1D counterparts: namely, the amplitude of the temporal model. 1D approaches initially fit the spectral peak amplitudes and then reintroduce an amplitude parameter in the temporal model (e.g., s ₀ in Equation (3)). It is this redundancy that is avoided by 2D approaches, in which all scaling is done only once in the combined 2D model.

The precision offered by 2D fitting improved exponentially when the spectral overlap between the peaks increased ($d\to 0$). This behavior was observed for both MTE and fMRS models, regardless of other parameter values. This strongly supports the notion that 2D fitting is a powerful tool for handling spectra with significant overlap—as is the case for proton and deuterium MRS, but less so for enriched carbon‐13 and phosphorus‐31 MRS. The effect of all other parameters was much less significant: The absolute value of the fractional change ($\delta$) in an fMRS experiment, or the $T_2$ relaxation time in an MTE experiment, has little effect on the relative quantification precision. In particular, as long as $T_{2,\mathrm{A}}=T_{2,\mathrm{B}}$ in an MTE experiment, its absolute value had virtually no effect on precision, and different $T_{2,\mathrm{B}}/T_{2,\mathrm{A}}$ ratios (from 0.3 to 3.0) led to only a $\pm 20\%$ deviation in relative precision.

Where do the substantial gains in precision come from as $d\to 0$? When the spectral peaks are far apart $(d\gg 1)$, the 6 × 6 CRLB matrix for the spectral components is block diagonal because the parameters of the first peak (amplitude, center, and width) are uncorrelated with those of the second peak. As the spectral peaks overlap, the CRLB deviates from this block diagonal form, and substantial spectral correlations form. 1D fitting records the individual values of the fitted spectral parameters, effectively tracing out these off‐diagonal matrix elements and discarding crucial information about their correlations. No such tracing occurs during 2D fitting.

To put the relative gains of 2D fitting in perspective, we note that an N‐fold increase in precision is equivalent to an N‐fold increase in SNR. Such gains can reduce the sample size N _s required to observe an effect with a given statistical significance $\alpha$ and power ($1-\beta$) ⁵⁴ :

$$N_{\mathrm{s}}=\frac{{\left(z_{1-\alpha }{\sigma }_B-z_{\beta {\sigma }_{\mathrm{A}}}\right)}^2}{{\left({\mu }_{\mathrm{B}}-{\mu }_{\mathrm{A}}\right)}^2}.$$

Here, ${\sigma }_{\mathrm{B}},{\mu }_{\mathrm{B}}$ are the SD and mean of the distribution of a quantity (e.g., percent change, or $T_2$) in population B (e.g., patients), whereas ${\sigma }_{\mathrm{A}},{\mu }_{\mathrm{A}}$ are the SD and mean in population A (e.g., controls). z _x is the inverse of the normal cumulative distribution function. For typical values of $\alpha =0.05$, $\beta =0.2$, one has $z_{1-\alpha }=1.645$ and $z_{\beta }=-0.842$. Reducing the SD of both populations by a factor of two reduces the required sample size by a factor of 4—a substantial gain in experimental time, cost, and complexity (however, it should be noted that in a real experiment, ${\sigma }_{\mathrm{A}},{\sigma }_{\mathrm{B}}$ will be determined by both the intrasubject precision—which 2D fitting improves—and intersubject variability, on which 2D fitting has no effect). Even for the case of no spectral overlap, where gains of about 20% in precision are to be expected, a commensurate reduction of ${1.2}^2\approx 1.44$ in the required sample size can be had. Similar substantive gains can be had in sensitivity and specificity, indicating 2D fitting can have a major impact on MRS in both the clinic and biomedical research.

4.1. Improvements to accuracy

The current work has examined gains to precision by calculating the CRLB for both 1D and 2D approaches to fitting spectral‐temporal data. The CRLB provides a lower bound for unbiased estimators; that is, this work has implicitly assumed that the fitting algorithms used are unbiased and therefore perfectly accurate. This is not uncommon: the Gauss–Markov theorem states that minimizing the least squares (i.e., L₂‐norm) between the data and model function—an approach often taken during fitting spectral data—produces unbiased parameter estimations witha precision that matches the CRLB (regardless of the SNR, and assuming noise is uncorrelated and has equal variances, which is the case for MRS data). However, our conclusions should be treated with some caution if the fitting is expected or known to produce biased parameter estimations, for example, if one chooses to minimize some other norm, such as L ₁.

Another source of bias occurs when either the spectral or temporal models do not describe the behavior of the data. Incorrect models will invariably bias the fitting results for both the 1D and 2D approaches, although it is unclear whether it should affect one or the other more severely. Assessing the effects of incorrect modeling is outside the scope of this work, which has carried out comparisons under the assumption that the temporal model is known and almost identical between the 1D and 2D approaches.

5. CONCLUSION

By calculating the theoretical CRLB for both 1D and 2D approaches, we have shown that 2D fitting uniformly outperforms 1D fitting, with exponential gains when peaks overlap spectrally. Our work strongly motivates the transition to spectral‐temporal fitting packages for all dynamic MRS datasets.

Supporting information

Appendix S1 Matlab computer co

Tal A. The future is 2D: spectral‐temporal fitting of dynamic MRS data provides exponential gains in precision over conventional approaches. Magn Reson Med. 2023;89:499‐507. doi: 10.1002/mrm.29456

DATA AVAILABILITY STATEMENT

The documented MATLAB code used to calculate the CRLB bounds for the 1D and 2D approaches described in this work is provided as‐is in the Supporting Information.