Hybrid U‐Net‐based deep learning model for volume segmentation of lung nodules in CT images

Abstract

Objective

Accurate segmentation of the lung nodule in computed tomography images is a critical component of a computer‐assisted lung cancer detection/diagnosis system. However, lung nodule segmentation is a challenging task due to the heterogeneity of nodules. This study is to develop a hybrid deep learning (H‐DL) model for the segmentation of lung nodules with a wide variety of sizes, shapes, margins, and opacities.

Materials and methods

A dataset collected from Lung Image Database Consortium image collection containing 847 cases with lung nodules manually annotated by at least two radiologists with nodule diameters greater than 7 mm and less than 45 mm was randomly split into 683 training/validation and 164 independent test cases. The 50% consensus consolidation of radiologists' annotation was used as the reference standard for each nodule. We designed a new H‐DL model combining two deep convolutional neural networks (DCNNs) with different structures as encoders to increase the learning capabilities for the segmentation of complex lung nodules. Leveraging the basic symmetric U‐shaped architecture of U‐Net, we redesigned two new U‐shaped deep learning (U‐DL) models that were expanded to six levels of convolutional layers. One U‐DL model used a shallow DCNN structure containing 16 convolutional layers adapted from the VGG‐19 as the encoder, and the other used a deep DCNN structure containing 200 layers adapted from DenseNet‐201 as the encoder, while the same decoder with only one convolutional layer at each level was used in both U‐DL models, and we referred to them as the shallow and deep U‐DL models. Finally, an ensemble layer was used to combine the two U‐DL models into the H‐DL model. We compared the effectiveness of the H‐DL, the shallow U‐DL and the deep U‐DL models by deploying them separately to the test set. The accuracy of volume segmentation for each nodule was evaluated by the 3D Dice coefficient and Jaccard index (JI) relative to the reference standard. For comparison, we calculated the median and minimum of the 3D Dice and JI over the individual radiologists who segmented each nodule, referred to as M‐Dice, min‐Dice, M‐JI, and min‐JI.

Results

For the 164 test cases with 327 nodules, our H‐DL model achieved an average 3D Dice coefficient of 0.750 ± 0.135 and an average JI of 0.617 ± 0.159. The radiologists' average M‐Dice was 0.778 ± 0.102, and the average M‐JI was 0.651 ± 0.127; both were significantly higher than those achieved by the H‐DL model (p < 0.05). The radiologists' average min‐Dice (0.685 ± 0.139) and the average min‐JI (0.537 ± 0.153) were significantly lower than those achieved by the H‐DL model (p < 0.05). The results indicated that the H‐DL model approached the average performance of radiologists and was superior to the radiologist whose manual segmentation had the min‐Dice and min‐JI. Moreover, the average Dice and average JI achieved by the H‐DL model were significantly higher than those achieved by the individual shallow U‐DL model (Dice of 0.745 ± 0.139, JI of 0.611 ± 0.161; p < 0.05) or the individual deep U‐DL model alone (Dice of 0.739 ± 0.145, JI of 0.604 ± 0.163; p < 0.05).

Conclusion

Our newly developed H‐DL model outperformed the individual shallow or deep U‐DL models. The H‐DL method combining multilevel features learned by both the shallow and deep DCNNs could achieve segmentation accuracy comparable to radiologists' segmentation for nodules with wide ranges of image characteristics.

1. INTRODUCTION

Lung cancer is one of the most common cancers and the leading cause of cancer‐related death in men and women in the United States. According to the American Cancer Society, about 13% of all new cancers are lung cancers, with about 235 760 new cases (119 100 in men and 116 660 in women) and about 131 880 deaths from lung cancer (69 410 in men and 62 470 in women) in 2021. ¹ The overall prognosis of lung cancer is poor, with a 5‐year survival rate of only 21%.

Computed tomography (CT) has become a preferred method for detecting and diagnosing lung cancer. Accurate segmentation of the lung nodule in CT images not only provides an objective measurement of nodule size for clinical surveillance of nodule growth ² but also constitutes a critical component for the development of a computer‐assisted lung cancer detection/diagnosis system.

Despite the development of computerized methods over the years, lung nodule segmentation remains a difficult task because of the wide range of heterogeneity in lung nodule characteristics such as shape, size, and attenuation. The complexity of the lung parenchyma surrounding the nodules further poses a challenge in developing robust segmentation models. ³ As the examples shown in Figure 1, it is challenging to segment the nodules with heterogeneous intensity distribution characterized by a wide range of varied x‐ray attenuation distributed within the nodules containing solid, sub‐solid, nonsolid ground glass opacity (GGO) or mixed components, the nodules with “irregular shapes” categorized as irregular or spiculated margins, and the juxtapleural or juxtavascular nodules attached to the chest wall, pleural surface, or pulmonary vessels.

FIGURE 1.

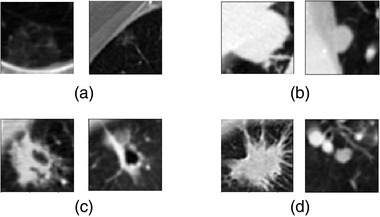
Examples of lung nodules from the Lung Image Database Consortium image collection (LIDC‐IDRI) dataset used in the test set of this study with different characteristics in computed tomography (CT) images: (a) ground‐glass opacity nodule. (b) juxtapleural nodule. (c) Cavitary nodule. (d) nodule with irregular margins

Conventional methods for automated lung nodule segmentation in CT images ⁴ , ⁵ commonly consist of two steps: the detection of nodule locations and then the segmentation of the detected nodules from the surrounding lung parenchyma. ⁶ The features characterizing nodule intensity, textures, and morphologies are usually extracted to differentiate nodules from other lung structures during nodule detection. Then, these features are used to segment the nodules by various methods such as intensity‐based methods with morphological operations, ⁷ , ⁸ region growing methods, ⁹ optimization methods with level set, ¹⁰ graph cut, ¹¹ or reinforcement‐learning techniques. ¹² In an early study, ¹³ we used 3D active contours guided by gradient and curvature energies for segmentation and extracted morphological and texture features to classify malignant and benign lung nodules. In our recent study, ¹⁴ we developed a 3D adaptive multicomponent expectation‐maximization (EM) analysis method to segment the nodule volume including the solid and nonsolid GGO components and the surrounding lung parenchyma region. Radiomic features were then extracted to characterize the CT attenuation distribution patterns of the nodule components. Our results demonstrated the feasibility of classifying pathologically invasive nodules, preinvasive nodules, or benign nodules using the proposed method. Although a wide variety of methods have been developed, the accuracy and robustness of the segmentation have yet to be further improved, especially for nodules with irregular shapes and heterogeneous intensity distribution within the nodules (e.g., partially solid and nonsolid GGO nodules). ⁸

Supervised deep learning methods are emerging technologies increasingly used in medical image analysis, shifting from the classical methods trained with handcrafted features to the training of deep learning models in which the features are learned automatically without manual extraction and selection. Deep convolutional neural network (DCNN)‐based deep learning methods have been used for learning discriminative features from the training data in various machine learning applications from image analysis to natural language processing. DCNN models, such as VGG, ¹⁵ , ¹⁶ DenseNet, ¹⁷ Fast‐CNN, ¹⁸ and some much deeper CNNs, have been successfully employed for a wide variety of tasks. The Mask R‐CNN ¹⁹ represents one of the state‐of‐the‐art DCNNs that uses a region proposal network followed by a region‐based CNN and a semantic segmentation model to simultaneously perform the tasks of detection and segmentation. Different network structures have been developed specifically for many types of lesions or organs to be segmented in various medical imaging modalities. The U‐Net ²⁰ model supplements the deeply supervised encoder sub‐network with a decoder sub‐network through simple skip connections that allow the network to propagate context information to higher resolution layers. The iW‐Net ²¹ was composed of two U‐Nets; the first performed automatic segmentation, while the second U‐Net allowed user correction by marking 2 points along the nodule boundary to refine the segmentation result of the first U‐Net. The PN‐SAMP ²² first segmented a nodule using U‐Net and then used the feature maps from the encoder and the segmentation output from the decoder as inputs to a CNN to predict the malignancy of the nodule. However, these previous methods relied on user interaction to refine the segmentation, such as iW‐Net or were trained for specific types of nodules such as PN‐SAMP. Continued effort is needed to develop new architectures to take advantage of the DCNN‐based approach for the segmentation of heterogeneous lung nodule volumes.

The key feature of the current U‐Net architecture and its variants for image segmentation is the use of two DCNN networks with a similar structure as the encoder and decoder for pixelwise image segmentation. However, there are still many significant challenges in advancing U‐Net segmentation approaches, including improving the learning capability of the encoder to discover enough useful hidden image patterns with large variations ²³ , ²⁴ so as to characterize the differences between lung cancer and lung parenchyma and a better understanding of the intricate relationships between a large number of interdependent variables, ²⁵ especially for segmentation of complex objects in medical images, such as highly heterogeneous lung nodules. Increasing the depth of a DCNN to generate deeper and diverse representations enables the network to progressively explore different levels of features with different sizes of the receptive field as it sequentially goes through each layer is a popular method in the previous years. However, an excessively deep network can result in saturation and cause performance degradation, ¹⁷ and a relatively small training set, such as our lung cancer dataset, is more prone to such risks.

Another approach to increasing the learning ability of a DCNN network is to combine multiple convolutional sequences that may better characterize complex image patterns. Convolutional sequences have different structures, depths, and receptive fields that may allow them to independently capture different features and focus on different kinds and levels of patterns. When these convolutional sequences are hybridized together, they can learn more complex patterns or capture a larger combination of patterns.

Following the second approach, in this study, we designed a new hybrid deep learning (H‐DL) model for the segmentation of lung nodules of a wide range of heterogeneous characteristics. Compared with the conventional U‐Net‐related methods, our H‐DL model was an ensemble of two U‐shaped architectures (U‐shaped deep learning [U‐DL]): one had a shallow DCNN as the encoder, and the other had a deep DCNN as the encoder with a different network structure to increase the learning capability so that different levels of features can be explored to characterize the highly heterogeneous lung nodules in CT images. Moreover, unlike the simple long skip connections utilized in the conventional U‐Net, we adapted a series of nested and dense skip structures ²⁵ to provide alternative pathways to connect the encoder and the decoder in each U‐DL network. These skip structures further alleviate the vanishing gradient problem that saturates gradient backpropagation in deeper networks. After a large number of patterns were captured independently by these two networks, an ensemble layer was used to hybridize the two different U‐DL networks to the H‐DL model to obtain the larger combinations of patterns. To increase the efficiency of our H‐DL model, we used an asymmetric encoder and decoder path structure in which the same decoder with only one convolutional layer at each level was used for both the shallow and deep U‐DL models. The simplified decoder could not only reduce computational and memory costs but also provides flexibility to further expand the H‐DL model by adding more DCNNs with different structures as encoders if needed.

To evaluate the effectiveness of our H‐DL model in segmenting heterogeneous lung nodules, we deployed the H‐DL and the individual U‐DL models separately to an independent test set with a wide range of characteristics manifested in CT images and demonstrated the increased learning capability resulting from the ensemble of two different feature extraction (encoding) networks. We also compared our method with other methods reported in the literature for lung nodule segmentation. To evaluate the generalizability and robustness of our H‐DL model, we deployed our H‐DL model with the trained weights frozen to the test set of an offline challenge, the Sub‐Challenge B (Nodule Segmentation) of the Grand Challenge on automatic lung cancer patient management (LNDb) challenge, ²⁶ and demonstrated that our H‐DL model can be directly deployed to an “external” dataset and achieve high accuracies in lung nodule segmentation.

This paper is organized as follows. Section 2 introduces our H‐DL model and the dataset used. Section 3 presents the results of our method. Section 4 provides the discussion, and Section 5 concludes the paper.

2. MATERIALS AND METHODS

2.1. Dataset

From 1010 patient cases publicly available through the Lung Image Database Consortium image collection (LIDC‐IDRI) with manually annotated lung nodules, ²⁷ a dataset of 847 cases containing lung nodules marked by at least two radiologists with nodule diameters greater than or equal to 7 mm and less than 45 mm were selected in our study. The CT images were acquired with different CT scanners manufactured by GE, Philips, Siemens, and Toshiba. The tube current ranged from 40 to 627 mA (mean: 221.1 mA), the tube peak potential energies ranged from 120 to 140 kV, the slice thickness ranged from 0.6 to 5.0 mm with reconstruction intervals from 0.45 to 5.0 mm, and the pixel size in the axial plane varied from 0.46 to 0.98 mm. We used 683 cases with 2558 nodules for training and validation and the remaining 164 cases with 327 nodules for independent testing.

In the LIDC dataset, the lung nodules were marked and manually segmented by at least two radiologists. The LIDC radiologists also subjectively assessed the nodule characteristics by descriptors and provided ratings on a scale from 1 to 5 for each marked nodule, including subtlety, spiculated margin, solid opacity, lobulated shape, and the likelihood of malignancy (e.g., nodule subtlety, 1 = extremely subtle, 5 = obvious). The typically used 50% consensus consolidation of radiologists' annotations for each nodule was calculated by the LIDC suggested python package “pylidc” and used as the reference standard for training and testing. That is, a voxel was labeled within the nodule when at least 50% of radiologists' segmentation included that voxel. Figure 2 shows examples of radiologists' variabilities in manual outlining of nodules of various sizes, shapes, and locations. The dashed contours with different colors (left) are the outlines by four different radiologists, and the red contour enclosed nodule (right) is the 50% consensus consolidation of radiologists' annotations for that nodule.

FIGURE 2.

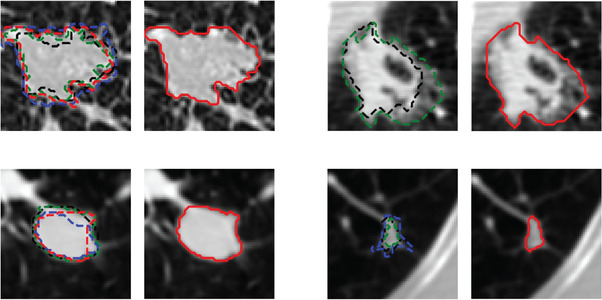
Examples of radiologists' annotations on four different nodules showing the variabilities among radiologists in manual outlining of nodules (left, dashed contours with different colors). The 50% consensus consolidation of radiologists' annotations for each nodule was used as the reference standard (right, red solid contour)

In general, lung nodules with smooth shapes and obvious margins resulted in more similar outlines by the radiologists, as the boundaries were clearly recognizable. In contrast, lung nodules with irregular shapes and fuzzy margins caused higher variabilities because their boundaries were difficult to be clearly identified.

2.2. U‐DL model for lung nodule segmentation

The U‐Net neural network architecture ²⁰ was initially developed for biomedical image segmentation and has been widely used in medical image analysis. Despite the outstanding overall performance, some studies suggested that the conventional U‐Net architecture still has room for improvement due to its simple series of convolutional layers, ²⁸ , ²⁹ plain probable sematic gap, ²⁵ , ²⁹ and relatively shallow network structures. ³⁰ Based on these previous observations, we made the following targeted innovation. Leveraging the basic U‐shaped architecture of the encoder and decoder paths in a conventional U‐Net, we redesigned the DCNN architectures of the encoder and decoder in two separate U‐shaped networks and combined them into an H‐DL model to improve the learning capabilities for segmentation of complex lung nodules that have large variations in the structural and attenuation characteristics. Each of the U‐DL networks consisted of a contracting (encoder) and an expanding (decoder) path (Figure 3a,b). Compared with the original U‐Net that contained five levels of the same number of nine convolutional layers, we expanded each of the U‐DL networks to six levels in both paths. In one U‐DL network, we used a relatively shallow DCNN structure containing 16 convolutional layers adapted from VGG‐19 (the three fully connected layers in VGG‐19 were not used). In the other U‐DL network, we used a deep DCNN structure containing 200 layers adapted from DenseNet‐201 (196 convolutional layers and four transitional layers in five dense blocks while dropping the one fully connected layer in DenseNet‐201). We referred to our two U‐shaped DCNN backbone networks as the shallow U‐DL (Figure 3a) and deep U‐DL (Figure 3b) models.

FIGURE 3.

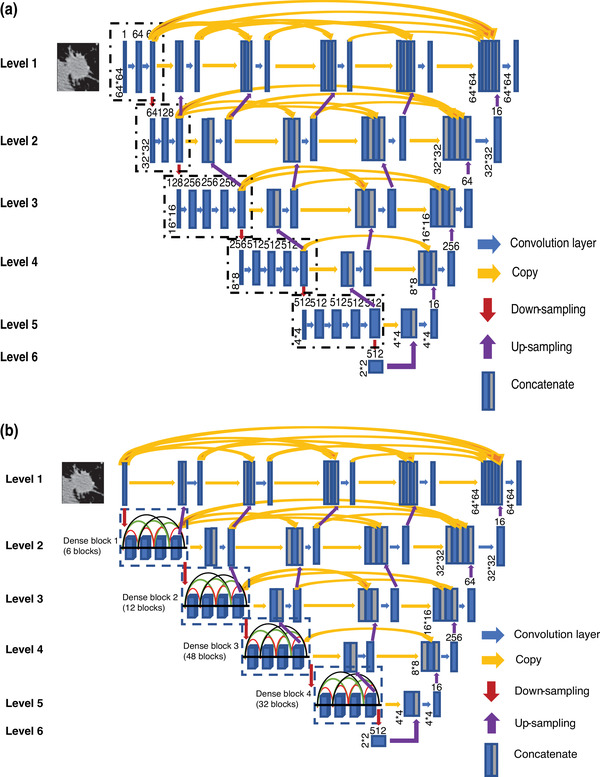
The architectures of our two asymmetric U‐shaped deep learning backbone networks for lung nodule segmentation in CT images. (a) VGG19‐based encoder path (Shallow U‐DL) (upper), and (b) deep DenseNet‐based encoder path (Deep U‐DL) (bottom). The size of each feature map is shown at the lower‐left edge of the box. The arrows of different colors represent different operations.

We also redesigned the decoder in the expanding path of the conventional U‐Net. In our U‐DL models, the expanding path consisted of only one convolutional layer at each level that was much fewer than those in the contracting path and was not symmetric to the contracting path. The simplified decoder can not only reduce computational and memory costs but also provide flexibility that allows further expansion of the H‐DL model by adding more DCNNs as encoders. Both the encoding and decoding paths used a 3 × 3 padded convolution followed by a rectified linear unit. A 2 × 2 max pooling operation with stride two was used for feature map downsampling in the contracting path. We experimentally chose the transpose convolution (inverse convolution) operations for the upsampling operation in the expanding path by comparing it to the interpolation (nearest neighbor or bilinear).

In a conventional U‐Net model, the supervised encoder and decoder sub‐networks were connected through simple long skip connections, allowing the network to propagate contextual information to higher resolution layers. As we utilized deeper encoder network structures in our U‐DL models, to further alleviate the vanishing gradient problem that saturates gradient backpropagation in deeper networks, we modified our U‐DL models by adding a series of nested and dense skip structures to provide alternative pathways to connect the encoder and the decoder as shown in Figure 3. This skipping scheme was derived and modified from U‐Net++, ²⁵ a U‐Net variant that has the advantage of reducing the semantic gap between the feature maps of the encoder and the decoder.

In our hybrid model, the two U‐DL models were separately trained with the training set, and then the probabilities predicted by the two U‐DL models were combined into the H‐DL model through an ensemble layer to maximize the probabilities of the pixels belonging to a nodule as shown in Figure 4. The ensemble layer concatenated the vectors output from the two U‐DL models, followed by a 3 × 3 convolutional layer with the sigmoid activation function and output the multicomponent vectors to a likelihood map indicating pixelwise the chance that a pixel was inside the lung nodule. A threshold of 0.5 likelihood value was determined during the training process to segment the likelihood map to a binary image that labeled the interior and exterior regions of the nodule.

FIGURE 4.

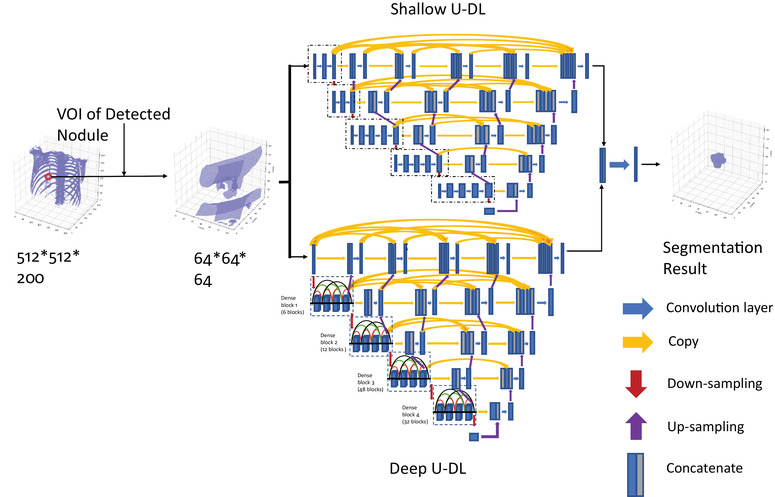
The overall framework of our hybrid DL (H‐DL) model

2.3. Data preparation

The Hounsfield unit (HU) is commonly used in CT scans that measure the radiodensity to characterize the tissue property. As the 12‐ or 16‐bit CT data read directly from the LIDC DICOM file is not the HU value, we first converted the data read from the DICOM file to the HU values by multiplying the pixel values with the rescaling slope and adding the intercept, which is stored in the metadata of the DICOM header. The CT scans were originally acquired with a slice interval ranging from 0.45 to 5.0 mm and a pixel size in the axial plane varying from 0.46 to 0.98 mm. We resampled all CT scans to isotropic volumes with a voxel size of 0.5 x 0.5 x 0.5 mm using the 3D spline interpolation method. For each reference standard nodule marked by radiologists, a volume of interest (VOI) of 64 × 64 × 64 pixels in size centered at the center of the nodule was cropped. For each VOI, the voxel values were scaled as follows:

$$\begin{array}{c}{f}^{\prime }\left(x,y,z\right)=\frac{f\left(x,y,z\right)-\min }{\max -\min }\end{array},$$ (1)

where $f(x,y,z)$ is the voxel value at $(x,y,z)$ min and max are the minimum and maximum voxel values within the VOI, respectively.

2.4. Training of H‐DL models

Our H‐DL models were trained with the set of 683 LIDC cases containing 2558 nodules marked by at least two radiologists. This dataset was separated randomly by case with a ratio of 9:1 as the training set and the validation set during the training process. For each 64 × 64 × 64‐pixel VOI, three 64 × 64‐pixel 2D patches in the axial plane, with the central patch centered at the nodule center, were sampled with a 1.5 mm interval and treated as three different training samples. With an image patch as input, the H‐DL model outputs the likelihood map, which indicates pixels the chance that a pixel is inside the nodule, in the same size as the input image patch (64 × 64 pixels).

Our H‐DL model was trained with mini‐batch training for stochastic optimization and the Adam optimizer. ³¹ The Dice coefficient combined with the binary cross‐entropy was used as the loss function during training. A mini‐batch size of 64 randomly divided from the training set was used in each training epoch. A normal distribution with a mean of 0 and a standard deviation of 0.02 was used to initialize the networks’ weights. The learning rate was initially set to 0.001 as a compromised balance of slow progress (with a lower learning rate) and undesirable divergences (with a larger learning rate) in the loss function and decreased by 10 times when the loss did not continuously decrease on the validation set after 10 consecutive epochs. The early stop strategy was used when the loss on the validation set did not decrease over 30 consecutive epochs.

2.5. Performance evaluation

The performances of our trained models in lung nodule segmentation were evaluated by comparing the segmentation results to the reference standard, defined as the 50% consensus consolidation of radiologists' annotations. Different from using only three image patches sampled from each VOI to train the models, the trained model was deployed to the entire 64 × 64 × 64 VOI slice by slice. For performance evaluation, the 3D Dice similarity coefficient (Dice) and Jaccard index (JI) applied to the 64 slices in each VOI were calculated as quantitative performance measures:

$$\begin{array}{c}DICE=\frac{2\left(Obj\cap Ref\right)}{Obj+Ref}\end{array},$$ (2)

$$\begin{array}{c}JI=\frac{Obj\cap Ref}{Obj\cup Ref}\end{array},$$ (3)

where Obj is the segmented volume, and Ref is the reference standard.

For comparison, we also calculated the 3D Dice coefficient and JI for each LIDC radiologist relative to the reference standard. Since the nodules were segmented by a different number of radiologists (N > = 2) in the LIDC dataset, we calculated the median (M) and minimum (min) of the 3D Dice and JI over all radiologists who segmented a given nodule, referred to as M‐Dice, min‐Dice, M‐JI, and min‐JI, respectively. The averages of the above quantitative measures over the entire test set of nodules were compared with the average 3D Dice coefficient and JI of the two U‐DL models and the combined H‐DL model. The two‐tailed paired t‐test was used to compare the differences between our models and the radiologists' manual segmentations.

3. RESULTS

3.1. LIDC independent test set

Table 1 summarizes the results of our H‐DL model, shallow U‐DL and deep U‐DL models, and radiologists' performance. Figure 5 shows the box and whisker plots of the distributions of the 3D Dice coefficients for the nodule segmentation.

TABLE 1.

Test results achieved by the hybrid deep learning (H‐DL) model, shallow U‐shaped DL (U‐DL) and deep U‐DL alone, and the performance of Lung Image Database Consortium radiologists' manual segmentations relative to the reference standard

		H‐DL		Radiologist				Shallow U‐DL		Deep U‐DL
Categories		Dice	Jaccard index (JI)	M‐Dice	min‐Dice	M‐JI	min‐JI	Dice	JI	Dice	JI
All nodules	N = 327	0.750 ± 0.135	0.617 ± 0.159	0.778 ± 0.102	0.685 ± 0.139	0.651 ± 0.127	0.537 ± 0.153	0.745 ± 0.139	0.611 ± 0.161	0.739 ± 0.145	0.604 ± 0.163
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05
Diameter (mm)	≥ 10.00 (N = 208)	0.782 ± 0.128	0.658 ± 0.152	0.790 ± 0.105	0.704 ± 0.135	0.667 ± 0.128	0.559 ± 0.150	0.777 ± 0.129	0.652 ± 0.154	0.766 ± 0.150	0.640 ± 0.166
	p‐value			0.423	< 0.05	0.434	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05
	< 10.00 (N = 119)	0.695 ± 0.131	0.547 ± 0.145	0.758 ± 0.093	0.652 ± 0.139	0.623 ± 0.121	0.499 ± 0.153	0.688 ± 0.137	0.540 ± 0.149	0.691 ± 0.125	0.541 ± 0.137
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	0.651	0.498
Subtlety	≥ 4.25 (N = 163)	0.798 ± 0.113	0.677 ± 0.140	0.785 ± 0.116	0.701 ± 0.148	0.662 ± 0.139	0.558 ± 0.163	0.796 ± 0.111	0.674 ± 0.138	0.785 ± 0.125	0.662 ± 0.149
	p‐value			0.210	< 0.05	0.222	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05
	< 4.25 (N = 164)	0.702 ± 0.139	0.557 ± 0.154	0.771 ± 0.086	0.670 ± 0.128	0.640 ± 0.112	0.517 ± 0.140	0.694 ± 0.145	0.549 ± 0.159	0.693 ± 0.150	0.548 ± 0.157
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	0.197	0.173
Malignancy	≥ 3.00 (N = 203)	0.783 ± 0.123	0.658 ± 0.149	0.785 ± 0.105	0.700 ± 0.134	0.660 ± 0.127	0.553 ± 0.147	0.778 ± 0.124	0.652 ± 0.148	0.773 ± 0.135	0.647 ± 0.155
	p‐value			0.842	< 0.05	0.855	< 0.05	< 0.05	< 0.05	0.078	0.058
	< 3.00 (N = 124)	0.697 ± 0.139	0.551 ± 0.157	0.767 ± 0.095	0.661 ± 0.145	0.636 ± 0.126	0.511 ± 0.160	0.690 ± 0.145	0.544 ± 0.16	0.683 ± 0.145	0.535 ± 0.152
	p‐value			< 0.05	0.056	< 0.05	0.051	< 0.05	< 0.05	0.100	< 0.05
Margin	≥ 4.25 (N = 175)	0.774 ± 0.126	0.647 ± 0.154	0.795 ± 0.094	0.710 ± 0.137	0.672 ± 0.123	0.567 ± 0.155	0.767 ± 0.135	0.640 ± 0.160	0.756 ± 0.149	0.627 ± 0.166
	p‐value			0.070	< 0.05	0.091	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05
	< 4.25 (N = 152)	0.723 ± 0.140	0.582 ± 0.157	0.759 ± 0.107	0.657 ± 0.136	0.627 ± 0.128	0.503 ± 0.144	0.719 ± 0.140	0.578 ± 0.156	0.720 ± 0.139	0.579 ± 0.156
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	0.667	0.584
Lobulated	≥ 1.75 (N = 165)	0.776 ± 0.120	0.648 ± 0.147	0.775 ± 0.113	0.682 ± 0.151	0.648 ± 0.136	0.536 ± 0.162	0.771 ± 0.121	0.642 ± 0.148	0.767 ± 0.131	0.638 ± 0.154
	p‐value			0.958	< 0.05	0.978	< 0.05	< 0.05	< 0.05	0.136	0.097
	< 1.75 (N = 162)	0.724 ± 0.145	0.586 ± 0.164	0.782 ± 0.089	0.689 ± 0.126	0.655 ± 0.117	0.539 ± 0.144	0.718 ± 0.151	0.579 ± 0.168	0.710 ± 0.154	0.570 ± 0.166
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	0.058	< 0.05
Spiculated	≥ 1.50 (N = 173)	0.767 ± 0.125	0.638 ± 0.150	0.774 ± 0.112	0.680± 0.142	0.648 ± 0.134	0.532 ± 0.153	0.764 ± 0.125	0.633 ± 0.149	0.755 ± 0.145	0.624 ± 0.162
	p‐value			0.515	< 0.05	0.443	< 0.05	0.767	0.739	0.250	0.309
	< 1.50 (N = 154)	0.731 ± 0.143	0.596 ± 0.164	0.783 ± 0.089	0.691 ± 0.136	0.655 ± 0.119	0.543 ± 0.154	0.723 ± 0.151	0.586 ± 0.17	0.721 ± 0.145	0.582 ± 0.162
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	0.587	0.608	0.494	0.431
Solid	≥ 5.00 (N = 167)	0.776 ± 0.125	0.649 ± 0.151	0.794 ± 0.099	0.709 ± 0.135	0.672 ± 0.126	0.564 ± 0.154	0.771 ± 0.131	0.644 ± 0.156	0.759 ± 0.150	0.631 ± 0.166
	p‐value			0.092	< 0.05	0.084	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05
	< 5.00 (N = 160)	0.723 ± 0.141	0.584 ± 0.160	0.762 ± 0.103	0.661 ± 0.139	0.629 ± 0.125	0.509 ± 0.147	0.717 ± 0.142	0.577 ± 0.160	0.718 ± 0.138	0.577 ± 0.156
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	0.630	0.457	0.685	0.447
Sphericity	≥ 4.00 (N = 179)	0.760 ± 0.139	0.632 ± 0.162	0.796 ± 0.085	0.706 ± 0.129	0.673 ± 0.112	0.561 ± 0.148	0.756 ± 0.144	0.626 ± 0.166	0.754 ± 0.143	0.623 ± 0.163
	p‐value			< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05	0.212	0.129
	< 4.00 (N = 148)	0.737 ± 0.129	0.600± 0.153	0.757 ± 0.116	0.660 ± 0.146	0.624 ± 0.139	0.509 ± 0.155	0.732 ± 0.131	0.593 ± 0.154	0.721 ± 0.147	0.582 ± 0.162
	p‐value			0.144	< 0.05	0.058	< 0.05	< 0.05	< 0.05	< 0.05	< 0.05

Note: The p‐values of the differences between H‐DL and others were calculated by paired t‐test. p < 0.05 indicated that the difference was statistically significant. M‐Dice and M‐JI are the averages of the median, and m‐Dice and m‐JI are the averages of the minimum Dice and JI by radiologists, respectively.

FIGURE 5.

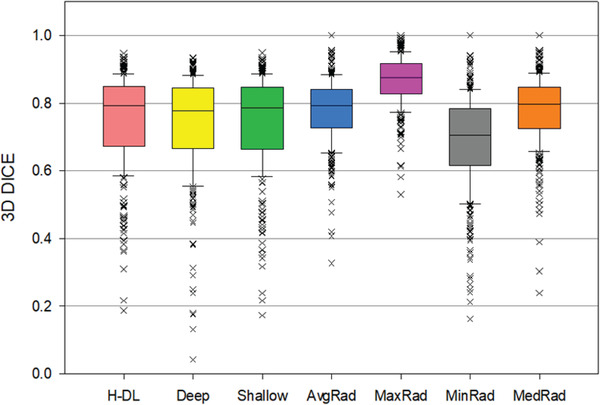
Box plots showing the distributions of the 3D Dice coefficients for the lung nodule segmentation achieved by the H‐DL model, deep U‐DL model, shallow U‐DL model, (H‐DL, deep, shallow, respectively) and average, maximum, minimum and median of the radiologists' manual outlines (AvgRad, MaxRad, MinRad, MedRad, respectively) relative to the reference standard. In this plot, the horizontal line represents the median value, the top line of the box is the 25% quartile, the bottom line of the box is the 75% quartile, the whiskers are the 10th and 90th percentiles, and the points are outliers.

For 164 test cases with 327 nodules, our H‐DL model achieved an average 3D Dice coefficient of 0.750 ± 0.135 and an average JI of 0.617 ± 0.159. The radiologists' average M‐Dice was 0.778 ± 0.102, and the average M‐JI was 0.651 ± 0.127; both were significantly higher than those achieved by the H‐DL model (p < 0.05). On the other hand, both the average min‐Dice (0.685 ± 0.139) and the average min‐JI (0.537 ± 0.153) were significantly lower than the corresponding average Dice and average JI achieved by the H‐DL model. The results indicated that the automated segmentation by the H‐DL model approached the average performance of radiologists and was superior to the radiologist whose manual segmentation had the minimum Dice and JI among the radiologists in the group outlining the same nodule. Note that, as the task of nodule marking was randomly assigned to different radiologists for each nodule in the LIDC study, the minimum Dice and JI could come from any radiologists.

To assess the effectiveness of combining the shallow U‐DL and deep U‐DL models into the H‐DL model, we deployed the separately trained shallow U‐DL and deep U‐DL models to the test set. The shallow U‐DL model achieved an average Dice of 0.745 ± 0.139 and an average JI of 0.611 ± 0.161. The corresponding average Dice and average JI achieved by the deep U‐DL model were 0.739 ± 0.145 and 0.604 ± 0.163, respectively. The average Dice and average JI achieved by our H‐DL model were significantly higher than those of the deep U‐DL and shallow U‐DL models (p < 0.05). Figure 6 shows examples of nodules segmented by the shallow U‐DL, the deep U‐DL, and the final H‐DL in comparison to the radiologists’ segmentation.

FIGURE 6.

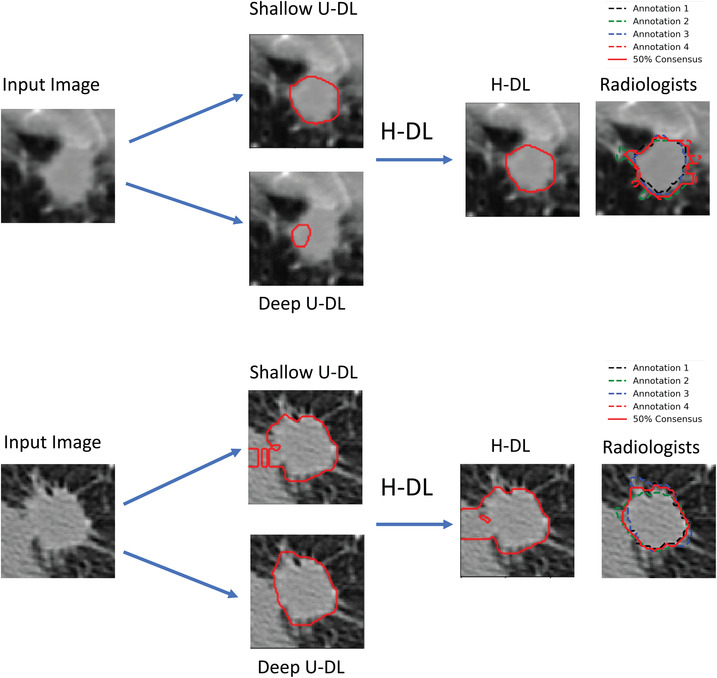
Examples showing the differences between the H‐DL, shallow U‐DL, and deep U‐DL models

For the nodules with different radiologic characterizations assessed by LIDC radiologists, we used the median of radiologists' ratings as the final rating for each nodule and then separated the nodules into two groups using the median of the nodules' final ratings for each descriptor. Table 1 shows the analysis for the two groups of each descriptor. For example, a nodule with diameters less than 10.02 mm was considered a small nodule, and a malignancy rating greater than or equal to 3.0 and a margin greater than or equal to 4.25 indicated that the nodules had a higher likelihood of malignancy and sharp margins, respectively. For the nodules with diameters greater than or equal to 10.02 mm or nodule subtlety rating greater than or equal to 4.25, the average Dice coefficients achieved by the H‐DL model were 0.782 ± 0.128 and 0.798 ± 0.113, compared to the radiologists' average M‐Dice of 0.790 ± 0.105 and 0.785 ± 0.116. Their differences did not achieve statistical significance (p > 0.05), indicating that the segmentation accuracies achieved by H‐DL were comparable to those of radiologists for relatively large and obvious nodules. For the nodules with other radiologic characterizations described by LIDC, the H‐DL model achieved average Dice coefficients of 0.774 ± 0.126, 0.776 ± 0.120, 0.767 ± 0.125, and 0.776 ± 0.125 for nodules with sharp margins (≥ 4.25), lobulated (≥ 1.75), spiculated (≥ 1.50), and solid (≥ 5.00) nodules, respectively, which were comparable (p > 0.05) to radiologists' average M‐Dice coefficients of 0.795 ± 0.094, 0.775 ± 0.113, 0.774 ± 0.112, and 0.794 ± 0.099, respectively. For malignant (≥ 3.00) nodules, the H‐DL model achieved an average Dice coefficient of 0.783 ± 0.123, compared to the average M‐Dice of 0.785 ± 0.105 achieved by radiologists (p > 0.05). Similar results of the JI metrics were achieved by the H‐DL model. The details of the comparisons are shown in Table 1.

To evaluate the robustness of the H‐DL model against the variability of centering the VOI at the nodule, we also deployed our H‐DL model to the VOI obtained by shifting the LIDC‐defined nodule center with a random distance (up to one‐third of the longest diameter of a nodule and at the same time keeping the nodule within the VOI) in the horizontal or vertical direction for each test nodule. This simulates the situation in which the nodule candidate is detected automatically in a computer‐aided diagnosis pipeline, where the centroid of the detected object may not be well centered because the object boundary is unknown before segmentation but the centroid is still located within the object region. The results showed that the average 3D Dice coefficient of 0.741 ± 0.142 using our H‐DL achieved at the shifted‐VOI was not significantly different (p > 0.05 by paired t‐test) from that of the VOIs centered at the LIDC‐defined nodule centers.

We also compared the segmentation results of our H‐DL model with four nodule segmentation methods reported in the literature, which were also tested by LIDC cases. Table 2 shows that our H‐DL achieved higher Dice coefficients and JIs (if reported in their studies).

TABLE 2.

Performance comparisons of our H‐DL model with other deep learning methods in the segmentation of lung nodules

	Dataset used	Volume of interest size	Dice	JI
H‐DL model	LIDC‐IDRI	64 × 64 × 64	0.750 ± 0.135	0.617 ± 0.159
3D U‐Net 32	LIDC‐IDRI	64 × 64 × 64	0.720 ± 0.049	0.380 ± 0.080
iW‐Net 21	LIDC‐IDRI	64 × 64 × 64	–	0.550 ± 0.140
PN‐SAMP 22	LIDC‐IDRI	64 × 64 × 64	0.741±0.357	–

Abbreviation: LIDC‐IDRI, Lung Image Database Consortium image collection.

3.2. LNDb: Grand Challenge on automatic lung cancer patient management

We deployed our H‐DL model that has been trained with the LIDC dataset directly without retraining to the test set of LNDb Sub‐Challenge B for lung nodule segmentation with CT images. ²⁶ The test set of LNDb Challenge B contained 58 CT scans. LNDb provided challenge participants with the VOI findings from an automated lung nodule detection method, in which each CT scan contained 50 VOIs of nodule candidates, resulting in a total of 2900 VOIs. Among those 50 VOIs for each CT, only one or two were the true positive of the nodule, others were false positives from the automated nodule detection, and LNDb only evaluated the segmentation performance for those true positive nodules that were manually outlined by LNDb but unknown to the challenge participants. During the LNDb Challenge B, the participants trained their lung nodule segmentation methods with an LNDb training set that contained only the true nodules with manual outlines and then applied them to the test set containing 2900 VOIs of true or false positives and submitted the segmentation results at the LNDb website for evaluation. Although the submission for the challenge ranking was closed, the submission still remains open for those who want to benchmark algorithms. Without retraining with the LNDb‐provided training set, we directly deployed our H‐DL model to the LNDb test set and submitted the segmentation results to the LNDb for evaluation. The LNDb evaluation results showed that our H‐DL model achieved a Hausdorff distance (HD) of 3.05 mm and a JI of 0.468. Compared with the participants in the leaderboard listed at the LNDb website, our H‐DL model would be ranked at the fifth place in the total ranking leaderboard, while the teams of first place achieved an HD of 2.028 mm and a JI of 0.522, and the original fifth place achieved an HD of 4.406 mm and a JI of 0.403.

4. DISCUSSION

In CT screening of lung cancer, the measurement of nodule size, especially the volume of a nodule, is a vital tool that can help differentiate malignant nodules from benign nodules by the nodule growth rate. The growth rate is estimated by monitoring the change in nodule volume in serial CT scans, such as between the baseline screening CT and the follow‐up scans. CT volumetry also plays an important role in lung cancer treatment by providing size change information to assess treatment response. Manual segmentation of lung nodules is a time‐consuming and tedious task, and substantial interradiologist variability exists as evident in the LIDC study. ³³ Automatic lung nodule segmentation can provide this valuable information without radiologists' effort or requiring only minimal effort in identifying the nodule of interest. Once developed and validated, computerized measurement can be more consistent and reproducible in segmenting the nodule boundaries and thus quantifying the volume changes without inter‐ and intraradiologist variabilities. Automated nodule segmentation is also a fundamental step in computer‐aided diagnosis that can assist radiologists in classifying lung nodules as malignant or benign by extracting radiomic features.

In recent decades, a large number of studies have investigated diverse methods, and most of the methods used a single model to segment lung nodules. These developed models cannot properly represent the decision bounds of a broad spectrum of nodules with high heterogeneity. In this study, we developed a hybrid model that combined two lung nodule segmentation models with different neural network architectures and demonstrated that combining multiple models may have the potential to better adapt to the heterogeneous data distribution in the lung nodule segmentation task. Although it has been shown that a feedforward neural network using only one single hidden layer that contains enough neurons can approximate any model, ³⁴ it is difficult to determine the number of nodes needed. As the number of neurons used in a multilayer network could be quite large, a deeper neural network with multiple layers could be more efficient and flexible to accomplish the tasks. ³⁵ With an increased number of network layers, expression and abstraction learning abilities will be increased in the network. ³⁶ , ³⁷ , ³⁸ However, in practice, the deepness of architecture has a significant drawback because excessive depth may degrade the accuracy. ³⁶ , ³⁹ In general, each layer will produce a lossy‐compression‐like effect after passing through the convolution kernel. A deeper neural network with multiple levels of convolutions may inevitably extract features of excessive abstraction and is more difficult to train than a shallow neural network. In this study, we balanced a deep network with a shallow network and leveraged state‐of‐the‐art network structures such as VGG and DenseNet to increase the learning capabilities of our H‐DL model and exploit different levels of image features from CT images (Figure 4). In Figure 7, we showed some examples to demonstrate that a deep or shallow network works better or worse than each other for different kinds of nodules. In summary, a shallow encoding path will focus on more high‐level features, and our results demonstrated that it had better segmentation for nodules of large sizes with smooth or sharp margins. On the contrary, a deep encoding path will focus more on detailed information, and our results demonstrated that it had better segmentation results for small, nonsolid nodules with poorly defined margins.

FIGURE 7.

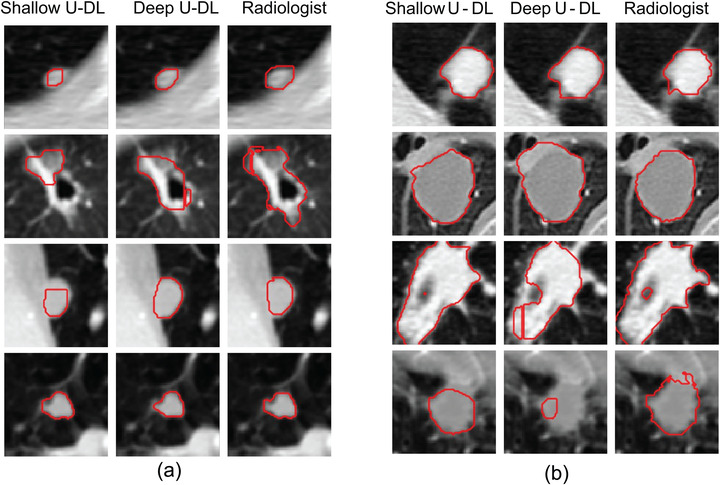
Examples showing the differences between the nodule segmentations by the shallow and deep U‐DL models alone. (a) Deep U‐DL outperformed shallow U‐DL, (b) shallow U‐DL outperformed deep U‐DL

Our results showed that although the segmentation results are different between shallow U‐DL and deep U‐DL when trained with the same training set, the segmentation accuracies achieved by the combined H‐DL model were superior to either one alone for most nodules (Table 1). This result indicated that the different network structures of the two U‐DL models can extract features at different levels of abstraction and provide complementary information in the hybrid model.

In the LIDC dataset, the ratings provided by radiologists for the descriptors of the different nodule characteristics as well as their manual outlines of nodule boundaries exhibited large variabilities. Table 3 shows the root‐mean‐square deviations of the ratings for individual nodules provided by radiologists, averaged over all nodules, for each of the descriptors. To evaluate the performance of our H‐DL model and the separate shallow U‐DL and deep U‐DL, we separated the nodules into two groups by using the radiologists’ ratings for each descriptor as described in the Results section. Although the segmentation accuracies achieved by our H‐DL model and those achieved by the radiologists showed a similar trend for most of the descriptors in each group (Table 1), there are exceptions. For example, both the H‐DL model and the radiologists achieved higher segmentation accuracies for the nodules with sharp margins (≥ 4.25) than for nodules with fuzzy margins. On the other hand, radiologists had lower accuracy in segmenting the spiculated nodules (spiculated ≥ 1.5), compared with nonspiculated nodules (M‐Dice of 0.774 vs. 0.783), whereas the H‐DL model achieved a better segmentation result for spiculated nodules than for nonspiculated nodules (Dice of 0.767 vs. 0.724). Similarly, radiologists achieved a lower accuracy in segmenting lobulated nodules (lobulated ≥ 1.75) than less lobulated nodules (M‐Dice of 0.775 vs 0.782), whereas the H‐DL model had much better performance with lobulated nodules than less lobulated nodules (Dice of 0.776 vs. 0.724). One reason could be the difficulty in visually judging the nodule boundaries in the presence of subtle spiculations and lobulations, and another reason could be that it was too time‐consuming for radiologists to consistently trace the spiculations or lobulations. Because the degree of spiculation or lobulation of the nodule boundary is strongly correlated with the probability of malignancy, an automated segmentation tool that can segment the boundary of these nodules accurately, reproducibly, and efficiently will be helpful in the assessment of screen‐detection lung nodules.

TABLE 3.

The root‐mean‐square deviation (RMSD) of the descriptors of nodule characteristics was provided by different radiologists in the test set. The ratings of the descriptors were given on a 5‐point scale except for the diameter

	Diameter (mm)	Subtlety	Malignancy	Margin	Lobulated	Spiculated	Solid	Sphericity
RMSD	1.725	0.659	0.787	0.706	0.79	0.709	0.51	0.691

We have conducted a preliminary exploration of methods to hybridize the two U‐DL networks. We compared our current method of using a trained ensemble convolutional layer to a simple voting method using a predefined voting threshold. We observed differences in the segmentation performance measures for the nodule sub‐groups of different characteristics; however, the latter method achieved an average 3D Dice coefficient of 0.749 ± 0.141 and an average JI of 0.617 ± 0.162, which were similar to the former method. This indicated that the ensemble layer might have learned a similar strategy as voting but used more adaptive weighting for different nodule characteristics. Although the results were similar on average, a potential advantage is that the ensemble layer method may be more robust as it achieved smaller variances. Further studies are needed to evaluate different fusion methods.

To evaluate the performance of our H‐DL model with the LNDb Challenge B test set, we directly deployed our H‐DL model to the LNDb test set that had several major differences from the LIDC dataset, including (1) our LIDC training set only included nodules with size > = 7 mm, and the LNDb included many small nodules down to 3 mm. (2) The annotations of LNDb nodules were relatively rough and lacked details of the nodule boundary compared with LIDC annotation, especially for the irregular‐shaped or spiculated nodules (Figure 8). (3) LNDb cropped the VOI to a size of 80 × 80 × 80 pixels with the image resolution normalized to 0.6375 x 0.6375 x 0.6375 mm, which was different from our VOI of 64 × 64 × 64 pixels with a resolution of 0.5 x 0.5 x 0.5 mm. Since we did not retrain the network and kept the input dimension as before, we automatically cut the VOI symmetrically from 80 × 80 × 80 to 64 × 64 × 64 and then padded zeros to the segmentation results’ periphery to recover 80 × 80 × 80 VOI.

FIGURE 8.

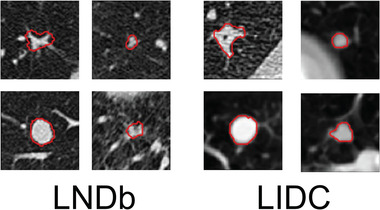
The annotations manually outlined by LNDb (left) and LIDC (right) readers, showing that the LIDC radiologist provided more refined outlines than those of LNDb, especially for the irregular‐shaped or spiculated nodules

Despite the differences, we were still able to achieve competitive performance without retraining with the LNDb training dataset, demonstrating the generalizability and robustness of our H‐DL model in lung nodule segmentation. Among the LNDb Challenge B leaderboards, most participants used the 3D U‐Net structure ⁴⁰ , ⁴¹ , ^{42 ,} which may have inherent advantages for volume segmentation of nodules in 3D CT images. However, the 3D U‐Net usually requires more training time and more GPU/CPU memories, and the accuracies achieved by those 3D networks were widely ranked across the leaderboard, indicating that the 3D network architectures may not be the major reason to achieve better results. Additionally, as the LNDb allowed the participants to submit their results multiple times, the higher‐ranked models also used some pre‐ or postprocessing methods to improve the test performance, such as the methods of attention mechanism convolutional block attention module (CBAM) and switchable normalization for fine‐tuning of the loss functions and hyperparameters based on the feedbacks of submitted test results ⁴³ or using a self‐supervised learning method ⁴⁴ combined with their own dataset with LNDb training set to train the model. Among the participated methods, a DL model ⁴⁴ used the similar training method as ours: It trained a model with the LIDC dataset and then deployed it to the LNDb test set. This model employed a conventional 3D U‐net structure and achieved an HD of 9.12 mm and JI of 0.22, which were significantly lower than those achieved by our H‐DL model.

There are several limitations in this study. In our H‐DL method, the two U‐DL base models shared a similar U‐shaped structure that could limit the networks to explore more diverse features to better characterize lung nodules. We will study other state‐of‐the‐art networks with different architectures, such as Mask R‐CNN ¹⁹ or YOLO ^{45 ,} that can be adapted to our U‐DL models to further improve the hybrid model for lung nodule segmentation. Another limitation is that we have not extensively optimized the fusion method and explored methods such as attention structures to hybridize the outputs from the U‐DL models. These limitations will be addressed in future studies.

5. CONCLUSION

In this study, we developed a new H‐DL method for volume segmentation of lung nodules with large variations in size, shape, margin, and opacity in CT scans. The H‐DL model combined two asymmetric U‐shaped network architectures, one with a 16‐layer shallow DCNN and the other with a 200‐layer deep DCNN as encoders for feature extraction. The results demonstrated that our H‐DL model outperformed the individual shallow or deep U‐DL models. The H‐DL method combining multilevel features learned by both the shallow and deep DCNNs could achieve high segmentation accuracy comparable to radiologists' segmentation for nodules with wide ranges of image characteristics.

CONFLICT OF INTEREST

The authors declare that they have no conflicts to disclose.

Wang Y, Zhou C, Chan H‐P, Hadjiiski LM, Chughtai A, Kazerooni EA. Hybrid U‐Net‐based deep learning model for volume segmentation of lung nodules in CT images. Med Phys. 2022;49:7287–7302. 10.1002/mp.15810

DATA AVAILABILITY STATEMENT

The Lung Image Database Consortium image collection (LIDC‐IDRI) is publicly available from the website ²⁷ (refer to https://wiki.cancerimagingarchive.net/display/Public/LIDC‐IDRI). The Grand Challenge on Automatic Lung Cancer Patient Management dataset is publicly available from the website ²⁶ (refer to https://lndb.grand‐challenge.org).