Using conditional independence tests to elucidate causal links in cell cycle regulation in Escherichia coli

Significance

Cells across all domains of life grow and divide such that their sizes are tightly regulated, yet the coordination of these processes remains poorly understood. Previous works proposed different models for this coupling in bacteria, in some of which division is controlled by DNA replication processes while in others it is uncoupled from them. We combine experimental data on single-cell E. coli growth with the powerful methodology of causal inference to show that constriction is a cell cycle checkpoint controlled exclusively by DNA replication processes in slow-growth conditions, while additional cues are at play in faster-growth conditions. We also show that control of the DNA replication cycles is more complex than previously thought, paving the way for future studies.

Abstract

How cells regulate their cell cycles is a central question for cell biology. Models of cell size homeostasis have been proposed for bacteria, archaea, yeast, plant, and mammalian cells. New experiments bring forth high volumes of data suitable for testing existing models of cell size regulation and proposing new mechanisms. In this paper, we use conditional independence tests in conjunction with data of cell size at key cell cycle events (birth, initiation of DNA replication, and constriction) in the model bacterium Escherichia coli to select between the competing cell cycle models. We find that in all growth conditions that we study, the division event is controlled by the onset of constriction at midcell. In slow growth, we corroborate a model where replication-related processes control the onset of constriction at midcell. In faster growth, we find that the onset of constriction is affected by additional cues beyond DNA replication. Finally, we also find evidence for the presence of additional cues triggering initiations of DNA replication apart from the conventional notion where the mother cells solely determine the initiation event in the daughter cells via an adder per origin model. The use of conditional independence tests is a different approach in the context of understanding cell cycle regulation and it can be used in future studies to further explore the causal links between cell events.

Cell size is regulated across all forms of life. The advent of single-cell experiments has advanced our understanding of these regulatory mechanisms over the past decade (1–3). Single cells growing in microfluidic channels when combined with fluorescence microscopy can be used to track the size and the timing of cell-cycle events such as birth, DNA replication initiation, termination, septum formation, and division (4–10). Existing models of cell-cycle regulation can be tested against the high-throughput data obtained from these experiments and the data can be used to hypothesize new models.

Previous studies have proposed cell cycle models where cells are assumed to initiate a round of DNA replication upon adding a constant size per origin, on average, from the previous initiation (8, 9, 11–13). This model of replication initiation control, referred to as “adder per origin”, predicts that the size added per origin between successive initiations of DNA replication is uncorrelated with the size at initiation for single cells, a prediction which has been observed experimentally (8, 9). However, the proposed cell cycle models differ in how the division event is controlled by the DNA replication process (8, 9, 11, 12, 14). Cooper and Helmstetter proposed that cell division follows the initiation of DNA replication after a constant time has elapsed (14) (we will refer to this as the CH model). Within this model, this constant time is the sum of the time taken for DNA replication (the C period) and the time from termination of DNA replication to division (the D period), Fig. 1. In the parallel adder model proposed for Mycobacterium smegmatis, cell division occurs after the cell has increased by a constant size per origin from replication initiation (15). This model was later proposed for E. coli, where it was referred to as “double adder” (9). We will use the term, parallel adder (PA), in this paper to describe two adders working in parallel (initiation to initiation and initiation to division). In both CH and PA models, division is controlled solely by the replication initiation event. A competing model (the independent adder (IA) model) suggests that division happens independently of the DNA replication process (8). In this model, the division is controlled by accumulation of a key protein to a threshold level, starting from cell birth. A middle ground is the concurrent processes model where division is controlled by a combination of cues, some of which originate from cell birth and others from the initiation of DNA replication (13, 16, 17). Identifying the correct statistical analysis method and model has been contentious.

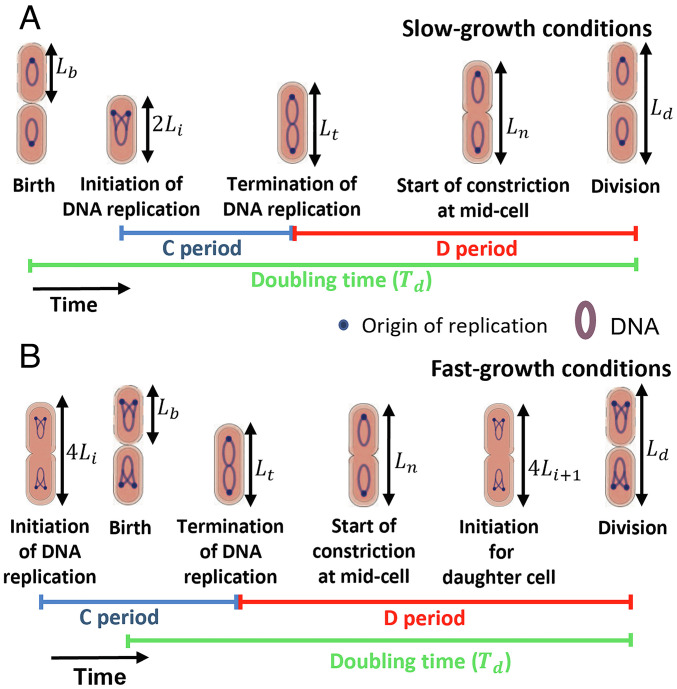
Fig. 1.

Key cell cycle events analyzed. (A) At slower-growth rates, cells are born with a single origin of replication. (B) In faster-growth conditions, cells are born with multiple origins. In the case of cells with two origins at birth, the initiation starts in the mother cell. The C period is the time taken for DNA replication and the D period is the time between termination of DNA replication and cell division. The lengths at these events considered in the data analysis are also shown. Here, L_i is the length per origin immediately after the initiation of DNA replication.

Much of the support for the models hypothesized above comes from the absence or presence of correlations between two variables describing the cell cycle. Recent studies have found different models described above to be consistent with the same data using the same analysis method (18–20). There is a lack of consensus on the use of a statistical method to study cell cycle regulation which leads to a lack of consensus on the underlying cell cycle model. To address this, we will go beyond two-variable correlations and use concepts of causal inference relying on conditional correlations involving more than two variables to study causal statements. Causal inference provides a systematic way to establish the phenomenological models for size control while being robust to the model details and helps us rule out the model where DNA replication and division happen independently.

While causal inference is widely used in epidemiology, sociology, economics, and computer science (21), it has not been utilized previously in testing cell cycle models. Specifically, we study the relation between replication and the onset of constriction and find that in the slowest growth conditions, replication is the limiting factor controlling the onset of constriction, but in faster-growth conditions, additional regulatory cues need to be invoked to explain the data. Furthermore, we find that the onset of constriction directly leads to division without the involvement of any additional regulatory mechanisms that retain the memory of birth size. Finally, the data suggest that replication initiation in the mother cell is not the sole factor controlling the initiation in the daughter cell, as was suggested previously (8, 9, 11–13). While the casual inference methodology we are using is agnostic to the details of the underlying molecular mechanisms, it allows us to gain important insights into the possible regulatory network architecture and narrow down the potential biological pathways.

Results

Replication Control on Division Is Growth Rate Dependent.

To investigate how the cell cycle events are controlled in E. coli, we used data from recent experiments in 6 different growth media (10). These data have been collected at slow (average number of origins at birth ∼1) and moderately fast growth rates (average number of origins at birth > 1). The experiments were conducted at 28 °C where the growth rates were about twice as slow as at 37 °C (22). The data contain the timings of cell cycle events such as birth, initiation of DNA replication, termination, start of septum formation, and division for hundreds of cell cycles and the corresponding cell lengths for those events.

Previous works have considered correlations between cell cycle variables such as the size at birth (L_b) and size at division (L_d) to infer cell cycle models (2). Using linear regression, we show the best linear fit between L_b and L_d for a fast-growth condition in Fig. 2A and a slow growth condition in Fig. 2B. For cells growing in fast-growth conditions (Fig. 2A), the underlying equation is close to L_d = L_b + ΔL and cells are assumed to be following an adder model where cells divide on the addition of constant size from birth (5, 8, 9). In slower-growth conditions, the cells have been shown to follow a near-adder (Fig. 2B and ref. 6). Ref. 23 provided a general framework to infer the cell cycle regulation strategy from L_d vs L_b plots. In this model, a cell born at size L_b divides at size L_d by employing a regulatory mechanism f(L_b) (a deterministic element), to which noise is added. Mathematically, for the case of size-additive noise, this corresponds to the equation L_d = f(L_b)+η, where η is the noise in division size, independent of L_b. This is an example of a structural causal model (SCM), widely used in causal inference (24). The SCMs can be visualized using directed acyclic graphs. The nodes in the graph are connected via directed edges with the direction of the arrows going from cause (variables on right side of the SCM) to effect (variable on left side of the SCM). Each node in the graph represents a variable which may either correspond to an observable quantity obtained in the experiments or to an unobserved variable. In the graphs that we will study in the paper, the nodes will correspond to cell lengths at cell cycle events (SI Appendix, section S2 for an explanation as to why using lengths is advantageous compared to using the timing of the events). In the graphs, the absence of an edge between two nodes shows that there is no direct causal effect between the two variables. In the case of cell cycle regulation models, the SCMs and the graphs are independent of the nature of noise and so will be our conclusions. The latter can be either size or time additive (25).

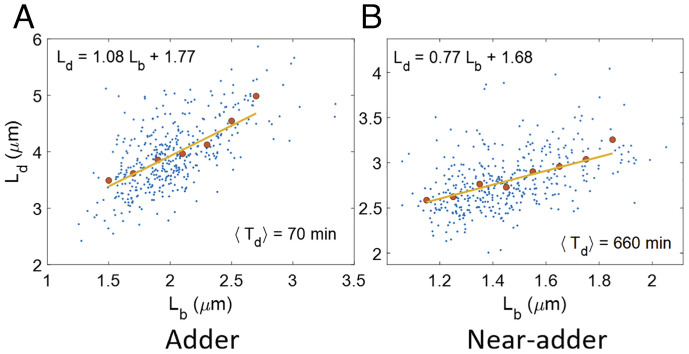
Fig. 2.

Correlation between birth and division: (A and B) L_d vs L_b graphs are plotted for data from ref. 10 in (A) Glucose-cas medium (generation time (⟨T_d⟩) = 70 min, N = 409 cells). The best linear fit has a slope = 1.08 (0.97, 1.19). (B) Acetate medium (generation time (⟨T_d⟩) = 660 min, N = 401 cells). The best linear fit has a slope = 0.77 (0.65, 0.89). The numbers in the parenthesis here represent the 95% confidence interval. In Fig. 2 A and B, the blue dots represent the raw data, the red dots represent the binned data, and the yellow line represents the best linear fit.

The linear relation between L_b and L_d can also be explained by other cell cycle models such as the CH and PA models. Next, we construct causal graphs for these E. coli cell-cycle models. In the CH and PA models, initiation of DNA replication controls when division happens. In slow-growth conditions where the number of origins at birth is 1, initiation and division occur in the same cell cycle (Fig. 1A). However, in the faster-growth conditions used in the experiments, replication initiation could start in the mother cell and the number of origins at birth is 2 (Fig. 1B). Mathematically, the size at division is determined by L_d = 2(L_i + Δ_id)+η for the PA model, where L_i is the initiation size per origin number taken right after initiation, Δ_id is the size per origin added between initiation and division, and η is a size additive noise. In the CH model where cells are undergoing exponential growth with growth rate λ, L_d = 2L_ie^{λ(C + D)} + η_t, where η_t is a size additive noise. This is shown as an arrow from L_i to L_d (Fig. 3A). In these models, initiation size $L_i=\frac{L_{i-1}+{\mathrm{\Delta }}_{\mathit{ii}}}{2}+\xi$, where L_i − 1 is the previous initiation size per origin, Δ_ii is the size per origin added between consecutive initiations and ξ is a size additive noise. This is shown as an arrow from L_i − 1 to L_i in Fig. 3A. The previous initiation event (L_i − 1) also controls the division event in the mother cell (L_d − 1) or equivalently the birth event of the current cell cycle (arrow from L_i − 1 to L_b). L_i − 1 is a confounder which means that it is a common cause of two events, in this case, L_b and L_i. In a second class of models referred to as “concurrent processes” (13, 16, 17), the division size is determined by the slowest of two processes: 1. constant size addition from birth (adder) at fixed growth rate 2. a time C+D from initiation of DNA replication (where each of the two processes is also subject to noise). The corresponding SCM for exponentially growing cells with growth rate λ is L_d = max(L_b + Δ_bd′+δ_bd′,L_ie^{λ(C′+D′+δ_C + D′)}) and it is represented by arrows from L_b to L_d and L_i to L_d, in the graph shown in Fig. 3B. L_d is a common effect of L_b and L_i, and in this case, L_d is said to be a collider. Note that the measured average C+D period will be determined by the competition between the two processes and, therefore, could be different from C′+D′. Similarly, the measured average size added between birth and division will be different from Δ_bd′. In the concurrent processes model’s SCM, δ_bd′ and δ_C + D′ are the noise terms in Δ_bd′ and C′+D′, respectively. The noise terms are independent of each other and are also uncorrelated with L_b and L_i. Similar to CH and PA models, birth (L_b) and initiation (L_i) are associated by a common cause, the initiation in the previous cell cycle (L_i − 1) (Fig. 3B). Note that the birth event in previous cell cycle (L_b − 1) also controls the division event in mother cell (L_d − 1) according to the concurrent process model, and hence, it controls birth in current cell cycle (L_b). We do not show the L_b − 1 to L_b causal link here as the omission of the link will have no effect on our analysis. For complete causal diagrams, see SI Appendix, section S3. A third model, the independent adder (IA) model is also shown in Fig. 3C where the division length is solely controlled by the birth length (arrow from L_b to L_d) independently of the initiation length (7, 8, 26). The initiation is controlled by the previous initiation as in the CH, PA, and concurrent processes models (arrow from L_i − 1 to L_i). Importantly, the links between L_i and L_b, and L_i and L_d are absent as initiation is independently controlled from division. Directed acyclic graphs (DAGs) such as the ones shown in Fig. 3 A–C can be used to determine correlations and conditional correlations.

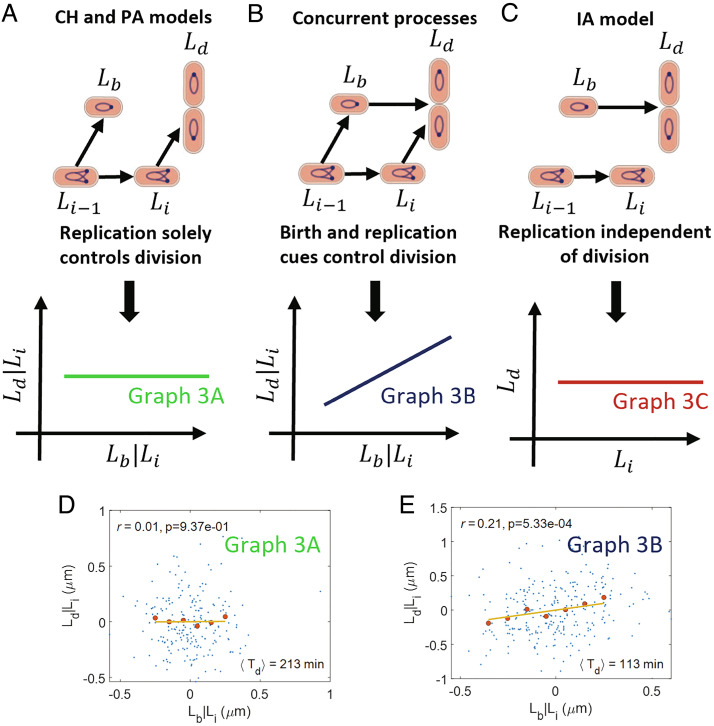
Fig. 3.

Causal graphs and CI tests linking birth, initiation, and division: (A) A causal graph linking lengths at birth (L_b), initiation (L_i), and division (L_d). In this graph, the replication initiation controls the division event. We predict r(L_b, L_d|L_i) =0 for the graph. (B) Both birth and initiation simultaneously control the division event. We predict r(L_b, L_d|L_i)≠ 0 for the graph. (C) A graph corresponding to the independent adder (IA) model. Here, the division process is independent of the replication process. L_b and L_d are uncorrelated from L_i. (D and E) Residuals obtained on linear regression of L_d on L_i (L_d|L_i) and L_b on L_i (L_b|L_i) are plotted for data from ref. 10 in (D) Alanine medium (generation time = 213 min, N = 215 cells, average number of origins at birth, ⟨n_ori⟩ = 1.07). (E) Glucose medium (generation time = 113 min, N = 259 cells, ⟨n_ori⟩ = 1.98). The conditional correlation, r(L_b, L_d|L_i), is negligible for the alanine medium (consistent with graph 3A) while it is nonzero for the glucose medium (consistent with graph 3B). In Fig. 3 D and E, the blue dots represent the raw data, the red dots represent the binned data, and the yellow line represents the best linear fit. r is the Pearson correlation coefficient between the variables in the x and y axes. p in the plots are the P values. We reject the null hypothesis that the correlation is zero if the P value is less than the significance level set at 0.05.

Correlations and conditional correlations are determined from the DAGs using a set of rules known as d-separation (21). These rules will be briefly explained below. In graph 3A, since L_i controls L_d, they will be correlated. L_b and L_i are correlated via the confounder, L_i − 1. Only under specific conditions where the effects of the two links cancel each other, L_b and L_i will be uncorrelated. Directed acyclic graphs encode information beyond two-variable correlations, namely conditional independencies (CI). Conditional correlation r(L_b, L_d |L_i) means finding the correlation between two variables, L_b and L_d, upon fixing the value of a third variable, L_i. In graph 3A, L_b and L_d are uncorrelated upon fixing the value of L_i and the path between L_b and L_d is then closed (in contrast, a path connecting two variables and leading to their correlations is defined as open, for example, the path between L_b and L_d without conditioning in graph 3A). In graph 3B, the collider L_d blocks the path between L_b and L_i and the path between L_b and L_i via L_d is closed. The path opens upon conditioning on a collider or any descendant of a collider: for instance, in graph 3B upon conditioning on the variable L_d, the path between L_b and L_i via L_d will be open. To summarize, a path is closed if a noncollider in the path is conditioned upon or if a collider and its descendants are not conditioned on. In the case of multiple paths between two variables, the variables are uncorrelated if all the paths between those variables are closed (SI Appendix, section S1). In this paper, we will go beyond the previously used methodology of using two variable correlations (Fig. 2 A and B) and use CI tests to select cell cycle models.

The model corresponding to graph 3C (IA model) predicts that L_i will be uncorrelated with L_b and L_d (prediction shown below the graph in panel 3C), as initiation is not linked to either birth or division. We find using experimental data that the Pearson correlation coefficients between L_b and L_i (r(L_b, L_i)) and L_i and L_d (r(L_i, L_d)) are nonzero in all six measured growth conditions (SI Appendix, Table S1). Note that we have excluded the two fastest growth conditions from (10) because of incomplete tracking of DNA replication initiation in these data sets. The result rules out IA model as a viable model for cell cycle regulation, as was previously argued in ref. 9. In contrast, both models shown in graphs 3 A and B predict that L_i will be correlated with L_b and L_d. Thus, we have to go beyond two variable correlations and use CI tests to distinguish between the two graphs.

To distinguish the models in graph 3 A and B, we will condition on the initiation length, L_i, and calculate the conditional correlation (r(L_b, L_d|L_i)) between L_b and L_d. We predict using d-separation that L_b and L_d are uncorrelated on fixing L_i in graph 3A. However, they are predicted to be correlated in graph 3B as there is a direct causal link between L_b and L_d. We validated the method using synthetic data generated by existing models following the methodology outlined in ref. 25 (SI Appendix, section S4).

The simplest way of calculating r(L_b, L_d|L_i) using experimental data is by evaluating the correlation between L_b and L_d in the small interval (L_i − dL, L_i + dL). We do not use this method because the number of data points of L_b and L_d corresponding to each interval in the available datasets is too small, making the conditional correlations hard to interpret (SI Appendix, Fig. S5). In order to obtain the conditional correlation, we will instead remove the influence of L_i from L_b and L_d using linear regression. To that end, we assume linear dependence of L_b and L_d on L_i. The linear relations can be rationalized as Taylor expansions around the mean of the nonlinear relations between L_b and L_i, and L_d and L_i. The residuals obtained upon carrying out the linear regression of L_b on L_i (L_b|L_i) and L_d on L_i (L_d|L_i) represent the effect of sources other than L_i on L_b and L_d, respectively. The correlation r(L_b, L_d|L_i) is calculated by obtaining the Pearson correlation coefficient between the residuals L_b|L_i and L_d|L_i (Materials and Methods and (27)). In this method of calculating the conditional correlation, we use the complete dataset available for each growth medium. Note that when we refer to conditional correlations as vanishing throughout the paper, we mean that the Pearson correlation coefficient is not statistically significant when using a P value as the metric at a significance level of 0.05.

Next, we use the experimental data to test whether r(L_b, L_d|L_i) is zero or not. We plot the residuals obtained using linear regression of L_d on L_i (L_d|L_i) and L_b on L_i (L_b|L_i). We find the correlation coefficients between the residuals to be negligible for the two slowest growth media (Fig. 3D and SI Appendix, Fig. S1A) and nonzero for the other growth conditions (Fig. 3E and SI Appendix, Fig. S1 B–D). Thus, graph 3A is consistent with the data in the two slowest growth conditions while the model in graph 3B is consistent with data in the faster-growth conditions. The correlations are tabulated for each growth medium in SI Appendix, Table S2. Accounting for possible outliers in the data (keeping the middle 95% percentile data of both axes), we find the P value to be above significance level of 0.05 in the three slowest growth condition (SI Appendix, Fig. S1E). This finding is in agreement with the hypothesis of the replication process becoming more limiting for determining division in slower-growth conditions. We also checked whether growth rate $\lambda =\frac{1}{T_d}ln(\frac{L_d}{L_b})$ affected the correlations between the residuals. The correlation coefficients between the residuals obtained using linear regression of L_d on L_i and λ (L_d|(L_i, λ)) and L_b on L_i and λ (L_b|(L_i, λ)) are shown in SI Appendix, Table S2. We still find the correlations to be close to zero for the two slowest growth conditions and nonzero for the others. In previous studies (13, 20), asymmetry in the partitioning of the mother cell into two daughter cells was shown to have important consequences on correlations. We, therefore, considered the effects of asymmetric divisions. For the small division ratio noise observed in the experiments for E. coli (10, 13, 28), we still expect r(L_b, L_d|L_i) to be close to zero. Moreover, asymmetric divisions can also be accounted for by replacing L_b with L_d − 1 (division size of mother cell) in the conditional correlation r(L_b, L_d|L_i) (SI Appendix, section S4). r(L_d − 1, L_d|L_i) is not affected by the division asymmetry as L_d − 1 is not affected by how the mother cell partitions into two daughter cells. We find that r(L_d − 1, L_d|L_i) also have values close to r(L_b, L_d|L_i) in the experiments and support our hypothesis that the replication process becomes more limiting in slow growth conditions (SI Appendix, Table S8). We also analyzed previously published datasets (8, 9, 13) and found that they were consistent with a model where both birth and replication processes limit division in fast growth and replication becomes more limiting in slower-growth conditions (SI Appendix, section S5).

To conclude, in the two slowest experimental growth conditions, division is solely controlled by replication (consistent with CH/PA models). However, in four faster-growth conditions, additional processes starting from cell birth also control division (consistent with concurrent processes model).

The Onset of Constriction Solely Controls the Division Size.

Previous studies propose the start of septum formation at midcell as an important checkpoint involved in length control (7, 10). However, most of the previous cell cycle models, including the aforementioned ones, did not explicitly contain this checkpoint, but only considered the division event. In this section, we show that cells exert size control at the start of constriction at midcell and the constriction process ultimately culminates in division, without additional regulation on the division timing. We will use cell lengths at birth, the onset of constriction (L_n), and division as a proxy to denote the events. The onset of constriction can be determined by labeling FtsN with a fluorescent fusion protein; FtsN is the last known essential component of the E. coli divisome to assemble at the midcell before constriction starts (29–34). The accumulation of FtsN at the midcell thus indicates the start of septum formation, as was validated in ref. 10.

We hypothesize a causal graph based on our prior knowledge about the start of septum formation at midcell. Previous works suggest that an accumulation of a threshold amount of cell division proteins such as FtsZ (8) or cell wall precursors (7) starting from birth is responsible for triggering constriction at midcell. For both scenarios and assuming also a balanced growth, we expect L_n = L_b + Δ_bn + ξ, where Δ_bn is the size added between birth and the onset of constriction and ξ is a size additive noise. This relation is depicted by an arrow from L_b to L_n in the graph of Fig. 4A, where the arrow from L_n to L_d represents commitment to division upon the onset of constriction. A competing model is shown in Fig. 4B, where in addition to the onset of constriction, another biochemical process starting at cell birth is limiting for the division event (for example, the accumulation of another key protein).

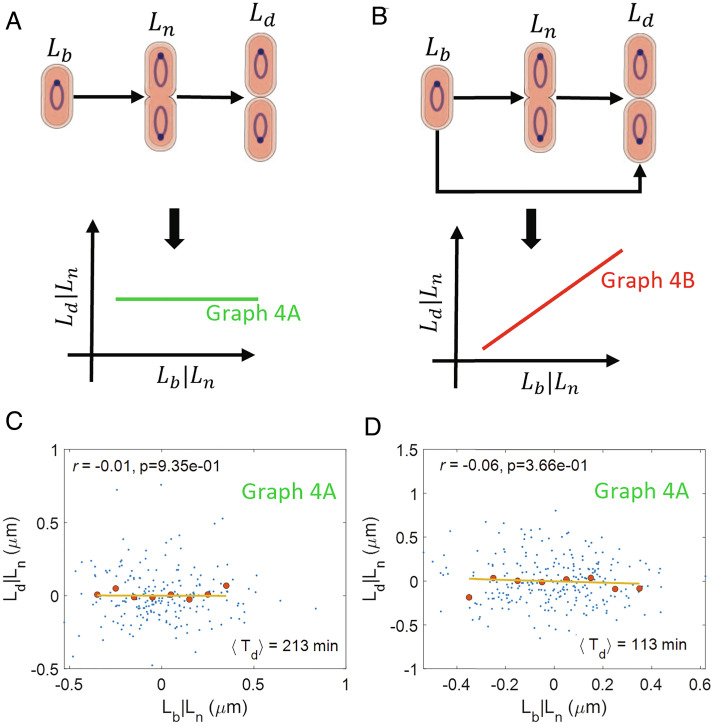
Fig. 4.

Linking birth, onset of constriction, and division: (A) A causal graph linking the length at birth (L_b), onset of constriction (L_n), and division (L_d). In this graph, division is solely controlled by the onset of constriction. We predict that r(L_b, L_d|L_n) = 0 for the graph. (B) A causal graph where multiple processes from birth and from the onset of constriction control division. We predict a nonzero r(L_b, L_d|L_n) for the graph. (C and D) Residuals obtained on linear regression of L_d on L_n (L_d|L_n) and L_b on L_n (L_b|L_n) are plotted for (C) Alanine medium (generation time = 213 min, N = 215 cells, ⟨n_ori⟩ = 1.07). (D) Glucose medium (generation time = 113 min, N = 259 cells, ⟨n_ori⟩ = 1.98). The conditional correlations, r(L_b, L_d|L_n) are close to zero for both of the growth conditions (consistent with graph 4A).

We expect that the variables L_b, L_n, and L_d will be correlated with each other for both graphs 4 A and B. This is because L_n shares a cause-and-effect relationship with L_d and L_b, respectively. This is indeed what we observe in the experimental data for all six growth media as shown in SI Appendix, Table S3. Note that the relation between birth and the onset of constriction deviated from an adder model in all growth conditions.

Next, we test the predictions of conditional independence obtained by applying d-separation on the graphs in Fig. 4 A and B. For the graph in Fig. 4A, we predict r(L_b, L_d|L_n) = 0 using d-separation while for Fig. 4B, r(L_b, L_d|L_n) is nonzero. To test these predictions, we find the correlation between the residuals obtained on linear regression of L_b on L_n (denoted as L_b|L_n) and L_d on L_n (L_d|L_n). The plots of the residuals are shown in Fig. 4 C and D for cells growing in a slow-growth medium (alanine, generation time = 213 min) and a fast-growth medium (glucose, generation time = 113 min), respectively. In Fig. 4 C and D, we show the correlation between the residuals to be close to zero. Similar negligible correlations are also obtained for four other growth media as shown in SI Appendix, Fig. S2 A–D and Table S3 with the corresponding P values (SI Appendix, Fig. S2E) above the significance level. Thus, the graph in Fig. 4A is consistent with the experimental data.

These results show that the onset of constriction can be regarded as a cell cycle checkpoint that solely controls the cell size at division without any additional cues from cell birth.

Cell Cycle Model Involving the Onset of Constriction.

In the previous section, we verified that the onset of constriction can be regarded as a cell cycle checkpoint. Previously, we showed that replication controls division in slow-growth conditions and is one of the factors controlling division in fast-growth conditions. In this section, we propose extensions of CH/PA and concurrent processes models that include the onset of constriction as a cell cycle checkpoint.

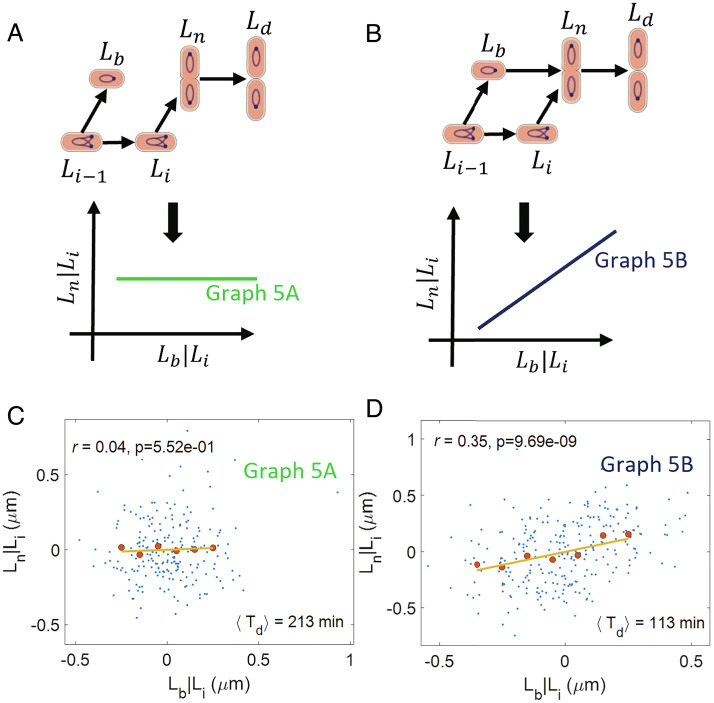
To this end, we adapt the cell cycle models of graphs 3 A and B by hypothesizing that birth size and replication initiation size control the size at the onset of constriction instead of division size. The graph in Fig. 5A corresponds to a model where initiation controls constriction (arrow from L_i to L_n). Such a control may be exerted by nucleoid occlusion, whereby a chromosome blocks the formation of FtsZ ring via DNA binding proteins (35) or sterically (36). Within this model, constriction may start when the chromosome segregation is underway, lowering the DNA density at the midcell and relieving the effects of nucleoid occlusion (10). Since termination of DNA replication follows causally from initiation, within the graph we depict this mechanism by an arrow from initiation of DNA replication to constriction. Thus, a limiting factor that controls the start of constriction may be the start of DNA replication (Fig. 5A). A competing model is shown in graph 5B where the size at the onset of constriction is simultaneously controlled by birth size (arrow from L_b to L_n) and initiation size (arrow from L_i to L_n). In this model, accumulation of division proteins and nucleoid occlusion may both play a limiting role on start of constriction (10). Based on the results in the previous section, constriction culminates in division. This is shown as arrows from L_n to L_d in Fig. 5 A and B.

Fig. 5.

Cell cycle regulation model: (A) A causal graph linking the lengths at birth (L_b), initiation (L_i), onset of constriction (L_n), and division (L_d). In this graph, constriction is controlled by the DNA replication process. We predict r(L_b, L_n|L_i) = 0 for the graph. (B) A causal graph in which the size at the onset of constriction is simultaneously controlled by the birth size and the initiation size. We predict a nonzero r(L_b, L_n|L_i) for the graph. (C and D) Residuals obtained on linear regression of L_n on L_i (L_n|L_i) and L_b on L_i (L_b|L_i) are plotted for (C) Alanine medium (generation time = 213 min, N = 215 cells, ⟨n_ori⟩ = 1.07). (D) Glucose medium (generation time = 113 min, N = 259 cells, ⟨n_ori⟩ = 1.98). The conditional correlation, r(L_b, L_n|L_i) is close to zero for the alanine medium (consistent with graph 5A) while it is nonzero for the glucose medium (consistent with graph 5B).

Both models predict that L_i and L_n will be correlated (in contrast to models where protein accumulation from birth triggers constriction, independently of DNA replication processes). We indeed find them to be correlated in experimental data in all six growth conditions (SI Appendix, Table S4). Next, we use d-separation to predict correlations and conditional correlations between the cell cycle variables in graphs 5 A and B. Graph 5A predicts L_b and L_n to be uncorrelated when conditioned upon L_i, while graph 5B predicts them to be correlated. To test these predictions, we plot the residuals L_n|L_i and L_b|L_i in Fig. 5 C and D, SI Appendix, Fig. S3 A–D. We find the correlations between the residuals to be zero for the two slowest growth conditions while it is nonzero for other growth conditions (P-values in SI Appendix, Fig. S3E). We also considered the correlations r(L_b, L_n|(L_i, λ)) (SI Appendix, Table S4) and r(L_d − 1, L_n|L_i) (SI Appendix, Table S8) to control for the effects of growth rate and asymmetric divisions, respectively. The results obtained are similar to that shown in Fig. 5 C and D, SI Appendix, Fig. S3 A–D. Thus, we find graph 5A to be consistent with data in the two slowest growth conditions while graph 5B to be consistent with data in faster-growth conditions.

Next, we show that our predictions of correlations and conditional correlations using graphs 5 A and B are in agreement with the conditional correlations discussed in the previous sections. Graph 5A predicts r(L_b, L_d|L_i) to be zero, while graph 5B predicts a nonzero correlation. These predictions are identical to those of graphs 3 A and B, respectively. As previously discussed, r(L_b, L_d|L_i) is nonzero in the four faster-growth conditions while it is zero in the two slowest growth conditions. Thus, we again find graph 5A to be consistent with the two slower-growth conditions while graph 5B is consistent with the other four growth conditions. We also showed that r(L_b, L_d|L_n) = 0 in the experiments for all growth conditions. This is consistent with our predictions obtained using d-separation for both graphs 5 A and B.

To probe the molecular mechanisms that might be involved in coupling of the replication cycle to the division cycle, we used mutants that lack proteins which link the replication and division processes. The ΔzapA, ΔzapB, ΔmatP, ΔslmA, FtsK K997A, and ΔminC mutants were grown in M9 glycerol+trace elements medium with T_d = 148 min in wildtype cells (WT) (10). In this growth condition, our analysis indicated the onset of constriction is controlled by two concurrent pathways (graph 5B). If these proteins were to mediate the coupling between the replication processes and the onset of constriction then on removing these proteins in the mutants, we expect the correlation between initiation and the onset of constriction upon conditioning on birth to be zero. However, we find that the correlation r(L_i, L_n|L_b) in both the WT and mutants is non-zero except in the Min mutants which undergo polar divisions (SI Appendix, section S6). One possible explanation for the difference in the correlation r(L_i, L_n|L_b) between cells undergoing midcell and polar divisions in the Min mutants is nucleoid occlusion as proposed previously in this section and in ref. 10. According to this idea, nucleoid density at midcell blocks the formation of the Z-ring until the later stages of the replication process, thus, coupling replication and the onset of constriction while polar divisions are not inhibited by such factors and they can happen independently of replication, thus, leading to a lack of causal link between replication and the onset of constriction.

To conclude, we showed that in slow-growth conditions, replication initiation controls the onset of constriction and hence, division, while in fast-growth conditions, there are additional limiting factors.

Initiation Is Not Solely Controlled by Initiation in the Previous Cell Cycle.

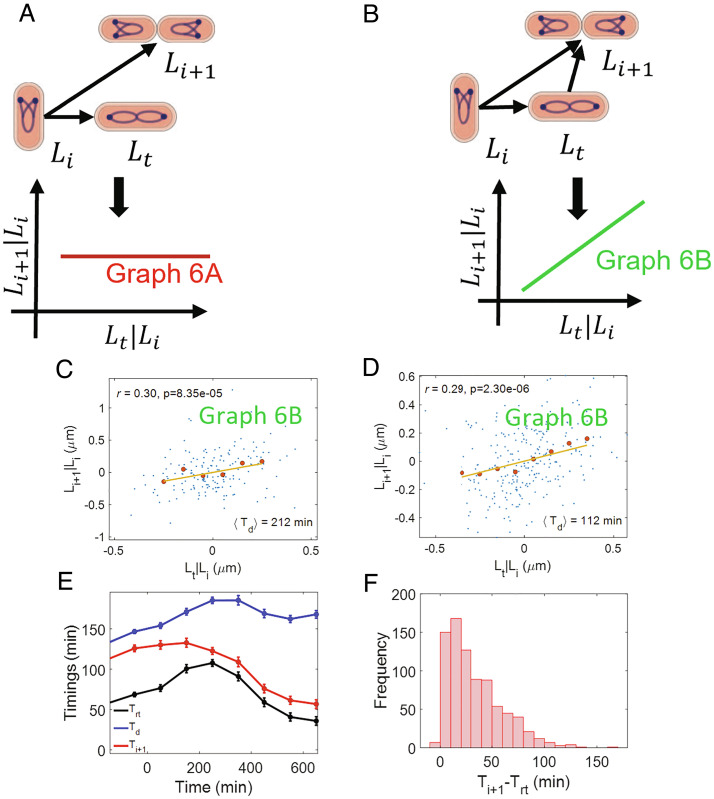
So far, we have discussed the control of the division cycle and the link between the replication and division cycle. A question that arises is what controls the DNA replication cycle. The main events in the DNA replication cycle are the initiation and termination of replication. As we discussed earlier, previous works suggested that the initiation happens via an adder per origin model (8, 9, 11, 16, 37). In the model, the initiation size per origin of the daughter cell (L_i + 1) is related to the initiation size per origin of the current cell cycle (L_i) as $L_{i+1}=\frac{L_i+{\mathrm{\Delta }}_{\mathit{ii}}}{2}+\xi$, and r(L_i, L_i + 1) is expected to be 0.5. The experimental data analyzed show the correlation to be close to 0.5 (SI Appendix, Table S7).

We also include replication termination in our model. Previous analysis suggests that termination occurs after a constant time from initiation (the C period) (11, 14), consistent with a constant speed of the replication forks as observed in single-molecule experiments (38, 39). We include this prior knowledge in graph 6A as a causal link between initiation and termination, where we denote the length at termination of DNA replication as L_t. L_i, L_t, and L_i + 1 are correlated with each other in graph 6A. These predictions are consistent with the correlations in experimental data for all six growth conditions (SI Appendix, Table S7). Furthermore, we predict that L_t and L_i + 1 will be uncorrelated upon conditioning on L_i in graph 6A. However, we find that r(L_t, L_i + 1|L_i) is nonzero in all growth conditions (Fig. 6 C and D and SI Appendix, Fig. S4 A–E and Table S7). In fact, this result is consistent with a model proposed in graph 6B which assumes that initiation in the daughter cell is also controlled by termination along with initiation in the current cell cycle. We predict using d-separation on graph 6B that r(L_i, L_i + 1|L_t) is nonzero which is consistent with our experiments. Graph 6B was also consistent with the data published in ref. 13 (SI Appendix, section S5). We also accounted for division asymmetry (=$\frac{L_b}{L_{d-1}}$) by calculating the conditional correlation $r(L_t,L_{i+1}|(L_i,\frac{L_b}{L_{d-1}}))$. We found its values close to that of r(L_t, L_i + 1|L_i) thus supporting graph 6B (SI Appendix, Table S9).

Fig. 6.

Control of replication initiation: (A) A causal graph linking the lengths at initiation per origin (L_i), termination (L_t), and the lengths at initiation per origin in the daughter cells (L_i + 1). In this graph, the initiation in the daughter cells is solely controlled by initiation in the current cell cycle. We predict r(L_t, L_i + 1|L_i) =0 for the graph. (B) A causal graph in which the initiation in the daughter cells is controlled simultaneously by initiation and termination in the current cell cycle. We predict a nonzero r(L_t, L_i + 1|L_i) for the graph. (C and D) Residuals obtained on linear regression of L_i + 1 on L_i (L_i + 1|L_i) and L_t on L_i (L_t|L_i) are plotted for (C) Alanine medium (generation time = 212 min, N = 167 cells, ⟨n_ori⟩ = 1.08). (D) Glucose medium (generation time = 112 min, N = 255 cells, ⟨n_ori⟩ = 1.98). The conditional correlation, r(L_t, L_i + 1|L_i) is nonzero for both alanine and glucose media (consistent with graph 6B). (E and F) ΔthyA cells are grown in a thymine concentration of 500 μ g/mL in M9 glycerol+trace elements medium at 28 °C. The cells are then shifted to a thymine concentration of 15 μ g/mL. Upon shifting to a lower thymine concentration, the C period of the cells increases. We measure the timings at the termination of DNA replication (T_rt) and the DNA replication initiation for the next cell cycle (T_i + 1) in multiple cells throughout the experiment (both before and after the shift). (E) Variation of timing (relative to cell birth) of termination, initiation for next cell cycle, and division are plotted. We show the binned data where the cell events’ timings are averaged in each bin based on the time when cell divides (x-axis). Time t = 0 in the x-axis represents the time when cells are shifted to the lower thymine concentration. (F) We plot the distribution of T_i + 1 − T_rt timings for all cells measured in the experiment.

To further test the model proposed in graph 6B, we use data from cells whose C period was longer as compared to the WT cells (10). This was achieved by deleting thyA and controlling the amount of thymine in the growth medium (40). ΔthyA cells grown in thymine concentrations of 500 μg/mL at 28 °C in glycerol + trace elements medium had identical replication period as WT cells. However, on decreasing the concentration to 15 μ g/mL, the C period showed a stepwise increase by approximately 40% (10). An increase in the C period may lead to termination in the current cell cycle happening after the initiation for the next cell cycle has started. Such a temporal order will violate the model presented in graph 6B where termination is a cause of initiation in daughter cells. The variation in timings at termination (T_rt), division (T_d), and initiation for the next cell cycle (T_i + 1) is shown in Fig. 6E for the ΔthyA strain. Time t = 0 on the x-axis corresponds to the time when cells were shifted to 15 μ g/mL thymine concentration. Strikingly, we find at the single-cell level that only few cells have the time T_i + 1 − T_rt ≤ 0 and it is always greater than −6 min (Fig. 6F). Since the measurement interval is 4 min, an error in the measurement of the initiation and termination events by one time frame can lead to a minimum time difference T_i + 1 − T_rt = −8 min even though the events coincide. Thus, the data are consistent with the temporal ordering of events in graph 6B even when the replication timings are perturbed. We note that graph 6B is unlikely to apply to faster-growth conditions where overlapping rounds of replication have been reported (14, 41).

To conclude, we rule out the model in which initiation in the next cycle is controlled solely by initiation in the current cycle, showing that control over replication initiation is more complex than previously thought.

Discussion

In the paper, we make use of causal inference, i.e., conditional independence tests, to interrogate cell-cycle models. An ideal cell-cycle model should be able to reproduce the joint probability density of all cell-cycle variables measured. Since the amount of data collected is finite, previous cell-cycle modeling studies have relied on using certain correlations (or lack of correlations) between cell-cycle variables to hypothesize models (6, 8, 9, 13, 17, 23, 42). The model simulations are then compared to experiments using specific correlations. The model which agrees the most with these chosen correlations is accepted as the underlying model. However, multiple models having different causal structures can agree with these limited correlations making it difficult to choose a particular causal model (20). Conditional independence tests allow us to reject models in a robust manner that do not depend on the fine-tuned details of the models but instead only relies on the structure of the causal network (i.e., which variables control which other variables). The framework relies on testing whether conditional correlations are zero or not—without resorting to their precise numerical values.

Our goal was to test several models previously proposed for the bacterial cell-cycle ranging from models in which DNA replication was assumed to control cell division to models where DNA replication cycles are independent of the cell division cycles (and a class of models interpolating the two, in which division couples not only to DNA replication but also to additional cues). Note that, generally, this framework of causal inference cannot determine the model structure de novo but rather allows us (in certain cases) to rule out particular models.

After validating our method on synthetic data, we used causal inference methods on recently obtained data measuring key cell-cycle variables (length and time of cell birth and division, initiation and termination of DNA replication, and constriction of the division ring) (10). We found that our data agreed with replication being the sole limiting factor for division in the two slowest growth conditions (Fig. 3D and SI Appendix, Fig. S1A). In faster-growth conditions, the data agreed with a model in which birth size and replication initiation size both controlled division size (Fig. 3E and SI Appendix, Fig. S1 B–D).

Although the onset of constriction has not been included in previous cell-cycle models, it can be expected to be an essential cell-cycle checkpoint in E. coli. We tested this idea using conditional correlations. We find the conditional correlations between birth and division lengths to be zero when conditioned on constriction length (Fig. 4 C and D, SI Appendix, Fig. S2 A–D). Note that we condition on the length at the start of constriction because of availability of data at that time point. However, a biochemical reaction leading to the onset of constriction may occur at some prior time close to the start of constriction (with lengths highly correlated with L_n) which may result in zero r(L_b, L_d|L_n). For example, the incorporation of one of the many proteins in the Z ring can be the limiting step. Once the protein is incorporated to form the Z ring, the constriction starts after a small time delay. The existing data are not sufficient to distinguish these molecular steps yet. Regardless of the nature of the biochemical processes, our analysis confirms that the onset of constriction controls cell-cycle progression from birth to division. Thus, including the constriction event into the cell cycle is important for theoretical and experimental studies involving cell-cycle regulation.

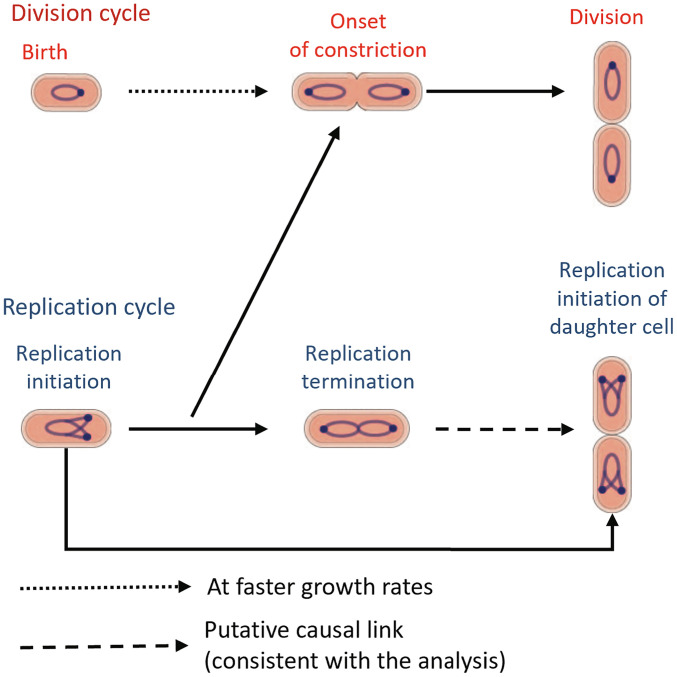
Combining these two results led us to envision a coarse-grained model for cell size regulation in which the constriction event is controlled by the DNA replication process alone in slow growth. In fast growth, the onset of constriction must be controlled by additional regulatory processes linked to cell birth and not controlling DNA replication initiation. In all growth conditions, division is downstream of the onset of constriction (Fig. 7). We corroborated the model predictions for the conditional correlation r(L_b, L_n|L_i), predicted to be zero in slow-growth conditions (Fig. 5C and SI Appendix, Fig. S3A) and nonzero in fast growth (Fig. 5D and SI Appendix, Fig. S3 B–D). An appealing molecular mechanism that explains the causal control of replication initiation over the onset of constriction is that of nucleoid occlusion, in which septum formation is blocked by a replicating nucleoid (35). The nucleoid occlusion or absence thereof at the cell poles explains the lack of correlations between replication and constriction in Min mutants undergoing polar divisions. Previous work also showed that in slow-growth conditions, increasing the DNA replication time, using mutants where external thymine levels determine the C period, delays the start of constriction (10). In both the wild-type and the thymine mutants, the constriction process does not start until the DNA density at the midcell has decreased. In fast-growth conditions, replication is not the sole limiting process, as evidenced by the nonvanishing conditional correlations. One possible additional mechanism is the accumulation of division proteins such as FtsZ (8) or cell wall precursors (7) that controls the trigger for constriction. The cell-cycle regulation model discussed here is in agreement with the models proposed in ref. 10 using correlations between the timings of different cell-cycle events. Our analysis of data in refs. 6, 8, 9 and 13 as well the analysis in ref. 13 itself are consistent with a model where the replication process becomes more limiting for determining division in the slower-growth conditions.

Fig. 7.

Schematics of the proposed cell-cycle model: In slow-growth conditions, replication-related processes, possibly nucleoid occlusion, limit the onset of constriction. In fast-growth conditions, additional processes, such as accumulation of cell division proteins, FtsZ, or cell wall precursors, might also control the onset of constriction independent of replication. Finally, the constriction process culminates in the division event. The start of the replication cycle is controlled by the replication initiation event in the previous cell cycle as well as an additional cue which is linked with the termination event.

We also studied the DNA replication cycle using the CI methodology. It has been suggested that accumulation of a threshold amount of the initiator protein DnaA in its ATP-bound form is needed to initiate DNA replication (43, 44). The accumulation starts from the previous initiation and the initiation size of the previous replication cycle controls the initiation size in the current replication cycle via an adder per origin model (9, 11, 12, 45). Furthermore, the termination of DNA replication happens after a C period elapses since the initiation (14). The adder per origin model predicts that r(L_i, L_i + 1) = 0.5. The correlations r(L_i, L_i + 1) reported in previous studies (8, 9) and observed in the experiments analyzed in this paper are close to 0.5, thus, lending support to an adder per origin model. However, such a model (Fig. 6A) would also predict that the correlation between initiation in the daughter cell and termination event when conditioned upon the initiation event in the current cell cycle is zero. We find the conditional correlations to be nonzero in all six growth conditions (Fig. 6 C and D and SI Appendix, Fig. S4 A–D). This agrees with the graph shown in Fig. 6B which suggests a more complicated model than previously thought. One possibility to explain this correlation is that the concentration of the replication initiator, DnaA-ATP, increases only after the termination of replication due to Hda-mediated regulatory inactivation of DnaA (RIDA) during the replication process ((46)). Alternatively, some replisome component other than DnaA limits replication initiation in these growth conditions. Once this replisome component becomes available after the termination, a new round of replication can start. Note that, in our paper, the validity of these results is tested at growth rates that do not necessitate overlapping rounds of replication forks (doubling times less than the C period).

The termination event was used for the conditional correlation analysis because of its availability from the experiments (10). However, we cannot rule out the possibility that other events (correlated with termination) instead of termination in graph 6B could also predict a nonzero correlation between L_t and L_i + 1 upon conditioning on L_i. However, such an event cannot be cell division. The data from almost all available growth conditions studied in the paper show that at least some initiation events can precede cell division. Such time ordering violates the causality principle. Furthermore, replication initiation can start without any division in filamentous E. coli cells (47). The presence of more than a single initiation event per cell cycle was also the basis for rejecting a cell-cycle model called the sequential adder, containing an adder from birth to initiation and another from initiation to division (15).

A possible alternative event for termination controlling the next initiation can be related to some replication-dependent conformational change within the nucleoid. It has been hypothesized that nucleoid tethered to the midcell (called the progression control complex or the PCC) inhibits both the onset of constriction and the next initiation (48). Once the cell has completed certain growth requirements, the PCC undergoes conformational changes permitting the next initiation and constriction formation to occur. These conformational changes could potentially happen at termination or close to it. If this hypothesis is correct, termination and the next initiation would be correlated upon conditioning on the initiation of the current cell cycle and as such this scenario will be able to explain the data.

It remains for future studies to determine at which growth rates the next initiation becomes uncorrelated from the previous termination event. The future studies can also identify if some conformational change in the nucleoid precedes the initiation or if there is some rate-limiting component beyond DnaA that controls the initiation. In the latter experiments, upregulation of the limiting component could shift initiation earlier and lead to disappearance of correlations.

To conclude, our analysis leads to a new cell-cycle model in E. coli linking division and replication cycles, which extends the previously developed concurrent processes model (Fig. 7). To come to this result, we used a versatile method of inference involving conditional independence tests. The technique may prove useful in analyzing and critically testing cell cycle models also in other organisms.

Materials and Methods

Obtaining Conditional Correlations.

The method used to calculate conditional correlations throughout the paper was introduced in Results. In this section, we discuss the method from a mathematical perspective.

Our aim is to calculate the correlation between variables A and B when conditioned upon variables X = {X₁, X₂, X₃...,X_n}. Here, X is a set of n variables which are being conditioned upon. Conditional correlation when conditioned upon X means finding the correlation on fixing the values of all variables in the set X. Fixing X would remove the effects of variability in X on other variables.

We use a method based on partial regression to calculate the conditional correlation (49). To achieve this, we try to find the effect of X on variables A and B. The random variables A, B, and X will correspond to cell lengths at various events in the manuscript. Since cell lengths are narrowly distributed about their means, we need to know the dependence/effects of X on A and B around their means. Hence, we can Taylor expand the nonlinear dependence of A and B on X around the means and consider terms to first order. We represent it as

$$\begin{array}{c}A={\displaystyle \sum _{i=1}^n{a}_i{X}_i+\eta },\end{array}$$ [1]

$$\begin{array}{c}B={\displaystyle \sum _{i=1}^n{b}_i{X}_i+\xi }.\end{array}$$ [2]

a_is and b_is are calculated by multiple linear regression of A on X and B on X, respectively. η and ξ capture the effects on A and B, respectively, from sources other than X, i.e., they represent variability in A and B on removing the effects of X. η and ξ are therefore the residuals obtained from the multiple linear regression of A on X and B on X, respectively. The conditional correlation between A and B when conditioned upon X (denoted as r(A, B|X)) is obtained by finding the Pearson correlation coefficient between the residuals η and ξ.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Previously published data were used for this work (10). The data analyzed in the paper can be found at https://data.mendeley.com/datasets/c8fh8jy78x.