Dissolved gases in the deep North Atlantic track ocean ventilation processes

Significance

The physicochemical transfer of gases between the atmosphere and the vast ocean interior occurs at a small number of high-latitude locations during winter months, often under extreme weather. As a result, few direct observations exist. Dissolved noble gases and their isotopes, which are chemically and biologically unreactive, are useful tools to quantify air-sea gas exchange. Here, we present high-precision dissolved noble gas data from the deep North Atlantic to evaluate gas exchange using an ocean circulation model. Our findings suggest a large role for bubble mediated-gas exchange, and our model allows us to isolate biological from physical sources of N₂ in the deep ocean, with relevance to the marine nitrogen cycle and its role in ocean carbon storage.

Abstract

Gas exchange between the atmosphere and ocean interior profoundly impacts global climate and biogeochemistry. However, our understanding of the relevant physical processes remains limited by a scarcity of direct observations. Dissolved noble gases in the deep ocean are powerful tracers of physical air-sea interaction due to their chemical and biological inertness, yet their isotope ratios have remained underexplored. Here, we present high-precision noble gas isotope and elemental ratios from the deep North Atlantic (~32°N, 64°W) to evaluate gas exchange parameterizations using an ocean circulation model. The unprecedented precision of these data reveal deep-ocean undersaturation of heavy noble gases and isotopes resulting from cooling-driven air-to-sea gas transport associated with deep convection in the northern high latitudes. Our data also imply an underappreciated and large role for bubble-mediated gas exchange in the global air-sea transfer of sparingly soluble gases, including O₂, N₂, and SF₆. Using noble gases to validate the physical representation of air-sea gas exchange in a model also provides a unique opportunity to distinguish physical from biogeochemical signals. As a case study, we compare dissolved N₂/Ar measurements in the deep North Atlantic to physics-only model predictions, revealing excess N₂ from benthic denitrification in older deep waters (below 2.9 km). These data indicate that the rate of fixed N removal in the deep Northeastern Atlantic is at least three times higher than the global deep-ocean mean, suggesting tight coupling with organic carbon export and raising potential future implications for the marine N cycle.

As a major reservoir of carbon and heat, the deep ocean exerts a fundamental impact on Earth’s climate (1–4). Global air-sea transfer of these properties is intimately tied to physical processes in the high latitudes where deep waters form. For example, the horizontal distribution of anthropogenic carbon within the ocean exhibits regional maxima in the Southern Ocean and North Atlantic, near the downwelling branches of the global meridional overturning circulation (2–4). Constraining the dynamics of deep-ocean ventilation (i.e., the physical air–sea exchange mechanisms that operate during deep water formation) is therefore key for predicting future climate change.

Despite its climatic importance, our understanding of gas exchange during deep water formation remains limited by a lack of observations. Recent advances, including airborne CO₂ observations over the Southern Ocean (5) and moored profiler O₂ measurements in the Labrador Sea (6, 7), represent promising steps that have provided opportunities to evaluate and refine physical models. However, in addition to these direct observations of air-sea fluxes at specific high-latitude sites, there exists a need for complementary observational constraints that provide broader spatiotemporal context.

Dissolved noble gases represent promising physical tracers of deep-ocean ventilation because they have a single well-characterized source—the atmosphere—and they are unmodified by chemistry or biology within the ocean. Moreover, the transport of noble gases within the ocean integrates across the short space and time scales of deep water formation, providing a climatologically useful average of highly variable conditions. The abundances and isotopic composition of dissolved noble gases in the deep ocean therefore reflect the imprint of physical air-sea exchange processes integrated across multiple deep water formation regions by circulation and mixing.

In recent years, multiple studies have demonstrated that noble gases in the deep ocean are not in equilibrium with the atmosphere (8–12), but rather exhibit a characteristic undersaturation of the heavier and more soluble noble gases (e.g., Xe) and supersaturation of the lighter and less soluble noble gases (e.g., Ne). These studies have linked solubility anomalies to various physical processes, such as rapid cooling during deep convection (8, 10) and submarine melting of glacial ice (11, 13). Here, we build upon prior work by i) introducing high-precision isotope ratio measurements to complement bulk elemental measurements and ii) comparing noble gas observations to model simulations (14, 15) to evaluate physical representations of air-sea exchange.

In this study, we present measurements of Ar, Kr, and Xe isotopic and elemental ratios from the deep North Atlantic and use these constraints to evaluate physical gas exchange parameterizations in an ocean general circulation model (GCM). Our measurements come from the Bermuda Atlantic Time Series (BATS) site (31°40 N, 64°10 W), which represents an ideal location to investigate air-sea gas exchange associated with North Atlantic Deep Water (NADW) formation, because it is located downstream of key places of wintertime deep convection. Properties of the deep ocean at BATS should therefore represent NADW formation conditions integrated over space and time by deep water transport and mixing.

Comparing noble gas observations to model simulations that implement different physical representations of gas exchange provides insight into fundamental processes and allows us to improve the parameterization of air-sea gas exchange in NADW formation regions. This, in turn, opens the door to physical simulation of other (noninert) gases in the deep North Atlantic. We demonstrate this potential through a case study to distinguish physical from biological N₂/Ar signals in the deep North Atlantic. Solubility disequilibrium of the N₂/Ar ratio has been suggested as a powerful top-down tracer of benthic denitrification, an important process that results in the addition of N₂, without Ar, to seawater (16, 17). While several studies of oxygen-deficient zones have found large (>1%) water column denitrification signals in N₂/Ar (18, 19), constraining benthic denitrification using N₂/Ar is challenging both because the signals are smaller and because N₂/Ar is impacted at the subpercent level by the same physical processes that lead to noble gas disequilibria during deep water formation. In this case study, we report N₂/Ar data from the deep North Atlantic across an east-west gradient in water mass age and combine measurements with physics-only model simulations of N₂ and Ar to resolve excess N₂ derived from benthic denitrification. Coupling excess N₂ constraints with water mass age estimates yields rate information regarding fixed N loss, with implications for the marine nitrogen cycle.

Results

Precise Constraints on Noble Gas Disequilibria.

Here we present measurements of dissolved heavy noble gas isotope ratios (⁴⁰Ar/³⁶Ar, ⁸⁶Kr/⁸²Kr, ¹³⁶Xe/¹²⁹Xe) and elemental ratios (⁸⁴Kr/⁴⁰Ar, ¹³²Xe/⁴⁰Ar) from the BATS site in the North Atlantic. Between two replicate deep casts (0 to 4,500 m) and a shallow cast (0 to 1,000 m), we collected 27 seawater samples for analysis of dissolved heavy noble gases (Dataset S1). These samples were analyzed using a technique for extraction, processing, and measurement of large samples (3 to 4 kg) via dynamic dual-inlet isotope-ratio mass spectrometry (20). These are the first Kr and Xe isotope data from the Atlantic Ocean. The precision of these measurements is considerably higher than the only two prior studies of heavy noble gas isotopes in seawater (9, 12), which laid the foundation for applying these tracers as sensitive constraints for air-sea gas exchange. Specifically, we achieved reproducibilities (1σ) of 0.007‰, 0.015‰, and 0.028‰ for dissolved ⁴⁰Ar/³⁶Ar, ⁸⁶Kr/⁸²Kr, and ¹³⁶Xe/¹²⁹Xe, respectively. The high-precision and large number of deep-ocean samples allow us to narrowly constrain the magnitude of solubility anomalies in the deep ocean at the BATS site.

Below 2 km, we find consistent heavy isotope depletion in each of these three ratios, with respect to solubility equilibrium values (Fig. 1). We report dissolved isotope ratios, δ_IR, as deviations from the well-mixed atmosphere (in ‰). Replicate-mean δ^40/36Ar and δ^86/82Kr are below solubility equilibrium at all nine depths sampled below 2 km, while δ^136/129Xe (the least precise isotope ratio) exhibits heavy isotope depletion at seven of nine depths. For elemental and isotopic ratios, we define solubility anomalies, Δ_ER (elemental ratio) and Δ_IR (isotope ratio), respectively, as deviations between measured ratios and solubility equilibrium between seawater and the atmosphere:

$$∆\equiv \frac{{\mathrm{R}}_{\mathrm{meas}}}{{\mathrm{R}}_{\mathrm{eq}\left(\theta ,\mathrm{S}\right)}}-1,$$ [1]

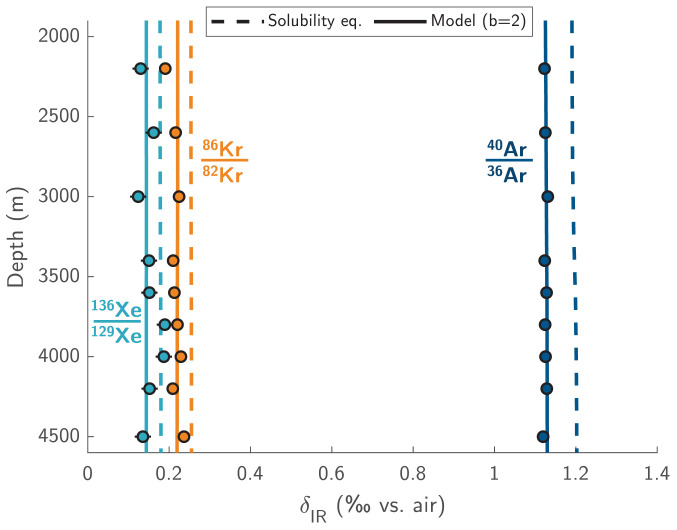
Fig. 1.

Ar, Kr, and Xe isotope ratios measured in the deep ocean at BATS show consistent heavy isotope undersaturation. Isotope ratios are reported as deviations (in ‰) from the well-mixed atmosphere. Markers show replicate-mean values and error bars indicate ±1σ analytical uncertainties (note: error bars may be smaller than markers). Dashed lines represent solubility equilibrium ratios, constrained by a compilation of published (12, 21) and experimental measurements at various temperatures and salinities. Solid lines represent model-simulated isotope ratios at BATS, using the gas-exchange parameterization of ref. 22 with a doubling of bubble-mediated gas exchange.

where R_meas is a measured isotope or elemental ratio and R_eq is the same ratio in seawater in equilibrium with the atmosphere at the measured potential temperature (θ) and salinity (S). We report Δ in units of ‰. Our ability to constrain Δ to high confidence is enabled, in part, by recent precise determinations of bulk noble gas solubility concentrations (23) and isotope ratios (12, 21). These were augmented by dozens of new air–water equilibration experiments carried out before, during, and after the BATS measurements in the same laboratory with same analytical technique (Materials and Methods). A major advantage of defining Δ for ratios, rather than gas abundances, is that it eliminates the need to conventionally assume that air–sea exchange occurs at a sea-level pressure of 1 atm, since pressure dependencies cancel in Eq. 1, leaving R_eq as a function of only θ and S.

As shown in Fig. 2, in the deep ocean (below 2 km) at the BATS site, we observe mean solubility disequilibria of −0.074 ± 0.006‰, -0.038 ± 0.009‰, and −0.026 ± 0.015‰ for ⁴⁰Ar/³⁶Ar, ⁸⁶Kr/⁸²Kr, and ¹³⁶Xe/¹²⁹Xe (±1 SE), respectively. We also observe mean Xe/Ar and Kr/Ar disequilibria of −16.3 ± 2.4‰ and −8.9 ± 0.9‰, respectively, over the same depth interval (±1 SE). These uncertainties account both for BATS sample measurement uncertainties and uncertainties in the solubility equilibrium ratios. We find remarkably close agreement between our deep BATS Δ(Xe/Ar) and Δ(Kr/Ar) measurements and previous measurements from the early 2000s (24, 25), adding confidence to these data (SI Appendix, Fig. S1 and Fig. 2). We also report a mean Δ(N₂/Ar) of 9.6 ± 1.0‰ below 2 km (Fig. 2) from a compilation of prior measurements (16, 25). Due to the inertness of N₂ and young age of deep western Atlantic waters (26–28), such that accumulation of N₂ from benthic denitrification is negligible (16), N₂/Ar provides an additional constraint on air–sea gas exchange that complements noble gas isotopic and elemental ratios.

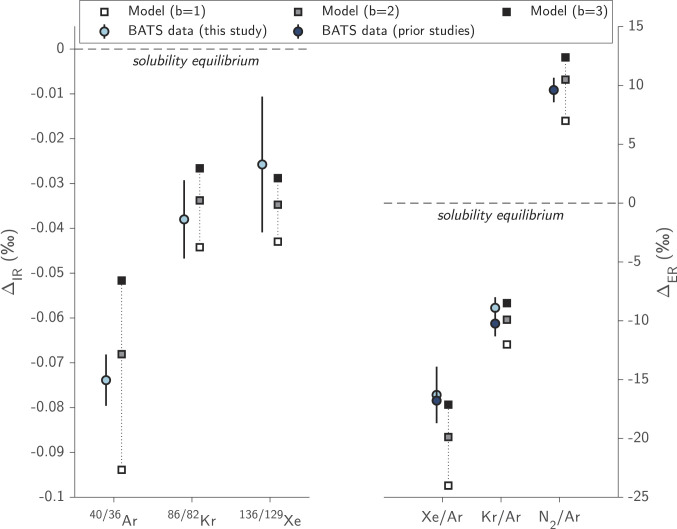
Fig. 2.

Comparison of mean deep-ocean (below 2 km) solubility anomalies measured at the BATS site with model predictions using the L13 gas exchange parameterization in which the bubble terms are multiplied by a scalar, b. Measured isotopic anomalies (Δ_IR; left-hand side) and elemental ratio anomalies (Δ_ER; right-hand side) both suggest that an enhancement of bubble fluxes is needed (i.e., b > 1), with an optimal value of b ≈ 2 compatible with five of six independent tracers. Error bars indicate ±1 SE, accounting for both measurement uncertainties and uncertainties in the solubility equilibrium values. Deep-ocean mean Δ(Kr/Ar) and Δ(Xe/Ar) values shown from this study (light blue) and ref 24 (dark blue), excluding artifactually low Δ(Kr/Ar) below −2% in ref 24. Modeled Δ(N₂/Ar) is compared with the below 2-km mean of published Δ(N₂/Ar) measurements from the BATS site (16, 25).

Inert Gas-Enabled GCM Simulations.

To evaluate observations of deep-ocean solubility disequilibria at BATS, we performed a set of ocean GCM simulations in which air-sea fluxes of Ar, Kr, Xe, N₂, and their isotopes were parameterized according to a diffusive- and bubble-mediated gas exchange formulation [(22); hereafter “L13”]. These simulations were carried out using the UVic Earth System Climate Model (29), which has a 1.8° latitude × 3.6° longitude grid with 19 vertical ocean layers, with preindustrial era boundary conditions and Coordinated Ocean Research Experiments version 2 (CORE-2) climatological surface wind fields (30). We apply the transport matrix method (31) for efficient offline simulation of dissolved gas tracers, using a modified version of an existing gas exchange toolbox (14, 15, 32, 33). Specifically, we updated the gas exchange toolbox to include Ar, Kr, and Xe isotopes and used the latest measurements of bulk gas and isotopic solubility and diffusivities (12, 21, 23). Given that noble gases are conservative tracers (i.e., lacking sources or sinks within the ocean interior), we assume that the simulated noble gas composition of the ocean interior is set by air-sea gas exchange influenced by physical conditions at the time and place of deep water formation. The transport of noble gases in the deep North Atlantic, which may vary between GCMs, is therefore likely to have little impact on the magnitude of noble gas saturation anomalies.

We carried out three separate sets of simulations with varying extents of bubble-mediated gas exchange. Following ref. 34, we adapted the L13 gas exchange parameterization to include a scalar, b, that enhances or diminishes bubble flux contributions to net gas exchange F_net:

$$F_{net} = F_S+ b (F_C + F_P),$$ [2]

where F_S, F_C, and F_P refer to surface diffusion, complete (small) bubble dissolution, and partial (large) bubble dissolution fluxes, respectively (22). In each simulation, dissolved N₂ and noble gases and their isotopes were integrated to steady state, and results in the model below 2 km near BATS were compared with observations (Fig. 2). Simulations were performed with three different values of b, namely, 1, 2, and 3.

We find that all deep-ocean measurements from BATS require an enhancement of bubble-mediated gas exchange, i.e., b > 1. Five of the six gas or isotope ratio anomalies are compatible with a doubling of the L13 bubble-flux terms. A possible explanation why measured Δ(Xe/Ar) values plot slightly above the b = 2 prediction is the representation of diapycnal mixing in the model. Mixing leads to greater supersaturation of Xe compared with any other gas considered in this study (23, 35, 36) due to the greater curvature of its solubility temperature dependence [e.g., the ratio of curvature between Xe and Ar solubility functions is ~2; (23)]. The slight Δ(Xe/Ar) disagreement with the model thus suggests a lower rate of mixing in the model than in reality. We also compared the L13 (b = 2) model simulations with additional simulations carried out with two other common diffusive- and bubble-mediated gas parameterizations (15, 37), finding that the L13 (b = 2) model exhibited closer agreement with BATS data (SI Appendix, Fig. S2). Given the physical basis of the L13 model and its performance in reproducing BATS data, the remainder of this study is focused on simulations using the L13 model with b = 2.

Discussion

Tracking the Origins of Inert Gas Disequilibria.

At the BATS site, these observations of undersaturation of heavy noble gas isotopes, Kr/Ar, and Xe/Ar, along with N₂/Ar supersaturation in published measurements (16, 25), together provide constraints to evaluate gas exchange parameterizations (Fig. 2) and explore fundamental physical mechanisms. The BATS site is situated in an ideal location for the interpretation of deep inert gas anomalies as faithful recorders of physical properties of NADW formation. Another advantage of focusing on the deep North Atlantic is that mean air-sea gas exchange conditions are reasonably well represented by modern climatological sea ice and wind fields, unlike the Southern Ocean where submarine glacial meltwater also likely impacts noble gases (11, 13), and the Pacific where present-day deep waters were formed up to two millennia before present under relatively unknown sea-surface conditions (38, 39).

The observed relative supersaturation of less soluble gases (e.g., N₂ relative to Ar) and undersaturation of more soluble gases (e.g., Xe relative to Ar) can be linked to i) bubble injection, ii) rapid cooling of the mixed layer, and iii) diffusive exchange through both the air–sea interface and large bubbles, as has been suggested by prior studies (8–10, 12, 40). Bubble injection by breaking waves leads to greater supersaturation of less soluble gases (37, 40–42). Rapid cooling incompletely restores gas concentrations to solubility equilibrium before deep water formation (8, 10). These cooling and bubble-induced disequilibria, which are preserved in the deep ocean, are enhanced by the slower diffusive exchange of the heavier noble gases (e.g., Xe and Kr) relative to the lighter gases (43) across the air-sea interface or in large bubbles. Previous idealized representations of noble gas disequilibria (10, 12, 42, 44) have, for simplicity, considered these mechanisms in isolation (or assumed they are linearly additive). These idealized approaches have either examined i) the instantaneous effect of each process (e.g., bubble injection without subsequent diffusive gas exchange), or ii) a quasi-steady state in which an individual process (e.g., bubble injection, or a cooling-driven solubility increase) is balanced by diffusive gas exchange such that the disequilibrium, Δ, for a single gas is constant in time. By convention, these single-process models also consider the impact of a mechanism acting on a mixed layer initially in equilibrium with the atmosphere (i.e., Δ = 0). Previous idealized models have been used to identify the key processes at play, and our study builds upon them in several important ways. First, the addition of noble gas isotope ratios provides a complementary set of independent constraints with unique sensitivities to these processes (12, 21). Second, the use of ratio anomalies (Eq. 1), rather than single gas anomalies, eliminates the influence of (unknown) barometric pressure anomalies during deep water formation on measured deep-ocean disequilibria. Third, by using a GCM instead of idealized single-process models, our simulations consider the impacts of multiple processes (e.g., bubble injection, rapid cooling) acting on a dynamic, seasonally varying ocean, circumventing the need to assume an initially equilibrated sea-surface saturation state prior to deep water formation.

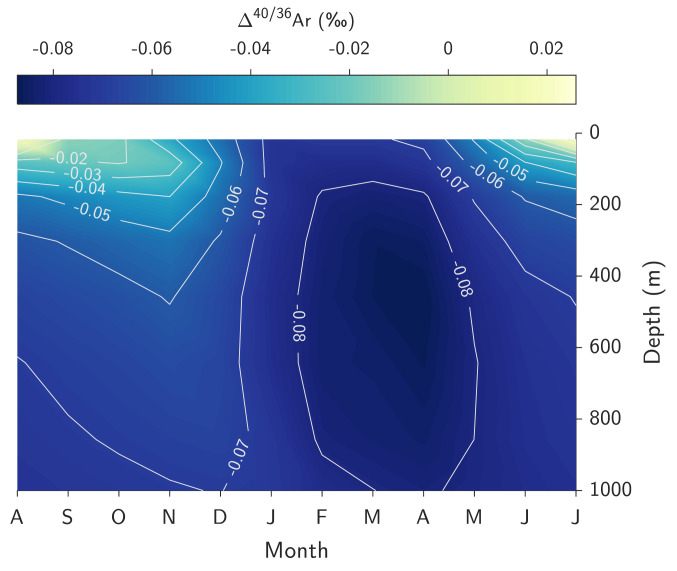
As an example of the insight gained from these simulations, Fig. 3 shows the modeled seasonal evolution of Ar isotope solubility disequilibrium in the Irminger Sea (60 to 65°N, 30 to 40°W). In this simulation, with an enhanced bubble flux constrained by deep BATS noble gas measurements (i.e., b = 2 in Eq. 2), we find a large amplitude of upper ocean Δ^40/36Ar in the Irminger Sea (0 to 35 m), varying by ~0.098‰ over the course of a year (SI Appendix, Fig. S3). Notably, we find similar patterns of seasonal disequilibria for Kr and Xe isotopes (SI Appendix, Figs. S4 and S5); however, here we focus on Ar for simplicity. In the summertime, radiative warming of the mixed layer and bubble injection both lead to supersaturation, which drives a net sea-to-air flux of Ar, leading to heavy-isotope enrichment in seawater owing to the slower diffusion of ⁴⁰Ar relative to ³⁶Ar (21, 45, 46). Conversely, during winter, cooling of the mixed layer increases noble gas solubilities, driving a net air-to-sea flux of Ar that induces the opposite sense of kinetic Ar isotopic fractionation due to diffusion (i.e., lowering the ⁴⁰Ar/³⁶Ar ratio due to faster diffusive ingassing of ³⁶Ar). This kinetic fractionation is accomplished by diffusion across both the air-sea interface and the large bubble-water interface. Notably, the minimum simulated surface Δ^40/36Ar (−0.073‰), which is sustained throughout wintertime deep water formation, closely matches the mean Δ^40/36Ar observed in the deep ocean at BATS (−0.074‰; SI Appendix, Fig. S3). This is consistent with the notion that the deep BATS inert gas composition accurately records information about air-sea gas exchange during NADW formation.

Fig. 3.

Simulated seasonal evolution of Ar isotope solubility disequilibrium (Δ^40/36Ar) in the Irminger Sea (area-weighted mean of model grid cells between 60 to 65°N and 30 to 40°W). Bottom axis tick labels are month name abbreviations consecutively from August through July. Simulations were performed using the L13 gas exchange parameterization with b = 2 (Eq. 2). Higher Δ^40/36Ar in the upper Irminger Sea during summer reflects kinetic fractionation associated with net air-to-sea gas exchange, whereas lower Δ^40/36Ar in the surface ocean (and propagating to depth due to deep convection) results from preferential in-gassing of ³⁶Ar relative to ⁴⁰Ar due to diffusion across air–sea and bubble–water interfaces.

Our measurements and model simulations together provide evidence in support of large bubble-mediated gas fluxes in the high-latitude North Atlantic (6, 7) and indicate that air-to-sea diffusion (across both bubbles and the sea surface), induced by wintertime upper ocean cooling, is key to driving heavy noble gas undersaturation in the deep ocean (8–10, 12). In the Southern and Pacific Oceans, we suspect that melting of glacial ice (specifically, the latent cooling and air injection associated with it) at depth may also contribute to noble gas disequilibrium (11, 13, 15). It is also important to note that at cold wintertime temperatures in regions of deep water formation, the kinetic fractionation associated with diffusive gas transfer across the air-sea interface and in large bubbles dominates the observed isotopic disequilibria. However, at warmer temperatures, and correspondingly higher specific humidity above the air–sea interface, fractionation due to the evaporative water vapor flux from the sea surface can be important (12). Our model accounts for this effect (Materials and Methods), and model-data agreement also remains consistent in the upper ocean (Dataset S1), although it is beyond the focus of this study. We also note that in other parts of the deep ocean with older mean ages, inert gas solubility disequilibria may in part reflect temporal shifts in deep water formation conditions during different climate periods. Thus, even though the observed Ar and Kr isotope disequilibria at BATS appear to agree in sign and approximate magnitude with recent measurements in the North Pacific (12), we caution against interpretation of Atlantic-Pacific differences. Instead, the focus of the present study is solely the deep North Atlantic, where the young ages of deep water allow for a more direct interpretation with respect to present-day NADW formation conditions.

These deep North Atlantic noble gas constraints have key implications for the rate of air-sea transfer of biogeochemically important gases like O₂, with particular relevance to the parameterization of physical gas exchange in models. For example, for a hypothetical scenario (SI Appendix, Table S1) in the wintertime North Atlantic with strong 10-m winds (20 m s⁻¹), 2 °C temperature, 35 psu salinity, and a 3% undersaturation of O₂ (i.e., C/C_eq = 0.97, driven both by cooling and entrainment of low O₂ waters), bubble-mediated gas exchange (F_P and F_C) represents ~91% of the net air-to-sea O₂ flux (Eq. 2) in the L13 (b = 2) parameterization. Partial (large) bubble dissolution (F_P) represents ~74% of the total flux, ~17% is accomplished via complete (small) bubble dissolution (F_C), and the remainder of air-sea exchange occurs through surface diffusion (F_S). By comparison, in this hypothetical scenario (SI Appendix, Table S1), ~84% of gas exchange in the L13 (b = 1) parameterization is accomplished via bubbles, while bubble-mediated exchange accounts for ~26% and ~58% of total gas exchange in the N16 (15) and S09 (37) parameterizations, respectively. Among these parameterizations, the simulation implementing L13 (b = 2) is in closest agreement with BATS noble gas data (SI Appendix, Fig. S2). The greater proportion of complete-to-partial bubble dissolution under the S09 parameterization (relative to L13) leads to weaker isotopic fractionation than observed in the deep North Atlantic (SI Appendix, Fig. S2). Notably, the net O₂ flux increases by 84% by doubling bubble fluxes in the L13 parameterization (SI Appendix, Table S2), consistent with a recent study in the Labrador Sea that showed the L13 model to underestimate the net air-to-sea O₂ flux by roughly half (6).

Importantly, the sensitivities of different gases to bubble-mediated exchange vary widely. To first order, bubble sensitivity is inversely proportional to solubility and can vary among common dissolved gas tracers by two orders of magnitude between a relatively insoluble gas (e.g., SF₆) and a more soluble gas (e.g., CO₂) (SI Appendix, Table S2). This study thus highlights the importance of explicitly considering bubble-mediated exchange in gas exchange parameterizations, especially partially dissolving bubbles, which dominate the total bubble flux in the L13 parameterization (22). Formulations of gas exchange that neglect separate bubble terms (e.g., parameterizations with a single diffusive term) could lead to large errors if extrapolated between less soluble and more soluble gases in windy regions with large bubble fluxes. Additionally, this study provides evidence that bubble-induced supersaturation is an important component to quantify when using SF₆ as a transient tracer of ocean circulation and water mass age (10, 47). For more soluble transient tracers such as chlorofluorocarbons (CFCs; SI Appendix, Table S2), these findings indicate that cooling-induced undersaturation should dominate bubble-induced supersaturation, in line with a recent study in the Labrador Sea (10). We suggest that implementation of SF₆ and CFCs into circulation models that utilize the updated L13 gas parameterization – which includes separate bubble-mediated exchange terms – would improve determination of initial air–sea disequilibria, which is critical for the application of these tracers.

These findings may also aid in future efforts to refine the formulation of gas exchange parameterizations. A recent study involving in situ N₂ observations in the North Pacific found that bubble flux estimates using the L13 parameterization were overpredicted by a factor of ~2.7 (34). If the L13 model under-predicts bubble fluxes in this study (windier wintertime high-latitude North Atlantic), but overpredicts bubble fluxes in the less windy mid-latitude North Pacific (34), this raises the possibility that the single correction factor (b in Eq. 2) proposed by ref. 34 is insufficient at all wind speeds, specifically that the exponential dependence of L13 bubble flux terms on wind speed may be too small. We propose that a correction of the form F_net = F_S + b₁(F_P + F_C)·u^b2 may offer a unified solution, where u is 10 m wind speed and b₁ and b₂ are tunable parameters. As a (nonunique) example, if b₁ = 1.3 × 10⁻³ and b₂ = 2.45, this correction would decrease the bubble flux by a factor of 2.7 for ~10 m s⁻¹ winds (in line with ref. 34) while increasing bubble flux by a factor of 2.0 for ~20 m s⁻¹ winds that are characteristic of NADW formation conditions (in line with our findings). While our study raises the possibility that global bubble-mediated gas fluxes are more sensitive to wind speed than previously thought, broader spatial data are needed to test this hypothesis. We also note that temporal resolution of wind-speed data products may also play a role, although we do not expect that differences between the 6-h resolution of winds and 3-h resolution of North Pacific N₂ observations used in this study (34) can explain the large differences in implied bubble fluxes. We suggest that future in situ measurements of gas fluxes in both windy and less windy regions, along with new measurements of noble gases and their isotopes in the surface ocean, would together provide additional insight into the wind speed dependence of bubble-mediated gas exchange.

Case Study: Disentangling Physical from Biogeochemical N₂/Ar Signals.

As an example of the insight gained from the implementation of a relatively insoluble gas into an ocean circulation model equipped with a noble gas-informed gas exchange parameterization, we present a case study in which N₂ is simulated as a physical tracer in our model. In this case study, we explore deep North Atlantic variability in N₂/Ar, using our physics-only simulations to isolate biogeochemical signals (Dataset S1). We present high-precision measurements of Δ(N₂/Ar) from 15 locations throughout the deep North Atlantic (SI Appendix, Fig. S6), measured in aliquots of gas from archived dissolved gas tanks from the eastern and western North Atlantic (between ~11°W and ~70°W) below 2,900 m that were originally collected in 1981 as part of the Transient Tracers in Oceanography North Atlantic (TTO/NAS) study. These dissolved gas samples were extracted at sea using a vacuum degassing apparatus with ~98% extraction efficiency for O₂ (48, 49). By measuring Δ(Kr/Ar), we were able to apply a physical correction to measured Δ(N₂/Ar) for fractionation associated with degassing (Materials and Methods). We validated the correction method by analyzing pairs of duplicate tanks from the same locations, finding that the correction reduces the root-mean-squared-deviation of Δ(N₂/Ar) from 4.9‰ to 0.4‰ (Materials and Methods).

By comparing these Δ(N₂/Ar) measurements to GCM simulations in which N₂ is treated as a fully abiotic tracer, we can gain insight into biological sources of N₂. At the locations of the 15 samples, we find remarkable consistency in modeled physics-only Δ(N₂/Ar) (SI Appendix, Fig. S7). Specifically, we find a mean simulated Δ(N₂/Ar) of 10.2 ± 0.8% (2σ) across these 15 locations, in close agreement with BATS Δ(N₂/Ar) measurements from below 2 km (9.6 ± 1.0%; Fig. 2). This provides a strong foundation upon which to interpret Δ(N₂/Ar), suggesting that values above this consistent baseline value are indicative of N₂ addition from a biological source. As shown in Fig. 4, we observe a positive linear correlation (r = 0.84) in Δ(N₂/Ar) with water mass age (26, 27), consistent with gradual accumulation of excess N₂ in the deep ocean. We also find inverse correlations with dissolved O₂ (SI Appendix, Fig. S8) and N* (SI Appendix, Fig. S9; N* = excess nitrate, relative to phosphate) and a positive correlation with longitude (SI Appendix, Fig. S11).

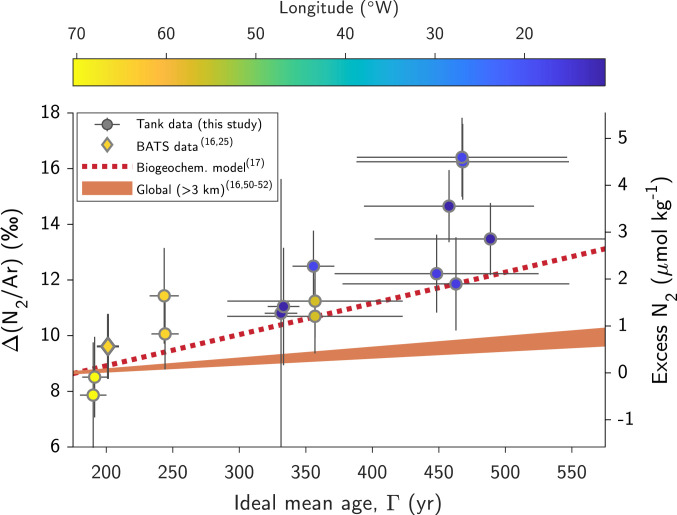
Fig. 4.

Spatial (increasing eastward) and temporal (increasing with time) trends in Δ(N₂/Ar) in the deep North Atlantic suggest a high rate of benthic denitrification, equal to or in excess of that suggested by a biogeochemical model (17) evaluated at the sample locations (dashed red line of best fit to model data, SI Appendix, Fig. S12). Circles represent TTO/NAS tank measurements from the deep North Atlantic (below 2.9 km) and diamond indicates the mean of deep BATS measurements (16, 25). Orange-shaded region shows global-mean rate estimates below 3 km (16, 50–52). Ideal mean ages reflect the mean of two inverse model estimates (26, 27) and X error bars indicate the spread between these estimates, while Y error bars indicate 95% CIs of Δ(N₂/Ar) based on analytical uncertainties (measurements and corrections). The second (Right) Y-axis shows apparent excess N₂ concentrations determined by comparing measurements to physics-only model Δ(N₂/Ar) in the deep North Atlantic, as described in the main text.

We employ a Monte Carlo approach to determine an apparent Δ(N₂/Ar) rate of change of 18.2 to 35.7‰ kyr⁻¹ (95% CI), considering analytical uncertainties and multiple estimates of ideal mean age (26, 27) at our sample locations (Materials and Methods). This rate is somewhat higher than the 11.2 ‰ kyr⁻¹ rate suggested by a recent biogeochemical modeling study [(17); SI Appendix, Fig. S12)], and well above the 2.5 to 3.9‰ kyr⁻¹ range based on global estimates of sedimentary denitrification rate below 3 km (16, 50–52). We suggest that the observed excess N₂ in the deep North Atlantic is primarily attributable to a high regional rate of benthic denitrification, such that exchange between the deep ocean and sedimentary pore waters (in which O₂ is consumed and N₂ is produced) acts to increase N₂ and reduce O₂ concentrations in the eastern North Atlantic. It is possible that a ~10% east-west difference in Antarctic Bottom Water fraction in the deep North Atlantic (28) may explain up to ~1‰ of the ~5‰ observed east-west difference in Δ(N₂/Ar), due to a glacial meltwater signal not captured by the model [(16); SI Appendix, Fig. S13]. Another possibility is that some portion of the observed temporal trend in Δ(N₂/Ar) reflects a paleoclimatic change in NADW formation conditions since the Little Ice Age (LIA). However, enhanced sea ice during the LIA would likely act to suppress bubble fluxes (producing the opposite temporal trend in Δ(N₂/Ar) to the one we observe), and the magnitude of the apparent LIA-to-present change (~5‰) suggests twice the amount of total disequilibrium, which is unlikely given that the LIA was a rather mild climate excursion (53). Thus, while we urge caution in interpreting the higher range of our estimated Δ(N₂/Ar) rate of change, our analysis provides independent evidence suggesting that the rate of benthic denitrification in the deep North Atlantic is at least three times higher than the global deep-ocean rate, in line with the biogeochemical model results (17).

The enhanced rate of benthic denitrification we observe in the deep North Atlantic supports the conceptual foundation underpinning the benthic denitrification transfer function derived by ref. 54 and the biogeochemical model of ref. 17, namely that benthic denitrification is controlled by the rain rate of particulate organic carbon (POC) to the seafloor and, to a lesser extent, bottom water O₂ and NO₃^- concentrations (17, 50, 51, 54). Although high-bottom water O₂ and low-bottom water NO₃^- in the deep North Atlantic are not considered favorable conditions for benthic denitrification, the overlying North Atlantic subpolar gyre is a region of high POC rain rate (54), which drives the relatively high rate of deep North Atlantic benthic denitrification in the parameterization employed by the biogeochemical model (17, 54). Because the oceanic fixed N budget regulates global marine productivity and thereby impacts the sequestration of atmospheric CO₂ by the biological pump (55), it is important to refine our understanding of the rate and spatial variability of fixed N loss from the global ocean. While the long-term global marine fixed N budget appears to be in balance based on N:P ratios (56, 57) and foraminifera-bound N isotope evidence for tight coupling between N₂ fixation and denitrification (58), it remains an open question as to how quickly inherent stabilizing feedbacks (59, 60) might compensate short-term changes driven by human activities. The residence time of fixed N in the ocean is ~2.5 to 3 kyr (61), suggesting that observations indicating a balanced preindustrial era fixed N budget do not preclude the possibility of substantial changes over the past few centuries (62). The global marine N cycle is unquestionably being altered by anthropogenic activities (63), as riverine and atmospheric input of fixed N to the ocean have substantially increased over the last century (64, 65). Since the North Atlantic contains the youngest deep water in the ocean, we suggest that it is the most likely region in which the fingerprint of an anthropogenic increase in benthic denitrification might be detected. Thus, this case study opens the door to future efforts to combine N₂/Ar, noble gases, and GCM simulations to provideindependent constraints on the magnitude and spatial variability of benthic denitrification within the deep North Atlantic, with implications for possible anthropogenic perturbations to the global fixed N budget. In particular, these findings demonstrate how noble gas constraints on bubble-mediated gas exchange are critical for properly understanding the physical disequilibrium of the N₂/Ar ratio, and thereby disentangling biogeochemical signals, since N₂ and Ar are both relatively low solubility gases (SI Appendix, Table S2) and therefore highly sensitive to the large bubble fluxes that are characteristic of deep water formation conditions.

Conclusions

The physical mechanisms of air–sea gas exchange during deep water formation play a key role in Earth’s climate system and impact inventories of climatically and biogeochemically important gases in the deep ocean. In this study, we have combined high-precision measurements of noble gases with tracer-enabled GCM simulations to evaluate physical mechanisms of gas exchange in the North Atlantic. Our findings have implications for the role of bubble-mediated gas exchange under the turbulent upper ocean conditions representative of wintertime deep water formation in the high northern latitudes, suggesting that the role of bubbles in enhancing air-sea gas exchange, especially for sparingly soluble gases like O₂, N₂, and SF₆, has been underappreciated (6, 7). Our noble gas validated model simulations also present a unique opportunity to disentangle physical from biological signals in the deep North Atlantic, exemplified by the N₂/Ar case study that represents the first detection of benthic denitrification in the North Atlantic using this technique. Our findings corroborate estimates of enhanced benthic denitrification in the deep Northeastern Atlantic from a recent biogeochemical modeling study (17), and thus provide independent support for the parameterization of benthic denitrification based on POC fluxes in biogeochemical modeling. Combining measurements of noble gas isotopes, elemental ratios, and biogeochemically important gases (e.g., N₂) with tracer-enabled modeling represents a promising approach to rigorously disentangle physical from biogeochemical signals and thereby provide insight into relevant processes.

Materials and Methods

Dissolved Noble Gas Sampling and Analysis.

We collected 27 ~ 3.5-L seawater samples on BATS cruise 10391 (30 Apr 2022 – 05 May 2022) between the surface and ~4,500 m on three separate casts at the BATS site (31°40 N, 64°10 W). Samples were collected by filling evacuated 6-liter stainless steel canisters with ~3.5 kg of seawater subsampled from 12-L Niskin bottles. Prior to sampling, Tygon® tubing was attached the Niskin bottle and flushed before connecting directly to the sample canister. Upstream of the sample, a valve was then opened (connected in line with a tee) to purge any air and ensure a direct, bubble-free connection between the Niskin bottle and sample canister. The sample was then collected by opening the canister valve (Swagelok SS-4H bellows-sealed valve) until the sample weight was ~3.5 kg, after which point the valve was closed, and the neck above the valve was flushed with deionized water and capped. In the Seltzer Lab at Woods Hole Oceanographic Institution (WHOI), samples were weighed and placed on a shaker table (at 45 rotations per minute, to agitate without bubble formation) in an isothermal chamber for a minimum of 3 d to equilibrate the sample headspace with dissolved gases, before samples were drained (leaving ~0.1 kg), and the headspace was analyzed, following a similar established technique for smaller dissolved gas samples (66). Corrections were made for the dissolved Ar, Kr, and Xe left behind during draining, as well as the small amount of water that was not drained, using the latest isotopic equilibrium fractionation factors, including dozens of recent air–water equilibration experiments that add to the measurements of ref. 21, and bulk gas solubility functions (23). Following ref. 20, samples were processed by first passing through a water trap at ~−95 °C and then gettering using Ti sponge at 900–1,000 °C to remove all reactive gases. Samples were analyzed for Ar, Kr, and Xe isotopic and elemental ratios using a Thermo MAT 253 Plus. Following ref. 20, we empirically corrected for matrix effects, using correction factors determined through an optimization routine to maximize agreement of measured air-equilibrated water samples with published solubility equilibrium values. The uncertainties associated with these matrix corrections are included in the final uncertainties reported in this study. Before, during, and after the BATS measurement campaign, air standards and air-equilibrated water standards were processed and analyzed following an identical methodology. We observed excellent reproducibility air and water standards. For δ^40/36Ar (the most susceptible of measured ratios to gas handling errors), we observed a SD of 0.006‰ across air standard measurements (six before the campaign, four during the campaign, and three after the campaign). In air-equilibrated deionized water samples (22.6 °C) prepared before the BATS campaign, stored for an equivalent period of time to BATS samples, and analyzed immediately before and after BATS samples, we observed δ^40/36Ar of 1.017‰ (before) and 1.015‰ (after), both within 1σ of the solubility equilibrium value (1.022‰).

GCM Simulations.

In this study, we simulated air-sea exchange and ocean transport of ⁴⁰Ar, ³⁶Ar, ⁸⁶Kr, ⁸²Kr, ¹³⁶Xe, ¹²⁹Xe, and N₂ using the transport matrix method (TMM), which facilitates efficient offline tracer simulations (31, 67, 68). Our study uses monthly mean ocean circulation transport matrices and forcing fields from a configuration of UVic ESCM (version 2.9) representing preindustrial conditions (69). Briefly, the UVic ESCM has a 1.8° × 3.6° × 19 vertical layer ocean coupled (in terms of energy and moisture) to an atmosphere, dynamic sea ice model, and land surface model (29). Our TMM simulations couple the circulation to a physical air-sea gas exchange model (14, 15) that solves for net diffusive- and bubble-mediated gas exchange between surface grid cells and a well-mixed atmosphere. We use the L13 gas exchange parameterization (22), with bubble fluxes modified by a scalar b as in Eq. 2, following ref. 34. Model simulations were forced with an annual cycle of 6-h surface winds from the CORE-2 dataset (30), and monthly mean sea ice area fraction, temperature, and salinity from UVic ESCM. Transport matrices and forcing fields were linearly interpolated to the current time step before being applied. In total, we carried out three sets of model experiments for varying bubble flux scalars b = 1, 2, or 3. For each gas tracer and each model experiment, we first initialized the tracer field at solubility equilibrium (at the potential temperature and salinity of each grid cell) and then ran the simulation for 8,000 y to steady state. All data reported in this study are either monthly mean or annual-mean results from the final year of these simulations.

To implement gas exchange using the L13 parameterization, we use modified a version of an existing gas exchange toolbox (15, 32) with updated solubility functions for noble gas isotopes and bulk concentrations (12, 21, 23) and diffusivity ratios for noble gas isotopes in water (12). We refer the reader to ref. 22 for the full set of equations for diffusive- and bubble-mediated gas exchange. The model includes the effect of steady-state kinetic fractionation of gases in the air-side molecular sublayer due to diffusion against a constant flux of water vapor evaporating from the ocean surface, as parameterized by ref. 12. At BATS, during deep-water formation, we assume a relative humidity of 2 m air of 75% based on 1959 to 2021 mean ERA5 reanalysis data (70), averaged between Nov and Mar (SI Appendix, Fig. S14). As described in ref. 12, the water-vapor flux kinetic fractionation effect is large for warmer upper ocean waters, but smaller (though still important) for colder waters relevant for deep-ocean ventilation. For example, for Δ^40/36Ar, Δ^86/82Kr, and Δ^136/129Xe, at 2 °C, the water-vapor flux effect at 75% relative humidity is −0.029‰, −0.007‰, and −0.005‰, respectively. Its effect on ΔXe/Ar and ΔKr/Ar is negligible relative to the magnitude of disequilibria (e.g., −0.06% for ΔXe/Ar at 2 °C), and the isotopic effect is not strongly dependent on the assumed relative humidity (e.g., between 75% and 80% relative humidity, the effect changes most for Δ^40/36Ar, but only by 0.006‰).

Analysis of TTO/NAS Dissolved Gas Tanks.

The stored tanks of dissolved gas analyzed in this study were originally collected from the North Atlantic in 1981 via the TTO/NAS program by degassing 250 L Gerard barrels at sea (48). While the original purpose of these dissolved gas sample extractions was the measurement of ⁸⁵Kr, many tanks were never analyzed and have remained carefully stored since their original collection. In this study, we measured 15 archived TTO/NAS tanks that had not previously been analyzed, from a total of six TTO/NAS stations throughout the North Atlantic (SI Appendix, Fig. S6). These samples were collected at depths between 2,946 and 5,442 m. Aliquots from stored gas tanks were analyzed in the Seltzer lab at WHOI using two instruments: i) Noble gas ratios were measured in ~35 mL aliquots of dissolved gas that were quantitatively gettered, following the same analytical procedure and MAT 253 Plus IRMS that was used for BATS dissolved gas measurements (20), and ii) N₂/Ar and O₂/Ar ratios in ~2 mL aliquots were measured on a Thermo MAT 253 IRMS following a similar method, but without gettering. Specifically, these ~2 mL aliquots were quantitatively transferred into dual-valve dip tubes by submerging the bottom compartment of the dip tubes, containing molecular sieve 13X, in liquid N₂. After allowing a minimum of 3 h at room temperature for N₂, O₂, and Ar to desorb and equilibrate within the dip tube body, the bottom valve was closed, and the sample was analyzed. Measured elemental ratios were normalized to the mean of atmospheric air measurements, which were processed and analyzed identically to TTO/NAS. Across replicate TTO/NAS measurements, we achieved a 1-σ reproducibility (i.e., pooled SD) of 0.72‰ for N₂/Ar and 0.48‰ for O₂/Ar. As an independent check on our noble gas measurements, we also analyzed tanks for noble gas elemental ratios in the Jenkins lab at WHOI, using a static mass spectrometer (71), finding a root-mean-squared deviation between the two labs for Kr/Ar and Xe/Ar of 2.4% and 2.0%, respectively. The uncertainties are nearly identical to the expected joint uncertainty (i.e., quadrature sum) of the individual analytical techniques. To test for sample integrity, we analyzed O₂/Ar ratios and compared against shipboard measurements of O₂ saturation. We find close agreement between original dissolved O₂ measurements (% saturation, from 1981) and Δ(O₂/Ar) measured in aliquots of stored gas in 2022 (SI Appendix, Fig. S15), indicating that these samples are well preserved.

For the purposes of our study, it is critical to correct for fractionation of N₂/Ar ratios due to slight (order 1%) extraction incompleteness from the at-sea degassing method (48). To do so, we make use of the fact that Δ(Kr/Ar) is remarkably constant in the deep North Atlantic throughout the study area (e.g., the SD of modeled Δ(Kr/Ar) at the locations of the 15 deep TTO/NAS samples is 0.08%, SI Appendix, Fig. S7). As a result, we posit that measured variability in Δ(Kr/Ar) across these 15 deep TTO/NAS samples reflects varying extents of kinetic fractionation due to extraction incompleteness, providing a useful tool with which to correct Δ(N₂/Ar) measurements. Here, we describe the physical basis for this correction and evaluate its robustness.

The fractionation induced by extraction incompleteness is controlled by the relative diffusive degassing rates of different gases. The diffusive flux of a gas is proportional to its gas transfer velocity and inversely proportional to its solubility (defined here as the equilibration concentration ratio between dissolved and free gas phases). For deep-ocean samples (temperature ~2 °C, salinity ~35), the ratio of N₂ to Ar gas transfer velocities (assuming a turbulent air–water interface in the degassing chamber) is 0.835 (43) and the inverse ratio of N₂ to Ar solubilities is 2.306 (72). Consequently, to first order, we expect that N₂ degasses ~1.926 times faster than Ar (i.e., 0.835 × 2.306 ≈ 1.926). We expect Kr, on the other hand, to degas ~2.526 times more slowly than Ar, due to its lower gas transfer velocity (43) and higher solubility (23). We therefore would predict that fractionation due to extraction incompleteness should lead to a positive bias in apparent (i.e., uncorrected) Δ(N₂/Ar) values and negative bias in apparent ΔKr/Ar values, with a slope of ~−0.762 (i.e., −1.926 divided by 2.526). Indeed, we observe a slope (reduced major axis regression) of −0.846 ± 0.192 (95% CI) by comparing apparent Δ(N₂/Ar) and Δ(Kr/Ar) in the 15 TTO/NAS samples below 2,900 m (SI Appendix, Fig. S16). We also find similar agreement between predicted (−0.334) and observed (−0.341 ± 0.074) slopes for apparent Δ(N₂/Ar) and Δ(Xe/Ar) (SI Appendix, Fig. S16), providing further support for the use of noble gas ratios to correct Δ(N₂/Ar) for physical fractionation.

Because of the close agreement between predicted and observed slopes for Δ(N₂/Ar) and Δ(Kr/Ar), and the similarity of simulated (b = 2) and observed Δ(Kr/Ar) at BATS, we use apparent Δ(Kr/Ar) measurements to correct Δ(N₂/Ar) in the following manner:

$$\begin{array}{c}\mathrm{\Delta }{(N2/Ar)}_{corr}=\mathrm{\Delta }{(N2/Ar)}_{raw}-(-0.846\pm 0.192)\times (\mathrm{\Delta }{(Kr/Ar)}_{raw}\hfill \\ -\mathrm{\Delta }{(Kr/Ar)}_{model}),\hfill \end{array}$$ [3]

where the subscripts “corr” and “raw” refer, respectively, to corrected and uncorrected (i.e., apparent) values, and Δ(Kr/Ar)_model is the Δ(Kr/Ar) value nearest to each TTO/NAS sample location within the UVic ESCM simulations in this study, using the modified L13 gas exchange parameterization with b = 2 (Eq. 2). We propagate the error from the Kr/Ar correction, along with the measurement uncertainty, to the final corrected Δ(N₂/Ar) value.

To evaluate the robustness of this correction, we explore five pairs of duplicate TTO/NAS tanks within our dataset (Dataset S1). Each of these duplicate pairs comprises two Gerard barrels that were collected at sea from the same station, at the same time, and at the same depth (within ~10 m). Each pair of duplicates was degassed separately at sea in 1981, and thus experienced a (random) different extent of incomplete degassing and associated fractionation. Because the true (i.e., original seawater) Δ(N₂/Ar) across each pair should be identical, but Δ(N₂/Ar)_raw should differ due to varying degrees of degassing-related fractionation, these duplicate pairs provide a useful opportunity to test the validity of our corrections. We find that pair differences in corrected Δ(N₂/Ar) are smaller than uncorrected differences for all five duplicate pairs (Dataset S1). Across these five duplicate pairs, the rmsd of Δ(N₂/Ar)_raw is 4.9‰, while the rmsd of Δ(N₂/Ar)_corr is 0.4‰, which is approximately equal to our analytical precision. The close agreement of corrected Δ(N₂/Ar) across duplicate pairs, as well as the similarity of observed fractionation slopes to theoretical predictions, both provide confidence in these corrections.

To determine an apparent temporal rate of change of Δ(N₂/Ar), we used two separate inverse model estimates of ideal mean age (Γ) evaluated a grid locations nearest to our TTO/NAS samples (26, 27). These inverse models are constrained by ¹⁴C and other tracers [e.g., ³He (73)]. As a first-order check, we verified that Δ(N₂/Ar) is anticorrelated with both ¹⁴C and ³⁹Ar activity in the Ocean Circulation Inverse Model version 2 [OCIM2, SI Appendix, Fig. S17, (27, 73, 74)]. Then, we adopted the mean of Γ estimates suggested by refs. 26 and 27 and carried out 10⁶ Monte Carlo simulations. In each Monte Carlo simulation, random perturbations were added to sample age (uniform distribution spanning the two age estimates) and Δ(N₂/Ar) (normal distribution based on both analytical and correction uncertainties), and a temporal trend was determined by reduced major axis regression. The 95% CI of these temporal trend estimates ranges from 18.2 to 35.7 ‰ ky⁻¹.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (XLSX)

Data, Materials, and Software Availability

All study data are included in the article or supporting information. Model results are freely and publicly available via BCO-DMO (https://www.bco-dmo.org/project/887496). Code, transport matrices and forcing data required to perform the simulations are available at https://github.com/samarkhatiwala/tmm and Zenodo (68).