An agent-based model of tissue maintenance and self-repair

Abstract

We hypothesized that a system that possesses the capacity for ongoing maintenance of its tissues will necessarily also have the capacity to self-heal following a perturbation. We used an agent-based model of tissue maintenance to investigate this idea, and in particular to determine the extent to which the current state of the tissue must influence cell behavior in order for tissue maintenance and self-healing to be stable. We show that a mean level of tissue density is robustly maintained when catabolic agents digest tissue at a rate proportional to local tissue density, but that the spatial heterogeneity of the tissue at homeostasis increases with the rate at which tissue is digested. The rate of self-healing is also increased by increasing either the amount of tissue removed or deposited at each time step by catabolic or anabolic agents, respectively, and by increasing the density of both agent types on the tissue. We also found that tissue maintenance and self-healing are stable with an alternate rule in which cells move preferentially to tissue regions of low density. The most basic form of self-healing can thus be achieved with cells that follow very simple rules of behavior, provided these rules are based in some way on the current state of the local tissue. Straightforward mechanisms can accelerate the rate of self-healing, as might be beneficial to the organism.

INTRODUCTION

Living systems are characterized by an ability to self-heal. That is, they respond to external attack by initiating a program that somehow neutralizes threats, repairs damage to the tissues, and then returns the system toward its original healthy state. Much is known about some of the specific cellular mechanisms involved in the repair of various tissues as evidenced by the burgeoning fields of regenerative medicine (1, 2) and bioinspired materials (3, 4). Nevertheless, self-healing in biology cannot be completely understood in terms of any single mechanism. Rather, it is a systems-level phenomenon resulting from the complex interactions between numerous players operating over wide ranges of length and time scales. Furthermore, living tissues are able to maintain internal order, and to restore that order after injury, without direction from any form of centralized sentient controller. Exactly how this happens remains incompletely understood. Nevertheless, biological tissues exhibit a wide range of maintenance and self-healing programs adapted to the specific challenges they face, such as the repair of barrier function in skin (5) and the retention of mechanical stiffness in lung parenchyma (6, 7). Despite this diversity of goals, however, we postulate the existence of a core set of necessary conditions for a system to exhibit self-healing.

The premise of the present study is that the fundamental effector of self-healing is the cell, since cells generate the extracellular matrix and are responsible for its subsequent maintenance and repair (8). How cells do this ultimately derives from complex sequences of intracellular chemical reactions. Regardless of these details, however, individual cells effectively behave as members of a cooperating community engaged in tasks that benefit the host. It is therefore useful to view cells as agents that operate according to evolved sets of rules that determine their behavior. A fundamental question, therefore, is how complex these behavioral rules need to be if cells are to automatically perform the crucial tasks of tissue maintenance and self-healing. Can we identify a minimal rule set that defines the baseline characteristics of a self-healing system? This question is not only of fundamental importance to the understanding of biology; it also pertains to the design of artificial self-healing systems (9).

Self-repair in biological systems is likely linked to morphogenesis and the subsequent ability to maintain homeostasis (10). That is, a system with the capacity for ongoing self-maintenance will necessarily also have the capacity to self-heal simply as a result of its ability to always return toward the homeostatic state following a perturbation. In the present study, we use an agent-based model of tissue maintenance to explore this idea in its most basic form, and to investigate the extent to which the current state of the tissue must influence cell behavior in order for maintenance and self-healing to be stable.

METHODS

The maintenance and repair of any structure necessarily requires the complementary abilities of being able to breakdown and remove damaged elements while also being able to replace them with new elements. Accordingly, we created a simple agent-based model representing a two-dimensional sheet of tissue upon which equal numbers of catabolic and anabolic cells operate. These cells are represented by catabolic and anabolic autonomous agents that move about at random on a matrix of 100 × 100 patches representing the tissue. Each patch may be occupied by any number of agents. At each time step, each agent moves to one of its randomly chosen neighboring patches, each of these options occurring with equal probability. The tissue sheet is closed such that if an agent moves off one of the four edges, it immediately appears on the adjacent patch at the opposite edge. The magnitude of the time step is linked to the time required for a cell to move to an adjacent patch, which in reality is determined by the patch size. We do not assign any particular value to either of these quantities here, since this does not play into the particular questions we address here, but scales of time and space could easily be imposed on the model for specific applications.

Each patch in the model comprises an amount M_i,j (i, j = 1,…,100) of tissue. At each time step, each catabolic agent removes a small amount δM_catab of tissue from the patch it occupies, whereas each anabolic agent increases the amount of tissue on its patch by δM_anab. The tissue is thus continually being degraded and replaced. The specific dynamics of the model are determined by the rules that define how both δM_catab and δM_anab are determined. We seek to make these rules as simple as possible in the interests of constructing a minimal model of homeostasis.

The simplest conceivable rules are that the catabolic and anabolic agents remove or add, respectively, the same amount of tissue at each time step (i.e., δM_catab = δM_anab = constant). In this scenario, tissue maintenance is an entirely open-loop process because no account is taken of the current tissue state. It is immediately apparent, however, that this is problematic because the maintenance of homeostasis would require exactly equal numbers of catabolic and anabolic cells; the slightest imbalance would lead to either progressive atrophy or hypertrophy. Furthermore, even if the overall rates of catabolism and anabolism were somehow to remain in perfect balance, this open-loop scheme still leads to progressively increasing tissue heterogeneity because the amount of tissue on each patch follows a random walk that results in a variance for M_i,j that increases linearly with time. We tested this in the model by running it for 5,000 time steps beginning with each patch having a value of M_i,j = 0.5. At each time step, each anabolic agent added 0.01 to the patch it was on, whereas each catabolic agent subtracted 0.01 from its patch. The square of the standard deviation of patch value increased linearly with time step, beginning at zero and reaching a maximum value of 0.0049, with a Pearson’s r value of 0.999 and a root mean squared residual of 7.2 × 10⁻⁵. Thus, while the mean amount of tissue per patch remains constant when δM_catab = δM_anab, its spatial variance increases progressively with the number of time steps.

The aforementioned considerations demonstrate that having fixed rates of degradation and replacement is not a viable strategy for maintaining tissue homeostasis. What is required is some form of feedback that causes agent behavior to change depending on the current state of the tissue. Accordingly, we modified the behavioral rules of our agents in the simplest way we could imagine. Each catabolic agent now removes a fraction α of the tissue from its current patch at each time step (i.e., δM_catab = αM_i,j). Each anabolic agent continues to add a fixed amount, αβ, of tissue to its current patch, where β is a constant (i.e., δM_anab = αβ). In other words, the action of each catabolic agent is influenced by the current state of the tissue upon which it sits, whereas each anabolic cell continues to operate in open-loop fashion.

We also investigated a simple form of durotaxis whereby cell movement is influenced by gradients in substrate stiffness (11), implemented in the model by having the cells move preferentially toward adjacent tissue patches with either low or high density. This was achieved by having each cell move from its current patch i, j to one of its eight immediate neighbors i + m, j + n (m, n = −1, 0, 1 excluding m = n = 0) with a probability proportional to either (1 − M_{i +m,j + n}) or M_{i + m,j + n}. We refer to the first case as negative durotaxis because it is a form of negative feedback whereby loss of tissue causes a corrective remodeling response, whereas the second case we call positive durotaxis.

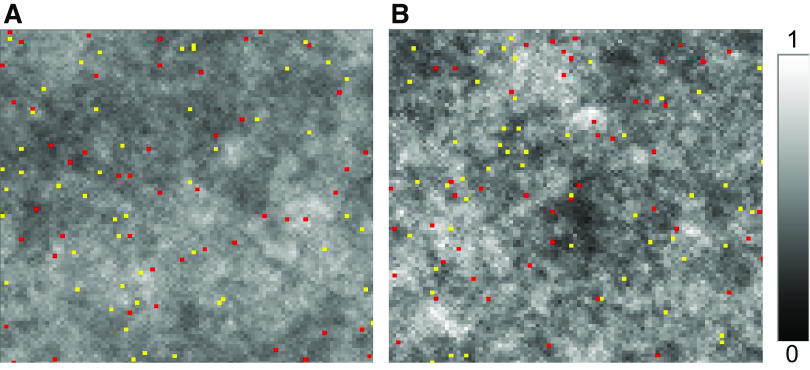
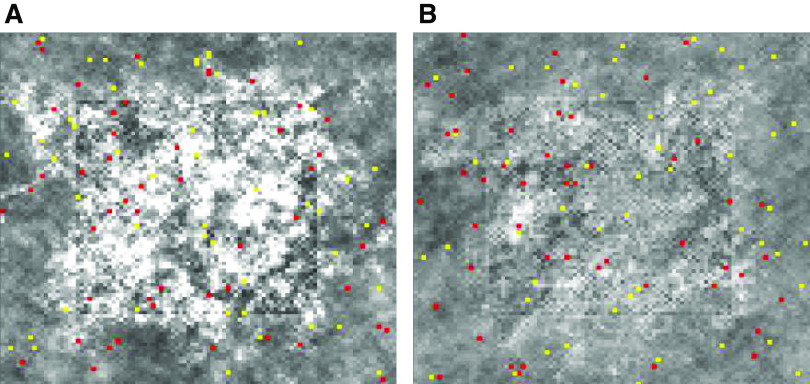
We implemented the agent-based model in Visual Basic 6. This implementation included a graphic representation of the model showing the different tissue patch densities and the positions of the two types of agents, which was used to make the images of the model shown in Figs. 1, 5, and 8. Running the model through 10⁵ time steps took a few minutes on a standardly configured personal computer.

Figure 1.

Tissue density maps obtained via agent-based model of tissue maintenance. Catabolic cells (red) digest a fixed fraction α of the tissue on each patch at each time step, whereas anabolic cells (yellow) lay down a fixed amount αβ of tissue on each patch, where β = 0.5 (the units of α and β are arbitrary). A: α = 0.01, the mean tissue density is 0.503, and the SD of the tissue density on each patch is 0.082. B: α = 0.02, the mean tissue density is 0.507, and the SD of the tissue density on each patch is 0.117. White corresponds to a tissue density of 1, whereas black corresponds to a tissue density of 0. The positions of the anabolic and catabolic cells shown correspond to the end of the simulation in each case.

Figure 5.

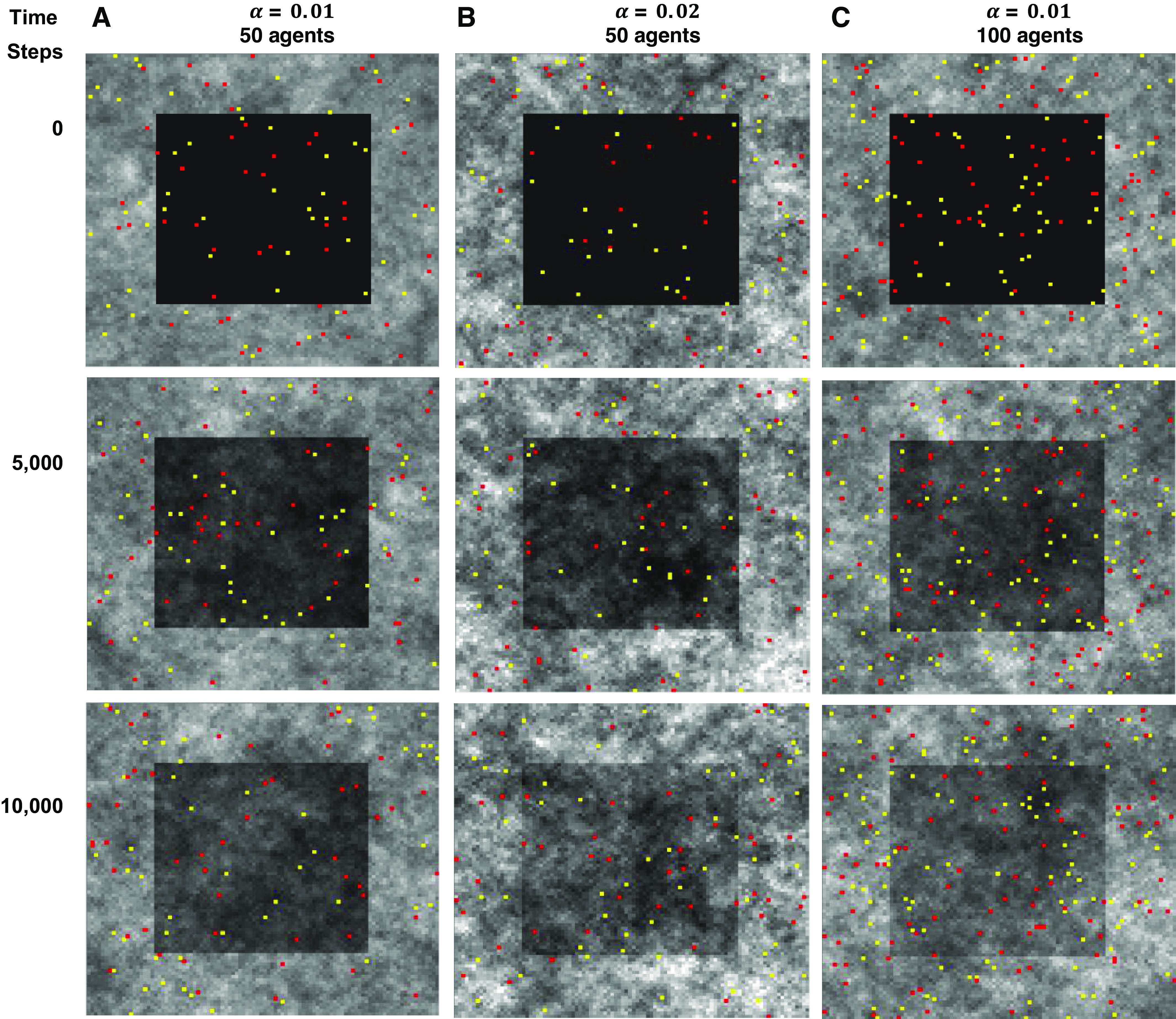
Healing of an injury. The injury is indicated by the dark central patch. A: fifty of each kind of agent with α = 0.01 beginning at the time of initial injury (time step 0) and at 5,000 and 10,000 time steps later. B: same as in A but with α = 0.02. C: same as in A but with twice the number of agents.

Figure 8.

Collateral fibrosis of self-repair. A: the model tissue after 10,000 time steps following injury with γ = 20 and T = 50 time steps. B: the tissue when durotaxis was implemented in the model (as described in the text).

RESULTS

Maintenance of Homeostasis

Figure 1 demonstrates the steady-state behavior of the agent-based model with 50 catabolic and 50 anabolic cells. The mean tissue density across the model is β = 0.5. We find that a finite degree of spatial heterogeneity develops across the tissue at steady state, and that this heterogeneity increases with the incremental tissue change, α, wrought by the catabolic agents at each time-step. Heterogeneity thus does not increase with the square root of the number of time steps as occurs in an open loop system in which both agent types simply subtract or add equal amounts of tissue at each time-step. In other words, if simple first-order behavior applies only to the rate of catabolism, this is sufficient to constrain the amount of heterogeneity that develops across the tissue over time.

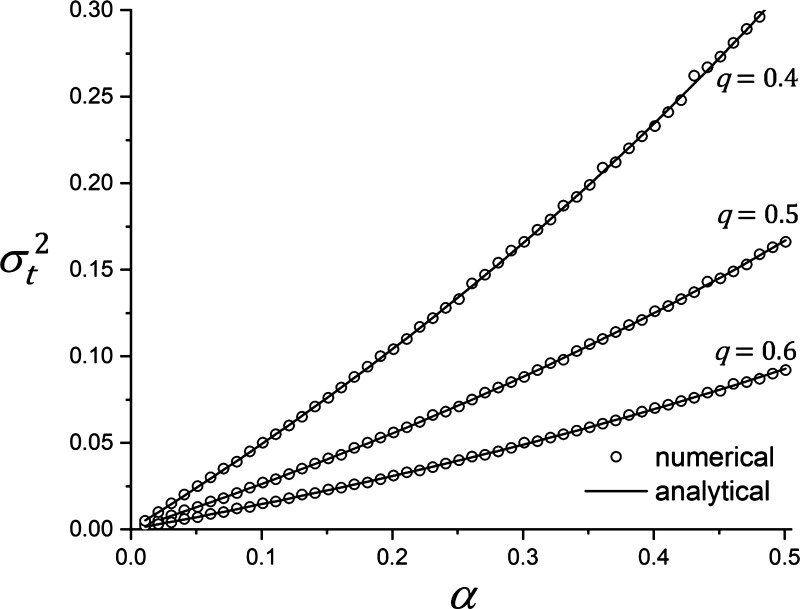
We found, however, that the spatial heterogeneity across the model tissue increases with the value of α. We were able to gain further insight into this phenomenon by investigating a single patch version of the model. Specifically, we determined how the amount, M, of tissue on the patch varies over time when either a fixed aliquot αβ of tissue is added or a fraction α of the current tissue amount is removed at each time step, either option being determined randomly. To increase the generality of our results, we relaxed the constraint that the number of anabolic and catabolic cells be equal by assigning a probability q to the likelihood that the tissue patch be visited by a catabolic agent, and a probability (1 − q) that it be visited by an anabolic agent. We imposed the initial condition that M start in the middle of its range (i.e., 0.5). In repeated runs of the model for a particular value of q, we let α take a range of values up to 0.5 so that it did not exceed the initial value of M. For each value of α, and for each of three different values of q, we ran the model for 10⁶ time steps, to establish steady state. We then continued for another 10⁶ iterations from which the temporal variance, ${\sigma }_{\text{t}}^2$, of M was calculated. Figure 2 shows that ${\sigma }_{\text{t}}^2$ increases monotonically with α in a slightly nonlinear manner. We were also able to derive an analytic expression for ${\sigma }_{\text{t}}^2$ (see appendix). The value of this expression is plotted as the solid lines in Fig. 2 and shows very close agreement with the numerically determined values of ${\sigma }_{\text{t}}^2$. Note that the numerical values of ${\sigma }_{\text{t}}^2$ in Fig. 2 were determined at each value of q using a different randomization for the agent behaviors, so the uncertainty in the individual values of ${\sigma }_{\text{t}}^2$, each determined from 10⁶ iterations, are reflected in the very small residuals that can sometimes be seen between the numerical values and the analytic solution.

Figure 2.

Dependence of the temporal variance of the time series produced by Eq. A3 at steady state, ${\sigma }_{\text{t}}^2$, vs. the size of the tissue digestion and replacement unit α for three different values of q.

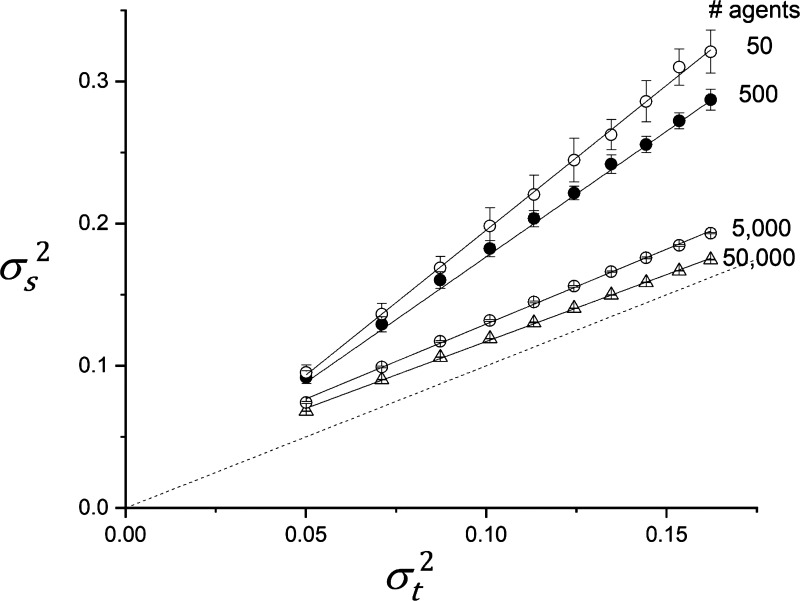
The two-dimensional agent-based model illustrated in Fig. 1 plays out the agent rules not on a single patch but on a two-dimensional grid. This results in the spatial statistics of M in the two-dimensional model being somewhat different to the temporal statistics of a single patch. We were not able to derive an analytic expression for these spatial statistics, so we determined them numerically by running the model to steady state for a range of different values of α and then calculating the spatial variance, ${\sigma }_{\text{s}}^2$, of M over all the model patches. Again, using β = 0.5, we determined ${\sigma }_{\text{s}}^2$ for values of α up to 0.1. Figure 3 shows ${\sigma }_{\text{s}}^2$ versus ${\sigma }_{\text{t}}^2$ with q = 0.5, determined over a range of α values, for different numbers of agents. When the agents are sparse (50 each of anabolic and catabolic), ${\sigma }_{\text{s}}^2$ depends linearly on ${\sigma }_{\text{t}}^2$ with a constant of proportionality of roughly 1.7. As the density of agents increases, the dependence of ${\sigma }_{\text{s}}^2$ on α remains linear but approaches the line of identity.

Figure 3.

Numerically determined spatial variance of tissue density, ${\sigma }_{\text{s}}^2$, vs. the temporal variance ${\sigma }_{\text{t}}^2$ predicted with q = 0.5 by Eq. A12 for different numbers of agents. The error bars indicate standard deviations obtained from 20 independent runs of the model. Linear regression lines through the points obtained with each number of agents are shown by the solid lines (r² > 0.998 in all cases). Dashed line is line of identity.

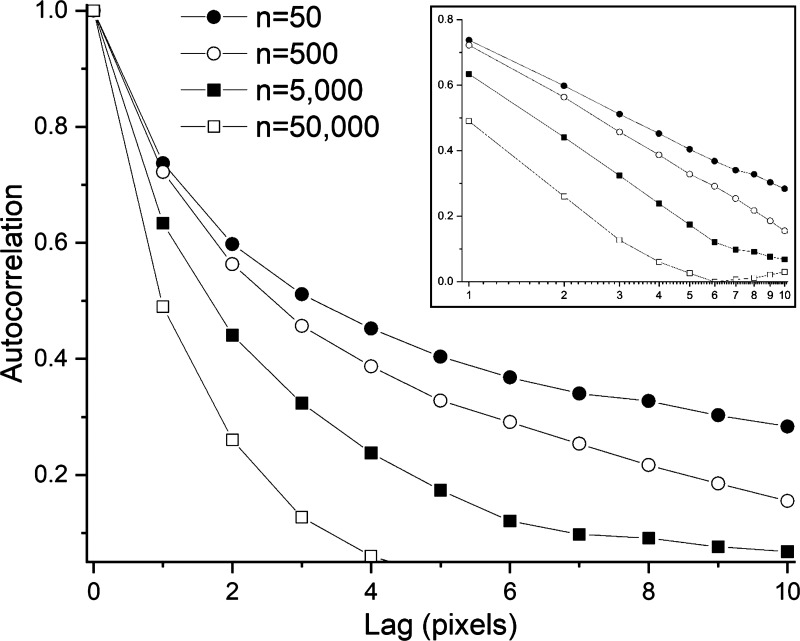
Visual inspection of Fig. 1 reveals that the spatial distribution of tissue in the agent-based model at steady state is not entirely random and uncorrelated. We quantified this by determining the autocorrelation of M_i,j of each row, j, in the model tissue and averaging over all rows. The normalized autocorrelation function C_j(l) was computed according to

$$C_j(l)=\frac{\eta }{100}\sum _{i=1}^{100}\left[\sum _{j=1}^{100}{M}_{i,j}{M}_{i,j+l}\right]$$ (1)

where l is the lag, the summation within the square brackets is performed cyclically such that when j + l > 100 it is replaced with j + l − 100, and η is a normalization factor that makes C_j(0) = 1. Figure 4 shows that C_j(l) decreases with l more rapidly as the density of agents in the model increases, approaching a delta function as the number of agents tends to infinity. The inset to Fig. 4 shows that the autocorrelation function decreases approximately linearly with the logarithm of l.

Figure 4.

Autocorrelation of tissue density at steady state calculated using Eq. 1 with α = 0.02. Inset: same plotted against the logarithm of time step. Lag is equal to the quantity l in Eq. 1.

Self-Healing

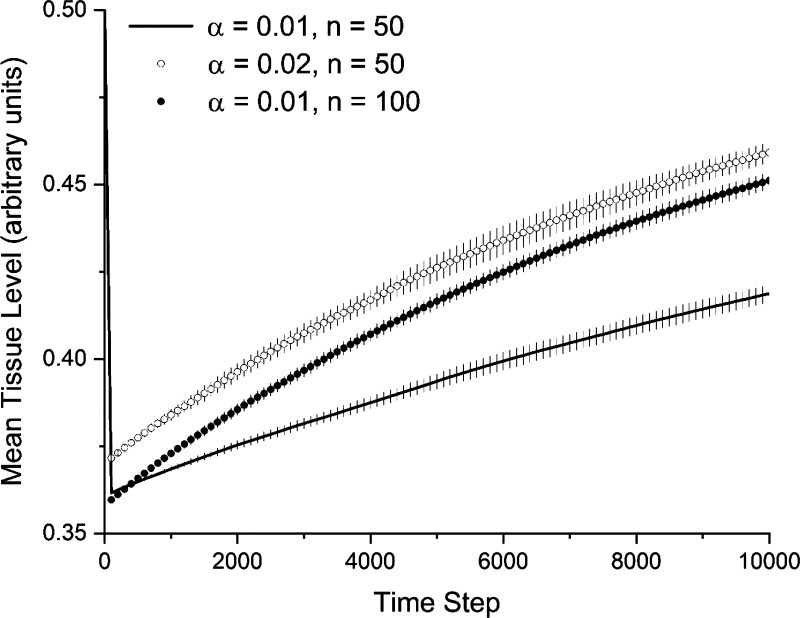
Figure 5 shows sequences of images of the two-dimensional agent-based model starting from a state of injury and then after 5,000 and 10,000 time steps, demonstrating a progressive repair of the injury and return toward homeostasis. The rates of self-healing with α = 0.02 (Fig. 5B) and when the number of agents is doubled (Fig. 5C) are clearly different to the control case when α = 0.01 (Fig. 5A). Figure 6 shows that these rates of healing are both increased as reflected in the rates of recovery of the mean values of M_i,j in the model. In each case, M_i,j is suddenly depressed by injury, and then returns monotonically toward 0.5 as the self-healing progresses. (Note that M_i,j at homeostasis was slighter greater in the α = 0.02 case because of a few tissue patches exceeding 1., which is why the tissue level immediately following injury is somewhat elevated compared with α = 0.01).

Figure 6.

Recovery from injury measured as deviation from baseline mean tissue level of 0.05. The injury used to generate the images in Fig. 5 caused the sudden initial drop in mean tissue level that then returns toward baseline as ongoing tissue maintenance proceeds. Increasing the amount of tissue removed and deposited (α) increases the rate of recovery, as does increasing the number of anabolic and catabolic agents (n). The lines show the mean of 20 stochastically independent simulations. The error bars show 1 standard deviation.

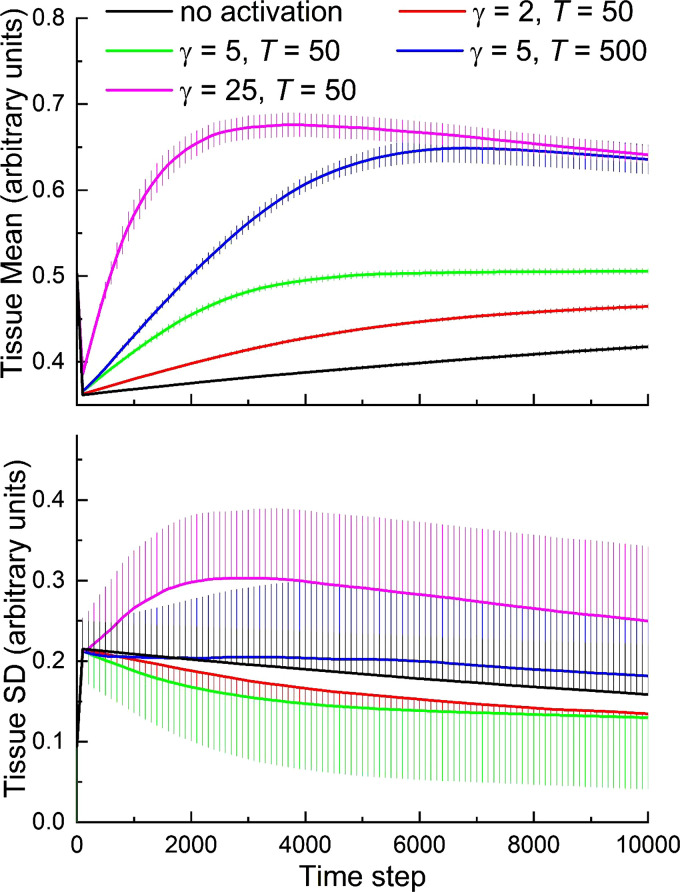
The aforementioned results demonstrate that a system that continually maintains itself will also repair itself following injury. However, the rate at which repair takes place may be a crucial consideration for the survival of an organism, and while this rate can be increased by increasing the value of α, it comes at the expense of increased tissue heterogeneity. In an attempt to mitigate this tradeoff, we modified the behavioral rules of the anabolic agents by letting them become temporarily activated whenever they found themselves on a patch for which M_i,j < 0.2. Activated anabolic agents added an amount αβγ of tissue to each patch at each time-step, instead of the original amount αβ, where γ > 1 is another constant. The temporary nature of this activation was achieved by deactivating each activated agent with a very small but fixed probability of P_apop at each time step. This gave the cells an exponentially distributed stochastic lifetime, which had the effect of simulating the apoptosis of activated cells and their immediate replacement with normal cells. The mean half-life of the activated agents produced by this scheme was T time steps, where $P_{\text{apop}}=1-{0.5}^{\frac{1}{T}}$. We chose T arbitrarily simply to demonstrate the dynamics of the model, but the value of T could potentially be tied to the lifetimes of key anabolic and/or catabolic cells. For example, chick embryo fibroblasts have a life span of ∼57 days (12), in which case each time step should correspond to roughly 57/T days.

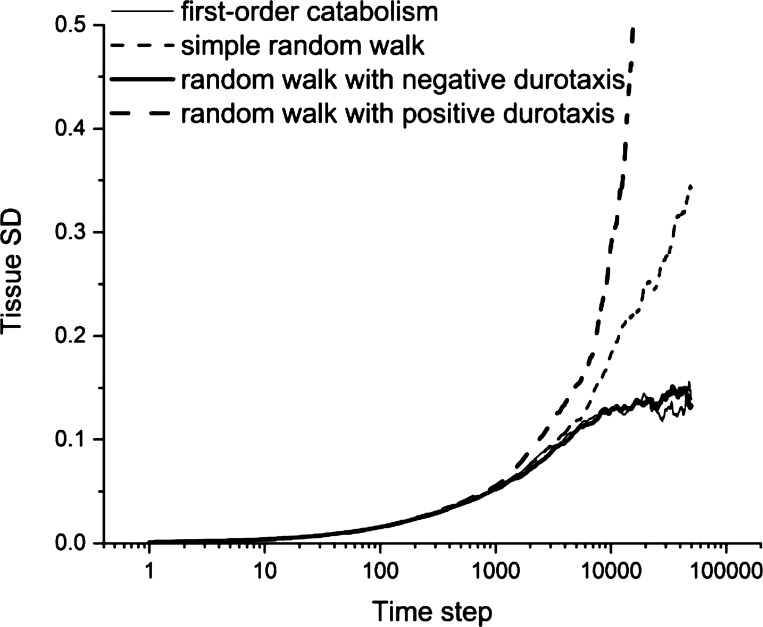
Figure 7 shows that temporarily increasing α and T results in substantial increases in the rate of healing. Interestingly, we observed an overshoot in the degree of repair when α and/or T were increased sufficiently, leading to temporary excess tissue deposition both within and around the site of injury (Fig. 8A). If such excess tissue is not eventually cleared, it would correspond to a scar. Adding negative durotaxis to both anabolic and catabolic cells resulted in a notable improvement in tissue repair (Fig. 8B). Importantly, it also led to a stable degree of tissue heterogeneity even when the amounts of tissue production and consumption were both fixed (Fig. 9). Alternatively, when positive durotaxis was implemented in the model (i.e., having both agent types move preferentially to regions of high tissue density), the rate of development of tissue heterogeneity was greatly amplified (Fig. 9). Breaking this down further, we found that stability was achieved when negative durotaxis was applied only to the anabolic cells, whereas the catabolic cells moved about randomly, and conversely when positive durotaxis was applied only the catabolic cells while the anabolic cells moved around randomly. Thus, negative feedback caused by either directing anabolic cells toward tissue-poor regions or catabolic cells toward tissue-rich regions is enough to constrain the amount of tissue heterogeneity that develops over time.

Figure 7.

Effects of injury-induced activation of anabolic agents on rate of recovery from injury. The parameter, α, that controls the amount of tissue produced or removed by each agent at each time step is increased by the factor γ. Activated cells persist for an average half-life of T time steps. The lines show the mean of 20 stochastically independent simulations. The error bars show 1 standard deviation.

Figure 9.

Evolution of tissue heterogeneity. The model was run for 50,000 time steps with 150 agents of each type and α = 0.02. Heterogeneity levels off after about 5,000 steps with both first-order catabolism (thin solid line) and the random walk modified by negative durotaxis (thick solid line), on contrast to the increase with the square root of the number of steps seen in heterogeneity with the simple random walk (thin dashed line) and the random walk modified by positive durotaxis (thick solid line).

These findings with simulated durotaxis mean that there is not a unique minimal rule set for tissue stability; both a catabolism rate proportional to the local tissue density and a biased random walk based on local tissue density can work equally well. The crucial feature of these strategies, however, is that they both involve agent behavior being influenced by feedback about the local state of the tissue.

DISCUSSION

We have used an agent-based model to explore minimal sets of behavioral rules that anabolic and catabolic cells must exhibit if they are to successfully collaborate on the maintenance and repair of the tissue within which they reside. Regardless of whether additional rules make repair more efficient and flexible, our study shows that some form of modulation of cell behavior by the current state of the tissue is necessary to prevent the tissue from becoming increasingly heterogeneous over time. Our study also demonstrates the power of agent-based modeling for addressing complex questions in cell biology. Computational modeling often involves advanced skills in mathematics, which tends to limit its accessibility to the biomedical community. The essential intellectual input required for agent-based modeling, on the other hand, is logic extracted from a detailed knowledge of relevant biology, which is the domain of the expert biologist.

Self-repair in the animal kingdom is exceedingly complex in all its details (13, 14), reflecting millions of years of evolutionary adaptation to countless challenges that have come in and out of existence over time. Nevertheless, there are certain general characteristics of living systems that would seem to be inextricably linked to their self-healing abilities. Key among these is that such systems are thermodynamically open (15, 16), meaning that they take in a continual supply of energy from the environment while excreting a corresponding amount of entropy (17). This gives them the resources to continually replace old tissue with new, thereby maintaining internal order throughout life in the face of perpetual assault by the second law of thermodynamics.

Ongoing tissue maintenance is a common program in biology. For example, epithelial layers such as skin are continually being sloughed off from the surface of the body by daily wear and tear while being replaced from below (5). Similarly, bone is continually being broken down by osteoclasts and rebuilt by osteoblasts (18). A program of continual tissue maintenance is also clearly an important component of lung tissue health as evidenced by the emphysema that develops due to protease/antiprotease imbalance (19, 20), and the corresponding imbalance in the opposite direction likely plays a key role in pulmonary fibrosis (21). These considerations suggest that self-repair is, at its most basic level, a natural consequence of the need for biological systems to self-maintain in the face of the ongoing challenges they face during life, at least until they can reproduce, and is thus central to development (10). The most extensively modeled situation is probably the repair of a physical tear in a layer of epithelium such as a cut in the skin where nearby cells move and divide in such a way as to bring the edges of the tear together (22–24). Nevertheless, exactly how self-repair comes about is still somewhat a mystery and thus remains a question of fundamental importance for both biology and artificially engineered systems (3, 4).

The results of our study indicate that repair cannot be accomplished satisfactorily without the current state of the tissue being taken into account in some way; simply removing and replacing fixed aliquots of tissue is fragile to an imbalance between the rates of catabolism and anabolism that would cause regional structural heterogeneities to grow inexorably without limit. Accordingly, for self-healing to be stable in the sense of respecting homeostasis, it must be regulated in some way by the local state of the tissue. Alves et al. (25) came to a similar conclusion when modeling the repair of elastic fibers under tension. Our model findings suggest that such regulation can be of an extremely basic nature if stability is the only requirement (Fig. 2). Indeed, regulation need only be applied to catabolism, as demonstrated in Fig. 1. Interestingly, applying the same strategy to anabolism alone leads to a diverging tissue state because it corresponds to Eq. A1 with the right-hand side multiplied by −1, that is, $\dot{M}\left(t\right)=-\alpha \beta +\alpha M(t)$. The solution to this equation is the increasing exponential function M(t) = [M(0) − β]e^αt + β, so there is no longer a fixed point.

Our numerical calculations of the temporal variance of tissue density, ${\sigma }_{\text{t}}^2$, in a single patch visited randomly at each time step by either agent type (Fig. 2) agree with theoretical predictions (see appendix). However, in a two-dimensional array of patches, when the density of agents is low, we find that ${\sigma }_{\text{s}}^2$ is significantly higher than ${\sigma }_{\text{t}}^2$. This discrepancy arises because an isolated agent is able to repeatedly affect its nearby patches, possibly multiple times, before an agent of the opposite type has time to move in and undo its work. This has essentially the same effect locally as an agent acting only once at each site but with an increased value of α, and would allow the development of islands of tissue that are substantially greater or less than the overall tissue mean. This also explains why ${\sigma }_{\text{s}}^2$ in the two-dimensional agent-based model does not conform precisely to the single-patch scenario and thus does not represent a discrete version of the continuous dynamics represented by Eq. A12. On the other hand, ${\sigma }_{\text{s}}^2$ approaches ${\sigma }_{\text{t}}^2$ as the number of agents increases (Fig. 3). Similarly, the autocorrelation of tissue density, C_j(l), decreases more quickly with increasing lag, l, as the number of agents increases (Fig. 4) because an agent of a given type becomes less able to dominate locally without interference from an agent of the opposite type.

But how can we justify the simple first-order catabolic mechanism leading to Fig. 1 biologically? Having an anabolic cell lay down a fixed amount of tissue at each step seems reasonable provided the necessary energy and raw materials continue to be available (26). However, having a catabolic cell remove an amount of tissue in proportion to that already present, while not inconceivable, would require some kind of mechanism that quantifies the tissue and directs the cell’s actions accordingly, which seems overly complex to be an absolute necessity. A simpler possibility might be that each catabolic cell secretes a fixed amount of proteolytic enzyme but that the amount of tissue accessible to the enzyme is proportional to the amount of tissue present (6). Alternatively, enzyme activity could be influenced by the mechanical stiffness of the substrate, which itself is modulated by the amount of anabolism or catabolism that has already taken place (27). On the other hand, implementing a simple form of durotaxis in the model shows that modulation of the amount of tissue removal is not necessary for stability if cells move preferentially toward regions of low tissue density (Figs. 8 and 9). What both these rules imply, therefore, is that to constrain the degree of steady-state tissue heterogeneity, some simple feedback mechanism is required whereby cellular activity is modulated by the local tissue state, be it the state itself or the spatial gradient of the state. In fact, Nature has equipped cells with both types of mechanism (11, 28), thereby providing redundancy against failure to maintain tissue homogeneity.

Figures 5 and 6 demonstrate that a mechanism that serves to maintain the homeostatic state of a tissue through a fixed program of ongoing breakdown and repair can also self-repair injury, which reflects the fact that Eq. A1 (see appendix) has a single fixed point toward which it will always asymptote. This does not, however, guarantee that the rate of healing will be rapid enough to allow an organism to deal successfully with all the other challenges inherent in remaining alive. One way to bring about a speedier recovery, as Figs. 5 and 6 show, is to have a larger value of α. However, as Figs. 5 and 6 also show, this will increase the degree of spatial heterogeneity across the tissue. At some point, this may become unacceptably large for appropriate biological function. An obvious compromise is to allow α to increase temporarily while the bulk of an injury is being repaired, and then have it return to its baseline value as the homeostatic state is approached, as demonstrated in Fig. 7. In fact, Nature has evolved mechanisms for achieving this. Reparative activities of cells are often upregulated in response to local cues reflective of injury, whereas eventual return to normal activity is usually achieved through apoptosis of the activated cells. For example, local chemical and mechanical cues can induce fibroblasts to become myofibroblasts that have high rates of collagen synthesis and secretion (29) and eventually undergo apoptosis. Indeed, most cells have lifetimes far shorter than that of the organism itself (30) and are continually being reborn either in the bone marrow or in local stem cell niches. Only the most highly differentiated of cell types are spared this fate (31), presumably because it is a better use of nature’s resources to support such highly trained cells in perpetuity rather than periodically trading them in for younger naïve models.

At the same time, apoptotic cells must be replaced by naïve progeny, so proliferation of cell types is critical to a self-repair program, and a temporary upregulation in the proliferation rate can increase the rate of repair. Interestingly, as illustrated in Fig. 7, this can lead to an overshoot in tissue properties such as occurs with the excessive collagen deposition that accompanies scar formation (32, 33). To avoid scarring, this excess deposition must eventually be rectified by baseline tissue maintenance once the activated cells have been eliminated. Although such evolutionary tricks bring clear survival advantages to the endowed organism, they also bring the specter of disease. For example, cellular replenishment requires appropriate rates of cell division and apoptosis, and dysregulation of either can lead to cancer (34, 35). Similarly, dysregulation of the collagen deposition that occurs when anabolic cells become activated can result in progressive fibrotic disease (36). Fibrosis can also result due to impaired apoptosis of anabolic cells (37). Indeed, even our simple model shows evidence of collateral fibrotic remodeling when cellular activation is overly exuberant (Fig. 8A). The extent of this remodeling is reduced by the phenomenon of durotaxis in which the direction of cell movement is affected by tissue mechanical properties (Fig. 8B), but some amount of excess deposition of collagen may be unavoidable for the timely repair of an injury so long as it is temporary. These events have analogs in the increased failure likelihood that inevitably plagues artificial systems as they increase in complexity (38).

It must be noted that our study has a number of limitations. The homeostatic self-healing scheme we have investigated here is an extremely simple model in two dimensions that does not purport to represent any biological system in particular. Vastly more complex and intricate feedback mechanisms are operative in three dimensions at the tissue-cell level of scale in real biological tissue. For example, the repair process can be further facilitated if cells are recruited to sites of injury from further afield by the deposition of chemotactic factors (39), which of course is another ubiquitous characteristic of biological systems. It may also be advantageous to have the mean tissue level, β, be temporarily modified following injury to accelerate self-repair. In addition, we have tacitly assumed that the catabolic and anabolic cells necessary to do the work of tissue removal and replacement somehow exist. This is not a trivial matter because these cells must be endowed with all the sophisticated machinery required to gather and utilize the energy and raw materials necessary to perform their respective functions. They are thus immensely complex machines that are themselves susceptible to sustaining injury, being killed, or acquiring aberrant behaviors in the course of their duties. Evolution has attended to this problem by giving cells finite lifetimes along with the ability to reproduce (30). In other words, biological self-repair involves removal and replacement of the agents as well as the tissue upon which the agents operate. It is thus important to realize that self-repair is an inherently multiscale process, and we have examined but one of these scales in the present study. Even at the level of the tissue considered here, however, self-repair in biology is much more complicated than our simple model. In particular, repair typically involves that a tissue progress through multiple phases that usually begin with inflammation that is followed by removal and eventual replacement of damaged tissue and eventual elimination of all excess repair machinery, including the inflammation (40).

In summary, we have attempted to identify the minimal characteristics required of a self-repairing biological system at the level of scale represented by connective tissues and the cells that maintain them. We have shown that homeostasis cannot be sustained when both catabolic and anabolic cells either remove or deposit fixed amounts of tissue at each time step. However, if the catabolic cells simply digest tissue at a rate proportional to local tissue density, a mean level of tissue is robustly maintained with a controllable degree of spatial heterogeneity. Alternatively, robust maintenance is also achieved by the durotactic mechanism of having cell movement influenced by the local spatial gradient of a surrogate for physical stiffness. The rate of self-healing from injury is increased by increasing either the amount of tissue removed or deposited at each time step, or by increasing the density of cells on the tissue. These correspond to the activation and proliferation, respectively, of reparative cells in nature. We conclude that self-healing at its most basic can be achieved with very simple rules of behavior by agents that alternately breakdown and rebuild tissue. We also conclude that there are a number of straightforward mechanisms that can accelerate the rate of self-healing, albeit at the expense of increased risk of chronic disease when such mechanisms operate in aberrant fashion.

DATA AVAILABILITY

Data will be made available upon reasonable request.

GRANTS

This work was supported by the NIH Grants U01 HL139466 and T32 HL076122.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.H.T.B. conceived and designed research; J.H.T.B. performed experiments; J.H.T.B. and B.S. analyzed data; J.H.T.B., J.H., D.T.C., and B.S. interpreted results of experiments; J.H.T.B. prepared figures; J.H.T.B. drafted manuscript; J.H.T.B., J.H., D.T.C., and B.S. edited and revised manuscript; J.H.T.B., J.H., D.T.C., and B.S. approved final version of manuscript.

APPENDIX

We are interested in understanding the nature of the spatial heterogeneity that arises in the model as a result of the actions of the anabolic and catabolic agents. Our approach to understanding these dynamics is to perform simulations with an agent-based model. This provides accurate depictions of what happens, but it is limited in terms of generality to the particular instantiations of the model that we investigate. As an informative adjunct to this investigation, we were able to derive an analytic, and therefore completely general, formula for the temporal variance of the amount, M, of tissue on a single patch when the patch has an equal likelihood of being visited by either a catabolic or anabolic agent at each successive time step.

The effective continuous time dynamics of M on a single patch are governed by the equation

$$\dot{M}\left(t\right)=\alpha \beta -\alpha M(t)$$ (A1)

(the units of the quantities M, α and β are arbitrary, although M and β must have the same units). Equation A1 has the solution

$$\text{M}\left(t\right)=\beta -\left[M\left(0\right)-\beta \right]e^{-\alpha t}=\text{β}-\left[M\left(0\right)-\text{β}\right]e^{-\frac{t}{\text{τ}}}$$ (A2)

where we have set τ = 1/α as the time constant of the system.

When there are different numbers of anabolic and catabolic agents, the more general finite difference version of Eq. A1 describes what happens to a single patch of tissue when there is equal probability of having an anabolic or a catabolic agent land on it, and is given by

$$M_{j+1}-M_j=\alpha \beta {\nu }_j-\alpha M_j\left(1-{\nu }_j\right)={\delta }_j$$ (A3)

where j is discrete time, ν_j is an uncorrelated random variable that takes a value of 0 with probability 0 < q < 1 and a value of 1 with probability 1 − q. The expected value of ν_j is then

$$\mathbb{E}\left\{{\nu }_j\right\}=0\times q+1\times \left(1-q\right)=1-q$$ (A4)

where $\mathbb{E}\{·\}$ denotes the statistical expectation operator. The right-hand side of Eq. A4 also applies to the expected value of ${\nu }_j^2$, so $\mathbb{E}\left\{{\nu }_j^2\right\}=1-q$.

The expectation of each side of Eq. A3 under these conditions is

$$\mathbb{E}\left\{{\delta }_j\right\}=\mathbb{E}\left\{\alpha \beta {\nu }_j-\alpha M_j\left(1-{\nu }_j\right)\right\}=\alpha \beta \left(1-q\right)-\text{α}q\mathbb{E}\left\{M_j\right\}$$ (A5)

where we have used the fact that since ν_j and M_j are uncorrelated, the expectation of their product is the product of their expectations.

If the sequence {M_j} converges on average toward a fixed point M^* for large j then, in the limit as j tends to infinity, $\mathbb{E}\left\{{\delta }_j\right\}=0$. Equation A5 then gives

$$\mathbb{E}\left\{M_j\right\}=M^{*}=\frac{\beta \left(1-q\right)}{q}$$ (A6)

We can derive an expression for the steady-state variance of {M_j} by first noting that

$$\mathbb{E}\left\{M_{j+1}^2\right\}=\mathbb{E}\left\{{\left(M_j+{\delta }_j\right)}^2\right\}=\mathbb{E}\left\{M_j^2\right\}+2\mathbb{E}\left\{M_j{\delta }_j\right\}+\mathbb{E}\left\{{\delta }_j^2\right\}$$ (A7)

The middle term on the right-hand side of Eq. A7 can be written as

$$\begin{array}{l}2\mathbb{E}\left\{M_j{\delta }_j\right\}=2\mathbb{E}\left\{M_j\left(\alpha \beta {\nu }_j-\alpha M_j+\text{α}{M}_j{\nu }_j\right)\right\}\\ =2\text{α}\left[\frac{{\text{β}}^2{\left(1-q\right)}^2}{q}-q\mathbb{E}\left\{M_j^2\right\}\right]\end{array}$$ (A8)

The last term on the right-hand side of Eq. A7 can be written as

$$\begin{array}{l}\mathbb{E}\left\{{\delta }_j^2\right\}=\mathbb{E}\left\{{\alpha }^2{\left(\beta {\nu }_j-M_j+M_j{\nu }_j\right)}^2\right\}\\ ={\alpha }^2\left[{\beta }^2\left(1-q\right)+q\mathbb{E}\left\{M_j^2\right\}\right]\end{array}$$ (A9)

Substituting Eqs. A8 and A9 into Eq. A7 gives

$$\begin{array}{l}\mathbb{E}\left\{M_{j+1}^2\right\}=\mathbb{E}\left\{M_j^2\right\}+2\alpha \left[\frac{{\beta }^2{\left(1-q\right)}^2}{q}-q\mathbb{E}\left\{M_j^2\right\}\right]+{\alpha }^2\left[{\text{β}}^2\left(1-q\right)+q\mathbb{E}\left\{M_j^2\right\}\right]\\ =\mathbb{E}\left\{M_j^2\right\}+\frac{2\alpha {\beta }^2{\left(1-q\right)}^2+{\text{α}}^2{\text{β}}^2\left(1-q\right)q}{q}+q\text{α}\left(\text{α}-2\right)\mathbb{E}\left\{M_j^2\right\}\end{array}$$ (A10)

Because $\mathbb{E}\left\{M_{j+1}^2\right\}=\mathbb{E}\left\{M_j^2\right\}$ in the limit as j tends to infinity, Eq. A10 reduces to

$$\mathbb{E}\left\{M_j^2\right\}=\frac{2{\beta }^2{\left(1-q\right)}^2+{\alpha \beta }^2\left(1-q\right)q}{q^2\left(2-\alpha \right)}$$ (A11)

The steady-state variance of M_j over time is therefore

$$\begin{array}{l}{\sigma }_{\text{t}}^2=\mathbb{E}\left\{M_j^2\right\}-\mathbb{E}{\left\{M_j\right\}}^2=\frac{2{\beta }^2{\left(1-q\right)}^2+{\alpha \beta }^2\left(1-q\right)q}{q^2\left(2-\text{α}\right)}-{\left[\frac{\text{β}\left(1-q\right)}{q}\right]}^2\\ =\frac{{\text{αβ}}^2\left(1-q\right)}{q^2\left(2-\alpha \right)}=\frac{{\text{β}}^2\left(1-q\right)}{q^2\left(2\text{τ}-1\right)}\end{array}$$ (A12)

Equation A12 has a singularity at α = 2 but this is moot because α is a fraction < 1. Equation A12 also shows that having the sequence {M_j} converge more slowly toward M^* by increasing τ leads to a reduction in its temporal variance at steady state.