Abstract
Acoustical behavior of semiconducting transition metal dichalcogenides determines the heat transfer pathway, and thus plays a crucial role in the electronics and optoelectronics design. In this research, van der Waals heterojunctions (vdWHs) consisting of transferred monolayer and bi-layer MoS2 on GaN substrate were studied. We observed an asymmetric bipolar acoustic strain wave with ∼5 ps duration, which describes the surface of substrate undergoing strong compressive deformation after weak tensile deformation in the out-of-plane direction. We developed a theory to explain the mechanisms responsible for the observed strain waveform in the vdWHs elastic system, and obtained the critical parameters of the carrier dynamics by temporal fitting. Our results not only report a coherent acoustic phonon generated in the vdWHs, which will complement our understanding of the thermal transfer at the 2D/substrate interface, but also provide information about the intrinsic properties in the vdWHs, which would benefit the design of the 2D-based devices in the future.
Keywords: MoS2, GaN, Van der Waals, Lattice vibration, Thermal phonon, Terahertz coherent acoustic phonon, Metal sulfurization
1. Introduction
Semiconducting 2D transition metal dichalcogenides (TMDs), such as MoS2, have been widely considered as a versatile platform for both electronics design [1] and novel physics research [2]. The bandgap tuning capability, owing to the multiple choices among the TMDs family and the stacking number of layers, enables the optoelectronic applications from visible to infrared wavelengths [3]. In addition, the formation of various types of heterojunctions [4] by contacting with different substrates could further enrich the properties for electronic operations. In recent years, MoS2/GaN heterojunction has attracted attention due to its promising application in the broadband photodetector [5], bipolar transistor devices [6], and photocatalytic for water splitting [7]. Because of the staggered type-II heterojunction, the optically excited electron-hole pairs in the van der Waals heterojunction (vdWHs) would be naturally spatially separated, and it would be beneficial for photon energy harvesting and detection [8]. Therefore, understanding the charge transfer at the interfaces is crucial for engineering flexibility. In addition, the performance of such 2D-based devices is also strongly affected by the temperature, and thus an efficient heat transfer path at such heterostructure is thus in demand.
To study the heat transfer properties of 2D nanostructures, optothermal Raman techniques [9], [10], [11] have been widely applied to directly determine the crucial parameters such as thermal conductivity and thermal interface conductance. The related research demonstrated a profound 100 times lower thermal conductivity for MoS2 compared to graphene. In recent years, ultrafast electron diffraction (UED) has also been developed to resolve the momentum dynamics of the lattice [12]. The electron-phonon coupling time can be obtained by analyzing the intensity of the diffraction pattern at the specific vector in the Brillouin zone. The reported energy coupling of hot carriers to the anisotropic phonon distribution can last up to 5 ps. However, this electron probing technique is often limited by the requirement of periodic crystal structure. On the other hand, picosecond ultrasonics has been widely regarded as a powerful method to probe the properties of charge transfer and the dynamics of carriers and phonons. Layer-dependent phonon lifetime of MoSe2 has been reported [13] with the coherent phonon spectroscopy, and ∼1 ps phonon lifetime has been measured for suspended bi-layer. For the vdWHs, our previous work has reported the graphene-to-substrate acoustic energy transfer induced by the excited charge and lattice temperature rise [14]. For charge transfer in vdWHs, the interlayer charge transfer time, such as MoSe2/MoS2, has been measured to be in the range of hundreds of femtoseconds to a few picoseconds [15].
In this research, monolayer and bi-layer large-area growth continuous MoS2 films were transferred onto the GaN substrate, forming a type-II heterostructure. We first applied picosecond ultrasonics measurement on bi-layer MoS2/GaN heterostructure and the observed Brillouin oscillation signal reveals the out-of-plane acoustic wave generation from the van der Waals (vdWs) interface into the substrate. We then designed a single quantum well (SQW) photoacoustic transducer embedded under the GaN substrate for monitoring the THz acoustic waveform. The carrier and thermal phonon dynamics following the excitation of MoS2 by a near-UV femtosecond laser pulse lead to a non-equilibrium state that drives the displacement of the interface. The generated acoustic strain wave propagated to the SQW, which functioned as a photoacoustic transducer, was temporally resolved. We found that the duration of the strain wave was less than 5 ps with a non-symmetric bipolar profile. The fast tensile followed by the slow compressive strain can be explained by the charge transfer at the heterojunction and the lattice temperature rise induced by the thermal phonon. Our observed acoustic phonon generation at the vdWHs and the establishment of the physical model will complement our understanding of the thermal transfer at the interface and the phonon induced by charge transfer at vdWHs.
2. Materials and methods
2.1. Growth and transfer methods for monolayer and bi-layer MoS2 samples
For the preparation of the 2D/substrate heterojunction, our monolayer and bi-layer MoS2 samples were first epitaxially grown by two different methods. Chemical vapor deposition (CVD) and transition metal sulfurization epitaxial growth methods were used to synthesize the as-grown monolayer and bi-layer MoS2 samples, respectively. The CVD-grown monolayer MoS2 continuous film was purchased and transferred to our GaN substrate by SixCarbon Technology. Co., Ltd. The polymethyl methacrylate (PMMA)-assisted transfer method was used to transfer the as-grown MoS2 monolayer film. Later, the PMMA was removed by acetone and the heating process to increase the adhesion. The growth condition for the epitaxially grown bi-layer MoS2 is the same as in our previous work [16]. To transfer the bi-layer MoS2 to our GaN substrate, a PDMS film was used as a stamp and attached to the MoS2. To separate the sapphire and MoS2, the sample was soaked in 2 M KOH solution. Later, the MoS2/PDMS was cleaned, dried and attached to the surface of our GaN substrate. Under 80 °C, the PDMS film can be removed and thus a MoS2/GaN heterostructures can be formed. A schematic illustration of the transfer process is shown in Fig. 1(a).
Fig. 1.
(a) Schematically illustrating the transfer process from sapphire to our GaN substrate and the transferred samples for Raman spectroscopy measurement and picosecond ultrasonics. The photo was taken for the 1L-MoS2/GaN sample from the top; (b) Schematically illustrating our ultrafast pump-probe system. (LPF: long pass filter; AOM: acousto-optic modulator; LNs: lens; BPF: band pass filter; HWP: half-wave plate; PBS: polarized beam splitter; NDW: neutral density wheel); (c-d) Raman spectra of 1L-MoS2/GaN and 2L-MoS2/GaN respectively.
2.2. GaN substrate for transfer and InGaN single quantum well as THz photoacoustic transducer
The substrate we designed for transfer was a 4 µm ultra-flat unintentionally doped GaN film grown on the c-plane of a 440 µm-thick (0001) double side polished sapphire substrate by metal-organic chemical vapor deposition. A 2.9 nm thick In0.25Ga0.75N SQW served as the THz photoacoustic transducer and was embedded below the surface of a 58.5 nm thick GaN cap layer. High resolution transmission electron microscopy (HRTEM) was used to confirm the thickness of the SQW and the GaN cap layer. The photoluminescence peak of the SQW was measured to be ∼460 nm.
After the transfer process, we applied Raman spectroscopy to characterize the vdWs heterostructure. For our GaN substrate before MoS2 transfer, two Raman peaks were measured at 417 cm-1 and 570 cm-1, which were related to the sapphire and E2 (high) modes of GaN, respectively. After transfer, in addition to the above Raman modes from the substrate, the and modes from the MoS2 were also observed. The difference of the two modes increased from 18.5 cm-1 to 21.0 cm-1 from monolayer to bi-layer (see Fig. 1(c-d)), showing a good agreement with the Davydov splitting feature with increasing layer number.
2.3. Ultrafast pump-probe system
Fig. 1(b) schematically shows our ultrafast pump-probe system. An 808 nm laser pulse from a Ti:sapphire laser oscillator was frequency doubled by a BBO nonlinear crystal. The near-UV laser output, corresponding to 3.1 eV, was split into two beams, considered as pump (30 mW) and probe (3 mW), by a polarized beam splitter. An autocorrelator was used to characterize the pulse width with 220 fs. The time difference between the pump and probe pulses was controlled by a retroreflector on the motorized stage. Finally, both beams were focused on the MoS2/GaN vdWs heterojunction and the SQW at the same spot location by an objective with a spot size of ∼10 µm. Considering the ∼30% optical absorption of the SQW, the maximum pump fluence at the focal point was kept below 3.44 J/m2, which corresponds to the maximum instantaneous laser power density of 13.8 TW/m2. To prevent the samples from oxidizing under the laser illumination, the following experiments were performed with the samples placed in a vacuum chamber under 10-6 mbar pressure.
3. Results and discussion
3.1. Measured Brillouin oscillation confirmed the acoustic phonon coupling from MoS2 vdWHs to GaN substrate
The acoustic phonon has been considered as the main heat carrier in semiconductors. The layer breathing mode of substrate-supported bi-layer MoS2 has been reported in numerous studies using Raman spectroscopy or picosecond ultrasonics. However, little is known about the complete motion behavior during the excitation for the initial displacement. For the monolayer and bi-layer MoS2/GaN vdWHs, the optical generation and coupling of the coherent phonons to the substrate has also not been thoroughly discussed as well. Therefore, we first experimentally measured the transmission change (see Fig. 2(b)) of the transferred 2L-MoS2 on GaN substrate without SQW (see Fig. 2(a)) to validate whether the MoS2/GaN vdWHs is able to generate and couple the coherent phonon into the substrate. The layer breathing mode at 1.2 THz was observed at the beginning of the response (see Fig. 2(c)) after background removal, which is the same result as the as-grown bi-layer samples on sapphire [16], indicating the transduction from the incident laser pulse to the acoustic energy. The leakage of coherent phonon into the substrate in the out-of-plane direction would cause the periodic optical interference, called Brillouin oscillation, and the frequency () can be calculated by the following equation:
| (1) |
where cS (=7950 m/s) is the sound velocity of the GaN substrate, n (=2.56 at 404 nm) is the refractive index of GaN, and θ (1.87°) and λ (404 nm) are the angle of incidence and the wavelength of the probe beam, respectively. Sinusoidal fitting and the calculated spectrum of the signal show a Brillouin oscillation at 102 GHz (see Fig. 2(d-e)), which agrees with the theoretically calculated value of 101 GHz. The pump-probe measurement was also performed on the GaN substrate without transferred MoS2, and we did not see the carrier relaxation signal or the Brillouin oscillation.
Fig. 2.
(a) Schematic illustration of the Brillouin oscillation resulting from the optical interference of laser pulse and the acoustic strain wave generated from the vdWHs; (b) Raw data of transmission change for 2L-MoS2/GaN; (c) Layer breathing mode of the bi-layer MoS2 on GaN substrate after transferring; (d) Oscillatory residual signal after decay background removal. Red solid line represents the sinusoidal fitting results; (e) Power spectral density of the Brillouin oscillation shows a single frequency peak at 102 GHz.
In addition, the leaked coherent phonon leading to Brillouin was not necessarily caused by the layer breathing mode (LBM) coherent phonon. Since the shift of the center of mass of the bi-layer MoS2 could not be detected by 2L-MoS2 itself, and the contribution from the transient state of the vdWHs system under the driving stress is still unknown at this moment. However, this experiment confirms the coupling of the generated coherent phonon into the substrate, and we would like to demonstrate the direct observation of the actual strain profile sent into the substrate by an additional photoacoustic transducer with THz bandwidth in the next section.
3.2. Background signal removal and the revealed coherent acoustic waves
From the experiments discussed in this section, the actual waveform of the coherent phonon coupling into the substrate and propagating to the SQW can be traced out by its strain-induced optical modulation properties. Fig. 3(a) shows the relative change in optical transmission for all three samples described in the subsections 2.1 and 2.2. The pump laser first passed through the samples and simultaneously excited the carriers in the MoS2 and the SQW at time zero. After the abrupt increase in transmission, the carriers in the two active regions would undergo a series of relaxations. The decay rate can be fitted by summing exponential decays with 2 and 3 different time constants for SQW and MoS2 +SQW, respectively. After removal of the relaxation background, the residuals were plotted in Fig. 3(b), and we can see three types of short-duration signals that were carried by a large negative cosinusoidal oscillation. The decaying oscillation signal between 0.9 ps and 6 ps, which exists only in the bi-layer case (blue color line), results from the LBM. Here, we used a target fitting function of () to fit the baseline change and then remove it to obtain the LBM oscillation (see the top panel of Fig. 3(c)).
Fig. 3.
(a) Relative optical transmission change of GaN with SQW (black solid line), 1L-MoS2 and 2L-MoS2 on GaN with SQW (green and blue solid lines); (b) Background signal fitting after the ΔT/T was fitted by exponential decay with different time constants. The red lines represent the fitting for Brillouin oscillation. The purple line represents the fitting for background signal near to the time zero for revealing the LBM oscillation. (each trace presented in this figure is from a single measurement); (c) Top panel: layer breathing mode of 2L-MoS2 on GaN. The inset shows the spectrum of the LBM vibration with peak frequency at 1.2 THz. Middle panel: coherent acoustic phonon generated by the vdWHs and detected by the SQW after 7.3 ps, which is the time required for the acoustic wave to propagate through the cap layer. Bottom panel: acoustic pulse launched by the SQW and was detected after round-trip-time of 14.6 ps (The shades on the traces represent the standard error of the mean).
When a longitudinal acoustic strain wave propagates through the SQW, the optical transmission of the probe beam would be linearly modulated by the Franz-Keldysh effect and thus could be used to visualize the acoustic waves. Considering the thickness of the cap layer and the sound velocity of GaN, the phonon propagation time through the cap layer is 7.3 ps. As we can see, an asymmetric bipolar signal with the duration of ∼5 ps can be observed after 7.3 ps as indicated by the first short-dashed line in the Fig. 3(b). This signal can be mainly attributed to the acoustic wave generated at the vdWHs and propagating the distance of the cap layer’s thickness to the SQW.
In addition, the peak of the negative unipolar pulse located at the round-trip-time of 14.6 ps (7.3 ps × 2) for the cap layer is considered to be the echo which was generated and detected by the SQW itself. When our InGaN SQW is irradiated by the near-UV femtosecond laser pulse, the electron-hole pairs are generated and then spatially separated due to the tilted electric field resulting from the piezoelectric effect of the strained quantum well. The separated charges would result in an instantaneous change of the electric field, leading to deformation of the SQW and launching an acoustic strain pulse on both sides of the SQW. Therefore, our SQW photoacoustic transducer can also generate a picosecond longitudinal acoustic wave in the out-of-plane direction, which could also induce a significant Brillouin oscillation. To isolate the signals, another target function () was introduced, which can describe the Brillouin oscillation with the nonuniform amplitude over time. All three types of isolated signals will be discussed in Section 3.3. In Fig. 4, we schematically showed the cross section of our transferred samples with MoS2/GaN vdWHs and InGaN SQW, and both of them contributed to the relaxation of the carrier dynamics and the generation and detection of coherent acoustic phonons.
Fig. 4.
Schematic of our MoS2/GaN vdWs heterostructure cross section.
3.3. Analysis and attribution of the acoustic coupling strength and the effective acoustic detection area
The vibrational lifetime of the LBM can give us an insight into the rate at which the coherent phonon decays into the thermal phonon [13]. See the top panel of Fig. 3(c), the ∼1 ps decay time of the interlayer vibration can be calculated by the full-width at half-maximum of the peak of the LBM (inset of top panel of Fig. 3(c)), and the value is close to the value of 2L-MoSe2 [13]. The peak at 1.2 THz is also consistent with our previous work [16] and low frequency Raman spectroscopy measurement. Since the bi-layer MoS2 is supported by the substrate and vdWs elastic coupling exists at the 2D/substrate interface, we must consider the phonon escaping into the substrate by introducing an additional time constant. The overall time constant can be written as , where and represent the time constants for the LBM phonon to scatter in the intralayer and couple its energy into the substrate, respectively. As the substrate changes, the substrate’s coupling strength would be different leading the change of the . By comparing the linewidth of the LBM for different substrates, including the sapphire [16], GaN, and quartz (see Fig. S1 in the supplementary materials), the overall time constants for the decay of the LBM remain at 1 ps. This indicates that the 1.2 THz phonon coupling to the substrate is weak and negligible, and we can consider the intralayer phonon lifetime as the only dominant term. The analytical solution leading to the same conclusion would be derived and discussed in the next section and the supplementary materials.
The middle panel of Fig. 3(c) shows our first observed acoustic strain waves between 7.3 ps and 12 ps with the help of the SQW, and the waveforms are asymmetric and bipolar-like for both 1L-MoS2 and 2L-MoS2. They are all consist of an initial weak negative strain followed by a large positive strain with longer pulse width. Our previous study showed that the compressive and tensile strain at the SQW would lead to the increase and decrease of the optical transmission change, respectively [17]. Therefore, we can realize that the surface of the GaN substrate at the vdWHs has been exerted negative stress (been pulled toward the MoS2) and positive stress (been pushed away from the MoS2) successively. Besides the larger peak-to-peak strain wave strength for the 2L-MoS2 vdWHs, the time for the acoustic strain waves to increase to their maximum and then finally decay to zero took a similar time ∼4.5 ps for both monolayer and bi-layer. Interestingly, there is a fluctuation feature between 8.5 ps and 11 ps for the monolayer case, and we think it can be attributed to the weak elastic response of the 1L-MoS2/GaN interface. In the bottom panel of Fig. 3(c), we have shown the round-trip echo that was launched by the SQW, reflected by the vdWHs, and detected by the SQW. We observed that the acoustic pulse width and the echo time for all three vdWHs structures are almost identical and this observation also suggests a weak coupling strength for the 2D/substrate interface.
Although the ability of the SQW to detect the incoming acoustic waves is phenomenal, we should also consider the possible detection sensitivity by the MoS2/GaN vdWHs. Considering the acoustic propagation in the opposite direction through the cap layer, the acoustic pulse generated by the SQW would propagate to the vdWHs interface and got reflected by the complete structure of the vdWHs (including the interface) at an exact probe delay time of 7.3 ps, which is half of the round trip time as shown by the bottom traces of Fig. 3(c). It is reasonable to assume that optical modulation may be present as the interface deforms, and its contribution to the signal right after 7.3 ps should be considered under this assumption. Since the MoS2/GaN interface and the thickness of the MoS2 layers are both thinner than the SQW, if there is any detection sensitivity contribution, the detection should also be instantaneous and provide a similar measurement for the pulse width. See the comparison between the middle and bottom panels of Fig. 3(c) around the gray dashed line. On the one hand, we observe that the first appearing negative pulse at 7.4 ps for the 1L-MoS2 case is weak and has a FWHM duration of ∼0.3 ps, which is much shorter than the 0.9 ps of the round-trip pulse. On the other hand, the 2L-MoS2 result not only shows a short pulse duration of less than 0.6 ps, but the peak time of the negative pulse has a non-negligible delay time of ∼0.4 ps. Our study thus does not provide any solid evidence to show the above-noise-level optical detection sensitivity of the strain pulse by the MoS2/GaN vdWHs.
It is also worth noting that the acoustic pulse launched by the SQW could couple its acoustic energy to the vdWHs and initiate the motion of the LBM and the center of mass of 2L-MoS2. However, we did not observe the 1.2 THz high-frequency oscillation in the bi-layer case after 7.3 ps. Based on the above discussion, our experimental results did not show sufficient necessity for us to consider the acoustic detection from the MoS2/GaN interface in our discussion. We thus conclude that the contribution may exist, but we think it may have been too weak and overwhelmed by the noise level. Therefore, the signals we observed between 7.3 ps and 12 ps in both the monolayer and bi-layer vdWHs were mainly the signal launched from the vdWHs and detected by the SQW after the traveling.
3.4. Theoretically derivation for the impulse response of an elastic vdWHs under driving stress
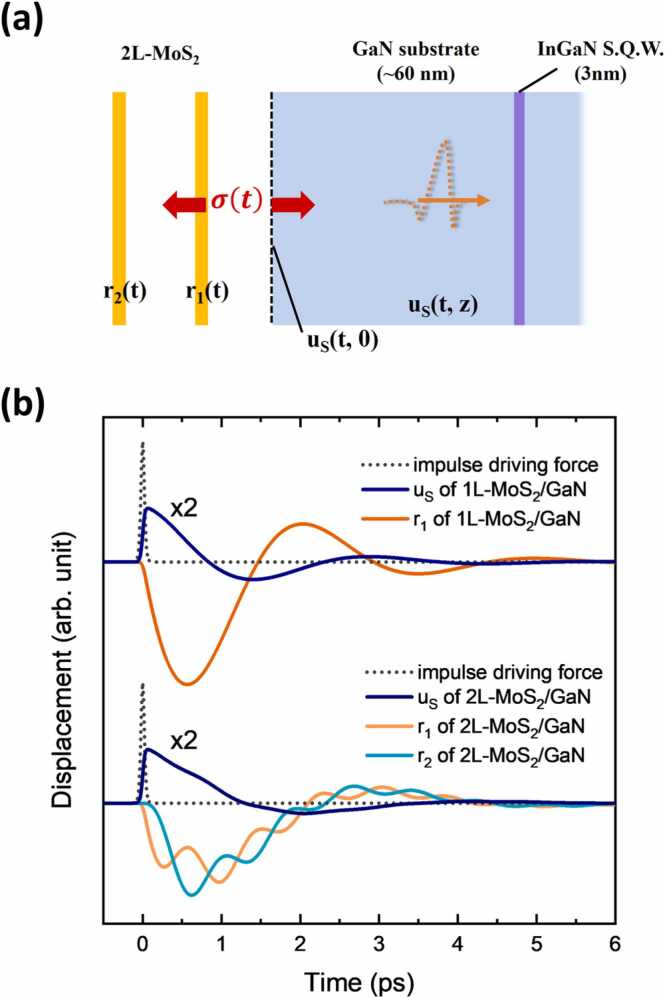
In order to give a physical explanation for the observed bipolar strain waves, we derived two theories describing the impulse response of such an elastic vdWHs system and the mechanisms of the driving stress resulting from the laser excitation, respectively. Eventually, the laser-induced displacement can be realized as the convolution result of the input driving stress with the impulse response of the elastic system of vdWHs (see Fig. 5). We first write down the equations of motion for discrete bi-layer MoS2 deposited on a continuum substrate with vdWs elastic coupling as the following:
| (2) |
| (3) |
| (4) |
where , , and denote the displacement of the 1st layer on the substrate, 2nd layer, and substrate respectively. μ is the area density. is the driving stress applied on the substrate and the 1st 2D layer in the opposite direction. The KS and K2L are the vdWs force constants of the substrate coupling and interlayer coupling respectively. The ρS and cS are the density and the longitudinal acoustic velocity of the substrate. The β in the equations describes the rate at which the vibrations are damped. Having derived the solution for the bi-layer case, we can simply set K2L and r2 to zero to obtain the solution for the monolayer case.
Fig. 5.
(a) Schematic of the elastic response of the vdWHs under interlayer driving force; (b) vdWHs elastic system’s impulse response of monolayer and bi-layer 2D films and substrate.
By Fourier transform, the phasor forms of the displacement for the substrate and the 2D materials can be represented as and respectively. Since is the conventional acoustic impedance, commonly referred to as Z, we let and to simplify the derived impulse response. The displacement solution for the 1st layer can be derived as (see the supplementary materials for the complete derivation):
| (5) |
and the displacement for the surface of the substrate can also be calculated using the following formula:
| (6) |
Since , we can obtain the complete displacement profile in the substrate once we convolute the impulse response to the driving stress, and the governing equation related to the driving stress is proposed and discussed in the next section.
The impulse response of the individual displacements of the substrate’s surface and the MoS2 layers are plotted in Fig. 5(b). Here we used the mechanical constants from our previous work [16] to simulate the response, and we can observe the following feature regarding to this vdWHs elastic system. Firstly, comparing the substrate surface (uS) with the first MoS2 layer (r1), the response for uS is faster than r1 and it is due to the phase delay nature of the oscillator, and the response for lower frequency is stronger as we can see in the bi-layer vdWHs. Secondly, the energy can be dissipated by both the damping term () and the substrate coupling, and the dominant term depends on the ratio of the acoustic impedance and the substrate force constant KS. Finally, we can see that although the LBM mode related displacement of the bi-layer vdWHs is significant, its coupling to the substrate is surprisingly low. This feature of the bi-layer impulse response could explain why we did not observe the LBM mode induced resonance by the acoustic-pulse-probed round-trip echo in the substrate. Taking into account the incident and reflected waves in the substrate by introducing the phasor of , we can further derive the acoustic reflectivity () for the strain waves of the vdWHs as the following equation (see the supplementary materials for the complete derivation):
| (7) |
3.5. Governing equation of the carrier dynamics under laser irradiation for simulating the driving stress
Here we would derive the indeterminate driving stress mentioned in the previous section for the simulation of the final strain. First, we write down the governing differential equations that describe how the energy is converted into different forms. When the femtosecond laser pulse was applied to the vdWHs, a fraction of the photons would be absorbed by the MoS2, causing the interband excitation and leading to the generation of electron-hole pair carriers. Later, the carriers would scatter with themselves through carrier-carrier scattering and become hot carriers () in tens of femtoseconds [18], [19], which was considered as instantaneous in our system. Due to the type-II heterojunction properties of the vdWHs, the electrons would transfer to the GaN substrate and the holes would instead be blocked by the large potential difference, as shown in Fig. 6(a). Meanwhile, high energy non-equilibrium electrons and holes in the MoS2 distributing in the band nesting region would scatter with the lattice, causing electron-phonon (e-ph) coupling. The typical electron-phonon coupling time is about 0.78 ps as reported in the literature [20] for MoS2, close to the value of 0.9 ps, which is the time when we can clearly see that the amplitude of LBM vibration reaches its maximum (see Fig. 3(c)). By the UED approach, the electrons undergoing scattering process with the lattice were directly visible below 5 ps [12], and the scattering would result in anisotropic phonon distribution.
Fig. 6.
(a) Type-II alignment band diagram of MoS2/GaN vdWHs and the carrier dynamics under laser excitation; (b) Carriers and phonon population change over time and thus induced driving force; (c) Displacement calculated by the measured strain waves (blue line: 2L-MoS2; green line: 1L-MoS2); (d) Fitting results (red dashed line) compared with averaged experimental data of 1L-MoS2 (green line) and 2L-MoS2 (blue line) (shifted −7.3 ps for the comparison with the simulation).
Because of the structural confinement of the TMDs, electrons and holes inside the MoS2 at the band edge would lose a small amount of their energy and form excitons or trions. Here we neglected the interlayer excitons, and the excitons would recombine and eventually disappear. The time constants representing the relaxation processes for electron-phonon scattering and exciton annihilation were denoted as and . The time constants for the exciton recombination rate can be obtained from the relaxation time fitting of our pump-probe experiments, which are on the time-scale of tens of picoseconds.
The complete process describing the hot carriers can be written as the following differential equation:
| (8) |
where is the time-domain intensity profile of the applied femtosecond laser, is the laser’s photon energy of the laser. Since the absorption rate would gradually decrease with increasing carrier density, a saturation laser intensity was introduced, which can be found in the reference [21] with a value of 413 GW/cm2. The saturation of the optical absorption rate () can be described as , and for monolayer and bi-layer were obtained by our transmission experiments with the value of 0.19 and 0.26 respectively.
During the cooling process of the hot carriers, carrier-phonon scattering would take place and the carriers would scatter with the optical phonon (including the ZA modes near the gamma point), giving its energy to the coherent lattice vibration. However, the phonon-phonon scattering would lead to the decrease of the coherence and the coherent phonon () would be reduced to the thermal phonon population and lead to the increase of the lattice temperature (). The above process is written as the following:
| (9) |
where is the decoherence time for the coherent phonon to generate the thermal phonon.
By density functional theory method and Raman spectroscopy, respectively, the phonon lifetimes have been reported to be ∼5 ps (for acoustic phonons) for graphene [22] and 5.1 ps (for E1 u mode) for bulk MoS2 [23]. In contrary, the acoustic phonon lifetime for MoS2 has been estimated by numerical methods to be less than 2 ps [24]. In addition, another first principle study [25] reported the acoustic phonon lifetime to be larger than 10 ps and increasing with decreasing frequency. Overall, the typical value for the optical phonon decay time has been reported with the value of 1–5 ps [26], which will be left as one of the fitting parameters to be determined.
The lattice temperature increase resulted from the energy of the photocarrier-released optical phonons (∼12 THz [27]). Therefore, the temperature increase rate can be estimated by the feed-in energy divided by the heat capacity () of the MoS2, and the value was taken as a constant of 5.81×10-4 (Joule∙K-1∙m-2) from the reference [28]. Finally, the heat inside the MoS2 would diffuse and conduct to the surrounding materials by in-plane and interfacial conductivity [29], which will occur on a longer time scale (>100 ps). The governing equation with the thermal phonon cooling time constant () can be written as:
| (10) |
where is the lattice temperature, and is the frequency of the coherent phonon.
The cascading steps for the thermal stress to eventually build up imply that it is a rather slow process compared to the charge transfer process. The rate equation for the transferred charges can be described by the following equation:
| (11) |
where is the time constants for the charge transfer process and is the decay time for the transferred charge in the bulk GaN.
The transferred charge would result in a driving stress that pulls the substrate and MoS2 closer together, and the thermal stress induced by the temperature rise would in turn push the vdWHs apart (see Fig. 6(b-c)). Thus, the driving force can be written as the linear combination of the transferred charge and the temperature rise with hidden variables as (), where p and q are the fitting parameters.
3.6. The fitted carrier parameters for acoustic strain wave simulation
The fitting parameters used to simulate the displacement for fitting were listed in the Table 1. The strain of the substrate can be obtained by differentiating the displacement with respect to time and then being divided by the sound velocity with minus sign. In addition, we considered the SQW width of 2.9 nm and assumed the spatial acoustic detection function as a Gaussian-like profile, and the measured waveform can be realized by convolving the simulated strain with the detection function. By fitting the experimental results to our theory, we have successfully simulated the strain waves we observed with the SQW (see Fig. 6(d)). The fitted time constants for the e-ph coupling are about hundreds of fs, which is close to the typical value we have discussed. Furthermore, the best-fit result shows that the charge transfer time (τCT) for monolayer and bi-layer vdWHs is ∼1 ps for both cases. We also obtained the τOP of ∼2 ps, which is close to the observed decay time for the LBM mode and the lower bounds of the previous references.
Table 1.
Parameters for the simulation of strain obtained by fitting.
| 1L-MoS2/GaN | 2L-MoS2/GaN | |
|---|---|---|
| τe-ph (ps) | 0.6 | 0.3 |
| τexciton (ps) | 41.4 (from exp.) | 64.1 (from exp.) |
| τOP (ps) | 2.2 | 1.8 |
| τcooling (ps) | 20 (insignificant to fitting) | |
| τCT (ps) | 1 | |
| τinterL (ps) | 40 (insignificant to fitting) | |
| β (N∙s/m3) | 3.6×106 | 6×106 |
| KS (N/m3) | 2.4×1019 | 1.6×1019 |
For the 1L-MoS2/GaN case, we experimentally observed a signal inversion in the range of 1.5–3.5 ps (in Fig. 6(d)). This feature can be attributed to the layer vibration resulting from the substrate vdWs elastic coupling. It is a highly damped system and thus the full damping of the oscillatory strain signal is difficult to observe. In particular, the last dip observed at 4.2 ps (in Fig. 6(d)) showed noisy and non-coherent behavior, and thus we should not rely on the measurement of the time-difference for the adjacent minimum as the period to calculate the elastic force constant. If we simply used method, the ∼1.5 ps period would correspond to the 4.7 × 1019 N/m3, which is too large for a typical transferred vdWs interface. Therefore, the reasonable retrieval of the substrate elastic constant would be applied by a good fit to the experimental data in an appropriate range using our model. Our best-fit results yield substrate elastic force constants of 2.4 × 1019 N/m3 and 1.6 × 1019 N/m3 for 1L-MoS2/GaN and 2L-MoS2/GaN, respectively.
We define the fitting error as the residual sum of squares, between experiment and theory, divided by the sum of squares of the experimental data. The best-fit error for monolayer and bi-layer are 12.4% and 2.8%, respectively. Varying the KS would increase the error. Under the error threshold of 15% for the monolayer, the fitted KS is ranging from 2.0 × 1019 N/m3 to 3.1 × 1019 N/m3. Under the 5% and 15% error thresholds for the bi-layer, the fitted KS are ranging from 1.2 × 1019 N/m3 to 1.9 × 1019 N/m3 and 0.9 × 1019 N/m3 to 2.9 × 1019 N/m3, respectively. The stronger substrate elastic force constant for the monolayer case can be explained by several reasons, such as the difference of the intrinsic vdWs coupling or less interfacial residue. Both transferred samples showed a stronger substrate elastic coupling compared to the as-grown MoS2/sapphire samples, which is 1.48 × 1019 N/m3, and it probably results from the lattice constant matching (<1%) for MoS2 and wurtzite GaN (0001). Finally, the lower damping constant for CVD synthesized monolayer MoS2 can be attributed to fewer defects and larger grain size leading to weaker grain boundary scattering.
4. Conclusion
In conclusion, we have used the InGaN SQW to investigate a series of carrier-induced coherent phonon phenomena in the MoS2/GaN vdWHs. We established a theory for the simulation of the observed acoustic coherent strain waves by calculating the convolution of the elastic impulse response to the driving stress resulting from the carrier dynamics and the charge transfer in the vdWHs. The first observed acoustic coherent phonon is generated from the vdWHs, and this observation describes a thermal energy transfer pathway that the high-frequency coherent phonon has to scatter to thermal phonon to efficiently couple with the substrate. The obtained parameters, including the charge transfer time, would benefit the design of the 2D-based devices in the future.
CRediT authorship contribution statement
Peng-Jui Wang: Conceptualization, Methodology, Experiments - ultrafast pump-probe measurements, Validation, Formal analysis, Writing – original draft, Writing – review & editing. Che-Jia Chang: Experiments – MoS2 transferring and Raman spectroscopy, Formal analysis, Writing – review & editing. Shih-Yen Lin: Writing – original draft, Writing – review & editing, Supervision. Jinn-Kong Sheu: Writing – original draft, Writing – review & editing, Supervision. Chi-Kuang Sun: Conceptualization, Methodology, Writing – original draft, Writing – review & editing, Supervision, Funding acquisition.
Declaration of Competing Interest
The authors have no conflicts of interest to disclose.
Acknowledgements
This project is sponsored by the National Science and Technology Council, R.O.C under MOST 110-2112-M-002-033 -MY3. We thank Yu-Tsun Yao for the MOCVD growth of the GaN film on the sapphire substrate. We thank Po-Cheng Tsai for the epitaxial growth of the bi-layer MoS2 on the sapphire substrate.
Biographies

Peng-Jui Wang received his B.S. degree in electrical engineering from National Taiwan University in 2014. He is currently a Ph.D. candidate in Graduate Institute of Photonics and Optoelectronics, National Taiwan University. His research focuses on THz photoacoustics, 2D materials, and ultrafast optics.

Che-Jia Chang received his M.S. degree in electrical and computer engineering from department of photonics, National Yang Ming Chiao Tung University, Hsinchu, Taiwan in 2022. He is currently studying for Ph.D. degree in Graduate Institute of Electronics Engineering, National Taiwan University, Taipei, Taiwan. His research interests include heteroepitaxy on 2D material surfaces and large-area 2D material for electrical devices.

Shih-Yen Lin received the Ph.D degree in electrical engineering from National Taiwan University at 2001. He was the deputy of manager of R&D department at Land Mark optoelectronics corp., Tainan, Taiwan during 2001–2003. From 2003–2006, he was with Electronics & Optoelectronics Research Laboratories, Industrial Technology Research Institute (ITRI), Hsinchu, Taiwan. He joined Research Center for Applied Sciences (RCAS), Academia Sinica, Taipei, Taiwan since 2006. He is now a research fellow at RCAS. His research interests are on the applications of MBE-prepared nano-structures and large-area 2-D crystals for opto-electrical devices. He is now a senior member of IEEE.

Jinn-Kong Sheu received the Ph.D. degree in electrical engineering from National Cheng Kung University (NCKU), Tainan, Taiwan, in 1999. From 1997–2000, he was a Senior Research and Development Engineer at Epistar Corporation Ltd., Taiwan, specializing in the manufacturing of high brightness LED chips and the growth of epitaxial wafers. He is currently a Distinguished Professor with the Department of Photonics, NCKU. He is a fellow of Optica.

Chi-Kuang Sun received his PhD in applied physics from Harvard University in 1995 and was an assistant researcher in the UCSB QUEST Center from 1995 to 1996. In 1996, he joined National Taiwan University, where he is now a distinguished professor of photonics and optoelectronics. He founded the NTU Molecular Imaging Center. His research focuses on nano-acoustics, femtosecond optics, THz optoelectronics, and biomedical imaging. He is a fellow of Optica, SPIE, and IEEE and is currently the present of Taiwan Photonics Society.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.pacs.2023.100477.
Appendix A. Supplementary material
Supplementary material.
.
Data availability
No data was used for the research described in the article.
References
- 1.Choi W., Choudhary N., Han G.H., Park J., Akinwande D., Lee Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today. 2017;20(3):116–130. [Google Scholar]
- 2.Costanzo D., Jo S., Berger H., Morpurgo A.F. Gate-induced superconductivity in atomically thin MoS2 crystals. Nat. Nanotechnol. 2016;11(4):339–344. doi: 10.1038/nnano.2015.314. [DOI] [PubMed] [Google Scholar]
- 3.Chaves A., Azadani J.G., Alsalman H., da Costa D.R., Frisenda R., Chaves A.J., Song S.H., Kim Y.D., He D., Zhou J., Castellanos-Gomez A., Peeters F.M., Liu Z., Hinkle C.L., Oh S.-H., Ye P.D., Koester S.J., Lee Y.H., Avouris P., Wang X., Low T. Bandgap engineering of two-dimensional semiconductor materials. npj 2D Mater. Appl. 2020;4(1) [Google Scholar]
- 4.Wang Q., Zhang L., Liu X., Li S. Two-dimensional semiconductor heterojunctions for optoelectronics and electronics. Front. Energy Res. 2021;9 [Google Scholar]
- 5.Jain S.K., Low M.X., Taylor P.D., Tawfik S.A., Spencer M.J.S., Kuriakose S., Arash A., Xu C., Sriram S., Gupta G., Bhaskaran M., Walia S. 2D/3D hybrid of MoS2/GaN for a high-performance broadband photodetector. ACS Appl. Electron. Mater. 2021;3(5):2407–2414. [Google Scholar]
- 6.Lee E.W., Lee C.H., Paul P.K., Ma L., McCulloch W.D., Krishnamoorthy S., Wu Y., Arehart A.R., Rajan S. Layer-transferred MoS2/GaN PN diodes. Appl. Phys. Lett. 2015;107(10) [Google Scholar]
- 7.Zhang Z., Qian Q., Li B., Chen K.J. Interface engineering of monolayer MoS(2)/GaN hybrid heterostructure: modified band alignment for photocatalytic water splitting application by nitridation treatment. ACS Appl. Mater. Interfaces. 2018;10(20):17419–17426. doi: 10.1021/acsami.8b01286. [DOI] [PubMed] [Google Scholar]
- 8.Jiang Y., Chen S., Zheng W., Zheng B., Pan A. Interlayer exciton formation, relaxation, and transport in TMD van der Waals heterostructures. Light Sci. Appl. 2021;10(1):72. doi: 10.1038/s41377-021-00500-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cai W., Moore A.L., Zhu Y., Li X., Chen S., Shi L., Ruoff R.S. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 2010;10(5):1645–1651. doi: 10.1021/nl9041966. [DOI] [PubMed] [Google Scholar]
- 10.Wang R., Zobeiri H., Xie Y., Wang X., Zhang X., Yue Y. Distinguishing optical and acoustic phonon temperatures and their energy coupling factor under photon excitation in nm 2D materials. Adv. Sci. 2020;7(13) doi: 10.1002/advs.202000097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yan R., Simpson J.R., Bertolazzi S., Brivio J., Watson M., Wu X., Kis A., Luo T., Hight Walker A.R., Xing H.G. Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent raman spectroscopy. ACS Nano. 2014;8(1):986–993. doi: 10.1021/nn405826k. [DOI] [PubMed] [Google Scholar]
- 12.Britt T.L., Li Q., Rene de Cotret L.P., Olsen N., Otto M., Hassan S.A., Zacharias M., Caruso F., Zhu X., Siwick B.J. Direct view of phonon dynamics in atomically thin MoS(2) Nano Lett. 2022;22(12):4718–4724. doi: 10.1021/acs.nanolett.2c00850. [DOI] [PubMed] [Google Scholar]
- 13.Soubelet P., Reynoso A.A., Fainstein A., Nogajewski K., Potemski M., Faugeras C., Bruchhausen A.E. The lifetime of interlayer breathing modes of few-layer 2H-MoSe2 membranes. Nanoscale. 2019;11(21):10446–10453. doi: 10.1039/c9nr02447f. [DOI] [PubMed] [Google Scholar]
- 14.Chen I.J., Mante P.A., Chang C.K., Yang S.C., Chen H.Y., Huang Y.R., Chen L.C., Chen K.H., Gusev V., Sun C.K. Graphene-to-substrate energy transfer through out-of-plane longitudinal acoustic phonons. Nano Lett. 2014;14(3):1317–1323. doi: 10.1021/nl404297r. [DOI] [PubMed] [Google Scholar]
- 15.Zheng T., Valencia-Acuna P., Zereshki P., Beech K.M., Deng L., Ni Z., Zhao H. Thickness-dependent interlayer charge transfer in MoSe(2)/MoS(2) heterostructures studied by femtosecond transient absorption measurements. ACS Appl. Mater. Interfaces. 2021;13(5):6489–6495. doi: 10.1021/acsami.0c18268. [DOI] [PubMed] [Google Scholar]
- 16.Wang P.-J., Tsai P.-C., Yang Z.-S., Lin S.-Y., Sun C.-K. Revealing the interlayer van der Waals coupling of bi-layer and tri-layer MoS2 using terahertz coherent phonon spectroscopy. Photoacoustics. 2022;28 doi: 10.1016/j.pacs.2022.100412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang P.-J., Shen C.-C., Chou K.-Y., Ho M.-H., Sheu J.-K., Sun C.-K. Studying time-dependent contribution of hot-electron versus lattice-induced thermal-expansion response in ultra-thin Au-nanofilms. Appl. Phys. Lett. 2020;117(15) [Google Scholar]
- 18.George P.A., Strait J., Dawlaty J., Shivaraman S., Chandrashekhar M., Rana F., Spencer M.G. Ultrafast optical-pump terahertz-probe spectroscopy of the carrier relaxation and recombination dynamics in epitaxial graphene. Nano Lett. 2008;8(12):4248–4251. doi: 10.1021/nl8019399. [DOI] [PubMed] [Google Scholar]
- 19.Song J.C.W., Tielrooij K.J., Koppens F.H.L., Levitov L.S. Photoexcited carrier dynamics and impact-excitation cascade in graphene. Phys. Rev. B. 2013;87(15) [Google Scholar]
- 20.Luo D., Tang J., Shen X., Ji F., Yang J., Weathersby S., Kozina M.E., Chen Z., Xiao J., Ye Y., Cao T., Zhang G., Wang X., Lindenberg A.M. Twist-angle-dependent ultrafast charge transfer in MoS(2)-Graphene van der Waals heterostructures. Nano Lett. 2021;21(19):8051–8057. doi: 10.1021/acs.nanolett.1c02356. [DOI] [PubMed] [Google Scholar]
- 21.Wang K., Wang J., Fan J., Lotya M., O’Neill A., Fox D., Feng Y., Zhang X., Jiang B., Zhao Q., Zhang H., Coleman J.N., Zhang L., Blau W.J. Ultrafast saturable absorption of two-dimensional MoS2 nanosheets. ACS Nano. 2013;7(10):9260–9267. doi: 10.1021/nn403886t. [DOI] [PubMed] [Google Scholar]
- 22.Bonini N., Garg J., Marzari N. Acoustic phonon lifetimes and thermal transport in free-standing and strained graphene. Nano Lett. 2012;12(6):2673–2678. doi: 10.1021/nl202694m. [DOI] [PubMed] [Google Scholar]
- 23.Sun Q., Mazumdar D., Yadgarov L., Rosentsveig R., Tenne R., Musfeldt J.L. Spectroscopic determination of phonon lifetimes in rhenium-doped MoS2 nanoparticles. Nano Lett. 2013;13(6):2803–2808. doi: 10.1021/nl401066e. [DOI] [PubMed] [Google Scholar]
- 24.Cai Y., Lan J., Zhang G., Zhang Y.-W. Lattice vibrational modes and phonon thermal conductivity of monolayer MoS$_{2}$ Phys. Rev. B. 2014;89(3) [Google Scholar]
- 25.Gu X., Yang R. Phonon transport in single-layer transition metal dichalcogenides: a first-principles study. Appl. Phys. Lett. 2014;105(13) [Google Scholar]
- 26.Kaasbjerg K., Bhargavi K.S., Kubakaddi S.S. Hot-electron cooling by acoustic and optical phonons in monolayers ofMoS2and other transition-metal dichalcogenides. Phys. Rev. B. 2014;90(16) [Google Scholar]
- 27.Su J., Liu Z.-t, Feng L.-p, Li N. Effect of temperature on thermal properties of monolayer MoS2 sheet. J. Alloy. Compd. 2015;622:777–782. [Google Scholar]
- 28.Saha D., Mahapatra S. Analytical insight into the lattice thermal conductivity and heat capacity of monolayer MoS 2. Phys. E Low Dimens. Syst. Nanostruct. 2016;83:455–460. [Google Scholar]
- 29.Suryavanshi S.V., Gabourie A.J., Barati Farimani A., Pop E. Thermal boundary conductance of two-dimensional MoS2 interfaces. J. Appl. Phys. 2019;126(5) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material.
Data Availability Statement
No data was used for the research described in the article.