Challenges in modeling the Agility multileaf collimator in treatment planning systems and current needs for improvement

Abstract

Background

The Agility multileaf collimator (MLC) mounted in Elekta linear accelerators features some unique design characteristics, such as large leaf thickness, eccentric curvature at the leaf tip, and defocused leaf sides (‘tilting'). These characteristics offer several advantages but modeling them in treatment planning systems (TPSs) is challenging.

Purpose

The goals of this study were to investigate the challenges faced when modeling the Agility in two commercial TPSs (Monaco and RayStation) and to explore how the implemented MLC models could be improved in the future.

Methods

Four linear accelerators equipped with the Agility, located at different centers, were used for the study. Three centers use the RayStation TPS and the other one uses Monaco. For comparison purposes, data from four Varian linear accelerators with the Millennium 120 MLC were also included. Average doses measured with asynchronous sweeping gap tests were used to characterize and compare the characteristics of the Millennium and the Agility MLCs and to assess the MLC model in the TPSs. The FOURL test included in the ExpressQA package, provided by Elekta, was also used to evaluate the tongue‐and‐groove with radiochromic films. Finally, raytracing was used to investigate the impact of the MLC geometry and to understand the results obtained for each MLC.

Results

The geometry of the Agility produces dosimetric effects associated with the rounded leaf end up to a distance 20 mm away from the leaf tip end measured at the isocenter plane. This affects the tongue‐and‐groove shadowing, which progressively increases along the distance to the tip end. The RayStation and Monaco TPSs did not account for this effect, which made trade‐offs in the MLC parameters necessary and greatly varied the final MLC parameters used by different centers. Raytracing showed that these challenging leaf tip effects were directly related to the MLC geometry and that the characteristics mainly responsible for the large leaf tip effects of the Agility were its tilting design and its small source‐to‐collimator distance.

Conclusions

The MLC models implemented in RayStation and Monaco could not accurately reproduce the leaf tip effects for the Agility. Therefore, trade‐offs are needed and the optimal MLC parameters are dependent on the specific characteristics of treatment plans. Refining the MLC models for the Agility to better approximate the measured leaf tip and tongue‐and‐groove effects would extend the validity of the MLC model, reduce the variability in the MLC parameters used by the community, and facilitate the standardization of the MLC configuration process.

1. INTRODUCTION

In modern radiotherapy, treatment planning systems (TPSs) generate highly conformal dose distributions using intensity modulated radiotherapy (IMRT) and volumetric modulated arc therapy (VMAT), in which the beam aperture is modulated by multileaf collimators (MLCs). In this context, accurate modeling of the MLC in the TPS is essential to guarantee that the planned dose is delivered to the patients. ¹ , ² , ³ , ⁴

However, the MLC configuration process is challenging because it is not standardized. A wide variety of methods and detectors for commissioning are recommended by TPS manufacturers and in international guidelines. ⁵ , ⁶ , ⁷ Additionally, plan‐specific quality assurance (PSQA) results obtained with commercial IMRT QA devices are often used for fine‐tuning the MLC model in the TPS despite many investigators having reported poor sensitivity of these devices to errors in the calculated doses. ⁸ , ⁹ , ¹⁰ Hence, it is not surprising to find a large variability in the MLC modeling parameters used by the community, which raises concerns about the MLC models used in the clinic. ¹¹ Furthermore, it is well known that MLC parameters have a strong impact on IMRT/VMAT dose calculations, and considerable dose calculation errors are present in 17% of the institutions participating in IROC's external end‐to‐end audits. ¹²

A novel procedure was recently proposed for standardizing the MLC configuration in TPSs using asynchronous sweeping gap (SG) tests and measurements with a Farmer‐type ion chamber. ¹³ The main concept behind this procedure is that the average dose in a region spanning several leaves can be used for characterizing and modeling fine details of the MLC such as the tongue‐and‐groove width and the leaf tip width. Analytical expressions for the determination of the MLC configuration parameters in the RayStation TPS were reported, but the method was applied only to the Millennium 120 and High Definition (HD120) Varian MLCs. ¹³

Elekta (Elekta AB, Stockholm, Sweden) linear accelerators (linacs) are also widely used in radiotherapy and all new Elekta linacs are equipped with the Agility MLC, which provides accurate and efficient IMRT treatments. ¹⁴ The Agility MLC features some unique design characteristics, such as a large leaf thickness, an eccentric curvature at the leaf tip, and defocusing of the leaf sides to minimize interleaf leakage (“tilting”), ¹⁵ which could be challenging for MLC models implemented in TPSs. Adequate clinical results can be obtained for the Agility MLC ¹⁶ but there is no consensus on the MLC configuration process to be used and discrepancies have been reported between MLC models obtained using either simple test fields or clinical plans. For instance, Snyder et al. pointed out that tuning the MLC model to match test field profiles did not maximize accuracy in clinical plans. ¹⁷ Similarly, Roche et al. reported that the effective tongue‐and‐groove on the Agility could not be accurately characterized in the Monaco TPS and recommended not using the QA field “FOURL” provided by Elekta to match the dose at the tongue‐and‐groove junctions. ¹⁸ The reasons for such discrepancies, however, remain unknown.

The aims of this study were to investigate the challenges in modeling the Agility MLC, to identify limitations in the MLC models implemented in two commercial TPSs (Monaco and RayStation), and to evaluate the need for future improvements in these models.

2. MATERIALS AND METHODS

2.1. Equipment used

Four Elekta linear accelerators located at four different centers were used, all equipped with the Agility MLC (Elekta AB, Stockholm, Sweden). Measurements and calculations were carried out at all participating centers using their own equipment and TPS models. Three of the centers use the RayStation TPS (RaySearch Laboratories, Stockholm, Sweden) and the fourth uses Monaco (Elekta AB, Stockholm, Sweden). Details on the equipment and TPSs used are given in Table 1. Although the present study focuses on the Agility, measurements from four TrueBeam systems (Varian Medical Systems, Palo Alto, CA) equipped with the Millennium 120 MLC were also included for comparison purposes.

TABLE 1.

Linacs, MLCs, and TPSs included in the study

Centre	Linac model	MLC model	TPS	Dose calculation engine
A	Versa HD	Agility	RayStation 10A	Collapsed Cone
B	Versa HD	Agility	RayStation 9B	Collapsed Cone
C	Synergy	Agility	RayStation 10B	Collapsed Cone
D	Versa HD	Agility	Monaco 5.51.10	Monte Carlo (XVMC)

The Agility MLC contains 160 leaves with a projected leaf width of 5 mm at the isocenter plane that can interdigitate to deliver complex IMRT and VMAT plans. ¹⁵ , ¹⁶ The Agility leaves can be modeled with a height of 90 mm and have rounded leaf ends with an eccentric curvature (center of the curvature located at 37.5 mm from the upper part of the leaves and at 52.5 mm from their lower part, that is, shifted 7.5 mm from the midleaf plane). ¹⁹ The leaf sides are flat and, to avoid direct beam irradiation through the small air gap between leaves, the leaves are rotated to defocus their sides from the source (“tilting”). Thus, there are no physical tongue‐and‐groove regions, but this tilted design with defocused leaves produces an effective tongue‐and‐groove width at the leaf sides. ²⁰

The leaf sides of the Millennium and High Definition (HD120) Varian MLCs, on the contrary, are designed with complementary tongue‐and‐groove regions extending outward and inward in such a way that adjacent leaf sides interlock to reduce interleaf transmission. Table 2 summarizes the main geometric characteristics of these MLCs typically used in C‐arm linacs. A sketch of the different tongue‐and‐groove designs can be found in section III.D (see leaf sections in Figure 6). More detailed information on the design and characteristics of these MLCs can be found in the literature. ¹⁵ , ²¹ , ²²

TABLE 2.

Main MLC geometric characteristics

MLC model	Leaf	Leaf	SCD	Radius	Eccentric	T&G leaf
and manufacturer	width*	thickness	(cm)	(cm)	curvature	design
Agility (Elekta)	5 mm	9.0 cm	34.93	17	Yes	Tilted
Millennium 120 (Varian)	5 & 10 mm	6.5 cm	51.0	8	No	Interlocking
HD120 (Varian)	2.5 & 5 mm	6.75 cm	51.0	16	No	Interlocking

SCD, source‐to‐collimator distance (measured at the center of curvature); T&G, tongue‐and‐groove. *Measured at the isocenter plane.

FIGURE 6.

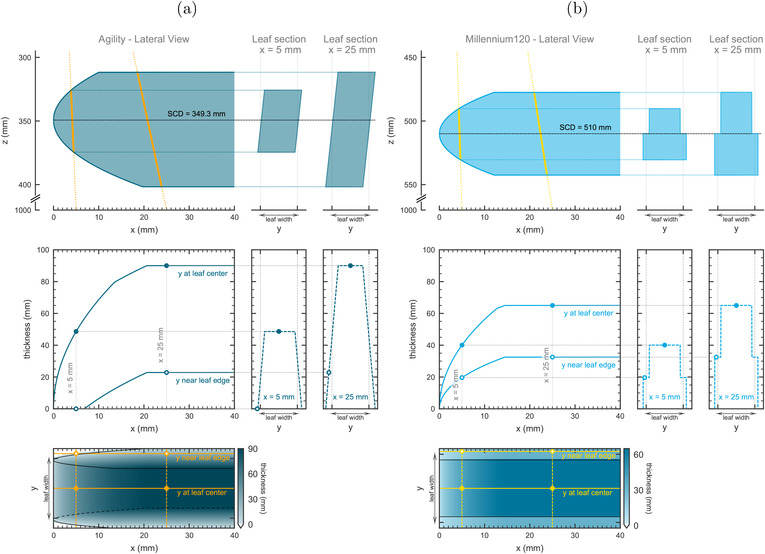
Results obtained with raytracing for the Agility (left) and Millennium MLC (right) Upper row: sketch with a lateral view of a leaf positioned at the central axis along with the leaf sections corresponding to projected positions at 5 and 25 mm. Middle row: traversed leaf thickness as a function of the off‐axis distance computed along lines in the x‐direction (at the leaf center and near the leaf edge) and in the y‐direction (at $x=$ 5 and 25 mm). The position of these lines is plotted in the lower row. Lower row: 2D map illustrating the traversed leaf thickness in the beam's eye view. All distances are indicated at the isocenter plane.

The RayStation TPS uses an analytical MLC transmission model with constant transmission regions from which a fluence is computed using projection of virtual sources, and the fluence is further traced into the patient using a collapsed cone or a Monte Carlo computation. ²³ The leaf tip and the tongue‐and‐groove regions are modeled with a partial transmission equal to T ^0.5, where T is the average MLC transmission. The widths of these regions can be configured with the user‐definable parameters leaf tip width and tongue‐and‐groove. Three additional parameters (offset, gain, and curvature) can be used to define the difference between the radiological leaf positions used in dose calculations and the nominal DICOM positions of the leaf tips. Different versions of RayStation were used in this study (see Table 1), but the MLC model was identical in all of them. A detailed description of the MLC model in RayStation can be found in the literature. ¹³ , ²³

The Monaco TPS uses three components for beam modeling: a virtual source model (VSM), transmission probability filters (TPFs) to model the jaws and the MLC, and an x‐ray voxel Monte Carlo (XVMC) engine to calculate the dose deposition in the patient. ²⁴ , ²⁵ The TPFs are characterized with geometric and probabilistic parameters that determine the probability of transmission through different regions of each collimator and 11 equally spaced transmission filters are used to characterize the MLC in three dimensions for a more accurate determination of oblique photons. ¹⁸ Some user‐definable MLC parameters in Monaco (MLC offset, leaf groove width, leaf transmission) resemble the ones in RayStation (MLC offset, tongue and groove, MLC transmission), whereas others address TPS‐specific features (leaf tip leakage, MLC leakage, interleaf leakage) ¹⁷ , ¹⁸ and produce differences in the final MLC models.

2.2. Tests and procedures used

2.2.1. Sweeping gap and asynchronous sweeping gap tests

SG and asynchronous SG (aSG) fields were used. In the SG tests, a dynamic MLC defines a rectangular beam aperture with the leaf pairs aligned (a “sliding slit” of a given gap size) that travels a certain distance d from left to right at a constant speed. The distance traveled was 12 cm and the dynamic sequence was defined with 13 control points. A dose rate of 500 MU/min was used and 200 monitor units (MU) were delivered for each field. The Y diaphragms were set to 10 cm and gap sizes of 5, 10, 20, and 30 mm were used. These tests were based on the SGs typically used for measuring the dosimetric leaf gap (DLG) in Varian linear accelerators. ²⁶ , ²⁷

The aSG tests are similar to the SG tests, but alternate leaves are offset a certain distance s in order to expose a controlled amount of the tongue‐and‐groove regions (leaf sides). ²⁸ The resulting aperture shape is no longer rectangular, but the gap size is the same for all leaf pairs and the same leaf pattern is kept across the dynamic sequence. These tests are illustrated in Figure 1.

FIGURE 1.

Schematic representation of the synchronous and asynchronous sweeping gap fields: (a) sweeping gap test for a gap size of 20 mm and (b) asynchronous sweeping gap test for the same gap size and distance between adjacent leaves $s=5$ mm

The doses for the SG/aSG tests were measured in water using a Farmer‐type ion chamber. Measurements were carried out with 6 MV photon beams at a depth of 10 cm and a source‐to‐surface distance of 90 cm. The gantry and the collimator angle were set to 0°.

In this approach, using a large ion chamber such as a Farmer chamber is crucial because its active length makes it adequate for measuring the average doses across several leaves. To that aim, the long axis of the Farmer chamber was placed perpendicular to the leaf motion direction (i.e., inplane). Furthermore, to average the doses better across different leaves, measurements were taken with the ion chamber at two longitudinal positions at +11.25 and −11.25 mm from the central axis, and the average reading was used.

2.2.2. Procedure to obtain the fluence reduction at the exposed leaf sides

As the distance between adjacent leaves in the aSG tests is increased, the amount of exposed leaf side also increases, which produces a reduction in the measured average doses due to the tongue‐and‐groove effect. This reduction can be characterized by the reduction in the total primary fluence or, more specifically, with the fluence reduction at the leaf sides as a function of the distance to the leaf tip end. This fluence reduction can be obtained from the average doses of the SG/aSG tests following the methodology proposed by Saez et al., ¹³ which we briefly explain below.

Let us first consider a regular SG field. The average dose for the SG is proportional to the total primary fluence ϕ_SG in the area under a leaf pair: ²⁹

$$D_{\mathrm{SG}}=k{\varphi }_{\mathrm{SG}},$$ (1)

where k is a constant that relates fluence values to dose units. The total primary fluence under a leaf pair can be approximated as

$${\varphi }_{\mathrm{SG}}=w_{\mathrm{leaf}}{\text{gap}}_{\mathrm{eff}}+w_{\mathrm{leaf}}\left(d-{\text{gap}}_{\mathrm{eff}}\right)T,$$ (2)

where w _leaf is the nominal leaf width at the isocenter plane (5 mm for the Agility), ${\text{gap}}_{\mathrm{eff}}$ is the effective gap size, d is the distance traveled by the leaves, and T is the average MLC transmission. The effective gap size can be obtained from the nominal gap size by adding an offset δ at each leaf position or, equivalently, by increasing the gap size by the DLG ²⁹ , ³⁰ :

$${\text{gap}}_{\mathrm{eff}}=\text{gap}+2\delta =\text{gap}+\mathrm{DLG}.$$ (3)

From these equations, it follows that

$$D_{\mathrm{SG}}=k{w}_{\mathrm{leaf}}\left[\text{gap}+2\delta (1-T)+dT\right],$$ (4)

which shows that, as pointed out by several authors, ²⁶ , ²⁷ D _SG depends linearly on the nominal gap size and can, consequently, be expressed as

$$D_{\mathrm{SG}}=\lambda \text{gap}+\gamma .$$ (5)

The parameters λ and γ can be experimentally obtained and using Equations (4) and (5), it can be deduced that

$$k=\frac{\lambda }{w_{\mathrm{leaf}}\left(1-T\right)},$$ (6)

$$\delta =\frac{1}{2}\left(\frac{\gamma }{\lambda }-\frac{dT}{1-T}\right).$$ (7)

Hence, k can be obtained from the readings of the SG fields, the nominal leaf width w _leaf and average transmission T using Equation (6). Similarly, the offset δ can be obtained using Equation (7), as well as the DLG as DLG $=2\delta$.

Let us consider next an aSG field with a distance s between adjacent leaves. The fluence at the exposed leaf sides will be reduced due to the tongue‐and‐groove effect. The fluence reduction at each leaf side for a given distance s can be expressed as $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ and the total primary fluence under a leaf pair for an aSG field results into

$${\varphi }_{\mathrm{aSG}}(s)={\varphi }_{\mathrm{SG}}-2\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s).$$ (8)

And the corresponding dose can be expressed as

$$D_{\mathrm{aSG}}(s)=k\left[{\varphi }_{\mathrm{SG}}-2\mathrm{\Delta }{\varphi }_{\mathrm{TG}}\right]=D_{\mathrm{SG}}-2k\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s).$$ (9)

For $s=0$, there is no tongue‐and‐groove, and the aSG is identical to the conventional SG field. For asynchronous SGs with $s>0$, there is a reduction in the total fluence and in the corresponding dose, which can be computed as

$$\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)=\frac{D_{\mathrm{SG}}-D_{\mathrm{aSG}}(s)}{2k},$$ (10)

where D _SG is the average dose for a synchronous SG of a certain gap size ($s=0$) and $D_{\mathrm{aSG}}(s)$ is the average dose for an aSG of the same gap size and distance between adjacent leaves equal to s. Hence, the fluence reduction at the leaf side can be derived from the measurements of the $D_{\mathrm{aSG}}(s)$ fields using Equation (10) and the k value from Equation (6).

The experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves for the Millennium and HD120 MLCs can be fitted to a function ³¹ such as:

$$\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)=a_1.s-a_2\left(1-e^{-a_1.s/a_2}\right),$$ (11)

which results in the first derivative

$$\frac{d\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)}{ds}=a_1\left(1-e^{-a_1.s/a_2}\right).$$ (12)

The first derivative (slope) of the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ function can be interpreted as an effective tongue‐and‐groove width, which depends on the distance to the leaf tip end. Further details on this methodology can be found in Saez et al. ¹³ and Hernandez et al. ³¹

Following this procedure, the experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves were computed from the doses measured with the Farmer chamber. The calculated $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves, corresponding to TPS calculations, were also obtained from the average doses calculated by each TPS. To obtain the average dose, a large evaluation structure mimicking the Farmer chamber was defined in the TPS and the average calculated dose to that structure was recorded for each beam. Finally, the calculated $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves were compared with the curves obtained experimentally.

Note that, for s values smaller than the gap, the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ values are independent of the gap size. For s values larger than the gap, however, there is interdigitation and the side of the leaf tip is not entirely exposed. In this study, measurements of the aSG tests were carried out for gap sizes of 5, 10, 20, 30, and 40 mm to characterize the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve up to 40 mm away from the leaf tip end.

2.2.3. FOURL test

Elekta provides a set of predesigned tests, known as the ExpressQA package, ¹⁷ , ¹⁸ as a tool to determine the MLC parameters in the TPS. This package contains QA fields for characterizing specific dosimetric features of the MLC. In the present study, we focused on the FOURL field to evaluate the tongue‐and‐groove models and we compared it with the results obtained with the SG/aSG tests. The FOURL is a step‐and‐shoot field with four segments of progressively smaller and nested L‐shaped apertures. The lower right part of the FOURL test field, with three junctions produced by abutting tongue‐and‐groove regions, was evaluated.

Measurements of the FOURL field were taken at all centers, at a depth of 10 cm with the gantry and the collimator rotation angle at 0°, a source‐to‐surface distance of 90 cm, and 10 cm slabs for backscatter. Film dosimetry was used to sample the dose at the junctions with a high‐spatial resolution. Gafchromic EBT3 films (ISP, Wayne, NJ) were calibrated in Solid Water^® against a Farmer‐type ion chamber following each center's film dosimetry protocol. Centers used the commercial software Radiochromic.com ³² (centers A and B) and home‐made software (centers C and D) using triple‐channel dosimetry protocols. ³³ , ³⁴ , ³⁵ RGB mode with 16 bits per channel with a resolution of 72 and 150 dpi was used. Dose profiles across the tongue‐and‐groove junctions were extracted at a position 4 cm off‐axis. To reduce the noise, the dose profiles were averaged over a 1 cm distance perpendicular to the profile direction.

Dose calculations were made with the TPSs and calculation engines given in Table 1 and dose profiles across the tongue‐and‐groove junctions were extracted and compared with those obtained with film dosimetry. A dose grid resolution of 1 mm was used, which was the finest resolution available in all TPSs. For Monte Carlo dose computations, the statistical uncertainty was set to 0.1% per control point and, to reduce the noise in the calculated profile, calculated doses were also averaged over a 1 cm distance perpendicular to the profile direction.

2.2.4. Raytracing computations

To facilitate the understanding and interpretation of the obtained $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves, we developed geometrical models for the Millennium and Agility MLCs. Raytracing was then performed considering a linear attenuation coefficient of 0.75 cm⁻¹ to obtain fluence maps through different leaf regions. The code was developed under Python 3.7. The fluence reduction $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ at the tongue‐and‐groove regions was derived from these geometrical models for both the Millennium and Agility MLCs.

Finally, we investigated the impact of differences in MLC geometry between Millennium and Agility on the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve. To evaluate the impact of each geometric parameter, the curve for the Millennium was first computed and MLC parameters were progressively changed, one at a time, until all the parameters were equal to those of the Agility. Starting from the Millennium, the first parameter changed was the curvature radius R, which was changed from R = 8 cm to R = 17 cm. Next, the leaf thickness was increased from 65 to 90 mm. After that, the SCD was reduced from 510 to 349.3 mm. Finally, the tilting and the leaf eccentricity were introduced. A tilting of 0.515º was used, which was the value that Gholampourkashi et al. found for the Agility using Monte Carlo techniques. ³⁶ The rationale behind this process was to illustrate the impact of each geometric parameter and to identify which ones contributed the most to the measured leaf tip effects.

3. RESULTS

3.1. Results with the asynchronous sweeping gap tests

To illustrate the dose variation as a function of s, Figure 2a gives the doses measured for aSGs with a gap size of 40 mm and shifts between adjacent leaves s of up to 40 mm for a representative case. It shows that the average doses decreased as s increased due to the tongue‐and‐groove effect. For small s values, the dose reduction for the Agility and the Millennium MLCs was similar. For large s values, on the contrary, the dose reduction for the Agility became more pronounced, which indicates a higher effective tongue‐and‐groove width.

FIGURE 2.

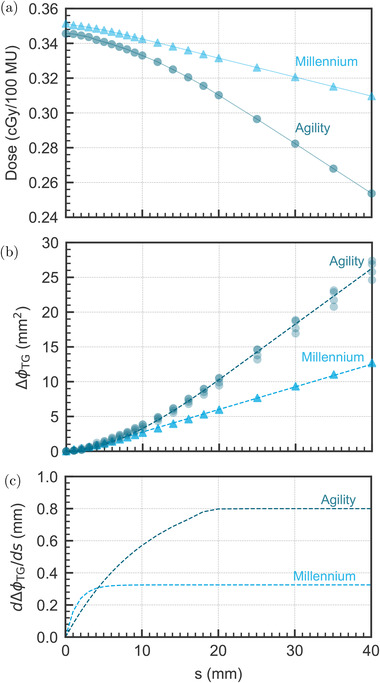
Asynchronous sweeping gap doses relative to the dose of the 10 × 10 cm² reference field are shown in (a) for representative linacs with the Agility and the Millennium MLC and the 40 mm gap size. The $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves for all the evaluated linacs are illustrated in (b), where symbols indicate results from each linac and dashed lines indicate the fit to average values across different linacs. The first derivative of $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ for the average curves is presented in (c).

The corresponding $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ values were computed for all linacs using Equations (6) and (10) and are plotted in Figure 2b. The $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ values for linacs with the same MLC were very similar; therefore, a fit to the average curves is used hereafter. Equation (11) was used for the fit and the fitting parameters were $a_1=0.33$, and $a_2=0.48$ for the Millennium and $a_1=0.95$, and $a_2=10.50$ for the Agility. The fit is illustrated in dashed lines in Figure 2b.

The experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves for the Agility and Millennium MLCs for small s values were also very similar. The Agility curve, however, showed a higher slope than the Millennium for large s values, notably for $s>20$ mm. Since the tongue‐and‐groove width is directly proportional to the slope of the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve, ¹³ these results indicate that the effective tongue‐and‐groove width near the leaf tip end is similar for both MLCs, whereas it is much larger for the Agility a few centimeters away from the leaf tip end.

To better evaluate this slope, the first derivative of the fitted function was computed with Equation (12) and is shown in Figure 2c. As can be seen, the tongue‐and‐groove width increases from zero (at the leaf tip) to a constant value (away from the leaf tip). For the Millennium, the first derivative stabilizes at s ∼ 6 − 7 mm with a value of 0.33 mm. For the Agility, however, the first derivative increases up to $s=20$ mm with a final value of 0.8 mm. This points out two important results. First, the initial build‐up region, where the first derivative increases, is approximately three times larger for the Agility than for the Millennium, which indicates a much larger impact of the rounded leaf end on the tongue‐and‐groove width. Second, the effective tongue‐and‐groove width at large distances away from the leaf tip for the Agility is also much larger than for the Millennium (by a factor of 2.4).

3.2. Fits and calculated $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves from TPSs

Once the experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves were obtained, the TPS‐calculated curves could be adjusted to the experimental ones by selecting the adequate MLC configuration parameters. Figure 3 shows the result of fitting the calculated $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curve in RayStation to the linear part of the averaged experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves, which was proposed by Saez et al. ¹³ and is hereafter named “Fit L.”

FIGURE 3.

Experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ values for the Agility and the Millennium MLCs and the corresponding fit to the linear part of the curves (“Fit L”). Symbols represent average measured data. Dotted lines indicate the result of fitting the calculated curves to the linear part of the experimental curves (Fit L).

As can be seen, a good agreement was found along the entire curve for the Millennium, with only some minor differences in the region below 5 mm. It was already shown that this fit to the experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curve produces a good calculation accuracy for clinical plans with the Millennium and the HD120 MLCs. ¹³ For the Agility, by contrast, the fit to the linear part ($s>20$ mm) produced large differences in the region below 15 mm. This fit does not seem adequate for clinical plans, especially for complex IMRT/VMAT plans involving small gap sizes, in which most leaf pair openings and distances between adjacent leaves (s) are typically below 20 mm.

Next, the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves configured within each center's clinical TPS for the Agility were evaluated. To that aim, the SG/aSG doses were computed and the corresponding $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves were obtained using Equations (6) and 10. As shown in Figure 4, remarkable differences were found between the calculated curves from different centers. These “clinical curves” exhibited a closer agreement with the experimental curve for low s values than the fit to the linear part (Fit L), at the expense of worsening the agreement for larger s values.

FIGURE 4.

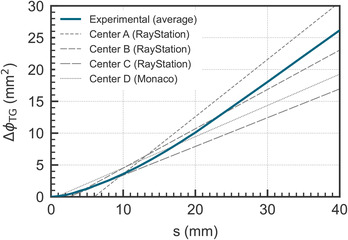
Experimental and calculated $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ values for the Agility. The solid curved line represents average measured data. Dashed and dotted lines show the calculated curves from each TPS.

The $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves from RayStation were zero until the s value reached the leaf tip width entered in the TPS. After that, the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curves increased linearly with a slope that was directly related to the value of the tongue‐and‐groove parameter. The curve from the Monaco TPS was quite similar to the curves from RayStation, except for an even smaller intersection with the x‐axis, which in Monaco seems to be fixed at around $s=0.5$ mm.

Table 3 gives the MLC parameters used clinically at each center (producing the plots shown in Figure 4 as well as the parameters used in the “Fit L” curve in Figure 3. Center D (Monaco) used the default MLC parameters provided by the manufacturer. ¹⁷ Centers A, B, and C (RayStation) fine‐tuned the MLC parameters locally and they all used lower values for the leaf tip width than the “Fit L” model.

TABLE 3.

TPSs and sets of MLC configuration parameters used. T&G, tongue‐and‐groove. *Fit to the linear part of the Agility $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}(s)$ curve, as shown in Figure 3

RayStation	Fit L*	Center A	Center B	Center C	Monaco	Center D
T&G (cm)	0.090	0.10	0.070	0.050	Interleaf leakage	3.0
Leaf tip width (cm)	0.89	0.60	0.25	0.20	MLC offset (mm)	0.0
MLC transmission	0.005	0.004	0.0055	0.005	Leaf transmission	0.5%
Offset (cm)	–	−0.02	−0.005	0.01	Leaf Tip Leakage	1.1
Gain	–	0.008	0.0007	0.0038	MLC Leakage	0.0
Curvature (1/cm)	–	0.0000	0.00015	0.0000	Leaf Groove Width (mm)	0.4

3.3. Results with the FOURL test field

Figure 5 shows a dose map for the FOURL test field obtained by film dosimetry for a representative center. Three horizontal bands are clearly visible in the dose map due to the lower delivered doses at the tongue‐and‐groove junctions. Calculated and measured dose profiles across these junctions are compared in Figure 5b for a representative center. As can be seen, the measured dose profiles exhibit dose minima at the leaf edge junctions due to the tongue‐and‐groove effect, with a reduction from maxima to minima of approximately 25–30%. The profile obtained was practically the same for the 72 and 150 dpi resolutions. The TPS dose profile clearly underestimated the dose reduction at the dose dips (calculated doses higher than measured doses), in agreement with the smaller tongue‐and‐groove value entered in the TPS. The comparison for the other centers can be found online as Supporting Information (see Figures S2 and S3). The only center with a good agreement for the Agility was center A, which used the highest tongue‐and‐groove parameter in the TPS (Table 3).

FIGURE 5.

FOURL test results. A dose map measured with film dosimetry for a representative center (center B) is shown in (a). Measured and calculated dose profiles along the dashed line indicated in (a) are shown in (b).

3.4. Raytracing

We used raytracing to investigate the relationship between the design and specific geometry of each MLC model and the differences experimentally obtained. Figure 6 shows, in its upper row, a lateral view of the rounded leaf end and the leaf cross‐sections at two different positions for the Agility and the Millennium MLCs. The lateral view is plotted as a function of the projected off‐axis distance, that is, as projected onto the isocenter plane. As can be seen, even if the leaf tip end of the Millennium MLC is more rounded than that of the Agility (R = 8 cm for the Millennium as opposed to R = 17 cm for the Agility), the projection of the rounded leaf end for the Agility at the isocenter plane extends farther away from the central axis, which indicates that the effect of the rounded leaf end for the Agility at the isocenter plane is more pronounced than for the Millennium. This is caused mainly by the smaller SCD for the Agility, which produces a larger projection at the isocenter plane, and, to a lesser degree, by the higher leaf thickness (“height” in the z direction) and the leaf eccentricity (curvature center shifted toward the upper part of the leaves) of the Agility. The leaf cross‐sections at $x=5$ mm (across the rounded sector of the leaf tip) and $x=25$ mm (across the rectangular part of the leaf) clearly illustrate their different tongue‐and‐groove designs: tilted leaf sides defocused from the beam source for the Agility and complementary regions of a fixed width extending outwards and inwards for the Millennium.

In the second row of Figure 6, the traversed leaf thickness is plotted as a function of the projected off‐axis distance in the leaf motion direction. Curves are represented at two different positions: at the leaf center and near the leaf edge. The thickness along the leaf center shows that the effect of the rounded leaf end for the Agility is visible up to $s\sim 20$ mm, whereas for the Millennium MLC, the effect is reduced (up to $s\sim 13$ mm). Interestingly, the difference between both MLCs is more marked near the leaf edge because for the Agility, there is a region with zero traversed thickness (full transmission). For the Millennium MLC, on the other hand, the traversed leaf thickness near the leaf edge is approximately half the thickness at the leaf center and there is no region with zero traversed thickness. This is due to differences in their tongue‐and‐groove and tilting geometry, as can be seen in the profiles along the y direction shown on the right.

A map illustrating the traversed leaf thickness is given in the lower row of Figure 6. For the Millennium, the thickness near the leaf tip end is reduced due to the leaf tip curvature, but the width of the tongue‐and‐groove regions (y direction) is fixed and constant up to the leaf tip end. Thus, the traversed thickness varies in the longitudinal direction (x‐axis, along the leaf motion) but the traversed thickness at the tongue‐and‐groove region is constant in the perpendicular direction (y‐axis). For the Agility, by contrast, the traversed thickness at the tongue‐and‐groove regions also varies in the y direction due to the tilting. An interesting consequence of this tilted design is the existence of regions with zero traversed thickness near the leaf edge, which extend up to 20 mm away from the leaf tip end. These regions are produced by the fact that the extent (width in the y direction) of the effective tongue‐and‐groove for the Agility depends on the leaf thickness and is therefore reduced near the leaf tip end. The extent of the tongue‐and‐groove regions for the Millennium, on the contrary, is fixed and independent of the distance to the leaf tip end.

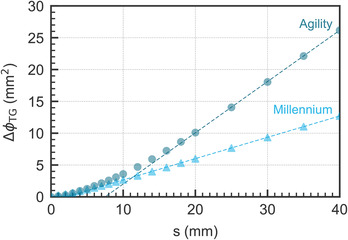
The $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves computed with raytracing for the Millennium and the Agility and their first derivatives are illustrated in Figure 7. The shape of these calculated curves was in line with the measured curves obtained for each MLC and shown in Figures 2b and 2c.

FIGURE 7.

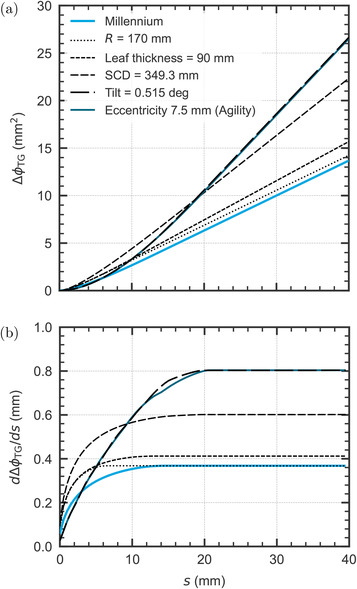
$\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves computed with raytracing (a) and their corresponding first derivatives (b). The $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ were curves progressively changed from the Millennium 120 (lower solid curve) to the Agility (upper solid curve) by modifying one parameter at a time: the leaf curvature radius (R), the leaf thickness, the source‐to‐collimator distance (SCD), the tilt, and the leaf eccentricity.

The results of progressively changing one parameter at a time, starting with the Millennium, to match the parameters of the Agility are also illustrated in Figure 7. As can be seen, changing the curvature radius from R = 8 cm to R = 17 cm produced a reduction in the rounded leaf effects, which resulted in a higher increase in the first derivative and its stabilization at a smaller s value. This new curve is similar to that of the Varian's HD120, which has a geometry similar to the Millennium 120 MLC except for its radius (R = 16 cm) and has, consequently, smaller leaf end effects. ³¹

Increasing the leaf thickness from 65 to 90 mm did not alter the initial shape of the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve but increased its first derivative farther away from the leaf tip end due to the larger extent of the rounded leaf end. Reducing the SCD from 510 to 349.3 mm produced a magnification of the entire curve caused by the larger projection of the leaf tip at the isocenter plane.

Finally, the tilting and the leaf eccentricity were evaluated. The tilting of 0.515º had a large impact on the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve and its first derivative, greatly increasing both the extent of the rounded leaf effects (s value at which the first derivative reaches a plateau) and its amount (distance from the horizontal line at small s values). The leaf eccentricity, on the other hand, had a mild impact on the curves; the only visible effect on the first derivative was a slight change in its slope between $s=12$ and 20 mm due to the different distances from the curvature center to the upper and lower leaf edges.

In summary, the first derivative of the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve facilitates the interpretation of the rounded leaf end effects and provides information on the dosimetric leaf end effects regarding both its amount (distance to the horizontal line) and extent (s value where the curve stabilizes and becomes horizontal). By changing one geometric parameter at a time, the dosimetric impact of each individual MLC parameter was evaluated and the parameters producing the large leaf tip effects measured for the Agility could be identified.

4. DISCUSSION

The Agility MLC exhibited challenging leaf tip end effects, with a large effective tongue‐and‐groove width progressively increasing up to 20 mm away from the leaf tip end (measured at the isocenter plane). The dosimetric impact of the rounded leaf end is larger for the Agility than for other commonly used MLCs, such as Varian's Millennium 120 and HD120. This seems surprising as the Agility has the largest radius (R = 17 cm as opposed to 8 and 16 cm for the Millennium and HD120, respectively), which ought to reduce the effects associated with the rounded leaf ends.

Raytracing provided a reasonable approximation to the measured $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves shown in Figure 2, as well as to their first derivatives, accurately replicating their shapes. Some differences were expected because the raytracing used did not take into account the source size, the energy spectrum of the photon beam or the MLC scatter. However, this simple approach was sufficient to illustrate that the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve is very sensitive to the MLC geometry and to investigate the impact of each geometric characteristic separately.

We found that the main reason for these effects was twofold: the tilting design of the Agility and its reduced SCD (see Figure 7). The tilting design introduces a variation in the traversed leaf thickness in the direction perpendicular to the leaf motion (y‐axis in Figure 6), which produces a high transmission region near the leaf tip end that increases the impact of the rounded leaves. The small SCD further magnifies the projection of the leaf tip at the isocenter plane, as well as the overall amount of these effects. The higher leaf thickness and the eccentric leaf end curvature of the Agility (see Table 2) also contribute to increasing the rounded leaf end effects, but to a lesser extent.

It is known that the Agility offers many important advantages, such as a very low MLC transmission, a consistent leaf tip penumbra across the whole range of leaf travel, and a high patient clearance, making the Agility well‐suited to delivering fast and accurate radiotherapy treatments. ¹⁵ Its design, however, makes the characterization of the Agility in TPSs challenging and requires a more sophisticated model of the leaf tip and of the tongue‐and‐groove than other MLCs.

The MLC models evaluated in this study assumed a null tongue‐and‐groove at the leaf tip and a fixed tongue‐and‐groove width starting at a certain distance from the leaf tip end, which produces a linear $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve. As shown in Figure 3, such a linear function cannot replicate the experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve obtained for the Agility. Therefore, these models could not accurately reproduce the increasing tongue‐and‐groove width as a function of the distance to the leaf tip end, and a trade‐off is required between modeling the tongue‐and‐groove near the leaf tip end (low s values) and away from the leaf tip end (high s values).

Remarkable differences were found in the MLC parameters used for the Agility, despite obtaining very similar experimental $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curves. We believe that this was due to the diverse approaches and methodologies used for configuring the MLC, as well as by the characteristics of the treatment plans used in that process. For instance, some users characterize the MLC with simple static tests, whereas others use clinical IMRT plans and iterative optimization strategies. Additionally, a small target modulated IMRT plan may require a good fit of the $\mathrm{\Delta }{\varphi }_{\mathrm{TG}}$ curve for small s distances, whereas a winding modulated H&N VMAT plan may require a compromise over the full range of s values.

The differences in MLC parameters found in the present study were compatible with the large variability in those used by the community in the clinical setting, which was recently reported by IROC. ¹¹ Interestingly, an analysis of the data reported in that study shows that the variability in the MLC parameters for the Agility was systematically higher than for the Varian's Millennium and HD120 MLCs regardless of the TPS evaluated, with an increase in the corresponding standard deviations by a factor of around 2. Our results can help explain this increased variability for the Agility because the trade‐offs needed in the MLC configuration give rise to larger differences in the parameters that are finally used.

The FOURL test or other similar tests can be used to characterize the tongue‐and‐groove of the MLC, but it is important to be aware that these tests are typically evaluated at large distances from the leaf tip. For instance, we evaluated the junction doses produced by abutting leaf sides in the FOURL test at distances between 5 and 9 cm away from the leaf tip, where the effects associated with the rounded leaf end are negligible. In clinical plans, on the contrary, distances between adjacent leaves are often smaller than 20 mm, which require a smaller tongue‐and‐groove width. This explains why only one center (A) had a good agreement between calculated and measured doses in the tongue‐and‐groove junctions of the FOURL test, whereas TPSs from the other centers clearly underestimated the dose reduction at the tongue‐and‐groove junctions. This reflects the fact that some centers consider static test fields and junction doses in their MLC configuration process, whereas other centers further focus on clinical IMRT/VMAT plans.

Additionally, the measurements of the FOURL test are dependent on the primary source size and can be affected by slight differences in the interleaf gap distances, which can explain the discrepancies in the dips of the experimental dose profiles from different linacs (see Figure S2 in the Supporting Information). Moreover, dose calculations for the FOURL test also depend on the source size used in the beam model and on the resolution of the calculation grid size.

The SG/aSG tests, on the contrary, are not affected by the primary source size or by aspects such as the resolution of the calculation grid size. ²⁸ , ³¹ The reason for this is that these tests are based on average doses obtained either by using a large Farmer ion chamber (in measurements) or by averaging the doses over a large structure (in calculations). Hence, these tests provide a robust determination of MLC parameters such as the leaf tip width and the tongue‐and‐groove width. ¹³

Our study has important implications regarding the commissioning of MLC models. Simple test fields can be useful to isolate specific features of the MLC, which should, in principle, facilitate the configuration of the MLC model. However, the characteristics of these test fields greatly differ from those used in clinical beams and an MLC model for the Agility optimized for such nonclinical conditions is not necessarily optimal for clinical IMRT/VMAT plans due to inherent limitations in the MLC model.

Alternatively, MLC models can be iteratively optimized using clinical IMRT/VMAT plans. To that aim, commercial IMRT QA devices can be used but ion chamber measurements have also been recommended. ⁶ , ⁷ , ³⁷ However, the effect of each separate MLC parameter is difficult to isolate in clinical plans, and the optimal value of one parameter can depend on the values of the others. ¹³ , ¹⁷ Consequently, this strategy is time‐consuming and could result in different MLC parameters. In this context, community average MLC parameters can provide a good starting point for optimizing MLC models and can also be useful as a final verification. We believe that these average parameters can guide users toward typical and safer MLC configurations and help prevent outliers. These parameters, however, might depend on the TPS version and substantially change in TPS upgrades if the MLC model is modified.

Our results are in agreement with previous findings from other investigators regarding MLC commissioning. Snyder et al. ¹⁷ found that replicating simple test fields led to a reduction in the agreement between calculations with the Agility and measurements for typical clinical dose distributions. Roche et al. ¹⁸ also reported that adjusting MLC parameters to match the FOURL test profiles for the Agility was not recommended. The present paper provides an explanation for these results, which are due to the challenging geometric characteristics of the Agility and to the limitations in the MLC models.

We believe that the procedure followed in this study, based on the SG/aSG tests, offers several major advantages for MLC configuration. The SG/aSG tests also lie within the category of “test fields,” but they provide information on the leaf tip width and on the tongue‐and‐groove attenuation as a function of the distance to the leaf tip end. Consequently, this methodology facilitates a better understanding of MLC models, exposes their limitations, and provides insight into trade‐offs that might be needed during their configuration. The optimal MLC parameters for the Agility are likely dependent on the treatment plan characteristics, but if the MLC model was improved to replicate the measured rounded leaf effects, the SG/aSG tests would provide a streamlined and robust MLC configuration process for the Agility, as has already been reported for other MLCs. ¹³ Additionally, such a model would also provide good accuracy for both simple test fields and clinical IMRT/VMAT plans of various characteristics, extending the range of validity of the MLC model.

A limitation of the present study is that only two TPSs were evaluated, although they are both widely used for Elekta linacs and cover a large part of this market. Furthermore, other commercial TPSs that implement similar or simpler MLC models will likely suffer from analogous limitations. Additionally, the methodology used can be readily applied to other MLCs and TPSs.

The potential impact of the MLC recalibrations was not thoroughly evaluated but centers had a good long‐term stability, and the SG/aSG results after carrying out the Elekta MLC calibration (AutoCal) procedure remained practically the same, with only minor dose variations compatible with differences in the MLC offset parameter within ± 0.05 mm.

Another limitation is that the accuracy of each MLC model for clinical plans was not evaluated. However, the aim of the study was not to assess the TPS accuracy, but to identify and describe the challenges in modeling the Agility, as well as to investigate why different MLC parameters are used in clinical practice, and how MLC models could be improved. It is of note that all participating centers reported good calculation and successfully complied with commissioning criteria from international guidelines. ⁵ , ⁶ , ⁷ In our opinion, the reason for this is that substantial differences in MLC parameters do not necessarily result in poor accuracy because some MLC parameters can compensate for each other over a certain range of treatment plan characteristics. Implementing improvements in MLC models for the Agility and evaluating the dosimetric impact of such improvements will be the object of future work.

5. CONCLUSIONS

The geometric characteristics of the Agility MLC produce dosimetric effects associated with the rounded leaf end up to a distance of 20 mm away from the leaf tip end measured at the isocenter plane. This affects the tongue‐and‐groove shadowing, which progressively increases along this distance. The MLC models implemented in RayStation and Monaco could not replicate this behavior, which makes it necessary to reach compromises in the MLC parameters configured in the TPS.

The optimal MLC parameters for the Agility in current commercial MLC models depend on the particular characteristics of the treatment plans used; consequently, MLC models must be carefully optimized for representative clinical plans. A refinement of MLC models is needed to better approximate the measured leaf tip and tongue‐and‐groove effects for the Agility, which would extend the validity of the MLC model, reduce the variability in the MLC parameters used by the community, and facilitate the standardization of the MLC configuration process.

CONFLICTS OF INTEREST

Agnes Angerud is an employee of RaySearch Laboratories. The rest of the authors have nothing to disclose.

Supporting information

Additional information is available online in the Supporting Information section.

Hernandez V, Angerud A, Bogaert E, et al. Challenges in modeling the Agility multileaf collimator in treatment planning systems and current needs for improvement. Med Phys. 2022;49:7404–7416. 10.1002/mp.16016