High‐dimensional propensity scores for empirical covariate selection in secondary database studies: Planning, implementation, and reporting

Abstract

Real‐world evidence used for regulatory, payer, and clinical decision‐making requires principled epidemiology in design and analysis, applying methods to minimize confounding given the lack of randomization. One technique to deal with potential confounding is propensity score (PS) analysis, which allows for the adjustment for measured preexposure covariates. Since its first publication in 2009, the high‐dimensional propensity score (hdPS) method has emerged as an approach that extends traditional PS covariate selection to include large numbers of covariates that may reduce confounding bias in the analysis of healthcare databases. hdPS is an automated, data‐driven analytic approach for covariate selection that empirically identifies preexposure variables and proxies to include in the PS model. This article provides an overview of the hdPS approach and recommendations on the planning, implementation, and reporting of hdPS used for causal treatment‐effect estimations in longitudinal healthcare databases. We supply a checklist with key considerations as a supportive decision tool to aid investigators in the implementation and transparent reporting of hdPS techniques, and to aid decision‐makers unfamiliar with hdPS in the understanding and interpretation of studies employing this approach. This article is endorsed by the International Society for Pharmacoepidemiology.

Key Points

• The high‐dimensional propensity score (hdPS) is an automated, data‐driven analytic approach for covariate selection that empirically identifies pre‐exposure variables and proxies to include in a propensity score model.

• This paper provides an overview of the hdPS approach, recommendations on the planning, implementation, and reporting of hdPS, and a checklist with key considerations in the use of hdPS.

• An hdPS implementation involves careful consideration of data dimensions, identification of empirical variables and proxies, prioritization and selection of empirically identified variables, and estimating the propensity score.

• To promote reproducibility and transparency of studies using real‐world data, reporting documentation should include all key decisions.

1. INTRODUCTION

Comparative effectiveness and safety studies using real‐world data are being adopted for regulatory, payer, and clinical decision‐making. ¹ However, one major criticism of these nonrandomized studies is the potential presence of unmeasured confounding, which can result in biased estimates of treatment effects. Real‐world evidence (RWE) used for high‐stakes decision‐making must follow the principles of epidemiology in design and analysis, ² and apply methods to minimize confounding given the lack of randomization. ³ Traditional propensity score (PS) analysis is a commonly used technique. As used in pharmacoepidemiology, a PS is the estimated probability that a patient will be treated with one drug versus an alternative, and summarizes a range of confounders; using a PS, investigators can adjust for a large number of measured preexposure covariates. ⁴ If all confounders are adjusted for, and the confounding does not vary after exposure, then the treatment effect estimate should be unbiased.

If some confounders are not able to be accounted for directly, in a PS or otherwise, the concept of proxy measures may help, particularly when working with secondary data that were not generated to answer a specific research question. ⁵ Proxy measure adjustment does not require investigators to measure confounders directly and exactly, but rather to measure observable markers correlated with these confounders. For example, frailty is a known confounder in studies examining interventions' effect on mortality in elderly populations, but frailty itself is difficult to measure in claims data. To capture frailty, investigators can use proxies such as use of a wheelchair or oxygen canisters, and use those proxies either directly or as part of a more complex algorithm. ⁶

Over the last decade, the high‐dimensional propensity score (hdPS) method has emerged as an approach that builds on the idea of large‐scale proxy measurements of unmeasured confounders for improved confounding adjustment in the analysis of healthcare databases. First introduced in 2009, ⁵ hdPS is an automated, data‐driven analytic approach for covariate selection that empirically identifies preexposure variables (“features” in data science parlance) to include in the PS model. hdPS confers several attractive advantages versus manual identification of confounders and proxies, including data source independence, data‐optimized covariate selection, and the ability to be coupled with traditional PS approaches. ⁷ The method has been shown to yield similar results as investigator‐driven approaches. ⁷

Existing guidance documents and user guides touch upon the use of hdPS in pharmacoepidemiology and comparative effectiveness research. ⁸ , ⁹ However, we currently lack best practice guidelines explaining when and how to implement hdPS, and we lack guidance to support decision‐makers in fully understanding this method where it has been applied.

The paper provides a comprehensive guide on the planning, implementation, and reporting of hdPS approaches for causal treatment effect estimations using longitudinal healthcare databases. We supply a checklist with key considerations as a supportive decision tool to aid investigators in the implementation and transparent reporting of hdPS techniques, and to aid decision‐makers unfamiliar with hdPS in the understanding and interpretation of studies employing this approach. This article is endorsed by the International Society for Pharmacoepidemiology.

2. PREIMPLEMENTATION STUDY PLANNING

2.1. Basic study design

The approach to designing and conducting a study that employs hdPS does not vary from other pharmacoepidemiologic analyses: core activities include developing a protocol that details data sources, study design, variable measurements, and a data analysis plan, executing the study according to best practices, and documenting the process following accepted guidelines. ¹⁰ , ¹¹ The guidelines for Good Pharmacoepidemiology Practice and ENCePP methodological standards recommend the development of a protocol prior to conducting a study and implementing the analysis, ⁸ , ¹¹ and this protocol should include known or suspected confounders that should be accounted for. hdPS can be a useful addition should the investigator believe that not all of the confounders are known a priori and/or can be suitably measured. The choice to use hdPS is no different than any other analytic technique in that it its rationale for use and implementation details should be shared as part of the study design.

2.2. Data sources

One of the benefits of employing hdPS is the ability to leverage comprehensive longitudinal claims data, and/or electronic health records (EHRs) with deep clinical information, to adjust for confounding. The hdPS approach is data source‐independent in that the hdPS algorithm operates without consideration of the semantics (clinical meaning) of coded or uncoded information; as such, any data source, regardless of data structure or coding systems, can be utilized. ⁷ While the hdPS approach was first developed using US‐based administrative claims data, the method has been used in geographically diverse datasets, such as UK EHRs, ¹² , ¹³ Danish registry data, ¹⁴ French claims data, ¹⁵ , ¹⁶ , ¹⁷ German claims data, ¹⁸ and Japanese claims data. ¹⁹

Being data source independent, however, does not imply that knowledge of the data source is not important: even with automated variable selection, one should have familiarity with the data source and content of the data to ensure optimal identification of variables to manually include or exclude, as well as for parameter specification for automated covariate identification.

Knowledge of the structure of underlying coding systems is particularly important, including how codes are utilized and whether hierarchies among codes may affect interpretation. For example, US administrative claims generally have longitudinal data with inpatient and outpatient diagnoses coded with the International Classification of Diseases, 10th Revision, Clinical Modification (ICD‐10‐CM) coding system, which is hierarchical. By contrast, UK EHRs using their National Health System's READ Codes, are less structured, have varying frequency of recorded data, and have lower granularity. ¹³ Even among countries that use the same coding systems—ICD‐10 codes are used in many countries worldwide—the way that codes are recorded may not be directly comparable. As an example, while US claims data typically include diagnosis and procedure codes from both inpatient and outpatient settings, the Nordic healthcare system does not capture codes observed in primary care. ¹⁴ Understanding the level of data capture, data granularity, and completeness of recording is critical: while the hdPS approach can extract all likely confounders in virtually any data source, it cannot overcome an inherent lack of information.

2.2.3. hdPS implementation steps

The following section discusses implementation of the hdPS algorithm, as applied to a specific study question and in specifically selected fit‐for‐purpose data sources. While choices of parameters are discussed through this section, a summarized checklist can be found in Table 1.

TABLE 1.

hdPS checklist

Guidance	Key concepts & considerations
Study planning, protocol and statistical analysis plan (SAP) development, and hdPS implementation
Specify parameters used for identifying and selecting empirically identified covariates in the statistical analysis plan: Select data dimensions Identify empirical variables and proxies Prioritize and select empirical variables	Variables automatically created from healthcare databases are called “empirically‐identified” variables Before the analysis, prespecify and decide how covariates will be identified, ranked, and selected A data dimension is a type of patient data—such as inpatient events, outpatient events, drug fills, or lab tests—recorded in healthcare data Parameters to specify with the hdPS approach include data dimensions, coding systems, level of hierarchy for the codes, number of variables to include, ranking method Consider the unique characteristics of each data source carefully when specifying parameters, such as data dimensions' capture of information and their coding systems
Define and identify investigator‐specified variables	Document known important confounders in the study protocol Recommend including patient characteristics such as age, sex, race, and important health service utilization variables such as, number of visits and number of prescriptions filled
Specify and exclude instrumental variables and colliders from the hdPS	Instrumental variables and colliders are often excluded from the hdPS to avoid bias amplification Variables noted by the investigator will be removed from the pool of covariates that the hdPS prioritizes
Document the method and software environment used for estimating the PS and how the PS will be used in the study in the protocol and statistical analysis plan. Estimate the PS Estimate the treatment effect	An hdPS functions similarly to a traditional PS As with a traditional PS, logistic regression is commonly used for estimating the hdPS Traditional approaches (e.g., matching, weighing, and stratification) apply to hdPS as well and should be selected a priori
Document planned diagnostics to be reported along with actions to take should anomalies be detected	Diagnostics to be employed include inspection of selected variables by creating a “Table 1” of baseline patient characteristics and any acceptable thresholds for summary measures, for example, maximum absolute standardized mean differences Other output often presented includes PS distribution plots and sequential additional of variable plots
Prespecify any other sensitivity analysis being conducted	A priori, investigators may vary certain parameters to determine the robustness of the results or test assumptions Note specifically any post hoc sensitivity analyses conducted over the course of the study
Reporting and transparency
Present diagnostic tables and graphs to show successful confounding adjustment and hdPS performance	Construct a “Table 1” showing baseline patient characteristics of patients between two treatment groups, using a summary measure such as the standardized mean difference Plotting PS distributions and standardized differences, or showing the sequential additional of prioritized covariates are useful visualizations to demonstrate hdPS performance
Consider completing Appendix Table 3F from the STaRT‐RWE framework to specify parameters used to identify and select empirically derived covariates to ensure reproducibility and transparency	STaRT‐RWE structured templates aid in the overall planning and reporting of study methods Supplemental Table 3F from STaRT‐RWE recommends specifying key parameters including algorithm for covariate definition, covariate assessment period, code types, and diagnosis positions If feasible, provide a detailed list of variables along with interpretable descriptions in a table in the supplemental appendix to aid transparency of the hdPS method

2.4. Selection of data dimensions

hdPS variable identification is built upon identifying codes present in one or more data dimensions. A data dimension is a type of patient data—such as inpatient events, outpatient events, drug fills, or lab tests—recorded in healthcare data (Figure 1). Rather than looking at all data taken together, hdPS considers data dimensions one at a time to avoid mixing measurements of heterogeneous meaning and quality. Within each dimension, variables are created from the presence of codes in patient records, such as diagnosis codes or drug identifiers; for each of often several thousand codes, patients are noted to have the code present or not present, thus creating a high‐dimensional variable space. Each dimension will have an associated coding system, such as ICD‐10‐CM codes for inpatient procedures, Current Procedural Terminology (CPT) codes for outpatient procedures, and National Drug Codes or generic drug names for outpatient pharmacy drug dispensing.

FIGURE 1.

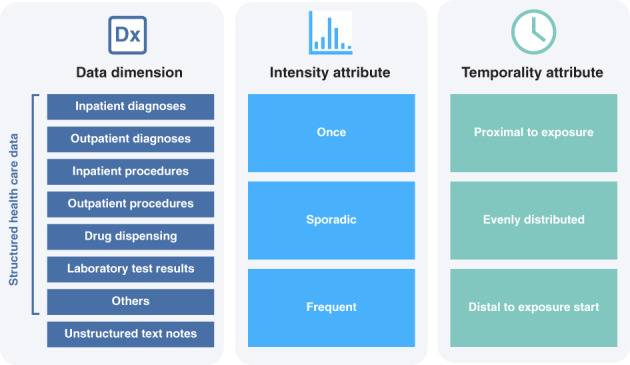
Classification of codes by data dimensions, frequency, and temporality. Adapted from Schneeweiss, Clin Epidemiol. 2018.

When coding systems are hierarchical, a decision must be made as to what level of the hierarchy to consider. Generally speaking, the lowest level of granularity (highest level of specificity) may be too granular for hdPS, as the prevalence of any given code will tend to be low. Selecting a level that gives an appropriate level of clinical context without too much detail will be most effective. For example, ICD‐10‐CM code E11.3 (Type 2 diabetes mellitus with ophthalmic complications) may provide sufficient confounding information as opposed to a code deeper in the hierarchy, such as E11.321 (Type 2 diabetes mellitus with mild nonproliferative diabetic retinopathy with macular edema) or even E11.3211 (as above, but left eye specifically).

To extract additional information from the presence of codes, codes can be further classified by frequency prior to exposure (occurring once, sporadically, or frequently). Extensions to hdPS have also considered temporality relative to exposure (proximal to exposure, evenly distributed, and distal to start) (Figure 1). ⁷ With the codes and the variations considered, a typical hdPS analysis may consider thousands of variables for each patient.

Table 2 contains examples of data dimensions used in various data sources in North America, Europe, and Japan. Typical data dimensions specified in US claims data are inpatient and outpatient diagnostic and procedures and drug dispensing. However, other data dimensions such as staging and biomarker information for an oncology study may be specified as needed for specific study questions, as available in specific data sources.

TABLE 2.

Example of data sources and data dimensions

Country	US	UK	Canada	Denmark	France	Japan
Data source type	Administrative claims data	Electronic health records	Medico‐administrative database	Administrative and health registries	National health care data system	Administrative claims database
Data source examples	MarketScan, Optum, Medicare	CPRD, THIN	Régie de l'assurance maladie du Québec (RAMQ) database Maintenance et Exploitation des Données pour l'Étude de la Clientèle Hospitalière (MED‐ECHO) database	Danish National Prescription Register, Danish National Patient Register	French National Healthcare System (Système National des Données de Santé [SNDS]	JMDC
Dimensions in noted data source(s)	Inpatient diagnoses (ICD codes)	Clinical (READ codes for diagnosis, signs and symptoms) (CPRD) Inpatient diagnosis (THIN)	Hospitalization discharge data for inpatient diagnostic code Physician claim for inpatient diagnostic codes	Inpatient diagnoses (ICD)	Inpatient diagnoses (ICD‐10 codes)	Inpatient diagnoses (ICD)
	Outpatient diagnoses (ICD codes)	Outpatient diagnoses (THIN)	Physician claim for inpatient and outpatient diagnostic codes	Outpatient diagnoses (ICD)	Long term disease registration for full reimbursement (ICD‐10 codes)	Outpatient diagnoses (ICD)
	Inpatient procedures (ICD codes or CPT codes)	Referral to specialists (READ codes) (CPRD) Inpatient procedures (THIN)	Hospitalization discharge data for inpatient procedure code Physician claim codes for inpatient procedures		Hospitalization discharge data for inpatient procedure code	Inpatient procedures (Japanese procedural codes)
	Outpatient procedures (ICD codes or CPT codes)	Outpatient procedures (THIN)	Physician claim codes for outpatient procedures Specialty of the physician providing care		Physician claim codes for outpatient procedures Specialty of the physician providing care	Outpatient procedures (Japanese procedural codes)
	Outpatient pharmacy dispensing (NDC, generic drug names)	Prescriptions (e.g., generic name, BNF codes) (CPRD) Outpatient drug use (THIN)	Drugs dispensed in outpatient setting	Drugs (ATC codes)	Outpatient Drug dispensing (ATC codes) inpatient expensive drugs (out of DRG cost coding system)	Inpatient and outpatient prescription (Japan‐specific drug coding system; ATC codes)
References/Source	Rassen 20	Toh 12 ; Tazare 13	Guertin 21 , 22	Hallas 14	Blin 15 , 17 ; Benzin 23	Ishimaru 19 , 24

Abbreviations: ATC, Anatomical Therapeutic Chemical Classification System; BNF, British National Formulary; CPRD, Clinical Practice Research Datalink; ICD, International Classification of Disease; THIN, The Health Improvement Network.

2.5. Identification of empirical variables and proxies

The hdPS algorithm begins with identification and measurement of variables and proxies (Figure 2, Step 1). ⁵ , ²⁰ All variables automatically created from healthcare databases are called “empirically‐identified” variables, which contrast with more traditional “investigator‐specified” variables. All of these variables, each a potential confounding factor, are identified during a covariate assessment window, usually defined as the time period covering the assessment of baseline patient covariates and prior to study entry (index date) (Figure S1). ²⁵ Typically, measurement of nontime‐varying factors after index date would lead to bias by adjustment for intermediates; whether to measure factors on the index date itself is a study‐specific choice.

FIGURE 2.

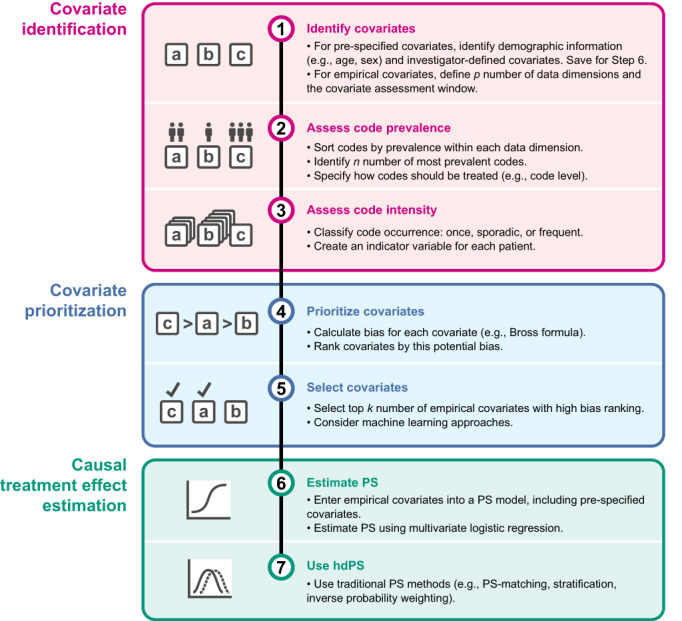
Overview of hdPS approach. The main phases of covariate adjustment with hdPS are (A) covariate identification, (B) covariate prioritization, and (C) causal treatment effect estimation, with specific steps 1 through 6 automated by the hdPS algorithm. hdPS, high‐dimensional propensity score; PS, propensity score.

The hdPS algorithm considers distinct codes as recorded in each dimension—without needing to understand their specific meaning—and turns these codes into dichotomous variables. Codes are considered as yes/no values indicating the presence of each code during the covariate assessment window, ⁵ and are ranked according to prevalence within the dimension (Figure 2, Step 2). Because the variable‐generating algorithm is agnostic to the semantics of each feature, it can therefore be applied to almost any structured or unstructured data source and coding systems. ⁷

The hdPS originally developed by Schneeweiss et al. ⁵ suggested considering the 200 most prevalent codes in each data dimension. There is debate as to the optimal maximum number of most prevalent codes to specify. In practice, going beyond 100 prevalent codes likely makes little difference, depending on the data source and data type. In Scandinavian data sources with less rich data than those in for example, US claims data, Hallas and Pottegård ¹⁴ showed that going above 100 covariates per dimension (200 total covariates in their case) demonstrated no additional improvement; the additional covariates added were false for almost all study individuals. Schuster et al. ²⁶ also explicitly omitted codes with very low prevalence or very infrequent occurrence, and it has been argued that the prevalence filter may not be necessary. At a number that's sufficiently large, the precise choice of n may not strongly impact study results.

Once the n most prevalent codes in each data dimension are identified, the algorithm creates three binary intensity variables for each code, indicating at least one occurrence of the code over the covariate assessment window, sporadic occurrences of the code, and many occurrences of the code (Figures 1 and 2, Step 3). ⁵

The high number of codes considered leads to the high dimensionality of the algorithm. A typical example with five data dimensions (inpatient diagnoses, inpatient procedures, outpatient diagnoses, outpatient procedures, pharmacy dispensing) yields up to 3000 binary variables per patient (five data dimensions * n = 200 prevalent codes per code dimension * three levels of frequency per code). Additional dimensions, such as lab test results, biomarker status, or words or phrases in free text notes, or more variables in each dimension, would lead to substantially larger numbers of candidate variables.

2.6. Prioritization and selection of empirical variables

Successful confounding adjustment with PSs controls for all risk factors associated with the outcome even if they are seemingly unrelated to treatment choice or weakly associated with the outcome of interest. ²⁷ , ²⁸ , ²⁹ One problem with a high number of risk factors in a PS model, however, is the practical challenge of estimating patients' PSs. For example, including all 3000 variables from the above example without prioritization or selection is likely unfeasible with standard logistic regression. Including too many variables would also lead to inefficiencies due to collinearity and possible bias amplification by including instrumental variables (IVs, variables associated with exposure but not associated with outcome, more below). ²⁹ Therefore, hdPS uses a heuristic process to determine which of the variables appear most important to include in the PS model.

The basic hdPS algorithm reduces the large number of candidate covariates by prioritizing covariates using a scoring algorithm and selecting covariates for inclusion into the PS the k of those that score highest (Figure 2, Steps 4 and 5). Schneeweiss et al. ⁵ noted that k = 500 compared with k = 200 covariates yielded little change to the effect estimate. Likewise, in an analysis using German statutory health insurance data, the authors noticed an insubstantial change in results when varying the number of covariates from k = 500 to k = 100, 200, and 1000 covariates. ³⁰

A traditional PS variable selection algorithm would prioritize variables according to their association with exposure (RR_CE). This may not work with hdPS, however, because as the candidate variables are empirically identified proxies as opposed to a priori specified confounders, the pool of candidates may contain both confounders and IVs. Alternatively, a scoring algorithm prioritizing variables by their outcome association (RR_CD) may not overlook variables that are important predictors of exposure (the focus of PS estimation), though with that said, debate is ongoing on the utility of the outcome ranking method. ³⁰ In most cases, a combination of the two is used: the original hdPS algorithm employed the formula by Bross which scores variables based on the observed joint association between covariate and outcome (RR_CD) and covariate and exposure (RR_CE) (Figure S3). ⁵ , ³¹ , ³² While hdPS to date has generally considered variables one by one, more advanced implementations, such as machine learning algorithms to identify predictors of the outcome or ensemble methods pooling multiple machine learning algorithms, ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ or the use of regularized regression in related techniques such as large‐scale propensity scores, ³⁸ have been demonstrated. ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ With that said, the Bross approach has been observed to be effective and durable, and is recommended for most applications.

2.7. Including investigator‐specified covariates

While hdPS is generally effective at identifying and selecting variables that are measured with recorded codes—so much so that investigator specification of such variables may not be required at all ⁷ —other variables will likely need to be entered specifically by the investigator. In any hdPS analysis, it is strongly recommended to specifically include patient attributes such as age, sex, and other measured factors that may be confounders. It is also recommended to include typical health service utilization variables such number of office visits, number of drug prescriptions filled, total cost of inpatient or outpatient care, or number of unique medications dispensed, as these are generally good markers of health status and disease severity. ¹⁵ , ¹⁷ , ³³ , ³⁹ Like other covariates, these markers are measured over the covariate assessment period, or over a standard period such as 6 months or 1 year prior to cohort entry.

Further investigator‐specified covariates can also be included. While doing so may introduce collinearity between investigator‐specified variables and those identified by hdPS—which can affect interpretability of the PS model coefficients but does not negatively impact the PS itself—explicitly incorporating the subject‐matter expertise of the investigator may provide additional levels of transparency and interpretability, since these prespecified variables are apparent and verifiable in a typical “Table 1.”

2.8. Excluding instrumental variables and colliders

While PSs tend to be forgiving with respect to what variables are included, two sources of bias introduced by variable inclusion are well‐documented: “Z‐bias” and “M‐bias,” each of which is described below. From the outset, however, we note that while Z‐bias should be actively avoided, M‐bias tends not to be an issue in day‐to‐day practice.

As briefly described above, an IV is a variable associated with the treatment assignment but not the outcome; the canonical IV is the random treatment assignment in an randomized clinical trial. ⁴⁰ Adjusting for an IV, often denoted Z, may increase the bias (Figure S2). It is well known that IVs should not be included in a PS, high‐dimensional or otherwise. ⁴ , ²⁸ , ²⁹ , ⁴¹ , ⁴² Using the typical prioritization with the Bross formula—which considers variables' joint association between exposure and outcome—may help avoid Z‐bias, as the Bross prioritization tends not select variables that only have an exposure association. ³³

However, to the extent that IVs can be identified either a priori or through inspection of hdPS's selected variables, they should be manually removed. One common way to identify potential IVs is to score all variables by quintile of exposure association and outcome association. Inspecting those variables in the top quintile of exposure association and bottom quintile of outcome association may help identify IVs. As a practical matter, if it is unclear whether a variable is an IV or confounder, erring on the side of assuming it is a confounder is likely the safer choice in nonrandomized research. ³⁴

Separately, colliders—variables that are the common effect of exposure and outcome, or a common effect of two variables that themselves each affect exposure or outcome—should also be excluded from a PS (Figure S2). ⁴³ Colliders may be more difficult to identify than IVs, though consistently measuring variables prior to the index date will tend to minimize their presence. A simulation study showed that bias due to controlling for a collider—M‐bias, so named because when collider relationships are plotted in a directed acyclic graph, they often resemble the letter M—was small, unless associations between the collider and unmeasured confounders were very large (relative risk > 8). As above, controlling for confounding should take precedence over avoiding M‐bias. ⁴⁴

2.9. Estimating the propensity score

The steps above will yield long lists of prioritized covariates, which should collectively capture a substantial portion of the underlying confounding. The final step is to estimate a PS, and to use that PS to control for confounding.

PSs are often estimated using logistic regression, ⁴ and as such, the standard estimation method for the hdPS is to use logistic regression to predict the probability of exposure as a function of all hdPS covariates, investigator‐specified and empirically identified. PSs are designed to reduce a large number of covariates into a single value, but in the hdPS case, the number of those covariates can be quite large. ⁴⁵ , ⁴⁶ Estimation of any PS is limited by the quantity of source data, and the usual recommendation is to not exceed 1 covariate in the model for every 7–10 exposed patients. ⁴⁷ For hdPS models, where the number of covariates can be large, a substantial number of exposed patients may be required for proper estimation of the hdPS.

This summary score is useful in many cases, including when there are a large number of covariates and a small number of outcomes. In those instances, parametric and regularized outcome regression have been recognized to have inadequate confounding adjustment. ⁴⁸ , ⁴⁹

2.10. Estimating the treatment effect

While the nuances of the application of PSs for confounding adjustment are outside the scope of this article, we note that once estimated, the hdPS will function as a traditional PS, and traditional approaches including matching, ⁵⁰ weighting, ⁵¹ , ⁵² , ⁵³ stratification, ⁵⁴ and fine stratification ⁵⁵ are all appropriate with hdPS (Figure 2, Steps 6 and 7).

3. MEASURING hdPS PERFORMANCE

Diagnostic tools are frequently used to evaluate the performance of analytic approaches, and the diagnostics for hdPS demonstrate or illustrate several of the items noted above: that balance on measured covariates has been achieved, that instruments have been removed, and that to the best of the investigator's ability, confounding has been accounted for.

3.1. Covariate balance diagnostics

Because PS methods are intended to control for confounding by balancing covariates between exposed and referent patients, demonstrating qualitative success in doing so is typically achieved by constructing a “Table 1” outlining baseline patient characteristics of study participants before and after PS adjustment, with the goal of showing that baseline characteristics are balanced between the two comparison groups. In a typical PS analysis, the variables in this Table 1 are generally those variables that were entered into the PS model; with hdPS, a typical Table 1 would have all investigator‐specified variables, with additional empirically identified variables appearing in a supplementary or online table. Inclusion of variables not specified by the investigator but that may have an expectation of imbalance in the Table 1 can help verify whether treatment group imbalance has in general been resolved by the hdPS.

More quantitatively, balance‐checking techniques are recommended for both investigator‐specified covariates (including key demographic variables like age and sex) and empirically identified variables. A common diagnostic to demonstrate balance between two comparison groups is to report for each variable the absolute standardized mean difference between the two treatment groups; this value is calculated as the absolute value of the difference in standardized mean in each group. An absolute standardized mean difference of 0.1 or less is an often‐used threshold to indicate adequate balance between treatment groups. ⁵⁶ A number of other diagnostics are also commonly employed. ⁵⁷

With that said, for empirically identified variables, imbalance may result for reasons that do not indicate lack of comparability between the exposure and comparator groups. For example, if an empirically identified variable impacts the outcome but not exposure, it may appear imbalanced; however, it may well be appropriate to include it in the PS, and since it is de facto not a confounder, no bias should result. Separately, if an empirically identified variable is strongly correlated with other empirically identified or investigator‐specified variable, balance may be achieved among the correlates but not the variable in question. ⁵⁸ For that reason, not all residual imbalances of individual variables result in bias, but they need inspection and explanation to the extent possible. ¹⁷ , ⁵⁹ , ⁶⁰

3.2. Graphical diagnostics

Visualizations are also helpful to visualize the performance of covariate balance and comparability between comparison groups. Typical visualizations include plots of the PS distribution before and after matching or weighting, and plots of standardized differences before and after application of the hdPS. For example, to demonstrate the performance of hdPS‐matching, Blin et al. ¹⁵ presented the standardized mean differences before and after matching as well as the overlap in hdPS distribution, which can help identify cases of nonpositivity (Figure 3). It is noted that these visualizations are not unique to hdPS and are suggested for any PS analysis.

FIGURE 3.

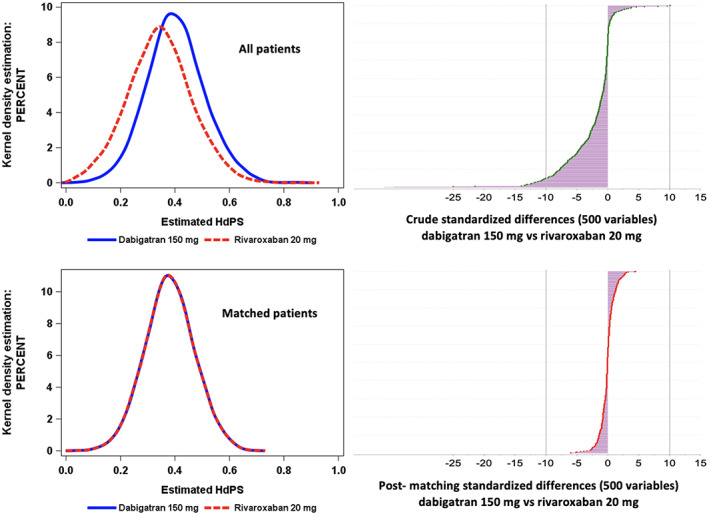
Examples of diagnostic output illustrating plots of the PS distribution and plots of standardized differences before and after hdPS‐matching for a study comparing anticoagulants dabigatran and rivaroxaban. Adapted from Blin et al., CPT 2019.

A useful hdPS‐specific diagnostic is a forest plot of the estimated treatment effects as sequentially more confounding adjustment is applied, displaying the unadjusted (crude) estimate, the estimate after adjustment with key demographic covariates (e.g., age and sex), the estimate with adjustment for all investigator‐identified covariates, and the estimate after hdPS has been applied. Such a plot has the ability to show the added value (or perhaps lack of value) of including the empirically identified covariates, as measured relative to a known ground truth.

Another visualization that can be useful is a plot of the treatment effect estimate as additional empirically identified covariates are added to the hdPS model (Figure 4). If the estimate with 50 versus 100 variables is substantially different, this implies that the addition of 50 variables to the hdPS was useful in additional confounding control. On the other hand, if a large number of variables are added and there is no change to the treatment effect estimate, then that suggests that a more parsimonious hdPS model may be appropriate.

FIGURE 4.

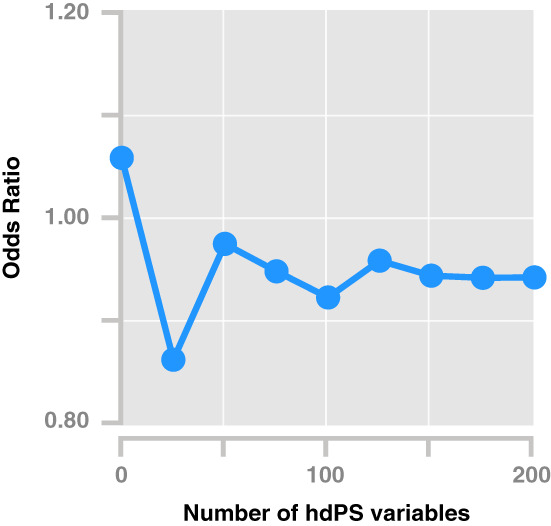
Sequential plot of odd ratios adjusted by hdPS with increasing size of empirically identified variables. The odds ratio broadly stabilizes after the addition of ~100–150 empirically identified variables. Hypothetical data following empirical analyses. ³³ hdPS, high‐dimensional propensity score.

4. TRANSPARENCY AND DOCUMENTATION

Overall efforts to improve the reproducibility and transparency of studies using real‐world data are broadly underway. ¹⁰ , ²⁵ For example, Wang et al. developed a structured template to aid in planning and reporting study methods, including hdPS if used, and recommend including key specifications such as the algorithm for covariate definition and other parameters (e.g., covariate assessment window, code type and granularity, diagnosis position) (Table S1).

Though not exhaustive, the following are items that should be reported and documented, first as part of a study protocol, and later as part of a final study report. By and large, the items below are syntheses of the decisions discussed above and thus will be familiar.

• Parameters for covariate identification. Within hdPS, decisions around how covariates will be identified, ranked and selected should be prespecified and documented. These parameters include which data dimensions will be considered (e.g., inpatient, outpatient, pharmacy); which coding systems will be used (e.g., ICD‐9‐CM, ICD‐10‐CM, CPT); to what level of detail the codes will be captured (e.g., the first three characters of ICD‐10‐CM codes); how many codes per dimension will be considered; how many variables will be included overall; and what ranking method will be applied (e.g., bias ranking, exposure association ranking).

• Investigator‐specified variables. As in all pharmacoepidemiology studies, noting a priori what confounders the investigators deem important to specifically adjust for is an important part of the analysis plan. Unlike typical protocols that include all variables, with hdPS, only investigator‐identified variables will be prespecified since the hdPS approach will empirically select further variables.

• Investigator‐specified excluded variables. Investigators should note any variables they consider instruments—and thus not appropriate to include in the hdPS—ahead of time. ²⁹ , ⁴¹ , ⁶¹ , ⁶² Such variables would include direct or near‐direct proxies for exposure. If further variables are excluded over the course of the study, those should be documented in the final study report.

• Estimation and use of PS. As with any PS, the method for estimating the hdPS (e.g., logistic regression) should be noted, along with any criteria for removing variables that may affect the estimation (e.g., employing a prevalence filter, such as not having at least five exposed and five referent patients). Furthermore, how the hdPS will be used in the analysis (e.g., matching, weighting) should be noted, as well as the software environment in which the score will be estimated and used.

• Diagnostics and reporting. The diagnostics to be employed (e.g., inspection of selected variables, surveilling for IVs) along with actions to take should anomalies be detected should be noted, as should other output (e.g., PS distribution plots, sequential addition of variables plot). ⁶⁰ We also recommend including a detailed list of variables included along with interpretable descriptions (e.g., the ICD‐10‐CM code description alongside the ICD‐10‐CM code) as a table or supplemental appendix. Software can aid in creating this list.

• Sensitivity analyses. While the decisions noted above should be made a priori, investigators may wish to vary certain parameters to determine robustness of the result or otherwise test their assumptions. For example, investigators may choose to conduct sensitivity analysis varying the confounder selection strategy with or without investigator‐identified covariates. To the extent possible, these sensitivity analyses should also be specified ahead of time, while acknowledging that certain variations may be made in response to observed data or observed performance of the hdPS. Any post hoc sensitivity analyses should be called out as such in the final study report.

5. LIMITATIONS AND MISCONCEPTIONS

Since its original publication, ⁵ a number of limitations and misconceptions regarding hdPS have emerged.

A first misconception is that data‐adaptive methods that consider hundreds of covariates for estimating the PS will lead to “over‐adjustment,” but it has been shown that the exposure effect size estimation should remain consistent even with additional covariates. ⁷ With that said, adjusting for too many preexposure may lead to statistical inefficiency, ³⁷ so if a larger number of covariates are desired, principled data‐adaptive PS estimation such as crossvalidation methods like Super Learning (SL) can be used to protect against overfitting when estimating the PS. ³⁷

There is also concern that liberal variable selection—including colliders and IVs—will lead to the introduction of M‐bias and Z‐bias, respectively. We would argue that the true threat to pharmacoepidemiology studies is unmeasured confounding, and as such, M‐ and Z‐bias are second‐order concerns. Furthermore, M‐ and Z‐biases are themselves mitigated with good study design (to avoid the introduction of colliders to begin with) and strong control of unmeasured confounding. As discussed earlier, any M‐bias will most likely be small, ²⁰ , ⁴⁴ and the careful measurement of covariates prior to exposure is a way to avoid including many colliders. Similarly, while Z‐bias may amplify any unmeasured confounding when IVs are included in the PS, Z‐bias's effect is greatly reduced by reducing the presence of unmeasured confounding. Unmeasured confounding remains the top problem to solve. ²⁰

Some consider hdPS to be a black box with limited transparency. While it is true that the hdPS method does not allow investigators to know the covariates that will be empirically identified a priori, the specific parameter settings of an hdPS algorithm can and should be prespecified and remain unchanged through the primary analysis. And while they are not known a priori, all selected variables are fully traceable back to source data, and their impact on baseline covariate balance can be assessed through the calculation and reporting of standardized differences. ⁷

hdPS can sometimes bring to light the limitations of the source data or of the research question asked. While hdPS extracts the maximum confounding information available in a database via proxy analytics to adjust for unmeasured confounding, ²¹ a given data source may inherently lack data dimensions that are required to reduce residual confounding to an acceptable level. ⁷ , ³⁷ hdPS is not a statistical technique to resolve poor data source selection, insufficient data content, or incorrect study design.

The performance of hdPS may be impacted by small sample sizes, including small cohorts, few exposures, and/or few outcome events. For example, because the PS model predicts exposure, PS estimation may be challenging when the number of exposed patients is small. However, in a study where investigators sampled data from four North American cohort studies and applied hdPS methods on the samples, they obtained similar hdPS‐adjusted point estimates in the samples relative to the full‐cohorts when there were at least 50 exposed patients with an outcome event. hdPS performed well in samples with 25–49 exposed patients with an outcome event when a zero‐cell correction was applied. ³³ Zero‐cell correction allows computation of the association between the variable and outcome by adding 0.1 to each cell in the 2 × 2 table, making computable values from values that are noncomputable due to division by zero. ²⁰

6. NEW DIRECTIONS

Since the publication of the original hdPS method, ⁵ a number of extensions and other developments have been shown. Below are several examples of new directions that hdPS has gone in.

6.1. Treatment effect estimation

The hdPS approach has most typically been applied to evaluate the effect of a static, binary treatment using PS matching. In more recent applications, hdPS was combined with alternate treatment effect estimation approaches such as inverse probability weighting and collaborative targeted minimum loss based estimation. ³⁷ , ⁶³ This was done to take advantage of these methods' improved statistical properties over PS matching, such as the ability to properly adjust for time‐dependent confounders and sources of selection bias, ⁶⁴ to employ double robustness, and to evaluate alternate causal estimands, such as the average effects of time‐varying dynamic treatment regimens. With that said, whatever the causal estimand and estimator chosen, hdPS at its core can be viewed as a pragmatic approach to automate selection of the covariate adjustment set in the analysis of healthcare databases.

6.2. Estimation of the PS

After identifying hdPS‐derived covariates, the investigator must use the covariates to estimate a PS for each patient, or for outcome regression in the case of doubly robust estimation of the causal effect. The standard logistic regression estimation methods rely on parametric assumptions such as the assumption that a PS or outcome regression model can be correctly represented by a logistic linear model with only main terms for each covariate and no interactions. Incorrect causal inferences are expected if these—often arbitrary—modeling assumptions do not hold, for example if the logit link between the linear part of the model and PS is incorrect. Finite sample bias and increased variability can also be expected when a large number of hdPS‐derived covariates are included in the parametric models. ³⁷ To protect against incorrect inferences due to mis‐specified parametric models and to automate dimensionality reduction of the covariate adjustment set (e.g., to reduce collinearity), statistical learning can be used to nonparametrically estimate a PS or outcome regression based on empirically identified and investigator‐specified variables while maintaining explainability using, for example, Shapley Additive Explanation values.

SL—an ensemble learning method—is one such approach that was proposed to improve confounding adjustment with hdPS covariates. SL is a data‐adaptive estimation algorithm that combines, through a weighted average, predicted values from a library of candidate learners such as neural networks, random forests, gradient boosting machines, and parametric models—all possible methods of estimating patients' PSs. The selection of the optimal combination of learners is based on crossvalidation to protect against overfitting. The resulting learner (called the “super learner”) is intended to perform asymptotically as well or better (in terms of mean error) than any of the candidate learners considered—and the number of candidate learners can grow as large as is computationally feasible. The practical performance of combining hdPS with SL for confounding adjustment has been illustrated using both real‐world and simulated data. ³⁶ , ³⁷ Future research is needed to evaluate the value of alternate methodologies such as deep learning.

6.3. Other new directions

6.3.1. Unstructured data

hdPS typically works with structured, coded data. However, using natural language processing methods, it is also possible to convert free‐text into tokens, which can stand on their own as potential variables. These data may give additional information beyond what is coded in diagnosis, procedure, medication and other fields, especially when electronic medical records are used as source data. ⁶⁵

6.3.2. Continuous covariates and outcomes

The Bross formula typically used is intended for use with binary covariates and outcomes, but in many cases, continuous values for one or both may be appropriate. Extensions to the ranking formula can incorporate such continuous values. ⁶⁶

6.3.3. Combination matching or weighting methods

Most studies that match or weight with a PS do so exclusively with the PS variable. However, it is also possible to match (weight) on specific key investigator‐identified factors, and then match (weight) on a PS. ⁶⁷

7. CONCLUSION

In this article, we provide an overview and guidance on the planning, implementing, and reporting of studies using the hdPS approach in the analysis of healthcare databases, an approach to minimize residual confounding by identifying and adjusting confounding factors or proxies for confounding factors. As illustrated by case examples included in the supplemental materials, a wide range of studies across different data sources have used hdPS over the past decade, and new applications with machine learning techniques are emerging. A basic understanding of the hdPS approach—for both researchers and decision‐makers consuming RWE—and recommendations for the planning, implementation, and reporting of hdPS process are critical for continued generation of transparent and robust RWE.

AUTHOR CONTRIBUTIONS

Jeremy A. Rassen drafted the manuscript from contributions from each author. Jeremy A. Rassen, Patrick Blin, Sebastian Kloss, Romain S. Neugebauer, Robert W. Platt, Anton Pottegård, Sebastian Schneeweiss, and Sengwee Toh all critically reviewed and revised the manuscript and gave final approval for publication.

CONFLICT OF INTEREST

Dr. Rassen is an employee of and has an ownership stake in Aetion, Inc. Dr. Kloss is an employee of Johnson & Johnson. Dr. Pottegård is an employee of the University of Southern Denmark, Clinical Pharmacology, Pharmacy and Environmental Medicine. He has participated in studies funded by pharmaceutical companies (Alcon, Almirall, Astellas, Astra‐Zeneca, Boehringer‐Ingelheim, Pfizer, Menarini, Servier, Takeda), with money paid to his employer and with no relation to the work reported in this article. Dr. Schneeweiss is participating in investigator‐initiated grants to the Brigham and Women's Hospital from Boehringer Ingelheim and UCB unrelated to the topic of this study. He is a consultant to Aetion Inc., a software manufacturer of which he owns equity. He is an advisor to Temedica GmbH, a patient‐oriented data generation company. His interests were declared, reviewed, and approved by the Brigham and Women's Hospital in accordance with their institutional compliance policies. Dr. Toh reports being a consultant to Pfizer and Merck on methodological issues unrelated to this study. Drs. Blin, Neugebauer, and Platt report no conflicts of interest.

Supporting information

APPENDIX S1: Supporting Information.

Rassen JA, Blin P, Kloss S, et al. High‐dimensional propensity scores for empirical covariate selection in secondary database studies: Planning, implementation, and reporting. Pharmacoepidemiol Drug Saf. 2023;32(2):93‐106. doi: 10.1002/pds.5566

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this study.