Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Mar 15;19(7):2048–2063. doi: 10.1021/acs.jctc.2c01170

Influence of the Lennard-Jones Combination Rules on the Simulated Properties of Organic Liquids at Optimal Force-Field Parametrization

Marina P Oliveira 1, Philippe H Hünenberger 1,*
PMCID: PMC10100539  PMID: 36920838

Abstract

graphic file with name ct2c01170_0011.jpg

We recently introduced the CombiFF scheme [Oliveira et al., J. Chem. Theory Comput. 2020, 16, 7525], an approach for the automated refinement of force-field parameters against experimental condensed-phase data for large compound families. Using this scheme, once the time-consuming task of target-data selection and curation has been performed, the force-field optimization itself is both straightforward and fast. As a result, CombiFF provides an ideal framework for evaluating the influence of functional-form decisions on the accuracy of a force field at an optimal level of parametrization. We already used this approach to assess the effect of using an all-atom representation compared to united-atom representations in the force field [Oliveira et al., J. Chem. Theory Comput. 2022, 18, 6757]. Here, CombiFF is applied to assess the effect of three Lennard-Jones combination rules, geometric-mean (GM), Lorentz–Berthelot (LB), or Waldman–Hagler (WH), on the simulated properties of organic liquids. The comparison is performed in terms of the experimental liquid density ρliq, vaporization enthalpy ΔHvap, surface-tension coefficient γ, static relative dielectric permittivity ϵ, and self-diffusion coefficient D. The calibrations of the three force-field variants are carried out independently against 2044 experimental values for ρliq, and ΔHvap concerning 1516 compounds. The resulting root-mean-square deviations from experiment are 30.0, 26.9, and 36.7 kg m–3 for ρliq and 2.8, 2.8, and 2.9 kJ mol–1 for ΔHvap, when applying the GM, LB, and WH combination rules, respectively. In terms of these (and the other) properties, the three combination rules perform comparatively well, with the GM and LB results being more similar to each other and slightly more accurate compared to experiment. In contrast, the use of distinct combination rules for the parameter calibration and property calculation leads to much larger errors.

1. Introduction

Classical atomistic simulation1−3 and, in particular, molecular dynamics4−8 (MD) has become an established tool complementary to experiment for investigating condensed-phase systems. Although classical models represent an approximation to quantum mechanics (QM), they can provide a realistic description of atom-based systems at a much lower computational cost. However, the accuracy of classical MD simulations depends crucially on the quality of the underlying potential-energy function or force field.9−15

The automatic optimization of force-field parameters16−22 has a long history in the context of target QM data23−27 (see also refs (28−33).). However, until recently, the refinement against experimental data has mainly relied on manual (thus laborious and time-consuming) procedures, with only a few attempts at automation, all in the context of atomic liquids34 or water.35−37 Recent attempts at automating the fitting against condensed-phase observables include the POP38,39 and the ForceBalance schemes29−31,40−45 (see also refs (46−51)).

Along these lines, the CombiFF22,52−54 approach developed in our group is an integrated scheme for the automated refinement of force-field parameters against experimental condensed-phase data, considering entire classes of organic molecules constructed using a fragment library via combinatorial isomer enumeration. The scheme is designed to achieve: (i) a comprehensive (although not exhaustive) coverage of the chemical space; (ii) an appropriate representation of induction effects; and (iii) a complete automation of the topology construction and parameter optimization. As initial applications, CombiFF was used to design GROMOS-compatible united-atom force fields for saturated acyclic compounds with halogen substitution22 or including common functional groups of oxygen and nitrogen.52

Using CombiFF, once the time-consuming task of target-data selection and curation has been performed, the force-field optimization itself is both straightforward and fast. As a result, CombiFF provides an ideal framework for assessing the influence of functional-form decisions on the accuracy of a force field at an optimal level of parametrization. The goal of the present study is to perform such an assessment considering the choice of a specific combination rule for the Lennard-Jones55 (LJ) potential. Despite a probably too steep short-range repulsion,29,56−58 the latter potential remains the most common function for representing the van der Waals interactions in condensed-phase (bio)molecular force fields (e.g., OPLS, AMBER, CHARMM, and GROMOS).

The application of combination rules is a widely used strategy to infer the parameters appropriate for LJ interactions between unlike atoms from the knowledge of those between like atoms, thereby reducing the number of parameters required in the definition of a force field. The combination is usually performed in terms of the LJ collision diameter σ (zero of the LJ curve) and well depth ϵ (energy drop at the minimum of the LJ curve). Three common rules are the geometric-mean (GM) rule,59,60 involving a geometric averaging of both σ and ϵ,

1. 1

the Lorentz–Berthelot (LB) rule,61,62 involving an arithmetic averaging for σ and a geometric averaging for ϵ,

1. 2

and the Waldman–Hagler (WH) rule,63 involving a sixth-power mean for σ and a geometric mean for ϵσ6,

1. 3

There is extensive literature discussing the accuracy and limitations of commonly used combination rules,64−68 including comparisons with results from using equations of state69,70 or molecular simulations71−73 in terms of the thermodynamic properties of fluid mixtures. It is well-known that the GM and LB rules lead to significant deviations from experimental data for rare gases, resulting in overly attractive unlike-pair potentials, while other rules, such as WH, provide a better description63 (see Section S.1 in the Supporting Information for a summary). In the condensed phase, the choice of a combination rule also significantly impacts the calculated thermodynamic properties of binary mixtures.71 For pure systems, their effect is expected to be more limited and, in large part, compensated for by the effective force-field parameters selected during the calibration.

In a recent study,54 we used the CombiFF approach to assess the effect of using an all-atom compared to a united-atom representation in the force field. Here, CombiFF is used to investigate the effect of the combination rule (GM, LB, or WH) on the accuracy of a force field in terms of condensed-phase observables for pure liquids at an optimal level of force-field parametrization.

2. Methodology

The CombiFF workflow for calibrating the parameters of a force field based on experimental data concerning a given compound family is described in our previous article.22 This section only provides information on its application to the present systematic comparison of combination rules. For ease of reference, a few key numbers (symbols and values) are summarized in Table 1.

Table 1. Key Numbers (Symbols and Values) Pertaining to the CombiFF Force-Field Calibrationa.

parameter value description
Nisocal 1516 compounds included in the calibration set
Nexpcal 2044 experimental data points for the calibration set
graphic file with name ct2c01170_m018.jpg
Nρcal 1440 experimental ρliq data points for the calibration set
NΔHcal 604 experimental ΔHvap data points for the calibration set
     
Nsimcal 1607 distinct compounds and P, T-points (i.e., simulations) for the calibration set
NattEE, Natt 56 number of EE types (or, equivalently, atom types)
NattLJ 17 number of LJ types
Nprmtot 289 total number of force-field parameters
graphic file with name ct2c01170_m019.jpg
Nprmcov 104 number of covalent parameters
Nprmnbd 185 number of nonbonded parameters
Nprmcal 137 number of parameters that are optimized
Open in a new tab
a

The structures of the Nisocal representative molecules considered in the calibration are shown in Section S.2 in the Supporting Information. The experimental data concerning these molecules is provided in Section S.3. The information concerning the Nprm covalent parameters is summarized in Section S.4. The optimized values of the Nprmnbd nonbonded parameters are provided in Section S.5. Note that the number Nprm of parameters optimized is smaller than the total number Nprmtot of force-field parameters, because only non-bonded parameters are optimized, and solely a subset thereof.

The set of compounds considered for the comparison is defined as the union of 11 subfamilies listed in Table 2. Besides alkanes, it includes homofunctional noncyclic aliphatic molecules with up to 10 carbon atoms representative of nine chemical functional groups, namely, halogen, ether, aldehyde, ketone, ester, alcohol, carboxylic acid, amine, and amide (with up to four occurrences of the given functional groups in the molecule), along with heterobifunctional molecules.

Table 2. Family of Compounds Used for the Force-Field Calibrationa.

function acronym char n m Nsim subfamily description
alkanes ALK A 1–10 – 150 C1–C10 alkanes
    F 1–10 1–4 27 C1–C10 fluoroalkanes
haloalkanes HAL C 1–10 1–4 33 C1–C10 chloroalkanes
    B 1–10 1–4 39 C1–C10 bromoalkanes
    I 1–10 1–4 28 C1–C10 iodoalkanes
ethers ROR O 1–10 1–3 123 C1–C10 ethers
aldehydes RCOH A 1–10 1–2 33 C1–C10 aldehyde
ketones RCOR K 1–10 1–2 85 C1–C10 ketones
esters RCOOR E 1–10 1–2 183 C1–C10 esters (only formates)
alcohols ROH L 1–10 1–3 358 C1–C10 alcohols
carboxylic acids RCOOH D 1–10 1 48 C1–C10 carboxylic acids
amines RN N 1–10 1–2 117 C1–C10 amines
amides RCON M 1–10 1 19 C1–C10 amides
mixed subfamilies MIX S 1–10 1–4 273 C1–C10 heteropolyfunctional molecules
             
total – – – – 1516 total over the 11 subfamilies
Open in a new tab
a

The family is defined as the union of 11 non-overlapping subfamilies, representative for alkanes, for nine chemical functional groups, and for hetero-bifunctional compounds of these groups. The acronyms retained for the different subfamilies (also distinguishing halogen types in the HAL subfamily) are further used in the text, tables, and figures. The one-character variant (Char) is used as a first letter in the acronyms of the corresponding molecules. For each subfamily, n stands for the number of carbon atoms, m for the number of occurrences of the functional group in the molecule (or total for the two types of group in the MIX subfamily), and Nsim for the number of isomers considered in the simulations (i.e., for which experimental data could be found). The structures of the Nisocal = 1516 representative molecules considered in the calibration are shown in Section S.2 in the Supporting Information (Figure S.2).

For the experimental data collection, the database (DBS) maintained in our group was queried for the liquid density ρliq, the vaporization enthalpy ΔHvap, the surface-tension coefficient γ, the static relative dielectric permittivity ϵ, and the self-diffusion coefficient D. The data sources accessed were refs (74−87). This resulted in values concerning Nisocal = 1516 compounds. The structures of these compounds are shown in Section S.2 in the Supporting Information (Figure S.2). The acronyms employed for the individual molecules involve one letter and four digits. The letter represents the chemical functional group (see Table 2). The first digit stands for the number of carbon atoms, with the number 10 mapped to the digit zero. The last three digits form a sequential index to further distinguish compounds for which the first two symbols are identical.

The experimental-data vector Xexp used to calibrate the force-field parameters has the dimension Nexpcal = 2044. It encompasses Nρ = 1440 values for ρliq and NΔHcal = 604 values for ΔHvap, and requires Nsim = 1607 independent simulations (i.e., distinct compounds and P,T-points) for its evaluation. The experimental reference values retained for ρliq and ΔHvap, along with the associated P,T-points, are listed in Section 3 in the Supporting Information (see Table S.2). After calibration based on ρliq and ΔHvap, experimental values of γ, ϵ, and D for 66 compounds were used to further test the accuracy of the optimized force fields. These values are listed in Section S.3 in the Supporting Information (See Table S.3). All the experimental data can also be freely downloaded from the Internet using ref (113), where the present data are labeled as version 1.0.

The force-field representation employed is compatible with the GROMOS force field88−93 in its 2016H66 variant,94 except for one important difference. The atomic partial charges are determined for each molecule based on an electronegativity equalization (EE) scheme.95 Similar to our previous work22 (see Appendix A.4 therein), charge flows are only allowed within overall neutral charge groups, and intramolecular Coulombic effects (J-terms in the EE scheme) are only included for first and second covalent neighbors.

The covalent interaction parameters relevant for the molecules considered here were taken or ported by analogy from the 2016H66 parameter set94 and kept unaltered. The corresponding information is summarized in Section S.4 in the Supporting Information (see Table S.4). Only the nonbonded interaction parameters were subjected to refinement and solely a subset thereof.

In GROMOS, charge groups are used for the application of the nonbonded interaction cutoff, which performs a group-based truncation in terms of the centers of geometry of the two charge groups. The relevant charge groups are illustrated in Figure 1. All the aliphatic (united) atoms of the molecule that are not explicitly included in one of these groups define separate one-particle charge groups with zero charge. Intramolecular Coulombic effects between first and second covalent neighbors within a charge group in the EE scheme are described using Gaussian-cloud interactions. The corresponding effective interatomic distances r̅ are calculated based on the reference bond lengths and angles of the covalent force field, along with effective radii set to the van der Waals radii of the involved (united) atoms. These radii are listed in Section S.4 (see Table S.5).

Figure 1.

Figure 1

Open in a new tab

Charge groups relevant for the compounds considered here. The symbol X denotes a halogen atom. Charge flows in the EE scheme are only permitted between atoms belonging to the same overall neutral charge group. All the aliphatic (united) atoms of the molecule (atom types CH0, CH1, CH2, CH3, and CH4 in Table 3) that are not explicitly included in these groups define separate one-particle charge groups with a charge of zero.

The atomic partial charges are determined indirectly via the EE scheme based on two types of atomic parameters: the hardness η and the electronegativity χ. Because of the use of a combination rule (GM, LB, or WH), the pairwise LJ coefficients are also constructed based on two types of atomic parameters, namely, the collision diameter σ and the well depth ϵ. Following the GROMOS design principles, the values σ and ϵ are only used in the combination rule for non-hydrogen-bonding LJ-type pairs (corresponding to the LJ parameters C6 and C12,I in GROMOS). For hydrogen-bonding LJ-type pairs, GROMOS relies on a modified set of LJ parameters with slightly enhanced repulsion. In this case, alternative values σ̃ and ϵ̃ are used instead (corresponding to the LJ parameters C6 and C12,II in GROMOS). For simplicity, the value of the dispersion coefficient C6 is kept identical in the two sets, so that only σ̃ needs to be specified, while ϵ̃ can be deduced as ϵ̃ = 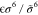Inline graphic. Finally, for third covalent neighbors, yet another pair of values σ* and ϵ* is used in the combination rule. Each atom type of the force field is thus associated with a unique selection for six (non-hydrogen-bonding type) or seven (potentially hydrogen-bonding type) parameters. However, the same σ and ϵ parameters are often used for different atom types of the same element. As a result, the present force field relies on a number Natt = 56 of atom types, which are equivalent to EE types Inline graphic, but involve a smaller number NattLJ = 17 of LJ types. The 56 atom types (or EE types) are listed in Table 3 along with a LJ type. The latter refers to the entries of Table 4. The correspondence between elements, LJ types, atom-types (EE types), and chemical functional groups is illustrated schematically in Figure 2. The final (optimized) values of the EE and LJ parameters are reported in Section S.5 in the Supporting Information (Tables S.6 and S.7) for the three choices of combination rules.

Table 3. Atom Types (or, Equivalently, EE Types) of the Force Fielda.

atom type (EE type) LJ type usage
Aliphatic Carbon (United) Atoms
CH0 CH0 CH0 carbon atom (methanetetryl group)
CH1 CH1 CH1 carbon united atom (methanetriyl group)
CH2 CH2 CH2 carbon united atom (methylene group)
CH3 CH3 CH3 carbon united atom (methyl group)
CH4 CH4 CH4 carbon united atom (methane group)
Halogen
F_hal F fluorine atom
Cl_hal Cl chlorine atom
Br_hal Br bromine atom
I_hal I iodine atom
CH0_hal CH0 halogenated CH0 atom
CH1_hal CH1 halogenated CH1 united atom
CH2_hal CH2 halogenated CH2 united atom
CH3_hal CH3 halogenated CH3 united atom
Ether
O_eth OC ether oxygen atom
CH0_O_eth CH0 alkoxylated CH0 atom
CH1_O_eth CH1 alkoxylated CH1 united atom
CH2_O_eth CH2 alkoxylated CH2 united atom
CH3_O_eth CH3 alkoxylated CH3 united atom
Aldehyde
H_CO_ald HC aldehyde hydrogen atom
C_ald C=O aldehyde carbonyl carbon atom
O_ald O=C aldehyde carbonyl oxygen atom
Ketone
C_ket C=O ketone carbonyl carbon atom
O_ket O=C ketone carbonyl oxygen atom
Ester
H_CO_est HC formate ester hydrogen atom
C_est C=O ester carbonyl carbon atom
O_est O=C ester carbonyl oxygen atom
O_C_est OC ester acylated oxygen atom
CH0_O_est CH0 ester oxygen-linked CH0 atom
CH1_O_est CH1 ester oxygen-linked CH1 united atom
CH2_O_est CH2 ester oxygen-linked CH2 united atom
CH3_O_est CH3 ester oxygen-linked CH3 united atom
Alcohol
H_ol HB hydroxyl hydrogen atom
O_ol OH hydoxyl oxygen atom
CH0_O_ol CH0 hydroxylated CH0 atom
CH1_O_ol CH1 hydroxylated CH1 united atom
CH2_O_ol CH2 hydroxylated CH2 united atom
CH3_O_ol CH3 hydroxylated CH3 united atom
Carboxylic Acid
H_CO_acd HC formic acid hydrogen atom
C_acd C = O carboxylic acid carbonyl carbon atom
O_acd O = C carboxylic acid carbonyl oxygen atom
H_O_acd HB carboxylic acid hydroxyl hydrogen atom
O_H_acd OH carboxylic acid hydroxyl oxygen atom
Amine
H_N_amn HB amine hydrogen atom
N_amn N_amn amine nitrogen atom
CH0_N_amn CH0 aminated CH0 atom
CH1_N_amn CH1 aminated CH1 united atom
CH2_N_amn CH2 aminated CH2 united atom
CH3_N_amn CH3 aminated CH3 united atom
Amide
H_N_amd HB amide nitrogen-linked hydrogen atom
C_amd C = O amide carbonyl carbon atom
O_amd O = C amide carbonyl oxygen atom
N_amd N_amd amide acylated nitrogen atom
CH0_N_amd CH0 amide nitrogen-linked CH0 atom (estimated)
CH1_N_amd CH1 amide nitrogen-linked CH1 united atom
CH2_N_amd CH2 amide nitrogen-linked CH2 united atom
CH3_N_amd CH3 amide nitrogen-linked CH3 united atom
Open in a new tab
a

The Natt = 56 atom types (or, equivalently, NattEE = 56 EE types) are listed, along with their usage and the associated LJ type (referring to the entries of Table 4). Initial (optimization start) and final (after optimization) values for these parameters can be found in Tables S.9 and S.7, respectively, in the Supporting Information.

Table 4. LJ Types of the Force Fielda.

LJ type usage
Carbon
CH0 CH0 carbon atom (methanetetryl group)
CH1 CH1 carbon united-atom (methanetriyl group)
CH2 CH2 carbon united-atom (methylene group)
CH3 CH3 carbon united-atom (methyl group)
CH4 CH4 carbon united-atom (methane group)
C=O carbonyl carbon atom
Halogen
F fluorine atom
Cl chlorine atom
Br bromine atom
I iodine atom
Oxygen
OC ether oxygen atom
O=C carbonyl oxygen atom
OH hydoxyl oxygen atom
Nitrogen
N_amn amine nitrogen atom
N_amd amide nitrogen atom
Hydrogen
HC carbonyl-linked hydrogen atom
HB oxygen- or nitrogen-linked hydrogen atom
Open in a new tab
a

The NattLJ = 17 LJ types are listed along with their usage. These LJ types are invoked in the specification of the Natt = 56 atom types of Table 3. Initial (optimization start) and final (after optimization) values for these parameters can be found in Tables S.8 and S.6, respectively, in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

Correspondence between the 8 elements, the 17 LJ types, the 56 atom types (EE types), and the 10 chemical functional groups. The first column refers to the elements, the second to the LJ types (see Table 4), the third to the atom or EE types (see Table 3), and the fourth to the chemical functional groups (see Table 2).

The five aliphatic atom types (CH0 to CH4) have no EE parameters, as their charge is always zero. The LJ parameters of the polar hydrogen atom type (HB) were also kept at zero and excluded from the optimization. The third-neighbor LJ interaction parameters were kept equal to those of the 2016H66 set94 for the GM combination rule, or made equal to the corresponding normal LJ parameters multiplied by 0.8 (σ* = 0.8σ and ϵ* = 0.8ϵ) for the LB and WH combination rules. This modification is inspired by the scaling applied to third-neighbor interactions in the AMBER force field.96 Note also that, in the absence of a parametrization target, the η and χ values of the EE-type CH0_N_amd could not be calibrated. The initial parameter values selected to start the optimization are reported in Section S.6 in the Supporting Information (Tables S.8 and S.9). They were taken from the previous application of the CombiFF scheme to the HAL and O+N families22,52, complemented when necessary by η and χ, as estimated from ref (95).

Following from the above choices, the present force field involves Nprmtot = 289 parameters, namely, Nprm = 104 covalent parameters and Nprmnbd = 185 nonbonded parameters (2 × 56 EE-types + 4 × 12 non-hydrogen-bonding LJ types + 5 × 5 potentially hydrogen-bonding LJ types), among which Nprm = 137 are subject to optimization (omitted are 2 × 17 third-neighbor LJ parameters, 2 × 1 LJ parameters for HB, and 2 × 6 EE parameters for aliphatic carbons and CH0_N_amd). Optimizing these parameters against Nexpcal = 2044 experimental data points leads to an observable-to-parameter ratio of ∼15. This ratio is further analyzed for each EE and LJ type separately in Section S.7 in the Supporting Information (Tables S.10 and S.11). A favorable observable-to-parameter ratio is achieved in most cases, although three EE types (CH3_O_ol, H_CO_acd, and CH1_N_amd) only occur in a single representative molecule, and one (CH0_N_amd) is not represented at all.

The search for optimal parameters was performed as in our previous work22 (see Appendix A.7 therein), by minimizing an objective function Q(P; Xexp) of the parameter vector P which accounts for the deviation between the simulated-data vector Xsim(P) and the reference-data vector Xexp. This function is

2. 4

with

2.

where the index n corresponds to the Nn observable types and the index m to the Nm molecules in the family. The sn coefficients eliminate the dependence on a unit system and adjust the relative weights of different observables in terms of the perceived (i.e., subjective) extent of “badness”. They are set here to 20 kg m–3 for ρliq and 1 kJ mol–1 for ΔHvap, i.e., we “decided” that it is equally bad for a force field to be off by 20 kg m–3 in terms of ρliq, or to be off by 1 kJ mol–1 in terms of ΔHvap. The coefficients wnm are set to one for all the combinations included (also considering observables at multiple state points).

The iterative parameter adjustments are is performed by assuming that Xsim(P) is approximately linear in parameter changes within a small trust region around a reference point P° in parameter space, i.e., using the local first-order approximation 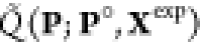Inline graphic to Q(P; Xexp), defined by

2. 5

where S(P°) is the sensitivity matrix of the different molecule/observable combinations, with respect to variations of the Nk parameters around the point P°, i.e.,

2. 6

This matrix is calculated next to the observables themselves during the MD simulations at P° using appropriate statistical-mechanical expressions.22,30,38−40,97 The trust region is defined here in terms of maximal allowed relative changes in each of the parameters over an iteration, set to 5% for all parameters optimized. Note that the MD simulations and the parameter changes are performed sequentially, not simultaneously. During the simulations, ρliq and ΔHvap are calculated and averaged, as well as the first derivatives of these observables with respect to all force-field parameters (with the parameters remaining fixed). Only after the simlations is a parameter adjustments undertaken.

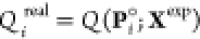In practice, the optimization algorithm involves the following steps over iterations i starting from zero: (1) select an initial guess P0° for the parameters; (2) run Nsim simulations to get the vector Xisim,° and the matrixInline graphic; (3) calculate the real value Inline graphic of the objective function at this point in parameter space using eq 4; (4) minimize 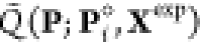Inline graphic in eq 5 with respect to P starting from Pi and staying within the trust region, leading to Pi*; (5) calculate the predicted value 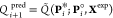Inline graphic of the objective function; (6) set Pi+1 to Pi*, increment i, and iterate to step (2) until convergence.

Convergence can be defined by an objective function that stops varying significantly upon further iteration, or by force-field parameters that also stop varying significantly upon further iteration. The two options will not differ much in terms of the accuracy reached for ρliq and ΔHvap (because it is what is measured by the objective function), but they may differ when other properties are calculated based on the optimized force fields (because their accuracy depends on the parameters retained). In this work, we took the first definition. Previous work involving multiple optimizations initiated from different starting parameters22 (see Section S.8 in the Supporting Information of this article) have shown that (i) different solutions of similar accuracies are obtained; (ii) the corresponding EE parameters evidence significant variations, while the LJ parameters and EE-derived partial charges are more similar. The force-field variants derived in this work are thus probably close to optimality, but not unique.

The full parameter optimization was performed twice for GM and LB, or three times for WH. The second optimization (and third for WH) were carried out with randomly perturbed parameters from the final parameters of the first optimization (changes in the range 20%, or 50% for the third run with WH). These repeats served to assess the robustness of the calibration with respect to variations of the initial parameters. Only the results for the three runs (one for each combination rule) leading to the minimum value of the target function are discussed in the main article. The results for the other runs are reported in Section S.13 in the Supporting Information.

The optimization against ρliq and ΔHvap was performed as in our previous work22,52 using an in-house GROMOS-compatible simulation engine in C++ called SAMOS. The GROMOS program92,98 was used for the calculation of all other properties. The pure-liquid MD simulations were carried out under periodic boundary conditions based on cubic computational boxes containing 512 molecules. They were performed in the isothermal–isobaric ensemble at the reference pressures P and temperatures T listed in Tables S.2 and S.3 in the Supporting Information.

The equations of motion were integrated using the leapfrog scheme99,100 with a time step of 2 fs. Constraints on all bond lengths were enforced using the SHAKE procedure101 with a relative geometric tolerance of 10–5. The nonbonded interactions were calculated using a twin-range scheme102 based on charge-group distances, with short- and long-range cutoff radii set to 0.8 and 1.4 nm, respectively, and an update frequency of 5 timesteps for the short-range pairlist and intermediate-range interactions. The mean effect of the omitted electrostatic interactions beyond the long-range cutoff was reintroduced by means of a reaction-field correction.103,104 The corresponding static relative dielectric permittivities were set to the experimental permittivity ϵ. The temperature was maintained close to its reference value using a Nosé–Hoover thermostat105 with a coupling time of 0.1 ps, and the pressure was maintained close to its reference value using a weak-coupling barostat106 with a coupling time of 0.5 ps and an isothermal compressibility set to 4.575 · 10–4 kJ–1 mol nm3. The ideal-gas simulations (required for ΔHvap) involved a single molecule and relied on stochastic dynamics100,107−110 (SD) with a friction coefficient set to 2 ps–1.

For the calculation of the five monitored properties (ρliq, ΔHvap, γ, ϵ, and D), three independent repeats were carried out each time, involving different initial coordinates and velocities. The average value is reported, along with an uncertainty estimate corresponding to the error on the mean over the three repeats with a 95% confidence interval.

The pure-liquid density ρliq and vaporization enthalpy ΔHvap were calculated based on pure-liquid and ideal-gas simulations at P,T-points specified in Table S.2. For ρliq, this required only a pure-liquid simulation at the indicated P,T-point. For ΔHvap, this also required an ideal-gas simulation at the same temperature T. For each repeat, the former simulation involved 0.6 ns equilibration followed by 0.6 ns production. The value of ρliq was calculated from the pure-liquid simulation as the ratio of the mass of the computational box to the corresponding average volume. The value of ΔHvap was calculated from the pure-liquid and gas-phase simulations as the difference between the average potential energies per molecule in the two phases (gas minus liquid), expressed on a per-mole basis and increased by RT, where R is the gas constant.

The surface-tension coefficient was calculated at the P,T-points listed in Table S.3. For each of the three repeats, the system was first equilibrated for 5 ns at constant pressure. The box was then extended by a factor of 5 in the z-direction, generating a system with two liquid-vacuum interfaces. The value of γ was calculated from a subsequent 5 ns constant-volume simulation as

2. 7

where Lz is the box length in the z-direction and Pαα (α = x, y, z) are the diagonal elements of the pressure tensor.

The static relative dielectric permittivity ϵ was calculated at the P,T-points listed in Table S.3. For each of the three repeats, ϵ was obtained from a 50 ns constant-pressure simulation using the Neuman relation,111

2. 8

where M is the box dipole moment vector, ϵo is the permittivity of vacuum, and ϵRF is the reaction-field permittivity (Table S.2).

The self-diffusion coefficient D was calculated at the P,T-points listed in Table S.3. For each of the three repeats, it was obtained based on a 5.0 ns constant-pressure simulation from the mean-square displacement of the molecules, using the Einstein relation112

2. 9

where ri is the instantaneous position of the center of geometry of molecule i, following molecules across periodic boundaries. The estimation of D relied in practice on a least-squares fit over the interval from 0 to 3 ns.

Additional details about the simulation protocols can be found in refs (22 and 52). The GROMOS-compatible molecular topologies and equilibrated liquid configurations for the Nisocal = 1516 molecules considered here can be downloaded from the Internet under ref (113) (version 1.0).

3. Results

The evolution of the objective function Q against the iteration number i is illustrated in Figure 3 for the three combination rules. The main graph shows the optimizations that led to the lowest final Q values. The inset shows the other optimizations (one for GM and LB, two for WH). The real values Qireal at iteration i as well as their predicted values Qi from iteration i – 1 are both shown. The objective function drops sharply during the first two iterations, converges after about four iterations (where Qpred and Qreal become almost identical), and the additional iterations bring only little further improvement. The three final force-field variants corresponds to iteration i = 10 for the main replica, with final values of 1.18, 1.15, and 1.45 for the objective function in the GM, LB, and WH cases, respectively. The final values for the alternative replicas are 1.21, 1.16, and 1.45 for the GM, LB, and WH combination rules. The third run using WH, which involved a more pronounced randomization of the initial parameters, gives a final value of 1.64. The value of Qireal using WH is always the highest, whereas the values for GM and LB are lower and closer together. For the sake of conciseness, only the three force-field variants with the lowest final Q value are further discussed here. The results for the other replicas evidence the same qualitative features, and are reported in Section S.13 in the Supporting Information for completeness.

Figure 3.

Figure 3

Open in a new tab

Evolution of the predicted (pred) and real (real) values of the objective function Q against the iteration number i along the force-field parameter optimization for geometric-mean (GM), Lorentz–Berthelot (LB), and Waldman–Hagler (WH) combination rules. The main graph shows the optimizations that led to the lowest final Q values. The inset shows the other optimizations (one for GM and LB, two for WH). For the main runs, 34, 7, and 17 molecules vaporized when optimizing with the GM, LB, and WH combinations rules, respectively. These are displayed in Section S.8 in the Supporting Information. The results discussed in the text exclude the set of 69 molecules that vaporized in any of these runs. Note that the lines have no physical meaning and are intended only as a guide to the eye.

The evolution of the Nprmcal = 137 nonbonded interaction parameters subject to calibration against the iteration number i is shown in Figures 4 and 5 for the LJ and EE parameters, respectively. The LJ interaction parameters σ and ϵ tend to converge to similar final values for the three combination rules, i.e., within relatively narrow ranges. The exceptions are the atom types CH0, CH1, and Cl. Note that CH0 is a special case, as it is a buried atom type. Compared to the LJ interaction parameters, the electrostatic parameters η and χ evidence more variations across the three optimizations. However, as shown in Figure 6, the atomic partial charges remain qualitatively consistent across the optimizations with the different combination rules. The charges tend to be positive for hydrogen and carbon atom types, and predominantly negative for oxygen and nitrogen types. Exceptionally, the alkoxyl-oxygen atom type (OC) in ester groups may present positive charges when using GM. This is because the electronegativity of the oxygen type O_C_est (7.6 V) is lower than of alkoxyl-carbon atom types (8.0 V for CH1_O_est, 7.8 V for CH2_O_est, and 8.1 V for CH3_O_est). Only when bound to CH0_O_est (6.4 V) is the alkoxyl-oxygen in ester groups negative. The corresponding atomic partial charges are shown in Section S.9 in the Supporting Information (Figure S.7) and compared to QM-derived charges.114−118

Figure 4.

Figure 4

Open in a new tab

Evolution of the 37 LJ interaction parameters against the iteration number i along the force-field parameter optimization for the geometric-mean (GM), Lorentz–Berthelot (LB), and Waldman–Hagler (WH) combination rules. The parameters considered are the collision diameter σ or σ̃ (the latter is applicable for hydrogen-bonding types) and the well depth ϵ. The NattLJ = 17 LJ types are listed in Table 4. The final parameter values are reported numerically in Table S.6 in the Supporting Information. Note that the parameters σ̃ are only relevant for potentially hydrogen-bonding LJ types (5 types), and that the LJ-type HB is omitted from the graph (σ and ϵ set to zero). The results with the alternative replicas are shown in Section S.13 in the Supporting Information. Note that the lines have no physical meaning and are intended only as a guide to the eye.

Figure 5.

Figure 5

Open in a new tab

Evolution of the 100 EE interaction parameters against the iteration number i along the force-field parameter optimization for geometric-mean (GM), Lorentz–Berthelot (LB), and Waldman–Hagler (WH) combination rules. The parameters considered are the electrostatic hardness η and electronegativity χ. The NattEE = 56 EE types are listed in Table 3. The final parameter values are reported numerically in Table S.7 in the Supporting Information. Note that the aliphatic united-atom EE types are omitted from the graph (5 types with zero charge) as well as the EE type CH0_N_amd (no representative molecule for calibration). The results with the alternative replicas are shown in Section S.13 in the Supporting Information. Note that the lines have no physical meaning and are intended only as a guide to the eye.

Figure 6.

Figure 6

Open in a new tab

Distribution of the EE-derived atomic partial charges for the different LJ types using the GM (top), LB (middle), and WH (bottom) combination rules. The boxes show the minimum, first quartile, median, third quartile, maximum, and outlier values of the distribution. Each possible value of the charge is only counted once in the distribution (irrespective of the number of molecules in which the particular charge occurs). The NattLJ = 17 LJ types are listed in Table 4.

The level of agreement between the optimized force fields and experiment in terms of ρliq and ΔHvap for each combination rule is illustrated in Figure 7. The corresponding numerical values can be found in Section S.10 in the Supporting Information (Tables S.15–S.17). The statistics per compound types are provided in Figure 8 for the three combination rules. In these statistics, four classes of compounds are also considered separately, namely, the compounds with two different functional groups (MIX), the halogen (HAL) ones, the non-hydrogen-bonding (NHB) ones (including ethers, ketones, aldehydes, and esters), and the hydrogen-bonding (HBD) ones (including alcohols, carboxylic acids, amines, and amides).

Figure 7.

Figure 7

Open in a new tab

Comparison of simulated and experimental properties based on the optimized force field for the GM (top), LB (middle), and WH (bottom) combination rules. The diagonal solid lines and the two parallel dashed lines indicate perfect agreement within ±80 kg m–3 for ρliq (left) or ±8 kJ mol–1 for ΔHvap (right). The corresponding numerical values are reported in Tables S.12–S.14 in the Supporting Information.

Figure 8.

Figure 8

Open in a new tab

Statistics concerning the discrepancies between simulated and experimental properties with the GM, LB, and WH combination rules using a set of 1447 molecules. The results are reported separately for the different chemical functions as listed in Table 2. Four classes of compounds are also considered separately, namely, the compounds with two different functional groups (MIX), the halogenated (HAL) ones, the non-hydrogen-bonding (NHB) ones (including ethers, ketones, aldehydes, and esters), and the hydrogen-bonding (HBD) ones (including alcohols, carboxylic acids, amines, and amides), along with the entire set of molecules (ALL). The root-mean-square deviation (RMSD) and average deviation (AVED) values are reported in terms of ρliq (left) and ΔHvap (right). The value of m indicates to the number of functional groups and N refers to the number of data points considered. The color coding underlines the sign and magnitude of the discrepancies.

Considering ρliq, the overall agreement with experiment in terms of root-mean-square deviation (RMSD) is good for the three combination rules, with values of 30.0, 26.9, and 36.7 kg m–3 for GM, LB, and WH, respectively. Overall, the results with LB are the most accurate, but this is not always true when considering the compound families separately. For example, the GM combination rule is generally more accurate for the halohydrocarbons. On the other hand, the results with WH are slightly less accurate compared to GM and LB, not only overall but also in terms of the different families. In particular, for the alkanes with WH, the RMSD is significantly higher (23.9 kg·m–3) than with the other combination rules (10.2 and 14.2 kg m–3). The only exceptions are trifluoromethane, tetrabromomethane, and carboxylic acids, for which WH performs slightly better.

In terms of ΔHvap, the three combination rules perform comparably well with overall RMSD values of 2.8, 2.8, and 2.9 kJ mol–1 for GM, LB, and WH, respectively. A similar observation also applies to the results for the individual families, where there is no significant difference between the combination rules, irrespective of the chemical functional group considered.

Although the agreement with experiment is good for most molecules (Figure 7), there are outliers for the three combination rules. The corresponding structures (with deviations higher than 80.0 kg m–3 for ρliq and/or higher than 8.0 kJ mol–1 for ΔHvap) are depicted in Section S.11 in the Supporting Information (Figures S.8–S.10). These molecules are predominantly tri- and tetrafluoromethane, diamines, diols, and small compounds with two distinct functional groups. Note that the number of such outliers is lowest when using the LB combination rule (61), compared to that observed for the GM rule (105) and the WH rule (91).

The level of agreement with experiment in terms of γ, ϵ, and D for each combination rule is illustrated in Figure 9. The corresponding numerical values are reported in Section S.10 (Tables S.15–S.17 in the Supporting Information). The statistics for the set of 66 compounds is provided in Table 5 for the three combination rules. The results do not evidence any pronounced systematic effect of the combination rule on these three properties. In terms of the comparison with experiment, however, significant deviations are observed. The errors concerning D are significant, but largely nonsystematic. They probably result from an interplay between different effects, such as the use of united atoms (expected to enhance diffusion, depending on their count in a given molecule), and the application of a cutoff with a reaction-field correction for the long-range electrostatic interactions in the absence of a correction for the long-range Lennard-Jones interactions (which may affect diffusion in different ways for different molecules). The errors concerning ϵ and γ are also significant, and now somewhat systematic. The deviations observed for ϵ, which are predominantly negative (especially for the most polar compounds), likely result from the use of a nonpolarizable force field, i.e., with an implicit treatment of the electronic-polarization effects. The deviations observed for γ, which predominantly occur at high γ and are then negative, likely result from the use of a mean-field treatment of the electrostatic interactions beyond the cutoff (reaction-field correction), i.e., that may not be very accurate/adequate in a heterogeneous environment like a liquid/vacuum interface.

Figure 9.

Figure 9

Open in a new tab

Comparison of the simulated and experimental surface-tension coefficient (γ), static relative dielectric permittivity (ϵ), and self-diffusion coefficient (D), based on the force-field variants optimized using the GM, LB, and WH combination rules. The corresponding numerical values are reported in Tables S.15–S.17.

Table 5. Statistics Concerning the Discrepancies between Simulated and Experimental Properties with the GM, LB, and WH Combination Rules for 66 Molecules in Terms of Surface-Tension Coefficient (γ), Static Relative Dielectric Permittivity (ϵ), and Self-Diffusion Coefficient (D)a.

  ρliq [kg m–3]
 ΔHvap [kJ mol–1]
 γ [mN m–1]
 ϵ
 D [ 10–9 m2 s–1]
combination rule RMSD AVED RMSD AVED RMSD AVED RMSD AVED RMSD AVED
GM 30.0 2.0 2.8 0.1 5.9 –1.9 19.0 –7.0 0.6 0.1
LB 26.9 0.0 2.8 –0.1 6.8 –2.0 20.9 –7.9 0.6 0.2
WH 36.7 –5.6 2.9 0.0 7.3 –1.5 19.0 –6.5 0.7 0.1
Open in a new tab
a

The results for the 1447 molecules in terms of the experimental liquid densities ρliq, and vaporization enthalpies ΔHvap are also shown. The root-mean-square (RMSD) and average (AVED) deviations are reported.

The force-field parameters obtained from the optimization with a given combination rule were also used to carry out simulations with the two other rules, to investigate the effect of a possible mismatch in this choice between force-field calibration and property calculation. The matrix with the statistics concerning ρliq and ΔHvap is shown in Figure 10. The corresponding data sorted by compound families can be found in Section S.12 (Figure S.11 in the Supporting Information). Expectedly, the best agreement with experiment is normally obtained when the force field is used together with the combination rule that was employed in the calibration (diagonal elements of the matrices). However, the exchange between the GM and LB combination rules has a limited effect. For the NHB and HBD groups, using the combination rule with parameters optimized for LB even leads to slightly more accurate results than with the GM parameters optimized for GM. On the other hand, replacing the combination rules GM or LB with WH significantly decreases the accuracy for both ρliq and ΔHvap.

Figure 10.

Figure 10

Open in a new tab

Statistics concerning the discrepancies between simulated and experimental properties considering the interchange of combination rules. Each entry corresponds to the results obtained with the combination rule specified in the given row and the parameters optimized using the combination rule specified in the given column. The root-mean-square deviation (RMSD) and the average deviation (AVED) are reported in terms of ρliq (left) and ΔHvap (right) for the common set of 1447 molecules. The same analysis separated per family of compounds is shown in Figure S.11 in the Supporting Information.

4. Conclusions

To assess in a fair way the effect of a specific functional-form choice on the intrinsic accuracy of the classical force-field representation, the comparison must ideally be performed at an optimal level of parametrization relative to a given set of molecules, observables, and target values.

Here, we performed such a comparison considering the choice different combination rules for the LJ interactions, namely geometric-mean (GM), Lorentz–Berthelot (LB), and Waldmann–Hagler (WH). This assessment was performed using 2044 experimental liquid densities ρliq and vaporization enthalpies ΔHvap concerning 1516 organic liquids. Three force-field variants (implementing the three alternative combination rules) were optimized independently and automatically against these target data using the CombiFF workflow.

The resulting RMSD values from the experiment are 30.0, 26.9, and 36.7 kg m–3 for ρliq and 2.8, 2.8, and 2.9 kJ mol–1 for ΔHvap, when using the GM, LB, and WH combination rules, respectively. Repeats of the optimizations were also performed, leading to similar deviations, which suggests that the calibrated parameters are close to optimal with respect to the target data. The comparison was then extended to three other properties that were not included as parametrization targets, namely, the surface-tension coefficient (γ), the static relative dielectric permittivity (ϵ), and the self-diffusion coefficient (D).

The main observation is that, provided that the parameters are optimized specifically for a given combination rule, the difference between the three rules is rather small. The simulation results with GM and LB are closer together and have a slightly higher accuracy compared to WH, but the effect is not very pronounced.

The slightly lower accuracy of the WH rule may come as a surprise, considering that this rule is demonstrably more accurate than the GM and LB rules for rare gases.63 Clearly, the presence of a slight suboptimality in the CombiFF optimization (convergence not entirely reached and/or reaching a local minimum) cannot be excluded. This could lead to a residual dependence of the optimized force field on the initial parameters of the optimization. Since these parameters are taken from GROMOS, which relies on the GM rule, this could penalize WH (and, to a lesser extent, LB). However, it is also possible that the WH rule is more accurate in the context of rare gases, but less accurate in the context of effective interaction functions for condensed-phase systems. In practice, the latter involve numerous approximations (united atoms, atomic partial charges, implicit electronic polarization, cutoff and mean-field corrections) leading to atom–atom interactions differing significantly from those corresponding to isolated pairs of neutral closed-shell noble-gas atoms in the gas phase.

Expectedly, the discrepancies relative to experiment are typically larger when the properties are calculated using a combination rule that differs from the one used in the parameter calibration. The discrepancies are in particular relatively large when the GM or LB rules are substituted by the WH rule.

Acknowledgments

Financial support by the Swiss National Science Foundation (Grant No. 200021-175944) is gratefully acknowledged.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c01170.

  • Detailed information concerning: (i) the influence of combination rules for rare gases; (ii) the compounds in the calibration set; (iii) the reference experimental data; (iv) the covalent interaction parameters; (v) the final values of the nonbonded parameters; (vi) the initial values of the nonbonded parameters; (vii) the observable-to-parameter ratio; (viii) the list of compounds that vaporized; (ix) the partial charges on oxygen and carbon for esters; (x) the comparison with experiment (experimental vs simulated properties); (xi) the outliers; (xii) the statistics concerning the discrepancies between simulated and experimental properties considering the interchange of combination rules; and (xiii) the results of the alternative replica sets (PDF)

The authors declare no competing financial interest.

Supplementary Material

ct2c01170_si_001.pdf (8.8MB, pdf)

References

  1. Allen M. P.; Tildesley D. J. In Computer Simulation of Liquids; Oxford University Press: New York, 1987. [Google Scholar]
  2. Berendsen H. J. C. In Simulating the Physical World; Cambridge University Press: Cambridge, U.K., 2007. [Google Scholar]
  3. Hirst J. D.; Glowacki D. R.; Baaden M. Molecular simulations and visualization: Introduction and overview. Faraday Discuss. 2014, 169, 9. 10.1039/C4FD90024C. [DOI] [PubMed] [Google Scholar]
  4. Alder B. J.; Wainwright T. E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208. 10.1063/1.1743957. [DOI] [Google Scholar]
  5. Alder B. J.; Wainwright T. E. Studies in molecular dynamics. I. General method. J. Chem. Phys. 1959, 31, 459. 10.1063/1.1730376. [DOI] [Google Scholar]
  6. van Gunsteren W. F.; Berendsen H. J. C. Computer simulation of molecular dynamics: Methodology, applications and perspectives in chemistry. Angew. Chem., Int. Ed. 1990, 29, 992. 10.1002/anie.199009921. [DOI] [Google Scholar]
  7. Karplus M.; McCammon J. A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646. 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
  8. van Gunsteren W. F.; Bakowies D.; Baron R.; Chandrasekhar I.; Christen M.; Daura X.; Gee P.; Geerke D. P.; Glättli A.; Hünenberger P. H.; Kastenholz M. A.; Oostenbrink C.; Schenk M.; Trzesniak D.; van der Vegt N. F. A.; Yu H. B. Biomolecular modelling: goals, problems, perspectives. Angew. Chem., Int. Ed. 2006, 45, 4064. 10.1002/anie.200502655. [DOI] [PubMed] [Google Scholar]
  9. Halgren T. A. Potential energy functions. Curr. Opin. Struct. Biol. 1995, 5, 205. 10.1016/0959-440X(95)80077-8. [DOI] [PubMed] [Google Scholar]
  10. Hünenberger P. H.; van Gunsteren W. F. In Computer Simulation of Biomolecular Systems, Theoretical and Experimental Applications, Vol. 3; van Gunsteren W. F., Weiner P. K., Wilkinson A. J., Eds.; Kluwer/Escom Science Publishers: Dordrecht, The Netherlands, 1997; pp 3–82. [Google Scholar]
  11. Hünenberger P. H.; van Gunsteren W. F. In Lecture Notes in Chemistry; Sax A. F., Ed.; Springer Verlag: Berlin, Germany, 1999; pp 177–214. [Google Scholar]
  12. MacKerell D. A. Jr. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004, 25, 1584. 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
  13. Monticelli L.; Tieleman D. P. Force fields for classical molecular dynamics. Methods Mol. Biol. 2013, 924, 197. 10.1007/978-1-62703-017-5_8. [DOI] [PubMed] [Google Scholar]
  14. Nerenberg P. S.; Head-Gordon T. New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol. 2018, 49, 129. 10.1016/j.sbi.2018.02.002. [DOI] [PubMed] [Google Scholar]
  15. Riniker S. Fixed-charge atomistic force fields for molecular dynamics simulations in the condensed phase: An overview. J. Chem. Inf. Model. 2018, 58, 565. 10.1021/acs.jcim.8b00042. [DOI] [PubMed] [Google Scholar]
  16. Brooks C. L. III Methodological advances in molecular dynamics simulations of biological systems. Curr. Opin. Struct. Biol. 1995, 5, 211. 10.1016/0959-440X(95)80078-6. [DOI] [PubMed] [Google Scholar]
  17. Elber R. Novel methods for molecular dynamics simulations. Curr. Opin. Struct. Biol. 1996, 6, 232. 10.1016/S0959-440X(96)80080-7. [DOI] [PubMed] [Google Scholar]
  18. Hansson T.; Oostenbrink C.; van Gunsteren W. F. Molecular dynamics simulations. Curr. Opin. Struct. Biol. 2002, 12, 190. 10.1016/S0959-440X(02)00308-1. [DOI] [PubMed] [Google Scholar]
  19. Norberg J.; Nilsson L. Advances in biomolecular simulations: Methodology and recent applications. Q. Rev. Biophys. 2003, 36, 257. 10.1017/S0033583503003895. [DOI] [PubMed] [Google Scholar]
  20. van Gunsteren W. F.; Dolenc J. Thirty-five years of biomolecular simulation: development of methodology, force fields, and software. Mol. Simul. 2012, 38, 1271. 10.1080/08927022.2012.701744. [DOI] [Google Scholar]
  21. Field M. J. Technical advances in molecular simulation since the 1980s. Arc. Biochem. Biophys. 2015, 582, 3. 10.1016/j.abb.2015.03.005. [DOI] [PubMed] [Google Scholar]
  22. Oliveira M. P.; Andrey M.; Rieder S. R.; Kern L.; Hahn D. F.; Riniker S.; Horta B. A. C.; Hünenberger P. H. Systematic optimization of a fragment-based force-field based on experimental pure-liquid properties considering large compound families: Application to the saturated haloalkanes. J. Chem. Theory Comput. 2020, 16, 7525. 10.1021/acs.jctc.0c00683. [DOI] [PubMed] [Google Scholar]
  23. Allinger N. L. Conformational analysis. 130. MM2. A hydrocarbon force field utilizing V1 and V2 torsional terms. J. Am. Chem. Soc. 1977, 99, 8127. 10.1021/ja00467a001. [DOI] [Google Scholar]
  24. Hagler A. T.; Ewig C. S. On the use of quantum energy surfaces in the derivation of molecular force-fields. Comput. Phys. Commun. 1994, 84, 131. 10.1016/0010-4655(94)90208-9. [DOI] [Google Scholar]
  25. Maple J. R.; Hwang M.-J.; Stockfisch T. P.; Dinur U.; Waldman M.; Ewig C. S.; Hagler A. T. Derivation of class-II force-fields. 1. Methodology and quantum force-field for the alkyl functional-group and alkane molecules. J. Comput. Chem. 1994, 15, 162. 10.1002/jcc.540150207. [DOI] [Google Scholar]
  26. Halgren T. A. Merck molecular force field. 1. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490.. [DOI] [Google Scholar]
  27. Ewig C. S.; Berry R.; Dinur U.; Hill J.-R.; Hwang M.-J.; Li H.; Liang C.; Maple J.; Peng Z.; Stockfisch T. P.; Thacher T. S.; Yan L.; Ni X.; Hagler A. T. Derivation of class II force fields. VIII. Derivation of a general quantum mechanical force field for organic compounds. J. Comput. Chem. 2001, 22, 1782. 10.1002/jcc.1131. [DOI] [PubMed] [Google Scholar]
  28. Pinnick E. R.; Erramilli S.; Wang F. Predicting the melting temperature of ice-Ih with only electronic structure information as input. J. Chem. Phys. 2012, 137, 014510. 10.1063/1.4731693. [DOI] [PubMed] [Google Scholar]
  29. Wang L.-P.; Chen J.; van Voorhis T. Systematic parametrization of polarizable force fields from quantum chemistry data. J. Chem. Theory Comput. 2013, 9, 452. 10.1021/ct300826t. [DOI] [PubMed] [Google Scholar]
  30. Wang L.-P.; Martinez T. J.; Pande V. S. Building force fields: An automatic, systematic, and reproducible approach. J. Phys. Chem. Lett. 2014, 5, 1885. 10.1021/jz500737m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Laury M. L.; Wang L.-P.; Pande V. S.; Head-Gordon T.; Ponder J. W. Revised parameters for the AMOEBA polarizable atomic multipole water model. J. Phys. Chem. B 2015, 119, 9423. 10.1021/jp510896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Prampolini G.; Livotto P. R.; Cacelli I. Accuracy of quantum mechanically derived force-fields parameterized from dispersion-corrected DFT data: The benzene dimer as a prototype for aromatic interactions. J. Chem. Theory Comput. 2015, 11, 5182. 10.1021/acs.jctc.5b00642. [DOI] [PubMed] [Google Scholar]
  33. Prampolini G.; Campetella M.; De Mitri N.; Livotto P. R.; Cacelli I. Systematic and automated development of quantum mechanically derived force fields: The challenging case of halogenated hydrocarbons. Chem. Theory Comput. 2016, 12, 5525. 10.1021/acs.jctc.6b00705. [DOI] [PubMed] [Google Scholar]
  34. Njo S. L.; van Gunsteren W. F.; Müller-Plathe F. Determination of force field parameters for molecular simulations by molecular simulation: An application of the weak-coupling method. J. Chem. Phys. 1995, 102, 6199. 10.1063/1.469065. [DOI] [Google Scholar]
  35. Berweger C. D.; van Gunsteren W. F.; Müller-Plathe F. Force field parametrization by weak coupling. Re-engineering SPC water. Chem. Phys. Lett. 1995, 232, 429. 10.1016/0009-2614(94)01391-8. [DOI] [Google Scholar]
  36. van der Spoel D.; van Maaren P. J.; Berendsen H. J. C. A systematic study of water models for molecular simulation: Derivation of water models optimized for use with a reaction field. J. Chem. Phys. 1998, 108, 10220. 10.1063/1.476482. [DOI] [Google Scholar]
  37. van Maaren P. J.; van der Spoel D. Molecular dynamics simulations of water with novel shell-model potentials. J. Phys. Chem. B 2001, 105, 2618. 10.1021/jp003843l. [DOI] [Google Scholar]
  38. Di Pierro M.; Elber R. Automated optimization of potential parameters. J. Chem. Theory Comput. 2013, 9, 3311. 10.1021/ct400313n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Di Pierro M.; Mugnai M. L.; Elber R. Optimizing potentials for liquid mixture: A new force field for a tert-butanol and water solution. J. Phys. Chem. B 2015, 119, 836. 10.1021/jp505401m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Wang L.-P.; Head-Gordon T.; Ponder J. W.; Ren P.; Chodera J. D.; Eastman P. K.; Martinez T. J.; Pande V. S. Systematic improvement of a classical molecular model of water. J. Phys. Chem. B 2013, 117, 9956. 10.1021/jp403802c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Qi R.; Wang L.-P.; Wang Q.; Pande V. S.; Ren P. United polarizable multipole water model for molecular mechanics simulation. J. Chem. Phys. 2015, 143, 014504. 10.1063/1.4923338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. McKiernan K. A.; Wang L.-P.; Pande V. S. Training and validation of a liquid-crystalline phospholipid bilayer force field. J. Chem. Theory Comput. 2016, 12, 5960. 10.1021/acs.jctc.6b00801. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wade A. D.; Wang L.-P.; Huggins D. J. Assimilating radial distribution functions to build water models with improved structural properties. J. Chem. Inf. Model. 2018, 58, 1766. 10.1021/acs.jcim.8b00166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Qiu Y.; Nerenberg P. S.; Head-Gordon T.; Wang L.-P. Systematic optimization of water models using liquid/vapor surface tension data. J. Phys. Chem. B 2019, 123, 7061. 10.1021/acs.jpcb.9b05455. [DOI] [PubMed] [Google Scholar]
  45. Kantonen S. M.; Muddana H. S.; Schauperl M.; Henriksen N. M.; Wang L.-P.; Gilson M. K. Data-driven mapping of gas-phase quantum calculations to general force field Lennard-Jones parameters. J. Chem. Theory Comput. 2020, 16, 1115. 10.1021/acs.jctc.9b00713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Yin J.; Fenley A. T.; Henriksen N. M.; Gilson M. K. Toward improved force-field accuracy through sensitivity analysis of host-guest binding thermodynamics. J. Phys. Chem. B 2015, 119, 10145. 10.1021/acs.jpcb.5b04262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yin J.; Henriksen N. M.; Muddana H. S.; Gilson M. K. Bind3P: Optimization of a water model based on host-guest binding data. J. Chem. Theory Comput. 2018, 14, 3621. 10.1021/acs.jctc.8b00318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Naden L. N.; Shirts M. R. Rapid computation of thermodynamic properties over multidimensional nonbonded parameter spaces using adaptive multistate reweighting. J. Chem. Theory Comput. 2016, 12, 1806. 10.1021/acs.jctc.5b00869. [DOI] [PubMed] [Google Scholar]
  49. Stroet M.; Koziara K. B.; Malde A. K.; Mark A. E. Optimization of empirical force fields by parameter space mapping: A single-step perturbation approach. J. Chem. Theory Comput. 2017, 13, 6201. 10.1021/acs.jctc.7b00800. [DOI] [PubMed] [Google Scholar]
  50. Messerly R. A.; Razavi S. M.; Shirts M. R. Configuration-sampling-based surrogate models for rapid parameterization of non-bonded interactions. J. Chem. Theory Comput. 2018, 14, 3144. 10.1021/acs.jctc.8b00223. [DOI] [PubMed] [Google Scholar]
  51. Messerly R. A.; Barhaghi M. S.; Potoff J. J.; Shirts M. R. Histogram-free reweighting with grand canonical Monte Carlo: Post-simulation optimization of non-bonded potentials for phase equilibria. J. Chem. Eng. Data 2019, 64, 3701. 10.1021/acs.jced.8b01232. [DOI] [Google Scholar]
  52. Oliveira M. P.; Hünenberger P. H. Systematic optimization of a fragment-based force-field against experimental pure-liquid properties considering large compound families: Application to oxygen and nitrogen compounds. Phys. Chem. Chem. Phys. 2021, 23, 17774. 10.1039/D1CP02001C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Oliveira M. P.; Hünenberger P. H. Force fields optimized against experimental data for large compound families using CombiFF: Validation considering non-target properties and polyfunctional compounds. J. Mol. Graph. Model. 2023, 118, 108312. 10.1016/j.jmgm.2022.108312. [DOI] [PubMed] [Google Scholar]
  54. Oliveira M. P.; Goncalves Y. M. H.; Ol Gheta S. K.; Rieder S. R.; Horta B. A. C.; Hunenberger P. H. Comparison of the united- and all-atom representations of (halo)alkanes based on two condensed-phase force fields optimized against the same experimental data set. J. Chem. Theory Comput. 2022, 18, 6757. 10.1021/acs.jctc.2c00524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Lennard-Jones J. E. The equation of state of gases and critical phenomena. Physica 1937, 4, 941. 10.1016/S0031-8914(37)80191-3. [DOI] [Google Scholar]
  56. Walz M.-M.; Ghahremanpour M. M.; van Maaren P. J.; van der Spoel D. Phase-transferable force field for alkali halides. J. Chem. Theory Comput. 2018, 14, 5933. 10.1021/acs.jctc.8b00507. [DOI] [PubMed] [Google Scholar]
  57. Burrows S. A.; Korotkin I.; Smoukov S. K.; Boek E.; Karabasov S. Benchmarking of molecular dynamics force fields for solid-liquid and solid-solid phase transitions in alkanes. J. Phys. Chem. B 2021, 125, 5145. 10.1021/acs.jpcb.0c07587. [DOI] [PubMed] [Google Scholar]
  58. Bernhardt M. P.; Nagata Y.; van der Vegt N. F. A. Where Lennard-Jones potentials fail: iterative optimization of ion– water pair potentials based on ab initio molecular dynamics data. J. Phys. Chem. Lett. 2022, 13, 3712. 10.1021/acs.jpclett.2c00121. [DOI] [PubMed] [Google Scholar]
  59. Hagler A. T.; Huler E.; Lifson S. Energy functions for peptides and proteins. I. Derivation of a consistent force field including the hydrogen bond from amide crystals. J. Am. Chem. Soc. 1974, 96, 5319. 10.1021/ja00824a004. [DOI] [PubMed] [Google Scholar]
  60. Lifson S.; Hagler A. T.; Dauber P. Consistent force field studies of intermolecular forces in hydrogen-bonded crystals. 1. Carboxylic acids, amides, and the C = O···H hydrogen bonds. J. Am. Chem. Soc. 1979, 101, 5111. 10.1021/ja00512a001. [DOI] [Google Scholar]
  61. Lorentz H. A. Über die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Ann. Phys. 1881, 248, 127. 10.1002/andp.18812480110. [DOI] [Google Scholar]
  62. Berthelot D. Sur le mélange des gaz. C. R. Acad. Sci. Paris 1889, 126, 1703. [Google Scholar]
  63. Waldman M.; Hagler A. T. New combining rules for rare gas van der Waals parameters. J. Comput. Chem. 1993, 14, 1077. 10.1002/jcc.540140909. [DOI] [Google Scholar]
  64. Duh D.-M.; Henderson D.; Rowley R. L. Some effects of deviations from the Lorentz-Berthelot combining rules for mixtures of Lennard-Jones fluids. Mol. Phys. 1997, 91, 1143. 10.1080/00268979709482801. [DOI] [Google Scholar]
  65. Boda D.; Henderson D. The effects of deviations from Lorentz–Berthelot rules on the properties of a simple mixture. Mol. Phys. 2008, 106, 2367. 10.1080/00268970802471137. [DOI] [Google Scholar]
  66. Rouha M.; Nezbeda I. Non-Lorentz-Berthelot Lennard-Jones mixtures: A systematic study. Fluid Phase Equilib. 2009, 277, 42. 10.1016/j.fluid.2008.11.007. [DOI] [Google Scholar]
  67. Forsman J.; Woodward C. E. Limitations of the Derjaguin approximation and the Lorentz-Berthelot mixing rule. Langmuir 2010, 26, 4555. 10.1021/la904769x. [DOI] [PubMed] [Google Scholar]
  68. Moučka F.; Nezbeda I. Water-methanol mixtures with non Lorentz-Berthelot combining rules: A feasibility study. J. Mol. Liq. 2011, 159, 47. 10.1016/j.molliq.2010.05.005. [DOI] [Google Scholar]
  69. Zarkova L.; Hohm U.; Damyanova M. Comparison of Lorentz-Berthelot and Tang-Toennies mixing rules using an isotropic temperature-dependent potential applied to the thermophysical properties of binary gas mixtures of CH4, CF4, SF6, and C(CH3)4 with Ar, Kr, and Xe. Int. J. Thermophys. 2004, 25, 1775. 10.1007/s10765-004-7735-4. [DOI] [Google Scholar]
  70. Reis R. A.; Paredes M. L. L.; Castier M.; Tavares F. W. Evaluation of mixing and combining rules for asymmetric Lennard-Jones chain mixtures: Effect of segment diameter, energy interaction, and chain length. Fluid Phase Equilib. 2007, 259, 123. 10.1016/j.fluid.2007.05.027. [DOI] [Google Scholar]
  71. Delhommelle J.; Millié P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation. Mol. Phys. 2001, 99, 619. 10.1080/00268970010020041. [DOI] [Google Scholar]
  72. Song W.; Rossky P. J.; Maroncelli M. Modeling alkane-perfluoroalkane interactions using all-atom potentials: Failure of the usual combining rules. J. Chem. Phys. 2003, 119, 9145. 10.1063/1.1610435. [DOI] [Google Scholar]
  73. Schnabel T.; Vrabec J.; Hasse H. Unlike Lennard-Jones parameters for vapor-liquid equilibria. J. Mol. Liq. 2007, 135, 170. 10.1016/j.molliq.2006.12.024. [DOI] [Google Scholar]
  74. Frenkel M.; Hong X.; Wilhoit R. C.; Hall K. R. In Thermodynamic Properties of Organic Compounds and Their Mixtures. Densities of Alcohols; Hall K. R., Marsh K. N., Eds.; Landolt-Börnstein Series, Vol. IV/8G; Springer-Verlag: Berlin/Heidelberg, 2000. [Google Scholar]
  75. Frenkel M.; Hong X.; Wilhoit R. C.; Hall K. R. In Thermodynamic Properties of Organic Compounds and Their Mixtures. Densities of Esters and Ethers; Hall K. R., Marsh K. N., Eds.; Landolt-Börnstein Series, Vol. IV/8H; Springer–Verlag: Berlin/Heidelberg, 2001. [Google Scholar]
  76. Frenkel M.; Hong X.; Dong Q.; Yan X.; Chirico R. D. In Thermodynamic Properties of Organic Compounds and Their Mixtures. Densities of Phenols, Aldehydes, Ketones, Carboxylic Acids, Amines, Nitriles, and Nitrohydrocarbons; Hall K. R., Marsh K. N., Eds.; Landolt-Börnstein Series, Vol. IV/8I; Springer-Verlag: Berlin/Heidelberg, 2002. [Google Scholar]
  77. Frenkel M.; Hong X.; Dong Q.; Yan X.; Chirico R. D. In Thermodynamic Properties of Organic Compounds and Their Mixtures. Densities of Halohydrocarbons; Frenkel M., Marsh K. N., Eds.; Landolt-Börnstein Series, Vol. IV/8J; Springer-Verlag: Berlin/Heidelberg, 2003. [Google Scholar]
  78. Frenkel M.; Chiroco R. D.; Diky V.; Dong Q.; Marsh K. N.; Dymond J. H.; Wakeham W. A.; Stein S. E.; Königsberger E.; Goodwin A. R. H. XML-based IUPAC standard for experimental, predicted, and critically evaluated thermodynamic property data storage and capture (ThermoML). Pure Appl. Chem. 2006, 78, 541. 10.1351/pac200678030541. [DOI] [Google Scholar]
  79. Wohlfahrt C. In Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures, Vol. IV/17; Springer, Berlin, Germany, 2008. [Google Scholar]
  80. Caleman C.; van Maaren P. J.; Hong M.; Hub J. S.; Costa L. T.; van der Spoel D. Force field benchmark of organic liquids: Density, enthalpy of vaporization, heat capacities, surface tension, isothermal compressibility, volumetric expansion coefficient, and dielectric constant. J. Chem. Theory Comput. 2012, 8, 61. 10.1021/ct200731v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Yaws C. L. In Thermophysical Properties of Chemicals and Hydrocarbons, 2nd Edition; Gulf Professional Publishing (Elsevier), Oxford, U.K., 2014. [Google Scholar]
  82. Suárez-Iglesias O.; Medina I.; Sanz M. A.; Pizarro C.; Bueno J. L. Self-diffusion in molecular fluids and noble gases: available data. J. Chem. Eng. Data 2015, 60, 2757. 10.1021/acs.jced.5b00323. [DOI] [Google Scholar]
  83. Wohlfahrt C. In Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures, Vol. IV/17S; Springer, Berlin, 2015. [Google Scholar]
  84. Acree W. Jr.; Chickos J. S. Phase transition enthalpy measurements of organic and organometallic compounds. Sublimation, vaporization and fusion enthalpies from 1880 to 2015. Part 1. C1-C10. J. Phys. Chem. Ref. Data 2016, 45, 033101. 10.1063/1.4948363. [DOI] [Google Scholar]
  85. NIST 103a database. https://www.nist.gov/mml/acmd/trc/thermodata-engine/srd-nist-tde-103a (accessed 2018). [Google Scholar]
  86. Springer Materials database. https://materials.springer.com (accessed 2018). [Google Scholar]
  87. Rumble J. R. In CRC Handbook of Chemistry and Physics. 98th Edition; CRC Press/Taylor and Francis, Boca Raton, FL, 2018. [Google Scholar]
  88. van Gunsteren W. F.; Billeter S. R.; Eising A. A.; Hünenberger P. H.; Krüger P.; Mark A. E.; Scott W. R. P.; Tironi I. G. In Biomolecular Simulation: The GROMOS96 Manual and User Guide; Verlag der Fachvereine, Zürich, Switzerland, 1996. [Google Scholar]
  89. van Gunsteren W. F.; Daura X.; Mark A. E. In Encyclopedia of Computational Chemistry, Vol. 2; Schleyer P v. r., Ed.; John Wiley & Sons, Chichester, U.K., 1998; pp 1211–1216. [Google Scholar]
  90. Scott W. R. P.; Hünenberger P. H.; Tironi I. G.; Mark A. E.; Billeter S. R.; Fennen J.; Torda A. E.; Huber T.; Krüger P.; van Gunsteren W. F. The GROMOS biomolecular simulation program package. J. Phys. Chem. A 1999, 103, 3596. 10.1021/jp984217f. [DOI] [Google Scholar]
  91. Oostenbrink C.; Villa A.; Mark A. E.; van Gunsteren W. F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656. 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
  92. Christen M.; Hünenberger P. H.; Bakowies D.; Baron R.; Bürgi R.; Geerke D. P.; Heinz T. N.; Kastenholz M. A.; Kräutler V.; Oostenbrink C.; Peter C.; Trzesniak D.; van Gunsteren W. F. The GROMOS software for biomolecular simulation: GROMOS05. J. Comput. Chem. 2005, 26, 1719. 10.1002/jcc.20303. [DOI] [PubMed] [Google Scholar]
  93. van Gunsteren W. F.The GROMOS Software for Biomolecular Simulation. Available via the Internet at: http://www.gromos.net (accessed May 5, 2011). [Google Scholar]
  94. Horta B. A. C.; Merz P. T.; Fuchs P.; Dolenc J.; Riniker S.; Hünenberger P. H. A GROMOS-compatible force field for small organic molecules in the condensed phase: The 2016H66 parameter set. J. Chem. Theory Comput. 2016, 12, 3825. 10.1021/acs.jctc.6b00187. [DOI] [PubMed] [Google Scholar]
  95. Verstraelen T.; Van Speybroeck V.; Waroquier M. The electronegativity equalization method and the split charge equilibration applied to organic systems: Parametrization, validation, and comparison. J. Chem. Phys. 2009, 131, 044127. 10.1063/1.3187034. [DOI] [PubMed] [Google Scholar]
  96. Wang J. M.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general Amber force field. J. Comput. Chem. 2004, 25, 1157. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  97. Bourasseau E.; Haboudou M.; Boutin A.; Fuchs A. H.; Ungerer P. New optimization method for intermolecular potentials: Optimization of a new anisotropic united atoms potential for olefins: Prediction of equilibrium properties. J. Chem. Phys. 2003, 118, 3020. 10.1063/1.1537245. [DOI] [Google Scholar]
  98. Schmid N.; Christ C. D.; Christen M.; Eichenberger A. P.; van Gunsteren W. F. Architecture, implementation and parallelisation of the GROMOS software for biomolecular simulation. Comput. Phys. Commun. 2012, 183, 890. 10.1016/j.cpc.2011.12.014. [DOI] [Google Scholar]
  99. Hockney R. W. The potential calculation and some applications. Methods Comput. Phys. 1970, 9, 135. [Google Scholar]
  100. van Gunsteren W. F.; Berendsen H. J. C.; Rullmann J. A. C. Stochastic dynamics for molecules with constraints. Brownian dynamics of n-alkanes. Mol. Phys. 1981, 44, 69. 10.1080/00268978100102291. [DOI] [Google Scholar]
  101. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the Cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  102. Berendsen H. J. C.; van Gunsteren W. F.; Zwinderman H. R. J.; Geurtsen R. G. Simulations of proteins in water. Ann. N.Y. Acad. Sci. 1986, 482, 269. 10.1111/j.1749-6632.1986.tb20961.x. [DOI] [PubMed] [Google Scholar]
  103. Barker J. A.; Watts R. O. Monte Carlo studies of the dielectric properties of water-like models. Mol. Phys. 1973, 26, 789. 10.1080/00268977300102101. [DOI] [Google Scholar]
  104. Tironi I. G.; Sperb R.; Smith P. E.; van Gunsteren W. F. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 1995, 102, 5451. 10.1063/1.469273. [DOI] [Google Scholar]
  105. Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  106. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; di Nola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684. 10.1063/1.448118. [DOI] [Google Scholar]
  107. Guàrdia E.; Padró J. A. Generalized Langevin dynamics simulation of interacting particles. J. Chem. Phys. 1985, 83, 1917. 10.1063/1.449379. [DOI] [Google Scholar]
  108. van Gunsteren W. F.; Berendsen H. J. C. A leap-frog algorithm for stochastic dynamics. Mol. Simul. 1988, 1, 173. 10.1080/08927028808080941. [DOI] [Google Scholar]
  109. Yun-yu S.; Lu W.; van Gunsteren W. F. On the approximation of solvent effects on the conformation and dynamics of cyclosporin A by stochastic dynamics simulation techniques. Mol. Simul. 1988, 1, 369. 10.1080/08927028808080959. [DOI] [Google Scholar]
  110. van Gunsteren W. F. In Computer Simulation of Biomolecular Systems, Theoretical and Experimental Applications, Vol. 2; van Gunsteren W. F.; Weiner P. K.; Wilkinson A. J., Eds.; ESCOM Science Publishers, B.V.: Leiden, The Netherlands, 1993; pp 3–36. [Google Scholar]
  111. Neumann M. Dipole moment fluctuation formulas in computer simulations of polar systems. Mol. Phys. 1983, 50, 841. 10.1080/00268978300102721. [DOI] [Google Scholar]
  112. Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549. 10.1002/andp.19053220806. [DOI] [Google Scholar]
  113. Hünenberger P. H.CombiFF Data Collection in the ETHZ. Research Collection (tar-file CombiFF_combination_rule_comparison, version 1.0 corresponds to the published article). 10.3929/ethz-b-000445271 (accessed 2022). [DOI] [Google Scholar]
  114. Manz T. A.; Limas N. G. Introducing DDEC6 atomic population analysis: Part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 6, 47771. 10.1039/C6RA04656H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  115. Bayly C. I.; Cieplak P.; Cornell W. D.; Kollman P. A. A well-behaved electrostatic potential based method using charge restraint for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269. 10.1021/j100142a004. [DOI] [Google Scholar]
  116. Staroverov V. N.; Scuseria G. E.; Tao J.; Perdew J. P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129. 10.1063/1.1626543. [DOI] [PubMed] [Google Scholar]
  117. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  118. Weigend F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct2c01170_si_001.pdf (8.8MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES