Automated Treatment Planning Framework for Brachytherapy of Cervical Cancer Using 3D Dose Predictions

Abstract

Objective:

To lay the foundation for automated knowledge-based brachytherapy treatment planning using 3D dose estimations, we describe an optimization framework to convert brachytherapy dose distributions directly into dwell times (DTs).

Approach:

A dose rate kernel $\dot{d}(r,\theta ,\phi )$ was produced by exporting 3D dose for one dwell position from the treatment planning system and normalizing by DT. By translating and rotating this kernel to each dwell position, scaling by DT and summing over all dwell positions, dose was computed (D_calc). We used a Python-coded COBYLA optimizer to iteratively determine the DTs that minimize the mean squared error between D_calc and reference dose D_ref, computed using voxels with D_ref 80-120% of prescription. As validation of the optimization, we showed that the optimizer replicates clinical plans when D_ref=clinical dose in 40 patients treated with tandem-and-ovoid (T&O) or tandem-and-ring (T&R) and 0-3 needles. Then we demonstrated automated planning in 10 T&O using D_ref=dose predicted from a convolutional neural network developed in past work. Validation and automated plans were compared to clinical plans using mean absolute differences $\left(MAD=\frac{1}{N}{\sum }_{n=1}^{N}abs\left(x-x\prime \right)\right)$ over all voxels (x=Dose, N=#voxels) and DTs (x=DT, N=#dwell positions), mean differences (MD) in organ D_2cc and high-risk CTV D90 over all patients (where positive indicates higher clinical dose), and mean Dice similarity coefficients (DSC) for 100% isodose contours.

Main Results:

Validation plans agreed well with clinical plans (MAD_dose=1.1%, MAD_DT=4s or 0.8% of total plan time, D_2cc MD=−0.2-0.2% and D90 MD=−0.6%, DSC=0.99). For automated plans, MAD_dose=6.5% and MAD_DT=10.3s (2.1%). The slightly higher clinical metrics in automated plans (D_2cc MD=−3.8-−1.3% and D90 MD=−5.1%) were due to higher neural network dose predictions. The overall shape of the automated dose distributions were similar to clinical doses (DSC=0.91).

Significance:

Automated planning with 3D dose predictions could provide significant time savings and standardize treatment planning across practitioners, regardless of experience.

1. Introduction

Brachytherapy for cervical cancer is complex, time-consuming and requires a skilled team. Despite its important role in the standard of care for cervical cancer (Hanks, Herring and Kramer, 1983; Eifel et al., 2004), brachytherapy utilization is declining (Han et al., 2013; Bagshaw et al., 2014; Gill et al., 2014), which may in part be due to the long procedure times, resource intensiveness, and need for specialized expertise (Ma et al., 2019). A large component of brachytherapy procedure time is treatment planning, which is performed real-time while patients are sedated and can take over an hour (Mayadev et al., 2014; Michaud et al., 2016). Current solutions to automate or improve the efficiency of gynecologic brachytherapy treatment planning have not achieved widespread adoption. While dose-volume histogram (DVH) based inverse optimization methods exist, it is challenging to produce the standard dose distributions for cervical brachytherapy because anatomy such as the uterus, parametrium and vagina are not typically contoured (Trnková et al., 2009). Some groups have found ways to work around these issues with inverse optimization, such as contouring additional dose-shaping structures (Lessard, Hsu and Pouliot, 2002; Oud et al., 2020) or locking certain dwell times during optimization (Trnková et al., 2009), but these methods still require some user intervention and thus are not fully automated. Many centers are still performing manual treatment planning under time constraints, which results in plan quality that is practitioner-dependent and variable, as has been observed in the external beam radiotherapy space (Moore et al., 2015).

Deep learning could provide value for automated brachytherapy planning as models can identify 3D anatomical and geometric features that relate to common dose distributions. Knowledge-based planning uses models trained on prior patient treatment plans to predict the optimal treatment for a patient based on anatomical and geometric inputs (Wu et al., 2009; Zhu et al., 2011; Appenzoller et al., 2012; Ge and Wu, 2019). In external beam radiotherapy, multiple groups have developed 3D knowledge-based dose predictions using neural networks (Shiraishi and Moore, 2016; Nguyen et al., 2019, 2020; Babier et al., 2020, 2021). The literature in brachytherapy is more scarce, though one group used a convolutional neural network to predict 3D dose for tandem-and-ovoid brachytherapy (Cortes et al., 2022), and two other groups used a neural network to predict 3D Monte Carlo calculated dose from imaging and treatment plan inputs such as dwell positions and times (Mao et al., 2020; Akhavanallaf et al., 2021). While 3D dose predictions could be useful for plan quality assurance, the highest clinical utility is provided when these predictions can be converted into deliverable treatment plans. For external beam radiotherapy, that would require determination of beam parameters such as multi-leaf collimator positions and gantry angles to achieve the desired dose distribution. For brachytherapy, dwell times would need to be computed for each dwell position within an applicator and/or needles. This critical step is challenging, and other than standard DVH-based inverse optimization using predicted doses in optimization objectives, little methodology has been developed thus far. While there are a few solutions for external beam radiotherapy planning (Fredriksson, 2012; McIntosh et al., 2017; Babier et al., 2018; Fan et al., 2019; Lempart et al., 2021), to our knowledge this has not been explored in the brachytherapy space.

The goal of this work was to develop a framework that would take 3D brachytherapy dose distributions as input and output dwell times to lay the foundation for automated brachytherapy treatment planning using knowledge-based dose estimations. Dose distributions from clinical treatment plans were used to validate optimizer performance by determining whether dwell times from clinical plans could be reproduced. We then demonstrated fully automated treatment planning in ten patients using 3D dose predictions from a neural network to derive dwell times. Automated planning for gynecological brachytherapy could drastically reduce the time patients spend under anesthesia and improve the ease of delivering high-quality treatments, enabling more centers to offer this crucial treatment for cervical cancer.

2. Methods and Materials

2.1. Patients and Clinical Data

This study was approved by our institutional review board (IRB Project #200065CX) and received a waiver of informed consent due to the minimal risk to human subjects. All patient data was anonymized. The research was conducted in accordance with the principles embodied in the Declaration of Helsinki and in accordance with local statutory requirements. 40 patients with cervical cancer treated with high dose-rate (HDR) brachytherapy between 2012 and 2019 were randomly selected for this study (see Table 1). A single fraction from a multi-fraction brachytherapy treatment was included for each patient. Patients were implanted with either a tandem-and-ovoids (T&O) or tandem-and-ring (T&R) applicator and 0 to 3 supplemental needles. High-risk CTV (HRCTV), bladder, rectum and sigmoid were manually contoured on CT imaging and then treatment planning was manually performed in a commercial treatment planning system (Brachytherapy Planning v8.9–v13.6, Varian Medical Systems, Inc., Palo Alto, CA). Applicators and needles were manually digitized by a physicist. Dwell times were activated in the ovoids or ring and up to the tip of the tandem, and in the needles within the HRCTV. Physicists typically produce an initial plan using the following process and then radiation oncologists review and adjust the plan further. First, standard loading patterns are set for the intracavitary applicator and dose is normalized to point A. For T&O treatments at out center, the standard loading most often consists of a 15 dwell time weighting in the dwell positions located in the upper third of the tandem and ovoids and 10 weighting in the bottom 2/3 of the tandem. For T&R, the most common loading used at our center is a 2 to 1 tandem to ring dwell time weighting.

Table 1.

Summary of patient characteristics;

Parameter	Specification	Value
Number of patients	Total	40
	T&O	10
	T&O + needles	10
	T&Rs	10
	T&R + needles	10
Tumor stage (FIGO 2009)	I	21
	II	21
	III	3
HRCTV Volume [cc]	Mean (Range)	19.6 (4.9 – 40.2)
HRCTV D90 [%]	Mean ± SD	112.5 ± 16.6
HRCTV V100 [%]	Mean ± SD	94.9 ± 10.1
Prescribed dose per fraction (Rx) [Gy]	Median (Range)	7 (5.5 – 8.5)
D2cc Bladder [Gy] (% Rx)	Mean ± SD	4.97 ± 1.15 (70 ± 15%)
D2cc Rectum [Gy] (% Rx)	Mean ± SD	2.56 ± 0.86 (36 ± 12%)
D2cc Sigmoid [Gy] (% Rx)	Mean ± SD	3.44 ± 1.25 (48 ± 18%)
Number of dwell positions	Mean ± SD	74 ± 12
Total dwell time [s]	Mean ± SD	54.58 ± 7.47

T&R = tandem and ring; T&O = tandem and ovoids; HRCTV = high-risk clinical target volume; SD = standard deviation.

When needles are present, small dwell times (physicist-dependent, but typically around 5 s) are then added to source positions located within needles inside the HRCTV to provide additional dose shaping and target coverage. Then the plans are optimized by manually dragging isodoses to cover the HRCTV and reduce dose to nearby organs to meet the following EMBRACE II EQD2 criteria (Pötter et al., 2018). Hard planning constraints included HRCTV D90 > 85 Gy, bladder D_2cc < 90 Gy, rectum D_2cc < 75 Gy, and sigmoid D_2cc < 75 Gy, while soft planning aims included HRCTV D90 < 95 Gy bladder D_2cc < 80 Gy, rectum D_2cc < 65 Gy, and sigmoid D_2cc < 70 Gy.

2.2. Optimization Framework

We propose an automated planning workflow using 3D dose predictions from a neural network (see Figure 1). 3D dose prediction methodology was developed in prior work (Cortes et al., 2022) and is described below in Section 2.4, but the ability to convert these predictions into deliverable treatment plans was missing. This fundamental building block of automated planning is the focus of this paper. We developed an optimizer that iteratively determines the dwell times required for a series of dwell positions to reproduce a given 3D dose distribution (see Figure 2). In order to compute dose, a dose rate kernel was produced by exporting the 3D dose for a single dwell position from the treatment planning system and normalizing by dwell time. The source was a VariSource VS2000 HDR Iridium 192 Brachytherapy Sealed Source AL09400000 (Varian Medical Systems, Inc., Palo Alto, CA), and the dose rate kernel was a 400x400x400 matrix with 0.625x0.625x0.625 mm³ resolution. Dwell positions for a given patient’s implant were extracted from the plan DICOM file. The kernel was translated and rotated to each dwell position in an applicator or needle and scaled by the dwell time for that position. Then the dose for the full applicator (D_calc) was computed by summing over all dwell positions and scaling by the ratio of the air kerma strength at the time of the patient’s treatment (AKS_current) to that of the kernel (AKS_kernel). This is described in equation (1), where $D_{calc}^k$ is the 3D dose computed in the kth iteration, M_n is the matrix required to translate and rotate the dose rate kernel $\dot{d}$ to the location of the nth dwell position and t_n is the dwell time for that dwell position. These terms are summed over the N total dwell positions contained within the applicator (and needles, if present).

Figure 1.

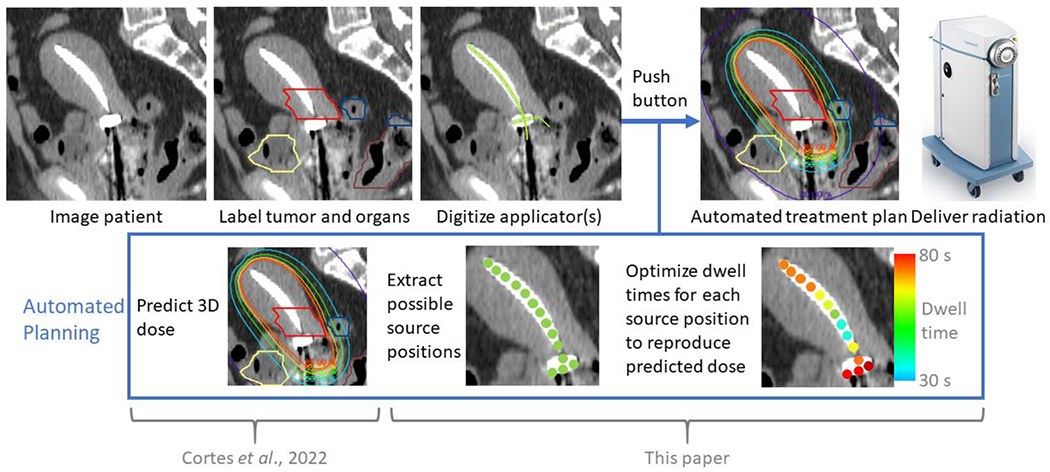
Proposed workflow for automated, knowledge-based planning. Contouring, applicator and needle digitization, and dwell position activation are performed manually at our institution, though these steps can be automated using other technology.

Figure 2.

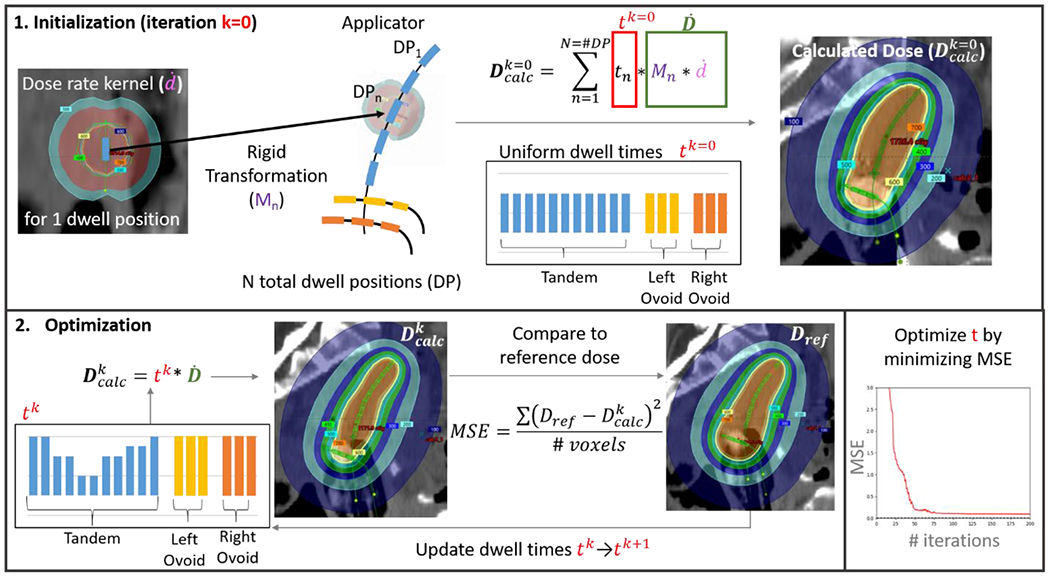
Schema of optimization workflow. First, a single dose rate kernel $\left(\dot{d}\right)$ was extracted from the treatment planning system. A rigid transformation matrix M_n translated and rotated the kernel to the location of each of the n=1-N dwell positions (DP) in a patient’s applicator and/or needles. Weighting these dose rate matrices by the dwell time (t_n) for each DP_n, scaling by the ratio of the current air kerma strength to that of the kernel (not shown in figure) and then summing over all N DPs gave the dose calculated for a particular iteration $\left(D_{calc}^k\right)$. Tandem-and-ovoid dwell times were initialized to 25 s, ring to 15s and needles to 5 s. To simplify the figure display, the summation in the top equation is replaced by t^k*$\dot{D}$, where t^k is meant to represent the dwell times of a current iteration. Dwell times are updated in each iteration to minimize the mean square error (MSE) between the reference dose (D_ref) and calculated dose. The MSE includes all voxels with reference doses between 80-120% of prescription.

$${\mathit{D}}_{calc}^k={\sum }_{n=1}^N{t}_n\ast M_n\ast \dot{d}\ast \frac{{AKS}_{current}}{{AKS}_{kernel}}={\sum }_{n=1}^N{t}_n\ast {\dot{D}}_n$$ (1)

To simplify computation, a dose rate matrix ${\dot{D}}_n$ was computed once for each dwell position, which was then weighted by the updated dwell time with each iteration before summation. For the few instances where the translated kernel did not cover the full extent of the considered field of view for a patient, the missing data in ${\dot{D}}_n$ was filled in with values approximated using inverse square fall-off in dose from the center of the source position. Dwell times were initialized to 25 s in the tandem and ovoids, 15 s in the ring and 5 s in the needles and updated iteratively to minimize the mean squared error (MSE) between the calculated and reference dose as shown in equation (2)

$$MSE=\frac{{\sum }_{i=1}^M{\left(D_{ref,i}-D_{calc,i}^k\right)}^2}{M}$$ (2)

where D_ref,i is the reference 3D dose for the ith voxel and M is the total number of voxels included in the computation. We included all voxels where the reference dose was between 80 to 120% of the prescription dose for that brachytherapy treatment fraction. A COBYLA (Constrained Optimization BY Linear Approximation) optimizer with a tolerance of 1 was coded using the SciPy 1.8.1 package, and all post-processing, optimization and analysis was performed in Python v3.10.5 unless otherwise stated. COBYLA is a numerical optimization method for constrained problems when the derivative of the objective function is not known (Powell, 1994). For each iteration, the actual optimization problem is approximated by linear programming problems, which are solved to obtain a possible solution. The solution is evaluated using the actual objective and constraint functions, yielding a new point in the optimization space. Dwell times were constrained to fall between 0 and 100s.

Optimization was performed on a Windows computer with an Intel(R) Core(TM) i7-5930K CPU @ 3.50GHz, 3501 Mhz, with 6 cores, 12 logical processors and 32 GB RAM. Multiprocessing was used to speed up computation and dose rate matrices $\left({\dot{D}}_n\right)$ were generated in parallel. To reduce computation time during optimization iterations, a sparse 1/4 voxel sampling was used, with a full 0.625 mm³ resolution dose calculation to achieve the final optimized dose.

2.3. Validating Optimization by Reproducing Clinical Plans

First, we demonstrated whether the optimizer could reproduce clinical treatment plans of 40 unique patients treated with T&O and T&R applicators and 0-3 needles (see Table 1). Dwell times, contours and dose distributions were extracted from the RT DICOM files. These 3D dose distributions were fed into the optimizer as the reference dose. Final optimized dwell times and dose distributions calculated from these dwell times (termed the “optimized plan” from here on) were compared to actual values from the clinical plans using the mean absolute difference (MAD) over all dwell times and voxels, which was defined using equation (3) below.

$$MAD=\frac{1}{N}{\sum }_{n=1}^{N}abs\left(x_{n,clinical}-x_{n,optimized}\right)$$ (3)

x refers to either the dwell time of an individual source position or the dose of a single voxel within a dose distribution. The absolute value of the differences between clinical and optimized plans were summed over all dwell times or voxels and divided by the total number (N) of dwell times or dose voxels within the plan. Mean differences (equation 3 without the absolute value) were also computed. Standard clinical metrics for assessing gynecological brachytherapy plan quality, including D90 and V100 of the HRCTV and D_2cc of the bladder, rectum and sigmoid were quantified for each plan and the mean and standard deviation of differences over all patients were computed. To assess the similarity in the shape of the dose distributions between optimized and clinical plans, Dice similarity coefficients (DSC) were determined for contours generated from the 100% isodose in each plan. The DSC is defined as $\text{DSC=}\frac{2\left(A\cap B\right)}{A+B}$ with values ranging from 0 to 1, where 1 indicates perfect agreement. In this work, A and B are the sets of all voxels in each dose distribution with dose greater than 100% of the prescription dose.

2.4. Automated Planning Using 3D Dose Predictions

To demonstrate the entire workflow of automated planning, we used 3D dose predictions computed in previous work to generate optimized dwell times (Cortes et al., 2022). Briefly, a 3D U-NET that uses applicator, HRCTV target and organ-at-risk (OAR) masks as inputs was trained on 273 T&O treatment plans, validated on 61 plans and tested on 61 plans. 10 plans from 10 unique patients were selected from the test set and the model-predicted 3D dose was fed into the optimizer as the reference dose. The optimized dwell times and dose (termed the “automated plan” from here on) were compared to those of the clinical plans using the same metrics described above. To better understand where the differences in automated and clinical plans arise from, the 3D dose prediction was also compared to the clinical plan dose and automated plan dose was compared to the 3D dose prediction. We created an in-house Python script that updates the exported plan DICOM with the optimized dwell times to generate a new optimized plan file that can easily be imported into the treatment planning system for delivery. Automated, optimized and actual clinical treatment plans were qualitatively evaluated in the treatment planning system. Using the known external beam dose and total number of brachytherapy fractions for a given patient, EQD2 values for clinical metrics were computed as if the automated plan or corresponding clinical plan were delivered for all fractions using an in-house script in MATLAB (R2019b, MathWorks, Inc., Natick, MA). EQD2s for automated and clinical plans were compared to each other and to the dose criteria described earlier to assess whether the automated plans were clinically acceptable.

3. Results

Table 2 summarizes optimization times and compares optimized plans to clinical plans, automated plans to clinical plans and automated dose to predicted dose. Table 3 compares clinical dose metrics used to assess plan quality. Optimization took an average of 1.6 minutes and ranged from a minimum of 1 minute for intracavitary plans up to 3.8 minutes for a hybrid case (i.e. one with additional needles). Although there were small differences in dwell times for optimized plans compared to clinical plans (mean difference 0.2s, MAD 4s or 0.8% of the total plan dwell time), the resulting dose distributions were nearly indistinguishable (see first two columns of Figure 3 and Figure 4). MAD over all voxels were under 2% for all patients (1.1% on average), and the mean dose difference over all patients was 0.2%. Mean differences in OAR D_2cc over all patients were −1.9 cGy (or −0.3% of prescription) for bladder, −0.4 cGy (0.0%) for rectum, and 0.7 cGy (0.1%) for sigmoid. On average, HRCTV D90 differed by 4.5 cGy (0.6%) and V100 differed by 0.4%. The average DSC between optimized and actual 100% isodose contours was 0.99.

Table 2.

Comparison of optimized plans (Opt) for validation to corresponding clinical (Clin) plans, predicted (Pred) doses to clinical plans, automated (Auto) plans to predicted doses, and automated plans to clinical plans, along with optimization times for optimized and automated plans.

	Mean Absolute Differences		Mean Differences		DSC	Mean (Range)
	Dwell Times	Overall Dosea	Dwell Times	Overall Dose	100% Isodose	Optimization Time
	s (%b)	cGy (%)	s	cGy (%)		s
Optimized Plan Results for Validation (Clin-Opt)
T&O	4.1 (0.9%)	6.9 (1.1%)	0.3	1.8 (0.3%)	0.99	75 (63-96)
T&O + N	5.6 (1.0%)	8.9 (1.3%)	0.2	1.7 (0.3%)	0.98	124 (80-227)
T&R	2.7 (0.7%)	6.1 (0.8%)	0.2	1.3 (0.2%)	0.98	90 (69-126)
T&R + N	4.0 (0.7%)	7.6 (1.0%)	0.2	2.0 (0.3%)	0.99	113 (94-130)
Automated Plan Results (All T&O)
Clin-Pred	NA	57.6 (9.1%)	NA	9.4 (1.7%)	0.90	NA
Pred-Auto	NA	38.8 (6.1%)	NA	−15.5 (−2.5%)	0.96	81 (70-92)
Clin-Auto	10.3 (2.1%)	40.9 (6.5%)	0.0	−6.2 (−0.8%)	0.91	81 (70-92)

T&O = tandem-and-ovoid, T&R = tandem-and-ring, N = needle(s), DSC = Dice similarity coefficient.

^aOver all voxels for each patient, where % is relative to prescription

^bRelative to the total plan dwell time (corresponding values for mean differences were less than 0.1% so are not shown)

Table 3.

Mean and standard deviation of differences in dose metrics between optimized plans (Opt) for validation and corresponding clinical plans (Clin), predicted (Pred) doses and clinical plans, automated (Auto) plans and predicted doses, and automated plans and clinical plans, over all patients.

	Bladder D2cc	Rectum D2cc	Sigmoid D2cc	HRCTV D90	HRCTV V100
	cGy (%a)	cGy (%)	cGy (%)	cGy (%)	%
T&O	−2.7±4.9 (−0.4±0.8)	1.8±0.0 (0.3±0.7)	0.2±2.2 (0.0±0.3)	4.1±10.4 (0.6±1.7)	0.7±0.6
T&O + N	−3.6±4.4 (−0.5±0.7)	−0.1±0.1 (0.0±0.8)	1.0±8.2 (0.2±1.2)	6.1±4.3 (0.9±0.6)	0.6±0.5
T&R	0.3±4.0 (0.0±0.5)	−2.0±0.0 (−0.3±0.5)	0.2±3.2 (0.0±0.4)	3.7±9.7 (0.5±1.3)	0.2±0.4
T&R + N	−1.7±6.0 (−0.2±0.8)	−1.2±0.1 (−0.2±0.9)	1.3±4.0 (0.2±0.6)	4.1±6.9 (0.6±1.0)	0.2±0.4
Clin-Pred	−25.6±59.6 (−3.8±9.3)	−25.0±44.8 (−3.8±7.0)	−13.5±32.7 (−2.1±5.4)	−29.2±73.0 (−4.3±11.6)	−2.0±6.1
Pred-Auto	−0.2±23.7 (0.1±3.8)	1.1±19.7 (0.2±3.2)	4.3±12.3 (0.7±2.0)	−4.9±23.1 (−0.8±3.8)	0.0±1.6
Clin-Auto	−25.7±61.2 (−3.8±9.3)	−23.8±44.5 (−3.5±6.7)	−9.2±33.0 (−1.3±5.4)	−34.1±79.1 (−5.1±12.7)	−1.9±5.6

T&O = tandem-and-ovoid, T&R = tandem-and-ring, N = needle(s).

^a% is relative to prescription

Figure 3.

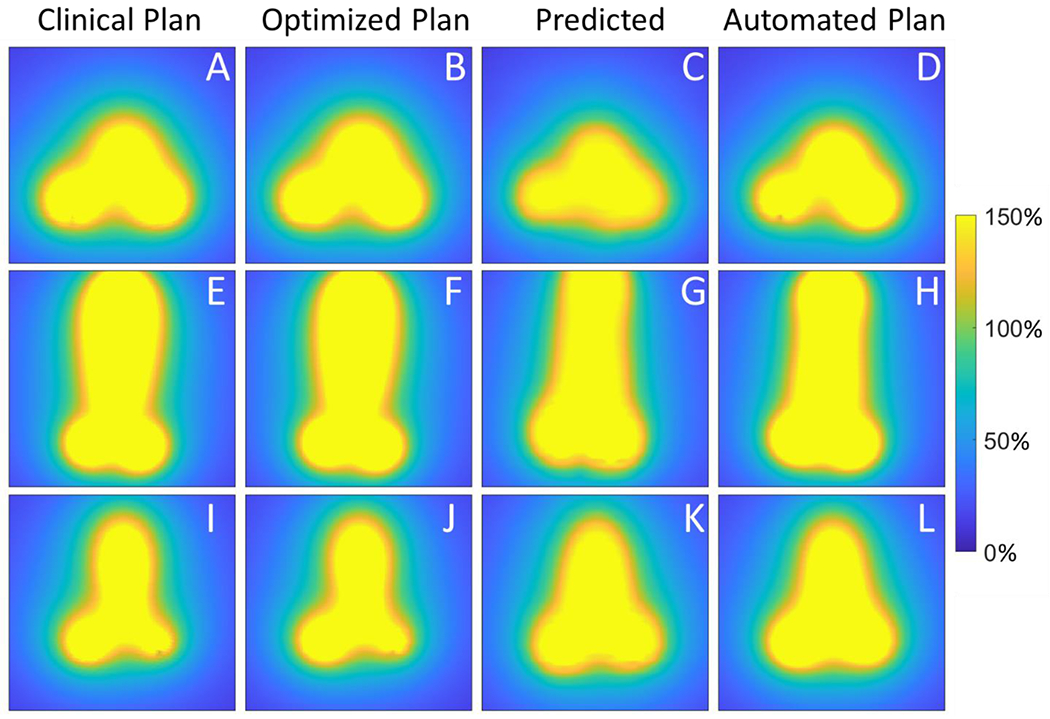
Coronal view of the dose from the clinical plan (A,E,I); dose from the optimized plan (B,F,J), which was proposed by optimizing using the clinical dose as the reference; dose predicted by the neural network (C,G,K); and dose from the automated plan (D,H,L), which was produced by optimizing using the predicted dose as the reference. The top row (A-D) displays subject 10, which had the best automated plan; the middle row (E-H) displays subject 4, whose automated plan featured the largest mean absolute difference in dwell times from the clinical plan; and the bottom row (G-I) shows subject 2, whose automated plan featured the largest mean absolute difference in dose from the clinical plan. Dose is shown relative to the prescription dose in %.

Figure 4.

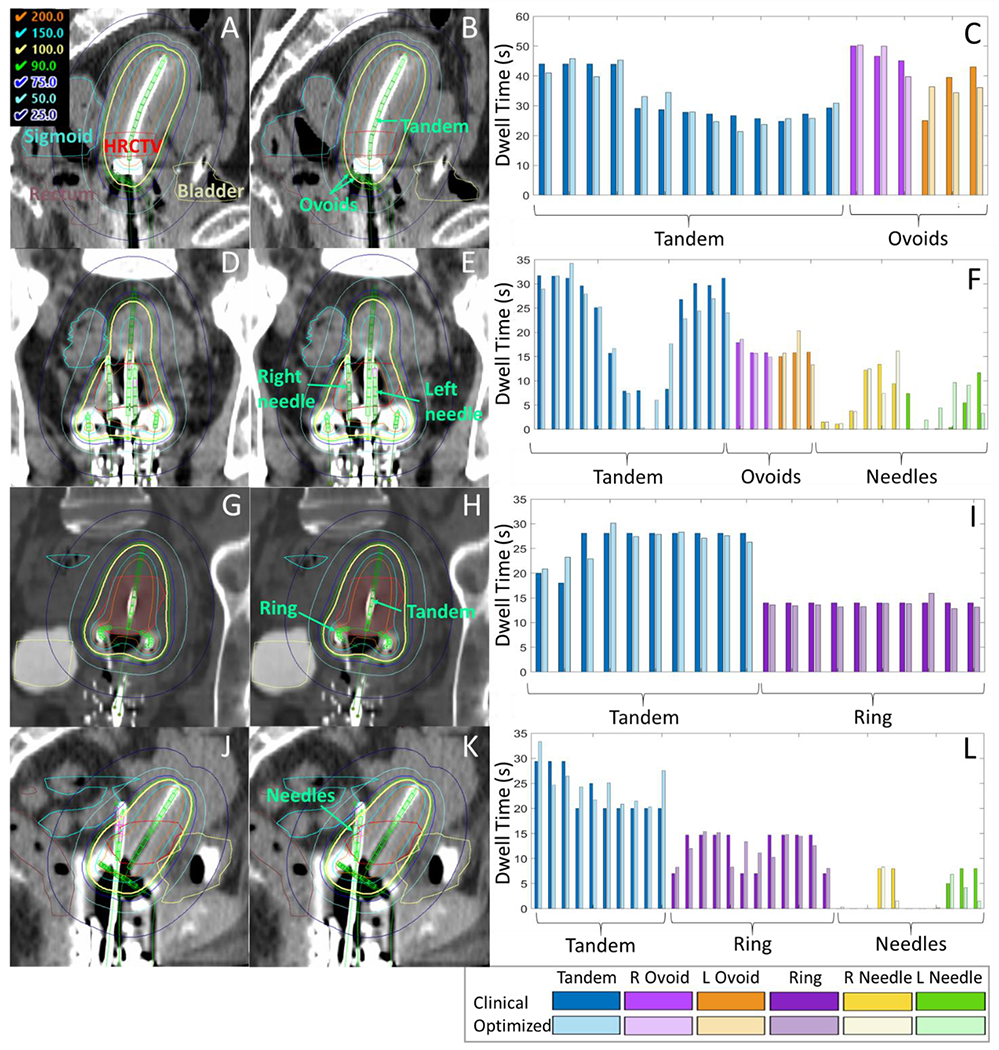
Example dose distributions from patient clinical plans (left column) and optimized plans for validation (middle column), and a comparison of clinical and optimized plan dwell times (right column). (A-C) displays a tandem-and-ovoid case and a sagittal view, (D-F) displays a tandem-and-ovoid plus two needles and a coronal view, (G-I) displays a tandem-and-ring and a coronal view, and (J-L) shows a tandem-and-ring with two needles and a sagittal view. Anatomy displayed on the CT scans includes the HRCTV (red), bladder (yellow), rectum (brown) and sigmoid (cyan), and the implanted applicators and needles are shown in green. Isodoses shown are relative to the prescription dose in %.

For the automated plans, dose and dwell time differences from the clinical plans were larger. The average dwell time difference was 10.3s, or 2.1% of the total plan dwell time. Automated plan dose over all voxels was on average 6.2 cGy (0.8%) higher than clinical dose, and the MAD in dose was 40.9 cGy (6.5%). When comparing the predicted dose to the clinical plan dose, predicted dose was on average 9.4 cGy (1.7%) lower, with MAD 57.6 cGy (9.1%). Comparing the automated plan dose to the predicted dose, the automated plan dose was on average 15.5 cGy (2.5%) higher, with MAD 38.8 cGy (6.1%).

On average, clinical plan quality metrics were higher for automated plans than the clinical plan (bladder D_2cc 25.7 cGy (3.8%), rectum D_2cc 23.8 cGy (3.5%), sigmoid D_2cc 9.2 cGy (1.3%) and HRCTV 34.1 cGy (5.1%)). The predicted dose metrics were higher than the clinical plans by similar magnitudes (bladder D_2cc 25.6 cGy (3.8%), rectum D_2cc 25.0 cGy (3.8%), sigmoid D_2cc 13.5 cGy (2.1%) and HRCTV 29.2 cGy (4.3%)). When comparing the automated plan dose to the predicted dose, these differences were smaller (ranging from 4.3 cGy (0.7%) lower than predictions for sigmoid to 4.9 cGy (0.8%) higher than predictions for HRCTV D90).

Table 4 displays the EQD2 values for each clinical metric for automated and clinical plans. In the left column, * indicates the plan was generally too hot (5/10 plans) and ** indicates the plan was generally too cold based on the hard planning constraints. Two automated plans (subjects 5 and 10) met all constraints, and one cool plan (subject 7) featured improved HRCTV coverage relative to the clinical plan. Although the automated plans tended to be a bit hot in general, the shape of the dose distributions qualitatively appeared to be very reasonable (see Figure 3 last column, which demonstrates the ideal pear-shaped dose distribution, and Figure 5). Figure 5 shows example dose distributions and dwell times for the best and worst automated plans, side-by-side with clinical plans.

Table 4.

Comparison of EQD2 dose metrics for automated plans compared to clinical plans. EQD2 incorporates the prior external beam radiotherapy dose and was computed assuming the dose for the single brachytherapy fraction was delivered for the entire course of treatment.

	HRCTV D90 [Gy]		Bladder D2cc [Gy]		Rectum D2cc [Gy]		Sigmoid D2cc [Gy]
Subject	Auto	Clinical	Auto	Clinical	Auto	Clinical	Auto	Clinical
1*	92.6	84.2**	59.1	56.7	71.7	63.6	77.4*	72.2
2*	97.7	85.5	96.7*	80.0	82.8*	73.4	75.9*	73.5
3*	98.2	96.6	95.9*	95.9*	80.8*	80.0*	73.9	72.7
4**	83.5**	84.4*	85.8	88.6	71.9	65.1	53.6	54.8
5	86.3	89.7	84.1	89.1	58.6	60.2	53.9	57.1
6*	99.2	96.3	60.6	59.2	68.0	65.5	78.0*	75.2*
7**	81.3**	79.8**	58.6	56.2	67.4	65.4	67.4	65.7
8**	81.5**	85.0	87.1	88.6	68.6	72.5	63.7	62.2
9*	111.0	90.5	79.6	72.4	55.3	54.9	77.1*	69.3
10	94.9	104.1	71.4	77.8	58.0	59.1	67.4	71.5

^*indicates the dose metric exceeded a hard maximum planning constraint (bladder D_2cc > 90 Gy, rectum D_2cc > 75 Gy, sigmoid D_2cc > 75 Gy), while

^**indicates that the minimum HRCTV coverage D90 constraint (85 Gy) was not met.

Stars in the left column indicate whether the automated plan was generally too hot (*) or too cold (**).

Figure 5.

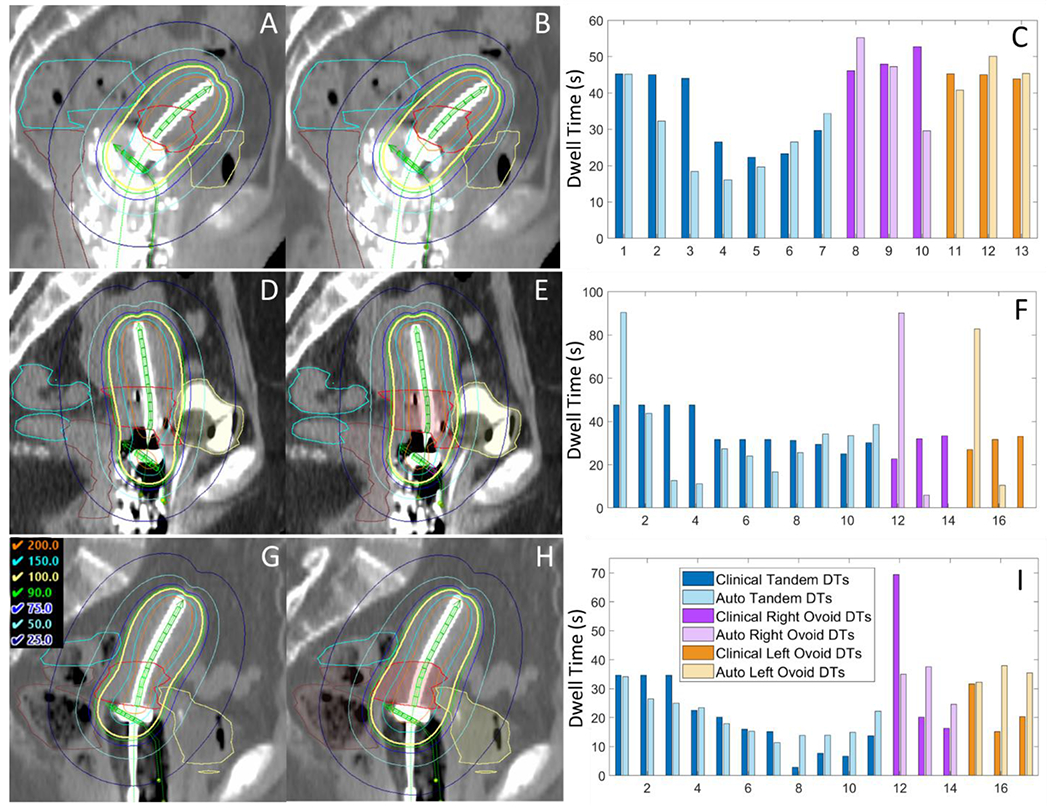
Sagittal view of clinical plan dose (left) compared to automated plan dose (center), as well as a comparison of dwell times (right). (A-C) shows the best automated plan (subject 10), which was clinically acceptable (top); (D-F) shows the automated plan which featured the largest mean absolute difference in dwell times from the clinical plan (subject 4); and (G-I) shows the automated plan which featured the largest mean absolute difference in dose from the clinical plan (subject 2). Despite the largely varying dwell times, the middle plan (D-F) nearly met all clinical plan constraints, though the HRCTV coverage was slightly too low (D90 EQD2 = 83.5 Gy instead of >85 Gy). The bottom plan (G-I) featured more smooth dwell times than the clinical plan, yet did not adequately spare the OARs and in general was too hot.

4. Discussion

4.1. Validating Optimization by Reproducing Clinical Plans

This paper provides a proof-of-concept for automated cervical brachytherapy treatment planning using 3D dose predictions from a neural network, as depicted in Figure 1. In order to convert 3D dose predictions to deliverable treatment plans, we developed an optimization framework that iteratively minimizes the difference between a calculated and reference dose distribution to compute dwell times. We first demonstrated that the optimizer could accurately reproduce dwell times and dose of clinical treatment plans by feeding in the 3D clinical plan dose as the reference dose. There were small dwell time differences between optimized and clinical plans (mean difference 0.2s); however, qualitatively the dose distributions appeared almost indistinguishable, the average dose error over all voxels was small (0.2%) and the differences between clinical metrics were 0.6% or less on average. The very high DSC (0.99 on average) indicated the shape of the optimized plan 100% isodose closely matched that of the clinical plan. We suspect that there are multiple dwell time solutions that give approximately the same dose distribution, which is why some slight variations in dwell time distributions can be observed in Figure 4.

There were some differences in results between applicator types. In general, optimization was slightly less accurate for cases with needles, likely due to the increased number of parameters. T&R featured the best performance, with mean absolute differences in dwell times and overall dose of 2.7s and 6.1 cGy, respectively, compared to 4.1s and 6.9 cGy of T&O. The better dwell time agreement for T&R was driven by the ring, which featured about half the MAD in dwell times compared to the tandems and ovoids. We do not have a good explanation for the better performance in the ring, but we suspect these differences are within the noise of the process and could differ depending on patient selection.

4.2. Automated Planning Using 3D Dose Predictions

We also presented an initial demonstration of automated treatment planning for 10 T&O patients using 3D dose predictions from a U-NET. Automated treatment plans featured standard pear-shaped dose distributions that closely matched that of the predicted doses and clinical plans, as indicated by the high DSC of the 100% isodose contours (0.96 and 0.91 on average, respectively). Automated plan clinical metrics were, on average, higher than clinical plan metrics, with mean differences ranging from 9-34 cGy. Most of this difference was due to the predictions, as the predicted metrics were on average 14-29 cGy higher than clinical. Automated plan clinical metrics were very similar to predicted dose metrics (mean OAR D_2cc and HRCTV D90 differences under 5 cGy, mean HRCTV V100 difference 0.0%).

When considering all voxels, the differences between automated and predicted doses were larger: on average, automated plan dose was 16 cGy higher than predicted dose, and MAD was 39 cGy. Since the predicted dose was, on average, lower than the clinical plan dose (mean difference 9 cGy and MAD 58 cGy), the overall voxel-based difference between automated and clinical dose averaged to a smaller value (6 cGy higher for automated, MAD 41 cGy). The greater differences when considering all voxels can be explained by the reduced accuracy of dose prediction for high doses, which were de-emphasized in the neural network to preferentially improve predictive accuracy in doses near OARs (Cortes et al., 2022). These high doses were also excluded from optimization, so it is unsurprising that there were larger discrepancies between predictions and automated plans in high doses and better agreement in intermediate doses near the OARs. As seen in Figure 3, the yellow high dose in the automated plan sometimes agreed better with the clinical plan than the physically impossible high doses of the predictions. It is encouraging that despite the differences between the clinical plan and predicted dose distributions, the optimization was able to correct for some of these differences. Thus, the predictions provided a good starting template for creating standard dose shapes, while the optimizer ensured the automated plan dose was physically possible.

Table 4 demonstrates that clinical EQD2 metrics of automated plans were close to acceptable levels. However, only 2 out of 10 automated plans met all hard planning criteria compared to 4 out of 10 clinical plans that met these same criteria. HRCTV coverage was most often greater in automated plans than clinical plans, which resulted in some overdosing of OARs. Five of the plans were too hot (most often overdosing the sigmoid), while 3 were too cold due to reduced HRCTV coverage. One of the cool automated plans featured improved HRCTV coverage than the clinical plan, so in total 3 out of 10 plans could be considered clinically acceptable. As mentioned above, most the differences in clinical metrics arose from the predictions themselves, and thus a more accurate neural network would likely results in a greater percentage of clinically acceptable automated plans produced with this framework. Despite these challenges, a qualitative analysis of the dose distributions and dwell times showed that the remaining 7 automated plans were very close to being clinically acceptable and likely would have required minor adjustments.

The automated plan with the largest deviations in dwell times from the clinical plan (subject 4) is shown in Figure 5 E and F. The clinical plan featured a smoother distribution of dwell times, while the automated plan featured larger jumps in time between adjacent source positions. However, the resulting dose met all planning constraints except the minimum target coverage, and HRCTV D90 was 83.5 Gy EQD2 compared to 84.4 Gy of the clinical plan. Likely a smoother dwell time distribution could be obtained by adding some form of regularization to optimization, and this will be the subject of future work. Furthermore, it is interesting that the dose prediction and automated plan were so reasonable given the retroverted uterus, which was not commonly observed in the training dataset. The automated plan with the largest discrepancy in dose from the clinical plan (subject 2) is shown in Figure 5 H and I. Here the dwell time distribution was smoother than the clinical plan, but the HRCTV was slightly over-covered, resulting in hotter doses to the OARs. While this initial demonstration reveals that further work is necessary to obtain clinically acceptable plans for all patients without further refinement, automated planning is feasible and the procedure could still save time by providing an excellent starting point in a matter of minutes.

It is important to note that the clinical EQD2s were computed as if that single fraction’s clinical plan was delivered for the entire treatment, and thus the reported EQD2s do not reflect what was actually delivered to the patient. The implants can vary day-to-day and physicians may choose to increase or decrease coverage for a given treatment fraction to compensate for other fractions. We felt it was most appropriate to compare automated and clinical plans for the same fraction of treatment, as if delivered for the entire course, as it represents the dose achievable on the same implant.

The combined time for the dose predictions (<1 minute) and optimization (1.6 minutes on average) would be about 3 minutes. While we have not formally evaluated treatment planning time at our center, the combination of manual loading, point A normalization and optimization typically takes at least 5 minutes, and upwards of an hour on more for challenging hybrid cases. One study reported an average of 138 minutes for total planning time, which included applicator digitization, contouring, optimization, physician review and quality assurance (Mayadev et al., 2014). Another study reported an average of 66 minutes for the above steps, minus physics quality assurance checks by physics (Michaud et al., 2016). These studies did not separate contouring and applicator digitization time from treatment plan optimization, but in our experience optimization typically occupies the majority of planning time. In addition, neither of these studies featured cases with supplemental needles, which would greatly increase total planning time (Dimopoulos et al., 2006). Given these points, we believe that reducing treatment plan optimization down to 3 minutes will significantly reduce overall planning time, particularly for complex cases. An in-depth timing analysis is beyond the scope of this work, but future work will test efficiency gains in clinical workflow once the automated planning pipeline has been fully validated.

4.3. Dwell Time Optimization

Numerous groups have developed techniques for DVH-based inverse optimization of brachytherapy plans (Sloboda, 1992; Lessard, Hsu and Pouliot, 2002; Lahanas, Baltas and Zamboglou, 2003; Trnková et al., 2009; Yao et al., 2014; Oud et al., 2020; Wang et al., 2020). These methods evaluate dose within specific target and OAR contours and iteratively attempt to maximize dose within targets, minimize dose within OARs, and/or meet user-defined clinical objectives on these contours. While these solutions have the potential to be faster than manual optimization, they do not use prior patient data to inform optimal planning. Additionally, DVH-based optimization is ill-suited for cervical brachytherapy since the anatomy and applicator geometry that result in the clinically standard pear-shaped dose distribution are not typically contoured. As mentioned previously, solutions for gynecologic brachytherapy typically require additional user-generated inputs or other work-arounds to preserve the standard pear-shaped distribution (Lessard, Hsu and Pouliot, 2002; Trnková et al., 2009; Oud et al., 2020).

We have shown that 3D patient-specific dose predictions from a neural network can produce plans with pear-shaped dose distributions for T&O intracavitary cases using only inputs that are commonly contained in DICOM RT files for gynecological brachytherapy (i.e., applicator geometry and contours of HRCTV, bladder, rectum and sigmoid). By training on prior treatments, the neural network learned to place dose in regions that were not contoured, such as the uterus. The 3D dose predictions remove the strong reliance on contoured targets, distinguishing our method from prior inverse optimization techniques. Our optimizer incorporates a voxel-wise comparison between dose computed in each iteration and the reference 3D dose. We chose to include all voxels with reference doses between 80-120% with equal weighting into a MSE cost function. Higher doses were excluded since the neural network dose prediction accuracy was worse in this range (Cortes et al., 2022). We tested many different dose ranges and found that 80-120% resulted in the best trade-off between computation speed and accuracy. Fredriksson implemented a similar voxel-based optimization for external-beam radiotherapy, where the goal of the optimization was to at least match or improve upon a 3D reference dose distribution (Fredriksson, 2012). However, his cost function applied constraints that no voxel outside of the target could receive a dose greater than the reference dose, and additional constraints to ensure uniform prescription coverage of the target. We could not apply such restrictions because some cervical brachytherapy targets are not contoured. Furthermore, in cervical brachytherapy dose heterogeneity is preferred as it contributes to the very good outcomes, although we do not yet know the best metric (such as V150 or V200) to quantify the heterogeneity. While we could have weighted voxels within the HRCTV and OARs higher in our MSE cost function, we found that equal weighting was fast, simple and sufficient for accurately reproducing the dose and dwell times of clinical treatment plans.

4.4. Knowledge-based Planning

Our automated planning method offers an additional benefit above standard DVH-based inverse optimization since it uses patient-specific predictions of optimal dose instead of population-based dose constraints. These predictions are derived from models trained on hundreds of past treatments, and thus can capture plan features common to a variety of different anatomical and applicator geometries. In the external beam radiotherapy space, knowledge-based planning has shown great benefit over traditional inverse optimization by improving plan quality, reducing plan quality variability, and reducing planning time (Moore et al., 2015; Cornell et al., 2019; Kaderka et al., 2019, 2021). The literature on knowledge-based planning in brachytherapy is much more scarce, though there are a few groups that have trained models on past treatment data to make dose predictions and/or automate planning for new patients (Damato, Viswanathan and Cormack, 2013; Nicolae et al., 2017, 2020; Shen et al., 2019; Yusufaly et al., 2020; Kallis, Mayadev, Covele, et al., 2021; Kallis, Mayadev, Kisling, et al., 2021; Cortes et al., 2022; Pu et al., 2022; Reijtenbagh et al., 2022). Prediction of DVHs and OAR D_2cc can be beneficial for plan quality control and determining which patients may require supplemental needles (Damato, Viswanathan and Cormack, 2013; Yusufaly et al., 2020; Fan, Xing and Yang, 2021; Kallis, Mayadev, Covele, et al., 2021; Kallis, Mayadev, Kisling, et al., 2021; Reijtenbagh et al., 2022), but converting these metrics to treatment plans would suffer from the challenges of DVH-based optimization. One group successfully automated prostate brachytherapy treatment planning using anatomical feature metrics to identify the most similar patient from a training dataset (Nicolae et al., 2017, 2020), though the planning process for cervical cancer is very different. Another study used deep reinforcement learning to automatically adjust inverse dose optimization priorities for cervical brachytherapy (Shen et al., 2019). While it was a nice proof-of-principle of AI-driven planning on 10 patients, the in-house inverse optimization method and automated plan quality were not rigorously evaluated. Pu et al. used deep reinforcement learning to intelligently adjust dwell times for cervical brachytherapy; however, the objective function was contour-based and the ability to reproduce a pear-shaped dose distribution was not discussed (Pu et al., 2022). Deep learning has also been used to predict dwell position coordinates and times for cervical brachytherapy plan verification, but this methodology has not been applied to automate planning (Fan, Xing and Yang, 2021).

4.5. Limitations of the Current Framework

The optimizer and automated planning framework developed in this study feature a few limitations. Ideally the optimizer should be able to exactly reproduce the dose distributions in the validation cases, but we found there were still small differences (around 1% mean absolute difference over all voxels). We suspect that these arose from slight variations in sampling and interpolation between our optimizer and the treatment planning system. The treatment planning system computes dose using TG-43 (Nath et al., 1995; Rivard et al., 2004), which requires interpolation of data tables, whereas our procedure involves translating and rotating matrices. The differences in dose tended to be larger in the high doses where gradients were steeper, which would support the notion that small shifts and sampling play a role. For cases with needles, larger differences could be observed in the smaller doses (around 30% of prescription) for some patients, and it was confirmed that these doses were located near needles, where steep dose gradients for single dwell positions would occur.

Dwell times were constrained to fall between 0 and 100 s during optimization. While dwell times greater than 100 s are very uncommon at our clinic, one clinical plan in this dataset featured a couple dwell times above 90 s; therefore, we may consider increasing this upper bound in future work. These constraints would need to be tailored for each institution based on the typical range of source strengths and dwell times.

The current deep learning model was only produced for T&O brachytherapy, so we were only able to demonstrate automated T&O planning in this work. In addition, the automated plan quality is limited by the quality of the dose predictions. In the dose range of 80 to 120% of prescription, the mean model bias and random error in the test set ranged from about 2-5% and 12-30%, respectively. Therefore, it is unsurprising that there are some differences between the automated and clinical plan doses. We are currently developing an updated neural network that uses applicator geometry inputs directly pulled from the RT DICOM plan file, as well as inputs that account for the physical properties of radiation to improve dose prediction accuracy. We are also investigating whether including the CT image as an input will improve model performance. The new model will be trained and validated on other implant types, such as T&R and interstitial cases, to improve applicability to all cervical cancer brachytherapy. Once a more accurate, generalized model is developed, automated planning will be investigated on a large scale with physician input.

The dose predictions and optimization are performed outside of the treatment planning system using Python programs, which requires export and subsequent import of DICOM plan files. Until very recently, the Varian brachytherapy planning system has provided little flexibility for user scripting. Future work will explore fully integrating our automated planning pipeline into the treatment planning system. In addition, we have only considered automating treatment optimization after contouring and applicator digitization steps are complete. There are multiple solutions for automating those other steps (Zhou et al., 2017; Jung et al., 2019; Zaffino et al., 2019; Dai et al., 2020; Zhang et al., 2020; Jiang et al., 2021; Mohammadi et al., 2021; Zabihollahy et al., 2021; Yoganathan et al., 2022). For instance, manual contouring of HRCTV and OARs can take 15 to 20 minutes per patient (Jiang et al., 2021), and deep learning based auto-contouring could reduce this time to less than 1 minute (Zhang et al., 2020; Mohammadi et al., 2021; Zabihollahy et al., 2021; Yoganathan et al., 2022). Future work will investigate combining all automation for fully-automated brachytherapy planning.

4.6. Benefits of the Current Framework

Despite these challenges, we believe that the current automated planning pipeline has the potential to significantly reduce planning time and improve the ease of treatment planning. Automated plans from the existing neural network could be used as-is or with minor manual adjustment, which may still be faster than manual loading and optimization. With a slightly improved neural network that generalizes to other implant types, we believe clinically acceptable intracavitary and hybrid treatment plans could be produced with a button-click and imported into the treatment planning system for immediate delivery. Models trained on patients treated by experienced clinicians at busy brachytherapy clinics, such as our own, could be used to guide automated planning at smaller centers with less brachytherapy expertise. Experienced clinics could benefit from the quality control, standardization and efficiency gains offered by automated, knowledge-based planning. Because automated treatment plans are produced in a few minutes, patients could either spend less time under sedation, or clinicians could use the remaining time to better optimize plans, which may enable toxicity reduction. Furthermore, the proposed framework could be extended to automate brachytherapy planning for other treatment sites, such as breast or prostate cancer.

The current automated planning method is based on a dose kernel calculated with the TG-43 formalism (Nath et al., 1995; Rivard et al., 2004). Model-based dose calculation algorithms can improve dose calculation accuracy, for example when considerable gas is present in the rectum (Abe et al., 2018), though for unshielded plastic gynecological applicators the dosimetric changes are often minimal (<5%) (Jacob et al., 2017; Abe et al., 2018). However, our method could be modified to use more complex, model-based dose calculation algorithms. Instead of exporting one kernel and translating and rotating it to the location of each dwell position, individual dose rate matrices $\dot{D_n}$ for each dwell position would need to be calculated separately using information from the CT image. Depending on the algorithm and treatment planning system, it may be achievable to compute this outside of the treatment planning system, or it may be possible to perform and export a dose calculation with each dwell time activated separately, within the system (provided this could be scripted for automation). Then the optimization could continue as-is, weighting each dose rate matrix by the dwell time and summing over all dwell positions to calculate total dose for each iteration. Neural network models would also need to be re-trained on dose calculated with that algorithm. Translating this methodology to other dose calculation algorithms will be the subject of future work.

5. Conclusions

We have presented a proof-of-concept for automated, knowledge-based brachytherapy planning for cervical cancer using 3D dose predictions from a neural network. In order to convert dose predictions to a deliverable treatment plan, we developed an optimizer that iteratively determines the dwell times required for a series known source positions to replicate a 3D reference dose. We demonstrated that this optimizer can accurately reproduce the dose and dwell times of clinical treatment plans when the clinical dose is used as the reference dose. Using dose predictions for 10 T&O patients from a convolutional neural network produced in prior work, we demonstrated that the full automated planning pipeline is feasible and can result in clinically acceptable treatment plans. With further improvements to dose prediction accuracy, it may be possible to achieve high quality, clinically acceptable plans for most, if not all, patients in a matter of minutes. This tool has the potential to drastically reduce brachytherapy procedure times and standardize brachytherapy planning.