Exergoeconomic analysis and multi-objective optimization of ORC configurations via Taguchi-Grey Relational Methods

Abstract

Recovery of low-grade waste heat in industrial processes is an essential energy management topic. Yet, most low-temperature heat sources discharge their heat directly into the environment. The Organic Rankine Cycle (ORC), which has the benefits of being energy-efficient, enabling investment savings, and being ecologically friendly, is crucial in recycling energy from low-temperature waste heat. Both the application of the optimum cycle design and the provision of optimum working conditions are the issues that need to be focused on efficiently using energy. This study performs the energy, exergy, and exergoeconomic analysis of four different organic Rankine cycle configurations operating with renewable or low grade waste heat. The effect degrees and ratios of selected control factors are calculated using Taguchi and variance analysis methods to compare thermal and exergy efficiencies, total system cost, and unit cost of electricity produced by the system. The objective function of the multi-objective optimization problem is defined, and its solution is realized with the Taguchi-Grey Relational Analysis method. The best thermodynamic and exergoeconomic performance result is calculated for the configuration of ORC with Feed Fluid Heater-Internal Heat Exchanger (IHE–FFH–ORC). As a result of Taguchi and ANOVA analysis, the factors that most affect the thermal efficiency of the system, the exergy efficiency, the total system investment cost, and the unit cost of the electricity produced are, respectively, the evaporation temperature (∼50%), turbine efficiency (∼25%), working fluid (∼20%), subcooling (∼4%), pump efficiency (∼0.05%), and superheating (∼0.05%). As a result of the optimization process, the thermal and exergy efficiencies, the total system cost and the unit cost of produced electricity for the IHE–FFH–ORC power system are calculated as 22.6% and 73.5%, 1.06 $/h, 0.039 $/kWh and 2.9 years, respectively.

1. Introduction

Since most electrical energy is generated through the combustion of fossil fuels, the necessity for high-efficiency alternative systems employing low grade thermal energy cannot be overstated. The need for the industry to continually improve the energy efficiencies of its systems and energy recovery from the low-grade waste heat produced during the production of primary energy is becoming more and more pressing due to problems and concerns like rising primary energy prices, the unequal distribution of primary energy reserves throughout the world, political unrest, and the current generation’s growing awareness of its responsibility to use primary energy reserves sustainably, to name just a few [1]. Various thermodynamic cycles such as the organic Rankine cycle, supercritical CO₂ cycle, Kalina cycle, Goswami cycle, and triple flash cycle have been proposed to recover this heat[2]. The organic Rankine cycle is the most chosen application due to its low complexity, great reliability, and ease of maintenance [[3], [4], [5], [6]]. The organic fluids that we are used to seeing in cooling systems, which may deliver higher vapor pressure at the same temperatures, are employed in the Organic Rankine Cycle (ORC), which generates mechanical energy from vapor, in place of the steam that drives the expander. In this way, electricity is produced effectively even at low temperature heat sources based on renewable energy sources (such as geothermal and solar energy) or the low-grade waste heat generated during any process in the industry [[7], [8], [9], [10], [11]].

The performance of ORC power systems depends on several factors, including operating conditions, capacity, appropriate system configuration and working fluid. At the same time, the design should be economical and environmentally friendly. Many studies have been published on novel configurations, arrangements, and technology in ORC-based power systems. The capacity and performance of the ORC systems are largely determined by the working fluids used in their design[12]. Yet, it is widely known that using regularly used refrigerants affects the stratospheric ozone layer and the rate of global warming. Hence, choosing a good working fluid also depends on a few factors, including flammability, toxicity, ozone depletion potential (ODP), and potential for global warming (GWP) [[13], [14], [15]]. In the ORC power systems, several types of working fluids are available in the market, such as hydrofluorocarbons (HFCs), chlorofluorocarbon (CFCs), hydrochlorofluorocarbon (HCFCs), and natural refrigerants (${\mathrm{C}\mathrm{O}}_2$, ammonia, propane, etc.). Some studies on the working fluid selection and appropriate configuration design in the literature are as follows. Shah et al. [16] performed the energy and exergy analysis of a basic and regenerative ORC sourced from waste heat for R113, R123, R236ea, R245fa, and R141b. As a result of the research, the regenerative ORC performed better. The most suitable fluid for the cycle was R113. In the study published by Rashwan et al. [17], the comparative thermodynamic analysis was performed for three different designs: basic ORC, ORC with recuperator, and integrated ORC with double turbine and two-fluid cascade closed loop. Waste heat was used as the heat source, and propane was used as the working fluid. According to the calculations, the cascade system gave better performance values than other designs. Abam et al. [18] performed a comparative performance analysis of different ORC configurations using thermo-sustainability indicators. The working fluids used in the systems were R245fa, R1234yf, and R1234ze. The designed configurations were basic ORC, ORC with internal heat exchanger, turbine bleeding ORC, and turbine bleeding/regeneration ORC. They stated that the best configuration, regarding maximum exergy efficiency and environmental aspects, was the turbine bleeding/regenerated ORC using R245fa fluid. Ozdemir and Kilic [19] performed a comparative energy and exergy analysis of waste heat-sourced basic and regenerative ORC systems. The selected fluids were R113, R114, R227ea, R245fa, and R600a. It was concluded that the regenerative cycle performs better than the basic cycle. Ataei et al. [20] analyzed different cycle configurations (basic ORC, ORC with internal heat exchanger, regenerative ORC, and regenerative ORC with internal heat exchanger) using R113, RC318, iso-pentane, and n-hexane dry organic fluids. As a result, regenerative ORC with an internal heat exchanger had the best performance values, with a thermal efficiency of 21.7% and the second-law efficiency of 64.2%. Energy and exergy analysis of four different configurations, namely basic ORC, turbine bleeding ORC, regenerative ORC, and both turbine bleeding and regenerative ORC, were performed by Safarian and Aramoun [21]. As a result of their analysis revealed the maximum thermal and exergy efficiency and minimum exergy loss between the four cycles with both turbine bleeding and regenerative ORC system. Mago et al. [22] compared basic and regenerative ORC systems that generate power using low-temperature waste heat. R113, R245ca, R123, and isobutane were selected from the dry fluids for analysis. According to the calculation results, it has been determined that the regenerative ORC provides higher efficiencies, a lower irreversibility ratio, and lower heat input at the same power generation compared to simple ORC.

To improve the ORC configurations' performance, several researchers conducted optimization studies [[23], [24], [25]]. Meanwhile, some multi-purpose optimization studies were reported to determine the optimum operating conditions of the system [[26], [27], [28], [29]]. Imran et al. [30] performed thermoeconomic optimization of three different ORC configurations from a waste heat source: basic ORC, single-stage regenerative ORC, and double-stage regenerative ORC. Maximum thermal efficiency and minimum specific investment cost (SIC) were taken as objective functions optimized with a Genetic Algorithm. Braimakis and Karellas [31] performed thermoeconomic optimization of basic and regenerative ORC systems. They investigated the effects of different heat source temperatures and capacities. They also evaluated different expander types and configurations. Nondy and Gogoi [32] compared the exergoeconomic performances of the basic ORC, recuperative ORC, regenerative ORC, and recuperative-regenerative ORC for R123 working fluid. They performed a parametric study and optimized the system’s performance by targeting maximum exergy efficiency and minimum system cost rate using Pareto Envelope-based Selection Algorithm-II (PESA-II). The authors reported that among the configurations studied, recuperative-regenerative ORC was the most efficient and economic system. Braimakis and Karellas [33] optimized three different regenerative ORC configurations. The first design included an open preheater where the fluid leaving the turbine and the fluid exiting the pump were mixed, while other configurations included a closed preheater. The systems are optimized for different working fluids, and their energy efficiency is compared with the standard ORC with and without a recuperator. Fang et al. [34] conducted the thermoeconomic multi-objective optimization of a basic ORC using a genetic algorithm. Fluids in the analysis were toluene, decane, R245fa, R123, and their zeotropic mixtures. The effect of four control factors, namely evaporation temperature, condensation temperature, superheat degree, and mass fraction of the zeotropic mixtures, were investigated on the thermodynamic and thermoeconomic parameters of the system. It was determined by the researchers that working fluids with high critical temperature and their zeotropic mixtures exhibit better thermodynamic and thermoeconomic performance. Zhang et al. [35] optimized the thermodynamic performance of ORC for waste heat recovery with exergy efficiency and levelized energy cost as an objective function by using the non-dominated sorting genetic algorithm-II. They selected six organic fluids, namely R141b, R142b, R245ca, R245fa, R600a, and R601a. According to the results, the ORC system using R245ca was more effective with a shorter payback period than other fluids. Laouid et al. [36] studied the multi-objective optimization of basic ORC, ORC-IHE, and regenerative ORC for twelve premium fluids. They accepted evaporation temperature, pinch point temperature difference (PPTD) in the evaporator and condenser, superheat degree, IHE effectiveness, and intermediate pressure as decision variables. Researchers examined two different combination cases as output parameters. The first is exergy efficiency and the electricity production cost (EPC), and the second is the net power output and EPC. The authors reported that when the second case is selected in the objective function, waste heat is maximized for all configurations. In addition, minimum EPC values were obtained in the second case. The thermodynamic and thermoeconomic analysis of the basic ORC, driven by exhaust gas of a solid waste power plant, was performed by Özahi et al. [37]. At the same time, the authors performed a multi-objective optimization by maximizing the net power output and minimizing the total cost rate of the system. As a result of the thermoeconomic analysis and multi-objective optimization for four different fluids, the best-performing fluid was toluene. Feng et al. [38] compared basic and regenerative ORC based on thermoeconomic multi-objective optimization using Pareto optimal solution. The effects of five parameters, namely evaporator outlet temperature, condenser temperature, superheating degree, most minor temperature difference, and subcooling degree, on exergy efficiency and leveled energy cost were investigated. At the end of the study, while regenerative ORC provided 8.1% higher exergy efficiency than basic ORC, it resulted in a 21.1% higher leveled energy cost value. Quoilin et al. [39] performed thermodynamic analysis and economic optimization in a small-scale ORC application with waste heat recovery. R245fa, R123, R134a, n-butane, n-pentane, HFE7000, SES 36, and R1234yf fluids were chosen as working fluids in the analysis. The objective function was taken as maximum economic profitability and efficiency in the optimization process. In the results obtained, maximum efficiency and minimum initial investment cost were achieved with n-butane. As a result of the thermoeconomic optimization, choosing a higher evaporation temperature is suggested as it increases the high-pressure steam density and reduces the cost of the expander and evaporator. Kermani et al. [40] optimized ORC architectures combined with an industrial waste heat recovery system for electricity generation. Optimum working fluid, ORC architecture, and equipment sizes were determined by applying a new optimization method by the researchers. Behzadi et al. [41] investigated the thermodynamic and exergoeconomic optimization of an ORC coupled with a gasifier and a Rankine cycle. As a result of the parametric analysis, the best-performing fluid was R123. With multi-objective optimization using a genetic algorithm, the maximum exergy efficiency was found to be 19.61%, and the minimum total product unit cost was found to be 24.65 $/GJ.

Another method applied for multi-objective optimization is the Grey Relational Analysis (GRA) method. In this method, the objective function for the multi-criteria optimization problem is obtained by calculating the general gray relationship degree for the output parameters in the system. Some authors have successfully applied this method in the performance evaluation of ORC systems. Xia et al. [42] performed optimization of turbine inlet pressure and pinch point temperature difference for six different working fluids in the basic ORC based on indicators of heat recovery efficiency, internal exergy efficiency, payback period, and annual emission reduction. In the analysis, entropy theory was used to calculate the weight coefficients of the output indicators. In another study published by the author and colleagues, a multi-objective optimization method with improved GRA was used to select a suitable fluid pair for a flue gas-powered dual-loop ORC system. Multi-purpose optimization was carried out by focusing on the system’s thermodynamic, economic, and environmental performance [43]. Wang et al. [44] performed comparative thermodynamic and thermoeconomic optimization using 14 different fluids for three different ORC configurations. The designed configurations were basic ORC, ORC-IHE, and extractive ORC. Exergoeconomic analysis, bi-objective optimization, and GRA were used to evaluate the system to obtain the configuration that provides the most comprehensive performance with the selected fluids. As a result of GRA, optimum results were obtained in terms of thermodynamics (energy and exergy efficiency) and thermoeconomics (cost of ORC per net output power and purchased equipment) with the basic ORC system R141b fluid used. In the study published by Bademlioglu et al. [45], the effect ratio and order of importance of nine control factors on the first and second law efficiency of the ORC-IHE were determined by Taguchi and ANOVA statistical analysis methods. In addition, the optimum combination of control factors was obtained by determining the parameter levels that provide the maximum value of the first and second law efficiency with the Taguchi-Grey Relational Analysis (Taguchi-GRA) method.

Studies in the literature show that there are various parameters affecting the performance of ORC power systems such as the boiler, condenser and absorber temperatures, expander and pump efficiencies and heat exchanger effectivenes. Yet, there hasn’t been a thorough research that examines all these variables and uses statistics to calculate their relative contributions to the system’s performance. As a result, the goal of this study is to investigate the parameters that have the greatest impact on the values of the ORC’s thermal and exergoeconomics parameter values, and to rank these parameters according to their significance using the Taguchi-GRA and ANOVA methodologies. Also, several statistical analysis techniques are used to establish the ideal working conditions, and the results are compared. As it is clear from the studies mentioned above, the system’s thermal efficiency increases with expanded configurations of ORC systems. In view of these, the main contribution of the present study can be stated as follows:

First, four different ORC configurations, basic ORC, ORC with internal heat exchanger (IHE-ORC), ORC with feed fluid heater (FFH-ORC), and ORC with both internal heat exchanger and feed fluid heater (IHE–FFH–ORC), powered by low-grade heat source were designed and modeled. These configuration enables to see the affects of internal heat exchanger and the feed fluid heater employed alone and together. Comparative thermodynamics and exergoeconomics analyses of these ORC configurations were performed and evaluated for seven selected working fluids.

Second, the impacts of the operational parameters, including evaporation temperature, condensation temperature, superheating degree, subcooling degree, expander and pump efficiencies on the thermodynamic and exergoeconomics performances of ORC system were conducted by utilizing Taguchi and ANOVA statistical analysis methods.

Third, a multi-objective optimization procedure by means of the Taguchi-Gray Relational Analysis method is performed to optimize the IHE–FFH–ORC configuration with the objective of maximum thermal efficiency, maximum exergy efficiency, minumum total system cost and minumum unit cost of produced electricity by using controllable factors, including working fluid, evaporator temperature, condenser temperature, turbine efficiency, pump efficiency, superheating temperature, and subcooling temperature. For the multi-objective optimization, Taguchi and ANOVA statistical analysis methods were used to obtain the control factors' effect degrees and ratios.

2. Methodology

2.1. System configurations

A schematic diagram of a basic organic Rankine cycle is shown in Fig. 1. This system includes four components: an evaporator, turbine (expander), condenser, and pump. Here, the heat required to operate the ORC is provided by the exhaust gas [46]. Waste heat enters the evaporator and transfers heat to the working fluid circulating in the cycle. The working fluid enters the expander at the evaporator pressure and expands isentropically to the condenser pressure. In the condenser, the working fluid condenses completely by giving its heat to the ambient air at constant pressure, and supercooling occurs. The fluid leaving the condenser enters the pump and is compressed isentropically, and its pressure reaches the evaporator pressure. The working fluid enters the evaporator and, utilizing the waste heat, completely evaporates, and superheating occurs. And then, the cycle continues like this.

Fig. 1.

The schematic diagram of basic ORC.

The schematic diagram of the ORC with an internal heat exchanger (IHE-ORC) is presented in Fig. 2. Unlike the basic ORC system, in this system, the high-temperature vapor phase organic fluid coming out of the turbine transfers its heat to the low-temperature liquid phase organic fluid coming from the pump. Hence, an internal heat recovery process is realized by employing IHE.

Fig. 2.

The schematic diagram of IHE-ORC.

One of the ORC configurations used to obtain energy from waste thermal energy is the regenerative (feed fluid heater) ORC. The schematic diagram of the FFH-ORC system is presented in Fig. 3. In the feed fluid heat exchanger, heat transfer occurs between the high-temperature vapor at the turbine outlet and the low-temperature liquid at the pump outlet to prevent energy loss [14,15,17]. In an FFH-ORC, vapor enters the expander (turbine) at evaporator pressure (state 5) and expands isentropically to an intermediate pressure. Meanwhile, some steam is taken and directed to the regenerator (state 6). The remaining steam continues to expand in the turbine, expanding isentropically to the condenser pressure (state 7). The fluid leaves the condenser (state 1). The condensed fluid enters pump-I, where its pressure increases, reaching the regenerator pressure (state 2). The liquid entering the FFH mixes with the vapor from the expander and exits the FFH as a saturated liquid (state 3). Then, the fluid enters pump-II and the pressure of the fluid rises to the evaporator pressure (state 4). The cycle is completed by the evaporation of the working fluid in the evaporator.

Fig. 3.

The schematic diagram of FFH-ORC.

Fig. 4 shows the schematic diagram of the IHE-FFH ORC system. Unlike the FFH-ORC system, there are two expanders in this cycle, a high-pressure expander, and a low-pressure expander. Some of the vapor coming out of the high-pressure expander goes to the FFH and the rest enters the low-pressure expander, and its pressure drops. It then enters the internal heat exchanger, where it transfers its heat to the fluid leaving the pump-I. Then it enters the regenerator and mixes with the fluid coming from the high-pressure expander and leaves the regenerator in the saturated liquid phase.

Fig. 4.

The schematic diagram of IHE-FFH ORC.

2.2. Energy analysis

The evaporator, turbine, condenser, and pump that make up the basic ORC system, as well as the regenerator and recuperator in the configurations of the ORC, are heat exchangers, and the inlet, outlet, and other operating conditions do not change during their operation. For this reason, they are called continuous-flow machines [47,48].

In a continuous flow open system, the total mass in the control volume does not change with time. In this case, the total mass flow entering the control volume must be equal to the total mass flow leaving the control volume as given in Eq. (1).

$$\sum {\dot{m}}_{in}=\sum {\dot{m}}_{out}$$ (1)

where, $\dot{m}$ is the mass flow rate, and the subscripts “in”, and “out” represent the inlet, and outlet, respectively. For an open system with a continuous flow where kinetic and potential energy changes are neglected, the conservation of energy equation is expressed by Eqs. (2), (3).

$${\dot{E}}_{in}={\dot{E}}_{out}$$ (2)

$$\dot{Q}-\dot{W}=\sum {\dot{m}}_{out}{h}_{out}-\sum {\dot{m}}_{in}{h}_{in}$$ (3)

The symbols $\dot{E}$, $\dot{Q}$, $\dot{W}$, and $h$ in these equations are energy per unit time (kW), heat rate (kW), power (kW), and specific enthalpy (kJ/kg), respectively.

The net power of an ORC system, as given in Eq. (4), is the difference between the total power produced by the plant and the total power supplied to the plant [42,49].

$${\dot{W}}_{net}={\dot{W}}_{out}-{\dot{W}}_{in}$$ (4)

The portion of the thermal energy entering a heat engine converted into net power is called thermal efficiency and is calculated by using Eq. (5) [[42], [43], [44], [45]].

$${\eta }_{th}={\dot{W}}_{net}/{\dot{Q}}_{ev}$$ (5)

2.3. Exergy analysis

The exergy balance of a steady state control volume is expressed by Eq. (6) [48].

$$0=\sum _j\left(1-\frac{T_0}{T_j}\right){\dot{Q}}_j-{\dot{W}}_{CV}+\sum _{in}\dot{m}ex-\sum _{out}\dot{m}ex-\dot{ED}$$ (6)

where, $T$, $ex$, and $\dot{ED}$ refer to temperature, specific exergy, and exergy destruction rate, respectively. Subscript “j” is the property value in case j. The subscript “cv” represents the control volume.

The physical exergy stream for flow whose kinetic and potential energy changes are neglected is given by Eq. (7) [48].

$$\dot{Ex}=\dot{m}\left[\left(h-h_0\right)-T_0\left(s-s_0\right)\right]$$ (7)

where subscript “0” indicates the dead state, which has the same temperature and pressure as the ambient conditions. The exergy efficiency of an ORC system is defined as the ratio of the exergy obtained in the system to the exergy supplied to the system and is calculated with Eq. (8) [[46], [47], [48], [49]].

$${\eta }_{ex}=\frac{Exergyinproducts}{totalexergyinput}=\frac{{\dot{W}}_{net}}{{\dot{Ex}}_{in}}$$ (8)

The second law of efficiency for a system, as given in Eq. (9), is the ratio of the actual thermal efficiency to the highest (reversible, r) thermal efficiency that can occur under the same conditions [47,48].

$${\eta }_{II}=\frac{{\eta }_{th}}{{\eta }_{th,r}}={\eta }_{th}{\left(1-\frac{T_{sink}}{T_{source}}\right)}^{-1}$$ (9)

The heat transfer rate, power, and exergy destruction rate realized by each subcomponent of the four ORC configurations developed were calculated using the equations given in Table 1. The thermal and exergy efficiency expressions of the designed ORC configurations are presented in Table 2.

Table 1.

Energy and exergy balance equations for the components of the ORC configurations.

Components	Energy Balance	Exergy Balance
Basic ORC
Pump	${\dot{W}}_p={\dot{m}}_{wf}\left(h_2-h_1\right)$	$\dot{{Ex}_1}+\dot{W_p}=\dot{{Ex}_2}+\dot{{ED}_p}$
Evaporator	${\dot{Q}}_{ev}={\dot{m}}_{wf}\left(h_3-h_2\right)$	$\dot{{Ex}_2}+\dot{{Ex}_5}=\dot{{Ex}_3}+\dot{{Ex}_6}+\dot{{ED}_{ev}}$
Expander	${\dot{W}}_{\mathit{exp}}={\dot{m}}_{wf}\left(h_3-h_4\right)$	${\dot{Ex}}_3={\dot{Ex}}_4+{\dot{W}}_{\mathit{exp}}+{\dot{ED}}_{\mathit{exp}}$
Condenser	${\dot{Q}}_c={\dot{m}}_{wf}\left(h_4-h_1\right)$	${\dot{Ex}}_4+{\dot{Ex}}_7={\dot{Ex}}_1+{\dot{Ex}}_8+{\dot{ED}}_c$
IHE-ORC
IHE	${\dot{Q}}_{IHE}={\dot{m}}_{wf}\left(h_2-h_3\right)={\dot{m}}_{wf}\left(h_6-h_5\right)$ ${\dot{Q}}_{IHE}={\epsilon }_{IHE}{C}_{\mathit{min}}\left(T_2-T_5\right)$	${\dot{Ex}}_2+{\dot{Ex}}_5={\dot{Ex}}_3+{\dot{Ex}}_6+{\dot{ED}}_{IHE}$
Pump	${\dot{W}}_p={\dot{m}}_{wf}\left(h_2-h_1\right)$	${\dot{Ex}}_1+{\dot{W}}_p={\dot{Ex}}_2+{\dot{ED}}_p$
Evaporator	${\dot{Q}}_{ev}={\dot{m}}_{wf}\left(h_4-h_3\right)$	$\dot{{Ex}_3}+\dot{{Ex}_7}=\dot{{Ex}_4}+\dot{{Ex}_8}+\dot{{ED}_{ev}}$
Expander	${\dot{W}}_{\mathit{exp}}={\dot{m}}_{wf}\left(h_4-h_5\right)$	${\dot{Ex}}_4={\dot{Ex}}_5+{\dot{W}}_{\mathit{exp}}+{\dot{ED}}_{\mathit{exp}}$
Condenser	${\dot{Q}}_c={\dot{m}}_{wf}\left(h_6-h_1\right)$	${\dot{Ex}}_6+{\dot{Ex}}_9={\dot{Ex}}_1+{\dot{Ex}}_{10}+{\dot{ED}}_c$
FFH-ORC
FFH	${\dot{m}}_{wf}X{h}_6+{\dot{m}}_{wf}\left(1-X\right)h_2={\dot{m}}_{wf}{h}_3$	$\dot{{Ex}_2}+\dot{{Ex}_6}=\dot{{Ex}_3}+{\dot{ED}}_{FFH}$
Pump-I	${\dot{W}}_{pI}={\dot{m}}_{wf}\left(1-X\right)\left(h_2-h_1\right)$	$\dot{{Ex}_1}+{\dot{W}}_{pI}=\dot{{Ex}_2}+{\dot{ED}}_{pI}$
Pump-II	${\dot{W}}_{pII}={\dot{m}}_{wf}\left(h_4-h_3\right)$	$\dot{{Ex}_3}+{\dot{W}}_{pII}=\dot{{Ex}_4}+{\dot{ED}}_{pII}$
Evaporator	${\dot{Q}}_b={\dot{m}}_{wf}\left(h_5-h_4\right)$	$\dot{{Ex}_4}+\dot{{Ex}_8}=\dot{{Ex}_5}+\dot{{Ex}_9}+{\dot{ED}}_{ev}$
Expander	${\dot{W}}_t={\dot{m}}_{wf}X\left(h_5-h_6\right)+{\dot{m}}_{wf}\left(1-X\right)\left(h_5-h_7\right)$	${\dot{Ex}}_5={\dot{Ex}}_6+{\dot{Ex}}_7+{\dot{W}}_t+{\dot{ED}}_{\mathit{exp}}$
Condenser	${\dot{Q}}_y={\dot{m}}_{wf}\left(1-X\right)\left(h_1-h_7\right)$	${\dot{Ex}}_7+{\dot{Ex}}_{10}={\dot{Ex}}_1+{\dot{Ex}}_{11}+{\dot{ED}}_c$
IHE–FFH–ORC
Pump-I	${\dot{W}}_{pI}={\dot{m}}_{lpe}\left(h_2-h_1\right)$	${\dot{Ex}}_1+{\dot{W}}_{p1}={\dot{Ex}}_2+{\dot{EY}}_{pI}$
IHE	${\dot{Q}}_{IHE}={\dot{m}}_{lpe}\left(h_3-h_2\right)={\dot{m}}_{lpe}\left(h_{10}-h_{11}\right)$ ${\dot{Q}}_{IHE}={\epsilon }_{IHE}{C}_{\mathit{min}}\left(T_2-T_{10}\right)$	${\dot{Ex}}_2+{\dot{Ex}}_{10}={\dot{Ex}}_3+{\dot{Ex}}_{11}+{\dot{ED}}_{IHE}$
FFH	${\dot{Q}}_{FFH}={\dot{m}}_{wf}{h}_4={\dot{m}}_{lpe}{h}_9+{\dot{m}}_{lpe}{h}_3$	${\dot{Ex}}_3+{\dot{Ex}}_9={\dot{Ex}}_4+{\dot{ED}}_{FFH}$
Pump-II	${\dot{W}}_{pII}={\dot{m}}_{ORÇ}\left(h_5-h_4\right)$	${\dot{Ex}}_4+{\dot{W}}_{p2}={\dot{Ex}}_5+{\dot{ED}}_{pII}$
Evaporator	${\dot{Q}}_b={\dot{m}}_{wf}\left(h_6-h_5\right)={\dot{m}}_{12}\left(h_{12}-h_{13}\right)$	${\dot{Ex}}_5+{\dot{Ex}}_{12}={\dot{Ex}}_6+{\dot{Ex}}_{13}+{\dot{ED}}_{ev}$
High-pressure expander	${\dot{W}}_{hpe}={\dot{m}}_{wf}\left(h_6-h_7\right)$	${\dot{Ex}}_6={\dot{Ex}}_7+{\dot{W}}_{hpe}+{\dot{ED}}_{hpe}$
Low-pressure expander	${\dot{W}}_{lpe}={\dot{m}}_{lpe}\left(h_8-h_{10}\right)$	${\dot{Ex}}_8={\dot{Ex}}_{10}+{\dot{W}}_{lpe}+{\dot{ED}}_{lpe}$
Condenser	${\dot{Q}}_c={\dot{m}}_{lpe}\left(h_{11}-h_1\right)={\dot{m}}_{14}\left(h_{15}-h_{14}\right)$	${\dot{Ex}}_{11}+{\dot{Ex}}_{14}={\dot{Ex}}_1+{\dot{Ex}}_{15}+{\dot{ED}}_c$

Table 2.

The thermal and exergy efficiency of the ORC configurations.

Efficiency	Thermal efficiency	Exergy efficiency
Basic ORC	${\eta }_{th}=\frac{{\dot{W}}_{\mathit{exp}}-{\dot{W}}_p}{{\dot{Q}}_{ev}}$	${\eta }_{ex}=\frac{{\dot{W}}_{net}}{{\dot{Ex}}_5-{\dot{Ex}}_6}$
IHE-ORC	${\eta }_{th}=\frac{{\dot{W}}_{\mathit{exp}}-{\dot{W}}_p}{{\dot{Q}}_{ev}}$	${\eta }_{ex}=\frac{{\dot{W}}_{net}}{{\dot{Ex}}_7-{\dot{Ex}}_8}$
FFH-ORC	${\eta }_{th}=\frac{{\dot{W}}_{\mathit{exp}}-{\dot{(W}}_{pI}+{\dot{W}}_{pII})}{{\dot{Q}}_{ev}}$	${\eta }_{ex}=\frac{{\dot{W}}_{net}}{{\dot{Ex}}_8-{\dot{Ex}}_9}$
IHE-FFH-ORC	${\eta }_{th}=\frac{{\dot{(W}}_{hpe}+{\dot{W}}_{lpe})-\left({\dot{W}}_{pI}+{\dot{W}}_{pII}\right)}{{\dot{Q}}_{ev}}$	${\eta }_{ex}=\frac{{\dot{W}}_{net}}{{\dot{Ex}}_{12}-{\dot{Ex}}_{13}}$

2.4. Exergoeconomic analysis

Exergoeconomic is an exergy-assisted cost reduction method that combines exergy and cost analysis [46]. Exergeconomic is also a powerful tool for understanding the interconnections between thermodynamics and economics, and therefore the behavior of an energy conversion plant in terms of cost. Exergy destruction and exergy losses are evaluated to evaluate the thermodynamic inefficiencies of these systems. Knowing the costs of such inefficiencies is very useful for increasing the economic efficiency of the system, i.e., reducing the costs of the final products produced by the system [23,30,38,50]. The Specific Exergy Costing method (SPECO), one of the thermoeconomic cost calculation methods available in the literature, was applied for the thermoeconomic analysis of ORC systems. The implementation of this method is carried out in three steps as follows:

• Step 1: All matter and energy flows that cross the boundaries of the considered component are identified and the exergy values associated with these flows are calculated.

• Step 2: Fuel and product definitions are made for each component of the system and auxiliary equations are formulated for each component.

• Step 3: Cost balance equations are developed for each component [23,51].

The cost balance equation for a stable system is formulated as given in Eq. (10) [52].

$${\dot{C}}_{P,tot}={\dot{C}}_{F,tot}+{\dot{Z}}_{tot}^{CI}+{\dot{Z}}_{tot}^{OM}$$ (10)

where ${\dot{C}}_P$ is the cost ratio associated with the product of the system, ${\dot{C}}_F$ is the ratio of the total expense to produce the product, i.e., the fuel cost ratio, ${\dot{Z}}^{CI}$ is the initial investment cost of the system, and ${\dot{Z}}^{OM}$ is the cost associated with the operation, maintenance and repair of the system. The average unit exergy cost for each flow is calculated with Eq. (11) [53].

$$c_i=\frac{{\dot{C}}_i}{{\dot{Ex}}_i}$$ (11)

where $\dot{C}$ and $c$ are expressed in $/h, and $/GJ, respectively. The exergy costs that occur with the exergy flow entering (${\dot{Ex}}_{in}$) and leaving (${\dot{Ex}}_{out}$) a system, power ($\dot{W}$), and heat transfer (${\dot{Ex}}_q$) are calculated with Eqs. (12), (13), (14), (15), respectively [52].

$${\dot{C}}_{in}=c_{in}{\dot{Ex}}_{in}$$ (12)

$${\dot{C}}_{out}=c_{out}{\dot{Ex}}_{out}$$ (13)

$${\dot{C}}_w=c_w\dot{W}$$ (14)

$${\dot{C}}_q=c_q{\dot{Ex}}_q$$ (15)

The $c_{in}$, $c_{out}$, $c_w$, and $c_q$ in these equations represent the unit cost of input flow, output flow, work, and heat, respectively. The exergy cost balance equation for each component of the system is given in Eq. (16) [52,54].

$$\sum {\dot{C}}_{out,k}+{\dot{C}}_{w,k}=\sum {\dot{C}}_{in,k}+{\dot{C}}_{q,k}+{\dot{Z}}_k$$ (16)

This equation states that the total cost of outgoing exergy transfers is equal to the total exergy cost of obtaining them (the cost of incoming exergy flows plus capital and other costs).

The ${\dot{Z}}_k$ in Eq. (16) is calculated by first calculating the capital investment and operating and maintenance costs associated with the kth component and then dividing the leveled values of these costs by the system uptime. ${\dot{Z}}_k$ for each component in the system is obtained with Eqs. (17), (18).

$${\dot{Z}}_k={\dot{Z}}_k^{CI}+{\dot{Z}}_k^{OM}$$ (17)

$${\dot{Z}}_k=\frac{{PEC}_{k}CRF\phi }{N3600}$$ (18)

In the above equation, ${PEC}_k$ is the purchased equipment cost, $\phi$ is the total operating and maintenance cost factor (1.06), $N$ is the operating time of the system in hours (7446 h), the $CRF$ is the capital recovery factor and is expressed by Eq. (19) [23].

$$CRF=\frac{i{\left(1+i\right)}^n}{{\left(1+i\right)}^n-1}$$ (19)

where $i$ is the interest rate and $n$ is the predicted life of the system’s constituents. In the thermoeconomic analysis, $i$ and $n$ were accepted as 10% and 20 years, respectively [23,55,56].

Various parameters have been defined to evaluate and compare the exergoeconomic performances of the system components. These are the average cost per unit exergy of the fuel ($c_{F,k}$), the average cost per unit exergy of the product ($c_{P,k}$), the relative cost difference ($r_k$), and the thermoeconomic factor ($f_k$). $c_{F,k}$, $c_{P,k}$, $r_k$, and $f_k$ for the kth component of a system are respectively computed by using Eqs. (20), (21), (22), (23) [52].

$$c_{F,k}=\frac{{\dot{C}}_{F,k}}{{\dot{Ex}}_{F,k}}$$ (20)

$$c_{P,k}=\frac{{\dot{C}}_{P,k}}{{\dot{Ex}}_{P,k}}$$ (21)

$$r_k=\frac{c_{P,k}-c_{F,k}}{c_{F,k}}$$ (22)

$$f_k=\frac{{\dot{Z}}_k}{{\dot{Z}}_k+{\dot{C}}_{D,k}}$$ (23)

The ${\dot{C}}_{D,k}$ in Eq. (23) is the cost of exergy destruction and is expressed as follows [57].

$${\dot{C}}_{D,k}=c_{F,k}{\dot{E}}_{D,k}$$ (24)

In Eq. (24), ${\dot{E}}_{D,k}$ represents the exergy destruction rate of the system component. The total system cost rate is calculated with Eq. (25).

$${\dot{C}}_{sys}=\sum _k{\dot{Z}}_k+\sum _k{\dot{C}}_{D,k}+{\dot{C}}_{L,k}$$ (25)

where ${\dot{C}}_L$ is the cost ratio associated with the exergy loss and the cost ratio is neglected as the exergy losses in the system are neglected [37].

$C_{el}$ is another important parameter in cost analysis. This value expresses the unit cost of electricity produced by ORC and is calculated with Eq. (26) [55,58].

$$C_{el}=\frac{{PEC}_{tot}CRF\phi }{{\dot{W}}_{net}N}$$ (26)

In the above equation, ${PEC}_{tot}$ denotes the total purchased equipment cost of ORC components and ${\dot{W}}_{net}$ denotes the net power produced by ORC.

The payback period of the designed ORC system is calculated by Eq. (27) [55].

$$PB=\frac{\log \frac{\left({\dot{W}}_{net}N{c}_{el}\right)-{PEC}_{top}\left(\phi -1\right)}{\left({\dot{W}}_{net}N{c}_{el}\right)-{PEC}_{top}\left(\phi -1\right)-\left(i{PEC}_{top}\right)}}{\log \left(1+i\right)}$$ (27)

In the above equation, $c_{el}$ represents the unit price of electricity and it is taken as 0.15 $/kWh in the analysis [58].

Cost balance and auxiliary equations are written for each component of the ORC configurations. Obtained equations are presented in Table 3.

Table 3.

Cost balance and auxiliary equations of ORC configurations.

Components	Cost Balance	Auxiliary equation
Basic ORC
Pump	$c_1\dot{{Ex}_1}+c_p\dot{W_p}+{\dot{Z}}_p=c_2\dot{{Ex}_2}$	$c_p=c_{\mathit{exp}}$
Evaporator	$c_2\dot{{Ex}_2}+c_5\dot{{Ex}_5}+{\dot{Z}}_{ev}=c_3\dot{{Ex}_3}+c_6\dot{{Ex}_6}$	$c_5=c_6$
Expander	$c_3\dot{{Ex}_3}+{\dot{Z}}_{\mathit{exp}}=c_4\dot{{Ex}_4}+c_{\mathit{exp}}{\dot{W}}_{\mathit{exp}}$	$c_3=c_4$
Condenser	$c_4{\dot{Ex}}_4+c_7{\dot{Ex}}_7+{\dot{Z}}_c=c_1{\dot{Ex}}_1+c_8{\dot{Ex}}_8$	$c_4=c_1,c_7=0$
IHE-ORC
IHE	$c_2\dot{{Ex}_2}+c_5\dot{{Ex}_5}+{\dot{Z}}_{IHE}=c_3\dot{{Ex}_3}+c_6\dot{{Ex}_6}$	$c_5=c_6$
Pump	$c_1\dot{{Ex}_1}+c_p\dot{W_p}+{\dot{Z}}_p=c_2\dot{{Ex}_2}$	$c_p=c_{\mathit{exp}}$
Evaporator	$c_3\dot{{Ex}_3}+c_7\dot{{Ex}_7}+{\dot{Z}}_{ev}=c_4\dot{{Ex}_4}+c_8\dot{{Ex}_8}$	$c_7=c_8$
Expander	$c_4\dot{{Ex}_4}+{\dot{Z}}_{\mathit{exp}}=c_5\dot{{Ex}_5}+c_{\mathit{exp}}{\dot{W}}_{\mathit{exp}}$	$c_4=c_5$
Condenser	$c_6{\dot{Ex}}_6+c_9{\dot{Ex}}_9+{\dot{Z}}_c=c_1{\dot{Ex}}_1+c_{10}{\dot{Ex}}_{10}$	$c_6=c_1,c_9=0$
FFH-ORC
FFH	$c_6\dot{{Ex}_6}+c_2\dot{{Ex}_2}+{\dot{Z}}_{FFH}=c_3\dot{{Ex}_3}$
Pump-I	$c_1\dot{{Ex}_1}+c_{pI}{\dot{W}}_{pI}+{\dot{Z}}_{pI}=c_2\dot{{Ex}_2}$	$c_{pI}=c_{\mathit{exp}}$
Pump-II	$c_3\dot{{Ex}_3}+c_{pII}{\dot{W}}_{pII}+{\dot{Z}}_{pII}=c_4\dot{{Ex}_4}$	$c_{pII}=c_{\mathit{exp}}$
Evaporator	$c_4\dot{{Ex}_4}+c_8\dot{{Ex}_8}+{\dot{Z}}_{ev}=c_5\dot{{Ex}_5}+c_9\dot{{Ex}_9}$	$c_8=c_9$
Expander	$c_5\dot{{Ex}_5}+{\dot{Z}}_{\mathit{exp}}=c_6\dot{{Ex}_6}+c_7\dot{{Ex}_7}+c_{\mathit{exp}}{\dot{W}}_{\mathit{exp}}$	$c_6=c_5,c_7=c_5$
Condenser	$c_7{\dot{Ex}}_7+c_{10}{\dot{Ex}}_{10}+{\dot{Z}}_c=c_1{\dot{Ex}}_1+c_{11}{\dot{Ex}}_{11}$	$c_7=c_1,c_{10}=0$
IHE–FFH–ORC
Pump-I	$c_1{\dot{Ex}}_1+c_{pI}{\dot{W}}_{pI}+{\dot{Z}}_{pI}=c_2{\dot{Ex}}_2$	$c_{pI}=c_{hpe}$
IHE	$c_{10}{\dot{Ex}}_{10}+c_2{\dot{Ex}}_2+{\dot{Z}}_{IHE}=c_{11}{\dot{Ex}}_{11}+c_3{\dot{Ex}}_3$	$c_{10}=c_{11}$
FFH	$c_3{\dot{Ex}}_3+c_9{\dot{Ex}}_9+{\dot{Z}}_{FFH}=c_4{\dot{Ex}}_4$
Pump-II	$c_4{\dot{Ex}}_4+c_{pII}{\dot{W}}_{pII}+{\dot{Z}}_{pII}=c_5{\dot{Ex}}_5$	$c_{pII}=c_{lpe}$
Evaporator	$c_5{\dot{Ex}}_5+c_{12}{\dot{Ex}}_{12}+{\dot{Z}}_{ev}=c_6{\dot{Ex}}_6+c_{13}{\dot{Ex}}_{13}$	$c_{12}=c_{13}$
High-pressure expander	$c_6{\dot{Ex}}_6+{\dot{Z}}_{hpe}=c_7{\dot{Ex}}_7+c_{hpe}{\dot{W}}_{hpe}$	$c_6=c_7,c_7=c_8,c_7=c_9$
Low-pressure expander	$c_8{\dot{Ex}}_8+{\dot{Z}}_{lpe}=c_{10}{\dot{Ex}}_{10}+c_{lpe}{\dot{W}}_{lpe}$	$c_{10}=c_8$
Condenser	$c_{11}{\dot{Ex}}_{11}+c_{14}{\dot{Ex}}_{14}+{\dot{Z}}_c=c_1{\dot{Ex}}_1+c_{15}{\dot{Ex}}_{15}$	$c_{11}=c_1,c_{14}=0$

For thermoeconomic analysis according to the SPECO method, after writing the cost balance and auxiliary equations for each component of the ORC configurations, the initial investment, operation, and maintenance cost values of the components should be calculated according to Eq. (18). The purchased equipment cost (${PEC}_k$), is calculated with the equations in Table 4 for each component. Since the initial investment cost of the three-way valve in the IHE–FFH–ORC system is much lower than the other components of the cycle, this value is neglected in the calculations.

Table 4.

Initial investment cost functions of ORC system components.

Components	Initial investment cost function ($)	Refs.
Pump	${PEC}_p=3540{\left(\dot{W_p}\right)}^{0.71}$	[33,45]
Evaporator	${PEC}_{ev}=130{\left(A_{ev}/0.093\right)}^{0.78}$	[33]
Expander	${PEC}_{\mathit{exp}}=4405{\left({\dot{W}}_{\mathit{exp}}\right)}^{0.7}$	[33]
Condenser	${PEC}_c=2143{\left(A_c\right)}^{0.514}$	[56]
IHE	${PEC}_{IHE}=2681{\left(A_{IHE}\right)}^{0.59}$	[56,57]
FFH	${PEC}_{FFH}=280.3{\left({\dot{m}}_{FFH}\right)}^{0.67}$	[52]

Evaporator, condenser, and IHE in the ORC system are assumed to be shell-tube type. The amount of heat transfer realized in the heat exchanger is modeled by Eq. (28), depending on the logarithmic temperature difference (${\Delta T}_k^{lm}$) and the total heat transfer coefficient ($U_k$) expressions according to the LMTD method.

$${\dot{Q}}_k=U_k{A}_k{\Delta T}_k^{lm}$$ (28)

For heat exchangers in ORC configurations, the logarithmic temperature difference is calculated by Eq. (29).

$${\Delta T}_k^{lm}=\frac{\left(T_{hot,in}-T_{cold,out}\right)-\left(T_{hot,out}-T_{cold,in}\right)}{\mathit{ln}\left(\frac{T_{hot,in}-T_{cold,out}}{T_{hot,out}-T_{cold,in}}\right)}$$ (29)

where, $T_{hot,in}$ and $T_{hot,out}$ represent the inlet and outlet temperature of the hot fluid to the heat exchanger, respectively. The inlet and outlet temperatures of the cold fluid in the heat exchanger are indicated by $T_{cold,in}$ and $T_{cold,out}$, respectively. The total heat transfer coefficient values taken for the evaporator, condenser, and IHE in the analysis are presented in Table 5.

Table 5.

Heat transfer coefficient of the heat exchangers.

Components	$\mathit{U}$ (kW/m2K)	Refs.
Evaporator	0.9	[59,60]
Condenser	1.1	[59,60]
IHE	0.7	[61]

2.5. The assumptions and input values in the analysis

The following simplifications and assumptions are considered for the analysis of ORC configurations [43,44].

• •Each component of the ORC configurations performs in a steady-state condition.
• •Negligible heat and friction losses occurred in the heat exchangers and pipes of the ORC configurations.
• •There are negligible changes in kinetic and potential energy.
• •Ambient temperature and pressure are 293.15 K and 101 kPa, respectively.
• •The hot waste fluid is air and has a pressure of 101 kPa and a mass flow of 10 kg/s.
• •The condenser is air-cooled and the pressure of the cold air entering the condenser is 101 kPa and its mass flow rate is 20 kg/s.

Other operating conditions and input values for the analysis are shown in Table 6.

Table 6.

Operating conditions and input values.

Parameter	Value	Unit	Refs.
Evaporation temperature	130	°C	[62]
Condensation temperature	30	°C	[63]
Evaporator capacity (${\dot{Q}}_{ev}$)	100	kW	[62]
Expander isentropic efficiency (${\eta }_{\mathit{exp}}$)	0.80		[51]
Pump isentropic efficiency (${\eta }_p$)	0.80		[51]
Pinch-point temperature difference in evaporator and condenser (${\Delta T}_{pp}$)	5	°C	[64]
Overheating in the evaporator	5	°C	[40]
Subcooling in the condenser	5	°C	[40]
Internal heat exchanger effectiveness (${\epsilon }_{IHE}$)	0.80		[65]

2.6. Working fluid selection

The working fluid properties that will circulate in the system play an important role in the performance of the ORC system. In the study, seven candidate refrigerants, R113, R141b, R123, R245fa, R114, R600, and R600a, were selected depending on the heat source temperature and fluid properties. Selected organic fluids are among the most recommended fluids in low-temperature ORC applications [16,30]. Thermo-physical properties and environmental effects of these evaluated fluids are presented in Table 7 [30,66].

Table 7.

Thermo-physical properties and environmental impact factors of the selected fluids.

Fluids	Molecular mass	Formula	Boiling temperature	Critical temperature	Critical pressure	ODP	GWP 100 yr
	g/mol		°C	°C	MPa
R113	187.38	C2Cl3F3	47.59	213.95	3.39	1.00	6130.0
R141b	116.95	C2Cl2FH3	32.06	204.35	4.21	0.00	713.0
R123	152.93	C2Cl2F3H	27.78	183.68	3.66	0.02	77.0
R245fa	134.05	C3F5H3	15.18	154.05	3.65	0.00	1030.0
R114	170.92	C2Cl2F4	3.79	145.68	3.26	1.00	3.9
R600	58.12	C4H10	−0.52	152.01	3.80	0.00	4.0
R600a	58.12	C4H10	−11.68	134.70	3.63	0.00	3.0

2.7. Taguchi experiment design and Analysis of Variance method (ANOVA)

Taguchi’s Experimental Design and Analysis of Variance (ANOVA) offers a systematic approach to identify optimized control factors and independent variables to ensure the best performance of the system. Many engineering problems solved using this method are in the literature [[67], [68], [69]]. The Taguchi method finds the optimal solution for an existing problem using orthogonal arrays. Orthogonal arrays used here are special arrays that reduce the number of experiments to be performed compared to the traditional experimental design. The number and levels of independent variables determined in the problem determine which orthogonal array will be used. In the Taguchi Experiment Design, the working fluid type (A), evaporator temperature (B), condenser temperature (C), expander efficiency (D), pump efficiency (E), superheating temperature (F) and subcooling temperature (G) seven control factors were selected. Among these factors, 6 levels (6¹) were taken for the working fluid type (A) factor and 3 levels (3⁶) for the other factors (Table 8).

Table 8.

Control factors and levels used in the analysis.

Symbols	Control Factors	1	2	3	4	5	6
A	Working fluid	R113	R141b	R123	R245fa	R114	R600
B	Evaporation temperature (°C)	100.0	130.0	145.0
C	Condensation temperature (°C)	25.0	35.0	45.0
D	Expander efficiency	0.7	0.8	0.9
E	Pump efficiency	0.7	0.8	0.9
F	Superheating (°C)	2.0	5.0	10.0
G	Subcooling (°C)	2.0	5.0	10.0

After determining the number of experiments in Taguchi analysis, the next step is to calculate the signal-to-noise ($S/N$) ratio for each experiment and each output parameter. In the $S/N$ ratio, the signal expresses the desired true value, while the noise expresses the undesired factors in the measured values. In Taguchi’s analysis, the $S/N$ ratio is a measure used in science and engineering to compare the level of the desired signal with the level of background noise [41,66]. The $S/N$ ratio operates mainly in three conditions: smaller better, nominal better, and larger better. Depending on the requirement of the output performance parameter, the corresponding $S/N$ ratio condition is selected. For the smaller the better ($SB$) condition, and the larger the better ($LB$) condition, the $S/N$ ratios are calculated by using Eqs. (30), (31), respectively [[67], [68], [69], [70]].

$$S/N=-10{\log }_{10}\left(\frac{1}{n}\sum _{i=1}^n{y_i}^2\right)$$ (30)

$$S/N=-10{\log }_{10}\left(\frac{1}{n}\sum _{i=1}^n\frac{1}{{y_i}^2}\right)$$ (31)

where, $n$ is the number of experiments, and $y_i$ defines the output value for the $i$ th performance parameter. The selection of the appropriate orthogonal array for the designed experiment is obtained by calculating the degree of freedom ($DOF$) of each factor determined in the analysis. The $DOF$ value for each factor is 1 minus the level of each factor [45]. There are 6 levels of the selected working fluid in the analysis. $DOF$ is 5. The other six factors have 3 levels and hence the $DOF$ value of 2. In this case, the total degree of freedom (${DOF}_{tot}$) is 17. Therefore, the Taguchi (L18) orthogonal array was chosen for the analysis.

In this study, four output parameters are considered. These are thermal efficiency (${\eta }_{th}$), exergy efficiency (${\eta }_{ex}$), total system cost (${\dot{C}}_{sys}$), and the unit cost of electricity produced ($C_{el}$). For the maximization of the ${\eta }_{th}$, and ${\eta }_{ex}$ of the ORC system from the output parameters, the $LB$ condition is applied in calculating the $S/N$ ratio. The $SB$ condition is chosen for minimizing the ${\dot{C}}_{sys}$, and $C_{el}$.

Another statistical method used in the analysis is the Analysis of Variance method (ANOVA). The ANOVA is used to determine the extent of the effects of the determined control factors on the output parameter and the objective function. In addition, the order of effectiveness of the parameters obtained by the Taguchi method is compared with the ANOVA results to control the reliability [71]. Minitab and Microsoft Excel software was used to perform the statistical analysis.

2.8. Grey Relational Analysis (GRA)

The traditional Taguchi method gives the optimum results of the specified output parameters one by one. However, it is not a suitable method to obtain the optimum solution to a multi-objective optimization problem. Taguchi-Grey Relational Analysis ($GRA$) technique, which is a hybrid approach, is used to optimize a multi-objective problem [45].

In this method, firstly, the experimental data is normalized between 0 and 1, and the matrix formed is called the gray relational generation matrix. The Gray Relational Coefficient ($GRC$) is calculated from the normalized matrix to represent the correlation between desired and actual experimental data. Finally, the overall Gray Relational Grade ($GRG$) is calculated by considering the weight factors for the output parameters in the objective function. Thus, the multi-response problem turns into a single-response optimization problem. Finally, optimal values are determined by performing Taguchi and ANOVA analysis [72].

In this study, the objective function that maximizes the values of the system, There are three different criteria for normalizing the output parameters in the GRA method. These are smaller better ($SB$), larger better ($LB$), and nominal best ($NB$) [72,73]. For ${\eta }_{th}$, and ${\eta }_{ex}$, based on the $LB$ criterion, with Eq. (32); for the ${\dot{C}}_{sys}$, and $C_{el}$ normalization was performed with Eq. (33) by taking the $SB$ criterion.

$$y_i\left(k\right)=\frac{x_i^0\left(k\right)-\mathit{min}{x}_i^0\left(k\right)}{\mathit{max}{x}_i^0\left(k\right)-\min x_i^0\left(k\right)}$$ (32)

$$y_i\left(k\right)=\frac{\mathit{max}{x}_i^0\left(k\right)-x_i^0\left(k\right)}{\mathit{max}{x}_i^0\left(k\right)-\min x_i^0\left(k\right)}$$ (33)

In these equations, $y_i\left(k\right)$ is the normalization value of the gray relational generation. $\mathit{max}{x}_i^0\left(k\right)$, and $\mathit{min}{x}_i^0\left(k\right)$ represent the largest and smallest values of $x_i\left(k\right)$ for the $k$ th response, respectively. The symbols $i$ and $k$ represent the number of experiments and the number of responses, respectively [[72], [73], [74]].

After the data are normalized, the gray correlation coefficient (${\xi }_i$), which relates the ideal and actual normalized experimental results, is calculated from Eq. (34) [45,[73], [74], [75]].

$${\xi }_i\left(k\right)=\frac{{\Delta }_{\mathit{min}}+\varnothing {\Delta }_{\mathit{max}}}{{\Delta }_{0i}\left(k\right)+\varnothing {\Delta }_{\mathit{max}}}$$ (34)

$${\Delta }_{0i}\left(k\right)=\Vert y_0\left(k\right)-y_i\left(k\right)\Vert$$ (35)

$${\Delta }_{\mathit{max}}=\underset{\forall j\mathrm{ℇ}i}{\max }\underset{\forall k}{\max }\Vert y_0\left(k\right)-y_i\left(k\right)\Vert$$ (36)

$${\Delta }_{\mathit{min}}=\underset{\forall j\mathrm{ℇ}i}{\min }\underset{\forall k}{\min }\Vert y_0\left(k\right)-y_i\left(k\right)\Vert$$ (37)

In Eq (35), ${\Delta }_{0i}\left(k\right)$ is the deviation between $y_0\left(k\right)$ and $y_i\left(k\right)$. Δ_max and Δ_min can be calculated by using Eqs. (36), (37), respectively. $\varnothing$ is in the range of 0–1 and is defined as the discriminating coefficient. In this study, $\varnothing$ was taken as 0.5 [45,73,76,77]. Gray Relational Grade (${\gamma }_i$) with normalized weighting factor is calculated by Eq. (38).

$${\gamma }_i=\frac{1}{n}\sum _{k=1}^n{w}_k{\xi }_i\left(k\right)$$ (38)

where high ${\gamma }_i$ indicates a strong correlation between $y_0\left(k\right)$ and $y_i\left(k\right)$. If the two series being compared have the same values, ${\gamma }_i=1$. That is, ${\gamma }_i$ is used to determine the closeness of the compared serial value to the reference serial value. Also in the above equation, $\sum _{k=1}^n{w}_k=1$ where $w_k$ is the normalized weighting factor for each response. The weight factor expresses the effect ratio of each output parameter on the objective function to reduce the multi-objective optimization problem to a single equation and is obtained with Eq. (39) [45,75].

$$w_i=\frac{{\sum }_{j=1}^p{Delta}_{i,j}}{\sum _{i=1}^t{\sum }_{j=1}^p{Delta}_{i,j}}$$ (39)

where $t$ is the number of responses, $p$ is the number of parameters, and $Delta$ is the range of $S/N$.

2.9. Validation of the simulation models

The study published by Safarian and Aramoun [21] was used to test the accuracy of the simulations of the designed ORC configurations developed with the Engineering Equation Solver program. In the reference study, the hot fluid source temperature is 300 °C, the evaporator heat rate is 252 kW, the condenser temperature is 25 °C, the evaporator pressure is 2500 kPa, the turbine efficiency is 0.80, the pump efficiency is 0.85 and the working fluid is R113. In addition, the regenerator pressure in the FFH-ORC system was accepted as 1000 kPa. Simulations developed in EES software for basic ORC, IHE-ORC and FFH-ORC systems were revised according to the assumptions made in the reference model. The results obtained are presented in Table 9.

Table 9.

Model validation for basic ORC, IHE-ORC, and FFH-ORC systems.

Parameters	Basic ORC [21]	Present study	Diff. Ratio (%)	IHE-ORC [21]	Present study	Diff. Ratio (%)	FFH-ORC [21]	Present study	Diff. Ratio (%)
${\eta }_{th}(\%)$	19.46	19.68	−1.13	21.5	22.0	−2.32	22.00	22.27	−1.23
${\dot{W}}_{net}\left(kW\right)$	49.04	49.60	−1.14	54.3	55.4	−2.02	55.53	56.11	−1.04
${\dot{m}}_{wf}\left(kg/s\right)$	1.06	1.05	0.94	1.15	1.17	−1.74	1.99	1.98	0.50

As can be clearly seen from the table, the results obtained for each configuration are very close to the results obtained in the reference study and the error rate is very low.

3. Results and discussion

3.1. Thermodynamic and exergoeconomic analysis results

By taking the operating conditions and input values in Table 6, energy, exergy and exergoeconomics analyses of ORC configurations were performed. The unit exergy cost of the low-grade waste heat supplied to the system is accepted as 4.00 $/GJ, and the unit exergy cost and exergy of the air used in the air-cooled condenser of the system is accepted as 0.00 $/GJ and 0.00 kW [52]. For the evaluation of systems, thermal efficiency (${\eta }_{th}$), exergy efficiency (${\eta }_{ex}$), net power obtained from the system (${\dot{W}}_{net}$), exergy input to the system (${\dot{Ex}}_{in}$), total exergy destruction rate (${\dot{ED}}_{tot}$), the mass flow rate of working fluid (${\dot{m}}_{wf})$, the total system cost (${\dot{C}}_{sys}$), the unit cost of electricity produced ($C_{el}$), and the payback period of the plant ($PB$) were calculated. The results obtained are presented in Table 10.

Table 10.

Energy, exergy and exergoeconomic analysis results of ORC configurations.

Fluids	${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{W}}}_{\mathit{n}\mathit{e}\mathit{t}}$	${\dot{\mathit{E}\mathit{x}}}_{\mathit{i}\mathit{n}}$	${\dot{\mathit{E}\mathit{D}}}_{\mathit{t}\mathit{o}\mathit{t}}$	${\dot{\mathit{m}}}_{\mathit{w}\mathit{f}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$	${\mathit{C}}_{\mathit{e}\mathit{l}}$	$\mathit{P}\mathit{B}$
	$(\%)$	$(\%)$	(kW)	$\left(kW\right)$	$\left(kW\right)$	(kg/s)	($/h)	$\left(\$/kWh\right)$	$\left(years\right)$
Basic ORC
R113	15.00	53.14	15.00	28.23	12.06	0.46	0.856	0.042	3.2
R141b	15.48	54.79	15.48	28.26	11.69	0.34	0.912	0.044	3.3
R123	15.08	53.54	15.08	28.17	11.96	0.42	0.886	0.044	3.4
R245fa	14.11	50.39	14.11	28.01	12.75	0.38	0.914	0.047	3.7
R114	12.89	46.15	12.89	27.93	13.85	0.54	1.057	0.053	4.4
R600	14.09	50.32	14.09	28.01	12.76	0.20	0.938	0.048	3.8
R600a	13.36	48.05	13.36	27.80	13.30	0.22	0.990	0.053	4.3
IHE-ORC
R113	17.22	60.73	17.22	28.36	10.11	0.53	1.013	0.047	3.7
R141b	16.62	58.65	16.62	28.33	10.69	0.36	1.047	0.049	3.9
R123	16.74	59.23	16.74	28.27	10.50	0.47	1.035	0.049	3.9
R245fa	15.82	56.32	15.82	28.09	11.24	0.43	1.069	0.052	4.3
R114	14.95	53.33	14.95	28.04	12.03	0.63	1.243	0.058	5.0
R600	15.89	56.55	15.89	28.10	11.17	0.23	1.104	0.054	4.5
R600a	14.85	53.32	14.85	27.86	11.96	0.25	1.157	0.059	5.1
FFH-ORC
R113	16.30	57.27	16.30	28.45	10.58	0.72	0.959	0.044	3.4
R141b	17.14	60.40	17.14	28.38	9.92	0.45	0.987	0.044	3.3
R123	16.92	59.73	16.92	28.32	10.03	0.57	0.961	0.044	3.4
R245fa	15.90	56.41	15.90	28.18	10.94	0.47	0.980	0.047	3.6
R114	14.48	51.49	14.48	28.12	12.27	0.65	1.124	0.052	4.3
R600	15.45	54.90	15.45	28.14	11.42	0.23	0.986	0.048	3.8
R600a	14.21	50.72	14.21	28.01	12.60	0.24	1.026	0.052	4.3
IHE-FFH-ORC
R113	18.07	63.49	18.07	28.46	10.01	0.57	0.909	0.041	3.0
R141b	18.04	63.34	18.04	28.49	10.07	0.41	0.936	0.041	3.1
R123	17.97	63.25	17.97	28.41	10.06	0.54	0.937	0.042	3.2
R245fa	17.15	60.67	17.15	28.26	10.73	0.51	0.975	0.045	3.5
R114	16.79	59.39	16.79	28.27	11.09	0.74	1.076	0.047	3.7
R600	17.13	60.59	17.13	28.27	10.76	0.26	1.014	0.046	3.6
R600a	16.33	57.60	16.33	28.36	11.63	0.31	1.089	0.051	4.1

As can be seen clearly from Table 10, the basic ORC system has lower thermal efficiency (${\mathit{\eta }}_{\mathit{t}\mathit{h}}$), exergy efficiency (${\mathit{\eta }}_{\mathit{e}\mathit{x}}$) and net power obtained from the system (${\dot{\mathit{W}}}_{\mathit{n}\mathit{e}\mathit{t}}$) for all fluids among the four ORC configurations. Meanwhile, it has the highest total exergy destruction rates (${\dot{\mathit{E}\mathit{D}}}_{\mathit{t}\mathit{o}\mathit{t}}$) compare to other ORC configurations. On the other hand, the exergoeconomic parameters ((${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$), (${\mathit{C}}_{\mathit{e}\mathit{l}}$), and ($\mathit{P}\mathit{B}$)) of the basic ORC system lower than the IHE-ORC and FFH-ORC ones. This is caused by the extra cost of inclusion of IHE and FFH into the system. They improve the system efficiencies and the net power production but increase the total system cost (${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$). Comparing the IHE-ORC and FFH-ORC performances, IHE-ORC presents higher increase on the system efficiencies as well as the total cost of the system. Therefore, exergoeceonomic parameters of IHE-ORC are worst comparing to the other ORC configurations. It is interesting to see that the IHE–FFH–ORC system among the four configerations shows better performance with respect to all considered parameters. Comparing to the basic ORC, the IHE–FFH–ORC system have about 17–22% higher ${\mathit{\eta }}_{\mathit{t}\mathit{h}}$, ${\mathit{\eta }}_{\mathit{e}\mathit{x}}$, and ${\dot{\mathit{W}}}_{\mathit{n}\mathit{e}\mathit{t}}$ values and about 2–7% lower ${\mathit{C}}_{\mathit{e}\mathit{l}}$, and $\mathit{P}\mathit{B}$ values. This means that inclusion of both IHE and FFH into the system significantly improves the system performance and reduces the total exergy destruction rate (${\dot{\mathit{E}\mathit{D}}}_{\mathit{t}\mathit{o}\mathit{t}}$) eventhough this increases the total system cost (${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$) about 2–8%.

As it is clearly seen from Table 10, the minimum total system cost rate (${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$) is calculated as 0.856 $/h for basic ORC. It was followed by IHE–FFH–ORC with 0.909 $/h, FFH-ORC with 0.959 $/h, and FFH-ORC with 1.013 $/h. The lowest values of the unit cost of electricity produced and payback period were obtained for the IHE–FFH–ORC system, with ${\mathit{C}}_{\mathit{e}\mathit{l}}$ calculated as 0.041 $/kWh and $\mathit{P}\mathit{B}$ as 3.0 years. The maximum ${\mathit{C}}_{\mathit{e}\mathit{l}}=\mathbf{0.059}\$/\mathit{k}\mathit{W}\mathit{h}$ and $\mathit{P}\mathit{B}=\mathbf{5.1}\mathit{y}\mathit{e}\mathit{a}\mathit{r}\mathit{s}$ values within the four ORC configurations were obtained for the IHE-ORC.

Considering the working fluids impacts on the system performances, the performances of the R113, R141b and R123 are notable better than other fluids for the all ORC configurations. The performance order of the working fluids stays almost same for the ORC configurations. The worst performances were observed with the R600a for all the cases considered. Considering ODP and GWP values in Table 7, R123 may be chosen as working fluid because of smaller environmental impact values.

According to the SPECO method, the fuel and product unit exergy cost was obtained with each component’s fuel and product approach. At the same time, the relative cost difference, exergoeconomic factor, cost rate of exergy destruction, capital cost rate, and exergy destruction rate of all system components was calculated. Accordingly, the exergoeconomic parameters mentioned for each component of the ORC configurations with R123 refrigerant as working fluid were summarized in Table 11. The high value of the relative cost difference means that the unit exergy cost of the product produced by the component is higher than the unit exergy cost of the fuel used. From this point of view, the maximum $r$ value belongs to the condenser in all ORC systems. It is possible to decrease the $r$ value by increasing the exergy efficiency of this component [52]. In the third and fourth columns of Table 11, the exergy destruction rate ($\dot{ED}$) and exergy destruction cost rate (${\dot{C}}_D$) of the components are given. As it is clearly seen from the table, the maximum exergy destruction occurred in the evaporator in basic ORC, IHE-ORC and FFH-IHE-ORC, while in the FFH-ORC cycle, it took place in the expander. In basic ORC, IHE-ORC and FFH-IHE-ORC systems, the maximum exergy destruction occurred in the evaporator, while in the FFH-ORC cycle, it took place in the expander. The highest exergy destruction cost was 0.091 $/h in the expander in the IHE-ORC system.

Table 11.

Exergoeconomic parameters of the ORC configurations.

Components	${\mathit{c}}_{\mathit{f}}$	${\mathit{c}}_{\mathit{p}}$	$\dot{\mathit{E}\mathit{D}}$	${\dot{\mathit{C}}}_{\mathit{D}}$	$\mathit{r}$	$\mathit{f}$	$\dot{\mathit{Z}}$
	$\left(\$/GJ\right)$	$\left(\$/GJ\right)$	$\left(kW\right)$	$\left(\$/h\right)$	$(\%)$	$(\%)$	$\left(\$/h\right)$
Basic ORC
Pump	16.63	45.18	0.09	0.006	171.7	85.83	0.0347
Evaporator	4.00	5.58	6.16	0.089	39.41	28.92	0.0361
Expander	6.27	16.63	3.42	0.077	165.1	86.69	0.5034
Condenser	6.27	40.78	2.23	0.051	550.0	63.31	0.0887
IHE-ORC
IHE	6.67	35.09	0.40	0.009	425.7	85.20	0.0551
Pump	16.84	44.71	0.11	0.006	165.5	85.30	0.0374
Evaporator	4.00	5.22	4.47	0.064	30.51	38.42	0.0402
Expander	6.67	16.84	3.80	0.091	152.3	85.58	0.5415
Condenser	6.67	58.12	1.72	0.041	770.8	78.13	0.1481
FFH-ORC
FFH	7.28	10.94	1.76	0.046	50.32	6.52	0.0032
Pump-I	16.30	55.62	0.03	0.002	241.3	89.90	0.0142
Pump-II	16.30	42.64	0.09	0.005	161.6	87.82	0.0365
Evaporator	4.00	4.99	2.39	0.034	24.85	62.83	0.0583
Expander	6.28	16.30	3.81	0.086	159.5	86.42	0.5479
Condenser	6.28	32.11	1.95	0.044	411.3	65.5	0.0839
IHE-FFH-ORC
IHE	5.55	9.60	0.40	0.008	73.0	10.49	0.0009
FFH	7.97	9.48	0.39	0.003	18.96	21.57	0.0031
Pump-I	16.93	58.25	0.02	0.001	244.0	90.09	0.0124
Pump-II	17.46	44.01	0.09	0.006	152.1	86.81	0.0371
Evaporator	4.00	4.47	2.96	0.042	11.7	0.05	0.0021
HPE	5.55	16.93	1.98	0.039	205.1	90.27	0.3673
LPE	5.55	17.46	1.89	0.038	214.5	89.83	0.3347
Condenser	5.55	42.3	2.33	0.046	662.1	6.94	0.0035

The minimum value of exergoeconomic factor ($f$) indicates that the cost rate from exergy destruction is quite dominant compared to the capital cost rate. Similarly, the relatively high exergooeconomic factor indicates that the capital cost rate is significant compared to the exergy destruction cost rate [37,52]. From Table 11 it can be seen that in all configurations, evaporator and condenser have lower exergoeconomic factor due to high exergy destruction. In addition, it is seen that the exergoeconomic factors of FFH and IHE components are low in FFH-ORC and IHE–FFH–ORC configurations. In order to improve the exergoeconomic factors of these components, it is necessary to reduce the exergy destruction and exergy destruction cost rates by improving their thermodynamic performances. In addition, the capital cost rate can be reduced and the exergoeconomic factor can be high. It can be seen in the same table that the highest capital cost rate ($\dot{Z}$) is calculated for the expander on a component basis in all configurations.

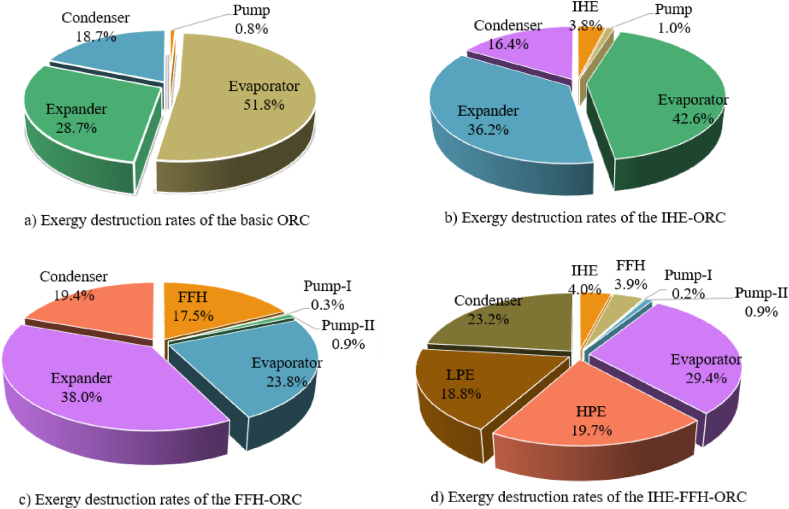
As a result of the exergy analysis applied to the ORC configurations, the exergy destruction rates of each equipment were calculated, and the results were given in Table 11. Fig. 5 shows the percentage shares of the components in the total exergy destruction rate for each cycle. The total exergy destruction rates of the basic ORC and IHE-ORC configurations are given in Fig. 5(a) and (b), respectively. The maximum exergy destruction ratios occur in the evaporator component with 51.8% and 42.6%. In both cycles, the second-highest exergy destruction was realized in the expander. The share of this component in the total exergy destruction rate was calculated as 28.7% for basic ORC and 36.2% for IHE-ORC. The share of the condenser in the total exergy destruction rate is 18.7% and 16.4% for basic ORC and IHE-ORC, respectively. The distributions of exergy destruction rates of FFH-ORC and IHE–FFH–ORC configurations on a component basis are presented in Fig. 5(c) and (d), respectively. It is noteworthy that the equipment most exergy destruction appears in the expander of the ORC systems, with the presence of intermediate steam removal from the expander (FFH-ORC configuration) or the use of double expanders (IHE–FFH–ORC configuration). The exergy destruction rate of the expander in the FFH-ORC system is 38%. In the IHE–FFH–ORC system, the share of the high-pressure expander exergy destruction rate is 18.8%, and the share of the low-pressure expander one is 19.5%; in total, 38.5% belongs to the expanders. Other equipment with high exergy destruction in both FFH-ORC and IHE–FFH–ORC systems were the evaporator and condenser, respectively. Notably, the percantage share of the exergy destruction in the FFH of the IHE–FFH–ORC is less compared to the exergy destruction ratio of the FFH in the FFH-ORC. The exergy destruction rates of the pumps and IHEs are quite low compared to other components for all configurations.

Fig. 5.

Exergy destruction rates of the ORC configurations: (a) Basic ORC, (b) IHE-ORC, (c) FFH-ORC, (d) IHE–FFH–ORC.

3.2. Taguchi and ANOVA analysis results of IHE–FFH–ORC system

Control factors and levels used in the analysis are given in Table 8. In the Taguchi Experiment Design, seven control factors were selected as the working fluid type (A), evaporator temperature (B), condenser temperature (C), expander efficiency (D), pump efficiency (E), superheating temperature (F) and subcooling temperature (G). Among these factors, 6 levels (6¹) were taken for the working fluid type (A) factor and 3 levels (3⁶) for the other factors. The levels of control factor values were determined in accordance with the designed L₁₈ orthogonal array. Then, the thermal efficiency of the system (${\eta }_{th}$), exergy efficiency (${\eta }_{ex}$), the total cost of the system (${\dot{C}}_{sys}$) and the unit cost of the electricity produced ($C_{el}$) by the system were calculated for these 18 cases. Calculations are performed with the EES software. The results are given under the “Responses” column heading of Table 12. Then, using Minitab software, $S/N$ ratios were calculated by taking the $LB$ approximation for ${\eta }_{th}$ and ${\eta }_{ex}$, and the $SB$ approximation for ${\dot{C}}_{sys}$ and $C_{el}$. In Table 12, the calculated $S/N$ ratio values of each output parameter are also presented.

Table 12.

${\mathit{\eta }}_{\mathit{t}\mathit{h}}$, ${\mathit{\eta }}_{\mathit{e}\mathit{x}}$, ${\dot{\mathit{C}}}_{\mathit{s}\mathit{i}\mathit{s}}$, and ${\mathit{C}}_{\mathit{e}\mathit{l}}$ results and S/N ratios according to L₁₈ orthogonal array.

Exp.No	Control factors and levels							Responses				$\mathit{S}/\mathit{N}$ ratios
	A	B	C	D	E	F	G	${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$ ($\$/h$)	${\mathit{C}}_{\mathit{e}\mathit{l}}$ $(\$/kWh$)	${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$	${\mathit{C}}_{\mathit{e}\mathit{l}}$
1	1	1	1	1	1	1	1	0.13	0.58	0.767	0.045	−17.5	−4.8	2.3	27.0
2	1	2	2	2	2	2	2	0.17	0.60	0.878	0.042	−15.3	−4.4	1.1	27.6
3	1	3	3	3	3	3	3	0.19	0.61	0.932	0.040	−14.3	−4.3	0.6	27.9
4	2	1	1	2	2	3	3	0.15	0.64	0.844	0.043	−16.4	−3.9	1.5	27.4
5	2	2	2	3	3	1	1	0.19	0.67	0.897	0.040	−14.4	−3.5	0.9	27.9
6	2	3	3	1	1	2	2	0.15	0.49	0.929	0.046	−16.4	−6.3	0.6	26.8
7	3	1	2	1	3	2	3	0.11	0.50	0.739	0.047	−18.8	−6.0	2.6	26.5
8	3	2	3	2	1	3	1	0.15	0.53	0.858	0.045	−16.2	−5.5	1.3	26.9
9	3	3	1	3	2	1	2	0.23	0.73	1.049	0.040	−12.9	−2.7	−0.4	28.1
10	4	1	3	3	2	2	1	0.12	0.53	0.684	0.048	−18.3	−5.5	3.3	26.3
11	4	2	1	1	3	3	2	0.16	0.55	1.005	0.045	−15.8	−5.2	0.0	26.9
12	4	3	2	2	1	1	3	0.17	0.56	1.099	0.048	−15.4	−5.1	−0.8	26.4
13	5	1	2	3	1	3	2	0.14	0.59	0.845	0.048	−17.1	−4.6	1.5	26.5
14	5	2	3	1	2	1	3	0.12	0.43	1.017	0.055	−18.2	−7.2	−0.1	25.4
15	5	3	1	2	3	2	1	0.19	0.61	1.192	0.046	−14.4	−4.3	−1.5	27.0
16	6	1	3	2	3	1	2	0.11	0.47	0.691	0.052	−19.3	−6.6	3.2	25.6
17	6	2	1	3	1	2	3	0.20	0.70	1.102	0.044	−14.1	−3.1	−0.8	27.0
18	6	3	2	1	2	3	1	0.16	0.49	1.090	0.050	−16.1	−6.1	−0.7	25.7

In Table 13, the calculated $S/N$ ratios of the control factors at the determined levels in the Taguchi analysis are presented. The difference between the largest and smallest values of the $S/N$ ratios calculated for each factor gives the $Delta$ value in table. A large value indicates that factor has the greatest effect on the output parameter. As it is clearly seen from the table, the B factor with $Delta=2.98$, namely the evaporation temperature, has the maximum degree of influence on the thermal efficiency. This result is in parallel with the studies in the literature [45]. This is followed by D-expander efficiency, C-condensation temperature, A-working fluid, F-superheating degree, E-pump efficiency, and G-subcooling degree. At the same time, the $Rank$ expression given in the table shows the order of the effect of the control factors on the thermal efficiency, in other words, the degree of importance. The weight coefficient calculated for thermal efficiency is $w=34.0\%$.

Table 13.

The $S/N$ ratios and the weight factors calculated for the ${\eta }_{th}$, ${\eta }_{ex}$, ${\dot{C}}_{sys}$, and $C_{el}$.

Thermal efficiency (${\mathit{\eta }}_{\mathit{t}\mathit{h}}$)
Levels	A	B	C	D	E	F	G
1	−15.72	−17.92	−15.21	−17.16	−16.12	−16.30	−16.16
2	−15.75	−15.67	−16.17	−16.19	−16.21	−16.22	−16.16
3	−15.99	−14.94	−17.14	−15.18	−16.19	−16.01	−16.21
4	−16.50
5	−16.59
6	−16.50
$Delta$	0.87	2.98	1.93	1.98	0.09	0.29	0.05
$Rank$	4	1	3	2	6	5	7
$\sum Delta$	8.19
$w$ (%)	34.0
Exergy efficiency (${\mathit{\eta }}_{\mathit{e}\mathit{x}}$)
1	−4.50	−5.22	−3.98	−5.93	−4.88	−4.97	−4.94
2	−4.54	−4.81	−4.94	−4.95	−4.98	−4.92	−4.94
3	−4.76	−4.79	−5.91	−3.94	−4.97	−4.93	−4.95
4	−5.24
5	−5.36
6	−5.26
$Delta$	0.86	0.43	1.93	1.99	0.10	0.05	0.005
$Rank$	3	4	2	1	5	6	7
$\sum Delta$	5.37
$w$ (%)	22.3
Total cost of the system (${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$)
1	1.35	2.40	0.16	0.77	0.68	0.85	0.94
2	1.02	0.40	0.77	0.80	0.77	0.89	1.00
3	1.18	−0.37	1.49	0.84	0.97	0.68	0.48
4	0.81
5	0.07
6	0.54
$Delta$	1.42	2.77	1.33	0.07	0.29	0.21	0.51
$Rank$	2	1	3	7	5	6	4
$\sum Delta$	6.61
$w$ (%)	27.4
Unit cost of the electricity produced (${\mathit{C}}_{\mathit{e}\mathit{l}}$)
1	27.50	26.56	27.21	26.38	26.76	26.73	26.80
2	27.34	26.93	26.77	26.81	26.75	26.85	26.91
3	27.13	26.96	26.48	27.27	26.95	26.88	26.75
4	26.53
5	26.29
6	26.12
$Delta$	1.38	0.40	0.73	0.90	0.20	0.15	0.17
$Rank$	1	4	3	2	5	7	6
$\sum Delta$	3.93
$w$ (%)	16.3

Fig. 6 shows the trend of the calculated $S/N$ ratios at the levels determined for the control factors. The highest performance is obtained if the level that gives the maximum $S/N$ for each parameter is selected. So, according to the graph, if A₁ (R113) for the working fluid, B₃ (145 °C) for the evaporation temperature, C₁ (25 °C) for the condensation temperature, D₃ (0.90) for the turbine efficiency, E₁ (0.70) for the pump efficiency, F₃ (10 °C) for superheating, and G₂ (5 °C) for subcooling (A₁B₃C₁D₃E₁F₃G₂) are selected, the maximum ${\eta }_{th}$ will be 22.9%.

Fig. 6.

Effects of control factors levels on ${\mathit{\eta }}_{\mathit{t}\mathit{h}}$.

Table 14 shows the ANOVA results obtained for the output parameters. The effect results of all parameters were found as a result of 95% reliability test comparisons. As can be seen from the table, the most effective parameter for thermal efficiency was the evaporation temperature with 50.48%. The effect rate obtained for expander efficiency is 24.73%. The total effect of these two control factors on ${\eta }_{th}$ is 75.21%. The effect rates of other parameters on the result are, respectively, the condensation temperature 20.34%, the working fluid 4.31%, subcooling 0.06%, pump efficiency 0.05%, and superheating 0.03%. When compared with the Taguchi analysis result, it seems that almost similar results are obtained. In this respect, the analysis is consistent and parallel to each other.

Table 14.

ANOVA results and the contribution ratios for the ${\eta }_{th}$, ${\eta }_{ex}$, ${\dot{C}}_{sys}$, and $C_{el}$.

Symbol	Control factors	$\mathit{D}\mathit{O}\mathit{F}$	Contribution (%)
			${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$	${\mathit{C}}_{\mathit{e}\mathit{l}}$
A	Working fluid	5	4.31	8.24	13.64	50.28
B	Evaporation temperature	2	50.48	3.37	67.48	5.34
C	Condensation temperature	2	20.34	42.20	15.63	17.30
D	Expander efficiency	2	24.73	46.00	0.07	23.34
E	Pump efficiency	2	0.05	0.08	0.49	1.60
F	Superheating	2	0.03	0.06	0.08	1.26
G	Subcooling	2	0.06	0.05	2.62	0.87
Error		0	–	–	–	–
Total		17	100.00	100.00	100.00	100.00

The effects of control parameters on exergy efficiency were analyzed by the Taguchi method and the results are presented under the ‘exergy efficiency’ line of Table 13. As can be seen from the table, D-expander efficiency was the most important parameter affecting the ${\eta }_{ex}$. This was followed by C-condensation temperature, A-working fluid, B-evaporation temperature, E-pump efficiency, F-superheating degree, and G-subcooling degree. In the multi-objective optimization process, the weight factor of the exergy efficiency was calculated as 22.3%.

According to Fig. 7, the parameter levels that maximize the ${\eta }_{ex}$ are A₁B₃C₁D₃E₁F₂G₂. In this case, the maximum ${\eta }_{ex}$ is obtained as 73.78%.

Fig. 7.

Effects of control factors levels on ${\mathit{\eta }}_{\mathit{e}\mathit{x}}$.

When the ANOVA results obtained for exergy efficiency were examined, it was determined that the parameter with maximum importance was the turbine efficiency with 46.00% (Table 14). The second most effective control factor is the condensation temperature with 42.20%. The total effect value of these two parameters is 88.20%. As can be seen from the table, the effect of other control factors on exergy efficiency is quite low.

Another purpose in the design of the ORC system is the minimization of the ${\dot{C}}_{sys}$. According to the results of the Taguchi analysis, the most effective parameter for obtaining the smallest value of ${\dot{C}}_{sys}$ is the B-evaporation temperature (Table 13). This was followed by A-working fluid, C-condensation temperature, G-subcooling degree, E-pump efficiency, F-superheating degree, and D-expander efficiency. For multi-objective optimization, the effect value (weighting factor, $w$) of the ${\dot{C}}_{sys}$ value on the objective function is 27.4%.

In Fig. 8, the calculated $S/N$ ratios of the control factors for the total system cost are given graphically. According to this figure, A₁B₁C₃D₃E₃F₂G₂ combination are taken, the minimum ${\dot{C}}_{sys}$ value is calculated as 0.655 $/h.

Fig. 8.

Effects of control factors levels on ${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$.

When the ANOVA analysis results obtained for the ${\dot{C}}_{sys}$ in Table 14 are examined, it has been determined that the parameter with the highest effect value to ensure the minimum value of ${\dot{C}}_{sys}$ is the evaporation temperature (B) with a rate of 67.48%. It seems that the evaporation temperature factor has a very large ratio when compared to other parameters. Therefore, this parameter should be the most concentrated to obtain the minimum result of the ${\dot{C}}_{sys}$ value.

In the analysis, the last output parameter affecting the objective function the unit cost of electricity produced ($C_{el}$). First, Taguchi analysis was performed to determine the order of effect values of the control factors that would minimize the $C_{el}$ value. The results obtained are presented in Table 13. Maximum $Delta=1.38$ has been calculated for the control factor A (working fluid). That is, the most effective parameter for $C_{el}$ is A (working fluid). This was followed by D-expander efficiency, C-condensation temperature, B-evaporation temperature, E-pump efficiency, G-subcooling degree and F-superheating degree. Also, the weight factor of $C_{el}$ was calculated as 16.3%.

The distribution of the $S/N$ ratios calculated for each level of each control factor is given in Fig. 9. According to this figure, if A₁B₃C₁D₃E₃F₃G₂ combination was selected, the minimum $C_{el}$ value was calculated as 0.0378 $/kWh.

Fig. 9.

Effects of control factors levels on ${\mathit{C}}_{\mathit{e}\mathit{l}}$.

The last column of Table 14 contains the results of the ANOVA analysis for the minimization of the ${\mathit{C}}_{\mathit{e}\mathit{l}}$ value. According to the results obtained, the most influential parameter on the ${\mathit{C}}_{\mathit{e}\mathit{l}}$ was the working fluid type with 50.28%. It is followed by expander efficiency with 23.34%, condensation temperature with 17.30%, evaporation temperature with 5.34%, pump efficiency with 1.60%, superheating degree with 1.26%, and subcooling degree with 0.87%, respectively. The order of importance obtained for the control parameters as a result of the ANOVA analysis seems to be the same as the results of the Taguchi analysis.

3.3. Multi-objective optimization of the IHE–FFH–ORC system with Taguchi-Gray relational analysis method

In this section, the output parameters (${\eta }_{th}$, ${\eta }_{ex}$, ${\dot{C}}_{s\mathit{y}\mathit{s}}$, and $C_{el}$) which were examined separately in the previous section, are integrated, and reduced to a single objective function. Taguchi-Grey Relational Analysis method was used to obtain and analyze the objective function. In this method, firstly, the four output parameters under the “Responses” column heading, which are calculated in accordance with the orthogonal array in Table 12, are normalized according to Eqs. (32), (33). The results are presented in Table 15.

Table 15.

Normalization, gray relational coefficient, gray relational grade, and order of output parameters.

Experiment	Normalization				Gray relational coefficient				$\mathit{G}\mathit{R}\mathit{G}$	Order
	${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{y}\mathit{s}}$	${\mathit{C}}_{\mathit{e}\mathit{l}}$	${\mathit{\eta }}_{\mathit{t}\mathit{h}}$	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$	${\dot{\mathit{C}}}_{\mathit{s}\mathit{i}\mathit{s}}$	${\mathit{C}}_{\mathit{e}\mathit{l}}$
1	0.21	0.48	0.84	0.68	0.39	0.49	0.75	0.61	0.55	8
2	0.54	0.57	0.62	0.87	0.52	0.54	0.57	0.79	0.58	5
3	0.72	0.58	0.51	0.95	0.64	0.54	0.51	0.91	0.62	3
4	0.36	0.69	0.68	0.79	0.44	0.61	0.61	0.71	0.57	6
5	0.71	0.79	0.58	0.95	0.63	0.71	0.54	0.90	0.67	2
6	0.37	0.18	0.52	0.59	0.44	0.38	0.51	0.55	0.46	15
7	0.06	0.22	0.89	0.49	0.35	0.39	0.82	0.49	0.51	11
8	0.40	0.32	0.66	0.63	0.45	0.42	0.59	0.57	0.50	12
9	1.00	1.00	0.28	1.00	1.00	1.00	0.41	1.00	0.84	1
10	0.12	0.32	1.00	0.44	0.36	0.42	1.00	0.47	0.57	7
11	0.45	0.40	0.37	0.63	0.48	0.45	0.44	0.58	0.48	14
12	0.53	0.41	0.18	0.46	0.52	0.46	0.38	0.48	0.46	16
13	0.27	0.53	0.68	0.47	0.41	0.51	0.61	0.49	0.50	13
14	0.13	0.00	0.34	0.00	0.36	0.33	0.43	0.33	0.37	18
15	0.69	0.60	0.00	0.59	0.62	0.55	0.33	0.55	0.52	10
16	0.00	0.12	0.99	0.22	0.33	0.36	0.97	0.39	0.52	9
17	0.77	0.90	0.18	0.71	0.68	0.83	0.38	0.63	0.62	4
18	0.42	0.20	0.20	0.30	0.46	0.38	0.38	0.42	0.42	17

In the next step, the normalized results were applied to Eqs. (34), (35), (36), (37)) and gray relational coefficient ($GRC$) was calculated for each output parameter (Table 15). Finally, gray relational grade ($GRG$) was obtained according to Eq. (38). For this, the weight factors calculated for each output parameter in Section 3.3 were considered and the following objective function was obtained as given in Eq. (40).

$$GRG=0.340{GRC}_{{\eta }_{th}}+0.223{GRC}_{{\eta }_{ex}}+0.274{GRC}_{{\dot{C}}_{sis}}+0.163{GRC}_{C_{el}}$$ (40)

In the last column of Table 15, there is the order of the $GRG$ calculated. Accordingly, the optimum result, namely the experimental design that maximizes the objective function, was obtained with the 9th experiment, A₃B₃C₁D₃E₂F₁G₂ (corresponds parameters as R123 working fluid, 145 °C evaporation temperature, 25 °C condensation temperature, 90% turbine efficiency, 80% pump efficiency, 2 °C superheating at the evaporator exit, and 5 °C subcooling at the condenser exit).

Taguchi analysis was performed to determine the effect degrees of control factors on the $GRG$ obtained and the result is presented in Table 16. When the $Delta$ and $Rank$ values in the table are examined, it is seen that the parameter that most affects the objective function is the D-expander efficiency. The order of importance of all parameters is as follows: D-expander efficiency > A-working fluid > C-condensation temperature > F-superheating degree > E-pump efficiency > G-subcooling degree > B-evaporation temperature.

Table 16.

$S/N$ ratios of the gray relational grade.

Level	A	B	C	D	E	F	G
1	−4.68	−5.42	−4.65	−6.73	−5.79	−5.20	−5.49
2	−5.02	−5.54	−5.73	−5.61	−5.38	−5.33	−5.16
3	−4.44	−5.40	−5.98	−4.02	−5.20	−5.83	−5.71
4	−6.01
5	−6.80
6	−5.77
$Delta$	1.91	0.14	1.32	2.71	0.59	0.62	0.55
$Rank$	2	7	3	1	5	4	6

The distribution of the $S/N$ ratio values calculated for each level of the examined control factors is given in Fig. 10. In this graph, the maximum value of each parameter is determined as the optimum value. Accordingly, the levels of control factors A₃, B₃, C₁, D₃, E₃, F₁, G₂ are the combination that maximizes the objective function. In this case, the thermal efficiency of the system is calculated as ${\eta }_{th}=22.62\%$, exergy efficiency ${\eta }_{ex}=73.48\%$, the total system cost ${\dot{C}}_{sys}=1.059\$/h$, the unit cost of electricity produced $C_{el}=0.0392\$/kWh$, and the payback period $PB=2.88years$.

Fig. 10.

Effects of control factors levels on $\mathit{G}\mathit{R}\mathit{G}$.

ANOVA analysis was performed on the objective function and the results are given in Fig. 11. Accordingly, the parameter that most affected the objective function among the control factors was the D-expander efficiency with a rate of 49.14%. This was followed by A-work fluid with a rate of 26.45%. The sequence of other parameters is as follows: C-condensation temperature, F-superheating degree, E-pump efficiency, G-subcooling degree and B-evaporation temperature. When the results of the Taguchi analysis are compared, it is determined that the order of importance of the control factors on the objective function is exactly the same.

Fig. 11.

Contribution ratio of control factors according to the ANOVA results obtained for the $\mathit{G}\mathit{R}\mathit{G}$ function.

4. Conclusion

In the present work, four different ORC configurations are designed, namely basic ORC, IHE-ORC, FFH-ORC, and IHE–FFH–ORC. The ORC configurations with seven different working fluids under same operating conditions are compared from the viewpoint of thermodynamic and exergoeconomic performance parameters. In the last stage, for the IHE–FFH–ORC system, by targeting maximum ${\eta }_{th}$ and ${\eta }_{ex}$, minimum ${\dot{C}}_{sys}$ and $C_{el}$, the effects of seven control factors on performance outputs separately selected by Taguchi and ANOVA statistical analysis methods are investigated. Furthermore, multi-objective optimization based on the Taguchi-Grey Relational Analysis method is applied to find the optimum control factors of the IHE–FFH–ORC power system considering the energy, the exergy and the exergoeconomic parameters. The main findings are summarized below:

• •Among the studied configurations under the same operating conditions, the highest ${\eta }_{th}$, ${\eta }_{ex}$ and ${\dot{W}}_{net}$ values for all fluids are calculated for the IHE–FFH–ORC configuration. The order from maximum to minimum performance according to ${\eta }_{th}$, ${\eta }_{ex}$ and ${\dot{W}}_{net}$ values is as follows based on configuration: IHE–FFH–ORC, IHE-ORC, FFH-ORC, and basic ORC.
• •Among the studied configurations under the same operating conditions, the smallest C_el and shortest PB values for all fluids are calculated for the IHE–FFH–ORC configuration. The order from maximum to minimum performance according to C_el and PB values is as follows based on configuration: IHE–FFH–ORC, basic ORC, FFH-ORC and IHE-ORC.
• •The performances of the R113, R141b and R123 are notable better than other fluids (named as R245fa, R600, R114, and R600a) for the all ORC configurations. The performance order of the working fluids stays almost same for the considered ORC configurations. The worst performances were observed with the R600a for all the cases considered.
• •The minimum and maximum total exergy destruction rates within the configurations are calculated for basic ORC and IHE–FFH–ORC, respectively.
• •As a result of Taguchi and ANOVA analysis, the importance order of control factors for ${\eta }_{th}$ is determined as follows: evaporator temperature, expander efficiency, working fluid, condenser temperature, subcooling degree, pump efficiency, superheating degree.
• •Expander efficiency and condenser temperature are the most essential parameters affecting the exergy efficiency, with rates of 41.80% and 39.49%, respectively.
• •Working fluid control factor has a dominant effect on the ${\dot{C}}_{sys}$ and $C_{el}$ output parameters with a ratio of 76.65% and 72.76%, respectively.
• •Maximization of the GRA objective function gives the optimum configuration of control factors as R123 (working fluid), 145 °C (evaporation temperature), 25 °C (condensation temperature), 90% (expander efficiency), 80% (pump efficiency), 2 °C (superheating), and 5 °C (subcooling). In this case, it is calculated as ${\eta }_{th}=\%\mathrm{22,62}$, ${\eta }_{ex}=\%\mathrm{73,48}$, ${\dot{C}}_{sys}=\mathrm{2,022}\$/h$, and $C_{el}=\mathrm{0,0286}\$/kWh$.

Author contribution statement

Esra Özdemir Küçük, Muhsin Kiliç: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Data availability statement

Data included in article/supplementary material/referenced in article.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Nomenclature

$c$

specific heat (kJ/kgK)

$C_{el}$

unit cost of electricity produced ($/kWh)

$\dot{C}$

cost rate ($/h)

${\dot{C}}_D$

cost of exergy destruction ($/h)

$f_k$

thermoeconomic factor

$\dot{E}$

energy (kW)

$\dot{ED}$

exergy destruction rate (kW)

$\dot{Ex}$

exergy rate (kW)

h

specific enthalpy (kJ/kg)

$i$

interest rate

$\dot{m}$

mass flow rate (kg/s)

$n$

predicted life of the system’s (years)

$N$

the operating time of the system (hours)

P

pressure (kPa)

PB

paybak period (year)

$r_k$

relative cost difference

s

specific entropy (kJ/kgK)

$S/N$

signal-to-noise ratio

$\dot{Q}$

heat rate (kW)

v

specific volume (m³/kg)

w

weighting factor

$\dot{W}$

power (kW)

T

temperature (K)

$U$

total heat transfer coefficient (W/m²K)

$\dot{Z}$

capital cost rate ($/h)

$\phi$

total operating and maintenance cost factor

$\epsilon$

effectiveness of heat exchanger

ƞ

efficiency

${\xi }_i$

gray correlation coefficient

$\varnothing$

discriminating coefficient

Abbreviations

$CRF$

capital recovery factor

$DOF$

degree of freedom

FFH

feed fluid heater

$GRA$

Grey Relational Analysis

$GRG$

Grey Relational Grade

IHE

internal heat exchanger

$LB$

larger the better

ORC

organic Rankine cycle

$NB$

nominal best

$PEC$

purchase equipment cost

$SB$

smaller the better

Subscripts

b

boiler

c

condenser

cv

control volume

c2

condenser-II

comp

compressor

exp

expander

ev

evaporator

ex

exergetic

F

fuel

heat

heat

hpe

high-pressure expander

$i$

the number of experiment

in

inlet

$k$

the number of responses

lpe

low-pressure expander

min

minimum

net

net

out

outlet

p

pump

P

product

sys

system

th

thermal

total

total

o

dead state condition

wf

working fluid