Behavioural strategies of manufacturing firms for high-quality development from the perspective of government participation: A three-part evolutionary game analysis

Abstract

The high-quality development of the manufacturing industry is not only a requirement of industrial transformation and upgrading but also an internal task for the sustainable development of manufacturing enterprises. The high-quality development of the manufacturing industry is a process of multi-participation and dynamic evolution. To understand the evolution of the high-quality development of the manufacturing industry, an evolutionary game model composed of local governments, leading enterprises, and following enterprises is constructed. The evolution process and the influence of internal factors such as innovation capability, organization construction and industry resources on the evolution and stability strategy are analysed. MATLAB software is used to perform numerical simulations. The results show that (1) there are two possible evolutionary stability strategy (ESS) models in the game, namely, {active supervision, positive participation, positive participation} and {active supervision, negative participation, negative participation}; (2) when the initial probabilities of leading and following enterprises are all at low levels, increasing any one of the local government's initial probability, innovation capability, organization construction and industry resources can promote tripartite evolution towards {active supervision, positive participation, positive participation}; and (3) the convergence rate of leading enterprises and following enterprises evolving towards a positive participation strategy will increase slightly with an increase in local government's initial probability, innovation capability, organization construction, and industry resources when both are at middle initial probability levels. The final policy suggestions can be used to help all parties choose the optimal strategy and to achieve the high-quality development target of the manufacturing industry as soon as possible.

1. Introduction

Manufacturing serves as the backbone of the real economy, a crucial area for supply-side structural reform, the primary scene of technological innovation, and the primary component of a contemporary economic system. As a pillar industry of the national economy [1], manufacturing is the key to innovation and technology diffusion and plays an important role in economic and social development. The recovery of major developed economies is feeble due to the extensive adjustment of the global economic situation, and the growth of emerging and developing countries is slowed dramatically [2]. Significantly promoting economic growth through the development of manufacturing has become the primary strategy for nations all over the world to achieve economic recovery [3,4]. In the face of complex international competition and challenges brought by domestic reform pressure, China's traditional manufacturing development model, which is characterized by high investment, high energy consumption, and high emissions, has resulted in increasingly serious issues such as environmental pollution, resource consumption, and energy shortages [5,6]. Additionally, this has also aggravated environmental pollution and ecological deterioration. The limits on domestic factor supply are tightening while pressure from global competition is growing. China's manufacturing industry is struggling to grow, which affects its high-quality development. Currently, China is focusing on the high-quality development of manufacturing [7]. Vigorously promoting the high-quality development of the manufacturing industry is the fundamental requirement for determining development ideas and implementing macro-controls at present and in the future [8]. The high-quality development of the manufacturing industry is of great strategic significance [9] for achieving the goals and tasks of China's new double-circulation development pattern. Therefore, it is urgent to improve the quality of China's manufacturing development.

Promoting the high-quality development of the manufacturing industry requires the joint efforts of the government and enterprises. Manufacturing enterprises can be thought of as a combination of leading enterprise populations and following enterprise populations [10]. The interaction and restriction between populations form the core driving force for the high-quality development of the manufacturing industry [11]. Therefore, how to address the interaction among the government, leading enterprises and following enterprises is a challenge for the high-quality development of the manufacturing industry. First, the government, as a top-level designer, not only grasps the overall policy of high-quality development [12] and formulates a long-term plan for the sustainable development of the manufacturing industry but also improves the regulatory mechanism for the high-quality development of this industry, cultivates multiple financing channels, optimizes a fair development environment and other policy initiatives [13] to serve the high-quality development of leading enterprises and following enterprises. Second, leading enterprises can benefit from advantages in knowledge, systems, talent, market, capital, etc., which creates a solid basis for the high-quality development of enterprises. However, as high-quality growth entails both a systematic shift and a fundamental revolution, the shift in human cognition and thinking is one of the most important steps towards achieving it. This process causes leading enterprises to increase the cost of several reforms. Due to the mismatch between the external environment and the internal resources of enterprise groups, for instance, risks and problems associated with the strategic transformation of enterprise groups will eventually develop [14]. Third, for the following enterprises, advanced knowledge and experience from leading businesses can be acquired relatively cheaply through observation, learning, and imitation in a short amount of time. This allows the following enterprises to avoid the significant development costs and risks associated with leading businesses' technological innovation [15]. However, the innovation resource base of the following enterprises is relatively weak, making it difficult for them to compete with the current leading pioneers. Moreover, the weak foundation of innovation resources will inevitably restrict the rapid improvement of innovation capability and make it difficult for the following enterprises to obtain innovation advantages under the existing technological economic model.

Given the different perspectives of the interests of these three players, the following observation arises: if the local government does not consider the actual development of manufacturing enterprises, oversees with blind supervision, or mainly relies on the market's automatic regulation, blind rewards and punishments may not be able to achieve the desired results. In addition, due to the uneven development level of leading enterprises and following enterprises, enterprises will also face development difficulties if they blindly participate in high-quality development out of their actual development status. The strategic interaction strategy among local governments, leading enterprises and following enterprises is an invisible challenge to the high-quality development of the manufacturing industry. How to address the strategic interaction among the government, leading enterprises and following enterprises is an urgent problem to be solved for the high-quality development of the manufacturing industry.

The remaining sections of this paper are organized as follows: Section 2 is the literature review, which introduces the status of the high-quality development of the manufacturing industry. The problem analysis, model assumptions, and payoff matrix are presented in Section 3. The stability of the equilibrium point is analysed by solving the evolutionary stability strategy. In Section 4, the model is simulated. Section 5 presents a discussion of the study. In Section 6, the conclusion and management recommendations are given, and further research directions are explained.

2. Literature review and conceptual background

2.1. Review of research status

The high-quality development of the manufacturing industry is a research hotspot for government workers and academic researchers, who focus on technological innovation, industrial structure, enterprise games and other perspectives. When studying the game of the high-quality development of enterprises, scholars mainly focus on the interactions among different departments within the enterprise, between enterprises and customers, between enterprises and enterprises, between enterprises and the government, and between different industries.

Domestic and foreign scholars' research on the game within enterprises mainly focuses on the collaborative innovation of various departments [16,17]. For the game study between enterprises and customers, Li et al. [18] used the evolutionary game analysis method to build an evolutionary game model of the behaviours of manufacturing enterprises and customers. They suggested that the servitization degree of enterprises and the degree of participation of customers would have an impact on the knowledge-based interaction between manufacturing enterprises and customers. Li et al. [19] constructed an evolutionary game model based on the participation of both enterprises and consumers. By solving the game model, we obtained the evolutionary stability strategy of the green product market. It was found that the higher the initial probability of enterprises producing green products or consumers consuming green products was, the more inclined enterprises were to carry out green production. For the game between enterprises, Levi et al. [20] studied two types of joint ventures using the method of game theory and proposed that the effective capacity of joint ventures was constrained by the scarcest resources. Meng et al. [21] constructed an evolutionary game model for the intelligent transformation and upgrading of high-end equipment manufacturing enterprises by combining data collection and analysis level, production process digitization level and other factors. They found that the data collection and analysis level, digitization level and other factors had a significant impact on the strategy evolution results of both sides of the game. Zhang et al. [22] simulated the effects of a carbon trading market, innovation subsidy, and environmental taxes on the green technology diffusion of manufacturing enterprises by constructing an evolutionary game model of technology diffusion between enterprises in the context of complex networks. In their study, they found that various levels of policy implementation lead to different rates of diffusion. Based on the open strategy, semi-open strategy and non-open strategy, Wang and Pan [23] constructed a game model for the selection of knowledge-sharing strategies for enterprise cooperative innovation and found that the risk coefficient of knowledge leakage has a certain impact on the speed and direction of system evolution. Sun et al. [24] used differential game theory to study the coordination of quality management behaviour in a supply chain composed of manufacturers, component suppliers and parts suppliers and found that under decentralized decision-making, manufacturers' quality management behaviour is the same. Xu et al. [25] used game models to study the collaborative relationship between enterprises and highlighted how to maximize the effect of collaborative innovation between enterprises. Through the evolutionary game model of tripartite enterprise game groups, Hao and Zhao [26] found that improved technology and other methods have an impact on the behaviour of manufacturing enterprises. For the game between enterprises and the government, Wang and Shi [27] constructed an evolutionary game model of industrial pollution between local governments and enterprises. They found that under the static punishment mechanism, the strategy between the government and the firm is uncertain. Under the dynamic punishment mechanism, the evolutionary path between government and enterprise tends to converge to a stable value. By introducing government behaviour, Wang and Chen [28] built an evolutionary game strategy between manufacturing enterprises and logistics enterprises under the government subsidy mechanism and found that the system of joint development between manufacturing enterprises and logistics enterprises has a distinct feature of “path dependence”. Li et al. [29] used the evolutionary game model to study the potential behaviour characteristics of the government and enterprises and their influencing factors and found that the ecological benefit index net income and weight played a decisive role.

The research on the game between different industries mainly includes the game between manufacturing enterprises and logistics enterprises [30], the game between manufacturing enterprises and high-tech enterprises [31], the three-party game among manufacturing enterprises, industrial internet platforms and third-party developers [32], and the four-party supply chain game with manufacturers, third-party logistics, retailers and banks as the main body [33]. In addition, Ma et al. [34] combined the typical evolutionary game model of individual decision-making mechanisms with the complex network theory of individual interaction behaviour in groups, revealing the impact of various factors on the willingness of enterprises to share knowledge in the dimensions of capacity and efficiency. The aforementioned literature states that promoting the high-quality development of the manufacturing industry is crucial for its sustainable growth and the green development of the economy for both manufacturing businesses and local governments.

2.2. Research gaps based on the literature review

First, the current research on the high-quality development of the manufacturing industry mostly focuses on the level of scientific and technological innovation, policy design and the game between the government and enterprises. There is still insufficient systematic analysis of the strategy of a tripartite evolutionary game involving the government and two types of enterprises. Second, there is a dearth of analysis on how internal elements, such as innovative capacity, organizational design, and industry resources, affect the evolution and stability strategy of manufacturing businesses. Finally, general game theory assumes that all rational players have perfect judgement and prediction ability. This completely rational assumption is difficult to realize in the game process, especially for the high-quality development of the manufacturing industry, which involves the dynamic behaviour choices of stakeholders.

2.3. Research problems and innovations

Based on the above research gaps, the primary research issues of this work are as follows: (1) From the perspective of local government participation, how can the stable strategy of the tripartite evolutionary game between leading enterprises and following enterprises in the high-quality development of the manufacturing industry be scientifically judged? (2) How can we scientifically analyse the mechanism of internal factors such as innovation capability, organization construction and industry resources on the main body strategy of high-quality development of the manufacturing industry? (3) How can we scientifically understand the evolution and stability strategies of local governments, leading enterprises and following enterprises in different situations under the condition of limited rationality?

Compared with the existing research results, the most notable innovation of this paper is the analysis of the impact of internal factors such as innovation capability, organization construction, industry resources, etc., on the evolution and stability strategies of different population entities. Traditional game theory assumes that players are completely rational. In contrast, the game model in this paper is based on the limited rationality of the players, which makes up for many defects of traditional game theory. Additionally, this study incorporates the local government into the model as the primary entity. Finally, a tripartite evolutionary game model is constructed and numerical simulation data are analysed.

The contributions of this study are as follows: First, the population evolution theory and bounded rationality hypothesis are introduced to analyse the dynamic evolution of the internal factors in the strategy of the enterprise subject in the high-quality development of the manufacturing industry. It is proposed that the strategy of high-quality development subjects of the manufacturing industry is the result of mutual learning and competition, which is consistent with the characteristics of an ecological population and environmental coevolution. Second, combined with the background of high-quality development in China and the production practice of enterprises, the dynamic evolution characteristics of the main strategy of high-quality development in the manufacturing industry are systematically analysed through the aspects of initial probability, innovation capability, organization construction, industry resources, etc. Thirdly, by using two complementary research methods, dynamic evolutionary game and simulation, this paper examines the evolutionary stability strategy of the three-party evolutionary game among local government, leading enterprises and following enterprises under different situations. This can provide theoretical support for the high-quality development of the manufacturing industry.

3. Construction of the evolutionary game model

3.1. Evolutionary game theory

In game theory, mathematical models can be used to analyse strategic choices among participating agents [35]. Under certain assumptions, game theory can effectively address the strategic choices that different agents make for their benefit under cooperative and competitive conditions [36]. This theory can be divided into complete information game theory and incomplete information game theory according to the strategy of participating subjects and the integrity of information [37]. In recent years, concepts such as evolutionary stable strategy (ESS) and replicator dynamics equations have replaced classical game theory. As an important branch of game theory, the strategy of evolutionary game theory can replace the mixed strategy in game theory with a certain proportion of group selection [38]. Evolutionary game theory differs from classical game theory in the following ways. First, according to evolutionary game theory, participating subjects have bounded rationality because people's cognition, perception and expression are limited [39]. Second, evolutionary game theory takes the population as the research object. Individuals can gradually correct their strategies through observation and learning in the course of multiple games and finally reach a stable state for all participants [40]. The framework of evolutionary game theory mainly consists of three parts: the game profit matrix, the replicator dynamic system and an evolutionary stability strategy. Evolutionary games as a descriptive theory are suitable for this study for two reasons. First, classical game theory assumes that the participants are completely rational and have comprehensive environmental information. Unlike in classical game theory, for evolutionary games, it is assumed that players are boundedly rational and exist in an environment of incomplete information. In some evolutionary games, evolutionary stable strategies (ESS) do not exist absolutely. Local governments, leading enterprises, and following enterprises neither fully understand the intentions of other participants nor fully understand environmental information. Evolutionary games provide a mechanism for analysing the behaviour of such systems. Second, the classical game model is difficult to calculate, and it usually cannot describe the optimal behaviour in terms of optimality and stability. In addition, evolutionary games are more advantageous for analysing the dynamics of strategy changes, various strategies sequentially dominate the game, and the evolutionary dynamics show the fluctuation cycles between each strategy.

In the process of the high-quality development of the manufacturing industry, local governments, leading enterprises, and following enterprises change their strategies over time to cope with the strategies of other participants. Evolutionary games provide a basis for analysing dynamic evolution in the context of strategic interactions. Local governments, leading enterprises and following enterprises have different interest demands. Therefore, there is a game among them in terms of high-quality development. General game theory assumes that all rational players have perfect judgement and forecasting abilities under known conditions. This completely rational assumption is difficult to realize in the game process, especially for the high-quality development of the manufacturing industry, which involves the dynamic behaviour choices of stakeholders. Evolutionary game theory starts from system theory and regards the adjustment process of group behaviour as a dynamic adjustment process. A tripartite evolutionary game is an effective method for studying the dynamic changes of multiagent strategies under bounded rationality in long-term repeated games, and it is suitable for describing complex problems [41]. Therefore, this theory is suitable for analysing behavioural evolution strategies among different subjects in the high-quality development of the manufacturing industry.

3.2. Problem description

The global manufacturing development pattern is currently adjusting relatively quickly, and China's economy is moving from a stage of rapid expansion to one of high-quality development. The high-quality development of the manufacturing industry in China is currently experiencing unstable conditions due to the complex and profound changes that have taken place in the local and global environments as well as those conditions themselves. In this study, a three-party game evolution model of local governments, leading enterprises, and following enterprises is constructed to address the question of how the internal elements of manufacturing enterprises influence the high-quality development of the manufacturing industry. Fig. 1 displays the relationships and set of strategies for the three game subjects.

Fig. 1.

The relationship and strategy set of the players.

In this study, the local government is the symmetry of the central government. It is the state organ responsible for administrative work in the local administrative regions at all levels. The local government has a public organization that decides and manages a limited range of public affairs. Leading enterprises are defined as enterprises that face the end market, provide complete (or overall) functional products and services, have a market share at the forefront of the industry, and meet one of the three leading conditions of leading industry price, leading industry technology innovation, and system and management innovation. Following enterprises are defined as backwards enterprises with low cost competitive advantage and lack of initial resources, and their main goal is to catch up with leading enterprises.

3.3. Model assumptions

The development environment in which enterprises are located is a critical factor affecting their level of high-quality development. However, in addition to the competition among enterprises, the government plays a significant role in the high quality development of manufacturing enterprises. The government acts as the creator of the environment for the high-quality development of manufacturing enterprises. When employing a strategy of “active supervision”, the government provides policy guidance and financial support for the high-quality development of manufacturing enterprises and other measures to promote the steady growth of the manufacturing industry. When the government employs a strategy of “passive supervision”, the development of manufacturing enterprises is carried out under the role of market economic laws. Therefore, the strategic choices of manufacturing enterprises for high-quality development in a differentiated environment are different. The participating entities of the evolutionary game have finite rationality and can evolve dynamically to reflect the decision-making behaviour of the participants and the influence of the external environment. Based on this, the following hypotheses are proposed.

Assumption 1

Manufacturing enterprises are regarded as a system. In the “natural” state, leading enterprises and following enterprises exist in the system and have limited rationality and subjective initiative, i.e., enterprises will choose the strategic decision that will be most advantageous to their development from their interests. In the process of the game between the government and multiple enterprises, there are three types of participants, namely, the local government, leading enterprises and following enterprises. It is assumed that the enterprises in this study are universal, i.e., there is no serious heterogeneity among enterprises. To promote the high-quality development of manufacturing enterprises, the local government mainly supervises and manages this process. Meanwhile, the high-quality development of manufacturing is a long-term realization process, and enterprises choose their strategies based on their strategic positioning. The late entrants can observe the actions and results of the first entrants, and the late entrants will adjust their behavioural strategies according to the behavioural strategies and behavioural results of the first entrants. Moreover, all three parties have finite rationality in the game process, and the game process is an iterative long-term process to find the optimal strategy through multiple games.

Assumption 2

G stands for local government, A stands for leading enterprise, and B stands for following enterprise. In the game process, the local government can choose the strategy of “active supervision” or “passive supervision”. When the local government selects the “active supervision” strategy, this means that the government provides services such as policy guidance and regulatory regulations to manufacturing enterprises for high-quality development, and the incurring cost is regarded as $C_G$. Thus, the incurring cost is recorded as $C_{Gi,}i=\left(A,B\right)$ if the government provides financial incentives to enterprises that choose the strategy of “positive participation”. When the local government selects the strategy of “passive supervision”, then the development of manufacturing enterprises proceeds under the action of the laws of the market economy. The strategy set of local governments is {active supervision, passive supervision}. Leading and following enterprises develop new strategies of action according to their needs. When an enterprise chooses the “positive participation” strategy, it will pay high costs but also gain more returns. When an enterprise chooses the strategy of “negative participation”, the enterprise will develop according to the original development strategic plan. Whether the expected return from selecting the “positive participation” approach is higher than the expected return from selecting the “negative participation” strategy determines which strategy should be chosen. Both leading enterprises and following enterprises can choose strategies from the strategy set {positive participation, passive participation}.

Assumption 3

The initial returns of the leading and following enterprises when negatively participating in high-quality development are $R_A$ and $R_B$, respectively. When only one of the leading and following enterprises chooses the “positive participation” strategy, the enterprise needs to invest many human, material and financial resources to induce the high-quality development of the enterprise, and the total cost incurred is $C_i,\left(i=A,B\right)$. Under the same circumstances, if enterprises choose a “positive participation” strategy, they can optimize the industrial structure, increase production efficiency, improve product quality and service quality, and encourage the market to favour their products or services. When the local government chooses the “active supervision” strategy, if the enterprise chooses the “negative participation” strategy, the government will punish it, which is regarded as $T$.

Assumption 4

Due to the synergy between enterprises, such as collaboration in resolving management or technological issues, if both the leading and following enterprises opt for a “positive participation” strategy, the input cost of doing so together is lower than the cost of one enterprise doing so alone. Therefore, the cost for both enterprises is referred to as $c_i,\left(i=A,B\right)$, $c_i<C_i$. When a local government chooses an “active supervision” strategy, the government's payoff is $R_G$. When the local government chooses the “passive supervision” strategy, the government's payoff is $k{R}_G,k\in \left(\mathrm{0,1}\right)$, where $k$ represents the ratio of the government's payoff from the “passive supervision” strategy to the government's payoff from the “active supervision” strategy.

Assumption 5

When both the leading enterprise and the following enterprise decide to positively participate in high-quality development strategies, the two enterprises' complementary capabilities and interenterprise synergy provide a synergistic impact that benefits both businesses indirectly. Han et al. [42] and Liu et al. [43] suggested that innovation is a key factor in the high-quality development of the manufacturing industry. As a result, this study holds that a company's ability to innovate is likely to shorten the innovation cycle, increase innovation efficiency, and encourage innovation dissemination, all of which lead to the creation of new value and increased profitability. Therefore, the innovation return is referred to as $R_{i1},i=\left(A,B\right)$ when enterprises strengthen their innovation capability. According to Mathieu [44], corporate culture and organizational capabilities play a role in how successfully the manufacturing industry undergoes a strategic change. On the other hand, Hu et al. [45] also proposed that soft resources, which are difficult to replicate within manufacturing enterprises, also have an important impact on the development of enterprises. Soft resources include the enterprise culture that encourages innovation, the management mechanism of coordination and linkage, the organizational system of cooperation and sharing, and the organizational staff that unites and forges ahead. Therefore, in this study, it is proposed that organizational construction elements such as enterprise human capital, style construction, enterprise culture, and stakeholder collaboration boost enterprise potential in a number of ways and can be used to adapt to changes in the external environment. These factors significantly contribute to the high-quality development of manufacturing enterprises, which leads to abnormal returns for enterprises, where the abnormal return is referred to as $R_{i2},i=\left(A,B\right)$. According to Song [46], a weak industrial foundation will obstruct the high-quality development of the manufacturing industry, while Pang [47] suggests that the industrial structure is a crucial support for encouraging the high-quality development and stable growth of the manufacturing industry. According to this study, the upgrading and rationalization of industry resources, such as the industrial base and industrial structure, can lower the cost for enterprises in choosing “active participation” strategies. The relevant parameters under this assumption are set as follows: the innovation capability coefficient is $\alpha$, the organization construction coefficient is $\beta$, and the industry resource coefficient is $\gamma$.

Based on the above assumptions, the profit and loss parameters of the three parties are shown in Table 1.

Table 1.

Parameter settings of the model.

Subjects	Parameter	Description
Local government	$R_G$	The government's profits when choosing the strategy of “active supervision"
	$k$	The ratio of the profit the government receives when it opts for the “passive supervision” strategy to the profit received when it opts for the “active supervision” strategy.
	$C_G$	The cost for the local government when choosing an “active supervision” strategy.
	$C_{GA}$	The financial subsidy given by the government when leading enterprises to choose the strategy of “positive participation”.
	$C_{GB}$	The financial subsidy given by the government when leading enterprises to choose the strategy of “negative participation".
	$T$	The punishment imposed by the government on enterprises when the latter choose the strategy of “negative participation".
Leading enterprises	$R_A$	Initial return of leading enterprises.
	$C_A$	The cost when only leading enterprises choose the “active participation” strategy.
	$c_A$	The cost for leading enterprises when both types of enterprises choose the strategy of “active participation".
	$R_{A1}$	The innovation benefit brought by leading enterprises when they improve their innovation capability.
	$R_{A2}$	The excess profit brought by leading enterprises when they improve the level of organization construction.
Following enterprises	$R_B$	Initial return of following enterprises.
	$C_B$	The cost when only following enterprises choose the “active participation” strategy.
	$c_B$	The cost for following enterprises when both types of enterprises choose the strategy of “active participation".
	$R_{B1}$	The innovation benefit brought by following enterprises when they improve their innovation capability.
	$R_{B2}$	The excess profit brought by following enterprises when they improve the level of organization construction.
	Variables	Description
	$\alpha$	Innovation capability coefficient
	$\beta$	Organization construction coefficient
	$\gamma$	Industry resources coefficient
	$x$	The probability of local government choosing the “active supervision” strategy
	$y$	The probability of leading enterprises choosing the “positive participation " strategy
	$z$	The probability of following enterprises choosing the “positive participation " strategy

3.4. Payoff matrix

In the game model, local governments, leading enterprises, and following enterprises make strategic choices according to their wishes. Assuming that the probability that the local government will choose the “active supervision” strategy is $x$, the probability that it will opt for the “passive supervision” strategy is $1-x$, where $0\le x\le 1$.

The probability that the leading enterprise chooses the “positive participation” strategy is $y$, and the probability that the leading enterprise chooses the “negative participation” strategy is $1-y$, where $0\le y\le 1$. The probability that the following enterprise chooses the “positive participation” strategy is $z$, and the probability that the following enterprise chooses the “negative participation” strategy is $1-z$, where $0\le z\le 1$. Given the above assumptions, the payoff matrix for the game of high-quality development of the manufacturing industry can be constructed, as shown in Table 2.

Table 2.

Tripartite evolutionary game payoff matrix.

Entities of the game				Following enterprises
				Positive participation $z$	Negative participation $1-z$
Local government	Active supervision $x$	Leading enterprises	Positive participation $y$	$R_G-C_G-C_{GA}-C_{GB}$	$R_G-C_G-C_{GA}+T$
				$R_A+\alpha R_{A1}+\beta R_{A2}-\left(1-\gamma \right)c_A+C_{GA}$	$R_A+R_{A1}+R_{A2}-C_A+C_{GA}$
				$R_B+\alpha R_{B1}+\beta R_{B2}-\left(1-\gamma \right)c_B+C_{GB}$	${\mathrm{R}}_B-R_{B1}-{R_B}_2-T$
			Negative participation $1-y$	$R_G-C_G-C_{GB}+T$	$R_G-C_G+2T$
				${\mathrm{R}}_A-R_{A1}-R_{A2}-T$	${\mathrm{R}}_A-T$
				$R_B+R_{B1}+R_{B2}-C_B+C_{GB}$	${\mathrm{R}}_B-T$
	Passive supervision $1-x$	Leading enterprises	Positive participation $y$	$k{R}_G$	$k{R}_G$
				$R_A+\alpha R_{\mathrm{A}1}+\beta R_{A2}-\left(1-\gamma \right)c_A$	$R_A+R_{A1}+{R_A}_2-C_A$
				$R_B+\alpha R_{\mathrm{B}1}+\beta R_{\mathrm{B}2}-\left(1-\gamma \right)c_B$	$R_B-R_{B1}-R_{B2}$
			Negative participation $1-y$	$k{R}_G$	$k{R}_G$
				$R_A-R_{A1}-R_{A2}$	$R_A$
				$R_B+R_{\mathrm{B}1}+R_{\mathrm{B}2}-C_B$	$R_B$

3.5. Model establishment and evolutionary stabilization strategy solution

3.5.1. Construction of the payoff expectation functions

The expected payoffs that the local government chooses the “active supervision” strategy or “passive supervision” strategy can be determined based on Table 2 and are denoted as $U_{G1}$ and $U_{G2}$, respectively. The average expected payoffs are represented by ${\bar{U}}_G$.

$$\begin{array}{l}{U}_{G1}=yz\left(R_G-C_G-C_{GA}-C_{GB}\right)+y\left(1-z\right)\left(R_G-C_G-C_{GA}+T\right)+\\ \left(1-y\right)z\left(R_G-C_G-C_{GB}+T\right)+\left(1-y\right)\left(1-z\right)\left(R_G-C_G+2T\right)\end{array}$$ (1)

$$U_{G2}=yzk{R}_G+y\left(1-z\right)k{R}_G+\left(1-y\right)zk{R}_G+\left(1-y\right)\left(1-z\right)k{R}_G$$ (2)

$${\bar{U}}_G=x{U}_{G1}+\left(1-x\right)U_{G2}$$ (3)

The expected payoffs that leading enterprises choose the “positive participation” strategy or “negative participation” strategy are then denoted as $U_{A1}$ and $U_{A2}$, respectively. The average expected payoffs are represented by ${\bar{U}}_A$.

$$\begin{array}{l}{U}_{A1}=xz\left[R_A+\alpha R_{\mathrm{A}1}+\beta R_{\mathrm{A}2}-\left(1-\gamma \right)c_A+C_{GA}\right]+x\left(1-z\right)\left(R_A+R_{\mathrm{A}1}+R_{\mathrm{A}2}-C_A+C_{GA}\right)+\\ \left(1-x\right)z\left[R_A+\alpha R_{\mathrm{A}1}+\beta R_{\mathrm{A}2}-\left(1-\gamma \right)c_A\right]+\left(1-x\right)\left(1-z\right)\left(R_A+R_{\mathrm{A}1}+R_{\mathrm{A}2}-C_A\right)\end{array}$$ (4)

$$U_{A2}=xz\left(R_A-R_{\mathrm{A}1}-R_{\mathrm{A}2}-T\right)+x\left(1-z\right)\left(R_A-T\right)+\left(1-x\right)z\left(R_A-R_{\mathrm{A}1}-R_{\mathrm{A}2}\right)+\left(1-x\right)\left(1-z\right)R_A$$ (5)

$${\bar{U}}_A=y{U}_{A1}+\left(1-y\right)U_{A2}$$ (6)

Subsequently, the expected payoffs that following enterprises choose the “positive participation” strategy or “negative participation” strategy are denoted as $U_{B1}$ and $U_{B2}$, respectively. The average expected payoffs are represented by ${\bar{U}}_B$.

$$\begin{array}{l}{U}_{B1}=xy\left[R_B+\alpha R_{\mathrm{B}1}+\beta R_{\mathrm{B}2}-\left(1-\gamma \right)c_B+C_{GB}\right]+x\left(1-y\right)\left(R_B+R_{\mathrm{B}1}+R_{\mathrm{B}2}-C_B+C_{GB}\right)+\\ \left(1-x\right)y\left[R_B+\alpha R_{\mathrm{B}1}+\beta R_{\mathrm{B}2}-\left(1-\gamma \right)c_B\right]+\left(1-x\right)\left(1-y\right)\left(R_B+R_{\mathrm{B}1}+R_{\mathrm{B}2}-C_B\right)\end{array}$$ (7)

$$U_{B2}=xy\left(R_B-R_{\mathrm{B}1}-R_{\mathrm{B}2}-T\right)+x\left(1-y\right)\left(R_B-T\right)+\left(1-x\right)y\left(R_B-R_{\mathrm{B}1}-R_{\mathrm{B}2}\right)+\left(1-x\right)\left(1-y\right)R_B$$ (8)

$${\bar{U}}_B=z{U}_{B1}+\left(1-z\right)U_{B2}$$ (9)

3.5.2. Solution of evolutionary stabilization strategy using the replicator dynamics equation

Following the solution of the replicator dynamic equation [48,49], according to Eq. (1) ∼ (3), we can obtain the replicator dynamic equation for the local government's strict supervision as follows:

$$F\left(x\right)=\frac{dx}{dt}=x\left(U_{G1}-{\bar{U}}_G\right)=x\left(1-x\right)\left(U_{G1}-U_{G2}\right)=x\left(1-x\right)\left[\left(1-k\right)R_G-C_G-y{C}_{GA}-z{C}_{GB}+T\left(2-y-z\right)\right]$$ (10)

According to Eq. (4) ∼ (6), we can obtain the replicator dynamic equation for leading enterprises implementing a high-quality development strategy as follows:

$$F\left(y\right)=\frac{dy}{dt}=y\left(U_{A1}-{\bar{U}}_A\right)=y\left(1-y\right)\left(U_{A1}-U_{A2}\right)=y\left(1-y\right)\left[R_{A1}\left(z\alpha +1\right)+R_{A2}\left(z\beta +1\right)-z\left(1-\gamma \right)c_A+x{C}_{GA}-\left(1-z\right)C_A+xT\right]$$ (11)

According to Eq. (7) ∼ (9), we can obtain the replicator dynamic equation for following enterprises implementing a high-quality development strategy as follows:

$$F\left(z\right)=\frac{dz}{dt}=z\left(U_{B1}-{\bar{U}}_B\right)=z\left(1-z\right)\left(U_{B1}-U_{B2}\right)=z\left(1-z\right)\left[R_{B1}\left(y\alpha +1\right)+R_{B2}\left(y\beta +1\right)-y\left(1-\gamma \right)c_B+x{C}_{GB}-\left(1-y\right)C_B+xT\right]$$ (12)

Finally, Eq. (10) ∼ (12) constitute a three-dimensional dynamic system for the evolutionary game, as follows:

$$\{\begin{array}{l}\frac{dx}{dt}=x\left(1-x\right)\left[\left(1-k\right)R_G-C_G-y{C}_{GA}-z{C}_{GB}+T\left(2-y-z\right)\right]\\ \frac{dy}{dt}=y\left(1-y\right)\left[R_{A1}\left(z\alpha +1\right)+R_{A2}\left(z\beta +1\right)-z\left(1-\gamma \right)c_A+x{C}_{GA}-\left(1-z\right)C_A+xT\right]\\ \frac{dz}{dt}=z\left(1-z\right)\left[R_{B1}\left(y\alpha +1\right)+R_{B2}\left(y\beta +1\right)-y\left(1-\gamma \right)c_B+x{C}_{GB}-\left(1-y\right)C_B+xT\right]\end{array}$$ (13)

In Eq. (13), when $\frac{dx}{dt}=0$, $\frac{dy}{dt}=0$, $\frac{dz}{dt}=0$, eight pure strategy equilibrium points of the system can be determined: $E_1\left(\mathrm{0,0,0}\right)$, $E_2\left(\mathrm{0,0,1}\right)$, $E_3\left(\mathrm{0,1,0}\right)$, $E_4\left(\mathrm{0,1,1}\right)$, $E_5\left(\mathrm{1,0,0}\right)$, $E_6\left(\mathrm{1,0,1}\right)$, $E_7\left(\mathrm{1,1,0}\right)$, and $E_8\left(\mathrm{1,1,1}\right)$. According to the assumptions, the equilibrium point must be in the three-dimensional space, i.e., the condition $V=\left\{\left(x,y,z\right)|0\le x\le 1,0\le y\le \mathrm{1,0}\le z\le 1\right\}$ is satisfied. According to Friedman's [50] analysis of dynamic stability using differential equations, the stability of the equilibrium point is assessed using a local stability analysis of the system's Jacobian matrix. If the eigenvalues of the related Jacobian matrix satisfy the requirement that they be all less than 0, it is an evolutionary stability point [51].

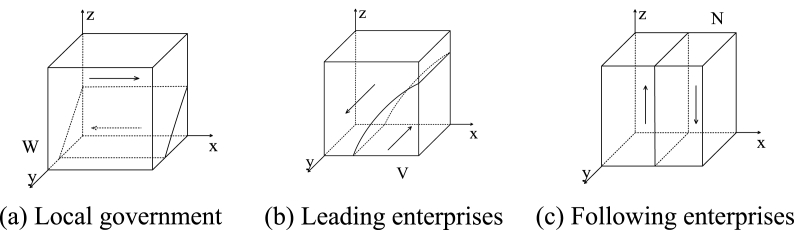
Based on the properties of the evolutionary stable strategy [52], the necessary condition that needs to be satisfied for a local government subject to reach the point of evolutionary stability is $dF\left(x\right)/dx<0$. According to replicator dynamic Eq. (10) for the local government, when $z=\frac{\left(1-k\right)R_G-C_G-y{C}_{GA}+T\left(2-y\right)}{T+C_{GB}}$, $F\left(x\right)=0$, then all values of $x$ are steady states. When $z>\frac{\left(1-k\right)R_G-C_G-y{C}_{GA}+T\left(2-y\right)}{T+C_{GB}}$, $x=1$ satisfies the necessary condition $dF\left(x\right)/dx<0$; therefore, $x=1$ is the evolutionary stability point. When $z<\frac{\left(1-k\right)R_G-C_G-y{C}_{GA}+T\left(2-y\right)}{T+C_{GB}}$, $x=0$ satisfies the necessary condition $dF\left(x\right)/dx<0$; therefore, $x=0$ is the evolutionary stability point. According to $z=\frac{\left(1-k\right)R_G-C_G-y{C}_{GA}+T\left(2-y\right)}{T+C_{GB}}$, the surface W is drawn as shown in Fig. 2(a). The points in surface W are stable in the $X$-axis direction, the points above surface W evolve towards $x=1$, and the points below surface W evolve towards $x=0$. Similarly, for the leading enterprises, the points in surface V are stable in the $Y$-axis direction, the points above surface V evolve towards $y=1$, and the points below surface V evolve towards $y=0$, as shown in Fig. 2(b). For the following enterprises, the points in surface N are stable in the $Z$-axis direction, the points above surface N evolve towards $z=1$, and the points below surface N evolve towards $z=0$, as shown in Fig. 2(c).

Fig. 2.

The strategy evolution process of the three-party game subjects.

3.6. Analysis of the evolutionarily stable strategy

The dynamical system M can be used to describe the entire high-quality development of the manufacturing industry. In the following, the dynamic change process of strategy selection of game entities is studied through M to explore the evolutionary path and law of high-quality development. The evolutionary stability strategy of the system of differential equations can be obtained from the local stability analysis of the Jacobi matrix of this system of differential equations.

$$\begin{array}{l}J=\\ \left[\begin{array}{ccc}\begin{array}{l}\left(1-2x\right)[\left(1-k\right)R_G-C_G-\\ y{C}_{GA}-z{C}_{GB}+T\left(2-y-z\right)]\end{array}& x\left(1-x\right)\left(-C_{GA}-T\right)& x\left(1-x\right)\left(-C_{GB}-T\right)\\ y\left(1-y\right)\left(C_{GA}+T\right)& \begin{array}{l}\left(1-2y\right)[R_{A1}\left(z\alpha +1\right)+R_{A2}\left(z\beta +1\right)-\\ z\left(1-\gamma \right)c_A+x{C}_{GA}-\left(1-z\right)C_A+xT]\end{array}& y\left(1-y\right)\left[\alpha R_{A1}+\beta R_{A2}-\left(1-\gamma \right)c_A{+\mathrm{C}}_{\mathrm{A}}\right]\\ z\left(1-z\right)\left(C_{GB}+T\right)& z\left(1-z\right)\left[\alpha R_{B1}+\beta R_{B2}-\left(1-\gamma \right)c_B{+\mathrm{C}}_{\mathrm{B}}\right]& \begin{array}{l}\left(1-2z\right)[R_{B1}\left(y\alpha +1\right)+R_{B2}\left(y\beta +1\right)-\\ y\left(1-\gamma \right)c_B+x{C}_{GB}-\left(1-y\right)C_B+xT]\end{array}\end{array}\right]\end{array}$$ (14)

The following is the analysis of the equilibrium point $E_1\left(\mathrm{0,0,0}\right)$. When $x=y=z=0$, the Jacobian matrix in Eq. (14) can be simplified as Eq. (15):

$$J_1=\left[\begin{array}{ccc}\left(1-k\right)R_G-C_G+2T& 0& 0\\ 0& R_{A1}+R_{A2}-C_A& 0\\ 0& 0& R_{B1}+R_{B2}-C_B\end{array}\right]$$ (15)

From the Jacobi matrix $J$, three eigenvalues can be derived as ${\lambda }_1=\left(1-k\right)R_G-C_G+2T$, ${\lambda }_2=R_{A1}+R_{A2}-C_A$, and ${\lambda }_3=R_{B1}+R_{B2}-C_B$. Similarly, the eigenvalues of the other equilibria are calculated as shown in Table 3.

Table 3.

The eigenvalues of each equilibrium point corresponding to the Jacobi matrix.

Equilibrium points	Eigenvalue ${\lambda }_1$	Eigenvalue ${\lambda }_2$	Eigenvalue ${\lambda }_3$
$E_1\left(\mathrm{0,0,0}\right)$	$\left(1-k\right)R_G-C_G+2T$	$R_{A1}+R_{A2}-C_A$	$R_{B1}+R_{B2}-C_B$
$E_2\left(\mathrm{0,0,1}\right)$	$\left(1-k\right)R_G-C_G-C_{GB}+T$	$R_{A1}\left(\alpha +1\right)+R_{A2}\left(\beta +1\right)-\left(1-\gamma \right)c_A$	$-\left({R_B}_1+R_{B2}-C_B\right)$
$E_3\left(\mathrm{0,1,0}\right)$	$\left(1-k\right)R_G-C_G-C_{GA}+T$	$-\left({R_A}_1+{R_A}_2-C_A\right)$	$R_{B1}\left(\alpha +1\right)+R_{B2}\left(\beta +1\right)-\left(1-\gamma \right)c_B$
$E_4\left(\mathrm{0,1,1}\right)$	$\left(1-k\right)R_G-C_G-C_{GA}-C_{GB}$	$-\left[R_{A1}\left(\alpha +1\right)+R_{A2}\left(\beta +1\right)-\left(1-\gamma \right)c_A\right]$	$-\left[R_{B1}\left(\alpha +1\right)+R_{B2}\left(\beta +1\right)-\left(1-\gamma \right)c_B\right]$
$E_5\left(\mathrm{1,0,0}\right)$	$-\left[\left(1-k\right)R_G-C_G+2T\right]$	$R_{A1}+R_{A2}+C_{GA}-C_A+T$	$R_{B1}+R_{B2}+C_{GB}-C_B+T$
$E_6\left(\mathrm{1,0,1}\right)$	$-\left[\left(1-k\right)R_G-C_G-C_{GB}+T\right]$	$R_{A1}\left(\alpha +1\right)+R_{A2}\left(\beta +1\right)-\left(1-\gamma \right)c_A+C_{GA}+T$	$-\left(R_{B1}+R_{B2}+C_{GB}-C_B+T\right)$
$E_7\left(\mathrm{1,1,0}\right)$	$-\left[\left(1-k\right)R_G-C_G-C_{GA}+T\right]$	$-\left(R_{A1}+R_{A2}+C_{GA}-C_A+T\right)$	$R_{B1}\left(\alpha +1\right)+R_{B2}\left(\beta +1\right)-\left(1-\gamma \right)c_B+C_{GB}+T$
$E_8\left(\mathrm{1,1,1}\right)$	$-\left[\left(1-k\right)R_G-C_G-C_{GA}-C_{GB}\right]$	$-\left[R_{A1}\left(\alpha +1\right)+R_{A2}\left(\beta +1\right)-\left(1-\gamma \right)c_A+C_{GA}+T\right]$	$-\left[R_{B1}\left(\alpha +1\right)+R_{B2}\left(\beta +1\right)-\left(1-\gamma \right)c_B+C_{GB}+T\right]$

In the game model established in this paper, the influence of four parameters (initial probability, $\alpha ,\beta \text{,}$ and $\gamma$) on the stability of the system is mainly considered. In this study, the tripartite initial probability refers to the initial possibility of the local government choosing the “positive supervision” strategy, the initial possibility of leading enterprises choosing the “active participation” strategy and the initial possibility of following enterprises choosing the “active participation” strategy. To facilitate the analysis of the sign of eigenvalues corresponding to different equilibrium points, under the assumption that $\left(1-k\right)R_G-C_G-C_{GA}-C_{GB}>0$, $R_{A1}\left(\alpha +1\right)+R_{A2}\left(\beta +1\right)-\left(1-\gamma \right)c_A>0$, $R_{B1}\left(\alpha +1\right)+R_{B2}\left(\beta +1\right)-\left(1-\gamma \right)c_B>0$, (The meaning of this assumption is: if the government chooses the strategy of “active supervision”, and the leading enterprises and the following enterprises choose “positive participation” strategy, the benefits will be greater than that of the opposite situation.), the following four scenarios are discussed:

Scenario 1. When $R_{A1}+R_{A2}+C_{GA}+T<C_A$ and $R_{B1}+R_{B2}+C_{GB}+T<C_B$ (that is, the sum of innovation gain, abnormal return, government financial support and government penalty of leading and following enterprises is less than the cost of the “positive participation” strategy, as shown in Table 4), the eigenvalues of the Jacobi matrix corresponding to equilibrium points $E_5\left(\mathrm{1,0,0}\right)$ and $E_8\left(\mathrm{1,1,1}\right)$ are less than 0, so the condition of the evolutionary stability point is satisfied. The corresponding evolutionary strategies are {active supervision, negative participation, negative participation} and {active supervision, positive participation, positive participation}. In the $E_5\left(\mathrm{1,0,0}\right)$ strategy, both leading and following enterprises choose the “negative participation” strategy, and the high-quality development of the manufacturing industry cannot be realized, so such situations should be avoided.

Table 4.

Equilibrium point stability analysis.

Equilibrium points	Scenario 1				Scenario 2				Scenario 3				Scenario 4
	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	Stability	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	Stability	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	Stability	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	Stability
$E_1\left(\mathrm{0,0,0}\right)$	+	–	–	Unstable point	+	+	+	saddle point	+	+	–	Unstable point	+	–	+	Unstable point
$E_2\left(\mathrm{0,0,1}\right)$	+	$\pm$	+	Unstable point	+	$\pm$	–	Unstable point	+	$\pm$	+	Unstable point	+	$\pm$	–	Unstable point
$E_3\left(\mathrm{0,1,0}\right)$	+	+	$\pm$	Unstable point	+	–	$\pm$	Unstable point	+	–	$\pm$	Unstable point	+	+	$\pm$	Unstable point
$E_4\left(\mathrm{0,1,1}\right)$	+	$\pm$	$\pm$	Unstable point	+	$\pm$	$\pm$	Unstable point	+	$\pm$	$\pm$	Unstable point	+	$\pm$	$\pm$	Unstable point
$E_5\left(\mathrm{1,0,0}\right)$	–	–	–	ESS	–	+	+	Unstable point	–	+	–	Unstable point	–	–	+	Unstable point
$E_6\left(\mathrm{1,0,1}\right)$	–	+	+	Unstable point	–	+	–	Unstable point	–	+	–	Unstable point	–	+	–	Unstable point
$E_7\left(\mathrm{1,1,0}\right)$	–	+	+	Unstable point	–	–	+	Unstable point	–	–	+	Unstable point	–	+	+	Unstable point
$E_8\left(\mathrm{1,1,1}\right)$	–	–	–	ESS	–	–	–	ESS	–	–	–	ESS	–	–	–	ESS

Scenario 2: When $R_{A1}+R_{A2}>C_A$ and $R_{B1}+R_{B2}>C_B$, (namely, the innovation and abnormal return of the leading and following enterprises are greater than the cost of choosing the “positive participation” strategy alone), only the eigenvalues of the Jacobi matrix corresponding to $E_8\left(\mathrm{1,1,1}\right)$ satisfy the condition that both are less than 0. Therefore, $E_8\left(\mathrm{1,1,1}\right)$ is the evolutionary stability point. The strategy combination at this point is {active supervision, positive participation, positive participation}.

Scenario 3: When $R_{B1}+R_{B2}+C_{GB}+T<C_B$ and $R_{A1}+R_{A2}>C_A$, (namely, the sum of innovation gains, abnormal return, government financial support and government penalties of the following enterprises is less than the cost of choosing the “positive participation” strategy alone, and the innovation gains and abnormal return of the leading enterprises are greater than the cost of choosing the “positive participation” strategy alone), only the eigenvalues of the Jacobi matrix corresponding to $E_8\left(\mathrm{1,1,1}\right)$ satisfy the condition that both are less than 0. Therefore, $E_8\left(\mathrm{1,1,1}\right)$ is the evolutionary stability point. The strategy combination at this point is {active supervision, positive participation, positive participation}.

Scenario 4: When $R_{A1}+R_{A2}+C_{GA}+T<C_A$ and $R_{B1}+R_{B2}>C_B$, (that is, the sum of innovation gain, abnormal return, government financial support and government penalty of the leading enterprise is less than the cost of choosing the “positive participation” strategy alone, and the innovation gain and abnormal return of the following enterprise is greater than the cost of choosing the “positive participation” strategy alone), only the eigenvalues of the Jacobi matrix corresponding to $E_8\left(\mathrm{1,1,1}\right)$ satisfy the condition that both are less than 0. Therefore, $E_8\left(\mathrm{1,1,1}\right)$ is the evolutionary stability point. The strategy combination at this point is {active supervision, positive participation, positive participation}.

In summary, based on the research assumptions, the stable points of Scenario 1 are $E_5\left(\mathrm{1,0,0}\right)$ and $E_8\left(\mathrm{1,1,1}\right)$, and the stable points of Scenario 2, Scenario 3 and Scenario 4 are E8. However, for the $E_5\left(\mathrm{1,0,0}\right)$ strategy, both leading and following companies choose the “negative participation” strategy, which will cause the high-quality development of the manufacturing industry to not be achieved; therefore, this kind of situation should be avoided. The results of Scenarios 1–4 above show that there are two probabilities of the evolution of the local government, leading enterprises and following enterprises, namely, {active supervision, positive participation, positive participation} and {active supervision, negative participation, negative participation}. However, this only proves the outcome of the evolutionary game and does not reveal the reasons for the final evolutionary outcome. Moreover, these results cannot fully provide the evolutionary process from the initial state to the final equilibrium.

4. Numerical simulations

In the evolutionary game analysis above, both the payoffs and the replicator dynamic equations are based on the estimation of the probabilities of the different strategies [27]. For example, the expected payoff when a local government selects a strict supervision strategy depends on the estimation of the probability of a leading enterprise subject choosing the “positive participation” strategy and the probability of a following enterprise subject choosing the “positive participation” strategy, as shown in Equation (1). The replicator dynamic equation for the strategy of local government agents is also based on the estimation of the probability of both strategies, as shown in Equation (10). However, the complexity of the real world restricts the applicability of the above evolutionary game research method. In the real world, the estimation of the strategy probability related to the game object, whether it is a local government subject, a leading enterprise subject, or a following enterprise subject, is biased and is a kind of strategy estimation under the condition of limited rationality. The introduction of the above uncertainty into the game analysis can deepen the conclusion of the analysis of the tripartite evolutionary game of high-quality development of the manufacturing industry. Therefore, based on the above evolutionary game model, by using the MATLAB simulation method, the evolutionary process of high-quality development of the manufacturing industry is simulated from the perspective of micro-interaction to macro emergence. Factors such as initial probability, innovation capability, organization construction and industry resources of participating entities are discussed to reveal the micro mechanism of the high-quality development of the manufacturing industry.

To understand the strategy choices of each game subject more intuitively, we simulate the ESS evolution track of the tripartite evolutionary game based on the abovementioned evolutionary game analysis, model assumptions and stability conditions. See Table 1 for the meaning of the parameter settings. To obtain the initial value of the evolution simulation, we investigated some representative provinces (such as Henan Province, Shaanxi Province, Shandong Province, Sichuan Province, Shanxi Province, Gansu Province Qinghai Province, the Ningxia Hui Autonomous Region, the Inner Mongolia Autonomous Region and other provinces) and some manufacturing enterprises (such as Weichai Group, Shandong Energy Group, AVIC Optoelectronics Technology Co., Ltd., Henan Shenhuo Group, Weihua Group, China Railway Engineering Equipment Group, CRRC Datong Electric Locomotive Co., Ltd., Shaanxi Automobile Holding Group, Jinchuan Group, Chengdu Aircraft Industry Group, Henan Kuangshan Crane Co., Ltd., Haier Group, Tongwei Group, Tianyuan Manganese Industry Group, Taiyuan Iron and Steel Group, Huayang New Material Technology Group, Yutong Group, Jiuquan Iron and Steel Group, Shaanxi Nonferrous Metals Holding Group, Western Mining Group, Qinghai Energy Development Group, and Maike Group). At the same time, initial parameters are estimated based on policies and regulations, the National Bureau of Statistics, research reports on the development of China's manufacturing industry and the literature [17,53,54]. Finally, the parameter values in Table 5 are sorted out. The value only represents a general proportion and is mainly used to verify the evolutionary game model and the related parameters of the high-quality development of the manufacturing industry.

Table 5.

Model parameters.

Parameters	$R_G$	$C_G$	$C_{GA}$	$C_{GB}$	$C_A$	$C_B$	$R_{A1}$	$R_{A2}$	$R_{B1}$	$R_{B2}$	$T$	$c_A$	$c_B$	$k$	$\alpha$	$\beta$	$\gamma$
Values	20	5	2	2	50	60	23	21	20	20	2	45	50	0.4	0.5	0.5	0.5

The benefit of the government's choice of the “active supervision” strategy is $R_G=20$, the cost of providing policy guidance and improving regulatory regulations is $C_G=5$, and the costs of giving financial support and tax incentives are $C_{GA}=2$, $C_{GB}=2$, and $k=0.4$. If an enterprise chooses the “negative participation” strategy when the local government chooses the “active supervision” strategy, the government will penalize it, which is denoted as $T=2$. When only one enterprise chooses the “positive participation” strategy, the cost is $C_A=50$, and $C_B=60$. When both companies choose the “positive participation” strategy, the costs are $c_A=45$ and $c_B=50$, respectively. The innovation benefit obtained by the leading enterprise is $R_{A1}=23$, and the excess benefits are $R_{A2}=21$. The innovation gain for the following enterprise is $R_{B1}=20$, and the excess gain is $R_{B2}=20$. The innovation capability coefficient is $\alpha =0.5$, the organization construction coefficient is $\beta =0.5$, and the industry resources coefficient is $\gamma =0.5$.

4.1. The effect of initial probability on the evolutionary game

With other parameters unchanged, the impact of the change in the three parties' initial probabilities on the high-quality development strategy is simulated in Fig. 3, where the $Y$-axis indicates the probability of the government adopting the strategy of “active supervision” $x$ or the probability of manufacturing enterprises choosing “positive participation” $y$ or $z$. The $X$-axis indicates the evolution process. When the initial probabilities of the local government, leading and following enterprises are the same and are all small, i.e., $x=y=z=0.2$, the final equilibrium point tends to be $E_8\left(\mathrm{1,1,1}\right)$, as shown in Fig. 3. Enterprises converge to 1 more slowly than the government does due to the cost of positively participating in high-quality development. When the three parties' initial probabilities are all at a middle level, i.e., $x=y=z=0.5$, the leading and following enterprises’ probabilities of positively participating rise rapidly, and the ultimate equilibrium point tends to be $E_8\left(\mathrm{1,1,1}\right)$. When the initial probabilities of the game participants ($x,y$, and $z$) are larger, i.e., $x=y=z=0.8$, x, y and z converge to 1, the enterprises converge to 1 faster than the government does, and the final equilibrium point converges to $E_8\left(\mathrm{1,1,1}\right)$. According to the simulation results, as initial probabilities $x,y$ and $z$ increase, the speed of $x$ converging to 1 decreases, the speed of $y$ and $z$ converging to 1 accelerates, and the final three-party game entities converge to the stable point $E_8\left(\mathrm{1,1,1}\right)$.

Fig. 3.

Evolution results of simultaneous changes of initial probabilities $x$, $y$, and $z$.

The simulation depicted in Fig. 4 is run with the other parameters left unaltered, and its purpose is to further investigate the impact of the change in the government's initial probability $x$ on the strategy of leading and following enterprises to participate in the high-quality development of the manufacturing industry. As seen from Fig. 4, when the initial probabilities of leading and following enterprises ($y$ and $z$) are at a low level, i.e., $y=z=0.2$, $y$ and $z$ rapidly rise and converge to 1 with the increases of $x$ (the government's initial probability), and the final equilibrium point converges to $E_8\left(\mathrm{1,1,1}\right)$. In other words, increasing the government's initial probability can induce leading and following enterprises to evolve towards a “positive participation” strategy.

Fig. 4.

Evolution results when the initial probability $x$ varies.

4.2. The effect of innovation capability on the evolutionary game

The impact of the innovation capability coefficient on the evolutionary game is explored by gradually increasing the innovation capability coefficient of the enterprise when the initial probabilities $x,y$ and $z$ are at low levels, i.e., $x=y=z=0.2$, with other parameters held constant. As shown in the numerical simulation in Fig. 5, it can be found that when the innovation capability coefficient increases from 0.2 to 0.5, the leading and following enterprises start to evolve from the strategy of “negative participation” to that of “positive participation”, but their convergence to the “positive participation” strategy is slower, and the final equilibrium point converges from $E_5\left(\mathrm{1,0,0}\right)$ to $E_8\left(\mathrm{1,1,1}\right)$. When the innovation capability coefficient increases from 0.5 to 0.8, the evolution of the leading and following enterprises towards the “negative participation” strategy is further accelerated, and the equilibrium point tends to $E_8\left(\mathrm{1,1,1}\right)$. It is evident that the increased level of corporate innovation capability plays a positive role in enterprises' choice of “positive participation” strategy. That is, when the initial probabilities of enterprises are low, the increased level of enterprises’ innovation capability can lead enterprises to evolve towards the “positive participation” strategy. However, it is worth noting that as the innovation capability coefficient rises from 0.5 to 0.8, the evolution speed at which the government chooses an “active supervision” strategy decreases slightly.

Fig. 5.

The evolution of innovation capability coefficient when all initial probabilities are 0.2.

To further investigate the effect of innovation capability on the evolutionary game when the initial probabilities of local government, leading and following enterprises are all at a middle level, i.e., $x=y=z=0.5$, with other parameters held constant, numerical simulations are conducted, as shown in Fig. 6. When the innovation capability coefficient rises from 0.2 to 0.8, the convergence rate of leading and following enterprises towards the “positive participation” strategy increases slightly, while the convergence rate of the government's preference for an “active supervision” strategy stays essentially unchanged. This indicates that the government's readiness to supervise is not significantly affected by an increase in innovation capability.

Fig. 6.

The evolution of innovation capability coefficient when all initial probabilities are 0.5.

4.3. The effect of organization construction on the evolutionary game

The impact of organizational construction on the evolutionary game is explored by gradually increasing the organizational construction coefficient of the enterprise when the initial probabilities $x,y$ and $z$ are at low levels, i.e., $x=y=z=0.2$, with other parameters held constant. As shown in the numerical simulation in Fig. 7, when the organization construction coefficient increases from 0.2 to 0.5, the leading and following enterprises start to evolve to a “positive participation” strategy. However, their speed of convergence to the “positive participation” strategy is slower, and the final equilibrium point converges from $E_5\left(\mathrm{1,0,0}\right)$ to $E_8\left(\mathrm{1,1,1}\right)$. By further increasing the organization construction coefficient from 0.5 to 0.8, the evolution of the leading and following enterprises towards the “positive participation” strategy is further accelerated, and the equilibrium point tends to $E_8\left(\mathrm{1,1,1}\right)$. It is evident that the improvement of organization construction plays a positive role in an enterprise's choice of “active participation” strategy. In other words, when the initial probabilities of enterprises are low, improving the level of organization construction can promote the evolution of enterprises to the strategy of active participation.

Fig. 7.

The evolution of organization construction coefficient when all initial probabilities are 0.2.

To further investigate the effect of organization construction on the evolutionary game when the initial probabilities of the government, leading and following enterprises are at a middle level, i.e., $x=y=z=0.5$, numerical simulations are conducted as shown in Fig. 8, with other parameters held constant. As the organization construction coefficient increases from 0.2 to 0.8, the rate at which leading and following enterprises converge to the “active participation” strategy increases slightly, and the equilibrium point eventually converges to $E_8\left(\mathrm{1,1,1}\right)$.

Fig. 8.

The evolution of organization construction coefficient when all initial probabilities are 0.5.

4.4. The effect of industry resources on the evolutionary game

The impact of industry resources on the evolutionary game is explored by gradually increasing the industry resources coefficient of the enterprise when the initial probabilities $x,y$ and $z$ are at low levels, i.e., $x=y=z=0.2$, with other parameters held constant. As shown in the numerical simulation in Fig. 9, when the industry resources coefficient increases from 0.2 to 0.5, the leading and following enterprises start to evolve to the “positive participation” strategy, but their convergence to the “positive participation” strategy is slower, and the final equilibrium point converges from $E_5\left(\mathrm{1,0,0}\right)$ to $E_8\left(\mathrm{1,1,1}\right)$. By further increasing the industry resources coefficient from 0.5 to 0.8, the evolution of the leading and following enterprises towards the “positive participation” strategy is further accelerated, and the equilibrium point tends to $E_8\left(\mathrm{1,1,1}\right)$. It is evident that the increased level of corporate industry resources plays a positive role in the implementation of high-quality development options for enterprises. That is, when the initial probabilities of enterprises are low, the increased level of industry resources can guide enterprises to evolve towards a “positive participation” strategy.

Fig. 9.

The evolution of industry resources coefficient when all initial probabilities are 0.2.

To further investigate the effect of industry resources on the evolutionary game when the initial probabilities of the government, leading and following enterprises are at a middle level, i.e., $x=y=z=0.5$, numerical simulations are conducted as shown in Fig. 10, with other parameters held constant. The final equilibrium point converges to $E_8\left(\mathrm{1,1,1}\right)$ when the industry resource coefficient increases from 0.2 to 0.8, and the rate of convergence of leading and following enterprises towards the “positive participation” strategy increases slightly.

Fig. 10.

The evolutionary of industry resources coefficient when all initial probabilities are 0.5.

5. Discussion

Based on the above analysis, this paper proposes the promotion mechanism of the high-quality development of the manufacturing industry in different stages, as shown in Fig. 11. With the upgrading of the high-quality development stage of the manufacturing industry, the sustainable benefits of the manufacturing industry are gradually enhanced.

Fig. 11.

Promotion mechanism for the high-quality development of the manufacturing industry at different stages.

In the initial stage of the high-quality development of the manufacturing industry, both leading and following enterprises have negative profits. In this case, the government should play a leading role to ensure that the high-quality development of the manufacturing industry proceeds smoothly. Due to issues such as technology and cost, the input costs are usually higher than the benefits when leading and following enterprises start to implement high-quality development in manufacturing. Promoting high-quality manufacturing development has become an important goal for the government. On the one hand, due to the insignificant economic benefits at this stage, it is difficult for enterprises to sustain high investment under great financial pressure. To fully mobilize the enthusiasm of manufacturing enterprises, the government should adopt a variety of economic incentives, introduce guiding industrial policies, and implement other measures for manufacturing enterprises, such as land concessions, tax exemptions, financial subsidies, special funds, business environments, and financial services. On the other hand, the government should impose fines on manufacturing enterprises when they choose the “negative participation” strategy. That is, the government should impose resource taxes and energy taxes on these enterprises if they continue to use the conventional manufacturing development model, which is characterized by high investment, high energy consumption, and high emissions. This will deter manufacturing enterprises from choosing the “negative participation” strategy.

In the development stage of high-quality development, manufacturing enterprises can cut losses by driving their high-quality development through innovation and producing high-quality products. Since enterprises are actors seeking to maximize economic benefits, effectively reducing the cost of implementing high-quality development is a crucial way to choose a “positive participation” strategy. To reduce costs, it is necessary to improve quality and efficiency, make technological innovations, improve the technology system, and build an entire industrial chain. This cannot be achieved by manufacturing enterprises alone but also relies on the government's participation. Local governments should vigorously support enterprises' technological research and development and innovation and help manufacturing enterprises solve basic problems through policies and subsidies. Local governments should adopt incentive policies such as subsidies and rewards to reduce the cost of the positive participation of enterprises in high-quality development. Additionally, after enterprises positively participate in high-quality development, their products or quality will be greatly improved, which will increase additional benefits for consumers. As a result of the enhanced benefits of using products, consumers on the market are more likely to prefer the products or services of enterprises that choose the “positive participation” strategy. Consumers' demands drive the supply of high-quality development by manufacturing enterprises. When consumers voluntarily choose to invest in high-quality products or services, the government should offer them financial incentives such as partial tax exemptions and corresponding financial subsidies.

In the mature stage of high-quality manufacturing development, both leading and following enterprises have positive profits. With the gradual improvement of the market for high-quality development, the government should establish an effective regulatory system for high-quality development. The government should improve laws and regulations to restrict the speculative behaviour of some enterprises seeking private benefits by choosing a “positive participation” strategy. The government can implement a series of effective regulatory systems, establish industry standards for manufacturing enterprises, and implement mandatory measures to regulate the behaviour of enterprises in choosing a “positive participation” strategy. Governments can reduce the cost of policy incentives, make full use of the media, the internet, and non-profit organizations for policy advocacy, and use market mechanisms and intangible resources for automatic regulation and policy promotion. In addition, the government should reduce direct subsidies to leading and following enterprises, give full play to the decisive role of the market in resource allocation, and better play its own role of governing.

6. Conclusions and managerial insights

6.1. Conclusions

The evolutionary game of high-quality manufacturing development is an emerging area. A game payoff matrix of the high-quality development of the manufacturing industry is established under the premise of limited rationality, which is composed of the local government, leading enterprises and following enterprises. A detailed discussion of the influence of factors on the evolutionary stability of the model of the high-quality development of the manufacturing sector is provided in this paper. These factors include initial probability, innovation capability, organization construction, and industry resources. The following findings and suggestions are drawn from this study:

• (1)According to evolutionary game theory, increasing the initial probabilities of local governments and leading and following enterprises can induce enterprises to choose “positive participation” strategies. When the initial probabilities of leading and following enterprises are at low levels, increasing the initial probability of local government can accelerate the evolution of enterprises to “positive participation” strategies.
• (2)When the initial probabilities of local governments and leading and following enterprises are all at low levels, increasing the innovation capability coefficient can motivate enterprises to choose the “positive participation” strategy. When the initial probabilities of local government, leading and following enterprises are all at middle levels, increasing the innovation capability coefficient can slightly increase the convergence speed of leading and following enterprises in choosing positive participation strategies.
• (3)When the initial probabilities of local governments and leading and following enterprises are all at low levels, increasing the organizational construction coefficient can motivate enterprises to choose the “positive participation” strategy. When the initial probabilities of local governments and leading and following enterprises are all at middle levels, increasing the organizational construction coefficient has a slight positive effect on the convergence speed of leading and following enterprises in choosing positive participation strategies.
• (4)When the initial probabilities of local governments and leading and following enterprises are all at low levels, increasing the industry resources coefficient can motivate enterprises to choose the “positive participation” strategy. When the initial probabilities of local governments and leading and following enterprises are all at middle levels, increasing the industry resources coefficient can improve the convergence speed of leading and following enterprises in choosing positive participation strategies.

6.2. Managerial insights

High-quality development is important for achieving sustainability in manufacturing. The positive participation strategy of enterprises has a significant impact on this process. The results of this study show that initial willingness, innovation capability, organizational construction and industry resources are key factors influencing the high-quality development of manufacturing. Therefore, the following policy implications are proposed in this paper:

First, the government should regularly increase the publicity of the high-quality development of the manufacturing industry, fully stimulate and mobilize the enthusiasm, initiative and creativity of the high-quality development of manufacturing enterprises, and strengthen the awareness of this development so that manufacturing enterprises pay attention to high-quality development. The government attaches great importance to the high-quality development of the manufacturing industry, which can effectively enhance the probability of enterprises participating in high-quality development.

Second, enterprises should attach great importance to innovation, put innovation capability first, and accelerate the overall innovation around the implementation of an innovation capability strategy. In this new development concept, innovation is the core of the high-quality development of the manufacturing industry and is the most fundamental and lasting source of power to provide support for the high-quality development of the manufacturing industry. To promote high-quality development, enterprises should strive to improve the scientific level, technological innovation, service innovation, product innovation, management innovation, and marketing innovation.

Third, enterprises should combine stakeholder synergy, human capital development, ideological and political work, corporate style construction and corporate culture construction to continuously improve their organization construction capabilities. Stakeholders play a role in promoting the development of the enterprise. Balancing each stakeholder is an important basis for promoting the high-quality development of an enterprise. Enterprises should increase the introduction of talent to provide strong intellectual support for the high-quality development of the manufacturing industry. At the same time, party construction, as an essential political resource for Chinese enterprises, is a necessary condition for enterprises to build a modern enterprise system and achieve high-quality development.

Fourth, manufacturing enterprises should improve the level of industry resources, accelerate the pace of industry structure upgrading and improve the level of industrial foundation. Industrial structure adjustment is the key path to coordinating the sustainable development of the manufacturing industry and environmental protection. Enterprises should strive to expand to the high end of the value chain and gradually change from production and manufacturing to production and service. An enterprise must strengthen its industrial foundation ability to achieve high-quality development. The industrial foundation ability is crucial to an enterprise's development because it controls the growth of other industries, influences the enterprise's development strategy, and affects how quickly it operates.

Fifth, the government should adopt stronger subsidies and penalties to prompt enterprises to evolve towards the “positive participation” strategy. The government should initially provide differentiated financial subsidies for high-quality development according to the characteristics of enterprises and penalize enterprises that do not implement high-quality development to enhance their willingness to engage in “positive participation”. The government should also create an environment for high-quality development. Only when enterprises and the government work together to maximize the willingness of the former to participate can the high-quality development of manufacturing enterprises be realized.

6.3. Limitations and research directions

This study analyses the behaviour strategy of the manufacturing high-quality development system composed of local governments, leading enterprises and following enterprises, as well as the influence of relevant factors on the equilibrium of the system. However, this study has the following limitations. First, the foundation of this study is a relative idealistic assumption. Regardless of the vertical cooperation between upstream and downstream of the industrial chain, local governments, leading enterprises and following enterprises are assumed to be independent stakeholders. Therefore, one of the next research goals will be to examine how to create a more realistic model to include the interests of the three parties in many fields in the complex real world. Second, even if the simulation results and model analysis agree, the parameter values are set in a quite abstract manner. To better match the actual situation, more data collection is needed, and empirical analysis is the next step in the research process. Finally, the evolutionary game model used in this study concentrates on local governments, leading enterprises, and following enterprises while ignoring other subjects such as customers and suppliers. These also contribute significantly to the high-quality development of the manufacturing industry. Future research should focus on how to construct a more useful model that considers more subjects and information based on the relationships between subjects.

Declarations

Author contribution statement

Jinfa Shi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Yongqiang Su: Conceived and designed the experiments; performed the experiments; Wrote the paper.

Funding statement

This study is supported by the Philosophy and Social Science Planning Project of Henan (2022BJJ066) and the National Natural Science Foundation of China (71371172).

Data availability statement

Data will be made available on request.

Declaration of interest's statement

The authors declare no competing interests.

Additional information

No additional information is available for this paper.