Chiral conformity emerges from the least-time free energy consumption

Abstract

The prevalence of chirally pure biological polymers is often assumed to stem from some slight preference for one chiral form at the origin of life. Likewise, the predominance of matter over antimatter is presumed to follow from some subtle bias for matter at the dawn of the universe. However, rather than being imposed from the start, handedness standards in societies emerged to make things work. Since work is the universal measure of transferred energy, it is reasoned that standards at all scales and scopes emerge to consume free energy. Free energy minimization, equal to entropy maximization, turns out to be the second law of thermodynamics when derived from statistical physics of open systems. This many-body theory is based on the atomistic axiom that everything comprises the same fundamental elements known as quanta of action; hence, everything follows the same law. According to the thermodynamic principle, the flows of energy naturally select standard structures over less-fit functional forms to consume free energy in the least time. Thermodynamics making no distinction between animate and inanimate renders the question of life’s handedness meaningless and deems the search for an intrinsic difference between matter and antimatter pointless.

1. Introduction

The prevalence of left-handed amino acids and right-handed sugars over their mirror-image molecules on the Earth is not truly comprehended. Likewise, the predominance of matter over antimatter in the universe is not well understood.

Here, I argue that chiral conformity, like all standards, emerges from minimizing free energy in the least time. This universal imperative states the common cause for molecular homochirality and corpuscular charge convention while leaving specific scenarios to these standards open.

In physics, a cause is a force, i.e. a difference in energy. However, it may seem as if forces are negligible to favour a form over its mirror image. There is hardly any difference in energy between two enantiomers when in a test tube [1–5] or between a particle and its antiparticle when in a cloud chamber [6,7]. Thus, under these reduced experimental conditions, the dissymmetry in abundance between left- and right-handed forms seems inexplicable indeed [8,9].

Then again, in the biosphere, the force for the enantiomeric excess is enormous. Wrong-handed molecules would block metabolism consuming free energy, ultimately totalling all energy absorbed in photosynthesis. Similarly, in the cosmos, the broken charge–parity symmetry for particles is compelling. Antiparticles would purge particles from participating in nuclear reactions powering stars, thereby eventually terminating all processes. And in an economy, non-standard components would jam assembly lines and shut down activity.

From this thermodynamic perspective, free energy minimization imposes molecular and corpuscular standards for systems to gain balance with their surroundings in the least time. Thus, the tellurian homochirality convention and the universal charge–parity violation emerged from evolution rather than from some subtle bias during abiogenesis [10,11] and baryogenesis [12]. I motivate this view with an all-inclusive theory of evolution derived from statistical physics.

Thinking of evolution to chirality standards, specifically, or in general as a series of changes—nothing more, nothing less—points to atomism. As the ancient Greeks reasoned, how else could one thing transform into another unless both are made of the same elemental entities? Indeed, everything comprising fundamental, indivisible elements seems all-inclusive enough of an axiom to found a universal theory of evolution. Ultimately, not only biota but everything is in flux.

The old atomistic idea entertained Galileo, Newton and undoubtedly Dalton, but notably in the context of evolution, Boltzmann. He pioneered statistical physics, the probability theory underlying thermodynamics. After all, among the laws of physics, the second law of thermodynamics is the one with time’s arrow, evolution’s unmistakable characteristic.

However, Boltzmann failed to derive the equation of probable motion towards thermodynamic balance [13]. Already, his contemporary Loschmidt wondered how time-symmetric motion, i.e. stochastic dynamics, proposed by Boltzmann, instead of irreversible thermodynamics, could possibly lead to the flow of time. Also, Zermelo remarked that Boltzmann’s H-theorem implied recurrence; a system, once in a state of imbalance, returns to that state of imbalance. But such things do not happen.

In precis, Boltzmann formulated a stationary-state condition, not an equation of evolution. Since a steady-state system can only lose its coherence, not its energy, increasing entropy became erroneously associated with increasing disorder. Due to this misunderstanding, the evolution into orderly structures, e.g. chiral conformity, became a puzzle.

At best, near balance, forces relate nearly linearly to flows so that the Onsager reciprocal relations hold well. Then the principle of minimum entropy production describes reproducible dynamical steady states, known as dissipative structures [14]. But in general, when out of balance, the equation of evolution has remained obscure.

From this historical perspective, thermodynamics deserves to be rederived from statistical physics. Then, as I show, evolution into chiral standards, or in general to orderly structures, can be understood as expressions of increasing entropy, equal to decreasing free energy, instead of being misunderstood as manifestations of decreasing entropy incorrectly equated with increasing order.

2. Statistical physics

Among the theories of physics, thermodynamics is considered a universal theory of macroscopic quantities [15], however, not a fundamental one deriving from microscopic entities. Thus, for formulating the theory of evolution from first principles, the crux of the matter is the fundamental element.

The old idea of seeing the light quantum as the basic building block of everything [16] is still motivated since all particles and antiparticles annihilate into light quanta [17]. This indivisible and indestructible element, known best as the photon, carries energy, E, on its period, t, totalling an invariant, Planck’s constant, h = Et [18].

As per thermodynamics, the flows of quanta, for example, from hot to cold, even out energy differences. Similarly, photosynthesis, employing chirally pure compounds, decreases the energy difference between insolation and matter. In turn, nuclear reactions, engaging standard particles, level the energy difference between matter in stars and the surrounding space. Also, societies establish and employ standard structures, e.g. right-handed bolts in their machinery consuming surrounding supplies.

So, energy does not flow whichever way. The flows naturally select paths that decrease differences in the least time, e.g. those equipped with chiral compounds. Conversely, less-efficient paths dry up [19,20]. Thus, nature is not wandering arbitrarily but evolving actively towards thermodynamic balance.

The equation of evolution, i.e. the series of changes towards thermodynamic balance, can be derived from statistical physics, the state of natural things, katástasi ta physiká (Greek). The resulting differential equation counts flows that transform the system from one state to another [21,22]. In this way, evolution is mathematized as a natural process consuming free energy in the least time in every detail and all enormity.

The general theory by expressing changes of any kind as flows of quanta—nothing more, nothing less—also describes the evolution from a racemic mixture into a chiral consonance. Irrespective of the complexity, such a detailed account can be given, even without knowing the entities explicitly, thanks to the fundamental simplicity of every entity basically comprising quanta.

2.1. The probability of an entity

To derive the state equation, consider the probability of finding a molecule, chiral or achiral, for example, in a primordial warm little pond, by asking what it takes for that molecule to exist. Clearly, if any one of its substrates, indexed with k, is absent altogether, the j-product cannot exist. This nil condition is guaranteed by including all ingredients in a mathematical product, ∏_k.

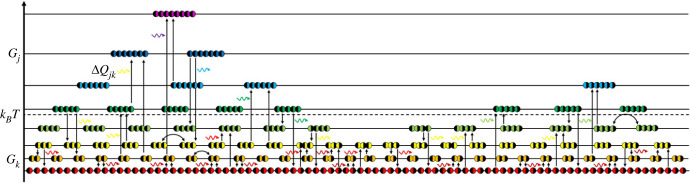
Besides the substrates in numbers, N_k, also the energy difference, −ΔG_jk, between the k-substrate and j-product narrows the existence of the j-molecule as apparent from an energy level diagram (figure 1). In turn, an influx of energy, ΔQ_jk, coupling to the jk-reaction, widens the existence. Thus, the probability of the j-molecule is the product over all k-ingredients,

$${\hspace{0.17em}}_1{P}_j=\prod _k{N}_k\exp \left[\frac{(-\mathrm{\Delta }{G}_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk})}{k_{B}T}\right],$$ 2.1

where the energy differences in the scale-free exponential form, d exp(x)/dx = exp(x), are relative to the average energy, k_BT [23]. In the exponent, the notation by i distinguishes energy in radiation from energy in matter. In this way, the textbook statistical mechanics of closed or stationary systems [24] opens up to account for evolution by endergonic and exergonic transformations also towards thermodynamic balance that displays chiral purity [22,25].

Figure 1.

Energy level diagram depicts a system evolving through chemical reactions of chiral residues (◐ and ◑). Compounds of the same energy, G_k, relative to the average energy, k_BT, are on the same level in numbers, N_k. Their exchange (curved arrows) is of no consequence, but reactions (vertical arrows) involving compounds with different energy, G_j, in numbers, N_j, coupled with the flux of quanta with energy, ΔQ_jk (wavy arrows), move the system towards thermodynamic balance with its energy-rich surroundings. In general, reactions yield mixed-handed polymers. Only if chiral-pure products turn out to catalyse their own enantioselective polymerization will the multiple mixed-polymer reactions fall behind in furthering the system towards thermodynamic balance.

2.2. The probability of a population

The probability of a population,

$$P_j=\frac{{({\hspace{0.17em}}_1{P}_j)}^{N_j}}{N_j!},$$ 2.2

of N_j molecules ensures that if any one j-molecule were missing, i.e. ₁P_j = 0 (equation (2.1)), then also P_j = 0. Since the number of ways of choosing identical molecules is inconsequential, the product is divided by the factorial N_j!.

Specifically, the probability of left-handed molecules differs from that of right-handed ones because of energy differences between the molecules and surroundings, not because of some minute differences between the molecules themselves. For example, machinery comprising chirally pure components can be more effective in consuming free energy than one made of mixed ingredients.

2.3. The probability of a system

Finally, the total probability for the whole system of populations (equation (2.2)),

$$P=\prod _j{P}_j=\prod _j\frac{{(\prod _k{N}_k\exp (-\mathrm{\Delta }{G}_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk})/k_{B}T)}^{N_j}}{N_j!},$$ 2.3

guarantees, again by the product ∏_j, that if any one population, say, a pool of chiral-pure catalysts, was absent altogether, i.e. P_j = 0, then also P = 0. As per equation (2.3), even if a single quantum were missing, the reaction mixture would not exist exactly as it does.

The total probability (equation (2.3)) is the main result of statistical physics. It gauges the state of a system by including all quanta. The formal precision of one quantum is a mere corollary of everything comprising quanta.

Next, deriving thermodynamics, i.e. changes from one state to another, is mere mathematical differentiation. Namely, energy differences force changes.

3. Thermodynamics

The total probability (equation (2.3)) is a precise measure of a macroscopic system comprising microscopic constituents, i.e. quanta. Its derivative, dP/dt, could be computed. But, in practice, the evolution with time, t, from one state to another is easier to derive from ln P, customarily multiplied by Boltzmann’s constant to entropy, S = k_B ln P [21].

It is worth emphasizing that entropy, S, as a mere logarithm of the probability (equation (2.3)), is a measure of energy per T, not of disorder. In other words, orderly structures, such as chirally pure biopolymers, emerge for the system to gain balance with its surroundings. Thus, their presence is not a sign of imbalance. For example, chromophores, plant leaves, and solar panels materialized to transfer energy from insolation to matter. Conversely, when a system loses energy on its way to balance with low-energy surroundings, the outcome may be disordered, such as broken photoreceptors, but also ordered, such as fluid frozen into a crystalline solid. Thus, by empirical evidence, disorder is no goal in itself. On the contrary, even on the cosmic scale, the projected heat death of the universe entails, by Bose–Einstein statistics, a highly structured vacuum [26,27].

Despite disorder being an outcome, just like order, rather than a universal objective, increasing entropy has been mistaken for increasing disorder ever since Boltzmann’s failure to derive the proper equation of state that includes free energy. Namely, Boltzmann’s steady-state system cannot change in energy but may only decohere through the exchange of quanta with incoherent surroundings. As the ergodic hypothesis states [28], such a phase-space evolution between conceptual microstates of equal energy is not the same as the state-space evolution between factual states of unequal energy.

Moreover, the evolution towards thermodynamic balance depends on the path, i.e. history. Therefore, the textbook equation, d̄$Q=T\hspace{0.17em}\mathrm{d}S$, denoting the consumed free energy, d̄Q, causing the change in entropy, dS, in a given temperature, T, is written using the inexact differential, d̄.

Expressly, forces imposing chiral purity increase along the path to chiral purity. In other words, evolution is virtuous circle for one form of handedness while vicious for the other. This interdependence between cause and consequences, i.e. forces and changes, is not circular reasoning but rationalizing non-determinism.

3.1. The equation of state

While the multiplicative probability (equation (2.3)) quantifies the state of a system perfectly, an additive measure is preferred as we are accustomed to adding things up when gauging the whole. To this end, the appropriate measure is entropy,

$$\begin{array}{rl}S& =k_B\ln P=k_B\sum _{\hspace{0.17em}j}\ln P_j\\ & \approx k_B\sum _{\hspace{0.17em}j}{N}_j(\sum _k\ln N_k+\frac{-\mathrm{\Delta }{G}_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}}{k_{B}T}-\ln N_j+1)\\ & =\frac{1}{T}\sum _{\hspace{0.17em}j,k}{N}_j(-\mathrm{\Delta }{\mu }_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}+k_{B}T),\end{array}$$ 3.1

where Stirling’s approximation lnN_j ! ≈ N_j ln N_j − N_j is excellent for a statistical system, i.e. one with many constituents.

Besides the energy bound in populations, $\sum N_j{k}_{B}T$, familiar from steady-state thermodynamics, equation (3.1) includes the energy difference, Δμ_jk = −μ_j + μ_k, between the j-product potential, μ_j = k_BT ln N_j + G_j, and k-substrate potential, μ_k = k_BT ln N_k + G_k, as well as the energy influx, ΔQ_jk, that couples from the surroundings to the jk-transformation. This free energy forces evolution from one state to another, e.g. from racemate to chiral purity.

Eventually, all free energy is consumed. At the dynamic steady state, |− Δμ_jk + iΔQ_jk| = 0, the flux, ΔQ_jk, balances the difference in potentials, Δμ_jk, and upholds a high-energy distribution of N_j, i.e. dissipative structures [29,30]. In other words, the state of balance should not be mistaken for an out-of-equilibrium state. Since a thermodynamic balance is between the system and its surroundings, a chirally pure state is not necessarily a sign of non-equilibrium but of balance in high-energy surroundings.

The total energy, TS = 2K, in a state of stationary motion adds up the energies of each and every quantum of action, h. Accordingly, the total action, $L=nh=\int 2K\hspace{0.17em}\mathrm{d}t$, integrates the kinetic energy of all quanta, 2K, over their periods (of time), t. Then, as by Noether’s theorem: every differentiable symmetry of the action of a physical system has a corresponding conservation law [31]. So, symmetry means that energy is conserved and time is invariant [32]. Conversely, symmetry is broken at every step of evolution when at least one quantum is either absorbed into the system or emitted from the system to its surroundings.

3.2. The equation of change

Differentiating the state equation (equation (3.1)) with respect to time gives the equation of evolution [32],

$$\frac{\mathrm{d}S}{\mathrm{d}t}=\sum _{\hspace{0.17em}j}\frac{\mathrm{d}S}{\mathrm{d}{N}_j}\frac{\mathrm{d}{N}_j}{\mathrm{d}t}=\frac{1}{T}\sum _{\hspace{0.17em}j,k}\frac{\mathrm{d}{N}_j}{\mathrm{d}t}(-\mathrm{\Delta }{\mu }_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}).$$ 3.2

As expected, free energy, −Δμ_jk + iΔQ_jk, causes changes in entropy. It makes things happen. For example, the chemical potential difference, −Δμ_jk, along with the influx of photons, ΔQ_jk, that couples to the jk-reaction, drives transformations between the k-substrates and j-products. Conversely, no change of state is non-dissipative. Thus, the accurate reduction of a system to its constituents counts as constituents also the dissipated quanta [33].

The jk-indexes show that a system taps into surrounding flux, ΔQ_jk, via its N_k and N_j constituents. Accordingly, novel constituents may draw from new forms of free energy. Conversely, without appropriate means, the system does not sense free energy potentials.

The system evolves until dS/dt = 0 (equation (3.2)). When all free energy is consumed, influx and efflux tally. Then entropy is at maximum, $S=k_B\sum N_j$, and free energy at minimum, $\sum _{\hspace{0.17em}j,k}{N}_j|-\mathrm{\Delta }{\mu }_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}|=0$ (equation (3.1)). In the dynamic balance, all populations are steady, dN_j/dt = 0, within the characteristic period of a system.

3.3. The rate equation

On the way to the free-energy minimum, the populations, N_j, change at the rate

$$\frac{\mathrm{d}{N}_j}{\mathrm{d}t}=\frac{1}{k_{B}T}\sum _k{\sigma }_{\hspace{0.17em}jk}(-\mathrm{\Delta }{\mu }_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}),$$ 3.3

proportional to the mechanisms, σ_jk ≥ 0, that transform energy free in differences into the energy bound in populations [34]. For example, an enzyme is a mechanism, σ_jk, that speeds up the jk-reaction over an innate reaction mechanism, ${\sigma }_{\hspace{0.17em}jk}^{\hspace{0.17em}\mathrm{\prime }}$. For example, carbonic anhydrase catalysis beats the intrinsically fast conversion of carbonic acid to carbon dioxide and water.

According to equations (3.2) and (3.3), the more effective the mechanism, the faster the increase in entropy, equivalent to a faster decrease in free energy. Therefore, to gain balance in the least time, the flows of energy naturally select paths with efficient mechanisms while leaving other paths to run dry [20]. It is the least-time imperative to consume free energy rather than energy differences as such, let alone the difference between a chiral compound and its mirror image, that matters when it comes to survival of the fittest.

In thermodynamic terms, the biological fitness criterion is the rate of free energy consumption, which in many cases displays as proliferation. From this perspective, it makes sense, for instance, that nucleotides enriched on the early Earth as they forwarded evolution first by absorbing sunlight, then catalysing polymerization, and eventually storing, carrying, and translating information [35–37]. In this light, difficulties in defining life and deciphering its origin follow from reductionism drawing groundless demarcation lines.

By the scale-free theory, a mechanism itself is a system of its own. For example, a molecule is a system of atoms that evolves through chemical reactions. Also, molecular evolution directs along the lines of force and the flows of energy naturally select those molecules that increase entropy in the least time. For example, the highly ordered genome, the oxymoronic ‘aperiodic crystal’ [38], emerged to serve evolution, not to supervise it [39,40]. Similarly, standard metabolites and rated octanes accelerate free energy consumption. Conversely, non-standard substances, like mixed-handed polymers, have gone almost extinct.

It is worth emphasizing that thermodynamics (equation (3.2)) by denoting the jk-paths of transformations is consistent with the least-time kinetics (equation (3.3)). Transformations always run downhill in free energy, never crossing energy barriers, just like water never climbs uphill. Also, in a rapid, having energy in motion, water rushes downhill over rocks. So, a catalyst does not alter energy differences, only the rate, σ_jk, at which free energy is consumed (equation (3.3)), for example, by binding to the reactants. Therefore, I argue that the least-time free energy consumption drives systems, one way or another, to emerge with standards such as homochirality that speed up the system’s evolution towards balance with its surroundings.

It is also worth noticing that evolution by equation (3.3) is non-deterministic because consequences, i.e. changes, dN_j/dt, are inseparable from causes, i.e. forces, since potentials, μ_j = k_BT ln N_j + G_j, contain N_j. Thus, it is not the complexity of evolution per se but the interdependence between causes and consequences that precludes determinism, calculating the final stationary state from an initial state. Customarily, the path dependence is known as history, the great chain of beings (scala naturae), the prime evidence of evolution.

Moreover, while near chemical equilibrium, the reaction rate is approximately proportional to the product of the reactant activities or concentrations [41,42], in general, the rate is proportional to free energy. This is to say, the law of mass action approximates the rate equation (equation (3.3)).

Inserting equation (3.3) into equation (3.2) proves the renowned inequality,

$$\frac{\mathrm{d}S}{\mathrm{d}t}=\frac{1}{k_B{T}^2}\sum _{\hspace{0.17em}j,k}{\sigma }_{\hspace{0.17em}jk}(\mathrm{\Delta }{\mu }_{\hspace{0.17em}jk}^2+\mathrm{\Delta }{Q}_{\hspace{0.17em}jk}^2)\ge 0.$$ 3.4

It follows from the conservation of quanta. The quanta do not appear out of nothingness or disappear into nothingness but move from the system to the surroundings or vice versa. So, the system and its surrounding system invariably evolve together. For example, an animal adapts to its habitat and the habitat to the animal. On the whole, the evolution of the biosphere altered Earth’s atmosphere [43,44]. And the more recent evolution of the anthroposphere affects the global climate, and the changing climate strikes back to human habitats.

The free energy consumption (equation (3.2)) sets the arrow of time locally and universally [32]. Conversely, natural processes are reversible as much as there is free energy and mechanisms to run reverse reactions.

In summary, every system evolves towards balance with its surrounding systems as flows of quanta even out energy differences in the least time. Thus, every system is at the mercy of its greater surrounding system. For example, a molecule cannot but react under reactive circumstances in a cell. Likewise, a cell cannot but differentiate under the conditions imposed by an organism. Since circumstances matter, the emergence of homochirality, let alone life, does not readily reduce to test-tube conditions. Similarly, the advent of particles in excess over antiparticles, let alone all matter, does not easily confine to artificial conditions.

3.4. The patterns in data

Throughout nature, we find that data closely follow power laws, sigmoid growth curves, and skewed, nearly lognormal distributions [45–47]. These patterns are the imprints of evolution resulting from the least-time free energy consumption [21].

The rate equation (equation (3.3)) shows that the ubiquitous, s-shaped curve builds up from an initial, nearly exponential, $N_j(t)\propto \exp (\sum _k{\sigma }_{\hspace{0.17em}jk}t)$, free energy consumption by primitive mechanisms, σ_jk, and from final, declining consumption, $N_j(t)\propto \exp (-\sum _k{\sigma }_{\hspace{0.17em}jk}t)$, of nearly exhausted resources by mature mechanisms, and from $\mathrm{d}{N}_j/\mathrm{d}t=$ $j{\alpha }_j{N}_1^{\hspace{0.17em}j-1}\hspace{0.17em}\mathrm{d}{N}_1/\mathrm{d}t=j(N_j/N_1)(\mathrm{d}{N}_1/\mathrm{d}t)$ in between that integrates into a power law, ln N_j = j ln N₁ + constant, as the elemental constituents, the quanta, N₁, amass through mn-transformations, α_j = ∏_mnexp[( − Δμ_mn + iΔQ_mn)/k_BT], into various entities $N_j=\prod _k{N}_k\exp [(-\mathrm{\Delta }{G}_{\hspace{0.17em}jk}+i\mathrm{\Delta }{Q}_{\hspace{0.17em}jk})/k_{B}T]={\alpha }_j{N}_1^j$.

Invariably, natural distributions of energy, bound in potentials, μ_j = k_BT ln ϕ_j, are skewed, nearly lognormal when the variation, n, is small, i.e. n ≪ j, around the average density in energy [23], ϕ_j = N_jexp(G_j/k_BT), because $\ln {\varphi }_{\hspace{0.17em}j-n\cdots j+n}=\ln {\varphi }_j+\sum _{n}n\ln {\varphi }_1$ distribute approximately in a normal manner according to the central limit theorem. For example, gene lengths distribute in this manner [48].

Since skewed distributions accumulate along sigmoid curves, deviating at low and high ends from the power law [49,50], the many patterns in data display one and the same principle, the least-time free energy consumption. Therefore, there are no grounds to regard evolution into homochirality as distinct from evolution in general.

4. Evolution into chiral uniformity

From the thermodynamic theory, as formulated above, the prominence of L-amino acids over D-amino acids and the dominance of matter over antimatter are not special cases of broken symmetry but manifestations of symmetry breaking in general. It is a sheer corollary of Noether’s theorem [31] that a change in energy accompanies a change in time. Thus, the broken symmetry between the amounts of mirror-image moieties is not a sign of minute imbalance between the left- and right-handed form but the signature of irresistible evolution towards balance.

According to the inequality dS/dt ≥ 0 (equation (3.4)), the more effective a transformation mechanism, σ_jk, the faster the increase in entropy. Thus, chirality consensus emerges when such a standard provides faster mechanisms for minimizing free energy and access to more free energy. Conversely, a standard will be loosened, even abandoned, when it curtails an increase in entropy.

In general, the larger the system, the bigger the benefits of standardization. So too, large reaction mixtures cross over more readily from achiral to chiral and further from racemate to chirally pure species [51]. Conversely, a chirality standard, like any other standard, is useless in a small system where there is no substantial potential for faster processing outweighing the costs of standardization. For example, screw standard becomes useful first when many screws are needed for the energy transduction machinery. Likewise, we should expect homochirality of molecular machinery to emerge along with increasing metabolism rather than budding from some subtle bias (figure 2).

Figure 2.

Energy level diagram depicts a system evolving into homochirality through chemical reactions of chiral residues (◐ and ◑). Compounds of the same energy, G_k, relative to the average energy, k_BT, are on the same level in numbers, N_k. Their exchange (curved arrows) is of no consequence, but reactions (vertical arrows) with compounds of different energy, G_j, in numbers, N_j, coupled with the flux of quanta with energy, ΔQ_jk (wavy arrows), forward the system towards thermodynamic balance. When the chiral-pure products (on the left and on the right) catalyse their own enantioselective polymerization, the mixed-handed polymers (in the middle) emerging from multiple reactions fall behind irretrievably. By the same token, improvements, for example, in the left-handed synthesis yield ever more powerful autocatalysts that shift the balance ever more in favour of the left-handed polymers.

According to the equation of evolution (equation (3.2)), a racemate becomes unstable when the chiral-pure polymer synthesis increases entropy faster than mixed-handed syntheses. The scenario is likely since even a single improvement on the enantioselective synthesis profits all the chirally pure polymers, whereas only multiple mutations may improve multiple reactions producing mixed-handed polymers (figure 2).

The ever more effective chiral constituents increase the influx of energy that, in turn, refuels the asymmetric steady state faster than racemization erodes it [30]. By the rate equation (equation (3.3)), the faster enantioselective synthesis becomes, the more it eclipses racemizing. And by the same argument, autocatalysis surpasses catalysis; the system adopts and advances one form of handedness while abandoning the other as disordering, even disruptive [52].

Moreover, chirally pure polymers, folding into supramolecular structures, may sustain the strain needed for catalysis [53] better than mixed-handed polymers in the same manner as pure substances maintain structure upon heating better than mixtures. Conversely, like other standards, chirality standards will be lost in circumstances where they no longer provide superior free energy consumption over random processes.

While initial improvements in facilitating free energy consumption might well have been marginal, ultimately, one mutation after another, the pure-handed polymers excelled mixed-handed enormously. Similarly, Darwin argued that even a slight ability to sense light was better than nothing. And one improvement after another eventually led to an advanced eye. Conversely, the eye began to atrophy when food was found only in the dark, of which some bat and cavefish species are glaring examples.

In particular, the enantioselective synthesis is open for chiral amplification through autocatalysis [54–56]. When products catalyse their own synthesis or cocatalyse each other’s production, like ribozymes and enzymes, only a small nudge may suffice to divert the course to the left or to the right [57,58]. So commences a virtuous cycle for more and more free energy, providing ever more powerful catalysts of the one hand kind, while the other hand is in for a vicious cycle.

Like other natural processes, also the evolution into homochirality is expected to follow a sigmoid course [21,57,59], akin to the evolutionary course framed by the theory of punctuated equilibrium [60]. As by the rate equation (equation (3.3)), the early phase is rapid, nearly exponential, since the newly introduced standard opens up substantial resources. Likewise, the late phase is slow, nearly exponential decay, since returns through further standardization are marginal. The track between closely follows a power law, the characteristic of multiplicative processes [61,62], where every step depends on all previous steps. Likewise, the law of proportionate effect, also known as Gibrat’s Law and Zipf’s Law [63,64], renders the growth of a population, company, city, etc. along a power law.

In teleological terms, the goal of evolution is the free energy minimum. However, the end state is not predestined because evolution exposes new forces that affect its own course, and so on. Accordingly, the future is foreseeable as much as the forces at present are sensed. Conversely, the past is deducible as much as history is preserved in the present. So, we might never know how L-amino acids outrivaled D-amino acids and matter outplayed antimatter. Still, we know that the least-time quest for free energy minimum forced matter to choose one way or the other.

The degree of standardization, such as enantiomeric excess, serves as a measure of the degree of integration [57], e.g. in a network [65,66]. Namely, enormous forces, such as those between subatomic particles, impose strict standards. Conversely, without any interaction, there is no transformation, and anything goes. Qualitatively speaking, the rule of traffic is more stringent on lanes than on sidewalks because the consequences of cars crashing are more severe than of people bumping into each other.

While standardization speeds up processing, both anabolism and catabolism, violation of standard serves the same purpose. For example, among enzymes decomposing L-amino acid polypeptides, some protect themselves by incorporating D-amino acids [67–69]. Similarly, reverse threads are used in specialized applications in which right-handed screws or bolts would come loose.

Moreover, the capacity to process non-standard compounds suggests access to slowly circulating supplies, like deep-sea organic debris, racemized further than rapidly circulating moieties of shallow sea [70].

5. Theorizing and modelling

The proposed tenet explains why systems evolve into standards, like chiral conformity, not how this happens. The cause is force, i.e. an energy difference. Any system changes its motion along paths that consume free energy in the least time. Thus, matter evolves into chirally pure compounds when such standards contribute to the consumption of free energy faster than non-standardized substances. Conversely, systems abandon standards that impede free energy consumption. Thus, thermodynamics explains both presence and absence of chiral purity.

Theorizing evolution as the least-time free energy consumption both compares to and contrasts with modelling evolution. Unlike a model based on data, thermodynamics is based on the axiom that everything comprises the same basic building blocks. Ergo, the theory can be falsified with any data, whereas a model may be modified to match additional data [71]. Accordingly, an axiomatic theory aims to explain the cause of data, whereas a model aims to predict the course of data.

For example, the information-theoretic free-energy principle [72–75] resembles the minimization of free energy contained in information [76] by minimizing the difference between evidence, E, i.e. data, and hypothesis, H, i.e. model, in terms of the logarithm of the likelihood, −log P(E|H), i.e. the probability of observing E given H. However, in contrast to refining H to match E, free energy is not consumed to reach a predestined goal but to arrive at thermodynamic balance, wherever that might be.

Moreover, the information-theoretic iteration may seem like an intractable process due to many alternatives, but actually, non-determinism is not due to complexity but interdependence; the improving model provides improving evidence for improving the model. Similarly, free energy consumption affects the future consumption of free energy.

In practice, natural distributions with long tails are hard to sample exhaustively. Therefore, variational Bayesian methods are used to minimize the Kullback–Leibler divergence between the variational distribution, Q, and the full distribution, P. Similarly, an approximate form, such as a lognormal distribution, can be used when simulating evolution instead of using the true probability, P, housing numerous terms (equation (2.3)). However, in any case, defining the end state of optimization is not a faithful model of discovering it through minimizing free energy.

Since our sense of reality is invariably incomplete, we act according to the set of forces we deem significant. This behaviour is modelled by bounding the inference to a subset of variables, called a Markov blanket [77]. However, just like overlooked forces might prove to be irresistible, disregarded model parameters might turn out to be essential. While such a simplification is subjective, an objective view is an illusion, too. It takes a flow of energy to see, but a photon propagates from one object to only one observer, not to all observers.

In physics, probability is a measure of energy (equation (2.3)), not odds. In the frequentist’s sense, the probability is a propensity of nature, yet unknown a priori in the Bayesian sense. For example, presumed balanced odds will be updated after rolling a loaded dice. While the imbalance may seem between the faces, the faces are not weighed against each other but in the surrounding field of gravity. Likewise, particles and antiparticles, as well as mirror-image molecules, seem equal in energy. Yet, they are not rated against each other but against their surroundings.

So, when modelling, it is worth recalling that everything depends on everything else. Therefore, evolution is neither deterministic, i.e. predestined, nor indeterministic, i.e. random, but a non-deterministic process. Thus, even though the choice for L-amino acids over D-amino acids and for matter over antimatter may seem arbitrary, there were forces, no matter how fleeting and feeble [78,79], that tipped the balance in favour of the standards we witness. In other words, the evolutionary theory based on statistical physics does not discredit the ideas about the causes of initial symmetry breaking and the mechanisms of ensuing chiral amplification [3,78] but presents the universal principle underlying the courses of events.

6. Discussion

On the one hand, scientists wonder how left-handed amino acids gained supremacy over right-handed ones in the primordial soup [80] and how matter outweighed antimatter in the nascent universe. On the other hand, everyone grasps that conventions, for example, the rule of the road, materialized for things to work.

Work, in terms of physics, measures transferred energy. However, energy does not flow in whichever way but towards thermodynamic balance along the lines of force. Thus, the flows naturally select those channels that even out energy differences in the least time while abandoning others. As a result, the fittest mechanisms survive and other species go extinct. So, proper physics speaks the lingo of biology [81].

Nature is evolving manifestly. Still, physics has focused on stationary states ever since its mathematization in the seventeenth century [82]. Physicists yearned for exactness with the equations that can be solved but at the cost of correctness. Since symmetry secured solutions, concurrent energy conservation and timeless orbits became the ideals of theorizing. Consequently, the inseparable flow of energy and time was no longer seen embodied in the propagation of a light quantum having energy, E, on its period, t [32,83].

In contrast to the tractable stationary trajectories, evolutionary courses are intractable because motion consuming its driving forces affects its own course. When variables cannot be separated, not only is the future unforeseeable as much as the forces are not present, but also the past is undecipherable as much as relics are lost. Therefore, we might never be able to pin down how the prebiotic integration for increased free energy consumption forced the synthesis of homochiral compounds [84] and how, eons earlier, the immense energy contained in the primordial substance forced transformation into characteristic chirality of matter [85–87]. But still, thermodynamics tells us why all this took place.

Accordingly, thermodynamic thinking favours scenarios to homochirality that are driven by the energy difference between the system and its surrounding rather than those that present a minute energy difference between the mirror-image compounds. From this stance, the enantiomer excess of amino acids in meteorites is taken as evidence but not the cause of the early drive towards chiral conformity [88]. By the same token, circularly polarized light from space might have biased primordial chemical synthesis slightly in favour of one enantiomer over the other [79]. Still, such an early preference might have been only fleeting and overruled by thermodynamic fluctuations later. While leaving it open which way, the overwhelming energy in insolation powered evolution in general and specifically to homochirality.

From the thermodynamic standpoint, it was a mistake to take homochirality as the signature of life [78,89], but not as fundamental as taking for granted that there is life [90,91]. Namely, data removed from the legends and labels we penned make no distinction between animate and inanimate. All data display the same statistical characteristics of skewed distributions that accumulate sigmoidally and hence follow mostly power laws [45,47,49,50,92]. Thus, the uniformity in data substantiates the universality of thermodynamics. Consequently, a phenomenon can be understood like another one across scales and scopes. Through this lens of empirical evidence, life’s origin seems a groundless supposition, and so too does the genesis of the universe. Logically, all we witness is the permanent and unbreakable quanta in evolution.

Understanding evolution as least-time free energy consumption—nothing more, nothing less—presents a paradigm shift [93]. It is no longer meaningful to contemplate why the natural compounds are homochiral and why the predominant particles are chirally defined. The irresistible force towards thermodynamic balance makes all things happen. It is the final cause in the Aristotelian sense.

Also, investigating efficient causes seems secondary because the final cause employs whatever mechanisms or agencies to attain balance in the least time. So, as much as the past is lost, it is hard to prove how exactly L-amino acids outperformed D-amino acids on the face of the early Earth. Instead, it stands to reason that the conformity in chirality, like other conventions, settled during abiogenesis [94] to consume free energy through functions that evolved further to those we label biological. Similarly, there is hardly any point in speculating that all matter would be the remnant of a massive initial annihilation [12]. Instead, it is reasonable to think that the charge–parity standard materialized during baryogenesis. The primordial, elementary substance took the form of particles to consume free energy through particle reactions. Thus, evolution into chemical and cosmic standards compares to adopting either left- or right-hand traffic as the traffic grew, not only after a dazzling demolition derby.

In summary, a handedness convention is pointless—perplexing—without hands to shake with. Accordingly, chirality standards did not emerge in isolation but evolved for the system to gain balance with its surroundings. Since profound problems originate from problematic premises of thought, focusing on ever finer details only distances us from holistic thinking that renders the problems of reductionism null and void. In this sense, the thermodynamic take on evolution is more rigorous than radical.

Data accessibility

This article has no additional data.

Authors' contributions

A.A.: conceptualization, writing—original draft, writing—review and editing.

Conflict of interest declaration

I declare I have no competing interests.

Funding

No funding has been received for this article.