Optimal vaccine allocation for the control of sexually transmitted infections

Abstract

The burden of sexually transmitted infections (STIs) poses a challenge due to its large negative impact on sexual and reproductive health worldwide. Besides simple prevention measures and available treatment efforts, prophylactic vaccination is a powerful tool for controlling some viral STIs and their associated diseases. Here, we investigate how prophylactic vaccines are best distributed to prevent and control STIs. We consider sex-specific differences in susceptibility to infection, as well as disease severity outcomes. Different vaccination strategies are compared assuming distinct budget constraints that mimic a scarce vaccine stockpile. Vaccination strategies are obtained as solutions to an optimal control problem subject to a two-sex Kermack–McKendrick-type model, where the control variables are the daily vaccination rates for females and males. One important aspect of our approach relies on conceptualizing a limited but specific vaccine stockpile via an isoperimetric constraint. We solve the optimal control problem via Pontryagin’s Maximum Principle and obtain a numerical approximation for the solution using a modified version of the forward–backward sweep method that handles the isoperimetric budget constraint in our formulation. The results suggest that for a limited vaccine supply ($20\%$–$30\%$ vaccination coverage), one-sex vaccination, prioritizing females, appears to be more beneficial than the inclusion of both sexes into the vaccination program. Whereas, if the vaccine supply is relatively large (enough to reach at least $40\%$ coverage), vaccinating both sexes, with a slightly higher rate for females, is optimal and provides an effective and faster approach to reducing the prevalence of the infection.

Introduction

According to global estimates of the World Health Organization (2021), the burden of sexually transmitted infections (STIs) remains high, counting over 350 million new infections annually with one of the four most common STIs—chlamydia, gonorrhea, syphilis, and trichomoniasis. Although the majority of these infections can be cured, when not treated, STIs might lead to serious health consequences. In 2020, the human papillomavirus (HPV) caused over 600,000 new cases of cervical cancer and 342,000 deaths (Sung et al. 2021). Mother-to-child transmission of syphilis, or congenital syphilis, leads to over 350,000 adverse birth outcomes such as early fetal and neonatal deaths, stillbirths, and preterm or low-birth-weight babies (Korenromp et al. 2019). Negative effects associated with untreated gonorrhea and chlamydia infections include reproductive tract morbidities, such as tubal factor infertility and pelvic inflammatory diseases among women (Tsevat et al. 2017). Gonorrhea, syphilis, or genital herpes simplex virus infection (HSV) are associated with an increased risk of acquiring or transmitting HIV (Unemo et al. 2017). Moreover, a recent observational trend study showed that the absolute incidence of STI cases increased in the last 30 years, especially in sub-Saharan Africa and Latin America (Zheng et al. 2022). In view of this, more attention should be given to the prevention and control of STIs, particularly in low- and middle-income countries, evaluating the benefits of implementing different public health control strategies.

The spread of STIs can be significantly reduced by a number of non-pharmaceutical interventions including sex abstinence, reduction in the number of sex partners, mutually monogamous relationships, and correct and consistent use of latex condoms (Workowski and Bolan 2015). Effective treatment is available for bacterial and parasitic STIs. For example, gonorrhea, syphilis, chlamydia, and trichomoniasis can be treated with antibiotics, often in a single dose (World Health Organization 2021; Workowski and Bolan 2015). Viral STIs including HIV, genital HSV, viral hepatitis B, and HPV have limited treatment options, but disease symptoms can be weakened or controlled with systematic treatment (World Health Organization 2021; Workowski and Bolan 2015). Antiviral drugs typically reduce the viral load limiting clinical symptoms, though virus eradication is difficult (World Health Organization 2021; Workowski and Bolan 2015). The spread of STIs can also be limited via vaccination, which is the main tool for the primary prevention of disease, and one of the most cost-effective public health measures. Therefore, the development of vaccines against STIs is essential to reduce the vast number of infections globally, and their adverse health outcomes (Gottlieb et al. 2016). Currently, there are vaccines for viral STIs that have been proven to be safe and effective, including vaccines against HPV and hepatitis B virus (Gottlieb et al. 2016). Major efforts continue in the development of vaccines against other STIs e.g. herpes and HIV, with several vaccine candidates in early clinical development (World Health Organization 2021). Nevertheless, as the COVID-19 pandemic has shown, even after successful vaccine development, vaccines usually come on a limited budget and the available stockpile is rarely enough to guarantee the immunization of the entire population (Yamey et al. 2022). Generally, in addition to non-pharmaceutical interventions, public health authorities rely on a fixed amount of vaccines to control an outbreak, and therefore, optimizing the allocation of scarce vaccines becomes an important problem.

For an effective vaccination program, it is extremely important to identify subgroups within the general population that should be prioritized to be vaccinated (Hansen and Day 2011). In the context of STIs, the key allocation problem is to investigate how to effectively distribute a limited vaccine stockpile among individuals, females and males, to minimize the prevalence of the infection in a population (Bogaards et al. 2015; Heffernan et al. 2014; Saldaña et al. 2019). Strategic mathematical modeling has already been directed to study resource allocation problems using different approaches such as mixed-integer linear programming models (Saif and Elhedhli 2016; Tavana et al. 2021), feedback control (Camacho et al. 2019), analytical insights from compartmental models (Bogaards et al. 2011; Duijzer et al. 2018; Heffernan et al. 2014; Gao et al. 2021; Vo et al. 2021), and optimal control (Estadilla et al. 2021; Malik et al. 2016; Saldaña et al. 2019). Here, we focus on optimizing time-dependent control interventions in an epidemiological model, using the optimal control theory (OCT) as a methodology for designing effective vaccination strategies. The OCT has been proven to be a powerful tool in the development and evaluation of intervention strategies to cope with the burden of infectious diseases (Bussell et al. 2019). Several studies have used Kermack–McKendrick-type models coupled with the optimal control theory to devise vaccine prioritization for specific diseases such as influenza (Matrajt et al. 2013; Shim 2013), dengue (Maier et al. 2017; Rodrigues et al. 2014), and COVID-19 (Estadilla et al. 2021; Libotte et al. 2020; Saldaña and Velasco-Hernández 2021). Nevertheless, to the best of the authors’ knowledge, the number of studies investigating vaccine allocation via optimal control theory for STIs is relatively low. For example, Brown and White (2011) used an optimal control model to investigate targeted immunization programs for HPV in the United Kingdom. They found that the inclusion of both males and females into vaccination programs would be cost-effective and that vaccinating older individuals is also relevant for controlling the infection. Malik et al. (2016), explored the optimal vaccination rates of the bivalent, quadrivalent and nonavalent HPV vaccines if all three vaccines are in use but only in the female population. Their main conclusion was that immunization programs can optimally administer the three vaccines simultaneously by administering the quadrivalent and nonavalent vaccines at the maximum rates and the bivalent vaccine at moderate rates. Camacho et al. (2019) used a compartmental pair model coupled with optimal and feedback control to explore different public health strategies for the control of trichomoniasis, gonorrhea, chlamydia, and HPV. Saldaña et al. (2019) used optimal control theory to investigate the best combination of vaccination and screening to reduce the spread of HPV infection, as well as the cost of the intervention strategy. The results in these previous studies are deduced by employing commonly used $L_2$-type objective functionals. The approach presented in this study differs from previous methodologies in the sense that we consider a limited but specific vaccine supply via an isoperimetric constraint.

In this work, we contribute to the vaccine allocation literature investigating how prophylactic vaccines are best distributed in a population. Assuming sex-specific differences in susceptibility and disease outcomes, the main focus of our study is to investigate under which conditions the inclusion of both sexes into vaccination programs adds to the population-level impact of one-sex-only interventions. Theoretically, high vaccination coverage for one sex might be enough to reach herd immunity and eradicate an STI in a heterosexual population (Bogaards et al. 2011). Yet, some complications can arise depending on many factors such as (i) the male-to-female sexual infectivity rate is generally higher than that of female-to-male (Low et al. 2006; Wong et al. 2004) (ii) the health risks associated with the infection are considerably higher for females e.g. pelvic inflammatory disease, chronic pelvic pain, ectopic pregnancy, infertility, and cervical cancers (Low et al. 2006; Wong et al. 2004). Further, in some cases, there can be a group who is reluctant towards the vaccination; thus, a high vaccination coverage can be difficult to achieve even when targeting one sex-specific group (Saldaña et al. 2019). Our approach to addressing these issues relies on an optimal control problem, where the cumulative level of infected individuals is minimized under a limited vaccine stockpile and subject to a two-sex epidemic model.

The rest of this paper is organized as follows. In Sect. 2, we propose a two-sex Kermack–McKendrick-type model to describe the spread of an STI in a heterosexual population. The model considers prophylactic vaccine strategies that might include both genders. The analysis of equilibria together with the basic and control reproduction numbers are also investigated in Sect. 2. In Sect. 3, we formulate an optimal control problem (OCP) to seek optimal sex-specific vaccination programs aiming to minimize the total number of infections in the population. In Sect. 4, we provide a numerical approximation to the solution of OCP for several realistic vaccine scenarios with budget constraints that mimic a scarce vaccine stockpile insufficient to immunize the total population. We conclude by discussing the implications of our findings for gender-specific vaccination programs against STIs.

Methods

Model formulation

The model stratifies the total population at time t, denoted N(t) according to gender, so $N(t)=N_f(t)+N_m(t)$, where $N_f$ and $N_m$ represent the number of sexually active females and males, respectively. Both populations $N_k$ ($k=f,m$) are subdivided into mutually exclusive compartments according to infection status as unvaccinated susceptible ($S_k$), vaccinated susceptible ($V_k$), and infectious individuals ($I_k$). Hence, $N_k(t)=S_k(t)+V_k(t)+I_k(t)$, ($k=f,m$). The transmission dynamics of a sexually transmitted infection in a heterosexual population are described by the following system of differential equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{S}}_k& =b_k{N}_k-({\lambda }_{j\to k}+u_k+d_k)S_k+{\alpha }_k{I}_k+{\theta }_k{V}_k,\hfill \\ \hfill {\dot{V}}_k& =u_k{S}_k-(1-{ϵ}_k){\lambda }_{j\to k}{V}_k-(d_k+{\theta }_k)V_k,(k,j=f,m,k\ne j)\hfill \\ \hfill {\dot{I}}_k& ={\lambda }_{j\to k}(S_k+(1-{ϵ}_k)V_k)-({\alpha }_k+d_k)I_k,\hfill \\ \hfill \end{array}\end{array}$$ 1

where all the parameters and initial conditions are non-negative.

We assume individuals are recruited into the sexually active population as unvaccinated susceptible at a constant rate $b_k$ proportional to $N_k$ and $1/d_k$ is the average duration of the sexual life for sex $k=f,m$. Prophylactic immunization occurs at a rate $u_k$. The vaccine reduces the force of infection by a factor ${ϵ}_k\in [0,1]$; thus, ${ϵ}_k$ is the vaccine effectiveness and the vaccine is $100\%$ effective when ${ϵ}_k=1$. Vaccine-induced immunity wanes at a rate ${\theta }_k$, thus if ${\theta }_k=0$, protection is lifelong. Individuals recover naturally from the infection at a rate ${\alpha }_k$. No immunity is assumed after recovery. The acquisition of infection occurs with a sex-specific force of infection given by

$$\begin{array}{c}\hfill {\lambda }_{f\to m}={\displaystyle \frac{{\beta }_{f\to m}{I}_f}{N_f}},{\lambda }_{m\to f}={\displaystyle \frac{{\beta }_{m\to f}{I}_m}{N_m}}.\end{array}$$ 2

Here, ${\beta }_{f\to m}$ (${\beta }_{m\to f}$) is the female-to-male (male-to-female) transmission rate. We remark that although system (1) is a minimalist model, it captures the core characteristics of sexually transmitted infections in a heterosexual population under vaccination. For a full description of model parameters, together with their ranges and baseline values see Sect. 4.1 and Table 1.

Table 1.

Baseline model (1) parameters ($k=f,m$). References for the parameter values are given in the main text. The total population is assumed to be $N=100,000$ with a gender distribution $N_f^{\ast }=0.5052N$ and $N_m^{\ast }=0.4948N$

Parameters	Values-ranges	Units
Female’s sexually active life expectancy $1/d_f$	30.7–(30, 31.4)	Year
Male’s sexually active life expectancy $1/d_m$	34.7–(34.1, 35.3)	Year
Average number of sexual contacts for males $c_f$	52–Tri(0, 100, 52)	Year${}^{-1}$
Average number of sexual contacts for females $c_m$	50–Tri(0, 97, 50)	Year${}^{-1}$
Probability of female infection $p_{m\to f}$	0.70–Tri(0, 1, 0.70)	dimensionless
Probability of male infection $p_{f\to m}$	0.40–Tri(0, 1, 0.40)	dimensionless
Vaccine efficacy ${ϵ}_k$	0.80–(0.60, 0.95)	dimensionless
Duration of the infectious period $1/{\alpha }_k$	20–(10, 100)	Days
Vaccination rates $u_k$	0.50–(0.0, 1.60)	Year${}^{-1}$
Duration of vaccine-induced protection $1/{\theta }_k$	20–(1, 30)	Year

Mathematical analysis

From system (1) it is immediate that the total population for sex $k=f,m$ satisfies ${\dot{N}}_k=(b_k-d_k)N_k$. Since we are interested in studying model (1) over a finite time interval $[0,t_f]$, we assume that the population for both sexes is constant i.e. $N_k(t)=N_k(0):=N_k^{\ast }$ for all $t\in [0,t_f]$, so $b_k=d_k$. We stress that the constant population size assumption is standard in epidemic modeling and is based on the fact the time scale of the epidemic process is considerably faster than that of the demographic one for a short time horizon. Therefore, the biologically feasible region for system (1) is given by $\mathrm{\Omega }={\mathrm{\Omega }}_f\cup {\mathrm{\Omega }}_m$, where

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_k=\left\{(S_k,V_k,I_k),\in ,{\mathbf{R}}_{+}^3,:,N_k^{\ast },=,S_k,(t),+,V_k,(t),+,I_k,(t),,,,t,\in ,[0,t_f]\right\}(k=f,m)\end{array}$$

Let $x_i$ be an state variable of model (1), then if $x_i=0$ then ${\dot{x}}_i\ge 0$. It follows that all solutions of the system (1) with an initial condition in $\mathrm{\Omega }$ remain in $\mathrm{\Omega }$ for all $t\ge 0$ and $\mathrm{\Omega }$ is forward invariant. The basic existence, uniqueness, and continuation results for model (1) hold in $\mathrm{\Omega }$ (Wiggins et al. 2003). Therefore system (1) is epidemiologically well-posed (Hethcote 2000) and it is sufficient to study its dynamics in $\mathrm{\Omega }$.

The disease-free equilibrium (DFE) of model (1) is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill E_0& =(S_f^0,V_f^0,I_f^0,S_m^0,V_m^0,I_m^0)\hfill \\ \hfill & =\left({\displaystyle \frac{(d_f+{\theta }_f)N_f^{\ast }}{u_f+d_f+{\theta }_f}},,,{\displaystyle \frac{u_f{N}_f^{\ast }}{u_f+d_f+{\theta }_f}},,,0,,,{\displaystyle \frac{(d_m+{\theta }_m)N_m^{\ast }}{u_m+d_m+{\theta }_m}},,,{\displaystyle \frac{u_m{N}_m^{\ast }}{u_m+d_m+{\theta }_m}},,,0\right).\hfill \end{array}\end{array}$$

Therefore, the susceptible and vaccinated fractions at equilibrium are

$$\begin{array}{c}\hfill s_k^0={\displaystyle \frac{S_k^0}{N_k^{\ast }}}={\displaystyle \frac{d_k+{\theta }_k}{u_k+d_k+{\theta }_k}},v_k^0={\displaystyle \frac{V_k^0}{N_k^{\ast }}}={\displaystyle \frac{u_k}{u_k+d_k+{\theta }_k}},(k=f,m).\end{array}$$ 3

Observe that in the absence of vaccination, at the DFE, the whole population remains susceptible. Using the next-generation operator (Diekmann et al. 1990) and the method of Van den Driessche and Watmough (2002) we obtain the following next-generation matrix

$$\begin{array}{c}\hfill \mathbf{K}=\left[\begin{array}{cc}0& {\displaystyle \frac{{\beta }_{m\to f}(S_f^0+(1-{ϵ}_f)V_f^0)}{({\alpha }_m+d_m)N_m^{\ast }}}\\ {\displaystyle \frac{{\beta }_{f\to m}(S_m^0+(1-{ϵ}_m)V_m^0)}{({\alpha }_f+d_f)N_f^{\ast }}}& 0\end{array}\right]\end{array}$$ 4

The control reproduction number is defined as the spectral radius $\rho (\mathbf{K})$, that is, the largest eigenvalue of the next generation matrix. Therefore, the analytic expression for the control reproduction number is

$$\begin{array}{c}\hfill R_c(u_f,u_m)=\sqrt{{\displaystyle \frac{{\beta }_{f\to m}(s_m^0+(1-{ϵ}_m)v_m^0)}{({\alpha }_f+d_f)}}\times {\displaystyle \frac{{\beta }_{m\to f}(s_f^0+(1-{ϵ}_f)v_f^0)}{({\alpha }_m+d_m)}}}.\end{array}$$ 5

The notation $R_c$ is used to emphasize that the reproduction number is derived under control measures, in this case, vaccination. The square root in (5) arises since it takes two generations for infected hosts to produce newly infected hosts of the same sex (Van den Driessche and Watmough 2008). For a biological intuition of $R_c$ observe that an infectious individuals of sex j produces on average ${\beta }_{j\to k}(s_k^0+(1-{ϵ}_k)v_k^0)$ infections on the opposite sex k $(k,j=f,m,k\ne j)$, during his/her infectious period $1/({\alpha }_j+d_j)$.

The basic reproduction number in the absence of vaccination, $R_0$, satisfies

$$\begin{array}{c}\hfill R_0=R_c(0,0)=\sqrt{{\displaystyle \frac{{\beta }_{f\to m}}{({\alpha }_f+d_f)}}{\displaystyle \frac{{\beta }_{m\to f}}{({\alpha }_m+d_m)}}}>R_c(u_f,u_m)\text{for}{u}_f,u_m>0.\end{array}$$ 6

As a direct consequence of Theorem 2 in Van den Driessche and Watmough (2002), we obtain the local stability for the DFE. The result is formalized as follows.

Theorem 1

The disease-free equilibrium $E_0$ for model (1) is locally asymptotically stable if $R_c<1$ and unstable if $R_c>1$.

We now investigate the existence of the endemic equilibria of the form $(S_f^{†},V_f^{†},I_f^{†},S_m^{†},V_m^{†},I_m^{†})$ where $0<I_f^{†}<N_f^{\ast }$, and $0<I_m^{†}<N_m^{\ast }$ (a straightforward computation can show that $I_f^{†}=0$ implies $I_m^{†}=0$, and vice-versa). Further, since we are dealing with constant population for both sexes, we can express the endemic equilibria for the susceptible as $S_k^{†}=N_k^{\ast }-V_k^{†}-I_k^{†}$ ($k=f,m$). Then we can solve the equilibrium equations for the vaccinated classes $V_f^{†}$ and $V_m^{†}$ in terms of the infected classes $I_f^{†}$ and $I_m^{†}$ as

$$\begin{array}{c}\hfill V_m^{†}=\frac{u_m(N_m^{\ast }-I_m^{†})}{d_m+u_m+{\theta }_m+(1-{ϵ}_m){\beta }_{f\to m}{I}_f^{†}/N_f^{\ast }},\\ \hfill V_f^{†}=\frac{u_f(N_f^{\ast }-I_f^{†})}{d_f+u_f+{\theta }_f+(1-{ϵ}_f){\beta }_{m\to f}{I}_m^{†}/N_m^{\ast }}.\end{array}$$

Next, defining

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \delta & =d_m+{\theta }_m+(1-{ϵ}_m)u_m,\hfill \\ \hfill \zeta & =({\alpha }_m+d_m)N_f^{\ast }\left((d_m+u_m+{\theta }_m),N_f^{\ast },+,(1-{ϵ}_m),{\beta }_{f\to m},I_f^{†}\right),\hfill \end{array}\end{array}$$

we can express the infected males as $I_m^{†}=I_f^{†}F(I_f^{†})$ where

$$\begin{array}{c}\hfill F(I_f^{†})=\frac{{\beta }_{f\to m}{N}_m^{\ast }(\delta N_f^{\ast }+(1-{ϵ}_m){\beta }_{f\to m}{I}_f^{†})}{{\beta }_{f\to m}\delta N_f^{\ast }{I}_f^{†}+(1-{ϵ}_m){({\beta }_{f\to m}{I}_f^{†})}^2+\zeta }.\end{array}$$ 7

Finally, the infected females at the endemic equilibrium $I_f^{†}$ correspond to the zeros of the following four order polynomial

$$\begin{array}{c}\hfill A{I}_f^{†}{(F(I_f^{†}))}^2+BF(I_f^{†})+C=0\end{array}$$ 8

where

$$\begin{array}{cc}\hfill A& ={\beta }_{m\to f}^2(1-{ϵ}_f)(N_f^{\ast }-I_f^{†})\hfill \\ \hfill B& ={\beta }_{m\to f}{N}_m^{\ast }\left(-,({\alpha }_f+d_f),(1-{ϵ}_f),I_f^{†},+,(N_f^{\ast }-I_f^{†}),(d_f+{\theta }_f+(1-{ϵ}_f)u_f)\right)\hfill \\ \hfill C& =-({\alpha }_f+d_f)(d_f+{\theta }_f+u_f){(N_m^{\ast })}^2\hfill \end{array}$$

In the particular case for which the vaccine efficacy is $100\%$, that is, ${ϵ}_f={ϵ}_m=1$, we can find a unique endemic equilibrium given by

$$\begin{array}{cc}\hfill {\displaystyle \frac{I_f^{†}}{N_f^{\ast }}}=& \frac{R_0^2(d_m+{\theta }_m)(d_f+{\theta }_f)-(d_m+{\theta }_m+u_m)(d_f+{\theta }_f+u_f)}{R_0^2(d_m+{\theta }_m)(d_f+{\theta }_f)+{\beta }_{m\to f}(d_m+{\theta }_m)(d_f+{\theta }_f+u_f)/({\alpha }_m+d_m)},\hfill \\ \hfill {\displaystyle \frac{I_m^{†}}{N_m^{\ast }}}=& \frac{({\alpha }_f+d_f)I_f^{†}}{{\beta }_{m\to f}{s}_f^0(N_f^{\ast }-I_f^{†})}.\hfill \end{array}$$ 9

Observe that the above equilibrium only exists if the condition

$$\begin{array}{c}\hfill R_0^2(d_m+{\theta }_m)(d_f+{\theta }_f)>(d_m+{\theta }_m+u_m)(d_f+{\theta }_f+u_f)\end{array}$$

is fulfilled. This occurs if and only if $R_c>1$, therefore the classical forward bifurcation occurs when the vaccine is $100\%$ effective and the two-sex epidemic model (1) presents a unique endemic equilibrium. In the general case, it is not possible to obtain a closed-form solution for the endemic equilibria but numerical results indicate that the number of endemic equilibria is at most two. Furthermore, a backward bifurcation can occur if the vaccine effectiveness ${ϵ}_k$ ($k=f,m$) is below a certain threshold. Figure 1 depicts the typical dynamics for the endemic equilibria of the infected female class where the backward bifurcation is present. The equilibrium dynamics for the male infected class follow the same qualitative behavior (not shown).

Fig. 1.

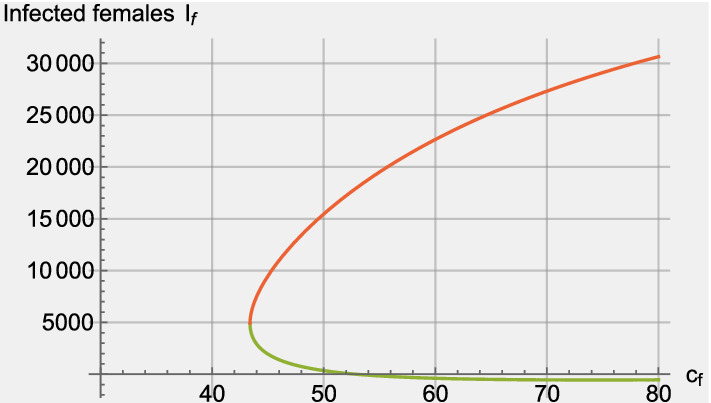
Endemic equilibria for the infected female sub-population, $I_f$, as a function of the expected number of sexual contacts that a typical man carries out per year $c_f$. Vaccine effectiveness for both sexes is $80\%$. Parameter values are shown in Table 1

Optimal vaccine allocation

In this section, we propose an optimal control problem with an isoperimetric constrain to investigate the best sex-specific vaccine deployment under a limited vaccine budget. For this, we consider time-dependent vaccination rates $u_f(t)$ and $u_m(t)$ per unit of time, thus the controlled model becomes

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{S}}_k& =b_k{N}_k-({\lambda }_{j\to k}+u_k(t)+d_k)S_k+{\alpha }_k{I}_k+{\theta }_k{V}_k,\hfill \\ \hfill {\dot{V}}_k& =u_k{S}_k-(1-{ϵ}_k){\lambda }_k{V}_k-(d_k+{\theta }_k)V_k,(k,j=f,m,k\ne j)\hfill \\ \hfill {\dot{I}}_k& ={\lambda }_k(S_k+(1-{ϵ}_k)V_k)-({\alpha }_k+d_k)I_k,\hfill \end{array}\end{array}$$ 10

subject to non-negative initial conditions. The vaccination rates will be called controls and denoted by the vector $\mathbf{c}(t)={(u_f(t),u_m(t))}^T$.

We conceptualize a limited vaccine supply assuming that the number of vaccines available under the time interval of interest $[0,t_f]$ is fixed with a value W and that all vaccines will be delivered to the population. We further assume that the vaccine stockpile is not enough to vaccinate the whole population i.e. $W<N$ since in another case there is no need to optimize vaccine allocation.

This condition can be modeled by the following isoperimetric constraint (Kamien and Schwartz 2012; Lenhart and Workman 2007):

$$\begin{array}{c}\hfill {\int }_0^{t_f}{u}_f(t)S_f(t)+u_m(t)S_m(t)dt=W.\end{array}$$ 11

The problem for public health officers is to choose an optimal vaccine deployment to minimize the prevalence of the infection, as well as the overall costs of vaccine deployment. In mathematical terms, such a goal can be achieved by minimizing the following objective functional

$$\begin{array}{c}\hfill J={\int }_0^{t_f}{A}_1{I}_f(t)+A_2{I}_m(t)+A_3{u}_f^2(t)+A_4{u}_m^2(t)dt.\end{array}$$ 12

The weight parameters $A_i$ $(i=1,\dots ,4)$ describe the relative impact of the control or state variables on the value of the objective functional (see Sect. 4.3). The dependence on the control in the objective functional (12) is assumed to be a quadratic function of the control itself. A reason for such a choice is that the quadratic terms penalize high levels of vaccine deployment in comparison with the cost of low levels (Saldaña et al. 2019). We follow this approach but we remark that this formulation offers important mathematical and numerical advantages, as for such $L_2$-type functionals, the application of Pontryagin’s Maximum Principle allows us to obtain a closed-form formula for the controls as a function of the states and adjoints that can be solved numerically as a boundary value problem (Lenhart and Workman 2007).

The control set is defined by

$$\begin{array}{c}\hfill \mathcal{U}=\{\mathbf{c}(t):u_k(t)\text{bounded and Lebesgue measurable on}[0,t_f],k=f,m\},\end{array}$$ 13

with bounds

$$\begin{array}{c}\hfill 0\le u_f(t),u_m(t)\le u_{\mathit{max}},\forall t\in [0,t_f].\end{array}$$ 14

Observe that besides the budgetary constraint (11), the vaccination rates should be constrained (due to logistic limitations) under a maximum vaccination rate $u_{\mathit{max}}$ per unit of time e.g. daily vaccination rate. As shown in Saldaña et al. (2022), a vaccination rate u can be approximated by

$$\begin{array}{c}\hfill u=-ln(1-V_c(t))/t\end{array}$$ 15

where $V_c(t)$ is the fraction of vaccinated individuals at time t, that is, the vaccination coverage. Considering a very optimistic case in which health authorities achieve a vaccination coverage $V_c(t)=80\%$ of the population in $t=1$ year, we obtain that the constant vaccination rate $u\approx 1.60$ per year. Therefore, we choose a maximum daily vaccination rate as $u_{\mathit{max}}=1.60/365$.

Given the special structure of (11), we can convert the isoperimetric constraint (11) into a fixed endpoint constrain (Kamien and Schwartz 2012), by defining

$$\begin{array}{c}\hfill Z(t)={\int }_0^t{u}_f(s)S_f(s)+u_m(s)S_m(s)ds.\end{array}$$ 16

The additional state variable, Z(t), represents the cumulative number of vaccines that have been given at time t, and satisfies

$$\begin{array}{c}\hfill \dot{Z}(t)=u_f(t)S_f(t)+u_m(t)S_m(t),Z(0)=0,Z(t_f)=W.\end{array}$$ 17

The Optimal Control Problem (OCP) is stated as follows:

$$\begin{array}{c}\hfill \underset{\mathbf{c}\in \mathcal{U}}{min}J(\mathbf{c})\text{subject to model}(10)\text{coupled with constrain}(17).\end{array}$$ 18

An application of the Fillipov-Cesari theorem (Fleming and Rishel 1975, Chapter III, Theorem 4.1) gives conditions to assert the existence of an optimal control pair

$$\begin{array}{c}\hfill {\mathbf{c}}^{\ast }(t)={(u_f^{\ast }(t),u_m^{\ast }(t))}^T\end{array}$$

and corresponding optimal state solutions

$$\begin{array}{c}\hfill {\mathbf{X}}^{\ast }(t)={(S_f^{\ast }(t),V_f^{\ast }(t),I_f^{\ast }(t),S_m^{\ast }(t),V_m^{\ast }(t),I_m^{\ast }(t),Z^{\ast }(t))}^T\end{array}$$

for the OCP (18). The proof is standard for $L_2$-type objective functionals and we omit it. Proofs of such statements can be found in Camacho et al. (2019); Saldaña et al. (2019); Sepulveda-Salcedo et al. (2020). We now use Pontryagin’s Maximum Principle to state the necessary criterion satisfied by an optimal control (Fleming and Rishel 1975; Kamien and Schwartz 2012).

Theorem 2

If ${\mathbf{X}}^{\ast }(t)$ and ${\mathbf{c}}^{\ast }(t)$ are optimal for the OCP (18), then there exist a constant ${\lambda }_0$ and piecewise differentiable functions $\lambda (t)=({\lambda }_1,\dots ,{\lambda }_7)$, where for all $t\in [0,t_f]$ we have $({\lambda }_0,\lambda (t))\ne (0,\mathbf{0})$, such that for every $t\in [0,t_f]$

$$\begin{array}{c}\hfill H(t,{\mathbf{X}}^{\ast }(t),{\mathbf{c}}^{\ast }(t),\lambda (t))\le H(t,{\mathbf{X}}^{\ast }(t),\mathbf{c}(t),\lambda (t))\end{array}$$ 19

for all admissible controls $\mathbf{c}\in \mathcal{U}$, where the Hamiltonian function H is defined by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H(t,\mathbf{X},\mathbf{c},\lambda )& ={\lambda }_0\left[A_1,I_f,+,A_2,I_m,+,A_3,u_f^2,+,A_4,u_m^2\right]\hfill \\ \hfill & +{\lambda }_1\left[b_f,N_f,-,({\lambda }_{m\to f}+u_f+d_f),S_f,+,{\alpha }_f,I_f,+,{\theta }_f,V_f\right]\hfill \\ \hfill & +{\lambda }_2\left[u_f,S_f,-,(1-{ϵ}_f),{\lambda }_{m\to f},V_f,-,(d_f+{\theta }_f),V_f\right]\hfill \\ \hfill & +{\lambda }_3\left[{\lambda }_{m\to f},(S_f+(1-{ϵ}_f)V_f),-,({\alpha }_f+d_f),I_f\right]\hfill \\ \hfill & +{\lambda }_4\left[b_m,N_m,-,({\lambda }_{f\to m}+u_m+d_m),S_m,+,{\alpha }_m,I_m,+,{\theta }_m,V_m\right]\hfill \\ \hfill & +{\lambda }_5\left[u_m,S_m,-,(1-{ϵ}_m),{\lambda }_{f\to m},V_m,-,(d_m+{\theta }_m),V_m\right]\hfill \\ \hfill & +{\lambda }_6\left[{\lambda }_{f\to m},(S_m+(1-{ϵ}_m)V_m),-,({\alpha }_m+d_m),I_m\right]\hfill \\ \hfill & +{\lambda }_7\left[u_f,S_f,+,u_m,S_m\right].\hfill \end{array}\end{array}$$ 20

Except at points of discontinuity of ${\mathbf{c}}^{\ast }(t)$, the adjoint variable $\lambda (t)$ satisfies

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{\lambda }}_1& ={\lambda }_1\left({\displaystyle \frac{{\beta }_{m\to f}{I}_m^{\ast }}{N_m^{\ast }}},+,u_f^{\ast },+,d_f\right)-{\lambda }_2{u}_f^{\ast }-{\lambda }_3{\displaystyle \frac{{\beta }_{m\to f}{I}_m^{\ast }}{N_m^{\ast }}}-{\lambda }_7{u}_f^{\ast },\hfill \\ \hfill {\dot{\lambda }}_2& =-{\lambda }_1{\theta }_f+{\lambda }_2\left[(1-{ϵ}_f),{\displaystyle \frac{{\beta }_{m\to f}{I}_m^{\ast }}{N_m^{\ast }}},+,(d_f+{\theta }_f)\right]-{\lambda }_3(1-{ϵ}_f){\displaystyle \frac{{\beta }_{m\to f}{I}_m^{\ast }}{N_m^{\ast }}},\hfill \\ \hfill {\dot{\lambda }}_3& =-{\lambda }_0{A}_1-{\lambda }_1{\alpha }_f+{\lambda }_3({\alpha }_f+d_f)+{\lambda }_4{\displaystyle \frac{{\beta }_{f\to m}}{N_f^{\ast }}}{S}_m^{\ast }+{\lambda }_5(1-{ϵ}_m){\displaystyle \frac{{\beta }_{f\to m}}{N_f^{\ast }}}{V}_m^{\ast }\hfill \\ \hfill & -{\lambda }_6{\displaystyle \frac{{\beta }_{f\to m}}{N_f^{\ast }}}(S_m^{\ast }+(1-{ϵ}_m)V_m^{\ast }),\hfill \\ \hfill {\dot{\lambda }}_4& ={\lambda }_4\left({\displaystyle \frac{{\beta }_{f\to m}{I}_f^{\ast }}{N_f^{\ast }}},+,u_m^{\ast },+,d_m\right)-{\lambda }_5{u}_m^{\ast }-{\lambda }_6{\displaystyle \frac{{\beta }_{f\to m}{I}_f^{\ast }}{N_f^{\ast }}}-{\lambda }_7{u}_m^{\ast },\hfill \\ \hfill {\dot{\lambda }}_5& =-{\lambda }_4{\theta }_m+{\lambda }_5\left[(1-{ϵ}_m),{\displaystyle \frac{{\beta }_{f\to m}{I}_f^{\ast }}{N_f^{\ast }}},+,(d_m+{\theta }_m)\right]-{\lambda }_6(1-{ϵ}_m){\displaystyle \frac{{\beta }_{f\to m}{I}_f^{\ast }}{N_f^{\ast }}},\hfill \\ \hfill {\dot{\lambda }}_6& =-{\lambda }_0{A}_2+{\lambda }_1{\displaystyle \frac{{\beta }_{m\to f}}{N_m^{\ast }}}{S}_f^{\ast }+{\lambda }_2(1-{ϵ}_f){\displaystyle \frac{{\beta }_{m\to f}}{N_m^{\ast }}}{V}_f^{\ast }-{\lambda }_3{\displaystyle \frac{{\beta }_{m\to f}}{N_m^{\ast }}}(S_f^{\ast }+(1-{ϵ}_f)V_f^{\ast })\hfill \\ \hfill & -{\lambda }_4{\alpha }_m+{\lambda }_6({\alpha }_m+d_m),\hfill \\ \hfill {\dot{\lambda }}_7& =0.\hfill \end{array}\end{array}$$ 21

Furthermore,

$$\begin{array}{c}\hfill {\lambda }_0=1\text{or}{\lambda }_0=0.\end{array}$$ 22

Last, the following transversality conditions are satisfied:

$$\begin{array}{c}\hfill {\lambda }_i(t_f)=0i=1,\dots ,6,{\lambda }_7(t_f)=\text{free}.\end{array}$$ 23

The adjoint variables ${\lambda }_i(t)$ ($i=1,\dots ,6$) have a classical interpretation in OCP as the marginal valuation of the associated state variable at time t (Kamien and Schwartz 2012). The value of the constant ${\lambda }_0$ in the Hamiltonian (20) is either 0 or 1. If ${\lambda }_0=1$, then the OCP (18) would have a solution in which the objective matters (Kamien and Schwartz 2012). In this scenario, the Hamiltonian function has the standard form, and minimization of the objective functional (12) is equivalent to minimization of H as a function of $\mathbf{c}(t)$ along the optimal path. This is not always possible for OCPs that include an isoperimetric constraint (Fleming and Rishel 1975). This results from the fact that the controlled system (10) coupled with (17), has more endpoint conditions than differential equations. Hence, the system is over-determined and the optimization problem may become unfeasible. If ${\lambda }_0=0$, one can handle the OCP finding an admissible control ${\mathbf{c}}^{\ast }(t)$ that satisfies the isoperimetric constrain (11). However, such control will neglect the value of the objective functional (Sepulveda-Salcedo et al. 2020). Problems in which ${\lambda }_0=0$ are called abnormal (Fleming and Rishel 1975) and the optimal control usually presents a bang-bang structure since H is a linear function in the control. A feasible control, in this case, is to start vaccinating with the maximal effort at the initial phase and to continue vaccinating with a maximal effort to deploy all the vaccines at a time $\widehat{t}\in (0,t_f)$ (Hansen and Day 2011; Sepulveda-Salcedo et al. 2020).

In our context, we cannot disregard the value of the objective functional since is essential to find the optimal vaccine deployment. Hence, hereafter we assume ${\lambda }_0=1$. From the first-order optimality conditions we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial H(t,{\mathbf{X}}^{\ast }(t),{\mathbf{c}}^{\ast }(t),\lambda (t))}{\partial u_f}}=2A_3{u}_f^{\ast }(t)-({\lambda }_1(t)-{\lambda }_2(t)-K)S_f^{\ast }(t)=0,\end{array}$$ 24

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial H(t,{\mathbf{X}}^{\ast }(t),{\mathbf{c}}^{\ast }(t),\lambda (t))}{\partial u_m}}=2A_4{u}_m^{\ast }(t)-({\lambda }_4(t)-{\lambda }_5(t)-K)S_m^{\ast }(t)=0.\end{array}$$ 25

Considering the lower and upper bounds for the controls and the optimality conditions (24)–(25), we obtain the following characterization of the optimal controls:

$$\begin{array}{c}\hfill u_f^{\ast }(t)=min\left\{max,\left\{0,,,{\displaystyle \frac{({\lambda }_1(t)-{\lambda }_2(t)-K)S_f^{\ast }(t)}{2A_3}}\right\},,,u_{\mathit{max}}\right\},\end{array}$$ 26

$$\begin{array}{c}\hfill u_m^{\ast }(t)=min\left\{max,\left\{0,,,{\displaystyle \frac{({\lambda }_4(t)-{\lambda }_5(t)-K)S_m^{\ast }(t)}{2A_4}}\right\},,,u_{\mathit{max}}\right\}.\end{array}$$ 27

The constant $K\in \mathbf{R}$ comes from the solution of the last equation in the adjoint system (21), which implies ${\lambda }_7=K$, where K should be chosen to fulfill the condition $Z(t_f)=W$.

Numerical results

Here, we complement the analytical results in the previous sections with the numerical computation of the optimal control. To obtain the optimal control solutions we must solve the optimality system which is a boundary value problem involving the state equations (10), coupled with the fixed endpoint constrain (17), and the adjoint system (21). The characterization of the optimal control (26)–(27) has to be substituted in the latter equations to get a system that only depends on the state and adjoint variables. Observe that although the model variables for the controlled system (10) have free end conditions, the additional state variable Z(t) has a specified endpoint (17). Therefore, the forward–backward sweep method (FBSM) cannot be applied directly to solve the optimality system (Lenhart and Workman 2007). Instead, we need to find the value K for the adjoint variable ${\lambda }_7=K$ such that $Z(t_f)=W$. To this end, we consider an adapted FBSM that takes as an input a guess for K, and solves the corresponding OCP. The solution obtained by the implementation of FBSM is denoted as $\phi (K)$, and the corresponding final value for the auxiliary function Z that computes the number of cumulative vaccinated individuals is denoted $Z_K(t_f)$. The adapted FBSM is an iterative process that seeks the value of K that minimizes the difference $Z_K(t_f)-W$. We use the classical secant method to solve this outer iterative process which usually involves several iterations of the FBSM.

The algorithm for the inner FBSM obtains a control update ${\widehat{\mathbf{c}}}^{(m)}$ for step m solving the optimality system. Often, a direct update of the control ${\mathbf{c}}^{(m)}={\widehat{\mathbf{c}}}^{(m)}$, $k=1,2,\dots$ is sufficient for convergence. Nevertheless, a weighted update such that

$$\begin{array}{c}\hfill {\mathbf{c}}^{(m)}=(1-\mu ){\widehat{\mathbf{c}}}^{(m)}+\mu {\mathbf{c}}^{(m-1)},\mu \in [0,1),k=1,2,\dots \end{array}$$ 28

is commonly used to improve convergence properties (Lenhart and Workman 2007). The choice of $\mu$ significantly accelerates convergence relative to the direct update (Sharp et al. 2021), particularly if $\mu$ is updated between iterations. However, since the optimal choice for $\mu$ is problem-dependent, here we use a constant $\mu =0.9$ for all iterations. Convergence properties for the FBSM for this case are discussed in Lenhart and Workman (2007); Sharp et al. (2021). As a convergence criterion, we require the relative error to be negligibly small so that

$$\begin{array}{c}\hfill \delta \Vert {\mathbf{c}}^{(m)}\Vert -\Vert {\mathbf{c}}^{(m)}-{\mathbf{c}}^{(m-1)}\Vert \ge 0,\end{array}$$ 29

is satisfied. Here, $\Vert ·\Vert$ is the Euclidean norm and $\delta$ is the accepted tolerance (fixed as $\delta =0.0001$). The equivalent convergence criteria should be satisfied by the state and adjoint variables. For the outer FBSM we seek that $Z_K(t_f)=W$ is satisfied with a desired tolerance using $\Vert Z_K(t_f)-W\Vert <{10}^{-4}W$.

Model parameters

We retrieved the baseline values for some of our model parameters using sexual behavior data from the United States of America (USA) and estimations from previous studies on STIs. Rather than studying a single disease, our approach is to investigate a set of scenarios of interest that might be plausible for the most common STIs. The selection of parameters is outlined as follows.

The sexually active life expectancy has been estimated to be on average higher for males than for females (Lindau and Gavrilova 2010). In particular, the sexually active life expectancy for males is 34.7 years with a $95\%$ confidence interval (34.1, 35.3). Thus, $1/d_m\in (34.1,35.3)$ years. The sexually active life expectancy for females is 30.7 years with a $95\%$ confidence interval (30, 31.4). Thus, $1/d_f\in (30,31.4)$ years. In 2020, it was estimated in the USA that the percentage of the female population is $50.52\%$ compared to $49.48\%$ in the male population (United Nations 2020). Therefore, $N_f^{\ast }=0.5052N$ and $N_m^{\ast }=0.4948N$. For simplicity, we assume that the total population is $N=100,000$.

The parameter ${\beta }_{m\to f}=c_m{p}_{m\to f}$ is the transmission rate from males to females, where $c_m$ is the expected number of sexual contacts with men that a typical woman carries out per unit of time and $p_{m\to f}$ is the probability of female infection given contact with an infectious male. Likewise, the transmission rate from females to males ${\beta }_{f\to m}=c_f{p}_{f\to m}$, is the product of the expected number of sexual contacts with women that a typical man carries out per unit of time $c_f$ and the probability of male infection given contact with an infectious female $p_{f\to m}$. To obtain the conservation of total sex contacts, the mixing function should satisfy the following condition (Busenberg and Castillo-Chavez 1991):

$$\begin{array}{c}\hfill c_f{N}_m^{\ast }=c_m{N}_f^{\ast }.\end{array}$$ 30

Observe that if $N_f^{\ast }\ne N_m^{\ast }$ then the parameters $c_f$ and $c_m$ can differ substantially. Under our conditions, if we assume that $c_f$ is fixed, we can obtain $c_m=0.4948c_f/0.5052=0.9794c_f$. Men and women in good health report frequent sex (once or more weekly) (Lindau and Gavrilova 2010). In our study, we assume that the expected number of sexual contacts that a typical man carries out follows a triangular distribution $c_f\sim Tri(0,100,52)$ per year (Lindau and Gavrilova 2010). Furthermore, there is evidence that the male-to-female sexual infectivity rate is generally greater than that for female-to-male (Low et al. 2006; Wong et al. 2004). For example, for genital herpes HSV-2, estimations indicate that $p_{m\to f}\approx 4p_{f\to m}$ (Heffernan et al. 2014). Therefore, we set $p_{m\to f}>p_{f\to m}$, and we propose $p_{m\to f}\sim Tri(0,1,0.70)$, and $p_{f\to m}\sim Tri(0,1,0.40)$.

According to the WHO, to be approved, vaccines are required to have a high efficacy rate of at least 50% (World Health Organization 2021). Current vaccines against STIs have been proven to be highly effective to prevent infection e.g. vaccines against HPV, and hepatitis B virus (Gottlieb et al. 2016). In this study, we consider vaccine efficacy between $60\%$-$95\%$ for both sexes (${ϵ}_f,{ϵ}_m\in [0.60,0.95]$). The average infectious period might vary substantially in STIs, depending on the disease, ranging from a few days up to several months (Workowski and Bolan 2015). As a consequence, we assume $1/{\alpha }_k\in [10,100]$ days ($k=f,m$). Regarding the duration of vaccine-induced immunity, we assume that the protection last from at least one year and can be maintained up to 30 years, hence $1/{\theta }_k\in [1,30]$ years ($k=f,m$). Model parameters are summarized in Table 1.

Global sensitivity analysis for the reproduction numbers

Here, a global sensitivity analysis is performed to provide a quantitative measure of the contributions of the model parameters on the reproduction numbers $R_0$ and $R_c$. We use a variance-based sensitivity analysis classically referred as the Sobol method which is, so far, one of the most powerful techniques among current global sensitivity analysis methods (Zhang et al. 2015). Sobol sensitivity analysis determines the contribution of input parameters to the overall variance of a model outcome of interest, in our case, the reproduction numbers. In particular, the so-called first-order Sobol indices measure the contribution to the output variance by a single model input alone. Whereas, the total-order index measures the contribution to the output variance caused by a model input, including both its first-order effects and all higher-order interactions (Saltelli et al. 2008). We perform numerical experiments (100,000 samples) using SALib, an open-source library written in Python for performing sensitivity analyses (Herman and Usher 2017). The ranges used for the parameters are listed in Table 1.

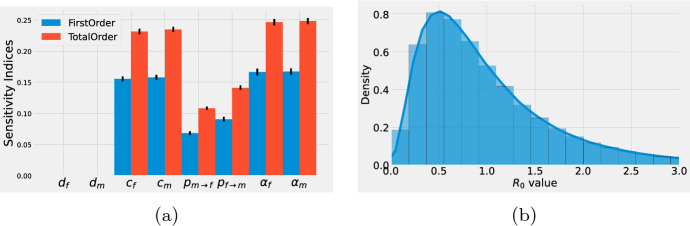
Figure 2a shows the first (blue) and total (red) Sobol’s indices for the basic reproduction number $R_0$. The dark marks on top of the bars in Fig. 2a represent 95% confidence intervals for the sensitivity indices. Notice that they are very small. Observe that the expected number of sexual contacts $c_k$ together with the recovery rates ${\alpha }_k$ ($k=f,m$) are the parameters that contribute the most to the variability of $R_0$. Whereas, the contribution to the variability of $R_0$ given by the mortality rates $d_k$ ($k=f,m$) is practically zero. Figure 2b shows a histogram for the distribution of $R_0$. The solid line represents a kernel density estimation for the continuous distribution. Observe that although in most cases $R_0$ value is below 1, in some extreme scenarios $R_0$ can be as high as 3.

Fig. 2.

a First (blue) and total (red) Sobol’s indices for the basic reproduction number $R_0$. The ranges for the parameters are listed in Table 1. The vertical black lines in the indices represent 95% confidence intervals. b Histogram for the distribution of $R_0$. The solid line represents a kernel density estimation for the continuous distribution (color figure online)

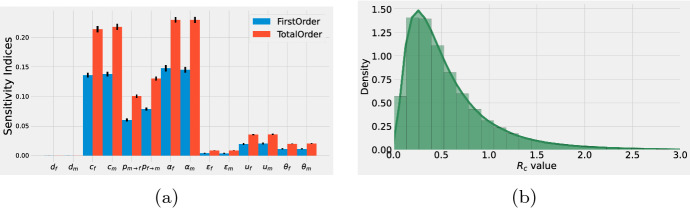
Figure 3a shows the first (blue) and total (red) Sobol’s indices for the control reproduction number $R_c$. As in the case for $R_0$, the parameters $c_k$ and ${\alpha }_k$ ($k=f,m$) contribute the most to the variance of $R_c$. Figure 3b shows a histogram for the distribution of $R_c$. Observe that the distribution for $R_c$ is closer to low values in comparison with the $R_0$ distribution (see Fig. 2b). Hence, even though the vaccine parameters (${ϵ}_k$, $u_k$, ${\theta }_k$) are not the most influential parameters on $R_c$, they still can significantly reduce the value of $R_c$.

Fig. 3.

a First (blue) and total (red) Sobol’s indices for the control reproduction number $R_c$. The ranges for the parameters are listed in Table 1. The vertical black lines in the indices represent 95% confidence intervals. b Histogram for the distribution of $R_c$. The solid line represents a kernel density estimation for the continuous distribution (color figure online)

Vaccination scenarios

We investigate several vaccination scenarios to evaluate the optimal sex-specific vaccine deployment among the population. The time horizon for our simulations is 365 days, that is, $t_f=365$ days and $t\in [0,t_f]$. In the objective functional (12), the parameters $A_1$ and $A_2$ balance the cost of the reduction in health and well-being of infected females and males, respectively. These costs related to pain and suffering are sometimes referred to as morbidity costs (Muennig and Bounthavong 2016). On the other hand, $A_3$ and $A_4$ represent the costs of vaccine deployment in females and males, respectively. In real-life scenarios, the monetary costs and side effects of a vaccination program are typically small compared with the potential losses that an outbreak can inflict. Hence, we assume $A_1,A_2>A_3,A_4$. Furthermore, females are more severely affected by STIs because of anatomical physiological characteristics. So in a heterosexual setting, women bear the largest burden (Workowski and Bolan 2015). The classical example is HPV infection. While HPV infection can lead to cervical cancer and death in women, the infection in men rarely leads to severe health problems (penile cancer from HPV might happen but the rate is far lower than the rate for cervical cancer) (Sung et al. 2021). Therefore, $A_1>A_2$. In particular, for the numerical simulations, we assume $A_1=10$, $A_2=1$. The cost of vaccine deployment is assumed to be the same for both sexes and is fixed as $A_3=A_4=A_2/2$.

To better quantify the gender-specific optimal vaccine deployment we define

$$\begin{array}{c}\hfill Z_f(t)={\int }_0^t{u}_f(s)S_f(s)ds,Z_m(t)={\int }_0^t{u}_m(s)S_m(s)ds.\end{array}$$ 31

Observe that $Z_f(t)$ and $Z_m(t)$ represent the cumulative number of vaccinated females and males, respectively, at time t, and $Z(t)=Z_f(t)+Z_m(t)$ for all $t\in [0,t_f]$. Furthermore, since vaccinated individuals can still get infected, it follows that $Z_f(t)\ge V_f(t)$, $Z_m(t)\ge V_m(t)$ for all $t\in [0,t_f]$.

A starting vaccination roll-out program

As a first scenario, we consider a starting vaccination roll-out program where no individuals in the population have been vaccinated. Initial conditions are set as follows: $I_f(0)=I_m(0)=10$, $V_f(0)=V_m(0)=0$, and $S_f(0)=N_f^{\ast }-I_f(0)-V_f(0)$, $S_m(0)=N_m^{\ast }-I_m(0)-V_m(0)$. Regarding the vaccine stockpile, we consider three cases corresponding to the supply of vaccines for 20% ($W=0.2N$), 30% ($W=0.3N$), and 40% ($W=0.4N$) of the total population.

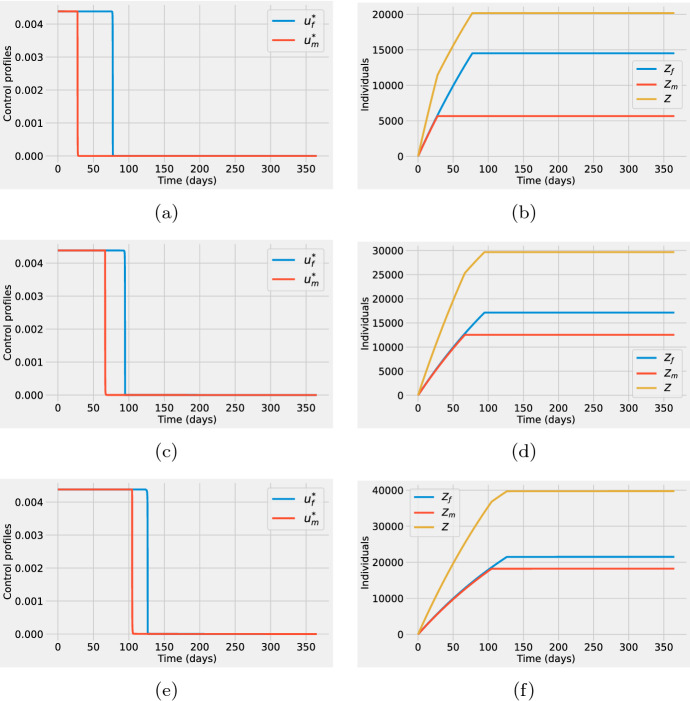
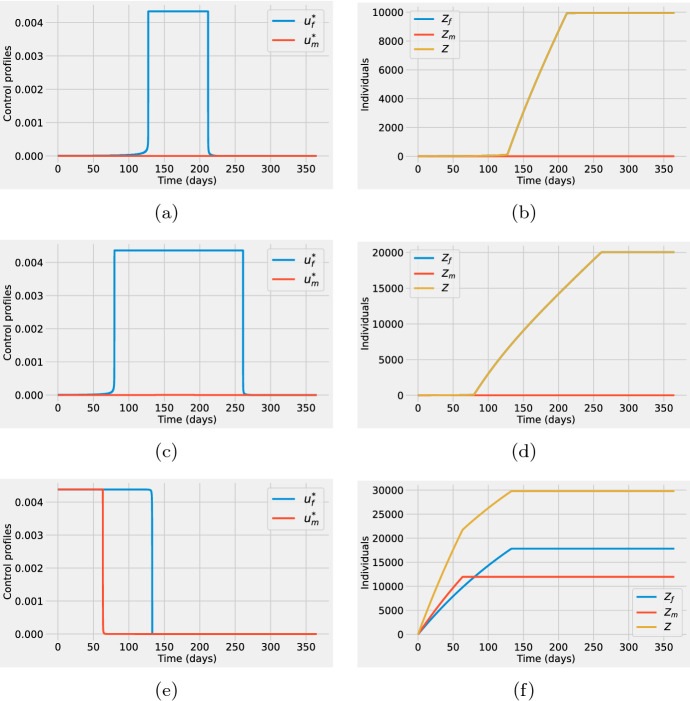
The first column in Fig. 4 shows the optimal control solutions, that is, the optimal time-dependent vaccination rates for females $u_f^{\ast }(t)$ (blue) and males $u_m^{\ast }(t)$ (red). The second column shows the sex-specific optimal vaccine deployment using cumulative vaccinated individuals. The cumulative number of vaccinated females $Z_f(t)$ (blue), and males $Z_m(t)$ (red) are obtained from the optimal states corresponding to the optimal controls on the first column. The variable Z(t) that represents the total cumulative number of vaccines administered is also shown. Observe that $Z(t_f)=W$ for each of the cases investigated: $W=0.2N^{\ast }$ (first row), $W=0.3N^{\ast }$ (second row) and $W=0.4N^{\ast }$ (third row). For all cases (see Fig. 4a, c, e), the optimal control solutions suggest that health officers must use all the vaccines available as soon as possible at the early phase of the outbreak.

Fig. 4.

First column: Optimal time-dependent vaccination rates for females $u_f^{\ast }(t)$ (blue) and males $u_f^{\ast }(t)$ (red). Second column: Cumulative number of vaccinated females (blue) and vaccinated males (red) computed from the optimal states corresponding to the optimal controls on the first column. The total cumulative number of vaccines administered, Z(t), is shown in yellow. For both columns, the supply of vaccines corresponds to 20% (a, b) (first row), 30% (c, d) (second row), and 40% (e, f) (third row) of the total population. Baseline parameter values are listed in Table 1. Initial conditions are $I_f(0)=I_m(0)=10$, $V_f(0)=V_m(0)=0$, and $S_f(0)=N_f^{\ast }-I_f(0)-V_f(0)$, $S_m(0)=N_m^{\ast }-I_m(0)-V_m(0)$ (color figure online)

One important result from Fig. 4a, c, d is that although the vaccination rate for females should be higher than the one for males, this difference is relatively small. Hence, under these conditions, men should be included in vaccination programs together with females. The right column in Fig. 4 shows, as expected from the optimal controls, that the cumulative number of vaccinated females is above the one for males. Nevertheless, the key point to notice is that the difference in the sex-specific cumulative vaccination increases as the vaccine stockpile reduces (note that the difference is bigger in Fig. 4b in comparison with Fig. 4f).

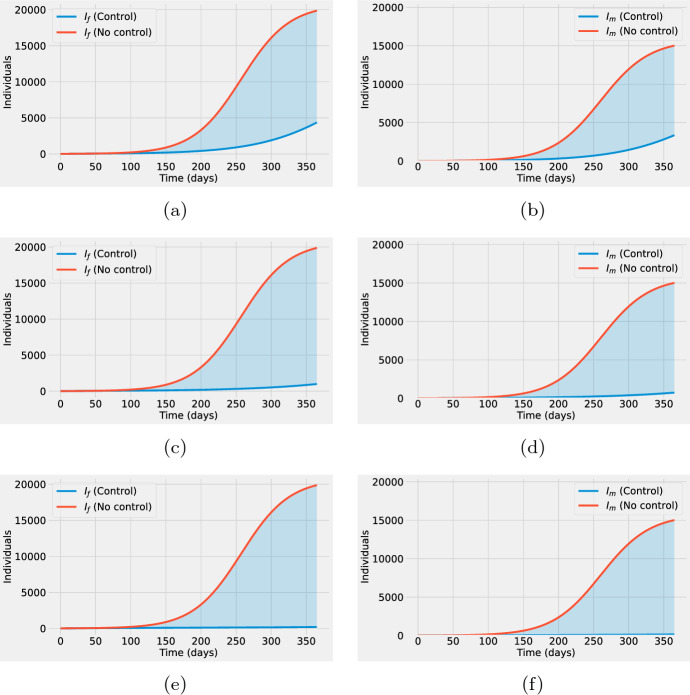
We remark that for all the scenarios explored, the implementation of the vaccination program manages to significantly reduce the prevalence of the infection in comparison with the no-control case. Figure 5 deploys the number of infected individuals without control (solid red line) and under the application of the optimal vaccination rates (solid blue line) corresponding to the three cases $W=0.2N$, $W=0.3N$, and $W=0.4N$. Females and males are presented in the left and right columns in Fig. 5, respectively. The integral of the shaded area corresponds to the number of infections averted by the vaccination programs.

Fig. 5.

(Left column) Number of infected females as a function of time without control (red line) and with optimal vaccination rates (blue line) for the three cases a $W=0.2N$, c $W=0.3N$, e $W=0.4N$. (Right column) The number of infected males as a function of time without control (red line) and with optimal control (blue line) for the three cases b $W=0.2N$, d $W=0.3N$, f $W=0.4N$. For all plots, the integral of the shaded area represents the number of infections averted by the optimal vaccination strategies (color figure online)

The case of an already existing single-sex vaccination program

The results in Fig. 4 were derived for a starting vaccination roll-out program. Another scenario of interest is when a single-sex vaccination strategy is already established. In this context, public health authorities would like to evaluate if it is better to increase coverage in the existing single-sex program or to vaccinate both sexes simultaneously (Bogaards et al. 2011). To simulate this scenario, we assume that $u_f(t)=u_{\mathit{max}}$ and $u_m(t)=0$ over an initial period such that at the end of the period 10000 females have been vaccinated. Hence, a substantial number of females have already been vaccinated, but no males have been vaccinated. Then, the optimal vaccine allocation begins. This scenario mimics HPV vaccination programs in several countries currently directed at females only (Bruni et al. 2021). Other model parameters are fixed as shown in Table 1, except the total vaccine stockpile W that now counts 10000 vaccines less (the ones that are already delivered for females).

The optimal control profiles and cumulative vaccinated individuals for these conditions are shown in Fig. 6. The resulting optimal control profiles for the cases $W=0.2N$ and $W=0.3N$ (see Fig. 6a, c), are significantly different in comparison with the corresponding cases (see Fig. 4a, c). The first difference is that now the control profiles no longer suggest that health authorities should deploy as many vaccines as possible at the beginning of the outbreak. Instead, immunization should be delayed by at least 60 days. Second, the optimal vaccination rate for males is now strictly zero i.e. $u_m^{\ast }(t)=0$. As a consequence, the total number of vaccinated individuals is equal to the number of vaccinated females, $Z(t)=Z_f(t)$ (see Fig. 6b, d). For the case of a starting vaccination roll-out program (see Fig. 4), results showed that females should be vaccinated at a higher rate than males. However, even in the scenario with the lowest vaccine supply, the optimal vaccination rate for males was greater than zero. Finally, observe that for the case $W=0.4N$ (see Fig. 6e, f), the control profiles present again the same qualitative behavior as the ones in the starting vaccination roll-out program. To summarize, for a scenario of very limited vaccine stockpile, i.e. $W<0.3N$, vaccine administration should continue prioritizing the female-only target population. However, if the stockpile is relatively large, i.e. $W>0.4N$, the inclusion of males in the vaccination program is the optimal strategy to effectively eliminate the epidemic in the population.

Fig. 6.

First column: Optimal time-dependent vaccination rates for females $u_f^{\ast }(t)$ (blue) and males $u_f^{\ast }(t)$ (red). Second column: Cumulative number of vaccinated females (blue), and males (red) computed from the optimal states corresponding to the optimal controls on the first column. The total cumulative number of vaccines administered, Z(t), is shown in yellow. For both columns, the supply of vaccines corresponds to 20% (first row), 30% (second row), and 40% (third row) of the total population but 10000 vaccines have already been directed to females. Baseline parameter values are listed in Table 1. Initial conditions $I_f(0)=1537$, $I_m(0)=1157$, $V_f(0)=10000$, $V_m(0)=0$, and $S_f(0)=N_f^{\ast }-I_f(0)-V_f(0)$, $S_m(0)=N_m^{\ast }-I_m(0)-V_m(0)$ (color figure online)

Discussion

The prevention and control of sexually transmitted infections have extensive public health benefits including the reduction of preventable deaths of newborns, and improved sexual and reproductive health (World Health Organization 2021). Vaccine development and successful implementation of effective immunization programs are critical actions to progress in the control of STIs (Gottlieb et al. 2019). Nevertheless, due to cost and logistical challenges, vaccine stockpile is typically limited and not enough to achieve high-immunization coverage, particularly in low-middle-income settings (Yamey et al. 2022). Data reports significant sex-specific differences in biological risks for STI acquisition, the clinical manifestation of the infection, and their potential for transmission to the opposite sex (Hook 2012; Wong et al. 2004). Hence, determining optimal sex-specific vaccination programs against STIs is a challenging task that deserves more attention. A major example are HPV vaccination programs which were introduced in several countries for young girls. These early female-only HPV immunization programs have been found to be cost-effective when cervical cancer prevention is the main objective (see Brisson et al. (2020) and the references therein). Yet, a number of studies (Elfström et al. 2016; Stanley 2012) have suggested that if rather than preventing cervical cancer alone, the aim is to reduce all HPV-associated diseases, then the inclusion of males can be cost-effective. Currently, more than 30% of the HPV programs are gender-neutral (GN), i.e. with both females and males receiving the vaccine. However, 79% of GN programs are from high-income countries whereas only 21% are from upper-middle-income countries (Bruni et al. 2021).

In this study, we investigate under which conditions the inclusion of both males and females into vaccination programs adds to the population-level impact of female-only interventions. Considering sex-specific differences in transmissibility and severity in disease outcomes, we compare vaccination strategies against STI transmission for different realistic settings described by distinct budget constraints associated with the vaccine supply. The vaccination strategies are obtained as solutions to an optimal control problem aiming to reduce the total prevalence of the infection subject to a minimalist two-sex Kermack–McKendrick-type model. The control variables are the daily vaccination rates for females and males, respectively, that mimic a prophylactic vaccine with effectiveness not necessarily equal to $100\%$. One important aspect of our approach relies upon modeling a limited but specific vaccine stockpile via an isoperimetric constraint (Kamien and Schwartz 2012). We solve the optimal control problem via Pontryagin’s Maximum Principle and obtain a numerical approximation for the solution using a modified version of the FBSM which handles the isoperimetric budget constraint in our formulation.

We considered two main scenarios regarding the current immunization coverage in the population (i) a starting vaccination roll-out program where no individuals in the population have been vaccinated (see Fig. 4) and (ii) a female-only vaccination strategy which is already established and has reached around 20% coverage in females (see Fig. 6). The second scenario is relevant for public health authorities who would like to evaluate if it is better to increase coverage in the existing female-only program or to vaccinate both sexes simultaneously. Each of these scenarios is further subdivided according to the total vaccine supply available which is incorporated via the isoperimetric constraint (11). The simulations for the first scenario show that although the vaccination rate for females should be higher than the one for males. Hence, under these conditions, vaccinating both sexes, with a slightly higher rate for females, is optimal and provides an effective and faster approach to reducing the prevalence of the infection. These results agree with the HPV immunization program currently used in Spain (Linertová et al. 2022). However, the difference in sex-specific vaccine distribution increases as the vaccine stockpile reduces. For the case in which a female-only program is already ongoing, vaccine administration should continue prioritizing the female-only target population and males should only be included if the vaccine stockpile is large (enough to reach at least $40\%$ total coverage). In other words, for a very limited vaccine supply ($30\%$ coverage or less), female-only vaccination can be more beneficial than the inclusion of both sexes into the vaccination program. Since the male-to-female sexual infectivity rate is generally higher than that of female-to-male, prioritizing female vaccination might seem counterintuitive, because vaccinating super-spreaders (in this case males) is usually effective to reduce the prevalence of the infection. Yet, this may be due to the fact that the health risks associated with STIs are considerably higher for females in comparison with men. This is considered in the solution of our optimal control problem using the weight parameters in the objective functional.

As with the majority of studies, we considered some simplifying modeling assumptions that can be improved in further studies. First, we assumed that single-dose vaccination is enough to reach full immunity. Nevertheless, a two-dose series is often needed and there might be a delay of some days (or weeks) to achieve full immunity. Second, we assumed that susceptible individuals are easily identified for a prophylactic vaccine that lacks therapeutic effects and is therefore not effective in already infected individuals. On the contrary case, some vaccines can be misdirected in the infected population. Finally, we have considered a heterosexual population but the inclusion of individuals with another sexual orientation can play a key role in disease dynamics. Future investigations are necessary to validate if the principal properties of the optimal vaccination policies drawn from this study are affected when these assumptions are relaxed.

Declarations

Conflict of interest

The authors declare they have no known competing financial interests that could have appeared to influence the results reported in this work.