An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges

Abstract

As the world moves towards industrialization, optimization problems become more challenging to solve in a reasonable time. More than 500 new metaheuristic algorithms (MAs) have been developed to date, with over 350 of them appearing in the last decade. The literature has grown significantly in recent years and should be thoroughly reviewed. In this study, approximately 540 MAs are tracked, and statistical information is also provided. Due to the proliferation of MAs in recent years, the issue of substantial similarities between algorithms with different names has become widespread. This raises an essential question: can an optimization technique be called ‘novel’ if its search properties are modified or almost equal to existing methods? Many recent MAs are said to be based on ‘novel ideas’, so they are discussed. Furthermore, this study categorizes MAs based on the number of control parameters, which is a new taxonomy in the field. MAs have been extensively employed in various fields as powerful optimization tools, and some of their real-world applications are demonstrated. A few limitations and open challenges have been identified, which may lead to a new direction for MAs in the future. Although researchers have reported many excellent results in several research papers, review articles, and monographs during the last decade, many unexplored places are still waiting to be discovered. This study will assist newcomers in understanding some of the major domains of metaheuristics and their real-world applications. We anticipate this resource will also be useful to our research community.

Introduction

The term ‘meta’ is becoming more prevalent nowadays; it generally translates to ‘beyond’ or ‘higher level’. Although there is no agreed mathematical definition, the continued development of heuristic algorithms is usually referred to as MAs (Yang 2020). A heuristic algorithm is a method for producing acceptable solutions to optimization problems through trial and error. Intelligence is found not only in humans but also in animals, microorganisms, and other minute aspects of nature, such as ants, bees, and other creatures. Nature serves as a source of inspiration for many MAs, which are referred to as nature-inspired algorithms (NIAs) (Yang 2010a). Nature performs all tasks optimally, whether it’s moving light through space in the shortest path, carrying out the work function of any living organ with the least amount of energy expansion, or forming bubbles with the least amount of surface area that is a sphere. Natural selection favors optimization. That is the most efficient method of completing any task successfully and hassle-free. This simple concept can be applied to any type of work that we perform in our everyday lives. However, when it comes to large-scale operations, such as those in businesses, national security, distribution in large areas, and the design of some structures, we require a concrete method or tool to ensure that resources are utilized properly and that are maximized, which leads to operations research (OR). During the last decade, metaheuristics have emerged as a powerful optimization tool in OR. Also, MAs are becoming more critical in computational intelligence because they are flexible, adaptive, and have an extensive search capacity. MAs are used in NP-Hard problems, fixture and manufacturing cell design, soft computing, foreign exchange trading, robotics, medical science, behavioral science, photo-voltaic models, and so on, which is evidence of the importance of MAs. As MAs are stochastic by nature, they cannot guarantee the achievement of the optimal solution. As a result, the question naturally arises: Is it a worthy choice? It is roughly akin to ‘something is better than nothing.’ When others fail, MAs provide us with a satisfactory ‘something’. In practice, we achieve a satisfactory or workable solution in a reasonable amount of time. Most of the algorithms have been tested for lower dimensions. It is necessary to test them for a higher dimensional problem and improve them if necessary to tackle the ‘curse of dimensionality’. A significant research gap between theory and implementation has been shown, which should be taken care of. As exploration and exploitation are the fundamental strategies of most MAs, balancing them is another challenge. The main contributions of this study can be summarized as:

• The article presents a recent metaheuristics survey. The data set for this study contains about 540 MAs.

• This study provides critical yet constructive analysis, addressing improper methodological practices to accomplish helpful research.

• A new classification of MAs is proposed based on the number of parameters.

• The limitations of metaheuristics, as well as open challenges, are highlighted.

• Several potential future research directions for metaheuristics have been identified.

The rest of this paper is organized as follows. A brief history is discussed in Sect. 2. A compilation of existing MAs and other literary works are provided in Sect. 3. In Sect. 4, few statistical data are provided, while constructive criticism has been done in Sect. 5. MAs are classified into subgroups based on four different points of view in Sect. 6. In addition, Sect. 7 contains some real-world metaheuristics applications. A few limitations, including some open challenges, are addressed in Sect. 8. A brief overview of the potential future directions of metaheuristics is provided in Sect. 9. Finally, conclusions are drawn in Sect. 10.

Brief history

What was the first use of (meta) heuristic? Because the heuristic process automatically dominates the human mind, humans may have employed it from the beginning, whether they realized it or not: the use of fire, the acquisition of number systems, and the usage of the wheel are all examples of heuristic process applications. Any practical problem can be modeled mathematically for optimization—this is a challenging task; even the more challenging task is to optimize it. To address this situation, scientists proposed several approaches that are now referred to as ‘conventional methods’. They are mainly as follows:

• Direct search: random search method, uni-variant method, pattern search method, convex optimization, linear programming, interior-point method, quadratic programming, trust-region method, etc.

• Gradient-based method: steepest descent method, conjugate gradient method, Newton–Raphson method, quasi-Newton method, etc.

Since the most realistic optimization problems are discontinuous and highly non-linear, conventional methods fail to prove their efficiency, robustness, and accuracy. Researchers devised alternative approaches to tackle such problems. It is worth noting that nature has inspired us since the beginning–whether making fire from a jungle blaze or making ships from floating wood. In general, all are gifted by nature, directly or indirectly.

However, Hungarian mathematician George Pólya wrote the book ‘How to Solve It’ about the subject in 1945, where he gave an idea about heuristic searches and mentioned four steps to grasping a problem as follows: (a) understand the problem, (b) devising a plan, (c) looking back, and (d) carrying the plan (Polya 2004). The book gained immense attraction and was translated into several languages, selling over a million copies. Still, the book is used in mathematical education, Pólya work inspired Douglas Lenat’s Automated Mathematician and Eurisko artificial intelligence programs.

Also, scientists all over the world tried to solve many practical problems. In this case, in 1945, the first success came by breaking the Enigma ciphers’ code at Bletchley Park by using heuristic algorithms; British scientist Turing called his method ‘heuristic search’ (Hodges 2012). He was one of the designers of the bombe, used in World War II. After then, he proposed a ‘learning machine’ in 1950, which would parallel the principle of evolution. Barricelli started work with computer simulation as early as 1954 at the Institute for Advanced Study, New Jersey. Although his work was not noticed widely, his work in evolution is considered pioneering in artificial life research. Artificial evolution became a well-recognized optimization approach in the 1960s and early 1970s due to the work of Rechenberg and Schwefel (sulfur 1977). Rechenberg solved many complex engineering problems through evolution strategies. Next, Fogel proposed generating artificial intelligence. Decision Science Inc. was probably the first company to use evolutionary computation to solve real-world problems in 1966. Owens and Burgin further expanded the methodology, and the Adaptive Maneuvering Logic flight simulator was initially deployed at Langley Research Center for air-to-air combat training (Burgin and Fogel 1972). Fogel and Burgin also experimented with simulations of co-evolutionary games in Decision Science. They also worked on the real-world applications of evolutionary computation in many ways, including modeling human operators and thinking about biological communication (Fogel et al. 1970). In the early 1970s, Holland formalized a breakthrough programming technique, the genetic algorithm (GA), which he summarised in his book ‘Adaptation in Natural and Artificial Systems’ (Holland 1991). He worked to extend the algorithm’s scope during the next decade by creating a genetic code representing any computer program structure. Also, he developed a framework for predicting the next generation’s quality, known as Holland’s schema theorem. Kirkpatrick et al. (1983) proposed simulated annealing (SA), which is a single point-based algorithm inspired by the mechanism of metallurgy’s annealing process. Glover (1989) formalized the tabu search computer-based optimization methodology. This is based on local search, which has a high probability of getting stuck in local optima. Another interesting artificial life program, called boid, was developed by Reynolds (1987), which simulates birds’ flocking behavior. It was used for visualizing information and optimization tasks. Moscato et al. (1989) introduced a memetic algorithm in his technical report inspired by Darwinian principles of natural evolution and Dawkins’ notion of a meme. The memetic algorithm was an extension of the traditional genetic algorithm. It was used as a local search technique to reduce the likelihood of premature convergence. Another nature-inspired algorithm from the early years was developed in 1989 by Bishop and Torr (1992), later referred to as stochastic diffusion search (SDS). Kennedy and Eberhart (1995) developed particle swarm optimization (PSO), which was first intended for simulating social behaviour. This is one of the simplest and most widely used algorithm. In the next two years, an appreciable and controversial work, the no free lunch theorem (NFL) for optimization, was introduced and proved explicitly by Wolpert and Macready (1997). While some researchers argue that NFL has some significant insight, others argue that NFL has little relevance to machine learning research. But the main thing is that NFL unlocks a golden opportunity to further research for developing new domain-specific algorithms. The validity of the NFL for higher dimensions is still under investigation. Later on, several efficient algorithms have been developed, such as differential evolution (DE) by Storn and Price (1997), ant colony optimization (ACO) by Dorigo et al. (2006), artificial bee colony (ABC) by Karaboga and Basturk (2007), and others, as shown in the following section.

Metaheuristics

It is difficult to summarize all existing MAs and other valuable data in a single article. In this section, we collect as many existing MAs as possible. Here about 540 existing MAs are complied. It enables us to comprehend the broader context in order to offer constructive criticism in this area, and this can be used as a toolbox (Table 1).

Table 1.

Metaheuristic algorithms (up to 2022)

SN	Algorithm	References
1	Across Neighbourhood Search (ANS)	Wu (2016)
2	Adaptive Social Behavior Optimization (ASBO)	Singh (2013)
3	African Buffalo Optimization (ABO)	Odili et al. (2015)
4	African Vultures Optimization Algorithm (AVOA)	Abdollahzadeh et al. (2021a)
5	African Wild Dog Algorithm (AWDA)	Subramanian et al. (2013)
6	Algorithm of the Innovative Gunner (AIG)	Pijarski and Kacejko (2019)
7	Ali Baba and the Forty Thieves Optimization (AFT)	Braik et al. (2022b)
8	Anarchic Socity Optimization (ASO)	Ahmadi-Javid (2011)
9	Andean Condor Algorithm (ACA)	Almonacid and Soto (2019)
10	Animal Behavior Hunting (ABH)	Naderi et al. (2014)
11	Animal Migration Optimization Algorithm (AMO)	Li et al. (2014)
12	Ant Colony Optimization (ACO)	Dorigo et al. (2006)
13	Ant Lion Optimizer (ALO)	Mirjalili (2015a)
14	Aphid-Ant Mutualism (AAM)	Eslami et al. (2022)
15	Aphids Optimization Algorithm (AOA)	Liu et al. (2022)
16	Archerfish Hunting Optimizer (AHO)	Zitouni et al. (2021)
17	Archery Algorithm (AA)	Zeidabadi et al. (2022)
18	Archimedes Optimization Algorithm (AOA)	Hashim et al. (2021)
19	Arithmetic Optimization Algorithm (AOA)	Abualigah et al. (2021b)
20	Aritificial Algae Algorithm (AAA)	Uymaz et al. (2015)
21	Artificial Atom Algorithm (A3)	Karci (2018)
22	Artificial Bee Colony (ABC)	Karaboga and Basturk (2007)
23	Artificial Beehive Algorithm (ABA)	Munoz et al. (2009)
24	Artificial Butterfly Optimization (ABO)	Qi et al. (2017)
25	Artificial Chemical Process (ACP)	Irizarry (2004)
26	Artificial Chemical Reaction Optimization Algorithm (ACROA)	Alatas (2011)
27	Artificial Cooperative Search (ACS)	Civicioglu (2013a)
28	Artificial Coronary Circulation System (ACCS)	Kaveh and Kooshkebaghi (2019)
29	Artificial Ecosystem Algorithm (AEA)	Adham and Bentley (2014)
30	Artificial Ecosystem-based Optimization (AEO)	Zhao et al. (2020b)
31	Artificial Electric Field Algorithm (AEFA)	Yadav et al. (2019)
32	Artificial Feeding Birds Algorithm (AFB)	Lamy (2019)
33	Artificial Fish Swarm Algorithm (AFSA)	Li (2003)
34	Artificial Flora Optimization Algorithm (AF)	Cheng et al. (2018)
35	Artificial Gorilla Troops Optimizer (GTO)	Abdollahzadeh et al. (2021b)
36	Artificial Hummingbird Algorithm (AHA)	Zhao et al. (2022b)
37	Artificial Infection Disease Optimization (AIO)	Huang (2016)
38	Artificial Jellyfish Search Optimizer (AJSO)	Chou and Truong (2021)
39	Artificial Lizard Search Optimization (ALSO)	Kumar et al. (2021)
40	Artificial Photosynthesis and Phototropism Mechanism (APPM)	Cui and Cai (2011)
41	Artificial Physics Optimization (APO)	Xie et al. (2009)
42	Artificial Plants Optimization Algorithm (APO)	Zhao et al. (2011)
43	Artificial Raindrop Algorithm (ARA)	Jiang et al. (2014)
44	Artificial Reaction Algorithm (ARA)	Melin et al. (2013)
45	Artificial Searching Swarm Algorithm (ASSA)	Chen et al. (2009)
46	Artificial Showering Algorithm (ASA)	Ali et al. (2015)
47	Artificial Swarm Intelligence (ASI)	Rosenberg and Willcox (2018)
48	Artificial Tribe Algorithm (ATA)	Chen et al. (2012)
49	Asexual Reproduction Optimization (ARO)	Farasat et al. (2010)
50	Atmosphere Clouds Model Optimization (ACMO)	Gao-Wei and Zhanju (2012)
51	Atomic Orbital Search (AOS)	Azizi (2021)
52	Backtracking Search Optimization (BSO)	Civicioglu (2013b)
53	Bacterial Chemotaxis Optimization (BCO)	Muller et al. (2002)
54	Bacterial Colony Optimization (BCO)	Niu and Wang (2012)
55	Bacterial Evolutionary Algorithm (BEA)	Numaoka (1996)
56	Bacterial Foraging Optimization Algorithm (BFOA)	Das et al. (2009)
57	Bacterial Swarming Algorithm (BSA)	Tang et al. (2007)
58	Bacterial-GA Foraging (BF)	Chen et al. (2007)
59	Bald Eagle Search (BES)	Alsattar et al. (2020)
60	Bar Systems (BS)	Del Acebo and de-la Rosa (2008)
61	Bat Algorithm (BA)	Yang and He (2013)
62	Bat Inspired Algorithm (BIA)	Yang (2010b)
63	Bat Intelligence (BI)	Malakooti et al. (2012)
64	Battle Royale Optimization (BRO)	Rahkar Farshi (2021)
65	Bean Optimization Algorithm (BOA)	Zhang et al. (2010)
66	Bear Smell Search Algorithm (BSSA)	Ghasemi-Marzbali (2020)
67	Bee Colony Optimization (BCO)	Teodorovic and Dell’Orco (2005)
68	Bee Conoly-Inspired Algorithm (BCIA)	Häckel and Dippold (2009)
69	Bee Swarm Optimization (BSO)	Akbari et al. (2010)
70	Bee System (BS)	Sato and Hagiwara (1998)
71	Bee System.1 (BS.1)	Lucic and Teodorovic (2002)
72	BeeHive (BH)	Wedde et al. (2004)
73	Bees Algorithm (BA)	Pham et al. (2006)
74	Bees Life Algorithm (BLA)	Bitam et al. (2018)
75	Beetle Swarm Optimization Algorithm (BSOA)	Wang and Yang (2018)
76	Beluga Whale Optimization (BWO)	Zhong et al. (2022)
77	Big Bang-Big Crunch (BBBC)	Erol and Eksin (2006)
78	Billiards-Inspired Optimization Algorithm (BOA)	Kaveh et al. (2020b)
79	Binary Slime Mould Algorithm (BSMA)	Abdel-Basset et al. (2021)
80	Binary Whale Optimization Algorithm (bWOA)	Reddy K et al. (2019)
81	Biogeography-Based Optimization(BBO)	Simon (2008)
82	Biology Migration Algorithm (BMA)	Zhang et al. (2019)
83	Bioluminiscent Swarm Optimization (BSO)	de Oliveira et al. (2011)
84	Biomimicry of Social Foraging Bactera for Distributed (BSFBD)	Passino (2002)
85	Bird Mating Optimization (BMO)	Askarzadeh (2014)
86	Bird Swarm Algorithm (BSA)	Meng et al. (2016)
87	Bison Behavior Algorithm (BBA)	Kazikova et al. (2017)
88	Black Hole Algorithm (BH.1)	Hatamlou (2013)
89	Black Hole Mechanics Optimization (BHMO)	Kaveh et al. (2020c)
90	Blind, Naked Mol-Rats Algorithm (BNMR)	Taherdangkoo et al. (2013)
91	Blue Monkey Algorithm (BM)	Mahmood and Al-Khateeb (2019)
92	Boids	Reynolds (1987)
93	Bonobo Optimizer (BO)	Das and Pratihar (2019)
94	Brain Storm Optimization (BSO)	Shi (2011)
95	Bull Optimization Algorithm (BOA)	FINDIK (2015)
96	Bumble Bees Mating Optimization (BBMO)	Marinakis et al. (2010)
97	Bus Transport Algorithm (BTA)	Bodaghi and Samieefar (2019)
98	Butterfly Optimization Algorithm (BOA)	Arora and Singh (2019)
99	Butterfly Optimizer(BO)	Kumar et al. (2015)
100	Buzzards Optimization Algorithm (BOA)	Arshaghi et al. (2019)
101	Camel Algorithm (CA)	Ibrahim and Ali (2016)
102	Camel Herd Algorithm (CHA)	Al-Obaidi et al. (2017)
103	Capuchin Search Algorithm (CapSA)	Braik et al. (2021)
104	Car Tracking Optimization Algorithm (CTOA)	Chen et al. (2018)
105	Cat Swarm Optimization (CSO)	Chu et al. (2006)
106	Catfish Particle Swarm Optimization (CatfishPSO)	Chuang et al. (2008)
107	Central Force Optimizartion (CFO)	Formato (2008)
108	Chaos Game Optimization (CGO)	Talatahari and Azizi (2021)
109	Chaos Optimization Alfgorithm (COA)	JIANG (1998)
110	Chaotic Dragonfly Algorithm (CDA)	Sayed et al. (2019b)
111	Charged System Search (CSS)	Kaveh and Talatahari (2010)
112	Cheetah Based Algorithm (CBA)	Klein et al. (2018)
113	Cheetah Chase Algorithm (CCA)	Goudhaman (2018)
114	Cheetah Optimizer (CO)	Akbari et al. (2022)
115	Chef-Based Optimization Algorithm (CBOA)	Trojovská and Dehghani (2022)
116	Chemical Reaction Optimization (CRO)	Alatas (2011)
117	Chicken Swarm Optimization (CSO)	Meng et al. (2014)
118	Child Drawing Development Optimization (CDDO)	Abdulhameed and Rashid (2022)
119	Chimp Optimization Algorithm (ChOA)	Khishe and Mosavi (2020)
120	Circle Search Algorithm (CSA)	Qais et al. (2022)
121	Circular Structures of Puffer Fish Algorithm (CSPF)	Catalbas and Gulten (2018)
122	Circulatory System-based Optimization (CSBO)	Ghasemi et al. (2022)
123	City Councils Evolution (CCE)	Pira (2022)
124	Clonal Selection Algorithm (CSA)	De Castro and Von Zuben (2000)
125	Cloud Model-Based Differential Evolution Algorithm (CMDE)	Zhu and Ni (2012)
126	Cockroach Swarm Optimization (CSO)	ZhaoHui and HaiYan (2010)
127	Cognitive Behavior Optimization Algorithm (COA)	Li et al. (2016b)
128	Collective Animal Behavior (CAB)	Cuevas et al. (2012a)
129	Collective Decision Optimization Algorithm (CDOA)	Zhang et al. (2017b)
130	Colliding Bodies Optimization (CBO)	Kaveh and Mahdavi (2014)
131	Color Harmony Algorithm (CHA)	Zaeimi and Ghoddosian (2020)
132	Community of Scientist Optimization (CoSO)	Milani and Santucci (2012)
133	Competitive Learning Algorithm (CLA)	Afroughinia and Kardehi M (2018)
134	Competitive Optimization Algorithm (COOA)	Sharafi et al. (2016)
135	Consultant Guide Search (CGS)	Wu and Banzhaf (2010)
136	Co-Operation of Biology Related Algorithm (COBRA)	Akhmedova and Semenkin (2013)
137	Coral Reefs Optimization (CRO)	Salcedo-Sanz et al. (2014)
138	Corona Virus Optimization (CVO)	Salehan and Deldari (2022)
139	Coronavirus Herd Immunity Optimizer (CHIO)	Al-Betar et al. (2021)
140	Coronavirus Optimization Algorithm (COVIDOA)	Khalid et al. (2022)
141	Covariance Matrix Adaptation-Evolution Strategy (CMAES)	Hansen et al. (2003)
142	Coyote Optimization Algorithm (COA)	Pierezan and Coelho (2018)
143	Cricket Algorithm (CA)	Canayaz and Karcı (2015)
144	Cricket Behaviour-Based Algorithm (CBA)	Canayaz and Karci (2016)
145	Cricket Chirping Algorithm (CCA)	Deuri and Sathya (2018)
146	Crow Search Algorithm (CSA)	Askarzadeh (2016)
147	Crystal Energy Optimization Algorithm (CEO)	Feng et al. (2016)
148	Crystal Structure Algorithm (CryStAl)	Talatahari et al. (2021b)
149	Cuckoo Optimization Algorithm (COA)	Rajabioun (2011)
150	Cuckoo Search (CS)	Yang and Deb (2009)
151	Cultural Algorithm (CA)	Jin and Reynolds (1999)
152	Cultural Coyote Optimization Algorithm (CCOA)	Pierezan et al. (2019)
153	Cuttlefish Algorithm (CA)	Eesa et al. (2013)
154	Cyclical Parthenogenesis Algorithm (CPA)	Kaveh and Zolghadr (2017)
155	Dandelion Optimizer (DO)	Zhao et al. (2022a)
156	Deer Hunting Optimization Algorithm (DHOA)	Brammya et al. (2019)
157	Dendritic Cells Algorithm (DCA)	Greensmith et al. (2005)
158	Deterministic Oscillatory Search (DOS)	Archana et al. (2017)
159	Dialectic Search (DS)	Kadioglu and Sellmann (2009)
160	Differential Evolution (DE)	Storn and Price (1997)
161	Differential Search Algorithm (DSA)	Civicioglu (2012)
162	Dolphin Echolocation (DE)	Kaveh and Farhoudi (2013)
163	Dolphin Partner Optimization (DPO)	Shiqin et al. (2009)
164	Dragonfly Algorithm (DA)	Mirjalili (2016a)
165	Driving Training-Based Optimization (DTBO)	Dehghani et al. (2022b)
166	Duelist Algorithm (DA)	Biyanto et al. (2016)
167	Dynamic Differential Annealed Optimization (DDAO)	Ghafil and Jármai (2020)
168	Dynastic Optimization Algorithm (DOA)	Wagan et al. (2020)
169	Eagle Strategy (ES)	Yang and Deb (2010)
170	Earthwarm Optimization Algorithm (EOA)	Wang et al. (2018a)
171	Ebola Optimization Search Algorithm (EOSA)	Oyelade and Ezugwu (2021)
172	Ecogeography-Based Optimization (EBO)	Zheng et al. (2014)
173	Eco-inspired Evolutionary Algorithm (EEA)	Parpinelli and Lopes (2011)
174	Egyptian Vulture Optimization (EV)	Sur et al. (2013)
175	Election-Based Optimization Algorithm (EBOA)	Trojovskỳ and Dehghani (2022a)
176	Electromagnetic Field Optimization (EFO)	Abedinpourshotorban et al. (2016)
177	Electro-Magnetism Optimization (EMO)	Cuevas et al. (2012b)
178	Electromagnetism-Like Mechanism Optimization (EMO)	Birbil and Fang (2003)
179	Electron Radar Search Algorithm (ERSA)	Rahmanzadeh and Pishvaee (2020)
180	Elephant Clan Optimization (ECO)	Jafari et al. (2021)
181	Elephant Herding Optimization (EHO)	Wang et al. (2015)
182	Elephant Search Algorithm (ESA)	Deb et al. (2015)
183	Elephant Swarm Water Search Algorithm (ESWSA)	Mandal (2018)
184	Emperor Penguin Optimizer (EPO)	Dhiman and Kumar (2018)
185	Emperor Penguins Colony (EPC)	Harifi et al. (2019)
186	Escaping Bird Search (EBS)	Shahrouzi and Kaveh (2022)
187	Eurasian Oystercatcher Optimiser (EOO)	Salim et al. (2022)
188	Evolution Strategies (ES)	Beyer and Schwefel (2002)
189	Exchange Market Algorithm (EMA)	Ghorbani et al. (2017)
190	Extremal Optimization (EO)	Boettcher and Percus (1999)
191	Farmland Fertility Algorithm (FFA)	Shayanfar and Gharehchopogh (2018)
192	Fast Bacterial Swarming Algorithm (FBSA)	Chu et al. (2008)
193	Fertilization Optimization Algorithm (FOA)	Ghafil et al. (2022)
194	Fibonacci Indicator Algorithm (FIA)	Etminaniesfahani et al. (2018)
195	FIFA Word Cup Competitions (FIFA)	Razmjooy et al. (2016)
196	Find-Fix-Finish-Exploit-Analyze Algorithm (F3EA)	Kashan et al. (2019)
197	Fire Hawk Optimizer (FHO)	Azizi et al. (2022)
198	Firefly Algorithm (FA)	Yang (2009)
199	Fireworks Algorithm (FA)	Tan and Zhu (2010)
200	Fireworks Optimization Algorithm (FOA)	Ehsaeyan and Zolghadrasli (2022)
201	Fish School Search (FSS)	Bastos Filho et al. (2008)
202	Fish Swarm Algorithm (FSA)	Tsai and Lin (2011)
203	Fitness Dependent Optimizer (FDO)	Abdullah and Ahmed (2019)
204	Flock by Leader (FL)	Bellaachia and Bari (2012)
205	Flocking Based Algorithm (FA)	Cui et al. (2006)
206	Flow Direction Algorithm (FDA)	Karami et al. (2021)
207	Flow Regime Algorithm (FRA)	Tahani and Babayan (2019)
208	Flower Pollination Algorithm (FPA)	Yang (2012)
209	Flying Elephant Algorithm (FEA)	Xavier and Xavier (2016)
210	Football Game Algorithm (FGA)	Fadakar and Ebrahimi (2016)
211	Forensic Based Investigation (FBI)	Chou and Nguyen (2020)
212	Forest Optimization Algorithm (FOA)	Ghaemi and Feizi-Derakhshi (2014)
213	Fox Optimizer (FOX)	Mohammed and Rashid (2022)
214	Fractal-Based Algorithm (FA)	Kaedi (2017)
215	Frog Call Inspired Algorithm (FCA)	Mutazono et al. (2009)
216	Fruit Fly Optimization Algorithm (FOA)	Pan (2012)
217	Gaining Sharing Knowledge Based Algorithm (GSK)	Mohamed et al. (2020)
218	Galactic Swarm Optimization (GSO)	Muthiah-Nakarajan and Noel (2016)
219	Galaxy Based Search Algorithm (GBS)	Shah-Hosseini (2011)
220	Gannet Optimization Algorithm (GOA)	Pan et al. (2022)
221	Gases Brownian Motion Optimization (GBMO)	Abdechiri et al. (2013)
222	Gene Expression (GE)	Ferreira (2002)
223	Genetic Algorithm (GA)	Holland (1991)
224	Genetic Programming (GP)	Koza et al. (1994)
225	Geometric Octal Zones Distance Estimation Algorithm (GOZDE)	Kuyu and Vatansever (2022)
226	Giza Pyramids Construction Algorithm (GPC)	Harifi et al. (2020)
227	Global Neighborhood Algorithm (GNA)	Alazzam and Lewis (2013)
228	Glowworm Swarm Optimization (GSO)	Zhou et al. (2014)
229	Golden Ball Algorithm (GB)	Osaba et al. (2014)
230	Golden Eagle Optimizer (GEO)	Mohammadi-Balani et al. (2021)
231	Golden Jackal Optimization (GJO)	Chopra and Ansari (2022)
232	Golden Search Optimization Algorithm (GSO)	Noroozi et al. (2022)
233	Golden Sine Algorithm (Gold-SA)	Tanyildizi and Demir (2017)
234	Good Lattice Swarm Optimization (GLSO)	Su et al. (2007)
235	Goose Team Optimizer (GTO)	Wang and Wang (2008)
236	Gradient Evolution Algorithm (GE)	Kuo and Zulvia (2015)
237	Gradient-Based Optimizer (GBO)	Ahmadianfar et al. (2020)
238	Grasshoper Optimization Algorithm (GOA)	Saremi et al. (2017)
239	Gravitational Clustering Algorithm (GCA)	Kundu (1999)
240	Gravitational Emulation Local Search (GELS)	Barzegar et al. (2009)
241	Gravitational Field Algorithm (GFA)	Zheng et al. (2010)
242	Gravitational Interactions Optimization (GIO)	Flores et al. (2011)
243	Gravitational Search Algorithm (GSA)	Rashedi et al. (2009)
244	Great Deluge Algorithm (GDA)	Dueck (1993)
245	Greedy Politics Optimization (GPO)	Melvix (2014)
246	Grenade Explosion Method (GEM)	Ahrari and Atai (2010)
247	Grey Wolf Optimizer (GWO)	Mirjalili et al. (2014)
248	Group Counseling Optimization (GCO)	Eita and Fahmy (2014)
249	Group Escape Behavior (GEB)	Min and Wang (2011)
250	Group Leaders Optimization Algorithm (GIOA)	Daskin and Kais (2011)
251	Group Mean-Based Optimizer (GMBO)	Dehghani et al. (2021)
252	Group Search Optimizer (GSO)	He et al. (2009)
253	Group Teaching Optimization Algorithm (GTOA)	Zhang and Jin (2020)
254	Harmony Element Algorithm (HEA)	Cui et al. (2008)
255	Harmony Search (HS)	Lee and Geem (2005)
256	Harris Hawks Optimizer (HHO)	Heidari et al. (2019)
257	Heart Optimization (HO)	Hatamlou (2014)
258	Heat Transfer Optimization Aalgorithm (HTOA)	Asef et al. (2021)
259	Heat Transfer Search Agorithm (HTS)	Patel and Savsani (2015)
260	Henry Gas Solubility Optimization (HGSO)	Hashim et al. (2019)
261	Hirerarchical Swarm Model (HSM)	Chen et al. (2010)
262	Honey Badger Algorithm (HBA)	Hashim et al. (2022)
263	Honeybee Social Foraging (HSF)	Quijano and Passino (2007)
264	Honeybees Mating Optimization Algorithm (HMOA)	Haddad et al. (2006)
265	Hoopoe Heuristic (HH)	El-Dosuky et al. (2012)
266	Human Evolutionary Model (HEM)	Montiel et al. (2007)
267	Human Felicity Algorithm (HFA)	Veysari et al. (2022)
268	Human Group Formation (HGF)	Thammano and Moolwong (2010)
269	Human Mental Search (HMS)	Mousavirad and Ebrahimpour (2017)
270	Human-Inspired algorithm (HIA)	Zhang et al. (2009)
271	Hunting Search (HuS)	Oftadeh et al. (2010)
272	Hurricane Based Optimization Algorithm (HOA)	Rbouh and El Imrani (2014)
273	Hydrological Cycle Algorithm (HCA)	Wedyan et al. (2017)
274	Hysteresis for Optimization (HO)	Zarand et al. (2002)
275	Ideology Algorithm (IA)	Huan et al. (2017)
276	Imperialist Competitive Algorithm (ICA)	Atashpaz-Gargari and Lucas (2007)
277	Improve Genetic Immune Algorithm (IGIA)	Tayeb et al. (2017)
278	Integrated Radiation Optimization (IRO)	Chuang and Jiang (2007)
279	Intelligent Ice Fishing Algorithm (IIFA)	Karpenko and Kuzmina (2021)
280	Intelligent Water Drop Algorithm (IWD)	Shah-Hosseini (2009)
281	Interactive Autodidactic School Algorithm (IAS)	Jahangiri et al. (2020)
282	Interior Search Algorithm (ISA)	Gandomi (2014)
283	Invasive Tumor Growth Optimization (ITGO)	Tang et al. (2015)
284	Invasive Weed Optimization Algorithm (IWO)	Karimkashi and Kishk (2010)
285	Ions Motion Optimization (IMO)	Javidy et al. (2015)
286	Jaguar Algorithm (JA)	Chen et al. (2015)
287	Japanese Tree Frogs Calling Algorithm (JTFCA)	Hernández and Blum (2012)
288	Jaya Algorithm (JA)	Rao (2016)
289	Kaizen Programming (KP)	De Melo (2014)
290	Kernel Search Optimization (KSO)	Dong and Wang (2020)
291	Keshtel Algorithm (KA)	Hajiaghaei and Aminnayeri (2014)
292	Killer Whale Algorithm (KWA)	Biyanto et al. (2017)
293	Kinetic Gas Molecules Optimization (KGMO)	Moein and Logeswaran (2014)
294	Komodo Mlipir Algorithm (KMA)	Suyanto et al. (2021)
295	Kril Herd (KH)	Gandomi and Alavi (2012)
296	Lambda Algorithm (LA)	Cui et al. (2010)
297	Laying Chicken Algorithm (LCA)	Hosseini (2017)
298	Leaders and Followers Algorithm (LFA)	Gonzalez-Fernandez and Chen (2015)
299	League Championship Algorithm (LCA)	Kashan (2014)
300	Lévy Flight Distribution (LFD)	Houssein et al. (2020)
301	Light Ray Optimization (LRO)	Shen and Li (2010)
302	Lightning Attachment Procedure Optimization (LAPO)	Nematollahi et al. (2017)
303	Lightning Search Algorithm (LSA)	Shareef et al. (2015)
304	Linear Prediction Evolution Algorithm (LPE)	Gao et al. (2021a)
305	Lion Algorithm (LA)	Rajakumar (2012)
306	Lion Optimization Algorithm (LOA)	Yazdani and Jolai (2016)
307	Locust Search (LS)	Cuevas et al. (2015)
308	Locust Swarm Optimization (LSO)	Chen (2009)
309	Ludo Game-Based Swarm Intelligence Algorithm (LGSI)	Singh et al. (2019)
310	Magnetic Charged System Search (MCSS)	Kaveh et al. (2013)
311	Magnetic Optimization Algorithm (MFO)	Tayarani-N and Akbarzadeh-T (2008)
312	Magnetotactic Bacteria Optimization Algorithm (MBOA)	Mo and Xu (2013)
313	Marine Predator Algorithm (MPA)	Faramarzi et al. (2020)
314	Marriage in Honey Bees Optimization (MHBO)	Abbass (2001)
315	Material Generation Algorithm (MGA)	Talatahari et al. (2021a)
316	Mean Euclidian Distance Threshold (MEDT)	Kaveh et al. (2022)
317	Meerkats Inspired Algorithm (MIA)	Klein and dos Santos Coelho (2018)
318	Melody Search (MS)	Ashrafi and Dariane (2011)
319	Membrane Algorithm (MA)	Nishida (2006)
320	Memetic Algorithm (MA)	Moscato et al. (1989)
321	Method of Musical Composition (MMC)	Mora-Gutiérrez et al. (2014)
322	Migrating Birds Optimization (MBO)	Duman et al. (2012)
323	Mine Blast Algorithm (MBA)	Sadollah et al. (2013)
324	MOEA/D	Zhang and Li (2007)
325	Momentum Search Algorithm (MSA)	Dehghani and Samet (2020)
326	Monarch Butterfly Optimization (MBO)	Feng et al. (2017)
327	Monkey Search (MS)	Mucherino and Seref (2007)
328	Mosquito Flying Optimization (MFO)	Alauddin (2016)
329	Moth Flame Optimization Algorithm (MFO)	Mirjalili (2015b)
330	Moth Search Algorithm (MSA)	Wang (2018)
331	Mouth Breeding Fish Algorithm (MBF)	Jahani and Chizari (2018)
332	Mox Optimization Algorithm (MOX)	Arif et al. (2011)
333	Multi-Objective Beetle Antennae Search (MOBAS)	Zhang et al. (2021)
334	Multi-Objective Trader algorithm (MOTR)	Masoudi-Sobhanzadeh et al. (2021)
335	Multi-Particle Collision Algorithm (M-PCA)	da Luz et al. (2008)
336	Multivariable Grey Prediction Model Algorithm (MGPEA)	Xu et al. (2020)
337	Multi-Verse Optimizer (MVO)	Mirjalili et al. (2016)
338	Naked Moled Rat (NMR)	Salgotra and Singh (2019)
339	Namib Beetle Optimization (NBO)	Chahardoli et al. (2022)
340	Natural Aggregation Algorithm (NAA)	Luo et al. (2016)
341	Natural Forest Regeneration Algorithm (NFR)	Moez et al. (2016)
342	Neuronal Communication Algorithm (NCA)	A Gharebaghi and Ardalan A (2017)
343	New Caledonian Crow Learning Algorithm (NCCLA)	Al-Sorori and Mohsen (2020)
344	Newton Metaheuristic Algorithm (NMA)	Gholizadeh et al. (2020)
345	Nomadic People Optimizer (NPO)	Salih and Alsewari (2020)
346	Old Bachelor Acceptance (OBA)	Hu et al. (1995)
347	OptBees (OB)	Maia et al. (2013)
348	Optics Inspired Optimization (OIO)	Kashan (2015)
349	Optimal Foraging Algorithm (OFA)	Sayed et al. (2019a)
350	Optimal Stochastic Process Optimizer (OSPO)	Xu and Xu (2021)
351	Orca Optimization Algorithm (OOA)	Golilarz et al. (2020)
352	Orca Predation Algorithm (OPA)	Jiang et al. (2021)
353	Oriented Search Algorithm (OSA)	Zhang et al. (2008)
354	Paddy Field Algorithm (PFA)	Kong et al. (2012)
355	Parliamentary Optimization Algorithm (POA)	Borji and Hamidi (2009)
356	Particle Collision Algorithm (PCA)	Sacco et al. (2007)
357	Particle Swarm Optimization (PSO)	Eberhart and Kennedy (1995)
358	Passing Vehicle Search (PVS)	Savsani and Savsani (2016)
359	Pathfinder Algorithm (PFA)	Yapici and Cetinkaya (2019)
360	Pearl Hunting Algorithm (PHA)	Chan et al. (2012)
361	Pelican Optimization Algorithm (POA)	Trojovskỳ and Dehghani (2022b)
362	Penguins Search Optimization Algorithm (PeSOA)	Gheraibia and Moussaoui (2013)
363	Photon Search Algorithm (PSA)	Liu and Li (2020)
364	Photosyntetic Algorithm (PA)	Murase (2000)
365	Pigeon Inspired Optimization (PIO)	Duan and Qiao (2014)
366	Pity Beetle Algorithm (PBA)	Kallioras et al. (2018)
367	Plant Competition Optimization (PCO)	Rahmani and AliAbdi (2022)
368	Plant Growth Optimization (PGO)	Cai et al. (2008)
369	Plant Propagation Algorithm (PPA)	Sulaiman et al. (2014)
370	Plant Self-Defense Mechanism Algorithm (PSDM)	Caraveo et al. (2018)
371	Plasma Generation Optimization (PGO)	Kaveh et al. (2020a)
372	Political Optimizer (PO)	Askari et al. (2020)
373	Poplar Optimization Algorithm (POA)	Chen et al. (2022)
374	POPMUSIC	Taillard and Voss (2002)
375	Population Migration Algorithm (PMA)	ZongXXSlahUndXXyuan (2003)
376	Prairie Dog Optimization (PDO)	Ezugwu et al. (2022)
377	Predator–Prey Optimization (PPO)	Narang et al. (2014)
378	Prey Predator Algorithm (PPA)	Tilahun and Ong (2015)
379	Projectiles Optimization (PRO)	Kahrizi and Kabudian (2020)
380	Quantum-Inspired Bacterial Swarming Optimization (QBSO)	Cao and Gao (2012)
381	Queen-Bees Evolution (QBE)	Jung (2003)
382	Queuing Search Algorithm (QSA)	Zhang et al. (2018)
383	Raccoon Optimization Algorithm (ROA)	Koohi et al. (2018)
384	Radial Movement Optimization (RMO)	Rahmani and Yusof (2014)
385	Rain Optimization Algorithm (ROA)	Moazzeni and Khamehchi (2020)
386	Rain Water Algorithm (RWA)	Biyanto et al. (2019)
387	Rain-Fall Optimization (RFO)	Kaboli et al. (2017)
388	Raven Roosting Optimization Algorithm (RRO)	Brabazon et al. (2016)
389	Ray Optimization (RO)	Kaveh and Khayatazad (2012)
390	Red Deer Algorithm (RDA)	Fard and Hajiaghaei k (2016)
391	Reincarnation Algorithm (RA)	Sharma (2010)
392	Remora Optimization Algorithm (ROA)	Jia et al. (2021)
393	Reptile Search Algorithm (RSA)	Abualigah et al. (2021a)
394	Rhino Herd Behavior (RHB)	Wang et al. (2018b)
395	Ring Toss Game-Based Optimization Algorithm (RTGBO)	Doumari et al. (2021)
396	Ringed Seal Search (RSS)	Saadi et al. (2016)
397	River Formation Dynamics (RFD)	Rabanal et al. (2007)
398	Roach Infestation Optimization (RIO)	Havens et al. (2008)
399	Root Growth Optimizer (RGO)	He et al. (2015)
400	Root Tree Optimization Algorithm (RTO)	Labbi et al. (2016)
401	RUNge Kutta optimizer (RUN)	Ahmadianfar et al. (2021)
402	Runner Root Algorithm (RRA)	Merrikh-Bayat (2015)
403	SailFish Optimizer (SFO)	Shadravan et al. (2019)
404	Salp Swarm Algorithm (SSA)	Mirjalili et al. (2017)
405	SaMW	Tychalas and Karatza (2021)
406	Saplings Growing Up Algorithm (SGUA)	Karci (2007)
407	Satin Bowerbird Optimizer (SBO)	Moosavi and Bardsiri (2017)
408	Scatter Search Algorithm (SS)	Glover (1977)
409	Scientific Algorithm (SA)	Felipe et al. (2014)
410	Search Group Algorithm (SGA)	Gonçalves et al. (2015)
411	Search in Forest Optimizer (SFO)	Ahwazian et al. (2022)
412	Seed based Plant Propagation Algorithm (SPPA)	Sulaiman and Salhi (2015)
413	Seeker Optimization Algorithm (SOA)	Dai et al. (2006)
414	See-See Partidge Chicks Optimization (SSPCO)	Omidvar et al. (2015)
415	Self-Organizing Migrating Algorithm (SOMA)	Zelinka (2004)
416	Self-Driven Particles (SDP)	Vicsek et al. (1995)
417	Seven-spot Labybird Optimization (SLO)	Wang et al. (2013)
418	Shark Search Algorithm (SSA)	Hersovici et al. (1998)
419	Shark Smell Algorithm (SSA)	Abedinia et al. (2016)
420	Sheep Flock Heredity Model (SFHM)	Nara et al. (1999)
421	Sheep Flock Optimization Algorithm (SFOA)	Kivi and Majidnezhad (2022)
422	Shufed Complex Evolution (SCE)	Duan et al. (1993)
423	Shuffled Frog Leaping Algorithm (SFLA)	Eusuff et al. (2006)
424	Shuffled Shepherd Optimization Algorithm (SSOA)	Kaveh and Zaerreza (2020)
425	Simple Optimization (SO)	Hasançebi and K Azad (2012)
426	Simulated Annealing (SA)	Kirkpatrick et al. (1983)
427	Simulated Bee Colony (SBC)	McCaffrey (2009)
428	Sine Cosine Algorithm (SCA)	Mirjalili (2016b)
429	Skip Salp Swam Algorithm (SSSA)	Arunekumar and Joseph (2022)
430	Slime Mold Optimization Algorithm (SMOA)	Monismith and Mayfield (2008)
431	Small World Optimization (SWO)	Du et al. (2006)
432	Smart Flower Optimization Algorithm (SFOA)	Sattar and Salim (2021)
433	Snake Optimizer (SO)	Hashim and Hussien (2022)
434	Snap-Drift Cuckoo Search (SDCS)	Rakhshani and Rahati (2017)
435	Soccer Game Optimization (SGO)	Purnomo (2014)
436	Soccer League Competition (SLC)	Moosavian and Roodsari (2014)
437	Social Cognitive Optimization (SCO)	Xie et al. (2002)
438	Social Cognitive Optimization Algorithm (SCOA)	Wei et al. (2010)
439	Social Emotional Optimization Algorithm (SEOA)	Xu et al. (2010)
440	Social Spider Algorithm (SSA)	James and Li (2015)
441	Social Spider Optimization (SSO)	Cuevas et al. (2013)
442	Society and Civilization Algorithm (SCA)	Ray and Liew (2003)
443	Sonar Inspired Optimization (SIO)	Tzanetos and Dounias (2017)
444	Space Gravitational Algorithm (SGA)	Hsiao et al. (2005)
445	Special Relativity Search (SRS)	Goodarzimehr et al. (2022)
446	Sperm Motility Algorithm (SMA)	Raouf and Hezam (2017)
447	Sperm Swarm Optimization Algorithm (SSO)	Shehadeh et al. (2018)
448	Sperm Whale Algorithm (SWA)	Ebrahimi and Khamehchi (2016)
449	Spherical Search Algorithm (SSA)	Misra et al. (2020)
450	Spherical Search Optimizer (SSO)	Zhao et al. (2020a)
451	Spider Monkey Optimization (SMO)	Bansal et al. (2014)
452	Spiral Dynamics Optimization (SDO)	Tamura and Yasuda (2011)
453	Spiral Optimization Algorithm (SOA)	Jin and Tran (2010)
454	Spotted Hyena Optimizer (SHO)	Dhiman and Kumar (2017)
455	Spring Search Algorithm (SSA)	Dehghani et al. (2017)
456	Spy Algorithm (SA)	Pambudi and Kawamura (2022)
457	Squirrel Search Algorithm (SSA)	Jain et al. (2019)
458	Star Graph Algorithm (SGA)	Gharebaghi et al. (2017)
459	Starling Murmuration Optimizer (SMO)	Zamani et al. (2022)
460	States Matter Optimization Algorithm (SMOA)	Cuevas et al. (2014)
461	Stem Cells Algorithm (SCA)	Taherdangkoo et al. (2011)
462	Stochastic Difusion Search (SDS)	Al-Rifaie and Bishop (2013)
463	Stochastic Focusing Search (SFS)	Weibo et al. (2008)
464	Stochastic Fractal Search (SFS)	Salimi (2015)
465	Stochastic Search Network (SSN)	Bishop (1989)
466	Strawberry Algorithm (SA)	Merrikh-Bayat (2014)
467	String Theory Algorithm (STA)	Rodriguez et al. (2021)
468	Student Psychology Based Optimization (SPBO)	Das et al. (2020)
469	Success History Intelligent Optimizer (SHIO)	Fakhouri et al. (2021)
470	Sunflower Optimization (SFO)	Gomes et al. (2019)
471	Superbug Algorithm (SA)	Anandaraman et al. (2012)
472	Supernova Optimizer (SO)	Hudaib and Fakhouri (2018)
473	Surface Simplex Swarm Evolution Algorithm (SSSE)	Quan and Shi (2017)
474	Swallow Swarm Optimizer (SWO)	Neshat et al. (2013)
475	Swarm Inspired Projection Algorithm (SIP)	Su et al. (2009)
476	Swine Influenza Models Based Optimization (SIMBO)	Pattnaik et al. (2013)
477	Symbiosis Organisms Search (SOS)	Cheng and Prayogo (2014)
478	Synergistic Fibroblast Optimization (SFO)	Subashini et al. (2017)
479	Tabu Search (TS)	Glover (1989)
480	Tangent Search Algorithm (TSA)	Layeb (2021)
481	Tasmanian Devil Optimization (TDO)	Dehghani et al. (2022a)
482	Teaching-Learning Based Optimization Algorithm (TLBO)	Rao et al. (2011)
483	Team Game Algorithm (TGA)	Mahmoodabadi et al. (2018)
484	Termite Colony Optimizer (TCO)	Hedayatzadeh et al. (2010)
485	Termite Life Cycle Optimizer (TLCO)	Minh et al. (2022)
486	Termite-hill Algorithm (ThA)	Zungeru et al. (2012)
487	The Great Salmon Run (TGSR)	Mozaffari et al. (2013)
488	Thermal Exchange Optimization (TEO)	Kaveh and Dadras (2017)
489	Tiki-Taka Algorithm (TTA)	Rashid (2020)
490	Transient Search Optimization Algorithm (TSO)	Qais et al. (2020)
491	Tree Growth Algorithm (TGA)	Cheraghalipour et al. (2018)
492	Tree Physiology Optimization (TPO)	Halim and Ismail (2018)
493	Tree Seed Algorithm (TSA)	Kiran (2015)
494	Trees Social Relations Optimization Algorithm (TSR)	Alimoradi et al. (2022)
495	Triple Distinct Search Dynamics (TDSD)	Li et al. (2020)
496	Tug of War Optimization (TWO)	Kaveh and Zolghadr (2016)
497	Tuna Swarm Optimization (TSO)	Xie et al. (2021)
498	Tunicate Swarm Algorithm (TSA)	Kaur et al. (2020)
499	Unconscious Search (US)	Ardjmand and Amin-Naseri (2012)
500	Vapor Liquid Equilibrium Algorithm (VLEA)	Taramasco et al. (2020)
501	Variable Mesh Optimization (VMO)	Puris et al. (2012)
502	Variable Neighborhood Descent Algorithm (VND)	Hertz and Mittaz (2001)
503	Vibrating Particles System (VPS)	Kaveh and Ghazaan (2017)
504	Virtual Ants Algorithm (VAA)	Yang et al. (2006)
505	Viral Systems Optimization (VS)	Cortés et al. (2008)
506	Virtual Bees Algorithm (VBA)	Yang (2005)
507	Virulence Optimization Algorithm (VOA)	Jaderyan and Khotanlou (2016)
508	Virus Colony Search (VCS)	Li et al. (2016c)
509	Virus Optimization Algorithm (VOA)	Juarez et al. (2009)
510	Virus Spread Optimization (VSO)	Li and Tam (2020)
511	Volcano Eruption Algorithm (VCA)	Hosseini et al. (2021)
512	Volleyball Premier League Algorithm (VPL)	Moghdani and Salimifard (2018)
513	Vortex Search Algorithm (VS)	Doğan and Ölmez (2015)
514	War Strategy Optimization (WSO)	Ayyarao et al. (2022)
515	Wasp Swarm Optimization (WSO)	Pinto et al. (2005)
516	Water Cycle Algorithm (WCA)	Eskandar et al. (2012)
517	Water Evaporation Algorithm (WEA)	Saha et al. (2017)
518	Water Evaporation Optimization (WEO)	Kaveh and Bakhshpoori (2016)
519	Water Flow Algorithm (WFA)	Basu et al. (2007)
520	Water Flow-Like Algorithm (WFA)	Yang and Wang (2007)
521	Water Optimization Algorithm (WAO)	Daliri et al. (2022)
522	Water Strider Algorithm (WSA)	Kaveh and Eslamlou (2020)
523	Water Wave Optimization (WWO)	Zheng (2015)
524	Water Wave Optimization.1 (WWO.1)	Kaur and Kumar (2021)
525	Water-Flow Algorithm Optimization (WFO)	Tran and Ng (2011)
526	Weed Colonization Optimization (WCO)	Mehrabian and Lucas (2006)
527	Weightless Swarm Algorithm (WSA)	Ting et al. (2012)
528	Whale Optimization Algorithm (WOA)	Mirjalili and Lewis (2016)
529	White Shark Optimizer (WSO)	Braik et al. (2022a)
530	Wind Driven Optimization (WDO)	Bayraktar et al. (2010)
531	Wingsuit Flying Search (WFS)	Covic and Lacevic (2020)
532	Wisdom of Artificial Crowds (WoAC)	Yampolskiy and El-Barkouky (2011)
533	Wolf Colony Algorithm (WCA)	Liu et al. (2011)
534	Wolf Pack Search (WPS)	Yang et al. (2007)
535	Wolf Search Algorithm (WSA)	Tang et al. (2012)
536	Woodpecker Mating Algorithm (WMA)	Karimzadeh Parizi et al. (2020)
537	Worm Optimization (WO)	Arnaout (2014)
538	Xerus Optimization Algorithm (XOA)	Samie Yousefi et al. (2019)
539	Yin-Yang-Pair Optimization (YYPO)	Punnathanam and Kotecha (2016)
540	Zombie Survival Optimization (ZSO)	Nguyen and Bhanu (2012)

Not only algorithms but also related research works have increased rapidly in the last decade (Fig. 4). Apart from algorithm development, the literature in this field mainly includes the following categories of studies:

Fig. 4.

Number of published documents with the word ‘optimization’ in the title/abstract/keywords and at least one of the words ‘meta-heuristic’, ‘metaheuristic’, ‘bio-inspired optimization’, ‘bio inspired optimization’, ‘nature-inspired algorithm’, ‘nature inspired algorithm’, ‘nature-inspired technique’, ‘nature inspired technique’, and ‘evolutionary algorithm’ in the title/abstract/keywords over the period 2000–2022. Data source—Scopus on December 31, 2022

Enhanced of algorithms

There are many techniques that can be employed to enhance the algorithm’s average performance. Such few techniques have been described by Wang and Tan (2017). Numerous improved methods have been developed to get better results in comparison with the original ones. Random grey wolf optimizer is such an efficient modified algorithm due to Gupta and Deep (2019). An enhanced salp swarm algorithm has propose by Hegazy et al. (2020). The chaotic dragonfly method is modified to an improved one, by Sayed et al. (2019b). Many more modified algorithms are available in literature, such as improved genetic algorithm (Dandy et al. 1996) and improved particle swarm optimization (Jiang et al. 2007). To achieve high computational efficiency, researchers introduce a powerful notion parallelism. Mainly three parallelism techniques have been recorded in literature as they are (a) parallel moves model, (b) parallel multi-start model, and (c) move acceleration model (Alba et al. 2005).

Hybridization of algorithms

The idea of hybridizing metaheuristics is not new but dates back to their origins. Several classifications of hybrid metaheuristics can be found in the literature. Hybrid metaheuristics can be classified based on many objectives as the level of hybridization, the order of execution, the control strategy, etc. (Raidl 2006).

Level of hybridization

Hybrid MAs are distinguished into two types based on the level (or strength) at which the various algorithms are combined: high-level and low-level combinations. High-level combinations retain the individual identities of the original algorithms while cooperating over a relatively well-defined interface. In contrast, low-level combinations heavily rely on each other, exchanging individual components or functions of the algorithms. Because both the original algorithms are strongly independent in high-level combinations, it is sometimes referred to as ‘weak coupling’. In contrast, in low-level combinations, it is referred to as ‘strong coupling’ because they are both dependent on each other.

Order of execution

Hybrid MAs can be divided based on the execution process as a batch, interleaved, and parallel. The batch model employs a one-way data flow in which each algorithm is executed sequentially. On the contrary, we have interleaved and parallel models in which the algorithms might interact in more sophisticated ways (Alba 2005).

Control strategy

Based on their control strategy, we may further subclass hybrid MAs into integrative (coercive) and collaborative (cooperative) combinations. In integrative approaches, one algorithm is considered a subordinate or embedded part of another. This method is quite common. For example, the memetic algorithm is embedded in an evolutionary algorithm for locally improving candidate solutions obtained from variation operators. Algorithms in collaborative combinations share information but are not embedded. For example, Klau et al. (2004) combined a memetic algorithm with integer programming to solve the prize-collecting steiner tree problem heuristically.

Comparison of MAs

In industries, determining which algorithm works best for a particular type of problem is a practical concern. Generally, the difficulty of an optimization task is measured based on its objective function. A fitness landscape consists essentially of the objective values of all variables within the decision variable space. To characterize the fitness landscape of a particular optimization problem, fitness landscape analysis (FLA) is a valuable and potent analytic tool (Wang et al. 2017). Thus, many research papers evolve by comparison of MAs. FLA is essential for studying how complex problems are for MAs to solve. The number of local optima is the first and most apparent fitness landscape characteristic to consider when determining the complexity of a particular optimization problem. Horn and Goldberg (1995) have found that multimodal optimization problems with half the points in the search space are more accessible to solve than unimodal problems. That is, only considering the number of local optima is neither sufficient nor necessary for an optimization algorithm. Another significant characteristic of the fitness landscape is the basin of attraction on local optima. Basins of attraction are classified into two types (Pitzer et al. 2010): strong basins of attraction, in which all individuals from the basin of attraction can approach a single optimum exclusively, and weak basins of attraction, in which some individuals from the basin of attraction can approach to another optimum. When determining the complexity of a specific optimization problem, basins of attraction might potentially offer additional helpful information about the size, shape, stability, and distribution of local optima. Recent developments in FLA can be found in (Zou et al. 2022).

Multi/many objective optimization

Most real life problems naturally involve multiple objectives. Multiple conflicting objectives are common and make optimization problems challenging to solve. Problems with more than one conflicting objective, there is no single optimum solution. There exist a number of solutions which are all optimal. Without more information, none of the optimum solutions may be deemed superior to the others. This is the fundamental difference between a single-objective (except in multimodal optimization scenarios where multiple optimal solutions exist) and multi-objective optimization task. In multi-objective optimization, a number of optimal solutions arise because of trade-offs between conflicting objectives.

To address multi-objective optimization, several extended versions of MAs are proposed. Few most popular examples are non-dominated sorting genetic algorithm II (NSGA-II) (Deb et al. 2002), multi-objective evolutionary algorithm based on decomposition (MOEA/D) (Zhang and Li 2007), and non-dominated sorting genetic algorithm III (NSGA-III) (Deb and Jain 2013). When the number of functions are greater than three, the majority of solutions in the NSGA-II search spaces become non-dominated, resulting in a rapid loss of search capability. MOEA/D decomposes a multi-objective optimization problem into a number of scalar optimization subproblems and optimizes them simultaneously. Also, each subproblem is optimized by only using information from its several neighbouring subproblems, which makes MOEA/D have lower computational complexity at each generation. NSGA-III uses the basic framework of NSGA-II. It uses a well-spread reference point mechanism to maintain diversity. NSGA-III was developed to solve optimization problems with more than four objectives.

Review articles

These studies offer young researchers a valuable perspective on the current state of existing works and their potential future prospects, which can be highly beneficial for their research. Some important articles are highlighted as follows. A novel taxonomy of 100 algorithms based on movement of population along with a few significant conclusions are given by Molina et al. (2020). Some significant future directions of metaheuristics are addressed by Del Ser et al. (2019). Tzanetos and Dounias (2021) have strongly criticised the unethical practises and have given few ideas for the future. A comprehensive overview and classification along with bibliometric analysis is given by Ezugwu et al. (2021). A recent survey of the multi-objective optimization algorithms, their variants, applications, open challenges and future directions can be found in (Sharma and Kumar 2022).

Benchmark test functions

Numerous test or benchmark functions have been reported in the literature; however, no standard list or set of benchmark functions for evaluating the performance of an algorithm exists. To combat this, CEC benchmark functions are published regularly (Liang et al. 2014). 175 benchmark functions are collected by Jamil and Yang (2013). Mirjalili and Lewis (2019) have provided a set of benchmark optimization functions considering different levels of difficulty. 67 non-symmetric benchmark functions have collected by Gao et al. (2021b).

Statistical analysis

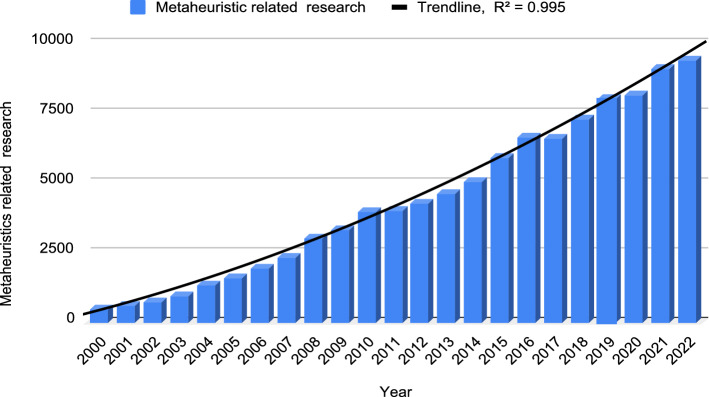
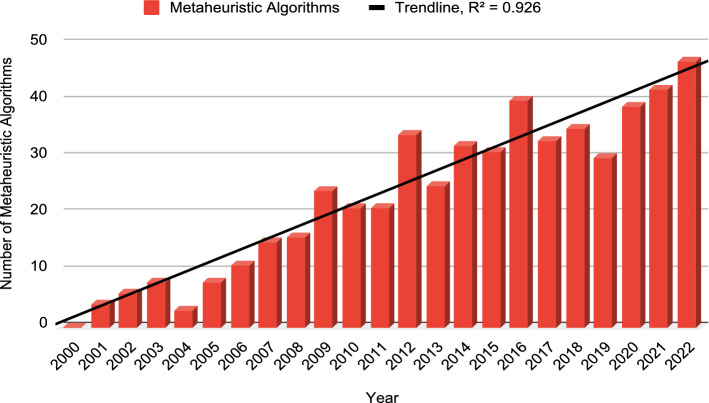
Approximate 540 new MAs have been developed, with about 385 of them appearing in the last decay. Furthermore, in the year 2022 alone, around 47 ‘novel’ MAs are proposed. A graphical representation is shown in Fig. 1. It can be seen in Fig. 1 that, the trend line, with coefficient of determination $(R^2)=0.926$, is highly upward. $R^2$ is a measure that provides information about the goodness of fit of a model. A trend line is most reliable when its $R^2$ value is at or near 1. It is clear from the high valuation of $R^2$ that, the development of ‘novel’ MAs is growing rapidly.

Fig. 1.

Number of metaheuristic algorithms developed during 2000–2022

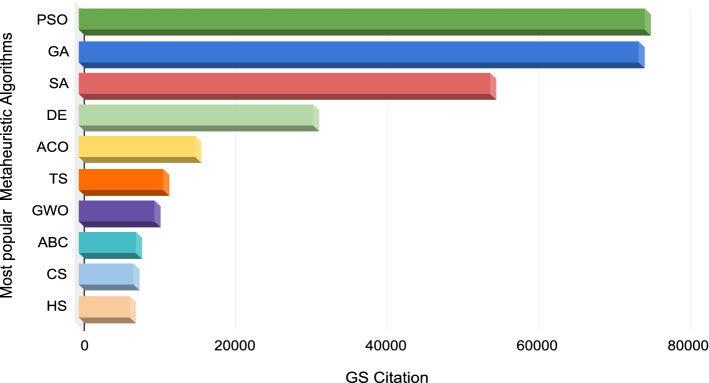
Figure 2 is a summary of the top 10 MAs that have been cited the most, based on Google Scholar (GS). The most widely used algorithm is particle swarm optimization (PSO), which has more than 75000 citations on its own. Genetic algorithm (GA) is ranked as the second most popular algorithm with more than 70000 citations. Ant colony optimization (ACO), differential evolution (DE), and simulated annealing (SA) are ranked third, fourth, and fifth, respectively, with more than 50,000, 30,000, and 15,000 citations respectively. In order of most-cited algorithms to date, tabu search (TS), grey wolf optimizer (GWO), artificial bee colony (ABC), cuckoo search (CS), and harmony search (HS) are rated fifth, sixth, seventh, eighth, ninth, and tenth, respectively.

Fig. 2.

Top ten cited MAs. Data source—Google Scholar (GS) on December 31, 2022

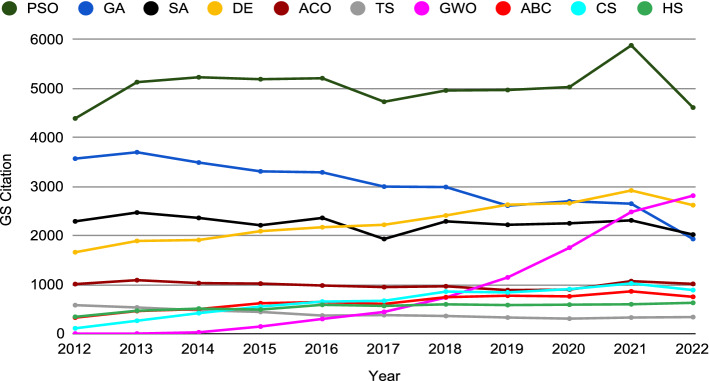
Additionally, Fig. 3 shows GS-citations for the most popular MAs during the last decade. The graph demonstrates how quickly these algorithms are gaining popularity. Grey wolf optimizer (GWO) has gained the attention of researchers and become one of the most popular in a short period of time. Other algorithms, such as the particle swarm optimization (PSO), genetic algorithm (GA), simulated annealing (SA), and differential evolution (DE), have attracted interest at a nearly steady pace during the last decade.

Fig. 3.

Citations of the top ten GS-cited MAs from 2012 to 2022. Data source—Scopus on December 31, 2022

Another very interesting question: How much metaheuristic research is being carried out now? We require data to address this question. Extraction of data from radically various types of repositories is a difficult task. However, we address this question and ascertain the present knowledge regarding metaheuristic studies. Our investigation is made based on available data in Scopus. Even though we do not have complete statistics, our data provide a picture of metaheuristics and leads to significant insights. To identify metaheuristic documents, we use two screening processes: The publications whose titles, abstracts, or keywords include the term ‘optimization’ are listed first. In the second step to identifying only the metaheuristic subdomain of optimization, we consider publications that contain at least one of the terms ‘meta-heuristic’, ‘metaheuristic’, ‘bio-inspired optimization’, ‘bio inspired optimization’, ‘nature-inspired algorithm’, ‘nature inspired algorithm’, ‘nature-inspired technique’, ‘nature inspired technique’, and ‘evolutionary algorithm’ in the titles, abstracts, or keywords. The period is taken from 2000 to 2022. Figure 4 depicts the search results. Each year there are more publications on metaheuristics than the year before. The trend line with $R^2=0.995$ indicates that metaheuristic research is expanding significantly. Table 2 lists the various document types. Statistics show that most of the weight in this metaheuristics domain publication comes from articles and conference papers.

Table 2.

Different types of published documents with the word ‘optimization’ in the title/abstract/keywords and at least one of the words ‘meta-heuristic’, ‘metaheuristic’, ‘bio-inspired optimization’, ‘bio inspired optimization’, ‘nature-inspired algorithm’, ‘nature inspired algorithm’, ‘nature-inspired technique’, ‘nature inspired technique’, and ‘evolutionary algorithm’ in the title/abstract/keywords

Document type	Total number	Percentage (%)
Article	54,158	54.22
Conference Paper	40,788	40.84
Conference Review	1292	1.29
Review	1093	1.09
Book	145	0.15
Editorial	88	0.09
Retracted	61	0.06
Erratum	37	0.04
Data Paper	9	0.01
Undefined	18	0.02
Total	99,877	100

Data source—Scopus on December 31, 2022

Constructive criticism

According to statistical data, numerous MAs appear one after the other; on average, approximately 38 algorithms have appeared yearly during the last decade. In light of this, it seems that metaheuristics is nearing the pinnacle of research effort, but is this the case? Many research community members have expressed alarm about this unanticipated scenario (Aranha et al. 2021; Del Ser et al. 2019). Genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO), and differential evolution (DE) were probably developed in a context when scientists lacked alternative optimization methods. Each has its own set of feathers and controlling equations. Many algorithms, particularly those of the most recent generation, are alleged to be non-unique. Furthermore, they are unable to deliver impactful effects. Criticizing this overcrowded situation, Osaba et al. (2021) have pointed out three factors: (a) being unable to provide beneficial containment rather than causing confusion in this area, (b) statistical data authenticity, and (c) unfair comparisons to promote own algorithms. Readers should be aware that several front-line algorithms have been claimed to have lost their novelty. Noted cases are BHO vs PSO (Piotrowski et al. 2014), GWO vs PSO (Villalón et al. 2020), FA vs PSO (Villalón et al. 2020), BA vs PSO (Piotrowski et al. 2014), IWD vs ACO (Camacho-Villalón et al. 2018), and HS vs ES (Weyland 2010). Constructive debate is essential to strengthening this area. Steer et al. (2009) separate the sources of inspiration for NIAs into two groups as well. The first group includes ‘strong’ inspiration algorithms, which mimic mechanisms that address real-world phenomena. Algorithms with ‘weak’ inspiration go into the second group since they do not precisely adhere to the norms of a phenomenon. A significant proportion of these algorithms are remarkably similar to other already available ones. Algorithms with little creativity usually keep their titles to distinguish themselves from other popular metaheuristic approaches that function similarly. Many algorithms, such as bacterial foraging optimization (BFO), birds swarm algorithm (BSA), krill herd (KH), cat swarm optimization (CSO), chicken swarm optimization (CSO), and blue monkey algorithm (BMA), are alleged to be PSO-like algorithms in (Tzanetos and Dounias 2021). Although there are numerous improved versions, new algorithms are frequently compared to older versions of well-known algorithms like GA and PSO. The intriguing aspect here is that each author individually codes these algorithms, and the results are often questionable due to the lack of transparency as the code is kept private. In another study, Molina et al. (2020) determine which algorithms are most influential for developing other algorithms. They compile other algorithms that can be considered variants of the classical algorithms. From this group, the following conclusions can be drawn: about 57 algorithms that are similar to PSO, including african buffalo optimization (ABO) and bee colony optimization (BCO), about 24 algorithms that are similar to GA, including crow search algorithm (CSA) and earthworm optimization algorithm (EOA), and about 24 algorithms that are similar to DE, including artificial cooperative search (ACS) and differential search algorithm (DSA). Research on ‘duplicate’ algorithms is just a repetition of research concepts already investigated in the context of the original algorithm, resulting in a waste of resources and time. However, several algorithms in recent years have demonstrated their efficacy in various real-world challenges, opening up new avenues for research. A new algorithm should be produced when the existing algorithms cannot generate a satisfactory solution to a real-world optimization problem or when a more intelligent mechanism is identified that makes the new algorithm more efficient than others.

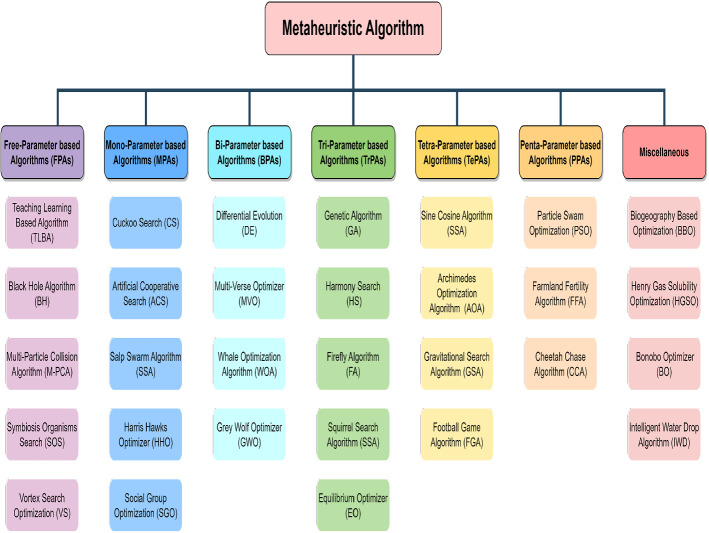
Taxonomy

In the literature, there are several classifications for MAs. For example, classification based on the source of inspiration (6.1) is the most common, but it does not provide us with any mathematical inside of algorithms. Another classification based on the number of finding agents (6.2) provides insight into the number of agents deployed in an iteration. However, this is highly non-uniform because relatively few algorithms fall into one group while the remainder falls into another. Molina et al. (2020) categorize MAs based on their behavior (6.3), rather than their source of inspiration, as (a) Differential Vector Movement and (b) Solution Creation, which provides additional information about the inner workings of MAs. An additional essential tool is employed in this study to classify the existing MAs. Parameters are pretty sensitive in any algorithm. Tuning a parameter for a new situation is difficult since we do not have a chart or set of instructions. Because of a lack of detailed mathematical analysis of algorithms and problems, we must execute the algorithms numerous times for different parameter values in this case. Thus, it is crucial to study the parameters of algorithms to improve the result. This study presents a novel classification based on the number of parameters (6.4).

Taxonomy by source of inspiration

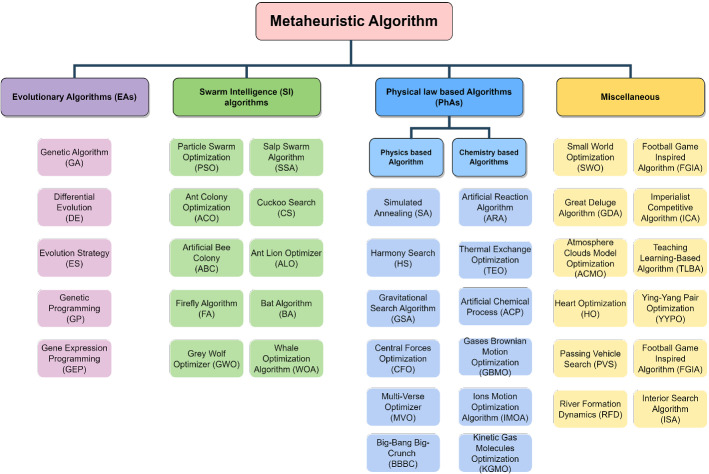
This is the oldest classification. Furthermore, it is a beneficial classification because nature-inspired algorithms or metaheuristics concept is primarily based on natural or biological phenomena. Depending on the source of inspiration, MAs have been categorized in various ways by different authors. Fister Jr et al. (2013) have classified it into four categories as swarm intelligence (SI) based algorithms, bio-inspired (not SI) based algorithms, physic-chemistry based algorithms, and the rest as another algorithm, whereas Siddique and Adeli (2015) have divided it into three subgroups as physics-based, chemistry-based and biology-based algorithms. Molina et al. (2020) have classified it into six subgroups as breeding-based evolutionary algorithms, SI-based algorithms, physics-chemistry-based algorithms, human social behavior-based algorithms, and plant-based algorithms, and the rest part are mentioned as miscellaneous. The widely recognized classification is addressed in this text. Hence, in this study, MAs are classified into four subgroups (Fig. 5), which are as follows:

Fig. 5.

Classification of MAs based on the source of inspiration

Evolutionary algorithms (EAs)

Darwinian ideas of natural selection or survival of the fittest inspired EAs. EAs start with a population of individuals and simulate sexual reproduction and mutation in order to create a generation of offspring. The practice is repeated to maintain genetic material that makes an individual more adapted to a particular environment while eliminating that which makes it weaker.

Charles Darwin’s theory of natural evolution motivates genetic algorithm (GA) and differential evolution (DE), while genetic programming (GP) is based on the paradigm of biological evolution. EAs examples include gene expression programming (GEP), learning classifier systems (LCS), neuroevolution (NE), evolution strategy (ES), and so on.

Swarm intelligence (SI) algorithms

Although Beni and Wang (1993) invented the term ‘Swarm Intelligence’ in 1989 in the context of cellular robotic systems, SI has since become a sensational topic in many industries. SI is defined as a decentralized and self-organized system’s collective behavior. The swarm system’s primary qualities are adaptability (learning by doing), high communication, and knowledge-sharing. While organisms cannot perform tasks like defending themselves against a vast predator or attacking for food on their own, they rely heavily on swarming. Even when they are looking for food, they swarm. SI has inspired a vast number of MAs; for example, the intelligent social behavior of birds flock motivates particle swarm optimization (PSO), the monkey climbing process on trees while looking for food motivates monkey search (MS), grey wolf leadership hierarchy and hunting mechanism motivates grey wolf optimizer (GWO), and so on. SI examples include, but are not limited to, ant lion optimizer (ALO), bat algorithm (BA), firefly algorithm (FA), ant colony optimization (ACO), cuckoo search (CS), artificial bee colony (ABC), and glowworm swarm optimization (GSO).

Physical law-based algorithms (PhAs)

Algorithms that are inspired by physical and chemical law fall under this subcategory. Furthermore, PhAs can be subclassified as:

• (i)Physics based algorithms:

  Gravitation, big bang, black hole, galaxy, and field are the primary key source of the idea of this subcategory. The consumption of stars by a black hole and the formation of new beginnings motivate the black hole algorithm (BH). Harmony search (HS) is developed based on the improvisation of musicians. Simulated annealing (SA) is based on metallurgy’s annealing process, where metal is heated quickly, then cooled slowly, increasing strength and making it simpler to work with. Among these are the big bang-big crunch algorithm (BBBC), central forces optimization (CFO), charged systems optimization (CSO), electro-magnetism optimization (EMO), galaxy-based search algorithm (GBS), and gravitational search algorithm (GSA).

• (ii)Chemistry based algorithms:

  MAs inspired by the principle of chemical reactions, such as molecular reaction, Brownian motion, molecular radiation, etc. come under this category. Gases brownian motion optimization (GBMO), artificial chemical process (ACP), ions motion optimization algorithm (IMOA), and thermal exchange optimization (TEO) are a few examples of this category.

Miscellaneous

Algorithms based on miscellaneous ideas like human behaviors, game strategy, mathematical theorems, politics, artificial thoughts, and other topics fall into this category. The creation, movement, and spread of clouds inspire the atmosphere clouds model optimization algorithm (ACMO), whereas trading shares on the stock market motivates the exchange market algorithm (EMA). Several other examples are the grenade explosion method (GEM), heart optimization (HO), passing vehicle search (PVS), simple optimization (SO), small world optimization (SWO), ying-yang pair optimization (YYPO), and great deluge algorithm (GDA).

Taxonomy by population size

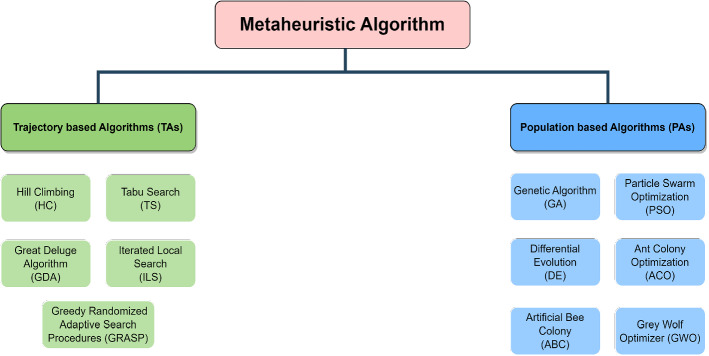
Multiple agents work better together than a single agent, and there are several advantages, such as information sharing, data remembering, etc. Inspired by it; researchers try to discover the best solution with multiple agents. When it comes to investigating a region, several agents have shown to be superior to a single agent. In our literature, existing algorithms are classified into two categories as trajectory-based and population-based algorithms (Fig. 6) (Yang 2020).

Fig. 6.

Classification of MAs based on the size of the population

Trajectory-based algorithms (TAs)

In contrast, most classical algorithms are built on trajectories, which implies that the movement of the solution during each iteration constitutes a single trajectory. At the beginning of the procedure, a random estimate was made, and the result was refined with each subsequent step. For example, simulation annealing (SA) involves a single agent or solution that moves piece-wise through the design or search space in which it is applied. Better moves and solutions are always welcome, whereas less-than-ideal moves are more likely to be accepted. These actions create a path through the search space, and there is a nonzero probability that this path will lead to the global optimal solution. Hill climbing (HC), tabu search (TS), great deluge algorithm (GDA), iterated local search (ILS), and greedy randomized adaptive search procedures (GRASP) are a few examples of this category.

Population-based algorithms (PAs)

This category encompasses all significant algorithms. Because population-based algorithm utilizes multiple finding agents, it enables an extraordinary exploration of the search space’s diversification, sometimes called an exploration-based algorithm. Elitism can be used easily here, which is a bonus point. Genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO), and firefly algorithm (FA) are a few examples of this category.

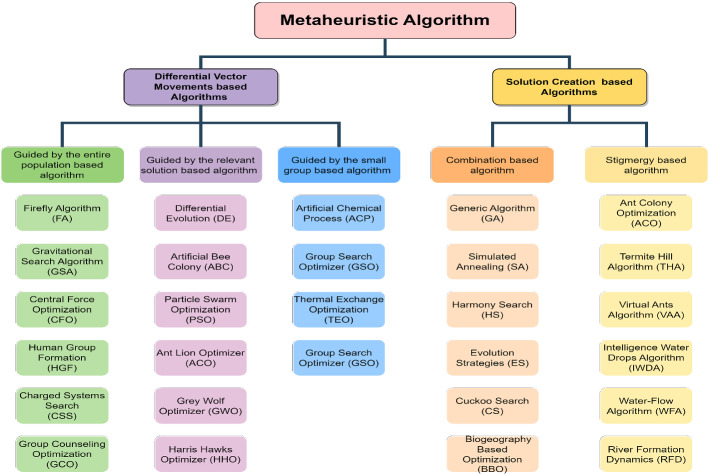
Taxonomy by movement of population

Molina et al. (2020) have attempted to categorize based on its behavior rather than its source of inspiration. How the population for the next iteration is updated remains the key feature of this classification. This classification is a good tool for understanding the same type of algorithms. According to them, MAs can be classified as algorithms based on differential vector movement and algorithms based on solution creation (Fig. 7).

Fig. 7.

Classification of MAs based on the movement of the population

Differential vector movement (DVM)

DVM is a method of creating new solutions by shifting or mutating an existing one. The newly generated solution could compete against earlier ones or other solutions in the population to obtain space and remain there in the following search cycles. That decision further subdivides this category. The movement—and thus the search—can be guided by (i) the entire population; (ii) only the meaningful/relevant solutions, e.g., the best and/or worst candidates in the population; and (iii) a small group, which could represent the neighborhood around each solution or, in subpopulation based algorithms, only the subpopulation to which each solution belongs.

Solution creation (SC)

New solutions are created by merging many solutions (such that there is no single parent solution) or another similar mechanism, rather than through mutation/movement of a single reference solution. This is further subdivided into two categories based on how the new solution is created as (i) a combination, or crossover, of several solutions, and (ii) stigmergy, in which there is indirect coordination between the different solutions or agents, usually through the use of an intermediate structure, to generate better ones.

Genetic algorithm (GA), gene expression (GE), harmony search (HS), bee colony optimization (BCO), cuckoo search (CS), and dolphin search (DS) are some examples of the first subcategory. In contrast, ant colony optimization (ACO), termite hill algorithm (THA), river formation dynamics (RFD), intelligence water drops algorithm (IWDA), water-flow optimization algorithm (WFOA), and virtual bees algorithm (VBA) are some examples of the second subcategory.

Taxonomy by number of parameters

Parameters are a critical component in the configuration of metaheuristics. The performance of MAs is highly dependent on the settings of the parameters. Choosing the best values of parameters for a MA (parameter tuning) is an intricate problem that may need its own study area for metaheuristics (Talbi 2009). MA’s flexibility and robustness are parameter-dependent. A smaller collection of parameters simplifies parameter tuning. In addition, the parameter values are defined by the optimization problem considered in the calculation. The number of parameters affects the complexity of an algorithm.

No classification in the literature takes this parametric trait into account. We require a classification based on this to identify algorithms that employ the same number of parameters. This classification will allow us to obtain an additional mathematical understanding of MAs. Many parameters influence an algorithm’s performance, including the population’s size and the number of iterations. Even though the population size and the number of iterations have a substantial impact on the output, these two parameters are shared by all algorithmic methods. In other words, these two parameters provide no information about the internal structure of algorithms. This type of parameter is referred to as a ‘secondary’ parameter. We concentrate on so-called ‘primary’ parameters that are not shared by all algorithms and are particularly sensitive to their values. This study proposes a novel classification framework for MAs based on the number of primary parameters employed.

The majority of algorithms are found to have between 0 and 5 primary parameters. Consequently, most algorithms are covered if we classify them into six categories based on the number of 0, 1, 2, 3, 4, and 5 primary parameters. Those not covered by the preceding six categories, i.e., those with more than five primary parameters, fall under the miscellaneous group. Accordingly, to maintain uniformity across subcategories and cover all MAs with a smaller number of classifications, we have classified them into seven subgroups as follows:

Free-parameter based algorithms (FPAs)

FPAs refer to algorithms that have no primary parameters in their structure. FPA is regarded as one of the most user-friendly of the various alternatives because no primary parameter is used. FPA is adaptive, flexible, and easy to utilize in different optimization problems. Generally, the governing equations of FPAs are pretty simple. It is potentially more generic to adapt to a broader class of optimization problems. FPA includes algorithms such as teaching-learning-based optimization (TLBO), black hole algorithm (BH), multi-particle collision algorithm (M-PCA), symbiosis organisms search (SOS), vortex search optimization (VS), forensic-based investigation (FBI), and lightning attachment procedure optimization (LAPO).

Mono-parameter based algorithms (MPAs)

MPAs refer to the algorithms that have single primary parameters in their structure. Mainly this parameter is used to change the state of exploration to exploitation and vice versa, which is extremely important. ‘Limit’ is the only primary parameter of the artificial bee colony (ABC) algorithm that determines the food source to be abandoned (Akay and Karaboga 2009). The parameter ‘$c_1$’ is utilized to balance exploration and exploitation in the governed Eq. (3.1) of the salp swarm algorithm (SSA) (Mirjalili et al. 2017). The probability of biological interaction (p) is the only primary parameter in artificial cooperative search (ACS) (Civicioglu 2013a). This value specifies the maximum number of passive individuals allowed in each sub-superorganism. The probability ($p_a$) is the only primary parameter in cuckoo search (CS) that essentially controls the elitism and the balance of the randomization and local search (Yang and Deb 2009). In harris hawks optimizer (HHO), the parameter ‘E’ is used to toggle between soft ($|E|\le 0.5$) and hard besiege ($|E|>0.5$) processes (Heidari et al. 2019).

Similarly, a few examples include gravitational interactions optimization (GIO), interior search algorithm (ISA), killer whale algorithm (KWA), kinetic gas molecules optimization (KGMO), social spider optimization (SSO), stochastic fractal search (SFS), social group optimization (SGO), and fitness dependent optimizer (FDO).

Bi-parameter based algorithms (BPAs)

BPAs refer to algorithms that have two primary parameters in their structure. Differential evolution (DE) comprises two direct control parameters, namely, the amplification factor of the difference vector and the crossover constant, which simultaneously regulate the exploration and exploitation search in different stages (Storn and Price 1997). Simulated annealing (SA) has two primary parameters: the initial temperature and the cool-down factor. Grey wolf optimizer (GWO) has only two primary parameters to be adjusted. They are ‘a’ and ‘C’ (Mirjalili et al. 2014). The parameter a is decreased from 2 to 0. The adaptive values of parameter a allow for a smooth transition between exploration and exploitation. Different places around the best agent can be reached concerning the current position by adjusting the value a and C vectors. The whale optimization algorithm (WOA) has two primary internal parameters that must be modified to transition from exploration to exploitation, namely A and C (Mirjalili and Lewis 2016). The parameter A enables the algorithm to transition seamlessly between exploration and exploitation: by decreasing A, specific iterations are allocated to exploration ($|A|\ge 1$), while the remainder is devoted to exploitation ($|A|<1$). By altering the values of the parameters A and C, several locations around the optimal agent can be attained relative to the current position. The marine predators algorithm (MPA) has two control parameters: FADs and P. The parameters FADs affect exploration, while the parameter P helps exaggerate the steps taken by predators or prey.

Crow search algorithm (CSA), flower pollination algorithm (FPA), grasshopper optimization algorithm (GOA), multi-verse optimizer (MVO), political optimizer (PO), seeker optimization algorithm (SOA), tunicate swarm algorithm (TSA), moth flame optimization (MFO), artificial chemical reaction optimization algorithm (ACROA), spiral dynamics optimization (SDO), zombie survival optimization (ZSO) and artificial jellyfish search optimizer (AJSO) are few examples of BPAs.

Tri-parameter based algorithms (TrPAs)

TrPAs refer to the algorithms that have three primary parameters in their structure. The genetic algorithm (GA) has three primary parameters: the selection criterion for the new population, the mutation rate, and the crossover rate (Holland 1991). The most often used selection methods are roulette wheel selection, rank selection, tournament selection, and Boltzmann selection, each of which has distinct advantages and disadvantages. Depending on the application, a suitable method of selection can be employed. Excavation from local minima is usually influenced by the rate of mutation, but the crossover rate impacts solution accuracy. Harmony search (HS) have three primary parameters: harmony memory considering rate (HMCR), pitch adjusting rate (PAR), and distance bandwidth (BW) (Kumar et al. 2012). The HMCR and PAR parameters are used for global searching and improving local solutions, respectively. Firefly algorithm (FA) is executed by three parameters: attractiveness, randomization, and absorption (Yang 2009). The attractiveness parameter is based on light intensity between two fireflies and defined with exponential functions. When this parameter is set to zero, it happens to the random walk corresponding to the randomization parameter, which is determined by the Gaussian distribution principle as generating the number from the [0, 1] interval. On the other hand, absorption parameters affect the value of attractiveness parameters as changing from zero to infinity. And, for the case of converging to infinity, the movement of fireflies appears as a random walk. Similarly, the squirrel search algorithm (SSA) has three parameters, namely: the number of food sources ($N_{\mathit{fs}}$), gliding constant ($G_c$), and predator presence probability ($P_{\mathit{dp}}$) (Jain et al. 2019). The parameter $N_{\mathit{fs}}$ is an attribute of the algorithm that provides flexibility to vary the exploration capability of the algorithm. The parameter Gc maintains a balance between exploration and exploitation. The natural behavior of flying squirrels is modeled by $P_{\mathit{dp}}$. Three parameters should be tuned in across neighborhood search (ANS) to suit different optimization problems: the cardinality of the superior solution set, the across-search degree, and the standard deviation of the Gaussian distribution (Wu 2016). The convergence curve formula, the effective radius, and epsilon are the three primary parameters for dolphin echolocation optimization (DEO) (Kaveh and Farhoudi 2013).

A few examples of TrPAs are the firefly algorithm (FA), krill herd (KH), spring search algorithm (SSA), artificial algae algorithm (AAA), gases brownian motion optimization (GBMO), hurricane based optimization algorithm (HOA), orca optimization algorithm (OOA), social spider algorithm (SSA), water cycle algorithm (WCA), equilibrium optimizer (EO), parasitism predation algorithm (PPA), and heap-based optimizer (HBO).

Tetra-parameter based algorithms (TePAs)

TePAs refer to the algorithms that have four primary parameters in their structure. In general, the algorithmic framework has many governed equations that are weighted according to the parameters for exploration and exploitation in subsequent iterations. Four primary parameters need to be selected in ant colony optimization (ACO): the information heuristic factor ($\alpha$), the expectation heuristic factor ($\beta$), the pheromone evaporation factor ($\rho$), and the pheromone strength (Q). Sine cosine algorithm (SSA) has four primary parameters: $r_1$, $r_2$, $r_3$, and $r_4$. The parameter $r_1$ specifies the next position’s area (or direction), which may be within or beyond the space between the solution and destination. The parameter $r_2$ specifies the direction of movement with respect to or away from the destination. The parameter $r_3$ brings a random weight for the destination in order to stochastically emphasize ($r_3>1$) or de-emphasize ($r_3\le 1$) the effect of the destination in defining the distance. Finally, the parameter $r_4$ equally switches between the sine and cosine components in Eq. (3.3) used in (Mirjalili 2016b). Archimedes optimization algorithm (AOA) has four parameters, namely $c_1$, $c_2$, $c_3$, and $c_4$ together control the exploration and exploitation (Hashim et al. 2021).

Similarly few examples of this category are football game algorithm (FGA), group counseling optimization (GCO), migrating birds optimization (MBO), space gravitational algorithm (SGA), spider monkey optimization (SMO), movable damped wave algorithm (MDWA), gravitational search algorithm (GSA), and football game algorithm (FGA).

Penta-parameter based algorithms (PPAs)

PPAs refer to algorithms that have five primary parameters in their structure. Particle swarm optimization (PSO) has five primary parameters: topology, cognitive constant ($C_1$), social constant ($C_2$), inertia weight (W), and velocity limit. The $g_{\mathit{best}}$ and the $l_{\mathit{best}}$ topologies were proposed in the original work. Many recent studies have investigated how different topologies, such as cycles, wheels, stars, and random graphs with N particles and N edges, affect the performance (Liu et al. 2016). A total of 1343 random topologies and six special topologies were tested in (Kennedy and Mendes 2002), including $g_{\mathit{best}}$, $l_{\mathit{best}}$, pyramid, star, small, and von Neumann. The parameters $C_1$ and $C_2$ control how much weight should be given between refining the particle’s search result and recognizing the swarm’s search result. There are also proposals to decrease the parameter $C_1$ while increasing the parameter $C_2$ to encourage exploration at the beginning and exploitation at the end. The parameter W specifies global and local search capabilities, whereas the parameter velocity limit serves as a convergent speed accelerator.

A few examples of this category are the cheetah chase algorithm (CCA), and farmland fertility algorithm (FFA) (Shayanfar and Gharehchopogh 2018).

Miscellaneous

This category includes algorithms with more than five primary parameters in their structure. Tuning all primary parameters simultaneously for a black-box optimization problem is complex, which is a disadvantage of this category. The six primary parameters of biogeography-based optimization (BBO) are the probability of modifying a habitat, the probability of immigration limits, the size of each step, the probability of mutation, I, and E (Simon 2008). The cluster number, $M_1$, $M_2$, $\alpha$, $\beta$, $\kappa$, $L_1$, $L_2$, $L_3$, $I_1$, $I_2$, and $I_3$ are the twelve primary parameters of henry gas solubility optimization (HGSO) (Hashim et al. 2019). Tuning them is a time-consuming task for a variety of optimization problems. We require sensitive analysis when dealing with a large number of parameter sets. The minimum and maximum temperatures, the initial supply and endurance, the visibility, the camel caravan, and the death rate are the seven primary parameters in the camel algorithm (CA) (Ibrahim and Ali 2016).

A few examples of miscellaneous are the cheetah chase algorithm (CCA), exchange market algorithm (EMA), forest optimization algorithm (FOA), african buffalo optimization (ABO), magnetic optimization algorithm (MFO), roach infestation optimization (RIO), worm optimization (WO), intelligent water drop algorithm (IWD), see-see partridge chicks optimization (SSPCO), ground-tour algorithm (GTA), bonobo optimizer (BO), hunting Search (HuS), and swallow swarm optimizer (SWO) (Fig. 8).

Fig. 8.

Classification of MAs based on the number of primary parameters

The classification based on the source of inspiration shows how researchers are convinced by various ideas found in nature and how they mathematically describe them to use them as an optimization tool. On the other hand, this classification reveals nothing about the mathematics hidden within. The classification based on the number of finding agents gives us a glimpse into each algorithm, allowing us to understand better how it operates. Multi-agent systems provide several advantages, including the ability to explore the environment and exploit elitism while increasing computing costs. The third classification is based on algorithmic behavior, giving us an essential insight into how the population is updated for the next generation. The classification according to the number of parameters allows us to look into the number of control parameters involved and their roles in each of the algorithms. Another aspect of the number of parameters is how algorithms are set up and how sensitive they are to changes in the parameters they contain. Less parameter-based MAs, in general, are easy to handle for any optimization problem. Consequently, fewer parameters with highly efficient MAs are preferable for industrial optimization problems.

Applications

MAs are usually more computationally expensive; it is not employed to solve simple real-world optimization problems that can be solved using standard gradient-based optimization tools. These problems are frequently non-linear and constrained by many non-linear constraints, raising numerous issues such as time restrictions and ‘cures of dimensionality’ in search of the optimal solution. We highlight a number of applications that are highly dependent on MAs.

NP-hard problems

NP-Hardness is a property of problems that are ‘at least as hard as the hardest problems in NP’. Exhaustive search methods are not applicable to find the best solution for large NP-Hard instances, due to their high computational cost.

• The most well-known problem in combinatorial optimization NP-Hard is the Travelling Salesman Problem (TSP), which poses the following question: ‘Given a list of cities and the distances between each pair of cities, what is the shortest route that visits each city precisely once and returns to the initial city?’ (Gutin and Punnen 2006). For example, there are approximately $1.22\times {10}^{17}$ feasible solutions for a TSP with 20 cities. Thus, an exhaustive search to find a global optimum solution would take a long time. The high computational cost involved in solving TSP problems can be significantly reduced by the use of MAs, which are often able to provide near-optimal solutions in reasonable time (Panwar and Deep 2021). A generalization of TSP is the vehicle routing problems (VRPs) that are more realistic since they typically correspond to industry challenges, notably in logistics. Because such problems are multi-objective, they are widely utilized to represent real-world settings. Metaheuristics such as ant colony optimization (ACO), particle swarm optimization (PSO), genetic algorithm (GA) are now frequently used to solve them (Jozefowiez et al. 2008).

• Job Shop Scheduling (JSS) is a well-known NP-Hard problem, which means no algorithm can solve it in polynomial time in terms of problem size. Because it contains a finite set of jobs that must be processed on a limited set of machines, JSS is the most general sort of scheduling problem. Numerous researchers have attempted to cope with JSS using simulated annealing (SA), firefly algorithm (FA), bat algorithm (BA), cuckoo search (CS), and artificial bee colony (ABC), among others (Zhang et al. 2017a). Prakasam and Savarimuthu (2015) have shown that it is possible to solve other related NP-Hard problems using the generic implementation based on polynomial turing reduction.

Medical science

Electronic chips and computers are the backbones of many medical imaging, diagnostic, monitoring, and treatment devices. These devices, made up of numerous hardware components, are maintained and controlled by software based on algorithms.

de Carvalho Filho et al. (2014) used a genetic algorithm to find a way to find and classify solitary lung nodules automatically. The designed algorithm could detect lung nodules with about $86\%$ sensitivity, $98\%$ specificity, and $98\%$ accuracy. In several studies, genetic algorithm (GA) was successfully employed to align MRI and CT scan pictures (Valsecchi et al. 2012). Another study used genetic algorithm (GA) to merge PET and MRI images to create coloured breast cancer images (Baum et al. 2011). Aneuploidy occurs when one or a few chromosomes in a cell’s nucleus are above or below the species typical chromosome count. However, the time required for these approaches necessitates the development of speedier diagnostic tests. To this objective, the proteomic profile of amniotic fluid samples was determined by mass spectrometry and analyzed by genetic algorithm (GA). The suggested approach could detect aneuploidy with $100\%$ sensitivity, 72–96% specificity and 11–50% positive and $100\%$ negative predictive values (Wang et al. 2005). Castiglione et al. (2004) devised a GA-based approach for selecting the optimal HAART treatment plan for HIV control and immunological reconstitution. The most common complication of insulin therapy in patients with type-1 diabetes mellitus is hypoglycemia (T1DM). Hypoglycemia can cause changes in electroencephalogram patterns (EEGs). Nguyen et al. (2013) used a combination of genetic algorithm (GA), artificial neural network, and Levenberg–Marquardt (LM) training techniques to detect hypoglycemia based on EEG signals. A more advanced computer-aided decision-support system for classifying tumors and identifying cancer stages through the use of neural networks in conjunction with particle swarm optimization (PSO) and ant colony optimization (ACO) is described in (Suganthi and Madheswaran 2012). In histopathology (to the microscopic examination of tissue to study the manifestations of the disease), artificial bee colon (ABC) has been used widely. To examine color, retinal scientists use the firefly algorithm (FA). A technique based on the artificial bee colony (ABC) algorithm is proposed for determining the IIR filter coefficients capable of removing doppler noise in the aortic valve efficiently (Koza et al. 2012). Particle swarm optimization (PSO) algorithm is used to improve the dynamic programming for segmenting the masses in the breast. Additionally, the ant colony optimization (ACO) hybridized Fuzzy technique is used to detect brain cancer. The capacity of these powerful algorithms to offer solutions to the myriad complicated difficulties physicians face every day has not been adequately explored in medicine.

Semantic web

The semantic web is an extension of the World Wide Web (WWW), whose primary goal is to make internet data machine-readable.The World Wide Web is a vast collection of web pages. SNOMED CT’s medical terminology ontology alone includes 370,000 class names, and current technology has not yet eliminated all semantically repetitive terms. GA-based algorithms and automated reasoning systems have been dealing with this currently. For the discovery of multi-relational association rules in the semantic web, Alippi et al. (2009) have used genetic algorithm (GA). Hsinchun et al. (1998) utilized genetic algorithm (GA) to develop a personalized search agent, and also he developed the quality of web search. Another multi-agent tool to perform a dynamic web search, Infospider, was developed by Menczer et al. (2004) with the help of genetic algorithm (GA) and artificial nural network. For the automatic composition of semantic web services, Wang et al. (2012) used ant colony optimization (ACO). Page classification, content mining, and also for organizing the web content dynamically scientists have used ant colony optimization (ACO).

Industry

Industry 4.0 is a result of next-level stuffs. The self-driving automobile is one of example. The automated control problem in self-driving cars includes routing. Shalamov et al. (2019) address the self-driving taxi routing problem formalized as the Pickup and Delivery Problem (PDP) by using common variable neighborhood search (VNS) algorithm and genetic algorithm (GA) for solution search. 5G will have more system capacity and spectral efficiency than 4G, as well as a greater number of network-connected wireless devices. Furthermore, the wireless communications infrastructure that exists today will not match the requirements of a 5G environment since a big number of traffic flows will be generated between a huge number of heterogeneous devices. The deployment strategy is one of the promising solutions to meet the expected demands of 5G. A major issue is the deployment of wireless communication and a hyper-dense deployment problem (HDDP) for 5G specifications. Tsai et al. (2015) provide a simple example of how a metaheuristic algorithm can solve the HDDP. Also, NSGA-II, MOEA/D, and NSGA-III are widely used in wireless sensor networks, electrical distribution system, and network reconfiguration for losses reduction (Sharma and Kumar 2022). The majority of optimization algorithms are only suitable to certain problems with superior characteristics. Thus, a hybrid of two or more algorithms is used to handle very complicated optimization problems in order to find the optimal solution. Ojugo et al. (2013) have proposed a hybrid artificial neural network-gravitational search algorithm model to train the neural network to simulate future flood occurrence and provides a lead time warning for flood management. A recent advances of metaheuristics in training neural networks for industrial applications can be found in (Chong et al. 2021).

Swarm drones and robotics

Unmanned Aerial Vehicles (UAVs) are widely favored for civil and military operations due to their vertical take-off and landing capabilities, stable hovering, and exceptionally agile movement in congested environments. It is critical for the success of the missions that the UAVs follow a desired trajectory accurately and quickly in civilian activities such as mapping, logistics, search and rescue, and exploration and surveillance, as well as a variety of military missions such as defense, attack, surveillance, and supervision. Numerous studies have implemented MAs for parameter optimization to accomplish these tasks. Altan (2020) uses particle swarm optimization (PSO) and harris hawks optimizer (HHO) to tune the parameters for this task. Both control algorithms have been evaluated on pathways with various shapes, including rectangle, circle, and lemniscate. The acquired findings have been compared to the performance of a conventional PID controller, and it has been found that the suggested controller outperforms both the conventional PID and PSO-based controllers. Goel et al. (2018) used metaheuristics for path planning of Unmanned Aerial Vehicles (UAVs) in three dimensional dynamic environment which is considered a challenging task in the field of robotics. Recently, metaheuristics have made a substantial effect on the application fields of collaborative robots. Improving the particle swarm optimization (PSO) algorithm to get a superior robotic search method seems to be on trend. Martinez-Soto et al. (2012) presented a hybrid PSO-GA strategy for creating the best fuzzy logic controller for each search robot. A review on metaheuristics applications in robotics can be found in (Fong et al. 2015).

Amazon and other online retailers are already filing patents for multi-level drone-beehive fulfillment centers, allowing for the deployment of this technology within the built environment. The use of drones for parcel delivery has been extensively studied in recent years, particularly in the area of logistics optimization.

Differential equation

Many highly non-linear problems in engineering and science involve one or more ordinary differential equations (ODEs). Analytic methods frequently fail to solve ODEs. To find ODE solutions, approximate analytical methods are used. The variational iteration method (VIM), the homotopy analysis method (HAM), the bilaterally bounded method (MBB), and the Adomian double decomposition method (ADDM) are a few examples. Approximation methods were used in many studies to solve integrodifferential equations (linear/non-linear). Each of these numerical approximation techniques, however, has its own set of operational constraints. As a result, these approximate techniques may fail to solve a particular problem. ADDM was unable to generate physically plausible data for the Glauert-jet problem (Torabi et al. 2012). Furthermore, the HAM and VIM failed to accurately predict solid particle motion in a fluid for some parameter values. It is clear that there is a lack of a proper approach that meets the majority of engineering demands with unconventional and non-linear ODEs. The approximation is the best solution for differential equations or other problems that cannot be solved analytically. In recent years, the use of MAs to approximate ODE solutions has grown rapidly. They differ in terms of the strategy employed and the base approximate function.

For example, Lee (2006) has used a different approach called the bilaterally bounded method in conjunction with particle swarm optimization (PSO) to solve the blasius equation. Sadollah et al. (2015) demonstrate an intriguing fact: harmony search (HS), particle swarm optimization (PSO), and genetic algorithm (GA) are used to approximate solve real-life ODEs for longitudinal heat transfer fins with a variety of profiles (rectangular, trapezoidal, and concave parabolic profiles). In engineering heat transfer problem, genetic algorithm (GA) and particle swarm optimization (PSO) have been the most widely used algorithms. Partial differential equations (PDEs) have also been attempted to solve by MAs because the existing techniques are not promising for a few extremely difficult problems. Panagant and Bureerat (2014) have successfully implemented the differential algorithm (DE) for the solution of a number of PDEs. By defining a global approximate function, a PDE problem is transformed into an optimization problem constrained by equality constraints imposed by the PDE boundary conditions. The acquired findings are displayed and contrasted with the actual solutions. It is demonstrated that the proposed method has the potential to become a future meshless tool if the metaheuristic’s search performance is significantly improved.

Image processing

Preprocessing, segmentation, object identification, denoising, and recognition are the most important tasks in image processing. Image segmentation is an important step to solve the image processing problems. Decomposing and partitioning a picture is computationally intensive. Chouhan et al. (2018) use genetic algorithm (GA) to solve this problem because of its greater search capabilities. Genetic algorithm (GA) has been used to eliminate noise from a noisy image. Also, it has been used to improve natural contrast and magnify images (Dhal et al. 2019). Li et al. (2016a) propose a modified discrete variant of grey wolf optimizer (GWO) to address the multi-level image thresholding problem. Also, to obtain optimal thresholds for multi-level thresholding in an image, cuckoo search (CS) algorithm is used (Agrawal et al. 2013). Particle swarm optimization (PSO) has been applied in many areas in image processing, such as color segmentation, clustering, denoising, and edge detection of images (Djemame et al. 2019).

Table 3 provides a quick summary of the many applications of the most prominent MAs, including their source of inspiration, number of parameters, solution updation equations/operators, and total number of function evaluations.

Table 3.

Summary of applications of most popular MAs with their source of inspiration and number of parameters

Algorithms	Source of inspiration	parameters	Updating equations/Operators	Function evaluations	Applications
Particle Swarm Optimization (PSO)	Bird swarm behaviour	5	$X_i(t+1)=X_i(t)+V_i(t+1)$	Population size (N) + N $\times$ number of iterations (T)	$\bullet$ Healthcare
					(i) Intelligence diagnosis
			$V_i(t+1)=V_i(t)+c_1·R_1·(P_i-X_i(t)$		(ii) Disease detection and classification
			$+c_2·R_2·(G-X_i(t)$
			Where		(iii) Medical image segmentation
			$P_i$: personal best
			G: global best		$\bullet$ Environmental
			$c_1$: cognitive coefficient, $0\le c1\le 4$		(i) Agriculture monitoring
			$c_2$: social coefficient, $0\le c2\le 4$		(ii) Flood control and routing
			$R_1,R_2$: uniform random number in (0, 1)		(iii) Pollutant concentration monitoring
					$\bullet$ Industrial
					(i) Economic dispatch problem
					(ii) Phasor measurement unit placement
					$\bullet$ Commercial
					(i) Risk assessment
					(ii) Predicting cost and price
					$\bullet$ Smart city
					(i) Smart home
					(ii) Traffic monitoring and scheduling
					(Gad 2022)
Genetic Algorithm (GA)	Darwin’s theory of evolution	3	Selection Operator	$N+N\times T$	$\bullet$ Operation management
					(i) Facility layout and Scheduling
			Crossover Operator		(ii) Inventory control
					(iii) Forecasting and network design
			Mutation Operator
					$\bullet$ Multimedia
					(i) Information security
					(ii) Image processing
					(iii) Video processing and Gaming
					$\bullet$ Wireless networking
					(i) Load balancing
					(ii) Localization
					(iii) Bandwidth and channel allocation
					(Katoch et al. 2021)
Ant Colony Optimization (ACO)	The foraging behaviour of ant colonies	5	Pheromones updation	Basic ACO was developed for TSP. The best path is chosen based on the density of pheromone. Pheromone is calculated for every path in each iteration.	$\bullet$ Transportation:
			${\tau }_{\mathit{ij}}^{\mathit{new}}=(1-\rho )·{\tau }_{\mathit{ij}}^{\mathit{old}}+\sum _k^{}\mathrm{\Delta }{\tau }_{\mathit{ij}}^k$		(i) Traveling salesman problem
			Where		(ii) Vehicle routing search
			$\rho$: evaporation rate
			$\mathrm{\Delta }{\tau }_{\mathit{ij}}^k$: pheromone amount laid by $k^{\mathit{th}}$ ant		$\bullet$ Set problems:
					(i) Set partitioning and covering
					(ii) Maximum independent set
					(iii) Bin packing
					$\bullet$ Scheduling:
					(i) Job shop scheduling
					(ii) Flow shop scheduling
					$\bullet$ Bio-informatics:
					(i) Protein folding
					(ii) DNA sequencing
					(Dorigo and Stützle 2019)
Differential Evolution Algorithm (DE)	Darwin’s theory of evolution	2	Mutation operator	$N+N\times T$	$\bullet$ Electrical and power systems:
					(i) Economic dispatch
			Crossover operator		(ii) Power system stabilizer
					(iii) Optimal power flow
			Selection operator
					$\bullet$ Robotics and Expert Systems:
					(i) Space trajectory optimization
					(ii) Satellite orbit reconfiguration
					(iii) Guidance of unmanned vehicles
					$\bullet$ Artificial Neural Networks:
					(i) Optimal network topology
					(ii) Neural network training
					(iii) Non-linear system identification
					$\bullet$ Operation Research:
					(i) Transport in docking systems
					(ii) Manufacturing optimization
					(iii) Scheduling
					(Das et al. 2016)
Simulated Annealing (SA)	Annealing process in metallurgy	2	Generate a new point x(k) randomly in a neighborhood of the current point	$1+T$	$\bullet$ Telecommunication:
					(i) Mobile network design
					(ii) Routing
					(iii) Channel allocation
					$\bullet$ Chemical industry:
					(i) Antenna array synthesis
					(ii) Refinery model problem
					$\bullet$ Operational:
					(i) Facility layout problems
					(ii) Flexible Manufacturing system
					(Suman and Kumar 2006)
					(Delahaye et al. 2019)
Tabu Search (TA)	Social tabu	2	Moves	1 + number of created neighbors in each iteration $\times T$	$\bullet$ Transportation:
					(i) Travelling salesman problem
					(ii) Vehicle routing Problem
					(iii) Quadratic assignment problem
					$\bullet$ Neural network:
					(i) Multi-layer network
					(ii) Training
					$\bullet$ Others:
					(i) Economic dispatch problems
					(ii) Telecommunication
					(iii) Clustering
					(Skorin-Kapov 1990)
					(Amuthan and Thilak 2016)
Grey Wolf Optimizer (GWO)	leadership hierarchy and hunting mechanism of grey wolves	2	$\overrightarrow{\mathbf{X}}(t+1)={\overrightarrow{\mathbf{X}}}_p(t)-A·D$	$N+N\times T$	$\bullet$ Medical and Bio-informatics:
					(i) Parkinson’s disease diagnosis
			Where		(ii) Breast cancer diagnosis
			$\overrightarrow{\mathbf{D}}=\overrightarrow{\mathbf{C}}·{\overrightarrow{\mathbf{X}}}_p(t)-\overrightarrow{\mathbf{X}}(t)$
			$\overrightarrow{\mathbf{A}}=2\overrightarrow{\mathbf{a}}·\overrightarrow{{\mathbf{r}}_{\mathbf{1}}}-\overrightarrow{\mathbf{a}}$		$\bullet$ Environmental applications:
			$\overrightarrow{\mathbf{C}}=2·\overrightarrow{{\mathbf{r}}_{\mathbf{2}}}$		(i) Water pollution assessment
					(ii) Thermal pollution assessment
			$\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{C}}$ are coefficient vectors
			${\overrightarrow{\mathbf{X}}}_p$: position vector of the prey		$\bullet$ Machine learning:
			$\overrightarrow{\mathbf{X}}$: position vector of a grey wolf		(i) Feature selection
			$r_1,r_2\in U[0,1]$		(ii) Training neural networks
					(iii) Clustering applications
					$\bullet$ Engineering applications:
					(i) Design and tuning controllers
					(ii) Power dispatch problems
					(iii) Robotics and path planning
					$\bullet$ Image processing:
					(i) Multi-level image threshold problem
					(ii) Template matching problems
					(iii) Hyper-spectral image classification
					(Faris et al. 2018)
Artificial Bee Colony (ABC)	the foraging behavior of honey bees when seeking a quality food source.	1	$v_{\mathit{ij}}=x_{\mathit{ij}}+{\varphi }_{\mathit{ij}}(x_{\mathit{ij}}-x_{\mathit{kj}})$	$N+[2N+$ number of scout bees]$\times T$	$\bullet$ Neural networks:
					(i) Signal processing applications
			Where		(ii) Machine learning
			$x_k$: randomly selected food source
			i: randomly chosen parameter index		$\bullet$ electrical engineering:
			${\varphi }_{\mathit{mi}}$: random number within the range [− 1,1]		(i) Distribution system
					(ii) Accident diagnosis in nuclear plant
					(iii) Radial distribution system
					$\bullet$ Civil engineering:
					(i) Grinding parameter optimization
					(ii) Heat exchangers
					(iii) Truss structures
					$\bullet$ Data mining:
					(i) Fuzzy clustering
					(ii) Chilli expert advisory system
					$\bullet$ Software engineering:
					(i) Automated maintenance of software
					(ii) Software test suite optimization
					(Karaboga et al. 2014)
Cuckoo Search (CS)	the brood parasitism of some cuckoo species	1	$x_i^{t+1}=x_i^t+\alpha \oplus$ Leavy$(\lambda )$	$N+2NT$	$\bullet$ Medical applications:
					(i) Medical image segmentation
			Where		(ii) Disease detection and classification
			$\alpha$ = Step size
			$\lambda$ = Levy exponent		$\bullet$ Image processing:
			$\oplus$ = Entry wise multiplication		(i) Image segmentation
					(ii) Enhancement
					(iii) Clustering
					$\bullet$ Engineering applications:
					(i) Economic dispatch problem
					(ii) Design and tuning controllers
					(Shehab et al. 2017)
					(Agrawal et al. 2013)
Harmony Search (HS)	musical performance process	3	$x_{\mathit{ij}}=x_{\mathit{ij}}+r_1\times BW$	$N+N\times T$	$\bullet$ Industrial application:
			$x_{\mathit{ij}}=l_{\mathit{ij}}+r_2\times (u_{\mathit{ij}}-l_{\mathit{ij}})$		(i) Logistics
					(ii) Tour planning
			Where		(iii) Self driving car
			BW: band width
			$r_1$, $r_2$: uniform random number in (0, 1)		$\bullet$ computer science:
			$u_{\mathit{ij}}$: upper bound of $x_{\mathit{ij}}$		(i) Web page and document clustering
			$l_{\mathit{ij}}$: lower bound of $x_{\mathit{ij}}$		(ii) Internet routing
					(iii) Robotics
					$\bullet$ electrical engineering:
					(i) Energy system dispatch
					(ii) Power system design
					(iii) Photo electronic detection
					$\bullet$ Medical Studies:
					(i) RNA structure prediction
					(ii) Medical image
					(iii) Forecasting influenza season
					(Ala’a et al. 2019)

Limitation and open problem

The main difference between deterministic and stochastic algorithms is that a deterministic algorithm, such as the simplex method, always provides the optimal solution. In comparison, a stochastic algorithm does not guarantee optimality, but rather a satisfactory solution. This is a significant disadvantage of MAs. However, the deterministic method fails miserably when confronted with increased complexity, such as a higher dimension or a non-differentiable function. This fact, however, can be interpreted as a ‘give and take’ policy. We must give up ‘something’ in order to gain ‘something’. We get a decent result, but we risk losing perfect precision. The ‘curse of dimensionality’ affects the performance of several MAs as the problem size increases. MAs used to solve problems involving a large number of choice variables, referred to as large scale global optimization (LSGO) problems, typically have a significant computational cost. A lack of mathematical analysis is a drawback for many MAs. There is currently no strong theoretical notion that overcomes this limitation: critics argue that, in comparison to physics, chemistry, or mathematics, the field of metaheuristics is still in its infancy. Despite the fact that metaheuristics have been demonstrated to handle a wide range of NP-Hard problems, this field is still missing in terms of convergence rate, complexity, and run time analysis, according to the study. Theoretically, if time is not a constraint, MAs can locate the optimal solution. However, since time is limited, we have to find a solution at a reasonable time. Therefore, there is a gap between theory and practical implementation. To prove the efficiency of the algorithm, a set of benchmark functions is chosen. How do these common benchmark test sets and evaluation criteria represent real-world problem characteristics? This benchmark function is complex but is these really can be used as a practical optimization problem? The answer is ‘No’. As a result, many algorithms can demonstrate their efficacy in papers yet fail miserably when applied to real-world problems. There is no single unified work to compare all MAs. Most of them need good parameter tuning and a better convergence rate. Many researchers work with them and find some way to enhance them by parallelism. We need a much stronger notion to cope with this situation. Some open challenges are as follows:

• How to provide a unified framework for mathematically analyzing all MAs to determine their convergence, rate of convergence, stability, and robustness? (Yang 2020)

• How to optimize an algorithm’s parameters for a certain group of problems? How to alter or adjust these parameters to optimize an algorithm’s performance? (Yang 2020)

• What benchmarks are useful? Do free lunches exist, and if so, under what circumstance? Can you prepare a genuine set of reliable benchmark functions? (Yang 2020)

• What performance measurements should be used to compare all algorithms fairly? Is it feasible to compare all algorithms honestly and rigorously? (Yang 2020)

• How to efficiently scale up algorithms that perform well for LSGO, real-world challenges? (Yang 2020)

• What is the NFL in terms of several dimensions?

• Two essential principles in the MAs are exploration and exploitation. These are diametrically opposed to one another, so how do you balance them for the best performance? (Črepinšek et al. 2013)

Future scope

Almost every science and engineering problem, and almost every life problem in general, can be framed as an optimization problem if we look closely enough. MAs, as given in the application Sect. 7, solve a wide range of problems. There are numerous future scopes. Several of them are listed below.

• Metaheuristics have been implemented to enhance parallel or distributed computation in modern technology of parallel computing. Alba (2005) explores metaheuristics in this domain and highlights relevant research paths to strengthen outcomes. They are unquestionably the most powerful optimization algorithms that will have a major impact on future generation computing.

• There have been very few efforts yet to further strengthen the scalability of the LSGO methods for addressing LSGO benchmark test sets with dimensions greater than 1000. Scalability of LSGO methods becomes a critical prerequisite, with significant implications for future study (Mahdavi et al. 2015).

• In NP-hard problems such as the TSP, JSS, and Knapsack Problems, metaheuristics are still in their infancy. Despite numerous scholars’ efforts to use metaheuristics to overcome these difficulties, they remain critical. For example, UAV (drone) task assignment in logistics, 3D path planning in dynamic environment, 5 G cell deployment challenge, etc. can all bring about a revolution. Consequently, scholars should focus on these challenges.

• A significant area of study that needs to explore is intelligent sampling and surrogate modeling. The boundaries of the issue space are decreased by intelligent sampling, allowing for confined searching to the best neighborhoods, whilst surrogate approaches aid metaheuristics in evaluating computationally costly functions by approximating the actual objective function. The limited work that has been done in this approach has shown tremendous promise. Mann and Singh (2017), for example, enhanced performance of artificial bee colony (ABC) by using a sampling technique called the Student’s-t distribution.

• Another useful study area is the evaluation of structural bias in population-based heuristics, which is the limitation of particular metaheuristics to focus on a subset of the solution space (Kononova et al. 2015). Due to the intrinsic algorithmic structure of such algorithms, they may sample solutions more frequently near the origin, near the boundary, or near any other specific area of the search space. Structural bias can drastically affect the performance of various popular MAs, as demonstrated by Piotrowski and Napiorkowski (2018). Similar research should be conducted with newer metaheuristics to clarify their behavior when sampling the solution space. Furthermore, Markov chain theory, self-organized systems, filter theory, discrete and continuous dynamical systems, Bayesian statistics, computational complexity analysis, and other frameworks can be used to investigate intriguing algorithmic aspects (Yang 2018).

• Numerous billions of pages compose the World Wide Web. SNOMED CT’s ontology of medical terminology contains 370, 000 in class names alone, and current technology has not yet eliminated all semantically redundant terms. Additionally, the Semantic Web’s shortcomings include ambiguity, inconsistency, and deception. Numerous studies have been undertaken in this area, and genetic algorithm (GA) addresses a number of the issues, while there are still a few unknown areas. One such area is the use of new generation algorithms such as grey wolf optimizer (GWO), cuckoo search (CS), and harmony search (HS) to semantic web reasoning, which is the future focus of study in this area.

• A promising but not fully explored direction is to solve highly non-linear ODEs and PDEs in engineering, physics, economics, fluids, and other disciplines. The ODEs and PDEs can be represented as an optimization problem with the Fourier series as the base approximate function.

• The algorithm selection task for black-box optimization problems is considered an important task. FLA has been demonstrated to be a useful tool for analyzing the hardness of an optimization problem by extracting its features. Wang et al. (2017) introduced the concept of population evolvability, which is an extension of dynamic FLA, to quantify the effectiveness of population-based metaheuristics for solving a given problem. This area should be investigated for more sophisticated user-friendly FLA techniques.

• According to Zelinka (2015), there are still many unsolved questions. Several of the problems may be consolidated into one: can controlling the dynamics of a swarm and evolutionary algorithms considerably increase their performance and diversity in search operations? The study suggests many prospective potential research avenues for the future, ranging from swarm robotics to evolvable hardware to disrupting terrorist communication.

• Metaheuristic and artificial intelligence can be combined to design a more effective optimization tool. In recent years, interest in the research of evolutionary transfer learning (ETO) has increased (Tan et al. 2021). ETO is a paradigm that combines EAs with knowledge learning and transfer across related domains to improve optimization efficiency and performance. Evolutionary multitasking is a very promising example of ETO, demonstrating that this might be a very valuable concept in the real world application (Gupta et al. 2015).

Conclusion

This study aims to conduct a state-of-the-art survey of metaheuristics. In order to develop a toolkit for researchers, this study assembled most of the existing MAs (approximately 540). Also, for better comprehension, statistical data is collected and analyzed. It can be concluded from the statistical data that during the last decade, approximately 38 MAs come on average each year. However, the majority of new generation algorithms lack originality and resemble to existing algorithms such as particle swarm optimization (PSO), genetic algorithm (GA), differential algorithm (DE), ant colony optimization (ACO), and artificial bee colony (ABC).

Various existing taxonomies of MAs based on source of inspiration, population size, and population movement are addressed along with their advantages and disadvantages. In this study, a novel taxonomy of MAs based of number of primary parameters is proposed. The existing MAs are classified in seven categories based on the different number of primary parameters. The MAs having 0, 1, 2, 3, 4, and 5 primary parameters are classified as free parameter, mono-parameter, bi-parameter, tri-parameter, tetra-parameter, and penta-parameter based algorithms respectively. The MAs having more than five parameters are kept in miscellaneous category. In general, increase in the number of parameters raises the complexity of parameter tuning. Also, when dealing with a black box problem, tuning large number of parameters is a laborious task. That is why, efficient algorithms with less parameters are welcome to solve the complex industrial optimization problems. Apart from the classification of algorithms, a handful of the remarkable application areas of MAs such as medical, industry, robotics and swarm drones have been highlighted in this study. Additionally, theoretical lacks of existing MAs and open problems are discussed which can be addressed in future. Several significant avenues for future research have been mentioned.

As an extension of this study, further investigation may be necessary to identify the overall level of complexity that arises as the number of primary parameters increase. In addition, a state-of-the-art survey of all the recent variants of most popular algorithms such as particle swarm optimization (PSO), genetic algorithm (GA), differential algorithm (DE), and ant colony optimization (ACO) can be done. We believe this extensive survey of metaheuristics will assist our research community and newcomers in seeing the broad domain of metaheuristics and give it the proper direction it deserves.