Considering light-matter interactions in Friedmann equations based on the conformal FLRW metric

Graphical abstract

Highlights

• •An alternative scenario of the evolution of the Universe is proposed.
• •The absorption of light by cosmic dust causes opacity that counterbalances gravitational forces.
• •The theory predicts cyclic model of the expansion and contraction of the Universe.
• •The maximum redshift of the Universe is about 15–17.
• •The proposed model removes some tensions of the standard cosmological model.

Abstract

Introduction

Recent observations indicate that the Universe is not transparent but partially opaque due to absorption of light by ambient cosmic dust. This implies that the current cosmological model valid for the transparent universe must be modified for the opaque universe.

Objectives

The paper studies a scenario of the evolution of the Universe when the cosmic opacity steeply rises with redshift, because the volume of the Universe was smaller and the cosmic dust density was higher in the previous epochs. In this case, the light-matter interactions become important, because cosmic opacity produces radiation pressure that counterbalances gravitational forces.

Methods

The radiation pressure due to cosmic opacity is evaluated and incorporated into the Friedmann equations, which describe cosmic dynamics. The equations are based on the conformal FLRW metric and are consistent with observations of the cosmological redshift as well as time dilation. Using astronomical observations of basic cosmological parameters, the solution of the modified Friedmann equations is numerically modelled.

Results

The presented model predicts a cyclic expansion/contraction evolution of the Universe within a limited range of scale factors with no Big Bang. The redshift of the Universe with the minimum volume is about 15–17. The model avoids dark energy and removes several fundamental tensions of the standard cosmological model. In agreement with observations, the modified Friedmann equations predict the existence of very old mature galaxies at high redshifts and they do not limit the age of stars in the Universe. The new model is consistent with theory of cosmic microwave background as thermal radiation of cosmic dust.

Conclusion

The paper demonstrates that considering light-matter interactions in cosmic dynamics is crucial and can lead to new cosmological models essentially different from the currently accepted ΛCDM model.

Introduction

The Big Bang (BB) theory as the mainstream theory of the evolution of the Universe and the ΛCDM model as the standard cosmological model bring many puzzles and tensions in cosmology [1], [2]. They assume the existence of cold dark matter (CDM) and dark energy (also called the cosmological constant Λ), which are of unknown physical nature. Dark matter is questioned for its mysterious nature and for discrepancies with observations on small scale [3], [4] such as observations of faint satellite galaxies of the Milky Way [5], [6] or observations of the radial acceleration relation of galaxies [7], [8]. Dark energy was introduced into the ΛCDM model to fit Type Ia supernovae (SNe Ia) observations [9], [10]. However, dark energy causes negative pressure lower by 120 orders than a theoretical value predicted by quantum field theory [11]. Dark energy also predicts the speeds of gravitational waves and light to be generally different [12], [13], but observations of the binary neutron star merger GW170817 and its electromagnetic counterparts proved that both speeds coincide with a high accuracy (<5x10^-16). In addition, the age of 14.46 ± 0.31 Gyr of a nearby star HD 140283 [14] is in conflict with the age of the Universe, 13.80 ± 0.02 Gyr, predicted by the BB theory based on the interpretation of the cosmic microwave background (CMB) as relic radiation of the Big Bang [15]. Similarly, mature galaxies observed by Watson et al. [16] or Laporte et al. [17] in the early Universe indicate that the predicted age of the Universe is incorrect.

The origin of the mentioned difficulties of the BB theory and the ΛCDM model lies most likely in unrealistic assumptions about the Universe made in the Friedmann equations. In order to manage the problem of the evolution of the Universe, Friedmann [18] applied many simplifications. Although the Universe is an extremely complex physical system described by a nonlinear fluid dynamics with chaotic features [[19], [20], [21], [22], [23], [24], [25], [26]], Friedmann modelled the Universe as a perfect isotropic fluid homogeneously distributed in space. The behaviour of the fluid was described by the so-called Friedmann-Lemaitre-Robertson-Walker (FLRW) metric [[18], [27], [28], [29]], which introduces a time-dependent space expansion characterized by the scale factor a(t). Friedmann inserted this metric into the Einstein equations of general relativity and obtained equations of the evolution of the Universe, which form fundamentals of the BB theory. Later, several authors pointed to the problem of the oversimplification due to neglecting inhomogeneities in the Universe and proposed new models, such as the Swiss-cheese cosmology [30], [31] or the timescape cosmology [32], [33]. These models are, however, complicated and not very usable for modelling. By contrast, Vavryčuk [34] pointed out that the Friedmann equations are too simplistic also for another reason. He emphasized that the standard FLRW metric used in the equations allows the space to be distorted by gravity, but the cosmic time is undistorted. If time distortion is allowed and the standard FLRW metric is substituted by the so-called conformal FLRW metric, the modified Friedmann equations behave much better: they fit the SNe Ia observations with no need to introduce dark energy or to consider inhomogeneities in the Universe.

Another severe simplification of the Friedmann equations lies in assuming that the Universe is transparent, in which the only force affecting its expansion is gravity. However, if the Universe is partially opaque, the radiation pressure produced by absorption of light could act against the gravity and affect the evolution history of the Universe and its age. Hypothetically, if radiation pressure is high enough in the early Universe, it can fully counterbalance the gravity. In this way, the evolution of the Universe would be described by a cyclic cosmology with no Big Bang. Consequently, the tension between the predicted age of the Universe and the observations of very old stars in our Galaxy [14] and of mature galaxies in the early Universe [16], [17] would be reconciled.

The idea that cosmic opacity might affect the cosmic dynamics looks apparently unrealistic but observations confirm that such process is plausible. We know that the interstellar medium (ISM) and the intergalactic medium (IGM) contain dust, which interacts with the stellar radiation. Dust grains absorb and scatter the starlight and reemit the absorbed energy at infrared, far-infrared and microwave wavelengths [35], [36], [37], [38], [39]. Since galaxies contain interstellar dust, they lose their transparency and become opaque [40], [41], [42]. Similarly, the Universe is not transparent but partially opaque due to ambient cosmic dust. The cosmic opacity is very low in the local Universe [43], but it might steeply increase with redshift [44], [45], [46].

Appreciable cosmic opacity at high redshift is documented by observations of (1) the evolution of the Lyα forest of absorption lines in quasar optical spectra, (2) the metallicity detected in the Lyα forest, and (3) emission spectra of high-redshift galaxies. In the Lyα forest studies, the evolution of massive Lyman-limit (LLS) and damped Lyman absorption (DLA) systems are, in particular, important, because they are self-shielded and serve as reservoirs of dust [47], [48]. It has been shown that the incidence rate and the Gunn-Peterson optical depth of the LLS and DLA systems increase with redshift as (1 + z)⁴ or more for z < 7 [49], [50], [51]. For higher z, the increase of the optical depth is even stronger. Another independent indication of dust at high redshifts is a weak or no evolution of metallicity with redshift. For example, observations of the C_IV absorbers do not show any visible redshift evolution over cosmic times suggesting that a large fraction of intergalactic metals may already have been in place at z > 6 [52]. In addition, the presence of dust in the high-redshift universe is documented also by observations of dusty galaxies even at z > 7 [16], [17] and dusty halos around star-forming galaxies at z = 5–7 [53]. Zavala et al. [54] measured a dust mass of ∼ 10⁷ M_ʘ for a galaxy at z ∼ 9. Since dust in high-redshift galaxies can efficiently be transported to halos due to galactic wind [55] and radiation pressure [56], the cosmic dust must be present even at redshifts z > 7–9.

The fact that the Universe is not transparent but partially opaque might have fundamental cosmological consequences. Neglecting cosmic opacity produced by intergalactic dust may lead to distorting the observed evolution of the luminosity density and the global stellar mass density with redshift [46]. Non-zero cosmic opacity affects the interpretation of the Type Ia supernova (SNe Ia) dimming as a result of dark energy and the accelerating expansion of the Universe [55], [57], [58], [59], [60], because the cosmic opacity can dim the SNe Ia luminosity. The cosmic microwave background (CMB) can be produced by cosmic dust instead of being relic radiation of the Big Bang [61], [62]. For example, it has been shown that thermal radiation of dust is capable to explain the spectrum, intensity and temperature of the CMB including the CMB temperature/polarization anisotropies [39].

If cosmic opacity and light-matter interactions are considered, the Friedmann equations must be modified and the radiation pressure caused by absorption of photons by dust grains must be incorporated. This was done by Vavryčuk [106], who assumed the standard FLRW metric when deriving the modified Friedmann equations. Since Vavryčuk [34] showed that the standard FLRW metric is inconsistent with observations of the cosmological redshift, the Friedmann equations based on the conformal FLRW metric are derived in this paper. It is demonstrated that the radiation pressure due to light absorption by cosmic dust is negligible at the present epoch, but it could be significantly stronger in the past epochs. Similarly as in Vavryčuk [106], the modified conformal Friedmann equations avoid the Big Bang and lead to a cyclic model of the Universe with repeating expansion/contraction epochs within a limited range of scale factors. As a consequence, the age of the Universe is not finite as predicted by the BB theory but infinite. The predicted parameters of the cosmic dynamics are, however, slightly different from those presented in Vavryčuk [106]. The redshift of the Universe with the minimum volume is about 15–17 and the maximum volume of the Universe is defined by the scale factor a of about 11. The presented model avoids dark energy and removes several fundamental tensions of the standard cosmological model.

The paper is organized as follows. The paper starts with section Theory, where novel equations for the expansion of the Universe are developed by assuming that the cosmic dynamics is driven not only by gravity but also by radiation pressure produced by interaction of light with cosmic dust ambient in the Universe. Section Results presents numerical tests, which show plausible scenarios of the evolution of the Universe. These scenarios predict a cyclic cosmology with no Big Bang, when the Universe is repeatedly expanding and contracting within a limited range of scale factors. Finally, sections Discussion and Conclusions summarize the most important cosmological consequences of the obtained results and recommendations for future research.

Theory

Standard and conformal FLRW metrics

The standard FLRW metric reads [[63], [64]]

$${\mathit{ds}}^2=-c^2{\mathit{dt}}^2+a^2\left(t\right)\left(\frac{{\mathit{dr}}^2}{1-k{r}^2}+r^{2}d{\mathrm{\Omega }}^2\right),$$ (1)

where c is the speed of light, $\mathit{ds}=cd\tau$ is the spacetime element, τ is the proper time, t is the coordinate time, k is the Gaussian curvature of the space, r is the comoving distance, Ω is the solid angle, and function a(t) is called the scale factor and describes the expansion history of the Universe.

The conformal FLRW metric [65], [66], [67] assumes the same scale factor a(t) for the space expansion as well as for time dilation,

$${\mathit{ds}}^2=a^2\left(t\right)\left(-c^2{\mathit{dt}}^2+\frac{{\mathit{dr}}^2}{1-k{r}^2}+r^{2}d{\mathrm{\Omega }}^2\right),$$ (2)

where time t has a different physical meaning than in Eq. (1) being often denoted as η. We can see that Eq. (2) is obtained from Eq. (1) by a simple transformation

$$\mathit{dt}=a\left(t\right)d\eta ,$$ (3)

where η is called the comoving time or the conformal time.

Obviously, Eqs (1), (2) define two physically different universe models. Eq. (1) assumes the cosmic time being invariant of the space expansion, but Eq. (2) assumes the cosmic time being dependent on the space expansion. Consequently, the proper speed of light is invariant in Eq. (1) but it depends on the scale factor a(t) in Eq. (2). In addition, Eq. (2) predicts cosmological redshift and time dilation in accordance with observations, while no such phenomena are predicted by Eq. (1), see Vavryčuk [34].

Conformal Friedmann equations for the transparent universe

Assuming the standard FLRW metric described by Eq. (1), the Friedmann equations for the perfect isotropic fluid read [[63], [64]]

$${\left(\frac{\dot{a}}{a}\right)}^2=\frac{8\pi G}{3}\rho -\frac{k{c}^2}{a^2},$$ (4)

$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left(\rho +\frac{3p}{c^2}\right),$$ (5)

where G is the gravitational constant, ρ is the mean mass density, p is the pressure, k/a² is the spatial curvature of the universe, and c is the speed of light at present.

In order to express the Friedmann equations for the conformal FLRW metric, we have to substitute time t by the conformal time η and time derivatives $\dot{a}=\frac{\mathit{da}}{\mathit{dt}}$ and $\ddot{a}=\frac{d^{2}a}{{\mathit{dt}}^2}$ by $a^{\text{'}}=\frac{\mathit{da}}{d\eta }=a\dot{a}$ and $a^{\text{'}\text{'}}=\frac{d^{2}a}{{d\eta }^2}=a^2\ddot{a}$. Hence, the conformal Friedmann equations read

$${\left(\frac{a^{\text{'}}}{a}\right)}^2=\frac{8\pi G}{3}\rho a^2-k{c}^2,$$ (6)

$$\frac{a^{\text{'}\text{'}}}{a}=-\frac{4\pi G}{3}\left(\rho +\frac{3p}{c^2}\right)a^2,$$ (7)

where $a^{\text{'}}$ denotes the derivative with respect to the conformal time. Considering a mass-dominated universe, we get

$$\frac{8\pi G}{3}\rho =H_0^2{\mathrm{\Omega }}_m{a}^{-3}.$$ (8)

Eq. (6) is rewritten as

$$H^2\left(a\right)=H_0^2\left[{\mathrm{\Omega }}_m{a}^{-1}+{\mathrm{\Omega }}_k\right]$$ (9)

with the condition

$${\mathrm{\Omega }}_m+{\mathrm{\Omega }}_k=1,$$ (10)

where $H\left(a\right)=a\text{'}/a$ is the Hubble parameter, H₀ is the Hubble constant, Ω_m is the normalized matter density, and Ω_k is the normalized space curvature.

For a comparison, the Hubble parameter for the common ΛCDM model based on the standard FLRW metric reads

$$H^2\left(a\right)=H_0^2\left[{\mathrm{\Omega }}_m{a}^{-3}+{\mathrm{\Omega }}_{\mathrm{\Lambda }}\right],$$ (11)

which describes a flat matter-dominated universe. The universe is transparent, because no interaction of radiation with matter is considered. The vacuum term Ω_Λ is called dark energy and it is responsible for the accelerating expansion of the universe. The dark energy is introduced to fit the ΛCDM model with observations of the Type Ia supernova dimming [9], [10]. By contrast, Eq. (9) fits observations of the Type Ia supernova without the necessity to introduce dark energy [34].

Light-matter interaction

The basic drawback of Friedmann equations is their assumption of transparency of the universe and the neglect of the universe opacity caused by interaction of light with intergalactic dust. Absorption of light by cosmic dust produces radiation pressure acting against the gravity, but this pressure is ignored in the Friedmann equations.

Let us consider light emitted by a point source with mass M (in kg) and luminosity L (in W) and absorbed by a dust grain with mass M_D, see Fig. 1. The light source produces the energy flux I (in Wm⁻²) and the radiation pressure p_D, which acts on the dust grain. The acceleration of the dust grain produced by the light source reads

$${\ddot{R}}_{\mathrm{\Lambda }}=\frac{S_D}{M_D}\frac{L}{4\pi v}\frac{1}{R^2},$$ (12)

where S_D is the absorption cross-section of the grain, L is the luminosity of the source, R is the distance of the dust grain from the light source, and v is the proper (rest-frame) speed of light. The ratio S_D/M_D in Eq. (12) can be expressed as

$$\frac{S_D}{M_D}=\frac{3}{4}\frac{Q_{\mathrm{a}\mathrm{b}\mathrm{s}}}{R_D{\rho }_D}=\kappa ,$$ (13)

where $S_D={n_{D}Q}_{\mathrm{a}\mathrm{b}\mathrm{s}}\pi R_D^2$ is the absorption cross-section of the dust grain, $M_D=n_D\frac{4}{3}\pi R_D^3{\rho }_D$ is the mass of the grain, R_D is the grain radius, Q_abs is the grain absorption efficiency, ρ_D is the specific mass density of grains, and κ is the mass opacity (in m²kg⁻¹). Inserting Eq. (13) into Eq. (12), and taking into account that dust mass forms just a fraction δ of the total mass of the universe, we write

$${\ddot{R}}_{\mathrm{\Lambda }}=\frac{\delta \kappa L}{4\pi v}\frac{1}{R^2}=\frac{\overline{\kappa }L}{4\pi v}\frac{1}{R^2},$$ (14)

where $\overline{\kappa }=\delta \kappa$ is the fractional (or effective) mass opacity. Expressing the gravitational acceleration ${\ddot{R}}_{\mathrm{g}}$ as

$${\ddot{R}}_{\mathrm{g}}=-\frac{\mathit{GM}}{R^2},$$ (15)

the total acceleration of a dust grain is

$$\ddot{R}={\ddot{R}}_{\mathrm{g}}+{\ddot{R}}_{\mathrm{\Lambda }}=\frac{1}{R^2}\left(-GM+\frac{\overline{\kappa }L}{4\pi v}\right).$$ (16)

Dividing Eq. (16) by distance R and substituting mass M (in kg) and luminosity L (in W) by mean mass density ρ (in kgm⁻³) and mean luminosity density j (in Wm⁻³), we get

$$\frac{\ddot{R}}{R}=-\frac{4}{3}\pi G\rho +\frac{\overline{\kappa }j}{3v}.$$ (17)

Fig. 1.

The scheme of gravitational forces (a) and radiation pressure (b) acting on dust grains. The blue and red arrows indicate a direction of the acting attractive and repulsive forces, respectively. The point source is characterized by mass M and luminosity L. The dust grains have mass M_D and the cross-section S_D.

Consequently, we obtain a Poisson equation for the scalar potential $\varphi$, which involves potentials for both gravitational and radiation-absorption fields

$$\mathrm{\Delta }\varphi =4\pi G\rho -\frac{\overline{\kappa }j}{v}.$$ (18)

Hence, the radiation-absorption term can be incorporated into the Friedmann equations in a very analogous way as the gravity. Its effect will be, however, opposite.

Conformal Friedmann equations for the opaque universe

Next, the Friedmann equations valid for the transparent universe will be modified for the universe with cosmic opacity caused by absorption of light by cosmic dust. Incorporating the radiation-absorption field into the Friedmann equations comprises several steps. First, we must modify the Einstein equations by incorporating a non-gravitational field ${\mathrm{\Lambda }}^{\mu \nu }$ described as a perfect isotropic fluid producing repulsive force acting against the gravity (see Appendix A)

$$G^{\mu \nu }+\frac{1}{c^4}{\mathrm{\Lambda }}^{\mu \nu }=\frac{8\pi G}{c^4}{T}^{\mu \nu },$$ (19)

$${\mathrm{\Lambda }}^{\mu \nu }=\left({\rho }_{\mathrm{\Lambda }}+\frac{p_{\mathrm{\Lambda }}}{c^2}\right)U^{\mu }{U}^{\nu }+p_{\mathrm{\Lambda }}{g}^{\mu \nu },$$ (20)

where ${\rho }_{\mathrm{\Lambda }}=2\frac{\overline{\kappa }j}{v}$ is the density and p_Λ is the repulsive pressure of the non-gravitational field produced by the light-matter interaction. Second, we assume the spacetime geometry described by the FLRW metric and density ${\rho }_{\mathrm{\Lambda }}$ dependent on the scale factor a as ${\rho }_{\mathrm{\Lambda }}={\rho }_{\mathrm{\Lambda }0}{a}^{-\beta }$. Consequently, the Friedmann equations for the opaque universe in the standard FLRW metric read (see Appendix A)

$${\left(\frac{\dot{a}}{a}\right)}^2=\frac{8\pi G}{3}\rho -\frac{k{c}^2}{a^2}-\frac{2}{3}\frac{\overline{\kappa }j}{v},$$ (21)

$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\rho +\frac{\beta -2}{3}\frac{\overline{\kappa }j}{v}.$$ (22)

Third, the Friedmann equations for the opaque universe in the standard FLRW metric will be transformed into the equations based on the conformal FLRW metric. The procedure is similar to that for the transparent universe. We just substitute time t in Eqs (21), (22) by the conformal time η and time derivatives $\dot{a}=\frac{\mathit{da}}{\mathit{dt}}$ and $\ddot{a}=\frac{d^{2}a}{{\mathit{dt}}^2}$ by $a^{\text{'}}=\frac{\mathit{da}}{d\eta }=a\dot{a}$ and $a^{\text{'}\text{'}}=\frac{d^{2}a}{{d\eta }^2}=a^2\ddot{a}$, see Eqs (6), (7). Hence,

$${\left(\frac{a^{\text{'}}}{a}\right)}^2=\frac{8\pi G}{3}\rho a^2-k{c}^2-\frac{2}{3}\frac{\overline{\kappa }j}{v}{a}^2,$$ (23)

$$\frac{a^{\text{'}\text{'}}}{a}=-\frac{4\pi G}{3}\rho a^2+\frac{\beta -2}{3}\frac{\overline{\kappa }j}{v}{a}^2.$$ (24)

Consequently, the Hubble parameter in the conformal FLRW metric is obtained by modifying Eq. (9) for the Hubble parameter in the standard FLRW metric as

$$H^2\left(a\right)=H_0^2\left[{\mathrm{\Omega }}_m{a}^{-1}+{\mathrm{\Omega }}_a{a}^{2-\beta }+{\mathrm{\Omega }}_k\right]$$ (25)

with the condition

$${\mathrm{\Omega }}_m+{\mathrm{\Omega }}_a+{\mathrm{\Omega }}_k=1,$$ (26)

where Ω_m, Ω_a and Ω_k are the normalized matter density, normalized radiation-absorption density and normalized space curvature, respectively,

$${\mathrm{\Omega }}_m=\frac{1}{H_0^2}\left(\frac{8}{3}\pi G{\rho }_0\right),$$ (27)

$${\mathrm{\Omega }}_a=-\frac{1}{H_0^2}\left(\frac{2}{3}\frac{\overline{\kappa }j}{v}\right),$$ (28)

$${\mathrm{\Omega }}_k=-\frac{k{c}^2}{H_0^2}.$$ (29)

The minus sign in Eq. (28) means that the radiation pressure due to the light-matter interaction acts against the gravity. Considering $a=1/(1+z)$, the comoving distance is expressed from Eq. (25) as a function of redshift as follows

$$\mathit{dr}=\frac{c}{H_0}{\left[{\mathrm{\Omega }}_m\left(1+z\right)+{\mathrm{\Omega }}_a{\left(1+z\right)}^{\beta -2}+{\mathrm{\Omega }}_k\right]}^{-1/2}dz.$$ (30)

This relation is needed for transforming observations of redshift for distant objects to their distance.

Redshift dependence of the light-matter interaction

The radiation-absorption term $\frac{\overline{\kappa }j}{v}$ in Eq. (23) is redshift dependent. Under the assumption that the number of sources (global stellar mass) and their luminosity conserves in time in the Universe, the rest-frame luminosity density j depends on redshift as ${\left(1+z\right)}^3$. Since the proper speed of light is $v=c/(1+z)$ in the conformal FLRW metric [34], we get

$$\frac{j}{v}=\frac{j_0}{c}{\left(1+z\right)}^4,$$ (31)

where subscript ‘0′ corresponds to the quantity observed at present. The assumption of the independence of the global stellar mass in the Universe looks apparently unrealistic but it is fully consistent with observations if corrections to the opacity of the Universe are applied [39], [46].

Also, the effective mass opacity $\overline{\kappa }=\delta \kappa$ in the radiation-absorption term $\frac{\overline{\kappa }j}{v}$ in Eq. (23) depends on redshift. Based on the extinction law, the mass opacity κ depends on the wavelength λ of absorbed radiation as ${\lambda }^{-\gamma }$, where γ is the spectral index ranging between 1.0 and 1.5 for grains with size of 0.2 μm or smaller [38], [68] and for wavelengths lower than 10 μm, see Fig. 2. Hence, if radiation changes its wavelength due to the redshift as ${\left(1+z\right)}^{-2}$ [34], the mass opacity κ depends on redshift as ${\left(1+z\right)}^{2\gamma }$. Consequently, the coefficient β describing the redshift-dependent radiation-absorption term $\frac{\overline{\kappa }j}{v}$ in Eqs (25), (30) is $\beta =4+2\gamma$ and ranges from 6 to 7. By contrast, the mass opacity is wavelength independent for large grains with size larger than wavelength λ and the radiation-absorption term depends on z as ${\left(1+z\right)}^4$ only.

Fig. 2.

The mass opacity κ as a function of wavelength for the so-called MRN dust model [68] defined by the power-law grains-size distribution with lower and upper size limits between ∼ 5 and ∼ 250 nm, see Tables 4–6 of Draine [37]. The red dashed line shows the power law with the spectral index γ of 1.3.

Limits of the scale factor a

Next, we assume that the mean spectral index γ characterizing the absorption of light by mixture of grains of varying size is 1. Consequently, the radiation-absorption term depends on a as $a^{-6}$. The scale factor a of the Universe with the zero expansion rate is defined by the zero Hubble parameter in Eq. (25), which yields the following algebraic equation in a

$${\mathrm{\Omega }}_k{a}^4+{\mathrm{\Omega }}_m{a}^3+{\mathrm{\Omega }}_a=0.$$ (32)

Assuming ${\mathrm{\Omega }}_k{a}^4\cong 0$ for $a\ll 1$ and taking into account that ${\mathrm{\Omega }}_m>0$ and ${\mathrm{\Omega }}_a<0$, Eq. (32) has one real positive root

$$a_{\mathrm{m}\mathrm{i}\mathrm{n}}\cong \sqrt[3]{\left|\frac{{\mathrm{\Omega }}_a}{{\mathrm{\Omega }}_m}\right|}.$$ (33)

Assuming ${\mathrm{\Omega }}_a\cong 0$ for $a\gg 1$ and taking into account that ${\mathrm{\Omega }}_m>0$ and ${\mathrm{\Omega }}_k<0$ (closed universe), Eq. (32) yields

$$a_{\mathrm{m}\mathrm{a}\mathrm{x}}\cong \left|\frac{{\mathrm{\Omega }}_m}{{\mathrm{\Omega }}_k}\right|\cong \left|\frac{1-{\mathrm{\Omega }}_k}{{\mathrm{\Omega }}_k}\right|.$$ (34)

Hence, Eq. (25) describes a closed universe with a cyclic expansion/contraction history and the two real positive roots a_min and a_max in Eqs (33), (34) define the approximate minimum and maximum scale factors of the Universe. Consequently, the maximum redshift is

$$z_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{1}{a_{\mathrm{m}\mathrm{i}\mathrm{n}}}-1.$$ (35)

Results

Parameters for modelling

For calculating the cosmic dynamics of the Universe, we need observations of the mass opacity of intergalactic dust grains, fraction of the dust mass to the total mass, the galaxy luminosity density, and the expansion rate and curvature of the Universe at the present time.

The size $d$ of dust grains is in the range of 0.01 – 0.2 μm with a power-law distribution $d^{-q}$ with q = 3.5 [68], but silicate and carbonaceous grains dominating the scattering are typically with d ∼ 0.1 μm [38]. The grains of size 0.07 μm ≤ d ≤ 0.2 μm are also ejected to the IGM most effectively [69]. The grains form complicate fluffy aggregates, which are often elongated or needle-shaped [70]. Considering the density of carbonaceous material ρ ∼ 2.2 g cm⁻³ and the silicate density ρ ∼ 3.8 g cm⁻³ [38], the average density of porous dust grains is ∼ 2 g cm⁻³ or less [71]. Consequently, the standard dust models [72] predict the wavelength-dependent mass opacity. For example, Draine [37] reports the mass opacity of 855 m²kg⁻¹ at the V-band and the mass opacity of 402 m²kg⁻¹ for a wavelength of 1 μm, which corresponds to the maximum intensity of the EBL. Since grains in the dust models are assumed to be of a spherical shape, the real mean cross-section of dust grains can be significantly different from theory. This effect can be included by introducing parameter ε as the ratio of the spheroidal to spherical dust grain cross-sections.

The fraction δ of the dust mass to the total mass is roughly estimated by measurements of the so-called dust-to-gas mass ratio in galaxies. Bohlin et al. [73] found that the ratio of the total hydrogen column density to the colour excess E(B-V) is roughly constant with value 5.8 × 10²¹ cm⁻² mag^-1. By fitting the extinction curve with various mixtures of the silicate and carbonaceous dust grains, it is possible to find the total volumes V_S and V_G of carbonaceous and silicate grain populations per H atom. For example, Weingartner & Draine [72] report for the silicate grains (their case B) V_S = 3.9 × 10^-27 cm³ H^-1 and for the carbonaceous grains V_G = 2.3 × 10^-27 cm³ H^-1, provided R_V = 3.1. This yields the dust-to-gas mass ratio of 0.01 for the Milky Way. A similar or lower value is presented also by other authors and for other galaxies [36], [74], [75], [76], [77], [78]. Here, the fraction δ of the dust mass to the total mass is assumed to vary from 0.3 % to 1.0 %.

The galaxy luminosity density j is determined from the Schechter function [79]. It has been measured by large surveys 2dFGRS [80], SDSS [81] or CS [82]. The luminosity function in the R-band was estimated at z = 0 to be (2.6 ± 0.3) × 10⁸h L_ʘ Mpc^-3 for the SDSS data [81] and (1.9 ± 0.6) × 10⁸h L_ʘ Mpc^-3 for the CS data [82]. The Hubble constant H₀ is measured by methods based on the Sunyaev-Zel’dovich effect [83], gravitational lensing [84], gravitational waves [85] or acoustic peaks in the CMB spectrum provided by Planck Collaboration et al. [15], and they yield values mostly ranging between 66 and 74 km s⁻¹ Mpc^-1. Here, we use an estimate H₀ = 69.8 ± 2.5 km s⁻¹ Mpc^-1 obtained by Freedman et al. [86] using the SNe Ia with a red giant branch calibration.

Assuming the ΛCDM model, the CMB and BAO observations indicate a nearly flat Universe [15]. This method is not, however, model independent and ignores an impact of cosmic dust on the CMB. A model-independent method proposed by Clarkson et al. [87] is based on reconstructing the comoving distances by Hubble parameter data and comparing with the luminosity distances or the angular diameter distances [88]. The cosmic curvature can also be constrained using strongly gravitational lensed SNe Ia [89] and using lensing time delays and gravitational waves [90]. The authors report the curvature term Ω_k ranging between −0.3 to −0.1 indicating a closed universe, not significantly departing from flat geometry.

Numerical results

Estimating the required cosmological parameters from observations, we calculate the upper and lower limits of the volume of the Universe and the evolution of the Hubble parameter with time using (25), (26), (27), (28), (29). The mass density of the Universe higher than the critical density is considered, and subsequently Ω_m is higher than 1. The Hubble constant is H₀ = 69.8 km s⁻¹ Mpc^-1, taken from Freedman et al. [86]. The mass opacity κ₀ of 402 m²kg⁻¹ is taken from table 4 of Draine [37]; which characterizes the opacity of dust at a wavelength of 1 μm. The mass opacity is further multiplied by factor ε ranging between 10 and 20 and reflecting that dust grains are not spherical but rather prolate spheroids having a larger effective cross-section. The fraction of the cosmic dust mass to the total mass δ ranges from 0.3 % to 1.0 %. The luminosity density is j₀ = 2.6 × 10⁸h L_ʘ Mpc^-3 [81]. The exponent β of the power-law decay of the radiation-absorption term in Eq. (24) ranges from 6.5 to 6.7. The results of modelling are summarized in Table 1.

Table 1.

Maximum redshift and scale factor in the cyclic model of the opaque universe.

Model	Input parameters						Output
	δ (%)	ε	Ωm	Ωa	β	Ωk	amax	zmax
A	1.0	20	1.2	−8.3x10-5	6.7	−0.200	6.0	12.2
B	0.3	10	1.2	−1.2x10-5	6.5	−0.200	6.0	25.7
C	0.7	15	1.2	−4.3x10-5	6.6	−0.200	6.0	16.1
D	0.7	15	1.1	−4.3x10-5	6.6	−0.100	11.0	15.7
E	0.7	15	1.3	−4.3x10-5	6.6	−0.300	4.3	16.5

Note: Parameter δ is the fraction of the cosmic dust mass to the total mass, ε is the ratio of the spheroidal to spherical dust grain cross-sections, Ω_m, Ω_a, and Ω_k are the matter, radiation-absorption and curvature terms, β is the power-law exponent describing a decay of the radiation-absorption term with the scale factor a in Eq. (25), and a_max and z_max are the maximum scale factor and redshift, respectively. Models A, B and C predict low, high and optimum values of z_max. Models E, D and C predict low, high and optimum values of a_max.

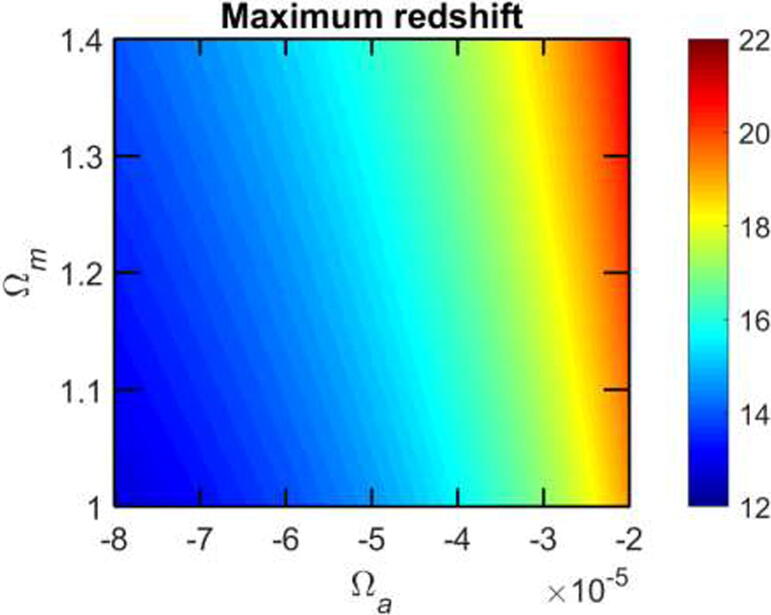
As seen in Fig. 3, the maximum redshift of the Universe depends on Ω_m and Ω_a, and ranges from 12 to 22 for β = 6.6. In contrast to a_min depending on both Ω_m and Ω_a, the maximum scale factor a_max of the Universe depends primarily on Ω_k only, see Eq. (34). The limiting value is Ω_k = 0, when a_max is infinite. For Ω_k = −0.1, −0.2, −0.3 and −0.5, the scale factor a_max is 11.0, 6.0, 4.3 and 3.0, respectively.

Fig. 3.

Maximum redshift as a function of Ω_m and Ω_a.

The history of the Hubble parameter, H(z), and its evolution in future, H(a), calculated by Eq. (25) is shown in Fig. 4 for five scenarios summarized in Table 1. The form of H(z) in Fig. 4a is controlled by Ω_a and the power-law exponent β, while the form of H(a) in Fig. 4b is controlled by Ω_k. The Hubble parameter H(z) in Fig. 4a increases with redshift up to its maximum that is lower than 300 km s⁻¹ Mpc^-1. After that the function rapidly decreases to zero. The drop of H(z) is due to a fast increase of light attenuation producing strong repulsive forces at high redshift. The maximum redshift z_max predicted by the considered scenarios ranges from 12 to 26. The maximum redshift for the optimum model is about 16. For future epochs, function H(a) in Fig. 4b is predicted to monotonously decrease to zero. The rate of decrease is controlled just by gravitational forces; the repulsive forces originating in light attenuation are negligible. The maximum scale factor a_max depends on the curvature of the Universe. Plausible values of a_max are in the range between 4 (${\mathrm{\Omega }}_k=-0.3$) to 11 (${\mathrm{\Omega }}_k=-0.1$).

Fig. 4.

The evolution of the Hubble parameter with redshift in the past and with the scale factor in future (in km s⁻¹ Mpc^-1). (a) The blue dashed, dotted and solid lines show Models A, B and C in Table 1. (b) The blue solid, dashed, and dotted lines show Models C, D and E in Table 1. The black dotted lines mark the predicted maximum redshifts (a) and maximum scale factors (b) for the models considered. The red solid line shows the flat ΛCDM model described by Eq. (11) with H₀ = 69.8 km s⁻¹ Mpc^-1, taken from Freedman et al. [86] and with Ω_m = 0.3 and Ω_Λ = 0.7.

For a comparison, Fig. 4 (red line) shows the Hubble parameter H(a) for the standard ΛCDM model [15], which is described by Eq. (11) with Ω_m = 0.3 and Ω_Λ = 0.7. The behaviour of H(a) and H(z) for the standard ΛCDM model is quite different from that for the cyclic model of the opaque universe. The Hubble parameter H(z) raises with redshift very steeply (Fig. 4a, red line) and goes to infinity when approaching the initial singularity with $z\to \infty$. For future epochs, the model predicts no maximum scale factor (Fig. 4b, red line), because it is continuously expanding for all times (flat universe).

The distance-redshift relation of the proposed cyclic model of the Universe is quite different from the standard ΛCDM model (see Fig. 5). In both models, the comoving distance monotonously increases with redshift, but the redshift can go possibly to 1000 or more in the standard model, while the maximum redshift is likely 15–17 in the optimum cyclic model. The increase of distance with redshift is remarkably steeper for the cyclic model than for the ΛCDM model.

Fig. 5.

Comoving distance as a function of redshift z. The blue dashed, dotted and solid lines show Models A, B and C in Table 1. The black dotted lines mark the predicted maximum redshifts for the models considered. The red solid line shows the flat ΛCDM model described by Eq. (11) with H₀ = 69.8 km s⁻¹ Mpc^-1, taken from Freedman et al. [86] and with Ω_m = 0.3 and Ω_Λ = 0.7.

Discussion

The radiation pressure as a cosmological force acting against the gravity has not been proposed yet, even though its role is well known in the stellar dynamics [[91], [92]], in supernovae stellar winds and in galactic wind dynamics [56]. The key role of the radiation pressure in cosmic dynamics was overlooked, because the Universe was assumed to be transparent. In the opaque universe model, the role of radiation pressure is essential. Since the cosmic opacity and luminosity density steeply rise with redshift, the radiation pressure becomes significant at high redshifts and stop the universe contraction driven by gravity. Small dust grains will probably be more important in this process, because the mass opacity responsible for the radiation pressure rapidly increases with decreasing size of grains. Similarly, the emission of high-energy photons will affect the universe dynamics more distinctly than the CMB, because they are absorbed more efficiently compared to the CMB photons, which are absorbed by dust very weakly.

Hence, the cyclic evolution of the Universe with repeating epochs of expansion and contraction might be produced by imbalance of gravitational forces and radiation pressure. If the global stellar and dust masses are independent of time with minor fluctuations only, the evolution of the Universe will be stationary. The age of the Universe is unconstrained and galaxies can be observed at any redshift less than z_max. The only limitation is high cosmic opacity, which can dim light of the most distant galaxies. Hypothetically, it could be possible to observe galaxies from previous cycle/cycles, if their distance is higher than that corresponding to z_max ∼ 15–17. However, the identification of galaxies from the previous cycles will not be easy, because distance will not be a unique function of redshift.

Obviously, a role of recycling processes is more important in the cyclic cosmological model than in the BB theory. The processes of formation/destruction of galaxies should play a central role in this model [[93], [94]]. Similarly, the formation of metals in nuclear fusion and their destruction should be balanced in the long term. For example, quasars might be recycling engines having an enormous destructive power. Indications supporting the recycling scenario are provided by studies of metallicity with cosmic time, when observations do not show convincing evidence of the metallicity evolution. By contrast, they point to an ambient metal pollution of the intergalactic medium in the early Universe [[47], [95]] and a failure to detect a pristine material with no metals at high redshifts.

Conclusions

The presented cosmological equations are novel in two basic aspects: (1) They incorporate light-matter interactions into the Friedmann equations similarly as done by Vavryčuk [106], and (2) they are based on the conformal FLRW metric, because the standard FLRW metric used in Vavryčuk [106] appeared to be inconsistent with observations of the cosmological redshift [34]. The model predicts a cyclic expansion/contraction evolution of the Universe within a limited range of scale factors with no initial singularity. The model avoids dark energy and removes some other tensions of the standard ΛCDM model, namely:

The model does not limit the age of stars in the Universe, being consistent with observations of a nearby star HD 140283 [14] with age of 14.46 ± 0.31 Gyr. By contrast, the existence of this very old star is in conflict with the age of the Universe, 13.80 ± 0.02 Gyr, determined from the interpretation of the CMB as relic radiation of the Big Bang [15]. The presented model predicts the existence of very old mature galaxies at high redshifts. The existence of mature galaxies in the early Universe was confirmed, for example, by Watson et al. [16] who analyzed observations of the Atacama Large Millimetre Array (ALMA) and revealed a galaxy at z > 7 highly evolved with a large stellar mass and heavily enriched in dust. Similarly, Laporte et al. [17] analyzed a galaxy at z ∼ 8 with a stellar mass of ∼ 2x10⁹ M_ʘ and a dust mass of ∼ 6x10⁶ M_ʘ. A large amount of dust is reported by Venemans et al. [96] for a quasar at z = 7.5 in the interstellar medium of its host galaxy. In addition, a remarkably bright galaxy at z ∼ 11 was found by Oesch et al. [97] and a significant increase in the number of galaxies for 8.5 < z < 12 was reported by Ellis et al. [98].

The model is capable to explain the SNe Ia dimming discovered by Riess et al. [9] and Perlmutter et al. [10] without introducing dark energy as the hypothetical energy of vacuum [34], which is difficult to explain under the quantum field theory [99]. Moreover, dark energy models predict different speeds of light and of gravitational waves [12], [13]. However, observations of the binary neutron star merger GW170817 and its electromagnetic counterparts proved that both speeds coincide.

The model avoids a puzzle, how the CMB as relic radiation could survive the whole history of the Universe without being distorted [100]. Also, why non-Gaussianity [[101], [102]] and a violation of statistical isotropy and scale invariance are observed in the CMB. Instead, theory of the CMB as thermal radiation of cosmic dust predicts the CMB temperature with the accuracy of 2% [39]. Anisotropies in the CMB temperature are satisfactorily explained by the presence of large-scale structures in the Universe and anisotropies in the CMB polarization are caused by dust grains aligned by magnetic fields around clusters and voids.

In summary, the BB theory and the cyclic cosmological model are essentially different concepts of the Universe. In contrast to the BB theory, the cyclic model of the eternal universe with high-redshift cosmic opacity is based on the standard physics, it is less speculative and predicts current observations comparably well with no free parameters such as dark energy or dark matter. Nevertheless, this model opens other questions, which need to be resolved. For example, the origins and role of recycling processes of stars, galaxies and other objects in the Universe should be clarified in detail. Essential progress in understanding the evolution of the Universe will bring the James Webb Space Telescope launched on December 25, 2021, which will be focused on observations of the early Universe [103], [104], [105]. This telescope can probe high-redshift galaxy populations and properties of the IGM including the distribution of the galactic and intergalactic dust at high redshifts. In particular, information on the high-redshift cosmic opacity will be the key for a more accurate modelling of the evolution of the Universe in future studies.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Considering light-matter interactions in Einstein equations of general relativity

The Einstein equations of general relativity read

$$G^{\mu \nu }+\mathrm{\Lambda }{\mathrm{g}}^{\mu \nu }=\frac{8\pi G}{c^4}{T}^{\mu \nu },$$ (A1)

where G^μν is the Einstein tensor, Λ is the cosmological constant, g^μν is the metric tensor, G is the gravitational constant, c is the speed of light, at present and T^μν is the energy–momentum tensor. The Einstein tensor G^μν describes the curvature of the spacetime associated with gravity produced by the presence of matter and/or energy described by the energy–momentum tensor T^μν. The cosmological term was introduced into the equation by Einstein as a non-gravitational term, which acts against the gravity.

Since ${G^{\mu \nu }}_{;\nu }=0$ and ${{\mathrm{\Lambda }g}^{\mu \nu }}_{;\nu }=0$, we get

$${T^{\mu \nu }}_{;\nu }=0,$$ (A2)

which expresses the energy–momentum conservation law. Obviously, the validity of the field equation (A1) is kept, if the cosmological term $\mathrm{\Lambda }{\mathrm{g}}^{\mu \nu }$ is substituted by a more general term $\frac{1}{c^4}{\mathrm{\Lambda }}^{\mu \nu }$,

$$G^{\mu \nu }+\frac{1}{c^4}{\mathrm{\Lambda }}^{\mu \nu }=\frac{8\pi G}{c^4}{T}^{\mu \nu },$$ (A3)

for which

$${{\mathrm{\Lambda }}^{\mu \nu }}_{;\nu }=0.$$ (A4)

Eq. (A4) expresses the energy–momentum conservation law for the non-gravitational field described by tensor ${\mathrm{\Lambda }}^{\mu \nu }$ and produced by the light-matter interactions. Formally, tensor ${\mathrm{\Lambda }}^{\mu \nu }$ can be considered as a part of the energy–momentum tensor T^μν, but it is useful to treat it separately, in order to emphasize its non-gravitational nature similarly as done by Einstein in the case of the original cosmological constant Λ. In this way, tensor T^μν is allocated for gravitational effects of mass and other physical fields only, but it does not reflect other non-gravitational forces. Obviously, both approaches are mathematically equivalent, because if ${\mathrm{\Lambda }}^{\mu \nu }$ is considered as a part of T^μν, matching the field equations for a weak non-relativistic field leads finally to decoupling of ${\mathrm{\Lambda }}^{\mu \nu }$ and canceling the factor $\frac{8\pi G}{c^4}$ standing at the term with ${\mathrm{\Lambda }}^{\mu \nu }$.

For a perfect isotropic fluid, the energy–momentum tensor T^μν reads

$$T^{\mu \nu }=\left(\rho +\frac{p}{c^2}\right)U^{\mu }{U}^{\nu }+p{g}^{\mu \nu },$$ (A5)

where ρ is the density, p is the pressure, and $U^{\mu }$ is the four-velocity. In analogy to Eq. (A5), the isotropic cosmological tensor ${\mathrm{\Lambda }}^{\mu \nu }$ can be described as

$${\mathrm{\Lambda }}^{\mu \nu }=\left({\rho }_{\mathrm{\Lambda }}+\frac{p_{\mathrm{\Lambda }}}{c^2}\right)U^{\mu }{U}^{\nu }+p_{\mathrm{\Lambda }}{g}^{\mu \nu },$$ (A6)

where ${\rho }_{\mathrm{\Lambda }}$ is the density and $p_{\mathrm{\Lambda }}$ is the pressure of the non-gravitational field produced by the light-matter interaction. Assuming the weak-field non-relativistic approximation, Eq. (A3) should yield the Poisson equation (18), which can be split into the equations for the gravitational potential ${\varphi }_{\mathrm{G}}$ and for the potential of the light-matter interaction ${\varphi }_{\mathrm{\Lambda }}$ as follows

$$\mathrm{\Delta }{\varphi }_{\mathrm{G}}=4\pi G\rho ,$$ (A7)

$$\mathrm{\Delta }{\varphi }_{\mathrm{\Lambda }}=-\frac{\overline{\kappa }j}{v}.$$ (A8)

Taking into account that ${\mathrm{\Lambda }}^{00}={\rho }_{\mathrm{\Lambda }}{c}^2$ and matching Eq. (A3) in the weak-field non-relativistic approximation with Eq. (A8), we get

$${\rho }_{\mathrm{\Lambda }}=\frac{2\overline{\kappa }j}{v}.$$ (A9)

Introducing the standard FLRW metric of the space defined by its Gaussian curvature k and by the scale factor a(t) [64], [65]

$$-c^2{d\tau }^2=-c^2{\mathit{dt}}^2+a^2\left(t\right)\left(\frac{{\mathit{dr}}^2}{1-k{r}^2}+r^2{d\mathrm{\Omega }}^2\right)$$ (A10)

into Eqs (A3), (A5), (A6), we get a modified form of the Friedmann equations, which involve effects of the non-gravitational field ${\mathrm{\Lambda }}^{\mu \nu }$

$${\left(\frac{\dot{a}}{a}\right)}^2=\frac{8}{3}\pi G\rho -\frac{1}{3}{\rho }_{\mathrm{\Lambda }}-\frac{k{c}^2}{a^2},$$ (A11)

$$\frac{\ddot{a}}{a}=-\frac{4}{3}\pi G\left(\rho +\frac{3p}{c^2}\right)+\frac{1}{6}\left({\rho }_{\mathrm{\Lambda }}+\frac{3p_{\mathrm{\Lambda }}}{c^2}\right).$$ (A12)

Considering $\rho$ and ${\rho }_{\mathrm{\Lambda }}$ depending on the scale factor a(t) as $\rho ={\rho }_0{a}^{-\alpha }$ and ${\rho }_{\mathrm{\Lambda }}={\rho }_{\mathrm{\Lambda }0}{a}^{-\beta }$, the equations of state for $T^{\mu \nu }$ and ${\mathrm{\Lambda }}^{\mu \nu }$ yield

$$p=\frac{\alpha -3}{3}{c}^2\rho ,$$ (A13)

$$p_{\mathrm{\Lambda }}=\frac{\beta -3}{3}{c}^2{\rho }_{\mathrm{\Lambda }},$$ (A14)

and Eq. (A12) reads

$$\frac{\ddot{a}}{a}=-\frac{4}{3}\pi G\left(\alpha -2\right)\rho +\frac{\beta -2}{6}{\rho }_{\mathrm{\Lambda }}.$$ (A15)

Specifying Eq. (A15) for the pressureless fluid (α = 3) and taking into account Eqs (A9) and (A14), the final form of the standard Friedmann equations for the opaque universe is expressed as

$${\left(\frac{\dot{a}}{a}\right)}^2=\frac{8}{3}\pi G\rho -\frac{2}{3}\frac{\overline{\kappa }j}{v}-\frac{k{c}^2}{a^2},$$ (A16)

$$\frac{\ddot{a}}{a}=-\frac{4}{3}\pi G\rho +\frac{\beta -2}{3}\frac{\overline{\kappa }j}{v}.$$ (A17)