Abstract
Nowadays, due to stricter pollution standards, more attention has been focused on pollutants emitted from cars. As a very dangerous pollutant, NOx has always triggered the sensitivity of the related organizations. In the process of developing and designing the engine, estimating the amount of this pollutant is of great importance to reduce future expenses. Calculating the amount of this pollutant has usually been complicated and prone to error. In the present paper, neural networks have been used to find the coefficients of correcting NOx calculation. The Zeldovich method calculated the value of NOx with 20% error. By applying the progressive neural network and correcting the equation coefficient, this value decreased. The related model has been validated with other fuel equivalence ratios. The neural network model has fitted the experimental points with a convergence ratio of 0.99 and a squared error of 0.0019. Finally, the value of NOx anticipated by the neural network has been calculated and validated according to empirical data by applying maximum genetic algorithm. The maximum point for the fuel composed of 20% hydrogen and 80% methane occurred in the equivalence ratio of 0.9; and the maximum point for the fuel composed of 40% hydrogen occurred in equivalence ratio of 0.92. The consistency of the model findings with the empirical data shows the potential of the neural network in anticipating the amount of NOx.
Keywords: Internal combustion engine, NOx, Neural network, Genetic algorithm
1. Introduction
The global determination for reducing the pollutants of engines and passing strict rules regarding pollutants is increasing. In this regard, an exact estimation of the amount of pollutants emitted by engines, especially NOx, is crucial. Different methods have been introduced for simulating the cycle of internal combustion engines and the amount of emitted pollutants. Karim et al. conducted many studies regarding the issue [1]. The majority of his studies have been focused on gas fueled engines [2]. In recent years, extensive researches have been conducted on hybrid fuel [3]. Shrestha and Karim studied the impact of adding hydrogen to methane in spark ignition engine [4]. Bauer et al. conducted extensive studies in this regard [5]. They conducted their research with four different combinations of methane and hydrogen (60%, 40%, 20%, and 0%) on the CFR engine and in two different periods. Their model had extensive errors with regard to calculating the pollutants. Polasek et al. studied NOx Pollutant in a hydrogen fueled engine using a two-zone model [6]. Ma et al. also optimized a hydrogen engine using a zero-dimensional model [7]. Based on empirical values they accessed, they fitted a vibe function on these values. Although their model was successful in simulating operating values of the engine, it was not able to exactly calculate the pollutants.
In 2012, Li et al. introduced a neural network model for anticipating the NOx of the engine based on the flame velocity [8]. Their model was able to correct the results of the NOx of the engine. Their neural network model was able to fit all of the experimental points. In 2018, Tan et al. also proposed a neural network model for anticipating the amount of NOx pollutant in the engines [9]. Their model was able to anticipate the NOx of the engine. Their model could anticipate the pollutants with great accuracy and showed the advantage of using the neural network.
Novel biodiesel was produced from Water Hyacinth by Jain et al. [10]. The twin influence of injection timing and load on the performance, exergy, and emission analysis for a Water Hyacinth (Eichhornia Crassipes) biodiesel-run diesel engine was investigated [11]. The highest BTE of 26.79% was obtained at IT of 20° bTDC for biodiesel mode and the lowest emission was measured at IT at 20° bTDC for biodiesel mode.
In 2019, Duan et al. studied spark ignition engine with different ratios of the combination of methane and hydrogen by applying a two-zone model [12]. Shi et al. conducted another model in which they focused on the pollutants of the engine in situation of hybrid fuel [13]. In this research, the produced pollutants have been studied in different equivalence ratios and different combinations of methane and hydrogen. They have used Woschni method for modeling heat transfer; they have also used the vibe function for modeling energy release rate. The amount of the pollutants produced is studied based on Crankshaft angle. In this research, in addition to this issue, the rate of the pollutants production has been also studied on the basis of temperature; they have also discussed the impact of temperature on the pollutants. But their model was prone to 20% error in calculating the NOx pollutant.
In the following sections of this paper, the adverse pollutants produced in the process of the gasoline engine combustion fueled with a combination of methane and hydrogen will be studied; This research introduces a neural network model for improving the estimation of NOx amount produced in the engine with a hybrid fuel of methane and hydrogen.
2. Methodology
2.1. Nitrogen oxides
A study has been conducted on CFR single cylinder engine with the characteristics summarized in Table 1 and its schematic in Fig. 1. Programming and simulating the engine has been conducted by MATLAB application [12]. The initial condition of the engine consists of an input air temperature of 300 K and a pressure of 1 bar. Due to the initial condition, the study has been conducted in full bar condition.
Table 1.
Geometric characteristics of the engine [8].
| Characteristic | Abbreviation | Value |
|---|---|---|
| The diameter of the cylinder | B | 83 mm |
| Piston stroke | L | 114 mm |
| The length of piston handle | l | 254 mm |
| The volume of total displacement | Vd | 0.62 L |
| Air valve closing time | IVC | 34 aBDC |
| Air valve opening time | EVO | 40 bBDC |
| The number of valves | – | 2 |
| The ratio of compression | rc | variable |
Fig. 1.
Schematic of the engine.
Chemical composition of unburned gas mixture and the input to the cylinder is based on the air only (21% oxygen and 79% Nitrogen); the hybrid fuel consists of methane and hydrogen gases [14]. In order to modeling this process and adding hydrogen, the raw material equation has been calculated based on the fixed and variable value of hydrogen indicated in the following equation (1); for determining the products of burning reaction an eleven-type chemical equilibrium combination has been created as equation (1) [12].
| (1) |
For calculating the values of n1 … n11, eleven equations are needed. Four equations are derived from the law of conservation of mass related to four atoms: H, N, C, O. Due to the fact that we consider the reactional products in equilibrium, seven other equations are derived from the fixed relations of equilibrium. These seven equilibrium reactions are as followed as equation (2):
| (2) |
In the fixed equations of equilibrium mentioned above, Xi, the Mole fraction each part equals to nj/Σ11j = 1 nj. Each kpi is just a temperature function, which has been calculated by polynomial of the fixed values of equilibrium based on temperature. The exhaust gases can have 2000 ppm nitrogen oxides [15], most of which consist of nitrogen oxide (NO); There is also a little amount of nitrogen dioxide (NO2) and other combinations of nitrogen and oxygen. All of the combinations of nitrogen oxides are categorized under NOx abbreviation in which x shows the related number. NOx is an inappropriate pollutant, therefore the regulations limiting its use is getting stricter. NOx reacts under the pressure of the environment which leads to ozone creation that is one of the main sources of Photochemical smog. This phenomenon is one of the main problems in many metropolises all over the world [16]. Smog is created through photochemical reaction of exhaust gases from engines and the atmosphere in the vicinity of the sunlight. Due to the importance of nitrogen oxides in air pollution, the mechanism of their production needs to be scrutinized.
2.2. Thermal mechanism or Zeldovich
Effects of ternary blends on the engine's performance and emission were explored by Ref. [17]. The blend of algal biodiesel and diesel was fortified with diethyl ether. The Bayesian approach was used to optimize the hyperparameters of GPR and A robust prediction model (R > 0.9746) to simulate the engine's performance was developed.
Thermal kinetic or Zeldovich mechanism is important in high temperature zones and for an extensive equilibrium ratio [18]. Thermal or Zeldovich mechanism consists of two chain reactions as shown in 3 [19]:
| (3) |
To which the following reaction can be added as 4:
| (4) |
Which is called developed Zeldovich mechanism. Generally, this mechanism will couple to the fuel combustion mechanism through the chemical components of O2, O, and OH. If the process of fuel combustion completes before producing NO, these two mechanisms function separately [20]. In this case, if the time scales are big enough, we can assume that the amount of density for N2, O2, O, and OH has been in balance and the density of N will be calculated in the permanent condition; these assumptions facilitates the resolve of producing NO. Zeldovich mechanism is severely dependent on the temperature and usually the thermal mechanism is important only if the temperature is bigger than 1700 k [21]. Therefore, this mechanism is applied after the creation of the flame.
NO can complete a reaction in different ways and produce NO2 as reaction (5) [22]:
| (5) |
Atmospheric nitrogen exists in low temperatures in the form of Stable diatom molecule and there are only a few amounts of nitrogen oxides in the atmosphere. But in very high temperatures which occur in engine combustion chamber, an amount of two-atom nitrogen decomposes to single-atom nitrogen which possesses the capability of reaction (6).
| (6) |
Chemical equilibrium for the above-mentioned equation is strongly dependent on the temperature and much greater amount of N – which can be stored in the engine – will be produced within the temperature range of 2500–3000 k. Other gasses which are stable in lower temperatures but reaction-prone in higher temperatures and participate in the composition of NOx, include oxygen and steam which break as follows reaction (7) [12]:
| (7) |
Fixed equilibrium reactions show that as the combustion chamber reaches higher temperatures, the reaction is more likely to occur from left to right. The higher the temperature of combustion reaction, more diatomic nitrogen will decompose to single-atom nitrogen and more NOx will be produced. In lower temperatures less NOx will be created.
Developed Zeldovich mechanism has been used for predicting the density of NOx. For this to happen and according to the explanations mentioned above and with the assumption of the stable situation as shown in equation (8) [12,23]:
| (8) |
Furthermore, assuming the values of equilibrium density for N2, O2, O, and OH, Zeldovich mechanism will calculate the rate of the changes of nitrogen oxide mole as explained below as equation (9) [24,25]:
| (9) |
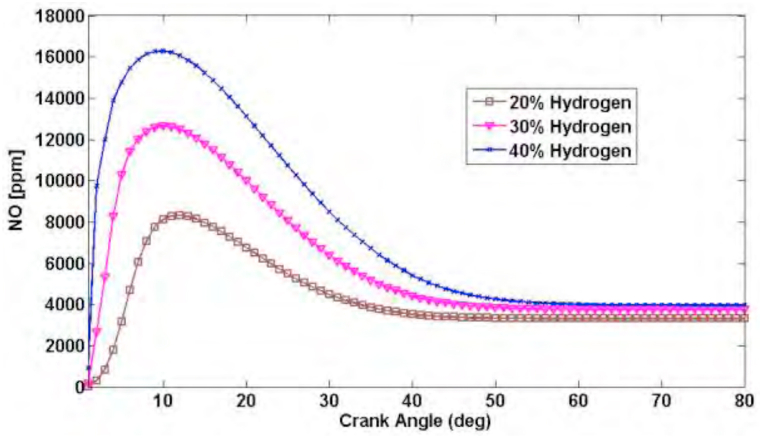
Fig. 2 shows the diagram of the changes of nitrogen oxide production during the cycle of three different blends. According to the diagram, with the increase in the percentage of the hydrogen, more nitrogen oxide will be produced. This difference is more significant on the peak of the diagram but in the end of expansion phase and the opening of the valve, in which the output chemical types are considered as a pollutant, this difference is lower.
Fig. 2.
Diagram of nitrogen oxide production during the cycle of the three different blends [26] (N = 900 = 8.5; φ = 1).
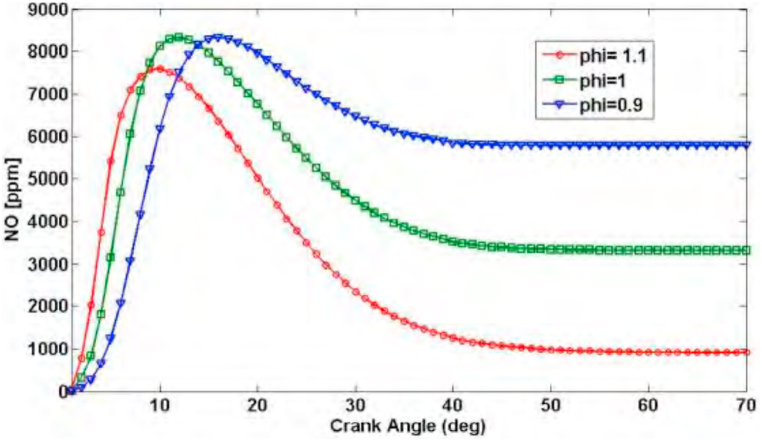
Fig. 3 shows the changes of nitrogen oxide production during the cycle for three equivalence ratios of one type of fuel. It is clear that the production rate of this chemical type is severely dependent on equivalence ratio.
Fig. 3.
Diagram of nitrogen oxide production during the cycle for three different equivalence ratios for the blend consisting of 20% hydrogen [27] (N = 900 ; = 8.5).
Fig. 4 also shows the diagram of changes in nitrogen oxide production on the basis of equivalence ratio which can be compared to empirical data. In this case, the model has predicted the amount of this pollutant with great error percentage.
Fig. 4.
Diagram of nitrogen oxide production according to the equivalence ratio and its comparison with empirical data [28] (N = 700 = 9).
The two diagrams above indicate that up to the equivalence ratio of 0.9 the amount of this pollutant increases and above that the amount of the pollutant decreases. Although the maximum temperature of the flame will occur at the ratio of air to stoichiometric fuel (φ = 1), but the maximum amount of NOx will be produced at the equivalence ratio of 90%. In this situation the flame temperature is extremely high; in addition, there is an extra amount of oxygen which combines with nitrogen to produce different oxides.
3. Results and discussion
3.1. The neural network model for predicting NOx
The influence of engine load, gaseous fuel flow rate, and injection advance on the combustion parameters of a diesel engine are investigated and optimized in Ref. [29]. At optimal operating settings, the engine's performance and combustion output were 21.34% brake thermal efficiency, 3.78 MJ/kWh brake specific energy consumption, 65.76% diesel savings, 84.37 ppm carbon monoxide, 101.7 ppm hydrocarbon and 303 ppm oxides of nitrogen (NOx). The usage of oxyhydrogen improved combustion, resulting in fewer total engine emissions. Except for NOx, the use of oxyhydrogen improved combustion and reduced engine emissions.
In most cases, researchers seek to find an equation which is consistent with empirical data by gathering laboratory data. In these cases, the mathematical concepts of fitting are raised. In many cases, fitting polynomials with the degree of 2 and 3 are not effective. In such cases, the neural networks are raised. For explaining a linear equation, if we introduce the slope and width of the equation by weight and bias and call the linear equation a neuron, then the only remaining task is to determine the weight and bias for adaptation to the data. Determining the equation for fitting the data and determining the passive coefficients of that equation will be the discussion topic of neural networks. In this study, the results found in diagram 3 have been amended by presenting a neural network model. The neural network used in this research is two-layered feed forward network. Such application is limited to the conventional compression-ignition and spark-ignition reciprocating engines.
The input of the neural network is the equivalence ratio of fuel and the percentage of hydrogen in the fuel. In fact, the input of the neural network is a matrix. In general, the model of mass neuron is expressed as follows equation (10):
| (10) |
In the above equations, p is the input, w stands for weight, b stands for bias, f stands for convert function, n stands for the total inputs and a stands for the output as 11 and 12.
| (11) |
| (12) |
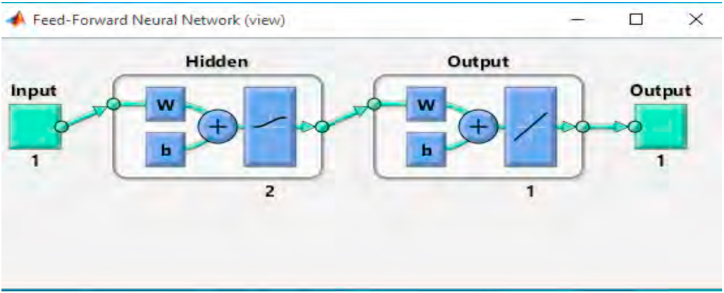
According to the mathematical theorem, for fitting an incessant function, a two-layered feed forward neural network is sufficient. This means that the output of the first layer will be attached to the second layer and this process goes on. It is necessary to mention that the number of the second layer's neuron must equal to the outputs because the output of this layer equals to the estimated amount of NOx. The hidden layers are the layers between the input and the output. Two hidden layers have been applied for solving the question using MATLAB Application and traingd network training model. The graphic output of the network is shown in Fig. 5.
Fig. 5.
Schematic of the neural network extracted from MATLAB Application.
The following diagram (Fig. 6) shows the performance of neural network in one iteration. P is the fuel equivalence ratio for different percentages of hydrogen which is considered as the network input. The output of the network is the amount of nitrogen oxide pollutant. The first empirical data of diagram 3 has been selected as the input.
Fig. 6.
Performance of neural network in one iteration.
The network starts with two neurons in the first layer. The first layer has been shown by full blue lines and the second layer has been shown by purple dash line. W1,1 stands for the weight of the first neuron in the first layer with the first input of equivalence ratio and w1,2 stands for the weight of second neuron in the second layer with the same equivalence ratio. B1 and b2 stand for the bias of the first and second neuron respectively. In the first step, 0.48 and 0.13 have been selected as the values of weight and bias accidently. In the next iterations, these values will be amended towards the empirical answers by the application. According to the above picture and equation (13), the first and second neuron functions have been selected based on the tangent logarithm function known as sigmoid function. The functions used in the neurons of hidden layers are usually tangent or logarithm. The output of these two neurons that acts according to equation (14) will be used as the input of the second layer [30,31]. Equations (15), (16)) show the weight of the first neuron and the bias of the first neuron respectively.
| (13) |
| (14) |
| (15) |
| (16) |
Superscript (1) in the above equation refers to the first layer which consists of two neurons. The weight of the second layer's neuron equals to the matrix of the outputs of the first layer's weights. The bias of the first layer's neuron will be selected accidently. By applying stair linear function for the second layer's neuron, NOx will be calculated according to Fig. 5 and equation (17). This value (a2) is in fact the corresponding width of the first equivalence ratio in diagram (3) as shown in equations (17), (18)).
| (17) |
| (18) |
W1,1 refers to the weight of the first layer resulted from the first neuron and W1,2 refers to the weight resulted from the second neuron of the same layer. This matrix is the weight of the second layer's neuron in the first iteration. Superscript (2) refers to the second layer. The input of second layer is the result of the first layer (a1). Therefore, the result of the second layer in which the amount of pollutant is specified in the equivalence ratio, will be achieved and compared with the empirical data. The above items will iterate until the amount of required empirical data is achieved in each iteration, the new weights and biases will be calculated and applied to the equation until the required error is achieved. The number of iterations equals to 100.000. This process will be applied to all point of fig. (4).
In summary, the neural network receives the value of equivalence ratio and then by using the accidental weights and biases and applying sigmoid function in the neurons of the first layer and then applying step function of the result of the first layer to the second layer, extracts the amount of pollutant and with plenty of iteration and amending the weights and biases, goes towards the right answer.
The result of the designed neural network for this issue has been shown in diagram (Fig. 7) based on 40% hydrogen. There is an acceptable consistency between the network function and empirical data. The comparison between this diagram and the diagram designed for the output of Zeldovich model for calculating NOx shows to what extent the neural network has been able to improve this estimation. The difference between these two estimations could be applied as a correcting coefficient in Zeldovich model.
Fig. 7.
Diagram of NOx production on the basis of equivalence ratio with neural network.
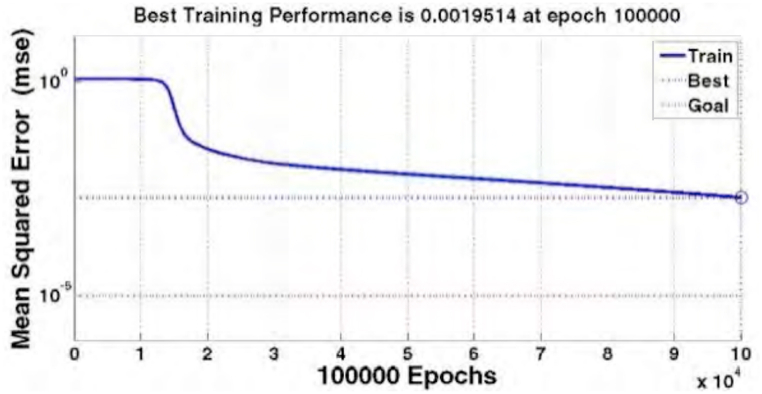
Diagram (Fig. 8) shows the convergence ratio and the error of neural network model compared to empirical data for educating the network. We can see that the network is able to predict the point with convergence ratio of 0.99 (R = 0.99). Diagram (Fig. 9) shows the mean square errors in the network which equals to 0.0019 (MSE = 0.0019) in 100.000 epochs.
Fig. 8.
Diagram of convergence ratio and the error of neural network.
Fig. 9.
MSE diagram of neural network in 100.000 epochs.
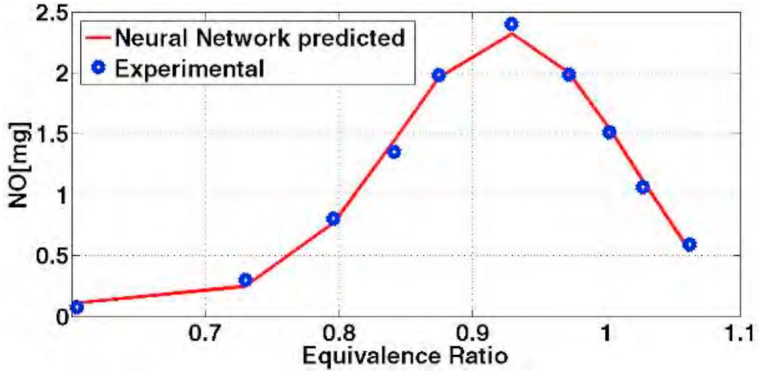
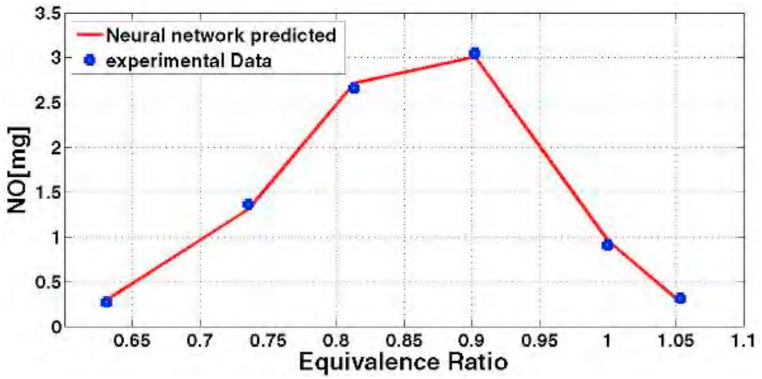
In the remaining of this article, the neural network model has been verified by other empirical data. The following Fig. 10 shows the prediction of neural network for NOx pollutant with the fuel consisting of 20% hydrogen and 80% methane. According to Fig. 9, the trained network correctly predicts NOx pollutant in different equivalence ratios.
Fig. 10.
Diagram of nitrogen oxide prediction with 20% hydrogen fuel in different equivalence ratios and its comparison with empirical data.
3.2. The genetic algorithm model for calculating NOx
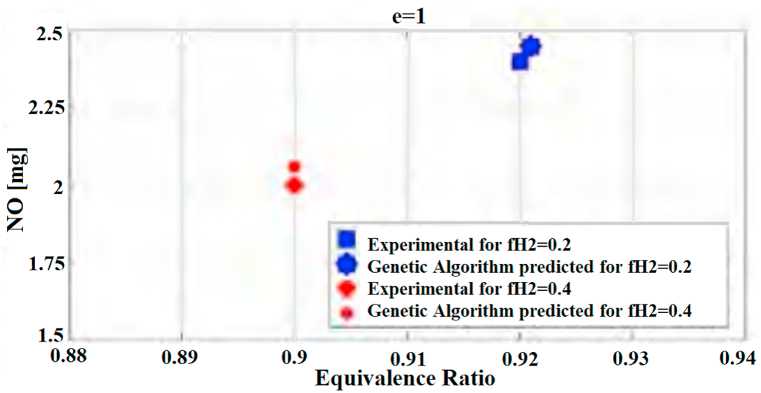
Finally, the maximum amount of NOx produced with different hydrogen rations in the fuel and in different equivalence ratios has been calculated using genetic algorithm. The mathematical method of genetic algorithm has been created based on Darwin's Natural Theory which states that those people who possess better and superior characteristics – compared to others – will survive and continue reproduction. According to this theory, the mathematical method of genetic algorithm states that the optimal point is in fact the superior characteristic. By applying the reproduction method of genetic algorithm, the optimal point can be finally converged. The optimization functions and orders of MATLAB application are to determine the minimum point of functions and therefore they cannot find maximum points. Due to this fact and considering the fact that the estimation of the maximum amount of NOx is important, symmetrizing technique has been used. By symmetrizing NOx data to the x axis and negating the values of NOx, a new neural network will be created which will perform as symmetry of the previous situation. The negative numbers do not have physical meanings and this function is just a mathematical technique. By applying genetic algorithm using the application with series of ga commands to neural network, the minimum points will be calculated. According to this process, after calculating each NOx related to equivalence ratio in 100.000 iterations, the application compares it with NOx related to other equivalence ratio, so that the minimum amount will be selected as the superior gene. With the iteration of this process, the algorithm will achieve the minimum point. The maximum values of NOx and their equivalence ratios will be determined by symmetrizing these values. Diagram (Fig. 11) shows the results of genetic algorithm in estimating the maximum values of NOx and its comparison to the empirical data. As we can see, the genetic algorithm has correctly predicted the maximum values of NOx with high accuracy.
Fig. 11.
Diagram of predicting maximum points of NOx in different ratios using genetic algorithm.
4. Conclusion
Temperature rise resulted from adding hydrogen to methane leads to increasing nitrogen oxides pollutant. In specified blend, by the increase in the equivalence ratio up to 0.9 the amount of nitrogen oxide production rises and above this figure this process becomes descending; the maximum amount of this pollutant is produces at equivalence ratio of 0.9.
The presented neural network has been able to predict the process of the production of this pollutant according to different equivalence ratios. Furthermore, the maximum amounts of NOx with different percentages of hydrogen and in different equivalence ratios has been presented and correctly estimated by genetic algorithm. This value has occurred for the fuel composed of 20% hydrogen and 80% methane at the equivalence ratio of 0.9; for the fuel composed of 40% hydrogen, this value occurred at the equivalence ratio of 0.92. Access to a model that can predict the NOx pollutant of this engine is practical for future research on this engine without the need for huge expenses.
Author contribution statement
Mansour Keshavarzzadeh: Contributed reagents, materials, analysis tools or data. Rahim Zahedi: Performed the experiments; Wrote the paper. Reza Eskandarpanah: Analyzed and interpreted the data. Sajad Qezelbigloo: Contributed reagents, materials, analysis tools or data. Siavash Gitifar:Performed the experiments; Wrote the paper. Omid Noudeh Farahani: Analyzed and interpreted the data. Amir Mohammad Mirzaei: Contributed reagents, materials, analysis tools or data.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Karim G., Gao J. SAE Technical Paper; 1993. Prediction of the Performance of Spark Ignition Gas Engines Including Knock. [Google Scholar]
- 2.Asemi H., Daneshgar S., Zahedi R. Experimental investigation of gamma stirling refrigerator to convert thermal to cooling energy utilizing different gases. Future Technol. 2023;2(2):1–10. [Google Scholar]
- 3.Zahedi R., Rad A.B. Numerical and experimental simulation of gas-liquid two-phase flow in 90-degree elbow. Alex. Eng. J. 2022;61(3):2536–2550. [Google Scholar]
- 4.Shrestha S.B., Karim G.A. IECEC-97 Proceedings of the Thirty-Second Intersociety Energy Conversion Engineering Conference. IEEE; 1997. Hydrogen as an additive to methane for spark ignition engine applications. No. 97CH6203. [Google Scholar]
- 5.Bauer C., Forest T. Effect of hydrogen addition on the performance of methane-fueled vehicles. Part I: effect on SI engine performance. Int. J. Hydrogen Energy. 2001;26(1):55–70. [Google Scholar]
- 6.Vudumu S.K., Koylu U.O. ASME International Mechanical Engineering Congress and Exposition. 2009. A computational study on performance, combustion and emissions characteristics of a hydrogen-fueled internal combustion engine. [Google Scholar]
- 7.Ma J., et al. Simulation and prediction on the performance of a vehicle's hydrogen engine. Int. J. Hydrogen Energy. 2003;28(1):77–83. [Google Scholar]
- 8.Li X., et al. IEEE International Conference on Imaging Systems and Techniques Proceedings. 2012. IEEE; 2012. Prediction of nox emissions throughflame radical imaging and neural network based soft computing. [Google Scholar]
- 9.Tan C., Bai Y., Li X. Dynamic prediction of NOx emissions based on factor analysis and NARX neural network. Chin. Autom. Congress (CAC). 2019. IEEE. 2018 [Google Scholar]
- 10.Jain A., et al. Application of hybrid Taguchi L16 and desirability for model prediction and optimization in assessment of the performance of a novel Water Hyacinth biodiesel run diesel engine. Fuel. 2023;339 [Google Scholar]
- 11.Jain A., et al. Theoretical potential estimation and multi-objective optimization of water hyacinth (Eichhornia crassipes) biodiesel powered diesel engine at variable injection timings. Renewable Energy. 2023;206:514–530. [Google Scholar]
- 12.Duan X., et al. Experimental study the effects of various compression ratios and spark timing on performance and emission of a lean-burn heavy-duty spark ignition engine fueled with methane gas and hydrogen blends. Energy. 2019;169:558–571. [Google Scholar]
- 13.Shi C., et al. Comparative evaluation of intelligent regression algorithms for performance and emissions prediction of a hydrogen-enriched Wankel engine. Fuel. 2021;290 [Google Scholar]
- 14.Asemi H., Zahedi R., Daneshgar S. Theoretical analysis of the performance and optimization of indirect flat evaporative coolers. Future Energy. 2023;2(1):9–14. [Google Scholar]
- 15.Ozgur T., et al. Effect of nanoparticle additives on NOx emissions of diesel fuelled compression ignition engine. Int. J. Glob. Warming. 2015;7(4):487–498. [Google Scholar]
- 16.Daneshgar S., Zahedi R. Optimization of power and heat dual generation cycle of gas microturbines through economic, exergy and environmental analysis by bee algorithm. Energy Rep. 2022;8:1388–1396. [Google Scholar]
- 17.Alruqi M., et al. Renewable energy approach towards powering the CI engine with ternary blends of algal biodiesel-diesel-diethyl ether: Bayesian optimized Gaussian process regression for modeling-optimization. Fuel. 2023;334 [Google Scholar]
- 18.Normann F., et al. High-temperature reduction of nitrogen oxides in oxy-fuel combustion. Fuel. 2008;87(17–18):3579–3585. [Google Scholar]
- 19.Zhang S., et al. Sustainable nitrogen fixation with nanosecond pulsed spark discharges: insights into free-radical-chain reactions. Green Chem. 2022 doi: 10.1039/D1GC03859A. [DOI] [Google Scholar]
- 20.Asemi H., Daneshgar S., Zahedi R. Experimental investigation of gamma Stirling engine coupling to convert thermal to cooling energy in different laboratory conditions. Resour. Environ. Inform. Eng. 2022;4(1):200–212. [Google Scholar]
- 21.Wang C., et al. Influence of chemical kinetics on detonation initiating by temperature gradients in methane/air. Combust. Flame. 2018;197:400–415. [Google Scholar]
- 22.Ignarro L.J. Academic press; 2000. Nitric Oxide: Biology and Pathobiology. [Google Scholar]
- 23.Khah M.V., et al. Thermal analysis and optimization of indirect flat evaporative coolers. Int. J. Thermofluids. 2022 [Google Scholar]
- 24.Preissing P., et al. Three-dimensional density distributions of NO in the effluent of the COST reference microplasma jet operated in He/N2/O2. Plasma Sources Sci. Technol. 2020;29(12) doi: 10.1088/1361-6595/abad01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Estelaji F., et al. Potential measurement and spatial priorities determination for gas station construction using WLC and GIS. Future Technol. 2023;2(4):24–32. [Google Scholar]
- 26.Imtenan S., et al. Effect of n-butanol and diethyl ether as oxygenated additives on combustion–emission-performance characteristics of a multiple cylinder diesel engine fuelled with diesel–jatropha biodiesel blend. Energy Convers. Manag. 2015;94:84–94. [Google Scholar]
- 27.Nadaleti W.C., Przybyla G. Emissions and performance of a spark-ignition gas engine generator operating with hydrogen-rich syngas, methane and biogas blends for application in southern Brazilian rice industries. Energy. 2018;154:38–51. [Google Scholar]
- 28.Otchere P., et al. Mixture formation and combustion process of a biodiesel fueled direct injection rotary engine (DIRE) considering injection timing, spark timing and equivalence ratio–CFD study. Energy Convers. Manag. 2020;217 [Google Scholar]
- 29.Sharma P., Bora B.J. Modeling and optimization of a CI engine running on producer gas fortified with oxyhydrogen. Energy. 2023 [Google Scholar]
- 30.Zuo Q., et al. Prediction of the performance and emissions of a spark ignition engine fueled with butanol‐gasoline blends based on support vector regression. Environ. Prog. Sustain. Energy. 2019;38(3) [Google Scholar]
- 31.Babaie Pirouziana A., et al. Integration of renewable energy-based systems for transport sector in 2050; a case study in Iran. Renew. Energy Res. Appl. 2023;4(1):21–30. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.