Abstract
One of the key challenges preventing the breakthrough of magnesium‐ion batteries (MIB) is the formation of a passivating boundary layer at the Mg anode. To describe the initial steps of Mg anode degradation by O2 impurities, a Mg/O ReaxFF (force field for reactive systems) parameter set was developed capable of accurately modeling the bulk, surface, adsorption, and diffusion properties of metallic Mg and the salt MgO. It is shown that O2 immediately dissociates upon first contact with the Mg anode (modeled as Mg(0001), Mg(10 0)A, and Mg(10 1)), heating the surface to several 1000 K. The high temperature assists the further oxidation and forms a rock salt interphase intersected by several grain boundaries. Among the Mg surface terminations, Mg(10 0)A is the most reactive, forming an MgO layer with a thickness of up to 25 Å. The trained force field can be used to model the ongoing reactions in Mg–air batteries but also to study the oxidation of magnesium metal in general.
Keywords: batteries, magnesium, multi-scale modeling, passivation, ReaxFF
Mg anode passivation: In this work, a Mg/O ReaxFF force field potential was developed that enables large‐scale simulations of Mg/O systems. Furthermore, deep insights into the ongoing passivation mechanism are provided by investigating the reaction processes of the Mg anode in an O2 atmosphere.
Introduction
The search for new energy storage technologies to promote electromobility and reduce global warming is one of the greatest challenges of our time. Magnesium‐ion batteries (MIB) are attracting increasing attention as an alternative to conventional lithium‐ion batteries (LIB) due to the unique properties of magnesium metal anodes, such as high volumetric capacity, low cost, and safe operation.[ 1 , 2 , 3 , 4 , 5 ] However, mass market adoption of MIBs is currently hindered by significant challenges. One of the biggest challenges is the formation of a passivating interface on the Mg surface which is impermeable to Mg cations and leads to battery failure.[ 6 , 7 , 8 ] Sun et al. have identified three reasons for Mg degradation in a recent review article. [9]
First, Mg has a higher charge density due to its bi‐valency, which leads not only to stronger coordination with solvent molecules and salt anions but also facilitates solvent decomposition at the anode. [10] For example, Lu et al. have shown that the salt anion ClO4 is chemically reduced at the Mg anode in carbonate‐containing solvents, forming a solid‐electrolyte interface (SEI) consisting of Mg‐halides, MgO, Mg(OH)2, MgCO3, and Mg(ROCO2)2. [11]
Second, short circuits are induced by non‐uniform Mg growth, which can be further subdivided into hemispherical, [12] porous, [13] or dendritic [14] growth morphologies. [9] Hemispherical 3D particles with different shapes have been detected in TFSI‐based electrolytes as a function of the applied current density. [12] In an Mg(TFSI)2 salt electrolyte with MgCl2 as additive, continuous stripping and plating leads to fracturing and reformation of the SEI layer, resulting in large effective current densities at the respective fracture sites and inhomogeneous Mg deposition. [13] Through this mechanism, hemispherical deposits are further degraded to porous morphologies and trapped sediments that are irreversibly lost for cycling. The most extreme form of non‐uniform Mg growth is the formation of dendrites, which occurs much less frequently at the Mg anode than in the Li equivalent. So far, dendrites have been detected only for a 0.5 mol dm−3 solution of MeMgCl in THF at a current density of 0.921 mA cm−2. [14]
Third, corrosion of the Mg surface upon contact with ambient air leads to the formation of inorganic compounds such as MgO and Mg(OH)2 at the interface. [9] During fabrication, transport, or storage of the Mg anode, contact with impurities such as O2 or H2O can hardly be avoided. In addition, traces of water in the electrolytes or oxygen residues under inert gas conditions can also lead to passivation.[ 15 , 16 ] According to Connell et al., impurities contribute even more to passivation than decomposition products of electrolytes. [17]
To study in detail the initial steps of the Mg anode passivation by oxygen impurities, we apply ReaxFF, a bond‐order based reactive force field method capable of large‐scale molecular dynamics simulations (cf. computational details).[ 53 , 54 ] ReaxFF has proven valuable for studying battery materials. For example, Islam et al. developed a ReaxFF potential for amorphous sulfur cathodes, allowing the group to model the volume expansion and associated strain hardening during lithiation. [18] In addition, the authors studied reductive decomposition pathways of ethylene carbonate (EC) using the eReaxFF method, which can explicitly describe electrons in a pseudoclassical manner.[ 19 , 20 ] The study demonstrated electron transfer from Li to EC to trigger ring‐opening to form the Li+/EC− radical, and predicted possible radical termination products which were also detected experimentally. O'Hearn et al. trained a force field for Li/O systems with the goal of improving the description of brittle fractures in Li2O slabs. [21] Although the force field was not directly trained for battery application, it should be able to describe oxidation processes at the Li anode. Recently, force field parameters for the study of lithium and sodium metal anodes were trained by Gaissmaier et al. [22] Ostadhossein et al. developed a Li/Si/O/Al force field to study lithium diffusion in silica anodes [23] and Bedrov et al. trained parameters for an ethylene carbonate description to investigate possible reactions of closed and open ring EC radical anions. [24] Moreover, Shin et al. investigated the ionic conductivity of Li in the Na super ionic conductor (NASICON)‐type solid‐state electrolyte Li1‐x Al x Ti2‐x (PO4)3. [25] A complete battery setup consisting of a sulfur cathode, a carbon nanotube anode and tetra(ethylene glycol) dimethyl ether as electrolyte was simulated by Islam et al. [26] One of the latest battery ReaxFF force fields was trained by Hossain et al. to study the influence of Li atoms and cations on organic compounds such as ethylene carbonate, ethyl methyl carbonate, vinylene carbonate, and LiPF6 salts. [27] Thereby, different parameter sets were trained for the Li cation and the atom and its interchange was simulated by a Monte Carlo type replacement. The group found that only the neutral Li atom could trigger ring opening, while the Li cation was inactive.
The oxidation of magnesium is not only of central importance in battery science but also in automotive and aerospace research. [28] There are many studies trying to understand and explain magnesium corrosion in a metallurgical context.[ 29 , 30 , 31 , 32 ] Thus, Mg/O ReaxFF parameters could also be beneficial to these research areas and further promote corrosion studies.
Until now, no suitable Mg/O parameters have been available to describe the passivation at the Mg anode. So far, only Cheung et al. have trained force field parameters for magnesium hydride systems [33] or Iype et al. to describe MgSO4 hydrates. [34] Additional parameters for Mg/O are available in a peptide force field developed by Zhu et al., whose training set was however limited to the bulk phases of Mg and MgO. [35] The parameters were recently reused by Yeon et al. to study magnesium aluminosilicate glasses, and the training set was extended to include additional bulk phases, heats of formation, and bond scans for the Mg/O description. [36]
The goal of the present study is to describe the initial steps of Mg anode degradation by oxygen impurities. To this end, we trained a reactive ReaxFF Mg/O force field that can accurately describe the properties of metallic Mg and MgO. The comprehensive training set included a variety of bulk, surface, and adsorption energies as well as diffusion barriers calculated at the level of density functional theory (DFT). In addition, we demonstrated the applicability of our force field by first completely oxidizing a Mg particle in a grand‐canonical Monte Carlo (GCMC) simulation and then recrystallizing it into the thermodynamically stable rock salt structure by simulated thermal annealing at 2000 K in a subsequent molecular dynamics (MD) simulation.
Results and Discussion
The following section first compares the DFT training data with the force field optimization results. In this context, we discuss the performance and limitations of the obtained ReaxFF parameters. We subsequently demonstrate the functionality of the force field by oxidizing a Mg nanoparticle in a GCMC simulation and then recrystallizing it into the thermodynamically stable rock salt structure in a subsequent MD simulation. Afterwards, we simulate and discuss the first steps of Mg anode passivation. All fitted ReaxFF force field parameters for the Mg/O interactions are given in the Supporting Information.
Magnesium‐magnesium interactions
The first milestone of ReaxFF parameter training for the Mg/Mg metal interactions was to reproduce the bulk properties of Mg. Therefore, lattice constants, cohesive energies [(Eq. (3)], and bulk moduli of the crystal phases hexagonal close‐packed (hcp), face centered cubic (fcc), body centered cubic (bcc), β‐tungsten type (a15), and simple cubic (sc) were introduced to the training set. Figure 1 and Table 1 compare the DFT training data and the results obtained with the fitted ReaxFF force field. We only trained bonding but excluded off‐diagonal, valence, or torsion parameters for the Mg/Mg interactions, which means that first, the ratio (a 0/c 0) of the lattice constants a 0 and c 0 in the hcp unit cell always corresponds with (8/3)1/2 to the ideal value of a closed‐packed crystal, and second, the hcp and fcc cohesive energy will be identical. [37]
Figure 1.
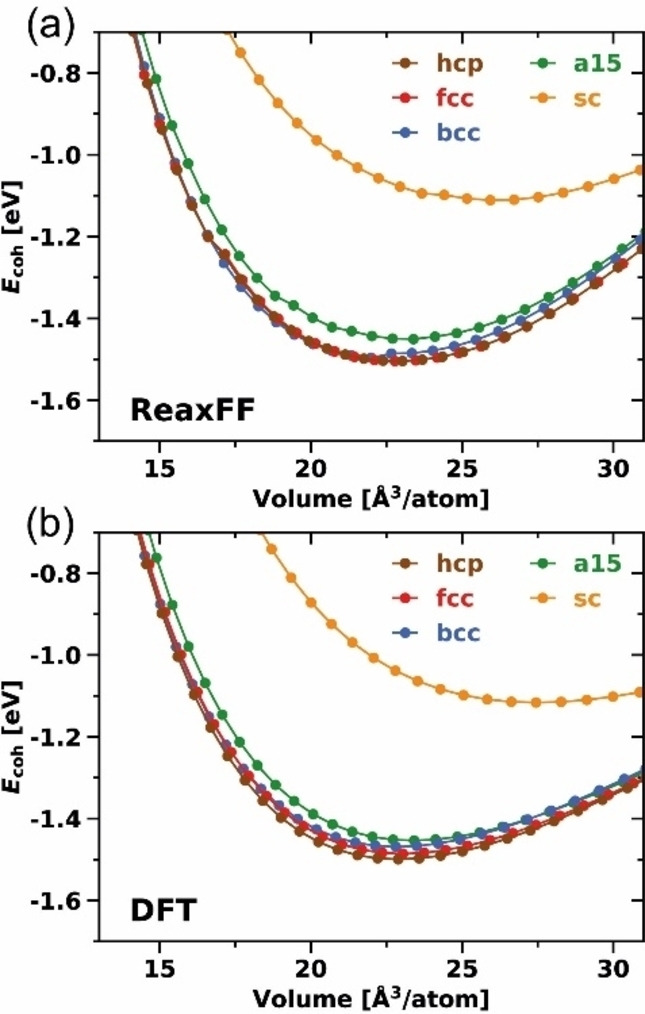
Equations of state (EOS) for bulk Mg crystal phases calculated with a) the trained ReaxFF force field and b) DFT. [38]
Table 1.
Lattice constants a 0 and c 0, bulk modulus B 0, and cohesive energies E coh calculated with Equation (3) for the Mg bulk crystal phases hcp, fcc, bcc, a15, and sc determined in ReaxFF and DFT. For the hcp phase, the experimental constants of Kittel were adopted and are given for comparison. [39]
|
Structure |
Method |
a 0 [Å] |
c 0 [Å] |
B 0 [GPa] |
E coh [eV] |
|---|---|---|---|---|---|
|
hcp – P63/mmc |
ReaxFF |
3.18 |
5.20 |
38.5 |
1.50 |
|
|
DFT [38] |
3.18 |
5.21 |
36.5 |
1.50 |
|
|
experiment [39] |
3.21 |
5.21 |
35.4 |
1.51 |
|
fcc – Fm m |
ReaxFF |
4.50 |
– |
42.9 |
1.50 |
|
|
DFT [38] |
4.52 |
– |
35.9 |
1.49 |
|
bcc – Im m |
ReaxFF |
3.53 |
– |
42.4 |
1.49 |
|
|
DFT [38] |
3.57 |
– |
35.3 |
1.48 |
|
a15 – Pm n |
ReaxFF |
5.72 |
– |
41.2 |
1.45 |
|
|
DFT [38] |
5.72 |
– |
34.7 |
1.46 |
|
sc – Pm m |
ReaxFF |
2.96 |
– |
28.7 |
1.11 |
|
|
DFT [38] |
3.02 |
– |
23.2 |
1.12 |
The lattice constants of the experimentally present [39] hcp crystal phase at ambient conditions are accurately reproduced by ReaxFF (a 0: both 3.18 Å, c 0: 5.20 Å vs. 5.21 Å), which is also true for the cohesive energy (both 1.50 eV) and bulk modulus (38.5 GPa vs. 36.5 GPa). The cohesive energy, in particular, is an important measure to describe bond strengths, and was therefore weighted more strongly during the training process; it varies at most by 0.01 eV for all crystal phases. This is also reflected in the relative stability between the crystal phases, which are in good agreement. ReaxFF slightly overestimates the bulk modulus for all crystal phases. This behavior is illustrated in the equation of state (EOS) curves presented in Figure 1 and is a result of an increase of the ReaxFF energy values at higher volumes.
In addition, we trained surface energies of the low index surfaces Mg(0001), Mg(10 0)A, Mg(10 0)B, Mg(10 1), Mg(10 0), and Mg(10 1), which were calculated using Equation (6). According to DFT calculations, Mg(0001) is the most stable Mg surface, followed by the surfaces Mg(10 0)A and Mg(10 1). [38] This trend is reproduced by the trained ReaxFF force field as illustrated in Table 2. The surface energy of Mg(0001) (31.6 meV Å−2 vs. 33.9 meV Å−2) is reproduced most accurately with an error below 10 %; however, this structure was also weighted most strongly during force field training. In general, the trained ReaxFF force field slightly underestimates all absolute surface energies.
Table 2.
Comparison of Mg surface energy results γ calculated with ReaxFF and DFT. The surface energy was obtained using Equation (6).
|
Surface |
γ [meV Å−2] |
|
|---|---|---|
|
|
ReaxFF |
DFT [38] |
|
Mg(0001) |
31.6 |
33.9 |
|
Mg(10 0)A |
34.1 |
40.3 |
|
Mg(10 0)B |
46.4 |
55.5 |
|
Mg(10 1) |
34.3 |
40.9 |
|
Mg(11 0) |
39.9 |
47.1 |
|
Mg(11 1) |
41.4 |
48.7 |
The calculated surface fractions in the Wulff construction (Table 3) were only indirectly part of the training set via the surface energies and can therefore be seen as a validation measure. Mg(10 1) has the largest area percentage (56.9 % vs. 48.6 %) in a Mg nanoparticle, followed by Mg(10 0)A (23.9 % vs. 27.9 %) and Mg(0001) (19.2 % vs. 23.7 %). The absolute values deviate up to 10 %, but the relative ratios agree. It is important to note that when studying Mg metal anodes, the surface Mg(10 1) should be considered equally as Mg(0001). [38] Despite its higher surface energy compared to Mg(0001), it has by far the largest area percentage in the Wulff construction, which is correctly reproduced in ReaxFF.
Table 3.
Calculated area fractions of Mg(0001), Mg(10 0)A, and Mg(10 1) in a Mg nanoparticle. The Wulff construction [40] and the area fractions were obtained using the Python package WulffPack from surface energies calculated with ReaxFF and DFT from Table 2. [41]
|
Surface |
Area fraction [%] |
|
|---|---|---|
|
|
ReaxFF |
DFT [38] |
|
Mg(0001) |
19.2 |
23.7 |
|
Mg(10 0)A |
23.9 |
27.9 |
|
Mg(10 1) |
56.9 |
48.6 |
We further included adsorption energies of atomic Mg on different sites on Mg(0001), Mg(10 0)A, and Mg(10 1) into the training set, calculated using Equation (7). Schematic representations of the underlying structures are shown in Figure S3. Adsorption energy results obtained with ReaxFF and DFT are compared in Table 4. It is noticeable that all adsorption energies for Mg(0001) are significantly overestimated by ≈0.2 eV. Moreover, according to DFT, adsorption at the fcc site is considered to be 0.02 eV more stable than at the hcp site. [38] However, it is impossible to distinguish between the two adsorption sites in ReaxFF without using angular terms or increasing the bond order cutoff, as already explained in the case of the cohesive energy of the hcp and fcc crystals. Besides, the relative stability sequence of the adsorption sites on Mg(0001) is well reproduced. For example, the fcc and meta‐stable ontop positions differ by 0.13 eV in ReaxFF and DFT. Additionally, the relative absorption energy trends between different surfaces are described well by ReaxFF. The ontop‐bottom position on Mg(10 0)A has the highest adsorption energy (−1.06 eV vs. −1.00 eV), followed by the hollow position on Mg(10 1) (−1.03 eV vs. −0.97 eV), and the fcc site on Mg(0001) (−0.80 eV vs.−0.58 eV).
Table 4.
Adsorption energies E ad of a Mg adatom on Mg(0001), Mg(10 0)A, and Mg(10 1) calculated with ReaxFF and DFT using Equation (7).
|
Surface |
Adsorption site |
E ad [eV] |
|
|---|---|---|---|
|
|
|
ReaxFF |
DFT [38] |
|
Mg(0001) |
fcc |
−0.80 |
−0.58 |
|
|
hcp |
−0.80 |
−0.56 |
|
|
bridge[a] |
−0.79 |
−0.56 |
|
|
ontop[a] |
−0.57 |
−0.45 |
|
Mg(10 0)A |
ontop‐bottom |
−1.06 |
−1.00 |
|
|
bidge‐bottom[a] |
−1.05 |
−0.97 |
|
|
ontop‐up[a] |
−0.35 |
−0.46 |
|
|
bridge‐up[a] |
−0.58 |
−0.58 |
|
Mg(10 1) |
hollow |
−1.03 |
−0.97 |
[a] Site not stable, relaxation of the adatoms was constrained in the x and y direction.
To obtain a smooth potential energy surface (PES), which is key to performing meaningful MD simulations, we added activation energies of selected self‐diffusion processes to the training set, calculated using Equation (8). Our goal was to introduce a diverse spectrum of different magnesium conformations but also of transition states into the training set. For the latter, we included terrace self‐diffusion barriers on Mg(0001), Mg(10 0)A, and Mg(10 1) (Figure 2, Table 5), but also additional diffusion processes of the terrace‐step‐kink (TSK) model [42] (like dimer, trimer, step‐edge, kink, inner‐corner, outer‐corner, step‐down on Mg(0001) and dimer, trimer on Mg(10 1)). To keep this section compact, we discuss only the performance of the terrace self‐diffusion barriers in the main text but refer to the Supporting Information for the additional diffusion processes (Figure S4, Table S1 for Mg(0001); Figure S5, Table S2 for Mg(10 1)). Overall, the trained force field reproduces the reference DFT activation energies of 32 of the 37 processes to an accuracy of |▵E a |≤0.2 eV. As a necessary trade‐off, the remaining 5 diffusion barriers, which include exchange terrace self‐diffusion, dimer formation, or the step‐down diffusion process on Mg(0001), show larger deviations. The trained ReaxFF force field describes all hopping terrace self‐diffusion processes within 0.1 eV accuracy but struggles to describe the corresponding exchange processes (▵|E a |≥0.3 eV). In an exchange process, the diffusing atom takes the place of a surface atom, which in turn is pushed to its destination. However, since these processes have much higher barriers than the hopping processes, they are of less importance for an accurate description of surface mobility. In general, terrace self‐diffusion on Mg(0001) (Figure 2a) has almost no barrier, which is also the case for diffusion within a channel on Mg(10 0)A (Figure 2b). [38] In contrast, the activation energy for diffusion across a channel is several times higher, which is in the same order of magnitude as diffusion on Mg(10 1) (Figure 2c).
Figure 2.
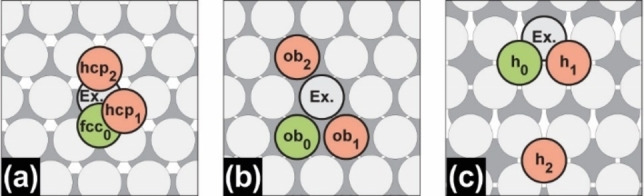
Overview and schematic representation of trained terrace self‐diffusion processes on a) Mg(0001), b) Mg(10 0)A, and c) Mg(10 1). Green atoms mark the initial, while red atoms mark the final position. The label Ex. marks the exchanged surface atom. Reproduced from Ref. [38] Copyright (2022), with permission from Wiley‐VCH.
Table 5.
Activation energies E a calculated with ReaxFF and DFT using Equation (8) for forward and backward terrace self‐diffusion processes on Mg(0001), Mg(10 0)A, and Mg(10 1). [38]
|
Surface |
Pathway |
[eV] |
[eV] |
[eV] |
[eV] |
||
|---|---|---|---|---|---|---|---|
|
|
|
ReaxFF |
DFT [38] |
|
ReaxFF |
DFT [38] |
|
|
Mg(0001) |
fcc0 ↔hcp1 |
0.01 |
0.02 |
0.01 |
0.01 |
0.01 |
0.00 |
|
|
fcc0 ↔hcp2 (Ex.) |
1.20 |
0.74 |
0.46 |
1.19 |
0.72 |
0.47 |
|
Mg(10 0)A |
ob0 ↔ob1 |
0.02 |
0.02 |
0.00 |
0.02 |
0.02 |
0.00 |
|
|
ob0 ↔ob2 |
0.49 |
0.42 |
0.07 |
0.49 |
0.42 |
0.07 |
|
|
ob0 ↔ob2 (Ex.) |
0.78 |
0.46 |
0.32 |
0.78 |
0.46 |
0.32 |
|
Mg(10 1) |
h0 ↔h1 |
0.39 |
0.30 |
0.09 |
0.39 |
0.30 |
0.09 |
|
|
h0 ↔h1 (Ex.) |
1.00 |
0.59 |
0.41 |
1.00 |
0.59 |
0.41 |
|
|
h0 ↔h2 |
0.41 |
0.42 |
0.01 |
0.41 |
0.42 |
0.01 |
Magnesium‐oxygen interactions
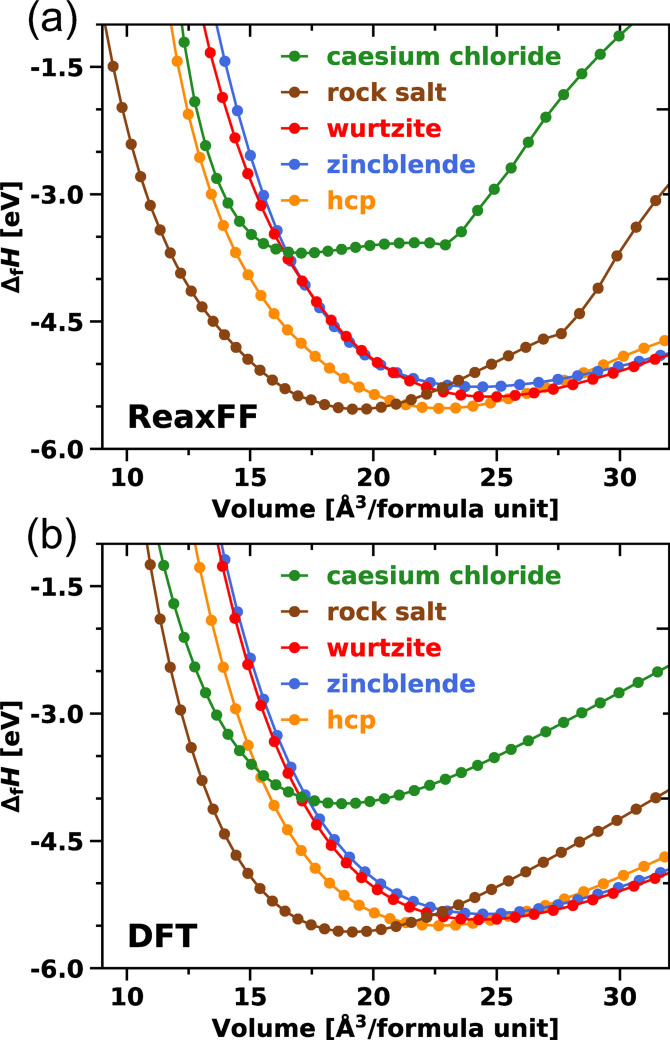
Our training focuses on introducing EOS curves for the MgO crystal phases rock salt, wurtzite, zincblende, cesium chloride, and hcp to the training set for the Mg/O interactions. This selection of structures represents different coordination environments, bond distances, and geometries to provide a broad overview of the configurational space. Each EOS was constructed from eleven data points. The rock salt structure was weighted most strongly during training as this represents the preferred structure of MgO at ambient conditions. [43] Figure 3 compares the DFT reference EOS with the ReaxFF data, which are in excellent agreement. In particular, the transitions from rock salt to the hcp (22 Å3 to 24 Å3) and wurtzite (>24 Å3) structures in the high volume region are well reproduced. The EOS for cesium chloride and rock salt exhibit a significant flattening in the ReaxFF method in general (Figure 3a) due to the exponentially decreasing bond order at long bond lengths. However, since the affected structures constitute high energy phases that are not sampled in simulations of MgO at ambient conditions, the impact of this methodological limitation on the intended scope of simulations with the trained force field is deemed negligible. The corresponding indicator, the heat of formation ▵f H [Eq. (4)], is reproduced for all structures with a relative error smaller than 10 % as shown in Table 6. The rock salt structure is calculated to give the lowest heat of formation with −5.49 eV with the trained force field compared to −5.57 eV in DFT. Furthermore, the relative stability sequence of all crystal phases is correctly reproduced as well.
Figure 3.
Equations of state (EOS) for MgO crystal phases calculated with a) the trained ReaxFF force field and b) DFT
Table 6.
Lattice constants a 0 and c 0, bulk moduli B0, heats of formation ▵f H and oxygen vacancy energies E v for the MgO crystal phases rock salt, wurtzite, zincblende, hcp, and cesium chloride determined in ReaxFF and DFT. ▵f H and E v were calculated using Equations (4) and (5). The experimental constants for the rock salt structure were adopted from Refs. [44] and [45].
|
Structure |
Method |
a 0 [Å] |
c 0 [Å] |
B 0 [GPa] |
▵f H [eV] |
E v [eV] |
|---|---|---|---|---|---|---|
|
rock salt – Fm m |
ReaxFF |
4.26 |
|
157.5 |
−5.49 |
−6.82 |
|
|
DFT |
4.25 |
|
154.6 |
−5.57 |
−6.71 |
|
|
4.21 |
|
155.0 |
−6.24 |
|
|
|
wurtzite – P 63 mc |
ReaxFF |
3.33 |
5.13 |
103.6 |
−5.34 |
|
|
|
DFT |
3.31 |
5.11 |
117.4 |
−5.43 |
|
|
zincblende – F 3m |
ReaxFF |
4.60 |
|
122.4 |
−5.23 |
|
|
|
DFT |
4.61 |
|
117.4 |
−5.36 |
|
|
hcp – P 63 /mmc |
ReaxFF |
3.52 |
4.23 |
116.3 |
−5.48 |
|
|
|
DFT |
3.52 |
4.23 |
128.0 |
−5.50 |
|
|
cesium chloride – Pm m |
ReaxFF |
2.59 |
|
210.4 |
−3.68 |
|
|
|
DFT |
2.65 |
|
142.2 |
−4.06 |
|
We incorporated the vacancy energy E v [Eq. (5)] of an oxygen atom in the rock salt bulk structure with a low weighting in the force field training to use it as a validation measure for the obtained bonding, off‐diagonal, and valance parameters. The vacancy energy calculated with the force field equals −6.82 eV and deviates very slightly from the DFT reference (−6.71 eV). The lattice constants and bulk moduli were only indirectly included in the force field training via the volume‐energy data points. In particular, the lattice constants deviate from the DFT values by at most 0.02 Å for the rock salt, wurtzite, zincblende, and hcp structures. The bulk modulus for the energetically favored rock salt structure is best described with less than 2 % error, while the other structures (wurtzite, zincblende, hcp) deviate around 5 % to 12 %. The cesium chloride structure, which is energetically unfavorable at ambient conditions, shows the largest deviation from the DFT reference data but constitutes the only experimentally confirmed structure, along with the rock salt phase. [43] However, the transition occurs at an extremely high pressure of 0.36 TPa.
Surface energy results γ were trained only for the stoichiometric surfaces MgO(100) and Mg(110), since it is difficult to calculate the surface energy for the non‐stoichiometric surface MgO(111) (cf. Table 7). Either the stoichiometric structure has different terminations (oxygen‐rich on the one side, magnesium‐rich on the other side), or it is impossible to reference the symmetric structure against the bulk energy. Reuter and Scheffler stated in this context that “in a purely electrostatic model in which all oxygen ions would be in their bulk formal oxidation state, polar surfaces would be charged and should thus exhibit an infinite surface energy”. [46] The surface energy results for MgO(100) and MgO(110) were calculated using Equation (6) and are shown in Table 7.
Table 7.
Calculated [Eq. (6)] and experimental surface energies γ of MgO(100) and Mg(110).
|
Surface |
Method |
γ [meV Å−2] |
|---|---|---|
|
MgO(100) |
ReaxFF |
71.4 |
|
|
DFT |
55.5 |
|
|
experiment |
64.9[a]; 71.8[b] |
|
MgO(110) |
ReaxFF |
117.7 |
|
|
DFT |
135.0 |
While the trained force field underestimates the DFT surface energy in case of all Mg surfaces, both MgO surfaces are overestimated as shown in Table 7. On the other hand, the experimental surface energy (64.9 meV Å−2) for MgO(100) at 0 K lies in between the values determined with ReaxFF (71.4 meV Å−2) and DFT (55.5 meV Å−2), respectively. [47]
In addition to bulk and surface energies for MgO, we trained oxygen adsorption energies for the surfaces Mg(0001), Mg(10 0)A, and Mg(10 1) to diversify the training data for the Mg/O parameters. Schematic illustrations of the adsorption sites are shown in Figure S6 and a comparison of the oxygen adsorption energy results obtained with ReaxFF and DFT is summarized in Table 8.
Table 8.
Oxygen adsorption energies E ad on Mg(0001), Mg(10 0)A, and Mg(10 1) calculated with ReaxFF and DFT using Equation (7).
|
Surface |
Adsorption site |
E ad [eV] |
|
|---|---|---|---|
|
|
|
ReaxFF |
DFT |
|
Mg(0001) |
fcc |
−4.01 |
−4.03 |
|
|
hcp |
−4.02 |
– |
|
|
tet‐1 |
−4.36 |
−4.42 |
|
|
tet‐2 |
−4.33 |
−4.30 |
|
|
tet‐3[a] |
– |
−3.79 |
|
|
oct |
−4.64 |
−3.92 |
|
|
sub‐tet‐1 |
−4.44 |
−4.26 |
|
|
sub‐tet‐2 |
−4.45 |
−4.28 |
|
|
sub‐oct |
−4.66 |
−4.05 |
|
Mg(10 0)A |
fcc |
−4.04 |
−4.07 |
|
|
hcp |
−3.96 |
– |
|
|
tet |
−4.53 |
−4.43 |
|
|
bdg |
– |
−4.14 |
|
|
oct |
−4.69 |
−4.09 |
|
Mg(10 1) |
fcc |
−3.93 |
−4.21 |
|
|
hcp |
−3.94 |
– |
|
|
tet‐1 |
−4.45 |
−4.31 |
|
|
tet‐2 |
−4.36 |
−4.20 |
|
|
tet‐3 |
−4.46 |
−4.34 |
|
|
tet‐4[a] |
– |
−3.90 |
|
|
oct |
−4.62 |
−3.94 |
|
|
hlw |
−4.44 |
−4.25 |
[a] Adsorption site is metastable.
According to DFT, the tetrahedral position tet‐1 between the first and second surface layer is the most stable adsorption site on Mg(0001), which is in agreement with the results of Francis and Taylor. [49] However, our adsorption energy of −4.42 eV is significantly less exothermic (vs. −7.69 eV [49] ), which is due to the group's chosen oxygen reference, a single oxygen atom in the gas phase, while we use half of the energy of an O2 molecule. In agreement with Francis and Taylor, we find that hcp adsorption sites are unstable in DFT; an atom placed there relaxes, in the case of Mg(0001), to the tet‐1 position. With the trained ReaxFF force field, the hcp sites are stable but, similar to fcc sites, the corresponding adsorption energy is less exothermic compared to the tet‐1 site with −4.02 eV and −4.01 eV for Mg(0001), respectively. A potential reason for the decreased adsorption energy could be the smaller coordination number. While four magnesium atoms surround the oxygen atom for the tetrahedral (tet) positions, there are only three surrounding atoms present for the fcc and hcp sites. The tet‐3 site on Mg(0001) was identified as a meta‐stable position with an energy of −3.79 eV in DFT but is calculated to be unstable with the force field. The most stable adsorption positions calculated with the force field are octahedral (oct) sites coordinated by six Mg atoms with −4.64 eV on Mg(0001), −4.69 eV on Mg(10 0)A, and −4.62 eV on Mg(10 1), while DFT predicts this site to be less stable compared to tet sites. During training, it became clear that a trade‐off would be required between the accurate description of the relative stability sequences of the adsorption sites and that of the bulk phases. If we assigned a higher weight to the adsorption energy values, the Mg−O−Mg equilibrium angle changed in tandem, which in the most extreme case caused the wurtzite structure to be more stable than the rock salt phase. We ultimately decided to constrain the Mg−O−Mg equilibrium angle at 180°, thereby placing more weight on the accurate reproduction of the bulk phases.
Furthermore, we trained the thermodynamic stability of subsurface (sub) adsorption positions between the second and third surface layers on Mg(0001). While in DFT, the tet positions in deeper surface layers become thermodynamically less stable (−4.26 eV/−4.28 eV vs. −4.42 eV/−4.30 eV), the opposite trend is calculated with the force field (−4.44 eV/−4.45 eV vs. −4.36 eV/−4.33 eV). With the force field, the sub‐oct position shows nearly the same adsorption energy (−4.66 eV) compared to an adsorption site just below the surface (−4.64 eV). In the DFT reference data, the site further away from the surface is more stable (−4.05 eV vs. −3.92 eV). In summary, DFT calculations suggest that on Mg(0001), the adsorption sites in between the first and second surface layers are the most stable. With the trained force field, diffusion to deeper layers is calculated to be more favorable from a thermodynamic point of view.
Finally, the activation barriers calculated using Equation (8) for the diffusion process between the oct adsorption site and its subsurface equivalent sub‐oct on Mg(0001) were part of the training set (Figure 4). According to our DFT calculations, an oxygen atom must overcome a barrier of 0.68 eV to diffuse from an oct position to a subsurface site and 0.81 eV to diffuse back. The corresponding barriers in ReaxFF are 0.71 eV and 0.73 eV and thus agree well. We calculated additional oxygen diffusion barriers for Mg(0001), Mg(10 0)A, and Mg(10 1) to validate the obtained parameters, which were not part of the training set. The performance of these diffusion processes is discussed in the Supporting Information (Figures S7, S8, and S9; Tables S3, S4, and S5.
Figure 4.
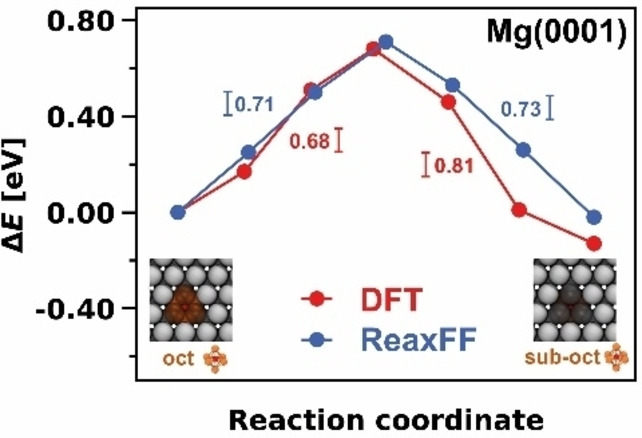
Comparison of the diffusion pathway from the oct to the subsurface oct site on Mg(0001) calculated with DFT and ReaxFF.
Grand‐canonical Monte Carlo simulations of the oxidation of a magnesium nanoparticle
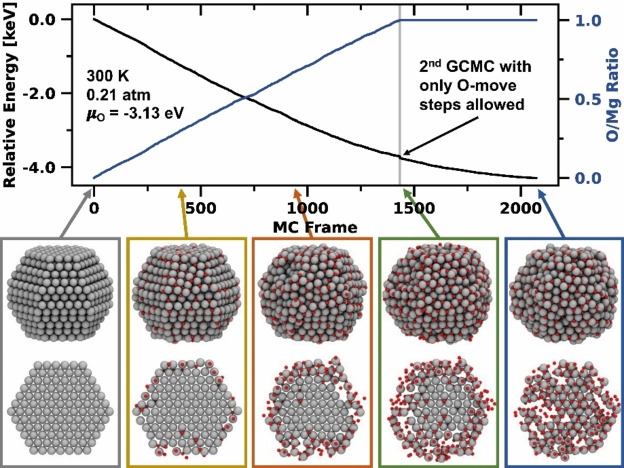
As initial test cases we applied the trained Mg/O potential in two subsequent GCMC simulations to investigate the thermodynamic oxidation behavior of a Mg nanoparticle. Therefore, we started with a clean, equilibrium‐shaped Mg978 nanoparticle and inserted in the first GCMC simulation oxygen atoms up to an O/Mg ratio of 1.0. As shown in Figure 5, oxygen is mainly inserted at the particle's surface during early stages of the simulation. Note that especially oct sites are populated first and that the surface starts to reshape into the rock salt structure. Upon reaching an O/Mg ratio of 1.0, the particle is not yet fully oxidized to the core – as shown in the cross‐section of the particle images in Figure 5 – but a series of non‐dissociated O2 molecules is adsorbed on the surface. As the simulation continues, the surface is covered with more and more O2 molecules but complete oxidation to the core was not achieved even after 10 000 iterations (see Figure S10). Thus, to accelerate the process, we decided to perform a second GCMC simulation, using a nanoparticle with an O/Mg ratio of 1.0 as the input structure from the first GCMC simulation. In 20 000 additional iterations, we allowed only O‐move steps but prohibited further oxygen atoms from being inserted or removed. As a result, now oxygen diffusion processes lead to oxidation of the particle's core. The final structure contains many patterns of the rock salt structure, which spread out in different spatial directions. Furthermore, grain boundaries are formed that make the particle appear amorphous. In summary, we show that a magnesium particle generated from Wulff construction oxidizes first at the surface oct sites from a thermodynamic point of view. Further oxygen adsorption is also thermodynamically favored despite the formed surface oxide layers. The fully oxidized particle exhibits an amorphous structure with rock salt structure elements but many grain boundaries.
Figure 5.
Grand‐canonical Monte Carlo simulation showing the oxidation of an equilibrium‐shaped Mg978 nanoparticle at 300 K and 0.21 atm first up to and then at an O/Mg ratio of 1.0. Oxidation first occurs on the surface oct sites and subsequently penetrates the particle's core.
Molecular dynamics simulation of the recrystallization of a magnesium oxide nanoparticle
We subsequently carried out an MD simulation to recrystallize the particle obtained from the GCMC simulations. To this end, we performed a simulated thermal annealing procedure where we first heated the particle to 2000 K at a rate of 80 K ps−1, maintained the temperature for 75 ps, and then slowly cooled the system down to 1 K at a rate of 16 K ps−1, as shown in Figure 6. The maximum temperature of 2000 K allowed for ample but non‐destructive mobility of atoms in the particle. At even higher temperatures, within the simulation time evaporation of small MgO clusters (about ten atoms) was observed and the nanoparticle became unstable. The recrystallization process took place between 25 ps and 100 ps at 2000 K, which is signified by a decrease of the relative energy in Figure 6. While the kinetic energy of the system remains constant in this range (temperature≙kinetic energy), the potential energy decreases due to the rearrangement process. The final structure of the MgO particle becomes visible after the cooling phase is completed. The particle has assumed rock salt structure and the initially round particle now has a cubic shape. In simulations with smaller periods than 75 ps at 2000 K, the recrystallization process was not yet complete and grain boundaries were present in the particle, even though the rock salt phase was already clearly apparent.
Figure 6.
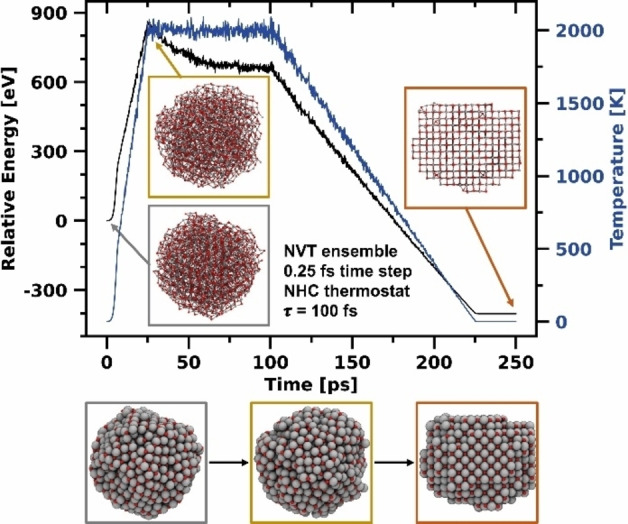
NVT simulation showing the recrystallization of an amorphous Mg nanoparticle into the rock salt structure by simulated thermal annealing at 2000 K.
Molecular dynamics simulation of the passivation of the magnesium anode
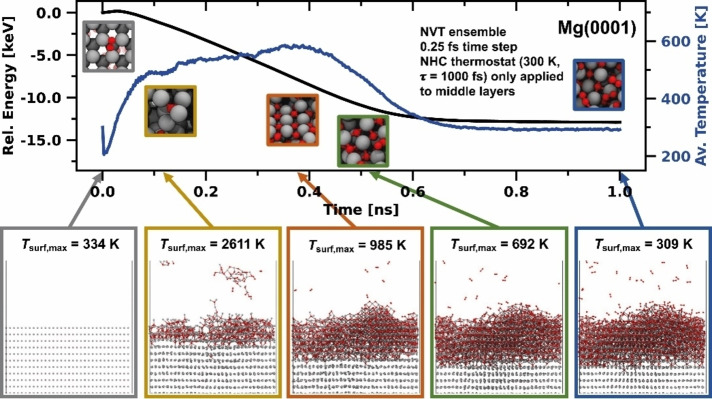
Contact of the Mg anode with oxygen impurities, traces of water, or decomposition products of the electrolyte results in an interface layer impermeable to Mg cations, leading to battery failure. [9] To investigate the initial steps of Mg anode passivation, we performed MD simulations of Mg(0001), Mg(10 0)A, and Mg(10 1) surfaces in contact with an oxygen atmosphere. A weakly coupled Nosé‐Hoover (NHC) thermostat set to 300 K was applied only to the ten innermost layers of the Mg slab to avoid quenching of surface reactions and to prevent surface melting which would otherwise have to be compensated by adding an inefficiently large number of surface layers. For Mg(0001), the energy evolution, average temperature in the simulation box, and snapshots at distinct time points are shown in Figure 7. Analogous results for Mg(10 0)A and Mg(10 1) are presented in the Supporting Information (Figures S11 and S12). Since the average temperature inside the cell is insufficient to understand the processes taking place at the surface, we divided the z‐axis into 500 equally sized sections and calculated the temperature of all atoms inside the corresponding box. In this way, we obtained a temperature profile along the z‐axis to calculate the surface temperature T surf. This compartmentalization also allowed us to analyze the individual temperature profiles of the oxygen atmosphere, the Mg/O interface, and bulk magnesium (Figures S14, S15, and S16).
Figure 7.
NVT simulation of the oxidation behavior of Mg(0001) at 300 K and an O2 partial pressure 10 atm. Upon contact of the first O2 molecules, the surface heats to several 1000 K. The high temperature fosters the formation of a rock salt interphase structure on top of the Mg anode. The maximum surface temperature T surf,max was determined from the temperature profiles in Figure S14.
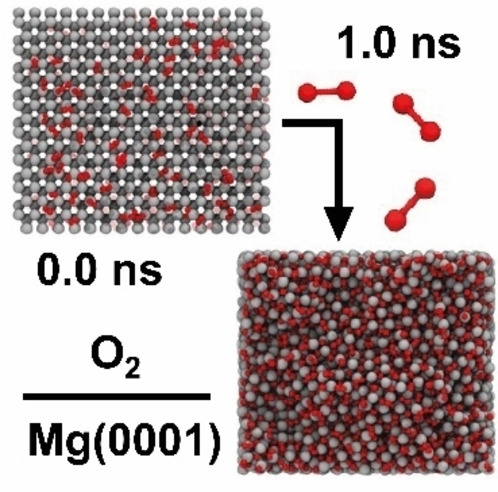
The first oxygen molecules hitting the metal surface instantaneously dissociate and heat the surface to several 1000 K within the first 0.1 ns. On Mg(0001), the high temperature causes short‐term detachment of individual MgO clusters, which later readsorb on the surface. In addition, the elevated temperature causes high mobility at the interface, leading to surface recrystallization into the rock salt structure. However, the structures observed in this simulation are significantly more disordered compared to the recrystallized MgO particle (Figure 7), showing a multitude of grain boundaries connecting several rock salt phase domains. The peak of the average temperature is reached at about 0.4 ns. From this point on, the thermostat extracts kinetic energy at a higher rate than the rate at which MgO formation releases energy. Nevertheless, the temperature at the surface of T surf,max=985 K remains significantly higher than in the bulk phase of the cell (Figure S14). At about 0.75 ns, equilibrium is reached, and MgO formation at the interface is complete, as underlined by molecular composition analysis (Figure S13). The number of intact O2 molecules in the atmosphere or adsorbed on the surface remains constant, which is also true for O‐atoms bound in the MgO boundary phase. Similar trends as for Mg(0001) are also observed in simulations with Mg(10 0)A and Mg(10 1) surfaces in contact with oxygen; in fact, we found these surfaces to be even more reactive. The relative energy decreases the most for Mg(10 0)A surface model and the oxidation penetrates the deepest, likely due to the more open surface structure. Over the course of oxidation, the average temperature reaches the highest values for Mg(10 0)A and remains on a plateau for the longest time before decreasing again (Figure S15). Similarly, molecular composition analysis in Figure S13 shows that on Mg(10 0)A, most O2 molecules were decomposed and bound in the MgO phase, followed by Mg(10 1) and finally Mg(0001) (Figure S13). This trend aligns with the relative surface energies, where Mg(10 0)A and Mg(10 1) surfaces are less stable than Mg(0001) (see Table 2).
Fournier et al. experimentally studied the oxidation of magnesium by exposing Mg to a pure oxygen atmosphere at 20 kPa and determined an MgO layer thickness of 260 Å at 300 K (170 Å at 150 K) for a 15 min exposure time. [29] A simulation over such a long time is currently impossible with the ReaxFF method. Our simulation covers the first nanosecond and describes the initial contact of O2 with the Mg surface. The thickness of the MgO resulting from our simulations constitute about one‐tenth of the overall surface thickness (Mg(0001)≈20 Å, Mg(10 0)A≈25 Å, Mg(10 1)≈21 Å). Larger oxide layer thickness could likely be observed by using significantly more surface layers, and by turning off the thermostat which dampens oxygen mobility increasingly the deeper that oxygen atoms penetrate into the slab. Fournier et al. also suggested that the surface oxide growth at 300 K follows an inverse logarithmic law. This is consistent with our observations that after initial contact, the surface is heated to such an extent that oxidation to deeper layers is facilitated. However, once the first oxide layer is formed and the surface temperature has normalized, diffusion of oxygen bound in the MgO interphase into deeper surface layers is likely the rate‐determining step. [32]
Conclusion
In this work, we developed a reactive force field description for Mg/O systems for the ReaxFF framework. Magnesium‐magnesium interactions were obtained using the KVIK optimization routine designed explicitly for metallic systems, while magnesium‐oxygen interactions were trained using the successive one‐parameter parabolic interpolation (SOPPI) optimizer. As a result, the force field can reliably reproduce the bulk, surface, adsorption, and diffusion properties of both metallic Mg and the MgO salt.
We first showed in a GCMC simulation that, from a thermodynamic point of view, a Mg nanoparticle (here 978 atoms) is first oxidized at surface oct sites. The structure obtained at the end of the simulation is mostly amorphous with individual domains showing rock salt ordering, separated by grain boundaries. For complete transformation to the rock salt structure, the particle must be heated to 2000 K in an MD simulation for at least 75 ps. If the thermal annealing is performed at too low temperatures or the system is cooled down too quickly, grain boundaries remain visible.
We further showed the effects of oxygen impurities on Mg surfaces. We demonstrated that O2 immediately dissociates upon first contact with the Mg surface, heating the surface to several 1000 K. The high temperature catalyzes further oxidation and causes the formation of rock salt phases separated by grain boundaries. Among the Mg surfaces, Mg(1010)A is the most reactive, forming an MgO layer with a thickness of up to 25 Å.
The future goal is to extend the presented force field by Mg/H and Mg/C parameters to obtain a full magnesium electrolyte description to model the initial steps of SEI formation in Mg batteries. For the moment, our trained force field offers the opportunity to study the passivation and oxidation of metallic Mg in more detail or to investigate the ongoing reactions in Mg‐air batteries.[ 50 , 51 , 52 ]
Computational Details
The ReaxFF reactive force field method
ReaxFF is a reactive force field method introduced by van Duin et al. that can model bond breakages and formations without explicitly describing the system's electronic structure.[ 53 , 54 ] To this end, ReaxFF employs an empirical approach that first translates the inter‐atomic distance across all atoms into a continuous bond‐order function BOij , which is further divided into σ ( ), π ( ), and ππ ( ) bond contributions [Eq. (1)]. The continuity of the function provides constant differentiability of the energy landscape, which is necessary to calculate the forces acting on the atoms. Thus, ReaxFF enables to accurately describe bond transitions and long‐distance covalent interactions which are necessary to account for transition states and reaction barriers. [55] The bond‐order formalism is defined as:
| (1) |
where BOij is the total bond‐order between two atoms i and j, rij is the inter‐atomic distance, r 0 are the equilibrium bond distances of the bonds, and p bo1 to p bo6 are empirical parameters. Thereupon, the system's total energy E system is calculated using Equation (2), which is composed of several bond‐order dependent energy terms like the binding energy E bond, three‐body angular E angle and four‐body torsional energy E tors, and penalty energy terms for over E over and under coordination E under. Non‐bond‐order dependent energy terms are the electrostatic Coulomb energy E Coulomb and the dispersive van der Waals interactions E vdWaals:
| (2) |
The last energy term E specific summarizes energy contributions that were not relevant to our force field, such as hydrogen bonding or the energy correction in conjugated systems. For a detailed description of the energy terms, we refer to the Supporting Information in the work of Chenoweth et al. [54] To calculate the non‐bond‐order dependent Coulomb energy, we applied the polarizable charge approach electron equilibration method (EEM) developed by Mortier et al., which provides a good description of metallic systems. [56] Moreover, we do not consider compressed systems in which EEM can lead to unrealistically high Coulomb attractions. [53]
ReaxFF force field training
The training set for the Mg/Mg and Mg/O parameters was entirely composed of quantum chemical calculations. The Mg/Mg parameters were trained against data from our previous publication, [38] while the Mg/O training data is presented in this work. The O/O parameters were adapted from the battery electrolyte force field from Hossain et al. [27] The Mg/Mg parameters were trained using the KVIK optimization routine, which was developed in particular for fast and accurate training of metal ReaxFF force fields. [22] After each optimization cycle, all structures are rescaled with the optimal lattice constant. Otherwise, stresses in the unit cell can significantly affect adsorption energy results or diffusion barriers as Stottmeister and Groß showed. [57] The Mg/O parameters, on the other hand, were trained with the classical successive one‐parameter parabolic interpolation (SOPPI). [58] In general, every optimizer has strengths and weaknesses with no guarantee of getting to the global minimum on the first try. [59] Instead, the training process involves many consecutive training cycles, in which the weighting of the training data is continuously adjusted.
The cohesive energies E coh for the following Mg crystal phases hcp, fcc, bcc, a15, and sc were calculated by Equation 3:
| (3) |
where is the energy of the Mg bulk crystal structure, is the energy of an isolated Mg atom and N is the amount of Mg atoms in the corresponding bulk unit cell.
In contrast, the heats of formation ▵f H for the MgO crystal phases rock salt, wurtzite, zincblende, cesium chloride, and hcp were obtained as follows:
| (4) |
where is the bulk energy of the MgO crystal phase, is the bulk energy of hcp Mg per Mg atom, is the gas‐phase energy of one oxygen molecule, is the vibrational zero point energy within the harmonic normal approximation, and N is the amount of MgO fragments within the MgO crystal phase.
The bulk modulus was obtained with the jellium equation of state[ 60 , 61 ] and the vacancy energy E v was calculated in a (2×2×2) MgO rock salt unit cell with the following equation:
| (5) |
where is the bulk energy of the rock salt structure, is the bulk energy of the rock salt structure with one missing oxygen atom and is the gas‐phase energy of one oxygen molecule.
The surface energy γ was determined as shown below:
| (6) |
where E slab is the energy of the surface slab, E bulk is the bulk energy per Mg atom/MgO fragment, N is the amount of Mg atoms/MgO fragments in the slab, and A is the surface slab area. The area A has to be multiplied by two because of the symmetric slab configuration. The Wulff construction [40] and the area fractions were obtained using the Python package WulffPack. [41]
The adsorption energies E ad were calculated by subtracting the energy of the slab E slab and the adsorbate E adsorbate from the energy of the relaxed structure E tot containing the slab and the adsorbate. For a magnesium adsorbate, E adsorbate equaled the energy of an isolated Mg atom E atom and for an oxygen adsorbate E adsorbate corresponded to half of the energy of an O2 molecule :
| (7) |
The activation energy equaled the energy difference between a stable adsorption position E IS/FS and the transition state energy E TS of a diffusion process from (forward or to (reverse) this position:
| (8) |
DFT calculations
All first principles calculations to obtain the training set for the parameterization of the Mg/O parameters were performed with the periodic plane‐wave DFT code Vienna ab initio simulation package (VASP).[ 62 , 63 ] The description of the core electrons was carried out using the projector augmented wave (PAW) method where the Mg 2s and O 2s4p electrons were considered as valence electrons.[ 64 , 65 ] The exchange and correlation energy was described using the Perdew, Burke, and Enzerhof (PBE) functional following the generalized gradient approximation (GGA) approach. [66] After a detailed convergence study, we chose the cutoff energy to be 500 eV (Figure S1a) and the k‐points sampling using a gamma‐centered mesh (due to the hexagonal symmetry of hcp Mg) with a minimum grid density of 0.14 Å−1 (Figure S1b). We also ensured that the number of k‐points in one direction was always rounded up to the next odd integer. To provide consistency with the Mg/Mg training set, we used Gaussian smearing with a width of 0.1 eV for the one‐electron states as we did for metallic magnesium. [38] The convergence criterion for the electronic self‐consistent field (SCF) was set to a maximum energy difference of 1×10−5 eV between two consecutive minimization cycles, and the norms of all forces had to be less than 1×10−3 eV Å−1. Surface energy results were calculated using (1×1) cells with a minimum thickness of 20 Å and an equally large vacuum region. Oxygen adsorption energy results and diffusion barriers were calculated on (4×4) Mg(0001), (4×2) Mg(10 0)A, and (4×2) Mg(10 1) periodic surface models with six surface layers where the coordinates of the lowest two layers were constrained to simulate bulk behavior. To find the transition state, we applied the climbing image nudged elastic band (CI‐NEB) method as implemented in the transition state tools for VASP (VTST) package.[ 67 , 68 ] Here, we used five images to represent the minimum energy path (MEP), each separated by a spring constant of 5.0 eV Å−2. We used the image‐dependent pair potential (IDPP) as the initial estimate for the MEP to achieve faster convergence.[ 69 , 70 ] To confirm stable adsorption positions and transition states, we determined the vibrational frequencies of the diffusing atom and its nearest neighbor atoms along the diffusion path. Stable adsorption sites were required to have no imaginary frequency while transition states must have exactly one imaginary frequency due to a maximum in the potential energy surface in one direction. To calculate harmonic normal modes, we used the dynamical matrix method from the VTST package where the respective atoms were displaced by 0.001 Å in each direction. To this end, we increased the electronic and ionic convergence criteria to 1×10−8 eV and 1×10−8 eV Å−1, respectively.
ReaxFF grand‐canonical Monte Carlo simulations
We used the GCMC algorithm implemented in the AMS driver program, [71] originally developed by Senftle et al. as an extension for standalone ReaxFF. [72] In a TVμ O N Mg ensemble, the algorithm randomly decides whether an oxygen atom should be (1) inserted, (2) removed, or (3) displaced in the system. The coordinates for the insertion and displacement steps are chosen randomly. The algorithm places atoms further than 1.85 Å to the nearest atom to prevent a Coulomb collapse (excessive Coulomb attraction) but closer than 3.0 Å to achieve faster convergence. Subsequently, the system's geometry is relaxed until the norms of all forces were less than 0.1 eV Å−1 or the maximum number of steps (1000) was reached. [73] Finally, the probabilities from Equations (9), (10), and (11) decided whether the executed Monte Carlo (MC) step is accepted or rejected:
| (9) |
| (10) |
| (11) |
In Equations (9), (10), and (11), N is equal to the the number of exchangeable particles in the system before the MC move, V is the volume of the system, Λ corresponds to the thermal de Brogli wavelength of the exchanged particle, β equals the Boltzmann factor (β=1/k B T), and E 1 and E 2 are the potential energy values of the system before and after the MC move. The chemical potential of the single oxygen atom is set to be μ O=3.13 eV and was calculated under ambient conditions at 300 K and 0.21 atm using Equation (12):
| (12) |
which is half the experimental chemical potential of an O2 molecule minus its zero‐Kelvin bond dissociation energy . The experimental oxygen chemical potential was determined via the Showmate equation using parameters from the thermochemical tables of the NIST‐JANAF. [74] The bond dissociation energy of the O2 molecule ( =5.59 eV) was calculated using ReaxFF.
The input structure of the Mg nanoparticle was obtained using the Python package WulffPack. [41] The surface energies calculated with ReaxFF presented in Table 2 served as input to generate a 978 atom‐sized particle in a 100 Å×100 Å×100 Å simulation box.
ReaxFF molecular dynamics simulations
MD simulations were performed within the AMS driver program [71] using the Velocity‐Verlet algorithm with a time step of 0.25 fs. [75] The geometry of the system was optimized before each MD simulation until the norms of all forces on all atoms were below 0.1 eV Å−1 to avoid simulation artifacts due to high‐energy starting configurations.
We performed the recrystallization of the MgO particle in an NVT ensemble using a NHC thermostat with a time constant τ of 100 fs. The initial geometry corresponded to the MgO particle obtained by the GCMC simulations, shown in the blue box in Figure 5. Simulations of the Mg anode used (16×16) Mg(0001), (16×8) Mg(10 0)A and (16×8) Mg(10 1) periodic surface model systems with 60 layers for 1 ns (≙4 000 000 iterations with 0.25 fs time step). On each side of the surface slab was a vacuum of 2000 Å thickness filled with 5504 O2 molecules whose atomic configurations were generated using the PACKMOL software. [76] We calculated the number of O2 molecules using the ideal gas law at 300 K at ten times atmospheric pressure (10 atm). The initial velocities of all atoms followed a Maxwell‐Boltzmann distribution for 300 K. Furthermore, we applied a weakly coupled NHC thermostat (τ=1000 fs) to the ten innermost Mg layers at 300 K to provide a heat sink for the reaction heat generated at the surface. The choice to use a heat sink region constitutes a compromise: in simulations without a thermostat, the Mg surface heated far beyond its melting temperature due to the strongly exothermic oxidation reaction taking place and evaporation was observed. The number of surface layers required to serve as a heat sink to compensate for this effect is computationally inefficient. In contrast, applying the thermostat to all atoms quenches the surface reactions altogether. With the thermostat layer used here, the surface heats up to several 1000 K for a short time upon first contact of the bare Mg surface with oxygen but the surface remains intact. An illustration of the cell setup and the simulation settings used are given in Figure S2.
Author Contributions
F.F. performed all the calculations except of the force field training of the magnesium‐magnesium interactions which was performed by D.G. F.F. analyzed and discussed all results together with D.G., M.B., and J.B. A.C.T.v.D. and T.J. supervised the research. The manuscript was written by F.F. and all authors commented on the manuscript.
Conflict of interest
The authors declare no conflict of interest.
1.
Supporting information
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supporting Information
Acknowledgments
This work contributes to the research performed at the Center for Electrochemical Energy Storage Ulm‐Karlsruhe (CELEST) and was partly funded by the German Research Foundation (DFG) under Project‐ID 390874152 (POLiS Cluster of Excellence). Further support through the DFG‐research unit FOR‐5065 (ELSICS) under Project‐ID 428906592 is gratefully acknowledged. The authors acknowledge support by the state of Baden‐Württemberg through bwHPC and the DFG through grant no INST 40/575‐1 FUGG (JUSTUS 2 cluster). F.F. sincerely thanks Dr. Björn Kirchhoff and Dr. Christoph Jung for helpful discussions and comments on the manuscript. A.C.T.v.D. acknowledges funding from a grant from the U.S. Army Research Laboratory through the Collaborative Research Alliance (CRA) for Multi‐Scale Multidisciplinary Modeling of Electronic Materials (MSME) under Cooperative Agreement No. W911NF‐12‐2‐0023. Open Access funding enabled and organized by Projekt DEAL.
Fiesinger F., Gaissmaier D., van den Borg M., Beßner J., van Duin A. C. T., Jacob T., ChemSusChem 2023, 16, e202201821.
A previous version of this manuscript has been deposited on a preprint server (https://doi.org/10.5281/zenodo.7074790)
Data Availability Statement
The data that support the findings of this study are openly available in zenodo at https://doi.org/10.5281/zenodo.7074790. Furthermore, the KVIK optimization routine is openly available in the GitHub repository at https://github.com/shk11/KVIKOptimizer.
References
- 1. Liang Y., Dong H., Aurbach D., Yao Y., Nat. Energy 2020, 5, 646. [Google Scholar]
- 2. Bonnick P., Muldoon J., Adv. Funct. Mater. 2020, 30, 1. [Google Scholar]
- 3. Liu F., Wang T., Liu X., Fan L., Adv. Energy Mater. 2021, 11, 2000787. [Google Scholar]
- 4. Song J., Sahadeo E., Noked M., Lee S. B., J. Phys. Chem. Lett. 2016, 7, 1736. [DOI] [PubMed] [Google Scholar]
- 5. Li D., Yuan Y., Liu J., Fichtner M., Pan F., J. Magnesium Alloys 2020, 8, 963. [Google Scholar]
- 6. Liang Z., Ban C., Angew. Chem. Int. Ed. 2021, 60, 11036. [DOI] [PubMed] [Google Scholar]
- 7. Shi J., Zhang J., Guo J., Lu J., Nanoscale Horiz. 2020, 5, 1467. [DOI] [PubMed] [Google Scholar]
- 8. Attias R., Salama M., Hirsch B., Goffer Y., Aurbach D., Joule 2019, 3, 27. [Google Scholar]
- 9. Sun Y., Ai F., Lu Y., Small 2022, 18, 2200009. [DOI] [PubMed] [Google Scholar]
- 10. Rajput N. N., Qu X., Sa N., Burrell A. K., Persson K. A., J. Am. Chem. Soc. 2015, 137, 3411. [DOI] [PubMed] [Google Scholar]
- 11. Lu Z., Schechter A., Moshkovich M., Aurbach D., J. Electroanal. Chem. 1999, 466, 203. [Google Scholar]
- 12. Eaves-Rathert J., Moyer K., Zohair M., Pint C. L., Joule 2020, 4, 1324. [DOI] [PubMed] [Google Scholar]
- 13. Yoo H. D., Han S.-D., Bolotin I. L., Nolis G. M., Bayliss R. D., Burrell A. K., Vaughey J. T., Cabana J., Langmuir 2017, 33, 9398. [DOI] [PubMed] [Google Scholar]
- 14. Davidson R., Verma A., Santos D., Hao F., Fincher C., Xiang S., Van Buskirk J., Xie K., Pharr M., Mukherjee P. P., Banerjee S., ACS Energy Lett. 2019, 4, 375. [Google Scholar]
- 15. van den Borg M., Gaissmaier D., Knobbe E., Fantauzzi D., Jacob T., Appl. Surf. Sci. 2021, 555, 149447. [Google Scholar]
- 16. van den Borg M., Gaissmaier D., Fantauzzi D., Knobbe E., Jacob T., ChemSusChem 2022, 15, e2021017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Connell J. G., Genorio B., Lopes P. P., Strmcnik D., Stamenkovic V. R., Markovic N. M., Chem. Mater. 2016, 28, 8268. [Google Scholar]
- 18. Islam M. M., Ostadhossein A., Borodin O., Yeates A. T., Tipton W. W., Hennig R. G., Kumar N., van Duin A. C. T., Phys. Chem. Chem. Phys. 2015, 17, 3383. [DOI] [PubMed] [Google Scholar]
- 19. Islam M. M., van Duin A. C. T., J. Phys. Chem. C 2016, 120, 27128. [Google Scholar]
- 20. Islam M. M., Kolesov G., Verstraelen T., Kaxiras E., van Duin A. C. T., J. Chem. Theory Comput. 2016, 12, 3463. [DOI] [PubMed] [Google Scholar]
- 21. O'Hearn K. A., Swift M. W., Liu J., Magoulas I., Piecuch P., van Duin A. C. T., Aktulga H. M., Qi Y., J. Chem. Phys. 2020, 153, 084107. [DOI] [PubMed] [Google Scholar]
- 22. Gaissmaier D., van den Borg M., Fantauzzi D., Jacob T., ChemRxiv preprint 2022, DOI: 10.26434/chemrxiv-2022-lrsjd-v2. [Google Scholar]
- 23. Ostadhossein A., Kim S.-Y., Cubuk E. D., Qi Y., van Duin A. C. T., J. Phys. Chem. A 2016, 120, 2114. [DOI] [PubMed] [Google Scholar]
- 24. Bedrov D., Smith G. D., van Duin A. C. T., J. Phys. Chem. A 2012, 116, 2978. [DOI] [PubMed] [Google Scholar]
- 25. Shin Y. K., Sengul M. Y., Jonayat A. S. M., Lee W., Gomez E. D., Randall C. A., v. Duin A. C. T., Phys. Chem. Chem. Phys. 2018, 20, 22134. [DOI] [PubMed] [Google Scholar]
- 26. Islam M. M., Bryantsev V. S., van Duin A. C. T., J. Electrochem. Soc. 2014, 161, E3009. [Google Scholar]
- 27. Hossain M. J., Pawar G., Liaw B., Gering K. L., Dufek E. J., van Duin A. C. T., J. Chem. Phys. 2020, 152, 184301. [DOI] [PubMed] [Google Scholar]
- 28. Song G., Atrens A., Adv. Eng. Mater. 2003, 5, 837. [Google Scholar]
- 29. Fournier V., Marcus P., Olefjord I., Surf. Interface Anal. 2002, 34, 494. [Google Scholar]
- 30. Song G., Atrens A., Adv. Eng. Mater. 2007, 9, 177. [Google Scholar]
- 31. Tan Q., Atrens A., Mo N., Zhang M.-X., Corros. Sci. 2016, 112, 734. [Google Scholar]
- 32. Nie H., Schoenitz M., Dreizin E. L., J. Phys. Chem. C 2016, 120, 974. [Google Scholar]
- 33. Cheung S., Deng W.-Q., van Duin A. C. T., Goddard W. A., J. Phys. Chem. A 2005, 109, 851. [DOI] [PubMed] [Google Scholar]
- 34. Iype E., Hütter M., Jansen A. P. J., Nedea S. V., Rindt C. C. M., J. Comput. Chem. 2013, 34, 1143. [DOI] [PubMed] [Google Scholar]
- 35. Zhu R., Janetzko F., Zhang Y., van Duin A. C. T., Goddard W. A., Salahub D. R., Theor. Chem. Acc. 2008, 120, 479. [Google Scholar]
- 36. Yeon J., Chowdhury S. C., Daksha C. M., Gillespie J. W., J. Phys. Chem. C 2021, 125, 18380. [Google Scholar]
- 37. Raymand D., van Duin A. C., Baudin M., Hermansson K., Surf. Sci. 2008, 602, 1020. [Google Scholar]
- 38. Fiesinger F., Gaissmaier D., van den Borg M., Jacob T., ChemSusChem 2022, 15, e202200414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Kittel C., Introduction to Solid State Physics, 8th Edition, Wiley, Hoboken: 2004. [Google Scholar]
- 40. Wulff G., Kristallogr. 1901, 34, 449. [Google Scholar]
- 41. Rahm J., Erhart P., J. Open Source Softw. 2020, 5, 1944. [Google Scholar]
- 42. Burton W. K., Cabrera N., Frank F. C., Phil. Trans. R. Soc. A 1951, 243, 299. [Google Scholar]
- 43. McWilliams R. S., Spaulding D. K., Eggert J. H., Celliers P. M., Hicks D. G., Smith R. F., Collins G. W., Jeanloz R., Science 2012, 338, 1330. [DOI] [PubMed] [Google Scholar]
- 44. Sangster M. J. L., Peckham G., Saunderson D. H., J. Phys. C 1970, 3, 1026. [Google Scholar]
- 45. Lide D., CRC Handbook of Chemistry and Physics, 90th Edition, CRC Press, Boca Raton: 2009. [Google Scholar]
- 46. Reuter K., Scheffler M., Phys. Rev. B 2001, 65, 035406. [Google Scholar]
- 47. Jura G., Garland C. W., J. Am. Chem. Soc. 1952, 74, 6033. [Google Scholar]
- 48. Westwood A. R. C., Goldheim D. L., J. Appl. Phys. 1963, 34, 3335. [Google Scholar]
- 49. Francis M. F., Taylor C. D., Phys. Rev. B 2013, 87, 075450. [Google Scholar]
- 50. Li C., Sun Y., Gebert F., Chou S., Adv. Energy Mater. 2017, 7, 1700869. [Google Scholar]
- 51. Lu Y.-T., Neale A. R., Hu C.-C., Hardwick L. J., Front. Energy Res. 2021, 8. [Google Scholar]
- 52. Hardwick L. J., De León C. P., Johnson Matthey Technol. Rev. 2018, 62, 134. [Google Scholar]
- 53. van Duin A. C. T., Dasgupta S., Lorant F., Goddard W. A., J. Phys. Chem. A 2001, 105, 9396. [Google Scholar]
- 54. Chenoweth K., van Duin A. C. T., Goddard W. A., J. Phys. Chem. A 2008, 112, 1040. [DOI] [PubMed] [Google Scholar]
- 55. Senftle T. P., Hong S., Islam M. M., Kylasa S. B., Zheng Y., Shin Y. K., Junkermeier C., EngelHerbert R., Janik M. J., Aktulga H. M., Verstraelen T., Grama A., Van Duin A. C., npj Comput. Mater. 2016, 2, 15011. [Google Scholar]
- 56. Mortier W. J., Ghosh S. K., Shankar S., J. Am. Chem. Soc. 1986, 108, 4315. [Google Scholar]
- 57. Stottmeister D., Groß A., ChemSusChem 2020, 13, 3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. van Duin A. C. T., Baas J. M. A., van de Graaf B., J. Chem. Soc. Faraday Trans. 1994, 90, 2881. [Google Scholar]
- 59. Shchygol G., Yakovlev A., Trnka T., van Duin A. C. T., Verstraelen T., J. Chem. Theory Comput. 2019, 15, 6799. [DOI] [PubMed] [Google Scholar]
- 60. Alchagirov A. B., Perdew J. P., Boettger J. C., Albers R. C., Fiolhais C., Phys. Rev. B 2001, 63, 224115. [Google Scholar]
- 61. Alchagirov A. B., Perdew J. P., Boettger J. C., Albers R. C., Fiolhais C., Phys. Rev. B 2003, 67, 026103. [Google Scholar]
- 62. Kresse G., Furthmüller J., Phys. Rev. B 1996, 54, 11169. [DOI] [PubMed] [Google Scholar]
- 63. Kresse G., Furthmüller J., Comput. Mater. Sci. 1996, 6, 15. [Google Scholar]
- 64. Blöchl P. E., Phys. Rev. B 1994, 50, 17953. [DOI] [PubMed] [Google Scholar]
- 65. Joubert D., Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758. [Google Scholar]
- 66. Perdew J. P., Burke K., Ernzerhof M., Phys. Rev. Lett. 1996, 77, 3865. [DOI] [PubMed] [Google Scholar]
- 67. Henkelman G., Jónsson H., J. Chem. Phys. 2000, 113, 9978. [Google Scholar]
- 68. Henkelman G., Uberuaga B. P., Jónsson H., J. Chem. Phys. 2000, 113, 9901. [Google Scholar]
- 69. Smidstrup S., Pedersen A., Stokbro K., Jónsson H., J. Chem. Phys. 2014, 140, 214106. [DOI] [PubMed] [Google Scholar]
- 70. Hjorth Larsen A., Jørgen Mortensen J., Blomqvist J., Castelli I. E., Christensen R., Dułak M., Friis J., Groves M. N., Hammer B., Hargus C., Hermes E. D., Jennings P. C., Bjerre Jensen P., Kermode J., Kitchin J. R., Leonhard Kolsbjerg E., Kubal J., Kaasbjerg K., Lysgaard S., Bergmann Maronsson J., Maxson T., Olsen T., Pastewka L., Peterson A., Rostgaard C., Schiøtz J., Schütt O., Strange M., Thygesen K. S., Vegge T., Vilhelmsen L., Walter M., Zeng Z., Jacobsen K. W., J. Phys. Condens. Matter 2017, 29, 273002. [DOI] [PubMed] [Google Scholar]
- 71.R. Rüger, M. Franchini, T. Trnka, A. Yakovlev, E. van Lenthe, P. Philipsen, T. van Vuren, B. Klumpers, T. Soini, AMS 2021, SCM, Vrije Universiteit, Amsterdam (The Netherlands) 2021.
- 72. Senftle T. P., Meyer R. J., Janik M. J., van Duin A. C. T., J. Chem. Phys. 2013, 139, 044109. [DOI] [PubMed] [Google Scholar]
- 73. Bitzek E., Koskinen P., Gähler F., Moseler M., Gumbsch P., Phys. Rev. Lett. 2006, 97, 170201. [DOI] [PubMed] [Google Scholar]
- 74. Chase M. W., NIST-JANAF Thermochemical Tables, 4th Edition, American Institute of Physics, College Park: 1998. [Google Scholar]
- 75. Verlet L., Phys. Rev. 1967, 159, 98. [Google Scholar]
- 76. Martínez L., Andrade R., Birgin E. G., Martínez J. M., J. Comput. Chem. 2009, 30, 2157. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supporting Information
Data Availability Statement
The data that support the findings of this study are openly available in zenodo at https://doi.org/10.5281/zenodo.7074790. Furthermore, the KVIK optimization routine is openly available in the GitHub repository at https://github.com/shk11/KVIKOptimizer.