Optical Spin Polarization of a Narrow‐Linewidth Electron‐Spin Qubit in a Chromophore/Stable‐Radical System

Abstract

Photoexcited organic chromophores appended to stable radicals can serve as qubit and/or qudit candidates for quantum information applications. 1,6,7,12‐Tetra‐(4‐tert‐butylphenoxy)‐perylene‐3,4 : 9,10‐bis(dicarboximide) (tpPDI) linked to a partially deuterated α,γ‐bisdiphenylene‐β‐phenylallyl radical (BDPA‐d ₁₆) was synthesized and characterized by time‐resolved optical and electron paramagnetic resonance (EPR) spectroscopies. Photoexcitation of tpPDI‐BDPA‐d ₁₆ results in ultrafast radical‐enhanced intersystem crossing to produce a quartet state (Q) followed by formation of a spin‐polarized doublet ground state (D ₀). Pulse‐EPR experiments confirmed the spin multiplicity of Q and yielded coherence times of T _m=2.1±0.1 μs and 2.8±0.2 μs for Q and D ₀, respectively. BDPA‐d ₁₆ eliminates the dominant ¹H hyperfine couplings, resulting in a single narrow line for both the Q and D ₀ states, which enhances the spectral resolution needed for good qubit addressability.

A promising approach to molecular qubits employs a photoexcited chromophore covalently linked to a deuterated stable radical (C−R⋅). Photoexcitation of the C within C−R⋅ results in ultrafast intersystem crossing to produce the spin‐polarized quartet state (Q) that decays to the spin‐polarized ground state (D₀ ). Both Q and D₀ have narrow linewidths that allow facile addressability using microwave pulses.

Introduction

Quantum bits, i.e. qubits, are essential to quantum computation, communication, and sensing technologies.[ ¹ , ² , ³ ] Aside from current qubit candidates, such as photons ^[4] and superconducting states in Josephson junctions, ^[5] solid‐state defects, such as the nitrogen vacancy (NV) center in diamond ^[6] and the neutral carbon divacancy center in silicon carbide, ^[7] have been investigated extensively because they can be optically pumped to achieve highly spin‐polarized states and read out using optically detected magnetic resonance (ODMR) spectroscopy. Despite these advantages, significant challenges remain in spatially controlling these defects with atomic precision in the diamond or SiC lattice. In contrast, molecular qubits have synthetic flexibility, can be positioned with atomic precision, have long coherence times, are capable of optical spin initialization and readout, ^[8] and their properties can be modified using different chemical environments. ^[9] Moreover, molecular qubits can be easily assembled into extended qubit arrays using various methods, including doping single crystals and incorporating the qubits into metal–organic frameworks. ^[10] The advantages of synthetic tunability and scalability have sparked recent efforts to prepare and characterize molecular qubits.[ ⁸ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ ]

A promising approach to molecular qubits having optical pumping and addressability properties like those of NV centers uses photoexcited covalently linked chromophore‐stable radical (C−R⋅) systems. Figure 1 depicts a typical photophysical pathway of a C−R⋅ molecule. Upon photoexcitation, the chromophore of the doublet ground state (¹C−²R⋅, D ₀) is optically pumped to its first excited state (¹*C−²R⋅, D ₁), followed by enhanced intersystem crossing (EISC) driven by the exchange interaction between the two spin paired electrons on ¹*C with the unpaired electron on ²R⋅ to generate ³*C−²R⋅. The resulting three‐spin system is best described at high magnetic fields as an excited doublet state [²(³*C−²R⋅), D ₂] and a quartet state [⁴(³*C−²R⋅), Q]. The transition from D ₁ to D ₂ is more rapid than that from D ₁ to Q because the former is spin allowed while the latter is spin forbidden. The spin Hamiltonian of a triplet chromophore spin coupled to a doublet radical is described as:

$${\displaystyle \mathbf{H}=\beta (\mathbf{S}{}_{T}g{}_T+\mathbf{S}{}_{R}g{}_R)\mathbf{B}-2J{}_{TR}\mathbf{S}{}_T\mathbf{S}{}_R+\mathbf{H}{}_{ZFS}}$$ (1)

Figure 1.

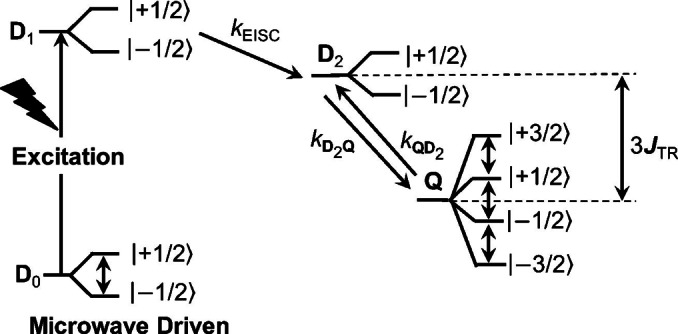
Schematic representation of the photophysical process of a photoexcited chromophore‐radical system. Detailed photophysical pathways are introduced in the text. The resonant microwave pulses induce the change of population in different spin sublevels, which can be detected through absorption or emission spectroscopies.

where the subscript symbols R and T represent the doublet radical and the photogenerated triplet chromophore, respectively. The first term in Eq. (1) is the Zeeman interaction, the second term is the spin‐spin exchange interaction (J_TR ) between the chromophore triplet and radical doublet states, and the third term is the zero‐field splitting (ZFS) between the two unpaired electrons on the chromophore triplet state. The D ₂ and Q states are separated by an energy difference of 3J_TR , and typically, Q is lower in energy than D ₂ due to the molecular extension of Hund's rule. ^[16] The spin states of D ₁, D ₂, and Q, are also often referred to as sing‐doublet, trip‐doublet, and trip‐quartet, respectively, to show the spin multiplicity of the overall state and that of the chromophore. ^[17] Since D ₁ and D ₂ have the same spin multiplicity, the transition from D ₁ to D ₂ is more rapid than that to Q, which is populated by spin‐orbit‐induced intersystem crossing (SO‐ISC) from the D ₂ state driven by the ZFS.[ ¹⁸ , ¹⁹ , ²⁰ ] Furthermore, decay of Q to the ground doublet state D ₀ is spin forbidden, allowing a sufficiently long lifetime to probe and manipulate Q using resonant microwave pulses. Eventually, a hyperpolarized ground doublet state (¹C−²R⋅, D ₀) can be achieved after multiple photoexcitation and relaxation cycles to serve as a qubit with a well‐defined spin state. Moreover, the three electronic spins in the photogenerated quartet state Q form a multi‐level qubit, or qudit that can reduce the number of entangled gates required in quantum algorithms, thus improving algorithmic efficiency. ^[21] C−R⋅ molecules also offer the possibility of optical readout of spin information because the chromophore excited state fluoresces as well as has readily observable excited‐state absorptions. Thus, C−R⋅ molecules satisfy key DiVincenzo criteria for a functional qubit. ^[22]

Early examples of photogenerated molecular quartet states were observed using porphyrin and fullerene chromophores connected to stable nitroxide radicals via covalent or coordination bonds.[ ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ ] Metalloporphyrins with paramagnetic metals also exhibit photogenerated quartet spin states.[ ¹⁷ , ²⁹ , ³⁰ , ³¹ ] In addition, our previous work has demonstrated that perylene‐3,4 : 9,10‐bis(dicarboximide) (PDI), 1,7‐bis(4‐tert‐butylphenoxy‐PDI (dpPDI), and 1,6,7,12‐tetrakis(4‐tert‐butylphenoxy)‐PDI (tpPDI) chromophores linked to nitroxide radicals can produce quartet states and subsequently spin‐polarize the nitroxide doublet ground state.[ ¹¹ , ³² ] However, the nuclear hyperfine splittings of the metals in the porphyrins and ¹⁴N in the nitroxide radicals increase the spectral complexity as well as broaden the signal linewidth. For example, in tpPDI‐TEMPO, the spin polarization pattern of central quartet transition exhibits an eae EPR pattern at X‐band due to the ¹⁴N hyperfine splitting of TEMPO, which reverses its phase to aea at Q‐band, where a=enhanced absorption and e=emission. ^[11]

In order to simplify manipulations of the three‐spin system using microwave pulses that target QIS applications, here we describe a new molecular spin qubit candidate featuring a partially deuterated α,γ‐bisdiphenylene‐β‐phenylallyl radical (BDPA‐d ₁₆) attached to a nitrogen atom of tpPDI (1) (Scheme 1). The PDI chromophore in 1 has demonstrated exceptional chemical, optical and electrical stability in various applications,[ ³³ , ³⁴ ] and the BDPA radical also shows excellent stability. ^[35] Upon photoexcitation, 1 produces a spin‐polarized quartet state Q, whose spin state is characterized using transient nutation spectroscopy. This photogenerated quartet state Q and the subsequent spin‐polarized D₀ ground state exhibit long coherence times, adequate for quantum logic gate operations. In contrast to the nitroxide radicals, BDPA‐d ₁₆ eliminates large nuclear hyperfine splittings, allowing a clear view of the spin dynamics of the three‐electron spin system. Moreover, the optical properties of tpPDI provide for future studies involving optical readout of the tpPDI‐BDPA‐d ₁₆ spin dynamics.

Scheme 1.

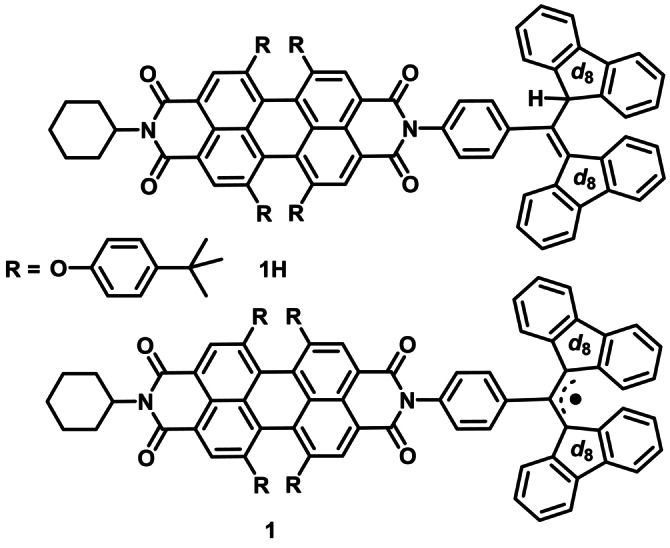
Structures of 1 and its precursor, 1H.

Results and Discussion

The steady‐state UV/Vis spectra of both 1 and its precursor 1H exhibit the well‐known tpPDI chromophore peaks located at 450 nm, 535 nm, and 580 nm (Figure 2a). ^[36] In comparison, 1 has an additional absorption with a maximum at 490 nm resulting from the BDPA‐d ₁₆ radical. ^[37] Covalently linking BDPAH‐d ₁₆ or BDPA‐d ₁₆ to tpPDI does not significantly alter the absorption spectra of these species, suggesting that they are weakly coupled electronically. Moreover, the steady‐state emission spectrum of 1 is typical of tpPDI derivatives but with a fluorescence quantum yield φ_F=0.01. ^[36] The absorption and emission spectra of 1 are in a convenient spectral region to permit future absorption and fluorescence detected magnetic resonance (ADMR/FDMR) experiments.

Figure 2.

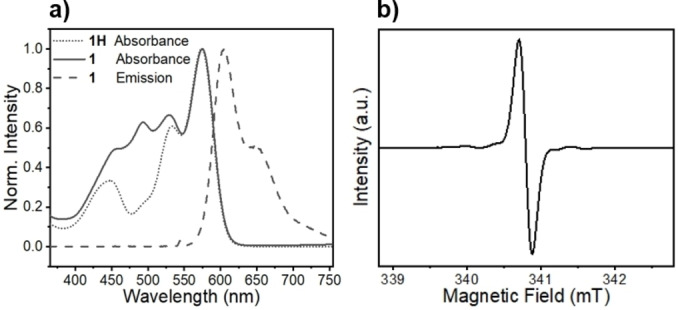
a) Steady state UV/Vis spectra of 1 (solid line) and 1H (dot line) The emission spectrum (dash line) of 1 recorded using 545 nm excitation. b) CW EPR spectra of 1. All spectra were acquired in toluene at 295 K.

The X‐band CW EPR spectrum of 1 acquired in toluene at 295 K exhibits a single, narrow resonance centered at g=2.0026 (Figure 2b). The absence of any significant structure on the line is indicative of the reduction in hyperfine splittings provided by the partial deuteration and demonstrates the low spin density delocalized onto the phenyl attached to tpPDI from the radical center (Figure S2). The single, narrow resonance of 1 simplifies the analysis of the transient EPR spectra produced by photoexcitation of the appended tpPDI chromophore. The weak satellite bands in the CW EPR spectrum of 1 likely result from hyperfine splittings of natural abundance ¹³C.[ ³⁸ , ³⁹ ]

Femtosecond and nanosecond transient absorption (TA) spectra of 1 were acquired in toluene at 295 K (Figure 3) following photoexcitation at 545 nm. The corresponding spectra of 1 in 2‐methyltetrahydrofuran (mTHF) at 85 K are given in Figure S3. Global kinetic fitting of the data yields the evolution‐associated spectra with the indicated time constants for formation and decay of the different species. The initial excited‐state absorption observed from 680–850 nm at 295 K is assigned to the singlet excited state of tpPDI, ^[40] within ¹*tpPDI‐²BDPA‐d ₁₆ or D ₁, which decays in τ=15±1 ps and is accompanied by partial recovery of the ground‐state bleach at 580 nm and the appearance of tpPDI triplet excited state absorption peaks at 450–550 nm.[ ⁴¹ , ⁴² ] This intermediate species then relaxes back to the ground state, ¹tpPDI‐²BDPA‐d ₁₆ or D ₀, in τ=8.7±0.4 μs. It is worth noting that the intrinsic triplet yield of tpPDI resulting from SO‐ISC is very low, so that the rapid ISC observed here is caused by the presence of the BDPA‐d ₁₆ radical. Magnification of the spectrum in Figure 3b shows that it possesses spectroscopic features similar to that of ³*tpPDI. ^[32] This can be rationalized by recognizing that although D ₂ and Q have different spin multiplicities, both states have two unpaired electrons localized on the tpPDI chromophore, leading to dominant TA spectra characteristic of ³*tpPDI. While the TA data shows that a long‐lived species results from the presence of BDPA‐d ₁₆, it does not provide information regarding the spin state(s) of photoexcited tpPDI‐BDPA‐d ₁₆, so that time‐resolved EPR spectroscopy was used to obtain that information.

Figure 3.

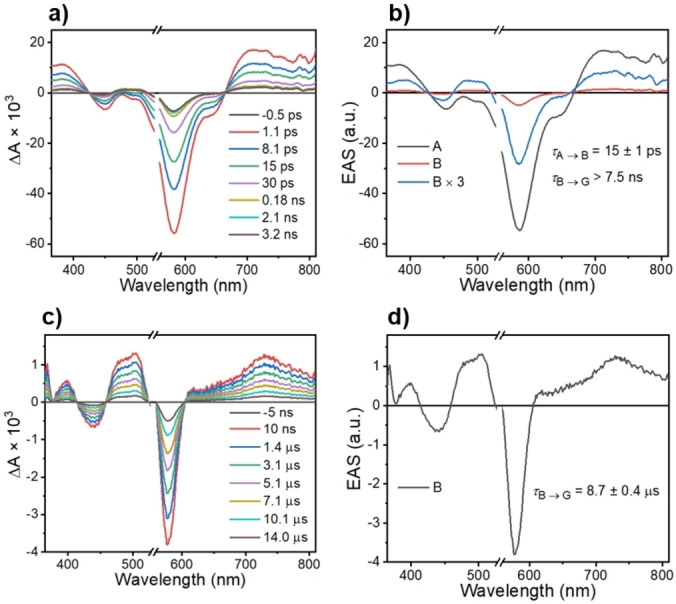
FsTA (a) and nsTA (c) spectra of 1 in toluene at 295 K at selected times following a 150 fs, 545 nm excitation pulse. b) and d) are the corresponding evolution‐associated spectra of 1 with kinetic values. Species A is assigned to ¹*tpPDI‐²BDPA‐d ₁₆, while the long‐lived intermediate B has absorption features of triplet tpPDI. G is the ground state.

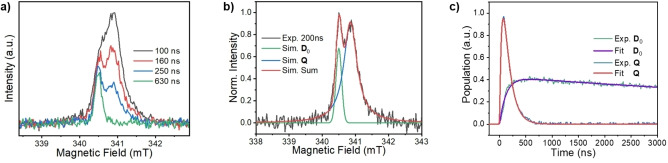
Time‐resolved EPR spectroscopy using CW microwaves (TREPR) as well as pulse microwaves (pulse‐EPR) was used to determine the spin dynamics of 1 following photoexcitation. TREPR measurements on 1 performed in toluene at 295 K show the presence of two partially overlapping resonances that display different decay rates (Figure 4a). Simulations resolve the g‐values of two signals as 2.0026 (340.5 mT) and 2.00054 (340.9 mT), respectively (Figure 4b). Pulse‐EPR experiments, discussed later, clarify that these transitions correspond to the ground state doublet D ₀ and excited quartet Q state, respectively. At 295 K, the initial signal resulting from Q decays to form spin‐polarized D ₀, the kinetics for which are plotted with fits in Figure 4c. The spin‐polarized signal of Q appears in τ=64±4 ns and decays with the concomitant appearance of the spin‐polarized D ₀ state in τ=125±4 ns. It should be noted that time constants obtained from TREPR experiments are limited by spin relaxation and are influenced by the continuous microwave irradiation, so should be viewed as a lower limit and generally do not necessarily agree with the population lifetimes obtained by nsTA spectroscopy (Figure S3).

Figure 4.

TREPR spectra of 1 in a) toluene at 295 K. b) Spectrum of 1 in toluene at 295 K obtained 200 ns after the laser pulse. The polarized ground state doublet D ₀ and the quartet Q states of 1 are observed at 340.5 mT and 340.9 mT, respectively, where c) shows the kinetics for Q and D₀ .

Pulse‐EPR techniques were used to unambiguously verify the spin multiplicity of Q and to gain further insight into the properties of the spin‐polarized Q and D ₀ states. The echo‐detected, field‐sweep (EDFS) spectra at three different times following laser excitation of 1 at 85 K and subtraction of the corresponding spectrum of 1 without photoexcitation are shown in Figure 5a. The light‐minus‐dark results are ratioed relative to the dark signal, offering a quantitative assessment of the magnitude of the spin polarization enhancement relative to the signal at the Boltzmann equilibrium. Similar to the TREPR spectra in Figure 4, the EDFS spectra at different times after the laser pulse consist of only two signals assigned to Q and D ₀. At early times after the laser pulse, the integrated echo intensity of the broader Q state signal is larger than that of D ₀, whereas at the later times D ₀ dominates. Here, the broadening of Q is likely due to the ZFS E‐parameter. This occurs because the central transition |+1/2>↔|−1/2> within the quartet manifold is not broadened by the ZFS D‐parameter, which is normally ≈1–2 GHz for PDI chromophores. ^[43]

Figure 5.

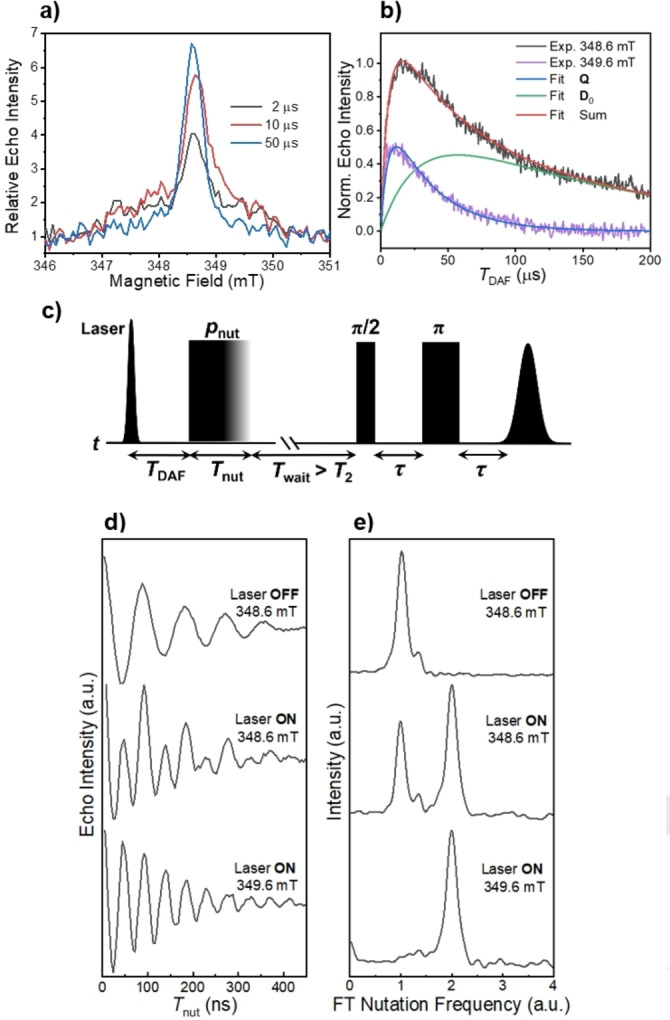
a) Three time slices of EDFS spectra of 1 obtained in mTHF at 85 K at varying time delays T _DAF, ratioed to the dark background spectrum. b) Time evolution of the amplitude following laser excitation at two field positions. Superimposed are the spectral fits. c) Pulse sequence of nutation experiments. d) Normalized echo intensities collected versus the nutation pulse length T _nut with and without laser excitation at different magnetic field positions (348.6 mT and 349.6 mT) and e) their corresponding Fourier‐transformed results normalized by the nutation frequency of the ground doublet state in the dark.

Figure 5b shows the echo intensities at 348.6 mT and 349.6 mT as a function of the time delay after the laser flash (T _DAF). The signal at 348.6 mT represents a mixture of both Q and D ₀ while at 349.6 mT only Q is present. By fitting these two traces, it was found that Q appears in τ=6.5±0.3 μs and decays in τ=33.4±0.6 μs, and the polarized D ₀ appears concomitantly with the decay of Q and decays in τ=152±3 μs, which is likely limited by T ₁ of the BDPA‐d ₁₆ radical. The decay time constant of Q derived from the pulse‐EPR measurements, although limited by T ₁ of the tpPDI triplet, is reasonably consistent with the kinetic component observed in the transient absorption spectra measured in mTHF at 85 K (Figure S3).

Transient nutation experiments were used to assign the spin multiplicity of each species observed in the EDFS data in Figure 5a. The pulse sequence shown in Figure 5c was used and the nutation pulse length (flip‐angle) was varied in 4 ns steps. The polarization nutation frequency under selective pulse irradiation is given by the equation 2:[ ²⁷ , ⁴⁴ , ⁴⁵ ]

$${\displaystyle {\omega }_{m_s,m_{s+1}}{=\omega }_0\sqrt{S\left(S+1\right)-m_s\left(m_s+1\right)}}$$ (2)

In our experiments, the microwave B ₁ field amplitude is much smaller than the ZFS magnitude, therefore, Equation (2) is applicable to 1. ^[46] The frequency axis was normalized by using the frequency ω₀ obtained for the D ₀ dark state of 1 (S=1/2). If the transition |+1/2>↔|+1/2> in D ₀ has a nutation frequency of ω₀, then within the quartet manifold, the selective satellite transitions (i.e., |±1/2>↔|±3/2>, termed multiplet polarization) are expected to have a frequency of $\sqrt{3}$ ω₀, and the central transition within the quartet manifold ( i.e. |+1/2>↔|−1/2>, termed net polarization) will have a nutation frequency of 2ω₀. Nutation experiments were performed under three different conditions: (1) the dark state of ¹tpPDI‐²BDPA‐d ₁₆ (D ₀), (2) the photoexcited state of 1 at the center of the EPR spectrum (348.6 mT), where both Q and the spin‐polarized D ₀ resonate, and (3) the photoexcited state of 1 at the off‐center position of the EPR signal (349.6 mT), where only Q resonates. Figure 5d shows the recorded Rabi oscillations, from which the nutation frequencies are derived using discrete Fourier transformation (FT) (Figure 5e). At 348.6 mT (the center of the EPR signal), two nutation frequencies are observed, ω₀ and 2ω₀, indicative of a mixture of hyperpolarized D ₀ and Q, respectively. On the other hand, at 349.6 mT, a sole nutation frequency of 2ω₀ is detected, suggesting an uncontaminated Q state with a transition between its |+1/2> and |−1/2> states, accounting for the “net polarization” in the excited state.[ ¹⁹ , ²⁰ ] The satellite multiplet transitions for 1 were not detected. The absence of the |±1/2>↔|±3/2> transitions in photogenerated quartet systems has been discussed previously, and it has been suggested that multiplet polarization occurs soon after photoexcitation and a rapid equilibrium between D ₂ and Q results in net polarization dominating the spectrum.[ ²⁹ , ³⁰ , ³¹ ] A fast equilibrium between D ₂ and Q is also supported by the transient absorption kinetics discussed above, in which only one decay constant is resolved from the excited states to D ₀. This model suggests that the energy gap between D ₂ and Q (3J_TR ) should be less than the thermal energy (k _BT≈60 cm⁻¹ at 85 K and 206 cm⁻¹ at 295 K) to facilitate thermal mixing of D ₂ and Q, which provides an estimate of the exchange coupling strength (J_TR ) of this system.

As discussed earlier, Q is largely generated from D ₂ via SO‐ISC. The H _ZFS operator in Equation (1) can mix the D ₂ and Q states to induce intersystem crossing, and the corresponding ISC rates between spin sublevels are governed by the energy differences:

$${\displaystyle k(\left|{\mathbf{D}}_2\right.\left(m_s\right)>\to \left|\mathbf{Q}\right.\left(m_s\right)>\propto {\left(\left|{\mathbf{D}}_2\right.\left(m_s\right)\left|{\mathbf{H}}_{ZFS}\left|\mathbf{Q}\right.\left(m_s\right)>\right.\right)}^2/{(E_{{\mathbf{D}}_2}\left(m_s\right)-E_{\mathbf{Q}}\left(m_s\right))}^2}$$ (3)

Although the nutation experiments cannot distinguish between a hyperpolarized doublet ground state (D ₀) from that of an excited state doublet (D ₂), it is evident that the observed doublet state is D ₀ because of its longer lifetime and the fact that it is the final spin state observed by EPR spectroscopy.

While the radical‐triplet pair mechanism (RTPM)[ ⁴⁷ , ⁴⁸ ] has been used successfully to explain spin polarization resulting from triplet‐radical pair interactions in a diffusive encounter, the chromophore and radical moieties studied in this work are covalently linked at fixed distances. The spin dynamics of 1 can be rationalized using the reverse quartet mechanism (RQM) (Figure S4) and the rapid thermal equilibrium between D ₂ and Q as described above.[ ³² , ⁴⁹ , ⁵⁰ ] Among all spin‐allowed transitions between spin sublevels (Δm_S =±1, ±2), Equation (3) suggests that |D ₂(−1/2)>→|Q(+3/2)> is most preferred due to the smallest energy gap. Thus, at early times, the depletion of |D ₂(−1/2)> is faster than |D ₂(+1/2)> because of energetically favored ISC pathways, leading to an overpopulation of |D ₂(+1/2)>. The decay from D ₂ to D ₀ carries the same population distribution and should yield an emissive signal of D ₀. The absence of such an emissive pattern in this system can be justified by the equilibrium between D ₂ and Q, which acts as the competing pathway and suppresses the initial decay from D ₂ to D ₀. At later times, Q relaxes to D ₀ via the |D ₂(−1/2)> sublevel due to the smaller energy gaps, which should produce an absorptive polarization feature of D ₀ as shown in Figures 4 and 5.

In designing a C−R⋅ molecule to execute quantum logic gate operations, it is essential for C−R⋅ to have a well‐defined initial spin state. The photogenerated hyperpolarized quartet Q and doublet D ₀ states of 1 can be utilized as qudit or qubit candidates, respectively. Selection of the Q state can be realized by optimizing T _DAF as well as T _nut in the pulse‐EPR experiments. For instance, a shorter value of T _DAF and/or T _nut will minimize the relative doublet contribution from D ₀. According to the nutation experiments in Figures 5d and 5e, the polarization of Q at the off‐center resonance position is free of any D ₀ interference, creating a clean Q state for quantum information input and output. In addition, it is essential that the spin qubit or qudit has a long coherence time. ^[51] The coherence time T ₂ is approximated by the phase memory time, T _m. ^[52] The echo intensity of photogenerated Q and D ₀ in 1 were recorded versus τ in Figure 6, where an exponential fit to the data gives T _m=2.1±0.1 μs and 2.8±0.2 μs, respectively, which is adequate to perform spin coherent spin manipulations to demonstrate logic gates. This value also compares favorably with previously reported molecular spin systems,[ ⁹ , ¹¹ , ⁵³ , ⁵⁴ ] as well as the measured T _m values of BDPA over a range of comparable temperatures. ^[55] Another important feature of 1 is the absence of large hyperfine splittings on BDPA‐d ₁₆, which results in a much simpler absorptive peak for the central transition of the Q manifold as compared to those we have reported for nitroxides appended to tpPDI derivatives. ^[11] Furthermore, mixing of D ₂ and Q via the ZFS interaction generates a net polarization |+1/2>↔|+1/2> in the Q manifold. The absence of multiplet polarization turns out to be advantageous for QIS applications not only because it results in narrower signal linewidths, but, more importantly, only one isolated transition (net polarization) can be probed and operated on with minimum interference from other spin processes. In addition, the highly spin‐polarized ground state D ₀ that results from decay of Q can also serve as qubit with a well‐defined initial quantum state that can be manipulated using microwave pulses.

Figure 6.

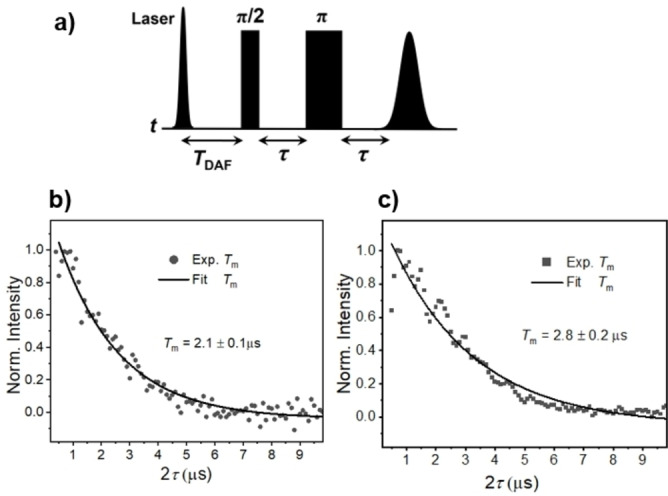
a) Pulse sequence to determine the coherence time T _m of Q and D ₀ of 1 in mTHF at 85 K, in which τ is varied. Coherence decay of Q (b) and D ₀ (c). The experimental data points are fit to a monoexponential decay.

Conclusion

We have synthesized and characterized a covalent chromophore‐radical system that upon photoexcitation produces spin‐polarized quartet Q and doublet D ₀ states at 85 K with lifetimes of τ=33.4±0.6 μs and τ=152±3 μs, respectively, which agree with the time constants obtained by transient absorption spectroscopy. The photogenerated Q and D ₀ states were further characterized using transient nutation experiments and exhibit coherence times T _m=2.1±0.1 μs and 2.8±0.2 μs, respectively, at 85 K in glassy mTHF, which is adequate for quantum logic gate operations. The main feature of this system is that the BDPA‐d ₁₆ radical has very small nuclear hyperfine couplings, which result in a single, relatively narrow resonance. Photo‐driven spin polarization of this resonance produces a well‐defined initial state for QIS applications. This system compares favorably with the porphyrin‐trityl system in which the radical resonance is also narrow. ^[56] Our next goal is to use the spin‐polarized states of 1 to implement an NV center surrogate that can be probed using ODMR methods.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Qiu Y., Equbal A., Lin C., Huang Y., Brown P. J., Young R. M., Krzyaniak M. D., Wasielewski M. R., Angew. Chem. Int. Ed. 2023, 62, e202214668; Angew. Chem. 2023, 135, e202214668.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.