Nomogram model and risk score to predict 5‐year risk of progression from prediabetes to diabetes in Chinese adults: Development and validation of a novel model

Abstract

Aim

To develop a personalized nomogram and risk score to predict the 5‐year risk of diabetes among Chinese adults with prediabetes.

Methods

There were 26 018 participants with prediabetes at baseline in this retrospective cohort study. We randomly stratified participants into two cohorts for training (n = 12 947) and validation (n = 13 071). The least absolute shrinkage and selection operator (LASSO) model was applied to select the most significant variables among candidate variables. And we further established a stepwise Cox proportional hazards model to screen out the risk factors based on the predictors chosen by the LASSO model. We presented the model with a nomogram. The model's discrimination, clinical use and calibration were assessed using the area under the receiver operating characteristic (ROC) curve, decision curve and calibration analysis. The associated risk factors were also categorized according to clinical cut‐points or tertials to create the diabetes risk score model. Based on the total score, we divided it into four risk categories: low, middle, high and extremely high. We also evaluated our diabetes risk score model's performance.

Results

We developed a simple nomogram and risk score that predicts the risk of prediabetes by using the variables age, triglyceride, fasting blood glucose, body mass index, alanine aminotransferase, high‐density lipoprotein cholesterol and family history of diabetes. The area under the ROC curve of the nomogram was 0.8146 (95% CI 0.8035‐0.8258) and 0.8147 (95% CI 0.8035‐0.8259) for the training and validation cohort, respectively. The calibration curve showed a perfect fit between predicted and observed diabetes risks at 5 years. Decision curve analysis presented the clinical use of the nomogram, and there was a wide range of alternative threshold probability spectrums. A total risk score of 0 to 2.5, 3 to 4.5, 5 to 7.5 and 8 to 13.5 is associated with low, middle, high and extremely high diabetes risk status, respectively.

Conclusions

We developed and validated a personalized prediction nomogram and risk score for 5‐year diabetes risk among Chinese adults with prediabetes, identifying individuals at a high risk of developing diabetes. Doctors and other healthcare professionals can easily and quickly use our diabetes score model to assess the diabetes risk status in patients with prediabetes. In addition, the nomogram model and risk score we developed need to be validated in a prospective cohort study.

1. INTRODUCTION

Around the world, diabetes affects millions of people, making it one of the most prevalent chronic diseases. ¹ Worldwide, in 2021, according to the International Diabetes Federation, approximately 536.6 million adults had diabetes. According to estimates, people with diabetes will account for 783.2 million of the world's population by 2045. ² In addition, diabetes and its complications constitute a worldwide public health problem that imposes a huge economic burden on society. ³ , ⁴ , ⁵

Diabetes is a chronic endocrine and metabolic disease that can be split into numerous types. Type 1 diabetes and type 2 diabetes (T2D) are the two main types. T2D accounts for 90%‐95% of all diabetes, primarily because of a lack of insulin production or impaired insulin sensitivity. The development of T2D normally has three stages: health, prediabetes and T2D. ⁶ , ⁷ Prediabetes generally refers to the presence of either or both impaired glucose tolerance and impaired fasting glucose. ⁸ Evidence suggests that after the diagnosis of T2D, the patient's blood glucose level will continue to rise, which is difficult to reverse with medical treatment. ⁹ Therefore, effective intervention for patients with prediabetes is the key to preventing diabetes. ¹⁰ , ¹¹ , ¹² , ¹³ Nevertheless, lifestyle modification programmes and drug costs limit population‐wide initiatives for prediabetes. Conversely, early identification of patients at a high risk of developing prediabetes into diabetes and timely management can avoid the burden of prevention and treatment in low‐risk populations.

However, the commonly used laboratory tests for risk stratification are limited, with fasting blood glucose (FPG) having an intermediate sensitivity and HbA1c being the most convenient but least sensitive. ¹⁰ However, other factors affecting the onset of diabetes, including hypertension, ¹⁴ dyslipidaemia, ¹⁵ body mass index (BMI), ¹⁶ waist circumference ¹⁷ and dietary patterns, ¹⁸ also have limited predictive value for the risk of prediabetes progression to diabetes. Risk score models are practical and efficient tools for screening high‐risk individuals with prediabetes. Currently, many diabetes risk score models can estimate diabetes risk and help physicians make appropriate treatment plans based on a patient's risk status. ¹⁹ , ²⁰ , ²¹ Several risk assessment tools for detecting the risk of progression from prediabetes to diabetes have been reported. ²² , ²³ , ²⁴ However, most studies employed logistic regression rather than the Cox proportional hazards model, considering follow‐up time. Besides, most studies lack an evaluation of model accuracy and clinical use value, which limits the generalization of the model. Most scoring systems are created for Whites in industrialized countries, and only a few are for Asians. Therefore, a diabetes risk score is needed for Chinese adults with prediabetes.

Our study uses a Cox proportional hazards model to develop a diabetes risk score and nomogram for individuals with prediabetes based on medical examination records in China. The model's discriminatory ability, clinical applicability, calibration and internal validation will all be assessed. We developed this model to help clinicians predict the risk of progression to diabetes in patients with prediabetes and to facilitate intervention programmes to delay or prevent the onset of diabetes.

2. METHODS

2.1. Study design

We performed a retrospective cohort study using data from the database provided by the China Rich Healthcare Group. ²⁵ Variables at baseline are included as screening variables in the prediction model in the current study. The dependent variable was diabetes diagnosed during the 5 years of follow‐up (dichotomous variable: 0 = non‐diabetes, 1 = diabetes).

2.2. Data source

The raw data were obtained freely from the DATADRYAD database (www.datadryad.org) provided by Chen et al. (Chen Y, Zhang XP, Yuan J, et al. [2018], Data from Association of body mass index and age with incident diabetes in Chinese adults: a population‐based cohort study, Dryad, Dataset, https://doi.org/10.5061/dryad.ft8750v). ²⁵ This is an open‐access article given in accordance with the Creative Commons Attribution Non Commercial (CC BY‐NC 4.0) license, and anyone may share, remix, change and produce a derivative work from it for non‐commercial use, as long as the authors and source are credited. ²⁵

2.3. Study population

Information was extracted from a computerized database established by the Rich Healthcare Group in China by the original researchers, which contains all medical records for participants who received health checks in 32 regions and 11 cities from 2010 to 2016. The Rich Healthcare Group Review Board initially approved the original study, and the information was retrieved retrospectively. ²⁵ For the retrospective study, no informed consent or approval was required by the institutional ethics committee. ²⁵ Therefore, ethical approval was not required for the current secondary analysis. Furthermore, the original study was carried out in compliance with the Helsinki Declaration, as was this secondary analysis.

The original study initially recruited 685 277 participants aged at least 20 years and with at least two health examinations. After that, 473,444 participants were excluded. Finally, the original study included 211 833 individuals in its analysis. Following are the exclusion criteria for the original study: (a) participants diagnosed with diabetes at enrolment; (b) no information about FPG value, sex, height and weight at baseline; (c) extreme BMI values (< 15 kg/m² or > 55 kg/m²); (d) participants with less than 2 years between visits; (e) and participants with unknown diabetes status at follow‐up. According to the American Diabetes Association (ADA) 2022 diagnostic criteria for prediabetes, ²⁶ we excluded 185 815 participants with baseline FPG less than 5.6 mmol/L and FPG greater than 6.9 mmol/L in the current study. Ultimately, 26 018 participants were included in the present study. Figure 1 shows how participants were selected.

FIGURE 1.

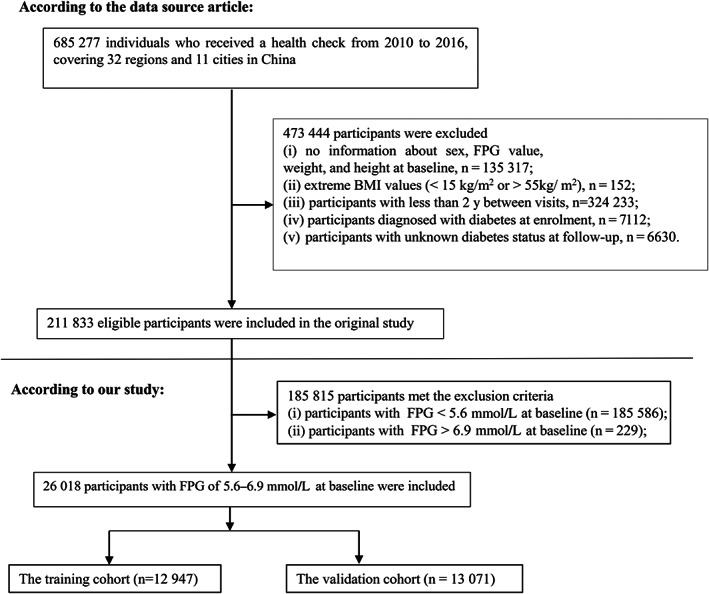
Flowchart of study participants. BMI, body mass index; FPG, fasting plasma glucose

2.4. Variables

2.4.1. Baseline variables

According to previous research and clinical experience, we selected the screening variables for the prediction model in this study. ²² , ²⁵ The following variables were therefore used as covariates based on the principles outlined above: (i) continuous variables: serum creatinine (Scr), systolic blood pressure (SBP), BMI, diastolic blood pressure (DBP), age, triglyceride (TG), total cholesterol (TC), FPG, low‐density lipoprotein cholesterol (LDL‐c), aspartate aminotransferase (AST), high‐density lipoprotein cholesterol (HDL‐c) and alanine aminotransferase (ALT); and (ii) categorical variables: smoking, sex, family history of diabetes and alcohol consumption.

2.4.2. Data collection

In the original study, trained investigators used standard questionnaires to collect baseline information, including alcohol consumption and smoking status, demographic characteristics (sex and age) and family history of diabetes. Smoking status was divided into three categories according to the smoking situation: currently smoking, ever smoking and never smoking. Alcohol consumption status was divided into three categories according to the situation: currently, ever and never alcohol consumption. The family history of diabetes was defined as diabetes history in at least a parent or sibling. Standard mercury sphygmomanometers measured blood pressure. During each visit, fasting venous blood samples were taken at least 10 hours after a fast. A Beckman 5800 autoanalyser was used to measure plasma glucose, TC, HDL‐c, TG and LDL‐c. ²⁵

2.4.3. Outcome measures

Our interesting outcome variable was diabetes (dichotomous variable: 0 = non‐diabetes, 1 = diabetes). Prediabetes was diagnosed based on FPG at baseline, and FPG values in patients with prediabetes are set at 5.6 to 6.9 mmol/L as part of the ADA's 2022 diagnostic criteria. ²⁶ Incident diabetes was based on either self‐report or FPG of 7.0 mmoL/L or higher at the last follow‐up evaluation, whichever came first. ²⁵ The follow‐up period was 5 years.

2.4.4. Handling missing baseline variables

The number of participants whose data were missing for SBP, DBP, Scr, ALT, LDL‐c, HDL‐c, AST, smoking status and alcohol consumption status was 7 (0.03%), 7 (0.03%), 1342 (5.16%), 234 (0.90%), 9958 (38.27%), 10 589 (40.70%), 14 708 (56.53%), 17 244 (66.28%) and 17 244 (66.28%), respectively. This study used multiple imputations for missing data to mitigate the variation caused by missing variables. ²⁷ The imputation model (type = linear regression, iterations = 10) included sex, age, DBP, HDL‐c, TC, AST, Scr, SBP, ALT, LDL‐c, alcohol consumption status, family history of diabetes and smoking status. Missing‐at‐random assumptions are used in missing data analysis procedures. ²⁷ , ²⁸

2.5. Statistical analysis

All participants were randomly assigned a random number generated by the Empower network random system. Randomized participants were stratified into training and validation cohorts according to a simple randomization procedure. Continuous variables with Gaussian distributions are presented as means and standard deviations, and skewed distributions are reported as medians. For categorical variables, percentages and frequencies are presented. We used Wilcoxon rank‐sum tests (skewed distribution), two‐sample t‐tests (normal distribution) or χ² (categorical variables) to test for differences between the training and validation cohorts. Additionally, we summarized the baseline characteristics of the training and validation cohorts stratified by incident diabetes.

We conducted two rounds of variable screening to identify a simple and reliable risk prediction model. The Least Absolute Shrinkage and Selection Operator (LASSO), a method suitable for reducing high‐dimensional data and for selecting the most useful prediction candidates, was used for the first variable screening of the model. ²⁹ , ³⁰ The LASSO model was established by selecting candidates with non‐zero coefficients. ³¹ We performed a second screening round based on the LASSO model's identified variables. First, we applied all risk factors to build a full model through the Cox proportional hazards model. Second, our method was to perform a step‐down selection process using the Akaike information criterion, so as to develop a parsimonious model (i.e. a stepwise Cox proportional hazards model). ³² Third, to establish a stable model (i.e. the multivariable fractional polynomials [MFP] model) in the real world, we used the iterative fashion to determine significant variables and functional form by backward elimination according to the MFP algorithm. ³³

In view of the fewer variables and reasonably good prediction performance of the stepwise model, we selected it for further analysis. To evaluate the discriminatory power of the prediction models, we plotted the receiver operating characteristic (ROC) curve and calculated the area under the curve (AUC) in the training and validation cohorts, respectively. We calculated the sensitivity, specificity, negative likelihood ratio (NLR), positive likelihood ratio (PLR), negative predictive value (NPV) and positive predictive value (PPV) for the stepwise model according to standard definitions. In addition, we obtained a diabetes risk prediction formula from the stepwise Cox proportional hazards model. Predicted risk (time t) = 1‐S0(t) Exp (LP), where the predicted probability is given at time t (in years) after the start of follow‐up using the stepwise model, Exp = exponential of e, LP is the linear predictor from the stepwise model and S0(t) = baseline survival at time t (for ease of calculation, an estimate was provided 5 years after the start of follow‐up). ³⁴ The nomogram was based on proportionally converting each regression coefficient in the stepwise Cox proportional hazards regression model to a 0‐to‐100‐point scale; 100 points were assigned to the variable with the highest β coefficient (absolute value). We added points across independent variables to obtain total points, which were then converted into predicted probabilities of progression to diabetes from prediabetes. Each patient's nomogram score was a numeric value representing their prediction model score. At different cut‐off points of nomogram scores, sensitivity and specificity were different for predicting diabetes. Also, the calibration plot for 5‐year diabetes probability was used to assess the accuracy of the nomogram. ³⁵ We assessed the clinical utility of the risk prediction model for diabetes in patients with prediabetes by conducting decision curve analysis: taking the proportion of individuals who showed a true positive result and subtracting the proportion who showed a false positive result, then weighting the relative hazard of the false positive and false negative results to obtain a net benefit of making a decision. ³⁶

The associated risk factors of prediabetes in the stepwise model were also categorized according to clinical cut‐points or tertiles to create the prediabetes score model. We put these risk factors that were treated as categorical variables into the stepwise Cox proportional hazards model and derived a new β coefficient. The scoring system was constructed according to regression coefficients multiplied by three and rounded to the nearest integer to calculate the weights. ³⁷ The scoring system was then implemented in a questionnaire form that primary care personnel could utilize easily. The total score was classified into four risk categories: low, middle, high and extremely high risk.

Additionally, we assessed the performance of our risk score model for the development of diabetes from prediabetes. The survival estimates and time‐to‐event variables were calculated using the Kaplan‐Meier method. Using the log‐rank test, we compared the probability of diabetes‐free survival among the four risk score groups (quartile of risk score). Using ROC curves, we also analysed the performance of each risk factor in the model for predicting diabetes performance and its optimal cut‐off.

All results are reported according to the TRIPOD statement. ³⁸ Statistical analyses were conducted with R (http://www.R-project.org; The R Foundation) and Empower‐Stats 2.0 (X&Y Solutions, Inc, Boston, MA). Two‐tailed tests were conducted and P less than .05 was statistically significant.

3. RESULTS

The present study included 26 018 eligible participants (66.34% men and 33.66% women). The mean age of all participants was 49.06 ± 13.82 years; 2640 (10.15%) participants developed diabetes during a median follow‐up period of 3.05 years.

3.1. Baseline characteristics of participants

Table 1 lists the eligible participants' basic demographic, clinical and anthropological information. Among all participants with prediabetes, 12 947 were in the training cohort and 13 071 were in the validation cohort; 1315 and 1325 participants developed diabetes over the 3.05‐year median follow‐up period in the training and validation cohorts, respectively. Training and validation cohorts did not differ in a statistically significant manner for any baseline characteristics (all P > .05).

TABLE 1.

Baseline characteristics of the training and validation sets

Characteristic	Training set	Validation set	P value
N	12 947	13 071
Age (y)	49.03 ± 13.82	49.08 ± 13.83	.751
Age groups
< 40 y	3926 (30.32%)	3961 (30.30%)	.949
40 to < 60 y	5856 (45.23%)	5893 (45.08%)
≥ 60 y	3165 (24.45%)	3217 (24.61%)
BMI (kg/m2)	24.77 ± 3.34	24.84 ± 3.39	.118
BMI groups			.305
< 18.5 kg/m2	257 (1.99%)	239 (1.83%)
18.5‐24.0 kg/m2	5061 (39.09%)	5135 (39.29%)
24.0‐28.0 kg/m2	5531 (42.72%)	5488 (41.99%)
≥ 28 kg/m2	2098 (16.20%)	2209 (16.90%)
SBP (mmHg)	127.15 ± 17.53	127.21 ± 17.61	.783
DBP (mmHg)	78.42 ± 11.23	78.38 ± 11.05	.772
FPG (mmol/L)	5.95 ± 0.32	5.95 ± 0.32	.985
TC (mmol/L)	4.97 ± 0.95	4.97 ± 0.96	.931
TG (mmol/L)	1.78 ± 1.43	1.80 ± 1.46	.191
HDL‐c (mmol/L)	1.33 ± 0.30	1.33 ± 0.31	.413
LDL‐c (mmol/L)	2.89 ± 0.72	2.88 ± 0.73	.604
ALT (U/L)	22.00 (15.30‐33.00)	22.00 (15.50‐33.45)	.400
AST (U/L)	26.40 ± 11.90	26.51 ± 12.31	.478
Scr (μmol/L)	72.72 ± 15.75	72.83 ± 16.36	.589
Sex			.903
Male	8594 (66.38%)	8667 (66.31%)
Female	4353 (33.62%)	4404 (33.69%)
Family history of diabetes			.091
No	12 610 (97.40%)	12 773 (97.72%)
Yes	337 (2.60%)	298 (2.28%)
Alcohol consumption			.928
No	10 610 (81.95%)	10 706 (81.91%)
Yes	2337 (18.05%)	2365 (18.09%)
Smoking			.674
No	9492 (73.31%)	9613 (73.54%)
Yes	3455 (26.69%)	3458 (26.46%)

Note: Continuous variables are summarized as mean (SD) or medians (quartile interval); categorical variables are displayed as a percentage (%).

Abbreviations: ALT, alanine aminotransferase; AST aspartate aminotransferase; BMI, body mass index; BUN, blood urea nitrogen; DBP, diastolic blood pressure; FPG, fasting plasma glucose; HDL‐c, high‐density lipoprotein cholesterol; LDL‐c, low‐density lipid cholesterol; SBP, systolic blood pressure; Scr, serum creatinine; TC, total cholesterol, TG triglyceride.

The baseline characteristics of both cohorts are shown in Table S1 according to incident diabetes status within the 5 years. The participants with incident diabetes had higher DBP, BMI, SBP, TG, FPG, age, TC, AST, LDL‐c, ALT, and higher rates of males, smokers, and family history of diabetes in the training and validation cohort (all P < .05). By contrast, the persons without incident diabetes had higher levels of HDL‐c. In addition, in the validation cohort, the proportion of participants with alcohol consumption was higher in those with incident diabetes than in those without incident diabetes. However, there was no statistically significant difference for Scr and alcohol consumption status in the training cohort.

3.2. Univariate and multivariate analyses of risk predictors of diabetes onset

Table S2 displays risk predictors for incident diabetes through the univariate and multivariate Cox proportional hazards model in the training cohort. The univariate analysis showed that age (HR = 1.03), female (HR = 0.84), BMI (HR = 1.13), SBP (HR = 1.02), DBP (HR = 1.02), FPG (HR = 9.77), TG (HR = 1.12), LDL‐c (HR = 1.08), TC (HR = 1.07), ALT (HR = 1.01), AST (HR = 1.01), family history of diabetes (HR = 1.45) and smoking (HR = 1.28) were related to incident diabetes (all P < .05); alcohol consumption status was not associated with the risk of diabetes (P = .986). The multivariate analysis showed that age (HR = 1.02), BMI (HR = 1.09), FPG (HR = 7.57), TC (HR = 0.62), TG (HR = 1.15), HDL‐c (HR = 2.07), LDL‐c (HR = 1.58), ALT (HR = 1.01) and family history of diabetes (HR = 1.71) were related to diabetes risk (all P < .05). However, SBP, Scr, DBP, AST, smoking status and alcohol consumption status were not associated with the risk of diabetes (all P > .05).

3.3. Candidate selection through LASSO regression

On the basis of 12 974 participants in the training set that had non‐zero coefficients in the LASSO regression, 16 clinical features (BMI, age, SBP, HDL‐c, Scr, sex, TC, DBP, ALT, TG, LDL‐c, FPG, alcohol consumption status, family history of diabetes, AST and smoking status) were reduced to eight potential predictors (Figure S1). These potential predictors were HDL‐c, BMI, FPG, TG, ALT, TC, age and family history of diabetes.

3.4. Identification of risk factors

According to the predictors selected by the LASSO regression model, we developed three further prediction models: the MFP model, the full Cox proportional hazards model and the stepwise Cox proportional hazards model. For the training set, the MFP model, full model and stepwise model had AUCs of 0.781, 0.782 and 0.782, respectively (Figure S2). The corresponding AUCs for these models were 0.789, 0.786 and 0.786 in the validation set (Figure S2). There were fairly similar AUCs in the three models. Compared with the MFP and the full model, the stepwise model has fewer risk factors, is simpler and better predicts diabetes risk. Therefore, we concluded that the stepwise model is the most suitable model for predicting diabetes risk. As shown in Table 2, seven variables were selected by the stepwise model, namely, FPG (HR = 7.5164, 95% CI 6.5201‐8.6650), BMI (HR = 1.0920, 95% CI 1.0739‐1.1105), age (HR = 1.0201, 95% CI 1.0157‐1.0246), TG (HR = 1.0374, 95% CI 1.0036‐1.0724), HDL‐c (HR = 1.4859, 95% CI 1.2325‐1.7914), ALT (HR = 1.0050, 95% CI 1.0031‐1.0068) and family history of diabetes (HR = 1.6380, 95% CI 1.2635‐2.1236). The results showed that all seven variables were positively associated with incident diabetes.

TABLE 2.

Variables selected using a stepwise Cox proportional hazards model

	Beta	Standard error	HR (95% CI)	P value
Age (y)	0.0199	0.0022	1.0201 (1.0157, 1.0246)	< .0001
BMI (kg/m2)	0.0880	0.0086	1.0920 (1.0739, 1.1105)	< .0001
FPG (mmol/L)	2.0171	0.0726	7.5164 (6.5201, 8.6650)	< .0001
TG (mmol/L)	0.0368	0.0169	1.0374 (1.0036, 1.0724)	.0296
HDL‐c (mmol/L)	0.3960	0.0954	1.4859 (1.2325, 1.7914)	< .0001
ALT (U/L)	0.0050	0.0009	1.0050 (1.0031, 1.0068)	< .0001
Family history of diabetes	0.4935	0.1325	1.6380 (1.2635, 2.1236)	.0002

Abbreviations: ALT, alanine aminotransferase; BMI, body mass index; CI, confidence interval; FPG; fasting plasma glucose; HDL‐c, high‐density lipoprotein cholesterol; HR, hazard ratios; TG, triglyceride.

Each risk predictor (except for family history of diabetes) was evaluated for its prediction performance in the training and validation cohorts of incident diabetes over 5 years (Table S3, Figure S3). The AUC of the FPG was greater than the AUC of the other risk factors for 5‐year incident diabetes in participants with prediabetes.

We also plotted the time‐dependent ROC curves for the stepwise model in the training and validation cohorts (Figure S4). The results suggest that the AUCs for predicting the risk of diabetes at different times in the future using the present stepwise model remained broadly consistent. This indicates that the current model has a better predictive value for the risk of developing diabetes in patients with prediabetes at different times in the future.

3.5. Development of the nomogram

We also drew a corresponding nomogram based on age, BMI, FPG, TG, ALT, HDL‐c and family history of diabetes, providing a quantitative and simple tool for predicting the 5‐year risk of progression from prediabetes to diabetes (Figure 2). Based on the nomogram, each variable was assigned a specific point, and the points were summed to determine the probability of diabetes onset at 5 years. The algorithm of diabetes risk in the stepwise model was as follows:

$$\text{Predicted risk}\left(5-\text{year}\right)=1-\text{S0}\left(5-\text{year}\right)\mathrm{Exp}\left(\mathrm{LP}\right)$$

$$\mathrm{LP}=0.01994^{*}\mathrm{Age}\left(\text{years}\right)+0.08802^{*}\mathrm{BMI}\left(\mathrm{kg}/{\mathrm{m}}^2\right)+2.01709^{*}\mathrm{FPG}\left(\text{mmol}/\mathrm{L}\right)+0.03675^{*}\mathrm{TG}\left(\text{mmol}/\mathrm{L}\right)+0.39602^{*}\mathrm{HDL}-\mathrm{c}\left(\text{mmol}/\mathrm{L}\right)+0.00498^{*}\mathrm{ALT}\left(\mathrm{U}/\mathrm{L}\right)+{0.49350}^{*}\left(\text{family history of diabetes}\right)$$

$$\text{S0}\left(5-\text{year}\right)=0.99999994$$

FIGURE 2.

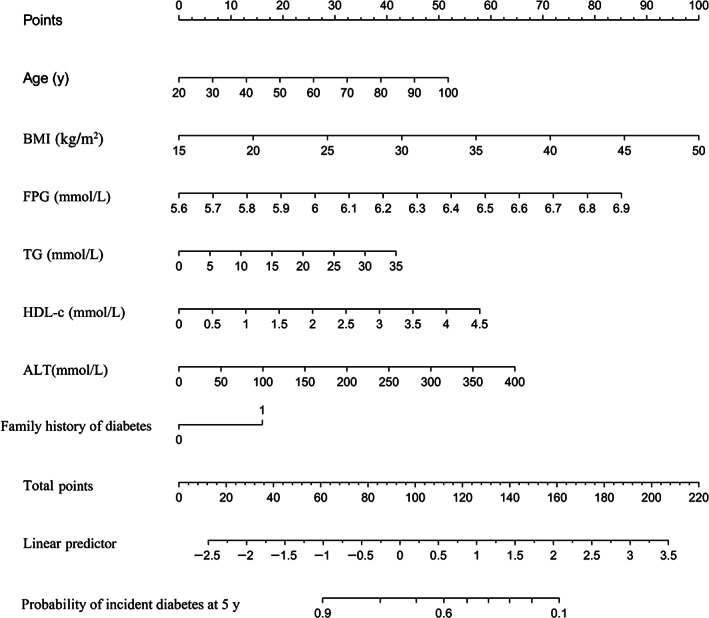
Nomogram to predict the risk of diabetes for patients with prediabetes. ALT, alanine aminotransferase; BMI, body mass index; FPG, fasting plasma glucose; HDL‐c, high‐density lipoprotein cholesterol; TG, triglyceride

3.6. Performance of nomograms to predict 5‐year incident diabetes

3.6.1. Discrimination

In the training cohort and the validation cohort, the AUCs of the nomogram were 0.8146 (95% CI 0.8035‐0.8258) and 0.8147 (95% CI 0.8035‐0.8259), respectively (Table S4, Figure S5). For the training and validation cohorts, at the best threshold, the sensitivity rates were 76.87% and 65.02%, respectively, and the specificity percentages were 71.63% and 82.57%. There was a comparatively high NPV in both the training and the validation cohorts.

3.6.2. Model accuracy evaluation

We also evaluated how close the predicted 5‐year diabetes risk was to the observed 5‐year diabetes risk for the nomogram in the training and validation cohorts. In both the validation and training sets, the calibration histograms for 5‐year incident diabetes probability showed excellent agreement between the predicted possibility and the actual observation (Figure S6). These results show that the nomogram could accurately predict the 5‐year diabetes risk in the Chinese population with prediabetes.

3.6.3. Clinical use of the nomogram

The training and validation cohorts of the stepwise model's decision curve analysis are shown in Figure S7. The black line represents the net benefit when no patient with prediabetes was considered to have diabetes. Conversely, the light grey line represents the net benefit if all patients with prediabetes were assumed to progress to diabetes. The area between the ‘all treatment line’ (light grey line) and the ‘no treatment line’ (black line) in the model curve represents the clinical utility of the model. In general, the further the model curve is from the black and light grey lines, the better the nomogram's clinical utility. Specifically, in the training cohort, the net benefit was about 23% if the threshold probability of a patient was 20% in the stepwise model, which corresponds to an additional 23 diabetes screenings per 100 Chinese adults with prediabetes in the absence of a significant change in diabetes incidence.

3.7. Associations between predicted diabetes probability and 5‐year incident diabetes

We further divided the training and validation cohorts into two groups according to whether they developed diabetes in the future, comparing the predicted diabetes probability between the two groups. The results showed that participants with diabetes had a higher predicted probability, whereas those without prediabetes had a lower predicted probability (Figure S8).

Next, we divided the participants into four groups based on the quartiles of predicted diabetes probability. Kaplan‐Meier survival curves for 5‐year diabetes‐free survival probability stratified by the predicted probability quartiles are shown in Figure S9. There were significant differences in the probability of diabetes‐free survival between the different predicted probability groups (log‐rank test, P < .0001). Diabetes‐free survival probabilities decreased as predicted probability increased, which indicated that those with the highest predicted probability faced the highest risk of diabetes. These results also indicated the good performance of the stepwise model.

3.8. The optimal cut‐off value for the nomogram score

In Table S5, we report the sensitivity and specificity for predicting diabetes at different cut‐off values in the training cohort. The specificity is 10.01% and the sensitivity is 99.70% based on a cut‐off value of 0.05. When the cut‐off value increased to 0.6, the specificity increased to 91.50%, while the sensitivity dropped to 41.22%. Overall, higher cut‐off values led to higher specificity, but the sensitivity rapidly decreased. In the validation cohort, we obtained similar results (Table S6).

3.9. Performance of nomograms to predict 5‐year incident diabetes in subgroups

We drew ROC curves to measure the ability of the nomogram to predict the onset of diabetes within 5 years in different subgroups. First, the ROC curves for the diabetes risk nomogram showed an AUC of 0.8091 and 0.8237 for male and female participants, respectively (Figure S10). For male and female cohorts, at the best threshold, the sensitivity rates were 72.30% and 76.42%, and the specificity was 75.46% and 75.05%, respectively. The NPV was higher in both male and female cohorts (Table S7). In addition, we stratified the participants of the training cohort according to age (< 40, 40‐60 and ≥ 60 years). The AUC of the nomogram predicting diabetes risk was 0.8538, 0.7947 and 0.7523 for those aged younger than 40, 40‐60 and 60 years or older, respectively (Figure S11). The NPV was higher in all age groups (Table S7).

3.10. Risk score model of progression from prediabetes to diabetes

We further categorized the risk factors, including age (< 40, 40‐60, ≥ 60 years), ³⁹ FPG (tertial), BMI (< 18.5, 18.5‐24, 24‐28, ≥ 28 kg/m²), ⁴⁰ HDL‐c (< 1.035, ≥ 1.035 mmol/L), ⁴¹ TG (< 1.7, ≥ 1.7 mmol/L) ⁴² and ALT (< 40, ≥ 40 U/L), ⁴³ according to clinical cut‐points, median or tertials, to create the diabetes score model. We put these categorical variables into the stepwise Cox proportional hazards model and derived a new β coefficient. The scoring system was constructed based on regression coefficients multiplied by three and rounded to the nearest integer to derive the weights of the scores (Table 3). Following this scoring rule, each participant's total score ranged from 0 to 13.5 points. Participants without diabetes risk factors received a minimum score of 0; those with seven diabetes risk factors received a maximum score of 13.5. The seven predictors (categorical variables) collectively yielded an AUC of 0.794 in the development model. The optimal cut‐point was selected to be 5.5 of the total score with 70.09% sensitivity and 75.2% specificity (Figure S12, Table S8).

TABLE 3.

Risk score model for diabetes in patients with prediabetes

	Coefficients	SE	HR (95% CI)	P value	Score
Age (y)
< 40	Ref.		Ref.		0
≥ 40, < 60	0.5125	0.0871	1.6695 (1.4076, 1.9801)	<.0001	1.5
≥ 60	0.8322	0.0909	2.2983 (1.9233, 2.7464)	<.0001	2.5
BMI (kg/m2)
< 18.5	Ref.		Ref.		0
≥ 18.5, < 25	0.0781	0.3220	1.0812 (0.5752, 2.0323)	.8084	0
≥ 25, < 30	0.3578	0.3211	1.4302 (0.7622, 2.6835)	.2651	1
≥ 30	0.6312	0.3239	1.8799 (0.9963, 3.5471)	.0513	2
FPG (mmol/L)
Low (< 5.74)	Ref.		Ref.		0
Medium (5.74‐6.0)	0.6716	0.1115	1.9575 (1.5731, 2.4357)	< .0001	2
High (≥ 6.0)	1.7354	0.0965	5.6713 (4.6942, 6.8519)	< .0001	5
HDL‐c (mmol/L)
Low (< 1.035)	Ref.		Ref.		0
High (≥ 1.035)	0.2354	0.0708	1.2654 (1.1013, 1.4538)	.0009	0.5
TG (mmol/L)
< 1.7	Ref.		Ref.		0
≥ 1.7	0.3182	0.0590	1.3747 (1.2245, 1.5432)	< .0001	1
ALT (U/L)
Low (< 40)	Ref.		Ref.		0
High (≥ 40)	0.2836	0.0665	1.3279 (1.1656, 1.5128)	< .0001	1
Family history of diabetes
No	Ref.		Ref.		0
Yes	0.4926	0.1320	1.6366 (1.2635, 2.1199)	.0002	1.5

Abbreviations: ALT, alanine aminotransferase; BMI, body mass index; CI, confidence interval; FPG, fasting plasma glucose; HDL‐c, high‐density lipoprotein cholesterol; HR, hazard ratios;TG, triglyceride.

Based on the quartile of the total risk score, we divided diabetes risk into four categories. The observed incidence of diabetes among low‐risk participants (0‐2.5 points) was 0.74% (19 out of 2564 participants), 3.44% (100 out of 2911 participants) among medium‐risk (3.0‐4.5 points), 8.92% (349 out of 3914 participants) among high‐risk (5‐7.5 points) and 23.81% (847 out of 3558 participants) among extremely high‐risk participants (8‐13.5 points) (Table S9). The dichotomizing scale at, for example, 5 points (non‐diabetes if risk score < 5; diagnosis of diabetes if risk score ≥ 5) yielded a sensitivity of 90.55%, a specificity of 46.05%, a PPV of 16.01% and an NPV of 97.83% (Table S9).

A Kaplan‐Meier survival curve for diabetes‐free survival stratified by risk score quartiles is shown in Figure 3A. The probability of diabetes‐free survival differed significantly between the quartiles of risk scores (log‐rank test, P < .0001). Diabetes‐free survival probabilities decreased as risk scores increased, which indicated that those in the extremely high‐risk group faced the highest risk of diabetes.

FIGURE 3.

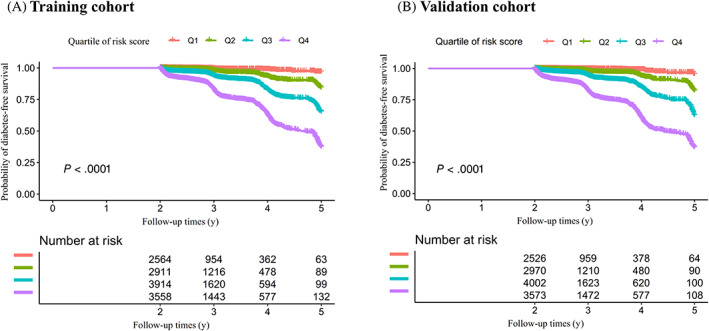
Kaplan‐Meier diabetes‐free survival curve stratified by the risk score quartiles. Kaplan‐Meier survival curves for 5‐year diabetes‐free survival probability stratified by the risk score quartiles in A, The training cohort and B, The validation cohort. There were significant differences in the probability of diabetes‐free survival between the different risk score groups (log‐rank test, P < .0001). Diabetes‐free survival probabilities decreased as risk scores increased, which indicated that those in the extremely high‐risk group faced the highest risk of diabetes

3.11. Validation stage of risk score

In the validation cohort, the optimal cut‐off point for the risk score was 6.5, which resulted in overall consistent test results with AUC = 0.7781, the optimal point with the optimal value of a sensitivity of 65.39% and a specificity of 78.46% (Figure S12, Table S8). This result suggested that the questionnaires filled out by participants in the training and validation cohorts had similar AUC values. According to the questionnaire formula in Table 3, we can estimate the probability of progression from prediabetes to diabetes based on the demographic and clinical characteristics of participants. The observed incidence of diabetes among low‐risk participants (0‐2.5 points) was 0.75% (19 out of 2526 participants), 3.2% (95 out of 2970 participants) among medium‐risk (3‐4.5 points), 8.27% (331 out of 4002 participants) among high‐risk (5‐7.5 points) and 24.63% (880 out of 3573 participants) among extremely high‐risk participants (8‐13.5 points) (Table S9). For example, the dichotomizing scale at 5.0 points (at < 5.0 points the diagnosis was non‐diabetes, and at ≥ 5.0 it was diabetes) yielded a sensitivity of 91.40%, a specificity of 45.82%, a PPV of 15.99% and an NPV of 97.93% (Table S9). Kaplan‐Meier survival curves yielded similar results to the training cohort (Figure 3B).

4. DISCUSSION

We developed and validated a personalized prediction nomogram and risk score for the 5‐year risk of incident diabetes in Chinese adults with prediabetes using cost‐effective and readily available variables in this study, assisting clinicians in identifying patients at a high risk of progression from prediabetes to diabetes. The prediction model included seven variables: BMI, ALT, TG, age, FPG, HDL‐c and family history of diabetes. Model evaluation and internal validation showed excellent prediction performance for our nomogram and risk score.

Several risk assessment tools have been reported for predicting progression from prediabetes to diabetes. In 2017, Yokota et al. ²⁴ performed a multivariate logistic regression analysis to develop a risk score to predict the risk of progression from prediabetes to diabetes based on family history of diabetes, sex, SBP, FPG, HbA1c and ALT. The AUC of the model was 0.80 (95% CI 0.70‐0.87), a specificity of prediction of 61.8% at 80% sensitivity. Although their study was a retrospective longitudinal study, they did not use a Cox proportional hazards model to build a predictive model, which takes into account factors of follow‐up time to build a model. After all, for predictive models, the effect of follow‐up time on the outcome must also be considered, as different follow‐up times may lead to differences in the performance of model predictions. Also, they did not perform decision curve analysis to evaluate the clinical usefulness of the model, nor calibration curve analysis to assess the model's accuracy. Furthermore, they did not try other methods to compare and screen the most suitable risk prediction model for incident diabetes. After all, because of the inherent collinearity and interaction effects of the screening factors, screening variables directly using logistic regression models is not a good choice. In 2020, Cahn et al. ²² developed a predictive model based on machine learning to predict the risk of progression from prediabetes to diabetes according to age, gender, glucose, HbA1c, BMI, TG, ALT, white blood cell count, HDL‐c, statins usage and aspirin usage. The AUC was 0.865 (95% CI 0.860‐0.869). However, they did not establish time‐dependent ROC curves and did not explicitly propose specific timing for predicting the risk of prediabetes. Also, they did not conduct decision curve analysis to assess the model's clinical suitability, nor did they measure how closely the predicted risk matches the actual risk. In addition, too many risk predictors for their model may limit further generalization of their model. Moreover, in 2021, Liang et al. ²³ developed a model to predict the risk of progression from prediabetes to diabetes using three predictors: FPG, 2‐hour postprandial blood glucose (2hPG) and HbA1c. Their model's predictive ability is comparatively low (AUC = 0.742). Besides, they did not perform variable screening and did not take into account predictors such as ALT, TG, HDL‐c, age and family history of diabetes, which are significantly associated with incident prediabetes or diabetes. ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ In addition, 2hPG is comparatively difficult to obtain, which affects the clinical application of the model. In 2022, Nicolaisen et al. ⁴⁹ developed a 5‐year risk prediction model for diabetes in patients with prediabetes based on factors including HbA1c, age, sex, BMI, treated hypertension, pre‐existing pancreatic disease, absence of cancer, unhealthy diet and physician recommendation to lose weight or change diet. The 5‐year AUC was 0.727 (95% CI 0.712‐0.743). Their model has too many predictors, and there are not easily measured and quantified predictors, which affects the clinical application of the model. Compared with the similar studies mentioned above, our nomogram and risk score filled those gaps. We used LASSO regression and the multivariate fractional polynomials algorithm in the screening process, considering the collinearity and interaction of the screened variables. Meanwhile, we established predictive equations by Cox proportional hazards regression models to fully account for the effect of follow‐up time on incident diabetes and established time‐dependent ROC curves. Besides, we performed a complete evaluation of the model for discrimination, clinical use and calibration, as well as an internal validation of the model. Moreover, for further convenience of clinical use, we also established a risk score, and risk stratification was performed.

The prevalence of prediabetes among adults reached 35.7% in a nationwide cross‐sectional survey in China. ⁵⁰ Therefore, effective intervention for patients with prediabetes is the key to preventing diabetes. It is important to note that only a subset of people with prediabetes will progress to diabetes, so intervention of the entire prediabetic population is not cost‐effective. Identifying those truly at a high risk of developing diabetes among individuals with prediabetes is particularly important, as this allows us to allocate medical costs for diabetes prevention and treatment rationally. In this study, we constructed a nomogram and risk score using the LASSO and stepwise Cox proportional hazards models. And we provided a formula that calculated the risk of progression from prediabetes to diabetes based on risk predictors, which could assist clinicians in identifying individuals with prediabetes at a high risk of diabetes and assist them in being screened for diabetes on time. Our nomogram model and risk score are routine clinical variables readily available to clinicians; thus, they can be easily applied in practice.

The present study has several strengths, including: (i) participants in this study came from multiple centres, and the sample size was large; (ii) we established four prediction models: the LASSO, full, stepwise and MFP. And we developed a simple stepwise model based on the LASSO model; (iii) we performed a nomogram and a risk score at the same time to ensure model precision and clinical practicability; (iv) we provided a formula to calculate the risk of diabetes in patients with prediabetes based on risk predictors, which can help clinicians calculate an individual's risk of developing diabetes quickly and accurately; (v) we performed a complete evaluation of the model for discrimination, clinical use and calibration; (vi) the decision curve analysis showed the nomogram's clinical value and could avoid additional diabetes screenings (such as the Oral Glucose Tolerance Test) in individuals with prediabetes who are at a low risk of incident diabetes; and (vii) we performed a series of internal validations to ensure the reliability of the results.

Despite the excellent performance of our nomogram and risk score, some potential limitations remain. First, this is a secondary analysis based on published data. The raw data did not include other diabetes risk factors, such as lifestyle factors, medical history and waist‐to‐hip ratio, which may influence the development of prediabetes or diabetes. In addition, although we performed subgroup analyses for age and sex during modelling, some population differences, such as regional and ethnic differences, were not addressed. We may attempt to design our studies or collaborate with other researchers in the future to collect as many variables as possible. Second, diabetes was defined as having an FPG level of 7.00 mmol/L or higher and/or having self‐reported diabetes during the follow‐up period, but not as a measurement of HbA1c or of a 2‐hour oral glucose tolerance test. Therefore, the incidence of diabetes may be underestimated. However, in such a large cohort, a 2‐hour oral glucose tolerance test was not easy to perform. Third, we used multiple imputations to replace missing values. This has the potential to lead to bias. Therefore, in the future, we can consider designing our studies or cooperating with other researchers to collect as many variables as possible and reduce the numbers of missing values. Finally, although we tested the performance of the predictive model, it still needs real clinical or other relevant work to test it before it can be widely accepted or applied.

In conclusion, we have developed and validated a personalized prediction nomogram and risk score for the 5‐year risk of incident diabetes among Chinese adults with prediabetes, including TG, BMI, age, FPG, HDL‐c, ALT and family history of diabetes. The nomogram and risk score have excellent prediction performance in both the training and validation cohorts for estimating the risk of developing diabetes and have high generalizability. Categorizing the entire risk relative to the risk status helps to create a diabetes intervention or prevention programme. Additionally, much clinical and other related work is required before this diabetes risk score and nomogram can be widely accepted and used.

AUTHOR CONTRIBUTIONS

YH, HH and YL contributed to the study design and drafted the manuscript. HH and YH are responsible for statistical analysis, research and interpretation of the data. They are responsible for the integrity of the data and the accuracy of the data analysis. ZW and DL contributed to the discussion and reviewed the manuscript. YH, HH and DL are the guarantors of this work. All the authors read and approved the final manuscript.

FUNDING INFORMATION

This study did not receive any funding.

CONFLICT OF INTEREST

There is no conflict of interest among the authors.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1111/dom.14910.

AVAILABILITY OF DATA AND MATERIALS

The “DATADRYAD” database (www.Datadryad.org) provides access to data.

Supporting information

Appendix S1. Supporting Information.

Figure S1. Risk predictors selection using the LASSO regression model. (A) Optimal predictor (lambda) selection in the LASSO model with 10‐fold cross‐validation by minimum criteria. The area under the receiver operating characteristic curve was plotted versus log (lambda). Dotted vertical lines were drawn at the optimal values by using the minimum criteria and the 1 SE of the minimum criteria. (B). LASSO coefficient profiles of the 17 predictors. A coefficient profile plot was developed against the log (lambda) sequence. A vertical line was drawn at the value selected with 10‐fold cross‐validation, where optimal lambda resulted in 8 predictors with nonzero coefficients (lambda = 0.0056).

Figure S2. The ROC curves of the full model, stepwise model and MFP model in the training cohort (A) and validation cohort (B). (A). In the training set, AUCs of the MFP model, full model and stepwise model were 0.781, 0.782 and 0.782, respectively. (B) In the validation set, the corresponding AUCs of those models were 0.789, 0.786 and 0.786, respectively.

Figure S3. The ROC curves of each risk predictor in our stepwise model, including age, BMI, FPG, ALT, HDL‐c, TG and family history of diabetes in the training cohort (A) and validation cohort (B). The AUC of the FPG was greater than the AUC of other risk factors for the 5‐year incident diabetes in patients with prediabetes both in in the training cohort and validation cohort.

Figure S4. Time‐dependent ROC curve. We plotted the time‐dependent ROC curves for the stepwise model in the training cohort (A) and validation cohort (B). The results suggested that the AUCs for predicting the risk of diabetes at different times in the next 5 years using the present stepwise model remained broadly consistent. It indicated that the present model had a better predictive value for all incident diabetes at different times in the next 5 years.

Figure S5. ROC curve for the nomogram model predicting the risk of developing diabetes at 5 years. In the training and validation cohorts, the AUCs of the nomogram was 0.8146 and 0.8147.

Figure S6. Calibration histograms. The calibration histograms for 5‐year incident diabetes probability showed excellent agreement between the predicted possibility and the actual observation in both the training and validation sets (A and B).

Figure S7. The decision curve analysis of the nomogram model for 5‐year diabetes risk in the training cohort(A) and validation cohort (B). The area between the “all treatment line” (light gray line) and the “no treatment line” (black line) in the model curve represented the clinical utility of the model. The farther the model curve is from the black and light gray lines, the better the clinical use of the nomogram.

Figure S8. Comparing the predicted diabetes probability between the diabetes and non‐diabetes groups in the training cohort (A) and validation cohort (B). Showed that participants with diabetes had a higher predicted probability, whereas those without diabetes had a lower predicted probability.

Figure S9. Kaplan‐Meier diabetes‐free survival curve stratified by the quartiles of predicted diabetes probability. Kaplan‐Meier event‐free survival curve in the training cohort(A) and validation cohort (B). we divided the participants into four groups based on the quartiles of predicted diabetes probability at baseline. Kaplan‐Meier survival curves for 5‐year diabetes‐free survival probability stratified by the predicted probability groups. There were significant differences in the probability of diabetes‐free survival between the different predicted probability groups(log‐rank test, P < .0001). Diabetes‐free survival probabilities decreased as predicted probability increased, which indicated that those with the highest predicted probability faced the highest risk of diabetes.

Figure S10. ROC curve for the nomogram model predicting the risk of developing diabetes in men and women with prediabetes. The AUC of the nomogram model for predicting the risk of developing diabetes in the female and male populations was 0.8237 and 0.8291, respectively.

Figure S11. ROC curve for the nomogram model predicting the risk of developing diabetes in different age groups. The AUCs of the nomogram model for predicting the risk of developing diabetes in participants <40 years, 40 to <60 years, and ≥ 60 years were 0.8538, 0.7947, and 0.7523, respectively.

Figure S12. ROC curve for the risk score model predicting the risk of developing diabetes at 5 years in the training cohort (A) and validation cohort (B). In the training and validation cohorts, the AUCs of the risk score model were 0.794 and 0.778.

Table S1. Baseline characteristics for the training and validation cohorts by incident diabetes status.

Table S2. Relationship between risk predictors and the risk of diabetes in patients with prediabetes in univariate and multivariate analyses

Table S3. Prediction performance of risk predictors in our nomogram.

Table S4. Prediction performance of the nomogram for the risk of diabetes.

Table S5. Values of sensitivity, specificity, and predictive values of the nomogram scores at different cut‐off values in the training sets.

Table S6. Values of sensitivity, specificity and predictive values of the nomogram scores at different cut‐off values in the validation sets.

Table S7. Prediction performance of the nomogram for the risk of diabetes in different subgroups.

Table S8. Prediction performance of the risk score for the risk of diabetes in patients with prediabetes.

Table S9. Risk status categorization

Han Y, Hu H, Liu Y, Wang Z, Liu D. Nomogram model and risk score to predict 5‐year risk of progression from prediabetes to diabetes in Chinese adults: Development and validation of a novel model. Diabetes Obes Metab. 2023;25(3):675‐687. doi: 10.1111/dom.14910

DATA AVAILABILITY STATEMENT

The 'DATADRYAD' database (www.Datadryad.org) provides access to data Chen, Ying et al. (2018), data from: Association of body mass index and age with incident diabetes in Chinese adults: a population‐based cohort study, Dryad, Dataset, https://doi.org/10.5061/dryad.ft8750v.;