Genetic sex determination, sex chromosome size and sex‐specific lifespans across tetrapods

Abstract

Sex differences in lifespan are ubiquitous across the tree of life and exhibit broad taxonomic patterns that remain a puzzle, such as males living longer than females in birds and vice versa in mammals. The prevailing unguarded X hypothesis explains sex differences in lifespan by differential expression of recessive mutations on the X or Z chromosome of the heterogametic sex, but has only received indirect support to date. An alternative hypothesis is that the accumulation of deleterious mutations and repetitive elements on the Y or W chromosome might lower the survival of the heterogametic sex (‘toxic Y’ hypothesis). Here, we use a new database to report lower survival of the heterogametic relative to the homogametic sex across 136 species of birds, mammals, reptiles and amphibians, as expected if sex chromosomes shape sex‐specific lifespans, and consistent with previous findings. We also found that the relative sizes of both the X and the Y chromosomes in mammals (but not the Z or the W chromosomes in birds) are associated with sex differences in lifespan, as predicted by the unguarded X and the ‘toxic Y’. Furthermore, we report that the relative size of the Y is negatively associated with male lifespan in mammals, so that small Y size correlates with increased male lifespan. In theory, toxic Y effects are expected to be particularly strong in mammals, and we did not find similar effects in birds. Our results confirm the role of sex chromosomes in explaining sex differences in lifespan across tetrapods and further suggest that, at least in mammals, ‘toxic Y’ effects may play an important part in this role.

Sex differences in lifespan are ubiquitous across the tree of life, and exhibit broad taxonomic patterns that remain a puzzle. Here, we first analysed sex differences in lifespan across 136 species of birds, mammals, reptiles and amphibians to show that genetic determination system is clearly linked with the sex gap in lifespan (Figure). Bars above the black line (the red ring) indicate that females live longer than males, while bars below the black line (the blue ring) indicate that males live longer than females; the log transformed ratio of female and male lifespan (lnR) is plotted for each species. ZW systems are coloured in blue and XY systems are coloured in red. Across six independent origins of both ZW (blue circles) and XY (red circles) systems, females tend to live longer lifespans in species with XY systems and vice versa in ZW systems. Second, we analysed whether the relative sizes of the sex chromosomes co‐vary with sex‐specific ageing. In line with the idea that sex differences in lifespan can be driven by the degeneration of the heteromorphic sex chromosome (the toxic Y hypothesis), we found that the relative size of the Y is negatively associated with male lifespan in mammals, so that small Y size correlates with increased male lifespan.

1. INTRODUCTION

Sexual dimorphism in lifespan is widespread across the tree of life, including among tetrapods (Maklakov & Lummaa, 2013). Which sex lives longer varies considerably in both direction and magnitude. For example, females live three times longer than males in the brown antechinus, a small marsupial, while males are twice as likely as females to survive from 1 year to the next in Arabian babblers, a passerine bird (Braithwaite & Lee, 1979; Clutton‐Brock & Isvaran, 2007). In humans, the average global lifespan gap is 4.8 years – female life expectancy is 74.7 years, whereas male life expectancy is 69.9 years (UN, 2019). Understanding the dynamic nature of sex differences in lifespan across taxa remains an unsolved problem in evolutionary biology. To date, empirical studies have focused on adaptive hypotheses stemming from sex‐specific differences in how natural selection operates on females and males (Bonduriansky et al., 2008; Maklakov & Lummaa, 2013; Moorad et al., 2019; Trivers, 1985; Williams, 1957). Despite their prominent role in explaining sex differences in lifespan, such processes seem unable to explain the observation that the homogametic sex tends to live longer than the heterogametic sex across a wide taxonomic range (Maklakov & Lummaa, 2013; Pipoly et al., 2015).

There are at least two reasons why the asymmetric inheritance of sex chromosomes could directly contribute to the evolution of different female and male lifespans (Maklakov & Lummaa, 2013; Marais et al., 2018). First, the unguarded X hypothesis (UXh) predicts increased mortality of the heterogametic sex due to the expression of deleterious recessive mutations that accumulate in the non‐recombining (i.e. haploid) parts of the X (or Z) chromosome (Trivers, 1985). Because these mutations are masked in the homogametic sex, females are predicted to live longer than males in XY systems (where females are the homogametic sex), and males longer than females in ZW systems (where males are the homogametic sex). This idea has received indirect support in the finding that adult sex ratios are typically female biased in tetrapods with XY systems, but male biased in taxa with ZW systems, as expected if biased adult sex ratios result from sex‐specific mortality (Pipoly et al., 2015). A recent study further shows that the heterogametic sex tends to exhibit higher mean/maximum lifespan across a wide taxonomic range, although phylogenetic inertia and sexual selection could also explain this relationship (Xirocostas et al., 2020). Experimental evidence also shows that ‘unguarding’ the X chromosome in females erases the sex gap in lifespan in Drosophila melanogaster (Carazo et al., 2016; Sultanova et al., 2018), but the latter effect may not be consistent, as it was not present in a more direct test of the unguarded X hypothesis where inbreeding was limited to the X chromosome (Brengdahl et al., 2018). Furthermore, Connallon et al. (2022) recently used a simple model to show that the magnitude of UXh effects should depend largely on evolutionary parameters such as the genomic deleterious rate, the fraction of the haploid genome that is X‐ or Z‐linked, the average dominance of deleterious mutations, sex biases in mutation rate and selection, and the average relative effects of mutations on survival and longevity vs. on fitness (Connallon et al., 2022). More importantly, they used published estimates of these parameters across different species to show that UXh effects are expected to be weak, and hence fall short of explaining the broadly observed sex gaps in lifespan.

A second hypothesis focuses on the role of the heteromorphic Y (or W) chromosome (the toxic Y hypothesis). Following recombination suppression, the non‐recombining regions of Y (or W) chromosomes tend to accumulate deleterious mutations through evolutionary time via Muller's ratchet (i.e. irreversible stochastic effects) and genetic hitchhiking (i.e. the fixation of deleterious alleles linked to strongly beneficial mutations), as well as loose beneficial mutations via the purging of beneficial alleles linked to strongly deleterious mutations (i.e. ‘Ruby in the rubbish’; see Bachtrog, 2013; Wright et al., 2016). Recombination suppression also leads to an accumulation of repetitive DNA in the Y and W chromosomes through evolutionary time (Bachtrog, 2013; Wright et al., 2016). Recent evidence has shown that this repetitive DNA on the Y chromosome negatively influences chromatin integrity and hence modulates gene expression profiles genome wide in D. melanogaster (Brown et al., 2020a). Furthermore, repetitive DNA is disproportionally de‐repressed, and hence mis‐expressed, in old males compared to old females (Brown et al., 2020b). Therefore, in D. melanogaster, toxic Y effects may result in increased mortality and accelerated ageing of the heterogametic sex (Brown et al., 2020b; Marais et al., 2018), but the role of this hypothesis in explaining broad patterns of sex differences in lifespan has yet to be addressed.

The UXh and the toxic Y hypotheses are not mutually exclusive, and both predict that sex differences in lifespan result from increased mortality of the heterogametic sex. However, as the former relates to the X (or Z) chromosome while for latter relates to the Y (or W), they bear different predictions regarding the relationship between female/male lifespan and the relative size of the non‐recombining haploid regions in both the X (or Z) and the Y (or W). Unfortunately, these data are not available for a broad enough sample of species, but here we used the relative size of the sex chromosomes, which is generally expected to covary positively with the haploid region, as a proxy to test the following predictions. First, the UXh predicts that the sex gap in lifespan (i.e. female–male lifespan) will be positively associated with the relative size of the X chromosome with respect to the rest of the genome (or vice versa for the Z), because this provides a measure of how much variability in lifespan we expect the X (or Z) chromosome to explain (Figure 1a). For example, all else being equal (e.g. per‐base mutation rate), X‐linked effects would be expected to be more significant in D. melanogaster, where the X chromosome constitutes ~20% of the genome (Mallet et al., 2011), than in polar bears (Ursus maritimus), where the X chromosome is <5% of the genome (O'Brien et al., 2006). Specifically, the UXh posits that the relative size of the X (or Z) chromosome with respect to the rest of the genome (as a proxy for the amount of X/Z‐linked deleterious mutations) will be negatively correlated with the survival of the heterogametic sex (Figure 1c). In contrast, toxic Y (or W) effects depend on the size of the non‐recombining region in the Y (or W) chromosomes. Thus, toxic Y effects predict a higher sex gap in survival and, in particular, lower survival of the heterogametic sex with increasing size of the Y (or W) chromosome relative to the autosomes (Figure 1d). Importantly, toxic Y effects are expected to be larger in XY than in ZW systems as degeneration of the Y chromosome is generally more likely than degeneration of the W chromosome (Bachtrog, 2013).

FIGURE 1.

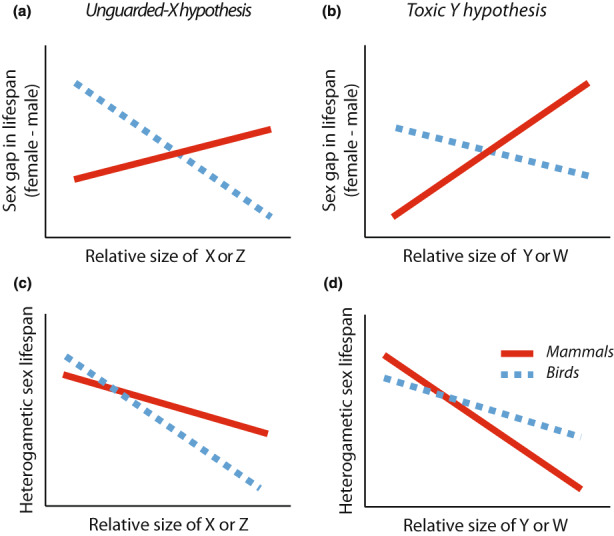
Predictions from the unguarded X and toxic Y hypotheses with respect to the expected relationship between the relative sizes of the sex chromosomes and: (a–b) the sex gap in lifespan, and (c–d) the lifespan of the heterogametic sex. (a) The unguarded X hypothesis predicts a positive relationship between the lifespan gap (i.e. female–male lifespan) and the size of the X relative to the autosomes in mammals (red line), and vice versa for the Z chromosome in birds (blue line). (c) This occurs because the unguarded X hypothesis predicts a negative relationship between survival/lifespan of the heterogametic sex and the size of both the X and Z chromosomes. Given that we expect a generally higher mutation load in males, unguarded effects may be expected to be clearer in birds (Z chromosome) than in mammals (X chromosome). (b) The toxic Y hypothesis predicts a positive relationship between the lifespan gap and the size of the Y chromosome relative to the autosomes in mammals and vice versa (albeit weaker, due again to a higher expected mutation load in males) in the case of the W chromosome in birds. (d) This occurs because the toxic Y predicts a negative relationship between survival/lifespan of the heterogametic sex and the relative size of both the Y and W chromosomes, although, again, a weaker relationship is expected in birds. Note that predictions are in relation to the direction and steepness of the slopes depicted, not the intercepts.

We, thus, first collected data on sex‐specific survival and mean age, as proxies for sex‐specific lifespan (hereafter, ‘lifespan’ for simplicity), across 136 species of birds, mammals, reptiles and amphibians. We then used phylogenetic meta‐analytic models to test the general prediction that females are longer lived than males in XY systems and vice versa in ZW systems. To test for unguarded X and toxic Y effects, we then collected published karyotype data for as many of the birds and mammals in our dataset as possible. We focused on birds and mammals as we needed substantial variation in the sizes of sex chromosomes across species, and we did not find enough currently available data (on both sex‐specific survival and karyotype data) for amphibians and reptiles. We then tested the following predictions separately for these two datasets. With respect to the sex gap in survival (i.e. female–male): (i) the UXh predicts higher female survival (vs. males) with increasing size of the X chromosome relative to the autosomes in mammals and vice versa with the Z chromosome in birds (Figure 1a), while (ii) the toxic Y makes the same predictions but regarding the Y/W chromosome (Figure 1b). With respect to survival of the heterogametic sex: (iii) the UXh predicts lower survival of the heterogametic sex as the size of the X (mammals) and Z (birds) chromosome increases relative to the autosomes (Figure 1c), while (iv) the toxic Y predicts lower survival of the heterogametic sex as the size of Y (mammals) and W (birds) increases relative to the autosomes, albeit a weaker relationship in birds (Figure 1d).

2. MATERIALS AND METHODS

2.1. Data collection

To test for unguarded X and toxic Y effects using comparative analyses, we required data on sex‐specific lifespans across multiple independent origins of XY (male heterogametic) and ZW (female heterogametic) systems as well as variation across species in the sizes of the sex chromosomes within each of these independent origins. We, therefore, limited our search to tetrapods (amphibians, reptiles, birds and mammals) with XY or ZW systems because of the abundance of species that have been relatively well studied with respect to sex‐specific lifespans (or proxies thereof, see below). We excluded fish because we did not find enough concurrent data on both sex‐specific lifespan and genetic sex‐determination system.

2.1.1. Sex differences in lifespan

We used sex‐specific adult survival rates and mean ages (years) as proxies for sex differences in lifespan to maximize available data across multiple independent origins of XY and ZW systems. Average lifespans are difficult to measure in wild vertebrate populations, and life tables (from which adult life expectancy can be calculated) have been reported for relatively few species, primarily mammals and birds (Clutton‐Brock & Isvaran, 2007; Jones et al., 2013). Both survival and mean age are directly related to lifespan: life history theory predicts a longer lifespan when extrinsic mortality is low and thus survival is high, while mean age will be lower in populations with a higher proportion of young individuals (Stearns, 1992). Furthermore, survival and mean age are typically estimated using mark‐recapture methods and so have the advantage of being reported with measurement error, which can be incorporated into statistical analyses. We excluded maximum lifespan as a proxy for average lifespan because it is strongly dependent on sampling effort, it is reported without error (by definition), and currently available data come from a mixture of wild and captive populations frequently based on few individuals (De Magalhaes et al., 2005).

We used Scopus and Web of Science (WoS) Core Collection to identify studies reporting sex‐specific survival rates and mean ages. First, we used the following topic search term: (male or female) AND mark‐recapture (studies published up to 31/12/2018). This returned 1647 studies from WoS and 2227 studies for Scopus. We also conducted backward and forward citation searches on the following review papers of survival rates (DeSante & Kaschube, 2007; Karr et al., 1990; McCarthy et al., 2008; Peach et al., 2001; Siriwardena et al., 1998; Yom‐Tov et al., 1992). This returned 168, 42, 118, 91, 8 and 31 studies from each review respectively. This search strategy primarily returned studies with suitable data on birds and mammals. To increase the number of amphibians and reptiles in our sample, we, therefore, conducted two additional searches in WoS and Scopus using the following topic search terms mean age OR average age AND male AND female AND amphibian OR reptile and skeletochronology AND male AND female. The first search terms returned 25 studies from WoS and 32 studies from Scopus, and the second search terms returned 205 studies from WoS and 207 studies from Scopus. We included ‘skeletochronology’ in our second search term because this is a widely used technique for determining mean age in reptiles and amphibians that is typically reported with error for both females and males. We screened the title of each study in our sample (N = 4801 studies) and the abstracts of those which appeared to contain relevant data and identified 156 studies which met our inclusion criteria (adult female and male survival/mean age reported with error) and that matched with the reptile and amphibians with known genetic sex‐determination systems (see below and Table S1).

2.1.2. Genetic sex‐determination system

We collected data on the genetic sex‐determination system for each species in our database using the tree of sex database (Ashman et al., 2014). We complemented this with individual searches for species for which we had data on sex‐specific lifespan (i.e. survival or mean age) but that did not appear in the tree of sex database, using the keywords species name AND karyotype OR sex chromosome in Google Scholar, Scopus and WoS and then examining the abstracts in search for data on the genetic sex‐determination system. All birds were assigned as ZW (N _species  = 69) and all mammals as XY (N _species  = 42). We assigned 6 amphibian and 7 reptile species as ZW and 10 amphibian and 2 reptile species as XY. We estimated the number of independent origins of XY and ZW systems in our sample of species using data from published sources (Evans et al., 2012). There were two independent XY origins and two independent ZW origins in our sample of reptiles and three independent XY origins and three independent ZW origins in amphibians. Therefore, in total, our sample included six XY origins and six ZW origins (see Table S1 for details).

2.1.3. Karyotypes

We collected karyotype data for all available bird and mammal species for which we also had sex‐specific survival data. We focused on birds and mammals as we needed variation in the sizes of the recombining and non‐recombining chromosomes across species that share the same origin of a genetic sex‐determination system. This was not possible for amphibians and reptiles where each independent origin of XY or ZW systems included seven or fewer species. We began by searching 14 chromosome atlases for the karyotypes of species for which we had data on sex differences in survival (Benirschke et al., 1967, 1973, 1975; Hsu & Benirschke, 1967, 1970, 1973, 1977; O'Brien et al., 2006). We identified karyotype images for 23 mammal and 4 bird species. For the species that were not present in these atlases, we did an additional search using the keywords species name AND karyotype in Web of Science and Scopus. We then examined the content of each article for karyotype images. From these searches, we found karyotype images for a further 9 mammal and 11 bird species. In total, we found suitable data for 32 mammal and 15 bird species. For each of these species, we used the karyotype image to calculate two ratios: (i) the ratio of X or Z to the rest of the chromosomes (X/autosomes or Z/autosomes) and (ii) the ratio of Y or W to the rest of the chromosomes (Y/autosomes or W/autosomes). Data are provided in Table S1. We used ImageJ (Abramoff et al., 2004) for calculating the relative size of the sex chromosomes from karyotype images. Briefly, after removing the labels or numbers around the chromosomes in the karyotype photos, we delimited chromosome boundaries using the ‘threshold’ plug‐in in Image J. Then, we measured the relative size of the sex chromosomes with respect to the autosomes using the ‘analyse particles’ plug‐in in Image J tool, which automatically provides an excel file listing the area of each delimited chromosome in pixels. For heterogametic sex karyotypes, the relative size of each sex chromosome was calculated by dividing the area of the corresponding sex chromosome by half the total area of the autosomes. For homogametic sex karyotypes, the relative size of the sex chromosome was calculated by dividing the total area of both sex chromosomes (XX or ZZ) by the total area of the autosomes.

2.1.4. Sexual size dimorphism

We used sexual size dimorphism as a proxy to control for the strength of sexual selection by including this variable as a covariate in our statistical models (see supplementary R code). We aimed to collect data on female and male head to body length for mammals, amphibians and reptiles. However, sex‐specific body lengths were not available for most of the birds and some of the mammals in our sample; therefore, we extracted data on female and male body mass instead (see Table S1). Note that for all the species included in the mammal‐ and bird‐specific analyses, size was measured as body mass (kg) for females and males. For mammals, we compiled data from two online resources: http://www.arkive.org and http://eol.org. For the species that were not present in these databases, we did an additional search using the keywords species name AND body size AND male AND female in WoS and Scopus, and we then examined each article to identify male and female body length data. For amphibians and reptiles, the studies from which we extracted sex‐specific mean age data also provided data on sex‐specific body size (see Table S1). For birds, sexual size dimorphism was taken from the Handbook of the Birds of the World (Lislevand et al., 2007). We took average values when a range was reported. Finally, we calculated sexual size dimorphism as the natural logarithm of the ratio of female to male body size: ln (female value/male value).

Importantly, we had sex‐specific size estimates in both mm and kg for 30 species in our sample (see ‘ssd in mm and kg’ in the Supplementary information), for which the log ratio of female to male size in mm and kg were highly correlated across species (Pearson's r = 0.90, 95% CI = 0.79 to 0.95) indicating that the different measurement used to estimate sexual size dimorphism give comparable results and do not bias our results.

2.1.5. Phylogenetic trees

We used the rotl R package, an interface to the Open Tree of Life (McTavish et al., 2015), to estimate a phylogenetic tree of the relationships among species in our sample. Branch lengths were estimated using Grafen's method (Grafen, 1989) in the APE package in R, with each node height raised to the power of 0.5. This tree was used in the analysis of sex differences in lifespan across tetrapods (see below). For the analyses involving birds only, we downloaded a sample of 1300 phylogenies (out of 10 000) from the birdtree.org (Jetz et al., 2012). Similarly, for the analyses involving mammals only, we downloaded a sample of 1300 phylogenies (out of 10 000) from Kuhn et al. (2011). We calculated a phylogenetic covariance matrix (branch lengths between species) from each of these trees which were then used to account for dependencies due to shared evolutionary history in our statistical models.

2.2. Effect size calculation

We compared female and male lifespans using an effect size which allows us to take a standardized measure of the magnitude of the difference between the sexes that is comparable across studies (Koricheva et al., 2013). We used the natural logarithm of the response ratio:

$$\mathit{lnR}=\ln \left({\overline{\mathrm{X}}}_1/{\overline{\mathrm{X}}}_2\right)$$

where $\overline{\mathrm{X}}$ ₁ is either female mean age or female annual survival and $\overline{\mathrm{X}}$ ₂ is either male mean age or male annual survival, depending on which measure was available for a given species. Positive values indicate that females live longer than males, and negative values indicate that males live longer than females. Each effect size was weighted by its inverse sampling variance in our statistical models to account for differences in sampling effort between studies:

$$\mathit{\text{VlnR}}=\left({\mathrm{SE}}_1^2/{\overline{\mathrm{X}}}_1^2\right)+\left({\mathrm{SE}}_2^2/{\overline{\mathrm{X}}}_2^2\right).$$

where SE₁ is the standard error of the female value and SE₂ is the standard error of the male value. In total, we obtained 253 effect sizes from 156 studies on 136 species across 6 independent origins of XY systems and 6 independent origins of ZW systems (Table S1; Figure S1). Full details of publication bias tests and heterogeneity estimates are provided in Table S2. Briefly, there was significant between‐study variance (τ² = 0.02, I ² = 97.7%, Cochran's Q = 7219, p < 0.001, N _{effect sizes}  = 253). We detected no evidence of publication bias using Egger's regression method (intercept = 0.01, se = 0.07, t = 0.18, p = 0.88). However, a trim and fill analysis suggested that 48 additional effect sizes are needed to generate a symmetric funnel plot (Figure S2). We report heterogeneity statistics for each of the phylogenetic meta‐analytic models described in Tables 1 and 2, including the percentage of variation in lnR attributable to phylogenetic history and repeated observations made on the same species (Nakagawa & Santos, 2012). Full details are provided in the supplementary R code.

TABLE 1.

The effects of genetic sex‐determination system and sexual size dimorphism on sex differences in survival (lnR) across tetrapods (N _{effect sizes}  = 253, N _species  = 136). I ² values refer to the percentage of heterogeneity in lnR explained by repeated measures made on the same species (I ² repeated) and phylogeny (I ² phylogeny).

Fixed terms	𝛽 a	lwr CI	upr CI	I 2 repeated	I 2 phylogeny
XY	0.15	0.01	0.26	3	82
ZW	−0.02	−0.13	0.10
Dimorphism	0.01	−0.02	0.04

^a 𝛽 is the parameter estimate, and lwr CI and upr are the lower and upper 95% credible intervals of this estimate.

TABLE 2.

Sex differences in survival (lnR) in relation to the relative sizes of the X chromosome in (A) mammals (N _{effect sizes}  = 70, N _species  = 32), the Z chromosome in (B) birds (N _{effect sizes}  = 29, N _species  = 15), the Y chromosome in (C) mammals (N _{effect sizes}  = 56, N _species  = 21) and the W chromosome in (D) birds (N _{effect sizes}  = 28, N _species  = 14). I ² values as in Table 1.

	Fixed terms	𝛽	lwr CI	upr CI	I 2 repeated	I 2 phylogeny
(A)	Intercept	0.19	0.01	0.44	3	86
	X / autosome ratio slope	0.05	0.01	0.11
	Dimorphism slope	−0.00	−0.06	0.07
(B)	Intercept	−0.04	−0.13	0.03	10	12
	Z / autosome ratio slope	−0.01	−0.06	0.05
	Dimorphism slope	0.01	−0.03	0.07
(C)	Intercept	0.18	−0.03	0.43	4	88
	Y / autosome ratio slope	0.09	0.01	0.18
	Dimorphism slope	0.03	−0.07	0.12
(D)	Intercept	−0.06	−0.13	0.06	15	20
	W / autosome ratio slope	−0.02	−0.08	0.05
	Dimorphism slope	0.02	−0.03	0.09

2.3. Statistical models

We used the Metafor (Viechtbauer, 2010) and MCMCglmm (Hadfield, 2010) R packages for model fitting when analysing lnR. Metafor uses restricted maximum likelihood for parameter estimation, whereas MCMCglmm uses the Markov chain Monte Carlo (MCMC) method in a Bayesian framework. For analyses of non‐Gaussian response variables (i.e. sex‐specific annual survival rates, described below), we used MCMCglmm only which has greater flexibility when fitting models with non‐normal distributions. We, therefore, report parameter estimates from MCMCglmm in the results section for consistency between analyses but show those from Metafor in Tables S3–S5. Parameters from the MCMCglmm models are reported as the posterior mode (ß) and 95% credible interval (CI) of the posterior distribution of the Markov chain, and significance is assessed by whether the CI includes zero. Where two parameter estimates are compared, significance is assessed by calculating the mean difference between the posterior samples for each parameter and the 95% CI of this difference. For the MCMCglmm models, we used uniform priors for fixed effects and inverse‐Wishart priors (v = 1 and nu = 0.002) for random effects and ran each model for 1 300 000 iterations with a burn in period of 300 000 and saving every 1000th iteration of the chain. Full details including model diagnostics are provided in the supplementary R script, and full model results are reported in Tables S2–S8.

2.3.1. Sex differences in lifespan and genetic sex‐determination system across tetrapods

To test whether females are longer lived than males in XY systems and males are longer lived than females in ZW systems, we modelled lnR (treated as Gaussian) as a function of genetic sex‐determination system (two‐level fixed effect: ZW or XY) with sexual size dimorphism included as a covariate (z transformed: mean = 0 and sd = 1). We supressed the intercept in this model to estimate mean values of lnR in XY and ZW systems separately. We included the phylogenetic covariance matrix from the tetrapod phylogeny as a random effect and a species‐specific random effect to account for repeated measures made on the same species, and each effect size was weighted by its inverse sampling variance, V _lnR (R code: mcmcMod1.fix.D and metaMod1.fix.D).

We examined whether the measure (annual survival vs. mean age) used to estimate sex differences in lifespan affects the relationship between sex differences in lifespan and genetic sex determination by contrasting female and male lifespans in XY and ZW systems separately for each lifespan measure. We found that females lived longer in XY systems and males live longer in ZW systems when lifespan was measured as annual survival (lnR estimates: XY = 0.09, ZW = −0.07, N _observations  = 219) and mean age (lnR estimates: XY = 0.17, ZW = 0.02, N _observations  = 34), suggesting that the proxy used to estimate sex differences in lifespan does not bias our results. To formally test this, we included measure (two levels: annual survival vs. mean age) as an additional fixed effect in the model described above, which we interacted with genetic sex determination (R code: mcmcMod1.sens.B and metaMod1.sens.B). A significant interaction would indicate that the sex difference in lifespan between XY and ZW systems depends on how the difference was measured. The interaction between genetic sex determination and measure was not significant (difference in slopes: = −0.01, CI = −0.35 to 0.18; Table S4), confirming that the proxy used to estimate sex differences in lifespan does not bias our results.

2.3.2. Sex differences in lifespan and the relative sizes of the sex chromosomes

The UX hypothesis predicts that sex differences in lifespan should correlate with the size of the X (or Z) chromosome relative to the rest of the genome, as this ratio measures the potential impact of recessive mutations on survival. Similarly, the toxic Y hypothesis predicts that sex differences in lifespan should correlate with the size of the Y (or W) chromosome relative to the rest of the genome.

We tested for UX effects by constructing two models. In mammals, we modelled lnR (treated as Gaussian and with each effect size weighted by its sampling variance) as a function of the X/autosomes ratio (z transformed) and sexual size dimorphism (z transformed) with a species identifier and a phylogenetic covariance matrix included as random effects (R code: mcmcMod2.XA.C and metaMod2.XA.C). We replaced the phylogenetic covariance matrix every 1000 iterations of the Markov chain with the next one in the sequence calculated from the 1300 mammal phylogenies from Kuhn et al. (2011). The values of the variance components and latent variables estimated using the previous phylogenetic covariance matrix were used as starting values for the next one in the sequence. This allowed us to incorporate uncertainty in the mammal phylogeny into our analyses. Note that this was not possible for the Metafor analysis and parameters were calculated based on one randomly sampled phylogenetic covariance matrix. We repeated this model for birds, substituting the X/autosomes ratio for the Z/autosomes ratio (R code: mcmcMod2.ZA.C and metaMod2.ZA.C). We compared the mammal and bird slopes by calculating the mean difference between the posterior samples for each parameter and the 95% CI of this difference.

We then tested for toxic Y effects in mammals and birds by repeating the above models but replacing the X/autosomes ratio with the Y/autosomes ratio (z transformed) in the mammal analysis (R code: mcmcMod2.YA.C and metaMod2.YA.C) and the Z/autosomes ratio for the W/autosomes ratio (z transformed) in the bird analysis (R code: mcmcMod2.WA.C and metaMod2.WA.C). All other fixed and random effects were the same. Again, we compared the mammal and bird slopes by calculating the mean difference between the posterior samples for each parameter and the 95% CI of this difference.

Note that we ran models with the X (or Z)/autosome ratio and the Y or (W)/autosome ratio included as predictors separately instead of a single model with these two parameters as predictors to maximize statistical power. For mammals, we had estimates of the X/autosome ratio for 32 species and Y/autosome ratio for 21 of these species (because only 21 of them had karyotype images from males). For birds, we had estimates of the Z/autosome ratio for 15 species and the W/autosome ratio for 14 of these species. Running an analysis with the relative sizes of both sex chromosomes as predictors would thus reduce our sample size to 21 mammal species (> 30% reduction) and 14 bird species, which would greatly reduce the power of our analyses. Furthermore, the relative sizes of the sex chromosomes correlate moderately in both mammals (r = 0.28, n = 21, t = 1.3, p = 0.22) and birds (r = −0.31, n = 14, t = −1.1, p = 0.28), so that including them both as predictors would violate the assumption of non‐collinearity.

For plotting, we ran the above models separately for birds and mammals and only included the X (or Y) to autosome ratio (untransformed) for mammals and the Z or (W) to autosome ratio (untransformed) for birds as fixed effects. This allowed us to plot separate slopes and intercepts for birds and mammals on the data scale. The results of these models are reported in Table S7.

2.3.3. Lifespan of the heterogametic sex and the relative sizes of the sex chromosomes

The unguarded X and toxic Y hypotheses predict reduced survival of the heterogametic sex specifically. We tested this in mammals by comparing male annual survival rates (males are XY) across species in relation to (i) the z transformed X/autosomes ratio (R code: mcmcMod3.XA.C) and (ii) z transformed the Y/autosomes ratio (R code: mcmcMod3.YA.C). Male annual survival was modelled using a binomial distribution (number alive vs. number dead) with a logit link function. The number alive vs. number dead was calculated from the sample size associated with each survival estimate. This sample size is based on the standard error associated with each survival estimate, using the formula for the standard error of a binomial response variable: sqrt((p*(1 − p))/n), where p is a proportion. We used this approach because the standard error was more likely to be reported than the underlying sample size in many of the studies included in our analysis and because reported sample sizes are normally ‘ringing effort’ rather than ‘study effort’ and for some species are extremely high. For example, a study might ring 2000 birds and recover just 50 because the birds aren't site‐faithful vs. a study which rings 50 birds and is able to track each one individually because they are philopatric. Thus, the standard error provides a good indication of the weight each study should be given. In both of these models, we included male body mass (z and log transformed) and sexual size dimorphism (z transformed) as covariates to control for variation in male annual survival rates across species explained by differences in the strength of sexual selection and size differences. A phylogenetic covariance matrix (updated as described above) and a species level identifier were included as random effects in each model.

Females are the heterogametic sex in birds; therefore, we modelled female annual survival rates (using a binomial distribution with a logit link function) as a function of (i) the z transformed Z/autosomes ratio (R code: mcmcMod3.ZA.C) and (ii) the z transformed W/autosomes ratio (R code: mcmcMod3.WA.C). Again, the number alive vs. number dead was calculated from the sample size (based on the standard error) associated with each survival estimate. In both of these models, we included female size as a covariate, to account for variation in female survival rates across species explained by differences in size, and a phylogenetic covariance matrix (updated as above) and a species‐level identifier were included as random effects.

For plotting, we ran the above models separately for birds and mammals and only included the X or Y to autosome ratio (untransformed) for mammals and the Z or W to autosome ratio (untransformed) for birds as fixed effects. This allowed us to plot separate slopes and intercepts for birds and mammals on the data scale. The results of these models are reported in Table S8.

We explored the sensitivity of our results to calculating the number alive vs. number dead from the standard error of each survival estimate by recalculating the number alive vs. number dead assuming a sample size of 100 for all survival estimates and treating the standard error as an additional fixed effect (z and log transformed) in the four models described above (R code: mcmcMod3.sens.MA, mcmcMod3.sens.MB, mcmcMod3.sens.BA and mcmcMod3.sens.BB). For example, if annual survival is 80%, then 80 individuals were assumed to be alive and 20 dead. Parameter estimates from these models are reported in Table S6 and are consistent with those from the models where the number alive vs. number dead was calculated from the standard error (Table 3).

TABLE 3.

Annual survival of the heterogametic sex in relation to the relative sizes of the X chromosome in (A) male mammals (N _estimates  = 70, N _species  = 32), the Z chromosome in (B) female birds (N _estimates  = 29, N _species  = 15), the Y chromosome in (C) male mammals (N _estimates  = 56, N _species  = 21) and the W chromosome in (D) female birds (N _estimates  = 28, N _species  = 14).

	Fixed terms	𝛽	lwr CI	upr CI
(A)	Intercept	0.23	−0.88	1.76
	X/autosome ratio slope	−0.12	−0.42	0.19
	Body size slope	0.66	0.17	1.09
	Dimorphism slope	0.30	−0.09	0.75
(B)	Intercept	1.31	0.01	2.46
	Z/autosome ratio slope	−0.17	−0.64	0.89
	Body size slope	0.31	−0.55	1.30
	Dimorphism slope	0.41	−0.62	0.99
(C)	Intercept	0.65	−0.76	1.83
	Y/autosome ratio slope	−0.53	−0.99	−0.08
	Body size slope	0.59	0.25	0.97
	Dimorphism slope	0.25	−0.26	0.79
(D)	Intercept	1.13	−0.23	2.42
	W/autosome ratio slope	0.24	−0.93	1.08
	Body size slope	0.34	−0.77	1.62
	Dimorphism slope	0.29	−0.71	1.18

3. RESULTS

3.1. Sex differences in lifespan and genetic sex‐determination system across tetrapods

In XY systems, females survived significantly longer than males on average (the log transformed ratio of female to male survival, lnR = 0.15, 95% credible interval [CI] = 0.01 to 0.26; N _{effect sizes}  = 118; N _species  = 54; Figure 2; Table 1), but there was no difference between the sexes in survival in ZW systems (lnR = −0.02, CI = −0.13 to 0.10; N _{effect sizes}  = 135; N _species  = 82; Figure 2; Table 1). When we compared the ratios to each other, we found a significant difference between XY and ZW systems (lnR difference between XY and ZW systems = 0.12, CI = 0.05 to 0.24; N _{effect sizes}  = 253; N _species  = 136; Figure 2). The effect of the genetic sex‐determination system on sex differences in lifespan was independent of phylogeny, which explained 82% of the heterogeneity in sex‐specific lifespans across species, and sexual size dimorphism (slope = 0.01, CI = −0.02 to 0.04; Table 1), suggesting that differences in lifespan between the sexes are not due to overall differences between species in the strength of sexual selection.

FIGURE 2.

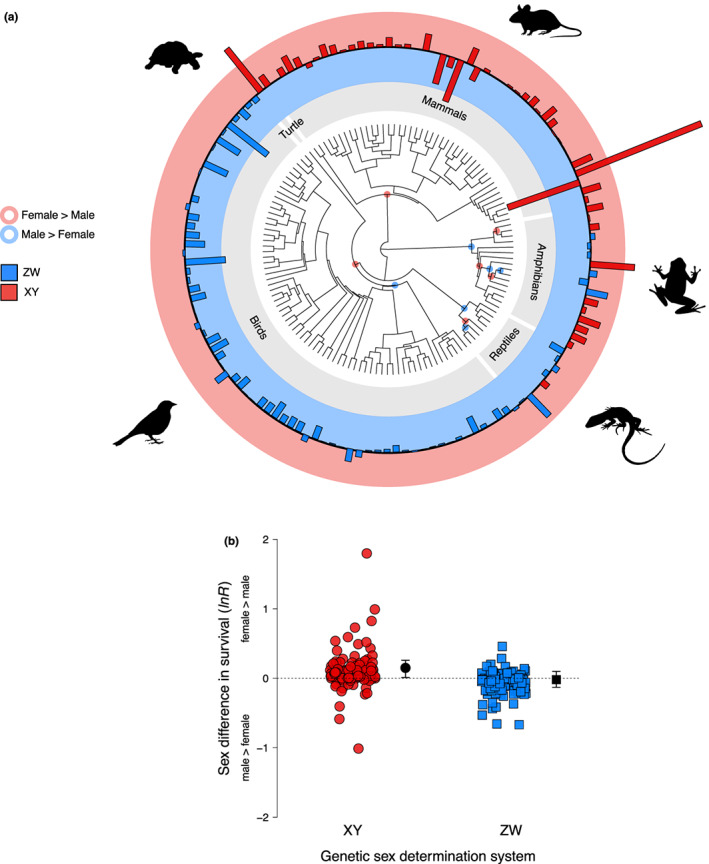
Sex differences in lifespan and sex‐determination systems across vertebrates. (a) Sex differences in lifespan across 136 species of birds, mammals, reptiles and amphibians. The log transformed ratio of female and male lifespan (lnR) is plotted for each species. When more than one lnR estimate was available per species, we took an average. Bars above the black line (the red ring) indicate that females live longer than males, while bars below the black line (the blue ring) indicate that males live longer than females. ZW systems are coloured in blue, and XY systems are coloured in red. The blue circles in the phylogeny show the six independent origins of ZW systems, and the red circles show the six independent of XY systems in our sample of species. (b) Sex differences in lifespan for XY and ZW systems, where each point represents estimates from a single species (i.e. some species have multiple estimates) and black bars denote 95% CIs around the mean estimated lnR within each genetic determination system (see Results).

3.2. Sex differences in lifespan and the relative sizes of the sex chromosomes

Across mammal species, the size of the X chromosome relative to the autosomes was significantly associated with sex differences in survival, consistent with the unguarded‐X hypothesis. Mammal species with relatively large X chromosomes showed larger differences in survival between the sexes, with females being increasingly long‐lived relative to males as the size of the X chromosome increased (mammal slope = 0.05, CI = 0.01 to 0.11; N _{effect sizes}  = 70; N _species  = 32; Table 2a; Figure 3a). In contrast, across bird species, the size of the Z chromosome relative to the autosomes was not associated with sex differences in survival (bird slope = −0.01, CI = −0.06 to 0.05; N _{effect sizes}  = 29; N _species  = 15; Table 2b; Figure 3b), contrary to the unguarded X hypothesis. The difference between the mammal and bird slope estimates, although positive, was marginally non‐significant (slope difference = 0.05, CI = −0.02 to 0.14).

FIGURE 3.

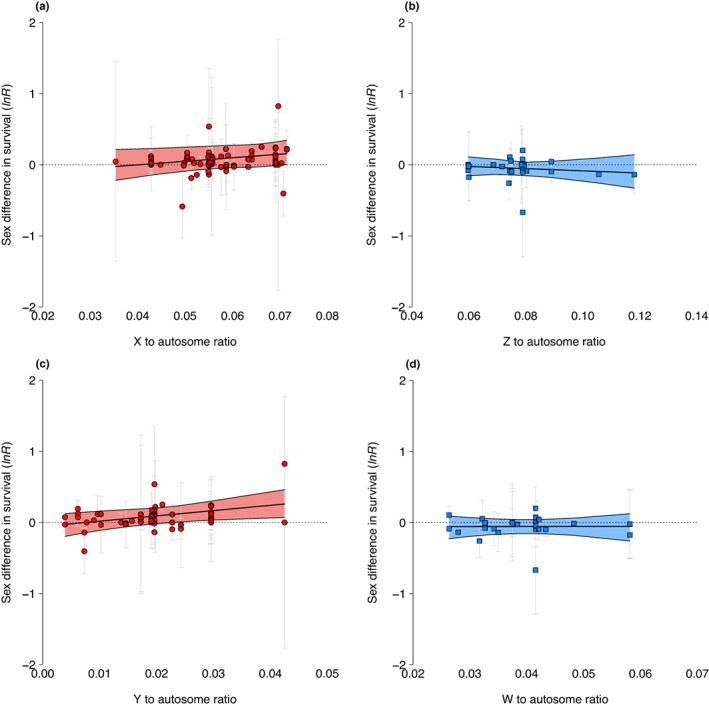
Sex differences in survival vs. (a) the relative size of X in mammals (red circles), (b) the relative size of Z in birds (blue squares), (c) the relative size of Y in mammals (red circles) and (d) the relative size of W in birds (blue squares). Each point is an effect size and is bracketed by its 95% confidence interval (multiple effect sizes per species are shown). Slopes and 95% credible intervals are estimated from phylogenetic mixed models run on untransformed data (see methods and Table S7).

Birds and mammals also differed in the relationship between the relative size of the Y and W chromosomes and sex differences in survival. Across mammal species, females were increasingly long‐lived relative to males as the size of the Y chromosome increased (mammal slope = 0.09, CI = 0.01 to 0.18; N _{effect sizes}  = 56; N _species  = 21; Table 2c; Figure 3c), as expected if the accumulation of deleterious mutations and repetitive elements on the Y chromosome lowers male survival. In birds, however, the size of the W chromosome relative to the autosomes was not associated with sex differences in survival (bird slope = −0.02, CI = −0.08 to 0.05; N _{effect sizes}  = 28; N _species  = 14; Table 2d; Figure 3d), contrary to the toxic Y hypothesis. The difference between the mammal and bird slope estimates was significant (slope difference = 0.11, CI = 0.01 to 0.21).

One species in our sample, the Virginia opossum, Didelphis virginiana, had extremely low male annual survival, <10%, and relatively large X and Y chromosomes (Table S1, the top right data point in Figure 3c). Given this is a representative outlier and not due to a measurement error (two survival estimates from two independent studies), we conducted a sensitivity analysis using the Winsor method (Chambers, 1986; Huber, 1981; Quinn & Keough, 2002) to confirm this species did not have an undue influence on the observed relationship between relative X and relative Y chromosome sizes and sex differences in survival across species and recovered the same results (X to autosome slope = 0.05, CI = 0.004 to 0.092, Y to autosome slope = 0.07, CI = 0.008 to 0.133).

3.3. Lifespan of the heterogametic sex and the relative sizes of the sex chromosomes

There was no effect of the relative sizes of the X or Z chromosomes on survival of the heterogametic sex in mammals (mammal slope = −0.12, CI = −0.42 to 0.19; N _estimates  = 70; N _species  = 22; Table 3a; Figure 4a) or birds (bird slope = −0.17, CI = −0.64 to 0.89; N _estimates  = 29; N _species  = 15; Table 3b; Figure 4b). A negative relationship was expected in both clades if recessive mutations on X and Z chromosomes lowered survival of the heterogametic sex. The relative size of Y chromosomes, however, had a strong effect on male survival in mammals. Males from mammal species with small Y chromosomes relative to the autosomes had high rates of annual survival, whereas males with relatively large Y chromosomes had low annual survival rates (mammal slope = −0.53, CI = −0.99 to −0.08; N _estimates  = 56; N _species  = 21; Table 3c; Figure 4c). Again, we confirmed the Virginia opossum did not have an undue influence on the observed relationship between relative Y chromosome size and male annual survival (the outlier in Figure 4c) using the Winsor method (mammal slope = −0.42, CI = −0.70 to −0.14). In contrast to the strong effect of Y chromosome size on male survival in mammals, female survival across bird species was not associated with the sizes of W chromosomes relative to autosomes (bird slope = 0.24, CI = −0.93 to 1.08; N _estimates  = 28; N _species  = 14; Table 3d; Figure 4d).

FIGURE 4.

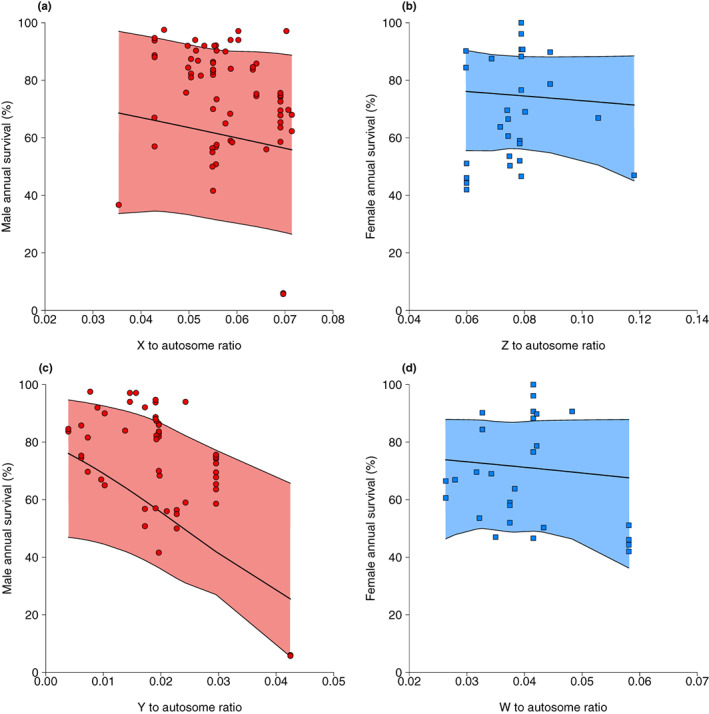
Annual survival of the heterogametic sex in mammals (males, red circles) and birds (females, blue squares) vs. the sizes of the sex chromosomes relative to the autosomes. (a) Male survival vs. the relative size of X in mammals, (b) female survival vs. the relative size of Z in birds, (c) male survival vs. the relative size of Y in mammals, and (d) female survival vs. the relative size of W in birds. Each point is an annual survival estimate (multiple survival estimates per species are shown). Slopes and 95% credible intervals are estimated from phylogenetic mixed models run on untransformed data (see methods and Table S8).

4. DISCUSSION

In this paper, we show a clear link between genetic sex‐determination system and the sex gap in lifespan. Across 136 species of vertebrates reflecting 6 independent origins of XY and ZW systems, females survived longer than males on average in XY systems, while there was no sex difference in survival on average in ZW systems (Figure 2). Previously, Pipoly et al. (2015) identified female‐biased adult sex ratios in taxa with XY systems and male‐biased adult sex ratios in taxa with ZW systems. Xirocostas et al. (2020) recently found that mean/maximum lifespan is shorter in the heterogametic sex across the tree of life. Our results use an independent dataset based on high‐quality data (see methods) to show that the relationship between sex differences in lifespan and sex‐determination system remains after accounting for phylogenetic signal (which explained 80% of the heterogeneity in the sex gap in lifespan), sampling error and sexual size dimorphism. Furthermore, our results suggest that in mammals, both sex differences in lifespan and male lifespan itself fit squarely with the existence of toxic Y effects. In birds, there was no clear signal of an unguarded X or toxic Y effect (Figures 3 and 4).

The most commonly cited hypothesis to explain broad patterns of sex‐specific lifespan across taxa is the UXh put forward by Trivers (1985). Recent works reporting a link between sex‐determination systems and different proxies for sex‐specific lifespan have been interpreted as supporting this hypothesis (Pipoly et al., 2015; Xirocostas et al., 2020). Here, we specifically tested the UXh by asking whether there is a correlation between the relative size of the sex chromosomes (X/Z relative to the autosomes) and (1) the sex‐gap in survival and (2) survival of the heterogametic sex. We found partial evidence that the UXh may drive sex‐specific mortality, as reflected by the association between the sex gap in survival and the size of the X chromosome in mammals (but not the Z chromosome in birds). However, we failed to find evidence for the more specific relationship between the relative size of X or Z chromosomes and survival of the heterogametic sex. Since it was first formulated, more than three decades ago, support for the UXh has been rare and indirect (Maklakov & Lummaa, 2013; Marais et al., 2018; Pipoly et al., 2015; Sultanova et al., 2018; Xirocostas et al., 2020). This may reflect the fact that the UXh does not actually play a major role in explaining sex‐specific lifespan. For example, there is likely to be strong selection against large effect X‐linked recessive mutations in nature (Vicoso & Charlesworth, 2006), meaning that any mutations that do accumulate on the recombining chromosome should have relatively minor effects. Alternatively, this paucity of evidence may be due to inherent difficulties in testing this hypothesis. In our case, given the relatively scarce karyotypic data generally available for vertebrates, our failure to find a correlation between the relative size of X/Z chromosomes (vs. autosomes) and the survival of the heterogametic sex may well be due to a lack of statistical power in our study. This problem is compounded by the general existence of collinearity between the size of the two sex chromosomes, and by the fact that both the X chromosome of mammals and the Z chromosome of birds seem to be highly conserved within each of these two lineages (Bachtrog et al., 2014; Graves, 2006, 2016), so that variation in the size of X and Z chromosomes between taxa within these groups may not be expected to correlate strongly with variation in gene content. Note, however, that the size (and gene content) of the rest of the genotype does vary substantially across taxa within both birds and mammals, and should hence modulate unguarded X effects; i.e. which fraction of the genome is hemizygous.

An alternative way to test the UXh would be to look at the extent to which the X chromosome is larger than the Y chromosome (and vice versa with Z/W), because unguarded recessive mutations have to accumulate in the functionally haploid non‐recombining regions of the X (or Z) chromosome and the overall size of these regions should in principle increase with the size difference between the sex chromosomes (Xirocostas et al., 2020). However, due to the accumulation of repetitive and non‐functional regions in the Y/W chromosomes, the size of the non‐recombining region between the two sex chromosomes can vary considerably, even across species with the same absolute X/Z vs. Y/W size differences (Bachtrog, 2013; Vicoso & Charlesworth, 2006; Wright et al., 2016). For example, the size of the X/Z vs. the Y/W may be generally indicative of the size of the non‐recombining region in young sex chromosomes, but not in old sex chromosomes (Wright et al., 2016), as are found in birds and mammals. Hence, while large differences in the size of sex chromosomes will reflect a large hemizygous fraction regardless of chromosome age, small differences in the size of old sex chromosomes will not necessarily reflect ample recombination. Unsurprisingly, when we examined the sex difference in survival in relation to the size difference between the sex chromosomes, we found no effect in mammals (Figure S3a; Table S5e; R code: mcmcMod2.XY.C and metaMod2.XY.C) or birds (Figure S3b; Table S5f; R code: mcmcMod2.ZW.C and metaMod2.ZW.C). Overall, we stress that our relative lack of support for predictions arising from the UXh should be taken with caution at this stage. First, due to the inherently noisy nature of using relative sex chromosome size as a proxy for the amount of sex chromosome linked deleterious mutations. Second, because there are other parameters that could potentially contribute to UXh effects that are currently not amenable to scrutiny (e.g. differences in deleterious mutation rate or the relative strength of selection between taxa; Connallon et al., 2022). Thus, we strongly suggest that future analysis with more exhaustive datasets should aim to replicate our analyses. For example, it would be interesting to replicate our study using absolute sex chromosome size and, ideally, gene content, but unfortunately these data are currently unavailable for most species. We note, however, that some of the above limitations of power should also affect our ability to detect toxic Y effects, a recent and until now empirically untested alternative to explain broad patterns of sex‐specific ageing that fits with the findings reported here. Furthermore, in a recent paper, Connallon et al. (2022) develop a population genetics model to identify what evolutionary parameters are relevant to unguarded X effects. They then use available estimates to parameterize their model and elegantly show that, while unguarded X effects are certainly expected, they would be too low to explain observed differences in lifespan between the sexes (Connallon et al., 2022). For example, in Drosophila, their estimations show that unguarded X effect can only account for 3% or less of the sex gap in lifespan, which led them to suggest that sex‐specific ageing must be predominantly attributable to other mechanisms, such as the toxic Y (Connallon et al., 2022).

According to theory, toxic Y effects can result in reduced survival of the heterogametic sex due to the accumulation of both deleterious mutations and repetitive DNA elements in the Y and W sex chromosomes (Bachtrog, 2013; Marais et al., 2018; Vicoso & Charlesworth, 2006; Wright et al., 2016). Two main predictions arise from this hypothesis. First, that genetic sex‐determination systems should predict the sex‐gap in lifespan so that the homogametic sex tends to live longer than the heterogametic sex across a wide range of taxa, as reported here (Figure 2) and in a recent study (Xirocostas et al., 2020). Second, that the size of the Y and W sex chromosomes should inversely predict the lifespan of the heterogametic sex in XY and ZW systems respectively. Our results show that there is indeed a negative correlation between the relative size of the Y chromosome and male lifespan in mammals (Figure 4c), although we did not find this effect in birds (Figure 4d). In fact, a stronger toxic Y effect is expected in XY than in ZW systems. This is due to the Y chromosome having a smaller effective population size than the W chromosome (higher variance in male than female reproductive success), and to Y chromosomes accumulating more mutations than W chromosomes because the male germ line undergoes more cell divisions than the female germ line (Drost & Lee, 1995). Thus, we expect a higher equilibrium load of mutations in the Y (vs. W) chromosome, which in turn makes degeneration of the Y chromosome (and hence accumulation of repetitive DNA) more likely (Bachtrog, 2013). For example, the mammalian Y chromosome is known to be significantly enriched in repetitive DNA compared to the W chromosome in birds (Bachtrog, 2013; Rutkowska et al., 2012; Wright et al., 2016; Zhou et al., 2014). Available evidence also suggests that non‐recombining regions are larger in mammal than in bird sex chromosomes, which also seem to exhibit less variability in the Z/W (vs. mammalian X/Y) size ratio (Bachtrog, 2013; Rutkowska et al., 2012; Wright et al., 2016; Zhou et al., 2014). In agreement with this, the X to Y chromosome ratio across mammals was twice as high as the Z to W chromosome ratio across birds in our sample of species (X to Y estimate = 4.96 ± 0.76 (se), N _species  = 21; Z to W estimate = 2.23 ± 0.19, N _species  = 14; Figure S4). This is unlikely to be a sampling artefact as evidence from the karyotypes of 200 bird species shows that the Z to W chromosome ratio does not extend beyond the limit we detected (Rutkowska et al., 2012). Lower variability in Z/W ratios may reflect the generally higher prevalence of homomorphic sex chromosomes in birds than in mammals. In line with this, avian W chromosomes have been found to maintain a higher proportion of pseudoautosomal regions than mammalian Y chromosomes (Zhou et al., 2014). Yet, the density of transposable elements on the W chromosome is greater than their genome‐wide density in at least six different bird species spanning the avian tree of life (Peona et al., 2021). Therefore, although avian W chromosome can potentially contain less transposable elements than mammalian Y chromosome, it still contains more than the rest of the genome. Our inability to detect effects predicted by a ‘toxic W’ may be simply due to the noise generated by a higher proportion of bird species with large pseudoautosomal regions because, by using karyotypic data, we are not able to detect whether a large W chromosome consists of a large amount of transposable elements or pseudoautosomal regions. Exploring the number and functional effects of transposable elements on the Y and W chromosomes instead of the size of these chromosomes would be more informative to understand the mechanistical basis of the toxic Y effects, which has started to gain attention (Peona et al., 2021). Similarly, directly examining deleterious mutation rates on the X and Z chromosomes would offer first‐hand evidence of how important unguarded X effects may be to explain sex‐specific lifespan (Connallon et al., 2022). Unfortunately, we are currently far from obtaining this type of data for a large enough sample of species to enable a comparative analysis. We hence suggest a priority for future studies will be to replicate our analyses with much higher sample sizes and detailed evidence about the size of transposable elements and pseudoautosomal regions.

An exciting possibility is that cyto‐nuclear interactions may contribute to explain marked toxic Y effects in mammals, but not in birds. Given that Y chromosomes are not inherited along with mitochondrial DNA (and other cytoplasmic products), there is less scope for cyto‐nuclear co‐evolution in males vs. females with X/Y genetic determination systems (but see Keaney et al., 2020). This is not the case in males of species with ZW sex‐determination systems because in these species females are the heterogametic sex, and hence, copies of both sex chromosomes are inherited maternally along with the cytoplasm. Indeed, recent evidence shows that cyto‐nuclear interactions have sex‐specific lifespan effects in D. melanogaster (Vaught et al., 2020), which opens yet another exciting line of research for future studies. Although it is tempting to interpret our negative finding of a toxic W effect in line with the predictions above, this finding must be taken with caution for two methodological reasons: our sample size for birds was approximately half that of mammals, and autosome size (on which our relative sex chromosome size measures are based) is more difficult to estimate in birds than in mammals due to bird karyotypes often including a large number of micro‐chromosomes that increased measurement error in our estimations of bird chromosome sizes.

Two further complementary hypotheses that could indirectly explain why sex chromosomes determine the sex gap in lifespan have to do with sexual selection and imperfect dosage compensation. First, sexual selection frequently favours the accumulation of mutations that increase male reproductive success at the expense of male survival (Bonduriansky et al., 2008). In both our study and in Pipoly et al. (2015), correlations between sex‐determination systems and survival/adult sex ratios were independent of sexual size dimorphism, a commonly used proxy for sexual selection intensity. However, it must be noted that sexual size dimorphism is far from being a perfect proxy of sexual selection, and thus sexual selection effects cannot be completely ruled out. Second, imperfect dosage compensation is in principle deleterious for the heterogametic sex, which could help explain why this sex is short‐lived relative to the homogametic sex (Mank, 2013). However, the mechanisms of sex chromosome dosage compensation vary greatly across taxa, defying strong predictions in this respect (Gu & Walters, 2017).

To conclude, we report compelling evidence of a link between sex‐determination systems and the sex‐gap in survival across tetrapods, which along with recent evidence (Xirocostas et al., 2020) strongly suggests that sex chromosomes play a key role in explaining broad patterns of sex differences in lifespan. Our data further suggest that toxic Y effects may contribute to explain this link. Future research should aim to explicitly test for toxic Y effects by means of direct empirical manipulations (Brown et al., 2020a, 2020b), by measuring the relative amount and activity of transposable elements on the Y/W chromosomes (Peona et al., 2021), and by expanding our comparative framework to other taxa (e.g. invertebrates).

CONFLICT OF INTEREST

Authors declare no competing interests.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1111/jeb.14130.

CODE AVAILABILITY

The code used to run all the analyses was uploaded during submission (Tetrapod_R_code.R, Mammal_R_code.R, Bird_R_code.R) and will be uploaded to a public repository, and the associated link will be provided in the paper before publication.

Supporting information

Data S1. Supporting Information

Figure S1. Forest plot showing all effect sizes (N = 253 from 136 tetrapod species). Blue squares are ZW systems, and red circles are XY systems. Each effect size is bracketed by its 95% confidence interval.

Figure S2. Funnel plot. Each effect size is plotted against its corresponding precision (standard error). Missing studies from the trim and fill analysis, those needed to make the funnel plot symmetrical, are shown in white (i.e. the filled studies in the figure legend).

Figure S3. Sex differences in survival and (a) the size of X relative to Y in mammals (slope = −0.03, CI = −0.12 to 0.04; Table S5e) and (b) the size of Z relative to W in birds (slope = 0.00, CI = −0.05 to 0.08; Table S5f). Each point is an effect size and is bracketed by its 95% confidence interval (multiple effect sizes per species are shown). Slopes and 95% credible intervals are estimated from phylogenetic mixed models run on untransformed data.

Figure S4. The X to Y chromosome ratio (bracketed by its 95% confidence interval) across mammals was twice as high as the Z to W chromosome ratio across birds in our sample of species (N = 21 mammals and 14 bird species).

Table S1.

Table S2. Heterogeneity and publication bias – I ² , Q and the trim and fill analysis are from random effect meta‐analytic models that did not control for phylogeny and repeated measures.

Table S3. Sex differences in lifespan and genetic sex‐determination system across tetrapods. N effect sizes = 253, N species = 136. R code models: mcmcMod1.fix.D and metaMod1.fix.D.

Table S4. Sensitivity analysis – how does lifespan measure (annual survival vs. mean age) affect GSD? N effect sizes = 256, N species = 138. R code models: mcmcMod1.sens.B and metaMod1.sens.B.

Table S5. Sex differences in lifespan and the relative sizes of the sex chromosomes.

Table S6. Sensitivity analyses – treating the standard error as an additional fixed effect and assuming a sample size of 100 (50 alive, 50 dead) for all sex‐specific models.

Table S7. Intercept and slope estimates for Figure 3. Models were constructed for birds and mammals separately (see methods).

Table S8. Intercept and slope estimates for Figure 4. Models were constructed for birds and mammals separately (see methods).

Sultanova, Z. , Downing, P. A. , & Carazo, P. (2023). Genetic sex determination, sex chromosome size and sex‐specific lifespans across tetrapods. Journal of Evolutionary Biology, 36, 480–494. 10.1111/jeb.14130

DATA AVAILABILITY STATEMENT

Data associated with this manuscript has been uploaded to Dryad (doi:10.5061/dryad.hhmgqnkm3).