Abstract
NADH and NADPH play key roles in the regulation of metabolism. Their endogenous fluorescence is sensitive to enzyme binding, allowing changes in cellular metabolic state to be determined using fluorescence lifetime imaging microscopy (FLIM). However, to fully uncover the underlying biochemistry, the relationships between their fluorescence and binding dynamics require greater understanding. Here we accomplish this through time- and polarization-resolved fluorescence and polarized two-photon absorption measurements. Two lifetimes result from binding of both NADH to lactate dehydrogenase and NADPH to isocitrate dehydrogenase. The composite fluorescence anisotropy indicates the shorter (1.3–1.6 ns) decay component to be accompanied by local motion of the nicotinamide ring, pointing to attachment solely via the adenine moiety. For the longer lifetime (3.2–4.4 ns), the nicotinamide conformational freedom is found to be fully restricted. As full and partial nicotinamide binding are recognized steps in dehydrogenase catalysis, our results unify photophysical, structural, and functional aspects of NADH and NADPH binding and clarify the biochemical processes that underlie their contrasting intracellular lifetimes.
Significance
The metabolic cofactors NADH and NADPH exhibit spectrally identical fluorescence, labeled NAD(P)H. The fluorescence lifetime of NAD(P)H is sensitive to shifts in metabolism, raising hope that FLIM could be used to determine the metabolic pathways active within the cells of living tissues. However, little is known about how the cofactor photophysics are mediated by the enzymes to which they bind, making NAD(P)H FLIM measurements difficult to interpret. Here we show that two distinct binding configurations, in which the nicotinamide chromophore either retains conformational freedom or becomes fully bound, are associated with distinct fluorescence lifetimes. These represent key steps in the dehydrogenase catalytic mechanism, demonstrating influence on NADH and NADPH fluorescence by the kinetics of the metabolic reactions they facilitate.
Introduction
The intracellular pools of nicotinamide adenine dinucleotide (NAD) and its phosphorylated analogue NADP are responsible for ferrying reducing equivalents between the redox reactions of metabolism (1). Their reduced forms (NADH and NADPH) are fluorescent, emitting at 460 (±50) nm after excitation at 340 (±30) nm, an absorption band that is absent when oxidized to NAD+ and NADP+ (2). The phosphate group that differentiates the two molecules allows enzyme binding sites to be specific to either cofactor, enabling their regulation of distinct sets of metabolic reactions (3). NAD is primarily involved in catabolic pathways in which molecules are broken down to provide energy in the form of adenosine triphosphate (ATP), such as glycolysis in the cytosol and the tricarboxylic acid (TCA) cycle in the mitochondria. In contrast, NADP primarily contributes to biosynthetic processes such as the production of lipids and nucleic acids and the maintenance of the glutathione and thioredoxin defenses against reactive oxygen species (ROS) (1).
The absorption and emission characteristics of NADH and NADPH are identical as the additional phosphate group is distant from the nicotinamide chromophore (Fig. 1) (1,2,4). The spectrally indistinguishable endogenous fluorescence of these molecules, labeled NAD(P)H (1), has been used to report the metabolic state of living cells and tissues since the 1950s (5). The lack of any fluorescence signal from oxidized NAD(P)+ allows changes in the NAD(P)H intensity to be directly correlated to the redox balance within a biological sample (1). Such measurements were crucial in early investigations of the mitochondrial electron transport chain (ETC) (6) and continue to be applied to this day using laser scanning confocal microscopy in the study of mitochondrial dysfunction (7,8). The commercialization of fluorescence lifetime imaging microscopy (FLIM) in the 1990s enabled work demonstrating the sensitivity of time-resolved NAD(P)H fluorescence to changes in the metabolic state of living samples (9). This was widely observed to contain two components, one with a short lifetime (∼0.4 ns) representing freely diffusing cofactors and one with a longer lifetime (2–4 ns) arising from enzyme-bound species (1). Both the average bound lifetime and the proportion of bound to free NAD(P)H change in response to metabolic perturbations (10,11,12,13,14). This has prompted the development of FLIM-based diagnostic tools (15) to exploit the close links between metabolism and pathology (16). However, both the clinical application of these and use of NAD(P)H FLIM to rigorously interrogate pathophysiological processes have been held back by inadequate knowledge of the molecular mechanisms that connect metabolic state with NAD(P)H lifetime (1). Key to rectifying this is to understand how metabolic enzyme binding perturbs the photophysics of these cofactors.
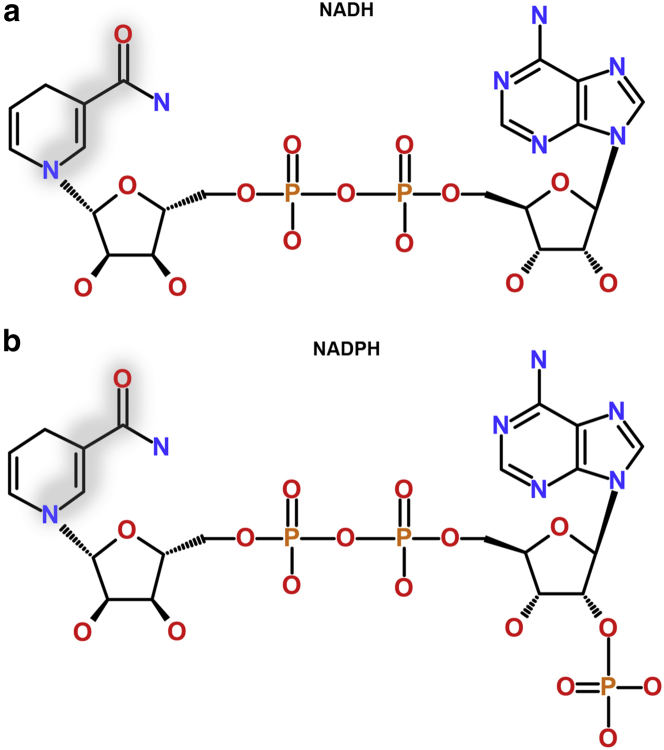
Figure 1.
NADH and NADPH are intrinsically fluorescent, structurally similar enzymatic cofactors that regulate contrasting sets of redox reactions within the cell. Absorption and emission are localized to the nicotinamide ring of both molecules, with the transition involving transfer of charge between the ring nitrogen to the oxygen of the amide group, shown in gray. NADPH (b) differs from NADH (a) only by the presence of a phosphate group at the adenine end of the molecule. Although the distance of this group from the chromophoric region results in identical photophysics of the molecules when isolated in solution, its negative charge allows enzyme binding sites to be specific for either cofactor. This allows NADH to regulate ATP-generating catabolic pathways, whereas NADPH is primarily involved in biosynthesis. To see this figure in color, go online.
We have demonstrated that changes in the fluorescence lifetime of the enzyme-bound NAD(P)H population reflect changes in the balance of NADPH and NADH (17). This allowed us to use FLIM to separately investigate the roles of the two cofactors for the first time, in diseases ranging from hearing loss (18) and cancer (19) to heart disease (20) and diabetes (21). Our results indicated that the separate binding sites of NADH and NADPH give rise to contrasting fluorescence lifetimes, which we predicted to be 1.5 (±0.2) ns and 4.4 (±0.2) ns respectively (17); however, the underlying mechanisms were unclear. We have recently studied the relationships between the fluorescence and conformational dynamics of NADH and NADPH in solution using polarized two-photon absorption and time-resolved intensity and anisotropy measurements. This demonstrated that small-scale motion of the nicotinamide ring and alterations to its geometry mediate their lifetimes (22,23). Here, we extend these investigations to study the fluorescence dynamics of NADH and NADPH when bound to two corresponding enzymes. These reveal heterogeneous fluorescent populations resulting from distinct binding configurations associated with the “open” and “closed” dehydrogenase conformational states.
Methods
NAD(P)H and enzyme solutions
NADH and NADPH were obtained from Sigma-Aldrich (Dorset, UK). Recombinant human lactate dehydrogenase (UniProtKB: P07195) and isocitrate dehydrogenase (UniProtKB: O75874), expressed in Escherichia coli and chromatography purified (>95% SDS-PAGE), were supplied by Abcam (Cambridge, UK). These were resuspended in 5 mL of 10 mM pH 7.4 Tris buffer (Sigma-Aldrich, Dorset, UK) containing 10 μM NADH or NADPH, and concentrated by spinning for 15 min at 2000 × g in a 10-kDa molecular weight cutoff Amicon Ultra-4 centrifugal filter unit (Merck, Watford, UK). Resuspension and centrifugation were repeated a further two times to ensure negligible presence of the original enzyme buffer. The final volume of the enzyme and cofactor mixture was between 90 and 100 μL. The mixtures were placed in a 50-μL, 3-mm path length quartz cuvette for measurements (Hellma, Southend on Sea, UK). Ternary complexes were produced by adding 10 μL of 1 mM sodium lactate or sodium isocitrate into the experimental sample, giving a final substrate concentration of at least 100 μM to ensure negligible levels of binary NAD(P)H-enzyme complexes.
Laser sources
Single-photon excitation at 340 nm was achieved by frequency doubling the 680-nm output of a tunable optical parametric amplifier (OPA 9400, Coherent, Cambridge, UK) using a β-barium borate (BBO) crystal. The OPA was pumped by a regeneratively amplified Ti:sapphire laser (Mira 900F and RegA 9000, Coherent, Cambridge, UK) operating at 800 nm with a repetition rate of 250 kHz, in turn pumped by an Nd:YVO4 laser (Verdi V18, Coherent, Cambridge, UK). The direct output of the OPA at 690 nm was used for two-photon fluorescence measurements.
Polarized time-correlated single-photon counting
Linearly polarized excitation was implemented by passage through a half-wave plate and Glan-Laser polarizer (Melles-Griot, New York, USA). A zero-order tunable quarter wave plate (Alphalas, Goettingen, Germany) was introduced for circularly polarized two-photon excitation (23). A 25-mm focal length achromatic doublet lens (Melles-Griot, New York, USA) was used to focus the polarized beam onto the sample cuvette. Fluorescence was collected in a 90° excitation-detection geometry by using a 25-cm focal length lens to direct the emission into a multichannel plate photomultiplier tube (MCP-PMT, R3809U, Hamamatsu Photonics, Welwyn Garden City, UK). 364-nm long-pass (BLP01-364R-25, Semrock, New York, USA) and 600-nm short-pass (BG39, Schott, Stafford, UK) filters were used to eliminate laser breakthrough during single- and two-photon excitation respectively. A modular time-correlated single-photon counting (TCSPC) system (Ortec, Oak Ridge, USA) was used for time- and polarization-resolved fluorescence measurements. A computer-controlled rotatable polaroid sheet was used to select the polarization of the collected fluorescence. This was alternated at 10-s intervals to transmit light polarized parallel or perpendicular to the symmetry axis of the excitation polarization (vertical for linear, horizontal for circular) (23). The corresponding decays, and , were built up from excitation-detection coincidence events allocated to 512 time bins spanning 27 ns and stored separately in computer memory.
For single-photon excitation, the incident intensity was reduced using an adjustable neutral density filter wheel to ensure average count rates below 2.5 kHz to avoid pulse pile-up effects. Excitation-emission coincidence events were collected for approximately 30 min, resulting in approximately 3 × 106 total photons collected. For two-photon excitation, count rates were around a factor of 40 lower. Data collection times were extended to an hour, resulting in approximately 105 photons per decay. Fluorescence intensity decays were constructed using
| (1) |
In the case of circularly polarized excitation, the symmetry axis is the direction of propagation of the excitation pulses and the fluorescence intensity is determined from (23),
| (2) |
For linearly polarized excitation, the time-resolved fluorescence anisotropy was calculated from
| (3) |
Fluorescence intensity and anisotropy decay fitting
The instrument response function (IRF) of our TCSPC system was measured, revealing an FWHM of 74 ps (Fig. S1). Its influence was therefore neglected in the analysis of our intensity and anisotropy decay measurements, given that this is significantly faster than the typical ∼400-ps (22) fluorescence lifetime and rotational correlation time of freely diffusing NAD(P)H. This allowed us to explore the application of decay models with complexity beyond the simple sum of exponentials typically offered by commercially available deconvolution software.
Fitting was performed using Origin 2019 (OriginLab, Northampton MA, USA). A least-squares algorithm was used to vary the parameters of the fitting model until the statistic was minimized. This was calculated using
| (4) |
where is the total number of time bins, is the number of freely varying parameters in the model, and and are the values of the fluorescence decay data and model at the time after excitation corresponding to bin . is the expected standard deviation of the data point, here given by (24)
| (5) |
Models of increasing complexity were attempted until the statistic of the best fit was no longer improved by the addition of further components. The 95% parameter confidence intervals were output by Origin using the model-comparison (F-test) approach. The quality of the fit was also assessed by inspection of the histogram of weighted residuals , calculated from
| (6) |
Histogram bin widths were chosen using the Freedman-Diaconis rule (25). Residuals were inspected for normal distribution about zero by calculating their arithmetic mean and visually comparing the histogram with a best-fit Gaussian. The lower count rates achievable with two-photon excitation resulted in systematically offset residuals, so a modified approach to the analysis of these measurements was necessary (see Appendix S1).
Composite fluorescence anisotropy decay models (e.g., Eq. 16) were fit using the same least-squares methods as for the single-photon fluorescence intensity decays, but with the lifetime () and amplitude () values (see Eq. 10) fixed using the results of the fluorescence intensity decay fitting and the expected standard deviation in each time bin becoming
| (7) |
by propagating the and uncertainties of the polarized fluorescence decays through Eq. 3 (24). Using both Eqs. 1 and 3 to eliminate and leads to the greatly simplified expression (26)
| (8) |
2PA polarization ratios
Average steady-state two-photon absorption (2PA) polarization ratios were determined by measuring the ratio of fluorescence intensities after circularly and linearly polarized excitation at constant incident power (23),
| (9) |
and were measured by setting the emission polarizer to the appropriate magic angle (54.7° and 35.3° to the vertical for linearly and circularly polarized excitation respectively) and recording fluorescence for 30 s. This was repeated five times for each excitation polarization, with the final value given by the ratio of average total photon counts.
Results
NADH and NADPH in binding equilibrium with their corresponding enzymes exhibit highly heterogeneous and contrasting fluorescence decay dynamics
The increased intensity of NAD(P)H fluorescence upon enzyme binding was recognized in the pioneering work of Britton Chance (27), with a corresponding increase in fluorescence lifetime first quantified by Gregorio Weber and co-workers in 1970 (28). In subsequent studies, the reported lifetimes of NADH and NADPH have varied between 1 and 6 ns depending on the specific enzyme under analysis and the presence of accompanying substrate molecules (29,30,31,32). Drawing conclusions from these data to determine the molecular mechanisms leading to fluorescence lifetime changes has proved difficult, presumably due to the limitations of the measurement techniques then available. For example, closely spaced lifetimes in multiexponential decays may have been obscured by early frequency domain techniques and in flash-lamp-based photon counting methods with low (∼102 Hz) count rates (33). In recent years, time-resolved fluorescence techniques have seen significant advances, and numerous studies have utilized two-photon excitation with mode-locked (∼108 Hz) Ti:sapphire lasers. These techniques are not without their drawbacks, as utilizing the full mode-locked pulse train may introduce inaccuracies due to the incomplete recording of the total fluorescence decay, limited to the ∼10-ns inter-pulse separation (34,35,36). Polarization artifacts may also be introduced by the high (>1) numerical aperture objectives used for two-photon excitation and fluorescence collection (37,38,39). To overcome such issues, we have employed low NA (0.1) excitation, 90° excitation-detection optics, and full fluorescence polarization analysis (22,23). Sample excitation was achieved using the frequency-doubled output of an OPA pumped by a 250-kHz regeneratively amplified Ti:sapphire laser. This permitted the simultaneous collection of fluorescence intensity and anisotropy decay data with 400-ns pulse-to-pulse separation at a maximum photon count rate of 2.5 kHz.
We performed polarization-resolved TCSPC on solutions of NADH and NADPH with lactate dehydrogenase and isocitrate dehydrogenase respectively. The total intensity decay data were fit to multiexponential functions of the form
| (10) |
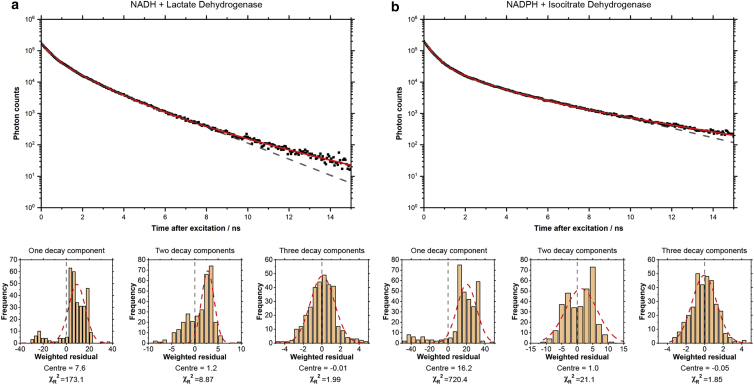
where accounts for any small contributions from time-uncorrelated background and is the fractional amplitude of species with lifetime . Best fit parameters are summarized in Table 1. Both solutions exhibited strongly heterogeneous fluorescence with three decay ( 3) components required for an acceptable fit ( = 1.99 for NADH and 1.85 for NADPH). Simpler decay functions gave poor fits, with asymmetrically distributed residuals and values of 173.1 and 720.4 (mono-exponential) and 8.87 and 21.1 (bi-exponential), respectively (Fig. 2). The majority (77% and 85.9%) decay component in both solutions, with a lifetime of approximately 0.4 ns , would correspond to free NADH or NADPH, in line with assignments in living cells (1). This is likely an average of the 0.3-ns and 0.7-ns decay components observed in aqueous solutions (22,40), suggested to correspond to cis and trans configurations of the amide group on the nicotinamide ring (23,41). An increase in the NAD(P)H fluorescence lifetime upon enzyme binding is well established (1). Here, introduction of an enzyme to solutions of NADH or NADPH resulted in the appearance of two longer (nanosecond) decay components of 1.34 and 1.59 ns (), and 3.2 and 4.4 ns () respectively. In the next section, time-resolved fluorescence anisotropy measurements will be used to correlate each lifetime to the corresponding global and internal motions of the bound cofactors. Considering the longer lifetime of bound NADPH inside the cell (1,17), it was also interesting to note that both and were longer for bound NADPH than bound NADH in solution. For , the difference between NADH and NADPH was only 0.25 ns, whereas for the increase was much larger at 1.2 ns. The relative proportion of and was also almost four times larger in NADPH bound to isocitrate dehydrogenase, with = 0.15 compared with 0.04 in NADH bound to lactate dehydrogenase. Although our prior 1.5 (±0.2) ns estimate of the lifetime of bound NADH in the cell agreed with the species of NADH bound in solution, it was the species of bound NADPH in solution that corresponded to the estimate of 4.4 (±0.2) ns for the lifetime of bound intracellular NADPH (17).
Table 1.
Fluorescence intensity decay parameters of NADH in solution with lactate dehydrogenase and NADPH with isocitrate dehydrogenase, and in ternary complex with reduced substrates
| NADH + LDH | +Lactate | NADPH + IDH | +Isocitrate | |
|---|---|---|---|---|
| /ns | 0.43 [0.42, 0.44] | 0.47 [0.46, 0.49] | 0.403 [0.397, 0.409] | 0.414 [0.406, 0.422] |
| /ns | 1.34 [1.30, 1.37] | 1.9 [1.8, 2.0] | 1.59 [1.54, 1.64] | 1.70 [1.63, 1.77] |
| /ns | 3.2 [3.0, 3.4] | 3.6 [3.5, 3.8] | 4.4 [4.2, 4.5] | 5.30 [5.2, 5.4] |
| /% | 77 [75, 78] | 59 [58, 61] | 85.9 [85.1, 86.7] | 86 [85, 88] |
| /% | 22.5 [21.7, 23.5] | 29 [28, 30] | 12.3 [11.9, 12.7] | 11.4 [10.9, 11.9] |
| /% | 0.9 [0.6, 1.1] | 11 [10, 13] | 1.8 [1.7, 2.0] | 2.3 [2.2, 2.5] |
Square brackets indicate 95% confidence intervals. IDH, isocitrate dehydrogenase; LDH, lactate dehydrogenase.
Figure 2.
Fluorescence intensity decays of NADH or NADPH in solution with an enzyme contained three distinct decay components. Time-resolved intensity datasets were constructed using Eq. 1 and the polarized fluorescence decays shown in Figure S2. For both (a) NADH mixed with lactate dehydrogenase and (b) NADPH mixed with isocitrate dehydrogenase, simpler models with one and two decay components gave unevenly distributed, non-Gaussian residuals and high values. The poor fit of two-component models, particularly at excitation-emission delay times beyond 10 ns, is shown as a dotted gray line. To see this figure in color, go online.
NADH and NADPH undertake their intracellular roles by donating hydride ions in the enzyme-catalyzed reduction of substrates. A number of previous studies have reported additional increases to the fluorescence lifetimes of bound NADH and NADPH when substrate molecules are simultaneously present in a ternary complex (28,30,31). To investigate the origins of these observations, we added a saturated solution of sodium lactate or sodium isocitrate into our enzyme and cofactor mixtures at the end of each initial experiment and undertook identical fluorescence decay measurements. As the products of the reactions catalyzed by the two enzymes when reduced cofactors are present, these substrates would occupy the binding site without causing oxidation to non-fluorescent NAD+ and NADP+ (42,43). The lifetimes of the two bound components were slightly longer in the ternary complex of NADH, lactate dehydrogenase and lactate, with increasing from 1.34 to 1.9 ns and increasing from 3.2 to 3.6 ns. More significant were the changes in the relative amplitudes of each decay component. Lactate was seen to drive the equilibrium toward the bound species, with decreasing from 77% to 59%. The relative abundance of the longer-lifetime bound species was also significantly higher, with the ratio increasing to 0.38 from 0.04. In contrast, we observed little change in the NADPH binding equilibrium induced by isocitrate and there was only a very minor increase in , from 1.59 to 1.70 ns. However, increased substantially, from 4.4 to 5.3ns. Potential mechanisms governing the contrasting influences of lactate and isocitrate on the NADH and NADPH binding equilibria, alongside the differences in their bound lifetimes, are explored in the “discussion” section.
Time-resolved fluorescence anisotropy reveals two distinct binding configurations
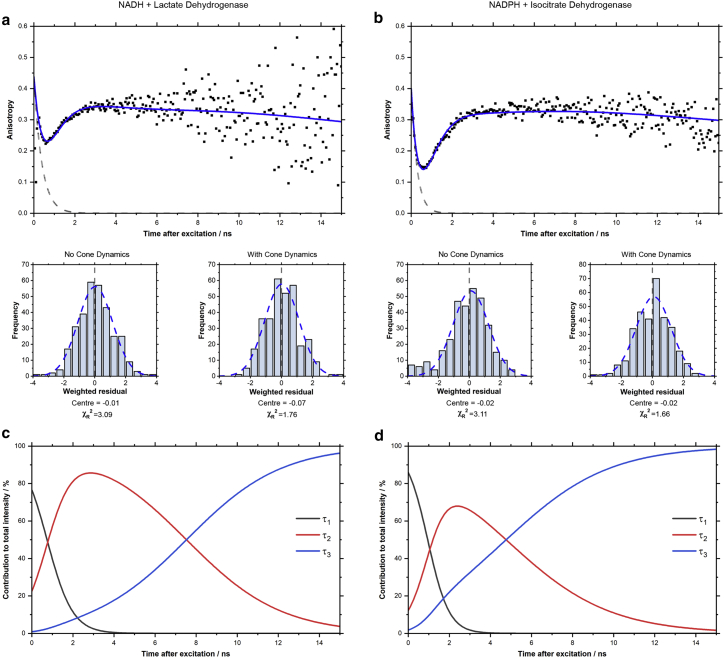
Time-resolved fluorescence anisotropy measurements were used to investigate differences in the environment and orientational dynamics of the three fluorescent populations observed in the intensity decays. The fluorescence anisotropy of such multi-component systems reports on the net transition dipole moment orientation of the excited state population (22,23). For a homogeneous emitting population in an isotropic solution, the time-dependent fluorescence anisotropy is sensitive to the global and internal motions of the chromophore and decays monotonically to zero (24). However, for the solutions of both NADH and lactate dehydrogenase and NADPH and isocitrate dehydrogenase, we observed a clear departure from such dynamics with a pronounced dip and rise in (Fig. 3 a and b). This phenomenon has previously been observed in a range of biological systems exhibiting heterogeneous fluorescence dynamics (32,44,45,46,47) and can be qualitatively interpreted by a comparison with the time-varying fractional contribution of each species to the overall fluorescence (Fig. 3 c and d). Before 1 ns, the short-lifetime population predominates and the anisotropy decays rapidly, indicating this to be a rapidly depolarizing species. Beyond 2 ns, the preponderance of the emission arises from the and species and the net anisotropy returns to 80%–90% of its maximum value (0.4), thereafter decaying monotonically and slowly, reducing by approximately 0.05 over the next 10 ns. This indicates that these populations are undergoing significantly slower rotational diffusion. This is consistent with the assignment of to freely diffusing NAD(P)H and and line to enzyme-bound species.
Figure 3.
The dip-and-rise dynamics of the time-resolved fluorescence anisotropies revealed that both longer-lifetime components were associated with slow rotational correlation times. Time-resolved anisotropy datasets were constructed using Eq. 3 and the same polarized fluorescence decays as the time-resolved intensity measurements in Fig. 1 (see Fig. S2). For both (a) NADH with lactate dehydrogenase and (b) NADPH with isocitrate dehydrogenase, acceptable composite anisotropy fits required the introduction of dynamics described by the wobbling-in-a-cone model to the bound components (Eq. 13). These revealed that the shorter-lifetime enzyme-bound component () possessed greater orientational freedom than the longer-lifetime species () in both cofactors. The gray dotted lines in each decay correspond to the anisotropy decay of free NAD(P)H measured in our previous work (22). The time-varying fractional intensities of each component (c and d), calculated using Eq. 12 and the parameters in Table 1, provide fit-free indication that both and are enzyme-bound species, with these components dominating the signal from 2 ns onward and the anisotropy remaining high. To see this figure in color, go online.
Quantifying the observed depolarization dynamics involves fitting of an appropriate decay model to the anisotropy data. is necessarily exponential for a homogeneous population of freely diffusing fluorophores (48). However, additional complexity will be introduced by the mixed populations of free and enzyme-bound cofactors studied here. For a heterogeneous population, the time evolution of the composite anisotropy is a sum of the individual anisotropy decays, each weighted by their time-varying fractional contribution to the overall fluorescence intensity (49),
| (11) |
| (12) |
In addition, although unbound NAD(P)H molecules will be expected to exhibit free diffusion, several X-ray diffraction studies have reported difficulties in resolving the nicotinamide moiety in the dehydrogenase-bound cofactor (50,51), implying it to be highly mobile (52,53). This has also been confirmed using nuclear magnetic resonance (NMR) spectroscopy (53). The diffusional motion of bound fluorophores is therefore likely to include contributions from both the global motion of the enzyme and the local motion of the cofactor itself (54). The time-resolved fluorescence anisotropy of such systems has been successfully described by the “wobbling-in-a-cone” model (24,55,56). This assigns a bi-exponential fluorescence anisotropy decay for each bound species,
| (13) |
The slower rotational correlation time results from the tumbling of the overall complex, whereas the faster time includes contributions from both the rates of tumbling and local diffusion. The fluorescence anisotropy immediately after excitation, , is determined by the angle between the absorption and emission transition dipoles and for single-photon excitation is 0.4 if these are collinear. The relative amplitudes of the two decay components relate to the angle of the cone swept out within the local motion ,
| (14) |
Using this angle, the contribution of the overall tumbling to can be removed to reveal the diffusion coefficient of the motion within the cone, , (56)
| (15) |
By assuming the slower rotational correlation time is shared between and , as they result from binding to identical enzymes, the composite anisotropy decay (Eqs. 11 and 12) becomes
| (16) |
where unbound NAD(P)H undergoes unrestricted rotational diffusion with correlation time . This model gave good fits to the experimental data, with evenly distributed residuals and = 1.76 for NADH and lactate dehydrogenase and 1.66 for NADPH and isocitrate dehydrogenase. The fit parameters were also physically realistic, with the ratio of the global rotational correlation times between the two enzymes equal to the ratio of their molecular weights, in agreement with the Stokes-Einstein-Debye equation (see Appendix S2). This was not the case for models in which the local NAD(P)H motion was not included (achieved by fixing both and at zero), which was also accompanied by an increase in the values to 3.09 and 3.11 respectively. Moreover, introducing separate values for each species gave no improvement in the fit quality.
In both mixtures, the parameters from fitting Eq. 16 revealed clearly differing local diffusive motion for the two enzyme-bound species (Table 2), returning in all cases with well-separated confidence intervals. In NADH bound to lactate dehydrogenase, corresponded to a binding state in which the cofactor was observed to diffuse within a cone angle of 20° at a rate of 0.03 ns−1, over 10 times slower than the equivalent rate of free NADH diffusion = = 0.43 ns−1. In contrast, was fully constrained, with = 0°, albeit with a 95% confidence interval up to 8°. This absence of local motion effectively removes from the model ( 0) and sets its diffusion coefficient to zero. For NADPH and isocitrate dehydrogenase, no local motion was again observed for the longest-lifetime species. However, although the shorter-lifetime bound species ( exhibited a similar degree of confinement to that for NADH bound to lactate dehydrogenase = 23°), they underwent a faster degree of local motion with = 0.5 ns−1. This would indicate that the nicotinamide of the population in NADPH, although constrained, appears to experience a greater exposure to the solvent. However, the corresponding rotational correlation time is close to the IRF of the TCSPC system, which likely introduces quantitative inaccuracies to this parameter value. The corresponding motion of the population in NADH must experience a larger degree of local friction, implying a greater degree of incorporation of the nicotinamide moiety into the binding site.
Table 2.
Measured (a) and derived (b) parameters describing the composite anisotropy decays of NADH with lactate dehydrogenase and NADPH with isocitrate dehydrogenase, and in ternary complexes
| a | NADH + LDH | +Lactate | NADPH + IDH | +Isocitrate |
|---|---|---|---|---|
| 0.409 [0.399, 0.417] | 0.41 [0.39, 0.43] | 0.40 [0.39, 0.42] | 0.40 [0.37, 0.43] | |
| /ns | 0.39 [0.38, 0.41] | 0.18 [0.17, 0.21] | 0.282 [0.281, 0.288] | 0.27 [0.25, 0.29] |
| 0.17 [0.15, 0.18] | 0.30 [0.27, 0.35] | 0.22 [0.21, 0.23] | 0.32 [0.26, 0.43] | |
| /ns | 1.1 [0.9, 1.3] | 1.4 [1.2, 1.9] | 0.09 [0.04, 0.13] | 0.5 [0.2, 0.6] |
| 0.00 [−0.11, 0.03] | 0.02 [0, 0.04] | 0.00 [−0.02, 0.01] | 0.00 [−0.01, 0.03] | |
| /ns | – | – | – | – |
| /ns | 38 [35, 49] | 45 [40, 51] | 51 [48, 57] | 26 [21, 29] |
| b | NADH + LDH | +Lactate | NADPH + IDH | +Isocitrate |
|---|---|---|---|---|
| /ns−1 | 0.43 [0.41, 0.44] | 0.9 [0.8, 1.0] | 0.591 [0.578, 0.592] | 0.63 [0.58, 0.66] |
| /ns−1 | 0.0044 [0.0034, 0.0048] | 0.0037 [0.0033, 0.0041] | 0.0032 [0.0029, 0.0035] | 0.006 [0.005, 0.008] |
| /° | 20 [19, 21] | 27 [26, 30] | 23.3 [22.7, 23.9] | 28 [25, 34] |
| /ns−1 | 0.03 [0.02, 0.05] | 0.04 [0.02, 0.08] | 0.5 [0.3, 1.2] | 0.1 [0.0, 0.7] |
| /° | 0 [−15, 8] | 7 [−4, 8] | 0 [−7, 5] | 0 [−5, 7] |
Square brackets indicate 95% confidence intervals.
After the addition of lactate, the time-resolved fluorescence anisotropy revealed that the only significant change in the diffusional characteristics of the nicotinamide moiety of bound NADH was a small (7°) increase in the cone angle of the species (Table 2). Any simultaneous increase in the cone angle of the species was obscured by its confidence interval overlapping with zero. A rise in was also observed upon the addition of isocitrate to the NADPH mixture with a possible decrease in the associated diffusion coefficient, from 0.5 to 0.1 ns−1, obscured, however, by the large uncertainty in the value for the binary complex. Interestingly, we also observed an increase in the diffusion coefficient of the overall tumbling motion of the isocitrate dehydrogenase ternary complex compared with the complex with NADPH alone, at 0.0032 ns−1 compared with 0.006 ns−1. Given that isocitrate is unlikely to significantly alter the volume or shape of the enzyme complex, this may suggest that its addition alters the solvent-solute boundary conditions (22). However, an alternative explanation may be provided by the results of a post hoc computational investigation into the impact on the fitting parameters resulting from the exclusion of the IRF (Appendix S3). Although this confirmed that the contrasting restriction of the two bound states () could indeed be successfully resolved using our approach, repeatedly re-generating Poisson noise on the simulated datasets resulted in a large spread in the returned values for , ranging from 29 to 52 ns. This would result from the low fluorescence signal at extended delay times due to and suggests that significantly extended acquisition times would be required to investigate these observations in more detail.
Two-photon polarization ratios indicate two differing nicotinamide enzyme-binding geometries for both NADH and NADPH
In previous work, we demonstrated that the fluorescence lifetimes of NADH and NADPH are mediated through constraints to the conformational freedom of the nicotinamide ring, reducing the rate of non-radiative transition from the excited to ground state by activated barrier crossing (22). Such constriction should manifest as a decreased diffusion coefficient in time-resolved fluorescence anisotropy measurements. In the mixture of NADH and lactate dehydrogenase, the longer lifetime of the bound species over that of the free species was indeed correlated with a smaller than . However, the equal diffusion rates of the and species in mixtures of NADPH and isocitrate dehydrogenase implied that the rate of activated barrier crossing was not reflected in the rate of local diffusional motion alone. We recently showed that changes in the fluorescence lifetimes of NADH and NADPH can also result from altered geometries of the nicotinamide ring, presumably through modifications to the barrier frequencies that control the non-radiative decay process (23). This was revealed by the polarization dependence of 2PA, measured by the ratio of absorption strengths with circularly and linearly polarized two-photon excitation. This value, denoted , reflects the symmetry of the two-photon transition (57). As this involves transfer of charge across the nicotinamide moiety in NADH and NADPH (2,4), altered values of may imply changes in the nicotinamide geometry (23). We therefore performed polarized 2PA measurements on the NAD(P)H-enzyme solutions to investigate whether this was occurring in the bound populations.
measurements are typically made by comparing the steady-state fluorescence intensity after circularly and linearly polarized two-photon excitation with equal incident power (58). In a heterogeneous mix of fluorophores, this will provide a population average (23) that we denote (see section “methods”). As the restricted two-photon excitation volume, localized to the beam waist of the excitation laser (59), leads to lower fluorescence intensities compared with single-photon fluorescence measurements, we carried out steady-state polarized 2PA measurements on new preparations in which we further concentrated the enzyme-bound population through repeated centrifugal filtration. From these, we measured = 1.04 (±0.01) for NADH with lactate dehydrogenase and = 0.94 (±0.01) for NADPH and isocitrate dehydrogenase. As we previously observed aqueous solutions of NADH and NADPH to exhibit = 0.8 (±0.1) (23), these results indicated that enzyme binding causes a change in the nicotinamide geometry in at least one of the species. The larger value for NADH and lactate dehydrogenase could have resulted from the presence of a larger proportion of enzyme-bound species relative to the NADPH and isocitrate dehydrogenase mixtures or may have reflected a fundamental difference in the individual values of the and species in NADH and NADPH. Determination of the component parameters required time-resolved two-photon fluorescence measurements using linearly and circularly polarized excitation. The polarization ratio for each component is then given by (23)
| (17) |
Our two-photon fluorescence decay measurements unavoidably contained an order of magnitude fewer photons than with single-photon excitation. This required us to adopt a maximum likelihood fitting approach (see section “methods” and Appendix S1). We sought to minimize the accompanying drop in precision by reducing the number of freely varying parameters. From Kasha’s rule (60), as both linearly and circularly polarized excitation would result in emission from the lowest energy excited state, the lifetimes of the three species would be expected to be equal in the two fluorescence decays. We therefore performed global fits in which the lifetimes , , and were shared between both datasets. This decreased uncertainties in the lifetimes by a factor of two. However, the individual lifetimes remained relatively imprecise compared with the single-photon measurements, with average uncertainties of 50% (see Table S1). Fortunately, the separate values of each decay component depend on the overall amplitude-weighted mean lifetime of the sample (Eq. 17) to account for changes in the average quantum yield of the mixtures with each excitation mode (23). The uncertainties in this composite parameter were more reasonable (10%–20%). Furthermore, the precision of the relative decay amplitudes of each component was sufficiently high to reveal clear differences between circularly and linearly polarized excitation. In NADH and lactate dehydrogenase, the amplitudes of the and components were larger with linearly polarized excitation, at = 21(±1)% compared to = 9(±1)% and = 10(±2)% compared to = 4(±5)%. In contrast, the amplitude of the component was larger for circularly polarized excitation, with = 87(±4)% and = 69(±1)%. This pattern of relative amplitudes was also observed for NADPH with isocitrate dehydrogenase.
Table 3 shows the clearly distinct values calculated for the two bound NADH species, with = 1.3 (±0.2) and = 0.4 (±0.4). Similar results were also found for NADPH, with = 1.2 (±0.1) and = 0.6 (±0.4). The 0.3- and 0.7-ns single-photon excited lifetimes present in aqueous NAD(P)H solutions were again represented by a single short lifetime component in these measurements, with corresponding values of 0.4 (±0.1) and 0.63 (±0.08) for NADH and NADPH respectively. Our earlier work revealed that the two free species exhibit values of 0.6 (±0.1) and 1.1 (±0.2), likely reflecting distinct values for the cis and trans geometries of the amide group of the nicotinamide (23). The lower values here might result from the experimental conditions pushing the equilibrium of the unbound cofactors toward one of the two forms, perhaps due to the preference of binding sites for the trans configuration (23,61). However, these small values are more likely an artifact of the low signal levels from the population. Only 3% of the photons counted from the NADH and lactate dehydrogenase measurements were emitted from this species (). This increased to 20% in the NADPH and isocitrate dehydrogenase mixtures, where was closer to our previously obtained values.
Table 3.
Polarized two-photon absorption ratios calculated for each species of NADH mixed with lactate dehydrogenase and NADPH mixed with isocitrate dehydrogenase, and in ternary complexes
| NADH + LDH | +Lactate | NADPH + IDH | +Isocitrate | |
|---|---|---|---|---|
| 0.4 (±0.1) | 0.4 (±0.2) | 0.63 (±0.08) | 0.27 (±0.04) | |
| 1.3 (±0.2) | 1.42 (±0.09) | 1.2 (±0.1) | 1.3 (±0.2) | |
| 0.4 (±0.4) | 0.82 (±0.05) | 0.6 (±0.4) | 0.5 (±0.4) |
values that exceed those measured from free NADH and NADPH confirmed an altered nicotinamide geometry in the shorter-lifetime bound species and hence may explain the increased lifetime of the component in NADPH bound to isocitrate dehydrogenase relative to even with equal diffusion coefficients. To within experimental accuracy, we found that the addition of substrate altered the 2PA polarization ratio only in the population of NADH bound to lactate dehydrogenase, increasing to 0.82 (±0.05) from 0.4 (±0.4). We also note that all values were within the theoretical limits of 0.25–1.5 for the planar two-photon transition in NAD(P)H (4,58), providing additional confidence in these measurements.
Discussion
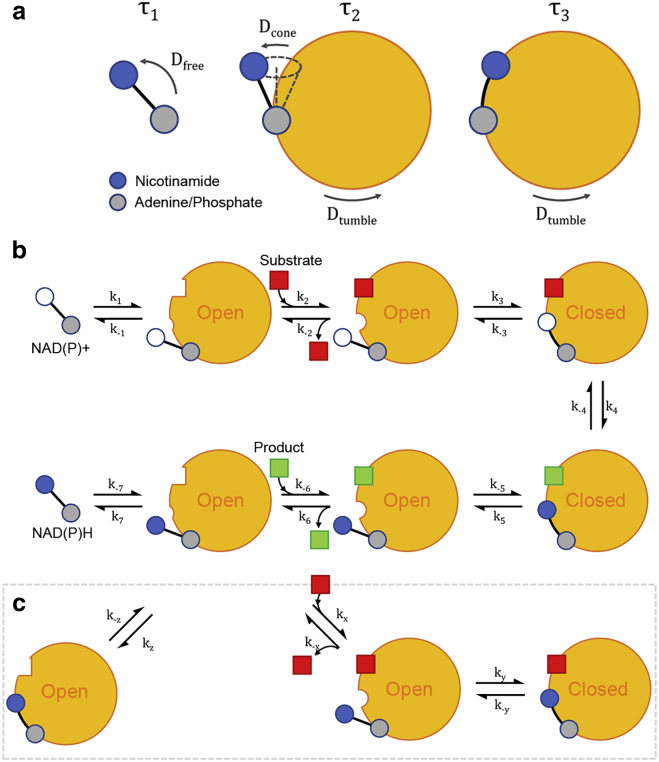
We have observed two distinct fluorescence lifetimes arising from the binding of NADH and NADPH to lactate dehydrogenase and isocitrate dehydrogenase respectively. For each enzyme, these correspond to two different configurations. The shorter lifetime () is associated with binding in which the cofactor is free to move within a cone angle of approximately 20°. As spontaneous emission in NADH and NADPH involves the nicotinamide moiety, the cofactors in this state must be bound at the opposing adenine/phosphate end. This conclusion is reinforced by circular dichroism studies that show a lower Michaelis constant associated with binding of the adenine moiety than the nicotinamide (62), reflected by our results with > in all mixtures. Eliminating local nicotinamide motion upon its binding then produces the longer-lifetime () bound species (Fig. 4). Local nicotinamide motion in the bound state has previously been recognized in time-resolved anisotropy measurements on NAD(P)H autofluorescence in living tissues (32). Here we took advantage of the extended collection times achievable when studying bound NADH and NADPH in solution, alongside recording of the complete polarized fluorescence decay, to apply composite wobbling-in-a-cone anisotropy models to quantify the distinct binding configurations and identify the fluorescence lifetimes associated with each for the first time.
Figure 4.
Conformational heterogeneity in the dehydrogenase reaction mechanism. (a) In solutions of NADH or NADPH with a corresponding enzyme, the shortest-lifetime species () exhibited rapid rotational diffusion, the intermediate-lifetime species () displayed rotational diffusion consistent with a cone model, and the longest-lifetime species () was associated with only the slow tumbling of the enzyme. (b) These configurations participate in the reaction mechanism of a dehydrogenase, in which the open form promotes the binding of substrate and the closed form facilitates hydride transfer. (c) Catalytically unproductive, abortive conformations are also possible, such as when reduced substrate binds alongside reduced cofactors. To see this figure in color, go online.
As inside cells (17), the fluorescence lifetimes associated with NADPH binding in solution were longer than for the corresponding species in bound NADH. This can be understood through the extensive efforts made to study differences in the NADH and NADPH binding sites to facilitate the creation of novel enzymes with the cofactor specificity switched (50,63,64,65). These are desirable for industrial biotechnology where the use of NADH, rather than NADPH, would be preferable due to its higher stability and lower production cost (3). X-ray diffraction studies have demonstrated that electrostatic effects are the principal means by which binding sites differentiate between the two cofactors (3). NADH binding sites contain negatively charged amino acids that form hydrogen bonds with the adenine ribose and cause repulsive forces toward the negatively charged phosphate group of NADPH. These are replaced by positively charged residues to confer specificity for NADPH and, importantly for the different fluorescence decay dynamics, result in a more rigid binding site (64). This would induce a longer fluorescence lifetime for NADPH by increasing conformational restriction and decreasing non-radiative relaxation (22,66). Supplementary mechanisms could nevertheless contribute; the nicotinamide moieties of NADH and NADPH may be constrained in different configurations (64) or be in direct contact with contrasting active site residues (63). Such contributions are indeed supported by our polarized two-photon absorption measurements on NADPH, where binding-induced alterations to the nicotinamide ring structure were resolved even in the absence of constraints to its diffusional motion. Such ring perturbations are known to facilitate hydride transfer in the active site (67).
Given our earlier predictions of 1.5 (±0.2) and 4.4 (±0.2) ns for the fluorescence lifetimes of enzyme-bound NADH and NADPH inside cells (17), our results suggest that intracellular NADPH is more likely to be found in the fully bound state, whereas intracellular NADH is bound more loosely in the state. To understand how this could occur, we must consider how the two binding configurations relate to the reaction mechanism of the enzymes and how these may differ inside the cell for NAD- and NADP-associated pathways. In general, enzymes must both sufficiently immobilize the reactants within the protein for catalysis but expose the binding sites to the surroundings for unimpeded ligand capture and release (68). Dehydrogenases overcome this apparent paradox by utilizing a structural change, transitioning between an open conformation, which allows substrate and cofactor binding and release, and a closed conformation, which facilitates the hydride transfer between the two (52,69). These conformations have been observed in structures of a wide range of enzymes, including isocitrate (70), glycerol 3-phosphate (71), glutamate (72), homoserine (73), malate (74), and alcohol (75) dehydrogenase. The reaction mechanism itself has been studied in most detail using lactate dehydrogenase as a model system (52,68,76). This has revealed that the adenine end of the cofactor must bind first. Subsequent binding of the substrate then initiates structural rearrangements that promote both the attachment of the nicotinamide and the open-to-closed transition of the ligand binding pocket, bringing the reactants close enough for hydride transfer. The process then occurs in reverse to reopen the binding pocket and release the product and cofactor.
In our experiments, the conformational freedom of the nicotinamide identified in the short-lifetime bound population () suggests this corresponds to NAD(P)H bound to the open-conformation enzyme. The complete restriction of local nicotinamide motion in the long-lifetime bound species () suggests this to be NAD(P)H bound to the enzyme in its closed conformation. The presence of this species even in the absence of substrate is in agreement with the work of Qiu et al., who observed the open and closed forms in fast equilibrium under these conditions (68). The substrate-induced nature of the open-to-closed transition was also evident in our measurements by the 10-fold increase of upon the introduction of lactate to NADH with lactate dehydrogenase. This may clarify recent work by Ranjit et al. in which the fluorescence decay of NADH bound to lactate dehydrogenase was measured to be mono-exponential with a lifetime of 3.4 ns (77). To optimize the accuracy of their lifetime measurements, the authors eliminated free cofactors by lowering the dissociation constant using high concentrations of oxalate. This will also have promoted the closed enzyme conformation, resulting in a single lifetime close to the 3.6 ns we measured as in the presence of substrate. The small difference could be attributable to a persisting minority of open-conformation enzymes that could not be resolved with the phasor method of fluorescence decay analysis. Only a 14% contribution from this species would be required if the single lifetime were an amplitude-weighted average of the substrate-associated and values that we observed.
In contrast to lactate dehydrogenase, isocitrate had no significant effect on the relative population of long- and short-lifetime bound species of NADPH and isocitrate dehydrogenase. The catalytic function of this enzyme is known to require a divalent metal ion to bind alongside the substrate to lower the activation energy by altering the redox potential of the reactants (78). Although these were absent from our solutions, the increase in the fluorescence lifetimes of each bound NADPH species upon isocitrate addition demonstrated that the substrate could nevertheless bind. The lack of a subsequent increase in implies a role for this ion in facilitating the transition between open and closed states. This is in agreement with structural studies in which the fully closed form could only be achieved with the metal ion present alongside substrate and cofactor (70).
To unite this model of dehydrogenase function with our knowledge of the time-resolved fluorescence of intracellular NADH and NADPH, we integrated our new understanding of their bound photophysics with a quantitative analysis of the reaction mechanism (see Appendix S4). This revealed two possible biochemical contributors to the longer lifetime of bound NADPH, relative to bound NADH, inside cells. The first involved an increased ratio of product binding to unbinding ( in Fig. 4) for NADPH-associated dehydrogenases in the complex cellular environment. Such a difference could facilitate the contrasting roles of the two cofactors; a higher ratio would favor the recruitment of substrates for reduction in NADPH-associated anabolic reactions, whereas a lower value would promote the release of the products of NADH-associated catabolic oxidations. However, this model relies upon the fluorescence lifetime of the reduced cofactor being the same in ternary complex with oxidized products (pyruvate, α-ketoglutarate) as with the reduced substrates (lactate, isocitrate) measured here. There is evidence that oxidized substrates can provide an additional excited state decay route for the reduced cofactor through photoinduced electron transfer (79), decreasing the fluorescence lifetime. Under these circumstances, a second contributor to the longer fluorescence lifetime of bound NADPH inside cells would be the characteristic lower NADP+ to NADPH ratio promoting the formation of “abortive” complexes of the reduced cofactor alongside the reduced substrate (42,43). To determine which of these mechanisms has the greater influence on the contrasting intracellular fluorescence lifetimes of NADH and NADPH, further experiments will be required to quantify both the reaction rates of their associated enzymes and their excited-state dynamics in ternary complex with oxidized substrates.
Conclusions
This work has established, for the first time, links between the time-resolved fluorescence of NADH and NADPH and the reaction mechanisms of the enzymes to which they bind. This will allow the interpretation of intracellular NAD(P)H FLIM measurements in greater biochemical detail in terms of the equilibria between different enzyme conformations and the cofactor redox balances that drive them. We have also demonstrated the sensitivity of the time-resolved anisotropy to conformational changes involved in the dehydrogenase reaction mechanism, which will be important for understanding polarization-resolved NAD(P)H fluorescence inside cells as this imaging technique becomes more widespread (32,38). Moreover, our work highlights the importance of recognizing heterogeneity in biological fluorescence measurements to ensure key phenomena are not overlooked. Although fluorescence has played a major role in the study of biological processes due to its molecular-level sensitivity, adaptability to most classes of intracellular molecules, and applicability in intact complex tissues and whole organisms under physiological conditions (80), the drive toward quantitative descriptions of living systems will place a greater burden on understanding probe photophysics to obtain accurate, precise, and artifact-free results (81). The extensive heterogeneity of fluorescent populations in biological systems will therefore present a significant challenge (82). Characterizing the multiple states with distinct lifetimes exhibited both intrinsically by autofluorescent biochemical molecules and by otherwise homogeneous synthetic probes within heterogeneous biological environments will be facilitated by the ongoing application of the tools and methodologies we have advanced in this work.
Author contributions
T.S.B. and A.J.B. designed the experiments. T.S.B. carried out the experiments and analyzed the data. All authors drafted the manuscript.
Acknowledgments
This work was supported by BBSRC grant “New approaches to studying redox metabolism using time-resolved NAD(P)H fluorescence and anisotropy” (BB/P018726/1) to A.J.B., M.R.D., and T.S.B., and BBSRC Discovery Fellowship “Autofluorescence across scales: an integrated understanding of redox cofactors as intrinsic probes of metabolic state” (BB/W009242/1) to T.S.B.
Declaration of interests
The authors declare no competing interests.
Editor: Jochen Mueller.
Footnotes
Thomas S. Blacker’s present address is Research Department of Structural & Molecular Biology, University College London, London, United Kingdom.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.02.014.
Supporting material
References
- 1.Blacker T.S., Duchen M.R. Investigating mitochondrial redox state using NADH and NADPH autofluorescence. Free Radic. Biol. Med. 2016;100:53–65. doi: 10.1016/j.freeradbiomed.2016.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.De Ruyck J., Famerée M., et al. Jacquemin D. Towards the understanding of the absorption spectra of NAD(P)H/NAD(P)+ as a common indicator of dehydrogenase enzymatic activity. Chem. Phys. Lett. 2007;450:119–122. [Google Scholar]
- 3.Chánique A.M., Parra L.P. Protein engineering for nicotinamide coenzyme specificity in oxidoreductases: attempts and challenges. Front. Microbiol. 2018;9:194. doi: 10.3389/fmicb.2018.00194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kierdaszuk B., Malak H., et al. Lakowicz J.R. Fluorescence of reduced nicotinamides using one- and two-photon excitation. Biophys. Chem. 1996;62:1–13. doi: 10.1016/s0301-4622(96)02182-5. [DOI] [PubMed] [Google Scholar]
- 5.Mayevsky A., Chance B. Oxidation-reduction states of NADH in vivo: from animals to clinical use. Mitochondrion. 2007;7:330–339. doi: 10.1016/j.mito.2007.05.001. [DOI] [PubMed] [Google Scholar]
- 6.Chance B., Cohen P., et al. Schoener B. Intracellular Oxidation-reduction states in vivo. Science. 1962;137:499–508. doi: 10.1126/science.137.3529.499. [DOI] [PubMed] [Google Scholar]
- 7.Gaude E., Schmidt C., et al. Frezza C. NADH shuttling couples cytosolic reductive carboxylation of glutamine with glycolysis in cells with mitochondrial dysfunction. Mol. Cell. 2018;69:581–593.e7. doi: 10.1016/j.molcel.2018.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thomas L.W., Esposito C., et al. Ashcroft M. CHCHD4 regulates tumour proliferation and EMT-related phenotypes, through respiratory chain-mediated metabolism. Cancer Metabol. 2019;7:7. doi: 10.1186/s40170-019-0200-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Becker W. Fluorescence lifetime imaging - techniques and applications. J. Microsc. (Oxf.) 2012;247:119–136. doi: 10.1111/j.1365-2818.2012.03618.x. [DOI] [PubMed] [Google Scholar]
- 10.Skala M.C., Riching K.M., et al. Ramanujam N. In vivo multiphoton fluorescence lifetime imaging of protein-bound and free nicotinamide adenine dinucleotide in normal and precancerous epithelia. J. Biomed. Opt. 2007;12:024014. doi: 10.1117/1.2717503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Barkauskas D.S., Medley G., et al. Roberts M.S. Using in vivo multiphoton fluorescence lifetime imaging to unravel disease-specific changes in the liver redox state. Methods Appl. Fluoresc. 2020;8:034003. doi: 10.1088/2050-6120/ab93de. [DOI] [PubMed] [Google Scholar]
- 12.Lukina M.M., Shimolina L.E., et al. Shirmanova M.V. Interrogation of tumor metabolism in tissue samples ex vivo using fluorescence lifetime imaging of NAD(P)H. Methods Appl. Fluoresc. 2019;8:014002. doi: 10.1088/2050-6120/ab4ed8. [DOI] [PubMed] [Google Scholar]
- 13.Chacko J.V., Eliceiri K.W. NAD(P)H fluorescence lifetime measurements in fixed biological tissues. Methods Appl. Fluoresc. 2019;7:044005. doi: 10.1088/2050-6120/ab47e5. [DOI] [PubMed] [Google Scholar]
- 14.Cao R., Wallrabe H., et al. Periasamy A. Optimization of FLIM imaging, fitting and analysis for auto-fluorescent NAD(P)H and FAD in cells and tissues. Methods Appl. Fluoresc. 2020;8:024001. doi: 10.1088/2050-6120/ab6f25. [DOI] [PubMed] [Google Scholar]
- 15.König K. Review: clinical in vivo multiphoton FLIM tomography. Methods Appl. Fluoresc. 2020;8:034002. doi: 10.1088/2050-6120/ab8808. [DOI] [PubMed] [Google Scholar]
- 16.Deberardinis R.J., Thompson C.B. Cellular metabolism and disease: what do metabolic outliers teach us? Cell. 2012;148:1132–1144. doi: 10.1016/j.cell.2012.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blacker T.S., Mann Z.F., et al. Duchen M.R. Separating NADH and NADPH fluorescence in live cells and tissues using FLIM. Nat. Commun. 2014;5:3936. doi: 10.1038/ncomms4936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Majumder P., Blacker T.S., et al. Gale J.E. Multiphoton NAD(P)H FLIM reveals metabolic changes in individual cell types of the intact cochlea upon sensorineural hearing loss. Sci. Rep. 2019;9:18907–18910. doi: 10.1038/s41598-019-55329-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tosatto A., Sommaggio R., et al. Mammucari C. The mitochondrial calcium uniporter regulates breast cancer progression via HIF -1α. EMBO Mol. Med. 2016;8:569–585. doi: 10.15252/emmm.201606255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nickel A.G., Von Hardenberg A., et al. Maack C. Reversal of mitochondrial transhydrogenase causes oxidative stress in heart failure. Cell Metabol. 2015;22:472–484. doi: 10.1016/j.cmet.2015.07.008. [DOI] [PubMed] [Google Scholar]
- 21.Haythorne E., Rohm M., et al. Ashcroft F.M. Diabetes causes marked inhibition of mitochondrial metabolism in pancreatic β-cells. Nat. Commun. 2019;10:2474. doi: 10.1038/s41467-019-10189-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Blacker T.S., Marsh R.J., et al. Bain A.J. Activated barrier crossing dynamics in the non-radiative decay of NADH and NADPH. Chem. Phys. 2013;422:184–194. [Google Scholar]
- 23.Blacker T.S., Nicolaou N., et al. Bain A.J. Polarized two-photon absorption and heterogeneous fluorescence dynamics in NAD(P)H. J. Phys. Chem. B. 2019;123:4705–4717. doi: 10.1021/acs.jpcb.9b01236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Blacker T.S., Chen W., et al. Bain A.J. Investigating state restriction in fluorescent protein FRET using time-resolved fluorescence and anisotropy. J. Phys. Chem. C Nanomater. Interfaces. 2017;121:1507–1514. doi: 10.1021/acs.jpcc.6b11235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhukov M., Popov A. IEEE 34th International Scientific Conference on Electronics and Nanotechnology, ELNANO 2014 Conference Proceedings. 2014. Bin number selection for equidistant mutual information estimaton; pp. 259–263. [Google Scholar]
- 26.Lidke K.A., Rieger B., et al. Jovin T.M. The role of photon statistics in fluorescence anisotropy imaging. IEEE Trans. Image Process. 2005;14:1237–1245. doi: 10.1109/tip.2005.852458. [DOI] [PubMed] [Google Scholar]
- 27.Chance B., Baltscheffsky H. Respiratory enzymes in oxidative phosphorylation. VII. Binding of intramitochondrial reduced pyridine nucleotide. J. Biol. Chem. 1958;233:736–739. [PubMed] [Google Scholar]
- 28.Scott T.G., Spencer R.D., et al. Weber G. Emission properties of NADH. Studies of fluorescence lifetimes and quantum efficiencies of NADH, AcPyADH, and simplified synthetic models. J. Am. Chem. Soc. 1970;92:687–695. [Google Scholar]
- 29.Yu Q., Heikal A.A. Two-photon autofluorescence dynamics imaging reveals sensitivity of intracellular NADH concentration and conformation to cell physiology at the single-cell level. J. Photochem. Photobiol., B. 2009;95:46–57. doi: 10.1016/j.jphotobiol.2008.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brochon J.C., Wahl P.H., et al. Iwatsubo M. Pulse fluorimetry study of beef liver glutamate dehydrogenase-reduced nicotinamide adenine dinucleotide phosphate complexes. Biochemistry. 1976;15:3259–3265. doi: 10.1021/bi00660a015. [DOI] [PubMed] [Google Scholar]
- 31.Gafni A., Brand L. Fluorescence decay studies of reduced nicotinamide adenine dinucleotide in solution and bound to liver alcohol dehydrogenase. Biochemistry. 1976;15:3165–3171. doi: 10.1021/bi00660a001. [DOI] [PubMed] [Google Scholar]
- 32.Vishwasrao H.D., Heikal A.A., et al. Webb W.W. Conformational dependence of intracellular NADH on metabolic state revealed by associated fluorescence anisotropy. J. Biol. Chem. 2005;280:25119–25126. doi: 10.1074/jbc.M502475200. [DOI] [PubMed] [Google Scholar]
- 33.Lakowicz J.R. Springer; 1999. Topics in Fluorescence Spectroscopy, Volume 1: Techniques. [Google Scholar]
- 34.Gorbunova I.A., Sasin M.E., et al. Vasyutinskii O.S. Two-photon excited fluorescence dynamics in enzyme-bound NADH: the heterogeneity of fluorescence decay times and anisotropic relaxation. J. Phys. Chem. B. 2021;125:9692–9707. doi: 10.1021/acs.jpcb.1c04226. [DOI] [PubMed] [Google Scholar]
- 35.Leung R.W.K., Yeh S.-C.A., Fang Q. Effects of incomplete decay in fluorescence lifetime estimation. Biomed. Opt Express. 2011;2:2517–2531. doi: 10.1364/BOE.2.002517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sakai Y., Hirayama S. A fast deconvolution method to analyze fluorescence decays when the excitation pulse repetition period is less than the decay times. J. Lumin. 1988;39:145–151. [Google Scholar]
- 37.Fisz J.J. Another look at magic-angle-detected fluorescence and emission anisotropy decays in fluorescence microscopy. J. Phys. Chem. A. 2007;111:12867–12870. doi: 10.1021/jp0775855. [DOI] [PubMed] [Google Scholar]
- 38.Cong A.T.Q., Pimenta R.M.L., et al. Heikal A.A. Associated anisotropy of intrinsic NAD(P)H for monitoring changes in the metabolic activities of breast cancer cells (4T1) in three-dimensional collagen matrix. Phys. Chem. Chem. Phys. 2021;23:12692–12705. doi: 10.1039/d0cp06635d. [DOI] [PubMed] [Google Scholar]
- 39.Devauges V., Marquer C., et al. Lévêque-Fort S. Homodimerization of amyloid precursor protein at the plasma membrane: a homoFRET study by time-resolved fluorescence anisotropy imaging. PLoS One. 2012;7:e44434. doi: 10.1371/journal.pone.0044434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Visser A.J.W.G., Hoek A.v. The fluorescence decay of reduced nicotinamides in aqueous solution after excitation with a UV-mode locked Ar ion laser. Photochem. Photobiol. 1981;33:35–40. [Google Scholar]
- 41.Gorbunova I.A., Sasin M.E., et al. Vasyutinskii O.S. Two-photon excited fluorescence dynamics in NADH in water-methanol solutions: the role of conformation states. J. Phys. Chem. B. 2020;124:10682–10697. doi: 10.1021/acs.jpcb.0c07620. [DOI] [PubMed] [Google Scholar]
- 42.Fromm H. Determination of dissociation constants of coenzymes and abortive. J. Biol. Chem. 1963;238:2938–2944. [PubMed] [Google Scholar]
- 43.Eggert M.W., Byrne M.E., Chambers R.P. Impact of high pyruvate concentration on kinetics of rabbit muscle lactate dehydrogenase. Appl. Biochem. Biotechnol. 2011;165:676–686. doi: 10.1007/s12010-011-9287-y. [DOI] [PubMed] [Google Scholar]
- 44.Steinmark I.E., Chung P.H., et al. Suhling K. Time-resolved fluorescence anisotropy of a molecular rotor resolves microscopic viscosity parameters in complex environments. Small. 2020;16:1907139. doi: 10.1002/smll.201907139. [DOI] [PubMed] [Google Scholar]
- 45.Smith T.A., Ghiggino K.P. A review of the analysis of complex time-resolved fluorescence anisotropy data. Methods Appl. Fluoresc. 2015;3:022001. doi: 10.1088/2050-6120/3/2/022001. [DOI] [PubMed] [Google Scholar]
- 46.Jha A., Udgaonkar J.B., Krishnamoorthy G. Characterization of the heterogeneity and specificity of interpolypeptide interactions in amyloid protofibrils by measurement of site-specific fluorescence anisotropy decay kinetics. J. Mol. Biol. 2009;393:735–752. doi: 10.1016/j.jmb.2009.08.053. [DOI] [PubMed] [Google Scholar]
- 47.Chib R., Raut S., et al. Gryczynski I. Associated anisotropy decays of Ethidium Bromide interacting with DNA. Methods Appl. Fluoresc. 2014;2:015003. doi: 10.1088/2050-6120/2/1/015003. [DOI] [PubMed] [Google Scholar]
- 48.Wahl P. Analysis of fluorescence anisotropy decays by a least square method. Biophys. Chem. 1979;10:91–104. doi: 10.1016/0301-4622(79)80009-5. [DOI] [PubMed] [Google Scholar]
- 49.Ludescher R.D., Peting L., et al. Hudson B. Time-resolved fluorescence anisotropy for systems with lifetime and dynamic heterogeneity. Biophys. Chem. 1987;28:59–75. doi: 10.1016/0301-4622(87)80075-3. [DOI] [PubMed] [Google Scholar]
- 50.Hurley J.H., Chen R., Dean A.M. Determinants of cofactor specificity in isocitrate dehydrogenase: structure of an engineered NADP+ → NAD+ specificity-reversal mutant. Biochemistry. 1996;35:5670–5678. doi: 10.1021/bi953001q. [DOI] [PubMed] [Google Scholar]
- 51.Hurley J.H., Dean A.M., et al. Stroud R.M. Catalytic mechanism of NADP+-Dependent isocitrate dehydrogenase: implications from the structures of magnesium-isocitrate and NADP+ complexes. Biochemistry. 1991;30:8671–8678. doi: 10.1021/bi00099a026. [DOI] [PubMed] [Google Scholar]
- 52.Deng H., Zhadin N., Callender R. Dynamics of protein ligand binding on multiple time scales: NADH binding to lactate dehydrogenase. Biochemistry. 2001;40:3767–3773. doi: 10.1021/bi0026268. [DOI] [PubMed] [Google Scholar]
- 53.Hammen P.K., Allali-Hassani A., et al. Weiner H. Multiple conformations of NAD and NADH when bound to human cytosolic and mitochondrial aldehyde dehydrogenase. Biochemistry. 2002;41:7156–7168. doi: 10.1021/bi012197t. [DOI] [PubMed] [Google Scholar]
- 54.Ko C.W., Wei Z., et al. Ying L. Probing nanosecond motions of plasminogen activator inhibitor-1 by time-resolved fluorescence anisotropy. Mol. Biosyst. 2009;5:1025–1031. doi: 10.1039/b901691k. [DOI] [PubMed] [Google Scholar]
- 55.Kinosita K., Ikegami A., Kawato S. On the wobbling-in-cone analysis of fluorescence anisotropy decay. Biophys. J. 1982;37:461–464. doi: 10.1016/S0006-3495(82)84692-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lipari G., Szabo A. Effect of librational motion on fluorescence depolarization and nuclear magnetic resonance relaxation in macromolecules and membranes. Biophys. J. 1980;30:489–506. doi: 10.1016/S0006-3495(80)85109-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Drucker R.P., McClain W.M. Polarized two-photon studies of biphenyl and several derivatives. J. Chem. Phys. 1974;61:2609–2615. [Google Scholar]
- 58.Bain A.J. Photonics: Scientific Foundations, Technology and Applications. Wiley; 2015. Multiphoton processes; pp. 279–320. [Google Scholar]
- 59.Larijani B., Bain A. Chemical Biology: Applications and Techniques. Wiley; 2007. Biological applications of single- and two-photon fluorescence; pp. 163–197. [Google Scholar]
- 60.Del Valle J.C., Catalán J. Kasha’s rule: a reappraisal. Phys. Chem. Chem. Phys. 2019;21:10061–10069. doi: 10.1039/c9cp00739c. [DOI] [PubMed] [Google Scholar]
- 61.Wu Y.D., Houk K.N. Theoretical study of conformational features of NAD+ and NADH analogs: protonated nicotinamide and 1,4-dihydronicotinamide. J. Org. Chem. 1993;58:2043–2045. [Google Scholar]
- 62.Delabar J.M., Martin S.R., Bayley P.M. The binding of NADH and NADPH to bovine-liver glutamate dehydrogenase: spectroscopic characterisation. Eur. J. Biochem. 1982;127:367–374. doi: 10.1111/j.1432-1033.1982.tb06881.x. [DOI] [PubMed] [Google Scholar]
- 63.Kalinina O.V., Gelfand M.S. Amino acid residues that determine functional specificity of NADP- and NAD-dependent isocitrate and isopropylmalate dehydrogenases. Proteins. 2006;64:1001–1009. doi: 10.1002/prot.21027. [DOI] [PubMed] [Google Scholar]
- 64.Mittl P.R., Berry A., et al. Schulz G.E. Anatomy of an engineered NAD-binding site. Protein Sci. 1994;3:1504–1514. doi: 10.1002/pro.5560030916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Scrutton N.S., Berry A., Perham R.N. Redesign of the coenzyme specificity of a dehydrogenase by protein engineering. Nature. 1990;343:38–43. doi: 10.1038/343038a0. [DOI] [PubMed] [Google Scholar]
- 66.Chen Y.Q., Van Beek J., et al. Callender R. Vibrational structure of NAD(P) cofactors bound to three NAD(P) dependent enzymes: an investigation of ground state activation. J. Phys. Chem. B. 2002;106:10733–10740. [Google Scholar]
- 67.Beis K., Allard S.T.M., et al. Naismith J.H. The structure of NADH in the enzyme dTDP-D-glucose dehydratase (RmlB) J. Am. Chem. Soc. 2003;125:11872–11878. doi: 10.1021/ja035796r. [DOI] [PubMed] [Google Scholar]
- 68.Qiu L., Gulotta M., Callender R. Lactate dehydrogenase undergoes a substantial structural change to bind its substrate. Biophys. J. 2007;93:1677–1686. doi: 10.1529/biophysj.107.109397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Suzuki K., Maeda S., Morokuma K. Roles of closed- and open-loop conformations in large-scale structural transitions of l -lactate dehydrogenase. ACS Omega. 2019;4:1178–1184. doi: 10.1021/acsomega.8b02813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Peng Y., Zhong C., et al. Ding J. Structural studies of Saccharomyces cerevesiae mitochondrial NADP-dependent isocitrate dehydrogenase in different enzymatic states reveal substantial conformational changes during the catalytic reaction. Protein Sci. 2008;17:1542–1554. doi: 10.1110/ps.035675.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Costa C.H.S.d., Bichara T.W., et al. Lameira J. Unraveling the conformational dynamics of glycerol 3-phosphate dehydrogenase, a nicotinamide adenine dinucleotide-dependent enzyme of Leishmania mexicana. J. Biomol. Struct. Dyn. 2021;39:2044–2055. doi: 10.1080/07391102.2020.1742206. [DOI] [PubMed] [Google Scholar]
- 72.Oide M., Kato T., Oroguchi T., Nakasako M. Energy landscape of domain motion in glutamate dehydrogenase deduced from cryo-electron microscopy. FEBS J. 2020;287:3472–3493. doi: 10.1111/febs.15224. [DOI] [PubMed] [Google Scholar]
- 73.Akai S., Ikushiro H., et al. Miyahara I. The crystal structure of homoserine dehydrogenase complexed with l-homoserine and NADPH in a closed form. J. Biochem. 2019;165:185–195. doi: 10.1093/jb/mvy094. [DOI] [PubMed] [Google Scholar]
- 74.Shimozawa Y., Himiyama T., et al. Nishiya Y. Structural analysis and reaction mechanism of malate dehydrogenase from Geobacillus stearothermophilus. J. Biochem. 2021;170:97–105. doi: 10.1093/jb/mvab027. [DOI] [PubMed] [Google Scholar]
- 75.Plapp B.V., Savarimuthu B.R., et al. Ramaswamy S. Horse liver alcohol dehydrogenase: zinc coordination and catalysis. Biochemistry. 2017;56:3632–3646. doi: 10.1021/acs.biochem.7b00446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Zhadin N., Gulotta M., Callender R. Probing the role of dynamics in hydride transfer catalyzed by lactate dehydrogenase. Biophys. J. 2008;95:1974–1984. doi: 10.1529/biophysj.108.132464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ranjit S., Malacrida L., et al. Gratton E. Determination of the metabolic index using the fluorescence lifetime of free and bound nicotinamide adenine dinucleotide using the phasor approach. J. Biophot. 2019;12:e201900156. doi: 10.1002/jbio.201900156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Neves R.P.P., Fernandes P.A., Ramos M.J. Unveiling the catalytic mechanism of NADP+-Dependent isocitrate dehydrogenase with QM/MM calculations. ACS Catal. 2016;6:357–368. [Google Scholar]
- 79.Peng H.L., Callender R. Mechanistic analysis of fluorescence quenching of reduced nicotinamide adenine dinucleotide by oxamate in lactate dehydrogenase ternary complexes. Photochem. Photobiol. 2017;93:1193–1203. doi: 10.1111/php.12775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sanderson M.J., Smith I., et al. Bootman M.D. Fluorescence microscopy. Cold Spring Harb. Protoc. 2014;2014 doi: 10.1101/pdb.top071795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Algar W.R., Hildebrandt N., et al. Medintz I.L. FRET as a biomolecular research tool — understanding its potential while avoiding pitfalls. Nat. Methods. 2019;16:815–829. doi: 10.1038/s41592-019-0530-8. [DOI] [PubMed] [Google Scholar]
- 82.Elson D., Requejo-Isidro J., et al. French P. Time-domain fluorescence lifetime imaging applied to biological tissue. Photochem. Photobiol. Sci. 2004;3:795–801. doi: 10.1039/b316456j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.