FERM domains recruit ample PI(4,5)P₂s to form extensive protein-membrane attachments

Abstract

The four-point-one ezrin-radixin-moesin homology (FERM) protein domain is a multifunctional protein-lipid binding site, constituting an integral part of numerous membrane-associated proteins. Its interaction with the lipid phosphatidylinositol-4,5-bisphosphate (PIP₂), located at the inner leaflet of eukaryotic plasma membranes, is important for localization, anchorage, and activation of FERM-containing proteins. FERM-PIP₂ complexes structurally determined so far exclusively feature a 1:1 binding stoichiometry of protein and lipid, with a few basic FERM residues neutralizing the −4 charge of the bound PIP₂. Whether this picture from static crystal structures also applies to the dynamic interaction of FERM domains on PIP₂ membranes is unknown. We here quantified the stoichiometry of FERM-PIP₂ binding in a lipid bilayer using atomistic molecular dynamics simulations and experiments on solid supported membranes for the FERM domains of focal adhesion kinase and ezrin. In contrast to the structural data, we find much higher average stoichiometries of FERM-PIP₂ binding, amounting to 1:3 or 1:4 ratios, respectively. In simulations, the full set of basic residues at the membrane interface, 7 and 15 residues for focal adhesion kinase and ezrin, respectively, engages in PIP₂ interactions. In addition, Na ions enter the FERM-membrane binding interface, compensating negative PIP₂ charges in case of high charge surpluses from bound PIP₂. We propose the multivalent binding of FERM domains to PIP₂ in lipid bilayers to significantly enhance the stability of FERM-membrane binding and to render the FERM-membrane linkage highly adjustable.

Significance

Four-point-one ezrin-radixin-moesin homology (FERM) domains are widespread modules that localize proteins to membranes by binding negatively charged phosphatidylinositol-4,5-bisphosphate (PIP₂) lipids. All current experimental PIP₂-FERM structures show one PIP₂ per FERM, but if this 1:1 stoichiometry holds at a dynamic FERM-membrane interface is unknown. Our atomistic simulations and biophysical experiments of two different FERM domains, those of focal adhesion kinase and ezrin, reveal that these FERM domains bind multiple PIP₂ molecules in a highly dynamic fashion. This highlights the importance of dynamic binding information in addition to static structures. Furthermore, we show how one principle, namely accumulation of basic residues on the FERM domain surface to recruit multiple PIP₂ molecules, apparently evolved independently at two distinct sites in the two model proteins studied.

Introduction

Located at the N-terminus of numerous peripheral membrane proteins, the band four-point-one ezrin-radixin-moesin homology (FERM) domain mediates the interaction with transmembrane proteins, signaling proteins, or lipids. It is involved in important signaling tasks and linking of the cortical actin cytoskeleton to the cytoplasmic leaflet of the plasma membrane (1). The FERM domain, as first discovered in the eponymous proteins ezrin, radixin, and moesin (ERM family), is composed of three subdomains (lobes), F1–F3, that arrange in the characteristic clover-leaf-shaped fold (Fig. 1).

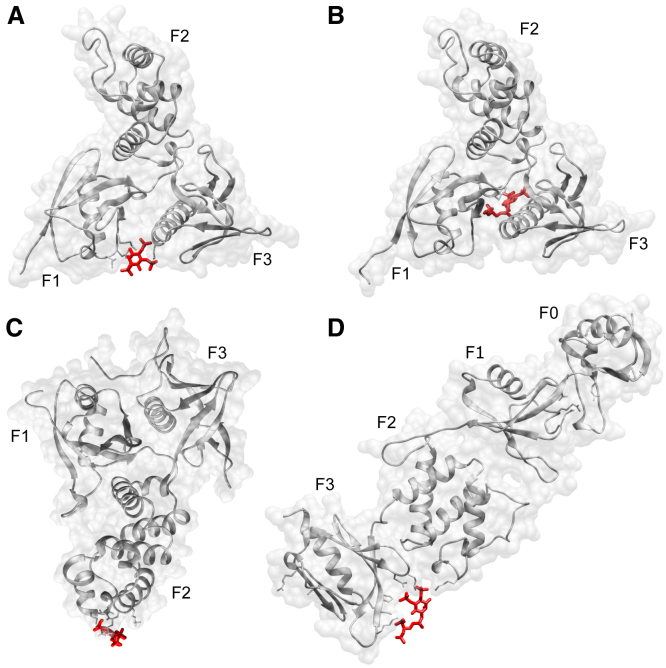
Figure 1.

The FERM domains (gray) of different proteins interact with PIP₂ via different binding sites. (A) Radixin-FERM in complex with inositol-(1,4,5)-triphosphate, (B) merlin-FERM-PIO complex (PIO = PIP2diC8), (C) FAK-FERM domain, and (D) talin-FERM-PIO. The PDB accession codes are PDB: 1GC6, 6CDS, 6CB0 (2), and 6MFS, respectively. The PIP₂ analogs are depicted in red. The location of the PIP₂ molecule bound to the FAK-FERM domain in (B) goes back to a model of focal adhesion kinase used in a previous MD simulation study (3). To see this figure in color, go online.

A common feature shared by many FERM domains is their high-affinity interaction with the lipid phosphatidylinositol-4,5-bisphosphate (PIP₂), which is often necessary for successful targeting and anchorage of FERM-containing proteins to the plasma membrane (4) and has been shown to constitute an integral part of the activation mechanism of several FERM-containing proteins (3,5).

Despite strong conservation of the FERM domain’s clover-leaf-shaped fold, past research has shown that different members of the FERM superfamily interact with PIP₂ via distinct binding sites on the FERM domain, partly assuming different binding poses with respect to the plasma membrane. While most FERM-containing proteins, including the ERM family members, orient the F1 and F3 lobes of their FERM domains toward the plasma membrane, focal adhesion kinase (FAK) presents the F2 lobe of its FERM domain to the plasma membrane, i.e., assumes a reversed binding pose (Fig. 1 C).

At the time of preparing this article, there are three FERM domain crystal structures complexed with PIP₂ analogs deposited on in the PDB. These FERM domains stem from the proteins radixin, merlin, and talin1. On the basis of the radixin-FERM-PIP₂ complex (PDB: 1GC6), radixin was suggested to possess a PIP₂-binding site in the basic cleft between its F1 and F3 lobes (6) (Fig. 1 A), which, in view of the high sequence identity of $\sim 85\%$ among ERM family FERM domains (7) and mutagenesis studies (4), is thought to be present in ezrin and moesin as well. Despite the still high sequence identity of $\sim 60\%$ between the FERM domains of merlin and radixin (8), the merlin-FERM-PIP₂ complex (PDB: 6CDS) is observed to have a unique PIP₂-binding site between the F1 and F3 lobes located approximately 17 Å away from radixin’s PIP₂-binding site (Fig. 1 B) (9). The cytoskeletal protein talin1 is an exceptional member of the FERM superfamily inasmuch as its FERM domain features a linear, rather than clover-leaf-shaped, arrangement, with an additional lobe F0 prepending the F1–F3 lobes. The talin1-FERM-PIP₂ complex (PDB: 6MFS) indicates yet another PIP₂-binding site between the F2 and F3 lobes (10) (Fig. 1 D).

Notably, all three abovementioned FERM-PIP₂ complexes are bound by a single PIP₂ analog at only one binding site, suggesting a stoichiometry of FERM-PIP₂ binding of 1:1.

Here, we performed molecular dynamics (MD) simulations and protein-binding studies of the FAK and ezrin FERM domains on phosphatidylcholine (POPC) lipid bilayers doped with PIP₂ to question the 1:1 stoichiometry observed in crystal structures. We chose these two FERM domain basic clefts as they differ in their position on the FERM domain as well as the local distribution of basic residues at the cleft (compare Fig. 1, A and C). We consistently identified higher numbers of PIP₂ bound to the proteins than the 1:1 ratio suggested by the crystal structures. We find the interaction surface of protein basic residues with the PIP₂ membrane to extend much beyond the known basic patch previously identified by crystallography or mutagenesis, thereby reaching out to rather $\sim$3–5 PIP₂ molecules at a time. Our joint experimental and simulation data reveal specific protein-PIP₂ interactions to be strongly multivalent and of surprisingly dynamic nature.

Materials and methods

Atomistic MD simulations

The starting structures for our MD simulations were modeled based on structures of the ezrin-FERM domain (PDB: 4RMA (11)) and the FAK-FERM domain (PDB: 6CB0 (2)). A structural fit of the ezrin-FERM domain to the sequentially and structurally very similar radixin-FERM domain of the FERM-PIP₂ complex in Fig. 1 A and repeated use of the functionalities provided by the CHARMM-GUI Membrane Builder (12,13) allowed us to obtain an ezrin-FERM-PIP₂ complex of reasonable orientation with respect to an underlying $9.1\times 9.1\text{nm}$ lipid bilayer (details in supporting material). To assemble the FAK-FERM-membrane starting structure, we used a previously modeled FAK-dimer-PIP₂ complex (3), based on a cryoelectron microscopy structure of a FAK dimer that was subjected to a rigorous PIP₂ docking procedure, as a template. Structurally fitting the FAK-FERM structure to one of the two FAK-FERM domains contained in this template structure and again making use of the CHARMM-GUI Membrane Builder, we assembled a reasonably oriented FAK-FERM-membrane starting structure (details in supporting material). The underlying lipid bilayer had dimensions $9.5\times 9.5\text{nm}$. In both systems, the lipid bilayer was composed of POPC lipids with $10\%$ PIP₂ in the protein-proximal leaflet. All MD simulations were performed with GROMACS (14) 2018.5 using the CHARMM36 (15) additive all-atom force-field (v.March 2019). The assembled ezrin- and FAK-FERM-membrane structures were placed in simulation boxes of sizes $9.2\times 9.2\times 15\text{nm}$ and $9.75\times 9.75\times 18\text{nm}$, respectively, and solvated in TIP3P water (16). All simulations were performed in the presence of NaCl specifying a target concentration of $150\text{mM}$. In energy minimization, using steepest descent, the systems were steered toward nearby local minima of the potential energy until the maximal occurring force dropped below $F_{\text{tol}}=1000\frac{\text{kJ}}{\text{nm}·\text{mol}}$. After initial temperature and pressure adjustment to $T=303\mathrm{K}$ and $p=1\text{bar}$ according to the CHARMM equilibration protocol (13), production runs were carried out in the NPT ensemble. To this end, temperature coupling was switched from velocity rescaling (17) to Nosé-Hoover coupling (18,19) with a coupling time constant of ${\tau }_{\text{tc}}=1\text{ps}$ and semiisotropic pressure coupling switched from Berendsen (20) to Parrinello-Rahmann (21,22) coupling with a coupling time constant of ${\tau }_{\text{pc}}=5\text{ps}$ and isothermal compressibility kept at $\kappa =4.5\times {10}^{-5}{\text{bar}}^{-1}$. Constraining bonds involving hydrogen with the LINCS algorithm (23), an integration time step of $\Delta t=2\text{fs}$ could be used. Van der Waals forces were smoothly switched to zero between $r_{\text{sw}}=1.0\text{nm}$ and $r_{\text{vdw}}=1.2\text{nm}$, and for both the evaluation of van der Waals interactions and the direct part of the Ewald sum, Verlet neighbor lists were used, which were updated every ${\mathrm{n}}_{\text{list}}\ge 20$ integration steps. Evaluation of the reciprocal part of the Ewald sum was done with the smooth particle mesh Ewald technique at a Fourier grid spacing of $0.14\text{nm}$. For the ezrin- and FAK-FERM domains, a total of $8.1$ and $6.9\mu$s of equilibrium simulation data were collected in 10 independent replicates, respectively. Additionally, for each FERM domain, six replicates were continued for a further $100\text{ns}$ with higher write-out frequency of ion coordinates (details in supporting material).

Based on stabilization of FERM-PIP₂ contact maps computed with ConAn as an equilibration criterion, we discarded the first $600\text{ns}$ of each ezrin-FERM simulation and the first $450\text{ns}$ of each FAK-FERM simulation as equilibration time (details in supporting material).

Evaluation of FERM-PIP₂ stoichiometry

The histograms of the stoichiometry of FERM-PIP₂ binding (Fig. 2) were obtained by counting for each simulation frame of the equilibrated portion of the MD data the number of PIP₂ molecules bound to the respective FERM domain. A PIP₂ molecule was considered to be bound to a FERM domain if at least one of its phosphate groups got within $0.6\text{nm}$ of the protonated end of a Lys or Arg residue (details in supporting material).

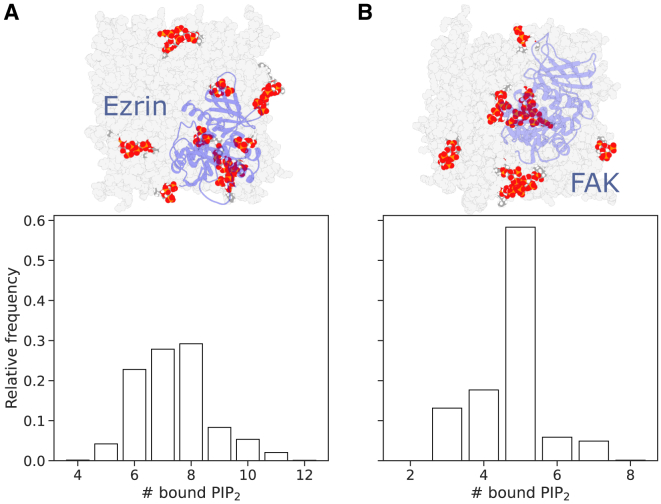
Figure 2.

The stoichiometry of FERM-PIP₂ binding is larger than suggested by FERM-PIP₂ complexes deposited on the PDB. Normalized stoichiometry histograms computed on the basis of MD simulation data are shown for (A) the ezrin-FERM and (B) the FAK-FERM domain. The simulation snapshots above the histograms show the FERM domains (blue) in interaction with PIP₂ molecules (red). The underlying membrane is colored in light gray. To see this figure in color, go online.

Contact analysis

To determine residue-wise FERM-PIP₂ contacts (Fig. 4, E and F) and the contributions of FERM-PIP₂ contacts to the overall FERM-membrane contacts (Table 1), ConAn was deployed, turning residue-lipid interactions on when interaction partners got within $d\le d_{\text{inter}}=0.4\text{nm}$ and off when they got separated by $d>d_{\text{high}}=0.6\text{nm}$ (details in supporting material).

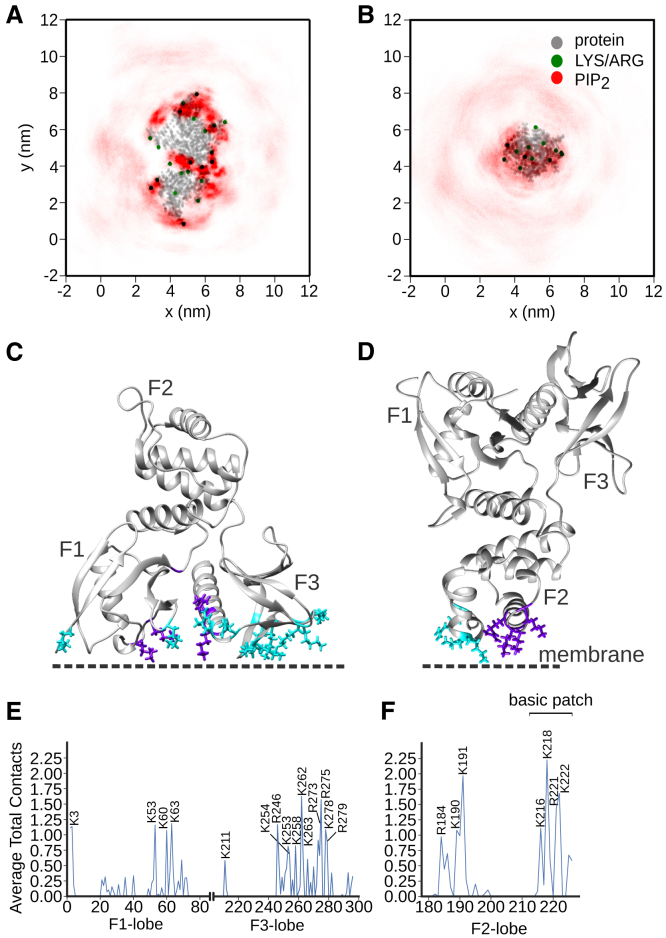
Figure 4.

The FERM domains of ezrin and FAK interact with PIP₂ via several different binding sites. (A and B) Lateral distribution of PIP₂ (red) around the ezrin- and FAK-FERM domains (gray). Green dots represent the protonated ends of Lys or Arg residues. The visualizations are based on simulation frames subjected to rotational and translational fits to a common reference structure (details in supporting information). (C and D) Sites of FERM-PIP₂ interaction on the ezrin- and FAK-FERM domains. The crystallographic basic cleft (ezrin) and basic patch (FAK) residues are colored purple. Additional, frequently interacting Lys and Arg are depicted in cyan. (E and F) Average total contacts per frame of ezrin-/FAK-FERM residues with PIP₂ molecules. We counted contacts when the minimal distance between a protein residue and PIP₂ was below 0.6 nm, summed the number of contacts of each residue, and averaged over the whole simulation time. Lys and Arg with ${\overline{n}}_{\text{res}}\ge 0.5$ average total contacts per frame were labeled in single letter amino acid code. To see this figure in color, go online.

Table 1.

Contribution of PIP₂ to overall FERM-membrane contacts

	Ezrin-FERM	FAK-FERM
FERM-membrane	$64\pm 5$	$20\pm 2$
FERM-PIP2	$23\pm 3$	$9.4\pm 1.3$

Average and standard error of the mean of contacts between FERM domain residues and all membrane lipids or only PIP₂ lipids are shown.

Isolation of recombinant ezrin-FERM and FAK-FERM

Proteins were recombinantly expressed in Escherichia coli as previously described by Schäfer et al. for ezrin-FERM and Ceccarelli et al. for FAK-FERM (24,25). The protocol for ezrin-FERM purification was followed strictly. The protocol for the FAK-FERM was adjusted starting with the pET28a vector with the respective DNA sequence kindly provided by Daniel Lietha (Margaritas Salas Center for Biological Research, Madrid, Spain). After transformation of the vector in a BL21(De3)pLysS strain (Novagen, Madison, WI, USA), the cells were grown to an OD₆₀₀ of 0.8, and protein expression was induced by the addition of 0.2 mM IPTG and incubated for 12–16 h at ${18}^{\circ }$C. The cells were pelleted and lysed in buffer A (20 mM Tris [pH 8], 10 mM β-mercaptoethanol, and 5 mM imidazole) with 200 mM NaCl and additionally containing an inhibitor cocktail tablet (cOmplete; Roche Diagnostics, Basel, Switzerland). The cells were sonicated and centrifuged for 1 h at 100,000 $\times g$. Afterward, the supernatant was loaded on a Ni-NTA column and eluted with buffer A containing 200 mM NaCl and 195 mM imidazole additionally. The His tag of the protein was cleaved off from the pooled fractions by a TEV protease (Merck KGaA, Darmstadt, Germany) using a ratio of 1:100 (w/w) at $4^{\circ }$C during dialysis to buffer A with 50 mM NaCl. The protein was loaded on a Mono Q 5/50 GL column (Merck KGaA, Darmstadt, Germany) and eluted with a buffer A gradient from 50 mM NaCl to 1 M NaCl. The fractions containing the FAK were combined and loaded onto a HiLoad 16/600 Superdex column (Merck KGaA, Darmstadt, Germany) equilibrated with buffer A containing 150 mM NaCl. The eluted protein was concentrated and stored at $4^{\circ }$C.

Reflectometric interference spectroscopy (RIfS)

RIfS experiments were performed using a custom-build instrument with a Flame-S-UV-visible spectrometer (OceanOptics Germany GmbH, Ostfildern, Germany). With the setup, the optical thickness of a thin layer on a SiO${}_2$ wafer can be determined by the reflection of white light, which was measured every 2 s (26). Si substrates with a 5 $\mu$m oxide layer were cleaned with an H${}_2$O/NH${}_3$/H${}_2$O${}_2$ (5:1:1) solution at ${70}^{\circ }$C for 20 min. The cleaned wafers were treated with an O${}_2$ plasma for 30 s and used directly afterward. After obtaining a baseline with Na-citrate buffer (50 mM NaCl, 20 mM Na-citrate, 0.1 mM EDTA, 0.1 mM NaN${}_3$ [pH 4.8]), small unilamellar vesicles were added to form a supported lipid bilayer. Small unilamellar vesicles were obtained by sonication of a lipid mixture of POPC and PIP₂ (Avanti Polar lipids, Alabaster, AL, USA) in Na-citrate buffer with different POPC:PIP₂ ratios (99:1–90:10). The quality of the supported lipid bilayers was proven by the $\Delta OT$ values after spreading. After a buffer exchange to buffer A with 150 mM NaCl for 10 min, a thoroughly mixed protein solution was added. FAK-FERM was added with a final concentration of 800 $\mu$M, whereas ezrin-FERM was added with a final concentration of 70 $\mu$M. The different concentrations take the different binding affinities into account, ensuring that all available PIP₂-binding sites are occupied. The obtained data were evaluated using a self-written MATLAB script (The MathWorks, Natick, MA, USA).

Results

Stoichiometry of FERM-PIP₂ binding is larger than expected

We determined the stoichiometries of FERM-PIP₂ binding of the ezrin- and FAK-FERM domains through MD simulations and stoichiometry experiments on lipid bilayers composed of POPC and PIP₂. By counting the number of PIP₂ molecules bound to the FERM domains for each simulation frame of the equilibrated portions of the MD trajectories, normalized histograms of stoichiometry were computed (Fig. 2).

For both FERM domains, the probability of binding PIP₂ increases up to an ideal range of bound PIP₂ molecules, above which probability drops markedly and decays to zero. While the ezrin-FERM domain is most likely bound by 6–8 PIP₂ molecules with an average binding count of ${\overline{\mathrm{N}}}_{\text{PIP}2,\text{ezrin}}=7.4\pm 0.4$ (standard error of the mean), the FAK-FERM domain is most often bound by 5 PIP₂ molecules with an average binding count of ${\overline{\mathrm{N}}}_{\text{PIP}2,\text{FAK}}=4.6\pm 0.3$ (standard error of the mean).

To investigate experimentally whether the hypothesis that both FERM domains bind more than one PIP₂ molecule as derived from our MD simulations, we analyzed the binding of FAK-FERM and ezrin-FERM to POPC lipid bilayers on Si substrates doped with different PIP₂ concentrations. By means of RIfS, we determined the change in optical thickness ($\Delta OT$) upon protein binding to the supported lipid bilayer dependent on the PIP₂ concentration (Fig. 3, A and B). $\Delta OT$ is a measure of the protein surface coverage. High protein concentrations were chosen to assume that all PIP₂ molecules are occupied by protein. The Hill equation (Eq. 1) was fitted to the sigmoidal change of $\Delta OT$ as a function of the total PIP₂ surface concentration ${\mathrm{\Gamma }}_{\text{PIP}\mathrm{2,0}}$:

$$\Delta OT=\Delta O{T}_{\max }\frac{{\mathrm{\Gamma }}_{\text{PIP}\mathrm{2,0}}^n}{K_{\mathrm{D}}+{{\mathrm{\Gamma }}^n}_{\text{PIP}\mathrm{2,0}}}$$ (Equation 1)

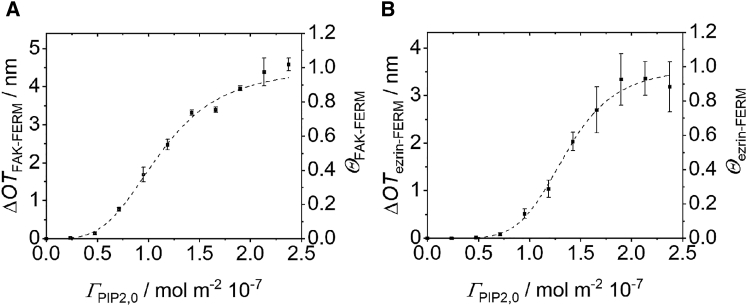
Figure 3.

Binding of FAK-FERM (A) and ezrin-FERM (B) on PIP₂-doped membranes. Change of the optical thickness ($\Delta OT$) upon binding of FAK-FERM (800 μM) or ezrin-FERM (70 μM) on POPC/PIP₂ SLBs with varying PIP₂ surface concentrations. Error bars indicate the standard error of the mean ($N\ge 4$). Eq. 1 was fit to the data (dashed lines), resulting in $\Delta O{T}_{\text{FAK}-\text{FERM}\left(\max \right)}=4.5\text{nm}$ with $n_{\text{FAK}-\text{FERM}}=3.6$ and $\Delta O{T}_{\text{ezrin}-\text{FERM}\left(\max \right)}=3.6\text{nm}$ with $n_{\text{ezrin}-\text{FERM}}=5.5$. ${\mathrm{\Theta }}_{\text{protein}}=\Delta OT/\Delta O{T}_{\max }$. To see this figure in color, go online.

For the FAK-FERM, a $\Delta O{T}_{\text{FAK}-\text{FERM}\left(\max \right)}=4.5\text{nm}$ was determined with $n_{\text{FAK}-\text{FERM}}=3.6$. For the ezrin-FERM, $n_{\text{ezrin}-\text{FERM}}=5.5$ and $\Delta O{T}_{\text{ezrin}-\text{FERM}\left(\max \right)}=3.6\text{nm}$ were found. $\Delta O{T}_{\text{FAK}-\text{FERM}\left(\max \right)}$ is defined as $n_{\text{protein}}\times d_{\text{FAK}-\text{FERM}}$, with $n_{\text{protein}}=1.455$ being the refractive index of the protein layer (27). That means that an average physical protein layer thickness of $d_{\text{FAK}-\text{FERM}}=3\text{nm}$ can be calculated for the FAK-FERM, whereas for ezrin-FERM, $d_{\text{ezrin}-\text{FERM}}$ would read $2.5\text{nm}$. Based on the $\Delta O{T}_{\max }$ values, we defined the surface coverage ${\mathrm{\Theta }}_{\text{protein}}=\Delta OT/\Delta O{T}_{\max }=1$. The exponent n in Eq. 1 refers to the cooperativity of binding and is often interpreted as the number of bound ligands. However, even though the Hill equation fits the data nicely, the assumption of a cooperative binding of ligands to a protein in three dimensions is not valid in a two-dimensional membrane system. To arrive at an equation (Eq. 2) that takes into account that only protein binding to the PIP₂-doped membrane surface can be measured by RIfS and where no direct information about the number of PIP₂ molecules per protein can be obtained, we defined multiple binding reactions at the membrane similar to the work of Mosior and co-workers (supporting material) (28,29):

$${\mathrm{\Theta }}_{\text{protein}}=A_{\mathrm{p}}{N}_{\mathrm{A}}\left({\mathrm{\Gamma }}_{\text{PIP}\mathrm{2,0}}-{\mathrm{\Gamma }}_{\text{PIP}2}\right)\frac{{\sum }_{i=1}^{\mathrm{n}}{\left(K_{\mathrm{S}}{\mathrm{\Gamma }}_{\text{PIP}2}\right)}^{\mathrm{i}-1}}{{\sum }_{i=1}^{\mathrm{n}}i{\left(K_{\mathrm{S}}{\mathrm{\Gamma }}_{\text{PIP}2}\right)}^{\mathrm{i}-1}}$$ (Equation 2)

$A_{\mathrm{p}}$ is the footprint of the protein, $N_{\mathrm{A}}$ the Avogadro constant, ${\mathrm{\Gamma }}_{\text{PIP}2}$ the free PIP₂ surface concentration, n the number of PIP₂ molecules bound to the protein and $K_{\mathrm{S}}$ the surface binding constant. We have taken the molecular protein area and the surface molecular coverage to calculate $A_{\mathrm{p}}=A_{\text{one}}/\alpha$ from the MD simulations leading to ${\mathrm{\Theta }}_{\text{protein}}=1$. $K_{\mathrm{S}}$ was calculated from the Gibbs free energies of binding (MD simulations; see supporting material) and the assumption that the surface is treated as a region of finite thickness with $h=10\text{nm}$ (28,29). The system is still underdetermined, and the free PIP₂ surface concentration cannot be determined independently. Thus, we calculated ${\mathrm{\Gamma }}_{\text{PIP}2}$ (${\mathrm{\Gamma }}_{\text{PIP}\mathrm{2,0}}$) plots for different n and found that ${\mathrm{\Gamma }}_{\text{PIP}2}$ becomes negative if n exceeds a certain value. We define this n as being the maximum PIP₂ molecules bound to the protein (supporting material). Using this approach, $n<3$ was determined for the FAK-FERM, whereas for the ezrin-FERM, $n<4$. The reduced n values compared with those obtained by fitting a Hill equation to the data are in agreement with the idea that the dimensionality is reduced upon the first binding of the protein to the quasi two-dimensional membrane (28,29).

Lateral PIP₂ distribution follows distribution of positive residues on the FERM domain surface

With average binding stoichiometries of five or even seven PIP₂ molecules per FERM domain in the simulations, it is not immediately clear where on the FERM domain surfaces all of these PIP₂ molecules could be accommodated. To get a first overview of the sites of FERM-PIP₂ interaction, we visualized the interaction surfaces of the ezrin- and FAK-FERM domains by plotting the lateral PIP₂ distribution around the two different FERM domains (Fig. 4, A and B).

For both FERM domains, lateral PIP₂ distribution closely follows the charge distribution generated by the Lys and Arg residues on the FERM domain surfaces of ezrin and FAK. The patch-like positively charged interaction surface (Fig. 4 B) the FAK-FERM domain’s F2 lobe offers the PIP₂ molecules for interaction is in stark contrast to the widespread charge distribution on the interaction surface of the ezrin-FERM domain (Fig. 4 A).

To quantitatively pin down the main sites of FERM-PIP₂ interaction, we computed the average total contacts formed by individual protein residues with PIP₂ molecules using the contact analysis tool ConAn (30) (Fig. 4, E and F).

The residue-wise average total contacts first of all indicate that it is indeed primarily Lys and Arg residues that frequently interact with PIP₂. As expected, the residues comprising the crystallographic binding site in the basic cleft between the F1 and F3 lobes of the ezrin-FERM domain (K60, K63, K83, K278, and R279) and the basic patch on the F2 lobe of the FAK-FERM domain (K216, K218, R221, and K222) are in pronounced interaction with PIP₂ molecules. Interestingly, however, the residue-wise contact analysis also reveals many other residues on the FERM domain surfaces that interact with PIP₂ at a comparable frequency. Whereas the ezrin-FERM residues K53 (F1 lobe) and R273 and R275 (F3 lobe) are found in close proximity to the basic cleft and thus effectively extend it, other strongly interacting residues like R246, K253, K254, K258, K262, and K263 are spread over the outer loops of the F3 lobe (Fig. 4 C). Noting also K3 and the less strongly interacting residues K35, K40, and K72 on the F1 lobe, as well as the residues R293 and K296 on the opposite side of a long α-helix of the F3 lobe, one realizes that positive residues are scattered all over the outer F1 and F3 lobes of the ezrin-FERM domain, thus maximizing its interaction surface. With R184, K190, and K191 on a neighboring α-helix of the F2 lobe, the FAK-FERM domain has three more strongly interacting protein residues beside the more prominent basic patch residues (Fig. 4 D) (3,31).

FERM-PIP₂ contacts contribute strongly to overall FERM-membrane contacts

Finding a large number of positively charged FERM residues in pronounced interaction with PIP₂, we became interested in the contribution of FERM-PIP₂ interactions to FERM-membrane binding strength. We therefore compared the number of contacts of protein residues with all membrane lipids and with only PIP₂ lipids (Table 1).

Since the PIP₂ content in the protein-proximal membrane leaflet is $10\%$, we would expect that FERM-PIP₂ contacts account for $10\%$ of the overall FERM-membrane contacts assuming an even distribution of PIP₂ lipids across the membrane as initially constructed. However, FERM-PIP₂ contacts contribute $36\%$ and $47\%$ of the overall ezrin-FERM- and FAK-FERM-membrane contacts, respectively. We conclude that PIP₂ accumulates below the proteins, while the unoccupied membrane regions consequentially possess a lower PIP₂ content.

Discussion

Here, we probed the stoichiometry of FERM-PIP₂ interaction of the proteins ezrin and FAK in atomistic MD simulations and in experiments on SLBs. Both simulations of single FERM domains on a PIP₂-containing lipid bilayer and stoichiometry experiments involving layers of typically oligomerized FERM domains suggest that the stoichiometry of FERM-PIP₂ binding is much larger than expected on the basis of the three FERM-PIP₂ complexes deposited on the PDB (PDB: 1GC6, 6MFS, and 6CDS). Our experimental data point at a stoichiometry of $\sim$3–4 PIP₂ molecules per FERM domain for FAK and ezrin, respectively.

To estimate the stoichiometry of FERM-PIP₂ binding experimentally, we analyzed the data first using a well-known Hill equation. The Hill equation describes protein-ligand binding and allows accessing the degree of cooperativity of reactions that occur in three dimensions, with the assumptions that the n binding sites are independent and identical (28). However, any reaction occurring at the membrane interface is subdivided into a first reaction taking place from solution but is then confined in the plane of the membrane, i.e., becomes two-dimensional. This reduction in dimensionality overestimates the stoichiometry given by the Hill coefficient n (28).

Thus, we applied a model following the assumption of Mosior and McLaughlin (28,29). The three-dimensional region, where the protein first binds to a ligand in the membrane is treated as a region of finite thickness of 10 nm. As the protein-ligand interaction at the membrane interface itself cannot be resolved by the measurement, the resulting set of equations is underdetermined. To still obtain a lower estimate of the number of ligands (PIP₂ molecules) bound to one protein, we defined the number of PIP₂ molecules, where ${\mathrm{\Gamma }}_{\text{PIP}2}$ = 0 applies. If n is an integer, n is defined where ${\mathrm{\Gamma }}_{\text{PIP}2}$ ¡ 0, defining the minimum number of bound PIP₂ molecules per FERM domain. The obtained n values derived from this model are for both proteins around one lower (n < 3 for FAK-FERM and n < 4 for ezrin-FERM) than the n values obtained from fitting the Hill equation to the data (n = 3.6 for FAK-FERM and n = 5.5 for ezrin-FERM) (Fig. 3, A and B). This is in agreement with our expectation that the Hill equation overestimates the number of bound ligands in a two-dimensional system.

In our simulations, we found even larger stoichiometries of 5 and 6–8 PIP₂ molecules per FERM domain for FAK and ezrin, respectively. These values are consistent with previous simulations. The ezrin-FERM domain’s stoichiometry reported here falls within a similar range as the PIP₂ binding count of $6\pm 0.3$ previously observed in atomistic MD simulations of the closely related protein moesin on a lipid bilayer with the composition POPC:POPE:POPS:PIP₂ 50:20:20:10 (mol/mol) (32). We note that our chosen cutoff for defining bound PIP₂ molecules, albeit being based on the Bjerrum length, is arbitrary. Additionally, the larger stoichiometry in simulations compared with experimental data could be explained by the finding that MD force-fields commonly overstabilize salt bridges (33). A previous attempt to avoid the overstabilization of salt bridges using the Amber99SB^∗ ILDN-DERK force-field, which applies adjusted charges for Glu, Asp, Arg, and Lys residues, has not improved this problem (34). Overall, both experiments and simulations agree that the stoichiometries for both proteins of binding PIP₂ are much larger than one and suggest a larger number of bound PIP₂ molecules for ezrin’s FERM domain with a larger, more diffuse basic interaction area compared with FAK.

The large stoichiometry of FERM-PIP₂ binding implies that the positive charges of the basic residues at the membrane surface are roughly compensated, if not overcompensated, by negative charges of PIP₂s. Experiments suggest $\sim$4 PIP₂s or charge $\sim -16e$ for 15 Lys/Arg of ezrin and $\sim$3 PIP₂s or charge $\sim -12e$ for 7 Lys/Arg of FAK, considering the experimentally determined (35) PIP₂ net charge at pH 7 of $\sim -4e$ per molecule. PIP₂ counts in our simulations translate to a charge of $\sim -30e$ and $\sim -18e$ for ezrin and FAK, respectively. At the same time, we observe a standard deviation of approximately $\sim$1 PIP₂, or a charge of $\sim -4e$, for the average number of bound PIP₂s in our MD simulations. As a consequence, negative charges dynamically vary and can exceed the positive protein charges at the interface. In such cases, our simulations predict that Na ions, being only partially displaced upon binding of PIP₂ to the protein, enter the binding interface, where they can neutralize a negative net charge of the protein-membrane interface (Figures S4–S6). However, this raises the question of why PIP₂ prefers to interact with the protein if Na ions could, in principle, compensate its charge. When we compared the charges of free and bound PIP₂ clusters, we found that Na ions and PIP₂ interact at a 3:1 ratio, leaving an excess charge of $\sim -1e$ for each PIP₂ molecule per cluster. This charge is neutralized by the positively charged protein residues, electrostatically biasing PIP₂ toward the protein interface, which also explains the large contribution of PIP₂ lipids to the overall FERM-membrane contacts (Table 1). We note that this simple consideration is based on charge summation and neglects the spatial distribution of charges or any less-simple contributions to the system’s free energy, which can further modify the stoichiometries. Also, our computational analysis is based on orientations of the FERM domains, as suggested by cocrystals with PIP2, while other orientations cannot be excluded and can only be partially covered by rocking motions within our submicrosecond simulations (Fig. S3).

Seeking to understand where on the ezrin- and FAK-FERM domains more than one PIP₂ molecule could be accommodated, we mapped out the FERM’s main PIP₂ interaction sites and visualized the interaction surfaces (Fig. 4). As expected in view of PIP₂’s substantial negative net charge, it was primarily the positively charged Lys and Arg that interacted frequently with PIP₂. Moreover, we observed lateral PIP₂ distribution to closely follow the distribution of positive charge determined by the Lys and Arg on the FERM domain surfaces. This type of visualization underlined the rather small patch-like interaction surface presented by the FAK-FERM domain to the membrane and showed that almost the entire surface of the ezrin-FERM domain is involved in the interaction. Residue-wise contact analysis further revealed that PIP₂ molecules interact frequently with many other Lys and Arg besides the well-established residues comprising the binding site in the basic cleft of the ezrin-FERM domain or the basic patch of the FAK-FERM domain.

Also taking into account less frequently interacting residues on the F1 and F3 lobes, our results are in keeping with the list of interacting residues reported in the abovementioned MD simulations of moesin (32). It is interesting to note that despite the FERM domains’ conserved fold, PIP₂-binding sites have apparently evolved at different positions. Yet, stable FERM-membrane binding relies on the same principle, namely a cluster of basic residues interacting electrostatically with PIP₂ lipids and, at least in simulations, charge neutralization by Na ions. When comparing the FERM domain with pleckstrin homology (PH) domains, which are another family of lipid recognition domains, one discovers that the FERM F3 lobe shares the same fold as PH domains. PH domains also rely on electrostatic interactions between positively charged residues and the phosphatidylintositol phosphate PIP₃. In contrast to FERM domains, a conserved canonical PIP₃-binding site could be defined for PH domains (36). However, a noncanonical site and further residues were also found to be important for thermodynamically stable membrane interactions in coarse-grained MD simulations of the GRP1 PH domain (37), which is in line with our finding that residues additional to the well-characterized FAK basic patch and ezrin basic cleft contribute to FERM domain PIP₂ binding.

From a biological perspective, the exhaustive use of the ezrin-FERM surface for interaction with PIP₂ conforms well with ezrin’s task to establish a robust link between the actin cortex and the plasma membrane. The usage of a smaller number of positive residues being concentrated on two neighboring α-helices on the F2 lobe might allow for a stable enough, but still readily detachable, membrane linkage, as required for a signaling enzyme like FAK. Membrane binding is required for autoactivation (38) and has to be strong enough to withstand the forces required for force activation (39,40). On the other hand, FAK has to be released from focal adhesions (FAs) for FA turnover. Therefore, carefully balanced thermodynamic and mechanical stability of membrane binding is crucial for normal cellular function. Stoichiometries of FERM-PIP₂ binding significantly beyond 1:1 render the protein-membrane interaction not only more stable but also adjustable. The PIP₂ concentration in the cytoplasmic leaflet of the plasma membrane depends on the activity of several enzymes, including, for example, the phosphatidylinositol phosphate kinase type Iγ, which synthesizes PIP₂ in FAs (41). Furthermore, we speculate that the ionic strength of the cytosol, importantly also the concentration of divalent ions, can regulate the strength of electrostatic FERM-PIP₂ binding.

In conclusion, our study quantifies and rationalizes the stoichiometry of the FERM-PIP₂ interaction of ezrin and FAK based on experiments and MD simulations performed on PIP₂-containing model membranes. The proposed rather large stoichiometry of FERM-PIP₂ binding ultimately entails a large contribution of the FERM-PIP₂ interaction to the overall FERM-membrane binding stability, which in turn results in a pronounced dependence of FERM-membrane interaction on local PIP₂ concentration. Our results underline the role of the FERM-PIP₂ interaction in controlling the activity of FERM-containing proteins. The mechanistic principles underlying the FERM-PIP₂ interaction uncovered here aid our understanding of the regulatory role of these proteins in cell adhesion, growth, and motility.

Author contributions

T.E., T.H., and S.d.B. designed and performed the research, analyzed the data, and wrote the manuscript. C.A.-S. performed research and analyzed data. F.G. and C.S. designed the research and wrote the manuscript.

Editor: Lucie Delemotte.

Supporting citations

References (2,3,6,11,12,13,30,35,42,43,44,45,46,47,48,49) appear in the supporting material.