Modeling the drivers of oscillations in COVID-19 data on college campuses

Abstract

Purpose

Incorporating human behavior in a disease model can explain the oscillations in COVID-19 data which occur more rapidly than can be explained by variants alone on college campuses.

Methods

Dampened oscillations emerge by supplementing a simple disease model with a risk assessment function, which depends on the current number of infected individuals in the student population and the institutional public health policies. After accounting for a rapid disease impulse due to social gatherings, we achieve sustained oscillations that follow the trend of 2020/2021 COVID-19 data as reported on the COVID-19 dashboards of US post-secondary institutions.

Results

This adjustment to the epidemiological model can provide an intuitive way of understanding rapid oscillations based on human risk perception and institutional policies. More risk-averse communities experience lower disease-level equilibria and less oscillations within the system, while communities that are less responsive to changes in the number of infected individuals exhibit larger amplitude and frequency of the oscillations.

Conclusions

Community risk assessment plays an important role in COVID-19 management in college settings. Improving the ability of individuals to rapidly and conservatively respond to changes in community disease levels may help assist in self-regulating these oscillations to levels well below thresholds for emergency management.

Background

The introduction of oscillations in disease models is a well-studied and important topic in public health management. Research shows that the infections of COVID-19 examine oscillatory behavior over long periods of time due to the development of new variants of the virus [1]. Seasonal changes in the environmental conditions lead to alterations in the virus stability, the host immune response, and the behavior of the susceptible individuals [2]. Therefore, these changes lead to oscillatory behavior in COVID-19 data over long periods of time.

However, oscillatory behavior also occurs at faster time scales. In contrast with the oscillations that occur over long time periods, this oscillatory behavior cannot be attributed to changing conditions or the development of new variants of the virus. Bukhari et al. [3] found that data for the COVID-19 daily reported cases and the overall positivity rate in Germany and Italy exhibit dampened oscillations with a frequency of 1 week. They hypothesize that these oscillations arise either due to differences in testing frequencies over the time span of a week or due to social factors. They prompt the scientific community to explore what could cause the observed oscillatory behavior.

Common methods for inducing periodicity in compartmental disease models account for processes that act on longer time scales. For example, including population dynamics (e.g., birth and death rates) allows for the consistent introduction of a new susceptible population—newborns [4]. Some models produce a yearly oscillation by imposing a seasonal forcing term to account for increased transmission as a result of high mixing in schools [5]. Oscillations could also arise due to a new strain of the disease, causing a peak in the data [6], in systems where the total population changes [7], or due to changes in testing patterns.

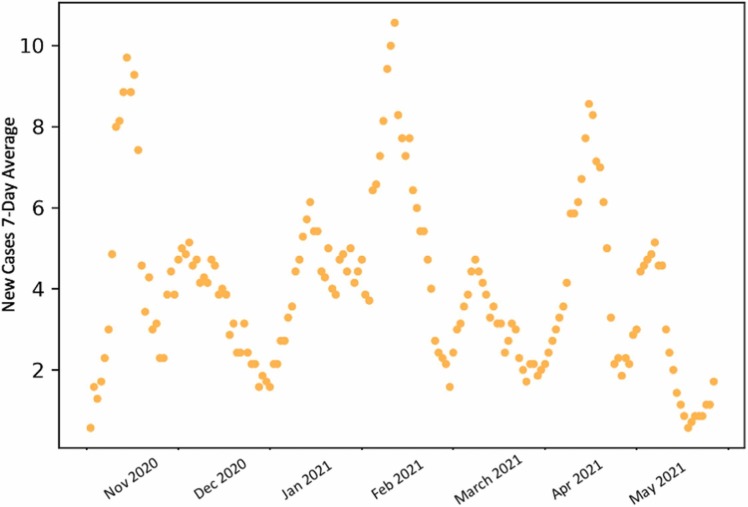
We present the COVID-19 data [8] from the 2020/2021 academic year at Tufts University (see Fig. 1), and we discuss the short-term oscillations that arise in the data for the infected. Then, we incorporate behavioral and social characteristics, specifically individual risk assessment, in a mathematical model. This results in dampened oscillations at a faster time scale. We then introduce a time-dependent impulse in our model, mimicking one-time large social gatherings, which results in sustained oscillations.

Fig. 1.

COVID-19 data for Tufts University during the academic 2020/2021 year.

Methods

Data analysis

We used data from Dr. Andrew Kennedy at Bates College, who collected data from several post-secondary institutions in the northeastern United States and posted the results daily to Twitter. These college campuses, during the 2020–2021 academic year, were testing all students twice per week and posting those results on their college’s COVID-19 reporting dashboard [9]. Employees were also tested, but they are not included in our data. Note that the data for the winter breaks are from a much smaller subset of the population that did not leave campus.

The highly residential colleges had rapid spiking and decline [9], presumably due to school holidays and subsequent rapid lockdowns. However, one of these institutions, Tufts University, experienced more regular oscillations. Notably, Tufts has a larger proportion of commuter students and has a large population size, reducing stochastic effects at small population sizes. The large peaks in the data for COVID-19 infected at Tufts are about 2 months apart; however, each peak is also followed by a smaller peak. So within a particular large period oscillation window, like Bukhari et al. [3], we observe dampened oscillations. In addition, Tufts University had regular weekly testing times, so these oscillations could not be due to differences in testing frequencies over the span of a week.

Epidemiological model

In order to understand the mechanisms behind high-frequency oscillatory behavior in COVID-19 data, we make the following simplifying assumptions to model disease dynamics and mimic the public health scenario at the small colleges from which we obtained data:

• •Vaccines have not been introduced.
• •Exposed individuals cannot transmit the disease until they would test positive as “Infected” and this process takes an average of 4 days.
• •Infected individuals can transmit the disease for 14 days, but the rate of transmission is low due to quarantine procedures.
• •Immunity after exposure is on average 90 days.
• •There is no change in population size, which implies there is no death due to COVID-19 or other circumstances. We use the published enrollment numbers to infer population size.
• •Populations are well mixed.

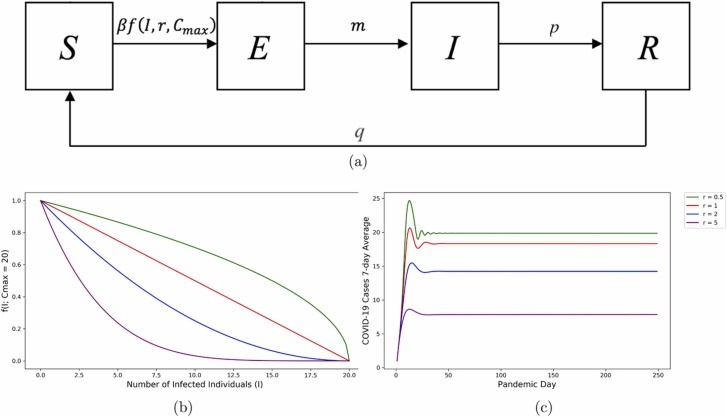
We use the Kermack and McKendrick SIR model [10], but with an exposed class (see Fig. 2). All susceptible individuals (S) move to the exposed class (E) when they have come into contact with an infected individual. COVID-19 takes time to build up enough viral load to transmit at which point, exposed individuals move to the infected (I) class, and can now transmit the disease. They will also test positive. Once they become healthy again, they move to the recovered (R) class. Recovered individuals move back to the susceptible class once their immunity wanes.

Fig. 2.

Panel (a): Compartmental Susceptible-Exposed-Infected-Removed (SEIR) model representing the movement between the classes for the COVID-19 spread. Panel (b): The risk assessment function with changes in the risk assessment parameter and keeping C_max = 20. Panel (c): Curve for infected, while changing the risk assessment parameter in the risk assessment function and keeping all the other parameters constant with C_max = 20.

The parameters m, p, q in Figure 2 represent the rates at which individuals move between the different compartments of the model and β is the probability of disease transmission per contact. Additionally, f(I; r, C _max) represents the risk assessment function that creates the oscillations in our model and we are going to discuss this in the Incorporating human behavior: Risk assessment subsection. The system of ordinary differential equations that represents the movement between the classes in the SEIR model in Figure 2(a) is:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{dt}}& \hfill =\hfill & -\beta f(I,r,C_{max})SI+qR,\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& \hfill =\hfill & \beta f(I,r,C_{max})SI-mE,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& \hfill =\hfill & mE-pI,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& \hfill =\hfill & pI-qR.\hfill \end{array}$$ (1)

This is a closed system (i.e., there are no birth or death rates incorporated in the model), as the right-hand side of the differential equations above sums up to zero.

Incorporating human behavior: Risk assessment

People change their behavior as the number of infected individuals in the community increases [11] and may begin practicing more preventative measures such as wearing masks and reducing close interactions. Likewise, as reports of infected cases drop, we expect individuals to engage again in higher-risk interactions. In the context of a small college campus, this may include interacting with more people, discontinuing any non-mandatory mask use, or partaking in unmasked gatherings around food and drinks. Before testing was widely available, the campuses we analyzed had privileged access to frequent and reliable information about their own infection status as well as census information about their communities’ overall status.

In order to model this response, we conceptualize that a person observing lower COVID-19 rates would reduce mitigation measures. For modeling purposes, this means that as infection rates decrease, the probability that an interaction between an infected and a susceptible will result in COVID-19 transmission increases. Because we do not know whether individuals respond slowly or quickly to daily infected case data, we define a function that is parameterized around one’s own “perception of risk,” r:

$$f(I;r,C_{max})=\left\{\begin{array}{cc}{\left(1-\frac{I}{C_{max}}\right)}^r\hfill & I<C_{max}\hfill \\ 0\hfill & I\ge C_{max},\hfill \end{array}\right)$$ (2)

where C _max is a parameter that indicates the number of cases that would prompt institutions to impose a total lockdown (when there is no movement between the susceptible and exposed class), and I is the number of infected individuals in the model. Defining C _max as a total lockdown parameter is possible because we work with data from a relatively small private institution, but this might not be possible for many larger organizations. Additionally, the risk assessment function f(I; r, C _max) is designed to take values between zero and one. Thus, it regulates the flow of individuals from the susceptible to the exposed class.

The parameter r represents the risk perception of the community. It can take any real positive value, as negative values of r would cause the risk assessment function to go out of its zero-to-one range. If we have a community with low-risk perception (r < 1, green in Fig. 2), then they do not change behaviors quickly as cases rise. In risk-averse communities (r > 1, blue and purple in Fig. 2)—even a small number of infected individuals leads to a fast reduction in the number of interactions and increased precautionary measures. In highly risk-averse populations (large r), even the smallest possibility of infection causes individuals to increase the practice of precautionary measures.

Linking behavior and disease introduction

We notice that the data for the infected class peaked during Halloween in almost all institutions. Family gatherings or holidays also may cause students to mix with off-campus individuals. Such events are also often unmasked and involve eating and drinking indoors, carrying a high risk of transmission. Thus, these events produce a one-time batch of new infections.

In order to represent this scenario with our model, we add a periodic impulse to the infected class. After holidays such as Halloween that induce social gatherings, we notice peaks in the data. We mimic this by modifying the parameters in the ordinary differential equation system in Equation (1) to have a temporarily heightened per capita transmission rate β, or a periodic impulse that creates the sustained oscillations in Figure 3(b). We also temporarily decrease m so that those infected with COVID do not artificially skip the exposed state because the infections have jumped. However, we maintain the recovery rate $p=\frac{1}{14}$ and immunity rate $q=\frac{1}{90}$ for 2 days. This process is repeated approximately every 60 days. Thus, we obtain periodic increases in the fit for infected. The code that generates all the figures and the impulse function is available at Ref. [9].

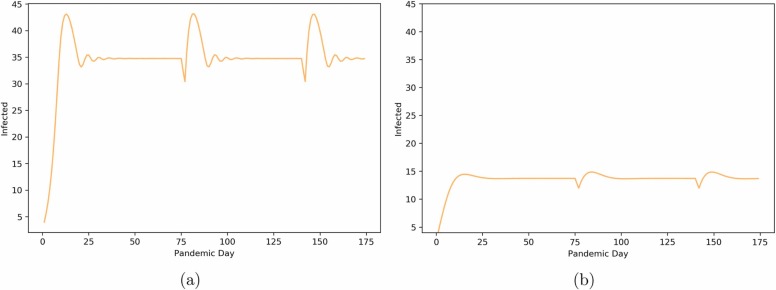
Fig. 3.

Oscillatory behavior we obtain from the SEIR model with introduced risk assessment and impulses and a C_max value of 35. Panel (a): Low risk perception (r = 0.5) Panel (b): High risk perception (r = 5).

This impulse can be repeated at any time the user wishes, but we chose to utilize a regular periodic impulse in this paper to illustrate that this model was capable of a stable periodic response from a mathematical perspective.

Results

The risk-assessment SEIR model produces well-defined dampened oscillations (Fig. 2), as observed by Bukhari et al. [3]. We also see that the level of community risk assessment affects the frequency and amplitude of the oscillations.

The more risk-averse a community is, the lower the disease level maintained in the system and the less it oscillates (both in frequency and amplitude). This behavioral characteristic helps the system maintain equilibrium below the C _max level that might trigger a lockdown. Thus, human behaviors can help mitigate the need for enacting a lockdown policy. The dependency of the oscillatory behavior is illustrated in Figure 3.

In communities that are less responsive to case change counts (see Fig. 3 a), we not only observe larger amplitude and frequency of oscillations but also a stabilized “viral load” above the institution’s own C _max policy level. This highlights the need for an overall lockdown policy in this circumstance, as some ecosystems may not be able to rely on self-regulation alone.

Additionally, changes in the C _max dictate the value at which the oscillations stabilize for low values of risk reception, r, as shown in Figure 3 a. However, in communities with high-risk perception, the number of infected individuals does not reach C _max so they stabilize at lower values (see Fig. 3 b).

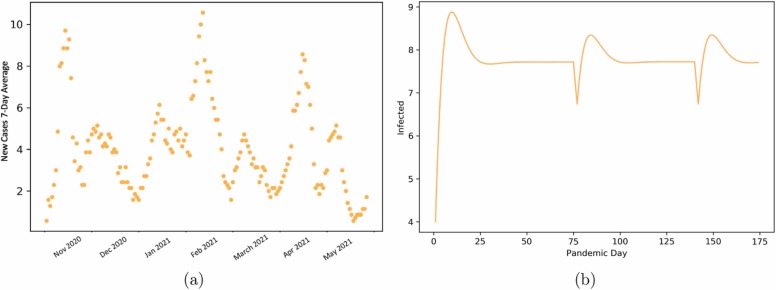
Thus, we can account for behaviors that can introduce new diseases into the system. Our model exhibits sustained oscillations of major peaks ( Fig. 4), similar to that observed at Tufts University for the 2020–2021 academic year.

Fig. 4.

Panel (a): COVID-19 data for Tufts University during the academic 2020/2021. Panel (b): Oscillatory behavior we obtain from the SEIR model with introduced risk assessment and impulses with a C_max value of 35 and risk assessment of r = 10.

Discussion

Oscillations in the infections for COVID-19 exist both over long periods of time and at faster time scales. As Bukhari et al. [3] discuss, models that produce oscillations as a result of incorporating behavioral characteristics in the system are important for the explanation of short-term periodicity in COVID-19 data.

The current methods used for introducing periodicity in disease models require either a change in the infectiousness of the disease over time or rapid changes in the number of susceptible individuals. However, these methods do not explain the short-period oscillations Bukhari et al. discuss, nor do they take into account human behavior as a factor.

Human behavior can play an important role in the spread of infectious diseases. Fenichel et al. [11] find that adaptive human behavior impacts the course of epidemics and that future research in disease modeling should acknowledge the effect that behavioral characteristics have on the development of infectious diseases. Individual decision-making driving a combination of community policy and self-regulation in response to COVID-19, modeled in Agusto et al. [12] has been found to generate oscillations.

We argue that one likely and explanatory reason for short-term oscillations in COVID-19 disease is due to the risk assessment behavior of susceptible individuals and social gatherings. Our model provides an epidemiological explanation for the observations of Bukhari et al. [3] and creates a structure that can be used in future research on short-term oscillations in disease models.

Unlike other studies that discuss oscillations in disease models [4], [5], [7], we manage to introduce dampened oscillations in a closed system with no stochasticity, without oscillatory forcing of the transmission rate. With periodic impulses due to social gatherings, the model predicts recurrent disease spiking. This is similar to patterns of COVID-19 data at a variety of small liberal arts colleges in New England. While our data exclude winter and summer break, in this study we do not use statistical techniques to fit data to our model, but rather model the overall patterns. Therefore, the effect of missing data on our findings is minimal.

The two parameters in the risk assessment function play an important part in the nature of the dampened oscillations that arise. As we increase the risk assessment parameter, r, the amplitude of the initial peak and the frequency of the subsequent oscillations decrease. Similarly, as lockdown ceiling C _max decreases, COVID disease stabilizes at lower rates. We define C _max as a parameter that would prompt the institution into a full lockdown because this was one of the main tools that institutions used to manage the COVID-19 pandemic at the time the data for this study was collected. Full lockdowns were implemented even in the spring of 2022 [13], 2 years after the pandemic started, and are a possibility in future epidemiological outbreaks as well.

One of the main implications of this study is highlighting the importance of human behavior and risk assessment in disease modeling for public health. Figure 3 a illustrates a hypothetical campus that depends on lockdowns to manage the disease. This is because individuals are not quick to adjust their contact behavior despite increasing disease levels—either because they lack the information to do so or for other reasons [7]. However, lockdowns are difficult to implement in many settings and are ideally only a last resort.

We find that one can manage disease oscillations when individuals in the community have information to monitor their risk and if their perception of risk is conservative. Figure 3 b relies on the same lockdown level, but individuals are responding more rapidly and conservatively to an impulse of disease, self-regulating disease levels to well below the lockdown threshold. Thus, understanding the behavior of the community is essential to institutional policy implementations.

Conclusion

This study reviews oscillations in disease modeling with an emphasis on COVID-19. Our tractable models build on prior work by introducing social behavior, such as social gathering and response to risk assessment. We show these models predict similar patterns to those at college campuses, which had extensive student testing data. We find that we are able to reproduce short-time scale oscillations discussed by Bukhari et al. [3]. We also find that communities with reliable disease dashboard information and which are risk-averse can self-regulate below emergency levels. However, communities that are less responsive to such dashboard information or may not have reliable information are primarily regulated through emergency quarantine policies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.