Abstract
Background
Functional Near-Infrared Spectroscopy is an optical brain monitoring technique which uses NIRS to perform functional neuroimaging. It uses near-infrared light for measuring brain activity and to estimate the cortical hemodynamic activity in the brain due to motor activity. Functional NIRS measures the changes in oxygen levels in oxygenated and deoxygenated hemoglobin by optical absorption. One of the main challenges in the analysis of fNIRS signals is the signal degradation due to the interference from noise and artifacts from multiple sources.
Methods
In this context, this research aims to analyze the connectivity between different regions of the brain using graph theory and hence the geometrical association of brain networks in terms of functional parameters. In this study, the impact of two noise removal processes (CBSI and TDDR), along with two types of correlation fNIRS such as Pearson's Correlation (PC), and Cross Correlation (CC) and various whole-brain network architectures on the reproducibility of graph measurements for individual participants has been carefully examined for different densities ranging from 5% to 50%.The graph measures' repeatability at the individual level was studied using the test-retest variability (TRT)
Results
The test-retest variability for global measurements in binary networks was substantially large at low densities, regardless of the noise removal method or the kind of correlation. Very low test –reset values are observed for weighted networks and great reproducibility for measures of the entire graph. When comparing the test-retest values for various methods, the kind of correlation, the absolute value of the correlation, and the weight calculation method on the raw correlation value all had significant major effects.
Conclusion
Based on a weighted network with the absolute cross correlation functioning as the weight, this study revealed that normalized global graph measurements were reliable. The node definition techniques that were utilized to remove noise were not essential for the normalized graph measures to be reproducible.
Keywords: Functional near-infrared spectroscopy (fNIRS), Pearson's correlation, Cross correlation, Neuroimaging, Graph theory
1. Introduction
Functional Near-Infrared Spectroscopy (fNIRS) analyses the variations in the intensity of near-infrared light measured between source and optodes placed on the scalp to determine the variations in the hemoglobin content in the cerebral cortex. This method was initially presented by Jobsis [1], which is now used predominantly in various neuroscience research analyses. fNIRS is used widely because of its promising attributes such as its cost effectiveness and practicality. Various researchers have used fNIRS to monitor the state of brain condition [[2], [3], [4], [5]]. However, there are certain challenges which affect the implementation of NIRS, such as the presence of motion artifacts. The fNIRS signals are highly sensitive to motion artifacts which appears due to the changes in the user's movement. The variations in the optical contact often result in the formation of artifacts in the fNIRS signal, and the amplitude of the artifacts has magnitude greater than the underlying hemodynamic variations. This increases the complexity of the analysis and makes it difficult to recover the original physiological NIRS signals from the motion artifacts [6].
fNIRS has a greater significance and superiority over other methods such as PET or fMRI in terms of portability, and hence is adopted in various sensitive neuroscience cases in infants or patients with neurological conditions. Especially, intrinsic cases such as Epilepsy is one such area which is highly menacing and fNIRS is an effective solution which can analyze epileptic seizures. A number of studies have implemented fNIRS for seizures in both adults and infants [[7], [8], [9], [10], [11]]. But, epileptic seizures often comprise excess and violent convulsions and motion artifacts increase the complexity to obtain relevant and accurate neurophysiological information about epileptic seizures. Hence it is essential to remove the motion artifacts prior to the analysis using an effective preprocessing technique. The preprocessing techniques must have an objective motion detection algorithm which can detect the changes such as heartbeat, various types of slow movement drifts such as baseline drifts, sudden frequency spikes like high-frequency spikes. Implementation of graph theory-based approaches to understand the functionality of the brain has provided a deeper analysis into the complicated investigation of different areas of the human brain [12].
This research aims to determine the effectiveness of graph theory in the analysis of resting state fNIRS data to ascertain the Functional Connectivity (FC) of the human brain [26]. The prime motivation behind this paper is to audit the new investigations using techniques that help to examine the availability designs in the human brain network utilizing fNIRS information. This research investigates the effectiveness of the proposed approach in its ability to acknowledge the cerebrum availability properties by diagram hypothesis (as estimated by fNIRS) and whether the proposed approach is capable of understanding the components basic human discernment in contrast with the conventional methodologies.
The main contributions of this study can be summarized in the below points:
-
●
This paper presents an analysis of fNIRS data based on graph theory to monitor the correlation of cognitive neural activity of the human brain.
●This paper analyses the functional connectivity of the brain using graph theory in order to determine the geometrical association of functional brain networks.
There has been a significant amount of research in the field of neuroscience and application of fNIRS for determining the correlation between different brain functions [[13], [14], [15]]. These research works mainly focused on the detection and removal of motion artifacts using different techniques. Recently graph theory-based approach for understanding the effectiveness of resting state fNIRS has gained a lot of significance [16]. This section discusses some of the prominent research works related to graph theory based fNIRS. The flexibility, efficacy and robustness of the construction techniques of brain networks with the help of various coupling and banalization techniques was discussed by Sun et al. [17]. For experimental analysis, 128 channel RS EEG related information were collected from sixteen Major Depressive Disorder (MDD) patients and normal controls. A spectral clustering-based resting network detection approach for analyzing fNIRS was proposed by Duan & Mai [18]. Their proposed clustering-based approach consisted of two steps wherein it initially determines the partition of the fNIRS analysis using the spectral clustering method which can determine the cluster number automatically. In the second stage, clustering is further performed on the individual-level partitioning results. The clusters which have high group consistency are considered as resting state network clusters. The performance of their proposed approach was validated using simulation results and fNIRS data. Their results show that the spectral clustering approach is effective for detecting fNIRS-RSN. The work proposed by Wang et al. [19] aimed to determine the minimum RS-fNIRS imaging duration for analyzing the accurate mapping of brain network connectivity in children and infants. 53 healthy children's RS-fNIRS imaging data set was used to determine the minimal imaging time necessary for obtaining a precise and stable functional connectivity as well as other performance metrics based on graph theory, such as nodal efficiency and network global and local efficiency of the brain network activity. Results of their experimental analysis show that the functional connectivity of the brain network was accurately obtained after 7 min of fNIRS imaging duration. However, the required scanning time for measuring the minimum time accurately was found to be 2.5 min at a lower network threshold. Their results provide a concrete proof for selecting the RS-fNIRS imaging time in children for studying the brain functional connectivity. The proposed work also validates the effectiveness of these techniques which can be used for applications developed for critically ill children and time-constrained infants. Table 1, enumerates the related research in this field specifically application of fNIRS brain connectivity.
Table 1.
Graph theory based functional connectivity research using fNIRS.
| Author | Journal | No of participants | Methods | Inference |
|---|---|---|---|---|
| Chong, J.S., Chan, Y.L., Ebenezer, E.G., Chen, H.Y., Kiguchi, M., Lu, C.K. and Tang, T.B [20] | Scientific reports, 10 (1), pp.1-12. (2020) | 39 (19 registered and 20 student) nurses | Differential Functional connectivity measures to detect dichotomy of stressed and emotional state of nursing student and registered nurses Heart Rate Variability and semi-metric analysis |
For nursing students, semi metric analysis percentage is higher in right pre-frontal cortex than left side. |
| Einalou, Z., Maghooli, K., Setarehdan, S.K. and Akin, A.21 | Neurophotonics4.4 041407. (2017) | 12 healthy participants | Wavelet based partial correlation and global efficiency graph theory method for analysis of fNIRS signal from Pre-Frontal Cortex. | Global efficiency metrics is used for metric measurement of graph theory Increase in cognitive load in right side has significant decrease in global efficiency values |
| Geng, S., Liu, X., Biswal, B.B. and Niu, H., 2017. k.22 | Frontiers in neuroscience, 11, p.392. (2017) | 18 participants | Independent Component Analysis for pre-processing. Intra class correlation coefficient network measure of the network properties of brain | Metric graph parameters are obtained by correlation based methods After 1 min of signal capture, nodal characteristics including nodal efficiency and betweenness were consistent, whereas efficiency parameters after 5 min. Results obtained only from healthy adults |
| Wang, J., Dong, Q. and Niu, H.[23] | Scientific reports, 7 (1), pp.1-10. (2017) | 53 healthy children | Images of resting state healthy children Quantified analysis of functional connectivity by Pearson correlation coefficients |
Accurate function connectivity metric can be obtained from short duration of resting state fNIRS data acquisition. Highly challenging for critically ill children and infants |
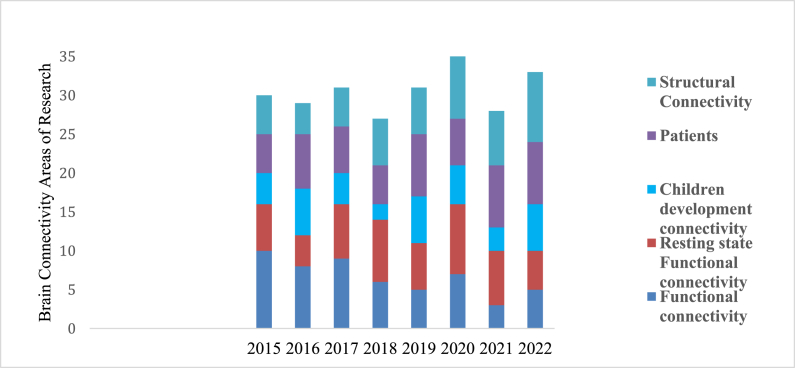
Despite the availability of different techniques like functional connectivity and structural connectivity in different regions of brain related with different task. Fig. 1, shows the statistics of the ongoing research in the field of fNIRS for the past seven years. Various research related to structural connectivity, functional connectivity, children development, resting state functional connectivity RS-fNIRS, patients with diseases like major depressive disorder (MDD) and Parkinson's diseases.
Fig. 1.
Recent Research work with specific application of brain connectivity using fNIRS.
In spite of these researches, still there is a great scope of research in this field. In this context, this research intends to contribute a comprehensive evaluation of the connectivity of brain based graph theory using fNIRS.
The organization of the paper is as follows: Section 2 presents the materials and methods related to data acquisition and preprocessing used. Section 3 provides a brief description of the results obtained. Section 4 presents the discussion related with consistency and repeatability of graph network measures in terms of binary and weighted networks along with simple and complex noise removal methods. Section 5 concludes the research with observations and future scope.
2. Materials and methods
2.1. Participants
The data was collected form Yücel et al. [20]. The dataset is of five healthy adults (1 female, 4 male) of age (23–52 years old (mean 35 ± 13). All adults were reported without any history of neurological disorder. While, have Yücel et al. [20] used this data for preprocessing analysis motion artifact study, we intend to analyze using graph theory.
2.2. Experiment
The participants participating in the experimental analysis are all right-handed and had a normal vision. All participants were healthy without any disorders related to neuromuscular, neurophysiological, visual, or cardiovascular abnormalities. All participants are scanned while their right hand is performing a tapping task. The tapping task is conducted with different durations with varying finger tapping or rest conditions. The samples of body movement are established using an approach discussed by Yücel et al. [20]. The data was acquired simultaneously while conducting the finger tapping or rest blocks and the samples of finger tapping are recorded. During this process, the participants were asked to perform different head and facial movements which were similar to the conventional movements observed during realistic and social communication.
2.3. Data acquisition
The optical changes of the hemodynamic signals for this study are acquired using a TechEn CW6 system which operates with LEDs emitting two different modulation wavelengths (690 and 830 nm). Temporal, parietal, occipital, frontal parts of cerebral cortex were covered using standard measurement system. The measuring cap consists of source detector optodes placed on the scalp with 15 sources with long separation of 18 detectors with a distance of 30 mm from sources and short separation of 8 mm from sources with sampling frequency of 50 Hz.The data was acquired from source detector pairs located on each side of the hemisphere similar to the placement of EEG electrodes. The subjects were asked to perform different task such as raising eyebrows, reading aloud, nodding head up and down, nodding head sideways, twisting head right, twisting head left and rapidly shaking head sideways. The entire time length of recording data was 6 min duration, each movement of task was performed for 3 s with 5 repetitive trials, and 5–10 s of random time interval between trials.
2.4. Data preprocessing
Data preprocessing is one of the important and initial steps to be carried out before performing the graph theoretical analysis. The fNIRS data is preprocessed to make the data suitable for further analysis. The process includes the conversion of raw light amplitude to optical density, by filtering the principal component and detecting and eliminating the motion artifacts. The impulsive spikes and uncertainties are modified by averaging the data segment adjacent to it.
A band-pass filter of frequency range 0.01–0.2 Hz is used to filter the raw intensity data and to eliminate the cardiac and respiratory waveforms and to remove the frequency fluctuation from the data. Once the intensity data is converted into optical density, the variations in oxy-Hb and deoxy-Hb concentrations are determined incorporating a modified Beer–Lambert equation. Preprocessing also includes other aspects of data processing such as filtering, motion correction, data sampling, de-trending with time point, noise regression, and customized processing techniques. Data shortening is required to make it appropriate for the experimental recording. A specific first or last time period recorded from the participants is deleted since it causes the shift in the physiological data and changes in the stability of the instrument. The linear and nonlinear changes in the signal are eliminated by subtracting the signal from the raw concentration signal.
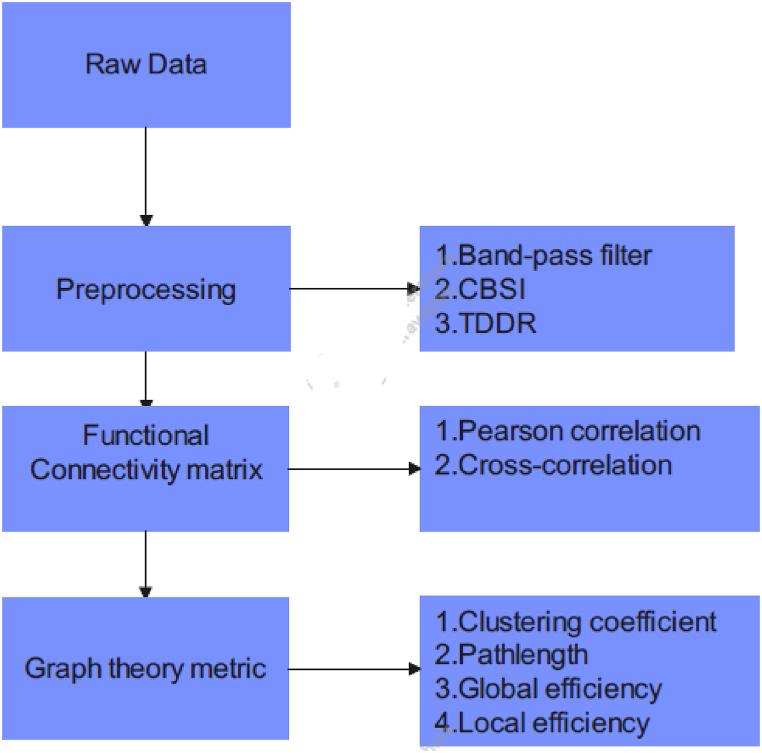
The general flow of processing is given as per the block diagram in Fig. 2.
Fig. 2.
Processing steps involved.
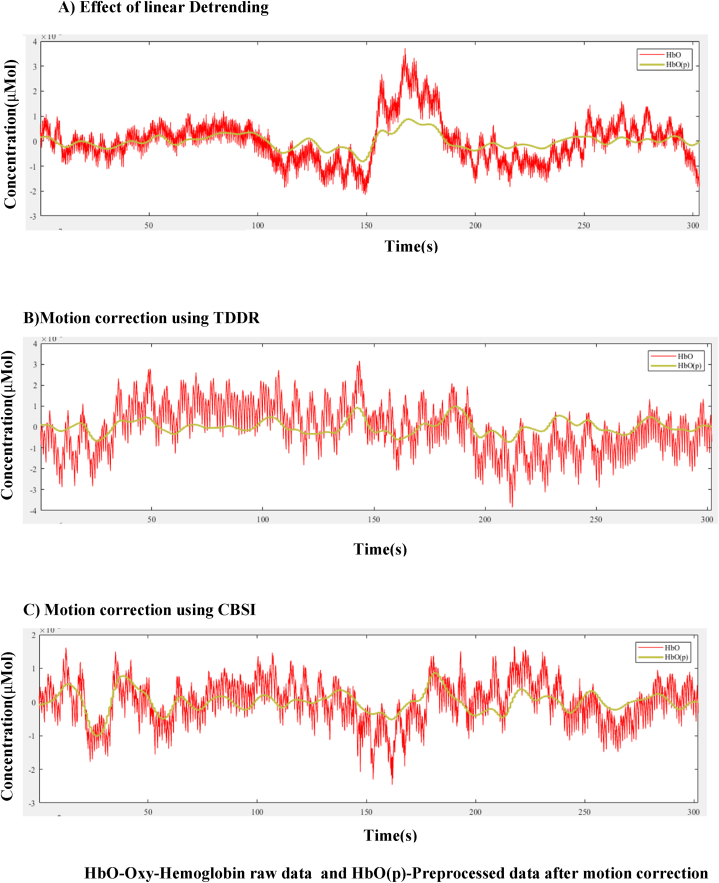
Motion correction is performed on data acquired on the source detector pair. The analysis includes the motion correction using Correlation Based Signal Improvement (CBSI). The CBSI process ensures that the oxy-Hb and deoxy-Hb signals are negatively correlated in resting state and become positively correlated due to the occurrence of motion artifacts in these signals [21]. Motion correction is also studied with another method known as Temporal Derivative Distribution Repair (TDDR). When the signal contains high frequency oscillation components, the distribution bias the estimates so the artifact that are closer to mean require less correction. The oscillations present in the high frequency increase the variance present in the temporal derivative. In this study, this method is taken as simple noise removal technique.TDDR method is based on the removal of baseline and spike shifts using a robust regression approach [22]. Fig. 3A shows the effect of linear detrending, CBSI and TDDR on raw data and preprocessed data are illustrated in Fig. 3B and C respectively. In Fig. 3, it can be noticed that preprocessed data has fine line representation compared to spiky signals of raw data (as depicted in the legends). The degradation in the signal is due to the interference of noise and instrumental disturbances. This TDDR is taken as complex noise removal method. To filter out the uncertainties, different filters such as Infinite impulse response (IIR) filter, finite impulse response (FIR) filter, and Fast Fourier transform-based ideal filter (FFT-based filter) are used. Band pass filtering is done using a Butterworth filter and finite impulse response filtering is done using a Hamming window since it is simple to control and has high stability compared to IIR filters. Here, the features of each channel is converted into frequency domain wherein.
Fig. 3.
Results of pre-processing methods of HbO (sub fig. A, B, C) using TDDR and CBSI.
HbO-Oxy-Hemoglobin raw data and HbO(p)-Preprocessed data after motion correction the signals of this domain are removed using a FFT filter. This is performed to remove different components such as heart rate (∼1.3 Hz), respiration (∼0.25 Hz), and the Mayer wave (∼0.09 Hz). The mean absolute error (ME) mean square error (MSE), SNR ratio and Peak SNR ratio measurements of IIR filter for different orders have been calculated and tabulated as in Table 2.
Table 2.
Performance parameters of filtered fNIRS signal using IIR filter.
| Parameters | IIR Filter 0 order | IIR Filter 1 order | IIR Filter 3 order |
|---|---|---|---|
| Mean absolute error (ME) | 0.007651 | 0.007853 | 0.07956 |
| Mean square error (MSE) | 0.009651 | 0.009853 | 0.09856 |
| Signal to noise ratio (dB) | 43.1805 | 44.5672 | 44.6782 |
| Peak Signal to noise ratio (dB) | 53.7834 | 54.8765 | 54.9821 |
From Table 2, IIR filter of order 3 shows significant performance with mean absolute error (ME) mean square error (MSE), SNR ratio and Peak SNR ratio measurements. In order to further smoothen the signal Hamming window is applied. The same parameters are calculated and tabulated in Table 3, after applying Hamming window.
Table 3.
Performance parameters of filtered fNIRS signal using Hamming window.
| Parameters | Hamming window order3 | Hamming window order 5 | Hamming window order10 |
|---|---|---|---|
| Mean absolute error | 0.4221 | 0.4231 | 0.4531 |
| Mean square error | 0.00354 | 0.00345 | 0.00364 |
| Signal to noise ratio (dB) | 40.0971 | 44.2367 | 47.8976 |
| Peak Signal to noise ratio (dB) | 54.8132 | 57.8926 | 59.3124 |
2.5. Graph theoretical analysis
In graphical networks, the edges and nodes are considered as the basic building blocks of a brain network. The functional connectivity between the nodes are represented by the edges and the nodes in the graphical network are considered as measurement channels. Definition of node determines the calculation of functional connectivity between nodes.
The functional connectivity is computed by evaluating the Pearson correlation (PC) coefficients for the time series between the nodes. Hence, for every individual, a correlation matrix (CM) of dimension N x N is obtained where N is the number of fNIRS channels. Further, an average value of all the individual correlation matrices are obtained and the matrices are converted from the mean CM into an adjacency matrix.
To get the average time series for each subject, the time series mean was calculated. The average time series allowed to establish whether any two subjects have a full or partial association. Any time series pair's cross correlations were determined using the other time series as controllers.The inversion of the covariance matrix served as the foundation for the calculation. In order to reduce the influence of other regions, cross correlations could be used as a more precise indicator of functional connectivity.
The main aim of the study is to use a weighted undirected network without self-connections and a binary network. The study of binary networks was conducted at various densities ranging from 5% to 50%. The issue of thresholding can be avoided by a weighted network, which also considers all weights ranging from 0 to 1, A fixed/preset correlation threshold denoted by ‘T’ is applied to ensure the edges with an absolute connectivity strength, greater than the threshold value, as illustrated in Equation (1):
| (1) |
In the proposed work, the threshold ‘T’ is determined in terms of sparsity and is determined as the ratio of the total actual edges to the maximum possible edges.T value is chosen to be 0.8 [24].
The graphical analysis of fNIRS coefficients for analyzing the cross - functional and cross relationships or functional connectivity (FC) is performed using Pearson correlation (PC) as in equation (2) and cross-correlation (CC) approaches as in equation (3). This research has investigated the significance of distinct network construction techniques on the stability of graph metrics and FC. The correlation matrix for each participant was determined individually using Pearson correlation and cross -correlation for a specific time period. The term PC was initially used to assess the degree of linear association between images acquired in time series.
| (2) |
where and denotes the average of M and N respectively.
| (3) |
where defines the delay between the mean time series of the i th and jth regions. The strength of the FC between two brain regions was determined by evaluating the maximum . Resting state functional connectivity matrix is shown for different head movements as in Fig. 4.
Fig. 4.
Resting state functional connectivity of different head movements task involved in fNIRS measurement.
In this work, the graph metrics measure the connectivity of each node. The clustering coefficients are used to measure the local neighborhood connectivity which is calculated as the likelihood of neighbors of the node. These neighbors are also the neighbors of the path length which measures the distance between nodes in the network, calculated using Equation (4) as given below,
| (4) |
Equation (4) defines the shortest geodesic distance between each node. Each node is associated with a global efficiency and measures the close association of the individual nodes with other nodes in the network. The local efficiency of the nodes determines the interconnection of the neighbors placed in the predefined network area.
Graphical network can be analyzed with respect to different network parameters such as nodal efficiency ), nodal betweenness, and network clustering coefficient, local and global efficiency of the network [22].
The term () is a metric that defines the communication capacity of the nodes and its ability to interact with other nodes in the network and is defined as shown in Equation (5).
| (5) |
where is the shortest path length between two nodes and , and N is the number of nodes. Another node metric known as nodal betweenness describes the node's global capacity in a brain network as shown in Equation (6).
| (6) |
where, ρhj defines the total shortest paths between two nodes h and j, and is the number of shortest paths between and that pass through . The term ( is defined [22] as a parameter which represent the capacity of the brain network to transform the information from one network to another globally. It is obtained by calculating the mean value of the nodal efficiency for all nodes27 as shown in Equation (7).
| (7) |
On the other hand, the term represents the node's ability to transfer the information locally i.e., within the network. It also defines the robustness of the network to withstand all types of network faults. Equation (8) defines the expression for calculating the local efficiency.
| (8) |
The average test-retest value was determined by combining the test-retest value between the two measures of the same subject across all subjects. The test-retest was determined as follows:
| (9) |
Higher variability and less reproducibility is indicated by higher value of TRT as given by equation (9).
3. Results
3.1. Impact of noise removal and correlation types
The performance of the proposed approach has been determined using different graph metrics such as path length, clustering coefficient, local efficiency, and global efficiency. Regardless of the noise removal method or the type of correlation, the TRT variability for global measurements was high at low density in binary networks. When evaluating different approaches TRT is significantly impacted by the type of correlation ( vs. ) (Table 4). There was no association between the noise removal pipelines and the type of correlation, nor did the noise removal pipelines have a serious impact TRT values.
Table 4.
Comparison Result for test-reset values of global graph measures of binary networks with df of value 1.324.
| Graph Measure | Density | Noise Removal methods |
Correlation methods |
||
|---|---|---|---|---|---|
| F | p | F | p | ||
| Path length | 5 | 0.0 | .995 | 0.0 | .980 |
| 10 | 0.0 | .989 | 0.2 | .974 | |
| 20 | 0.4 | .988 | 0.3 | .973 | |
| 30 | 0.2 | .990 | 0.2 | .980 | |
| 40 | 0.7 | .988 | 0.3 | .975 | |
| 50 | 0.9 | .988 | 0.3 | .982 | |
| Clustering coefficient | 5 | 0.0 | .932 | 1.3 | .270 |
| 10 | 0.2 | .833 | 2.3 | .302 | |
| 20 | 0.5 | .818 | 2.2 | .370 | |
| 30 | 1.3 | .802 | 3.5 | .083 | |
| 40 | 1.2 | .839 | 2.8 | .111 | |
| 50 | 1.7 | .838 | 0.7 | .344 | |
| Nodal Efficiency | 5 | 2.1 | .331 | 1.1 | .285 |
| 10 | 1.2 | .280 | 0.8 | .389 | |
| 20 | 3.6 | .087 | 1.5 | .290 | |
| 30 | 1.6 | .203 | 1.4 | .168 | |
| 40 | 0.7 | .456 | 1.2 | .269 | |
| 50 | 1.7 | .269 | 0.8 | .353 | |
| Betweenness Centrality | 5 | 0.8 | .330 | 2.4 | .111 |
| 10 | 1.3 | .288 | 2.3 | .203 | |
| 20 | 0.9 | .379 | 2.2 | .269 | |
| 30 | 1.2 | .239 | 5.4 | .053 | |
| 40 | 0.7 | .314 | 5.3 | .073 | |
| 50 | 0.6 | .073 | 4.5 | .468 | |
3.2. Weighted networks
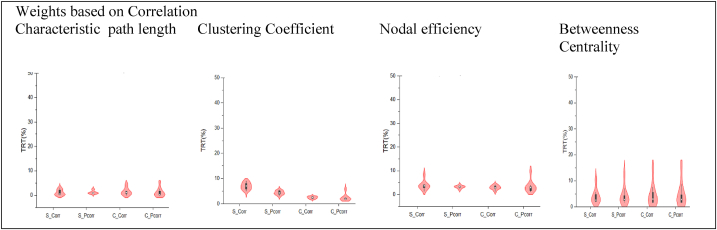
Weighted networks were calculated using simple (CBSI) complex (TDDR) noise removal technique for Pearson and cross correlation network. The following technique was employed for plotting S_Cor simple noise removal of cross correlation S_PCor for simple noise removal of Pearson correlation. C_Cor for complex noise removal of cross correlation and C_Pcorr for complex noise removal of Pearson correlation. Regardless of the chosen technique, weighted networks displayed extremely low TRT values for global graph metrics as in Fig. 5. There were significant main effects of the type of correlation when comparing the TRT values for various strategies. Low level of TRT values are obtained for path length and clustering coefficient but betweenness centrality has higher TRT values.
Fig. 5.
Comparison Result for test-reset values of global graph measures of weighted networks.
4. Discussion
In this study, careful analysis of network design and noise removal processes affects the reproducibility of graph metrics were studied. Additionally, the graph metrics of individual binary networks repeatability were insufficient, particularly when the network density was low. The repeatability of nodal graph measurements, in particular local betweenness centrality and nodal efficiency, were also analyzed.
4.1. Simple versus complex noise removal
By using a model with a simple (CBSI) or complex number of parameters (TDDR), basic and a sophisticated noise removal technique is used. The simple model has fundamental head movements. The parameters of the complex model were the same as those of the simple model, but they were also expanded with their temporal derivatives, their squared values, and their temporal derivatives squared values. In this analysis it is found that the graph measures of networks that had been preprocessed using either the simple or complex technique had extremely similar reproducibility and did not significantly differ from one another [25].
4.2. Binary and weighted networks
This analysis provided evidence that the weight choice has an impact on the TRT values of graph measurements. Until now there has not been a detailed examination of how to produce weights while using a weighted network analysis. Combining it with other network architectural elements its impact on TRT of graph measurements were studied. To conduct a valid statistical analysis when examining differences at the functional connectivity level, the number of data point used in the analysis is important. The derivation of graph metrics in this study was based on functional connectivity. Therefore, when weights are determined the quantity of data points is also a factor. Since binary networks are frequently studied at different densities, they can be built independently of the weight definition method. Additionally, since raw correlations, and weights all maintain the order of highest connections, they can all be used to select the highest connections. However, the binary networks at the subject level have poor repeatability, particularly at lower densities like 5%–10%. Although group-based binary networks are more repeatable in the current investigation, graph measures derived from single patients was examined because this is the recommended approach to employ in a clinical environment.
4.3. Limitations
This study has shortcomings. First, the study was examined using a dataset that was openly accessible and for which the diagnostic settings and the procedure were already established Because of this, we were unable to assess the impact of the sample rate (repetition time) or protocol modifications like keeping the eyes open (with or without a fixation point) or keeping them closed.
Second the impact of noise removal pipelines on functional connectivity has already been explored to investigate the reproducibility of graph measures, potent noise removal techniques based on a similar class was explored, Third, we examined graph metrics that took into account overall functional connectedness. Future research can examine the reproducibility of graph metrics for various brain states. Since networks are frequently studied at different densities, they can be built independently of the weight definition method.
5. Conclusion
The reliability of graph metrics of subject-level brain networks were thoroughly examined. The repeatability was unaffected by the noise removal techniques. Particularly when the network density was low, the graph metrics of individual binary networks did not reproduce well enough. The repeatability of nodal graph measures based on weighted or binary networks can be examined with absolute values of weights in future studies. This work can also be extended for studying early brain development in children and for clinical studies.
Production notes
Author contribution statement
V. Akila, Anita Christaline Johnvictor: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
No data was used for the research described in the article.
Declaration of interest’s statement
The authors declare no competing interests.
Contributor Information
V. Akila, Email: akilav@srmist.edu.in.
Anita Christaline Johnvictor, Email: anitaj@srmist.edu.in.
References
- 1.Jobsis F.F. Noninvasive, infrared monitoring of cerebral and myocardial oxygen sufficiency and circulatory parameters. Science. 1977;198(4323):1264–1267. doi: 10.1126/science.929199. [DOI] [PubMed] [Google Scholar]
- 2.Ayaz H., Onaral B., Izzetoglu K., Shewokis P.A., McKendrick R., Parasuraman R. Continuous monitoring of brain dynamics with functional near infrared spectroscopy as a tool for neuroergonomic research: empirical examples and a technological development. Front. Hum. Neurosci. 2013;7:871. doi: 10.3389/fnhum.2013.00871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Davies D.J., Su Z., Clancy M.T., Lucas S.J., Dehghani H., Logan A., Belli A. Near-infrared spectroscopy in the monitoring of adult traumatic brain injury: a review. J. Neurotrauma. 2015;32(13):933–941. doi: 10.1089/neu.2014.3748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gurel N.Z., Jung H., Hersek S., Inan O.T. Fusing near-infrared spectroscopy with wearable hemodynamic measurements improves classification of mental stress. IEEE Sensor. J. 2018;19(19):8522–8531. doi: 10.1109/jsen.2018.2872651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu Y.C., Yang Y.R., Tsai Y.A., Wang R.Y., Lu C.F. Brain activation and gait alteration during cognitive and motor dual task walking in stroke—a functional near-infrared spectroscopy study. IEEE Trans. Neural Syst. Rehabil. Eng. 2018;26(12):2416–2423. doi: 10.1109/TNSRE.2018.2878045. [DOI] [PubMed] [Google Scholar]
- 6.Cooper R.J., Caffini M., Dubb J., Fang Q., Custo A., Tsuzuki D., Boas D.A. Validating atlas-guided DOT: a comparison of diffuse optical tomography informed by atlas and subject-specific anatomies. Neuroimage. 2012;62(3):1999–2006. doi: 10.1016/j.neuroimage.2012.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Roche-Labarbe N., Wallois F., Ponchel E., Kongolo G., Grebe R. Coupled oxygenation oscillation measured by NIRS and intermittent cerebral activation on EEG in premature infants. Neuroimage. 2007;36(3):718–727. doi: 10.1016/j.neuroimage.2007.04.002. [DOI] [PubMed] [Google Scholar]
- 8.Singh H., Cooper R.J., Lee C.W., Dempsey L., Edwards A., Brigadoi S.…Austin T. Mapping cortical haemodynamics during neonatal seizures using diffuse optical tomography: a case study. Neuroimage: Clinica. 2014;5:256–265. doi: 10.1016/j.nicl.2014.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chiarelli A.M., Zappasodi F., Di Pompeo F., Merla A. Simultaneous functional near-infrared spectroscopy and electroencephalography for monitoring of human brain activity and oxygenation: a review. Neurophotonics. 2017;4(4) doi: 10.1117/1.NPh.4.4.041411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ulate-Campos A., Coughlin F., Gaínza-Lein M., Fernández I.S., Pearl P.L., Loddenkemper T. Automated seizure detection systems and their effectiveness for each type of seizure. Seizure. 2016;40:88–101. doi: 10.1016/j.seizure.2016.06.008. [DOI] [PubMed] [Google Scholar]
- 11.Peng K., Pouliot P., Lesage F., Nguyen D.K. Multichannel continuous electroencephalography-functional near-infrared spectroscopy recording of focal seizures and interictal epileptiform discharges in human epilepsy: a review. Neurophotonics. 2016;3(3) doi: 10.1117/1.NPh.3.3.031402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hendrikx D., Thewissen L., Smits A., Naulaers G., Allegaert K., Van Huffel S., Caicedo A. Complexity; 2018. Using Graph Theory to Assess the Interaction between Cerebral Function, Brain Hemodynamics, and Systemic Variables in Premature Infants. 2018. [Google Scholar]
- 13.Balconi M., Molteni E. Past and future of near-infrared spectroscopy in studies of emotion and social neuroscience. J. Cognit. Psychol. 2016;28(2):129–146. [Google Scholar]
- 14.Liu T., Pelowski M. A new research trend in social neuroscience: towards an interactive‐brain neuroscience. PsyCh J. 2014;3(3):177–188. doi: 10.1002/pchj.56. [DOI] [PubMed] [Google Scholar]
- 15.Khan M.J., Hong K.S., Naseer N., Bhutta M.R. 2015 54th Annual Conference of the Society Of Instrument And Control Engineers Of Japan (SICE) IEEE; 2015, July. Hybrid EEG-NIRS based BCI for quadcopter control; pp. 1177–1182. [Google Scholar]
- 16.Geng S., Liu X., Biswal B.B., Niu H. Effect of resting-state fNIRS scanning duration on functional brain connectivity and graph theory metrics of brain network. Front. Neurosci. 2017;11:392. doi: 10.3389/fnins.2017.00392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sun S., Li X., Zhu J., Wang Y., La R., Zhang X.…Hu B. Graph theory analysis of functional connectivity in major depression disorder with high-density resting state EEG data. IEEE Trans. Neural Syst. Rehabil. Eng. 2019;27(3):429–439. doi: 10.1109/TNSRE.2019.2894423. [DOI] [PubMed] [Google Scholar]
- 18.Duan L., Mai X. Spectral clustering-based resting-state network detection approach for functional near-infrared spectroscopy. Biomed. Opt Express. 2020;11(4):2191–2204. doi: 10.1364/BOE.387919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang J., Dong Q., Niu H. The minimum resting-state fNIRS imaging duration for accurate and stable mapping of brain connectivity network in children. Sci. Rep. 2017;7(1):1–10. doi: 10.1038/s41598-017-06340-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yücel M.A., Selb J., Boas D.A., Cash S.S., Cooper R.J. Reducing motion artifacts for long-term clinical NIRS monitoring using collodion-fixed prism-based optical fibers. Neuroimage. 2014;85:192–201. doi: 10.1016/j.neuroimage.2013.06.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cui X., Bray S., Reiss A.L. Functional near infrared spectroscopy (NIRS) signal improvement based on negative correlation between oxygenated and deoxygenated hemoglobin dynamics. Neuroimage. 2010;49(4):3039–3046. doi: 10.1016/j.neuroimage.2009.11.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fishburn F.A., Ludlum R.S., Vaidya C.J., Medvedev A.V. Temporal derivative distribution repair (TDDR): a motion correction method for fNIRS. Neuroimage. 2019;184:171–179. doi: 10.1016/j.neuroimage.2018.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Latora V., Marchiori M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001;87(19) doi: 10.1103/PhysRevLett.87.198701. [DOI] [PubMed] [Google Scholar]
- 24.Ghafoor U., Lee J.H., Hong K.S., Park S.S., Kim J., Yoo H.R. Effects of acupuncture therapy on MCI patients using functional near-infrared spectroscopy. Front. Aging Neurosci. 2019;11:237. doi: 10.3389/fnagi.2019.00237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Parkes L., Fulcher B., Yücel M., Fornito A. An evaluation of the efficacy, reliability, and sensitivity of motion correction strategies for resting-state functional MRI. Neuroimage. 2018;171:415–436. doi: 10.1016/j.neuroimage.2017.12.073. [DOI] [PubMed] [Google Scholar]
- 26.Akila V., Christaline J.A., Thinesh V.S., Hariharan V. Neuro cognitive activator. Mater. Today Proc. 2021 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.