Numerical investigation of shock-induced bubble collapse dynamics and fluid–solid interactions during shock-wave lithotripsy

Abstract

In this paper we investigate the bubble collapse dynamics under shock-induced loading near soft and rigid bio-materials, during shock wave lithotripsy. A novel numerical framework was developed, that employs a Diffuse Interface Method (DIM) accounting for the interaction across fluid–solid-gas interfaces. For the resolution of the extended variety of length scales, due to the dynamic and fine interfacial structures, an Adaptive Mesh Refinement (AMR) framework for unstructured grids was incorporated. This multi-material multi-scale approach aims to reduce the numerical diffusion and preserve sharp interfaces. The presented numerical framework is validated for cases of bubble dynamics, under high and low ambient pressure ratios, shock-induced collapses, and wave transmission problems across a fluid–solid interface, against theoretical and numerical results. Three different configurations of shock-induced collapse applications near a kidney stone and soft tissue have been simulated for different stand-off distances and bubble attachment configurations. The obtained results reveal the detailed collapse dynamics, jet formation, solid deformation, rebound, primary and secondary shock wave emissions, and secondary collapse that govern the near-solid collapse and penetration mechanisms. Significant correlations of the problem configuration to the overall collapse mechanisms were found, stemming from the contact angle/attachment of the bubble and from the properties of solid material. In general, bubbles with their center closer to the kidney stone surface produce more violent collapses. For the soft tissue, the bubble movement prior to the collapse is of great importance as new structures can emerge which can trap the liquid jet into induced crevices. Finally, the tissue penetration is examined for these cases and a novel tension-driven tissue injury mechanism is elucidated, emanating from the complex interaction of the bubble/tissue interaction during the secondary collapse phase of an entrapped bubble in an induced crevice with the liquid jet.

1. Introduction

The understanding of cavitation in biological systems as the synergy of interfacial and flow dynamic interactions that include thermodynamic and compressibility effects are of vital importance in a range of medical procedures [1], [2], [3], [4], [5]. Cavitation is a dynamic phenomenon that occurs when the static pressure drops below the vapor saturation pressure and results in the formation of bubbles. In biological flows cavitation can occur in the proximity of soft matter at instances of advancing ultrasound pulsations [6], shock waves [7], or during impacts [8] and sudden pressure changes. In principle, cavitation can either result in beneficial medical treatment, or can have adverse side effects. Extracorporeal Shock-Wave Lithotripsy (ESWL), employed for the treatment of kidney stone disease is among the most common medical procedures for which cavitation is prominent. Kidney stone disease is frequent with 12% lifetime risk for men and 6% for women [9]. For Kidney Stones (KS) larger than $5\text{mm}$ surgical removal is the optimal treatment [10], making ESWL the only non-invasive surgical practice available. Kidney stones are fragmented into smaller parts by focusing pressure shock waves [11] until they reach a passable size through the unitary track.

The exact mechanism of stone fracture is not yet fully understood [12], although two primary mechanisms have been identified. The shock impact on the stone produces distinct P and S waves that propagate within the stone, along with surface waves that are generated on the circumference interface of the stone. The superposition of these waves leads to higher stress development than the yield limit, producing thus internal crack formation [13], [14]. Additionally, the repeated shock impacts result in dynamic loading and fatigue, under the constant tension cycles. The second mechanism is cavitation erosion on the stone’s surface [15], [16], [17]. Although ESWL is effective, renal injury of some degree is common, and severe tissue damage can occur [18]. Tissue injury in ESWL can be attributed to two causes. The first one is due to the shear stresses produced by the compressible wave interaction with the tissue in the pre-focal region [19]. The second one is due to cavitating bubbles that either form after the passage of the tensile part of the lithotripter shock, or pre-exist as gas nuclei and can lead to blood vessel dilation and even rapture [20], [21]. Furthermore, it has been suggested that inertial cavitation inside blood vessels can be responsible for hemorrhage [22], [23]. In the work of Chen et al. [24] high-speed images show that bubble collapse can lead to vessel invagination, in ex vivo rat mesenteries. Experimental studies [25] have repeatedly shown the adverse effect of cavitation in ESWL, however, the exact mechanism of vessel rapture and tissue injury still remains unknown [24]. Thus, this paper aims to investigate cavitation-induced tissue injury and “further understanding of the precise mechanism of bubble action in SWL” [26].

Experimental and computational studies have shown that the collapse of a bubble is not spherical for non-symmetrical configurations such as in the proximity to a rigid surface, or a free boundary of a deformable solid or neighboring bubble [27]. Thus, simplified one-dimensional models, first developed to capture the non-linear oscillation of bubbles under constant or time-varying pressure, such as Rayleigh-Plesset type models can not be used. To capture those complex bubble dynamics, Plesset and Chapman [28] first employed a potential flow model and a Marker-and-Cell solver technique, to resolve the collapse of a gas bubble near a rigid wall. Similar strategies that employ potential flow solvers and Boundary Elements Methods (BEM) can be found in [29], [30]. The main advantage of the BEM method is that only the surface of the bubble is resolved. Following these initial studies, Godunov-type schemes enabled computational studies of the complete 3-dimensional flow structures, with complex compressible multi-material interaction and shock propagation. In order to address, however, the problem of the interface discontinuity two different approaches have been developed. The first approach considers these interfaces as sharp boundaries; thus an interface tracking method is required. Such methods introduce Lagrangian descriptions of the interface, where the computational mesh deforms, following the flow-field, Level-Set or Ghost Fluid Methods (GFM) [31], [32], Volume of Fluid (VOF) methods [33], and front tracking methods [34]. Even though most of these techniques can produce high-fidelity results with large deformations, their caveat is in the required complexity for the topological changes during the collapse [35], as well as in the explicit enforcement of the conservativeness of the discretization [36]. The second approach is the Diffuse Interface Model (DIM), where the different substances are represented in a unified Eulerian framework. The interfaces among the different materials arise from the distribution of the volume fraction for each material across the domain. This class of modeling approaches circumvents the difficulty of tracking interfaces, thus allowing for arbitrary interface geometries, large deformations, and the dynamic appearance or redundancy of new interfaces.

Numerical simulations of shock propagation dynamics, stress development, and cavitation phenomena in shock wave lithotripsy reported in the literature present a wide variety of modeling complexity. Numerical studies of ESWL configurations can be divided into two different categories. Starting with those focused solely on the wave propagation within the kidney stone and ignore cavitation effects, Cleveland et al. [37] showed that the peak loading within the kidney stone is the result of the constructive interference between the initial longitudinal waves and the shear waves generated by the traversal of the incident shock wave along the outer surface of the kidney stone. The experimental work of [15] shows that the tensile phase of the lithotripter pulse generates a bubble cloud around the surface of the stone. When the pressure is restored, the resulting collapsing cloud erodes the surface of the stone. Thus, accounting for the fluid–structure interaction between the kidney stone and the cavitating bubbles is imperative to elucidate this mechanism. The second category of studies focuses on shock-induced bubble collapses, utilizing pressure waveforms from experimental data. Johnsen and Colonius [38] first revealed that shock induce bubble collapse near a wall, can have a high potential for damage during ESWL. The main constraint of these studies is that the solid wall is modeled as an impermeable boundary with infinite acoustic impedance. Wang [39] simulated the shock-induced bubble collapse near kidney stones, highlighting the importance of the amplitude of the reflected shock wave from the solid wall. In this study, a two-way coupling between the Eulerian flow-field solution and the finite element model for the solid was incorporated. Cao et al. [40] elaborated on this approach, revealing the intricate effect of acoustic impedance on bubble dynamics, reporting differences up to 30% in shock wave emissions, liquid jet formation, and collapse time. Turangan et al. [41] presented simulations of erosion damage from shock-induced collapse close to stiff materials, using a free Lagrangian method. Freund et al. [42] investigated the jet impingement response of tissue during ESWL, by modeling tissue as a viscous fluid. Kobayashi et al. [43] using an improved GFM and the stiffened gas equation of state performed similar simulations, near various materials, such as kidney stones, and soft tissues. These materials were modeled as liquids, by matching the speed of sound and density to recover the correct acoustic impedance. Elasticity effects and shear stresses, however, were not accounted for. A similar approach was used by Coralic et al. [44] to simulate capillary rapture in a 3D domain.

The bubble dynamics close to rigid or soft surfaces can be affected by multiple factors. Lauer et al. [45] reported on the symmetry of the collapse mechanisms of detached and attached bubbles to rigid walls. Koukouvinis et al. [46] expanded on this mechanism by highlighting the influence of the angle of attachment between the near-wall liquid/vapor interface with the wall. For attachment angles greater than $90°$, the collapse is focused away from the wall, resulting in the “jetting and wall hammer” effect. In contrast, for angles smaller than $90°$, the collapse is driven by a local pressure increase in the circumference of the bubble leading to pin-type collapse. Kyriazis et al. [47] further report similar findings. Trummler et al. [48] showed the influence of stand-off distance on jet formation, rebound, and maximum wall pressures, as well as the importance of grid resolution on peak pressure estimation. Even though the above-mentioned studies utilized different numerical models and assumptions, they predict a similar collapse behavior, due to the common inertia-driven mechanism of the phenomenon. The collapse dynamics of attached bubbles to soft solids, however, still remain not fully understood.

In this paper, we aim to expand on previous studies by investigating the collapse dynamics in the vicinity of deformable solids by modeling them as elastic solids. For this, we have performed and presented a limited number of shock-induced bubble collapse simulations of detached and attached bubbles in the proximity of bio-materials for the first time. Specifically, three configurations were investigated. The first corresponds to a detached gas bubble with an initial stand-off distance of $S/R_0=1.2$ to the solid boundary collapsing under the effect of a lithotripter pulse, commonly used in numerical and experimental studies [49]. The second and third configurations correspond to bubbles attached to the solid surface with stand-off distances equal to $S/R_0=0.6$ and $S/R_0=-0.2$ respectively. The solid materials selected for this computational study are a uric acid type kidney stone and a soft tissue, with properties close to those of liver tissue. It should be noted that only one shock wave profile and bubble size were considered, thus limiting the generality of the conclusions. Our aim is to expand on the previous studies by revealing the complex fluid–solid interactions of these bubbles, i.e.: how they deform the surface of kidney stones and how they penetrate and damage soft tissues.

To this end, a new computational multi-material framework was developed, that enables fluid–structure interaction, shock capturing, and accurate bubble dynamics. The 6-equation pressure disequilibrium DIM model of Saurel et al. [50] was employed to simulate the shock-induced inertial collapse of bubbles. The specific implementation of DIM is derived from the 7-equation model of Baer and Nunziato [51] by assuming kinematic equilibrium. The mechanical equilibrium is imposed explicitly by a relaxation procedure. The model of Saurel et al. [50] was extended to account for Fluid–Structure Interaction (FSI) [52]. The mechanical properties of the solid continuum are integrated by incorporating 9 additional equations for the deformation Jacobian matrix. The deformation matrix is used for the evaluation of the full three-dimensional stress tensor for the solid. The Equation of State (EoS) for the solid and liquid materials is also extended with the addition of the elastic energy. This model poses the unique advantage of an Eulerian description, within a single hyperbolic system of equations governing both pure phases and mixture zones. Additionally, it is able to capture bubble dynamics, shock wave propagation, gas-fluid–solid interaction, extreme deformations, and dynamic creation and redundancy of interfaces.

To address the numerical diffusion of the material interfaces as described by the DIM volume fraction, high-order interpolations and mesh refinement at the interfaces are employed. To this end, the Forest of oct-trees AMR technique for unstructured hybrid meshes Papoutsakis et al. [53] was used. This approach offers an on-the-fly refinement of the grid to self-similar cells to an arbitrary level. The connectivity of the elements, their genealogy, and their partitioning have been described by linked lists of pointers. These pointers are attached to the tree data structure. This facilitates the on-the-fly splitting, merging, and repartitioning of the computational mesh by rearranging the links of each node of the tree. AMR aims to address the variety of different spatial scales observed in compressible, dispersed, multiphase flows reflecting the more general problem of the interaction between the micro- and the macro-scales in fluid mechanics by focusing the discretization resolution on the proximity of the fine structures. The ability to handle wide ranges of levels of adaptation and rearrange the grid to the new conditions makes it ideal for tracking moving flow structures and perform grid refinement to very high local resolution. The ForestFV AMR implementation aims to resolve the detailed structure of the interface of the bubbles and to resolve the shocks and refraction waves emitted during the bubble collapse. It is expected that the fine spatial resolution will minimize the discrepancies stemming from the resolution of the interface discontinuity, providing an interface-capturing approach. Second-order accurate DIM approaches that satisfy the conservation of the total energy among the pure phases and across the artificial mixture zones [50] have been used in cavitation modeling [36].

This paper is structured as follows. In Section 2 the governing equations of the physical model are presented. In Section 3 the numerical implementation of the DIM is described. In Section 4, three test cases are presented and validated, against other numerical models. In Section 5 the problem description and the numerical setup for specific shock-induced bubble collapse cases are presented, followed by the main findings for detached and attached bubble collapses in the proximity of a soft tissue and a kidney stone. Specifically, the bubble’s dynamics, the solid response to the liquid jet, the stresses developed, and the shock wave emission are investigated. In addition, the appearance of a novel secondary collapse mechanism that results in tissue penetration and injury is reported. Finally, in Section 6 the findings of this paper are summarized.

2. Governing equations

The principal flow features during the inertial collapse of a gas bubble in SWL include the shock-wave interaction between the incident and reflected shock waves on the interfaces of the bubble and the solid surfaces, the large deformation of solids as a result of the collapse of the bubble, and the induced compressibility effects. Therefore, in the specific inertia-driven configuration, surface tension, mass transfer, phase change between phases, and viscous forces are neglected [54]. The 6-equation DIM model [50] and its extension for isotropic elastic solids [52] is adopted. It should be noted that strain-stiffening or visco-elastic effects are not considered. The specific model has been validated for bubble dynamics and has been used to capture the fluid–structure interaction and the extreme deformations for soft and rigid solids. The governing equations are:

$$\begin{array}{cc}\frac{\partial \left({\alpha }_i{\rho }_i\right)}{\partial t}+\nabla \left({\alpha }_i{\rho }_i\overrightarrow{\mathit{u}}\right)\hfill & =0,i=1,\dots ,N\hfill \\ \frac{\partial \left(\rho \overrightarrow{\mathit{u}}\right)}{\partial t}+\nabla \left(\rho \overrightarrow{\mathit{u}}\otimes \overrightarrow{\mathit{u}}-\mathit{S}\right)\hfill & =0\hfill \\ \frac{\partial {\alpha }_i}{\partial t}+\overrightarrow{\mathit{u}}\nabla {\alpha }_i\hfill & =\mu (p_k-p_I),i=1,\dots ,N-1\hfill \\ \frac{\partial \left({\alpha }_i{\rho }_i{e}_i\right)}{\partial t}+\nabla \left({\alpha }_i{\rho }_i{e}_i\overrightarrow{\mathit{u}}\right)+{\alpha }_i\mathit{tr}\left({\sigma }_i\frac{\partial \overrightarrow{\mathit{u}}}{\partial \overrightarrow{\mathit{x}}}\right)\hfill & =-p_I\mu (p_K-p_I),i=1,\dots ,N\hfill \end{array}$$ (1)

$$\frac{\partial e^{\beta }}{\partial t}+\frac{\partial e^{\beta }}{\partial \overrightarrow{\mathit{x}}}\overrightarrow{\mathit{u}}+{\left(\frac{\partial \overrightarrow{\mathit{u}}}{\partial \overrightarrow{\mathit{x}}}\right)}^T{e}^{\beta }=0$$

where the scalar fields ${\alpha }_i,{\rho }_i,p_i,e_i,{\sigma }_i$ correspond to the volume fraction, the density, the pressure, the internal energy, and the stress tensor for each material $i,\rho$ is the mixture density, $\mathbf{u}$ is the velocity vector, $\mathbf{S}$ is the stress tensor, $\delta p$ is the pressure difference between the phases, ${\mathit{e}}^{\mathit{\beta }}$ are the columns of $F^{-T}$ (i.e. the local cobasis) with F being the Jacobian of the deformation defined as $F=\partial x/\partial X$ with x being the Eulerian coordinates and X the Lagrangian, while $p_I$ is the interfacial pressure defined as:

$$p_I=\frac{\sum \frac{p_k}{Z_k}}{\sum \frac{1}{Z_k}},$$ (2)

where $Z_i$ is the acoustic impedance of the material i. The total density and the saturation constrain are defined as:

$$\rho ={\displaystyle \sum _k^N}{\left(\rho \alpha \right)}_k,{\displaystyle \sum _k^N}{\alpha }_k=1\text{.}$$ (3)

Given the non-conservative formulation of the specific energy equations in Eq. (1), an additional equation for the total mixture energy is introduced, to ensure the numerical conservation of the total energy, in the presence of shocks [50]. The total mixture energy conservation equation is defined as:

$$\frac{\partial \left(\rho E\right)}{\partial t}+\nabla \left[(\rho E+\mathit{S})\overrightarrow{\mathit{u}}\right]=0\text{.}$$ (4)

The closure of the system of Eqs. 1, is achieved by the relation between the pressure density and the internal energy as dictated by the material EoS, as:

$$e_i=e_i({\rho }_i,p)\text{.}$$ (5)

For liquid substances, the stiffened gas equation of state is used:

$$p_i=({\gamma }_i-1){\rho }_i{e}_i-{\gamma }_i{\pi }_{\infty i},$$ (6)

where, $\gamma$ and ${\pi }_{\infty }$ are parameters of the EOS. For solids, the stiffened gas EoS is extended to account for the elastic energy as:

$$e_i=e_i^h({\rho }_i,p)+e_i^e(\rho ,\stackrel{\sim }{G})$$ (7)

In Eq. 7, $e_i^h$ is the hydrodynamic component which depends solely on density and pressure, while the second part corresponds to the elastic component dependent on the tensor $\stackrel{\sim }{G}$. The tensor $\stackrel{\sim }{G}$ is defined as:

$$\stackrel{\sim }{G}=\frac{G}{|G{|}^{1/3}},$$ (8)

where G is the finger tensor, i.e. the inverse of the left Cauchy-Green tensor $B={\mathit{FF}}^T$, thus, $G=F^{-T}{F}^{-1}$. The components of $F^{-T}$ are the vectors ${\mathit{e}}^{\mathit{\beta }}$. The elastic component ${\epsilon }_{\mathrm{s}}^e$ of the specific energy for a solid as described in the Eq. (7) is:

$${\epsilon }_{\mathrm{s}}^e=\frac{{\mu }_s}{4{\rho }_{s0}}\mathrm{tr}\left({(\stackrel{\sim }{G}-I)}^2\right)\text{.}$$ (9)

Finally, the stress tensor for solids is:

$${\sigma }_s=-2\rho \frac{\partial e}{\partial \stackrel{\sim }{G}}\stackrel{\sim }{G}=-p_{s}I-{\mu }_s\frac{{\rho }_s}{{\rho }_{s0}}\left(\frac{1}{|G{|}^{2/3}}\left(G^2-\frac{J_2}{3}I\right)-\frac{1}{|G{|}^{1/3}}\left(G-\frac{J_1}{3}I\right)\right),$$ (10)

where $\mu$ is the shear modulus, ${\rho }_s$ is the density of the solid phase, ${\rho }_{s0}$ is the initial density of the material, $p_s$ is the hydrodynamic pressure and $J_i=\mathit{tr}\left(G^i\right)$.

3. Numerical method

The system of Eqs. (1) can be written as:

$$\frac{\partial {\mathrm{U}}_{\mathrm{i}}}{\partial \mathrm{t}}+\frac{\partial {\mathrm{F}}_{\mathrm{ij}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+H_{\mathit{ikl}}\frac{\partial {\mathrm{u}}_{\mathrm{l}}}{\partial {\mathrm{x}}_{\mathrm{k}}}=\mu S_i,i=1,\dots ,3·N_{\mathit{mat}}+12,$$ (11)

where $U_i$ are the components of the state vector $\mathbf{U},F_{\mathit{ij}}$ is the flux vector, $H_{\mathit{ikl}}$ is the non-conservative source term, $S_i$ corresponds to the source terms and the $u_k$ are components of the velocity vector $\overrightarrow{u}$ at the direction k (A). The total number of equations is equal to $3·N_{\mathit{mat}}+12$, where $N_{\mathit{mat}}$ is the number of the different materials. The presence of non-conservative and relaxation terms perplexes the integration of the set of governing equations. The integration of the governing equations is achieved by an explicit density-based implementation of the Finite Volume methodology [55], [52] for hybrid unstructured grids incorporating hexahedral prismatic and tetrahedral elements (ForestFV). The specific implementation developed utilizes a graph representation of the computational domain as a dynamically evolving forest of oct-trees [53], [56].

The integration of the governing equations is achieved by employing the splitting procedure described in [52] in the following consecutive steps:

• 1.A hyperbolic step, i.e. solving (1) without the source terms.
• 2.A pressure relaxation step to restore the mechanical equilibrium and re-initialize the internal energies of each phase.
• 3.A Ghost Fluid Method (GFM) for the correct treatment of solid–fluid/gas interfaces.

3.1. Hyperbolic step

The system of Eqs. (1) in the absence of source terms can be expressed in a homogeneous formulation as:

$$\frac{\partial {\mathrm{U}}_{\mathrm{i}}}{\partial \mathrm{t}}+\frac{\partial {\mathrm{F}}_{\mathrm{ij}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+H_{\mathit{ikl}}\frac{\partial {\mathrm{u}}_{\mathrm{l}}}{\partial {\mathrm{x}}_{\mathrm{k}}}=0,i=1,\dots ,3·N_{\mathit{mat}}+12,$$ (12)

In the current implementation, the system of Eqs. (11) is discretized following an explicit finite-volume Godunov method for a general 3-dimensional non-Cartesian computational mesh as:

$${\mathbf{U}}_i^{n+1}={\mathbf{U}}_i^n-\frac{\mathrm{\Delta }t}{V_i}\left({\displaystyle \sum _{f=1}^N}{A}_f{\mathbf{F}}_f^{☆}·{\mathbf{n}}_f+{\displaystyle \sum _{f=1}^N}{A}_f\left({\displaystyle \sum _{k=1}^3}{n}_k{\displaystyle \sum _{l=1}^3}{H}_{\mathit{ikl}}{u}_l^{☆}\right)\right),$$ (13)

where $V_i,A,n_f$ are the volume of the cell, area, and the normal vector of a face respectively. ${\mathbf{F}}_f^{\ast }$ is the flux tensor computed at the interfaces with the HLLC approximate Riemann solver [55], and ${\mathbf{u}}_f^{\ast }$ is the flow velocity vector.

3.2. Pressure relaxation step

At the end of the hyperbolic step, the first stage of the splitting procedure for the numerical solution of the model (1) is complete. The obtained solution corresponds to a mechanical disequilibrium state in which the relaxation term is neglected: $\mu \to 0$. At this stage, the $N_{\mathit{mat}}$ discrete materials are under different pressures. A stiff relaxation step with $\mu \to \infty$ is necessary to restore the mechanical equilibrium by re-arranging the volume fractions of the components. This step entails the solution of:

$$\frac{\partial {\mathrm{U}}_{\mathrm{i}}}{\partial \mathrm{t}}=\mu S_i,i=1,\dots ,3·N_{\mathit{mat}}+12,$$ (14)

where $\mu S_i$ is composed of the right hand-side terms of (1).

By combining the equations of the specific energies, the mass conservation, and the saturation constrain, the following relation is obtained, [57]:

$$\frac{\partial e_k}{\partial t}+p_k\frac{\partial v_k}{\partial t}=0,$$ (15)

where $v_k=1/{\rho }_k$ is the specific volume. Integration over time, yields:

$$e_k^f-e_k^i-p_k\left({\tau }_k^f-{\tau }_k^i\right)=0,$$ (16)

where f denotes the final relaxed state and i is the initial disequilibrium state after the hyperbolic step. Substituting the internal energy using the stiffened gas EoS, and using the saturation constrain (3), an implicit relation of the pressures $p^f$ and $p^i$ with the volume fractions $a_k^i$ is derived:

$${\displaystyle \sum _{k=1}^N}\frac{{\alpha }_k^i}{{\gamma }_k}\left(\frac{p_k^i+{\pi }_{\infty ,k}}{p_{\mathit{rel}}+{\pi }_{\infty ,k}}\right)={\displaystyle \sum _{k=1}^N}\frac{{\alpha }_k^i}{{\gamma }_k}\text{.}$$ (17)

Eq. (17) is solved with an implementation of the Newton–Raphson method. The resulting relaxed pressure $p_{\mathit{rel}}$, and the new volume fractions that correspond to the relaxed pressure field can now be updated. It is noted that the relaxed pressure will not, in general, satisfy the total energy of the mixture or the equation of the state of the mixture. For this reason, a correction is needed using the total mixture energy E which is intrinsically conservative. Given the relaxed volume fractions, the mixture equilibrium pressure will be determined by the mixture EoS as:

$$p_{\mathit{eq}}=\frac{\rho {\epsilon }^h-\left({\displaystyle \sum _i^{N_{\mathit{mat}}}}\frac{{\alpha }_i{\gamma }_i{p}_{\mathit{xi}}}{{\gamma }_i-1}\right)}{{\displaystyle \sum _i^{N_{\mathit{mat}}}}\frac{{\alpha }_i}{{\gamma }_i-1}},$$ (18)

where ${\epsilon }^h$ is the hydrodynamic part of the mixture energy given by:

$${\epsilon }^h=E-\frac{1}{2}(u^2+v^2+w^2)-e_{\mathit{elastic}},$$ (19)

with the elastic energy defined as:

$$e_{\mathit{elastic}}={\displaystyle \sum _i^{N_{\mathit{solid}}}}{Y_s}_i{e}_i^e\text{.}$$ (20)

Finally, the mixture equilibrium pressure and the internal energies of the N materials can be re-initialized following the equation of state, as:

$$\begin{array}{ccc}{e}_k^h\hfill & =e_k^h\left(p_{\mathit{eq}},\frac{{\left(\alpha \rho \right)}_k}{{\alpha }_k}\right),k=s,g{e}_s^e\hfill & =e_s^e\left(A_{\mathit{ij}}\right),k=s\text{.}\hfill \end{array}$$ (21)

3.3. Ghost fluid method

The DIM framework introduces certain complexities at the material interfaces of solids with gases or fluids. The first one is that the tangential stresses ${\sigma }_{12},{\sigma }_{13}$ will not be zero in the gas/fluid region of the interface due to the presence of a small volume fraction of solid. For this, a correction to the Riemann problem solution is introduced to prohibit the tangential stresses influencing the solution across a solid/fluid interface. This correction guarantees that ${\sigma }_{13}^{\ast }={\sigma }_{12}^{\ast }=0,\mathrm{if}{\varphi }_L{\varphi }_R<0$, where $\varphi$ is defined as ${\varphi }_i={\alpha }_i-0.5$. The sign of $\varphi$ indicates the presence of a dominant solid phase and the product of $\varphi$ of two neighboring cells indicates the type of the interface. A negative product reveals a solid–gas or fluid interface whereas a positive all the others types of interfaces. A second technicality lies in solid interfaces with a fluid or gas, where the numerical diffusion of the transverse velocities creates nonphysical stress waves in the solid. Thus, a GFM approach [58], [52], [59] is employed. If an interface is found across the face of two neighboring cells, then two numerical fluxes, $F_{i+1/2,L}^{\ast }$ and $F_{i+1/2,R}^{\ast }$, will be computed for the current face, by modifying the primitive variables of the corresponding cells, using the neighboring tangential velocities:

$$F_{i+1/2,L}^{\ast }=F(V_{i,L}^n,V_{i+1}^n),F_{i+1/2,R}^{\ast }=F(V_i^n,V_{i+1,R}^n),$$ (22)

where $V_{i,L}^n$ has the tangential velocity of $V_{i+1}^n$, and $V_{i+1,R}^n$ has the tangential velocity of $V_i^n,i$ corresponds to the current cell under consideration and $i+1$ to the neighboring cell. For this, the interface needs to be captured and its movement needs to be predicted. Thus, the calculation of a temporary solution for the current cell is required, using Eq. (13), modified with the correct fluxes from Eq. (22). For advected interfaces, the transverse speed of the upwind cell is considered.

$${\overrightarrow{v}}_i^{n+1}=\left\{\begin{array}{ccc}\hfill {\overrightarrow{v}}_i^{n+1},\hfill & \hfill \mathrm{if}\hfill & \hfill {\varphi }_i^n{\varphi }_i^{n+1}<0\hfill \\ \hfill {\overrightarrow{v}}_{i+1}^{n+1},\hfill & \hfill \mathrm{if}\hfill & \hfill {\varphi }_i^n{\varphi }_i^{n+1}>0\hfill \end{array}\right)$$ (23)

where $\overrightarrow{v}$ is the vector of the transverse velocity. For multidimensional cases, the interface may not lie on a single face, rather it is defined as a plane for each cell. For that, a local 3D reconstruction of the interface is required. The flow velocities can be projected onto the reconstructed plane’s normal and tangential vectors.

3.4. Second order extension

In order to preserve the flow structures and the interfaces, a higher-order extension to the first-order Godunov scheme is needed. To this end, a second-order MUSCL-type scheme is used, formulated for unstructured grids [60]. For the spatial reconstruction, the gradient is computed using the least squares method, and the minmod limiter is used to suppress spurious oscillations. The two-step integration scheme is summarized as:

$$\begin{array}{cc}{U}_i^{n+\frac{1}{2}}\hfill & =U_i^n+\frac{\mathrm{\Delta }t}{2}\mathrm{RHS}\left({\mathrm{V}}_{\mathrm{i}}^{\mathrm{rec}}\right)\hfill \\ {\mathrm{U}}_{\mathrm{i}}^{\mathrm{n}+1}\hfill & ={\mathrm{U}}_{\mathrm{i}}^{\mathrm{n}}+\mathrm{\Delta }\mathrm{t}\mathrm{RHS}\left({\mathrm{V}}_{\mathrm{i}}^{\mathrm{n}+\frac{1}{2}}\right)\hfill \end{array},$$ (24)

where $\mathrm{RHS}$ is the right-hand side of the Eqs. (13), evaluated using the primitive reconstructed variables on the faces of the cells $V_i^{\mathit{rec}}$. $V_i^{n+1/2}$ is the primitive reconstruction of the half-time evolution of the state vector $U_i^{n+\frac{1}{2}}$. The reconstruction with the conservative variables was found to lead to spurious oscillations in the solution. Similar findings have been reported in [36], [60]. Thus, it is deemed necessary that the primitive variables are used for the spatial reconstruction.

3.5. Adaptive mesh refinement

Bubble collapse and multi-material interaction are the results of a closely-bound synergy of phenomena occurring at different scales across fine interfacial structures. These structures present a dynamically changing spatial distribution, are not known apriori and require a localized fine resolution of the flow field.

For the Finite Volume implementation presented in this paper the Forest of oct-trees AMR framework has been used [53]. This approach is based on a topological representation of the computational mesh by a hierarchical structure consisting of oct- quad- and binary trees. The ancestral elements of the mesh are split into self-similar elements allowing each tree to grow branches to an arbitrary level of refinement. The developed h-refinement method enables us to increase the spatial resolution for the computational mesh in the vicinity of the points of interest such as interfaces, geometrical features, or flow discontinuities. The connectivity of the elements, their genealogy, and their partitioning have been described by linked lists of pointers. These pointers are attached to the tree data structure. This facilitates the on-the-fly splitting, merging, and repartitioning of the computational mesh by rearranging the links of each node of the tree.

In the current FV implementation presented here (ForestFV), the partitioning of the connectivity graph has been upgraded thus, allowing the sending and receiving of individual trees of the forest and their topological characteristics across processors in addition to the field variables. This ensures a balanced computational load and memory allocation across processors. Changes in the forest topology are expressed by re-stitching pointers and relations, rather than moving and rearranging data structures.

This on-the-fly AMR implementation allows for the continuous refinement and coarsening of the grid. As such, it presents shock-capturing characteristics and enhances the resolution of the interface discontinuities. It has proven to be a powerful tool for modeling the complex mechanism of bubble growth [56], tracking the volatile topology of the bubble interface during bubble collapse, and capturing the progression of pressure wave fronts.

Splitting or merging cells is decided based on the basis of desirable mesh resolution needed to capture the flow characteristics. Those can be shock waves, interface tracking for low numerical diffusion, high velocities, or density gradients. Refinement based on geometrical characteristics of the flow field initialization is also incorporated.

For each cell the presence of significant gradients [36] serves as an indicator for refinement and is based on the following expression:

$$\frac{\left|U_{\mathit{Neig}}^i-U_{\mathit{current}}^i\right|}{\min \left(U_{\mathit{Neig}}^i,U_{\mathit{current}}^i\right)}>∊,$$ (25)

where $\mathbf{U}$ is the vector of the conservative variables. $∊$ serves as a cut-off limit for the refinement.

The conservativeness of the discretization for non-conforming faces in the Finite Volume framework presented here is ensured by treating the non-conforming faces as individual faces of polyhedral elements. After every adaptation of the mesh, a smoothing pass is executed to ensure a $1:1,1:2$, or $2:1$ connectivity. Finally, the resulting sum of the numerical fluxes from the refined cells up to level l is used in the lower level $l-1$ nonconforming neighboring cell with level $l-1$.

4. Validation

4.1. Wave transmission across a solid/fluid interface

The first validation case presented here is a 2-D problem of a pressure wave impacting a planar fluid–solid interface. The objective of this case is to verify the fluid–structure interaction and the correct prediction of the transmission and reflection of the pressure wave across interfaces. The configuration of the case is presented in Fig. 1. A square with edges of $40\text{mm}$ is considered with the top half being the fluid-subdomain, and the bottom half solid.

Fig. 1.

Wave propagation across a fluid–solid interface case setup and velocity magnitude distribution. Top half: fluid region, bottom half: solid region. (a)-(d) pressure sensors with $S_x=S_y=2.5\text{mm}$. The initial area of high pressure ($10\text{KPa}$) is denoted with red. Wave structure in the fluid region consists of the incident wave, the reflection, and the Schmidt head wave. In the solid region S/P and leaky Rayleigh waves.

A spherical high-pressure region at $10\text{kPa}$ higher than the ambient, is considered within a fluid region. The pressure around this high-pressure region smoothly transitions to the ambient following a tangent function distribution as described in [26]. This configuration replicates a pressure wave, similar to one that is emitted during a bubble collapse. The initial condition for the pressure across the fluid is given by:

$$p=p_0+\beta \left(1-\alpha \left(\tanh \left(2\pi \right(2\beta r-\alpha \left)\right)+1\right)\right)$$ (26)

where r is the distance from the source, $p_0$ is the hydrostatic pressure and $\alpha$ and $\beta$ are scaling parameters equal with $0.5$ and 1000, respectively. The initial position of the high-pressure area is located $5.0\text{mm}$ above the solid/fluid interface. The initial condition for the velocity field as provided by the acoustic theory [40] is initialized as:

$$u=\frac{p-p_0}{\rho c_0},$$ (27)

where $c_0$ is the speed of sound of water and $\rho$ the density. The parameters of the equation of state for water is $\rho =1000.0\text{kg}/{\text{m}}^3,{\pi }_{\infty }=6.0·{10}^8\text{Pa}$ , $\gamma =4.4$. For the solid $\rho =8900.0\text{kg}/{\text{m}}^3$ ${\pi }_{\infty }=342.0·{10}^8\text{Pa},\gamma =4.22$, $\mu =9.2·{10}^{10}\text{Pa}$ which corresponds to the properties of copper.

The computational mesh consists of a total number of 12.8 million hexahedral elements. The characteristic element size is uniform and equal $10\mu m$ throughout the Eulerian field and the time-step is held constant at $0.5\mathit{ns}$ for the entirety of the simulation.

Fig. 1 presents the velocity magnitude for the numerical solution at a time instance where the high-pressure wave has impacted the interface and has propagated inside the solid. The velocity magnitude colormap scale is adjusted to the different characteristic values of the maximum velocity in the solid and the fluid. The reflection of the pressure wave can be clearly seen in the fluid region, alongside the incident wave, which propagates outwards. In the same Fig., the transmitted P and S waves can be identified in the solid phase region. The generation of surface waves, emanating from the interface is also apparent, with Schmidt head waves in the fluid region and leaky Rayleigh waves in the solid. A similar wave structure is reported in [61]

To validate the developed numerical solver, the same case is simulated with a linear acoustic model that accounts for homogeneous fluids and elastic solids. This is accurate due to the small magnitude of the incident pressure wave, and the absence of solid deformation. The solution to this problem thus can be simulated by K-Wave [62] which employs such a model and has been validated against numerous other wave propagation problems [63]. In Fig. 2, the pressure time-series is given for two sensors (a), (c) located at (0,2.5) mm and (0,−2.5) mm, alongside the numerical solution of K-Wave. The two solutions are in close agreement, with minor differences of less than $1\%$ in magnitude.

Fig. 2.

Comparison of numerical solution of the wave transmission across a fluid/solid interface, using the developed ForestFV solver presented in this paper and the K-Wave [64] linear elastic-acoustic model. Left: Pressure time series at probe point (a) (0,2.5) mm. Right: Pressure time series at probe point (c) (0,-2.5) mm.

4.2. Spherical bubble collapses in an infinite medium

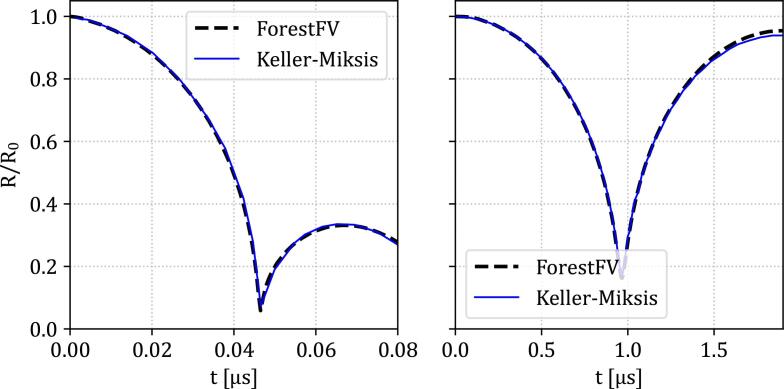
The validation case presented in this paragraph corresponds to the high/low-pressure collapse of a gas bubble in water. A typical benchmark case that can be easily verified against simple one-dimensional semi-analytical models such as the Rayleigh-Plesset and the Keller-Miksis [65] equations. In both cases, viscosity and surface tension are not accounted for. The computational domain spans to a far-field distance equal to $L=50R_0$ to avoid any boundary interference effects. The initial bubble radius for all cases is $R_0=1.0\text{mm}$. Symmetry boundary conditions were assumed in all boundaries, except the outer boundary of the domain, where an outflow boundary condition was imposed at the external face of the outermost cell. A grid independence investigation carried out resulted in a sufficient resolution of at least 35 cells for the initial radius. Similar findings were found in [36], [66]. Here the initial number of elements is 175 for the whole domain, with 50 corresponding to the initial bubble radius.

For the first case, a high-pressure ratio collapse at $p_l/p_g=352$ is considered. The gas is considered ideal with $\gamma =1.4,{\pi }_{\infty }=0\text{Pa}$, and the gas initialization pressure is considered as atmospheric ${10}^5\text{Pa}$. For the low-pressure bubble collapse test case, a pressure ratio of $p_l/p_g=20$ is assumed. In Fig. 3 we show the bubble radius evolution for both cases and are in excellent agreement, compared with the Keller-Miksis model. In particular, the high-pressure ratio collapse results in a much faster collapse time and reaches a smaller rebound radius $\approx 0.35R_0$. due to the surrounding liquid pressure than the low-pressure ratio which reaches $\approx 0.97R_0$. The details of the initial value problem formulation for the Keller-Miksis model, along with the parameters for the cases can be found in [66]. The results from the Keller-Miksis model where obtained, by integrating the corresponding equation, using a third-order Runge–Kutta with the same pressure ratios as in the numerical simulations.

Fig. 3.

Temporal evolution of the normalized bubble radius for the symmetric gaseous bubble collapse and rebound test case validation. Dashed line: (—) ForestFV result. Solid line (—): Keller-Miksis model. Left: High-pressure ratio case. Right: Low-pressure ratio case. 50 cells were used for the initial bubble radius $R_0$.

4.3. Shock induce bubble collapse close to a wall

Finally, to validate the resolution of the shock-induced bubble collapse dynamics, the validation case first presented in [49] and later in [39] is considered. This case is composed of a gas bubble collapsing after the impact of a lithotripter’s shock wave (LSW). The gas bubble has an initial radius $R_0=0.05\text{mm}$ and is at a distance $S/R_0=2$ from the wall. The surrounding media is water with the same properties as defined in the previous cases. The lithotripter pulse can be fitted from experimental data [67], with $p$+ and $p$- equal to $35\text{MPa}$ and $-10\text{MPa}$ respectively. The pulse is modeled as planar given that a typical focal width FW is much larger than the radius of the bubble $\mathit{FW}/R_{0}200$.:

$$p\left(t\right)=p_0+2p_s{e}^{-\alpha t}\mathit{cos}(\omega t+\pi /3),$$ (28)

where $\alpha =1.48·{10}^6{s}^{-1},\omega =1.21·{10}^6{s}^{-1}$are equal to the parameters values used in [49] and the maximum over-pressure is $p_s=35\text{MPa}$. The pulse is introduced into the domain by modifying the initial conditions for the pressure, total energy, and velocities according to the acoustic theory [40]. The rest of the domain is initialized with atmospheric pressure and zero velocity.

The computational domain is presented in Fig. 4. Due to the symmetry of the problem around the z-axis, the computational domain consists of a $2°$ degrees slice. Symmetry boundary conditions are assumed at the limiting planes while the out-most boundaries are modeled by outflow conditions. The rigid wall was modeled using reflective boundary conditions. The initial mesh consists of 125,000 elements. A grid convergence study was carried out with uniform and local mesh refinement up to 2,3 and 4 levels respectively. The resulting meshes have 0.5,2 and 8 million cells for the uniform re-meshing, whereas the local refinement is focused on the bubble interface and on significant pressure gradients, leading to at most 0.5 million elements. The results show (Fig. 5) that the local mesh refinement preserves the bubble’s interface in the same as in the uniform meshes. Additionally, the pressure loss due to numerical diffusion is minimized, with the 4-level AMR run having less than 5% difference from the 3 levels of uniform refinement. Thus, the strategy that was employed for this simulation is a combination of 2 levels of uniform refinement in the area close to the bubble with additionally two more levels on the interface and in the proximity of significant pressure gradients.

Fig. 4.

Shock-induced gas bubble collapse near a wall with stand-off distance $S/R_0=2$. (a) Case configuration. (b) Initial conditions. (c) $t/t_R=0.204$, (d) $t/t_R=1.266$, (e) $t/t_R=1.429$, gray-scale colormap: magnitude of the pressure gradient, blue iso-surface: bubble interface, rainbow colormap: pressure distribution on the wall surface. (f) Pressure time series probed at $r/R_0=0.0$, (g) pressure time series probed at $r/R_0=1.0$, pressure time series comparison between the present results with ForestFV and published results in [49], [39].

Fig. 5.

Shock-induced bubble collapse close to a rigid wall. Colormap: volume fraction (${\alpha }_0$) contour of water. Gray-scale: density gradient magnitude. Black iso-surface: bubble interface. Left: AMR with 3 levels of refinement on the interfaces, Right: Uniform refinement with 3 levels.

To compare and validate the present methodology, two pressure sensors are assumed along the wall. The sensors are located in the same radius from the center-line as in [39], [49] i.e $r/R_0=0$ and $r/R_0=1$. The time history of the pressure evolution at those probing stations is presented in Fig. 4(f and g). The first spike in pressure is the result of the LSW impacting the wall. The small time delay in the two sensors is due to the shielding effect of the bubble. After the reflection of the LSW of the wall, the bubble is loaded even more from the right side, accelerating the collapse. The bubble collapses and emits a shock wave which reaches a ratio of $p/p_s=10$. As shown in Fig. 4 a liquid jet forms from the distal side and towards the wall which finally results in a bubble that presents the classical pattern of the near-wall collapse toroidal shape and a vortical structure that stretches the bubble radially towards the wall [56]. The recorded time series of pressure are in good agreement with those reported in [39], [49], with a less than 10% difference in the peak pressure, at both sensors.

5. Results and discussion

In this section, we present the collapse dynamics of a gas bubble for varying stand-off distances and attachment styles for two different solids materials relevant to shock-wave lithotripsy, and the results are discussed and compared with similar findings in the literature. The first material studied is a uric type of KS, a common type formed in human kidneys. The material properties of the KS are taken as: $\rho =1546.0\text{kg}/{\text{m}}^3,{\pi }_{\infty }=8.37·{10}^9\text{Pa},\gamma =1.7,\mu =3.0·{10}^9\text{Pa}$. To investigate tissue damage during shock-wave lithotripsy, a soft tissue material is also studied with the following properties: $\rho =1060.0\text{kg}/{\text{m}}^3,{\pi }_{\infty }=1.43·{10}^8\text{Pa},\gamma =4.3,\mu =1.0·{10}^3\text{Pa}$. The properties of this second material are akin to the properties of human liver tissue. Following the approach of Kobayashi et. al. [43], the parameters for the equation of state for the soft tissues and the kidney stone, are calculated by matching the acoustic impedance and the speed of sound. The surrounding medium was modeled as fluid, as it was found that cavitation in the renal collecting system (urine) was immediately detected after the passage of the shock wave [68].

In the analysis presented in this work, three distinct stand-off distances S of the bubble’s center to the surface of the solid are considered. In the first configuration the bubble is not attached, i.e $S/R_0>1$. In the second configuration, the bubble is attached to the solid with an acute angle, i.e. $1>S/R_0>0$, and finally, a closely attached configuration where an obtuse angle of attachment is considered, i.e. $S/R_0<0$. The initial size of the bubble is $R_0=0.04\text{mm}$ which is a typical radius for bubbles formed during shock-wave lithotripsy. From a purely numerical viewpoint, the work of Wang [39] addressed the question of the critical bubble size by doing a parametric study of the effect of bubble size. It was found that bubbles larger than $R_0>0.13\text{mm}$ do not collapse in the time frame of the shock wave propagation across a kidney stone with a size $1.5\text{mm}$. It should be noted that the same shock wave profile was used thus the result from that study should hold for our cases. In principle, larger bubbles will tend to take longer to collapse. Similar findings were reported in the work of Sankin et al. [69]. Additionally, in the work Philipp et al. [70] it is stated that after the shock impact the bubble wall will accelerate to twice the material velocity behind the shock front. An explicit correlation between the bubble size and the jet velocity, however, was not identified. The same behavior is apparent in our findings as well. An optimal bubble size was established in the work of Philipp et al. [70] that characterizes the intensity of the bubble rebound which was highly correlated to the shock wave profile, as the collapse might be hindered by the tensile part of the shock wave. In our study, we did not observe such mechanism for the initial collapse as the shock impact set in motion the collapse of the bubble. This mechanism, however, can indeed play a role in the secondary bubble expansion. For all cases, the same shock wave, as in the validation case presented in Section 4.3 is considered. The shock is modeled by its corresponding spatial pressure distribution in the initial conditions of the simulation and is positioned at a distance $d/R_0=1.25$ away from the bubble’s center. The rest of the domain is initialized with atmospheric pressure and zero velocity.

The axis-symmetric configuration of the problem, allows the use of an unstructured hybrid computational grid for a $2°$ sector of the computational domain. The initial ancestral mesh consists of 125.000 hexahedral and prismatic elements. The assumption of symmetry greatly reduces the computational cost and enables a higher resolution on the solid–fluid-gas interface dynamics, which otherwise would elude. In principle, however, there are two distinct processes that cannot be investigated under this assumption. The first is related to the shock wave alignment to the bubble and solid interfaces. In the work of Johnsen et al., [38] and Coralic et al. [44], it is stated that the shock will dictate the direction of the collapse and the jet formation. Thus, a relative angle of 0 degrees, i.e., the symmetry assumption, leads to the most energetic collapse and is the most detrimental for vessel injury which is the case under investigation in this work. The second is that inherently the bubble collapse dynamics are fully three-dimensional processes. Theoretical studies [71] have suggested that during the collapse and rebound phases, bubbles do no remain spherical. The loss of sphericity has been reported by many authors [36], [49], and can be attributed to Rayleigh–Taylor, shape instabilities, and numerical schemes [66]. A numerical study that embodies this assumption [38], however, presents a good agreement with experimental results. More precisely it is stated that the location of the collapse does not vary significantly, although wall pressure might be overestimated by the simulations. This was attributed to the infinite acoustic impedance used in that study. Later work by Wang [39], revealed that by modeling an elastic solid with a finite impedance, this overestimation is substantially lower by 60% to 90%. Thus, the assumption of symmetry can have applicability, with future three-dimensional studies to fully investigate the aforementioned aspects of bubble dynamics.

A mixed refinement strategy, similar to the one discussed in Section 4, was used. The interfaces were resolved using 4 levels of refinement and significant pressure gradients, while 2 to 3 levels of refinement were used in the area around the collapsing bubble. The final dynamic mesh reaches a maximum of 1 million cells during the collapse of the bubble. An equivalent uniform mesh would have resulted in a prohibitive mesh size of two orders of magnitude more cells for the resolution of the dynamically developing interfaces. The time step was adjusted so that CFL would not exceed $0.1$, thus, ensuring numerical stability.

To facilitate the comparison of the various cases presented in this work, the results are presented as nondimensional values. Specifically, time is non-dimensionalized against the Rayleigh collapse time $t_R$,

$$t_R=0.915R_0\sqrt{\frac{{\rho }_l}{\mathrm{\Delta }p}},$$ (29)

where $R_0$ is the initial radius of the bubble ${\rho }_l$ is the fluid density of the surrounding liquid and $\mathrm{\Delta }p$ is the pressure difference between the two fluids [72]. Similarly, the velocities and pressures scales are normalized as in, [48]:

$$p_c=c_l\sqrt{\mathrm{\Delta }p{\rho }_l},u_c=\sqrt{\frac{\mathrm{\Delta }p}{{\rho }_l}}$$ (30)

5.1. Detached bubbles: $S/R_0>1$

The impact of the incident shock wave on a detached bubble near a KS is presented in Fig. 7. The initial configuration of the simulation is presented in Fig. 7a with an initial stand-off distance of $S/R_0=1.2$. The incident shock wave is initially placed at $1.25R_0$ upstream from the bubble’s center. At the instance $t/t_R=0.127$ the shock has impacted the bubble, resulting in the formation of an expansion pressure wave due to the difference in acoustic impedance between the gas content of the bubble and the surrounding water. The impact of the shock wave increases the pressure of the liquid around the bubble, Fig. 7b, inducing the asymmetric collapse of the bubble [73].

Fig. 7.

Contour map of the evolution of shock structure before the bubble collapse. The gray-scale colormap corresponds to the magnitude of the pressure field gradient. Blue iso-surface: The gas volume fraction level at $a_g=0.5$, representing the bubble interface. Red iso-surface: The solid volume fraction at $a_s=0.5$ represents the solid interface. (a) The initial configuration before the shock wave impact. (b) The expansion wave, (c) and (d) The reflection of the shock wave in the fluid and its transmission inside the solid phase.

In the last two instances presented in Fig. 7, (c-d) the shock wave has been reflected by the KS. The reflected shock impacts the bubble again, inducing a further secondary pressure loading on the bubble interface. The formation and the characteristics of the reflected pressure wave are governed by the mechanical properties of the solid surface [74]. The magnitude of the deformation induced by the solid is also a function of the properties of the solid material. The intensity of the reflected shock is of the same order of magnitude as the incident shock given the stiffness of the material, as highlighted in the validation case in Section 4.1. Due to the high shear and elastic modulus of the KS, the solid interface deformation is minimal and the solid does not deform for more than $0.1\%R_0$ under the effect of the incident shock wave. The acoustic impedance for the kidney stone is $5909.94\mathit{MPa}·s/m^3$. Following the analysis of Brekhovskikh and Godin [75], the amplitude of the reflected $p_r$ and the transmitted and $p_t$ waves are:

$$p_{\mathit{rf}}=p_i\frac{Z/Z_0-1}{Z/Z_0+1},p_{\mathit{tr}}=p_i\frac{2Z/Z_0}{Z/Z_0+1},$$ (31)

where $p_i$ is the intensity of the incident shock, Z is the acoustic impedance of the material, and $Z_0$ is the acoustic impedance of the surrounding liquid.

For the cases presented here, the incident shock wave intensity is $p_i=35\text{MPa}$, thus Eq. 31 results in $p_{\mathit{rf}}=19.9\text{MPa}$ and $p_{\mathit{tr}}=55\text{MPa}$ for the reflected and transmitted wave intensities. The numerical analysis presented here compares well with the simplified model described in [75] providing similar predictions for the kidney stone configuration with the reflection and the transmission as measured in the simulation being $p_{\mathit{rf}}=19.8\text{MPa}$ and $p_{\mathit{tr}}=54.9\text{MPa}$ respectively. The agreement between the numerical simulation results and the analytical model of Brekhovskikh and Godin seems to hold for the softer material studied.

Similar conclusions can be drawn for the soft tissue with the acoustic impedance equal with $Z=2349.58\mathit{MPas}/m^3,p_r=6.1\mathit{MPa},p_t=41.3\text{MPa}$ from the analytical expression and $p_r=6.0\text{MPa},p_t=41.1\text{MPa}$ from the simulations. These values are in close agreement with both the acoustic theory and the results published by [40]. In both cases, the reflection is a compressive pressure wave. It should be noted that the aforementioned pressures were measured $25R_0$ from the center of the axis, in order to minimize the effect of the expansion wave from the LSW-bubble interaction prior to the shock impact to the solid surface.

The pressure field distribution at different instances for the shock-induced bubble collapse in the proximity of KS is presented in Fig. 8a-a4. The result for the same configuration in the proximity of soft tissue is shown in Fig. 8b-b8. All cases shown in Fig. 8 correspond to detached bubbles with the same initial stand-off distance $S/R_0=1.2$.

Fig. 8.

Shock-induced collapse of a detached gas bubble with initial stand-off distance $S/R_0=1.2$. Colormap: pressure distribution. Black iso-surface: The gas volume fraction level at $a_g=0.5$ corresponds to the bubble interface. Red iso-surface: The solid volume fraction at $a_s=0.5$ represents the solid interface. (a-a4) Collapse near the KS, (b-b8) collapse near the soft tissue. (a) Detail of the jet formation (arrows velocity magnitude) and the impact of the shock on the KS (pressure contour on the KS surface), (b) detail of tissue deformation. Same magnification in all figures, except the (a/b), and (b5-b8).

Figs. 8a1 and 8b1 correspond to the start of the formation of the shock wave which initiates the collapse of the bubble. A time difference between the kidney stone and soft tissue is apparent in these figures, with the former being further into the collapse phase than the latter for the same time step. This is attributed to the increased intensity of the incident shock wave’s reflection on the bubble interface. For the KS configuration, it presents a value that is higher by $13.6\text{MPa}$. In general, the collapse is faster near solids with higher acoustic impedance, such as kidney stones, which is expected due to the additional loading of the reflection of the incident shock wave. Similar findings have been reported in [40].

The shrinking of the bubble during the initial collapse phase induces a characteristic sink flow [43]. In contrast to the rigid KS, the soft tissue has lower elastic modulus and thus deforms and moves upwards towards the adjacent interface of the bubble, (see Fig. 8b1 and 8b2).

In the frames of Fig. 8a2 and 8b2 the collapse of the bubble is presented. During the collapse, the distal bubble interface is gaining momentum moving rapidly towards the proximal bubble interface resulting in increased pressure distribution and rapidly moving towards the solid surfaces. In the present cases the direction of the collapse and the jet formation are dictated by the shock wave impact, as the bubble is initially in equilibrium. In principle, under other initial conditions, the jet might form in the opposing direction to the solid boundary [76]. For the KS simulation at $t/t_R=1.22$ (Fig. 8a) the bubble volume reaches a minimum. The impact of the two opposing moving liquid masses at the upper and lower interfaces of the bubble results in the emission of a water hammer shock wave directed toward the solid interface. The same mechanism is observed for the collapse near the soft tissue with the main difference that the toroidal shape is wider and shorter (Figs. 8a2 and 8b2). Specifically, the ratios between the two are: $d_{\mathit{KS}}/d_{\mathit{ST}}=1.017$ and $L_{\mathit{KS}}/L_{\mathit{ST}}=1.734$.

The emitted shock wave reaches $p/p_c=0.370$ for the KS case while for the soft tissue case, it reaches $p/p_c=0.183$. The induced impingement jet impacts on the surface of the kidney stone (Fig. 8a3) which further compresses the surface, at $t/t_R=1.22$. This impact results in compression loading. The reflection of the shock wave impacts again the collapsing bubble. The effect of this secondary impact is more pronounced in the case of the kidney stone. In the KS case, a characteristic toroidal vortical structure is formed for both cases in Figs. 8a2 and 8b3.

The induced velocities, from the liquid jets, on the solid interface at $r/R_0=0$ are presented in Fig. 10a. In this figure, we present the initial upward movement of the soft tissue, due to the sink flow, which reaches a maximum velocity of $u/u_c=-0.25$. Following the collapse of the bubble, the strong shock wave compresses the interface of the solid, specifically for the soft tissue case, the interface is abruptly changing its direction of movement. Following the impact of the liquid jet the interfaces further gain momentum. Due to the high shear and elastic modulus of the kidney stone, the maximum induced velocity is almost half of the corresponding in the soft tissue. Finally, the surface of the kidney stone rebounds, due to the high elastic energy gained by the initial compression.

Fig. 10.

Effect of stand-off distance/attachment on solid boundary’s velocity overtime at $r/R_0=0$. (a) Detached bubbles with stand-off distance $S/R_0=1.2$, (b) Attached bubbles with stand-off distance $S/R_0=0.6$ and an acute angle, (c) Attached bubbles with stand-off distance $S/R_0=-0.2$ and obtuse angle. Time instances given are: (a-a4) for KS, and for ST (b-b8) from Fig. 8, Fig. 12, Fig. 14. References to secondary collapse Fig. 11, Fig. 13, Fig. 15 are given with their corresponding number.

In the work of P. Zhong et al. [77] and Heymann [78] the pressure rise due to liquid jet’s impact on a solid boundary was investigated and a contact angle dependency was found. In both studies the authors considered a jet formation with clear boundaries and uniform velocity to derive the exact relations for the pressure rise. In our simulations, a pressure rise upon the jet’s impact on the solid surface can be identified, which is in agreement with the reported correlation between the pressure rise and the contact angle.

As the bubbles continue to move towards the solid interfaces, the gas contained in the toroidal cavities expands, and the bubble rebounds, similar to a Rayleigh-spherical collapse. At $t/t_R=1.5$ the bubble has reached the kidney stone and expands radially and in the proximity to the solid surface. This results in a secondary collapse shown in Fig. 9a and presented in more detail in Fig. 11a1-a2. The secondary collapse is weaker, due to the reduced pressure difference of the gas bubble content.

Fig. 9.

Effect of stand-off distance/attachment on non-dimensionalized gas volume evolution over time and non-dimensionalized pressure on the solid interface at $r/R_0=0$. (a)/(b) Detached bubbles with stand-off distance $S/R_0=1.2$, (c)/(d) Attached bubbles with stand-off distance $S/R_0=0.6$ and acute angle, (e)/(f) Attached bubbles with stand-off distance $S/R_0=-0.2$ and obtuse angle. Time instances given are: (a-a4) for KS, and for ST (b-b8) from Fig. 8, Fig. 12, Fig. 14. References to secondary collapse Fig. 11, Fig. 13, Fig. 15 are given with their corresponding number. Same magnification in all figures, except the (a/b), and (b5-b8).

Fig. 11.

Secondary collapses for detached bubbles with initial stand-off distance $S/R_0=1.2$. Colormap on solid surface: pressure distribution. Green iso-surface: The gas volume fraction level at $a_g=0.5$. Colormap on cross-section: maximum tensile stress distribution. (a1/a2) Collapse near the KS, with torus break up (b1/b2) Collapse near the soft tissue, tissue penetration, and tension-driven tissue injury.

The bubble collapse close to the soft tissue exhibits a different mechanism as it expands further and impinges the solid surface, forming a circular crevice, Fig. 8b6 within the solid. The strong liquid jet thus greatly deforms the soft tissue creating the space for the torus to penetrate inside of it.

In Fig. 8b6 the bubble has penetrated the soft tissue, has reached its maximum volume, and thus the second collapse phase has started. As the bubble moves further inside the soft tissue, the soft tissue exerts a radial pressure, due to the elasticity of the pre-loaded material. This mechanism in addition to the pressure drop inside the bubble, due to its expansion, leads to the secondary collapse shown in detail in Fig. 11(b1 and b2). Two main features can be identified. The first is that the bulk of the bubble volume has created a circular crevice with $R_{\mathit{cr}}/R_0=0.482$, whereas the second one is that the fast-moving jet has impinged the tissue forming a long neck-like structure (see Fig. 11b1). The secondary collapse emits shock waves that originate from the 4 toroidal cavities that collapse, with some additional auxiliary pockets of gas not visible in Fig. 11a1-a2 [56]. The resulting collapse and shock wave emission, generate vortexes around the expanding torus, that in terms exert high tensile stress on the tissue. The induced stressing is forcing strips of tissue to elongate. Additionally, this phenomenon produces high shear stresses, highlighted by the red and black areas of the maximum tensile stress contour map in Fig. 11. This can be identified as a secondary mechanism for tissue injury during ESWL. The expanding toruses further thicken the neck of the injury crevice. At the head of the crevice located at the very bottom, the same mechanism of tension-driven tissue injury takes place. In the experimental work of Kodama et al. [79] (see Fig. 5(c)) a qualitatively similar structure can be identified for a bubble collapsing close to a gelatin surface. In total three different bubble sizes were examined namely, $R_e=0.61\text{mm},R_e=0.33\text{mm},R_e=0.21\text{mm}$, utilizing a shock wave with a lower amplitude $p_s=10.2\pm 0.5\text{MPa}$ than in our case. For the first two bubble sizes, the collapse dynamics and the gelatin response exhibit rather different behavior than the one discussed presently. This can be attributed to mainly to the bubble size difference. The third and smaller bubble size, however, appears to produce the same structure with both the circular crevice and the neck-like structure and even the expansion of the $4^{\mathit{th}}$ torus which will lead to the head-like structure. Additionally, the secondary collapse mechanism, and tissue penetration, are also reported in the study. Comparing the first and secondary collapse mechanisms (see Fig. 9a), the equivalent bubble radius exhibits a damped oscillatory behavior, with most of the energy of the system having decayed after $t/t_R=7$. The resulting shape of the torus and the deformation of the tissue are presented in Fig. 8b, after which the elasticity of the tissue is the main driving restoring force.

5.2. Attached bubbles with acute interface angle, $1>S/R_0>0$

In the following, we investigate the bubble dynamics of bubbles that are initially attached to solid surfaces, that form an interface at an acute angle at the solid surface, see Fig. 6b. Previous research by Lauer et al. [45] and others [46], [48], [56] have studied the collapse dynamics close to a rigid wall, under uniform high pressure. The findings indicate the formation of a high-pressure region on the top of the bubble, while the attached face, due to the depressurization of the surrounding liquid, lags behind. Thus, the collapse is predominately driven by the high-pressure region on the distal interface of the bubble. The collapse takes place in the locality of the wall and gives rise to a torus after the impact of the jet on the wall.

Fig. 6.

Shock-induced gas bubble collapse case configurations. Types of bubble attachment on the solid surface based on the angle $\alpha$.

In Fig. 12 pressure contours for the shock-induced bubble collapse are presented for attached bubbles with distance to the wall equal to $S/R_0=0.6$. Similar findings to the aforementioned studies can be observed for the case of a bubble collapse near a kidney stone Fig. 12a-a4. After the impact of the incident shock wave, the distal side of the bubble starts accelerating toward the interface. The rest of the bubble’s interface is radially loaded as the incident shock wave transverses toward the solid. Depending on the acoustic impedance of the solid the reflected shock wave will further load the bubble interface. Thus, the proximal interface of the bubble starts to slide on the solid, and collapse radially (see Fig. 12a1-a2). Due to the depressurization of the liquid, however, the axial velocity, by which the bubble slides on the solid, is one order of magnitude lower with a ratio of $\left|u\right|/\left|v\right|=7.53$. The axial velocity is denoted with u and v is the radial slipping velocity on the kidney stone surface, at $t/t_R=1.13$.

Fig. 12.

Shock-induced collapse of an attached gas bubble with initial stand-off distance $S/R_0=0.6$. Colormap: pressure distribution. Black iso-surface: The gas volume fraction level at $a_g=0.5$ corresponds to the bubble interface. Red iso-surface: The solid volume fraction at $a_s=0.5$ represents the solid interface. (a-a4) Collapse near the KS, (b-b8) collapse near the soft tissue. (a) Detail of the jet formation (arrows velocity magnitude) and the impact of the shock on the KS (pressure contour on the KS surface), (b) detail of tissue deformation. Same magnification in all figures, except the (a/b), and (b5-b8).

After the collapse phase near the kidney stone, a water hammer shock wave impacts the surface, (see Fig. 12(a/a3). In Fig. 9d we present the pressure, probed on a Lagrangian sensor that follows the interface of the solid at $r/R_0=0$. The water hammer shock impact reaches $p/p_c=0.462$. This value is greater than the one observed for the detached collapse case close to the KS. This can be explained as the liquid jet rapidly decelerates when it impacts the surface of the kidney stone. Similar findings are reported at [45]. Due to the constrained space, the liquid jet then expands radially, forming the toroidal shape shown in Fig. 12a/a3. Due to the abrupt change of the liquid jet direction, vortex rings appear at the upper interface of the torus, which can be seen in Fig. 12a.

In Fig. 10b the solid boundary velocities are presented, for a sensor located at the axis of symmetry $r/R_0=0$. Initially, the KS interface starts accelerating due to the impact of the incident shock wave. Following the collapse and the impact of the liquid jet, the main compression of the interface is apparent. The interface rebounds back due to the significant elasticity of the KS, and releases the stored elastic energy. In Fig. 9c the rebound of the torus is shown with the maximum volume reached at $t/t_R=3.17$. Smaller secondary collapses induce additional velocities of the interface and lower shock wave emissions at later stages. The final stable shape is reached after $t/t_R\approx 7$. The torus has detached from the kidney stone, expanded radially, and formed two new toruses, which remain in the proximity of the solid (see Fig. 13b).

Fig. 13.

Secondary collapses for detached bubbles with initial stand-off distance $S/R_0=0.6$. Colormap on solid surface: pressure distribution. Green iso-surface: The gas volume fraction level at $a_g=0.5$. Colormap on cross-section: maximum tensile stress distribution. (a1/a2) Collapse near the KS, with torus break up (b1/b2) Collapse near the soft tissue, tissue penetration, and tension-driven tissue injury.

Similar to the detached bubbles, there is a time lag of the initiation of the collapse phase as shown in Fig. 12a1 and Fig. 12b1. This is the result of the difference in the acoustic impedance between the kidney stone and the soft tissue, as explained in Section 5.1. For the attached bubble cases this mechanism is less prominent. In later stages of the first collapse phase (see Fig. 9c), the time difference in the collapse is negligible.

As the bubble is getting compressed and finally collapses, a suction pressure is applied on the surrounding tissue by the inwards radial movement of the attached interface. This results in a wave-like formation seen in Fig. 12b1. In the next stage of the collapse (Fig. 12b2), and before the bubble reaches it’s minimum volume, a more prominent wave-like structure has been created, which further deforms the soft tissue, resulting in its stretching and the increase of its tensile stress. The maximum upwards displacement reaches $d/R_0=0.427$ at $t/t_R=1.218$.

In the same Fig. 12b2, it is apparent that the formation of the wave-like structure coincides with the creation of circular crevices. Similar to the detached bubble movement prior to the collapse, the soft tissue interface moves upwards, (Fig. 10b). Thus, when the bubble collapses the liquid jet gets trapped in this crevice, further intensifying the penetration of the tissue. In the same Fig., the maximum velocity of the jet is presented, which reaches $u/u_c=4.12$. Additionally, the impact of the axial jet with the inwards radial velocity results in vortexes which in turn, create a radially and axially expanding torus as seen in Fig. 12b3/b4. The shock emission is presented in Fig. 9d and reaches $p/p_c=0.539$, which is higher than the collapse near the kidney stone $p/p_c=0.462$. This comes in contrast to the detached bubbles, presented in the previous section. Two main factors contribute to this behavior. The first is that the pressure loading is caused by the incident and the reflected shock wave on the entire bubble interface, whereas for the attached bubble this pressure stress is applied only to a fraction of the bubble interface. The second factor is that the jet is entrapped within the circular tissue crevice that has formed.

As the bubble expands, following the initial collapse, the tissue is further compressed both axially and radially. The rebound phase ends after $t/t_R=3.46$ where the maximum bubble volume is reached. In a similar way as the detached bubble collapse near the soft tissue, the latter exerts radial pressure on the bubble during the rebound. This mechanism alongside the gas expansion, and the subsequent pressure drop inside the bubble, leads to the secondary collapse phase. In the Fig. 12b5 we present the penetration of the soft tissue at $t/t_R=3.46$. It is apparent that the wave-like formation has now been collapsed inwards, leading to a similar tensile-driven tissue injury mechanism. As the bubble collapses the main torus breaks into smaller toruses, shown in Fig. 12b7 and in more detail in Fig. 13b1. The shock emission from these secondary collapses can be seen in Fig. 9d. The creation of vortexes on the tissue/gas interface and the shock emissions result in the same tension-driven elongation of the tissue from the toruses/tissue interfaces, similar to the initial collapse phase. This tissue injury mechanism is yet again notable for attached bubbles to soft tissue. High shear stresses are observed in Fig. 13, in these tension-driven areas, as well as in the imminent surroundings of the expanding torus. As the gas expands inside the tissue, a similar structure to the detached bubble emerges, with a long neck-like structure followed by the main torus. The final deformation after $t/t_R=7.5$ is presented in Fig. 12b.

5.3. Attached bubbles with obtuse interface angle $S/R_0<0$

Shock-induced attached bubble collapses with initial stand-off distance to the wall equal with $S/R_0=-0.2$ are presented in Fig. 14. The initial attachment of the bubble relative to the solid surface forms an obtuse angle shown in Fig. 6c. As explained in the work of Koukouvinis et al. [46], the bubble collapse dynamics change compared to the previous cases. This is driven by the rapid local pressure increase in the circumference of the bubble, close to the solid surface, which leads to a momentum focusing. The increased pressure is the result of the velocity component normal to the solid interface, at the bubble/solid boundary. In this case, this velocity component causes a compression of the solid, contrary to the case before (see Section 5.2) where this velocity component caused tension, and depressurization of the liquid that surrounded the bubble solid interface. The main difference between the presented results and the aforementioned studies is the incident shock wave loads the surface of the bubble gradually. Thus, the distal part of the bubble accelerates first, with the attached face of the bubble starting to slide on the kidney stone after $t/t_R=0.141$.

Fig. 14.

Shock-induced collapse of an attached gas bubble with initial stand-off distance $S/R_0=-0.2$. Colormap: pressure distribution. Black iso-surface: The gas volume fraction level at $a_g=0.5$ corresponds to the bubble interface. Red iso-surface: The solid volume fraction at $a_s=0.5$ represents the solid interface. (a-a4) Collapse near the KS, (b-b8) collapse near the soft tissue. (a) Detail of the jet formation (arrows velocity magnitude) and the impact of the shock on the KS (pressure contour on the KS surface), (b) detail of tissue deformation. Same magnification in all figures, except the (a/b), and (b6-b8).

In the Fig. 14(a-a4), the collapse near the kidney stone is presented. It is apparent that a circumferential pressure increase is the main driving force for this attachment style. The mechanism mentioned above, of the increased pressure close to the bubble/solid interface results in a higher radial acceleration of the interface than the acceleration at the distal face of the bubble. Thus the collapse of the bubble can be characterized as a radial collapse. Thus, the same bubble dynamics are present for a shock-induced bubble collapse, similar to the findings presented in literature [45], for bubbles under high ambient pressure. When the bubble interface collapses in the axis of symmetry, a water hammer shock wave is emitted. In Fig. 9f, the maximum amplitude of the shock is presented, which reaches $p/p_c=0.689$. In Fig. 10c the jet velocities on the solid boundary are shown. The impact of the liquid jet on the solid surface induces the highest velocities amongst the cases presented in Sections 5.1, 5.2. Here the maximum velocity observed is reaching $u/u_c=4.609$. The stored elastic energy results in a restoring upwards movement of the solid surface.

The resulting collapse is depicted in Fig. 14a, producing a needle-like shape. The liquid jet abruptly changes direction, by $\pm 90°$ degrees, creating an upwards and downwards jet. This upwards motion, in addition to the high vorticity around the top of the needle-like shape, creates the characteristic mushroom rebound of the bubble, presented in Fig. 14a3. In the rebound phase, the bubble expands away from the kidney stone, creating a torus from the mushroom cap, which collapses again at $t/t_R=5.172$, (Fig. 9e), and in more detail in Fig. 15a1/a2). Due to the vortexes around the torus, gas pockets detach and collapse producing secondary shock emissions, apparent in Fig. 9f. The remaining gas volume of the initial bubble stays attached to the kidney stone surface as it can be seen in Fig. 14b4, with some smaller collapses happening at times $t/t_R=3.07,4.03,5.02$. This collapse also induces the motion of the solid surface.

Fig. 15.

Secondary collapses for detached bubbles with initial stand-off distance $S/R_0=1.2$. Colormap on solid surface: pressure distribution. Green iso-surface: The gas volume fraction level at $a_g=0.5$. Colormap on cross-section: maximum tensile stress distribution. (a1/a2) Collapse near the KS, with torus break up (b1/b2) Collapse near the soft tissue, tissue penetration, and tension-driven tissue injury.

In Fig. 14(b-b8), the shock-induced collapse of the bubble attached to the soft tissue is presented. After the incident shock wave impacts the bubble, the circumferential pressure rise around the bubble close to the soft tissue is apparent. The soft tissue is thus deformed upwards, following the motion of the bubble resulting in a similar wave-like structure observed in the Section 5.2. Gas pockets get trapped inside the soft tissue as the bubble collapses, which will lead to secondary collapses and rebounds at later stages. Additionally, a small torus is detached from the bubble in the upper part of the bubble interface (see Fig. 14b2) at $t/t_R=0.976$ and collapses before the main bubble.

The hammer shock wave emitted during the secondary collapse which takes place within the initial crevice reaches a pressure maximum $p/p_c=1.259$. This confined collapse leads to a needle-shaped structure that is forming after $t/t_R=1.15$ (Fig. 14).

The inwards radial jet has collapsed and produced a water hammer shock wave, similar to the case of the collapse near the kidney stone. A double wave-like structure has been created and shown in the same Fig. This structure is the result of the high radial velocities during the collapse, and the inability of the soft tissue to follow the bubble motion due to its elasticity. The downwards-moving liquid/gas jet impacts the soft tissue and creates an inner and an outer crevice, shown in Fig. 14b4. As the bubble expands and rotates inside the inner crevice, a strip of tissue is elongated under tension giving rise to the exact same mechanism of tension-driven injury as presented before. Furthermore, in the outer crevice, an expanding gas pocket, trapped in the initial stages of the bubble collapse, produces a similar feature with an additional tissue layer, that is tension driven by the liquid jet inside the main crevice. Thus, in this case, an extended tissue injury mechanism can be identified (see Fig. 14(b5-b8)).

The liquid jet velocities on the solid interface at $r/R_0=0$ are presented in Fig. 10c. The same prevailing dynamics are present during the initial upwards movement, followed by the violent liquid jet compressing the soft tissue interface. For this attachment configuration, the velocities induced in the soft tissue boundary are the highest. A detail observed in the same figure is that the strong vortex that develops during the collapse induces a momentary upwards movement on the soft tissue at $t/t_R=1.33$. This sudden change of velocities can be an indication of an additional mechanism of tissue injury, in which high acceleration of the soft tissue boundary and compression/tension loading can result in localized tearing.

In the later stages of the collapse, the liquid jet has further deformed the tissue, resulting in a crevice with part of the gas torus being enclosed between two layers of soft tissue. The tension-driven elongation of the tissue is still prominent, driving the collapse of the tissue in itself, $t/t_R=4.7-\approx 10.0$, (Fig. 15). No strong secondary collapses are present in this case, as the collapse splits the gas volume into two parts and the vortexes surrounding the gas toruses, restore the pressure without a rapid expansion, which could have led to a secondary collapse similar to the detached bubble collapses and attached with acute angle cases. The final shape of the deformed tissue after $t/t_R=10.85$ is presented in Fig. 14b. High shear stresses can be seen in the same figure, in the base of the circular crevice, as well as inside the elongated part of the soft tissue which has trapped the rest of the gas torus between the two layers.

6. Conclusions

In this work, we presented a unified Eulerian numerical investigation of the dynamic solid-liquid–gas interactions occurring during shock-induced bubble collapse for detached and attached bubbles in the proximity of a kidney stone and soft tissue. To this end, a novel numerical framework was developed, aiming to capture the fluid–solid interaction and the bubble collapse dynamics by employing a DIM approach [52], and preserve sharp interfaces incorporating an AMR strategy for unstructured grids utilizing a dynamically evolving Oct-tree graph. The presented framework was validated against theoretical and numerical results. The method presented was applied for shock-induced bubble collapse configurations against soft and rigid biomaterials with varying stand-off distances. Specifically, detached and attached bubbles were studied with acute or obtuse angles of contact.

The results revealed the effect of the stand-off distance of the bubble and the acoustic impedance of the solid material on the collapse dynamics characteristics. For detached bubbles with an initial stand of distance $S/R_0=1.2$, the influence of higher acoustic impedance leads to more violent collapse and higher primary shock wave emissions. The induced jet leads to the bubble’s entrapment in an induced crevice formation within the soft tissue that is leading to a secondary collapse. A tension-driven tissue injury mechanism is detailed, where tissue filaments are stretched during the secondary collapse, and the subsequent bubble rebound. The secondary shock waves emitted were found to be of lower intensity than in the primary collapse. The secondary jet velocity magnitude, however, is comparable to the initial jet produced during the primary collapse.

For attached bubble collapses with an initial stand-off distance of $S/R_0=0.6$ the collapse dynamics are significantly different. The collapse is driven by a synergy of radial and axial movement of the bubble’s interface, leading to a more violent collapse. No significant difference, however, was found in the collapse time. The primary shock wave emission in both solid materials is higher in relation to detached bubbles. Specifically, for the soft tissue case, a wave-like formation was observed. These wave formations entrapped the collapsing bubble within a crevice that enhanced the focusing of the shock wave and the impact of the resulting liquid jet. The tissue penetration from the initial collapse is thus more prominent, leading to greater penetration depth. The same tension-driven tissue injury mechanism is present during the secondary collapse phase.

For attached bubbles at an initial stand-off distance of $S/R_0=-0.2$, the collapse dynamics present a significant deviation. The radial movement of the bubble is dominating the collapse, leading to a characteristic needle-like shape at the collapse. The radially converging liquid jet split the bubble into two toruses. No difference in the collapse time is present. The primary shock wave emission is higher for the kidney stone due to the rigidity of the specific material. For the soft-tissue case, a double-wave-like structure emerges on the interface, which leads to the elongation of a circular tissue filament during the liquid jet penetration of the tissue. Thus, the same tension-driven tissue injury mechanism is also apparent for this standoff distance. For this case, however, no instances of secondary collapse were detected inside the soft tissue.

In this work, we have demonstrated the complex bubble dynamics close to rigid and soft bio-materials and elucidated a novel tissue injury mechanism for attached and detached gas bubbles during shock wave lithotripsy applications. This mechanism of tissue penetration and tension-driven tissue injury paves the way to a robust understanding of the mechanisms of hemorrhage and tissue injury in shock wave lithotripsy and ultrasonic-related procedures. It should be noted, that the generality of the results presented is only valid under the conditions that were investigated, and a subsequent study will address the influence of bubble size, shock wave profile, and a broader range of stand-off distances. The developed framework is intended for the study of cavitation in complex geometries, spatial mapping of material properties, and bubble cloud interactions with soft tissue.

CRediT authorship contribution statement

Evangelos Koukas: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing - original draft, Writing - review & editing, Visualization. Andreas Papoutsakis: Conceptualization, Methodology, Software, Validation, Formal analysis, Data curation, Writing - review & editing, Supervision. Manolis Gavaises: Conceptualization, Resources, Writing - review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. .

Starting from Eq. (12) the flux vector F and non-conservative terms H can be written in the following form:

$$\begin{array}{cc}\frac{\partial {\mathrm{U}}_{\mathrm{i}}}{\partial \mathrm{t}}+\frac{\partial {\mathrm{F}}_{\mathrm{ij}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+H_{\mathit{ikl}}\frac{\partial {\mathrm{u}}_{\mathrm{l}}}{\partial {\mathrm{x}}_{\mathrm{k}}}\hfill & =0,i=1,\dots ,3·N_{\mathit{mat}}+12\hfill \\ \frac{\partial {\mathrm{U}}_{\mathrm{i}}}{\partial \mathrm{t}}+\frac{\partial {\mathrm{F}}_{\mathrm{i}1}}{\partial \mathrm{x}}+\frac{\partial {\mathrm{F}}_{\mathrm{i}2}}{\partial \mathrm{y}}+\frac{\partial {\mathrm{F}}_{\mathrm{i}3}}{\partial \mathrm{z}}+H_{i1l}\frac{\partial u_l}{\partial \mathrm{x}}+H_{i2l}\frac{\partial u_l}{\partial \mathrm{y}}+H_{i3l}\frac{\partial u_l}{\partial \mathrm{z}}\hfill & =0\hfill \end{array}$$ (A.1)

where ${\mathrm{F}}_{\mathrm{i}1},{\mathrm{F}}_{\mathrm{i}2},{\mathrm{F}}_{\mathrm{i}3}$ and $H_{i1l},H_{i2l},H_{i3l}$ are components of the F and H vectors for the flux and the non-conservative terms respectively. The complete set of the state vector U, the flux vector F, and the H non-conservative terms are presented below in a matrix form.

$$U=\begin{array}{cc}\hfill & \left[\begin{array}{c}{\alpha }_1{\rho }_1\hfill \\ {\alpha }_2{\rho }_2\hfill \\ \rho u_1\hfill \\ \rho u_2\hfill \\ \rho u_3\hfill \\ \rho E\hfill \\ {\alpha }_1\hfill \\ {\alpha }_1{\rho }_1{e}_1\hfill \\ {\alpha }_2{\rho }_2{e}_2\hfill \\ A_1\hfill \\ A_2\hfill \\ A_3\hfill \\ B_1\hfill \\ B_2\hfill \\ B_3\hfill \\ C_1\hfill \\ C_2\hfill \\ C_3\hfill \end{array}\right]\hfill \end{array},F_1=\begin{array}{cc}\hfill & \left[\begin{array}{c}{\alpha }_1{\rho }_1{u}_1\hfill \\ {\alpha }_2{\rho }_2{u}_1\hfill \\ \rho u_1^2+S_{11}\hfill \\ \rho u_1{u}_2+S_{12}\hfill \\ \rho u_1{u}_3+S_{13}\hfill \\ \rho {\mathit{Eu}}_1+S_{1i}{u}_i\hfill \\ {\alpha }_1{u}_1\hfill \\ {\alpha }_1{\rho }_1{e}_1{u}_1\hfill \\ {\alpha }_2{\rho }_2{e}_2{u}_1\hfill \\ A_1{u}_1\hfill \\ A_2{u}_1\hfill \\ A_3{u}_1\hfill \\ B_1{u}_1\hfill \\ B_2{u}_1\hfill \\ B_3{u}_1\hfill \\ C_1{u}_1\hfill \\ C_2{u}_1\hfill \\ C_3{u}_1\hfill \end{array}\right]\hfill \end{array},F_2=\begin{array}{cc}\hfill & \left[\begin{array}{c}{\alpha }_1{\rho }_1{u}_2\hfill \\ {\alpha }_2{\rho }_2{u}_2\hfill \\ \rho u_2{u}_1+S_{21}\hfill \\ \rho u_2^2+S_{22}\hfill \\ \rho u_2{u}_3+S_{23}\hfill \\ \rho {\mathit{Eu}}_2+S_{2i}{u}_i\hfill \\ {\alpha }_1{u}_2\hfill \\ {\alpha }_1{\rho }_1{e}_1{u}_2\hfill \\ {\alpha }_2{\rho }_2{e}_2{u}_2\hfill \\ A_1{u}_2\hfill \\ A_2{u}_2\hfill \\ A_3{u}_2\hfill \\ B_1{u}_2\hfill \\ B_2{u}_2\hfill \\ B_3{u}_2\hfill \\ C_1{u}_2\hfill \\ C_2{u}_2\hfill \\ C_3{u}_2\hfill \end{array}\right]\hfill \end{array},F_3=\begin{array}{cc}\hfill & \left[\begin{array}{c}{\alpha }_1{\rho }_1{u}_3\hfill \\ {\alpha }_2{\rho }_2{u}_3\hfill \\ \rho u_3{u}_1+S_{31}\hfill \\ \rho u_3{u}_2+S32\hfill \\ \rho u_3^2+{\sigma }_{33}\hfill \\ \rho {\mathit{Eu}}_3+S_{3i}{u}_i\hfill \\ {\alpha }_1{u}_3\hfill \\ {\alpha }_1{\rho }_1{e}_1{u}_3\hfill \\ {\alpha }_2{\rho }_2{e}_2{u}_3\hfill \\ A_1{u}_3\hfill \\ A_2{u}_3\hfill \\ A_3{u}_3\hfill \\ B_1{u}_3\hfill \\ B_2{u}_3\hfill \\ B_3{u}_3\hfill \\ C_1{u}_3\hfill \\ C_2{u}_3\hfill \\ C_3{u}_3\hfill \end{array}\right]\hfill \end{array},$$ (A.2)

$$H_1=\begin{array}{cc}\hfill & \left[\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ -{\alpha }_1\hfill & 0\hfill & 0\hfill \\ {\alpha }_1{\sigma }_{11}\hfill & {\alpha }_1{\sigma }_{12}\hfill & {\alpha }_1{\sigma }_{13}\hfill \\ {\alpha }_2{\sigma }_{11}\hfill & {\alpha }_2{\sigma }_{12}\hfill & {\alpha }_2{\sigma }_{13}\hfill \\ 0\hfill & -B1\hfill & -C1\hfill \\ 0\hfill & -B2\hfill & -C2\hfill \\ 0\hfill & -B3\hfill & -C3\hfill \\ B1\hfill & 0\hfill & 0\hfill \\ B2\hfill & 0\hfill & 0\hfill \\ B3\hfill & 0\hfill & 0\hfill \\ C1\hfill & 0\hfill & 0\hfill \\ C2\hfill & 0\hfill & 0\hfill \\ C3\hfill & 0\hfill & 0\hfill \end{array}\right]\hfill \end{array},H_2=\begin{array}{cc}\hfill & \left[\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & -{\alpha }_1\hfill & 0\hfill \\ {\alpha }_1{\sigma }_{21}\hfill & {\alpha }_1{\sigma }_{22}\hfill & {\alpha }_1{\sigma }_{23}\hfill \\ {\alpha }_2{\sigma }_{21}\hfill & {\alpha }_2{\sigma }_{22}\hfill & {\alpha }_2{\sigma }_{23}\hfill \\ 0\hfill & A1\hfill & 0\hfill \\ 0\hfill & A2\hfill & 0\hfill \\ 0\hfill & A3\hfill & 0\hfill \\ -A1\hfill & 0\hfill & -C1\hfill \\ -A2\hfill & 0\hfill & -C2\hfill \\ -A3\hfill & 0\hfill & -C3\hfill \\ 0\hfill & C1\hfill & 0\hfill \\ 0\hfill & C2\hfill & 0\hfill \\ 0\hfill & C3\hfill & 0\hfill \end{array}\right]\hfill \end{array},H_3=\begin{array}{cc}\hfill & \left[\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & -{\alpha }_1\hfill \\ {\alpha }_1{\sigma }_{31}\hfill & {\alpha }_1{\sigma }_{32}\hfill & {\alpha }_1{\sigma }_{33}\hfill \\ {\alpha }_2{\sigma }_{31}\hfill & {\alpha }_2{\sigma }_{32}\hfill & {\alpha }_2{\sigma }_{33}\hfill \\ 0\hfill & 0\hfill & A1\hfill \\ 0\hfill & 0\hfill & A2\hfill \\ 0\hfill & 0\hfill & A3\hfill \\ 0\hfill & 0\hfill & B1\hfill \\ 0\hfill & 0\hfill & B2\hfill \\ 0\hfill & 0\hfill & B3\hfill \\ -A1\hfill & -B1\hfill & 0\hfill \\ -A2\hfill & -B2\hfill & 0\hfill \\ -A3\hfill & -B3\hfill & 0\hfill \end{array}\right]\hfill \end{array}$$ (A.3)