Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Apr 4;8(15):14122–14130. doi: 10.1021/acsomega.3c00801

Sensitivity Analysis of Thermal Degradation of Plastic Waste Using Statistically Assumed Exponential Factors and Activation Energies

Rao Adeel Un Nabi †, Hammad Hussain ‡, Muhammad Yasin Naz †,*, Shazia Shukrullah †,*, Hassan Abbas Khawaja §, Muhammad Irfan ∥, Saifur Rahman ∥, Abdulnour Ali Jazem Ghanim ⊥
PMCID: PMC10116507  PMID: 37091425

Abstract

graphic file with name ao3c00801_0008.jpg

The rise in the production of plastic waste has prompted the exploration of various recovery options instead of landfilling, burning, and other unethical ways of decomposing. The experimentally generated rate constants for the thermal processing of plastic waste do not yield enough liquid fuels and gases for commercial-scale usage. It is imperative to predict kinetic rate constants statistically using an appropriate combination of activation energies (Ea) and frequency factors (Ao) for the optimized thermal valorization of plastic waste. This approach also assists in controlling the selectivity and quantity of the pyrolysis products. A statistical kinetic model was tested to find the best combination of rate constants from different combinations of Ea and Ao to pyrolyze the high-density polyethylene. Two series of Ea and Ao were first assumed using R software. These series were then used to predict kinetic rate constants and analyze their sensitivity independently using MATLAB. The rate constants were varied from their originally predicted values during the sensitivity analysis. It was found that the rate constant k(7) dominated the other predicted rate constants where high oil and gas yields were concerned. The gas yield increased from lower to higher extreme positions in the range of 60%–74% with the first series and from 65% to 81% with the second series. The maximum oil content was found around 74% and 65% with the first series and second series, respectively.

1. Introduction

Plastics have surpassed natural materials as home products due to their diversity, ease of use, and low cost. Roughly, 350–400 million tons of nonbiodegradable plastic are generated each year, and 5–13 million tons of leftover plastic are dumped into the ocean.1 According to one assessment of the Great Pacific Rubbish Patch, 80 000 tons of plastic garbage have been detected in the Pacific latitudes.2 Plastic bags, bottles, containers, and packaging are all made from polyethylene and polypropylene. The environment is impacted by the use of 500 billion to 1 trillion bags globally. The widespread use of high-density polyethylene (HDPE) and low-density polyethylene (LDPE) poses major environmental concerns to terrestrial and marine ecosystems. Additionally, a large number of species from various habitats are on the verge of going extinct due to plastic-based pollution. The use of HDPE in boosting agricultural production has also resulted in a severe societal dilemma. Mulching waste vinyl impedes the soil animals like earthworms as well as the flow of essential elements like air, moisture, and nutrients, as reported by the Chinese Academy of Agricultural Sciences in 2014.3 These factors are causing physiological issues with plant growth, including germination of seed, root growth, and agricultural output. Therefore, managing polyethylene and other plastic wastes, as well as creating effective technology for plastic breakdown and recycling, is a current necessity.4,5

All recycling activities are classified based on the byproducts and treatment method. Pyrolysis is the use of heat to convert polymers into flammable liquids and gases.6,7 Plastic waste is cut into tiny pieces before being heated endothermically.8 Depending on the heating method, pyrolysis might be traditional heating or microwave heating of the plastic.9 It is critical to understand that decomposition necessitates a great deal of chemistry. To forecast the physicochemical traits of the pyrolysis products, systematic experimental and computational testing is required. A substantial study has been conducted to investigate the degradation of polyethylene (PE) utilizing physicochemical or microbiological techniques or a combination of the two.10,11 Thermal, UV, or a mixture of the two is used to shorten polymer chains and produce oxidized groups, including carbonyl, hydroxyl, and carboxyl, on the polymer surface. These treatments alter the original polymer’s crystallinity and surface shape, facilitating polymer biodegradation. Polyethylene films have been shown to fragment due to nitric acid oxidation, which is followed by microbial deterioration. Microorganisms or microbial colonies biodegrade PE by altering it and using it as a source of energy. The polymer’s physical and chemical characteristics change as a result, including weight loss, structural degradation, and organic matter carbon fixation.12 On the other hand, PE’s high level of hydrophobicity, low specific surface area, and flat surface topography prevent bacteria that break down polymers from forming a biofilm on it.13 Additionally, it is yet unknown which specific biochemical processes and enzymes are required for the breakdown of PE.14

For maximum production and excellent product selectivity, statistical optimization of the process parameters is necessary by applying suitable statistical models. In order to evaluate the effects of modifying operational parameters on process effectiveness, it is critical to create a model that simulates the pyrolysis of polymers. The statistical sensitivity of calculated rate constants for plastic pyrolysis has not been investigated in the published literature. It is possible to examine the efficacy and role of individual rate constants in a pyrolysis process by performing sensitivity analysis. In this study, we conducted a sensitivity analysis by varying values of rate constants from the predicted ones to a level where maximal oil yield is possible. The sensitivity analysis of rate constants has not yet been the subject of past investigations. The Ao and Ea factors can be critical in such analysis to maximize the yield of valuable products. A suitable mix of Ea and Ao is the foundation for forecasting the rate constants that are used to promote oil yield on a commercial basis. Each kinetic rate constant efficiency is solely assessed using sensitivity analysis. This research will show a number of ways for enhancing yields and understanding how temperature affects the kinetic rate constant. What effects do the frequency variables have on the kinetic rate reactions? This study will also provide recommendations for choosing an optimal mix of Ea and Ao to provide an efficient combination of kinetic rate constants. It will be possible to identify which combination of assumed parameters is ideal for increasing gas output while preserving industrial oil production using this model in the R program. Despite the importance of kinetic rate constants in yield efficiency, no research has been performed to examine how they work.

2. Methodology

Equation 1 is used to suppose two sets of Ea and Ao for predicting the rate constants. Equation 2 is applied to the supposed series factors am and bm in the R software, and rate constants k(1)–k(9) are predicted.15 In these equations, k is the rate constant, Ao is the frequency factor, Ea is the activation energy, and(Inline graphic) is the absolute temperature. The rate constant number (1–9) is denoted with M, and supposed values of Ea and Ao are denoted with m. Table 1 lists the values of two series of Ea, Ao, and anticipated rate constants.

2. 1
2. 2

Table 1. Rate Constants Predicted Using Two Series of Ea and Ao.

first assumed series
 second assumed series
Ea (J/mol) Ao (L-mol/s) predicted rate constant (kA) Ea (J/mol) Ao (L-mol/s) kB
80625.019 33.615 k_1 = 0.1086754 84686.595 33.608 k_1 = 0.08139305
80625.019 32.664 k_2 = 0.1056029 81443.176 32.469 k_2 = 0.09903624
124686.886 42.988 k_3 = 0.006052518 120686.723 41.349 k_3 = 0.007737653
122916.918 42.6119 k_4 = 0.006804437 109352.352 39.533 k_5 = 0.01656573
113732.624 41.088 k_5 = 0.01260851 106092.446 40.026 k_6 = 0.02114894
109446.245 41.256 k_6 = 0.01717254 111473.947 43.572 k_7 = 0.01570102
113878.971 44.5344 k_7 = 0.01352471 82618.8433 31.383 k_8 = 0.08804619
85148.665 32.268 k_8 = 0.07562118 130076.545 49.308 k_9 = 0.004731786
133160.256 50.432 k_9 = 0.003886529 109352.352 39.533 k_5 = 0.01656573
Open in a new tab

The rate constants in Table 1 are then used in MATLAB to analyze the sensitivity of the predicted rate constants by employing eqs 3 and 4. Using sensitivity analysis, we can examine the influence of individual rate constants on the products by varying their values from the predicted values up to a certain level wherever optimum product yield is possible. In this model, eq 3 is utilized in MATLAB to investigate the efficacy of rate constants, while eq 4 indicates a maximum and minimum change in each predicted rate constant. In these equations, t stands for time, B indicates % yield, k refers to the reaction constant, D0 stands for initial conditions, and P shows a change in the original value. Figure 1 gives a graphical representation of the conducted work. The mass of HDPE was taken as 150 kg, the pyrolysis time was varied from 1 to 240 min, and the response of reaction after 60 min of processing time was analyzed. The increasing and decreasing actual values of the projected rate constants imply that each reaction has two extreme positions: the lower extreme and the higher extreme.

2. 3
2. 4

Figure 1.

Figure 1

Open in a new tab

Flowchart of the methodology of the conducted work.

3. Model Framework

The proposed equations were solved using the approach described in the literature.16Figure 2 depicts a hypothetical workflow for this analysis.17 It reveals strong dependence of heavy wax (HW), light wax (LW), oil, and gas on k(1), k(2), and k(3) reaction constants, and k(4), respectively. These products are commonly obtained during the pyrolysis of plastic under optimum conditions. Free radicals cause the oxidation reactions that change LW into oil using the rate constant k(5), LW into gas using the rate constant k(6), HW into gas using the rate constant k(8), and HW into oil using the rate constant k(9). Using the k(7) reaction constant, some of the oil was instantly transformed into gas. The sensitivity of each rate constant to the yield is checked in a small temperature window of 370–380 °C. The thermal decomposition of PDPE could release gas, oil, and carbon black. Before reaching a steady state, HDPE is broken down into various organic species, primarily LW and HW.18 The most often used waxes nowadays are kerosene, paraffin, and aromatics. The high temperature may cause these waxes to break down into smaller molecules, which could eventually result in the formation of carbon black. This material is extremely stable; therefore, it will not undergo further chemical changes.19 The other reaction parameters, including Ea, Ao, temperature, and catalysts, might also alter the reaction rate and the nature of the products.

Figure 2.

Figure 2

Open in a new tab

Hypothetical workflow of the thermal pyrolysis of plastic.

4. Results and Discussion

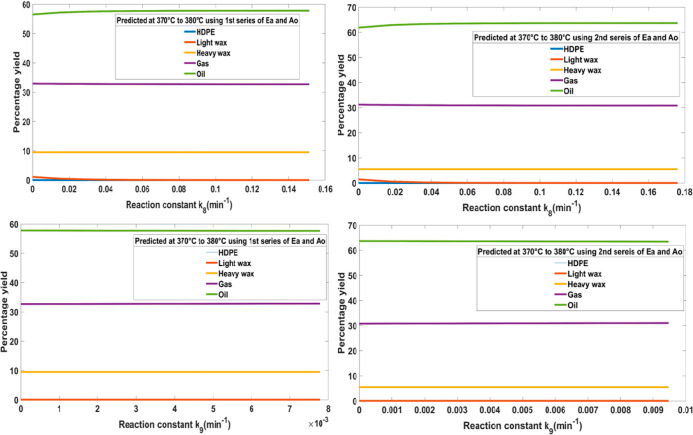
Table 2 shows initial, lower extreme, and higher extreme values of k(8) and k(9) constants and the corresponding product yield. For the supposed series of Ea and Ao, these rate constants were responsible for the transformation of HW into gas and oil, respectively. Figure 3 shows that for both assumed series, k(8) and k(9) rate constants ensure a constant flow of oil, gas, HW, and LW at a constant temperature. This phenomenon can be influenced by temperature and incomplete conversion of HDPE into HW. As a result, the oil and gas yields remain unchanged after 60 min of response time. For an efficient chemical rate, the reactant molecules must have enough kinetic energy to have collisions among themselves to initiate a proper reaction.16

Table 2. Different Values of k(8) and k(9) Kinetic Rate Constants and Their Effect on the Pyrolysis Products.

          yield (%)
rate constant initial value lower extreme higher extreme HDPE oil gas HW LW
First Assumed Series
k(8) 0.07562118 0 0.15 0 58 32 10 0
k(9) 0.003886529 0 0.0074 0 59 32 7 0
Second Assumed Series
k(8) 0.08804619 0 0.17 0 61 31 10 0
k(9) 0.004731786 0 0.0097 0 62 30 7 0
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

Behavior of k(8) and k(9) kinetic rate constants.

The rate responses k(1) and k(2) in both assumed series play a dominant role in the conversion of HDPE into LW and oil, respectively. Table 3 shows the initial, lower, and higher extreme values and their effect on the product yield. Figures 4a and 4b indicate that k(1) behaved a way opposite to that of the k(2) rate constant. At the initial value of k(1), the HW was 10% and 8%, and the gas and oil yields were 32% and 58% for the first assumed series and the second assumed series, respectively. No LW was observed in the case of the first assumed series. However, HW was predicted around 3–12% and oil around 55–59%. The gas yield, on the other hand, decreased from 41% to 28% for series 1. In the second assumed series, HW, oil, and gas remained in the range of 1–7%, 36–27%, and 59–64%, respectively. When the k(1) rate constant is evaluated, one of the constraints of this reaction is the rising amount of HW. The amount of HW reduced significantly with the k(2) rate constant, from 16% to 5% and 10% to 3% for the first series and second series, respectively.

Table 3. Different Values of k(1) and k(2) Kinetic Rate Constants and Their Effect on the Pyrolysis Products.

rate constant oil gas HW LW
First Series
k(1) initial 0.108 57 30 11 0
lower extreme 0 55 41 3 0
higher extreme 0.217 59 28 12 0
k(2) initial 0.106 57 35 12 0
lower extreme 0 59 24 5 0
higher extreme 0.211 56 37 16 0
Second Series
k(1) initial 0.111 64 30 5 0
lower extreme 0 63 36 1 0
higher extreme 0.162 62 27 7 0
k(2) initial 0.133 63 30 5 0
lower extreme 0 65 23 10 0
higher extreme 0.198 62 34 3 0
Open in a new tab

Figure 4.

Figure 4

Open in a new tab

(a) Efficiency of the k(1) kinetic rate constant and (b) the efficiency of the k(2) kinetic rate constant.

According to the lower extreme and higher extreme kinetic rate constants, when the HW dropped, the oil yield climbed from 24% to 37% for the first series and second series, respectively. The gas yield in both assumed series remained nearly identical, as shown in Figure 4b. Since minor differences in Ea and Ao in the assumed series did not affect the reaction rate, these rate constants behaved similarly. The moisture content of the feedstock can only affect gas yield when the temperature is kept lower as in this study. The higher the moisture content, the more gas is produced.20 The wax formation dominates the other products in the first series. In the second series, the wax formation witnessed a decreasing trend while gas and oil formation was more pronounced.21

The used values of k(3) and k(4) kinetic rate constants and the corresponding product yields are reported in Table 4. Figure 5 confirms the complete absence of LW in the product while HW was predicted around 9–10% using the first assumed series for both kinetic rate constants. The oil production with k(3) and k(4) constants was almost the same for both assumed series. The oil production ranged from 56% to 65% with a shift in rate constants from lower to higher values.21 The gas yield remained at 30–34% with the same rate constants. According to Figure 5, the oil yield increased with processing time for both series due to a decrease in gas and HW yield.22 The gas and oil yield trend was nearly identical for both the reaction rates and the assumed series.

Table 4. Different Values of k(3) and k(4) Kinetic Rate Constants and Their Effect on the Pyrolysis Products.

rate constant oil gas HW LW
First Series
k(3) initial 0.006 57 34 10 0
lower extreme 0 56 33 10 0
higher extreme 0.012 59 31 0 0
k(4) initial 0.007 57 32 9 0
lower extreme 0 56 33 10 0
higher extreme 0.013 59 31 9 0
Second Series
k(3) initial 0.008 63 30 7 0
lower extreme 0 62 31 7 0
higher extreme 0.015 65 29 7 0
k(4) initial 0.009 63 30 7 0
lower extreme 0 62 31 7 0
higher extreme 0.019 65 29 7 0
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Efficiency of k(3) and k(4) kinetic rate constants.

Table 5 provides information about the initial, lower, and higher extreme values of k(5) and k(6) kinetic rate constants and the product yields obtained using these rate constants. As shown in Figures 6a–6d, the rate constants k(5) and k(6) were responsible for converting LW into oil and gas at a fixed temperature. The maximum oil yield, obtained with lower to higher extreme values of k(5), ranged from 56% to 58% with the first series and 63% to 62% with the second series (Figures 6a and 6c). In the first series, the oil yield slightly increased while a slight decrease was observed in the second series. Figures 6b and 6d demonstrate that the gas yield increased with both assumed series, which was confirmed by assessing the lower and higher extreme values of the kinetic rate constants. This increase in gas yield is attributed to a decrease in HW with the processing time.23 The lower Ea in the second assumed series compared to the first series increases the reaction rate and consequently the gas yield. The decreasing byproducts result in an increase in primary products at constant temperatures.24,25

Table 5. Different Values of k(5) and k(6) Kinetic Rate Constants and Their Effect on the Pyrolysis Products.

rate constant oil gas HW LW
First Series
k(5) initial 0.012 57 32 2 0
lower extreme 0 58 25 16 0
higher extreme 0.025 56 38 4 0
k(6) initial 0.017 55 28 19 0
lower extreme 0 40 37 5 0
higher extreme 0.034 67 29 3 0
Second Series
k(5) initial 0.016 63 30 2 0
lower extreme 0 64 24 11 0
higher extreme 0.331 62 35 1 0
k(6) initial 0.021 65 29 13 0
lower extreme 0 51 35 2 0
higher extreme 0.042 71 27 1 0
Open in a new tab

Figure 6.

Figure 6

Open in a new tab

(a) Efficiency of the k(5) rate constant predicted using the first series, (b) efficiency of the k(5) rate constant predicted using the second series, (c) efficiency of the k(6) rate constant predicted using the first series, and (d) efficiency of the k(6) rate constant predicted using the second assumed series.

Table 6 summarizes the initial, lower, and higher extreme values of the k(7) kinetic rate constant and the corresponding product yield. The LW was completely decomposed for both assumed series, whereas the HW was in constant flow at 10% and 5% for the first series and second series, respectively. Interestingly, the oil yield increased drastically with a shift in the k(7) value from the lower to the higher extreme. As shown in Figure 7, the oil yield increased from 35% to 74% and 37% to 81% for the first series and second series, respectively. The percentage gas yield decreased from 55% to 15% and from 56% to 13% with the first and second assumed series, respectively. It is also revealed that the oil yield can be increased by adjusting the initial value of k(7). The HW formation decreases with an increase in oil yield. Other kinetic rate constants did not show the same authority on the pyrolysis reaction as the k(7) rate constant, indicating the high commercial significance of this rate constant.

Table 6. Different Values of the k(7) Kinetic Rate Constant and Its Effect on the Pyrolysis Products.

rate constant oil gas HW LW
First Series
k(7) initial 0.013 60 55 10 0
lower extreme 0 35 28 10 0
higher extreme 0.027 74 15 10 0
Second Series
k(7) initial 0.015 65 56 5 0
lower extreme 0 37 28 5 0
higher extreme   81 13 5 0
Open in a new tab

Figure 7.

Figure 7

Open in a new tab

Efficiency of the k(7) kinetic rate constant.

5. Conclusions

This work is focused on extracting experimental rate constants from pyrolysis experiments that do not produce enough liquid fuels and gases for commercial application. Using information from experimental rate constants, we forecasted statistical rate constants and analyzed their sensitivity in the thermal pyrolysis of plastic waste. Only sensitivity analysis of kinetic rate constants can determine their efficiency during a pyrolysis reaction. This study advances our understanding of how temperature affects the kinetic rate constant and what effect frequency factor changes have on the rate of chemical reactions. Two sets of Ea and Ao at 370–380 °C in the R software were assumed with the Arrhenius equation to predict rate constants and analyze the sensitivity of each kinetic rate constant. The statistically predicted k(7) rate constant outperformed the other rate constants for high oil and gas yield. Using this rate constant, the gas amount decreased from 55% to 15% and from 56% to 13% with first series and second series, respectively. It is also revealed that the oil yield can be increased by adjusting the initial value of k(7). These results confirm the high significance of the conducted analysis for commercial-scale pyrolysis of plastic waste.

Acknowledgments

The authors acknowledge the support from the Deanship of Scientific Research, Najran University, Kingdom of Saudi Arabia, for funding this work under the Research Groups funding program grant code number (NU/RG/SERC/12/9).

Data Availability Statement

The reported data is available from the corresponding authors upon valid request.

The authors declare no competing financial interest.

References

  1. Jambeck J. R.; Geyer R.; Wilcox C.; Siegler T. R.; Perryman M.; Andrady A.; Law K. L.; Narayan R. Plastic waste inputs from land into the ocean. Science 2015, 347 (6223), 768–771. 10.1126/science.1260352. [DOI] [PubMed] [Google Scholar]
  2. Lebreton L.; Slat B.; Ferrari F.; Sainte-Rose B.; Aitken J.; Marthouse R.; Reisser J.; Hajbane S.; Cunsolo S.; Schwarz A.; et al. Evidence that the Great Pacific Garbage Patch is rapidly accumulating plastic. Sci. Rep. 2018, 8 (1), 1–15. 10.1038/s41598-018-22939-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Liu E. K.; He W. Q.; Yan C. R. ‘White revolution’to ‘white pollution’—agricultural plastic film mulch in China. Environmental Research Letters 2014, 9 (9), 091001. 10.1088/1748-9326/9/9/091001. [DOI] [Google Scholar]
  4. Ghatge S.; Yang Y.; Ahn J. H.; Hur H. G. Biodegradation of polyethylene: A brief review. Appl. Biol. Chem. 2020, 63 (1), 1–14. 10.1186/s13765-020-00511-3. [DOI] [Google Scholar]
  5. Santo M.; Weitsman R.; Sivan A. The role of the copper-binding enzyme–laccase–in the biodegradation of polyethylene by the actinomycete Rhodococcusruber. International Biodeterioration & Biodegradation 2013, 84, 204–210. 10.1016/j.ibiod.2012.03.001. [DOI] [Google Scholar]
  6. Inayat M.; Sulaiman S. A.; Kurnia J. C.; Naz M. Y. Catalytic and noncatalytic gasification of wood–coconut shell blend under different operating conditions. Environmental Progress & Sustainable Energy 2019, 38, 688–698. 10.1002/ep.13003. [DOI] [Google Scholar]
  7. Ndolomingo M. J.; Bingwa N.; Meijboom R. Review of supported metal nanoparticles: synthesis methodologies, advantages and application as catalysts. J. Mater. Sci. 2020, 55, 6195–6241. 10.1007/s10853-020-04415-x. [DOI] [Google Scholar]
  8. Suriapparao D. V.; Vinu R. Resource recovery from synthetic polymers via microwave pyrolysis using different susceptors. J. Anal. Appl. Pyrolysis 2015, 113, 701–712. 10.1016/j.jaap.2015.04.021. [DOI] [Google Scholar]
  9. Inayat M.; Sulaiman S. A.; Aini A. J.; Guangul F. M.; Atnaw S. M.. The Study of Temperature Profile and Syngas Flare in Co-gasification of Biomass Feedstock in Throated Downdraft Gasifier. In ICGSCE 2014; Hashim M. A., Ed.; Springer: Singapore, 2015; pp 203–210. [Google Scholar]
  10. Restrepo-Flórez J. M.; Bassi A.; Thompson M. R. Microbial degradation and deterioration of polyethylene–A review. International Biodeterioration & Biodegradation 2014, 88, 83–90. 10.1016/j.ibiod.2013.12.014. [DOI] [Google Scholar]
  11. Sen S. K.; Raut S. Microbial degradation of low density polyethylene (LDPE): A review. J. Environ. Chem. Eng. 2015, 3 (1), 462–473. 10.1016/j.jece.2015.01.003. [DOI] [Google Scholar]
  12. Sen S. K.; Raut S. Microbial degradation of low density polyethylene (LDPE): A review. J. Environ. Chem. Eng. 2015, 3 (1), 462–473. 10.1016/j.jece.2015.01.003. [DOI] [Google Scholar]
  13. Miandad R.; Rehan M.; Barakat M. A.; Aburiazaiza A. S.; Khan H.; Ismail I. M. I.; Dhavamani J.; Gardy J.; Hassanpour A.; Nizami A. S. Catalytic Pyrolysis of Plastic Waste: Moving Toward Pyrolysis Based Biorefineries. Front. Energy Res. 2019, 7, 1–27. 10.3389/fenrg.2019.00027. [DOI] [Google Scholar]
  14. Zhang H.; Perez-Garcia P.; Dierkes R. F.; Applegate V.; Schumacher J.; Chibani C. M.; Sternagel S.; Preuss L.; Weigert S.; Schmeisser C.; Danso D.; Pleiss J.; Almeida A.; Höcker B.; Hallam S. J.; Schmitz R. A.; Smits S. H. J.; Chow J.; Streit W. R. The Bacteroidetes Aequorivita sp. and Kaistellajeonii Produce Promiscuous Esterases With PET-Hydrolyzing Activity. Front. Microbiol. 2022, 12, 1–15. 10.3389/fmicb.2021.803896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Alqarni A. O.; Nabi R. A. U.; Althobiani F.; Naz M. Y.; Shukrullah S.; Khawaja H. A.; Bou-Rabee M. A.; Gommosani M. E.; Abdushkour H.; Irfan M.; Mahnashi M. H. Statistical Optimization of Pyrolysis Process for Thermal Destruction of Plastic Waste Based on Temperature-Dependent Activation Energies and Pre-Exponential Factors. Processes 2022, 10 (8), 1559. 10.3390/pr10081559. [DOI] [Google Scholar]
  16. Roisman I. V. Hydrodynamic model of a collision of a spherical plastic ice particle with a perfectly rigid substrate. International Journal of Impact Engineering 2022, 159, 104019. 10.1016/j.ijimpeng.2021.104019. [DOI] [Google Scholar]
  17. Eidesen H.; Khawaja H.; Jackson S. Simulation of the HDPE Pyrolysis Process. Int. J. Multiphys. 2018, 12 (1), 79–88. 10.21152/1750-9548.12.1.79. [DOI] [Google Scholar]
  18. Guo Z.; Lan X.; Xue P. High-precision monitoring of average molecular weight of polyethylene wax from waste high-density polyethylene. Polymers 2020, 12 (1), 188. 10.3390/polym12010188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mohamad Aini N. A.; Othman N.; Hussin M. H.; Sahakaro K.; Hayeemasae N. Effect of hybrid carbon black/lignin on rheological, mechanical and thermal stability properties of NR/BR composites. Plastics, Rubber and Composites 2022, 51 (6), 293–305. 10.1080/14658011.2021.1981718. [DOI] [Google Scholar]
  20. Antonyuk S.; Heinrich S.; Tomas J.; Deen N. G.; Van Buijtenen M. S.; Kuipers J. A. M. Energy absorption during compression and impact of dry elastic-plastic spherical granules. Granular Matter 2010, 12 (1), 15–47. 10.1007/s10035-009-0161-3. [DOI] [Google Scholar]
  21. Zhou Y. A theoretical model of collision between soft-spheres with Hertz elastic loading and nonlinear plastic unloading. Theoretical and Applied MechanicsLetters 2011, 1 (4), 041006. 10.1063/2.1104106. [DOI] [Google Scholar]
  22. Praveen Kumar K.; Srinivas S. Catalytic co-pyrolysis of biomass and plastics (polypropylene and polystyrene) using spent FCC catalyst. Energy Fuels 2020, 34 (1), 460–473. 10.1021/acs.energyfuels.9b03135. [DOI] [Google Scholar]
  23. Wirawan R. P.Plastic waste pyrolysis optimization to produce fuel grade using factorial design. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Vol. 125, p 13005. [Google Scholar]
  24. Shah S. H.; Khan Z. M.; Raja I. A.; Mahmood Q.; Bhatti Z. A.; Khan J.; Farooq A.; Rashid N.; Wu D. Low temperature conversion of plastic waste into light hydrocarbons. J. Hazard. Mater. 2010, 179 (1–3), 15–20. 10.1016/j.jhazmat.2010.01.134. [DOI] [PubMed] [Google Scholar]
  25. Jin X.; Lee J. H.; Choi J. W. Catalytic co-pyrolysis of woody biomass with waste plastics: Effects of HZSM-5 and pyrolysis temperature on producing high-value pyrolytic products and reducing wax formation. Energy 2022, 239, 121739. 10.1016/j.energy.2021.121739. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The reported data is available from the corresponding authors upon valid request.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES