We are all exposed, but some are more exposed than others

ABSTRACT

This paper defines functional cold exposure zones that illustrate whether a person is at risk of developing physical performance loss or cold weather injuries. Individual variation in body characteristics, activity level, clothing and protective equipment all contribute to variation in the effective exposure. Nevertheless, with the right education, training, and cold-adapted behaviours the exposure differences might not necessarily lead to increased risk for cold injury. To support the preparation process for cold weather operations, this paper presents a biophysical analysis explaining how much cold exposure risk can vary between individuals in the same environment. The results suggest that smaller persons are prone to be underdressed for moderate activity levels and larger persons are prone to be overdressed. The consequences of these discrepancies place people at different risks for performance loss or cold weather injuries. Nonetheless, even if all are well-dressed at the whole-body level, variation in hand morphology is also expected to influence hand skin temperatures that can be maintained; with smaller hands being more prone to reach skin temperatures associated with dexterity loss or cold weather injuries. In conclusion, this work focusses on bringing cold science to the Arctic warrior, establishing that combating cold stress is not a one size fits all approach.

Introduction

Orchestrating successful Arctic operations is extremely challenging due to the logistical complexities of moving troops in such remote regions of the globe. The Arctic and extreme cold environments in general also bring particularly inhospitable conditions for human survival. Our bodies are particularly ill-adapted to prevent hypothermia and function even in mild cold exposure [1,2]. This reality brings forth the importance for military operators to have adequate cold-protection equipment, training and operational behaviours to help recognise functional cold exposure zones as well as prevent and treat cold weather injuries (CWI) [3]. CWI vary in gravity from debilitating, local, non-life-threatening injuries (e.g., non-freezing or freezing cold injuries) to severe hypothermia or a potentially lethal decrease in core temperature. While some solutions seem simple at first glance, it remains that understanding how to best protect military operators in extreme cold is extremely complex due to differences in body shape and body composition, activity level, and experience, as well as due to the ever-changing climate of the Arctic.

Clearly, from an operational standpoint, simple solutions for improving cold tolerance are essential to ensure feasibility, compliance, and mission success. Current military behavioural doctrines are aimed to provide one size fits all solutions to minimise actual cold exposure (e.g., the TB-MED508 COLD acronym: Keep it Clean, avoid Overheating, wear it Loose and in Layers, keep it Dry; or its NL-Marines variant COLDFEET – Keep it Clean, avoid Overheating, wear it Loose and in Layers, keep it Dry, Fit your clothing, Exercise your extremities, Eat your rations and Tight boots are terrible) [2,4]. Furthermore, good leaders commonly stress the importance of protecting skin by considering local meteorological conditions, such as the windchill index. It is also possible that adherence to such protection levels may not always be feasible due to operational requirements. Moreover, when a group is operating in a cold weather environment, all are exposed to the same environment, yet some might be more exposed than others. Even when all are dressed in a similar clothing, individual variations in body characteristics may contribute to variation in the effective exposure [1,5]. In any event, individuals must learn to recognise, prevent and treat cold weather injuries. In this context, it is crucial that cold weather operators have the adequate knowledge to assess thermal demand and make appropriate decisions to identify risks for CWI. One might be inclined to think of using wearable sensing technology to measure individual body temperatures that predict the onset of performance loss or a CWI. However, with the current level of understanding, there is no clear delineation at what tissue temperature and duration of exposure CWI or performance degradation occurs on an individual level; with the exception for the risk of freezing cold weather injury [6]. Nevertheless, humans share an orderly recruitment of thermoregulatory mechanisms, which provides cues for individuals to understand the thermal state of the body and how to respond appropriately before it is too late [7,8]. Therefore, there are functional cues that can be recognised by individuals and followed on with appropriate actions to prevent performance degradation and CWI.

This paper is an effort to define functional cold exposure zones that convey whether a person is at risk of developing performance loss or CWI; both for the whole-body and for extremities, such as the hands and feet. Consequently, the main objective of this paper is two-fold: 1) to help recognise key functional cold exposure zones and, 2) to prevent cold injuries by combining individualised activity level and clothing solutions. In essence, this work focusses on bringing science to the Arctic warrior, establishing that combating cold stress is not a one size fits all approach. This paper presents a modelling study and is thereby hypothesis-driving, that is, it should be considered as a sensitivity analysis and reflects the consequences of the underlying mechanisms. It should be noted, however, that the concepts proposed here from modelling require extensive verification with experimental data before absolute values are taken into practice.

Assessment of the cold environment

The windchill index is frequently used to express the level of cold exposure for a combination of air temperature and wind speed. The windchill index can be used to assess the risk of freezing injury of exposed skin, specifically the cheek [2,9]. For bare fingers a separate windchill index has been developed, however it has not gained as much traction as the windchill index for the cheek [10]. The windchill index provides a method to assess the cold environment for exposed skin, but does not inform about the cold exposure on the whole-body, nor can it take into account the protective effect of gloves or mittens.

The determination and assessment of a cold environment for the whole-body is described in International Standard ISO 11079 “Ergonomics of the thermal environment – Determination and interpretation of cold stress when using required clothing insulation (IREQ) and local cooling effects” [11]. The method describes a heat balance calculation to derive the required clothing insulation to maintain the whole-body in thermal equilibrium with the environment. That is, the ISO 11079 expresses the level of cold stress that the environment imposes on a person by the required clothing insulation.

The analysis presented in this paper will use ISO 11079 to determine how the required clothing insulation to maintain thermal comfort may differ for a range of body sizes, whilst all are performing a similar marching task in the same cold environment. The outcome of the analysis will show whether persons of varying body size are either underdressed, well-dressed or overdressed for a specific cold exposure. The clothing-state directly corresponds to the physiological demand to defend body temperature:

• In an underdressed state, the body has to defend itself against the cold via central thermoregulatory mechanisms, such as skin vasoconstriction which reduces heat transport to the skin and cold-induced thermogenesis, which increases body heat production (e.g., non-shivering thermogenesis and shivering thermogenesis) [1,2]. Through a cold thermal sensation and thermal discomfort an underdressed state will also increase the drive for behavioural changes, such as fidgeting, being more active, changing the dress state and/or avoiding the cold. The thermoregulatory vasoconstriction response reduces blood flow to the skin of the extremities and thereby increases the risk of excessive cooling of the hands and feet, even when these body parts are covered by insulating gloves, mittens or boots.

• In a well-dressed state the body is in thermal balance and there is no central thermoregulatory drive for vasoconstriction, vasodilation, shivering or sweating. Skin blood flow is, however, still governed by local regulatory mechanisms that follow the Q10-effect [12,13]. That is, skin blood flow is halved for every 10°C decrease in local skin temperature. The local cooling effect may cause a feedback loop where heat transport to the skin is continuously decreased due to cold skin, and thereby skin cools further until equilibrium is reached. Thus, keeping the extremities warm and maintaining blood flow, either by insulation or by behaviour such as exercising the extremities is an important countermeasure.

• In an overdressed state, the body has to defend itself against overheating via central thermoregulatory mechanisms, such as skin vasodilation, which increases heat transport to the skin, and sweating, which increases evaporative heat transport [2]. An overdressed state is commonly reached with moderate-to-high activity levels. According to cold weather operational guidelines sweating should be avoided at all times as it will make clothing wet and reduce its insulative properties. Wet clothing becomes a risk factor when the activity level is reduced, and the person becomes effectively underdressed. Moreover, freezing of wet clothing may create avenues of direct skin contact with ice, greatly increasing the risk of cold weather injuries.

Clearly, both overdressed and underdressed states should be avoided. But that may not be realistic in practice. As mentioned above, the whole-body dress state influences both the thermal balance of the whole-body as well as the thermal balance of the extremities.

The extremities such as the hands and feet are sensitive to performance loss or CWI due to cold exposure. To assess the effect of individual variation on effective cold exposure it is warranted to both express the exposure on a whole-body level and on an extremity level. The windchill index does not take into account differences in hand size or potential protective and insulative properties of gloves or mittens. Therefore, the windchill index cannot be used for the current analysis. However, in this paper, the hand segment of the internationally recognised Fiala thermophysiological simulation model is adapted to determine the effect of individual variation in hand size on effective cold exposure whilst wearing a common mitten [12,14]. For the extremities, the effective cold exposure is expressed in functional cold zones as described below.

Experiencing cold during cold weather operations may be expected [3]. However, it is the dose of cold that may determine whether the cold only affects the subjective perception of the environment, or that it progresses into performance degradation or CWI. For hands in contact with a cooling surface, comfortable hand skin temperature is typically close to 33°C; comfortably cool hands are reported between 27°C and 20°C; thermal discomfort is reported between 25°C and 15°C and pain is reported from hand skin temperatures below 24°C [15]. Performance degradation of the extremities is usually expressed by dexterity loss. Dexterity can further be classified into gross (e.g., loosening of nuts) and fine dexterity (e.g., inserting pins) and is generally found to decrease when hand skin temperature reaches below 22°C and becomes critical below 15°C [2,16–18]. Furthermore, non-freezing CWI can develop when skin temperature is maintained below 15°C for long durations, and general risk for CWI is expected when skin temperatures are below 5 °C for long durations [1,19]. It is important to note that there is considerable individual variation in the thermal sensitivity to cold and its potential implications for cold mitigating behaviour. Considering the overlapping temperature ranges, the perception of cold discomfort at the extremities should at all times be an alarming signal that performance degradation and cold weather injury may occur. Therefore, the following functional cold zones of hand skin temperature are proposed as:

• (green) Comfortably cold, hand skin temperature 27°C and above.

• (yellow) Dexterity loss and pain, starting from hand skin temperature 22°C and below.

• (orange) Pain and non-freezing cold injury risk if sustained for long time from 15°C and below.

• (red) CWI risk, starting from hand skin temperature 5°C and below.

Methods

The methods section first describes the overall analysis method and consequently dives deeper into the models that are used for the analysis.

The analysis consists of two stages: 1) the determination of the expected whole-body dress state, 2) the determination of the expected functional hand skin temperature for a given air temperature.

The two analyses are linked in that heat transport from the body to the hands is dependent on the whole-body dress state as described below.

The whole-body dress state is determined by iterating the ISO 11079 model for a cold environment (−20 °C) and a low wind speed at ground level (5 km/h), relative humidity is kept at 85% and mean radiant temperature is equal to air temperature. Furthermore, the activity level is set to a moderate activity (walking 4 km/h) whilst carrying a 20 kg load; the walking is assumed to take place on a small slope, and lastly the analysis is performed for a hypothetical set of soldiers (see Figure 1).

Figure 1.

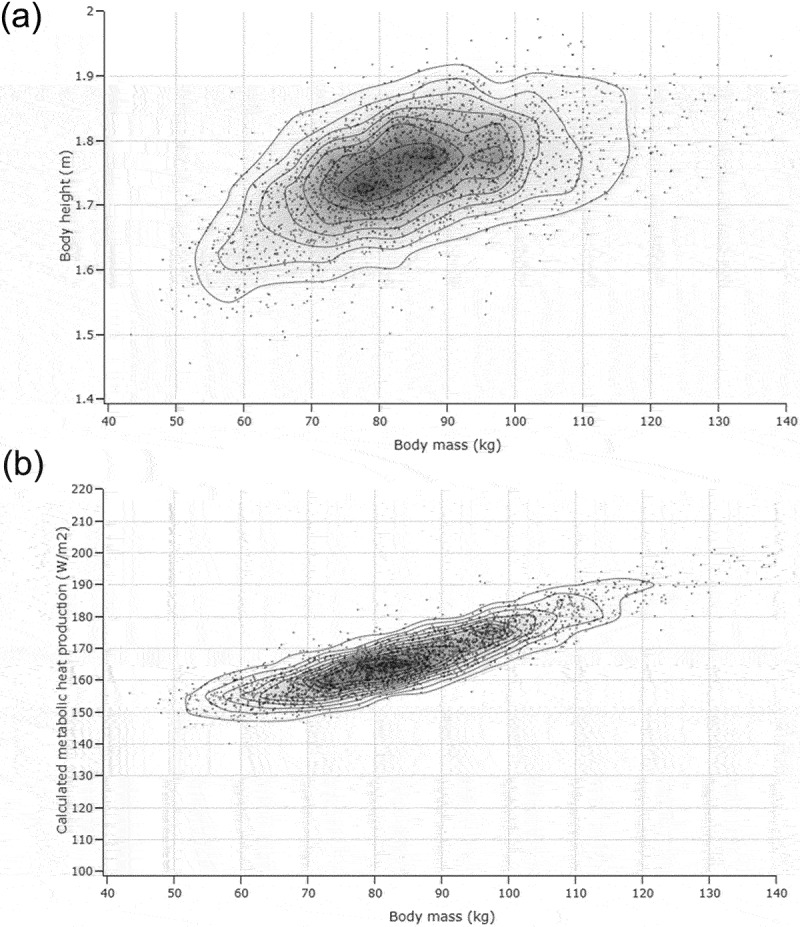
A) set of soldiers (n=2189) with varying body size (height and weight) for which the required clothing insulation analyses have been performed. B) calculated metabolic rate of the set of soldiers for a 4km/h walking activity on a small slope (2%) road, carrying a 20kg load.

Body surface area is determined according to Du Bois and Du Bois [20]. The metabolic rate associated with the walking speed, body weight and carried load is determined according to Pandolf, assuming a 2% incline on a flat top road [21]. The Pandolf equation is described below with P the metabolic rate in Watts, W the body weight in kg, L the mass of the load carried in kg, $\eta$ is a terrain factor ($\eta =1)$, V is the walking speed in m/s and G is the grade (fraction, %).

$$P=1.5\cdot W+2.0\cdot \left(W+L\right)\cdot {\left(\frac{L}{W}\right)}^2+\eta \cdot \left(W+L\right)\cdot {\left(1.5\cdot V^2+0.35\cdot V\cdot G\right)}_{\hspace{0.17em}}$$

The thermal properties of the clothing ensemble are chosen as a realistic arctic clothing attire with an intrinsic clothing insulation of 2.8 clo (0.434 m²KW⁻¹) and low wind permeability (p = 8 lm⁻²s). The weight of the clothing is not added to the carried load due to limitations in the calculation of the insulation required. To account for readjusting clothing or opening and closing parts of the ensemble 0.1 clo margin is considered when comparing the required clothing insulation with the provided clothing insulation for the determination of the clothing-state (underdressed, well-dressed, or overdressed).

For the second stage, a steady state biophysical hand model is used to calculate heat balance for a given combination of hand skin temperature, insulation, evaporative resistance and environmental conditions. Heat gain of the hand (through blood flow, arterial blood temperature and metabolism) is derived as described in the passive part of the Fiala model and heat loss from the hand skin surface (convection, radiation and evaporation) is calculated using the effective local thermal and evaporative resistances and their relation to heat flow as described in ISO 9920 [12,22].

Furthermore, the analysis is performed for two hand sizes with varying surface to volume ratio: an average female hand (278 ml total hand volume, 0.037 m² total hand surface area) and an average male hand (406 ml total hand volume, 0.040 m² total hand surface area) [23]. The hand is protected with a realistic windproof mitten configuration with the following thermal properties: a local intrinsic clothing insulation of 1.85 clo (0.287 m²KW⁻¹), local total evaporative resistance of 51 m²PaW⁻¹ and zero wind permeability.

The extremity steady state air temperature is influenced by blood flow and heat transport to the hands and the local insulation of the mittens. The Fiala thermoregulatory model follows the original Stolwijk description that the baseline blood flow (B₀) to tissues scales with the product of centrally mediated neurophysiological mechanisms (N) and local mechanisms (Q10-effect) [12,24,25].

$$B_i=B_0\cdot N\cdot Q_{10}$$

Baseline blood flow to a hand and metabolic heat production depends on hand size and is estimated using the Fiala hand segment (see values in Appendix Table A1). In the well-dressed state there is no central vasoconstriction drive, nor vasodilatory drive (N = 1), yet local blood flow regulation is still taken into account. Local regulation of skin blood flow follows the Q10-effect with a base of 2 which means that for each 10°C decrease of local skin temperature blood flow reduces by 50%. This has been shown experimentally for skin at the ventral forearm and both sides of the hand [13]. For the underdressed state, the centrally mediated vasoconstriction is estimated as significant vasoconstriction (N = 0.3; 70% below baseline from centrally mediated mechanisms alone), and for the overdressed state the centrally mediated vasodilation is assumed as a modest vasodilation (N = 1.2; 20% increase above baseline from centrally mediated mechanisms). These values are considered as illustrative for the principle, but may vary considerably in a practical situation. An example of the resulting scaling of blood flow to the hands relative to baseline, assuming the baseline hand skin temperature is 33.5°C, is shown in Appendix Table A2.

According to the Pennes bioheat equation, the amount of heat transported by blood flow is equal to the product of the density of blood (1060 kgm⁻³) [3], the specific heat capacity of blood (3.56 J kg⁻¹K⁻¹), the amount of blood flow (m³ s⁻¹) and the temperature difference between the arterial blood temperature and tissue temperature (K). The Fiala thermoregulatory model describes that the arterial blood temperature can be estimated from central body temperature, local end point tissue temperature and blood flow, taking into account the counter current heat exchange that occurs between arteries and veins [12]. For this analysis central body temperature is assumed to be 37.0°C, and blood flow is scaled from baseline blood flow for the functional hand skin temperatures as shown in Appendix Table A2, and the estimated arterial blood temperatures and estimated heat transport to the hand by blood flow are given in Appendix Table A3.

Following the description above, the heat balance is calculated over a range of hand skin temperature (−10 °C-+35 °C) and air temperature (−50 °C - +10 °C), at a wind speed of 1 km/h for bare hands and 5 km/h for hands with a mitten configuration. The procedure results in a matrix of heat balances for each combination of hand temperature and air temperature; and has been repeated for an underdressed state, well-dressed state and overdressed state; and as well as for bare hands and hands with a common military mitten configuration. The regions where the heat balance equals 0, correspond to combinations of hand temperature and air temperature for which there is no heat gain nor heat loss, and are therefore stable zones that can be maintained in steady state. The analysis result is shown in a contour plot that shows which hand temperature zone is in thermal balance vs. air temperature for a person in an underdressed, well-dressed and overdressed state.

Results

The expected whole-body dress state for the fictive set of soldiers performing the same activity is shown in Figure 2. The most common required clothing insulation is 2.8 clo, and coincides with a majority of people with a body mass of about 80 kg. In case all are using a similar clothing level of 2.8 ± 0.1 clo, 54% of the population will be well-dressed and will not need significant whole-body responses to defend against cold. In contrast, 18% will be underdressed, who will experience reduced blood flow to the extremities; and 28% will be overdressed and experience increased blood flow to the extremities and potentially sweating.

Figure 2.

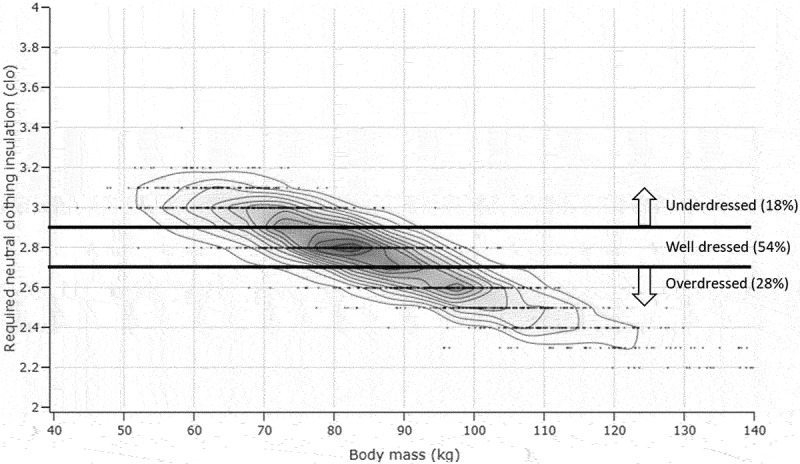
Calculated required clothing insulation for a varying set of body sizes. Relative to the average required clothing level (2.8±0.1 clo) 18% is underdressed, 28% is overdressed and 54% is well-dressed. The calculations have been performed using the metabolic rates shown in Figure 1b.

The second stage of the analysis is the calculation of expected functional hand skin temperature zones for a low wind situation. The influence of whole-body dress state and hand size on functional hand temperature zones is shown for bare hands in 1 km/h wind in Figure 3. Overall, Figure 3 shows that gloves or mittens are crucial for sustained exposure in cold environments, regardless of dress state and hand size. For underdressed individuals, there is little heat transport to the hands and therefore the hands cool linearly with decreasing air temperature with no benefit of having larger hands. For well-dressed individuals with bare average female hands discomfort and pain is already expected above 5°C air temperature, whereas for average male hands these issues are expected below 5 °C air temperature. Being overdressed increases blood flow to the extremities and therefore hand temperatures can be sustained at lower air temperatures.

Figure 3.

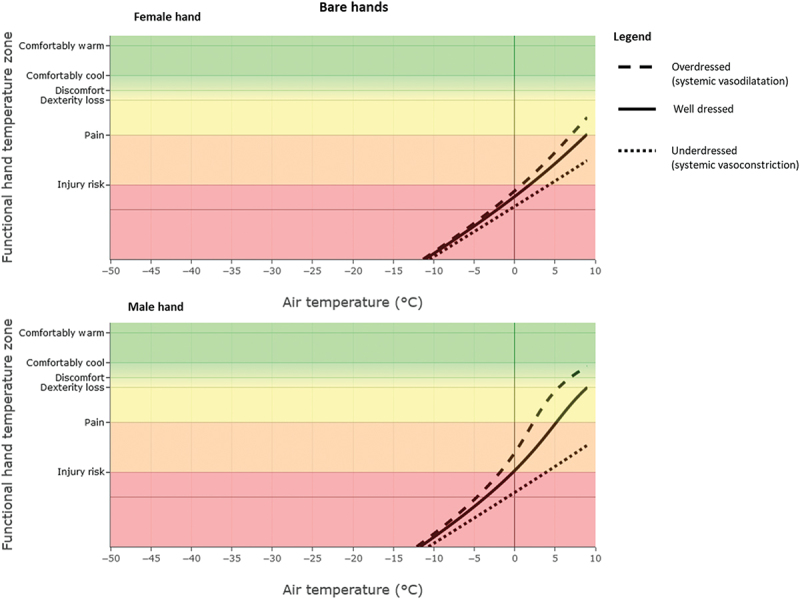
Bare hands functional hand temperature zones vs air temperature for three levels of dress state (1 km/h wind). Top: a female hand. Bottom: a male hand. The lines indicate heat balance and hand temperature will not change. Points on the right side of a line coincide with positive heat balance and hands will warm up. Points on the left side of a line coincide with negative heat balance and the hands will cool down.

Next, the functional hand temperature zones are shown for wearing common military mittens (Figure 4). Overall, Figure 4 shows that being underdressed is catastrophic for maintaining hand function in arctic conditions. For well-dressed or overdressed individuals with average male hands performance loss can be prevented at −20°C, as long as blood flow is maintained, but this analysis also suggests that the average female hand requires either more insulation from the mittens or more vasodilation to prevent injury or pain. Interestingly, regardless of dress state and hand size, the lowest air temperature that can be sustained coincides with the functional hand temperature zone where discomfort and dexterity loss become plausible. Therefore, these functional zones may also be used as critical zone indicators that behavioural action has to be taken.

Figure 4.

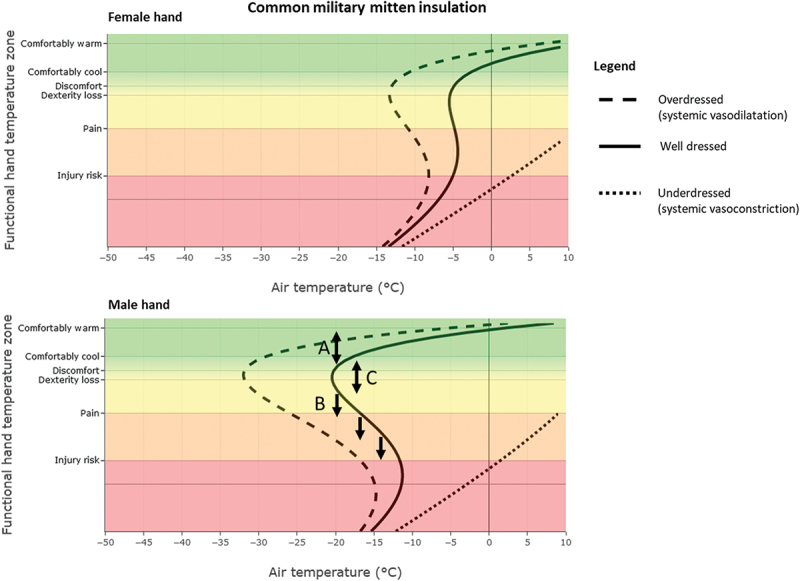
Common mitten hands functional hand temperature zones vs air temperature for three levels of dress state (5 km/h wind). Top: a female hand. Bottom: male hand. The line indicates heat balance and hand temperature will not change. Points on the right side of a line coincide with positive heat balance and hands will warm up. Points on the left side of a line coincide with negative heat balance and the hands will cool down. The letters in the bottom panel are supportive of three thought experiments: (A) starting from the solid line, if the hand accidentally warms up, it will cool down again until settling on the solid line. (B) If the hand accidentally cools down and ends on the left side of the solid line, it will continue to cool down. (C) In case the hand temperature drops from the solid line and ends up at the right side of the solid line, the hands will be in positive heat balance and automatically warm up again.

The example given in Figure 4 top panel suggests that an average female hand is able to maintain comfortably cool hands around −5°C when well dressed, and −15°C with modest vasodilation following being overdressed, yet not able to maintain a stable functional hand temperature at − 20 °C. It might be sustained with a higher insulative mitten configuration, or more heat input from blood flow (e.g., greater vasodilation due to increased activity levels). In contrast, Figure 4 bottom panel suggests that the average male hand is able to maintain a comfortably cool hand close to −20 °C, and even <−30 °C when modestly overdressed. Neither hand can sustain functional in case the whole body is underdressed. Points on the right side of a line coincide with positive heat balance and hands will warm up again (Figure 4). Points on the left side of a line coincide with negative heat balance and the hands will cool down. From this perspective, we suggest a thought experiment: consider that the hand incidentally heats up, a temporary excursion to the green zone may be the result, but it will cool down again until settling back on the line (bidirectional arrow A in Figure 4). In contrast, if the hands incidentally cool down near point B, the hands will continue to cool down; yet if it happens near point C, the hands will warm up by themselves. For hands cooling down near point B, the only solution is to increase heat flow to the hands again. For instance, when activity level is increased (e.g., by increasing carried load). This may cause the person to become overdressed and consequently achieve warmer hands.

Discussion

The analyses presented in this paper show that small persons are prone to be underdressed during moderate activity levels, whereas large persons are prone to be overdressed when all are exposed to the same cold environment wearing similar protective clothing. Moreover, even if all are well-dressed such that no central thermoregulatory mechanisms are active and all are wearing protective mittens to protect the extremities from the cold, still people with relatively long and thin hands are prone to suffer from dexterity loss and CWI compared to their large counterparts with larger hands. The latter is supported by experimental data, at least for the dexterity issue, but the authors are not aware if that is also supported for the risk of injury [26]. The analysis also shows the importance of maintaining blood flow, or warm hands for the ability to maintain hand temperature. For instance, if hand skin temperature drops due to an operational task that requires removal of a mitten, the associated reduction in skin blood flow and reduced heat transport to the hands prevents the rewarming of the hand without behavioural actions such as exercising of the extremities or active rewarming. The results presented in this paper are hypothesis-driving, and require extensive verification by experimental data before practical use.

The choice of the underlying models to calculate the body surface area and metabolic rate may influence the outcome. For instance, the equation from Du Bois and Du Bois for body surface area can be replaced by a more contemporary version for physically active men and women such as that from Looney et al. [27]. Likewise, the Pandolf equation for heat production can be replaced by a different equation that is specific to the metabolic costs of standing and walking for military age adults [28]. However, replacing both the equations for body surface area and metabolic costs does not change the outcome of the analysis on required clothing insulation, other than that the range of required clothing insulation becomes wider. That is, low mass individuals need an even higher clothing level and high mass individuals need even lower clothing insulation, yet the average remains the same.

The analyses shown in Figures 3 and 4 also differ in shape. With bare hands (Figure 3), the functional hand temperature follows an intuitive near linear relation with air temperature, with each air temperature coinciding with only a single hand temperature. Figure 4 however shows a parabolic relation and reveals the possibility that a specific air temperature can yield two stable hand temperatures. The authors are not aware of experimental physiological data that shows similar results. However, the behaviour can be explained from the physiological principles that are included in the model: 1. Reduced blood flow due to vasoconstriction causes a linear reduction in heat transport to the hands; and 2. Reduced blood flow to the hands also causes a reduced arterial blood temperature to the hands via the counter current heat exchange principle, and reduced arterial blood temperature also has a linear relation to heat transport. 3. Combining the effects of reduced blood flow and reduced arterial blood temperature results in a quadratic effect (parabola), and hence there are two solutions possible for heat balance. It is interesting that this behaviour only shows up when taking into account the insulation of the mittens (Figure 4) and not for bare hands (Figure 3). Apparently, the increased heat loss from bare hands dampens the underlying physiological dynamics and its heat transport consequences. The other way around, increased insulation by mittens amplifies the underlying mechanisms at play.

The model to calculate the insulation required for the whole-body level and the hand heat balance model are both steady state models. They allow to calculate what is a stable condition, or what eventually will be the stable equilibrium, but they do not directly provide an answer to how long it takes to reach a certain equilibrium, or to the consequences of dynamic changes in the environment, activity or clothing characteristics. Insight in the aforementioned questions may be obtained by using dynamic thermoregulatory simulation models for the whole body as well as specifically for the hands [29,30].

The analyses in this paper are conclusive that people with smaller and thinner hands are prone to experiencing colder hand skin temperatures. Nevertheless, the results that are presented in this document are not conclusive to the hypothesis that people with small hands will get CWI more often, it is well possible that behavioural components in those people are strong developed to avoid such cooling of the skin; thereby effectively reducing the risk for cold weather injuries. That is, with the right education, training and adapted behaviours, biological differences might not necessarily lead to increased risk for cold injury.

Conclusion

This paper presents a series of biophysical analyses to show how individual variation in body size and hand morphology influence the variation of cold exposure even when all are exposed to the same environment and in a similar uniform. In general, smaller persons are prone to be underdressed for moderate activity levels and larger persons are prone to be overdressed. The thermoregulatory consequences of these discrepancies displace people at different risks for performance loss or CWI. Nonetheless, even if all are well-dressed at the whole-body level, variation in hand morphology is also expected to influence functional hand skin temperatures that can be maintained; with smaller hands being more prone to reach skin temperatures associated with dexterity loss or CWI. The findings in this paper can be used for educational purposes aimed at mitigation and prevention of performance loss and CWI by behavioural measures.

Appendix.

Table A1.

Estimated properties of baseline gross blood flow to hand and local metabolic rate of the hand.

	Baseline blood flow (m3 s−1)	Metabolic rate (Wm−2
Female hands	2.00 E-7	3.2
Male hands	2.91 E-7	4.2

Table A2.

Estimated fraction of remaining blood flow to the hands due to centrally mediated neurophysiological mechanisms ($N$) and locally mediated mechanisms ($Q_{10}$) per functional hand skin temperature class.

	Estimated fraction remaining blood flow from baseline represented as $N\cdot Q_{10}=x$
Dress level	Underdressed	Well-dressed	Overdressed
Comfortably cold (27°C)	$0.3\cdot 0.66=0.20$	$1\cdot 0.66=0.66$	$1.2\cdot 0.66=0.79$
Dexterity loss (22°C)	$0.3\cdot 0.45=0.14$	$1\cdot 0.46=0.46$	$1.2\cdot 0.45=0.54$
Pain and NFCI (15°C)	$0.3\cdot 0.28=0.09$	$1\cdot 0.28=0.28$	$1.2\cdot 0.28=0.34$
Injury risk (5°C)	$0.3\cdot 0.14=0.04$	$1\cdot 0.14=0.14$	$1.2\cdot 0.14=0.17$

Table A3.

Estimated arterial blood temperature and estimated heat transport to the hands for functional hand skin temperature for the well-dressed situation.

	Estimated arterial blood temperature reaching hand skin (°C)		Estimated heat transported to hands by blood flow (W)
Hands	Average male	Average female	Average male	Average female
Comfortably cold (27°C)	34.4	33.5	5.4	3.3
Dexterity loss (22°C)	31.9	30.5	5.1	3.0
Pain and NFCI (15°C)	27.8	25.7	4.9	2.8
Injury risk (5°C)	16.6	14.0	1.9	1.3

Funding Statement

BK was funded through Ministerie van Defensie V1917, V2316 and ITP CWO.

Disclosure statement

The authors report there are no competing interests to declare. The views, opinions and/or findings contained in this article are those of the authors (Karl Friedl, John Castellani) and should not be construed as an official United States Department of the Army position, or decision, unless so designated by other official documentation. This article is approved for public release, and distribution is unlimited.