A machine-vision-based frailty index for mice

Abstract

Heterogeneity in biological aging manifests itself in health status and mortality. Frailty indices (FIs) capture health status in humans and model organisms. To accelerate our understanding of biological aging and carry out scalable interventional studies, high-throughput approaches are necessary. Here we introduce a machine-learning-based visual FI for mice that operates on video data from an open-field assay. We use machine vision to extract morphometric, gait and other behavioral features that correlate with FI score and age. We use these features to train a regression model that accurately predicts the normalized FI score within 0.04 ± 0.002 (mean absolute error). Unnormalized, this error is 1.08 ± 0.05, which is comparable to one FI item being mis-scored by 1 point or two FI items mis-scored by 0.5 points. This visual FI provides increased reproducibility and scalability that will enable large-scale mechanistic and interventional studies of aging in mice.

Aging is a terminal process that affects all biological systems. Biological aging, in contrast to chronological aging, occurs at different rates for different individuals. There is an observed heterogeneity in mortality risk and health status among individuals within an age cohort^1,2. The concept of frailty is used to quantify this heterogeneity and is defined as the state of increased vulnerability to adverse health outcomes³. Identifying frailty is clinically important as frail individuals have an increased risk of diseases and disorders, worse health outcomes from the same disease and even different symptoms of the same disease².

An FI is an invaluable tool for quantifying frailty^4,5. In this method, an individual is scored on a set of age-related health deficits to produce a cumulative score⁴. The presence and severity of each health deficit is scored as 0 for not present, 0.5 for partially present or 1 for present. The health deficits scored can vary between indices but still show similar characteristics and utility; two sufficiently large frailty indices (FIs) with different deficits would similarly predict an individual’s risk of adverse health outcomes and mortality⁴. FI scores outperform other developed measures, including molecular markers and frailty phenotyping at predicting mortality risk and health status^5–7.

FIs have since been adapted for use in mice^2,5,8. The mouse FI shows many of the characteristics of human FIs, including a submaximal limit and a strong correlation with mortality⁹. Mouse FIs have been used successfully to evaluate a variety of aging interventions¹⁰ and for construction of models of chronological age and mortality⁵. Unlike human FIs, the majority of mouse frailty indexing has been performed using the same set of health deficits as Whitehead et al.², although some studies have substituted a small number of mouse FI items for ones that better fit their specific strain or experiment¹⁰.

The successful creation of the mouse FI is a major step forward in aging research, particularly for long-term interventional studies that may be carried out by multiple laboratories; however, mouse FI scoring requires trained individuals, which limits the scalability of the tool. Manually scoring thousands of mice is labor intensive and so mouse studies that employ FIs are much smaller⁹. Furthermore, as many of the FI metrics require some level of subjective judgment, there are concerns about scorer-based variability and reproducibility^10–12. The reliability of FI between scorers has been found to be very good in general, but these studies on inter-scorer agreement strongly emphasize the importance of inter-scorer discussion and refinement in obtaining high agreement^10–12. Discussion and refinement is not always feasible in multi-site or long-term studies. Therefore, although an FI is an extremely useful tool for aging research, an increase in its scalability, reliability and reproducibility through automation would enhance its utility.

Toward this end, we developed an automated visual FI (vFI) using videos of mice in the open field. The open field is one of the oldest and most widely used assays for rodent behavior¹³. Commonly, measures such as locomotion, thigmotaxis, grooming and defecation have been used¹⁴; however, advances in machine-learning techniques have greatly expanded the types of metrics that can be extracted from the open-field assay^15,16. These advances are largely due to discoveries in the computer vision and statistical learning field^17–22. We, along with a number of other groups, have applied these new methods to animal behavior analysis. Our group has developed methods for image segmentation and tracking in complex environments²³, action detection²⁴ and pose-based gait and whole-body coordination measurements in the open field²⁵. These and other highly sensitive methods have advanced animal behavior extraction^15,26–28.

Our goal was to develop an efficient scalable method to determine frailty in the mouse using computer vision-based features. We hypothesized that biological aging produces changes in behavior and physiology that are encoded in video data (we can visually determine the frailty of an animal based on their open-field behavior). Additionally, sex differences in the FI are still an active area of research^9,29–32. Therefore, we generated one of the largest mouse FI datasets consisting of both males and female C57BL/6J. We extracted measures from video data using machine-learning methods. We used these features to construct a vFI model that has high prediction accuracy. Through modeling, we also gained insight into which video features are important to predict FI score across age and frailty status. Our automated vFI will increase efficiency and accuracy for large-scale studies that explore mechanisms and interventions of aging.

Results

Data collection and study design.

Our overall approach is described in Fig. 1a. The study was conducted with 643 data points (371 males and 272 females) taken over three rounds of testing with 533 unique mice (Supplementary Table 1). Top-down video of each mouse in a 1-h open-field session was collected according to previously published protocols^16,23 (Methods, Fig. 1a and Supplementary Videos 1 and 2 as examples of a young and old mouse). Following the open field, each mouse was scored using a mouse FI by a trained expert to assign a manual FI score³³ (Supplementary Fig. 2a). Despite bi-modality in age (Hartigan’s test³⁴, $D=0.07$, $P<2.2\times {10}^{-16}$) of our data, we found that the Simpson’s paradox³⁵ did not manifest in any of the top 15 features in our data (Supplementary Fig. 4a,b).

Fig. 1 |. Approach overview to build a visual frailty index.

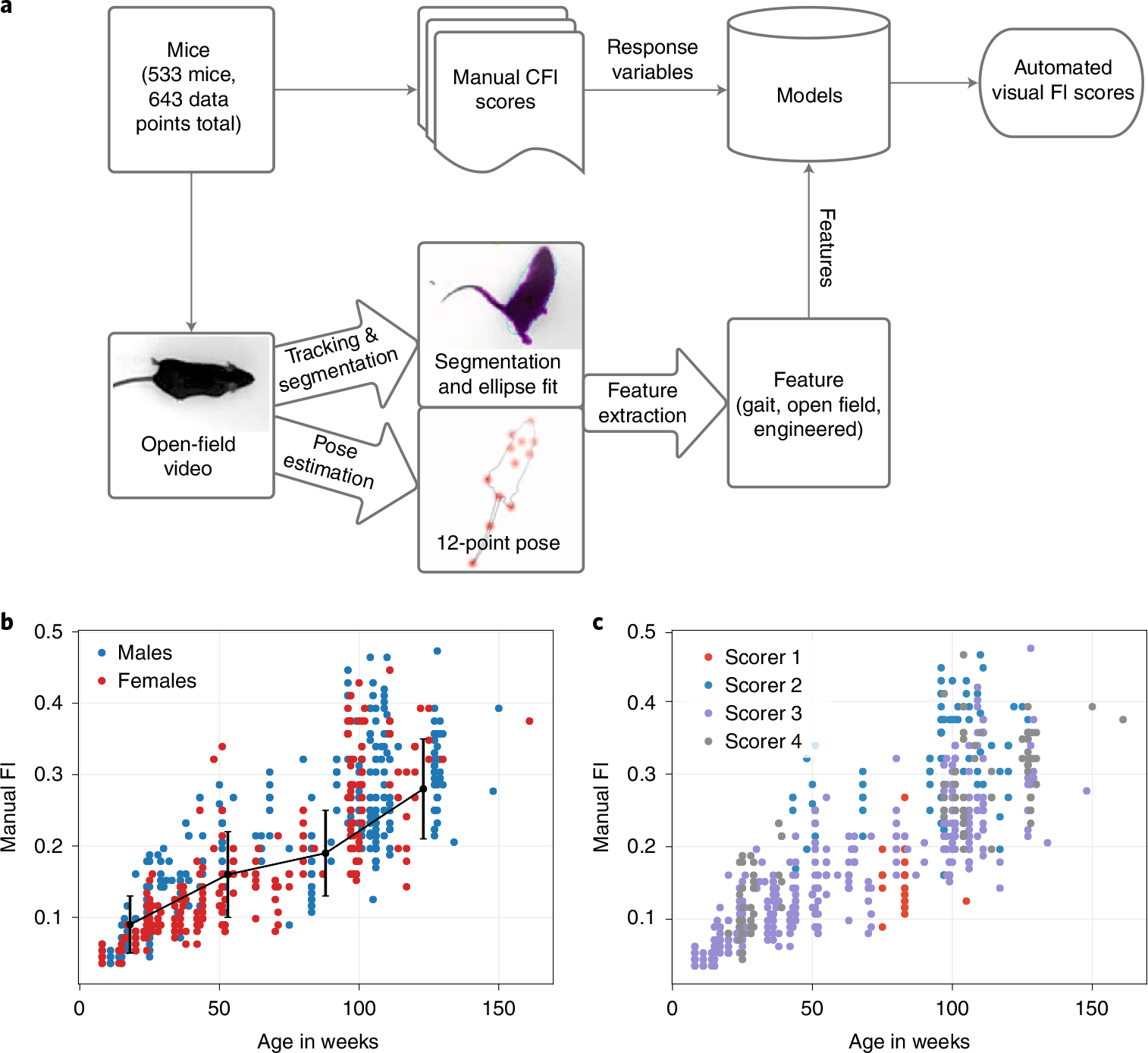
a, Pipeline for automated vFI. Top-down videos of the open field for each mouse are processed by a tracking and segmentation network and a pose estimation network. The resulting frame-by-frame ellipse-fits and 12-point pose coordinates are further processed to produce per-video metrics for the mouse. The mouse is also manually frailty indexed to produce an FI score. The video features for each mouse are used to model its FI score. b, Distribution of FI score by age. The black line shows a piece-wise linear fit (n = 160, 146, 50, 287 mice) to the data. The center point is the mean, and the error bars are the s.d. values. c, Effect of scorer on FI data; 42% of the variability in manual FI scores was due to a scorer effect (RLRT = 183.85, P < 2.2 × 10⁻¹⁶).

Consistent with previous data, in our dataset, the mean FI score increases with age (Fig. 1b). The heterogeneity of the FI scores also increases with age. We found a submaximal limit of the FI score slightly below 0.5 for our data, which falls within a range of submaximal limits shown in mice^2,9. These results show that our FI data are typical of other mouse data and mirror the characteristics of human FIs⁹. Over the course of the data collection, four different scorers conducted the manual FI. Inspection of the data showed a scorer effect on the manual FI score (Fig. 1c). For instance, scorer 1 and 2 tended to generate high and low frailty scores, respectively (Supplementary Fig. 1b). The modeling indicated that 42% of the variability in manual FI scores was due to a scorer effect (Fig. 1c). Piloerection, kyphosis and vision are the most affected items (Supplementary Fig. 1a).

Feature extraction.

The open-field video was processed by a tracking network and a pose estimation network, to produce an ellipse fit and a 12-point pose of the mouse for each frame^23,25. These frame-level measurements were used to calculate a variety of per-video features, including traditional open-field measures²³, grooming²⁴, gait and postural measures²⁵ and engineered features. All extracted features with explanation and source of the measurements can be found in Supplementary Table 2. Overall, there was a very high correlation between median and mean video metrics (Supplementary Fig. 3a,b). We decided to use only medians and interquartile ranges (IQRs) in modeling where possible for two reasons: medians tend to have higher correlation with FI score than mean and median and IQRs are more robust to outlier effects than means and s.d. values, respectively. This gave us a total of 44 video features (Supplementary Tables 3 and 2). We first looked at metrics taken in standard open-field assays, such as total locomotor activity, time spent in the periphery and center and grooming bouts (Fig. 2a). All standard open-field measures showed low correlation with both FI score and age (Supplementary Tables 3 and 4).

Fig. 2 |. Sample features used in the vFI.

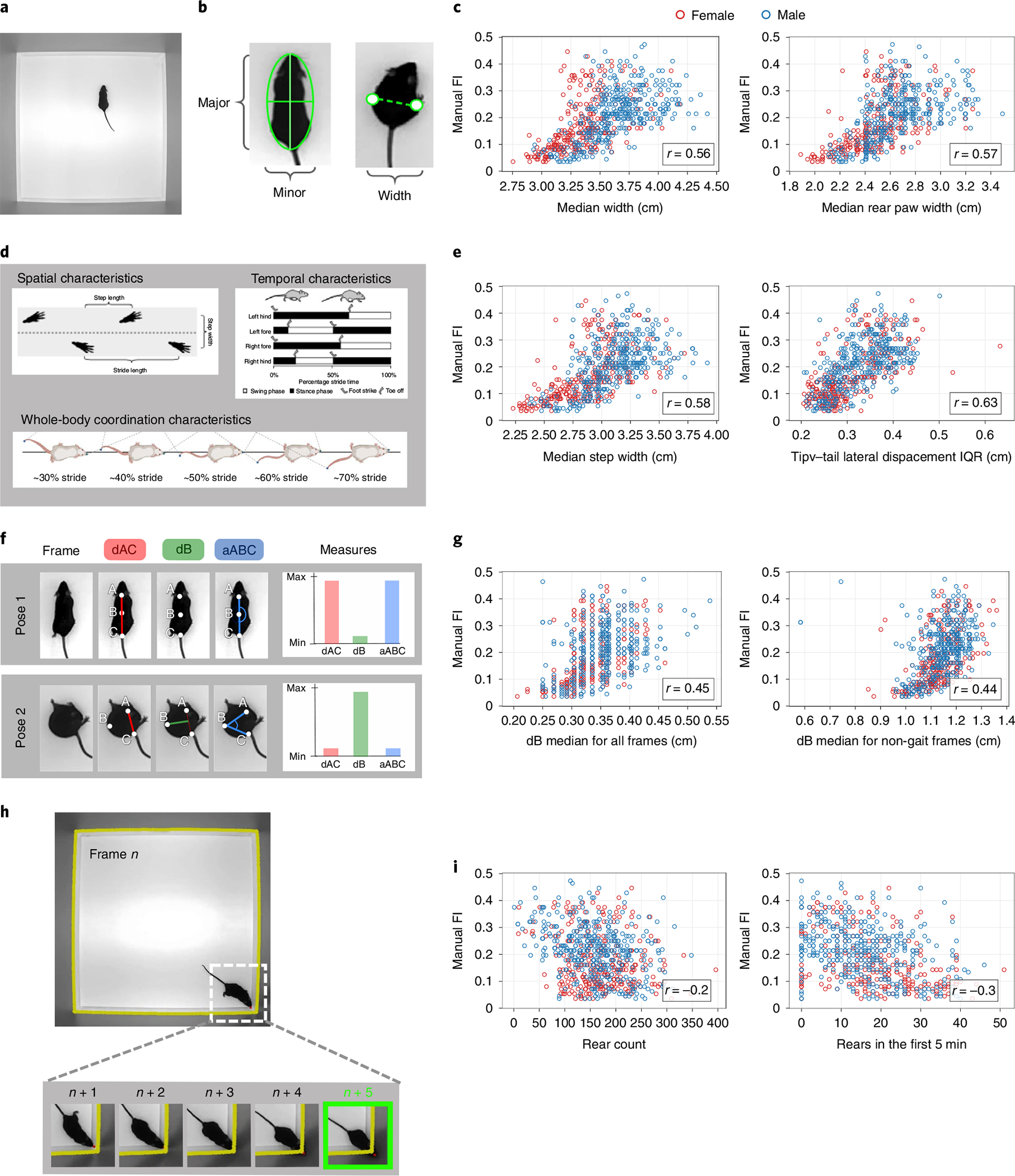
a, Single frame of the top-down open-field video. b, Morphometric features from ellipse fit and rear-paw distance measure performed on the mouse frame by frame. The major and minor axis of the ellipse fit are taken as the length and width, respectively. c, The median ellipse fit width and the median rear-paw distance taken over all mouse frames are highly correlated with FI score. d, Spatial, temporal and whole-body coordination characteristics of gait used to create metrics²⁵. e, The median step width and the IQR of tip-tail lateral displacement taken over all strides for a mouse are highly correlated with FI score. f, Spinal mobility measurements taken at each frame. dAC is the distance between point A and C (base of head and base of tail, respectively) normalized for body length, dB is the distance of point B (mid-back) from the midpoint of the line AC and aABC is the angle formed by the points A, B and C. When the mouse spine is straight, dAC and aABC are at their maximum value, whereas dB is at its minimum. When the mouse spine is bent, dB is at its maximum value, whereas dAC and aABC are at their minimum (Supplementary Video 3). g, The median of dB taken over all mouse frames and the median dB taken only over frames where the mouse is not in gait, shows a correlation with FI score. h, Wall-rearing event. The contour of the walls of the open field are taken and a buffer of five pixels is added (yellow line), marking a threshold. The nose point of the mouse is tracked at each frame. A wall-rearing event is defined by the nose point fully crossing the wall threshold (Supplementary Video 4). i, The total count of rearing events and the number of rears in the first 5 min of the open-field video show some correlation with FI score.

In addition to the existing features, we designed a set of features that we hypothesized may correlate with FI. These include morphometric features that capture the animal’s shape. Changes in body composition and fat distribution with age are observed in humans and rodents³⁶. We hypothesized that body composition measurements may show some relationship to aging and frailty. We took the median measurement of major and minor axes of the ellipse fitted to the mouse over all frame as an estimated length and width of the mouse, respectively (Fig. 2b). The median distance between the rear-paw coordinates over all frames was taken as another width measurement. Many of these morphometric features showed high correlations with FI score and age (Supplementary Tables 3 and 4), for example, median width and median rear-paw width had correlations of $r=0.56\text{and}0.57$, respectively (Fig. 2c).

Changes in gait are a hallmark of aging in humans^37,38 and mice^39,40. Recently, we established methods to extract gait and posture measures from freely moving mice in the open field²⁵. We carried out similar analysis to explore age-related gait changes in our dataset (Fig. 2d,e). Each stride was analyzed for its spatial, temporal and posture measures (Fig. 2d) and we took the medians of these measure over all strides for each mouse. We also looked into intra-mouse heterogeneity of gait features by calculating IQR over all strides for each mouse. Many of these measures showed a high correlation with the FI score and age (Supplementary Tables 3 and 4), for example, the median step width and tip-tail lateral displacement IQR ($r=0.58$ and $r=0.63$, respectively) (Fig. 2e).

We next investigated the bend of the spine throughout the video (Supplementary Video 3). We hypothesized that aged mice may bend their spine to a lesser degree, or less often due to reduced flexibility or spine mobility. This change can be captured by the pose estimation coordinates of three points on the mouse at each video frame: the back of the head (A), the middle of the back (B) and the base of the tail (C). At each frame, the distance between points A and C normalized for mouse length (dAC), the orthogonal distance of the middle of the back B from the line (dB) and the angle of the three points (aABC) were calculated (Fig. 2f) (Methods). We found some correlations showing relationships between spinal bend and FI score that contradicted our hypothesis (Supplementary Tables 3 and 4); while we expected dB median for all frames and dB median for non-gait frames to decrease with age, we found that they increase ($r=0.45\text{and}0.44$, respectively) (Fig. 2g). High-frailty mice may have higher dB medians partially due to body composition, as dB median has a correlation of 0.496 with body weight. It is important to note that these bend metrics cast a wide net; they are an inexpensive and general account of all the activity of the spine during the 1-h open field. Thus, these measures capture the interaction between body composition and behavior.

We also looked at occurrences of rearing supported by the wall (Fig. 2h and Supplementary Video 4). We hypothesized that frailer mice may rear less due to reduced lateral spinal mobility and/or reduced exploratory activity. We heuristically scored rearing by tracking the nose point of the mouse and the edges of the arena (Methods). We determined the number of rears and the average length of each rearing bout (Supplementary Table 2). We found that some metrics related to rearing bouts show signal for frailty, specifically total count of rears and rears in the first 5 min ($r=0.2\text{and}0.3$, respectively; Fig. 2i).

Notably, most of the correlations with age were slightly higher than correlations with FI score (Supplementary Tables 3 and 4). Of further note is the increase of heterogeneity in many of these measures with both age and FI score (for example, median width, median step width and dB median).

Sex differences in frailty.

The sex-specific characteristics of aging are important considerations. To visualize sex differences in frailty, we stratified the FI score data into four age groups and compared the box-plots for each age group between males and females (Fig. 3a). The oldest age group included 25 females compared to 122 males. The range of females’ frailty scores for each age group tended to fall lower than males except for the oldest age group. The middle two age groups showed highly significant differences in distribution between males and females.

Fig. 3 |. Comparison of male and female measures.

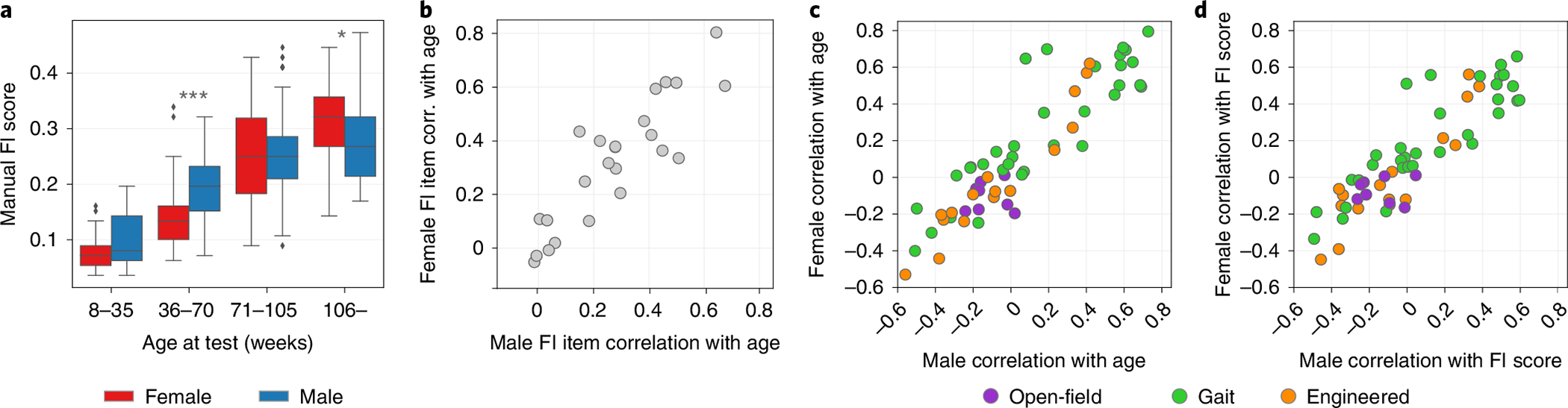
a, The distribution of FI scores for males and females when the data are split into four age groups of equal range. Significant differences in the distributions of male and female scores for that age group are determined by the two-sided Mann–Whitney U-test and are indicated by an asterisk (*). For each successive age group, $P=0.524$ ($n=78\text{females}$, $n=81\text{males}$), $P=3.38\times {10}^{-12}$ ($n=85\text{females}$, $n=61\text{males}$), $P=2.27\times {10}^{-12}$ ($n=107\text{females}$, $n=107\text{males}$) and $P=0.269$ ($n=25\text{females}$, $n=122\text{males}$). The box shows the quartiles of the dataset, while the whiskers extend to show the rest of the distribution, except for points that are determined to be ‘outliers’ using a method that is a function of the IQR. b, Pearson correlations of FI items with age for males compared to females ($r=0.85$). c, Pearson correlations of video metrics with FI score for males compared to females ($r=0.88$). d, Pearson correlations of video metrics with age for males compared to females ($r=0.90$).

Comparisons between the correlations of male and female FI item scores with age showed an overall high correlation (Fig. 3b and Supplementary Table 5). The average difference between male and female correlations of FI index items with age was 0.08, but a few index items showed notable differences. Alopecia and menace reflex have the highest sex differences in their correlation to age (0.29 and 0.21, respectively), with females having a higher correlation for alopecia and males having a higher correlation for menace reflex (Supplementary Table 5).

The correlations of male and female video features with both FI score and age were also high overall (Fig. 3c,d and Supplementary Tables 3 and 4). In both FI score and age, the video features with the highest sex differences were gait measures. Females had a higher correlation for median base-tail lateral displacement and median tip-tail lateral displacement to both FI score and age. For the metrics related to stride length and step length, males had a higher correlation to FI score and age. These results show that with age, females increase their base-tail and tip-tail lateral displacement in gait while males show little change in this feature, whereas males show a greater reduction in stride length with age compared to females.

Prediction of age and frailty index from video data.

Once we established that our video features correlated with aging and frailty, we used these features as covariates in a model to predict age and manual FI scores (Fig. 4a; model vFRIGHT and vFI, respectively). Age is an empirical ground truth and has a strong relationship to frailty. We compared the prediction of age using video features (Fig. 4a; Model vFRIGHT) to the prediction of age using manual FI items, a method referred to as the FRIGHT age clock⁵ (Fig. 4a; Model FRIGHT). We first tested four models, penalized linear regression (LR*)⁴¹, support-vector machine (SVM)⁴², random forest (RF)⁴³ and extreme gradient boosting (XGB)⁴⁴ (Fig. 4b; panel 1). We selected the RF regression model as our vFRIGHT model to predict age on unseen future data due to its superior performance over other models (Fig. 4b, panel 1, Supplementary Fig. 2c). Our vFRIGHT model was able to more accurately and precisely predict age (mean absolute error (MAE) 13.1 ± 0.99 weeks) than the FRIGHT clock (15.7 ± 4 weeks) (Fig. 4b, panel 2 and Supplementary Fig. 2d). The variance of prediction errors was noticeably reduced for vFRIGHT compared to FRIGHT (Fig. 4b, panel 2). We also plotted the predicted versus actual values for the train and test sets for the vFRIGHT model (Fig. 4g) and the FRIGHT model (Supplementary Fig. 2g). We find that for the youngest and oldest terciles, the model does better at predicting age than at the middle tercile. These results show that the automated video features offer information about age beyond what is addressed in the manual FI items. The video features may also provide information of aging which overlap with the health deficits scored in the manual FI.

Fig. 4 |. Prediction of age and frailty from video features.

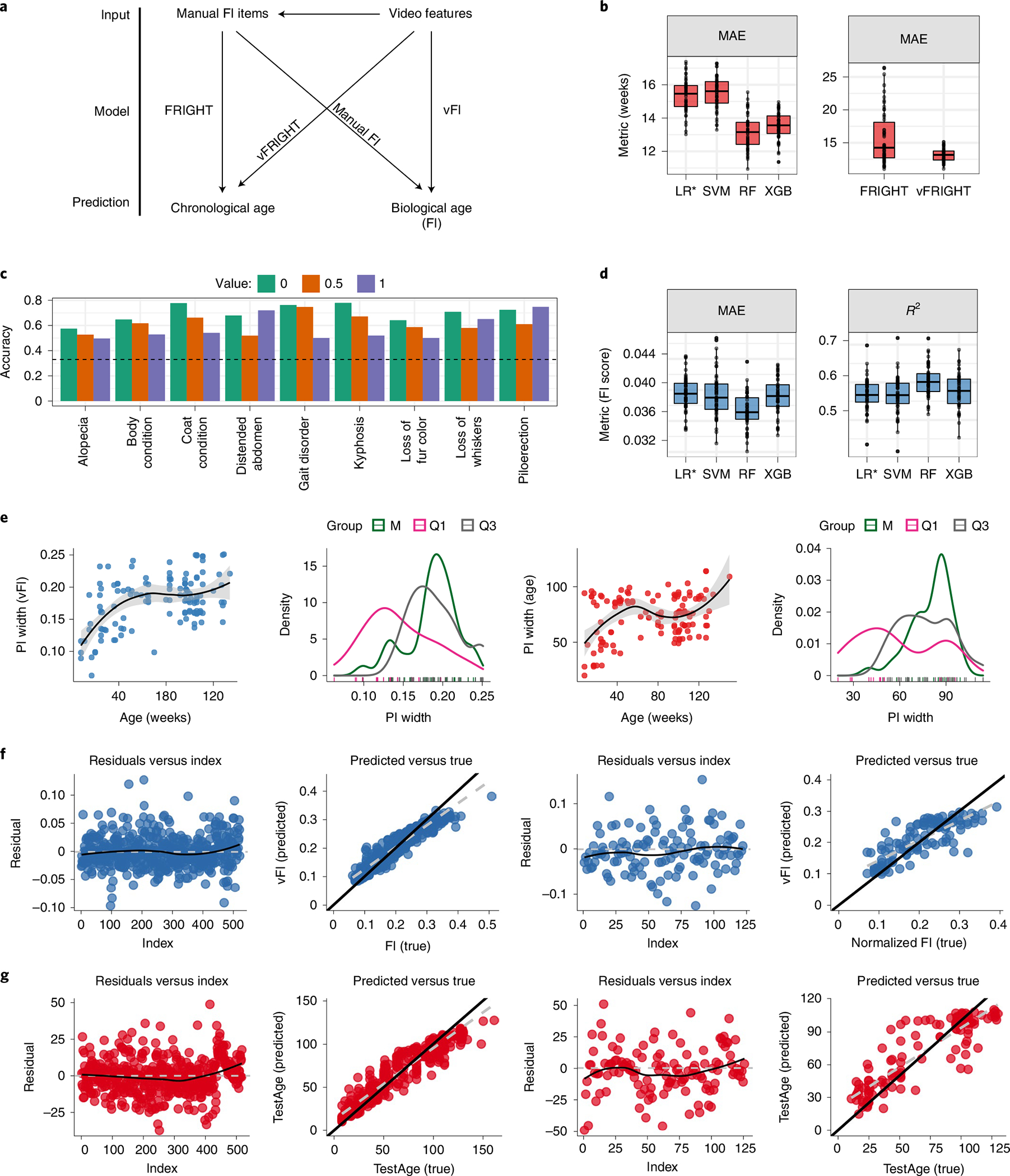
a, A graphical illustration shows the different models we fit. b, Video features are more accurate in predicting age than clinical frailty index items. Comparison among four models (LR*, SVM, RF and XGB) show that the RF predicted age on unseen future data better than other models with a lower MAE ($n=50$ independent train–test splits, $P<2.2\times {10}^{-16}$, ${\text{F}}_{3,147}=190.43$) when compared using repeated-measures ANOVA. We then compared the performance of RF models using frailty parameters (FRIGHT) and video-generated features (vFRIGHT) in predicting age. vFRIGHT had a superior performance ($n=50$ independent train–test splits, $P<4.7\times {10}^{-5}$, ${\text{F}}_{1,49}=19.9$, using repeated-measures ANOVA) with a lower MAE (13.1 ± 0.99 weeks) compared to the FRIGHT clock using FI items (15.7 ± 4 weeks). c, The performance of our ordinal regression models (classifiers) in terms of accuracy (accurately predicting the value of the frailty parameter in the test using the model trained on the training data). The black dotted line superimposed on the plot shows the accuracy that one would obtain if one guessed the values instead of using the video features. We found that the video features encode useful information that improves the models’ ability to predict frailty parameter values accurately. d, Comparison among four models (LR*, SVM, RF and XGB) show that the RF regression model predicted FI score on unseen future data better than all other models, with a lowest MAE ($n=50$ independent train–test splits, $P<2.1\times {10}^{-15}$, ${\text{F}}_{3,147}=30.53$) and highest $R^2$ ($P<4.7\times {10}^{-14}$, ${\text{F}}_{3,147}=27.2$) when compared using repeated-measures ANOVA. e, Uncertainty in predicting age (red) and FI score (blue) plotted as a function of age (weeks). The black curve shows the loess fit. These plots show less uncertainty in predicting age and FI scores for very young mice. We plot the distributions of PI widths and find that the PI widths for predicting age are wider (increased uncertainty in predictions) for mice belonging to the M age group. Similarly, the PI widths for predicting FI scores increase with age in our data. The shaded gray region is the 95% confidence interval for predicted values from the fitted linear model. f, The residuals versus the index and predicted FI score versus true for training (columns 1 and 2; residual s.e. 0.020(0.001), difference in slopes (black versus gray) = 0.23) and test sets (columns 3 and 4; residual s.e. 0.036, difference in slopes (black versus gray) = 0.37) for the RF model. We calculated the difference in the slopes between the diagonal line (black) and gray line. g, The residuals versus the index and predicted age versus true for training (columns 1 and 2; residual s.e. 9.051(1.585), difference in slopes (black versus gray) = 0.17) and test sets (columns 3 and 4; residual s.e.14.27, difference in slopes (black versus gray) = 0.29) for the RF model. The train–test splits in f and g are independent of each other. In b,d, the lower and upper hinges correspond to the first and third quartiles (the 25th and 75th percentiles), respectively, the line in the middle corresponds to the median, the upper (lower) hinge extends from the upper (lower) hinge to the largest (smallest) value not bigger (smaller) than 1.5 × IQR.

To address this, we predicted individual FI items using video features (Fig. 4a). Of the 27 items, many had no to almost no non-zero scores, which shows that in our genetically homogeneous dataset at least, most of the information in the manual FI are coming from a subset of index items (Supplementary Fig. 2f). We selected only index items with a balanced ratio of 0 to 0.5 and 1 scores for prediction (Fig. 4c). We then built a classifier for each of the nine index items to predict the score given a mouses video features. We predicted the individual FI items’ scores using an ordinal elastic-net regression model. For all nine, we were able to predict the score at an accuracy above what would be expected by randomly guessing (Fig. 4c; dotted line shows guessing accuracy). Many of these FI items have implicit relationships to video features such as grooming (coat condition and alopecia), gait/mobility (gait disorders and kyphosis) and body composition (distended abdomen and body condition). In the FRIGHT model, we found that gait disorders, kyphosis and piloerection had the highest contribution to age prediction in our dataset, followed by distended abdomen and body condition (Supplementary Fig. 2b), all items that our video features were able to predict the score for (Fig. 4c). These results together showed that most of the information for aging and frailty came from a small subset of manual FI items and that we are able to predict the information in this subset with video data. Furthermore, as we were able to predict age more accurately and precisely with video data than with manual FI items, video data may also contain additional signals for aging.

Next, we addressed the goal of a vFI (Fig. 4a; Model vFI): prediction of manual FI score with video data. Similarly to the vFRIGHT modeling, the RF regression model predicted FI score on unseen future data better than all other models (Fig. 4d and Supplementary Fig. 2e). The model could predict the FI score within 0.04 ± 0.002 of the actual FI score (FI scores have a possible range of 0 to 1, in our dataset we find a range of 0.04 to 0.47). This error is akin to 1 FI item mis-scored at one or two items mis-scored at 0.5 and demonstrates the robustness of the model. The residuals computed from the training data show that their distribution is symmetric around zero for both models and most residuals fall around the black diagonal line. The residuals for the test set follow similar patterns (Fig. 4f,g and Supplementary Fig. 2g). Age has a correlation with manual FI score of $r=0.81$ which is higher than any video feature. Thus, when we use a model with only age as feature, we find a higher prediction accuracy (Supplementary Fig. 5a). The model using both video features and age (All_RF) does notably better than the model with age alone, showing that the video features provide important information about frailty (Supplementary Fig. 5a). When we looked specifically at mice whose FI scores deviated from their age group, younger mice with higher frailty and older mice with lower frailty, the vFI model (Video_RF) performs better than the model using age and even the model using video features + age (All_RF) (Supplementary Fig. 5b). For mice who are outliers of their age group, video features provide better information about frailty than age. All together, we conclude that the vFI successfully predicts frailty beyond chronological age.

Finally, to see how much training data are realistically needed for high performance prediction with vFI and vFRIGHT, we performed a simulation study where we allocated different percentage of total data to training. We found that a training set of <80% of our current dataset achieved similar performance, whereas a decrease below this shows a general downward trend in performance (Supplementary Fig. 5e). As open-field tests are sometimes shorter than 1 h, we next investigated the accuracy for vFI predictions using shorter tests by truncating videos to the first 5 and first 20 min (Supplementary Fig. 5d). We observed a significant drop in performance accuracy when the open-field test length is reduced from a 60 to 20-min video.

Quantification of uncertainty in frailty index predictions.

In addition to quantification of an average accuracy, we investigated prediction errors more closely within our dataset to see how performance changes across frailty and age. We quantified the prediction error by providing prediction intervals (PIs)⁴⁵. For mice in the test set, we use generalized RFs based on quantiles to provide the point predictions of the FI score (age resp.) and PIs, which give a range of FI (age resp.) values that will contain the unknown FI scores (resp. age) with 95% confidence (Supplementary Fig. 2h,i). We find that the widths of the PIs are mouse and age-group specific. We plotted a smoothed regression fit for PI width versus age, which indicated that the widths increased with mouse age (Fig. 4e). The variability of 95% PI widths (Fig. 4e) showed higher variability for mice belonging to the middle (M) age groups (labeled M in green). We went beyond simple point predictions by providing PIs of the FI to quantify our predictions’ uncertainty. This allowed us to pinpoint the FI score and age with higher accuracy for some mice than others.

Feature importance for prediction of frailty.

A useful vFI should depend on several features that can capture the mouse’s inherent frailty and simultaneously be interpretable. Interpretability can prevent bias^46,47 and can guide the design of new features and improve later iterations of the vFI. We took two approaches to identify the features important for making vFI predictions using the trained RF model: (1) feature importance and (2) feature interaction strengths.

A comparison of the feature importance’s for the vFI and vFRIGHT (age prediction) models (Fig. 4a) shows that though many of the most important video features to the model are shared, there are a couple key differences (Supplementary Fig. 5c). For example, step width IQR is much more important for the vFI than for vFRIGHT and tip-tail lateral displacement (LD) IQR is much more important for vFRIGHT than for vFI. We next obtained a more complete picture of the feature importance by modeling three different quantiles of the conditional distribution of the FI score: low frail (Q1), intermediate frail (M) and high frail (Q3) mice. We found that different sets of features were crucial for mice belonging to different frailty groups (Fig. 5a). For the feature interaction strength approach, we measured the fraction of variability in predictions explained by feature interactions after considering the individual features⁴⁸ (Fig. 5c). For example, we can explain ⇡ 15% of the prediction function variability due to interaction between step width IQR and other features after considering the individual contributions due to step width IQR and other features.

Fig. 5 |. Quantile regression modeling of vFI using generalized random forests.

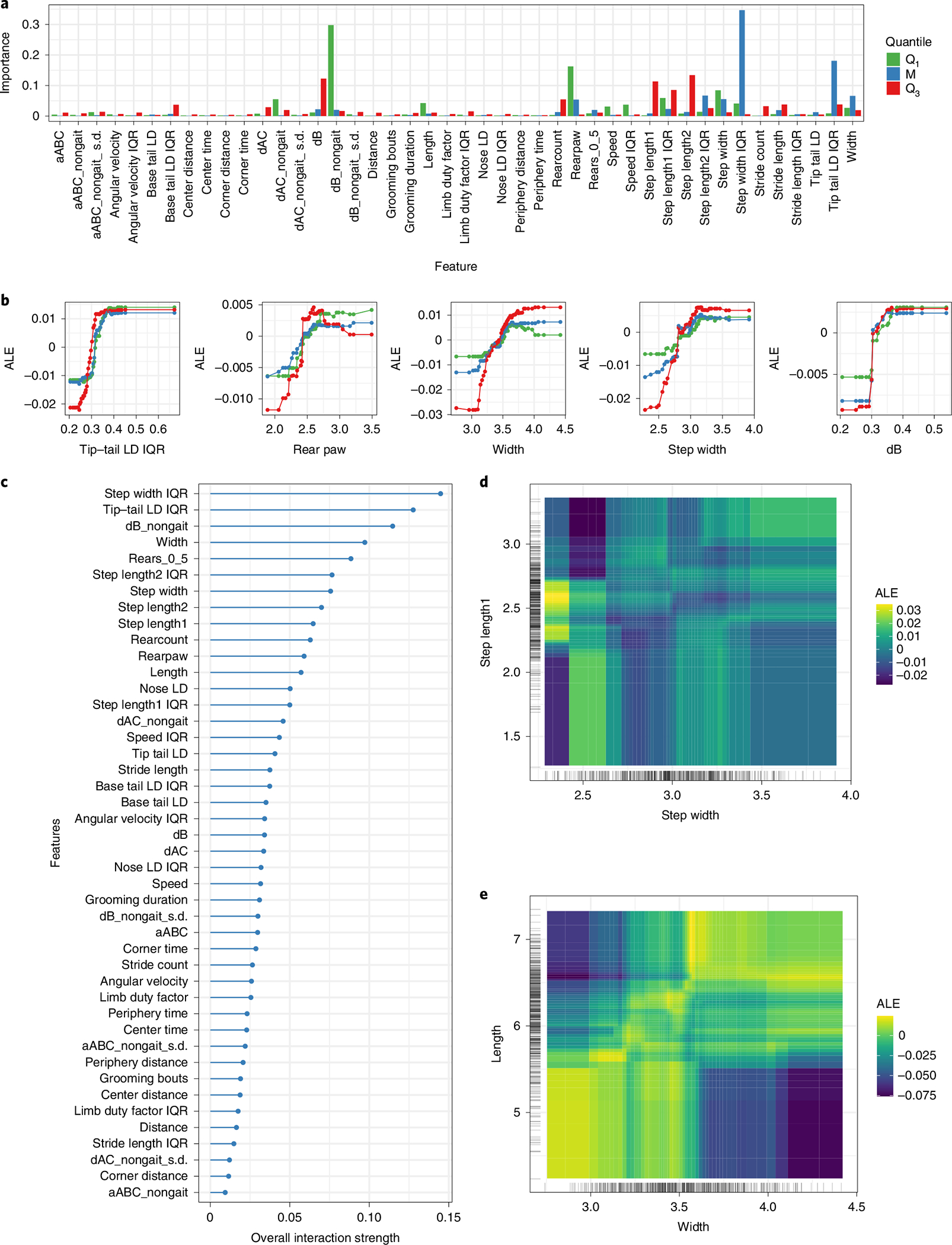
a, Variable importance measures for three quantile RF models (lower tail, Q_.025; median, Q_.50; upper tail, Q_.975). Mice in lower and upper tails correspond to mice with low and high frailty scores respectively. b, Marginal ALE plots show how important features influence the predictions of our models on average. For example, the average predicted FI score rises with increasing step width, but falls for values greater than three in mice belonging to lower and upper tail. c, A plot showing how strongly features interact with each other. d,e, ALE second-order interaction plots for step width and step length1 (E, width and length) on the predicted FI score. Lighter shade indicates an above average and darker shade a below average prediction when the marginal effects from features are already taken into account. d,e, Weak (resp. strong) interaction between step width (d) and step length1 (e) (resp. width and length). Large step width and step length1 increases the vFI score.

Both feature importance and feature interaction strengths informed us that the trained RF for vFI depends on several features and their interactions; however, they did not tell us how the vFI depends on these features and how the interactions look. We used the accumulated local effect (ALE) plots⁴⁹ that describe how features influence the RF model’s vFI predictions on average (Fig. 5b). For example, an increasing tip-tail lateral displacement positively impacts (increases) the predicted FI score for mice in all groups. We explored the ALE second-order interaction effect plot for the step length1-step width (Fig. 5d) and body length-width (Fig. 5e) predictors. Figure 5d revealed an interaction between step width and step length: mice with the lowest step widths and step length1 between 2.2 and 2.7 have a higher vFI on average (yellow area) compared to mice with lower step lengths (dark blue area). Similarly, larger widths (3.7–4.5) and smaller lengths (4.5–5.5) had a negative impact on the average FI scores predictions (Fig. 5e).

To summarize, we established vFI’s utility by demonstrating its dependence on several features through marginal feature importance and feature interactions. Next, we used the ALE plots to understand the effects of features on the model predictions, which help us relate the black-box models’ predictions to our video-generated features, an essential final step in our modeling framework.

Discussion

The mouse FI is an invaluable tool in the study of biological aging. Here we sought to extend it by producing a scalable automated vFI using video-generated features to model FI score. We generated one of the largest frailty data sets for the mouse with associated open-field video data. We used machine-vision techniques to extract an array of features, many of which show strong correlations with aging and frailty. We also analyzed sex-specific aging in mice. We then trained machine-learning models that can accurately predict age and frailty from video features.

We collected our data at a national aging center with a similar design as expected in a high-throughput interventional study that may run for several years. The mice were tested by the trained scorer who was available; four different scorers were used to FI test the different batches of mice. Further, we had some personnel changes between batches. These conditions may provide a more realistic example of inter-laboratory conditions, where discussion and refinement would be difficult. We found that 42% of the variability in our dataset could be accounted for by the scorer, indicating the presence of a tester effect. This variability and affected some items, such as piloerection, more than others. Although previous studies looking at tester effect found good to high inter-reliability between testers in most cases, FI items showing lower inter-reliability required discussion and refinement for improvement^10,12.

Top-down videos of mice in the open field were processed by previously trained neural networks to produce an ellipse fit, segmentation and pose estimation of the mouse for each frame. These frame-by-frame measures were used to engineer features. In humans, changes in age-related body composition and anthropometric measures such as waist-to-hip ratio are predictors of health and mortality risk^50–52. There are observed changes in body composition in rodents similar to humans^51,53. We found high correlation between morphometric features and both FI score and age, in particular median width and median rear-paw width.

The prevalence of gait disorders and irregularities increase with age^37,38. We looked at the spatial, temporal and postural characteristics of gait for each mouse and found many features with a strong correlation with both frailty and age. We found a decrease in stride speed with age, as well as an increase in step width variability³⁸. As gait is thought to have both cognitive and musculoskeletal components, it is a compelling area for frailty research.

Spinal mobility in humans is a predictor of quality of life in aged populations⁵⁴. Notably, although some spinal bend metrics showed moderately high correlations with the FI score and were deemed important features in the model, the relationship was the opposite of what we initially hypothesized. As these metrics are a general account of all the activity of the spine, they are likely capturing a combination of behaviors and body composition that gave this result.

Many age-related biochemical and physiological changes are known to be sex-specific^30–32. In humans, there is a known ‘sex-frailty paradox’, where women tend to be more frail but paradoxically live longer²⁹. However, in C57BL/6J mice, the evidence is mixed^2,29,55. We found that more males survived to old age and further, we found females tended to have slightly lower frailty distributions than males of the same age group. These results suggest that in C57BL/6J mice, the sex-frailty paradox may not exist or may be reversed. We also found a number of starkly different correlations of certain gait features with age and FI score between males and females.

The manual FI evaluates a wider range of body systems than vFI; however, we believe that the complex behaviors we measure contain implicit information about many body systems. We found that in our isogenic dataset, most information in the manual FI was came from a limited subset of index items. Of the 27 manual FI items scored, 18 items had little to no variation in score in our dataset (almost all mice had the same score) and only 9 items had a balanced distribution of scores. Our video features can accurately predict those nine FI items. Our model using video features also predicted age more accurately with much less variance than the model using manual FI items (FRIGHT versus vFRIGHT). This suggests that our video features can not only predict the relevant FI items but also contain signals for aging beyond the traditional manual FI. We find that the model does better at predicting age for the youngest and oldest terciles than for the middle tercile. This may be partially due to having fewer data at the middle tercile.

Finally, using the video features as input to the RF model, we were able to predict the manual FI score within 0.04 ± 0.002 of the actual score on average. Unnormalized, this error is 1.08 ± 0.05, which is comparable to one FI item being mis-scored by 1 point or two FI items being mis-scored by 0.5 points. We went beyond simple point predictions by providing 95% PIs. We then applied quantile RFs to low and high quantiles of the FI score’s conditional distribution that revealed how certain features affected frail mice differently.

Ease of use of the trained model by non-computational labs is an important challenge. Therefore, in addition to implementation details in the Methods, we have detailed our integrated mouse phenotyping platform, a hardware and software solution that provides tracking, pose estimation, feature generation and automated behavior analysis⁵⁶. This platform requires a specific open-field apparatus; however, researchers would be able to use the trained model if they generate the same features as our model using their own open-field data collection apparatus.

The vFI can be further improved with the addition of new features through reanalysis of existing data and future technological improvements to data acquisition^57,58. For instance, new behaviors could provide information about additional systems, while higher camera quality could provide information about fine-motor movement-based behaviors and appearance-based features. Additionally, this approach could be applied to a long-term home cage environment. Not only would this reduce handling and environmental factors, features such as social interaction, feeding, drinking, sleep and others could be integrated. Given the evidence of a strong genetic component to aging⁵⁹, application of this method to other strains and genetically heterogeneous populations, such as Diversity Outcross and Collaborative Cross, may reveal how genetic variation influences frailty. Further, as predicting mortality risk is a vital function of frailty, video features could be used to study lifespan. We also imagine that the value of this work could go beyond community adoption and toward community involvement; training data from multiple laboratories could provide an even more robust and accurate model. This could provide a uniform FI across studies. Overall, our approach has produced insights into mouse frailty and shows that video data of mouse behavior can be used to quantify aggregate abstract concepts such as frailty. Our work enables high-throughput, reliable aging studies, particularly interventional studies that are a priority for the aging research community.

Methods

Mice.

C57BL/6J mice were obtained from the Nathan Shock Center at The Jackson Laboratory. A total of 533 male and female mice from the ages of 8 to 161 weeks old were tested in accordance with approved protocols from The Jackson Laboratory Institutional Animal Care and Use Committee guidelines. This is an aging colony and were originally house eight mice to a pen. Each pen had an amber tunnel, chew block, shack and nestlet. The average temperature is 69 °F with 45% humidity. The first round (batch 1) of tests included 222 mice (141 males and 81 females). The second round (batch 2) of tests occurred about 5 months later and included 319 mice (173 males and 146 females). Of those mice, 105 were repeated from the first batch. The third round (batch 3) of testing occurred about a year later in response to reviewer comments with 102 mice (57 males and 45 females). Of these mice, 18 had previously been tested in the first round and 15 had been tested in the second round

Open-field assay and frailty indexing.

Mice were shipped from Nathan Shock Center aging colony, which resides in a different room in the same animal facility at The Jackson Laboratory. The mice were acclimated for 1 week to the Kumar Laboratory animal holding room, adjacent to the behavioral testing room. During the day of the open-field test, mice were allowed to acclimate to the behavior testing room for 30–45 min before the start of test. Open-field testing was performed by placing the mouse in the open field arena for 1 h for recording^16,23,56. After open-field testing, mice were returned to the Nathan Shock Center for manual FI (Supplementary Table 6). Manual FI was performed by trained experts in the Shock Center within 1 week of the open-field assay on each mouse. Mice were brought into the procedure room, body weights are recorded and mice were left undisturbed to acclimate to the procedure room for a minimum of 60 min. Mice were assessed one at a time for the multiple characteristics with the approximate time to complete the battery of 3–4 min per mouse (Fig. 1). With the exception of quantitative measures of body weight (g) and core body temperature (°C), all other characteristics were assessed on a scale of 0, 0.5 or 1 by a trained technician blinded to genotype or age^2,33. Body temperature was taken via a glycerol lubricated thermistor rectal probe (Braintree Scientific product RET 3; measuring 3/4 inches L 0.028 dia. 0.065 tip) inserted 2 cm into the rectum of the mouse for approximately 10 s and body temperature recorded (to the nearest 0.1 °C (Braintree Scientific product TH5 Thermalert digital thermometer). Between subjects, the thermistor probe was wiped with 70% ethanol and re-lubricated with glycerol. FI testing sheet with all items can be found in Supplementary Materials.

Video, segmentation and tracking.

Our open-field arena, video apparatus and tracking and segmentation networks are detailed elsewhere^23,56. Briefly, the open field arena measures 20.5 inches by 20.5 inches with Sentech camera mounted 40 inches above. The camera collects data at 30 fps with a 640 × 480-pixel resolution. We use a neural network trained to produce a segmentation mask of the mouse to produce an ellipse fit of the mouse at each frame as well as a mouse track.

Pose estimation and gait.

The 12-point two-dimensional pose estimation was produced using a deep convolutional neural network²⁵. The points captured are nose, left ear, right ear, base of neck, left forepaw, right forepaw, mid-spine, left rear-paw, right rear-paw, base of tail, mid-tail and tip of tail. Each point at each frame has an an $x$ coordinate, a $y$ coordinate and a confidence score. We use a minimum confidence score of 0.3 to determine which points are included in the analysis.

The gait metrics were produced by a trained neural network²⁵. Briefly, stride cycles were defined by starting and ending with the left hind paw strike, tracked by the pose estimation. These strides were then analyzed for several temporal, spatial and whole-body coordination characteristics, producing the gait metrics over the entire video.

Open-field measures and feature engineering.

Open-field measures were derived from ellipse tracking of mice^23,24,56. The tracking was used to produce locomotor activity and anxiety features. Grooming was classified using an action detection network²⁴. The other engineered features (spinal mobility, body measurements and rearing) were all derived using the pose estimation data. The spinal mobility metrics used three points from the pose: the base of the head (A), the middle of the back (B) and the base of the tail (C). For each frame dAC, dB and aABC were measured. The means, medians, maximum values, minimum values and s.d of dAC, dB and aABC were taken over all frames and over frames that were not gait frames (where the animal was not walking). For morphometric measures, we measured the distance between the two rear-paw points at each frame and also the means, medians and s.d. of that distance over all frames. For rearing, we took the coordinates of the boundary between the floor and wall of the area (using OpenCV contour) and added a buffer of four pixels. Whenever the mouse’s nose point crossed the buffer, this frame was counted as a rearing frame. Each uninterrupted series of frames where the mouse was rearing (nose crossing the buffer) was counted as a rearing bout. The total number of bouts, the average length of the bouts, the number of bouts in the first 5 min and the number of bouts within 5–10 min were calculated.

Modeling.

We investigated the effect of the scorer using a linear mixed model with scorer as the random effect and found that 42% of the variability (restricted likelihood-ratio test (RLRT) = 183.85, $P<2.2\times {10}^{-16}$) in manual FI scores could be accounted for by scorer (Fig. 1c). An RLRT⁶⁰ provided strong evidence of scorer (random) effect with non-zero variance. We fit a cumulative link model (logit link)⁶¹ to the ordinal response (frailty parameter) with weight, age and sex as fixed effects and the tester as a random effect. The effects are estimated variances associated with the random tester effect in the model ($y$ axis) across each FI item. We removed the tester effect from the FI scores using a linear mixed model

$$y_{ij}={\mathit{\mu }}_i+{\mathit{e}}_{ij}{\mathit{e}}_{ij},\leftarrow N\left(0,s^2\right),{\mu }_i\leftarrow P⌘N\left(0,t^2\right)$$

with the lme4 R package⁶². The following model was fit:where $y_{\mathrm{i}\mathrm{j}}$ is the jth animal scored by tester $\mathrm{i},{\mathit{\mu }}_{\mathrm{i}}$ is a tester-specific mean, $e_{\mathrm{i}\mathrm{j}}$ is the animal-specific residual, $s^2$ is the within-tester variance and $P$ is the distribution of tester-specific means. We had four testers with different number of animals tested by each tester $(i=1,\dots ,4)$. The tester effects, estimated with the best linear unbiased predictors using restricted maximum likelihood estimates⁶³ were subtracted from the FI scores of the animals, $y_{ij}^{\sim }=y_{ij}-{\hat{\mathit{\mu }}}_i$.

We modeled tester-adjusted FI scores, $y_{ij}^{\sim }$, with video-generated features as covariates/inputs using linear regression model with elastic-net penalty⁴¹, SVM⁴², RF⁴³ and gradient-boosting machine⁴⁴. We split the data randomly into two parts: train (80%) and test (20%). We ensured that the repeat measurements from the same mouse belonged to either the training or the test data and not both. We used the training data to estimate and tune the models’ hyper-parameters using tenfold cross-validation; the test set served as an independent evaluation sample for the models’ predictive performance. We performed 50 different splits on the data to allow for a proper assessment of uncertainty in our test set results. The models were compared in terms of MAE, root-mean-squared-error (RMSE) and $R^2$. These metrics were compared across the four models using repeated-measures ANOVA through $F$ test with Satterthwaite approximation⁶⁴ applied to the test statistic’s denominator d.f.

For FRIGHT modeling to predict age with manual FI items, we removed frailty parameters with a single value to avoid unstable model fits (zero-variance predictors). We fitted the ordinal regression models⁶⁵ without any regularization term and used a global likelihood-ratio test ($P<2.2\times {10}^{-16}$) to determine whether the video features show any evidence of predicting each frailty parameter separately (evidence of a predictive signal). Next, we used the ordinal regression model with an elastic-net penalty⁴¹ to predict frailty parameters using video features.

For predicting manual FI items, we selected frailty parameters for which $P_{\text{i}}<0.80$, where i is the mode of the parameters’ count distribution. For example, menace reflex is excluded, as i = 1 is the mode for menace reflex’s count distribution with $P_1>0.95$.

We obtained the $\text{100(1}-a\text{)\%}$ out-of-bag PIs $\left(\mathbf{X},{\mathbf{C}}_{\mathbf{n}}\right)$, where $\mathbf{X}$ is the vector of covariates and $P_1>0.95$ is the training set, via quantile RFs⁶⁶ with the grf package⁶⁷. PIs produced with quantile regression forests often perform well in terms of conditional coverage at or above nominal levels that is $P\left[y^{~}2{\text{I}}_a\left(\mathbf{X},{\mathrm{C}}_n\right)\mid \mathbf{X}=\mathbf{x}\right]1-a$, where we set $a=0.05$.

We picked animals whose ages and FI scores had an inverse relationship (younger animals with higher FI scores and older animals with lower FI scores). We formed five test sets containing animals with these criteria and trained the RF model on the remaining mice. We evaluated the predictive accuracy for predicting FI scores for the five test sets and displayed the results (Supplementary Fig. 5b). We defined the test sets using ${\text{age}}_L$, ${\text{age}}_U$, ${\text{FL}}_L$ and ${\text{FL}}_U$, which denote age and FI cutoffs for young and old animals, respectively. For the five test sets, we set the parameters as follows:

$${\mathrm{a}\mathrm{g}\mathrm{e}}_L=60,{\mathrm{a}\mathrm{g}\mathrm{e}}_U=90,{\mathrm{F}\mathrm{I}}_L=0.20\text{and}{\mathrm{F}\mathrm{I}}_U=0.15(n=43)$$

$${\mathrm{a}\mathrm{g}\mathrm{e}}_L=60,{\mathrm{a}\mathrm{g}\mathrm{e}}_U=100,{\mathrm{F}\mathrm{I}}_L=0.20\text{and}{\mathrm{F}\mathrm{I}}_U=0.15(n=38)$$

$${\mathrm{a}\mathrm{g}\mathrm{e}}_L=50,{\mathrm{a}\mathrm{g}\mathrm{e}}_U=90,{\mathrm{F}\mathrm{I}}_L=0.20\text{and}{\mathrm{F}\mathrm{I}}_U=0.20(n=45)$$

$${\mathrm{a}\mathrm{g}\mathrm{e}}_L=60,{\mathrm{a}\mathrm{g}\mathrm{e}}_U=110,{\mathrm{F}\mathrm{I}}_L=0.20\text{and}{\mathrm{F}\mathrm{I}}_U=0.20(n=42)$$

$${\mathrm{a}\mathrm{g}\mathrm{e}}_L=70,{\mathrm{a}\mathrm{g}\mathrm{e}}_U=100,{\mathrm{F}\mathrm{I}}_L=0.25\text{and}{\mathrm{F}\mathrm{I}}_U=0.15(n=20)$$

Statistics and reproducibility.

Both behavioral testing and FI were performed by trained experts who were blind to the age of the mice. Behavioral testing and FI were performed one cage at a time. Once a cage was selected, all mice in the cage was tested. Cages were randomized by age and sex to insure that each testing group had both males and females from each age group. We removed nine animals from the data as they contained missing values for many features. We removed approximately 20 videos due to technical data collection failures (video capture failures). Data distribution was assumed to be normal, but this was not formally tested in tests that were used to compare different predictive models. No statistical method was used to predetermine sample size, but our sample size was larger than similar studies⁵. We evaluated the predictive performance of our methods by randomly splitting the data into disjoint training and test sets. We ensured that the repeat measurements from the same animal belonged to either training or test set and not both. We performed 50 different splits on the data to allow for a proper assessment of uncertainty and reproducibility in our reported results. All attempts at replication were successful.

Extended Data

Extended Data Fig. 1 |. Estimation of the scorer effect in clinical FI items.

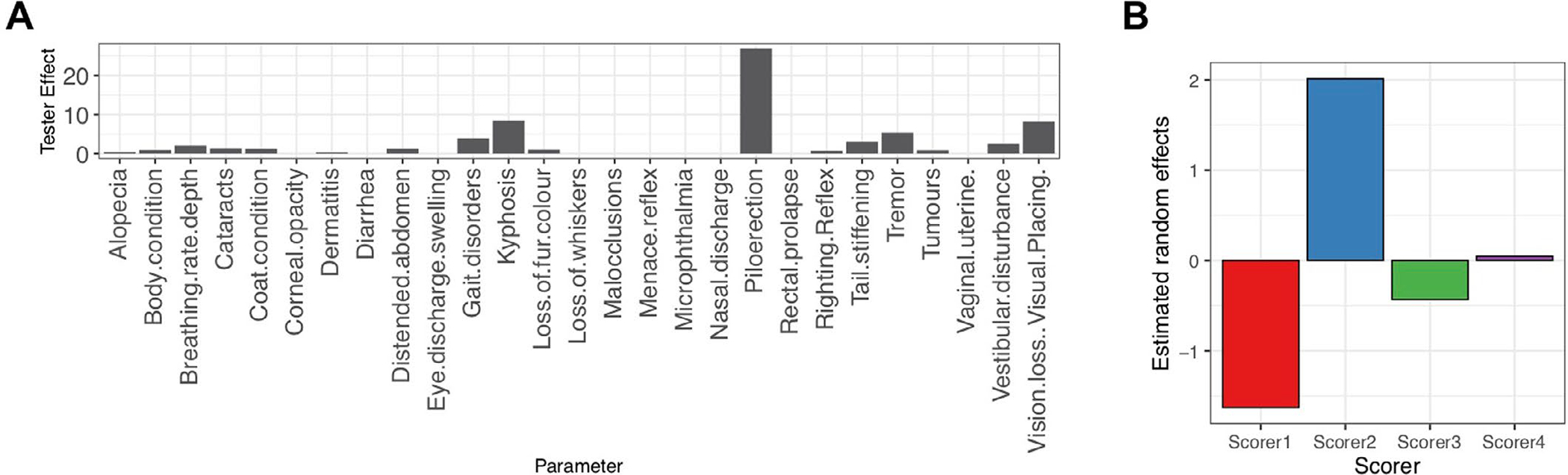
A, The effect of tester varies across FI items. B, The estimated random effect across 4 scorers in the data set.

Extended Data Fig. 2 |. Detailed modeling analysis.

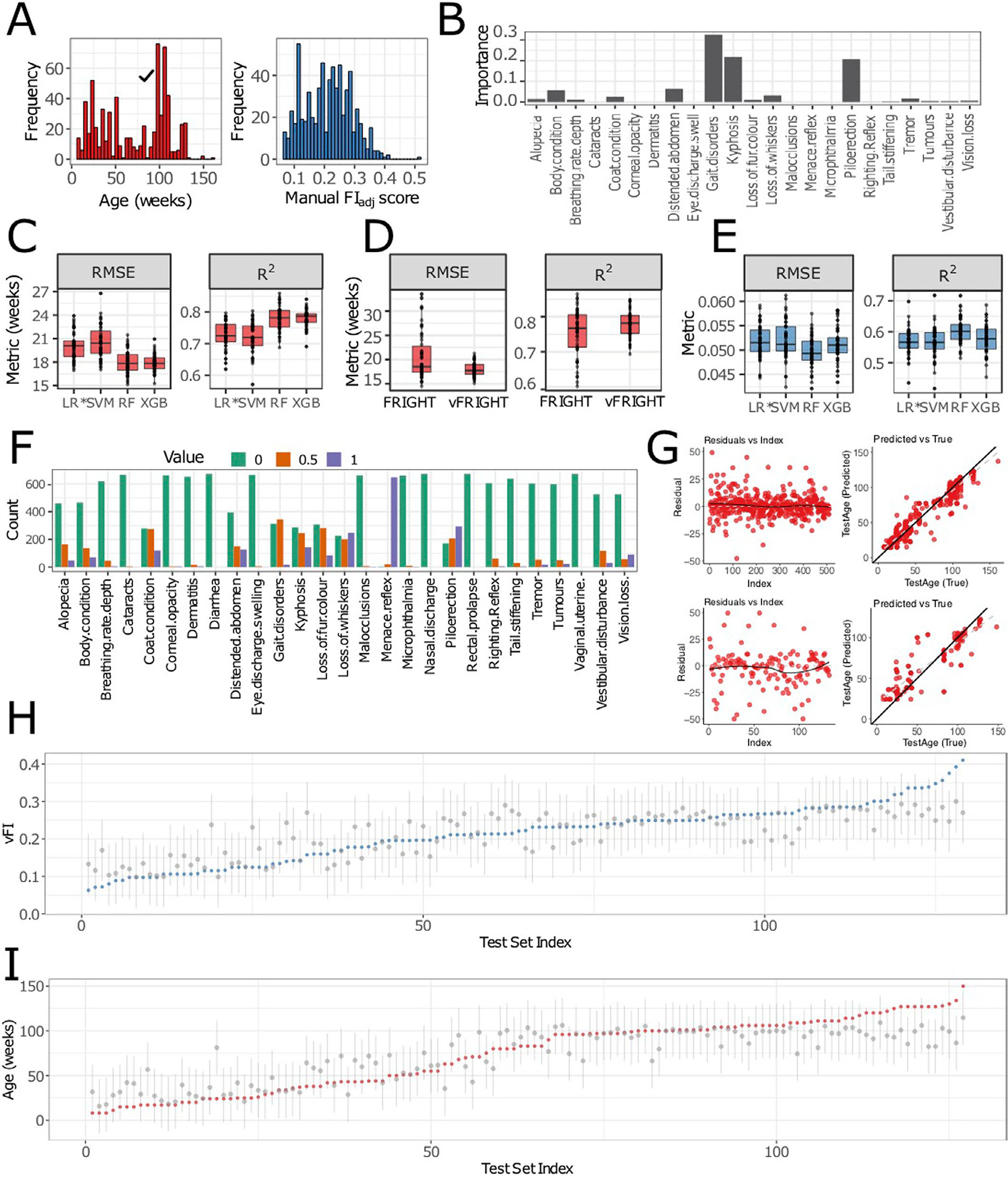
A, The distribution of age across 643 data points (533 mice). The distribution of manual FI_adj scores across 643 data points (533 mice). B, To determine the contributions of frailty parameters in predicting Age, we calculated the feature importance of all frailty parameters. We discover that gait disorders, kyphosis and piloerection have the highest contributions. C, The random forest regression model performed better than other models with the lowest root-mean-squared error (RMSE) (n = 50 independent train-test splits, p < 2.2e − 16, F3,147 = 59.53) and highest R2 (p < 2.2e − 16, F3,147 = 58.14) when compared using repeated-measures ANOVA. D, The vFRIGHT model performed better than the FRIGHT model with a lower RMSE (n = 50 independent train-test splits, RMSE_vFRIGHT = 17.97 ± 1.44, RMSE_FRIGHT = 20.62 ± 4.78, p < 6.1e − 7, F1,49 = 32.84) and higher R2 (RMSE_vFRIGHT =0.78 ± 0.04, RMSE_FRIGHT = 0.76 ± 0.07, p < 2.1e − 8, F1,49 = 44.54) when compared using repeated-measures ANOVA. E, The random forest regression model for predicting FI score on unseen future data performed better than all other models, with a lowest root-mean-squared error (RMSE) (n = 50 independent train-test splits, p < 8.3e − 14, F3,147 = 26.62) and highest R2 (p < 4.7e − 14, F3,147 = 27.2). F, The plot shows the counts distribution (0 - green, 0.5 - orange, 1 - purple) for individual frailty parameters— for many parameters such as Nasal discharge, Rectal prolapse, Vaginal uterine and Diarrhea, the proportion of 0 counts is 1 (p0 = 1). Similarly, Dermatitis, Cataracts, Eye discharge swelling, Microphthalmia, Corneal opacity, Tail stiffening and Malocclusions have p0 > 0.95. G, The residuals versus the index and predicted versus true for training (Column 1; residual standard error = 8.5, difference in slopes (black vs gray) = 0.11) and test sets (Column 2; residual standard error = 15.87, difference in slopes (black vs gray) = 0.30) for the model that predicts Age using frailty index items for both training and test data. H, I, Out-of-bag (OOB) error based 95% prediction intervals (PIs) (gray lines) quantifying uncertainty in point estimates/predictions (gray dots). There is one interval per test mouse (n = 107 unique mice, the test data contains some repeats of the same mice tested at different ages) and approximately 95% of the PI intervals contain the correct Age (red dots) and FI scores (blue dots). We ordered the x-axis (Test set index) in ascending order (from left to right) of the actual age/FI. The average PI width for all test mouse’s predicted FI score is 0.18 ± 0.04 (resp. 71.96 ± 18.52 for the predicted Age), while the PI lengths range from 0.08 to 0.29 (resp. 28 to 113 for Age). n (C, D and E), the lower and upper hinges correspond to the first and third quartiles (the 25th and 75^th percentiles) respectively, the line in the middle corresponds to the median, the upper (lower) hinge extends from the upper (lower) hinge to the largest (smallest) value not bigger (smaller) than 1.5 × IQR where IQR is the interquartile range.

Extended Data Fig. 3 |. Correlation between video metrics.

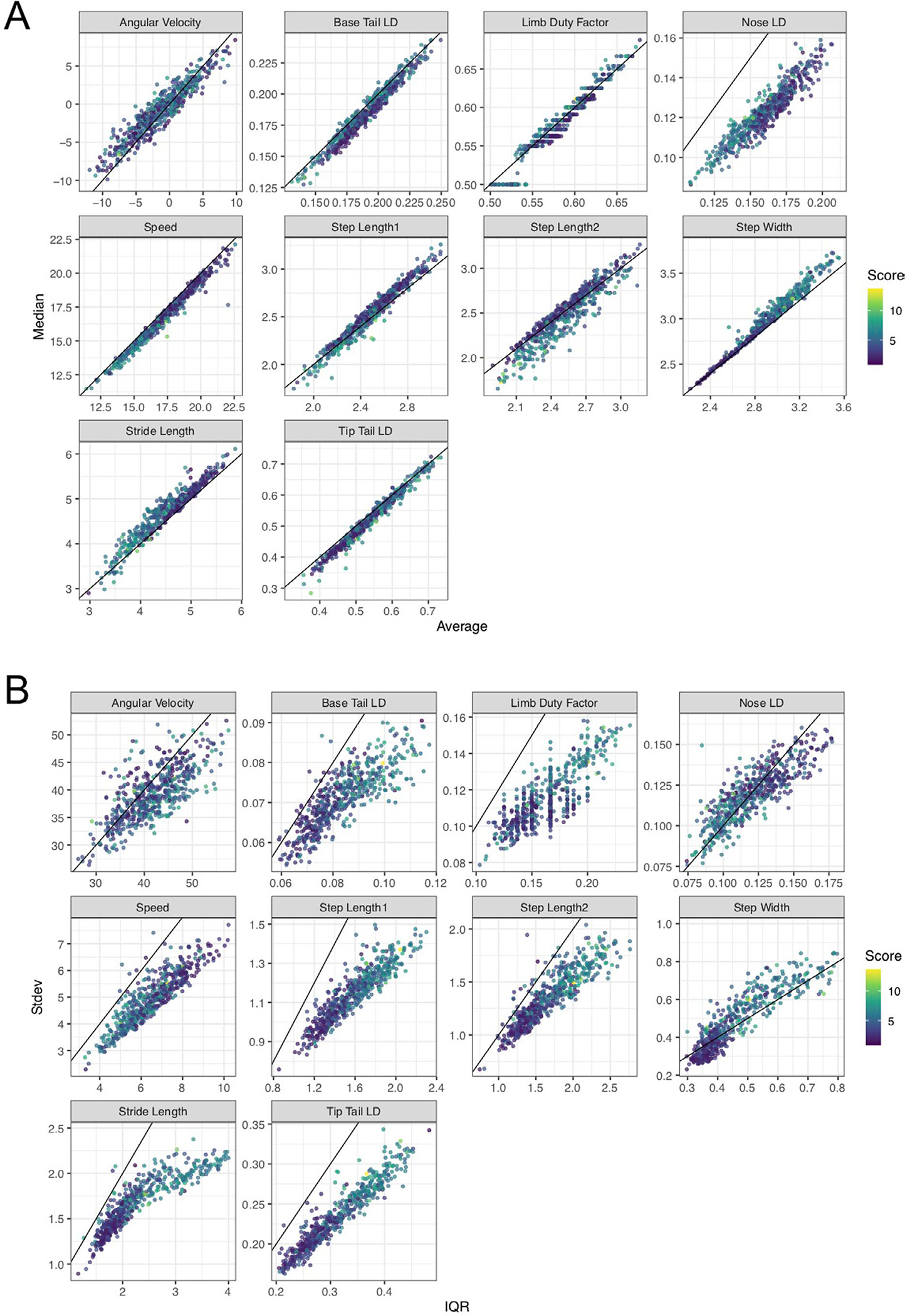
A, Correlation between average/mean (x-axis) and median (y-axis) video gait metrics. The diagonal line corresponds to maximum correlation i.e. 1. B, Correlation between inter-quartile range (IQR, x-axis) and standard deviation (Stdev, y-axis) video gait metrics. The diagonal line corresponds to maximum correlation i.e. 1. A tight wrap of points around the diagonal line indicates a high correlation between mean and median or IQR and standard deviation for the respective metric.

Extended Data Fig. 4 |. test for Simpson’s paradox.

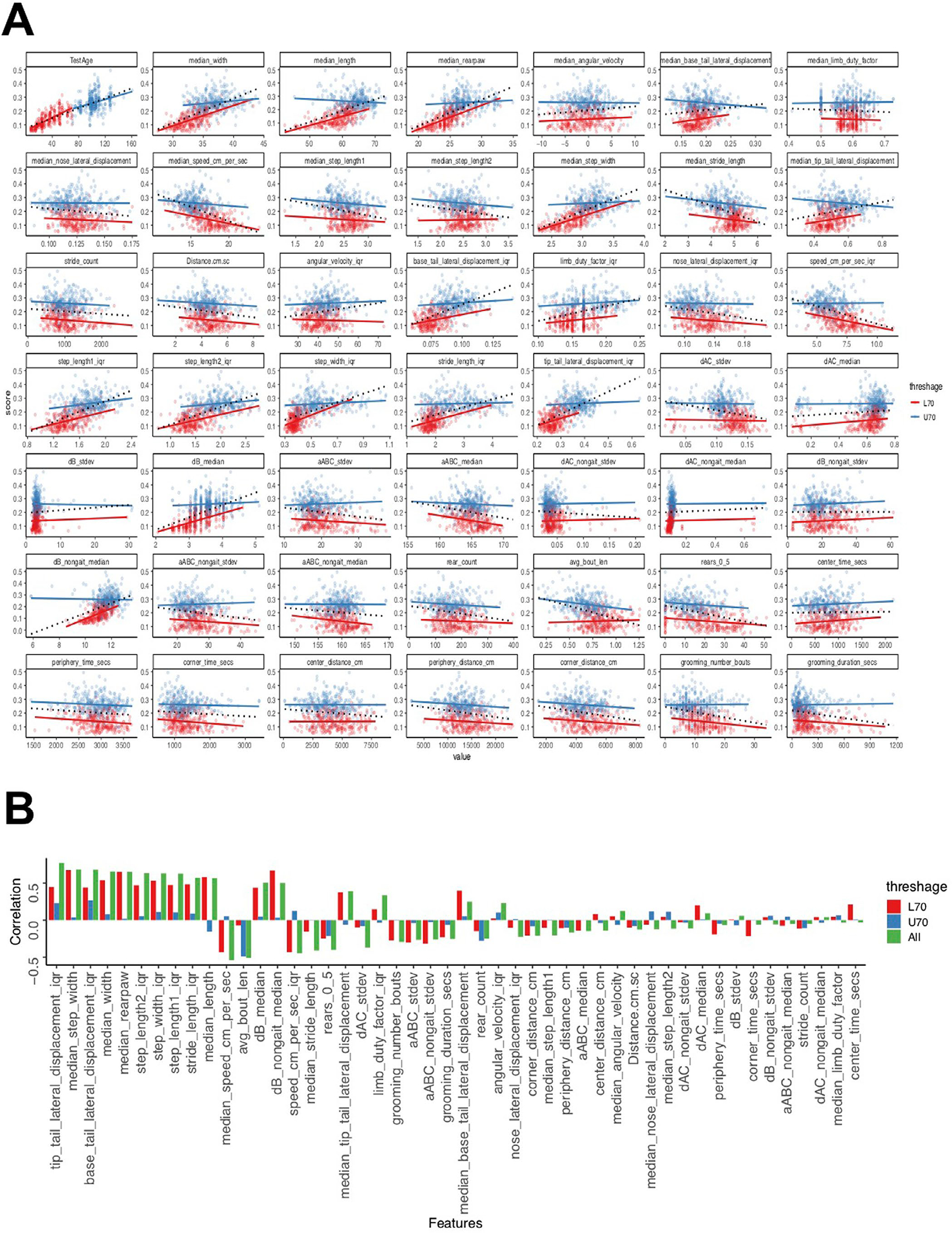
A, Simpson (1951) showed that the statistical relationship observed in the population could be reversed within all of the subgroups that make up that population, leading to erroneous conclusions drawn from the population data. To test for the manifestation of Simpson’s paradox in our data, we split the bimodal Age distribution into two separate unimodal distributions (clusters), that is, less than 70 weeks old (L70, red) versus more than 70 weeks old (U70, blue). Next, we plotted the dependent variable (frailty) against each of the independent variables/features in our data and fit a simple linear regression model to each subgroup separately (solid red and blue lines) as well as to the aggregate data (black dotted line). B, We quantified the correlations by measuring the slope of the linear fits of the features (Y) on Age (X). We computed the slopes for L70, U70 and overall (All), then plotted the slopes for features in decreasing order of their relevance to the model (where we predict Age from these features). We went further and performed one-way ANOVA to test for differences in slopes between L70 and U70 sub-groups and the overall data (one-way ANOVA, F_2,141 = 1.162, p > 0.32). Next, we performed a false discovery rate adjusted post hoc pairwise comparisons using the t-test. We found no significant differences in the comparisons (L70 versus U70, p = 0.38, L70 versus All, p = 0.77 and U70 versus All, p = 0.38). We found that Simpson’s paradox does not manifest in any of the top fifteen features in our data.

Extended Data Fig. 5 |. Further experiments to test model performance and parameters.

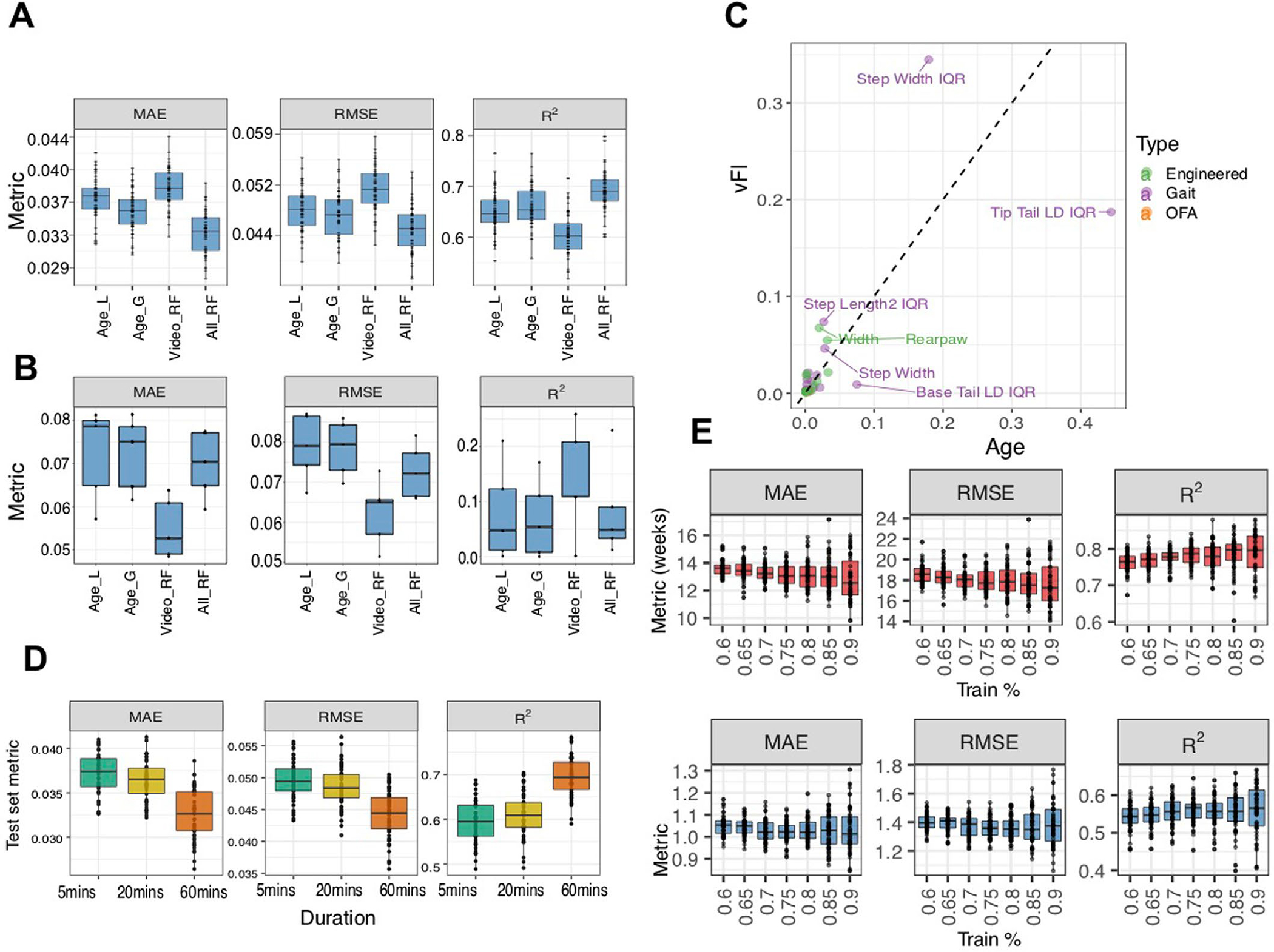
A, We compare the performance of different feature sets, 1) age alone, 2) video and 3) age + video, in predicting frailty across n = 50 independent train-test splits. We use age alone as a feature in a linear (Age_L) and a generalized additive non-linear model (Age_G). Although we didn’t notice a clear improvement of the random forest model (Video_RF) using video features over a vFI prediction based on age alone, a clear improvement in prediction performance is seen for the model (All_RF), which contains video features + age with lowest MSE (p < 2.2e − 16, F_3,147 = 213.79, LMM post hoc pairwise comparison with Age_G, t₁₄₇ = −12.21, FDR-adjusted p < .0001), lowest RMSE (p < 2.2e − 16, F_3,147 = 172.88, LMM post hoc pairwise comparison with Age_G, t₁₄₇ = −14.12, FDR-adjusted p < .0001) and highest R2 (p < 2.2e − 16, F_3,147 = 171.12, LMM post hoc pairwise comparison with Age_G, t₁₄₇ = 14.07, FDR-adjusted p < .0001). This shows that video features add important information pertaining to frailty that age alone does not. B, We picked animals whose ages and FI scores had an inverse relationship, that is, younger animals with higher FI scores and older animals with lower FI scores. We formed 5 test sets (n = 43, 38, 45, 42, 20) containing animals with these criteria and trained the random forest (RF) model on the remaining mice. The model using only video features (Video_RF) does better than all other models for these mice with lowest MSE (p < 1.6e − 08, F_3,12 = 91.07, LMM post hoc pairwise comparison with AgeG, t₁₂ = 13.60, FDR-adjusted p < .0001), lowest RMSE (p < 1.6e − 08, F_3,12 = 93.88, LMM post hoc pairwise comparison with AgeG, t₁₂ = 14.15, FDR-adjusted p < .0001) and highest R2 (p < 1.31e − 08, F_3,12 = 94.32, LMM post hoc pairwise comparison with AgeG, t₁₂ = 14.10, FDR-adjusted p < .0001). C, We further investigate the difference between Age and vFI predictors in terms of feature importance. Features lying along the diagonal are important for both Age and vFI predictions. D, Predicting FI score from video features extracted from videos of shorter durations. We used video features generated from videos with shorter durations (first 5 and 20 minutes) to investigate the loss in accuracy in predicting age and FI score. We used the random forest model trained with features generated from 60-minute videos as a baseline model for comparison. We found a diminished loss in accuracy using shorter videos. The features associated with 60-minute videos had the best accuracy for vFI prediction (LMM where ‘simulation’ is the random effect, nsim = 50; lowest MAE, F_2,98 = 178.39, p < 2.2e − 16; lowest RMSE, F_2,98 = 156.93, p < 2.2e − 16); highest R2 (p < 2.2e − 16, F_2,98 = 297.3). We observed a significant drop in performance accuracy when the open field test length is reduced from 60 to 20-minute video (LMM with post hoc pairwise comparisons - MAE, t₉₈ = 14.82, FDR-adjusted p < 0.0001; RMSE, t₉₈ = 13.69, FDR-adjusted p < 0.0001; R2, t₉₈ = −19.22, FDR-adjusted p < 0.0001). E, To see how much training data is realistically needed, we performed a simulation study (n = 50 independent train-test splits) where we allocated different percentage of total data to training. As expected, there is a general downward (upward) trend in MAE, RMSE (R2 with an increasing percentage of data allocated to training set. Indeed, a smaller training set (< 80% training) can reach a similar training performance. In A, B, E and D, the lower and upper hinges correspond to the first and third quartiles (the 25th and 75th percentiles) respectively, the line in the middle corresponds to the median, the upper (lower) hinge extends from the upper (lower) hinge to the largest (smallest) value not bigger (smaller than 1.5 × IQR where IQR is the interquartile range.

Data availability

Files containing the manual FI scores and vFI features for all mice in our dataset have been submitted as the source data for figures. Both files can also be found on the GitHub repository https://github.com/KumarLabJax/vFI-modeling and on the Zenodo repository https://zenodo.org/badge/latestdoi/412051716.