Effects of Selection at Linked Sites on Patterns of Genetic Variability

Abstract

Patterns of variation and evolution at a given site in a genome can be strongly influenced by the effects of selection at genetically linked sites. In particular, the recombination rates of genomic regions correlate with their amount of within-population genetic variability, the degree to which the frequency distributions of DNA sequence variants differ from their neutral expectations, and the levels of adaptation of their functional components. We review the major population genetic processes that are thought to lead to these patterns, focusing on their effects on patterns of variability: selective sweeps, background selection, associative overdominance, and Hill–Robertson interference among deleterious mutations. We emphasize the difficulties in distinguishing among the footprints of these processes and disentangling them from the effects of purely demographic factors such as population size changes. We also discuss how interactions between selective and demographic processes can significantly affect patterns of variability within genomes.

INTRODUCTION

A consistent pattern that has emerged from over 30 years of investigations of DNA sequence variability within species is that the level of selectively neutral or nearly neutral variability in a given region of the genome is usually positively correlated with its rate of genetic recombination (Begun & Aquadro 1992, Charlesworth & Campos 2014, Cutter & Payseur 2013), as illustrated in Figure 1. Regions of genomes that completely lack crossing over—sections of chromosomes near centromeres or telomeres and all or parts of Y and W chromosomes—can have levels of variability as low as one-tenth, or even less, of the genome-wide average (B. Charlesworth et al. 2010). Such regions also often show evidence of reduced levels of adaptation, including low codon usage bias and increased levels of nonsynonymous nucleotide substitutions between related species. Similar patterns are also found in asexual and highly self-fertilizing species, in which recombination is either absent or ineffective (Bast et al. 2018, D. Charlesworth 2003, Cutter & Payseur 2013). In such cases, it is difficult to distinguish the consequences of reduced rates of recombination from the effects of confounding ecological factors, such as a liability to local extinction and recolonization events (D. Charlesworth 2003). We therefore focus on patterns within the genome of a single sexual, outcrossing species.

Figure 1.

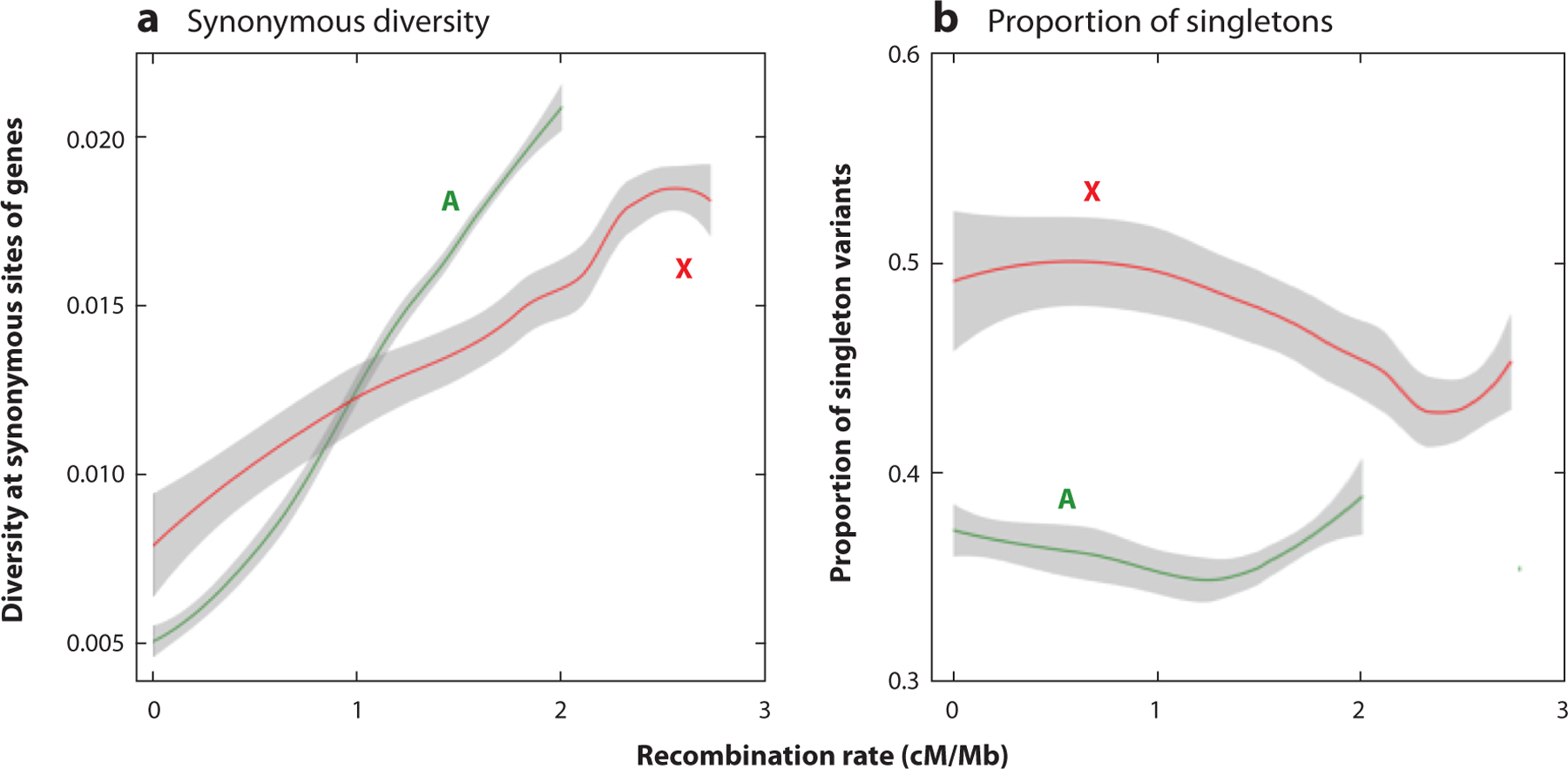
(a) The y-axis shows the pairwise diversity per nucleotide site at synonymous sites of genes in a sample of 17 haploid genomes of Drosophila melanogaster from a Rwandan population (Campos et al. 2014). (b) The y-axis shows the proportion of singleton variants (those present as a single copy in the sample). The x-axis of panels a and b displays the estimated rate of crossing over per megabase for each gene, corrected for the absence of crossing over in males. The plots are Loess regression fits with 95% confidence intervals (gray shading). The green curves are for autosomal genes (A), and the red curves are for X-linked genes (X). Panel a shows that diversity increases with the rate of crossing over experienced by a gene, whereas panel b shows that the proportion of singletons has a complex relationship with the rate of crossing over, although on autosomes it tends to decline with the rate of crossing over in the lower part of the range of crossing over rates. The difference between the proportions of singletons on the X chromosome and autosomes is striking and is suggestive of stronger hitchhiking effects on the X chromosome (Campos et al. 2014).

The generality of these observations implies that ubiquitous population genetic forces must be involved. Much effort has been expended in characterizing these forces and attempting to assess their relative roles. A major factor is hitchhiking, whereby selection at a given site in the genome influences the frequencies of variants at genetically linked sites. There are two main types of hitchhiking, selective sweeps (SSWs) (Berry et al. 1991, Maynard Smith & Haigh 1974) and background selection (BGS) (B. Charlesworth et al. 1993). A SSW involves the spread of a new, selectively favorable mutation. In the absence of recombination, any variants present on the chromosome in which the mutation arose will be carried along with it, and its fixation in the population wipes out variability at nearby sites. Recombination allows variants linked to the mutation to escape onto the wild-type background, reducing the loss of variability. BGS involves the reverse situation, in which new deleterious mutations that enter a population are eliminated by selection, together with any linked neutral variants. In the absence of recombination, the effective size of the population is multiplied by a factor approximately equal to the proportion of the population that carries one or more deleterious mutations, provided that selection is sufficiently strong that deleterious mutations have a high probability of becoming extinct.

There are two complementary ways of describing the general effects of selection on the variation and evolution at linked sites. First, selection at one locus causes heritable variation in fitness at other loci as a result of linkage disequilibrium (LD), reducing the apparent effective population size (N_e) that they experience, because of the well-known effect of variation in fitness in reducing N_e (B. Charlesworth 2009; Hill & Robertson 1966; Santiago & Caballero 1995, 1998). This reduces variability at these loci and reduces the fixation probabilities of new advantageous mutations, as both of these decrease with N_e (Kimura 1983); conversely, the fixation probabilities of deleterious mutations are increased. This reduction in N_e provides a useful heuristic, despite important qualifications that are described below. In the case of two or more selected loci, the effects on fixation probabilities are known as Hill–Robertson interference (Felsenstein 1974).

The second approach uses the finding that the expected change in the mean of a trait over one generation is proportional to the additive genetic covariance between the trait and fitness—the Price–Robertson equation (Crow & Nagylaki 1976, Price 1970, Robertson 1968). The additive covariance between the allelic state at a focal biallelic locus and fitness at a linked biallelic locus is equal to the product of the coefficient of LD between the two loci (D) and the average excess in fitness at the linked locus, a_w, of a selectively favored allele with frequency p (see the terms in the margins for definitions of the main symbols used here). With weak selection, the change in p over one generation is approximately equal to p(1 − p)a_w. If x is the allele frequency at the focal locus, its frequency change due to selection at the other locus is Δx ≈ Da_w, and its allelic diversity, 2x(1 − x), is changed by approximately 2(1 − 2x)Δx. Hitchhiking thus alters diversity by approximately 2(1 − 2x)Da_w, an expression used in several analyses of the different forms of hitchhiking (Barton 2000, Santiago & Caballero 1995, Zhao & Charlesworth 2016). This result implies that variability may not necessarily be reduced by hitchhiking; as we describe below, the type of hitchhiking known as associative overdominance (AOD) causes an increase in variability (Zhao & Charlesworth 2016).

This general framework for understanding hitchhiking effects neither distinguishes between the effects of different types of selection nor explicitly predicts important quantities such as levels of variability and fixation probabilities. More detailed analyses are needed in order to make such predictions and to assess which processes are likely to be involved in causing observed patterns of variability. In this article, we focus on BGS, the related process of AOD, and SSWs. In addition, we discuss how demographic factors such as population subdivision and size changes must be considered jointly with the effects of selection in order to make sense of data on patterns of variability across genomes.

Selective processes other than hitchhiking can, however, also affect variability at linked sites. If two or more alleles are maintained for a long time by balancing selection, genetic drift and mutation cause them to diverge at closely linked neutral or nearly neutral sites, in much the same way as local populations diverge when migration is limited (B. Charlesworth et al. 1997, Hudson 1990). A similar effect occurs if alleles at a locus in a spatially subdivided population are maintained at different frequencies by spatially divergent selection acting on different local populations (Barton 1979, B. Charlesworth et al. 1997). Divergence at linked sites in a subdivided population can also arise from hybrid incompatibilities among two or more loci (Bengtsson 1985). These findings have led to the hope that signals of balancing or divergent selection can be identified by genome scans of patterns of variability (Fijarczyk & Babik 2015, Hoban et al. 2016). Considerable progress has been made in both theoretical and empirical studies of these processes, although many problems remain to be solved. For brevity, we do not discuss them further, although they must be considered for a full understanding of natural variability.

THE NEUTRAL NULL MODEL OF VARIABILITY

Before describing the effects of different types of hitchhiking and demographic changes, we briefly review the properties of the simplest null model: a neutral locus in a population of constant effective population size, N_e, whose value is determined by the nature of the genetic system under consideration (e.g., haploidy, mitochondrion, autosome, sex chromosome) together with the breeding system (e.g., discrete generations, overlapping generations, random mating, partial inbreeding) (B. Charlesworth 2009).

Consider a set of n haploid genomes sampled from the population. At a nucleotide site in a genomic region of interest, either the n copies of this region (alleles) include two or more variants (i.e., the site is polymorphic) or the alleles are all identical (i.e., it is monomorphic). Under the infinite sites model of sequence evolution, variability is assumed to be sufficiently low that sites show at most two variants, one ancestral and one derived (Kimura 1971). We can then describe the state of the sample with respect to a sequence of m nucleotide sites by the variant frequencies at the polymorphic sites: f _i is the proportion of sites where the rarer variant is present in i copies (this is called the folded site frequency spectrum). A frequently used descriptor of the overall level of diversity for a genomic region consisting of m nucleotide sites is the pairwise nucleotide site diversity, π, given by the mean of 2i(n − i)/n over all sites, including sites where i is 0. Another way of quantifying variability uses the number of polymorphic sites in the sample, P. This yields the measure called Watterson’s theta, defined as θ_w = P/(ma_n), where a_n is the harmonic series, 1 + 2⁻¹ +···+ (n − 1)⁻¹. If the population size has been constant for a long time, the expectations of both π and θ_w are equal to θ = 4N_eu, where u is the probability of a neutral mutation per base pair per generation. These fundamental results can be most easily derived using neutral coalescent theory (Figure 2a), as explained in more detail in section 1 of the Supplemental Material (see also Hudson 1990 and Wakeley 2008). Observed values may, of course, deviate considerably from these expectations.

Figure 2.

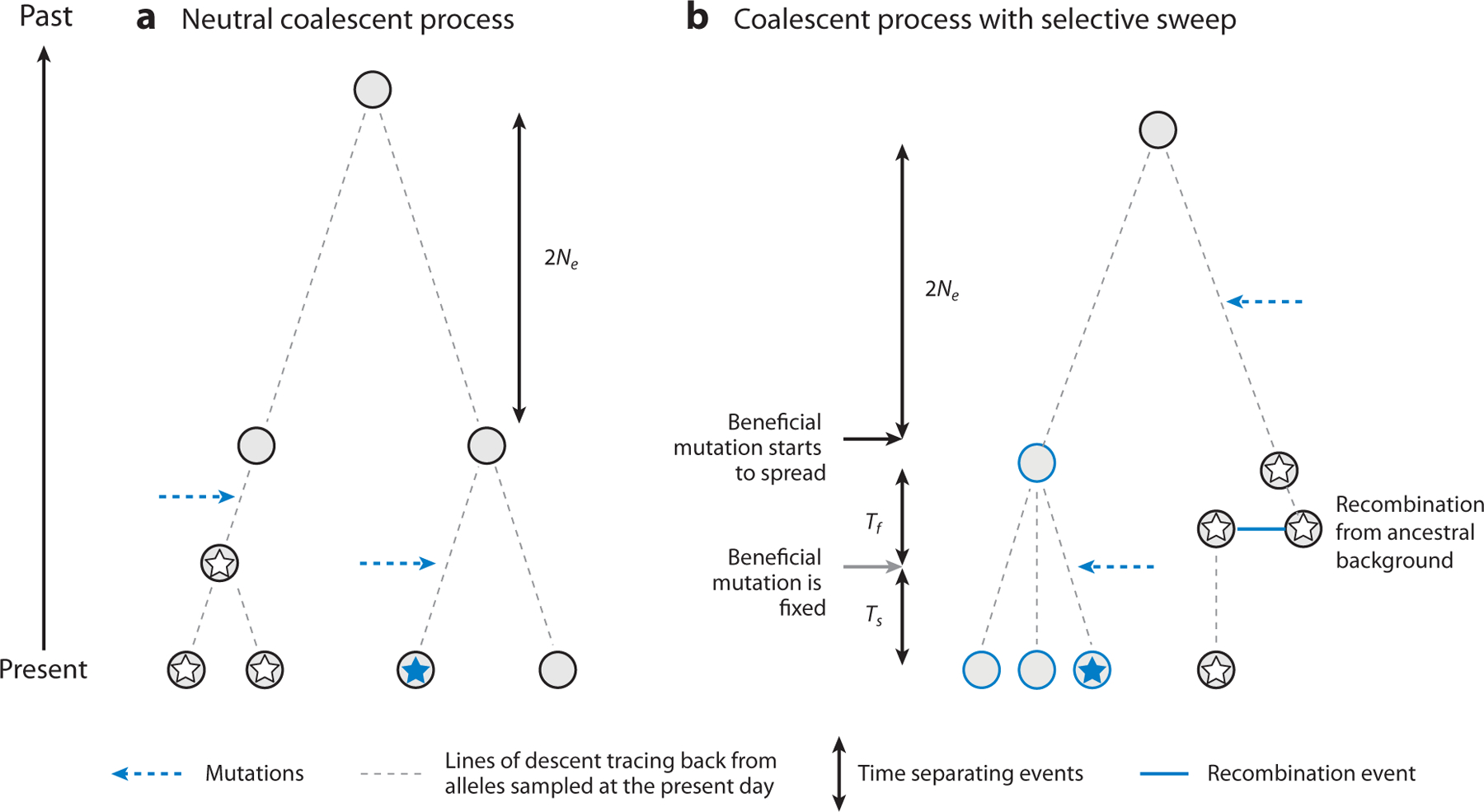
(a) Neutral coalescence and (b) coalescence with a selective sweep. The dashed black lines represent lines of descent tracing back from alleles sampled at the present day (bottom, gray circles). The coalescence of two alleles into an ancestral allele from which they are descended is indicated by the merger of the pair of lines connecting them to the ancestor. The horizontal dashed blue arrows represent occurrences of mutations at different sites in the sequence. (a) The neutral coalescent process for a sample of four alleles. The first mutation (white star) occurred after the first coalescent event (looking back in time), such that its frequency is 1/2; the second mutation (blue star) occurred before the first coalescent event on its branch of the tree, such that its frequency is 1/4. The double-headed arrow to the right of the tree indicates the expected time to the last coalescent event (2N_e generations). (b) Coalescence for a neutral locus linked to a site that has experienced a selective sweep, which finished T_s generations ago. The blue outlines indicate alleles carrying the beneficial mutation, all of which coalesced at the start of the sweep and whose duration is T_f generations. The solid black and gray arrows indicate the times of spread and fixation of this mutation, respectively. The solid blue line indicates a recombination event, such that the neutral site in question traced its ancestry to a wild-type background at the selected locus; its expected time to coalescence with the ancestor of all the nonrecombinant alleles counting back from the start of the sweep is 2N_e generations. The white stars indicate a mutation that arose in an ancestor of the recombinant allele; the blue star indicates a mutation that arose at a different site in an ancestor of a nonrecombinant allele. Both mutations have a frequency of 1/4 in the sample.

Theory shows that a population expansion, a recent SSW, and BGS all cause an excess of rare variants at neutral sites, compared with the equilibrium site frequency spectrum. This is because they cause the gene trees generated by the coalescent process to have longer external branches (the branches that have not yet experienced a coalescent event, looking back in time) relative to the total sizes of the trees, such that more mutations are represented only once in the sample than under strict neutrality (see Figure 2b), as explained in section 1 of the Supplemental Material. With a population expansion, the reason for this effect is simple; in the recent past, coalescent events take longer to occur because N_e is larger than it is in the more remote past. The effects of SSWs and BGS are discussed below. The expected value of π is then smaller than that of θ_w; conversely, population contractions, AOD, or balancing selection has the reverse effect (Wakeley 2008). Subdivision into partially isolated subpopulations also affects the site frequency spectrum in a way that depends on how the different subpopulations are sampled (Chikhi et al. 2018, Wakeley 2008). This greatly complicates inferences, and we largely evade this difficulty by focusing on organisms, such as Drosophila, for which it is reasonable to assume that the population is close to being panmictic.

BACKGROUND SELECTION AND ASSOCIATIVE OVERDOMINANCE

The Abundance of Deleterious Mutations in Natural Populations

Here, we review theory and evidence concerning the hitchhiking effects of purifying selection against deleterious mutations. Analyses of sequence data have shown that deleterious mutations are abundant in natural populations, both in coding sequences (Galtier & Rousselle 2020) and in functional noncoding sequences, such as the untranslated but transcribed regions adjacent to coding sequences, some components of introns, and many intergenic sequences (e.g., Casillas et al. 2007). For these mutations to be effective at causing BGS, they must be sufficiently strongly selected that their frequencies are controlled largely by selection rather than by genetic drift, thus requiring estimates of the strength of selection in order to assess the effects of BGS. Population genomic analyses of the distribution of fitness effects (DFEs) of new deleterious mutations for autosomal loci in randomly mating populations show that most of these mutations have small heterozygous selection coefficients (t, where t = hs), with a wide distribution about a mean so that $N_e\overline{t}\gg 1$, although the conclusions about the form of their distribution, and the means and variances of t, differ considerably among studies (Campos et al. 2017, Eyre-Walker & Keightley 2009, Galtier & Rousselle 2020, Johri et al. 2020, Kousathanas & Keightley 2013). But there is general agreement that a substantial fraction of deleterious mutations behave nearly deterministically; for example, in Drosophila melanogaster, only approximately 10% of new nonsynonymous mutations appear to be in the nearly neutral category (4N_et < 1), where variant frequencies are controlled largely by genetic drift ( Johri et al. 2020, Kousathanas & Keightley 2013).

The Classical Background Selection Process

These results imply that the elimination of recurrent deleterious mutations by purifying selection may cause hitchhiking effects on linked neutral and weakly selected mutations (B. Charlesworth et al. 1993). Much progress has been made in developing models of these effects. The basic model of BGS assumes deterministic mutation–selection balance at the sites responsible, with sufficiently frequent recombination among them that Hill–Robertson interference can be ignored. For an autosomal locus in a randomly mating population of constant size, this assumption leads to the following prediction for the mean pairwise coalescence time at a focal neutral site surrounded by m sites subject to selection, measured relative to its value in the absence of selection (Hudson & Kaplan 1995, Nordborg et al. 1996). This quantity is commonly denoted by B,

$$B\approx \exp -\sum _{i=1}^m\frac{u_i}{{\left[1+r_i\left(1-t_i\right)/t_i\right]}^2}.$$ 1.

Here, u_i is the mutation rate to deleterious alleles at the ith selected nucleotide site, t_i is the selection coefficient against heterozygous carriers of mutations at this site, and r_i is the recombination frequency with the focal site.

If the assumptions of the infinite sites model are met (see above), B corresponds to the expected pairwise nucleotide site diversity (π) relative to its purely neutral expectation (π₀). The formula implies that, all else being equal, π increases as the recombination rate increases. In the absence of recombination, B ≈ f₀, where $f_0=\exp -{\mathrm{\Sigma }}_i\left(u_i/t_i\right)$ is the equilibrium frequency of the mutation-free or least-loaded haplotype. This is equivalent to assuming that coalescence of a pair of alleles sampled from the population can occur only in a mutation-free background, because haplotypes carrying deleterious mutations are quickly eliminated from the population (D. Charlesworth et al. 1995, Hudson & Kaplan 1994, Nicolaisen & Desai 2013).

Equation 1 has been used in attempts to interpret observed levels of variability in genomic regions with differing local recombination rates (e.g., B. Charlesworth 1996, Comeron 2017, Elyashiv et al. 2016, Hudson & Kaplan 1995) (Figure 1a), as well as observations of increases in diversity in intergenic sequences at increasing distances from coding sequences ( Johri et al. 2020, McVicker et al. 2009, Pouyet et al. 2018). An example of the second type of pattern is shown in Figure 3a. The results strongly suggest that BGS contributes significantly to these observed patterns but is not the sole factor involved (Booker et al. 2017). For example, although 60% of the variance in diversity at putatively neutral noncoding sites in D. melanogaster can be explained by BGS (Comeron 2017) and the pattern in Figure 3a is consistent with BGS alone ( Johri et al. 2020), BGS cannot explain the negative relationship between a gene’s synonymous site diversity and the divergence of its protein sequence from that of a related species, as shown in Figure 3b (Campos et al. 2017).

Figure 3.

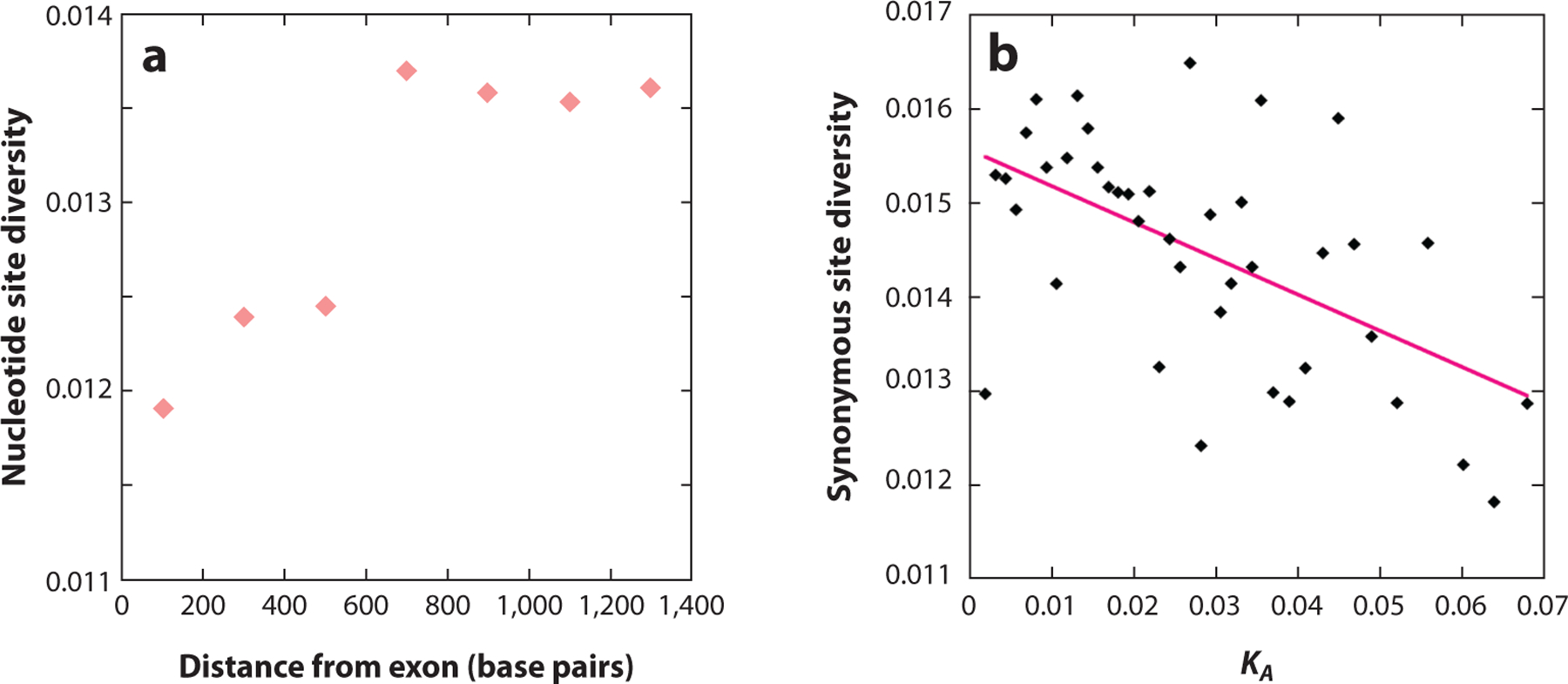
(a) The y-axis is the mean nucleotide site diversity in 200-bp sliding windows of intergenic sequence, and the x-axis is the distance of the middle of each window from the 5’ end of the exon. The data are for 94 single-exon genes sequenced in 76 haploid genomes from Drosophila melanogaster individuals sampled in Zambia; noncoding sites under strong selective constraints have been masked ( Johri et al. 2020). The Pearson correlation coefficient is r = 0.88, p < 0.01. (b) The points represent the mean synonymous site diversities of sets of autosomal genes from the Rwandan population of D. melanogaster used in Figure 1, grouped into 40 bins with respect to their divergence at nonsynonymous sites from the related species D. yakuba (K_A). The solid pink line is the least-squares linear regression of diversity on K_A (y = 0.0156 – 0.0385x, r =− 0.563, p < 0.001).

In addition to its effects on nucleotide site diversity, BGS affects the shape of the gene tree connecting a sample of alleles from a population. It distorts the site frequency spectrum toward a higher frequency of rare variants than is expected under neutrality, because alleles in a sample from the population that carry a deleterious mutation at a particular site cannot coalesce with mutant-free alleles but must wait until the time of origin of the mutation for such coalescent events to be possible. This increases the contribution from the external branches of the gene tree relative to its total size (see section 1 of the Supplemental Material). This effect is stronger when N_et is relatively small, because the mutation can persist in the population for a longer time than it can with large N_et (D. Charlesworth et al. 1995, Hudson & Kaplan 1994, Nicolaisen & Desai 2013). This weakens the effect of BGS on π compared with the classical expression (B is increased), but θ_w is less affected.

Overall, BGS seems to cause only relatively small distortions in the site frequency spectrum in genomic regions with recombination rates typical of most outcrossing species of multicellular organisms, even at synonymous sites in coding sequences (Campos & Charlesworth 2019, B. Charlesworth et al. 1993, D. Charlesworth et al. 1995, Hudson & Kaplan 1994, Zeng 2013). Nevertheless, these distortions can result in substantial errors in estimates of patterns of population change based on purely neutral models, as we discuss below. With large samples of alleles (B. Charlesworth et al. 1993, D. Charlesworth et al. 1995, Hudson & Kaplan 1994, Cvijović et al. 2018), excesses of both low- and high-frequency-derived variants are clearly visible under BGS. The excess of high-frequency-derived variants arises because new neutral mutations sometimes arise on a background with a mean fitness that is higher than average and then hitchhike to a high frequency (B. Charlesworth et al. 1993, Cvijović et al. 2018).

Muller’s Ratchet

This model of BGS breaks down when applied to regions of the genome where recombination is rare or absent, and selective interference among the deleterious mutations involved reduces the effective strength of selection. It also fails when 2N_es is approximately 5 or less, such that individual mutation frequencies experience significant stochastic fluctuations (B. Charlesworth et al. 1993, D. Charlesworth et al. 1995, Nordborg et al. 1996).

Muller’s ratchet (Felsenstein 1974, Muller 1964) is widely assumed to be the paradigm for the first situation, but this is an oversimplification. Models of Muller’s ratchet assume unidirectional mutation from wild-type to deleterious alleles, as well as an almost complete absence of recombination; they also usually assume that all mutations have similar fitness effects, although this assumption can be relaxed (Söderberg & Berg 2007). Under these assumptions, if a finite population that lacks recombination is founded from an initial equilibrium population, and the population size is sufficiently large that some least-loaded haplotypes are initially present, haplotypes carrying the current smallest number of deleterious mutations are successively and irreversibly lost from the population—the ratchet (Felsenstein 1974, Jain 2008). Each loss event is accompanied by the fixation of a deleterious mutation (Charlesworth & Charlesworth 1997). However, if reverse mutations can occur, as is the case for single-nucleotide mutations, these ultimately halt the ratchet, resulting in a statistical equilibrium under which the mean number of deleterious mutations per individual remains constant (B. Charlesworth et al. 2010).

There are two circumstances under which the ratchet is likely to accurately describe the behavior of a nonrecombining genomic region: when mutations are irreversible, such as deletions and complex sequence rearrangements, and when a nonrecombining genome, such as a new asexual lineage, has recently been formed, such that the system is far from the final equilibrium. Sequencing of the relatively long-established nonrecombining neo-Y chromosome of Drosophila miranda, formed by fusion of an autosome with the ancestral Y chromosome, has revealed that many genes have acquired loss-of-function mutations that are probably irreversible, such as frameshifts and deletions, and it seems likely that the ratchet has contributed to this process (Kaiser & Charlesworth 2010). Its role in other situations is plausible but hypothetical; for example, a role for the ratchet as well as other forms of Hill–Robertson interference in cancer progression has been proposed (McFarland et al. 2013).

The Interference Selection Limit

Theoretical work has shown that, especially with the wide distributions of mutational effects suggested by the population genomic analyses mentioned above, Hill–Robertson interference occurs among the deleterious mutations responsible for BGS, greatly reducing the effective strength of selection against individual mutations and resulting in an interference selection limit (Comeron & Kreitman 2002, Good et al. 2014). It is also necessary to consider the reverse mutations that occur with base substitutions (which constitute the majority of mutations) in order to understand the long-term properties of a low-recombination genomic region. Simulations with reverse mutations show that, at statistical equilibrium under mutation, drift, and selection, the effect of BGS on nucleotide site diversity at neutral sites is greatly reduced in a low-recombination region and is accompanied by a large increase in the abundance of low-frequency neutral variants and in the frequencies of deleterious variants (B. Charlesworth et al. 2010, Comeron & Kreitman 2002, Kaiser & Charlesworth 2009). This explains why low-recombination genomic regions, such as the neo-Y chromosome of D. miranda, often have much greater variability than is predicted by Equation 1 (B. Charlesworth et al. 2010, Kaiser & Charlesworth 2009).

Associative Overdominance

Another consequence of linkage and selection is associative overdominance (AOD). In its original formulation, AOD involves apparent heterozygote advantage at biallelic neutral loci caused by associations either with a linked selected locus that is subject to a genuine heterozygote advantage or with linked loci subject to recurrent mutations to recessive or partially recessive (h < 0.5) deleterious alleles. Here, we discuss the effects of deleterious mutations in randomly mating populations, where genetic drift can cause nonrandom associations between alleles at selected loci and alleles at closely linked neutral loci. This causes homozygosity for alleles at the neutral loci to be correlated with homozygosity at the selected loci, creating apparent heterozygote advantage at the neutral loci (Ohta 1971). In contrast, AOD in partially inbreeding populations is caused mainly by associations between the frequencies of heterozygotes at different loci caused by the different levels of homozygosity of outbred versus inbred individuals and does not involve drift (D. Charlesworth 1991).

This apparent heterozygote advantage was originally thought to retard the loss of neutral variability by genetic drift (Ohta 1971), the opposite effect of BGS. This raises the question of how deleterious mutations can apparently either retard or enhance the loss of variability, depending on the parameter values, as has been found in computer simulations (Gilbert et al. 2020, Latter 1998, Palsson & Pamilo 1999, Zhao & Charlesworth 2016). This paradox is partially resolved by the fact that substitution of the apparent selection coefficients against homozygotes into the standard equation for allele frequency change shows that they do not affect allele frequencies at the neutral locus and hence cannot influence its diversity (Zhao & Charlesworth 2016). Nevertheless, according to the Price–Robertson equation, diversity at the neutral locus must be changed by the hitchhiking effects of the selected loci, as described in the Introduction.

A detailed analysis of the case of a single selected locus and a linked neutral locus shows that neutral variability is increased only when the deleterious mutations are partially recessive (h < 0.5) and the scaled selection coefficient 2N_es is ≤ 2, such that genetic drift causes a substantial variance in the frequencies of deleterious mutations around their deterministic equilibrium values, especially when h is small. Otherwise, BGS operates and variability is reduced, not enhanced (Zhao & Charlesworth 2016). The intuitive basis for this result comes from the seemingly paradoxical fact that weakly selected recessive or partially recessive deleterious mutations have slightly longer mean sojourn times between their origination and their fixation or loss than do neutral mutations (Mafessoni & Lachmann 2015), whereas more strongly selected mutations have short sojourn times (see section 2 of the Supplemental Material for more details). When selection is sufficiently weak and mutations are sufficiently recessive, a linked neutral locus can therefore experience coalescence times that are longer than expected under neutrality. With multiple selected loci, simulations show that the conditions for AOD are somewhat relaxed compared with the analytical predictions for a single selected locus and confirm that a transition from BGS to AOD occurs as h and population size are reduced for a given strength of selection (Gilbert et al. 2020, Palsson & Pamilo 1999, Zhao & Charlesworth 2016).

The requirement for a small value of 2N_es suggests at first sight that AOD is likely to operate only in small populations, such as laboratory populations or closed populations of domestic animals. Evidence for its action in such populations is indeed seen in their rates of loss of variability at molecular marker loci (Latter 1998, Zhao & Charlesworth 2016). However, even in large natural populations the small N_e of low-recombination regions of the genome, and the accompanying interference among loci under selection, could reduce 2N_es below the threshold needed for AOD, at least for weakly selected deleterious mutations. Given the evidence from the parameters of the DFE mentioned above, most sites in low-recombination regions are probably subject to BGS rather than AOD, such that the mean diversity at neutral sites is expected to be much lower than the genome-wide average. However, some sites will fall into the region where AOD operates. This indeed occurs in computer simulations, whose predictions compare well with population genomic data (Becher et al. 2020). The excess of low-frequency synonymous variants in low-recombination regions of several Drosophila species is much less than expected under BGS alone (Becher et al. 2020). In humans, there is a decrease in the skew of the site frequency spectrum toward low-frequency variants in regions with low recombination, compared with regions with slightly more recombination, whereas the skew decreases with increasing recombination rate elsewhere (Gilbert et al. 2020, Pouyet et al. 2018). Both of these patterns indicate the action of AOD.

SELECTIVE SWEEPS AND THEIR FOOTPRINTS ACROSS THE GENOME

Effects of a Single Selective Sweep

Although beneficial mutations are a comparatively small fraction of all new mutations (Bank et al. 2014), they are obviously important in evolution. There is great general interest in studying adaptation, as well as in identifying loci underlying desirable traits in domesticated and cultivated species or undesirable traits, such as drug resistance in viral and bacterial populations (e.g., Xia et al. 2009, Foll et al. 2014). Maynard Smith & Haigh (1974) significantly enhanced our understanding of the genomic consequences of such positive selection by analyzing the reduction in variability at a linked site as a new beneficial mutation spreads toward fixation in a population, a process commonly referred to as a selective sweep (SSW) (Berry et al. 1991).

If selection favoring a beneficial mutation is sufficiently strong, it reaches fixation much faster than under neutrality, greatly reducing variability in the genomic region surrounding the target of selection, whose physical size is inversely related to the local rate of recombination. After the completion of a sweep, neutral variability gradually recovers as new mutations enter the population over a period of the order of 2N_e generations (Wiehe & Stephan 1993), although the time during which the genomic patterns associated with a sweep are statistically identifiable is generally much shorter (Przeworski 2002).

The set of events that occurs during a sweep can be understood with the help of the coalescent process, as illustrated in Figure 2b for the case of a sample of four alleles. In a sample of n alleles taken after a beneficial mutation has become fixed, all alleles will carry the mutation. If we trace the ancestry of these alleles back in time, we can see that a given linked neutral site in one or more of them can be derived by recombination from a wild-type allele that was still present in the population and whose ancestor was present before the sweep occurred. In contrast, all nonrecombinant alleles are derived from the single ancestral haplotype in which the beneficial mutation arose, and their expected time to coalescence is much shorter than in the absence of selection, causing a reduction in the expected value of π at the neutral site relative to π₀, the purely neutral value. Prior to the origin of the beneficial mutation, coalescence with respect to the neutral site for any extant alleles follows the standard neutral model.

These considerations suggest that the overall reduction in diversity caused by a sweep will be inversely related to the product of the time taken for the beneficial mutation to become fixed (T_f) and the recombination rate (r) between the selected and neutral sites, as this product determines the probability of occurrence of one or more recombination events during the sweep. For beneficial mutations that are sufficiently strongly selected that their trajectories of allele frequency change are close to those in an infinite population, T_f is inversely related to the selection coefficient s_a that measures the increase in fitness of heterozygotes for the mutation relative to wild-type homozygotes (B. Charlesworth 2020b, Haldane 1924). The reduction in diversity caused by a sweep, Δ = 1 − π/π ₀, should thus be inversely related to r/s_a. Furthermore, if T_f is sufficiently small, and there is only a short time T_s between the end of the sweep and the time of sampling, nonrecombinant alleles can coalesce only at the start of the sweep, creating a star-shaped genealogy, in which any new mutations are present only once in the sample (Figure 2b). The site frequency spectrum is thus expected to be skewed toward low-frequency variants compared with the standard neutral model (Barton 2000, Braverman et al. 1995).

Multiple extensions have been made to the theory of SSWs since the work of Maynard Smith & Haigh (1974) (for a recent overview, see Stephan 2019). In particular, Kaplan et al. (1989) used coalescent theory to develop a stochastic treatment that includes the initial phase when the beneficial mutation is rare and vulnerable to loss from the population. On the assumption that all nonrecombinant alleles coalesce at the start of the sweep, and that at most one recombination event occurs during the sweep, Barton (2000) derived a simple approximation for how a semidominant autosomal mutation affects the expected coalescence time for a pair of alleles sampled immediately after a sweep,

$$\mathrm{\Delta }=1-\frac{\pi }{{\pi }_0}\approx {\left(2N_e{s}_a\right)}^{-4r/s_a}.$$ 2.

This formula has been used in several methods for detecting sweeps, as has a different approximation due to Stephan et al. (1992).

The advent of high-throughput sequencing technologies has focused interest on characterizing patterns of variation associated with recent sweeps, potentially allowing them to be detected in population genomic data. As well as the reduced local variability and excess of low-frequency variants just mentioned, these patterns include high frequencies of derived variants around a recent sweep in a recombining genome region (Fay & Wu 2000) and an excess of LD during a sweep and a break in LD across the target of selection at the time of fixation of a beneficial mutation ( Jensen et al. 2007, Kim & Nielsen 2004, McVean 2007, Stephan et al. 2006).

These various expected signatures have been utilized in several tests for recent sweeps (reviewed by Bank et al. 2014, Booker et al. 2017, Stephan 2019). For example, Kim & Stephan (2002) developed a composite-likelihood ratio test, comparing the probability that the site frequency spectrum in a given genomic region was drawn from a neutral model versus a SSW model. Jensen et al. (2005) extended this approach, showing that violations of demographic equilibrium (i.e., population size changes) could result in high false-positive rates, and proposed an additional goodness-of-fit test to evaluate the fit of a SSW model. Nielsen et al. (2005) extended the composite-likelihood framework to use a null model, rather than the standard neutral model, based on the observed frequency spectrum across the genome as a whole; DeGiorgio et al. (2016) incorporated mutation rate variation, and information from LD patterns was added by Pavlidis et al. (2013).

These methods all assume a hard sweep (Figure 4), in which positive selection has acted on a new or rare variant and has driven it to fixation in the population, resulting in the fixation of a single haplotype in a region where recombination has failed to occur around the target of selection; methods for detecting ongoing or incomplete sweeps have also been developed (e.g., Ferrer-Admetlla et al. 2014). Two other alternatives to the hard sweep model must also be considered, which, although different from each other, are often collectively called soft sweeps because of their similar expected patterns of variation. In a soft SSW, multiple nonrecombinant haplotypes can be present after the initial wild-type state has been replaced (Figure 4). This can happen in two ways. First, positive selection can act on a variant that was initially present on multiple genetic backgrounds in the initial population, for example, a neutral or weakly deleterious variant that was segregating when a shift in selective pressure caused it to become beneficial (Hermisson & Pennings 2005). Second, either there is a high rate of input of beneficial mutations at a given locus or the locus represents a large mutational target. In this case, multiple mutations with identical fitness effects could arise on different genetic backgrounds, each remaining in the population after the wild-type state has been replaced (Pennings & Hermisson 2006).

Figure 4.

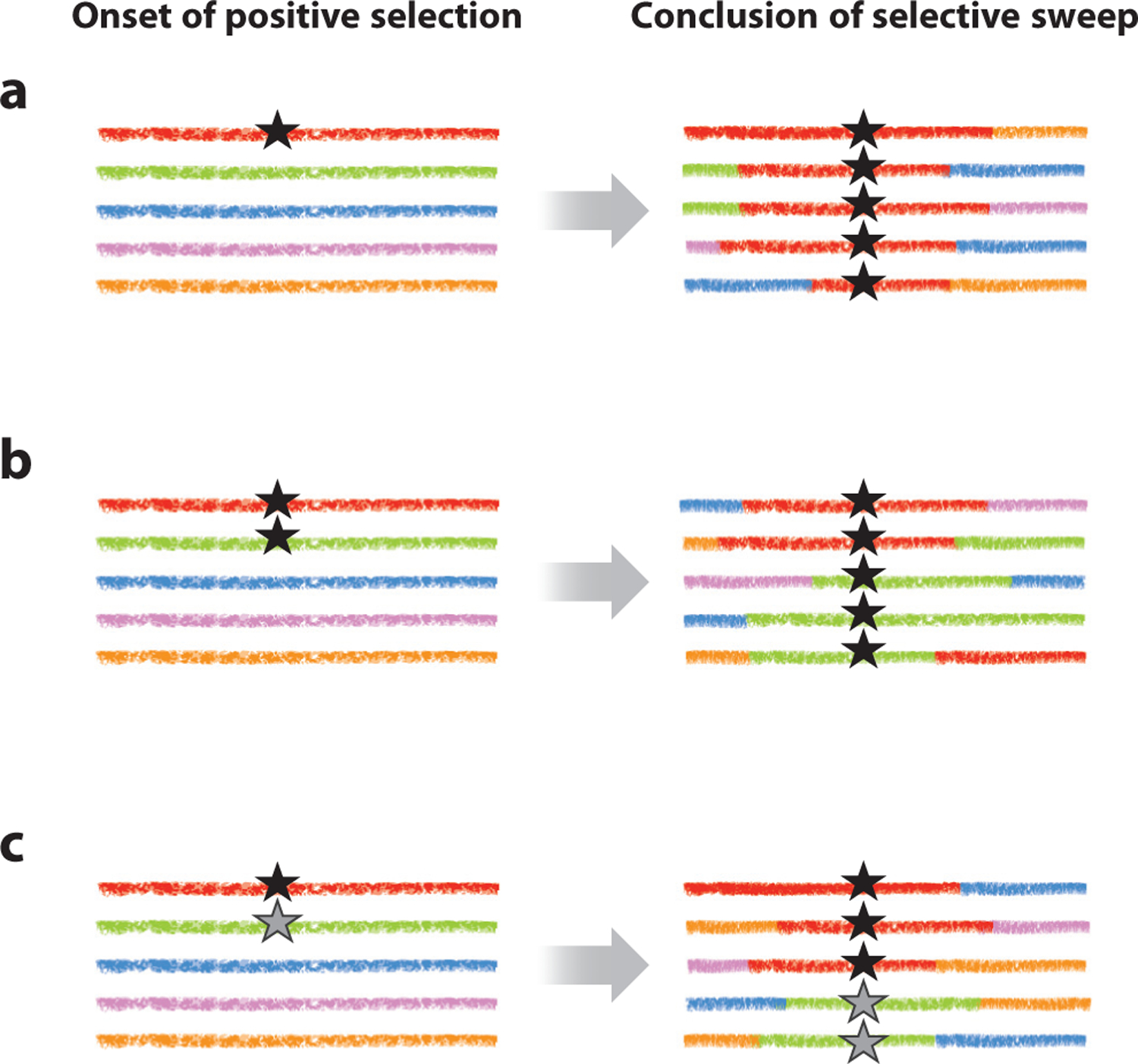
Diagram of three model realizations at two timepoints for five chromosomes sampled from a population subject to a selective sweep. Each colored line represents a unique chromosome-wide haplotype segregating in the population at the onset of selection, carrying a unique combination of polymorphic variants. The black and gray stars indicate distinct new mutations that are subject to positive selection. The left-hand column represents the state of the population at the onset of a selective sweep, and the right-hand column represents the state at the end of the sweep, when all individuals carry a beneficial variant. All models are characterized by hitchhiking effects due to associations with the beneficial mutation, as well as by breaks in these associations at various distances from the selected site caused by recombination events. (a) Hard sweep, i.e., selection on a rare variant. This is characterized by fixation of a single haplotype close to the target of selection (red haplotype). (b) Soft sweep in which selection acts on a common variant that was formerly neutral or deleterious. (c) Soft sweep in which selection acts on two independently occurring, beneficial variants with the same selection coefficient (black and gray stars). Both soft selective sweep models are characterized by multiple haplotypes segregating immediately around the target of selection (the red and green haplotypes, on which the beneficial variant was previously segregating neutrally or on which two beneficial variants arose independently).

A soft sweep can generate LD across the target of selection at the time of fixation (rather than only on opposite sides of the target) and produces a pattern of intermediate- and high-frequency variants close to the target of selection (rather than only in flanking regions) (Figure 4). This creates the problem that a region flanking a hard sweep (with strong LD and high-frequency-derived alleles) could be misinterpreted as a soft SSW (Schrider et al. 2015), as could gene conversion events that move the beneficial allele onto ancestral haplotypes. Furthermore, the soft sweep outcome requires an unusual situation to occur. For selection on standing variation to result in the continued presence of multiple haplotypes, the initial frequency of the advantageous allele must be considerable; if the hypothesized standing variants are rare, stochastic loss of all but one of the haplotypes carrying the beneficial variant is likely (Orr & Betancourt 2001). Generalizing this argument, Jensen (2014) argued that hard sweeps are the most likely outcome across much of the biologically relevant parameter space; for counterarguments, see Hermisson & Pennings (2017).

Several statistical tests aim to detect hitchhiking patterns associated with soft sweeps. For example, Garud et al. (2015) proposed a haplotype-based statistic based on the expectation that hard sweeps result in the fixation of a single haplotype close to the target of selection, whereas soft sweeps result in multiple common haplotypes. Schrider & Kern (2016) developed a machine learning–based approach using multiple summary statistics that utilizes sliding windows across a genome to classify patterns of variation in each region as being the result of a hard sweep (with no recombination), linkage to a hard sweep, a soft sweep, linkage to a soft sweep, or neutrality.

Finally, SSW-like effects are not limited to beneficial mutations. Conditional on its fixation, the fixation time of a semidominant deleterious mutation is the same as that of an advantageous one with the same selection coefficient (Maruyama & Kimura 1974). The fixation of a deleterious mutation by genetic drift can thus generate the same sweep effect as the fixation by selection of a beneficial mutation ( Johri et al. 2021a). A recent fixation of a neutral mutation is also associated with reduced variability at closely linked sites (Tajima 1990). Although the probabilities of fixation differ greatly between beneficial, neutral, and deleterious mutations, the far higher rates of occurrence of the last two suggest that recent fixations of such mutations could significantly affect the levels and patterns of variation at nearby sites when scanning genomes for fixation events (as was done by Sattah et al. 2011 and Elyashiv et al. 2016). However, these effects are likely to be highly localized to a few dozen base pairs except in low-recombination regions, as weak selection is required (Mafessoni & Lachmann 2015).

Recurrent Selective Sweeps

All the approaches described above suffer from the difficulty that many selective events may have occurred so far back in time that they leave little trace in the population statistics that we have just discussed. Given the evidence from population genomic studies that a substantial fraction of nucleotide differences between related species in functionally important regions of the genome reflect past positive selection (Booker et al. 2017), it is important to examine the expected effects of recurrent SSWs distributed across the genome.

The most commonly used underlying theory was developed by Kaplan et al. (1989), Wiehe & Stephan (1993), and Kim & Stephan (2000). It assumes that the reduction in diversity (relative to the neutral value) caused by a single sweep, Δ, is equal to the probability of coalescence of a pair of nonrecombinant alleles, as is assumed in Equation 2. If SSWs at a given selected site j occur at rate ω_j, causing an expected reduction in diversity Δ_j at a focal neutral site, then the rate of coalescence at the focal site caused by sweeps is equal to ${\mathrm{\Sigma }}_j{\omega }_j{\mathrm{\Delta }}_j$, ignoring any selective interference among the different beneficial mutations involved. With a BGS effect of B, the rate of coalescence due to drift is 1/(2BN_e); under this competing coalescent model, the net rate of coalescence $\approx {\left(2B{N}_e\right)}^{-1}+{\mathrm{\Sigma }}_j{\omega }_j{\mathrm{\Delta }}_j$ (Kim & Stephan 2000). The mean pairwise coalescence time is the reciprocal of this expression, which yields the following expected value of π at the focal site relative to the neutral value,

$$\frac{\pi }{{\pi }_0}\approx \frac{1}{{(2B)}^{-1}+2N_e{\mathrm{\Sigma }}_j{\omega }_j{\mathrm{\Delta }}_j}.$$ 3.

Equation 3 has been used in several attempts to estimate the rate of occurrence of SSWs and the strength of selection on beneficial mutations. These attempts exploit patterns such as the relationship between π and recombination rate (Wiehe & Stephan 1993), the relationship between π and recent nonsynonymous substitutions at nearby sites (Sattah et al. 2011), and the negative relationship between the value of synonymous site π for a gene and its level of protein sequence divergence from a related species, as seen in Figure 3b (Campos et al. 2017), as well as a composite-likelihood method that uses a combination of several such statistics (Elyashiv et al. 2016). The negative relationship between the proportion of rare variants in a sample and the level of recombination over the lower part of the range of recombination rates, as seen in Figure 1b, is suggestive of the effects of recurrent SSWs, as is the larger proportion of rare variants on the X chromosome compared with the autosomes, although a full quantitative analysis of these patterns is lacking (Campos et al. 2014).

These methods agree in suggesting that diversity at putatively neutral sites close to functional sites is significantly affected by recurrent substitutions. However, there are disagreements about the frequency at which sweeps occur and the strength of selection—indeed, the assumption that these patterns involve only the fixation of beneficial mutations as opposed to deleterious or neutral mutations is not entirely correct. In addition, both the competing coalescent model and the expressions for Δ described above are only approximate. Their use could lead to errors in estimates of sweep parameters, especially if the assumption of semidominance used in Equation 2 is relaxed (Campos & Charlesworth 2019, B. Charlesworth 2020a, Hartfield & Bataillon 2020). More work is needed before firm conclusions can be drawn.

THE INTERPLAY BETWEEN DEMOGRAPHIC CHANGES AND SELECTION AT LINKED SITES

These theoretical expectations for the effects of BGS and SSWs can be used to investigate the power and false-positive rates of the statistical tests based on them, particularly under demographic models relevant to natural populations, given that population size changes can produce genomic signatures similar to those of selection at linked sites. For example, the coalescent trees generated by a population size bottleneck, followed by rapid expansion, resemble those caused by a SSW, as most of the alleles in a sample coalesce at the time of the bottleneck (Barton 2000). Similarly, as already noted, both BGS and recent population growth generate a site frequency spectrum with an excess of low-frequency variants (B. Charlesworth et al. 1993, D. Charlesworth et al. 1995, Ewing & Jensen 2016, Nicolaisen & Desai 2013, Zeng 2013), especially in low-recombination genomic regions under the interference selection regime (Becher et al. 2020, B. Charlesworth et al. 2010, Kaiser & Charlesworth 2009).

In order to solve this problem, selective effects are often assumed to be locus specific, whereas demographic effects are genome wide. Population bottleneck/expansion patterns in individual genomic regions are then attributed to sweeps, whereas a similar genome-wide pattern is used to infer population history (Galtier et al. 2000). However, this is problematic because, under neutrality, population bottlenecks inflate the variance of commonly used summary statistics, such that many more outlier regions are generated than in a stationary population and can be mistaken for localized sweeps (Teshima et al. 2006, Thornton & Jensen 2007). Furthermore, any outlier detection approach relies on several specific, and often unsubstantiated, assumptions: (a) that selected regions reside in the tails of the distributions across the genome of test statistics (which is not always true, because this depends on the type and strength of selection as well as on the population’s demographic history), (b) that recent sweeps have indeed occurred (any model, including neutrality, will have outliers for any given test statistic), and (c) that sweeps are rare (if they were common, an outlier approach would fail to recognize the regions as unusual).

Selective and demographic effects may thus be confounded. Multiple studies have sought to quantify true- and false-positive rates for tests for recent sweeps. For statistics aiming to detect hard sweeps, Crisci et al. (2013) evaluated the performance of the commonly used methods of Nielsen et al. (2005) and Pavlidis et al. (2013) (described above) under various nonequilibrium demographic models. The approach by Nielsen et al. (2005) had low false-positive rates under a variety of neutral bottleneck models (generally under 5%) but true-positive rates for identifying sweeps were also low (generally under 10%), implying that their method simply lacks power to distinguish bottlenecks from sweeps. Conversely, the method of Pavlidis et al. (2013) had greater true-positive rates (up to 50% under certain models) at the expense of many false positives (approaching 90% under extreme bottleneck models). Therefore, under some demographic histories (such as recent bottlenecks; Poh et al. 2014), SSWs cannot be distinguished from genome-wide events, although in other situations the same statistics perform well and sweeps are identifiable.

Harris et al. (2018) similarly investigated the performance of tests for soft sweeps, examining the claims of Garud et al. (2015) and Schrider & Kern (2017) for frequent genome-wide soft sweeps in D. melanogaster and humans, respectively. Owing to the lack of appropriate null models, the validity of these claims was questioned. The top outlier regions of the D. melanogaster genome in Garud et al. (2015) were consistent with soft sweeps but also with hard sweeps or neutrality, and the population’s demographic history alone could have generated the empirically observed haplotype structure attributed to genome-wide positive selection effects. Similarly, the approach of Schrider & Kern (2017) had a high false-positive rate for detecting soft sweeps under virtually every model examined, and the number of sweeps detected across human populations was consistent with that expected from the false-discovery rate.

This misinference can act in the other direction—demographic models can be misinferred through a lack of consideration of selective effects. Population history is often estimated using intronic or synonymous sites, which are affected by selection at nearby directly selected exonic sites and may experience direct selection themselves (Machado et al. 2020, Parmley & Hurst 2007). Patterns of variation attributed to a neutral demographic model may therefore be the result of either purifying selection or positive selection (Messer & Petrov 2013, Zeng 2013). Ewing & Jensen (2016) showed that the skew toward low-frequency variants caused by BGS effects can lead to the inference of rapid population growth, even under a constant population size. Johri et al. (2021b) examined the widely used demographic estimators fastsimcoal2 (Excoffier et al. 2013) and the multiply sequential Markovian coalescent (MSMC) (Li & Durbin 2011, Schiffels & Durbin 2014) and found misinferred demographic histories in the presence of BGS, even after masking functional regions. This misinference was amplified as the strength of purifying selection and the density of directly selected sites increased. Notably, the pattern of past changes in N_e inferred by MSMC frequently had a characteristic shape indicating ancient decline and recent growth (as has been observed in studies of several species), even in a sample from a population at strict neutral equilibrium. These findings imply a need for caution when inferring population size changes if selection could be acting at linked sites; similar concerns have been raised about the effects of population structure (Chikhi et al. 2018).

Conversely, changes in population size can strongly affect the estimated values of the BGS parameter B, even when its true value remains constant, because differences in N_e affect the rate at which variability responds to a population size change ( Johri et al. 2021b). In addition, regions of the genome that differ in N_e because of recombination rate differences may exhibit different degrees of skew in their variant frequencies caused by their different rates of response to population size changes rather than by differences in the effects of SSWs or BGS. There is evidence for this effect in Drosophila, in which the skew toward low-frequency variants can increase rather than decrease with the recombination rate over some of the range of recombination rates, as shown in Figure 1b (Becher et al. 2020, Campos et al. 2014). This observation seems paradoxical at first sight, as recombination is expected to counteract hitchhiking effects.

These findings indicate the need for an appropriate null model, incorporating the effects of population processes that are certain to be constantly occurring across the genome (e.g., genetic drift under a realistic demographic history, purifying selection and BGS, and mutation and recombination rate variation), in order to accurately quantify the role of processes hypothesized to operate episodically or locally, such as positive selection (Comeron 2017, Johri et al. 2020). Johri et al. (2020) used an approximate Bayesian approach, which used statistics such as π, the site frequency spectrum, LD, and between-species divergence, to obtain the first joint estimate of the DFE together with population history. Their simulations showed that stepwise inferences, in which a demographic model is first estimated and then used to obtain an estimate of the DFE (as in the DFE-alpha method of Eyre-Walker & Keightley 2009), are prone to error when synonymous sites are under selection, because fitting a demographic model that corrects for the associated skew in variant frequencies leads to misinference of the DFE. Specifically, the excess of rare variants leads to populations being incorrectly inferred as growing rapidly. Consistent with this effect, they found less evidence for growth in a Zambian population of D. melanogaster than did earlier studies, and a substantial amount of weak purifying selection at functional sites was detected. Although a model with strong, frequent beneficial mutations was rejected, addition of a component of rare, weakly selected beneficial mutations could not be rejected (but did not improve the fit).

Recent efforts have also been made to extend inference methods beyond the standard neutral coalescent process described here (Figure 2), which assumes that N_e is so large, and the variance in the number of successful progeny per individual is so small, that at most one coalescent event can occur per generation (Hudson 1990, Wakeley 2008). While these assumptions are probably appropriate for many commonly studied organisms (including mammals, birds, and Drosophila), a wide variety of species, including many plants, marine spawners, and pathogens, exhibit large progeny number distributions better represented by multiple-merger coalescent models, in which more than one coalescent event can occur in a given generation (Irwin et al. 2016, Tellier & Lemaire 2014). This feature alone can radically alter expected levels and patterns of variation under neutrality, and its neglect could lead to serious misinference of both selection and demography. Recent theoretical and computational efforts have identified patterns that may allow population growth and neutral multiple-merger coalescence to be distinguished (Eldon et al. 2015, Matuszewski et al. 2018), and tests for SSWs under these alternative coalescent models have recently been proposed (Sackman et al. 2019). Such model development is feasible (Harris & Jensen 2020), given that SSWs themselves involve a localized multiple-merger coalescent event (Figure 2). Further theoretical studies of these alternative coalescent models are needed for analyses of organisms such as viruses (Irwin et al. 2016).

CLOSING THOUGHTS

The theoretical underpinnings of genetic hitchhiking models, and the development of statistical inference approaches for detecting and quantifying hitchhiking effects in genomic data, have proliferated over the past few decades. These advances have made it increasingly clear that the effects of selection at linked sites need to be considered for a full understanding of the levels and patterns of variation in natural populations. Both genetic drift, as modulated by population history, and purifying selection (with the associated effects of BGS) are pervasive factors determining the fates of new mutations, consistent with the neutral theory of molecular evolution (Kimura 1983). However, there is also strong evidence that positive selection plays an important role in between-species sequence divergence at functional sites. Through its associated SSW effects, positive selection modulates both the amount of DNA sequence variability and the shape of the site frequency spectrum, especially at sites within or close to coding sequences and certain types of noncoding sequences.

It remains a formidable challenge to estimate the individual contributions of these evolutionary processes accurately, but two things seem clear. First, ignoring one process in order to estimate another (e.g., neglecting direct and indirect effects of selection when estimating population history or neglecting population history when estimating the effects of selection) can lead to serious misinference. Second, any analysis of population genomic data must use a proper null model, capturing the roles of mutation and recombination rate variation, purifying selection and BGS in and around functional elements, and using the underlying history of population size change, structure, and migration. Encouragingly, theoretical and computational approaches are emerging that appear to be capable of jointly estimating the parameters of such an evolutionary null model. It may therefore become possible to accurately characterize the expected effects of processes such as hard versus soft sweeps, as well as complete versus incomplete sweeps, on levels and patterns of variability across genomes.

Glossary

N_e

the effective population size, such that the rate of coalescence of a pair of neutral alleles is 1/(2N_e)

D

the coefficient of linkage disequilibrium, equivalent to the covariance between the allelic states of a pair of biallelic loci

a_w

the average excess, measured by the difference in fitness between the carriers of the alleles at a biallelic locus

π

the mean value of the pairwise nucleotide site diversity over a set of nucleotide sites

θ_w

Watterson’s estimator of the scaled mutation rate from the number of polymorphic sites

θ = 4N_eu

the scaled neutral mutation rate, where u is the mutation rate per nucleotide site

s

the reduction in fitness to homozygotes for a deleterious mutation, relative to the fitness of wild-type homozygotes

t = hs

the reduction in fitness to heterozygotes for a deleterious mutation; h is the dominance coefficient

B

the ratio of the mean coalescence time at a neutral site under BGS, relative to its value without selection

r

the frequency of recombination between a pair of loci