Neuromorphic learning, working memory, and metaplasticity in nanowire networks

Abstract

Nanowire networks (NWNs) mimic the brain’s neurosynaptic connectivity and emergent dynamics. Consequently, NWNs may also emulate the synaptic processes that enable higher-order cognitive functions such as learning and memory. A quintessential cognitive task used to measure human working memory is the n-back task. In this study, task variations inspired by the n-back task are implemented in a NWN device, and external feedback is applied to emulate brain-like supervised and reinforcement learning. NWNs are found to retain information in working memory to at least n = 7 steps back, remarkably similar to the originally proposed “seven plus or minus two” rule for human subjects. Simulations elucidate how synapse-like NWN junction plasticity depends on previous synaptic modifications, analogous to “synaptic metaplasticity” in the brain, and how memory is consolidated via strengthening and pruning of synaptic conductance pathways.

Cognitive learning and memory are demonstrated in a brain-like physical substrate.

INTRODUCTION

The brain’s powerful information processing capacity can be largely attributed to neuronal microcircuits established by synaptic connectivity patterns (1, 2). Precisely how neurosynaptic connectivity gives rise to higher-order cognitive functions such as learning and memory remains elusive (3). However, an important clue is that neural connectivity is spatiotemporally sparse and dynamic (4, 5). Here, learning and memory are demonstrated in a unique physical substrate with these properties.

Nanowire networks (NWNs) emulate the physical nature of neurons and synapses in the brain (6). They are “neuromorphic” by virtue of not only their efficient integration of processing and memory in nanowire-nanowire cross-point junctions (7, 8) but also their ability to mimic both threshold-driven spike-like neuronal dynamics and conductance-based synapses (9, 10). Nanowire junctions exhibit resistive memory (“memristive”) switching between high and low resistance states (11). Because of NWN self-assembly, these memristive junctions are interconnected in a heterogeneous circuitry with recurrent feedback loops (12). Thus, NWN devices operate in a fundamentally different way from top-down fabricated memristor devices in a cross-bar architecture (8). In particular, NWNs exhibit emergent nonlinear dynamics as a result of the interplay between their memristive junctions and heterogeneous, recurrent network connectivity (13–15).

Previous studies have demonstrated how nonlinear dynamics can be harnessed for learning by treating the NWN as a physical “reservoir” in a reservoir computing paradigm [e.g., (9, 13, 15–23)]. This paradigm exploits the network’s ability to nonlinearly transform dynamical input signals into a higher-dimensional feature space, such that the outputs are linearly separable (24–26). NWN device readouts can then be used in a highly computationally efficient linear output layer, where only linear weights need to be trained to complete a desired machine learning task (27). In contrast, learning in the brain is thought to occur via three main mechanisms (28): supervised learning, typically linked to the cerebellum (29–32); reinforcement learning (33), typically linked to the basal ganglia (33–37); and unsupervised learning, typically linked to the cerebral cortex (28). In our recent study (38), we demonstrated Hebbian-like unsupervised learning via signal transduction pathways in NWNs. We reshaped these conductance pathways by altering the spatial location of input and output electrodes, as well as the order in which they were activated.

Such “dynamic pathway tuning” revealed that NWNs preserve information from previously established pathways when forming new pathways through the network, analogous to how synaptic plasticity in the brain depends on previous synaptic modifications (39). Here, we investigate the other two mechanisms of learning, which are more context dependent. Supervised learning encapsulates an iterative process whereby the system’s response to a given input is evaluated against a desired outcome, and deviations from that outcome are used to adjust adaptive elements within the system (40).

In reinforcement learning, synaptic weights are modified in response to information related to positive (or negative) feedback (33). Here, these brain-inspired learning mechanisms are physically implemented in NWNs, extending previous studies (38, 41) by explicitly applying context-dependent external feedback.

In addition to demonstrating brain-like learning in NWNs, we also demonstrate working memory (WM) by implementing sequence memory tasks inspired by the well-known cognitive task, the n-back task (42–45). In experiments with human subjects, the n-back WM task requires participants to identify whether each stimulus (e.g., visual pattern) in a sequence matches a stimulus that was presented n-steps back (43). As n increases, reaction times tend to increase, and accuracy tends to decrease due to processing load (44, 46). Furthermore, regions of the brain related to verbal WM processes tend to show increasing magnitudes of activation during large n values (46). WM is thought to pertain to short-term memory and involve information manipulation (47, 48). The ability to temporarily hold and manipulate information requires adaptive processing of multiple incoming dynamical inputs while retaining information about previously encoded input. This means that synaptic connections that form memories must be protected from being overwritten when storing new information (49, 50).

Through sequence memory tasks inspired by the n-back WM task, we demonstrate the ability of NWNs to recall previous information while continually processing new information. In addition, we show how information initially in short-term WM may be consolidated into long-term memory through physical reinforcement learning (PRL), which manipulates topological reconfiguration of NWNs via pathway strengthening and pruning.

RESULTS

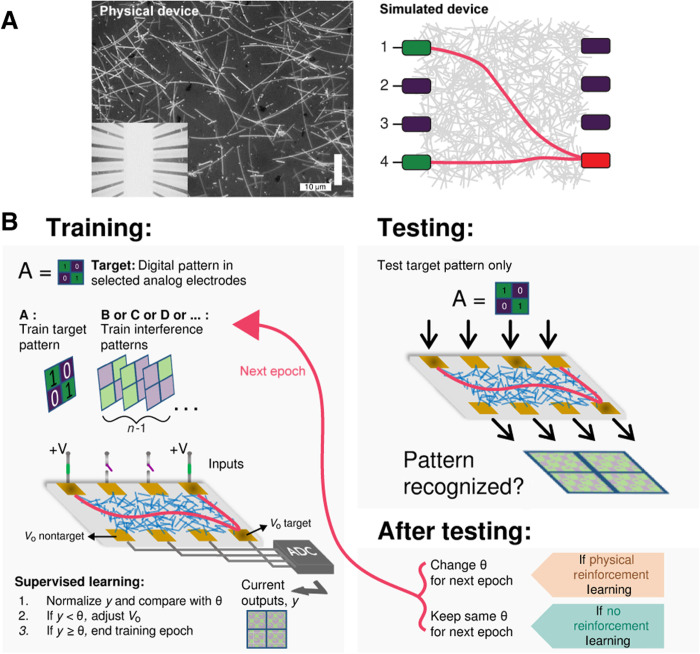
Figure 1 presents an overview of the NWN device (both physical and simulated) and the setup designed to implement supervised learning and PRL in tasks inspired by the n-back protocol. The average network density for the physical system shown in Fig. 1A is ≈0.76 nanowires/μm², similar to that used in the study by Diaz-Alvarez et al. (14). The simulated network had 698 nanowire nodes and 2582 edge junctions (0.12 nanowires/μm²). See Methods for full details of the physical and simulated NWN device.

Fig. 1. Overview of NWN device and setup for supervised learning, PRL, and the n-back task protocol.

(A) Left: Optical micrograph showing physical silver nanowires dropcast onto a substrate between 9 × 9 contact electrodes (nine inputs and nine outputs; inset). Scale bar, 10 μm. Right: Schematic of simulated NWN device with four input electrodes and four output electrodes, showing conductance pathways from source to drain electrodes (green and red, respectively). (B) Schematic of one epoch (training + testing) of an n-back task protocol. Training: Summary of training protocol in which presentation of target pattern A is followed by n-1 interference (nontarget) patterns. Schematic illustration of the NWN multielectrode device setup demonstrating the training protocol. During training, a digital pattern (A) is cued to analog electrodes and fed into the device inputs; outputs are recorded and compared with the target, after which drain currents are adjusted, nudging target output currents closer toward a fixed current threshold θ via supervised learning, and nontarget outputs away from θ. Testing: Summary of testing protocol in which the target pattern A is presented after n training patterns, and device outputs are compared with the target before the next epoch starts. After testing: If the outputs do not match the target and PRL is not applied, then the epoch fails; if this occurs with PRL, then θ is increased for the target and decreased for the nontargets for the next epoch.

Figure 1B summarizes one sample epoch, consisting of training and testing strategies developed to demonstrate the n-back protocol using the device. During training, the n-back protocol involves the NWN receiving n-1 unique nontarget samples after receiving a target pattern cue. The NWN is trained to recognize the target cue via a supervised learning strategy, which nudges a selected output toward a fixed current threshold θ, with all other outputs nudged away from θ. The nudging protocol occurs via a gradient descent-like method (see Eq. 2 in Methods), using the discrepancy between actual and desired output currents. While supervised learning is implemented during training, PRL is instead implemented after testing recall of the target cue, when the value of θ can be modified to provide feedback to the NWN. To test the network’s WM, θ is kept unmodified, corresponding to no PRL implemented. With PRL, θ is changed ahead of the next epoch based on the network’s performance: Target outputs receive more current, and nontargets receive less current. This tests the network’s consolidation of items initially held in short-term WM into long-term memory. In summary, supervised learning nudges the output currents toward θ during training, while PRL controls the value of the current threshold θ after testing. See Methods for full details.

Task 1: Physical binary classification

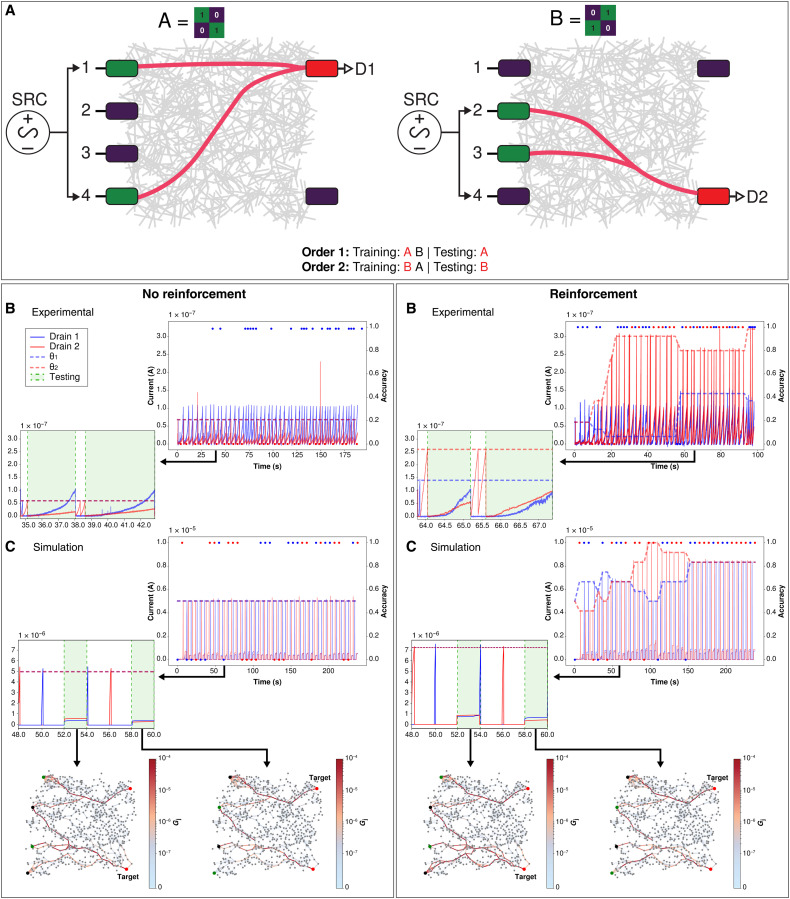
Figure 2 compares results for classification of two 2 × 2 patterns (i.e., four inputs to the network) for n = 2 without and with reinforcement (see full task 1 description in Methods, including Algorithm 1). Both experimental (Fig. 2A) and simulation (Fig. 2B) results demonstrate that once PRL is introduced, it markedly improves binary classification accuracy under the n = 2 protocol (i.e., testing after two training samples of the nontarget pattern are presented to the network). In experiment, 44 of 50 epochs achieve an accuracy of 100% with PRL, compared to only 23 of 50 without. Similarly, in simulation, 32 of 40 epochs are 100% accurate with PRL and 23 of 40 without. The worse performance without PRL results from the network successfully training and recalling the primary conduction pathway for one target drain, but not the other. This is most evident in the experimental results. Inset panels in Fig. 2 show that supervised learning increases current toward the respective threshold (θ₁ or θ₂) of the target drain as a consequence of voltage adjustments on the corresponding electrode (see fig. S1 for drain voltages).

Fig. 2. Binary classification of 2 × 2 patterns with n = 2 (task 1).

Top: (A) Experimental setup schematic of training a NWN for two unique 2 × 2 patterns. Green electrodes represent active sources (inputs), purple electrodes are inactive, and red electrodes are active drains (outputs; D1 = drain 1, D2 = drain 2). Patterns can be presented in two possible orders (order 1 or 2), for each of which the target pattern is different. Bottom left: Without reinforcement: (B) Experimental results. Drain currents (solid blue and red lines, left axis) and classification accuracy (blue and red dots, right axis) versus time. Horizontal dashed lines represent training threshold θ₁ for drain 1 (blue) and θ₂ for drain 2 (red). Inset shows close-up of drain current over two training and testing (green shade) epochs in Δt = 35 to 43 s. During the first testing period (t = 35 to 38 s for no reinforcement and t = 64 to 65 s for reinforcement), order 1 is presented to the network. During the second testing period, order 2 is presented to the network. (C) Simulation results. Inset shows close-up of drain current over two epochs in Δt = 48 to 60 s. Simulated network visualization snapshots (nodes = nanowires and edges = junctions) showing junction conductance states (G_j, colorbar) during testing at t = 53.0 (drain 2 target) and t = 59.0 (drain 1 target). Active and inactive source nodes are in green and purple, respectively, with active drain nodes in red and target drain labeled. Bottom right: Same as left but with reinforcement. Insets show zoom-in over epochs in (B) Δt = 64 to 68 s and (C) Δt = 48 to 60 s.

Simulated network connectivity maps (Fig. 2B) qualitatively show the conductance pathways that form between source and drain electrodes for each pattern. Quantitatively, memristive junctions along the pathways experience a conductance gain under PRL, whereas without reinforcement, junctions can decay and reset (see fig. S2).

Task 2: Complex binary classification

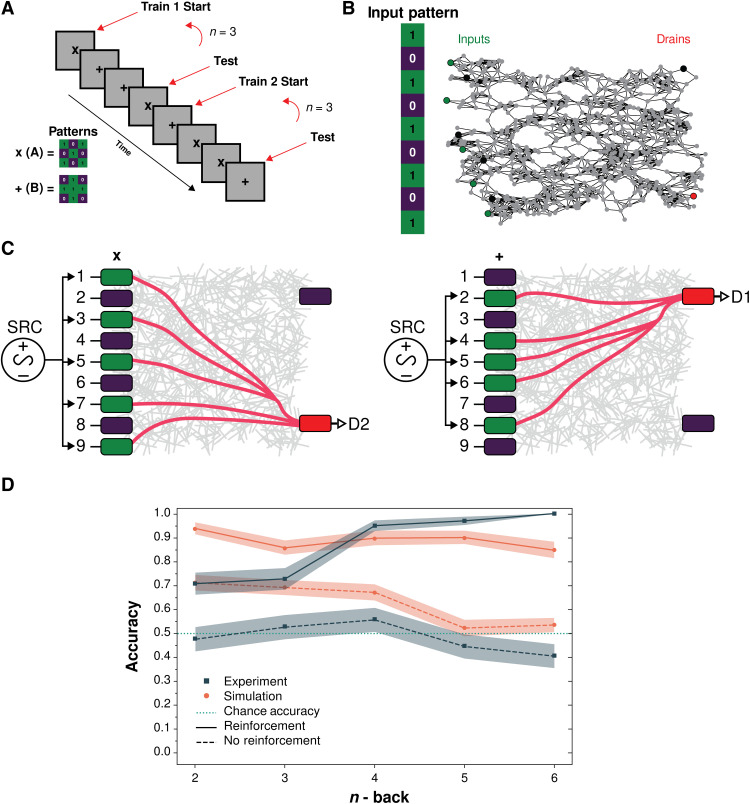
Figure 3 shows results for binary classification of 3 × 3 patterns (nine inputs) of either “+” or “x” (5-bits). For this task, the number of samples, n-1, between the first training sample and the testing sample was increased. This meant that n-back increased as n = 2,3,4,5, or 6 (see Fig. 3A and task 2 description in Methods). Otherwise, task setup and implementation were similar to task 1.

Fig. 3. Binary classification of 3 × 3 patterns for varying n (n ≥ 2) with and without physical reinforcement (task 2).

(A) Experimental schematic of task 2 n-back variation for two unique 3 × 3 patterns, “x” (pattern A) and “+” (pattern B), respectively. In epoch 1, x is presented during training as the target, followed by two (if n = 3) interference patterns +, and then x is presented again during testing. In epoch 2, the opposite order occurs. (B) Input pattern (as 1D vector) and corresponding input nodes of graphical network representation used in simulation with two drain nodes (target in red, nontarget in purple). (C) Same as Fig. 2A but for five voltage inputs (green) corresponding to 5-bit patterns x (left) and + (right). (D) Experimental (navy) and simulation (orange) results with (solid lines) and without (dashed lines) reinforcement. Chance accuracy (teal) is shown for comparison. Shaded areas represent SEM across epochs.

Both experimental and simulation results in Fig. 3D show a marked improvement in classification accuracy with reinforcement compared to without reinforcement. In experiment, accuracy increases from 0.48 to 0.71 for n = 2, and the maximum increase is from 0.41 to 1.00 for n = 6. Similarly, in simulation, accuracy increases from 0.71 to 0.93 for n = 2, and the maximum increase is from 0.53 to 0.85 for n = 6. In experiment, mean accuracy ranges from 0.71 to 1.00 when reinforcement is applied, while without reinforcement, it is similar to chance levels (mean accuracy ranges from 0.41 to 0.56). In contrast, simulation results with reinforcement show a narrower accuracy range (0.93 to 0.85), and simulation results without reinforcement show a steady decline with n (0.71 to 0.53). This is not observed in the experimental results, which show a marked increase in accuracy under reinforcement for n > 3.

These results can be understood in terms of the memristive switching junctions responsible for the conductance pathways that represent the physical manifestation of binary classification by the network. During training, the NWN establishes input-output conductance paths for each of the two patterns (Fig. 3C). As n increases, the NWN receives more training samples from nontarget patterns than the target. When this occurs without reinforcement, the memristive junctions corresponding to the target pattern decay, so that when the target pattern is next presented, the decaying conductive nanofilaments must reform. In experiment, a 3-hour wait time between each n is implemented (see Methods); however, it is difficult to determine to what extent the conductive pathways have decayed. In task 2 simulations, all junctions were completely reset between each n trial, so the accuracy without reinforcement decreases consistently with n. The higher accuracy for n = 2 to 3 compared to the experimental results can be attributed to the assumption made in the model that all junctions decay at the same rate (see fig. S4 for additional results on varying the junction decay parameter). With reinforcement, the conductance pathways are prevented from decaying, so the NWN is able to recall the target pattern, even for large n. The increase in accuracy with n evident in the experimental results may be attributed to nanofilaments forming faster than they decay. This is not observed in the simulation results due to the model assumptions mentioned above. This reinforcement effect is similar to the notion of population coding in the mammalian brain (51), although it is difficult to disentangle innate from learned features of classification in in vivo biological brains (52). This highlights the importance of using nonbiological, physical neural networks to understand how information is processed in networks like the brain.

Task 3: Working memory

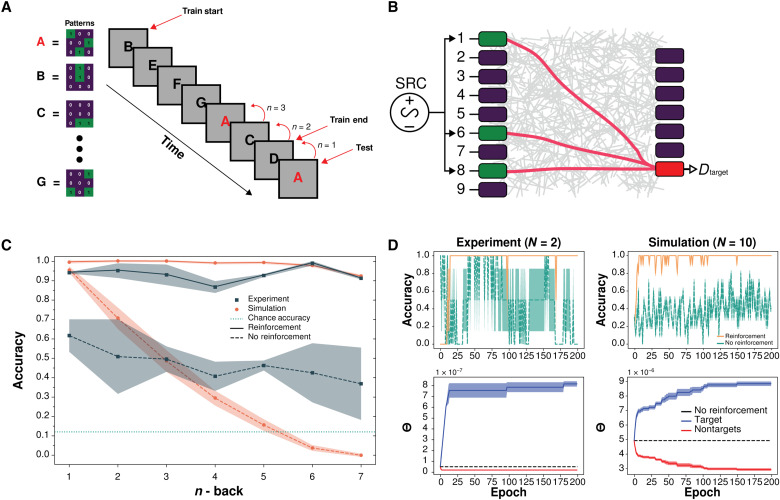
Figure 4 (A and B) show a schematic of the WM n-back task, where the NWN receives varying nonrepeat sample 3 × 3 patterns both before and during the n-back sequence (see task 3 description in Methods, including Algorithm 2). During training, each pattern is presented only once and in random order. Unlike the previous tasks, therefore, no repeat training is possible during a single training-testing epoch, and n varies from epoch to epoch.

Fig. 4. WM multipattern n-back task (task 3).

(A) Experimental schematic of task 3 n-back variation for seven unique 3 × 3 patterns. Pattern A is always selected as the target; however, its location is semirandomly varied, to change n. The order of the interference patterns (B to G) is random. (B) Same as Fig. 3C but for three voltage sources (green) corresponding to target pattern (A shown) and seven output electrodes (one target drain, red). (C) Mean recall accuracy in experiment (navy) and simulation (orange), with and without reinforcement, for varying n (sorted by n). Shaded regions represent SEM. Chance accuracy (teal) represents a one-in-seven chance of correctly classifying the target pattern over the six alternative patterns. (D) Mean accuracy sorted by epoch and corresponding θ threshold values; N is the number of trials.

Figure 4C shows the experimental and simulation recall accuracy results, sorted by n, while Fig. 4D shows the corresponding results plotted per epoch. Both the experimental and simulation results show that the mean accuracy in recalling the target pattern improves markedly under reinforcement compared to no reinforcement. Without reinforcement, the experimental accuracy declines steadily with n from 0.61 (n = 1) to 0.37 (n = 7), while the simulation accuracy declines more steeply from 0.95 (n = 1) to below chance accuracy (1/7 ≈ 0.14 odds of correctly selecting the target pattern at random).

Although a contributing factor may be differences between simulation and experimental time scales (as the experimental NWN has many more wires and junctions and a 3-hour rest period was included between each trial), the difference between experimental and simulation results without reinforcement may be primarily attributed to differences in junction decay rates. Specifically, the simulation model assumes that all junctions decay at the same rate, whereas experimental NWNs are heterogeneous, with a range of filament formation and decay rates due to varying nanowire thicknesses and stochastic effects in the nanoscale junctions. The simulation results reveal that, with no reinforcement, recall is highly sensitive to junction decay rates; both recall accuracy and maximum n-back values decline with faster decay (see fig. S5), i.e., as previously established pathways are more quickly forgotten. This is analogous to metaplasticity in the brain, which describes the dependence of synaptic plasticity on the history of synaptic modifications (39) .

Without reinforcement, the n-back task is a measure of WM. With reinforcement, both experimental and simulation results in Fig. 4 (C and D) show a high recall accuracy is maintained for all n. This indicates that short-term WM has changed to a longer-term memory that is independent of forgetting associated with junction decay. The mechanism responsible for this memory consolidation under PRL is explored next.

Network connectivity

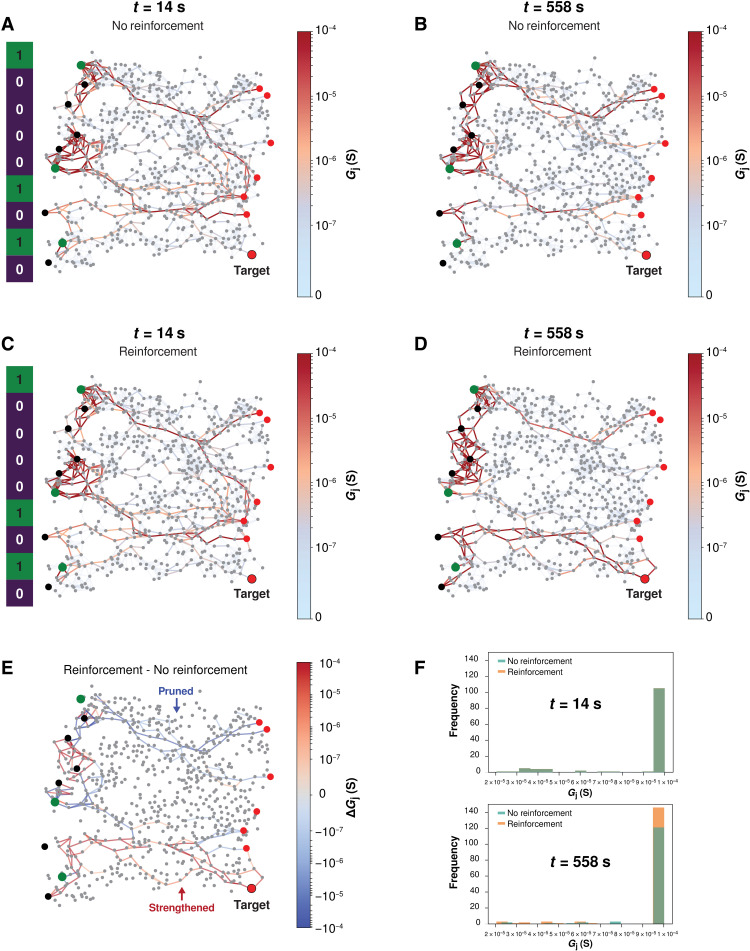
The network connectivity snapshots presented in Fig. 5 reveal the simulated NWN states during early (t = 14 s) and middle (t = 558 s) stages of testing target pattern recall from WM during the n-back task (for n = 3). The corresponding input pattern is shown on the left of Fig. 5 (A and C), with zeros (purple) and ones (green) corresponding to inactive and active sources, respectively. During the first testing epoch (t = 14 s), the connectivity maps (Fig. 5, A and C) and G_j histograms (Fig. 5F) with and without reinforcement are identical. This is because conductance paths are not yet conditioned by PRL. By the later testing epoch (t = 558 s), however, the effect of reinforcement is noticeable, with a strong conductance path to the target drain now evident (Fig. 5D) and weaker paths to nontarget drains. This occurs because the target drain is reinforced by increasing the current output threshold, while all other nontarget drains are “punished” with lower current thresholds. Consequently, conductance pathways to the target drain are strengthened and remembered by the network, while pathways to nontargets are pruned and forgotten.

Fig. 5. Simulated NWN connectivity snapshots during memory recall.

(A and B) Network connectivity maps visualizing junction conductance (G_j) snapshots at early (t = 14 s) and middle (t = 558 s) testing periods of the WM n-back task (with n = 3), respectively, without reinforcement. Active and inactive input electrodes are highlighted in green and purple, respectively, with active drain electrodes in red and target drain indicated. (C and D) Same as (A) and (B) but with reinforcement. (E) Topological reconfiguration map highlighting the junction conductance change ΔG_j between reinforced and nonreinforced paths. Values are calculated by comparing connectivity maps as follows: (d − c) − (b − a). (F) G_j histograms corresponding to (A) and (C) (top) and (B) and (D) (bottom). For clarity, G_j is thresholded at 2 × 10⁻⁵ S.

The effect of reinforcement is visualized in Fig. 5E, where red paths represent pathways strengthened by reinforcement (i.e., higher G_j) over time, and blue paths represent pruned pathways. The difference ΔG_j is calculated by first subtracting the maps at t = 14 s and t = 558 s [i.e., Fig. 5 (A and B) without reinforcement and Fig. 5 (C and D) with reinforcement] and then subtracting nonreinforced paths from reinforced paths. What remains is a topological reconfiguration map, highlighting the paths strengthened and pruned by reinforcement. Pathway strengthening occurs in regions closer to the target drain, while pruned pathways are in nontarget regions. See fig. S6 for intermediate connectivity maps.

Differences in pathway strengths are quantified by G_j histograms in Fig. 5F, which are identical during early testing, while during late testing, more junctions exhibit higher G_j values as a result of reinforcement. For these simulation results, a stronger filament decay parameter (b = 2) was used to enhance the visual contrast of conductance pathways in the functional connectivity maps in Fig. 5, but this does not change the fundamental nature of pathway selectivity that PRL produces. Other connectivity maps with varying b values are presented in fig. S7. The full videos from which these snapshots were taken are also available in the Supplementary Materials.

These findings highlight two unique memory capabilities in NWNs. First, the supervised learning paradigm without PRL reveals the importance of the history of junction changes to WM. The second memory capability is that of memory consolidation and occurs with the help of PRL. By manipulating the current threshold θ, specific pathways are reinforced with substantially greater current output, while other pathways are suppressed. This is realized as long-term memory for the strengthened pathways. Simulation results suggest that this activity is akin to memory consolidation via synaptic strengthening (1).

DISCUSSION

This study is the first to demonstrate a nontrivial cognitive task—inspired by the WM n-back task—in a physical non–CMOS (complementary metal-oxide semiconductor) substrate with native neuromorphic properties (i.e., not requiring implementation of neuromorphic algorithms).

In a previous study, Neftci and colleagues (53) demonstrated a simple cognitive task by emulating spiking neurons in a CMOS system. Their method used an intermediate computational layer in which silicon neurons are configured as soft winner-take-all (WTA) networks (54). The WTA mechanism has been reported in previous NWN studies (14, 15, 38, 41, 55, 56). Functional connectivity maps in the current study, generated by the simulations, indicate that the network uses more than one key pathway, in contrast to previous findings. This is because of the low voltages used in this study, which are well below the threshold needed to activate the WTA path. This is to ensure that the network is maintained in an intermediate conductance state, enabling control of conductance paths via the electrodes. We previously visualized conductance pathway formation in a similar multielectrode NWN device using lock-in thermography (38). Despite the poor spatial resolution, we were able to demonstrate the principle of reshaping conductance paths in the network by dynamically changing the spatiotemporal patterns of input signals delivered by the electrodes. In that study, we used Ag@TiO₂ nanowires as Ag–polyvinyl pyrrolidone (PVP) nanowires, used in this study, are difficult to image using this technique due to their much lower resistance, making them more susceptible to damage by Joule heating.

The training methods introduced here for learning a cognitive task have strong links to two unique neuroscientific learning theories. The first method, in which “nudging” was used, is similar to supervised learning in the brain (29). This method is also similar to the gradient nudging described in Æqprop (57) or other in materio gradient descent methods such as described by Boon and colleagues (58). Diaz-Alvarez et al. (41) previously demonstrated associative routing in an Ag-PVP NWN using the same multielectrode device configuration as used in this study. They effectively trained pathways by opening and closing selected electrodes to prompt the network to use specific pathways and associate them with specific spatiotemporal patterns delivered by the electrodes. However, they found that this technique was unable to maintain reliable pathway selectivity, particularly as more paths became established, which limited the ability to train multiple different patterns. By implementing selective feedback (PRL), our study demonstrates how the strengthening and pruning mechanism underlying PRL can control specific unique pathways to enable training of multiple distinct patterns and long-term memory of a target pattern.

When supervised learning is implemented in NWNs without any reinforcement, drain electrode voltages are altered and nudged closer to the target. However, because of the finite decay rate of NWN junctions (59), coupled with a fixed current threshold (θ), the conductance pathways are only remembered temporarily, reflecting the network’s WM capacity. In humans, WM is an example of information retention and consistent manipulation via synaptic modifications until the information is no longer needed (48), at which point it decays in seconds up to minutes or is encoded (60).

The cognitive task used in this study, a sequence memory task inspired by the n-back task, is extensively used in cognitive psychology for testing WM in humans (42–44, 61). Sequence memory and n-back memory tasks have also been applied to recurrent neural networks with bio-inspired topology (62). Well-known studies in humans originally suggested a capacity to store 7 ± 2 items in WM (63), although subsequent studies estimate it at closer to three to five “chunks” of memory (64, 65). Here, the n-back task was adapted into subtasks that could be implemented in NWNs. Task 3, the most similar to the original n-back task (61), showed that NWNs can store up to seven items in memory (and potentially more) at substantially higher than chance levels without reinforcement training and near-perfect accuracy with reinforcement training. One theory of WM at the synaptic level describes how an item is maintained in WM via increased residual calcium levels at presynaptic terminals of the neurons that code for that item (66). Since removal of residual calcium is a relatively slow process (around 1 s in humans), memories can be held over this time without the need for further spiking (67). The depletion of residual calcium is conceptually similar to atomic filament decay in NWNs (6).

The second method of learning implemented in this study, PRL, is similar to reinforcement in the brain, which is thought to occur, at least in part, via strengthening of synaptic dopamine channels through Hebbian plasticity, in response to a positive (or negative) outcome (35, 68). Contrastingly, and particularly during early development, when a synaptic pathway is unused, unwanted, or punished, it is pruned (69). Pruning occurs via a weight-dependent synaptic modification process called neuronal regulation (70). This study showed both reinforcement of desired pathways via PRL, as well as pruning of penalized pathways in NWNs.

A clear distinction must be made between non-PRL results and PRL results in the n-back task. Without PRL, task performance reflects the network’s WM capacity, i.e., its ability to temporarily recall information pathways while establishing new ones. When PRL is introduced, however, memory is consolidated. Memory consolidation in the brain involves the process of encoding information in a long-term manner via strengthening of synaptic pathways and brain regions that activate in response to that information (1, 71). These long-term modifications can last from hours up to an entire lifetime (1, 60).

In NWNs, PRL allows for strengthening specific pathways over time (and weakening of others), based on a desired output. Once pathways are consistently and repeatedly activated, they take notably longer to decay. In experiment, 3-hour rest was allocated between trials for the physical network. However, this was likely not long enough for conductance pathways to fully decay, particularly once PRL was introduced. NWNs have previously been shown to retain information even 24 hours after dynamic pathway tuning (38). Consequently, after reinforcement or repeated prolonged activation of specific pathways, NWNs’ memory for those pathways is also lengthened and consolidated. In contrast, memristive junctions and pathways in simulated NWNs were completely reset between each trial and displayed a lower WM capacity. These results are consistent with findings by Benna and Fusi (39), which suggest that synaptic plasticity depends on the history of synaptic modifications, referred to as synaptic metaplasticity. In physical NWNs, memory of previous junction modifications is carried on between epochs and trials more effectively than in simulation, increasing the WM capacity of the network.

Similar behavior was previously reported in Ag-PVP NWNs by Milano et al. (72), who found that the structural topology of NWNs evolves depending on synaptic history. In that study, however, rerouting of conductance pathways was demonstrated by applying sufficiently high current densities to rupture physical connections between wires. In contrast, the present study uses much lower voltages, which maintains persistent activity in the network. This is identified with WM (1). Synaptic metaplasticity as described here is a result of external feedback signals into the network rather than physical restructuring.

In task 3, the network was charged with only retaining pathway information for one target pattern. While the NWNs still had to contend with six interference patterns and therefore provided a comprehensive insight into the WM capabilities of the networks, the capacity for multiple classes to be held in memory and recalled was not measured. Consequently, NWNs demonstrate stimulus-specific manipulation, while WM in humans also involves domain-specific manipulation (73). The latter of these would require memory across multiple classes of stimuli, not just a single target pattern. To properly mimic large-scale parallel information manipulation in the brain, future studies into the network’s capacity to remember and recall multiple pathways associated with different input patterns are warranted. However, it may be that multiple, highly modular NWNs will be required to be linked up in parallel to demonstrate such information processing abilities (21). While NWNs are highly scalable as they are straightforwardly synthesized by bottom-up self-assembly, device scalability is limited by fabrication of the multielectrode system. Previously, other NWN devices have been fabricated in CMOS multielectrode arrays (MEAs) for implementing reservoir computing. These devices have not shown marked performance improvements when scaling from a 16-electrode MEA (10, 18, 23) to a 64-electrode MEA (74). The present study implements cognitive tasks rather than reservoir computing, and therefore an increased number of electrodes would allow demonstration of the n-back WM task with more complex patterns.

Neuromorphic systems that can learn, remember, and adapt to external time-varying stimuli would represent a breakthrough platform for neuro-inspired computing (75). The present study demonstrates the potential for NWNs to achieve this. The ability to process dynamically changing information is key in many real world applications, such as robotics and sensor edge devices, where there is a need to make on-the-fly decisions in a nondeterministic environment (76) .

In conclusion, by applying supervised and reinforcement learning strategies similar to those operating in the brain, we have demonstrated WM and memory consolidation in NWNs. These higher-order cognitive functions were achieved by implementing a nontrivial cognitive task routinely applied to human subjects. Results reveal that neuromorphic learning paradigms implemented in NWNs leverage similar mechanisms to the brain, namely, synaptic metaplasticity and synaptic strengthening and pruning, to optimize WM and memory consolidation.

METHODS

Experimental setup

Silver NWNs were synthesized by following the well-known Polyol method, as described previously (14), which produces an ethanol solution of Ag nanowires coated with the polymer PVP. Nanowires were directly deposited by drop-casting on a glass substrate to create dense and homogeneous networks of interconnected Ag-PVP nanowires, resulting from the random dispersion of nanowires once the ethanol droplet evaporates. A multielectrode Ag-PVP NWN device (Fig. 1A) was constructed by depositing two regular arrays of rectangular gold electrodes facing each other at a distance of 3 mm. Electrodes were 200 μm wide and 600 μm apart from each other. The electrodes were deposited onto the glass substrate by magnetron sputtering before depositing the nanowires. Depending on the task, a selection of electrodes out of the two arrays were connected to serve, respectively, as source or drain electrodes. The electronic setup is similar to the one described in Diaz-Alvarez et al. (41), comprising a digitally controlled switch box connected to the electrodes in use for the given task, which sequentially opens and closes the respective electrodes that form the patterns used in all the tasks (cf. Fig. 1B). Source voltage was delivered and controlled with a National Instruments data aqcuisition (NI-DAQ) card, and drain current was controlled using an array of in-house biased operational amplifiers (OPAs), serving as current-voltage converters with amplification of 10⁷ V/A. Voltage signal from the OPA array was sent to a digital acquisition card (NI-DAQ). In all tasks and experiments, the rate of acquisition was the same (1 kHz). This rate was further down-sampled for storage, analysis, and presentation purposes. Software to control voltage sources, digital switches, the acquisition cards, and the different algorithms for training/testing was developed using Python.

Full characterization of Ag-PVP NWNs, including the mechanisms of activation and decay are reported in our previous studies (9, 14, 38, 41), where we found that memory of previous conductance pathways begins to fade at 35 to 90 s, although networks can take much longer to decay (up to hours) due to many junctions in different states. Using the same multiterminal (nine input and nine output electrode) device configuration, Diaz-Alvarez et al. (41) demonstrated the ability to dynamically control conductance pathways in Ag-PVP NWNs by maintaining low input voltage levels, effectively keeping junctions in intermediate “metastable” states between low and high conductance. This was similarly later demonstrated by Li et al. (38) using the same electrode configuration but with Ag@TiO₂ NWNs. Consequently, the present study adopts a similar protocol, using low voltages during training and testing (0.1 to 0.2 V), and input samples are presented for relatively short durations (within the ∼1-min memory window). Networks were also rested for 3 hours between trials to allow decay of conductance pathways. Further characterization is shown in figure 3 and figure S3 of the study of Diaz-Alvarez et al. (14), although they used double-probe electrodes rather than a multiterminal device.

Two unique network samples were prepared and assessed for the different tasks, each with different input patterns and order of sample presentation. While results do vary from device to device (see source data file S1), they tend to follow similar trends within a range [see also Diaz-Alvarez et al. (14)] (fig. S1).

Simulation setup

Ag-PVP NWNs were modeled as described in previous studies (9, 12, 21). All simulations were conducted using Python. Briefly, nanowires were modeled as one-dimensional (1D) objects of length drawn from a gamma distribution (mean wire length = 10 μm), placed randomly within a 2D plane of fixed size (75 μm by 75 μm). The vertical and horizontal positions of wires were generated from a uniform distribution on 2π. In this study, NWN simulations used 698 nanowires (nodes) and 2582 junctions (edges), giving an average degree of 7.40. While the number of modeled nanowires is smaller than in the experimental network, NWN memory capacity is determined by the number of junctions, which was chosen to achieve simulation results that most closely matched experimental measurements. Previous NWN simulation studies (12, 15, 21) using the same model demonstrate the influence of topology and density on network functionality.

Nanowire-nanowire cross-points were modeled as ideal, electrically insulating, ionically conducting junctions, with threshold-driven bipolar memristive switching (14, 17, 59, 77, 78), modulated by electron tunnelling transport (9, 15). Junction conductance, G_j = G_j(λ), depends on a state variable λ(t) that parametrizes the conducting nanofilament responsible for memristive switching due to electrochemical metallization (6). The evolution of λ(t) is described by a polarity-dependent voltage threshold model (9, 15, 59, 78, 79) as shown in Eq. 1

$$\frac{d\mathrm{\lambda }}{dt}=\{\begin{array}{cc}(\mid V(t)\mid -V_{\mathrm{set}})\mathrm{sgn}[V(t)],& \mid V(t)\mid >V_{\mathrm{set}}\\ 0,& V_{\mathrm{reset}}<\mid V(t)\mid <V_{\mathrm{set}}\\ b(\mid V(t)\mid -V_{\mathrm{reset}})\mathrm{sgn}[\mathrm{\lambda }(t)],& \mid V(t)\mid <V_{\mathrm{reset}}\end{array}$$ (1)

where V is the voltage across a junction, and V_set and V_reset are the junction on and off thresholds, respectively. A positive constant parameter b was also used to quantify the filament decay rate due to stochastic thermodynamic breakdown (80–82). This parameter was varied (see fig. S3) to explore its effect on WM. For simulation results shown in this paper, b = 0.5 was used, unless otherwise indicated.

Experimental validation of the model used to simulate these networks can be found in Hochstetter et al. (9) (figs. S19 and S20). The choice of model parameters used in this study is based on an extensive parameter sensitivity analysis by Hochstetter and colleagues (9) in their Supplementary Notes.

The simulation duration and time steps used in all tasks were t = 2 s (for each sample) and Δt = 0.01 s, respectively. Input voltage amplitude was 0.3 V for training and 0.1 V for testing. For simulation results, the same network was used 10 times, each with different input patterns and order of sample presentation. Network junction states were completely reset between trials in simulation.

Implementation of supervised learning and PRL in classification and WM tasks

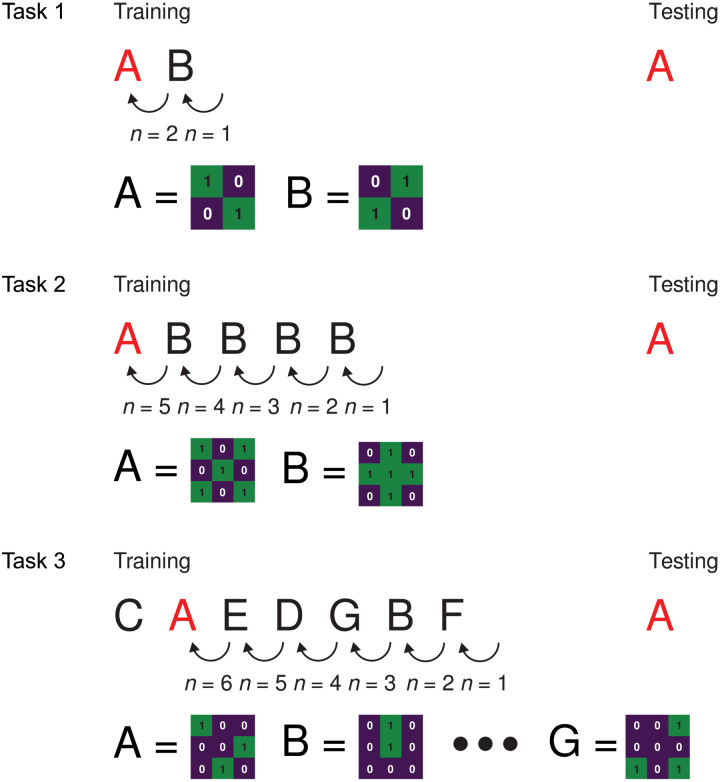
Figure 6 summarizes the three variations of n-back task presented in this study. For tasks 1 and 2, the target pattern is randomly switched between A and B in each epoch, and for task 3, the position of the target A is semirandomly changed at each training-testing epoch.

Fig. 6. Summary of n-back task protocols.

Top (task 1): Binary classification of two 2 × 2 patterns (A and B; two nonzero inputs each) and n = 2. Middle (task 2): Binary classification of 3 × 3 patterns (five nonzero inputs) and varying n. Bottom (task 3): WM task using multiple randomly selected, nonrepeated 3 × 3 patterns (A to G; example sequence shown) and varying n. Characters in red represent target pattern tested in each task.

Algorithm 1 describes the methodology for one training-testing epoch (for tasks 1 and 2), while Table 1 lists and describes all the parameters. A gradient descent–like algorithm (see Eq. 2) was used during training to implement supervised learning and change the relative voltage between the input and output electrodes, by increasing or decreasing the output voltage (V_o) of the drain electrodes. Changes in V_o are described by the following equation pair on lines 17 and 18 of Algorithm 1, respectively

$$\text{Δ}=\mathrm{\beta }(y_{\mathrm{target}}-d_{\mathrm{target}})$$ (2)

$$V_{\mathrm{o}}=V_{\mathrm{o}}+\text{Δ}$$ (3)

where y_target is the target drain output (current), d_target is the set target current, and β is the learning rate. Both y_target and d_target are normalized and therefore dimensionless, meaning that Δ is also dimensionless. By changing V_o, corresponding output drain currents were nudged toward a target current threshold (θ). Input electrodes remained unchanged from V_i. Experimentally, training stops once y_target reaches θ or the training time per sample ends. In the latter case, the sample was stopped even if the current had not reached the threshold θ, and the next sample was presented. The maximum training time was set to t = 15 s. If θ was reached before 15 s (which typically occurred after 1 to 3 s), the sample was considered trained, training was halted, and the next sample was presented. In simulation, each training sample was shown for all t = 2 s (200 time steps). If θ was reached before 2 s, V_i and all V_o were reset to zero for the rest of the sample duration.

Table 1. Experimental and simulation parameters and variables.

Parameter	Description
y	Normalized current (I) outputs of the drains, vector [ytarget,ynontarget]
d	Normalized current (I) that target drain is trained to reach (ytarget)
V o	Output (drain) voltages (1 × 2 vector)
I o	Nonnormalized output (drain) currents (1 × 2 vector)
V i	Input voltage (scalar)
β	Learning rate
λ	A state variable that parametrizes the conducting filament responsible for memristive switching
∆	Amount of adjustment required to Vo at each time step
b	Junction filament decay parameter (lower = slower decay)
Acc	Classification accuracy
Accθ	Accuracy threshold for reinforcement
θ	Reinforcement learning threshold, vector [θtarget,θnontarget]. Once the target output current (ytarget) reaches this threshold, it is considered trained for that sample.
θtest	Current threshold for testing used only in experimental setup. Once the current reaches this threshold, testing is halted.
incV al	Increase θtarget by incV al when Acc < Accθ
decV al	Decrease θnontarget by decV al when Acc < Accθ
x train	Input voltage during training
x test	Input voltage during testing, with xtest ≪ xtrain, so that new pathways are not formed during testing.

During testing, all the output electrodes were opened and reset to 0 V. An input that matches the same pattern as sample 1 (i.e., n samples before testing) was then delivered to the network. The input voltage was ramped up from 0 V until a current threshold (θ_test) is reached at the drain electrodes or until the testing time (typically t = 7 s) ends. The voltage does not exceed x_test. This procedure is used only in the experimental setup, as it is difficult to know a priori how much voltage is required for drain current to be measurable. In simulation, however, drain currents can be measured for any arbitrary voltage, so samples were delivered at a set voltage (V_i = x_test), which is lower than training.

Four possible scenarios can occur as a result of supervised learning

1) If y_target < d_target, then Δ < 0. Therefore, based on Eq. 3, V_o is reduced for the next time step. This, in turn, means that the voltage difference between the input electrodes (V_i) and V_otarget decreases, and more current flows to the target drain than the other drain electrodes.

2) If y_target ≥ d_target, then θ is reached, and the present sample is trained. Voltages are reset to 0.

3) If y_nontarget < d_target, the current outputs from the nontarget drains are likely lower than the outputs from the target drains.

4) If y_nontarget ≥ d_target, in this scenario, Δ ≥ 0, meaning that V_onontarget increases, and less current flows to the nontarget drains.

Once the test sample ended, the current of each output channel during testing time was averaged. The channel for which the average current was greater is considered the winner of the epoch (i.e., argmax is applied). If the winning output electrode matches the target that was trained for the testing electrode pattern (i.e., the corresponding drain from sample 1), then it is considered a successful epoch (Acc = 1), and the current threshold level (θ) stays the same. Otherwise, the epoch is considered unsuccessful (Acc = 0), and θ is increased for the target drain (reinforcement), while the threshold of the nontarget drain is decreased (penalty).

Task 1

A simple binary classification task was implemented (using four inputs and two outputs) to demonstrate supervised learning and PRL in NWNs. Each of two nonoverlapping 2 by 2 sample grid patterns (A and B) was associated with a corresponding grounded output electrode (drain 1 or 2) with a one-to-one correspondence. Each pattern was input as a voltage bias (V_i) applied to the selected source electrodes for t = 2 s, while the other input electrodes were electromechanically closed. The target output electrode was opened, while the other output electrode was electromechanically closed. After n = 2 cycles of training, a testing sequence was performed, in which the network’s efficacy in reproducing the trained pattern that presented n-steps previously was measured and analyzed. Training and testing for the selected input-output patterns were performed in sequence over multiple training-testing epochs.

Algorithm 1: Binary classification procedure

1: n ⇐ 2; d ⇐ 1 2: xtrain ⇐ 0.3 V; xtest ⇐ 0.1 V 3: incV al ⇐ θ/3; decV al ⇐ θ/6 4: θ⇐ [0.5, 0.5] 5: Vo ⇐ [0, 0] 6: for s in range(length(samples)) do 7:    if TRAINING then 8:        target ⇐ random (1, 2) ▷ Choose a class (1 or 2) at random and set as target 9:        Vi ⇐ xtrain 10:        Close Vonontarget 11:        RUN SIMULATION 12:        y⇐ Normalize(Io) 13:        if ytarget > θtarget then    ▷ If θ is reached, reset voltages to 0 14:            Vo ⇐ [0, 0] 15:            Vi ⇐ 0 16:        else 17:            ∆ ⇐ β(ytarget − dtarget)    ▷ Supervised learning 18:            Vo ⇐ Vo + ∆▷ External feedback 19:        end if 20:    else if TESTING then 21:            Vi⇐ xtest 22:            Vo ⇐ [0, 0] 23:            target ⇐ samples[s − n]    ▷ Target pattern is same as pattern n training samples prior. 24:            Open Vonontarget 25:            RUN SIMULATION 26:            y ⇐ Normalize(Io) 27:            if mean(ytarget) > mean(ynontarget) then 28:              Acc ⇐ 1 29:            else 30:              Acc ⇐ 0 31:            end if 32:            if Acc < Accθ then ▷ Reinforcement (PRL) 33:              θtarget ⇐ θtarget + incV al 34:              θnontarget ⇐ θnontarget − decV al 35:            end if 36:          end if 37:    end for

In experiment, parameters used for task 1 were as follows: x_train = 0.2 V; for x_test, voltage was ramped up from 0 V until a current was measurable in the target drain; θ= 6 × 10⁻⁸ A; θ_test= 1 × 10⁻⁷ A; training time: t = 15 s or until θ was reached; testing time: t = 7 s or until θ_test was reached, with 7-s rest between each training sample and 1-s rest between training and testing. In simulation, parameters used were as follows: x_train = 0.3 V; x_test = 0.1 V; θ= 5 × 10⁻⁶ A; training time: t = 2 s; testing time: t = 2 s, with no rest between each training sample and no rest between training and testing.

Task 2

The input pattern was expanded to 3 × 3 (nine inputs, two outputs), and more n values were added to the testing procedure: n = 2,3,4,5, and 6. Training and testing were implemented in the same way as in Algorithm 1, using more complex input patterns: “x” and “+” (5 bits each). One training-testing cycle made up an epoch. Each trial lasted 40 epochs of one n value. For example, in trial 1, n = 2, in trial 2, n = 3, and so on. A total of 50 trials were run, 10 for each n value, each with a different random seed. Figure 6 shows a schematic of the setup and methodology. The two classes of 3 × 3 patterns (+ and x) correspond to five nonzero inputs. If sample 1 is +, subsequent training samples were all x and vice versa. This way, during testing, conduction pathways formed by sample 1 are not stimulated for n-1 samples beforehand. Thus, the network relies on memory of pathways activated by the target input.

In experiment, parameters used for task 2 were as follows: x_train = 0.1 V; for x_test, voltage was ramped up from 0 V until a current was measurable in the target drain; θ= 2 × 10⁻⁸ A; θ_test= 1 × 10⁻⁷ A; training time: t = 15 s or until θ was reached; testing time: t = 6 s or until θ_test was reached, with 5-s rest between each training sample and 5-s rest between training and testing. In simulation, parameters used were as follows: x_train = 0.3 V; x_test = 0.1 V; θ= 5 × 10⁻⁶ A; training time: t = 2 s; testing time: t = 2 s, with no rest between each training sample and no rest between training and testing.

Task 3

A multiple pattern n-back task was implemented to test the WM capacity of NWNs while minimizing the influence of previous trials. This was operationalized by testing how accurately the NWN recalls a test sample from n-steps ago, without being reminded of that sample within the same epoch. To overcome the potential extra training of pathways during a single epoch due to repeating patterns (e.g., “A” repeated four times in the n-back = 5 pattern “ABBBBA” shown in Fig. 6), random, distinct patterns were generated.

Here, seven random 3 × 3 patterns were generated (named patterns A, B, C, … G). The number of pixels per pattern was limited to three, so that each pattern could have 1, 2, or 3 pixels randomly selected as inputs from the nine available pixels. The supervised learning and PRL algorithm used for one epoch (training + testing) is presented in Algorithm 2.

Pattern A was selected as the target for each testing epoch in the experiment. To vary n, the position at which pattern A was presented during training was varied, so that for testing, n-steps back varies. For example, if n = 3, pattern A is presented as the fifth training sample. In this case, the other six samples (four presented before A and two after) are randomly selected from patterns B to G without replacement. This meant that each training epoch included additional nonrepeated samples that precede the n-back sequence. In the example sequence shown in Fig. 6, the training order is [B, E, F, G, A, C, and D], which is followed by testing only for [A].

One training-testing cycle made up an epoch. Each trial lasted 200 epochs. The location of pattern A was semirandomized, so that each n was sampled around 28 times, for a total of 200 epochs. In other words, pattern A was presented at training position 1, 28 times over 200 epochs, at position 2, 28 times, and so on. A total of 10 trials were run, each with a different random seed.

Algorithm 2: Multipattern n-back procedure

1: patterns ⇐ [A, B, C, D, E, F, G] 2: d ⇐ 1 3: xtrain ⇐ 0.3 V; xtest ⇐ 0.1 V 4: incV al ⇐ θ/6; decV al ⇐ θ/12 5: θ ⇐ [0.5, 0.5] 6: Vo ⇐ [0, 0] 7: nV als ⇐ sample(length(patterns), replace = False)    ▷ Randomly sample positions at which target pattern (A) will be located. Repeat around 28 times for a total of 200 positions. 8: for s in range(length(samples)) do 9:    if TRAINING then 10:        target ⇐ A 11:        for pattern in patterns do 12:          n⇐ nV alss 13:          Vi ⇐ xtrain 14:          Close Vonontargets 15:          RUN SIMULATION 16:          y⇐ Normalize(Io) 17:          if ytarget > θtarget then    ▷ If θ is reached, reset voltages to 0 18:            Vo ⇐ [0, 0] 19:            Vi ⇐ 0 20:          else 21:            ∆ ⇐ β(ytarget − dtarget)    ▷ Supervised learning 22:            Vo ⇐ Vo + ∆▷ External feedback 23:          end if 24:        end for 25:      else if TESTING then 26:        Vi ⇐ xtest 27:        Vo ⇐ [0, 0] 28:        target ⇐ A 29:        Open Vonontargets 30:        RUN SIMULATION 31:        y ⇐ Normalize(Io) 32:        if mean(ytarget) > mean(ynontargets) then 33:          Acc ⇐ 1 34:        else 35:          Acc ⇐ 0 36:        end if 37:        if Acc < Accθ then    ▷ Reinforcement (PRL) 38:          θtarget ⇐ θtarget + incV al 39:          θnontargets ⇐ θnontargets − decV al 40:        end if 41:      end if 42: end for

In experiment, parameters used for task 3 were as follows: x_train = 0.1 V; for x_test, voltage was ramped up from 0 V until a current was measurable in the target drain; θ= 6 × 10⁻⁸ A; θ_test= 1 × 10⁻⁷ A; training time: t = 15 s or until θ was reached; testing time: t = 6 s or until θ_test was reached, with 5-s rest between each training sample and 5-s rest between training and testing. In simulation, parameters used were as follows: x_train = 0.3 V; x_test = 0.1 V; θ= 5 × 10⁻⁶ A; training time: t = 2 s; testing time: t = 2 s, with no rest between each training sample and no rest between training and testing.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S7

Legends for movies S1 to S4

Legend for Source Data File S1

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S4

Source Data File S1

View/request a protocol for this paper from Bio-protocol.