Abstract
Information in digital mammogram images has been shown to be associated with the risk of developing breast cancer. Longitudinal breast cancer screening mammogram examinations may carry spatiotemporal information that can enhance breast cancer risk prediction. No deep learning models have been designed to capture such spatiotemporal information over multiple examinations to predict the risk. In this study, we propose a novel deep learning structure, LRP-NET, to capture the spatiotemporal changes of breast tissue over multiple negative/benign screening mammogram examinations to predict near-term breast cancer risk in a case-control setting. Specifically, LRP-NET is designed based on clinical knowledge to capture the imaging changes of bilateral breast tissue over four sequential mammogram examinations. We evaluate our proposed model with two ablation studies and compare it to three models/settings, including 1) a “loose” model without explicitly capturing the spatiotemporal changes over longitudinal examinations, 2) LRP-NET but using a varying number (i.e., 1 and 3) of sequential examinations, and 3) a previous model that uses only a single mammogram examination. On a case-control cohort of 200 patients, each with four examinations, our experiments on a total of 3200 images show that the LRP-NET model outperforms the compared models/settings.
Keywords: Breast cancer, Risk prediction, Deep learning, Digital mammogram, Longitudinal data
1. Introduction
Based on the American Cancer Society (ACS)’s report in 2019, more than 3 million women have been diagnosed with breast cancer. In the last 30 years, the mortality rate of breast cancer has steadily decreased due to early detection, increased awareness, and treatment improvement [1]. Currently, the standard breast cancer screening is digital mammograms for women at average risk for breast cancer. Breast cancer risk models can provide a risk assessment to guide the screening strategies.
Imaging information, such as mammographic breast density [2] and breast parenchymal texture [3], has been shown useful for breast cancer risk prediction. Lately, deep learning has been studied to learn information from normal screening mammograms for predicting breast cancer risk, such as using a single prior mammogram [4] and the hybrid modeling of mammographic images and non-imaging risk factors [5]. These studies indicate that deep learning may be capable of identifying more predictive information in the screening mammograms and outperform existing statistically derived risk models for risk prediction.
In breast cancer screening by digital mammography, it is usual that a patient has multiple consecutive mammogram examinations. Longitudinal imaging data can provide spatiotemporal information than a single time point data, but also poses challenges on how to best integrate and capture the spatiotemporal information over longitudinal image examinations for analysis. Using longitudinal screening mammography for breast cancer risk prediction has a significant clinical value but is poorly studied in current literature. In this paper, we propose a novel deep learning structure, i.e., LRP-NET (Longitudinal Risk Prediction Network), to capture the spatiotemporal breast tissue variation over multiple longitudinal negative/benign screening mammogram examinations, for predicting breast cancer risk in a case-control setting. Specifically, LRP-NET is designed to capture the contralateral breast tissue variations between left and right breasts and over a time period for risk prediction. We evaluate LRP-NET on a case-control cohort of 200 women (100 with breast cancer and 100 breast-cancer free; a total of 1600 mammogram images). We also compare LRP-NET’s effects to a loose deep learning model (i.e., without capturing temporal relationships of longitudinal data) as well as a published model that uses only a single time point mammogram examination.
The rest of the paper is structured as follows: Section 2 gives a short review of related works. Section 3 describes our study cohort/datasets and details of the proposed LRP-NET structure. Section 4 presents the results of our model with a comparison to other models. Section 5 provides a discussion of our findings and conclusion.
2. Related work
In this section, we briefly summarize previous works in two related areas: breast cancer risk prediction models and longitudinal data modeling.
2.1. Breast cancer risk prediction models
A disease risk model is usually a tool to estimate the probability that a currently healthy individual may develop a future condition (e.g., cancer) within a specific time period. Earlier and existing breast risk models are usually based on conventional statistical modeling of clinical, personal, demographic, and/or genetic risk factors, such as the Gail model [6], Tyrer-Cuzick model [7], BOADICEA model [8], or a combination of multiple risk models [9]. A recent review paper [10] conducted a systematic quality assessment to several breast risk models.
Using pre-extracted features from breast images, machine learning methods have been adapted for breast cancer analysis [11], especially for risk prediction. Examples include Linear Discriminant Analysis (LDA) [12], Support Vector Machine (SVM) [13,14], and K-Nearest Neighbors (KNN) [14], using mammographic imaging features such as textures, textons, or density features. Logistic regression is also used to explore the association between texture/radiomic features and breast cancer risk [3,15]. Artificial neural networks (ANN) are used by Tan et al. [16] to fuse global texture and tissue density to predict near-term risk. Convolutional neural network (CNN) has also been employed to study the risk of developing breast cancer [17] and risk of recurrence for women undergoing chemoprevention treatment [18].
More recently, deep learning techniques were used to build end-to-end breast cancer risk prediction models. A deep learning-based risk score was shown to outperform the density-based score [19]. A GoogLeNet-LDA model was developed in [4] with a comparison to an end-to-end GoogleNet model for near-term risk prediction, where the study only used a single mammogram examination per patient. A recent work [5] investigated 3–5 years risk prediction using the ResNet18 model, where multiple (average number: 2 examinations) prior mammogram examinations were included but used independently; a follow-up study [20] also included demographic information for the risk prediction. However, inter-examination relationships among longitudinal imaging examinations were not explicitly captured in these studies [5,20].
2.2. Longitudinal imaging data modeling
Longitudinal imaging data have been extensively studied in brain [21], lung [22], etc., where the focus was to improve tumor segmentation or lesion detection [23]. In breast imaging, temporal analysis techniques have been applied in computer-aided diagnosis (CAD) studies intending to find temporally changing characteristics of mass lesions [24,25] as well as to detect micro-calcification (MC) in temporal mammogram pairs [26,27]. In [24], regional registration of current and prior images was first performed, and then extracted features from the registered regions were used in SVM models to classify mammographic mass lesions. In [25], a mapping between two prior mammogram examinations was used by a CNN model for mass detection. The temporal subtraction approach was used in [26,27] to detect MC by using classifiers such as LDA and SVM. In [28], three quantitative numbers about breast density were calculated over longitudinal examinations to assess breast cancer risk. A recent work [29] showed that information/knowledge extracted from distant/earlier normal mammograms could be used as a pre-trained model to train the recent mammograms to enhance breast cancer risk prediction. In general, these previous studies showed that when using temporal information between current and prior examinations, improved effects can be achieved for various tasks. However, no previous deep learning-based methods on using longitudinal mammogram imaging data for breast cancer risk prediction have been reported.
2.3. Our contribution
In this work, we propose a novel end-to-end deep learning structure (i.e., LRP-NET) to capture spatiotemporal breast tissue variations over four longitudinal normal screening mammogram examinations for predicting breast cancer risk. Our contributions are summarized as:
We propose a novel deep learning model (LRP-NET) to capture spatiotemporal changes of breast tissue over longitudinal mammographic imaging examinations.
We leverage clinical knowledge on capturing bilateral breast tissue changes in designing the structures of the LRP-NET model.
We evaluate the LRP-NET model with two ablation studies and compare it to three other related models/settings, showing outperforming results for breast cancer risk prediction in a case-control study.
3. Methods
3.1. Problem formulation and dataset
Our study received Institutional Review Board (IRB) approval at our institution. We perform a retrospective case-control study on 200 patients who underwent general breast cancer screening at our institution from 2007 to 2014, consisting of 100 breast cancer patients (“cases”) and 100 matched breast cancer-free patients (“controls”). For all the 200 patients, each has 4 longitudinal prior normal (i.e., negative or benign) screening mammogram examinations before the “current” mammogram with the diagnosis outcome (breast cancer or breast cancer-free). We use prior-4 (most distant), prior-3, prior-2, and prior-1 (most recent) to denote the four longitudinal mammogram examinations relative to the “current” examination (Fig. 1). We formulate the problem as a process of computational modeling using the 4 prior examinations to predict the “current” outcome (i.e., the cancer case vs. control status) of a patient.
Fig. 1.
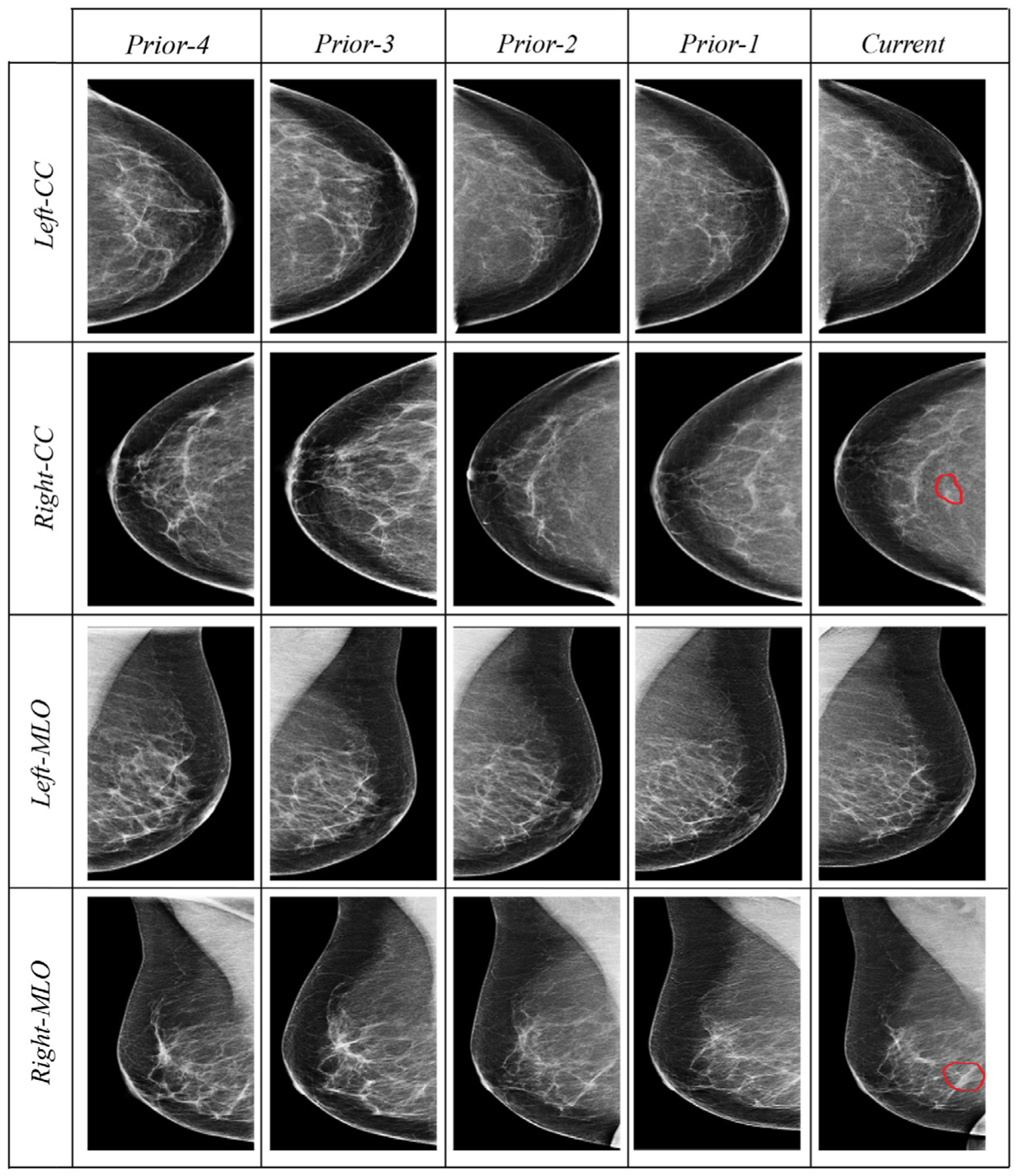
Examples of four longitudinal prior mammogram examinations (16 mammogram images) belonging to a 54-year-old woman diagnosed with nuclear grade 2 ductal carcinoma in situ manifest as microcalcifications in the right breast (red contours outlining the tumor region in the “current” column). Prior-1 through prior-4 are respectively captured at 1, 2, 3, and 4 year(s) earlier the cancer diagnosis at the current mammogram. Each prior includes four images: two projections (mediolateral oblique, MLO, and craniocaudal, CC) of each of the right and left breasts. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
All the 200 patients do not have any prior biopsy or recall on digital mammography. The 100 breast cancer cases are diagnosed with unilateral pathology-confirmed breast cancer. The 100 asymptomatic breast cancer-free controls are matched to the 100 cancer cases by patient age (±1 year old) at the “current” diagnosis outcome (i.e., breast cancer or breast cancer-free) and by the year (±1 year) of acquiring the “current” mammogram images. All controls remain breast cancer-free for at least one-year follow-up after the “current” image examination. For each prior examination, four mammographic images are collected including the left- and right-side breast, each in two views (i.e., craniocaudal (CC) view and mediolateral oblique (MLO) view). Thus, a total of 16 images are collected from 4 mammographic examinations for each patient. This leads to a total of 3200 mammogram images for the 200 patients for modeling and analysis. All mammographic examinations are acquired by Hologic/Lorad Selenia (Marlborough, MA) full-field digital mammography units.
Some key patient characteristics are summarized in Table 1. The mean age of patients at the “current” mammograms is 61.8 ± 9.0 years for the cancer cases and 61.0 ± 9.6 years for the controls. The average time period between prior-4 and current is 4.7 ± 0.82 (range 4 – 7) years for the cancer cases and 4.7 ± 1.02 (range 4 – 8) years for the controls. The average time period between prior-1 and current is 15 (range 7–23) months for cancer cases with 4 cases less than a year, and this average time between prior-1 and current for the control cohort is 16 (range 12–23) months. Comparing breast density, both cancer and control groups show a similar distribution across the four Breast Imaging-Reporting and Data System (BI-RADS) [30] breast density categories.
Table 1.
Key patient and imaging characteristics of the study cohort (200 patients including 100 breast cancer cases and 100 matched controls). Each patient has four prior mammogram examinations.
| Cases (N=100) n (%) | Controls (N=100) n (%) | |
|---|---|---|
| Patient/Imaging characteristics | ||
| Age (years): mean ± SD (range) | 61.8 ± 9.0 (39–88) | 61.0 ± 9.6 (41–88) |
| Time frame between 4th prior and current (years): mean ± SD (range) | 4.7 ± 0.8 (4–7) | 4.7 ± 1.0 (4–8) |
| Time frame between 1st prior and current (months): mean (range) | 15 (7–23) | 16 (12–23) |
| Menopausal status | ||
| Premenopausal | 10 (10%) | 20 (20%) |
| Postmenopausal | 81 (81%) | 76 (76%) |
| Hysterectomy | 3 (3%) | 3 (3%) |
| Uncertain | 6 (6%) | 1 (1%) |
| Family history of breast cancer | ||
| No family history | 40 (40%) | 54 (54%) |
| With family history | 59 (59%) | 46 (46%) |
| Unknown | 1 (1%) | 0 (0%) |
| Mammographic density (visual BI-RADS density categories) | ||
| Fatty | 7 (7%) | 9 (9%) |
| Scattered fibroglandular tissue | 42 (42%) | 37 (37%) |
| Heterogeneously dense | 50 (50%) | 51 (51%) |
| Extremely dense | 1 (1%) | 2 (2%) |
3.2. Proposed deep learning architecture: LRP-NET
We propose a novel deep learning CNN structure (Fig. 2) to capture the spatiotemporal imaging feature changes of the bilateral breast tissue over the four longitudinal mammograms for predicting the “current” outcome (i.e., breast cancer vs. control status). The CNN structure LRP-NET represents a Longitudinal Risk Prediction Network.
Fig. 2.
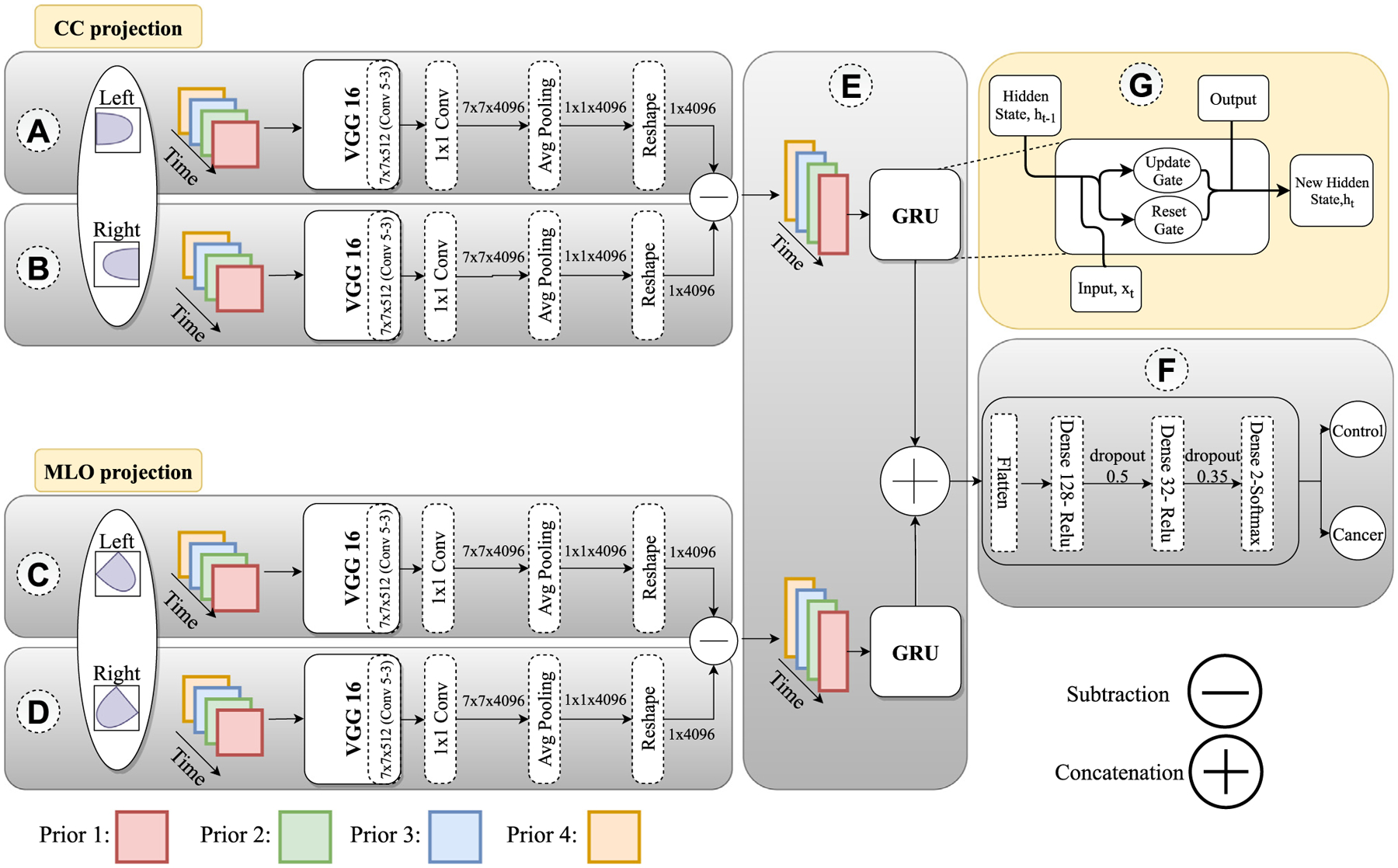
The proposed deep learning structure (LRP-NET) to capture changing pattern of longitudinal mammogram examinations for predicting breast cancer risk. The prediction is based on 16 images per patient. Eight CC-projections are fed into the top-left network and eight MLO projections into the bottom-left network. For each projection, 4 feature vectors belonging to the 4 corresponding priors go into the GRU model. Then the outputs of the two GRUs are concatenated to pass to the three dense layers followed by a flatten operation.
A pre-processing step is applied to all images before LRP-NET modeling. First, we run the LIBRA software package version 1.0.4 (Philadelphia, PA, 2016) [31] to segment the whole breast region out for subsequent analysis and exclude other imaged regions that are not related to the breast. Then all mammogram images are normalized to a fixed intensity range of 0 to 1 and are resampled to the same size of 224 × 224 by the nearest-neighbor interpolation technique. To make the image’s direction consistent for machine learning, we flip the direction of the right-side breast mammograms to appear as the left-side breast. In order to align each breast across the four longitudinal examinations for each patient, we apply the affine registration to account for partial deformation between the examinations, and we use the Elastix toolbox [32] to implement the affine registration. The left-side breast of prior-1 in both MLO and CC views is chosen as the reference to register all other mammogram images of the same patient.
As shown in Fig. 2, there are several main components in the proposed LRP-NET. Assume we have N cancer patients and N control patients where the cancer labels are assigned to 1 and control labels are assigned to 0. We define as a set of patient’s identifications. As mentioned, we have 4 priors per patient and for each prior we have two views and two sides S = {s1 : Left, s2 : Right}. This way, each image is denoted as , where and with label .
LRP-NET is composed of four blocks, A, B, C, and D, and each block contains an individual CNN model. The four blocks receive the left CC view images , right CC view images , left MLO view images , and right MLO images of the same patient as the input, respectively.
CNN Model Design:
The individual CNN models in the four blocks are responsible for extracting breast tissue imaging features, and their weights are shared across each view (i.e., between left CC and right CC as well as between left MLO and right MLO). Let denote our model with learnable parameter, . Corresponding to the 4 prior examinations, the 4 individual CNN models in the 4 blocks learn simultaneously from the 4 priors. Thus, the overall inputs of the CNN structure are 16 mammogram images with the size of 224 × 224 × 3, where the three channels are three duplicates of the gray image to enable ImageNet-based transfer learning. The output of each CNN model for an image I at the prior is denoted as , and it has a vector of size 1 × 4096. In implementing our CNN models, we used VGG16 as the backbone of the 4 CNN models. In order to reduce potential overfitting, we reduce the number of trainable network parameters/layers by modifying the layer types after the last original convolution layer (conv5_3). This means that 1 pooling layer and 3 dense layers in the original VGG16 structure are substituted with 1 convolution layer, 1 average pooling layer, and 1 reshape layer in our proposed structure. Each VGG16 model is pre-trained on ImageNet. For training, we freeze all the CNN layers except the last added layers to reduce the number of trainable parameters.
Subtraction layer:
In order to capture the breast tissue changing patterns from the difference between left and right breasts, we design a subtraction layer that is placed between blocks A & B and blocks C & D. In this layer, two feature vectors from the CNN models are subtracted, resulting in the output with the size of 1 × 4096, which is denoted by and as follows:
| (1) |
| (2) |
Gated Recurrent Unit (GRU) layer:
In order to capture the temporal relations between the subtracted feature vectors from the 4 priors, we use the many-to-one GRU model [33]. GRU is a gated version of the recurrent neural networks (RNN), and it uses the update gate and reset gate to solve the vanishing gradient problem of standard RNNs (block F). In this model, GRU receives four feature vectors (1 × 4096), each considered a one timestep and outputs a vector of 1 × 128. Given a sequence of input is an output of GRU with learnable parameters as following:
| (3) |
| (4) |
| (5) |
| (6) |
Initially, is set to 0 for . Here refers to each timestep, is a sigmoid function (Eqs. (3), (4)) and is a hyperbolic tangent (Eq. (5)). Because this is a many-to-one model, the final output of is the last output vector . Block E includes two GRU models corresponding to the two views (CC and MLO). The outputs of the two GRUs are concatenated to produce a vector of 1 × 256, which is denoted by .
Decision layer:
After the concatenation step, we place the decision layers, which include two dense layers (size 1 × 128 and 1 × 32), followed by a flatten layer fed into the last softmax layer (1 × 2). The dropout layers between the dense layers are employed to learn more robust features with rates 0.5 and 0.35, as shown in block F. Subsequently, the last layer of our CNN structure outputs a prediction probability of the outcome, namely, the status of cancer case or control. In this step we define the layers for patient with learnable parameter :
| (7) |
We run the training for 30 epochs with a batch size of 4 (indicating the number of patients in each batch since the data are split patient-wise) using the binary cross entropy (BCE) loss (Eq. (8)). We optimize the network’s hyperparameter using the RMSprops method with a start learning 0.01, and using the decay of 0.1 every five epochs with a minimum learning rate of . We incorporate an L2 kernel regularizer with a 0.01 rate. Data augmentation is not used. All these parameters are finalized through grid search on the training set and evaluation on the validation set using five-fold cross validation.
| (8) |
Our CNN structure is implemented using Python (version 3.6), TensorFlow (version 1.13), Keras (version 2.1.6). The prediction model is run on a CPU@3.60GHZ with 8 GB RAM and a Titan X Pascal Graphics Processing Unit (GPU).
3.3. Model evaluation and comparison with other methods
We evaluate the proposed LRP-NET structure at several different settings. In the main analysis, we test the model with both CC and MLO view images. Then, CC and MLO views are individually used to examine the respective prediction effect of a single view images (this is a clinically important setting because certain patients may only have one view images available); to do so, only one branch (i.e., blocks A & B or blocks C & D) is kept in the CNN structure, and one softmax layer is applied on top of the GRU’s output to generate the prediction of risk. Furthermore, in order to examine the robustness of the LRP-NET and the prediction effects of multiple but less than 4 prior mammograms, we assess our model using 3 priors as well. To do this, only the number of input to the GRU model is changed to 3 with the input sequences . This experiment includes the following combinations of examinations: prior-4→prior-3→prior-2, prior-4→prior-3→prior-1, prior-4→prior-2→prior-1, and prior-3→prior-2→prior-1. Note that we do not evaluate the effects of using only 2 priors because our proposed structure requires/prefers at least 3 examinations in order to perform the longitudinal analysis (because recurrent networks would need enough previous timesteps to decide the next). In addition, in order to highlight some of the regions that are potentially identified as relevant to the risk prediction, we use the GradCAM [34] method to visualize some imaging features identified by the VGG16 network.
To further investigate the effects of utilizing the CNN modules to identify the differences of features between left and right breast in LRP-NET, we conduct an ablation experiment by not using the CNN modules in all the four blocks of A, B, C, and D. Specifically, we replace the first CNN modules and the subsequent layers (i.e., Convolution, Pooling and Reshape) with a literal difference (i.e., subtraction in imaging space) of left and right breast followed by a Flatten layer and Dense layer, which generates a vector size of 4096 to feed to block E. This ablation experiment is denoted as “left/right breast difference in imaging space,” and we compare its effects to the original structures of LRP-NET, using 4 priors as well as 3 priors, respectively.
In order to assess the effects of the spatiotemporal relationships explicitly captured by LRP-NET among the four mammogram examinations, we also compare LRP-NET to a “loose” deep learning model that uses all the same four priors of each patient but without explicitly capturing the spatiotemporal relationships like LRP-NET does. Figure 3 shows the loose model, where we adopt ResNet18 referring to [5] as the main model to extract features from mammogram images. As can be seen, for each view (i.e., MLO and CC), ResNet18 is applied on four priors with shared parameters. The output of each individual prior is a score, and we used an average component to combine those scores. At the end, we average the score for each view to assign the final labels per patient. As a further examination to the loose model’s performance, we also directly calculate the absolute differences of sequential priors (i.e., |prior-3 - prior-4|, |prior-2 - prior-3|, and |prior-1 - prior-2|) and input them to the loose model. This experiment represents a simple implementation of capturing the temporal changes in the image space between two consecutive priors.
Fig. 3.
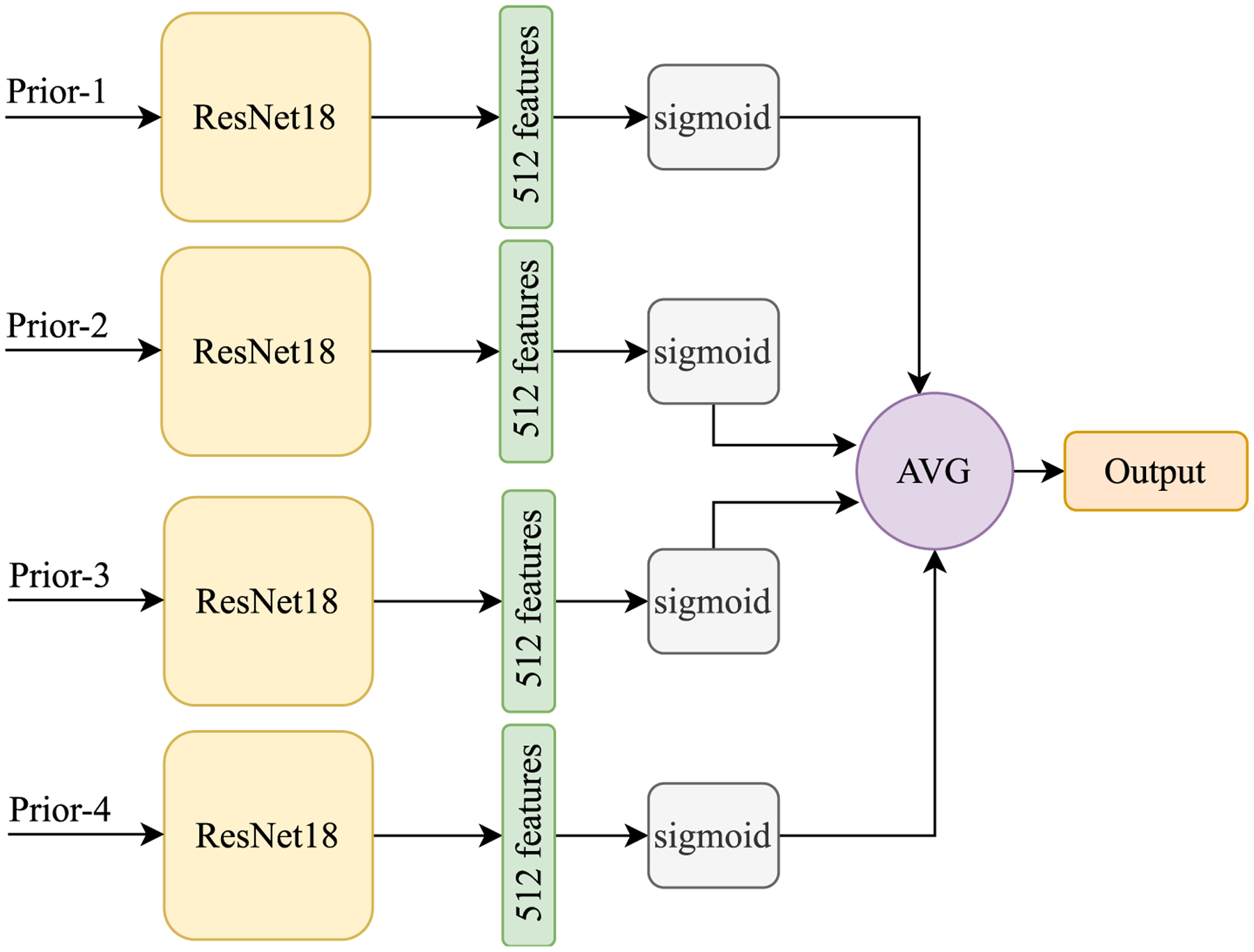
The “loose” model is used to incorporate the four longitudinal priors but without explicitly capturing the spatiotemporal relationships like LRP-NET does for breast cancer risk prediction.
Furthermore, we compare our model to a recent work [29] that also used longitudinal information for breast cancer risk prediction. On our dataset in this study, we implement the “prior data-enabled transfer learning” method (i.e., using older priors to inform newer priors) and the “multi-task learning” method proposed in that work [29] and we report the model performance on five-fold cross-validation.
Finally, we compare our risk prediction using all the 4 longitudinal examinations to the risk prediction using only a single examination (i.e., prior-4, prior-3, prior-2, or prior-1 individually), in two settings. For Setting 1 (denoted by “LRP-NET with Single-Prior Input”), we use the LRP-NET, but the inputs of blocks A, B, C, D are only a single prior (can be different views, i.e., CC, MLO, or CC+MLO). In order to do this, we maintain the original LRP-NET structure except to remove the GRUs for each view. In replacement of GRU, we put a Dense layer to reduce the size of features from 4096 to 128 to keep the number of features the same as the original to feed to block F. The purpose of this comparison is to isolate the effect of using longitudinal data from a full non-temporal model on a single-prior input (this is considered the second ablation experiment). For Setting 2 (denoted by “Single-Prior Model”), we implement a straightforward deep learning-based risk prediction method that uses only a single prior examination, as reported in the previous study [4] (i.e., GoogLeNet-LDA model). The purpose of this comparison is to reveal how the information captured by LRP-NET on longitudinal data can potentially enhance the risk prediction from using non-longitudinal data (i.e., a single prior examination).
3.4. Statistical analysis
We use patient-wise stratified 5-fold cross-validation (CV) for evaluating the model performance. In each fold, the proportions of the cancer cases and controls are balanced in patient stratification, and the data split is maintained the same across the different settings of experiments for comparison purposes. In each CV iteration, we assign one-fold as a test set and split the remains into 85% for training and 15% as a validation set. The area under the receiver operating characteristic (ROC) curve (AUC) and accuracy are calculated as the model performance metrics. We use bootstrapping methods to compute the 95% confidence interval (CI) for the average AUC values. Statistical significance between differences in AUC values are measured via Delong’s methods [35] and two-sample -test. All statistical analyses are performed using MATLAB software, version R2019a (The MathWorks, Natick, MA). Also, two-sided p-values < 0.05 is considered as statistically significant.
4. Results
When using all the four priors and both the CC and MLO views in LRP-NET, the AUC is 0.67 (95% CI: 0.59–0.75), and the accuracy is 0.61. The AUC value for the CC view only is 0.57 (95% CI: 0.49–0.64), while the MLO view only exhibits an AUC value of 0.60 (95% CI: 0.49–0.68). The AUC differences between MLO+CC view and a single view are statistically significant for MLO+CC vs. CC; for MLO+CC vs. MLO).
Table 2 compares the results of LRP-NET using four priors and the results of using a single prior (Setting 1: LRP-NET with Single-Prior Input and Setting 2: Single-Prior Model), with the following views: CC+MLO, MLO, and CC views. As can be seen, when comparing within the four individual priors, prior-1 shows the highest performance at MLO+CC view in both settings, with an AUC of 0.61 for Setting 1 and an AUC of 0.60 for Setting 2.
Table 2.
AUC values of using the four priors in LRP-NET and of using a single prior in two settings: Setting 1: LRP-NET with Single-Prior Input and Setting 2: Single-Prior Model. Here prior-1, prior-2, prior-3, and prior-4 denote from the most-recent to the most-distant examination relative to the current examination.
| Model | CC view AUC | MLO view AUC | MLO+CC view AUC |
|---|---|---|---|
| LRP-NET (prior-4 → prior-3 → prior-2 → prior-1) | 0.57 | 0.60 | 0.67 (referent) |
| Setting 1: | |||
| LRP-NET with Single-Prior Input (prior-1) | 0.56 | 0.55 | 0.61 (p = 0.05) |
| LRP-NET with Single-Prior Input (prior-2) | 0.53 | 0.55 | 0.60 (p = 0.05) |
| LRP-NET with Single-Prior Input (prior-3) | 0.55 | 0.57 | 0.59 (p = 0.03) |
| LRP-NET with Single-Prior Input (prior-4) | 0.54 | 0.54 | 0.59 (p = 0.03) |
| Setting 2 [4]: | |||
| Single-Prior Model (prior-1) | 0.61 | 0.52 | 0.60 (p = 0.04) |
| Single-Prior Model (prior-2) | 0.53 | 0.57 | 0.59 (p = 0.02) |
| Single-Prior Model (prior-3) | 0.53 | 0.59 | 0.53 (p = 0.01) |
| Single-Prior Model (prior-4) | 0.54 | 0.60 | 0.54 (p = 0.04) |
When both CC and MLO views are used, the AUC values of using a single prior (regardless of Setting 1 or Setting 2) are all significantly lower (all than that (i.e., 0.67) of using all the four priors in LRP-NET. When using a single view (CC or MLO), the differences between the AUC value of using a single prior (regardless of Setting 1 or Setting 2) and the AUC of LRP-NET on the four priors are not statistically significant (all In addition, when using a single view (CC or MLO), the Single-Prior Model outperforms LRP-NET with Single-Prior Input on most single priors. However, when CC and MLO views are combined, LRP-NET with Single-Prior Input outperforms the Single-Prior Model.
In terms of the effects observed when using different mammogram views (CC, MLO, or both), while it is not surprising to see that the combination of the two views shows the highest AUC, the MLO view outperforms the CC view in the main setting (i.e., using LRP-NET and four priors). When only the most recent prior (prior-1) is used, the CC view performs better than MLO, which is in line with the findings in a previous study [4]. However, the effects are opposite when using other single priors (i.e., MLO outperforms the CC view). These findings may indicate that the effects of the CC vs. the MLO view may be similar to each other for breast cancer risk prediction.
Table 3 shows that when using three continuous priors (i.e., prior-4→ 3 → 2 and prior-3 → 2 → 1), the AUC values are close to using all the four priors in the LRP-NET, and the AUC differences are not statistically significant (all ). However, when three discontinuous priors were used (i.e., prior-4 → 3 → 1 and prior-4 → 2 → 1), the AUC differences with using all the four priors are larger and statistically significant (all ). The performances drop, as expected when using three priors instead of the full four priors in our deep learning structure (LRP-NET). Furthermore, it looks like when the three priors are temporally continuous (i.e., prior-4 → 3 → 2 and prior-3 → 2 →1), the performance drop is less than when the three priors are not continuous (i.e., prior-4 → 3 → 1 and prior-4 → 2 → 1). This may indicate that the consistency of the time period gaps between two priors may largely affect the proposed model’s prediction effects. The results show that our model can still function when less than four priors are available for a given patient. Table 3 also shows the AUCs of the ablation experiment using “left/right breast differences in imaging space.” As can be seen, the direct use of left/right breast differences results in worse performance than using the CNN modules in the original LRP-NET. This indicates that it is hard to capture predictive features by simple subtraction of the images.
Table 3.
Performance of LRP-NET using its original CNN modules in comparison with the ablation experiment using “left/right breast differences in imaging space”.
| Model | LRP-NET with original CNN modules AUC | Left/right breast differences in imaging space AUC |
|---|---|---|
| LRP-NET (prior-4 → 3 → 2 → 1) | 0.67 (referent) | 0.59 |
| LRP-NET (prior-4 → 3 → 2) | 0.66 (p = 0.36) | 0.58 |
| LRP-NET (prior-4 → 3 → 1) | 0.60 (p = 0.01) | 0.59 |
| LRP-NET (prior-4 → 2 → 1) | 0.61 (p = 0.04) | 0.55 |
| LRP-NET (prior-3 → 2 → 1) | 0.64 (p = 0.16) | 0.56 |
As shown in Table 4, the AUC of using all the four priors but without capturing the spatiotemporal relationships (i.e., using the loose model) is 0.63, which is significantly lower than 0.67, the AUC obtained when using LRP-NET. Note that when the input of the loose model is the literal difference of the priors, the model performance drops significantly . This indicates that the simple subtractions of sequential priors are a sub-optimal choice as the input of the loose model.
Table 4.
Performance of the loose model by 1) using four priors but without capturing spatiotemporal relationships and 2) by directly using the differences of sequential priors.
| Model | MLO+CC view AUC |
|---|---|
| LRP-NET (prior-4 → prior-3 → prior-2 → prior-1) | 0.67 (referent) |
| Loose model using four priors (prior-4, 3, 2, 1) | 0.63 (p = 0.03) |
| Loose model using differences of sequential priors (| prior-3 - prior-4 |, |prior-2 - prior-3 |, |prior-1 - prior-2 |) | 0.57 (p < 0.01) |
Furthermore, regarding the effects of performing the affine registration between priors, we repeat all the experiments without the affine registration, and observe decreases in AUCs (~ 3 to 4 percentage drops; results not shown in the paper). This shows that having the prior registration is a helpful step for LRP-NET modeling. Of note, replacing the original backbones of the Single-Prior Model (i.e., GoogLeNet) and the loose model (i.e., ResNet18) consistently with VGG16 does not produce outperforming results.
The results of the two methods proposed in [29] are shown in Table 5. As can be seen, both the two methods have lower performance than our method. It should be noted that in the “prior data-enabled transfer learning” method, the use of all four priors leads to higher performance than using two or three priors, which is in line with what we observe in our method.
Table 5.
Results of the breast cancer risk prediction methods proposed in [29]. The expression e.g., “Prior-4 → Prior-3”, denotes transfer learning of a model trained on Prior-4 for training the model on Prior-3.
| Method | CC view AUC | MLO view AUC |
|---|---|---|
| Prior data-enabled transfer learning (Prior-4 → Prior-3) | 0.54 | 0.55 |
| Prior data-enabled transfer learning (Prior-4 → Prior-3 → Prior-2) | 0.58 | 0.56 |
| Prior data-enabled transfer learning (Prior-4 → Prior-3 → Prior-2 → Prior-1) | 0.61 | 0.60 |
| Multi-task learning using four priors | 0.60 | 0.59 |
Figure 4 shows eight representative ROC curves at eight different experimental settings. Figure 5 shows a visualization example of the CC view images from all the four priors on a randomly selected cancer patient. The heatmaps highlight potentially related regions where the proposed LRP-NET structure identifies predictive imaging features for the breast cancer risk. While we understand this visualization is a preliminary process, the regions behind the nipple seem to contain the most relevant features with regards to risk prediction, which is in line with previously reported studies [36]
Fig. 4.
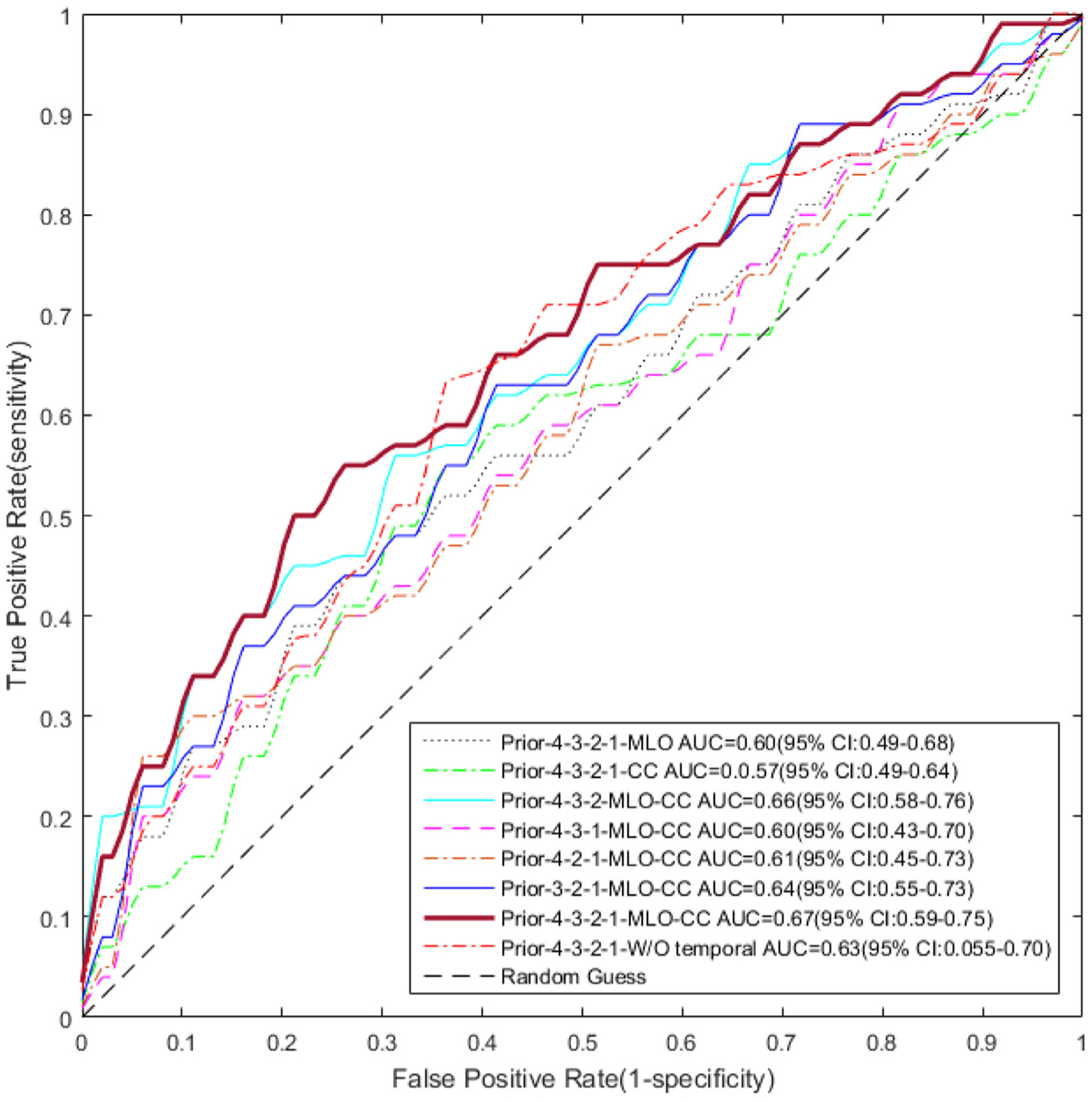
ROC curves for the risk prediction models which are evaluated at various settings. The proposed deep learning structure LRP-NET shows the highest AUC value of 0.67 (95% CI: 0.59–0.75).
Fig. 5.
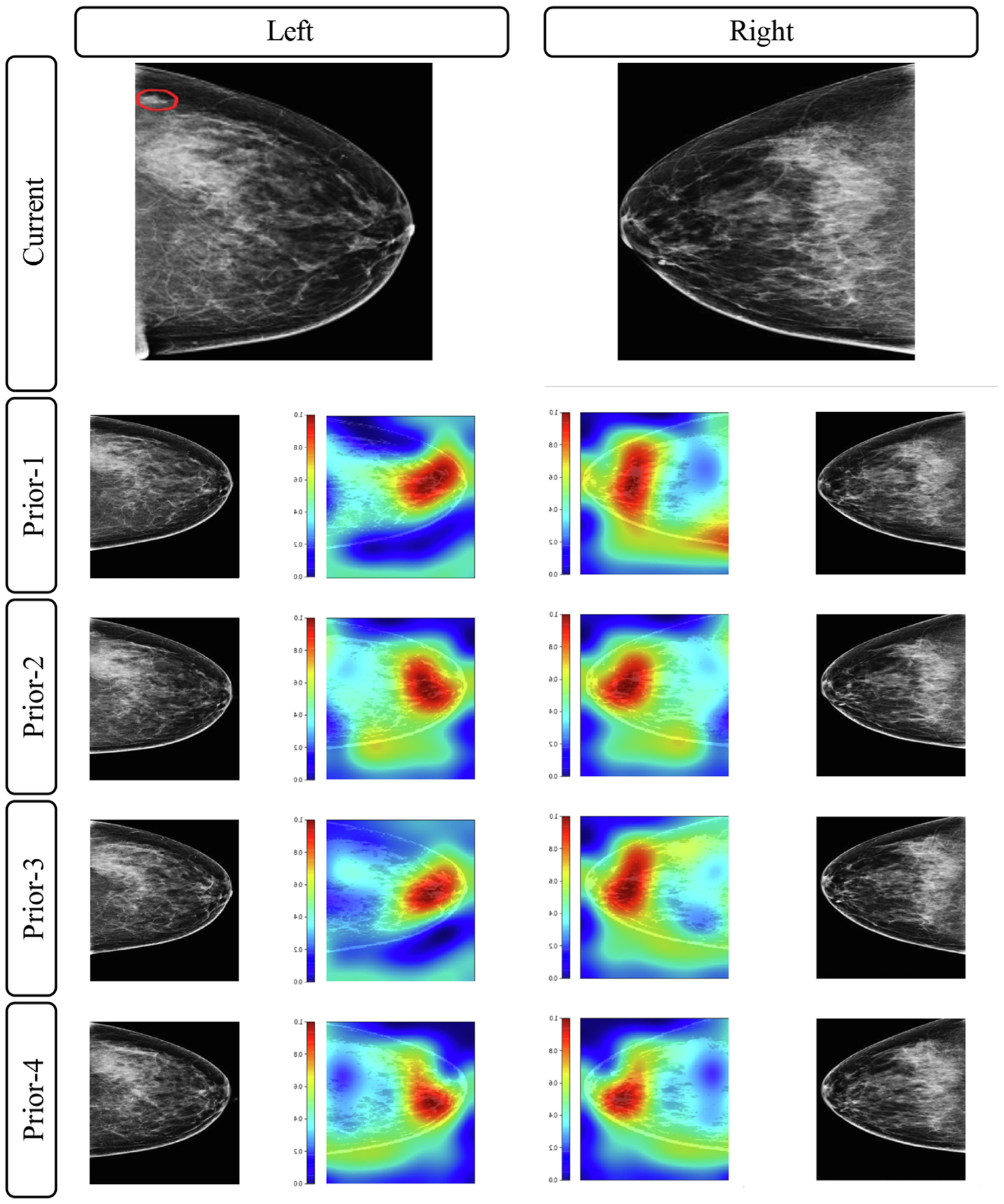
An illustrative example of imaging feature visualization for the VGG16 network. These mammograms belong to a 56-year-old woman diagnosed with grade 1 invasive ductal carcinoma and ductal carcinoma in situ in her left breast manifest as a developing irregular mass as outlined by red contours (ER positive, PR negative, HER-2 negative, Ki-67 10%, tumor size 6-mm, sentinel node negative). This patient is correctly predicted as a breast cancer case by the LRP-NET model. The brighter the color, the more relevant the pixel is for the risk prediction. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
5. Conclusion
In this paper, we design a new deep learning structure, LRP-NET, to investigate the association between spatiotemporal changes of breast tissue in longitudinal normal screening mammograms and the risk of developing breast cancer. We use four consecutive prior negative/benign mammographic examinations to extract spatiotemporal features in a case-control setting. In the two ablation studies (i.e., removal of the GRUs and replacement of the CNNs with literal differences of left and right breast), sub-optimal model performance is observed, indicating the efficacy of the original structure of LRP-NET. We also compare the effects of using a single prior examination, using 3 examinations, and using all the 4 priors but without explicitly capturing the spatiotemporal relationships between multiple priors. Our experiment results show that the proposed deep learning structure achieved the highest AUC for breast cancer risk prediction on the four priors, outperforming other compared models.
Breast cancer risk prediction using deep learning modeling has been reported in recent studies. Arefan et al. [4] studied ~ 1.5 year short-term risk prediction using a single prior mammogram examination. Yala et al. [5] reported a risk prediction study using mammograms of 3 to 5 years priors (on average 2 priors per patient), where, however, the spatiotemporal relationships of the priors were not taken into account in the modeling. A more recent work [29] evaluated effects of transfer learning from distant priors to recent priors and also a multi-task learning-based method. In this study, we propose LRP-NET to specifically identify and incorporate the spatiotemporal relationship information extracted from breast tissue changes over multiple longitudinal examinations. In contrast, the loose model is not designed to explicitly capture this relationship between the priors, hence the observed lower performance. When multiple longitudinal examinations are available, their spatiotemporal changes are informative for risk assessment as shown by the proposed LRP-NET model.
It should be noted that the spatiotemporal breast tissue changes captured by our model may have to do with the clinical notion of “developing asymmetry”, which is a sign that is associated with breast cancer risk and that radiologists seek to identify when viewing longitudinal mammogram examinations [37]. According to the BI-RADS atlas, developing asymmetry is defined as a bilateral asymmetry that is new or increased in conspicuity compared to previous mammogram examinations. The proposed LRP-NET can be viewed as a computational implementation of capturing the information related to the developing asymmetry from 4 longitudinal mammogram examinations. In this sense, LRP-NET can be reviewed as a deep learning architecture that incorporates medical knowledge to support the logic of the proposed model structures and to facilitate the modeling process. This may also partly explain the improved performance of LRP-NET in comparison to the loose model.
In future work, we will further evaluate the proposed model’s performance on a larger dataset, ideally from multi-center patient cohorts. In addition, we understand it is important to visualize the features associated with risk prediction in order to improve the interpretability of model [38]. The current image feature visualization techniques through gradient backpropagation only apply to the convolution layers. As a limitation, we cannot use this method to visualize the subtraction layers. This is because this visualization method captures the contribution of each pixel to the model prediction and subtraction in the feature space will result in a mixture of these effects. In next steps, we plan to develop methods to extend the visualization to other layers of the whole deep learning network for enhanced feature visualization. In addition, a recent study [39] showed that near-term breast cancer risk prediction models could be affected by early signs of cancer in the priors. Therefore, it will be helpful to have expert radiologists review all the priors to identify potential cases, if any, with early signs of cancer, in future work.
In summary, we propose a new deep learning structure to investigate the spatiotemporal mammographic information among multiple longitudinal examinations for breast cancer risk prediction. Clinical knowledge on risk assessment is incorporated in the design of our model structure. Extensive evaluation and comparisons to other related models/settings show the outperforming results of the proposed LRP-NET model. We are ready to share the code of our methods to the public via a GitHub link after acceptance of this paper.
Acknowledgment
This project is supported in part by National Institutes of Health (NIH)/National Cancer Institute (NCI) grants (1R01CA193603, 3R01CA193603-03S1, and 1R01CA218405), the grant 1R01EB032896 as part of the National Science Foundation (NSF)/NIH Smart Health and Biomedical Research in the Era of Artificial Intelligence and Advanced Data Science Program, a NSF grant (CICI: SIVD: 2115082), an Amazon Machine Learning Research Award, the UPMC Hillman Cancer Center Developmental Pilot Program, and a Developmental Pilot Award of the Pittsburgh Center for AI Innovation in Medical Imaging and the associated Pitt Momentum Funds through a Scaling grant from the University of Pittsburgh (2020). This work used the computational support by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF grant number ACI-1548562. Specifically, it uses the Bridges system, which is supported by NSF award number ACI-1445606, at the Pittsburgh Supercomputing Center. The content of this study is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the NSF.
Biographies
Saba Dadsetan, is a PhD student in the Intelligent Systems Program at the University of Pittsburgh. She got her BSc degree from the University of Tehran majoring in Information Technology Engineering. She is pursuing her academic research in medical image analysis using deep learning models.
Dooman Arefan, has MS and PhD degrees in Medical Imaging Engineering. He was a postdoctoral researcher from 2017 to 2020 at the University of Pittsburgh, PA, USA. He is currently a faculty member at the University of Pittsburgh. His current research interest is in artificial intelligence in medical imaging.
Wendie Berg, MD, PhD, FACR, is a Professor of Radiology at Magee-Womens Hospital of the University of Pittsburgh Medical Center. Her overarching interest is in improving methods for early detection of breast cancer. Refining risk assessment, tailoring screening, and optimizing implementation of new technologies are her primary research interests.
Margarita Zuley, MD, FACR, is a Professor of Radiology and Chief of Breast Imaging at Magee-Womens Hospital of the University of Pittsburgh Medical Center. As a diagnostic radiologist, the majority of her career has been focused on research that investigates novel beast imaging technologies for improved interpretation quality.
Jules Sumkin, DO, FACR, is a Professor and the Chairman of the Department of Radiology and endowed chair of women’s imaging at University of Pittsburgh and University of Pittsburgh Medical Center. His main research interest is in breast cancer imaging and computer-aided diagnosis.
Shandong Wu, PhD, is an Associate Professor of Radiology, Biomedical Informatics, Bioengineering at the University of Pittsburgh. He leads the Intelligent Computing for Clinical Imaging Lab and the Pittsburgh Center for AI Innovation in Medical Imaging. His main research interests include medical imaging analysis, artificial intelligence, and clinical/translational studies.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Siegel RL, Miller KD, Jemal A, Cancer statistics, 2019, CA Cancer J. Clin. 69 (1) (2019) 7–34. [DOI] [PubMed] [Google Scholar]
- [2].Nazari SS, Mukherjee P, An overview of mammographic density and its association with breast cancer, Breast Cancer 25 (3) (2018) 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kontos D, Winham SJ, Oustimov A, Pantalone L, Hsieh M-K, Gastounioti A, Whaley DH, Hruska CB, Kerlikowske K, Brandt K, et al. , Radiomic pheno-types of mammographic parenchymal complexity: toward augmenting breast density in breast cancer risk assessment, Radiology 290 (1) (2019) 41–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Arefan D, Mohamed AA, Berg WA, Zuley ML, Sumkin JH, Wu S, Deep learning modeling using normal mammograms for predicting breast cancer risk, Med. Phys 47 (1) (2020) 110–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yala A, Lehman C, Schuster T, Portnoi T, Barzilay R, A deep learning mammography-based model for improved breast cancer risk prediction, Radiology 292 (1) (2019) 60–66. [DOI] [PubMed] [Google Scholar]
- [6].Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Schairer C, Mulvihill JJ, Projecting individualized probabilities of developing breast cancer for white females who are being examined annually, J. Natl. Cancer Inst 81 (24) (1989) 1879–1886. [DOI] [PubMed] [Google Scholar]
- [7].Tyrer J, Duffy SW, Cuzick J, A breast cancer prediction model incorporating familial and personal risk factors, Stat. Med 23 (7) (2004) 1111–1130. [DOI] [PubMed] [Google Scholar]
- [8].Lee A, Mavaddat N, Wilcox AN, Cunningham AP, Carver T, Hartley S, de Villiers CB, Izquierdo A, Simard J, Schmidt MK, et al. , BOADICEA: a comprehensive breast cancer risk prediction model incorporating genetic and nongenetic risk factors, Genet. Med 21 (8) (2019) 1708–1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Guan Z, Huang T, McCarthy AM, Hughes KS, Semine A, Uno H, Trippa L, Parmigiani G, Braun D, Combining breast cancer risk prediction models, arXiv preprint arXiv:2008.01019 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Louro J, Posso M, Boon MH, Román M, Domingo L, Castells X, Sala M, A systematic review and quality assessment of individualised breast cancer risk prediction models, Br. J. Cancer 121 (1) (2019) 76–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Schaefer G, Závišek M, Nakashima T, Thermography based breast cancer analysis using statistical features and fuzzy classification, Pattern Recognit. 42 (6) (2009) 1133–1137. [Google Scholar]
- [12].Sun W, Zheng B, Lure F, Wu T, Zhang J, Wang BY, Saltzstein EC, Qian W, Prediction of near-term risk of developing breast cancer using computerized features from bilateral mammograms, Comput. Med. Imaging Graph 38 (5) (2014) 348–357 [DOI] [PubMed] [Google Scholar]
- [13].Tan M, Mariapun S, Yip CH, Ng KH, Teo S-H, A novel method of determining breast cancer risk using parenchymal textural analysis of mammography images on an Asian cohort, Phys. Med. Biol 64 (3) (2019) 035016. [DOI] [PubMed] [Google Scholar]
- [14].Li X-Z, Williams S, Bottema MJ, Constructing and applying higher order textons: estimating breast cancer risk, Pattern Recognit. 47 (3) (2014) 1375–1382 [Google Scholar]
- [15].Zheng Y, Keller BM, Ray S, Wang Y, Conant EF, Gee JC, Kontos D, Parenchymal texture analysis in digital mammography: a fully automated pipeline for breast cancer risk assessment, Med. Phys 42 (7) (2015) 4149–4160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Tan M, Pu J, Cheng S, Liu H, Zheng B, Assessment of a four-view mammographic image feature based fusion model to predict near-term breast cancer risk, Ann. Biomed. Eng 43 (10) (2015) 2416–2428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Gastounioti A, Oustimov A, Hsieh M-K, Pantalone L, Conant EF, Kontos D, Using convolutional neural networks for enhanced capture of breast parenchymal complexity patterns associated with breast cancer risk, Acad. Radiol. 25 (8) (2018) 977–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Manley H, Mutasa S, Chang P, Desperito E, Crew K, Ha R, Dynamic changes of convolutional neural network-based mammographic breast cancer risk score among women undergoing chemoprevention treatment, Clin. Breast Cancer (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Dembrower K, Liu Y, Azizpour H, Eklund M, Smith K, Lindholm P, Strand F, Comparison of a deep learning risk score and standard mammographic density score for breast cancer risk prediction, Radiology 294 (2) (2020) 265–272. [DOI] [PubMed] [Google Scholar]
- [20].Yala A, Mikhael PG, Strand F, Lin G, Smith K, Wan Y-L, Lamb L, Hughes K, Lehman C, Barzilay R, Toward robust mammography-based models for breast cancer risk, Sci. Transl. Med 13 (578) (2021). [DOI] [PubMed] [Google Scholar]
- [21].Pei L, Bakas S, Vossough A, Reza SM, Davatzikos C, Iftekharuddin KM, Longitudinal brain tumor segmentation prediction in MRI using feature and labe fusion, Biomed. Signal Process. Control 55 (2020) 101648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Wang C, Rimner A, Hu Y-C, Tyagi N, Jiang J, Yorke E, Riyahi S, Mageras G, Deasy JO, Zhang P, Toward predicting the evolution of lung tumors during radiotherapy observed on a longitudinal mr imaging study via a deep learning algorithm, Med. Phys. 46 (10) (2019) 4699–4707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Fartaria MJ, Kober T, Granziera C, Cuadra MB, Longitudinal analysis of white matter and cortical lesions in multiple sclerosis, NeuroImage 23 (2019) 101938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Timp S, Varela C, Karssemeijer N, Computer-aided diagnosis with temporal analysis to improve radiologists’ interpretation of mammographic mass lesions, IEEE Trans. Inf. Technol. Biomed 14 (3) (2010) 803–808. [DOI] [PubMed] [Google Scholar]
- [25].Kooi T, Karssemeijer N, Classifying symmetrical differences and temporal change for the detection of malignant masses in mammography using deep neural networks, J. Med. Imaging 4 (4) (2017) 044501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Filev P, Hadjiiski L, Chan H-P, Sahiner B, Ge J, Helvie MA, Roubidoux M, Zhou C, Automated regional registration and characterization of corresponding microcalcification clusters on temporal pairs of mammograms for interval change analysis, Med. Phys. 35 (12) (2008) 5340–5350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Loizidou K, Skouroumouni G, Nikolaou C, Pitris C, An automated breast micro-calcification detection and classification technique using temporal subtraction of mammograms, IEEE Access 8 (2020) 52785–52795. [Google Scholar]
- [28].Krishnan K, Baglietto L, Stone J, Simpson JA, Severi G, Evans CF, MacInnis RJ, Giles GG, Apicella C, Hopper JL, Longitudinal study of mammographic density measures that predict breast cancer risk, Cancer Epidemiol. Prev. Biomarkers 26 (4) (2017) 651–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Dadsetan S, Arefan D, Zuley M, Sumkin J, Sun M, Wu S, Learning knowledge from longitudinal data of mammograms to improving breast cancer risk prediction, in: Medical Imaging 2021: Imaging Informatics for Healthcare, Research, and Applications, vol. 11601, International Society for Optics and Photonics, 2021, p. 116010M. [Google Scholar]
- [30].Spak DA, Plaxco J, Santiago L, Dryden MJ, Dogan B, Bi-rads® fifth edition: a summary of changes, Diagn. Interv. Imaging 98 (3) (2017) 179–190. [DOI] [PubMed] [Google Scholar]
- [31].Keller BM, Nathan DL, Wang Y, Zheng Y, Gee JC, Conant EF, Kontos D, Estimation of breast percent density in raw and processed full field digital mammography images via adaptive fuzzy c-means clustering and support vector machine segmentation, Med. Phys. 39 (8) (2012) 4903–4917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Klein S, Staring M, Murphy K, Viergever MA, Pluim JP, Elastix: a toolbox for intensity-based medical image registration, IEEE Trans. Med. Imaging 29 (1) (2009) 196–205. [DOI] [PubMed] [Google Scholar]
- [33].Cho K, Van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, Bengio Y, Learning phrase representations using RNN encoder-decoder for statistical machine translation, arXiv preprint arXiv:1406.1078 (2014). [Google Scholar]
- [34].Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D, GradCAM: visual explanations from deep networks via gradient-based localization, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 618–626 [Google Scholar]
- [35].DeLong ER, DeLong DM, Clarke-Pearson DL, Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach, Biometrics (1988) 837–845. [PubMed] [Google Scholar]
- [36].Li H, Giger ML, Huo Z, Olopade OI, Lan L, Weber BL, Bonta I, Computerized analysis of mammographic parenchymal patterns for assessing breast cancer risk: effect of ROI size and location, Med. Phys. 31 (3) (2004) 549–555. [DOI] [PubMed] [Google Scholar]
- [37].Price ER, Joe BN, Sickles EA, The developing asymmetry: revisiting a perceptual and diagnostic challenge, Radiology 274 (3) (2015) 642–651. [DOI] [PubMed] [Google Scholar]
- [38].Dadsetan S, Wu S, A data interpretation approach for deep learning-based prediction models, in: Medical Imaging 2019: Imaging Informatics for Healthcare, Research, and Applications, vol. 10954, International Society for Optics and Photonics, 2019, p. 109540M. [Google Scholar]
- [39].Liu Y, Azizpour H, Strand F, Smith K, Decoupling inherent risk and early cancer signs in image-based breast cancer risk models, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, 2020, pp. 230–240 [Google Scholar]


