Highlights
-
•
Anchor competitive adaptive reweighted sampling (A-CARS) was proposed.
-
•
Monte Carlo synergy interval PLS (MC-siPLS) was used to find feature intervals and determine anchor points.
-
•
A-CARS-PLS was used to predict the protein content in corn.
-
•
The results of A-CARS-PLS were compared with 6 methods (GA-PLS, random frog PLS and CARS-PLS, siPLS and MWPLS).
-
•
We built the accurate model for prediction of protein content in corn via near-infrared spectroscopy and A-CARS.
Keywords: Corn protein, Near-infrared Spectroscopy, Monte Carlo method, Partial least-squares, Wavelength selection
Abstract
In order to quickly and accurately determine the protein content of corn, a new characteristic wavelength selection algorithm called anchor competitive adaptive reweighted sampling (A-CARS) was proposed in this paper. This method first lets Monte Carlo synergy interval PLS (MC-siPLS) to select the sub-intervals where the characteristic variables exist and then uses CARS to screen the variables further. A-CARS-PLS was compared with 6 methods, including 3 feature variable selection methods (GA-PLS, random frog PLS, and CARS-PLS) and 2 interval partial least squares methods (siPLS and MWPLS). The results showed that A-CARS-PLS was significantly better than other methods with the results: RMSECV = 0.0336, R2c = 0.9951 in the calibration set; RMSEP = 0.0688, R2p = 0.9820 in the prediction set. Furthermore, A-CARS reduced the original 700-dimensional variable to 23 variables. The results showed that A-CARS-PLS was better than some wavelength selection methods, and it has great application potential in the non-destructive detection of protein content in corn.
1. Introduction
Corn is one of the most important grains in the world. According to the United States Department of Agriculture (USDA), the total global corn production in 2020/21 was 1207 million metric tons, however, wheat was only 778.6 million metric tons and rice was only 509.8 million metric tons (https://www.ers.usda.gov/data-products/international-baseline-data/). In terms of yield, it is enough to show that corn is the most important grain, and corn has high nutritional value. The high nutrients such as riboflavin contained in corn are very beneficial to the human body. Corn is rich in nutrients such as starch and protein that are needed for human health (Shen et al., 2018). Therefore, it is important to determine the protein content in corn.
In recent years, near-infrared (NIR) spectroscopy has been widely used for qualitative and quantitative analysis of foods. Costa Pereira et al. applied NIR and interval partial least-squares (iPLS) regression combined with variable selection method to determine the quality parameters in vegetable (Costa Pereira et al., 2008). Lan et al. made use of NIR spectroscopy to describe and predict pure quality from the non-destructive apple measurements (Lan et al., 2020). Basile et al. utilized NIR Spectroscopy and Artificial Neural Networks to predict grape texture (Basile et al., 2022). The above studies show that NIR spectroscopy plays an important role in food non-destructive testing. Furthermore, Li et al. carried out the non-destructive identification and monitoring of Cu-Pb pollution in corn based on near-infrared spectroscopy (Li et al., 2023). Liu et al. processed near-infrared hyperspectral images of both sides of corn seeds to determine single-grain starch content (Liu et al., 2020). Zhang et al. used near-infrared spectroscopy to detect moisture content in corn stalk silage (Zhang et al., 2019). Zhang et al. classified the frozen corn seeds via hyperspectral VIS/NIR reflectance imaging (Zhang, Dai & Cheng, 2019). The above studies show that near-infrared spectroscopy plays an important role in the field of corn research.
Characteristic wavelength selection, as a hot research field in recent years, is often combined with spectral techniques to simplify the final model. It is one of the important methods of spectral multivariate calibration. During the last 20 years, many single variable selection algorithms based on model population analysis (MPA) have been proposed including ant colony (AO) (Dorigo et al., 2006), uninformative variable elimination (UVE) (Cai et al., 2008), Monte Carlo uninformative variable elimination (MC-UVE) (Han et al., 2008), competitive adaptive reweighted sampling (CARS) (Li et al., 2009), margin influence analysis (MIA) (Li et al., 2011), random frog (RF) (Li et al., 2012), variable iterative space shrinkage approach (VISSA) (Deng et al., 2014), variable in projection (VIP) (Galindo-Prieto et al., 2015), and bootstrapping soft shrinkage (BOSS) (Deng et al., 2016). Most of the variable selection algorithms use statistical methods to evaluate model performance. At the same time, these variable selection algorithms are also widely applied in non-destructive detection. For example, Wang et al. evaluated maize photosynthetic pigment contents of maize with continuous wavelet transform and UVE-PLS (Wang et al., 2020). Guo et al. predicted antioxidant capability and active constituents of green tea by AO-PLS, SA-PLS, and GA-PLS, combined with NIR spectroscopy (Guo et al., 2020). Sun et al. used fractional Savitzky-Golay derivation coupled with wavelength selection algorithm CARS to estimate moisture content in corn leaves (Sun et al., 2021). Yang et al. utilized CARS-SVM and Terahertz spectroscopy combined with chemometrics to identify corn varieties with 100% accuracy (Yang et al., 2021). From the foregoing, researchers make use of variable selection algorithms to simplify the model in order to improve the accuracy of the model. Therefore, the variable screening method is an important modeling method. However, some researchers believe that due to the high collinearity of NIR spectroscopy, variable selection methods are unstable and weak interpretable compared with the interval selection algorithms (Yun et al., 2019).
The competitive adaptive reweighted sampling (CARS) was based on Darwin’s theory of evolution, and the variables are selected according to survival of the fittest (Li et al., 2009). The CARS builds a PLS model on a randomly selected subset of variables from the calibration set by Monte Carlo method, and then adaptive reweighted sampling (ARF) and exponential descending Function (EDF) are served as important indicators for wavelength selection. After that, a partial least squares model is established for each newly generated subset, and the model with the smallest RMESE will be used as the calibration model (Li et al., 2009).
In this work, we proposed a new characteristic variable selection method called anchor competitive adaptive reweighted sampling (A-CARS) to determine the relationship between protein content in corn and near-infrared spectra of corn. Monte Carlo synergy interval PLS (MC-siPLS) was used to combine with CARS to improve the reliability of the model, and it eliminated irrelevant variables and selected relevant variables at the same time. MC-siPLS was used to filter the interval in which the characteristic variable exists, and combine the results of each selection until the interval size no longer changes. CARS could reduce variables based on the previously selected intervals by MC-siPLS. The purpose of MC-siPLS was to select intervals as many characteristic variables as possible and then combine them. This allows CARS to make further selections in intervals containing a large number of correlated variables and it can significantly improve the interpretability of the model.
2. Materials and methods
2.1. Corn dataset
The corn dataset contains NIR spectra of 80 corn samples. The spectral wavelength range 1,100–2,498 nm consisted of 700 wavelength points, which were scanned at the interval of 2 nm. The dataset collected at Cargill was from an m5 instrument and the protein of each sample was considered as the independent variable. The Kennard-Stone (KS) method was used to divide the samples (Morais et al., 2019), and the ratio of the calibration dataset and prediction dataset was 3:1. The calibration dataset contains 60 samples, and the prediction dataset contains 20 samples. The advantage of using KS to divide samples is that it can effectively improve the generality of the model. More information on corn dataset can be found at: https://www.eigenvector.com/data/Corn/index.html.
2.2. Monte Carlo synergy interval PLS(MC-siPLS)
For the traditional siPLS, its steps are as follows:
Step 1: Divide the spectrum into equal intervals.
Step 2: Combine 2, 3, or 4 sub-intervals.
Step 3: Build PLS models for each combination, and the number of sub PLS models established by siPLS can be known from the combination number formula as , of which, n is the number of combined intervals and m is the number of intervals (Nørgaard et al., 2005).
Step 4: Choose the best interval combination as the calibration model according to the minimum root mean square error of cross validation (RMSECV).
As an improved version of the iPLS algorithm, siPLS adds an interval combination function base on iPLS. But it does not optimize the interval division method. Therefore, the model will always choose the interval combination with the smallest RMSE, and it is easy to fall into the local minimum situation (Hulland, 1999). Therefore, the Monte Carlo (MC) method (Shapiro, 2003) was used to optimize the interval division. The intervals were divided using the Monte Carlo method as follows: at the stage of dividing P-1 points were randomly generated in the whole spectrum by the Monte Carlo method. The number of variables between each point including the start and end should be larger than the maximum number of components. If conditions were unsatisfactory, the program would regenerate the points. Through the MC method, each interval division was different, so more interval combinations could be generated. Therefore, the intervals with the most feature variables could be further searched, and MC-siPLS was used to screen characteristic variable intervals.
2.3. Anchor competitive adaptive reweighted sampling (A-CARS)
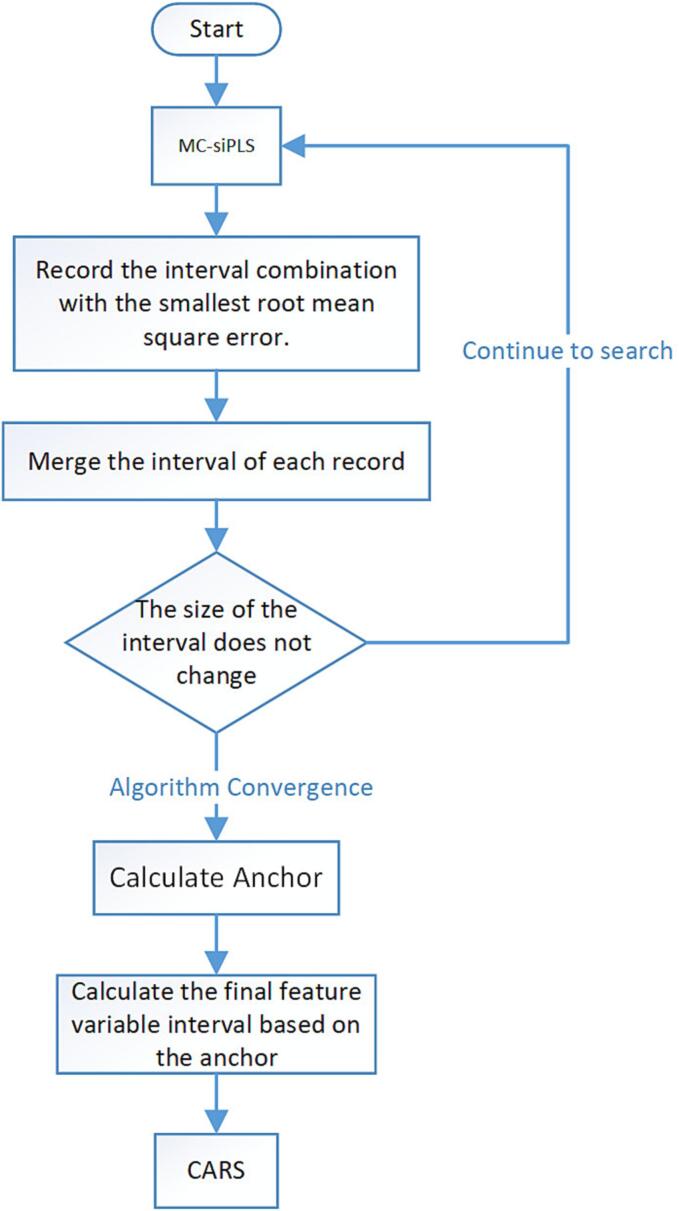
In this section, A-CARS will be introduced in detail. First of all, MC-siPLS will give the best way to divide the interval and the best interval combination (Zeng et al., 2023). Suppose that the characteristic variable interval selected by MC-siPLS each time is (), where is the number of times that MC-siPLS is run. The interval is the final selected interval. The definition of is given as follows:
| (1) |
The convergence conditions are as follows:
| (2) |
The above convergence conditions indicate that the algorithm converges when the size of does not change after the interval selected from the to the is merged with the previous.
After the algorithm converges, the interval boundary of each interval in is the anchor point. Finally, the selected feature variable intervals are sent to CARS for further variable screening.
As is shown in Fig. 1, before using CARS, the Monte Carlo method was used to divide the intervals, and then the intervals or interval combinations were selected with the lowest RMSE. At the same time, the selected intervals were recorded for each time, and then they were merged. The reason for using MC-siPLS is that the principle of interval partial least squares is to find one or several intervals with the most correlated variables and exclude intervals with a large number of uncorrelated variables as much as possible. At the same time, MC-siPLS divides intervals with unequal intervals through the MC method, and the combination of intervals with different sizes is more conducive to screening the intervals where the characteristic variables exist.
Fig. 1.
A simple flowchart of A-CARS method.
2.4. Estimation of model performance
In the experiments, RMSECV, R2c and bias were used to evaluate the calibration model. At the same time, root mean squared error of the prediction (RMSEP), R2p and bias were applied to evaluate the model performance of the tested model on the predict samples. The RMSE, R2, and the formula for the bias are as follows:
| (3) |
| (4) |
| (5) |
where and are the observed value and the predicted value, respectively. is the mean value of observations value; is the number of samples; is the number of samples from 1 to . The smaller the RMSE, the higher the prediction accuracy. R2 is also known as the coefficient of determination, and it is used to evaluate the ability of the model to predict. The closer R2 is to 1, the better the interpretation of the independent variable to the dependent variable in regression analysis.
2.5. Hardware and software
The experimental platform configuration is as follows: CPU E3-1230 V2 with 16G RAM, GPU: GTX1080, and all algorithms are run in MATLAB 2016b. PLS, MWPLS and siPLS algorithms can be found at the following URL: https://www.models.kvl.dk. Random Frog, CARS and GA-PLS come from the following URL https://www.libpls.net.
3. Results
3.1. Studies on model performance
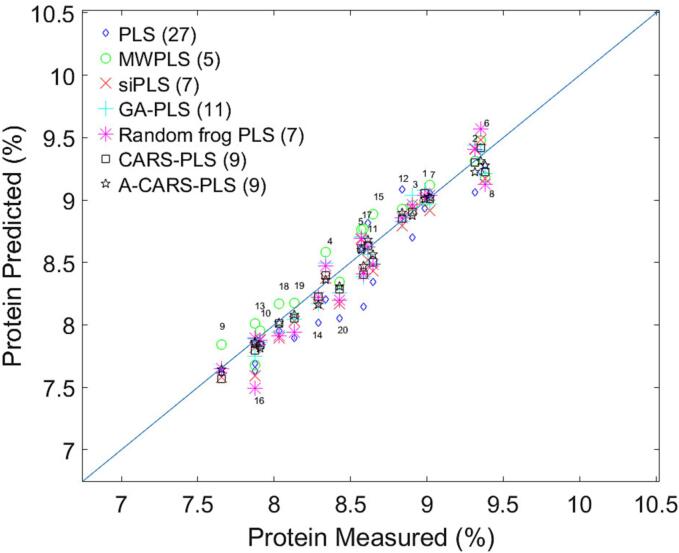
Table 1 shows the detailed results of seven different algorithms on the corn dataset. Overall, the partial least squares algorithm has the worst results and the result of A-CARS-PLS is the best among the seven algorithms. In the results of the interval partial least squares algorithm, the result of MWPLS is slightly better than that of siPLS. Among the results of the feature variable extraction algorithm, the result of A-CARS-PLS is the best, and the result of random frog is the worst. It is worth noting that the results of GA-PLS and Random frog-PLS in the test dataset are not as good as the interval partial least squares algorithms, but they are better than the interval partial least squares algorithm in the calibration dataset. This suggests that the two algorithms may be overfitting. The following will show more detailed results analysis and comparison.
Table 1.
Detailed results of seven different algorithms applied to the corn dataset.
| Method | selected variables | nVAR. | nLv. | Calibration |
Prediction |
||||
|---|---|---|---|---|---|---|---|---|---|
| RMSECV | R2c | Bias | RMSEP | R2p | Bias | ||||
| PLS | 1–700 | 700 | 27 | 0.0947 | 0.9808 | −0.0061 | 0.1307 | 0.9070 | −0.1290 |
| MWPLS | 535–555 | 21 | 5 | 0.0841 | 0.9846 | 0.0005 | 0.1402 | 0.9697 | 0.0619 |
| siPLS | 491–560 | 70 | 7 | 0.0588 | 0.9926 | −0.0012 | 0.1381 | 0.9615 | −0.0728 |
| GA-PLS | 47 57 321 441 486 493 511 515 524 525 528 529 530 532 536 537 539 543 549 553 554 561 594 610 | 24 | 11 | 0.0369 | 0.9941 | −0.001 | 0.1154 | 0.9493 | 0.0154 |
| Random frog-PLS | 518 534 535 529 531 532 536 520 546 528 | 10 | 7 | 0.0517 | 0.9885 | −0.001 | 0.1544 | 0.9093 | −0.044 |
| CARS-PLS | 298 340 341 342 344 346 385 513 515 518 519 530 532 558 | 14 | 9 | 0.0382 | 0.9937 | 0.001 | 0.0852 | 0.9724 | −0.0408 |
| A-CARS-PLS | 295 341 342 343 384 399 474 497 516 517 518 519 520 529 531 532 534 535 536 558 563 588 652 | 23 | 9 | 0.0336 | 0.9951 | −0.001 | 0.0688 | 0.9820 | −0.0350 |
3.2. Result of PLS
The PLS model was optimized by 5-fold cross-validation, and the best calibration model was determined by the lowest RMSECV. As could be seen from Table 1, the optimal number of PLS components was 27, and the result of the full-band PLS was the worst predicted result of all the algorithms with RMSECV = 0.0947, R2c = 0.9808 on the calibration set, and RMSEP = 0.1307, R2p = 0.9070 on the prediction set, respectively. The result of the prediction set was shown in the Fig. 4. From the prediction set results, it could be seen that there were some outliers, and the predicted results were less than expected. It is not difficult to infer that due to the wide spectral range, there are a large number of irrelevant and low-correlation variables, and the existence of these variables must affect the final model. Therefore, the interval selection method and variable selection method are used to eliminate irrelevant and poorly correlated variables to improve model accuracy and relevance.
Fig. 4.
The results of seven different PLS algorithm on the prediction set and the corresponding optimal number of PLS components.
3.3. Result of MWPLS and SiPLS
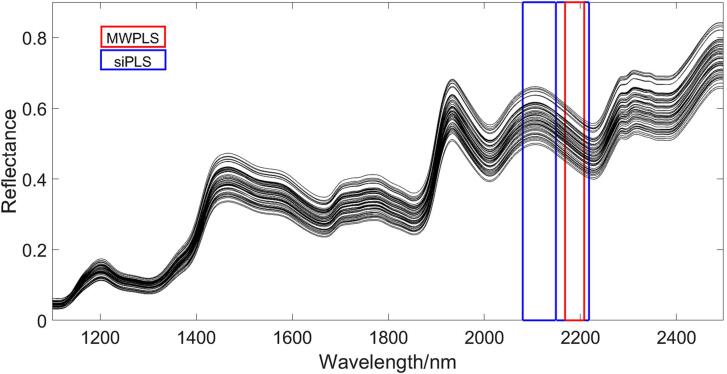
The size of the moving window in MWSPLS was 21; the number of sub-intervals was 20 and the combined intervals was 2 in siPLS, respectively. The result of siPLS was obtained by combining two subintervals, noted as RMSECV = 0.0588, R2c = 0.9926, RMSEP = 0.1381, and R2p = 0.9615. Meanwhile, MWPLS selected the interval between 2168 and 2208 nm, with RMSECV = 0.0841, R2c = 0.9846, RMSEP = 0.1402, and R2p = 0.9697.
The RMSE of siPLS was 0.0588, which was much smaller than the RMSE of MWPLS (0.0841) in the calibration dataset. But RMSEP and R2 of siPLS and MWPLS were very close on the prediction set. Compared with other feature variable extraction algorithms, their results were unsatisfactory, but they have been greatly improved compared to full-band PLS. RMSE of the full-band PLS on the prediction set was smaller than both, but R2 and bias of the full-band PLS were much worse than those of siPLS and MWPLS. Fig. 2 shows the intervals selected by siPLS and MWPLS. The red wireframe was the interval selected by MWPLS, and the blue wireframe was selected by siPLS. The area selected by siPLS covered the area selected by MWPLS completely. The results of siPLS show that there were characteristic variables between the variable numbers 491–560 corresponding spectral range 2080–2218 nm, and the results of MWPLS algorithm show that characteristic variables were located between the variable number 535–555 corresponding spectral range 2168–2208 nm. The reason for this situation lies in the difference in the principles of the two algorithms. The principle of siPLS is the combination of fixed-size intervals using the enumeration method. However, the feature of MWPLS is that the window it generates can move on the entire band. Compared with siPLS, the selection of windows is more diverse. But, due to the lack of a combination function, the variables selected by MWPLS are continuous variables in a single interval. Although the window can be moved freely, it is difficult for MWPLS to obtain an accurate model in spectral data with uneven distribution of characteristic variables. If the window is too large, it will cover more irrelevant variables, and if it is too small, it will lead to the incomplete selection of feature variables. In spite of the performance of MWPLS was not as good as siPLS, the result of MWPLS also has certain reference significance. It can tell us that in the current fixed-size interval, the interval with the most characteristic variables was located at 2168–2208 nm.
Fig. 2.
The selected intervals on the corn dataset by MWPLS and siPLS.
3.4. Result of RF-PLS and GA-PLS
On the corn dataset, the number of iterations of the random frog was 10000, and the number of variables selected was 2 at first. Finally, GA selected 24 feature variables, and the random frog gave the top ten variables with probability.
The results of GA-PLS were second only to A-CARS-PLS. However, the results were unsatisfactory on the prediction dataset, and the RMSEP and R2 were 0.1154 and 0.9493, respectively. At the same time, prediction results were quite different from the training results, which indicates that GA-PLS may produce a certain degree of overfitting. The reason why the Random Frog results were not good was that only the top 10 variables with the highest frequency in 10,000 iterations were selected. From the results, it can be found that the results of the calibration and prediction sets were very different, and they showed that GA-PLS and random frogs have different degrees of overfitting. It is worth noting that the correlation coefficient gap between the calibration set and the prediction set of the Random Frog algorithm is particularly obvious. This shows that it is unreasonable to choose 10 variables to replace the original 700 variables. The reason for the overfitting of the genetic algorithm is that the algorithm has a certain dependence on the selection of the initial population. At the same time, the setting of the crossover rate and mutation rate will also affect the result (Katoch et al., 2021). Although the results of the random frog were not very good, we could find that the variable numbers selected by the random frog were between 510 and 530 corresponding spectral range of 2110–2158 nm, which also confirmed that this interval contained some characteristic variables. The intervals were also overlapped with the interval selected by MWPLS and siPLS.
3.5. Result of CARS-PLS and A-CARS-PLS
The iterations of CARS and A-CARS were both 500. CARS-PLS generated RMSECV = 0.0382, R2c = 0.9937 in the calibration set; RMSEP = 0.0852, R2p = 0.9724 in the prediction set, and A-CARS generated RMSECV = 0.0336, R2c = 0.9951 in the calibration set; RMSEP = 0.0688, R2p = 0.9820 in the prediction set.
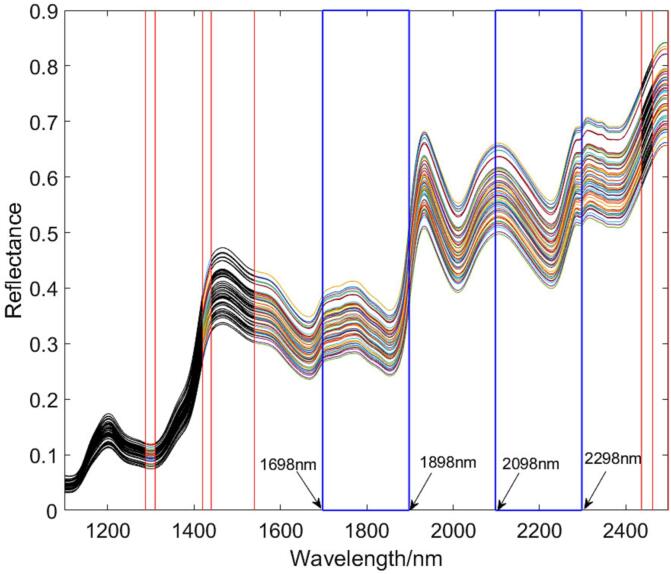
The red vertical line in Fig. 3 indicates the interval boundary after the interval converges, which is the anchor point. The colored intervals were the area where the characteristic variable exists. After that A-CARS screened characteristic wavelength on those intervals. The indexes of characteristic variable were mostly found at 300–400 and 500–560, which correspond to the spectral wavelengths 1698–1898 nm and 2098–2218 nm by CARS. At the same time, A-CARS selected the number of characteristic variables from 300 to 400 and 500–600, which correspond mostly to spectral wavelength 1698–1898 nm and 2098–2298 nm, respectively. A total of 23 variables were selected by A-CARS, and 14 feature variables were selected by CARS. It should be noted that CARS only selected 7 variables between 2098 and 2298 nm, and the variable data selected by the two algorithms between 300 and 400 nm was not very different. Notably, the 6 variables were selected at the same time, and they were 341, 342, 518, 519, 532, 558, respectively. This shows that these six variables had a high correlation with the model. From the results of the model, there is no doubt that A-CARS has the best performance on the calibration set and the prediction set at the same time. It was not difficult to find that the results of A-CARS and CARS on the calibration set were very close, but the results of A-CARS on the prediction set were better than those of CARS. This also proves from another aspect that A-CARS can effectively suppress overfitting while increasing the interpretability and correlation of the model.
Fig. 3.
The region where the characteristic variable exists.
The reason why A-CARS can effectively suppress overfitting is that its search space has been filtered by MC-siPLS. It is not difficult to find from Fig. 1 that MC-siPLS will merge the interval with the best result in a single iteration every time. After a certain number of iterations, the final feature interval size will not change. Through multiple cycles, MC-siPLS can help CARS narrow the search space to avoid the interference of irrelevant variables, and it can also improve the efficiency of feature variable screening.
4. Discussion
Overall, the prediction results of GA-PLS, CARS-PLS, and A-CARS-PLS were significantly better than those of full-band PLS and iPLS. This shows that the band extraction algorithm was efficient and meaningful. Fig. 4 shows the results of seven different algorithms on the prediction set, in which the optimal number of PLS components is in parentheses. The small font numbers in the figure are the sample number of the prediction set. It can be seen from the prediction results that the results of MWPLS and PLS are not very good and are far from the diagonal. The results of PLS in the prediction set are generally too small, and the results of MWPLS are generally too large. The squares and stars in the figure represent the results of A-CARS-PLS and CARS-PLS, respectively. The prediction results of A-CARS-PLS and CARS-PLS are closest to the diagonal line, which shows that the predicted values are close to the measured values. Combined with the deviation values in Table 1, the deviation values of the seven algorithms on the calibration set are not much different, and the corresponding R2 differences are not large, which shows that the calibration set model has a strong correlation. But the R2 gap is large on the prediction set. The deviation of the PLS algorithm comes to −0.1290, and R2 is also the worst among all algorithms. The situation of Random frog-PLS is similar to that of PLS. The prediction set results are quite different from the calibration set results, and the model correlation is far worse than other algorithms. Compared with other algorithms, the results of the A-CARS-PLS on the prediction set are closer to the calibration set, and it shows that the correlation of the A-CARS-PLS model is strong, but the prediction result is slightly smaller. It shows that the model has a strong correlation, but considering the deviation value, it can be concluded that the overall prediction result is small.
From the interval of the selected variables, except for the full-band PLS, the intervals or variables selected by other algorithms were located between 500 and 600. A-CARS and CARS selected several additional variables between 300 and 400. Due to the selection of variables between 300 and 400, the results of CARS and A-CARS are much better than other algorithms. The reason why siPLS and MWPLS did not select the variables interval between 300 and 400 may be that the calculation unit of these two algorithms is interval, and therefore they selected one or more intervals with a large number of characteristic variables. However, in the interval of 300–400, the number of irrelevant variables may be much larger than the relevant variables, so siPLS and MWPLS did not select the intervals between 300 and 400.
From the above model results and analysis, it is not difficult to conclude that the characteristic variable selected by A-CARS is the best regression variable with the 23 wavelengths (1688 nm, 1780 nm, 1782 nm, 1784 nm, 1866 nm, 1896 nm, 2046 nm, 2092 nm, 2130 nm, 2132 nm, 2134 nm, 2136 nm, 2138 nm, 2156 nm, 2160 nm, 2162 nm, 2166 nm, 2168 nm, 2170 nm, 2214 nm, 2224 nm, 2274 nm, and 2402 nm). Based on 23 feature wavelengths, a linear protein content percentage formula can be established:
| (6) |
Furthermore, the wavelengths selected by A-CARS were concentrated around 1700–1900 nm and 2000–2400 nm. This region is consistent with complex structural features of proteins, such as the bending or stretching of C—H, O—H, and N—H bonds as well as complex environments and their interactions. The characteristic wavelengths of protein in corn have been investigated in previous research (Li et al., 2009). Compared with the observations of Li etal., the results of the prediction set and the calibration set of A-CARS were better than the former. At the same time, this paper not only reduced the 700-dimensional full spectrum to 23 characteristic wavelengths but also gave the complete regression equation. Equation (6) shows the relationship between the percentage of corn protein content and the corresponding characteristic wavelengths. The A-CARS algorithm makes the linear formula for the determination of corn protein content simpler, which brings great convenience to the determination of protein content in corn.
The A-CARS algorithm takes into account the reliability and accuracy of the model and greatly reduces the number of variables. We believe that if portable near-infrared equipment can be combined with this technology in the future, large-scale non-destructive detection can be performed more quickly and accurately. At the same time, the cost of testing will be greatly reduced due to fewer variables, which can be done using embedded devices.
5. Conclusions
In order to determine the protein content in corn quickly and accurately, a new wavelength selection algorithm, called A-CARS, based on CARS and MC-siPLS was proposed. A-CARS selected 23-dimensional characteristic variables from a 700-dimensional full spectrum on the corn dataset. At the same time, A-CARS-PLS was compared with six algorithms including PLS, siPLS MWPLS, GA-PLS, random frog PLS, and CARS-PLS. The results show that A-CARS had good robustness and accuracy, and it can effectively extract feature variables and prevent overfitting. Furthermore, we built an accurate model for the prediction of protein content in corn via near-infrared spectroscopy and A-CARS, with the results: RMSECV = 0.0336, R2c = 0.9951 in the calibration set; RMSEP = 0.0688, R2p = 0.9820 in the prediction set. Furthermore, we also give a detailed linear regression equation for the prediction of corn protein content based on the 23 characteristic wavelengths. A-CARS-PLS proposed in this paper can be combined with portable near-infrared equipment for faster and more accurate large-scale nondestructive detection. At the same time, the reduction in the number of variables can effectively reduce the detection cost.
CRediT authorship contribution statement
Xiaohong Wu: Conceptualization, Methodology, Project administration, Supervision, Writing – review & editing. Shupeng Zeng: Investigation, Methodology, Software, Writing – original draft. Haijun Fu: Investigation, Supervision, Writing – review & editing. Bin Wu: Funding acquisition, Resources, Visualization, Software. Haoxiang Zhou: Conceptualization, Methodology, Validation, Supervision. Chunxia Dai: Validation, Formal analysis, Visualization, Data curation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research was funded by Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), the Undergraduate Scientific Research Project of Jiangsu University (20AB0011), the Major Natural Science Research Projects of Colleges and Universities in Anhui Province (2022AH040333), the Talent Program of Chuzhou Polytechnic (YG2019026 and YG2019024) and Key Science Research Project of Chuzhou Polytechnic (YJZ-2020-12).
Contributor Information
Xiaohong Wu, Email: wxh419@ujs.edu.cn.
Haoxiang Zhou, Email: zhx05150515@163.com.
Data availability
This data can be found here: https://www.eigenvector.com/data/Corn/index.html.
References
- Basile T., Marsico A.D., Perniola R. Use of artificial neural networks and NIR spectroscopy for non-destructive grape texture prediction. Foods. 2022;11(3):281. doi: 10.3390/foods11030281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai W., Li Y., Shao X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemometrics and Intelligent Laboratory Systems. 2008;90(2):188–194. [Google Scholar]
- Deng B.C., Yun Y.H., Liang Y.Z., Yi L.Z. A novel variable selection approach that iteratively optimizes variable space using weighted binary matrix sampling. Analyst. 2014;139(19):4836–4845. doi: 10.1039/c4an00730a. [DOI] [PubMed] [Google Scholar]
- Deng B.C., Yun Y.H., Cao D.S., Yin Y.L., Wang W.T., Lu H.M., Luo Q.Y., Liang Y.Z. A bootstrapping soft shrinkage approach for variable selection in chemical modeling. Analytica Chimica Acta. 2016;908:63–74. doi: 10.1016/j.aca.2016.01.001. [DOI] [PubMed] [Google Scholar]
- Dorigo M., Birattari M., Stutzle T. Ant colony optimization. IEEE Computational Intelligence Magazine. 2006;1(4):28–39. [Google Scholar]
- Galindo-Prieto B., Eriksson L., Trygg J. Variable influence on projection (VIP) for OPLS models and its applicability in multivariate time series analysis. Chemometrics and Intelligent Laboratory Systems. 2015;146:297–304. [Google Scholar]
- Guo Z.M., Barimah A.O., Shujat A., Zhang Z.Z., Ouyang Q., Shi J.Y., Hesham R.E.S., Zou X.B., Chen Q. Simultaneous quantification of active constituents and antioxidant capability of green tea using NIR spectroscopy coupled with swarm intelligence algorithm. LWT-Food Science and Technology. 2020;129 [Google Scholar]
- Han Q.J., Wu H.L., Cai C.B., Xu L., Yu R.Q. An ensemble of Monte Carlo uninformative variable elimination for wavelength selection. Analytica Chimica Acta. 2008;612(2):121–125. doi: 10.1016/j.aca.2008.02.032. [DOI] [PubMed] [Google Scholar]
- Hulland J. Use of partial least squares (PLS) in strategic management research: A review of four recent studies. Strategic Management Journal. 1999;20(2):195–204. [Google Scholar]
- Katoch S., Chauhan S.S., Kumar V. A review on genetic algorithm: Past, present, and future. Multimedia Tools and Applications. 2021;80:8091–8126. doi: 10.1007/s11042-020-10139-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan W., Jaillais B., Leca A., Renard C.M., Bureau S. A new application of NIR spectroscopy to describe and predict purees quality from the non-destructive apple measurements. Food chemistry. 2020;310 doi: 10.1016/j.foodchem.2019.125944. [DOI] [PubMed] [Google Scholar]
- Li H., Liang Y., Xu Q., Cao D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Analytica Chimica Acta. 2009;648(1):77–84. doi: 10.1016/j.aca.2009.06.046. [DOI] [PubMed] [Google Scholar]
- Li H.D., Liang Y.Z., Xu Q.S., Cao D.S., Tan B.B., Deng B.C., Lin C.C. Recipe for uncovering predictive genes using support vector machines based on model population analysis. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2011;8(6):1633–1641. doi: 10.1109/TCBB.2011.36. [DOI] [PubMed] [Google Scholar]
- Li H.D., Xu Q.S., Liang Y.Z. Random frog: An efficient reversible jump Markov Chain Monte Carlo-like approach for variable selection with applications to gene selection and disease classification. Analytica Chimica Acta. 2012;740:20–26. doi: 10.1016/j.aca.2012.06.031. [DOI] [PubMed] [Google Scholar]
- Li Y., Yang K., Wu B., Zhang J., Han Q., Gao W. Non-destructive study on identifying and monitoring of Cu-Pb pollution in corn based on near-infrared spectroscopy. Environmental Science and Pollution Research. 2023;30:14155–14164. doi: 10.1007/s11356-022-23206-2. [DOI] [PubMed] [Google Scholar]
- Liu C., Huang W., Yang G., Wang Q., Li J., Chen L. Determination of starch content in single kernel using near-infrared hyperspectral images from two sides of corn seeds. Infrared Physics & Technology. 2020;110 [Google Scholar]
- Morais C.L., Santos M.C., Lima K.M., Martin F.L. Improving data splitting for classification applications in spectrochemical analyses employing a random-mutation Kennard-Stone algorithm approach. Bioinformatics. 2019;35(24):5257–5263. doi: 10.1093/bioinformatics/btz421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nørgaard L., Hahn M.T., Knudsen L.B., Farhat I.A., Engelsen S.B. Multivariate near-infrared and Raman spectroscopic quantifications of the crystallinity of lactose in whey permeate powder. International dairy journal. 2005;15(12):1261–1270. [Google Scholar]
- Pereira A.F.C., Pontes M.J.C., Neto F.F.G., Santos S.R.B., Galvao R.K.H., Araujo M.C.U. NIR spectrometric determination of quality parameters in vegetable oils using iPLS and variable selection. Food Research International. 2008;41(4):341–348. [Google Scholar]
- Shapiro A. Monte Carlo sampling methods. Handbooks in operations research and management science. 2003;10:353–425. [Google Scholar]
- Shen S.Y., Li T., Liu R.H. Corn phytochemicals and their health benefits. Food Science and Human Wellness. 2018;7(3):185–195. [Google Scholar]
- Sun J., Yang W., Zhang M., Feng M., Xiao L., Ding G. Estimation of water content in corn leaves using hyperspectral data based on fractional order Savitzky-Golay derivation coupled with wavelength selection. Computers and Electronics in Agriculture. 2021;182 [Google Scholar]
- Wang Z.L., Chen J.X., Fan Y.F., Cheng Y.F., Wu X.L., Zhang J.W., Wang B.B., Wang X.C., Yong T.W., Liu W.G. Evaluating photosynthetic pigment contents of maize using UVE-PLS based on continuous wavelet transform. Computers and Electronics in Agriculture. 2020;169 [Google Scholar]
- Yang S., Li C., Mei Y., Liu W., Liu R., Chen W.…Xu K. Discrimination of corn variety using Terahertz spectroscopy combined with chemometrics methods. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. 2021;252 doi: 10.1016/j.saa.2021.119475. [DOI] [PubMed] [Google Scholar]
- Yun Y.H., Li H.D., Deng B.C., Cao D.S. An overview of variable selection methods in multivariate analysis of near-infrared spectra. TrAC Trends in Analytical Chemistry. 2019;113:102–115. [Google Scholar]
- Zeng S., Wu X., Wu B., Zhou H., Wang M. Rapid determination of cadmium residues in tomato leaves by Vis-NIR hyperspectral and Synergy interval PLS coupled Monte Carlo method. Food Science and Technology. 2023;43:e113422. [Google Scholar]
- Zhang M., Zhao C., Shao Q., Yang Z., Zhang X., Xu X., Hassan M. Determination of water content in corn stover silage using near-infrared spectroscopy. International Journal of Agricultural and Biological Engineering. 2019;12(6):143–148. [Google Scholar]
- Zhang J., Dai L., Cheng F. Classification of frozen corn seeds using hyperspectral VIS/NIR reflectance imaging. Molecules. 2019;24(1):149. doi: 10.3390/molecules24010149. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This data can be found here: https://www.eigenvector.com/data/Corn/index.html.