Abstract
Ground vibration due to blasting is identified as a challenging issue in mining and civil activities. Peak particle velocity (PPV) is one of the blasting undesirable consequences, which is resulted during emission of vibration in blasted bench. This study focuses on the PPV prediction in the surface mines. In this regard, two ensemble systems, i.e., the ensemble of artificial neural networks and the ensemble of extreme gradient boosting (EXGBoosts) were developed for PPV prediction in one of the largest lead–zinc open-pit mines in the Middle East. For ensemble modeling, several ANN and XGBoost base models were separately designed with different architectures. Then, the validation indices such as coefficient determination (R2), root mean square error (RMSE), mean absolute error (MAE), the variance accounted for (VAF), and Accuracy were used to evaluate the performance of the base models. The five top base models with high accuracy were selected to construct an ensemble model for each of the methods, i.e., ANNs and XGBoosts. To combine the outputs of the top base models and achieve a single result stacked generalization technique, was employed. Findings showed ensemble models increase the accuracy of PPV predicting in comparison with the best individual models. The EXGBoosts was superior method for predicting of the PPV, which obtained values of R2, RMSE, MAE, VAF, and Accuracy corresponding to the EXGBoosts were (0.990, 0.391, 0.257, 99.013(%), 98.216), and (0.968, 0.295, 0.427, 96.674(%), 96.059), for training and testing datasets, respectively. However, the sensitivity analysis indicated that the spacing (r = 0.917) and number of blast-holes (r = 0.839) had the highest and lowest impact on the PPV intensity, respectively.
Subject terms: Environmental sciences, Solid Earth sciences, Engineering
Introduction
Mining activities and civil projects are carried out using one of the most important operations, namely rock blasting, as a wide and economical way to rock breakage and displacement of them1. In this regard, the rock mass is drilled (drilling operations), and then many blast-holes are charged using explosive materials (blasting operations). Inevitably, blasting operations are caused several side environmental consequences/issues such as flyrock, back-break, dust pollution, air-overpressure, and ground vibration2–7. The blast-induced, air over-pressure, ground vibration, and flyrock are the most adverse phenomenon among them1,8,9. Therefore, the blasting sites and mine environment must be safe by monitoring and eliminating the adverse effects of the aforementioned consequences. It should be noted that the accurate amount of each phenomenon should be determined/predicted before conducting the operations. The pre-split and power-deck methods can be used to minimization adverse effects1.
Ground vibration is the most crucial side environment effect due to bench blasting based on previous investigations10,11. The effective parameters on ground vibration should be identified for its prediction/evaluation. The ground vibrations can be measured/recorded based on two different terms: peak particle velocity (PPV) and frequency12–15. According to various standards, the PPV is the most famous representative for estimating and evaluating blast-induced ground vibration in surface mines1,16,17. The most significant parameters on PPV are the number of blast-holes, hole depth, burden, spacing, powder factor, the charge per delay, and the distance between installed seismograph and blasting bench18–21.
In recent decades, many models have been introduced for PPV prediction in mines and open pits. The empirical models have been developed by Davis et al.22, Ambraseys and Hendron23, Dowding24, Roy25, and Rai and Singh26 for estimation of blast-induced PPV. However, the performance of empirical predictive models is weak and unacceptable. In addition, the empirical equations do not have the ability to accurately predict the PPV values while they must be accurately estimated to overcome the adverse effects. On the other hand, new computational techniques i.e., soft computing (SC) and artificial intelligence (AI) are capable to resolve science and engineering problems in terms of accuracy level27–30.
In the field of PPV, a vast range of SC/AI techniques have been proposed for prediction purposes7,31–35. For example, Hasanipanah et al.35 predicted the PPV values using a genetic algorithm. They concluded that this optimization algorithm can predict PPV values with high accuracy. Imperialist competitive algorithm (ICA) as another optimization algorithm was employed to estimate the value of PPV in the research conducted by Armaghani et al.6. They concluded that the ICA algorithm is capable for PPV prediction with high performance. In another study, Taheri et al.36 combined artificial neural network (ANN) and artificial bee colony (ABC) to the prediction of PPV; then results were compared to empirical equations. Their results indicated that the performance of the ANN-ABC model is higher than empirical models. Fuzzy system (FS) combined with ICA was introduced in the study conducted by Hasanipanah et al.13 to predict PPV. The results of their hybrid model showed that FS-ICA can forecast PPV with a high level of accuracy. Fouladgar et al.37 used the cuckoo search (CS) as a novel swarm intelligence algorithm for PPV prediction induced by mine blasting. Additionally, Hasanipanah et al.38 established a particle swarm optimization (PSO) technique for forecasting PPV values. In other studies, different techniques such as adaptive neuro-fuzzy inference system (ANFIS) were developed by Iphar et al.39 for the estimation of PPV with an acceptable degree of prediction performance. Table 1 summarises the most important studies related to PPV estimation by utilizing the AI and SC techniques.
Table 1.
Literature review of PPV estimation using AI and SC methods.
| References | Year | Model | Inputs | Model performance (R2) |
|---|---|---|---|---|
| Singh et al.40 | 2005 | ANN | D, N, HD, B, S, ST, MC, HDI, RDI | 0.82 |
| Iphar et al.39 | 2007 | ANFIS | DI, CD | 0.99 |
| Monjezi et al.41 | 2011 | ANN | CD, DI, ST, HD | 0.95 |
| Mohamed42 | 2011 | ANN, FIS | DI, MC |
ANN = 0.94 FIS = 0.90 |
| Khandelwal et al.43 | 2011 | ANN | DI, MC | 0.92 |
| Fişne et al.44 | 2011 | FIS | DI, MC | 0.92 |
| Mohamadnejad et al.11 | 2012 | SVM, ANN | DI, MC |
SVM = 0.89 ANN = 0.85 |
| Ghasemi et al.45 | 2013 | FIS | B, S, ST, N, MC, DI | 0.95 |
| Masoud et al.46 | 2013 | ANN | MC, DI, TC | 0.93 |
| Armaghani et al.47 | 2014 | PSO-ANN | S, B, ST, PF, MC, D, N, RD, SD | 0.94 |
| Hajihassani et al.20 | 2015 | ICA-ANN | BS, ST, PF, MC, DI, Vp, E | 0.98 |
| Dindarloo48 | 2015 | SVM | RD, E, UCS, TS, Js, B, S, HD/B, SC, ST, DPR, DI | 0.99 |
| Hajihassani et al.49 | 2015 | PSO-ANN | BS, MC, HD, ST, SD, DI, PF, RQD | 0.89 |
| Hasanipanah et al.50 | 2015 | SVM | DI, MC | 0.96 |
| Armaghani et al.51 | 2015 | ANFIS | DI, MC | 0.97 |
| Ghoraba et al.52 | 2016 | ANN, ANFIS | DI, MC |
ANFIS = 0.95 ANN = 0.89 |
| Faradonbeh et al.10 | 2016 | GEP | B, S, ST, D, HD, PF, MC, DI | 0.88 |
| Hasanipanah et al.53 | 2017 | CART | DI, MC | 0.95 |
| Shahnazar et al.54 | 2017 | PSO-ANFIS | DI, MC | 0.98 |
| Armaghani et al.6 | 2018 | ICA | DI, MC | 0.95 |
| Nguyen et al.55 | 2019 | HKM-CA | DI, MC, PF, B, S, HD | 0.99 |
| Nguyen et al.56 | 2020 | SVR-GA | DI, MC, B, S, N | 0.99 |
| Zhang et al.57 | 2020 | RF,CART,CHAID | B/S, DI, ST, MC, PF, HD |
RF = 0.94 CART = 0.97 CHAID = 0.91 |
| Zhou et al.58 | 2020 | RF | DI, ST, MC, PF, HD | 0.93 |
| Huang et al.21 | 2020 | FA-ANN | B/S, DI, ST, MC, PF, HD, RQD, N, SD | 0.91 |
| Zhou et al.12 | 2021 | GEP-MC | B/S, DI, ST, MC, PF, HD | 0.91 |
| Lawal et al.59 | 2021 | ANN-MFO | DI, MC, N, HD, RMR | 0.97 |
| He et al.60 | 2022 | RF-WOA | B/S, DI, ST, MC, PF, HD | 0.99 |
| Ragam et al.61 | 2022 | XGBoost-RF | N, B, S, HD, D, HD, ST, MC, DI | 0.95 |
| Nguyen et al.62 | 2023 | SSO-ELM | B, S, PF, MC, f | 0.91 |
B Burden, S Spacing, HL Hole length, ST Stemming, PF Powder factor, B Blastability index, SVM Support vector machine, MC Maximum charge per delay, RD Rock density, D Hole diameter, HD Hole depth, BS Burden to spacing, N Number of row, PSO Particle swarm optimization, SD Sub-drilling, DI Distance from the blast face, TC Total charge, RQD Rock quality designation, E Young’s modulus, ICA Imperialist competitive algorithm, Vp p-wave velocity, ANFIS Adaptive neuro-fuzzy inference system, FIS Fuzzy inference system, R2 Coefficient of determination, UCS Uniaxial compression strength, TS Tensile strength, Js Joint spacing, HD/B Hole depth-to-burden ratio, SC Specific charge, DPR Delay per row, GEP Gene expression programming, RMR Rock mass rating, f Rock hardness, CART Classification and regression tree, CHIAD Chi-square automatic interaction detection, RF Random forest, HKM K-means clustering, FA Firefly algorithm, WOA Whale optimization algorithm, XGBoost Extreme gradient boosting, SSO Sparrow search optimization, ELM Extreme learning machine.
An overview of the literature demonstrated that various SC/AI models have been established to estimate the PPV values. Nevertheless, scholars are always looking for models with the highest performance to enhance the accuracy of developed predictive models and decrease the adverse effect of PPV on the environment. Hence, in this study, to increase the accuracy and performance of AI models in the estimation of PPV, an ensemble of XGBoost as well as ANN models are proposed. According to certain research, no machine learning algorithm could ever consistently outperform every other algorithm. In reaction to this assertion, the ensemble learning method was created. Contrary to traditional machine learning approaches, which try to learning a single hypothesis from train dataset, ensemble learning algorithms develop numerous hypotheses and integrate them to solve a specific issue. Ensemble algorithms have resulted in significant improvements and minimized the overfitting issue by integrating numerous learners and fully using these learners. They also offer the flexibility to handle various jobs. Three well-known ensemble approaches include bagging, boosting, and stacking, while there are a few variations and more ensemble algorithms that have been put to use in real-world scenarios63. In this way, several publications analysed the performance capability of ensemble models in the various fields such as health science64, sport science65, agriculture66,67, finance68, wireless sensor network (WSN)69 and geosciences70.
The combination of multiple networks and creating an ensemble system can reduce the risk of incorrect results and potentially improve the accuracy and generalization capability. Indeed, an ensemble technique is a robust machine learning method that combines several learners, e.g., ANNs or any other machine learning methods, to improve overall prediction accuracy. In most cases, an ensemble of machine learning methods in comparison to a single learner gives better results70–72. This study will introduce a new viewpoint of ensemble modeling to estimate PPV based on two machine learning methods, i.e., XGBoost and ANN models as a stacked generalization technique. For comparison purposes, the performance of the ANNs ensemble method is compared to the XGBoost ensemble method. The more accurate model in forecasting blast-produced PPV will be selected based on the statistical results of all proposed models.
The main research questions are presented as follows:
How to increase the accuracy of predictive models?
How is the accuracy level of the model evaluated?
How is the performance of the proposed model compared to the literature?
How to measure the validity of the model?
How is output parameter performance measured against input parameters?
Case study and data preparation
This study was focused on the Anguran lead–zinc open-pit mine (Iran), which is located at between longitudes 47° 23′ 27″ N and 47° 25′ 50″ N, and between latitudes 36° 36′ 37″ N and 36° 38′ 04″ N. In addition, the altitude of this mine reported about 2935 m above sea level. Anguran is one of the largest mines in the Middle East (Fig. 1), which is operated with an annual 1.2 Mt extraction rate.
Figure 1.
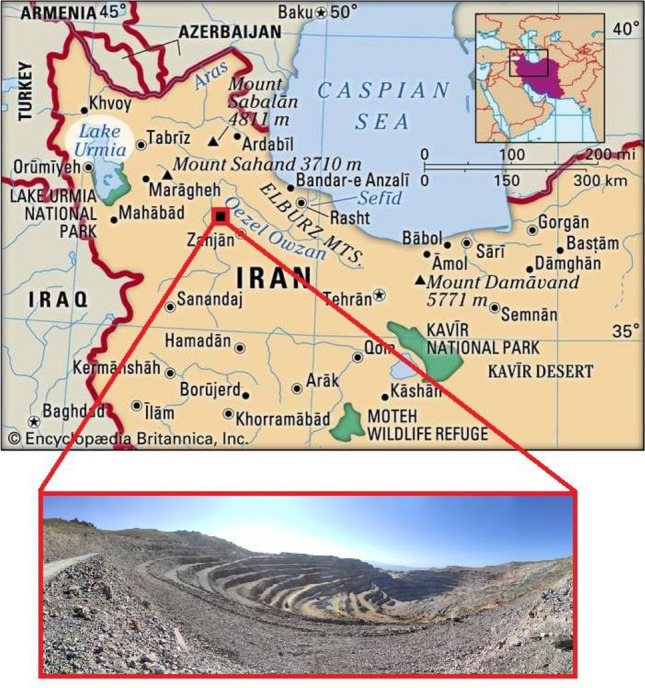
Location of Anguran lead–zinc mine and designed pit73 (this figure is modified by EdrawMax, version 12.0.7, www.edrawsoft.com).
The previous studies considered the blast design parameters as effective parameters on PPV intensity. In this study, we considered the seven blasting pattern design parameters which are used as models’ inputs. These parameters include the number of blast-holes (n), hole depth (ld), burden (B), spacing (S), powder factor (q), the charge per delay (Q), and the distance between installed seismograph and blasting bench (d). A total number of 162 blasting rounds were monitored and the effective parameters were measured during operations. The descriptive statistics of the aforementioned parameters are tabulated in Table 2. In the Anguran mine, initiation sequence is inter-row with the time delay of 9 to 23 ms.
Table 2.
The properties of the parameters and their ranges.
| Parameter | Sign | Unit | Minimum | Maximum | Mean | Standard deviation |
|---|---|---|---|---|---|---|
| Inputs | ||||||
| Number of blast-holes | n | – | 10 | 323 | 77.28 | 45.05 |
| Hole depth | ld | m | 2 | 12 | 9.95 | 2.65 |
| Burden | B | m | 3 | 4.2 | 4.02 | 0.33 |
| Spacing | S | m | 3.5 | 6 | 4.85 | 0.31 |
| Powder factor | q | Kg/m3 | 0.06 | 0.75 | 0.35 | 0.11 |
| Charge per delay | Q | Kg | 43.06 | 697.72 | 187.43 | 88.83 |
| Distance | d | m | 305 | 1167 | 741.22 | 248.32 |
| Output | ||||||
| Peak particle velocity | PPV | mm/s | 1.25 | 28.15 | 15.08 | 4.35 |
The significant relationships between effective parameters and PPV were determined using Pearson cross-correlation. The Pearson test measured the linear correlation of bivariable. The Pearson correlation between parameters and PPV is demonstrated in Table 3, in which the values are calculated in the range of − 1 to + 1. The positive and negative values indicated the positive and negative dependence degree, respectively. Besides, the value of 0 denoted no correlation between the two parameters74.
Table 3.
Pearson’s correlation matrix of parameters and PPV.

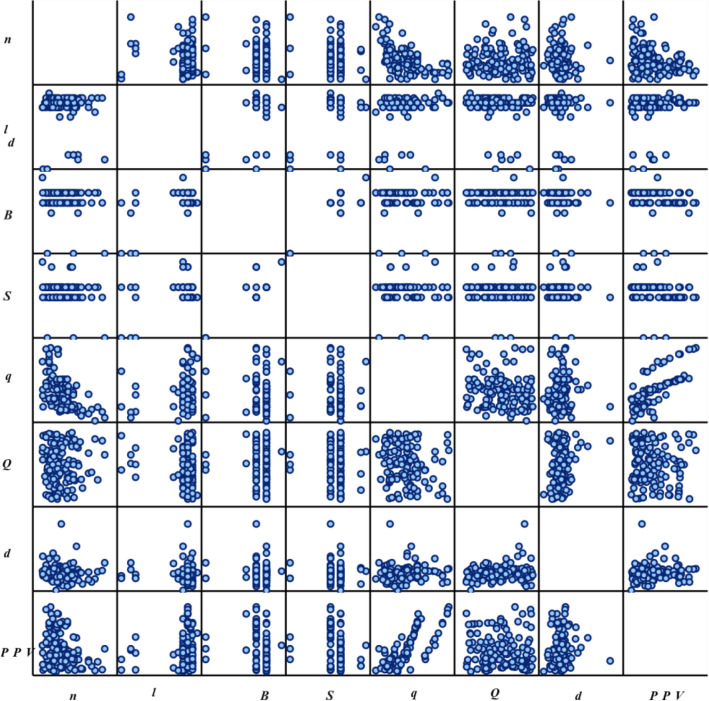
As can be found, the correlation between PPV and PF is high and positive; while PPV and Di have a low and negative correlation. The matrix plot of all parameters is shown in Fig. 2.
Figure 2.
Scatter matrix plot of all parameters considered in this study.
Method background
Artificial neural network (ANN)
ANN is one of the AI techniques, which first presented in the 1970s. The application of ANN has penetrated various fields of science75. A model of ANN is designed based on activities of artificial neural of the human brain. The architecture of an ANN is constructed using the input layer, hidden layer(s), and output layer76. Noteworthy, each layer includes many nodes (neurons) which are linked to each other by the weight of the processing components (connections). Input signals, which are the same as input data, are propagated throughout the network using input neurons. Then, input signals pass through the hidden layer(s) and access the output layer. In other words, some calculations are performed during passing signals in each layer and then delivered to the subsequent layer77–79. These calculations are formulated in Eq. (1) which simulated the training process of the network80
| 1 |
where f denotes activation function, w is the weight of connections, b indicates bias, and x is input data. Notably, the monolayer architecture of the neural network is suitable for simple problems, as well multi-layer architecture is used for complex problems81. However, an ANN architecture with two hidden layers for solving engineering problems is usually efficient75.
Extreme gradient boosting (XGBoost)
XGBoost is one of the applicable artificial intelligence techniques, which is firstly introduced by Chen et al.82 in 2015. XGBoost, as an AI method, is developed based on the gradient boosting decision. The most important characteristic of this method is creating boosted trees effectively and generating them in parallel. Besides, XGBoost deals with well-known classification and regression problems e.g., Bhattacharya et al.83, Duan et al.75, Nguyen et al.84, Ren et al.85, and Zhang and Zhan86. In XGBoost, gradient boosting (GB) creates a status under which an objective function (OF) is determined. The optimization of the value of OF is the core of the XGBoost algorithm, which operating to each various optimization technique. Overcoming the problems of data science has made it a robust algorithm. In XGBoost, parallel tree boosting of GB decision tree and GB machine can accurately solve many problems75,84. Training loss (L) and regularization (Ω) are the two main components of an OF in this algorithm that defined as follows:
| 2 |
The model performance related to training data is measured using training loss. Notably, the control and overcome overfitting problem as a model complexity is performed by the regularization term. In this regard, the complexity associated with each tree is calculated in several ways; nevertheless, the following formula is widely used to determine the complexity:
| 3 |
where n indicates the number of leaves and denotes the vector of scores on leaves. In XGBoost, the structure score is the OF represented as:
| 4 |
| 5 |
where q is the best for a presented structure (a quadratic form). Noteworthy, the is an independent vector.
Ensemble modeling
The ensemble of multiple individual learners (base models) is a robust way to enhance the performance and accuracy of artificial intelligence predictive models. In other words, the ensemble model deals with the combination of various models with different results87. In general, ensemble modeling includes two components, i.e., an ensemble of base models and a combiner. Training several base models/networks by different subsets of the training data, and employing the different architectures for each of the base models are two common techniques to build the base models71, which in current work later method for constructing the base models are used. Also, to the combination of base models, different strategies are proposed where all attempt to reduce the error of estimation.
Generally, combiners are divided into two main groups, i.e., trainable and non-trainable methods. For the combination of the outputs of the base models to achieve a single solution two non-trainable methods, i.e., majority voting and averaging methods, are widely used by scholars, e.g., Barzegar and Asghari Moghaddam88, Dogan and Birant89, and Krogh and Vedelsby90. As such, the mixture of experts and stacked generalization are two trainable combiners that are successfully used in different studies, e.g., Alizadeh et al.70, Jacobs et al.91, and Wolpert92. The trainable combination methods are trained by outputs of base models and expected correct results to predict the final results. The trainable combiners for predicting models that there are complex relations between inputs and targets are more efficient.
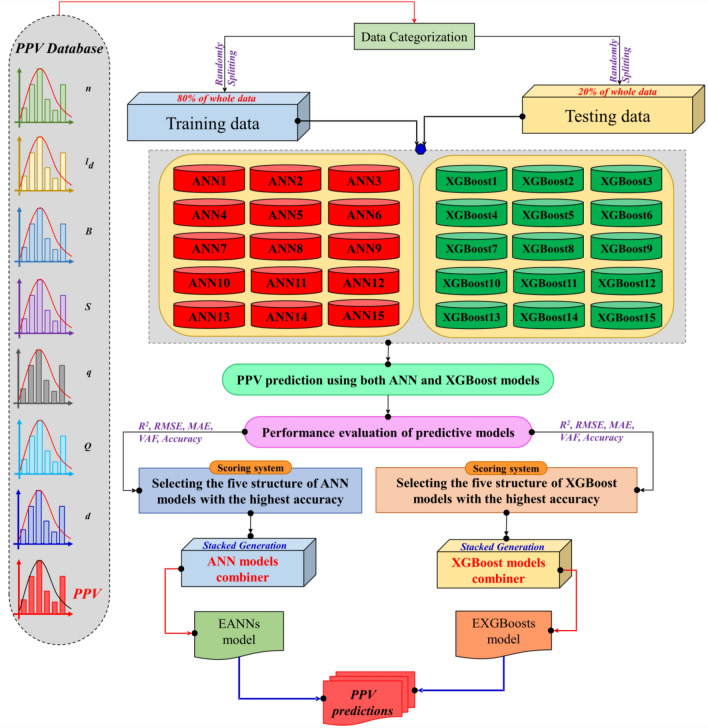
In this study, for each of the methods, i.e., XGBoost and ANN, several models to predict the PPV by stacked generalization technique were combined. In this regard, some ANNs models with a different number of hidden nodes, various activation functions, and different training algorithms for predicting PPV were used. Then top ANNs architectures were combined by the stacked generalization methods to construct the ensemble ANNs that named EANNS model. Notably, various XGBoost models as individual models are developed with different nrounds and different maximum depth for PPV estimation, and then top XGBoost models were combined by the stacked generalization technique, which this newly constructed model is called ensemble XGBoosts (EXGBoosts) model. Figure 3 represents the framework of EANNs and EXGBoosts methods, respectively.
Figure 3.
A schematic representation of EANNs and EXGBoosts methods for predicting PPV.
Stacking ensemble model
The stacking model basis is divided into two main phases, which are referred to as level-0 and level-1 structures, respectively. Base models are referred to as level-0, whereas the meta model at level-1 allows base-model predictions to be combined. Estimates provided by base-models are employed throughout the meta-training model's phase. In the case of regression or classification, the predictions result of the basic-models are utilized as inputs and can be of genuine use to the meta-model69. The methods of ANN and XGBoost are employed as the base-models in our research. Noteworthy, these models' several separately architectures are each employed individually as meta-learners.
Pre-analysis of modeling process
This study develops EXGBoosts and EANNs models with seven effective variables and only one output variable to estimate PPV in Anguran lead–zinc mine. In the first step of modeling, all data were normalized in the interval of [0,1], for better network training. Equation (6) was used for normalization of data:
| 6 |
where xnorm denotes normalized value, xmax and xmin are the maximum and minimum values, and xi indicates the input value. In the second step, to present the PPV predictive models, the collected data from the blasting site is randomly divided into two parts, i.e., training and testing datasets. In this regard, 80% of the whole data, namely approximately 130 blasting events, were specified randomly to the training part of models. While the remaining data (approximately 32 blasting events) were used for evaluation of the models' performance.
In the third step, several base models are developed for PPV estimation and the performance of models is compared and evaluated using several statistical indicators such as coefficient determination (R2), root mean square error (RMSE), mean absolute error (MAE), the variance accounted for (VAF), and Accuracy (Eqs.7 to 11). These indices are calculated to evaluate the relationship between measured PPV values and estimated one by developed models.
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
where Oi, Pi, and are measured value, predicted value, and the average of the predicted values, respectively. Also, n indicates the number of datasets. However, the value of R2, RMSE, MAE, VAF, and Accuracy for the most accurate system are one, zero, zero, 100, and 100, respectively.
PPV predictive models
ANN model
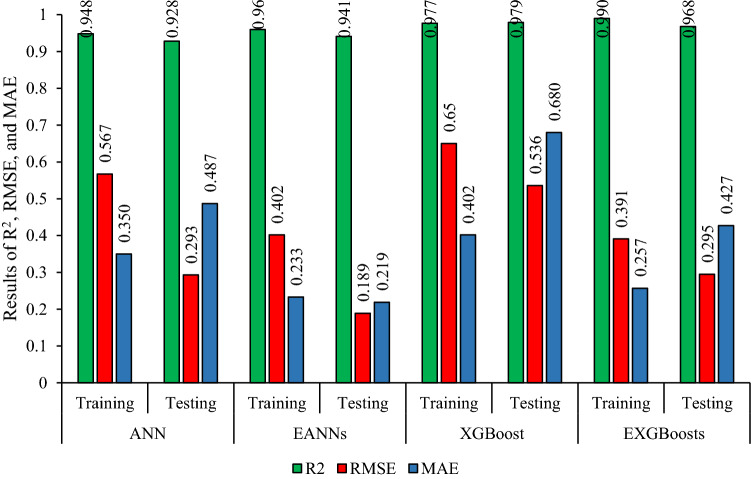
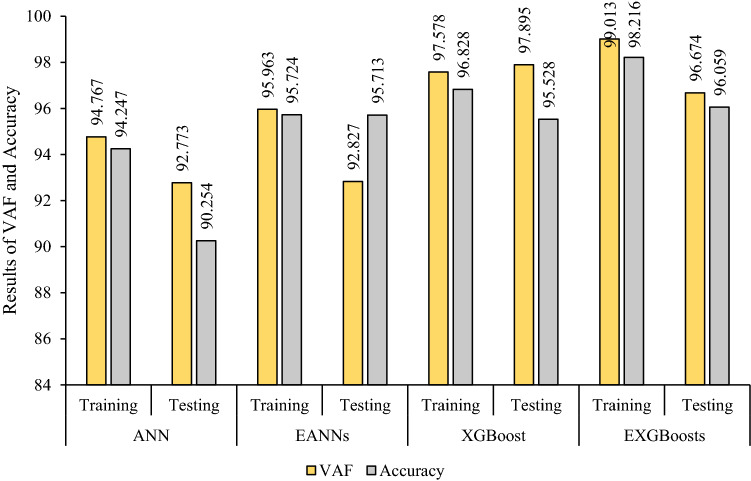
In the present study, for PPV prediction in a surface mine the multi-layer perceptron (MLP) artificial neural network as the most popular structure of ANN was used. The MLP structure contains at least one hidden layer. Hence, the determination of the training algorithm, number of hidden nodes, and hidden layers is a challenge in MLP modeling. In other words, the MLP structure must be designed to train optimally. The feedforward-backpropagation algorithm was used for MLP structure training. In addition, the “trial-and-error” procedure was employed to achieve an MLP model with an optimal structure to predict accurately PPV value. Therefore, 15 different MLP models as base models were developed (Table 4). As can be found, each of the models was trained with different training algorithms, hidden activation functions, output activation functions, and architectures. To determine the optimal architecture, the validation indices of R2, RMSE, Accuracy, MAE, and VAF that were formulated in Eqs. (7) to (11) were separately calculated for ANN training and testing datasets. Remarkably, the scoring system proposed by Zorlu et al.93 was applied to calculate the rate of each indices for MLP developed models. Table 5 shows the rating indices and ranking of MLP models. Based on results, base model number three with two hidden layers, “tansig” as hidden and output activation functions, and Levenberg–Marquardt (LM) training algorithm is the best base model for PPV prediction. This base model had the 141 total rates out of 150, that the values of (0.948, 0.567, 0.350, 94.767, 94.247) and (0.928, 0.293, 0.487, 92.773, 90.254) are obtained for R2, RMSE, MAE, VAF, and Accuracy of training and testing datasets, respectively.
Table 4.
The base models of ANN and their evaluations.
| ANN models | Training algorithm | Number of total hidden nodes | Hidden activation function | Output activation function | Architecture | Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | VAF | Accuracy | R2 | RMSE | MAE | VAF | Accuracy | ||||||
| ANN1 | TrainSCG | 4 | Tansig | Tansig | 7-4-1 | 0.934 | 0.660 | 0.428 | 93.415 | 91.471 | 0.724 | 1.193 | 0.724 | 68.725 | 87.644 |
| ANN2 | TrainSCG | 7 | Logsig | Tansig | 7-7-1 | 0.937 | 0.693 | 0.283 | 93.100 | 94.829 | 0.643 | 1.459 | 0.756 | 57.458 | 85.260 |
| ANN3 | TrainLM | 10 | Tansig | Tansig | 7-4-6-1 | 0.948 | 0.567 | 0.350 | 94.767 | 94.247 | 0.928 | 0.293 | 0.487 | 92.773 | 90.254 |
| ANN4 | TrainLM | 12 | Purelin | Tansig | 7-5-7-1 | 0.883 | 0.864 | 0.535 | 87.290 | 89.503 | 0.802 | 1.395 | 0.820 | 77.386 | 85.371 |
| ANN5 | TrainOSS | 13 | Logsig | Logsig | 7-5-8-1 | 0.932 | 0.672 | 0.411 | 93.213 | 91.816 | 0.850 | 0.492 | 0.508 | 84.935 | 90.061 |
| ANN6 | TrainGDX | 14 | Tansig | Logsig | 7-7-7-1 | 0.939 | 0.684 | 0.483 | 93.774 | 91.529 | 0.906 | 0.754 | 0.666 | 89.952 | 87.247 |
| ANN7 | TrainLM | 16 | Logsig | Logsig | 7-7-9-1 | 0.930 | 0.643 | 0.332 | 92.783 | 94.510 | 0.924 | 0.589 | 0.360 | 96.392 | 90.164 |
| ANN8 | TrainGDX | 14 | Purelin | Purelin | 7-9-5-1 | 0.906 | 0.799 | 0.499 | 90.543 | 91.588 | 0.841 | 0.850 | 0.622 | 83.640 | 87.034 |
| ANN9 | TrainSCG | 17 | Tansig | Purelin | 7-9-8-1 | 0.947 | 0.677 | 0.432 | 94.696 | 91.873 | 0.816 | 0.993 | 0.606 | 80.912 | 88.465 |
| ANN10 | TrainGDX | 24 | Logsig | Logsig | 7-11-13-1 | 0.915 | 0.913 | 0.624 | 88.188 | 88.413 | 0.879 | 1.126 | 0.985 | 80.926 | 79.481 |
| ANN11 | TrainSCG | 26 | Tansig | Tansig | 7-11-15-1 | 0.938 | 0.619 | 0.336 | 93.654 | 93.553 | 0.882 | 1.023 | 0.586 | 88.018 | 90.555 |
| ANN12 | TrainGDX | 32 | Purelin | Tansig | 7-15-17-1 | 0.922 | 0.680 | 0.387 | 92.201 | 93.114 | 0.866 | 0.978 | 0.392 | 86.559 | 88.953 |
| ANN13 | TrainLM | 37 | Tansig | Tansig | 7-17-20-1 | 0.906 | 0.900 | 0.628 | 88.409 | 87.744 | 0.763 | 0.992 | 0.822 | 73.105 | 85.883 |
| ANN14 | TrainSCG | 39 | Purelin | Logsig | 7-17-22-1 | 0.855 | 0.916 | 1.501 | 87.608 | 64.877 | 0.765 | 0.596 | 1.357 | 79.748 | 87.901 |
| ANN15 | TrainLM | 42 | Tansig | Logsig | 7-17-25-1 | 0.913 | 1.035 | 0.844 | 90.418 | 87.033 | 0.758 | 0.981 | 0.893 | 75.765 | 82.328 |
LM Levenberg–Marquardt, GDX Adaptive learning rate, SCG Scaled conjugate gradient, OSS One-step secant.
Table 5.
Performance of the base models of ANN and their rankings.
| ANN models | Training | Testing | Total rate | Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 rating | RMSE rating | MAE rating | VAF rating | Accuracy rating | R2 rating | RMSE rating | MAE rating | VAF rating | Accuracy rating | |||
| ANN1 | 10 | 12 | 9 | 11 | 6 | 2 | 3 | 7 | 2 | 8 | 70 | 9 |
| ANN2 | 11 | 7 | 15 | 9 | 15 | 1 | 1 | 6 | 1 | 3 | 69 | 10 |
| ANN3 | 15 | 15 | 12 | 15 | 13 | 15 | 15 | 13 | 14 | 14 | 141 | 1 |
| ANN4 | 2 | 5 | 5 | 1 | 5 | 6 | 2 | 5 | 5 | 4 | 40 | 12 |
| ANN5 | 9 | 11 | 10 | 10 | 9 | 9 | 14 | 12 | 10 | 12 | 106 | 4 |
| ANN6 | 13 | 8 | 7 | 13 | 7 | 13 | 11 | 8 | 13 | 7 | 100 | 5 |
| ANN7 | 8 | 13 | 14 | 8 | 14 | 14 | 13 | 15 | 15 | 13 | 127 | 2 |
| ANN8 | 4 | 6 | 6 | 6 | 8 | 8 | 10 | 9 | 9 | 6 | 72 | 8 |
| ANN9 | 14 | 10 | 8 | 14 | 10 | 7 | 6 | 10 | 7 | 10 | 96 | 7 |
| ANN10 | 6 | 3 | 4 | 3 | 4 | 11 | 4 | 2 | 8 | 1 | 46 | 11 |
| ANN11 | 12 | 14 | 13 | 12 | 12 | 12 | 5 | 11 | 12 | 15 | 118 | 3 |
| ANN12 | 7 | 9 | 11 | 7 | 11 | 10 | 9 | 14 | 11 | 11 | 100 | 5 |
| ANN13 | 3 | 4 | 3 | 4 | 3 | 4 | 7 | 4 | 3 | 5 | 40 | 12 |
| ANN14 | 1 | 2 | 1 | 2 | 1 | 5 | 12 | 1 | 6 | 9 | 40 | 12 |
| ANN15 | 5 | 1 | 2 | 5 | 2 | 3 | 8 | 3 | 4 | 2 | 35 | 15 |
XGBoost model
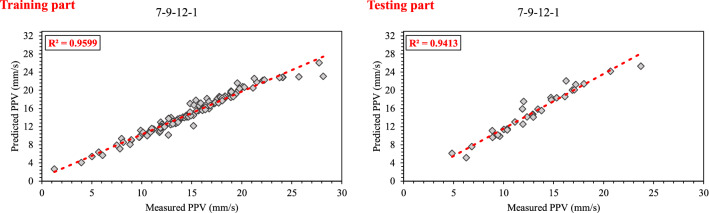
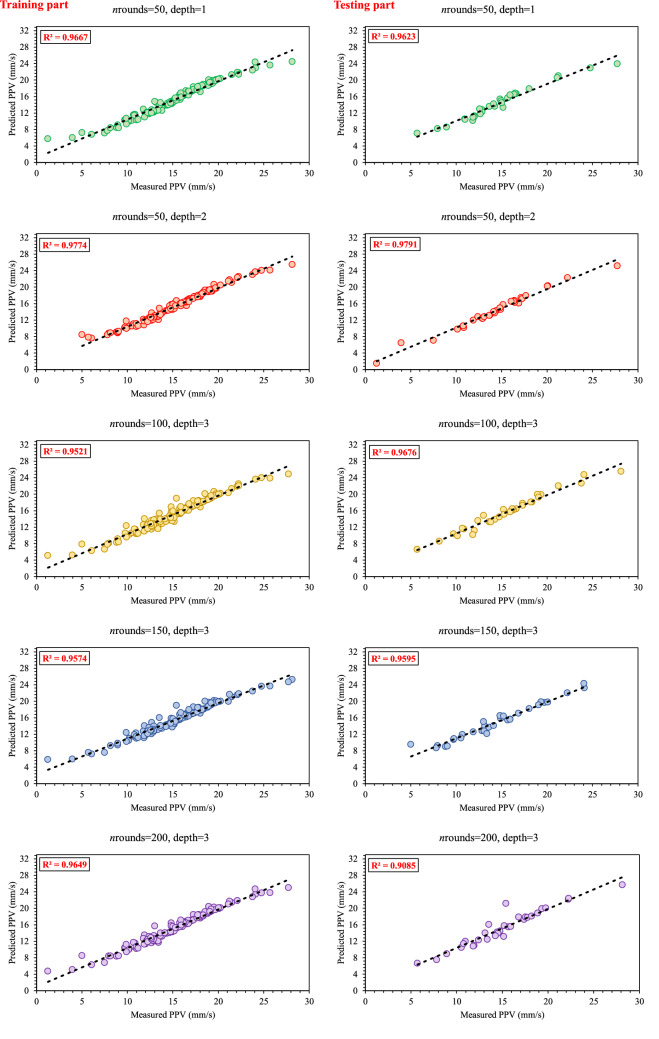
Herein, the XGBoost algorithm is used for PPV prediction. Before that, two main stopping criteria, including maximum tree depth and nrounds, were determined. These criteria have a significant impact on the performance of models. Similar to MLP networks, the overfitting problem there is also in XGBoost, which is occurred when the tree depth and the nrounds are set in the much values. Therefore, the range of [1–3] and [50–200] are considered for the maximum tree depth and nrounds. Similar to the ANN, the “trial-and-error” technique was used to determine an XGBoost model with the best performance. As shown in Table 6, the validation indices were computed to evaluate the base models of XGBoost performance. To construct the ensemble of XGBoost, 15 base models with different values of nrounds and maximum tree depth were developed. Based on Table 7, 15 base models of XGBoost were evaluated using Zorlu et al.93 scoring system. The results were shown that XGBoost base model number two, with the values of 50 and 1 for nrounds and maximum tree depth had the best performance in the PPV prediction, which this base model of XGBoost gets the score of 145 out of 150. The validation indices, i.e., R2, RMSE, MAE, VAF, and Accuracy were calculated as (0.977, 0.650, 0.402, 97.578 (%), 96.828) and (0.979, 0.536, 0.680, 97.895(%), 96.528) for training and testing datasets, respectively. However, a comparison between top base models of XGBoost and ANN reveals the superiority of the XGBoost method in the prediction of PPV.
Table 6.
The base models of XGBoost and their evaluations.
| XGBoost models | nrounds | Maximum tree depth | Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | VAF | Accuracy | R2 | RMSE | MAE | VAF | Accuracy | |||
| XGBoost1 | 50 | 1 | 0.967 | 0.803 | 0.526 | 96.502 | 95.315 | 0.962 | 0.966 | 0.645 | 95.760 | 95.293 |
| XGBoost2 | 50 | 2 | 0.977 | 0.650 | 0.402 | 97.578 | 96.828 | 0.979 | 0.536 | 0.680 | 97.895 | 96.528 |
| XGBoost3 | 50 | 3 | 0.904 | 1.395 | 0.876 | 90.053 | 92.825 | 0.899 | 1.122 | 0.848 | 89.762 | 93.295 |
| XGBoost4 | 100 | 1 | 0.957 | 0.896 | 0.629 | 95.593 | 94.562 | 0.952 | 0.943 | 0.723 | 94.777 | 95.340 |
| XGBoost5 | 100 | 2 | 0.938 | 1.112 | 0.764 | 93.474 | 93.579 | 0.937 | 1.175 | 0.805 | 93.248 | 94.695 |
| XGBoost6 | 100 | 3 | 0.952 | 0.923 | 0.626 | 95.169 | 94.595 | 0.968 | 0.795 | 0.651 | 96.645 | 95.387 |
| XGBoost7 | 100 | 1 | 0.950 | 0.990 | 0.66 | 94.773 | 94.442 | 0.943 | 0.906 | 0.679 | 94.238 | 94.612 |
| XGBoost8 | 150 | 2 | 0.923 | 1.182 | 0.771 | 92.003 | 93.397 | 0.882 | 1.598 | 1.241 | 85.342 | 92.732 |
| XGBoost9 | 150 | 3 | 0.957 | 0.973 | 0.631 | 94.796 | 94.741 | 0.959 | 1.033 | 0.723 | 95.330 | 93.528 |
| XGBoost10 | 150 | 1 | 0.909 | 1.367 | 0.861 | 90.419 | 92.900 | 0.900 | 0.653 | 0.791 | 90.020 | 94.786 |
| XGBoost11 | 150 | 2 | 0.935 | 1.160 | 0.762 | 93.092 | 93.567 | 0.951 | 1.144 | 0.461 | 93.577 | 91.276 |
| XGBoost12 | 150 | 3 | 0.928 | 1.219 | 0.828 | 92.017 | 93.046 | 0.952 | 0.942 | 0.814 | 94.961 | 94.355 |
| XGBoost13 | 200 | 1 | 0.943 | 1.059 | 0.708 | 94.131 | 93.913 | 0.924 | 0.684 | 0.644 | 92.392 | 95.753 |
| XGBoost14 | 200 | 2 | 0.963 | 0.812 | 0.568 | 96.507 | 94.978 | 0.904 | 1.007 | 0.85 | 90.304 | 94.105 |
| XGBoost15 | 200 | 3 | 0.965 | 0.811 | 0.547 | 96.402 | 95.117 | 0.909 | 0.863 | 0.795 | 90.701 | 94.561 |
Table 7.
Performance of the base models of XGBoost and their rankings.
| XGBoost models | Training | Testing | Total rate | Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 rating | RMSE rating | MAE rating | VAF rating | Accuracy rating | R2 rating | RMSE rating | MAE rating | VAF rating | Accuracy rating | |||
| XGBoost1 | 14 | 14 | 14 | 13 | 14 | 13 | 7 | 13 | 13 | 11 | 126 | 2 |
| XGBoost2 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 10 | 15 | 15 | 145 | 1 |
| XGBoost3 | 1 | 1 | 1 | 1 | 1 | 2 | 4 | 3 | 2 | 3 | 19 | 15 |
| XGBoost4 | 10 | 11 | 10 | 11 | 9 | 10 | 8 | 9 | 10 | 12 | 100 | 4 |
| XGBoost5 | 6 | 6 | 5 | 6 | 6 | 7 | 2 | 5 | 7 | 9 | 59 | 11 |
| XGBoost6 | 9 | 10 | 11 | 10 | 10 | 14 | 12 | 12 | 14 | 13 | 115 | 3 |
| XGBoost7 | 8 | 8 | 8 | 8 | 8 | 8 | 10 | 11 | 9 | 8 | 86 | 8 |
| XGBoost8 | 3 | 4 | 4 | 3 | 4 | 1 | 1 | 1 | 1 | 2 | 24 | 14 |
| XGBoost9 | 11 | 9 | 9 | 9 | 11 | 12 | 5 | 8 | 12 | 4 | 90 | 6 |
| XGBoost10 | 2 | 2 | 2 | 2 | 2 | 3 | 14 | 7 | 3 | 10 | 47 | 13 |
| XGBoost11 | 5 | 5 | 6 | 5 | 5 | 9 | 3 | 15 | 8 | 1 | 62 | 10 |
| XGBoost12 | 4 | 3 | 3 | 4 | 3 | 11 | 9 | 4 | 11 | 6 | 58 | 12 |
| XGBoost13 | 7 | 7 | 7 | 7 | 7 | 6 | 13 | 14 | 6 | 14 | 88 | 7 |
| XGBoost14 | 12 | 12 | 12 | 14 | 12 | 4 | 6 | 2 | 4 | 5 | 83 | 9 |
| XGBoost15 | 13 | 13 | 13 | 12 | 13 | 5 | 11 | 6 | 5 | 7 | 98 | 5 |
Ensemble model of ANNs (EANNs) to predict PPV
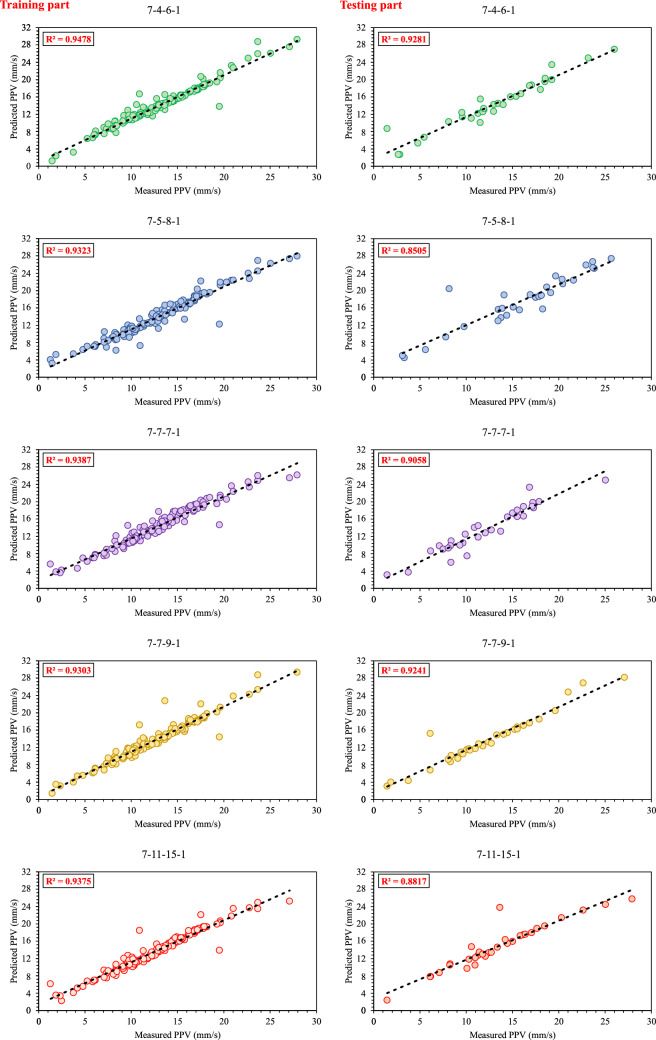
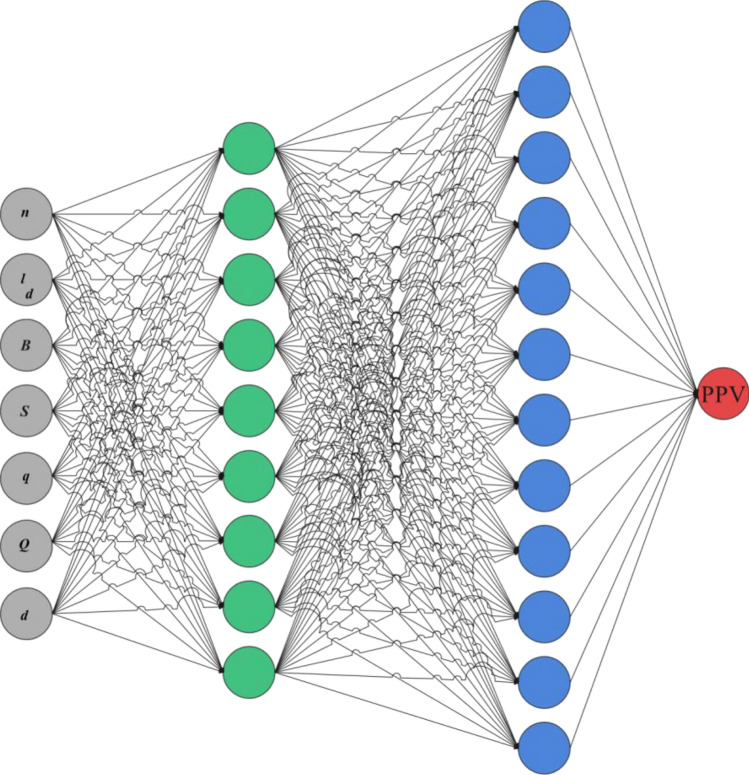
For the ensemble model of ANN, first, 15 base models for ANN are developed, and then after evaluation of the base models, five top base models for combination were chosen, that the scores of these models were 141, 127, 118, 106, and 100 out of 150, respectively. The correlation of measured PPV and predicted ones by five base models are illustrated in Fig. 4. After that, the stacked generalization combination technique was employed to combine the selected base models. For combination, the results of selected base models a feed-forward neural network with sigmoid activation function for hidden layers were used (Fig. 5). The input data of the combiner network consists of seven variables and the target dataset is the measured value of PPV.
Figure 4.
Correlation graph between measured and predicted values of PPV, using five top base models of ANN.
Figure 5.
The architecture of the ensemble ANN model for PPV prediction in Anguran mine (this figure is generated by EdrawMax, version 12.0.7, www.edrawsoft.com).
The correlation graph of predicted values using the stacked generalization technique and measured values is illustrated in Fig. 6. The values of (0.960, 0.402, 0.233, 95.963(%), 95.724) and (0.941, 0.189, 0.219, 92.827(%), 95.713) were obtained for both R2, RMSE, MAE, VAF, and Accuracy of training and testing datasets, respectively. Results proved that the EANNs model predicts PPV better than individual ANN (base models), so that the EANNs model 41% and 55% improved the RMSE of PPV prediction for training and testing part, respectively, in comparison with the best base model.
Figure 6.
Correlation graph between predicted data (EANNs model) and measured data.
Ensemble model of XGBoosts (EXGBoosts) to predict PPV
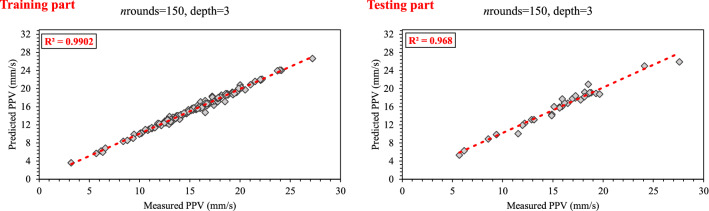
To construct EXGBoosts model for the prediction of PPV, first, several XGBoost models were developed. In this regard, 15 constructed XGBoost models were analyzed, and the five top base models with the highest score were selected. The numbers 145, 126, 115, 100, and 98 were the scores of the five top base models. The EXGBoosts model was structured based on a combination of five XGBoost base models. The base models using stacked generalization technique was combined to predict PPV. Figure 7 showed the correlation of PPV estimations by five XGBoost base models and measured values of PPV. The combiner was structured using a nrounds of 15 and a maximum tree depth of three. The results of stacked generalization show, the accuracy of the EXBoosts model in comparison with the best XGBoost base models is better (Fig. 8 and Table 8). To better comparing of the applied methods capability in estimating of PPV value, the performance of developed ANN, EANNs, XGBoost, and EXGBoosts models are tabulated in Table 8. The obtained statistical indices indicated that the EXGBoosts model with the value of (0.990, 0.391, 0.257, 99.013(%), 98.216) and (0.968, 0.295, 0.427, 96.674(%), 96.059) for R2, RMSE, MAE, VAF, and Accuracy of training and testing datasets, respectively, represents the highest performance for prediction of PPV among all applied models. Besides, EXGBoosts model 66% and 82% improved the RMSE of PPV prediction for training and testing part, respectively, in comparison with the best base model. The obtained results of performance indices regarding to our model presented in Table 9. This table compares the prediction accuracy and performance level of out proposed approach with three latest research. The results demonstrates that EXGBoost model has more performance capacity in model and estimation of PPV in comparison with the other methods.
Figure 7.
Correlation graph between predicted PPV by various XGBoost base models and measured data.
Figure 8.
Correlation graph between predicted data (EXGBoosts model) and measured data.
Table 8.
Performance of the ensemble and the best individuals of ANN and EXGBoosts.
| Techniques | Part | R2 | RMSE | MAE | VAF | Accuracy |
|---|---|---|---|---|---|---|
| ANN | Training | 0.948 | 0.567 | 0.350 | 94.767 | 94.247 |
| Testing | 0.928 | 0.293 | 0.487 | 92.773 | 90.254 | |
| EANNs | Training | 0.960 | 0.402 | 0.233 | 95.963 | 95.724 |
| Testing | 0.941 | 0.189 | 0.219 | 92.827 | 95.713 | |
| XGBoost | Training | 0.977 | 0.650 | 0.402 | 97.578 | 96.828 |
| Testing | 0.979 | 0.536 | 0.680 | 97.895 | 95.528 | |
| EXGBoosts | Training | 0.990 | 0.391 | 0.257 | 99.013 | 98.216 |
| Testing | 0.968 | 0.295 | 0.427 | 96.674 | 96.059 |
Table 9.
Accuracy comparison of our proposed technique with other reseach.
| Author | Year | Method | R2 |
|---|---|---|---|
| Huang et al.21 | 2020 | FA-ANN | 0.91 |
| Zhou et al.12 | 2021 | GEP-MC | 0.91 |
| Lawal et al.59 | 2021 | ANN-MFO | 0.97 |
| Ragam et al.61 | 2022 | XGBoost-RF | 0.95 |
| Nguyen et al.62 | 2023 | SSO-ELM | 0.91 |
| Proped technique | EXGBoosts | TR = 0.99, TS = 0.97 | |
| EANNs | TR = 0.96, TS = 0.94 | ||
TR Train, TS Test.
It is known that the significance of the estimation of level l (where l reveals the percentage of estimation) stands the quotient of the number of samples in which the estimations are within l absolute limit of measured values divided by the total number of samples. A common metric for evaluating the best models is P(0.25) ≥ 0.75 or 75%94. The level of 25% was used to test model in our study.
In which, where n is the number of dataset, Pi denotes the predicted value, and Oi indicates the observed values.
The 25% level estimation of ANN, XGBoost, EANNs, and EXGBoosts are showed in Table 10. As can be seen, the ANN at P(0.25) is not acceptable in validation dataset, but other models is acceptable in both testing and validation datasets. It can be concluded that the ensemble models developed in this study have the highest performance and capability in predicting PPV.
Table 10.
Estimation level at 25% in testing and validation datasets.
| Techniques | Part | P(0.25) |
|---|---|---|
| ANN | Testing | 76.254 |
| Validation | 33.563 | |
| EANNs | Testing | 100 |
| Validation | 92.987 | |
| XGBoost | Testing | 97.255 |
| Validation | 79.654 | |
| EXGBoosts | Testing | 100 |
| Validation | 100 |
Multiple parametric sensitivity analysis (MPSA)
In this part, a parametric analysis was conducted to specify which influential parameters have the highest impact on the average PPV value. In this regard, a multiple parametric sensitivity analysis (MPSA) was performed that follows the six main steps for applying to the outputs of the system for a specific set of parameters. These steps are as follows:
Step 1 Selecting the effective parameters to be subjected.
Step 2 Adjusting the range of input parameters.
Step 3 Generating a set of independent parameters in the form of random numbers with a uniform distribution for each parameter.
Step 4 Running the machine learning method utilizing the generated series and calculating the objective function using Eq. (12). The objective function was computed using the sum of square errors between measured and predicted values95:
| 12 |
where fh denots the objective function value for a particular PPVt variable h; xo,h indicates the measured values; xc,h(i) is the calculated value xc for variable h for each generated inputs; and n is the number of variables contained in the random set. In the computation process, the Monte Carlo simulation was used to generate 162 random data for seven effevtive parameters used in this study. At each iteration of the model, the trained models were provided with the newly produced values for one parameter.
Step 5 Determining the relative importance of effevtive parameters separately using Eq. (13)95:
| 13 |
In which, h is the variable that is used to introduce pairs of effective parameters. The outcomes that were achieved for each of the evaluated parameters were produced by using the technique that was provided to the PPVt model. Equation (13) had a significant importance in the accomplishment of these results.
Step 6 Evaluating parametric sensitivity and determining relative relevance of effective parameters using Eq. (14)95:
| 14 |
where the δt is computed from the first series of dataset (h = 1) to the maximum values (), which is 162 data for developed model in this study. Table 11 provides a tabular breakdown of the value spectrum that was employed throughout the evaluating of each parameter.
Table 11.
The range of γ index to determine sensitivity of each parameter95.
| γ Index | Model parameter sensitivity |
|---|---|
| γ ≤ 1 | Insensitive |
| 1 < γ ≤ 100 | Sensitive |
| γ ≥ 100 | Highly sensitive |
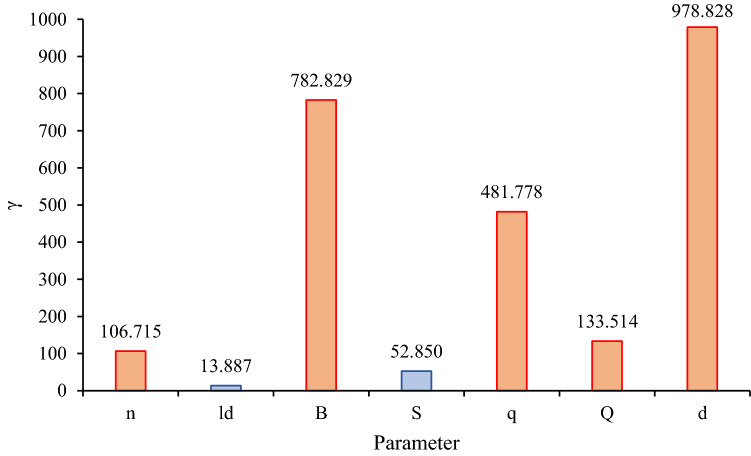
The lower the γ index value for each parameter, the less sensitive the st model is to that parameter, and the higher the γ index, the more sensitive the model is to the parameter under consideration. Table 11 has presented the γ index to evaluate the impact of model parameters and identify the most sensitive parameters. The calculated γ index for each parameter is depicted in Fig. 9. It can be found that the order of the sensitivity of the PPV to the parameters is ld < S < n < Q < q < B < d. It can be concluded that the PPV is highly sensitive to d, B, q, Q, and n, as well as sensitive to S and ld.
Figure 9.
The impact of effective parameters on PPV.
Influence of delay sequence on PPV
The seismic energy is what causes the blasting vibrations to be generated, and it also literally symbolizes the problems created to the rock-mass that extends beyond the boundaries of the explosion patch. The blasting pattern design specifications, explosives type and properties, and the physio-mechanical characteristics of the rock-mass all affect how much PPV occurs. The generation of PPV for several experimental implementing blasting has been obtained; the PPV value is reported as 5.12–17.23, 3.91–12.14, and 1.48–5.93 in the delay sequence (row to row) of 9, 15, and 23 ms. It can be concluded that the 23 ms delay between the rows will assist in lowering the PPV, which may be lowered up to a particular value by choosing the right delay sequence in production blast, according to field observations and data analysis.
The superimposition of waveform due to delay sequence refers to the effect of time delays on the coherence of signals. When two or more signals are delayed relative to each other, their waveforms may overlap and interfere with each other, resulting in a composite waveform that may be difficult to interpret. The impact of this effect on the outcome of a result depends on the specific context of the analysis. In some cases, such as in signal processing or communication systems, delay sequences are intentionally introduced to improve signal quality or reduce interference. In these cases, the superimposition of waveforms may be a desirable effect. However, in other cases, such as in physiological or biological signal analysis, the superimposition of waveforms due to delay sequences can lead to a loss of information and inaccuracies in the analysis. For example, in electroencephalogram (EEG) recordings, time delays between signals from different brain regions can result in overlapping waveforms that make it difficult to identify the underlying brain activity.
Results and discussions
This paper was accurately focused on estimation PPV due to mine blasting. In this way, the most effective parameters on PPV variation were identified. Two AI-based models i.e., ANN and XGBoost, were considered for choosing the best between PPV predictive models. For each predictive method, an ensemble model, i.e., EANNs and EXGBoosts, was developed, and the best one was chosen. The obtained results from statistical indicators (R2 and RMSE) associated with the best predictive models of ANN, XGBoost, EANNs, and EXGBoosts for training and testing parts were illustrated in Figs. 10 and 11.
Figure 10.
The value of R2, RMSE, and MAE for selecting the best model in the predicting PPV values.
Figure 11.
The value of VAF and accuracy for selecting the best model in the predicting PPV values.
The predictive model of EXGBoosts has specified capable of presenting the highest performance prediction level in train and test parts. Therefore, EXGBoosts was found a superior accuracy level regarding statistical indicators values among other predictive models. The R2 values of (0.948, 0.977, 0.960, and 0.990) and (0.928, 0.979, 0.941, and 0.968) were calculated for training and testing phases of ANN, XGBoost, EANNs, and EXGBoosts models, respectively. Besides, RMSE values of (0.567, 0.650, 0.402, and 0.391) and (0.293, 0.536, 0.189, and 0.295) were obtained for training and testing parts of ANN, XGBoost, EANNs, and EXGBoosts models, respectively. The EXGBoosts model revealed a maximum performance and minimum system error between other predictive models. In situations where the testing datasets reflect adequate generalizability of predictive techniques, the excellent efficiency of the train phases suggests the success of the learning procedures of the predictive models.
Benefits and drawbacks of the study
The main benefit of this study is in improving the performance and accuracy of the proposed ANN and XGBoost models. These models separately provide lower accuracy than the ensemble models. Therefore, using the combination of these methods and constructing an ensemble model, it is possible to predict the PPV with acceptable accuracy. Noteworthy, neural network base models each have different results and have uncertainty due to being a black-box. However, the ensemble model solves this problem to an acceptable. This study also has drawbacks. In this study, only two AI models have been used i.e., ANN and XGBoost. However, the number of AI models can be increased to reach maximum accuracy. It should be noted that the number of base models in this study is acceptable; nevertheless, more models can be obtained and run the ensemble model based on them.
Conclusions
In this study, the PPV induced from bench blasting is studied in Anguran lead–zinc mine, Iran. Considering the crucial importance of the adverse effects of ground vibration in blasting operations, the prediction of PPV at a high level of accuracy is essential. Therefore, this study investigates the ensemble of various artificial intelligence models to construct an accurate model for PPV estimation using 162 blasting datasets and seven effective parameters. For this aim, several ANN and XGBoost base models were developed and the five top base models among them were combined to generate EANNs and EXGBoosts models. To combination of top base models’ outputs and achieve a single result stacked generalization technique was used. The statistical indexes of R2, RMSE, MAE, VAF, and Accuracy were used to evaluate the performance of developed models and a scoring system was applied to select the best ANN and XGBoost base models with optimal structure. The results revealed that the EANNs with R2 of (0.960, and 0.941), RMSE of (0.402, and 0.189), MAE of (0.233, and 0.219), VAF of (95.963(%), and 92.827(%)), and Accuracy of (95.724, and 95.713) for training and testing datasets, respectively, and EXGBoosts model with R2 of (0.990, and 0.968), RMSE of (0.391, and 0.295), MAE of (0.257, and 0.427), VAF of (99.013(%), and 96.674(%)), and Accuracy of (98.216, and 96.059) for training and testing datasets, respectively, were two efficient machine learning ensemble methods for forecasting PPV. Comparison of the results of developed ensemble methods, i.e., EANNs and EXGBoosts, with the best individual models showed the superiority of ensemble modeling in predicting PPV in surface mines. Moreover, EXGBoosts model was most accurate compared to the EANN model. In the final step of this study, the effectiveness of each input variable on PPV intensity is determined using the CA method, which results denoted the spacing has the most impact on PPV. From practical applications, the proposed model can be updated for other engineering fields, specially mining and civil activities. Meanwhile, the ensemble machine learning approach can be applied to improve performance capacity of machine learning techniques and increase the accuracy level of prediction targets. The proposed models can be used to analyze safety data and identify potential hazards, blasting safety zone, and risks in blasting operations. The PPV values can be predicted before blasting operations to check any potential issues or damage to the workers, equipment and surrounding residential area. If the predicted results are higher than those suggested in literature or standards, the blasting pattern/design can be reviewed again to have a predicted PPV values within the suggested safe ranges. Generally, machine learning algorithms can be used to analyze environmental data and monitor the impact of mining operations on the environment.
Author contributions
S.H.: Data collection, conceptualization, methodology, results, analysis, writing. R.P.: Conceptualization, methodology, writing and editing, supervision. D.J.A: Writing, reviewing and editing, supervision. M.M.S.S: Writing, reviewing and editing, resources, funding.
Funding
The research is partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program ‘Priority 2030’ (Agreement 075-15-2021-1333 dated 30 September 2021).
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Jiang W, Arslan CA, Tehrani MS, Khorami M, Hasanipanah M. Simulating the peak particle velocity in rock blasting projects using a neuro-fuzzy inference system. Eng. Comput. 2019;35:1203–1211. doi: 10.1007/s00366-018-0659-6. [DOI] [Google Scholar]
- 2.Bakhtavar E, Hosseini S, Hewage K, Sadiq R. Green blasting policy: Simultaneous forecast of vertical and horizontal distribution of dust emissions using artificial causality-weighted neural network. J. Clean. Prod. 2021;283:124562. doi: 10.1016/j.jclepro.2020.124562. [DOI] [Google Scholar]
- 3.Bakhtavar E, Hosseini S, Hewage K, Sadiq R. Air pollution risk assessment using a hybrid fuzzy intelligent probability-based approach: Mine blasting dust impacts. Nat. Resour. Res. 2021 doi: 10.1007/s11053-020-09810-4. [DOI] [Google Scholar]
- 4.Hosseini S, Monjezi M, Bakhtavar E, Mousavi A. Prediction of dust emission due to open pit mine blasting using a hybrid artificial neural network. Nat. Resour. Res. 2021 doi: 10.1007/s11053-021-09930-5. [DOI] [Google Scholar]
- 5.Hosseini S, Mousavi A, Monjezi M. Prediction of blast-induced dust emissions in surface mines using integration of dimensional analysis and multivariate regression analysis. Arab. J. Geosci. 2022;15:163. doi: 10.1007/s12517-021-09376-2. [DOI] [Google Scholar]
- 6.Armaghani DJ, Hasanipanah M, Amnieh HB, Mohamad ET. Feasibility of ICA in approximating ground vibration resulting from mine blasting. Neural Comput. Appl. 2018;29:457–465. doi: 10.1007/s00521-016-2577-0. [DOI] [Google Scholar]
- 7.Nguyen H, Bui X-N. Soft computing models for predicting blast-induced air over-pressure: A novel artificial intelligence approach. Appl. Soft Comput. 2020;92:106292. doi: 10.1016/j.asoc.2020.106292. [DOI] [Google Scholar]
- 8.Faradonbeh RS, Armaghani DJ, Amnieh HB, Mohamad ET. Prediction and minimization of blast-induced flyrock using gene expression programming and firefly algorithm. Neural Comput. Appl. 2018;29:269–281. doi: 10.1007/s00521-016-2537-8. [DOI] [Google Scholar]
- 9.Koopialipoor M, Fallah A, Armaghani DJ, Azizi A, Mohamad ET. Three hybrid intelligent models in estimating flyrock distance resulting from blasting. Eng. Comput. 2019;35:243–256. doi: 10.1007/s00366-018-0596-4. [DOI] [Google Scholar]
- 10.Shirani Faradonbeh R, et al. Prediction of ground vibration due to quarry blasting based on gene expression programming: A new model for peak particle velocity prediction. Int. J. Environ. Sci. Technol. 2016 doi: 10.1007/s13762-016-0979-2. [DOI] [Google Scholar]
- 11.Mohamadnejad M, Gholami R, Ataei M. Comparison of intelligence science techniques and empirical methods for prediction of blasting vibrations. Tunn. Undergr. Sp. Technol. 2012;28:238–244. doi: 10.1016/j.tust.2011.12.001. [DOI] [Google Scholar]
- 12.Zhou J, Li C, Koopialipoor M, Armaghani DJ, Pham BT. Development of a new methodology for estimating the amount of PPV in surface mines based on prediction and probabilistic models (GEP-MC) Int. J. Mining Reclam. Environ. 2020;35:48–68. doi: 10.1080/17480930.2020.1734151. [DOI] [Google Scholar]
- 13.Hasanipanah M, et al. Prediction of an environmental issue of mine blasting: An imperialistic competitive algorithm-based fuzzy system. Int. J. Environ. Sci. Technol. 2018;15:551–560. doi: 10.1007/s13762-017-1395-y. [DOI] [Google Scholar]
- 14.Agrawal H, Mishra AK. Modified scaled distance regression analysis approach for prediction of blast-induced ground vibration in multi-hole blasting. J. Rock Mech. Geotech. Eng. 2019;11:202–207. doi: 10.1016/j.jrmge.2018.07.004. [DOI] [Google Scholar]
- 15.Nguyen H, Drebenstedt C, Bui X-N, Bui DT. Prediction of blast-induced ground vibration in an open-pit mine by a novel hybrid model based on clustering and artificial neural network. Nat. Resour. Res. 2020;29:691–709. doi: 10.1007/s11053-019-09470-z. [DOI] [Google Scholar]
- 16.Duvall, W. I. & Fogelson, D. E. Review of Criteria for Estimating Damage to Residences from Blasting Vibrations, vol. 5968 (US Department of the Interior, Bureau of Mines, 1962).
- 17.Siskind, D. E. Structure Response and Damage Produced by Ground Vibration from Surface Mine Blasting, vol. 8507 (US Department of the Interior, Bureau of Mines, 1980).
- 18.Qiu, Y. et al. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 1–18 (2021).
- 19.Zeng J, et al. Prediction of peak particle velocity caused by blasting through the combinations of boosted-CHAID and SVM models with various kernels. Appl. Sci. 2021;11:3705. doi: 10.3390/app11083705. [DOI] [Google Scholar]
- 20.Hajihassani M, Armaghani DJ, Marto A, Mohamad ET. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bull. Eng. Geol. Environ. 2015;74:873–886. doi: 10.1007/s10064-014-0657-x. [DOI] [Google Scholar]
- 21.Huang J, Koopialipoor M, Armaghani DJ. A combination of fuzzy Delphi method and hybrid ANN-based systems to forecast ground vibration resulting from blasting. Sci. Rep. 2020;10:1–21. doi: 10.1038/s41598-020-76569-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Davies, B., Farmer, I. W. & Attewell, P. B. Ground vibration from shallow sub-surface blasts. Engineer217, (1964).
- 23.Ambraseys, N. R. & Hendron, A. J. Dynamic Behavior of Rock Masses, Rock Mechanics in Engineering Practice (eds. Stagg, K. G. & Zienkiewicz, O. C.) (1968).
- 24.Dowding CH. Blast Vibration Monitoring and Control. Prentice-Hall Inc; 1985. pp. 288–290. [Google Scholar]
- 25.Roy, P. P. Putting ground vibration predictions into practice. Colliery Guard. (Kingdom)241 (1993).
- 26.Rai, R. & Singh, T. N. A new predictor for ground vibration prediction and its comparison with other predictors. (2004).
- 27.Mottahedi A, Sereshki F, Ataei M. Development of overbreak prediction models in drill and blast tunneling using soft computing methods. Eng. Comput. 2018;34:45–58. doi: 10.1007/s00366-017-0520-3. [DOI] [Google Scholar]
- 28.Sadeghi F, Monjezi M, Armaghani DJ. Evaluation and optimization of prediction of toe that arises from mine blasting operation using various soft computing techniques. Nat. Resour. Res. 2020;29:887–903. doi: 10.1007/s11053-019-09605-2. [DOI] [Google Scholar]
- 29.Xie C, et al. Predicting rock size distribution in mine blasting using various novel soft computing models based on meta-heuristics and machine learning algorithms. Geosci. Front. 2021;12:101108. doi: 10.1016/j.gsf.2020.11.005. [DOI] [Google Scholar]
- 30.Gao W, Alqahtani AS, Mubarakali A, Mavaluru D. Developing an innovative soft computing scheme for prediction of air overpressure resulting from mine blasting using GMDH optimized by GA. Eng. Comput. 2020;36:647–654. doi: 10.1007/s00366-019-00720-5. [DOI] [Google Scholar]
- 31.Nguyen H, Bui NX, Tran HQ, Le GHT. A novel soft computing model for predicting blast-induced ground vibration in open-pit mines using gene expression programming. J. Min. Earth Sci. 2020;61:107–116. [Google Scholar]
- 32.Mokfi T, Shahnazar A, Bakhshayeshi I, Derakhsh AM, Tabrizi O. Proposing of a new soft computing-based model to predict peak particle velocity induced by blasting. Eng. Comput. 2018;34:881–888. doi: 10.1007/s00366-018-0578-6. [DOI] [Google Scholar]
- 33.Arthur CK, Temeng VA, Ziggah YY. Soft computing-based technique as a predictive tool to estimate blast-induced ground vibration. J. Sustain. Min. 2019;18:287–296. [Google Scholar]
- 34.Bui X-N, Nguyen H, Le H-A, Bui H-B, Do N-H. Prediction of blast-induced air over-pressure in open-pit mine: Assessment of different artificial intelligence techniques. Nat. Resour. Res. 2019 doi: 10.1007/s11053-019-09461-0. [DOI] [Google Scholar]
- 35.Hasanipanah M, Golzar SB, Larki IA, Maryaki MY, Ghahremanians T. Estimation of blast-induced ground vibration through a soft computing framework. Eng. Comput. 2017;33:951–959. doi: 10.1007/s00366-017-0508-z. [DOI] [Google Scholar]
- 36.Taheri K, Hasanipanah M, Golzar SB, Abd Majid MZ. A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Eng. Comput. 2017;33:689–700. doi: 10.1007/s00366-016-0497-3. [DOI] [Google Scholar]
- 37.Fouladgar N, Hasanipanah M, Amnieh HB. Application of cuckoo search algorithm to estimate peak particle velocity in mine blasting. Eng. Comput. 2017;33:181–189. doi: 10.1007/s00366-016-0463-0. [DOI] [Google Scholar]
- 38.Hasanipanah M, Naderi R, Kashir J, Noorani SA, Qaleh AZA. Prediction of blast-produced ground vibration using particle swarm optimization. Eng. Comput. 2017;33:173–179. doi: 10.1007/s00366-016-0462-1. [DOI] [Google Scholar]
- 39.Iphar M, Yavuz M, Ak H. Prediction of ground vibrations resulting from the blasting operations in an open-pit mine by adaptive neuro-fuzzy inference system. Environ. Geol. 2008 doi: 10.1007/s00254-007-1143-6. [DOI] [Google Scholar]
- 40.Singh TN, Singh V. An intelligent approach to prediction and control ground vibration in mines. Geotech. Geol. Eng. 2005 doi: 10.1007/s10706-004-7068-x. [DOI] [Google Scholar]
- 41.Monjezi M, Ghafurikalajahi M, Bahrami A. Prediction of blast-induced ground vibration using artificial neural networks. Tunn. Undergr. Sp. Technol. 2011;26:46–50. doi: 10.1016/j.tust.2010.05.002. [DOI] [Google Scholar]
- 42.Mohamed MT. Performance of fuzzy logic and artificial neural network in prediction of ground and air vibrations. JES. J. Eng. Sci. 2011;39:425–440. [Google Scholar]
- 43.Khandelwal M, Kumar DL, Yellishetty M. Application of soft computing to predict blast-induced ground vibration. Eng. Comput. 2011 doi: 10.1007/s00366-009-0157-y. [DOI] [Google Scholar]
- 44.Fişne A, Kuzu C, Hüdaverdi T. Prediction of environmental impacts of quarry blasting operation using fuzzy logic. Environ. Monit. Assess. 2011 doi: 10.1007/s10661-010-1470-z. [DOI] [PubMed] [Google Scholar]
- 45.Ghasemi E, Ataei M, Hashemolhosseini H. Development of a fuzzy model for predicting ground vibration caused by rock blasting in surface mining. JVC/J. Vib. Control. 2013 doi: 10.1177/1077546312437002. [DOI] [Google Scholar]
- 46.Monjezi M, Hasanipanah M, Khandelwal M. Evaluation and prediction of blast-induced ground vibration at Shur River Dam, Iran, by artificial neural network. Neural Comput. Appl. 2013 doi: 10.1007/s00521-012-0856-y. [DOI] [Google Scholar]
- 47.Armaghani DJ, Hajihassani M, Mohamad ET, Marto A, Noorani SA. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab. J. Geosci. 2014;7:5383–5396. doi: 10.1007/s12517-013-1174-0. [DOI] [Google Scholar]
- 48.Dindarloo SR. Peak particle velocity prediction using support vector machines: A surface blasting case study. J. S. Afr. Inst. Min. Metall. 2015 doi: 10.17159/2411-9717/2015/v115n7a10. [DOI] [Google Scholar]
- 49.Hajihassani M, Armaghani DJ, Monjezi M, Mohamad ET, Marto A. Blast-induced air and ground vibration prediction: A particle swarm optimization-based artificial neural network approach. Environ. Earth Sci. 2015;74:2799–2817. doi: 10.1007/s12665-015-4274-1. [DOI] [Google Scholar]
- 50.Hasanipanah M, Monjezi M, Shahnazar A, Jahed Armaghani D, Farazmand A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Meas. J. Int. Meas. Confed. 2015 doi: 10.1016/j.measurement.2015.07.019. [DOI] [Google Scholar]
- 51.Armaghani DJ, Momeni E, Abad SVANK, Khandelwal M. Feasibility of ANFIS model for prediction of ground vibrations resulting from quarry blasting. Environ. Earth Sci. 2015 doi: 10.1007/s12665-015-4305-y. [DOI] [Google Scholar]
- 52.Ghoraba S, Monjezi M, Talebi N, Armaghani DJ, Moghaddam MR. Estimation of ground vibration produced by blasting operations through intelligent and empirical models. Environ. Earth Sci. 2016 doi: 10.1007/s12665-016-5961-2. [DOI] [Google Scholar]
- 53.Hasanipanah M, Faradonbeh RS, Amnieh HB, Armaghani DJ, Monjezi M. Forecasting blast-induced ground vibration developing a CART model. Eng. Comput. 2017 doi: 10.1007/s00366-016-0475-9. [DOI] [Google Scholar]
- 54.Shahnazar A, et al. A new developed approach for the prediction of ground vibration using a hybrid PSO-optimized ANFIS-based model. Environ. Earth Sci. 2017 doi: 10.1007/s12665-017-6864-6. [DOI] [Google Scholar]
- 55.Nguyen H, Bui X-N, Tran Q-H, Mai N-L. A new soft computing model for estimating and controlling blast-produced ground vibration based on hierarchical K-means clustering and cubist algorithms. Appl. Soft Comput. 2019;77:376–386. doi: 10.1016/j.asoc.2019.01.042. [DOI] [Google Scholar]
- 56.Nguyen H, Choi Y, Bui XN, Nguyen-Thoi T. Predicting blast-induced ground vibration in open-pit mines using vibration sensors and support vector regression-based optimization algorithms. Sensors (Switzerland) 2020 doi: 10.3390/s20010132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhang H, et al. A combination of feature selection and random forest techniques to solve a problem related to blast-induced ground vibration. Appl. Sci. 2020 doi: 10.3390/app10030869. [DOI] [Google Scholar]
- 58.Zhou J, Asteris PG, Armaghani DJ, Pham BT. Prediction of ground vibration induced by blasting operations through the use of the Bayesian Network and random forest models. Soil Dyn. Earthq. Eng. 2020 doi: 10.1016/j.soildyn.2020.106390. [DOI] [Google Scholar]
- 59.Lawal AI, Kwon S, Kim GY. Prediction of the blast-induced ground vibration in tunnel blasting using ANN, moth-flame optimized ANN, and gene expression programming. Acta Geophys. 2021 doi: 10.1007/s11600-020-00532-y. [DOI] [Google Scholar]
- 60.He B, Lai SH, Mohammed AS, Sabri MMS, Ulrikh DV. Estimation of blast-induced peak particle velocity through the improved weighted random forest technique. Appl. Sci. 2022;12:5019. doi: 10.3390/app12105019. [DOI] [Google Scholar]
- 61.Ragam P, Komalla AR, Kanne N. Estimation of blast-induced peak particle velocity using ensemble machine learning algorithms: A case study. Noise Vib. Worldw. 2022;53:404–413. doi: 10.1177/09574565221114662. [DOI] [Google Scholar]
- 62.Nguyen H, Bui X-N, Topal E. Reliability and availability artificial intelligence models for predicting blast-induced ground vibration intensity in open-pit mines to ensure the safety of the surroundings. Reliab. Eng. Syst. Saf. 2023;231:109032. doi: 10.1016/j.ress.2022.109032. [DOI] [Google Scholar]
- 63.Zhang Y, Liu J, Shen W. A review of ensemble learning algorithms used in remote sensing applications. Appl. Sci. 2022;12:8654. doi: 10.3390/app12178654. [DOI] [Google Scholar]
- 64.Doğru, A., Buyrukoğlu, S. & Arı, M. A hybrid super ensemble learning model for the early-stage prediction of diabetes risk. Med. Biol. Eng. Comput. 1–13 (2023). [DOI] [PubMed]
- 65.Buyrukoğlu, S. & Savaş, S. Stacked-based ensemble machine learning model for positioning footballer. Arab. J. Sci. Eng. 1–13 (2022).
- 66.Buyrukoğlu S. New hybrid data mining model for prediction of Salmonella presence in agricultural waters based on ensemble feature selection and machine learning algorithms. J. Food Saf. 2021;41:e12903. doi: 10.1111/jfs.12903. [DOI] [Google Scholar]
- 67.Buyrukoğlu G, Buyrukoğlu S, Topalcengiz Z. Comparing regression models with count data to artificial neural network and ensemble models for prediction of generic Escherichia coli population in agricultural ponds based on weather station measurements. Microb. Risk Anal. 2021;19:100171. doi: 10.1016/j.mran.2021.100171. [DOI] [Google Scholar]
- 68.Buyrukoğlu, S. Promising cryptocurrency analysis using deep learning. In 2021 5th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT) 372–376 (IEEE, 2021).
- 69.Akbas, A. & Buyrukoglu, S. Stacking ensemble learning-based wireless sensor network deployment parameter estimation. Arab. J. Sci. Eng. 1–10 (2022).
- 70.Zhou Z-H, Wu J, Tang W. Ensembling neural networks: Many could be better than all. Artif. Intell. 2002;137:239–263. doi: 10.1016/S0004-3702(02)00190-X. [DOI] [Google Scholar]
- 71.Alizadeh, S., Poormirzaee, R., Nikrouz, R. and Sarmady, S. Using stacked generalization ensemble method to estimate shear wave velocity based on downhole seismic data: A case study of Sarab-e-Zahab, Iran. J. Seism. Explor. (2021).
- 72.Nadeem F, Alghazzawi D, Mashat A, Faqeeh K, Almalaise A. Using machine learning ensemble methods to predict execution time of e-science workflows in heterogeneous distributed systems. IEEE Access. 2019;7:25138–25149. doi: 10.1109/ACCESS.2019.2899985. [DOI] [Google Scholar]
- 73.Production, I. M. Supply Company (IMPASCO). Final Rep. Complement. Explor. Oper. Anguran Lead Zinc Depos. Zanjan, Dandi, Iran313 (2019).
- 74.Khoshalan HA, Shakeri J, Najmoddini I, Asadizadeh M. Forecasting copper price by application of robust artificial intelligence techniques. Resour. Policy. 2021;73:102239. doi: 10.1016/j.resourpol.2021.102239. [DOI] [Google Scholar]
- 75.Duan, J., Asteris, P. G., Nguyen, H., Bui, X.-N. & Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 1–18 (2020).
- 76.Yegnanarayana B. Artificial Neural Networks. PHI Learning Pvt. Ltd.; 2009. [Google Scholar]
- 77.Fausett LV. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications. Prentice-Hall, Inc.,; 1994. [Google Scholar]
- 78.Dragičević T, Novak M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2018;66:8870–8880. doi: 10.1109/TIE.2018.2875660. [DOI] [Google Scholar]
- 79.Sengupta A, Shim Y, Roy K. Proposal for an all-spin artificial neural network: Emulating neural and synaptic functionalities through domain wall motion in ferromagnets. IEEE Trans. Biomed. Circuits Syst. 2016;10:1152–1160. doi: 10.1109/TBCAS.2016.2525823. [DOI] [PubMed] [Google Scholar]
- 80.Hodo, E. et al. Threat analysis of IoT networks using artificial neural network intrusion detection system. In 2016 International Symposium on Networks, Computers and Communications (ISNCC) 1–6 (IEEE, 2016).
- 81.Bui DT, Tuan TA, Klempe H, Pradhan B, Revhaug I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides. 2016;13:361–378. doi: 10.1007/s10346-015-0557-6. [DOI] [Google Scholar]
- 82.Chen, T. et al. Xgboost: Extreme gradient boosting. R Packag. version 0.4-2 1, 1–4 (2015).
- 83.Bhattacharya S, et al. A novel PCA-firefly based XGBoost classification model for intrusion detection in networks using GPU. Electronics. 2020;9:219. doi: 10.3390/electronics9020219. [DOI] [Google Scholar]
- 84.Nguyen H, Bui X-N, Bui H-B, Cuong DT. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: A case study. Acta Geophys. 2019;67:477–490. doi: 10.1007/s11600-019-00268-4. [DOI] [Google Scholar]
- 85.Ren, X., Guo, H., Li, S., Wang, S. & Li, J. A novel image classification method with CNN-XGBoost model. In International Workshop on Digital Watermarking 378–390 (Springer, 2017).
- 86.Zhang, L. & Zhan, C. Machine learning in rock facies classification: An application of XGBoost. In International Geophysical Conference, Qingdao, China, 17–20 April 2017 1371–1374 (Society of Exploration Geophysicists and Chinese Petroleum Society, 2017).
- 87.Nguyen H, Bui X-N, Nguyen-Thoi T, Ragam P, Moayedi H. Toward a state-of-the-art of fly-rock prediction technology in open-pit mines using EANNs model. Appl. Sci. 2019;9:4554. doi: 10.3390/app9214554. [DOI] [Google Scholar]
- 88.Barzegar R, Asghari Moghaddam A. Combining the advantages of neural networks using the concept of committee machine in the groundwater salinity prediction. Model. Earth Syst. Environ. 2016 doi: 10.1007/s40808-015-0072-8. [DOI] [Google Scholar]
- 89.Dogan, A. & Birant, D. A weighted majority voting ensemble approach for classification. In 2019 4th International Conference on Computer Science and Engineering (UBMK) 1–6 (IEEE, 2019).
- 90.Krogh A, Vedelsby J. Neural network ensembles, cross validation, and active learning. Adv. Neural Inf. Process. Syst. 1995;7:231–238. [Google Scholar]
- 91.Jacobs RA, Jordan MI, Nowlan SJ, Hinton GE. Adaptive mixtures of local experts. Neural Comput. 1991;3:79–87. doi: 10.1162/neco.1991.3.1.79. [DOI] [PubMed] [Google Scholar]
- 92.Wolpert DH. Stacked generalization. Neural Netw. 1992;5:241–259. doi: 10.1016/S0893-6080(05)80023-1. [DOI] [Google Scholar]
- 93.Zorlu K, Gokceoglu C, Ocakoglu F, Nefeslioglu HA, Acikalin S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008;96:141–158. doi: 10.1016/j.enggeo.2007.10.009. [DOI] [Google Scholar]
- 94.Sharma, M., Agrawal, H. & Choudhary, B. S. Multivariate regression and genetic programming for prediction of backbreak in open-pit blasting. Neural Comput. Appl. 1–12 (2022).
- 95.Corrêa JM, Farret FA, Popov VA, Simões MG. Sensitivity analysis of the modeling parameters used in simulation of proton exchange membrane fuel cells. IEEE Trans. Energy Convers. 2005 doi: 10.1109/TEC.2004.842382. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.