Shaping bacterial gene expression by physiological and proteome allocation constraints

Abstract

Networks of molecular regulators are often the primary objects of focus in the study of gene regulation, with the machinery of protein synthesis tacitly relegated to the background. Shifting focus to the constraints imposed by the allocation of protein synthesis flux reveals surprising ways in which the actions of molecular regulators are shaped by physiological demands. Using carbon catabolite repression as a case-study, we describe how physiological constraints are sensed through metabolic fluxes, and how flux-controlled regulation gives rise to simple empirical relations between protein levels and the rate of cell growth.

Introduction

The mechanics of protein expression in bacteria follow straightforwardly from the Central Dogma of molecular biology: a gene designated for expression is transcribed into mRNAs by RNA polymerases and subsequently translated into proteins by ribosomes. Regulatory mechanisms modulating each step of this process, including transcriptional and post-transcriptional control, have been studied in detail for numerous systems^1–5. Yet, the Central Dogma is only one part of what it takes to determine the concentrations of proteins in living cells (Fig. 1A).

Figure 1: Physiological constraints on gene expression.

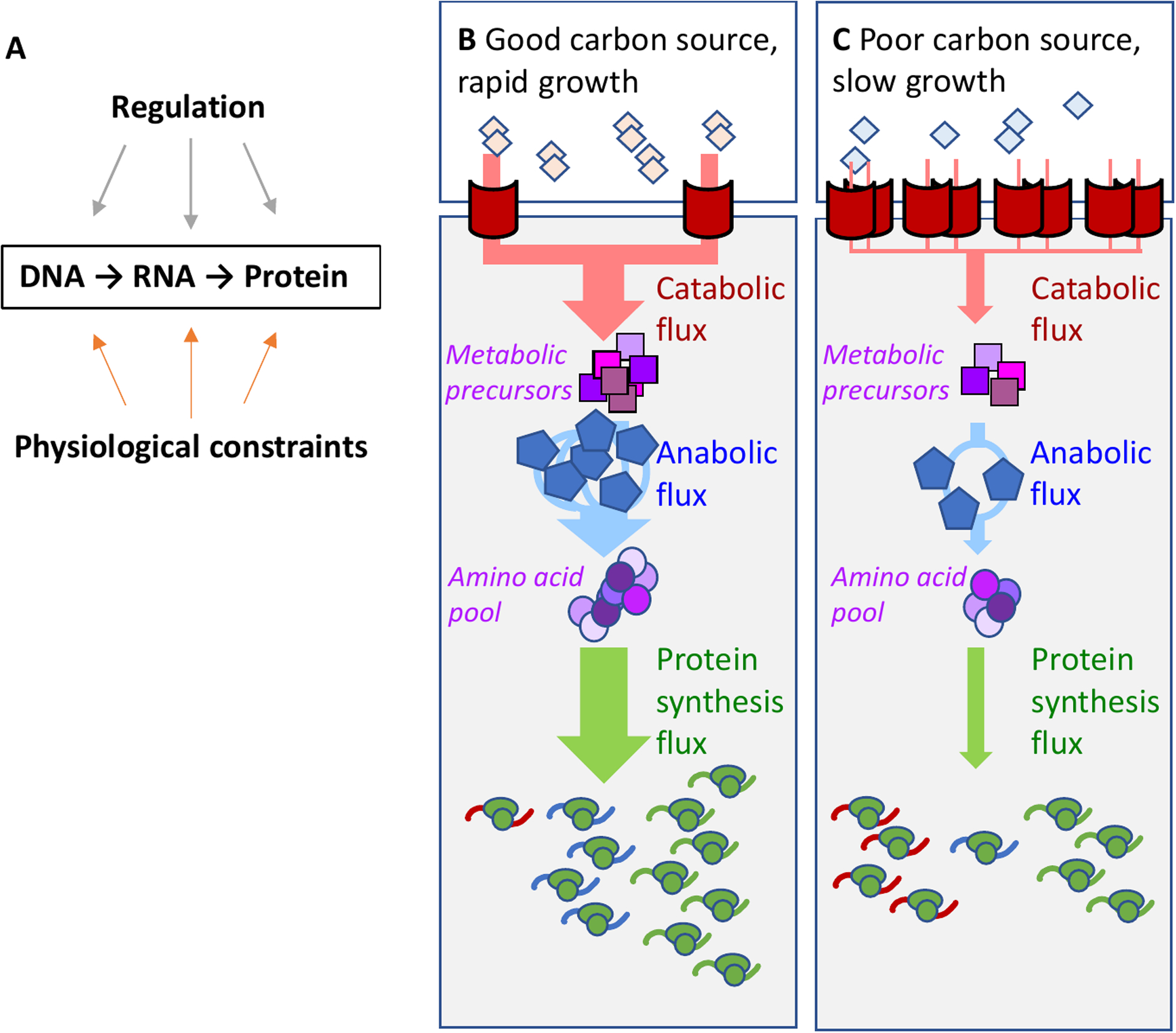
a. Protein expression in bacteria follow straightforwardly from the central dogma of molecular biology: a gene designated for expression is transcribed into mRNAs by RNA polymerases and subsequently translated into proteins by ribosomes. Protein expression is constrained by direct regulation and physiological constraints arising from cell growth. b,c. The external carbon source (diamonds) is imported and processed to metabolic pre-cursors (purple squares) via catabolic proteins (here represented by the red transporters), then converted into amino acids (purple circles) via anabolic enzymes (blue pentagons), and further assimilated into peptides via ribosomes (green ovals). The curly lines in the lower part of each panel denote the mRNAs, with color corresponding to each protein type. In a good carbon source (b), rapid exponential growth necessitates high metabolic fluxes (thick arrows). This requires a large concentration of ribosomes and anabolic enzymes; the concentration of catabolic proteins must be small to satisfy the constraint on total protein density. To maintain this proteome composition, more ribosomes must be allocated to synthesize ribosomes and anabolic enzymes than catabolic proteins, represented by a larger fraction of ribosomes translating the ribosomal and anabolic enzyme mRNAs. In a poor carbon source (c), the growth rate, and hence the metabolic fluxes, are greatly reduced (thin arrows). The demand for anabolic enzymes and ribosomes is reduced, and their concentrations are therefore reduced; whereas the concentration of catabolic proteins is increased to increase the carbon influx. This altered proteome composition is maintained by a larger fraction of ribosomes translating the catabolic enzyme mRNAs. The constraint on protein density is illustrated by having the same number of proteins (red, blue and green) in panels b and c.

Protein concentrations are affected not only by their synthesis, degradation, and dilution, but also by the cytoplasmic volume. The bacterial cytosol is densely packed with proteins that catalyze biochemical reactions, anchor structural components, and regulate gene expression, as well as macromolecular machinery responsible for transcription and translation⁶. Keeping protein concentrations high is obviously an advantage as it increases all the metabolic fluxes for the same number of proteins per cell; however, overly crowded cytoplasm would slow down molecular diffusion and eventually limit key cellular processes^7–9. Empirically, the biomass density is found to be approximately constant for several microorganisms grown under a variety of conditions^6,10–13. This constraint is not related to cell size and may arise from the homeostatic control of cytoplasmic water volume through intracellular osmolarity, as the biomass density changes primarily upon changes in external osmolarity^13,14.

Because protein is the major component of biomass and the lengths of typical proteins are similar, the invariance of the biomass density implies an approximate constancy of the total cellular protein density (also referred to as concentration)¹⁵. (in Escherichia coli, the protein concentration seems to vary less than 10% (Refs.^13,16)). This global constraint has a profound impact on the canonical notion of protein expression via the Central Dogma: Suppose the transcriptional activities of all genes are doubled and there is no post-transcriptional regulation in play, then one would naively expect all protein concentrations to be doubled. But this is not possible given the protein density constraint. Instead, if the concentrations of certain proteins are to be upregulated, then the concentration of other proteins need to be reduced to keep the protein density approximately constant. This can be achieved by downregulating the synthesis of designated proteins; if not, then the cytoplasmic water volume can increase to implement the total density constraint, resulting in an effective reduction in the concentration of all other proteins.

Protein density (or concentration):

The buoyant density is growth-rate independent under isotonic conditions. A constant density constraint (biomass/cell volume) therefore implies a constant concentration constraint (biomass / cell water volume). The cellular volume has strong growth-rate dependence, consequently we do not use protein-number-per-cell as an abundance measure in this Review.

For growing cells, another important constraint is that the macromolecular machinery needed for RNA and protein synthesis are required at different concentrations under different growth conditions17–19. In good nutrient conditions supporting fast growth, cells must maintain a high concentration of ribosomes and related translational machinery to satisfy the demand for a high flux of protein synthesis (because the speed of peptide elongation does not vary strongly across growth conditions²¹). This, coupled with the protein density constraint, immediately imposes the requirement that the concentration of non-ribosomal proteins must be reduced in fast growth. As a result, a growing bacterium is faced with a fundamental engineering problem of balancing the need for protein synthesis machinery to fuel biomass growth and the need to maintain sufficient concentrations of enzymes to generate fluxes of amino acids, nucleotides and energy to fuel protein synthesis and cell growth.

The focus of this review will be on the model bacterium Escherichia coli, for which these constraints have been quantitatively characterized. Consider, for example, adjustments in the macromoleular composition of the cell when the growth rate is modulated by the carbon source, as illustrated by the schematic shown in Fig. 1. With good carbon sources such as glucose (Fig. 1B), E. coli doubles quickly, which requires high metabolic fluxes (thick arrows) mediated by high concentrations of ribosomes (in green) and enzymes for biosynthesis (in blue). Maintaining high concentrations requires high synthesis rates of these proteins (indicated by mRNA of like-color in the lower part of Fig. 1). In poor nutrient conditions (Fig. 1C), the metabolic fluxes are reduced (thin arrows), with a consequent reduction in the concentrations of biosynthetic enzymes and ribosomes, and increased concentrations of catabolic proteins including transporters (in red).

The approximate constancy of protein density and the required allocation of macromolecular machinery for growing cells are two important examples of ‘physiological constraints’ that sculpt the outcome of direct regulatory interactions in the cell. In this review, we will describe several features of protein expression that appear surprising when viewed as a result of the Central Dogma modulated by regulators but become quite natural when viewed as consequences of these physiological constraints. Physiological constraints are meant as inviolable, operating independently of possible notions of optimality. In fact, as we detail below, the regulation that E. coli uses to satisfy these operating constraints can be sub-optimal in terms of, for example, growth-rate maximization.

Physiological constraint on protein synthesis

The constraints that exponential growth imposes on the protein synthetic machinery are revealed by tracking the cellular ribosome concentration²². The total cellular RNA is proportional to the number of ribosomes across growth conditions¹⁷, so total RNA-per-total protein-mass abundance is a convenient proxy for ribosome concentration²². Fig. 2A shows that for an exponentially growing culture, the RNA-protein ratio exhibits a simple linear correlation with the growth rate (solid black line), one of the “bacterial growth laws” known since 1960s²³. This linear relation, also referred to as the ‘R-line’²⁴, , was understood early on^23,25: To grow twice as fast requires the cell to synthesize proteins twice as quickly. Under moderate-to-fast growth conditions where empirically the peptide elongation rate by the ribosome is nearly constant²¹, the only way to double the protein synthesis rate is by doubling the ribosome concentration²³. Along with the R-line, the constancy of protein density imposes a complementary constraint: if the cell is to allocate more of its protein synthesis flux towards ribosomal proteins, then the synthesis (and hence concentrations) of some other proteins must decrease. Therein lies the fundamental constraint on protein synthesis. An illustrative case is provided by the growth dependence of the concentration of an unregulated protein (which provides the starting-point for analyzing the growth dependence of more complex regulatory motifs²⁶). Fig. 2B uses the activity-per-total protein-mass of a reporter enzyme (β-galactosidase) as a proxy for its abundance in terms of reporter concentration. When growth rate is modulated by changes in the nutrient quality , the concentration of an unregulated protein exhibits the opposite growth-rate dependence from the ribosome concentration, decreasing as the growth rate increases^22,27 (solid line, Fig 2B).

Figure 2: Growth-dependence of ribosomal and non-ribosomal proteins.

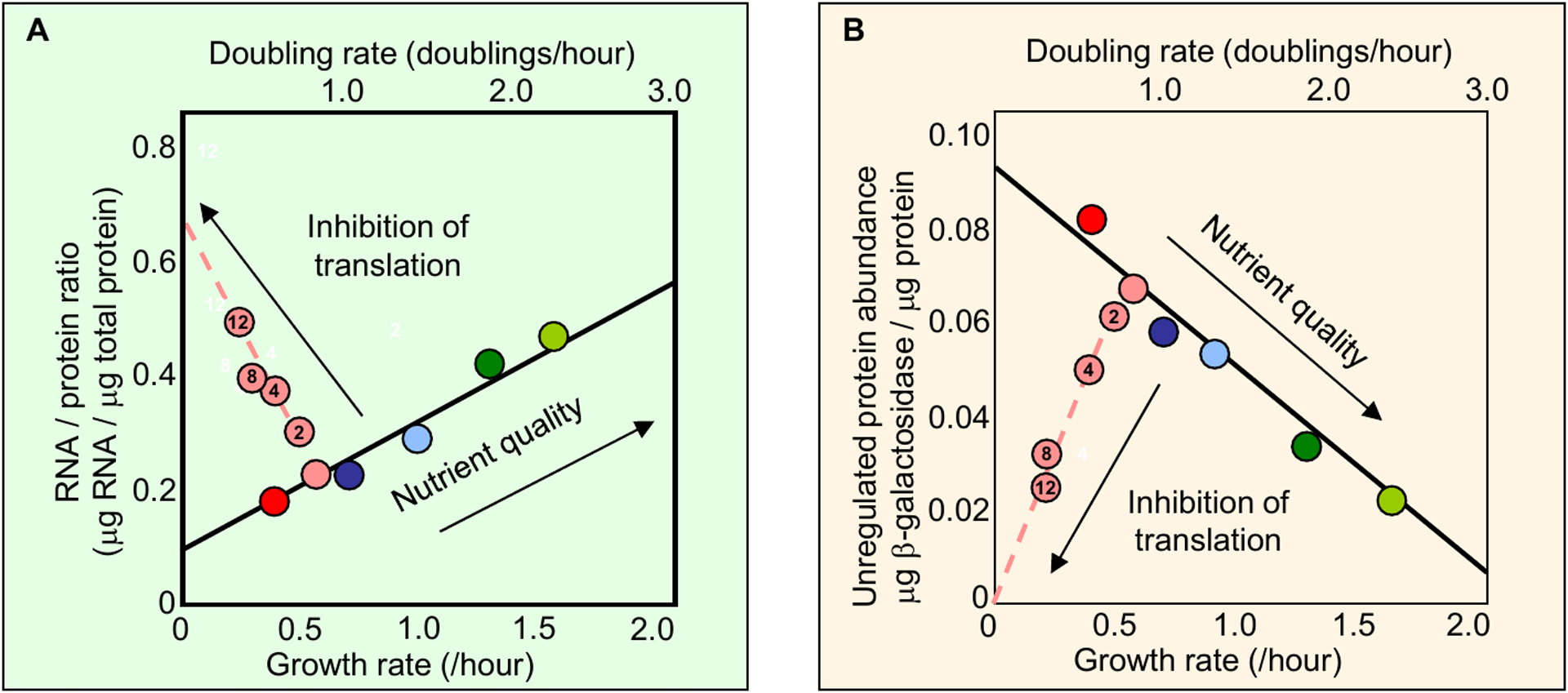
Escherichia coli cells are cultured to grow exponentially at different growth rates by using different nutrients (colored symbols along the solid black lines) or by applying various sub-lethal concentrations of translation-inhibiting antibiotics for a given nutrient (dashed lines, μM chloramphenicol shown inside the circles). Panel a shows that the RNA:total protein ratio, which is proportional to the ribosome concentration, exhibits approximate linear dependence on the growth rate: the dependence is positive when changing nutrient quality (solid line) and negative when changing antibiotic concentration (dashed line). Panel b shows that the concentration of an unregulated protein (pTetO1 driving lacZ (β-galactosidase) expression, using the activity:total protein ratio as a proxy) also exhibits approximate linear dependence on the growth rate, but in the opposite directions from that of the RNA:protein ratio shown in a. Comparing both panels, the strong anti-correlation between the concentration of ribosomes and the concentration of a constitutive protein suggests a linear constraint (like a see-saw) operating between them. The data are taken from Figs 2A and 2C of Scott et al.²².

Per-total protein-mass abundance:

The concentration constraint (biomass/cell water volume) allows a direct conversion between the concentration ((number of a particular molecule)/(cell water volume)) and its abundance relative to total protein mass ((number of a particular molecule) /(total protein mass)) assuming that the biomass contains a fixed fraction of protein.

R-line:

R-line: The positive correlation between the abundance of protein-synthetic machinery (chiefly ribosomes) and growth rate when growth rate is modulated by nutrient quality.

Unregulated protein:

Protein expression not subject to any transcriptional or post-transcriptional regulation.

Nutrient quality:

The exponential growth rate can be modulated by changing the carbon source, nitrogen source or enriching the medium with amino acids and nucleotides.

Experimentally, there are a variety of methods to investigate the coupling between growth rate and ribosome concentration. Early studies used changes in nutrient quality to modulate growth^23,28; other modes of growth-rate modulation include physical methods (e.g., changes in temperature^28,29, or osmolarity⁹), biochemical methods (e.g., using sub-inhibitory levels of antibiotics²²), and genetic methods (e.g., auxotrophy²⁸, or via expression of toxic³⁰ or unnecessary proteins²²). Sub-lethal levels of translation-inhibiting antibiotics provide a particularly illuminating method of growth modulation. In contrast to nutrient-limited growth with unperturbed translational elongation rate, ribosome-targeting antibiotics probe an ‘orthogonal’ scenario: translation-limited growth with nutrient quality held fixed. Under conditions of translational inhibition, the ribosome concentration exhibits a strong (near-linear) negative correlation with growth rate. As with nutrient-modulated growth, the concentration of unregulated proteins exhibits the opposite growth-rate dependence from that of the ribosomes (dashed lines, Figs. 2A, 2B). Translation-inhibited growth highlights the fundamental constraint on protein synthesis: whatever growth dependence is observed in the ribosomal concentration, the opposite growth dependence is observed in the concentration of an unregulated protein. The near-perfect anticorrelation between the two solid and two dashed lines in Figs. 2A, 2B suggests a linear constraint operating between ribosomal protein concentration and the concentration of all other proteins in the cell. The bulk of non-ribosomal proteins are devoted to metabolic enzymes. Below, we consider carbon-catabolite repression to illustrate the dramatic effect that the protein-synthesis constraint can have on shaping the regulation of metabolic gene expression.

Effect of the protein-synthesis constraint on carbon catabolite repression

Metabolic proteins are responsible for assimilating environmental nutrients to fuel biomass growth. Core metabolic tasks, including catabolism and anabolism, must be coordinated to ensure balanced growth³¹. Carbon catabolite repression (CCR) refers to reduction in the expression of carbon catabolic proteins during steady-state growth on a good carbon source compared to a poor one³². The phenomenon of choosing a distinct carbon substrate for consumption in media with multiple carbon substrates, sometimes referred to interchangeably with catabolite repression^33,34, will be discussed further below in the context of hierarchical carbon utilization.

Carbon catabolic proteins:

Proteins responsible for the transport and break-down of extracellular carbon sources. Operationally, these are genes regulated by cAMP-Crp.

Early studies of CCR focused on the chemical origin of the substrate for the apparent suppression of specific catabolic enzymes in the presence of glucose³⁵ (Box 1). Later, CCR came to be understood as a manifestation of a more general strategy whereby the accumulation of a group of intermediate metabolites produced by carbon catabolism (‘catabolites’) signal a flux-mismatch between carbon catabolism and consumption of these catabolites by anabolism³². Beyond catabolic proteins that are directly induced by their cognate substrate, in E. coli a large fraction of the proteome is coregulated to respond to changes in carbon availability even though many of these proteins carry no flux under these conditions¹⁹. Cyclic adenosine monophosphate (cAMP) antagonizes CCR^36,37; with the subsequent discovery of the cAMP receptor protein (Crp) and its role in activating the expression of induced carbon-catabolic gene expression³⁸, the direct regulatory mechanism responsible for catabolite repression in E. coli was resolved.

Box 1: The glucose effect and carbon catabolite repression.

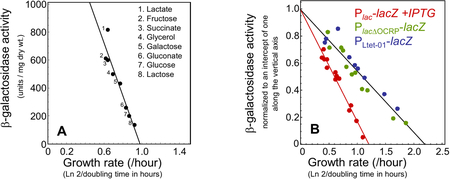
‘Carbon catabolite repression’ (CCR) was coined by Magasanik³² to replace what had previously been referred to as the ‘glucose effect,’ whereby the presence of glucose in the growth medium was seen to correlate with a reduction in the synthesis of catabolic enzymes responsible for breaking down carbon substrates other than glucose. Data by Mandelstam³⁹ illustrates the phenomenon: Carbon sources (such as glucose) that support rapid growth result in lower catabolic enzyme expression as compared to carbon sources (such as lactate) that support slower growth. A scatter plot of the data (A) shows a striking negative linear correlation between the activity of β-galactosidase (Plac-lacZ) and the growth rate; see also red symbols in (B) for β-galactosidase in a wildtype E. coli strain fully induced by IPTG.

Regulation by cAMP-Crp is necessary to produce the distinct growth dependence of carbon catabolic gene expression. If the Crp binding site in the lac promoter in scrambled (B, PlacΔOCRP green symbols), then the growth dependence of the expressed gene reverts to the canonical unregulated growth dependence (B, PLtet-O1 blue symbols; compare with the solid line in Fig. 2B). To facilitate comparison, the activities in panel B were scaled so that a linear fit through the data intercepts the vertical axis at 1. Data in panel A is from Mandelstam³⁹; data in panel B is from Figs. 1A (red), S10A (green) and S10B (blue) of You et al.²⁴.

Yet the physiological trigger of cAMP synthesis was never settled conclusively, and seemingly anomalous results kept the case from being closed: It has been long established that the synthesis of cAMP is inhibited by glucose transport⁴⁰, via the the phosphoenolpyruvate-dependent carbohydrate:phosphotransferase system (PTS)^41–44; however, growth on PTS-independent carbohydrates, as well as limitations in nitrogen or phosphorous, also affected the cAMP pool and consequently the degree of CCR^45–49. These anomalies, and subsequent work^52,53, brought into question the unique role of cAMP-Crp in the modulation of carbon catabolic protein expression⁵⁰, and began an unsuccessful search for additional regulators⁵¹.

Growth on single carbon sources

By attending to the carbon flux carried by catabolism and anabolism, in addition to constraints on protein synthesis, it becomes possible to disentangle the regulation-centric view of CCR from intrinsic protein-synthesis constraints on gene expression. Recent work supports the view that CCR acts primarily to coordinate metabolic flux, and identifies ketoacids as the metabolic node responsible for conveying a flux-mismatch between catabolism and anabolism²⁴.

Similar to the protein-synthesis constraints on ribosomal and non-ribosomal proteins (Figs. 2A, 2B), the protein-synthesis constraints on catabolism and anabolism are characterized by independently varying carbon and nitrogen flux, then observing how the cell adjusts the concentration of flux-carrying enzymes. The balance between carbon catabolic flux and anabolic flux can be shifted in several ways. Early studies focused on varying the composition of the growth medium^39,52 and using amino-acid auxotrophs^51,53; more recent work uses inducible promoters to dial the expression of key metabolic enzymes. Figure 3 shows a concrete example from You et al.²⁴, who dialed the expression of lactose permease to modulate carbon (lactose) influx in lactose minimal media, and dialed the expression of glutamate dehydrogenase (GDH) to modulate anabolic flux via limiting amino acid synthesis (Fig. 3A, dashed boxes). A proxy for the concentration of carbon catabolic proteins is (IPTG-induced) β-galactosidase (Fig. 3B), whereas a proxy for the concentration of anabolic proteins is glutamine synthetase (Fig 3C).

Figure 3: Modulation of carbon and nitrogen flux reveals protein-synthesis constraints on catabolic and anabolic proteins.

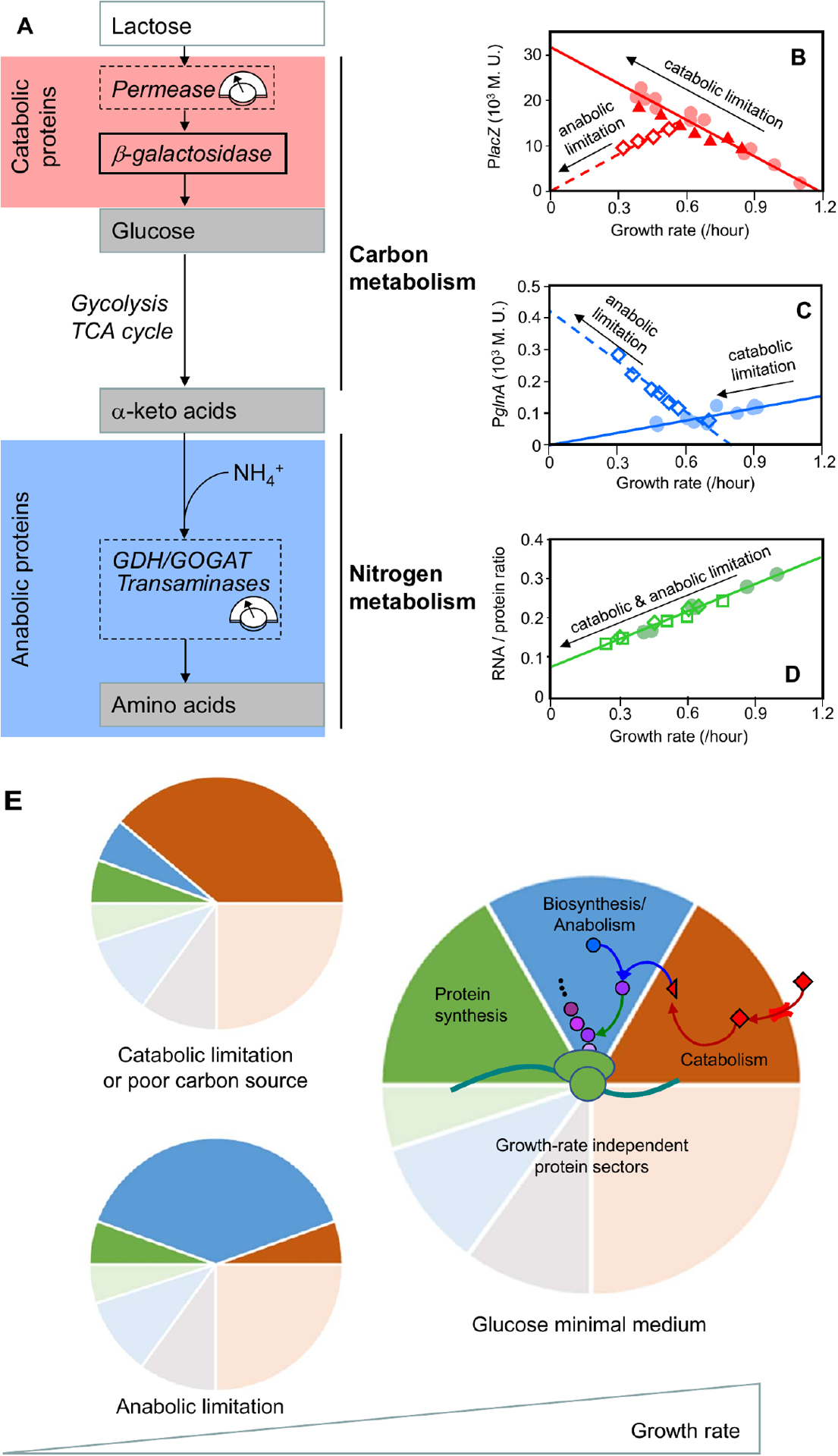
a. In a minimal growth medium without externally supplied amino acids, the bacterium must synthesize amino acids via amination of carbon precursors (ketoacids)⁵⁴. These precursors are supplied through the carbon-catabolic enzymes, glycolysis, the tricarboxylic acid (TCA) cycle, and various biosynthesis pathways. To minimize substrate-specific effects, carbon influx was modulated by titrating the expression of the uptake system (lactose permease for growth on lactose²⁴) or by changing the carbon source in minimal medium. The nitrogen flux was modulated by titrating glutamate dehydrogenase (GDH) in a glutamine oxoglutarate aminotransferase (GOGAT)-deleted background²⁴, or by titrating GOGAT in a GDH-deleted background²⁷. The flux-control points are denoted by dashed boxes. b–d. Proxies for the carbon-catabolic and anabolic protein concentrations are β-galactosidase activity (lacZ; panel b) and glutamine synthetase activity (glnA; panel c), respectively. These proxies quantitatively capture the behavior of many other catabolic and anabolic proteins, as validated by later proteomic work^15,27. Carbon-catabolic and anabolic enzyme concentrations exhibit obvious anti-correlation and near-linear growth dependence under various growth perturbations, whereas the ribosomal proteins exhibit a positive linear correlation with growth rate irrespective of the metabolic limitation that is used (RNA:protein ratio; panel d. The red line in panel b is sometimes called the ‘C-line’²⁴, and can be taken as a defining feature of carbon catabolite repression (Box 1). Carbon flux was modulated by a change in carbon source (filled circles), or by titrating lactose permease (filled triangles); nitrogen flux was modulated by titrating GDH in a GOGAT-deleted background (open diamonds). e. The correlations among the abundances of catabolic, anabolic and ribosomal proteins can be understood quantitatively if abundance is measured in units of protein mass fraction. The constancy of protein density and the allocation constraint on the protein synthetic machinery are both captured by a coarse-grained partitioning of the proteome. For simplicity, only four sectors are shown: growth-rate dependent ribosomal (and ribosome-affiliated) (green), biosynthetic/anabolic (blue) and catabolic (red) sectors, along with their associated growth-rate independent basal expression (pale sectors), and a growth-rate independent sector (gray)²⁷. The near-linear response of the growth-dependent sectors is rationalized by invoking a simple flux balance: external nutrients are converted to carbon precursors by the catabolic proteins (red arrows) and converted into amino acid precursors (purple circles) by the biosynthetic proteins (blue arrow), at a rate matched with amino acid consumption by protein synthesis (green arrow). Catabolic limitation leads to increased expression of catabolic proteins (top left), whereas anabolic limitation leads to increased expression of anabolic proteins (bottom left). Rightmost figures from Figs. 1A, 1C, 1D of You et al.²⁴.

Under conditions of lactose limitation, the concentration of β-galactosidase exhibits a negative correlation with growth rate, and a zero-expression intercept at a specific growth rate of λ_C ≈ 1.2 /h (Fig. 3B, red solid line; contrast with the zero-expression limit of an unregulated protein, which is at approximately 2.2 /h as shown in Box 1B). The same growth-dependent behavior in the concentration of carbon-catabolic proteins is produced when growth rate is modulated by changes in the carbon source (see Box 1A). Other forms of carbon limitation (e.g., titration of glycerol uptake) exhibit an identical response, and so we will refer to the negative correlation between the concentration of β-galactosidase and the growth rate as the ‘carbon catabolism-limited response’ of the carbon catabolic genes. This negative linear correlation of carbon catabolic gene expression is synonymous with carbon catabolic repression, and has been referred to as the ‘C-line’²⁴.

Box 2: Equivalence between ribosome allocation and proteome mass fraction.

During balanced growth, the allocation of shared macromolecular machinery provides a characteristic profile of the cell physiology. Because the lengths of most proteins are similar, the protein mass fraction gives approximately the protein number fraction; the latter is approximately proportional to the cellular concentration of that protein because the total protein content per-cell-volume is approximately constant (see text). Using the estimate of 19 ±1 × 10⁻⁸ mg of total protein per μm³ of cell volume^12,16 and a typical protein length of 250 amino acids^16,19 (with an average molecular weight of 108 Daltons per amino acid), a protein mass fraction of 1% in E. coli corresponds to a number density of 4.2 ± 0.3×10⁴/μm³ (see, also, the estimate of 3.4×10⁴/μm³ by Milo¹⁵).

In the absence of substantial proteolysis and secretion^55–57, the mass M_i of a given protein accumulates exponentially at rate λ, with the synthesis proportional to the total protein synthesis rate J_R and the fraction χ_i of translating ribosomes dedicated to that protein. Summing over all expressed proteins,

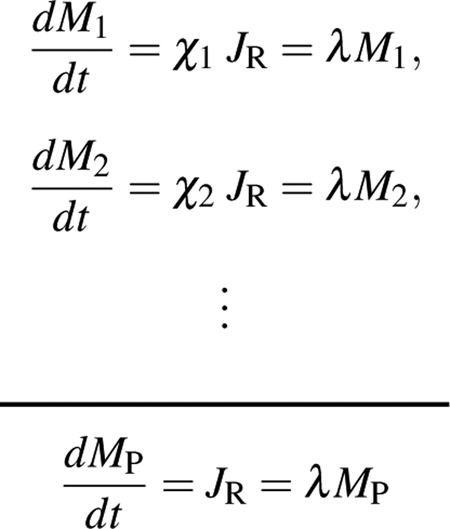The total protein mass M_P is the sum of all the constituent protein masses, M₁ + M₂ + … = M_P, and the fraction of translating ribosomes sums to one: χ₁ + χ₂ + … = 1. Dividing each individual protein accumulation equation by the sum,

$$\frac{{\chi }_i{J}_{\text{R}}}{J_{\text{R}}}=\frac{\lambda M_i}{\lambda M_{\text{P}}}\Rightarrow {\chi }_i=\frac{M_i}{M_{\text{P}}}={\varphi }_i$$

i.e., the steady-state fraction of ribosomes χ_i dedicated to translating a particular protein is identical to the protein mass fraction ϕ_i of that protein. This mathematical result has been exploited to yield accurate estimates of absolute abundances (in terms of the protein mass fraction ϕ_i) of stable proteins using the dedicated ribosome fraction obtained from ribosome profiling^58,59. Note that even for stable proteins, the dedicated ribosome fraction χ_i is generally different from the proteome fraction outside of steady-state; see Erickson et al.⁶⁰ and Fig. 5 in the main text.

C-line:

The negative correlation between catabolic enzyme expression and growth rate in minimal media when growth rate is modulated by carbon source.

The expression of the anabolic enzymes, using the reporter glutamine synthetase (GS, glnA) as a proxy, exhibits a clear anti-correlation with those of the carbon catabolic proteins. Under conditions of anabolic limitation, the concentration of anabolic proteins exhibit a negative linear correlation with growth rate (Fig. 3C, blue dashed line), whereas the carbon catabolic proteins exhibit a positive linear correlation with growth rate, passing through the origin (Fig. 3B, red dashed line). Under conditions of carbon catabolic limitation, the concentration of anabolic proteins exhibit positive linear correlation with growth rate, passing through the origin (Fig. 3C, blue solid line). Subsequently, carbon catabolism-limited and anabolism-limited response of the reporter enzymes was validated by proteomics measurements for a large number of catabolic and anabolic enzymes^19,27. The ribosomal concentration (which is proportional to the RNA/protein ratio under both carbon-catabolic and anabolic limitation) exhibits a positive linear correlation with growth rate (Fig. 3D) irrespective of growth limitation by catabolism or anabolism.

Anabolic enzymes:

Enzymes responsible for biosynthesis, including amino acid and nucleotide synthesis.

Using the protein mass fraction ϕ_i of an individual protein as a measure of cellular abundance (which we adopt henceforth) provides several advantages over concentration. First, in exponential growth the protein mass fraction of a given protein is equal to the fraction of ribosomes actively translating that particular protein (thereby manifesting the macromolecular machinery constraint; see Box 2). Second, all protein fractions must sum to one, thereby conveniently enforcing the constant-protein-density constraint.

Protein mass fraction:

The total number of a particular protein is proportional to its protein mass. Using the per-total protein-mass abundance defined above, the protein mass fraction ((protein mass of a particular protein)/(total protein mass)) is therefore a direct measure of concentration.

Using a series of growth perturbations and protein mass spectrometry, Hui et al.²⁷ found that individual proteins could be grouped together into a small number of sectors sharing a common response to growth rate change (Fig. 3E) (this was confirmed in a recent large-scale study by Mori et al.¹⁹). The cellular abundance of each individual protein is expressed as a protein mass fraction ϕ_i composed of a growth-independent (basal) component ${\varphi }_i^0$ and a growth-dependent component Δϕ_i(λ), where λ denotes the exponential growth rate,

$${\varphi }_i={\varphi }_i^0+\Delta {\varphi }_i(\lambda ).$$

With the proteome partitioned into proteome sectors, it becomes clear that if proteins in one sector increase in mass fraction, then other sectors must decrease to accommodate the change (Fig. 3E, small panels). Thus, the combination of constraints on total protein synthesis flux and on total cellular protein concentration leads to a constraint on the composition of individual protein concentrations as represented by the pie chart (Fig. 3E), which we call the ‘proteome allocation constraint.’

Proteome:

The set of all expressed proteins in a given growth condition.

Proteome sectors:

Subsets of the proteome that exhibits similar growth-rate dependence under various growth conditions.

Irrespective of the method of growth perturbation, all of the growth-dependent protein sectors exhibit a linear dependence on growth rate, and enzymes with correlated expression are found to largely share common functionalities (e.g. protein synthesis, carbon catabolism, amino acid biosynthesis)²⁷. This behavior is rationalized by assuming that the flux carried by enzymes in that sector is proportional to the sum of the growth-dependent fractions of those enzymes^27,61,

$$\begin{array}{cc}\begin{array}{l}\Delta {\Phi }_{\alpha }=\sum _{i\subset \alpha }\Delta {\varphi }_i,\\ \text{enzymes in sector }\alpha \end{array}& \begin{array}{l}\text{flux through enzymes}\\ \text{contained in proteome }={\kappa }_{\alpha }\Delta {\Phi }_{\alpha }(\lambda )\\ \text{sector }\alpha \end{array}\end{array}$$

where κ_α is a growth-rate independent factor characterizing the effective catalytic constant for the coarse-grained activity of that sector. It is important to note that although all proteins within a given sector α are co-expressed, not all proteins in that sector may be carrying flux in any particular growth condition¹⁹. The proteomic data of Hui et al.²⁷, which support the hypothesis that the enzyme-catalyzed reaction flux is proportional to the growth-dependent protein mass fraction ΔΦ_α, provides a quantitative, empirical framework for coupling flux-balance analysis with proteome allocation constraints⁶².

Assuming a flux balance between carbon catabolism and anabolism, as required by exponential growth, the linearity of the growth-dependent response of each metabolic sector implies that the flux is proportional to the growth-dependent protein fractions. Denoting the growth-dependent mass fraction of carbon-catabolic proteins by ΔΦ_C and the growth-dependent mass fraction of anabolic proteins by ΔΦ_A, the flux balance constraint is expressed succinctly as,

$${\kappa }_{\text{C}}\Delta {\Phi }_{\text{C}}={\kappa }_{\text{A}}\Delta {\Phi }_{\text{A}}$$

where κ_C and κ_A are proportionality constants that quantify the overall catalytic efficiency of each sector. Beyond the linearity of the response, the second striking feature of the data shown in Figs. 3B, 3C is the anti-correlation between the catabolic and anabolic protein sectors, implying a second proteome allocation constraint operating in addition to the overarching constraint illustrated in Fig. 2.

Altogether, the data suggest a hierarchical scheme of proteome allocation – first, the amino acid demands of protein synthesis determine the allocation of the growth-dependent sectors of the proteome between ribosomal proteins (setting amino acid consumption flux) and metabolic proteins (setting the amino acid supply flux; see Fig. 2)⁶³. Within the metabolic proteins, a second balance is struck between carbon catabolism and anabolism.

Coordination of flux-balance and proteome allocation constraints

The proteome allocation constraints lead to simple, linear dependence of the protein mass fractions on the steady-state growth rate. Yet the constraints themselves reveal little about the underlying regulation responsible for this apparent simplicity. Much is known about the molecular regulators that control expression of these large proteome sectors, ppGpp⁶⁴ in the case of the ribosomal proteins and cAMP-Crp⁴¹ in the case of carbon catabolic proteins. Here we discuss these signaling pathways in the context of proteome-allocation constraints and flux-balance.

The ribosomal protein mass fraction (denoted by Φ_R in Fig. 4) is set by the flux of ribosome biogenesis, which is inhibited by ppGpp through the synthesis of ribosomal RNA⁶⁷. The synthesis rate of ppGpp itself responds negatively to the rate of translational elongation⁶⁹, with translation rate acting as an integrated sensor of the availability of all 20 amino acids. An accumulation of the amino acid pools relieves repression of ribosomal RNA transcription, leading to feedforward activation of ribosome synthesis. Subsequently, the increased rate of amino acid consumption reduces amino acid accumulation (Fig. 4, green box). In this way, the amino acid pools serve to balance protein synthesis and amino acid biosynthesis fluxes.

Figure 4: Coordination of catabolic and anabolic flux via cAMP–Crp signaling.

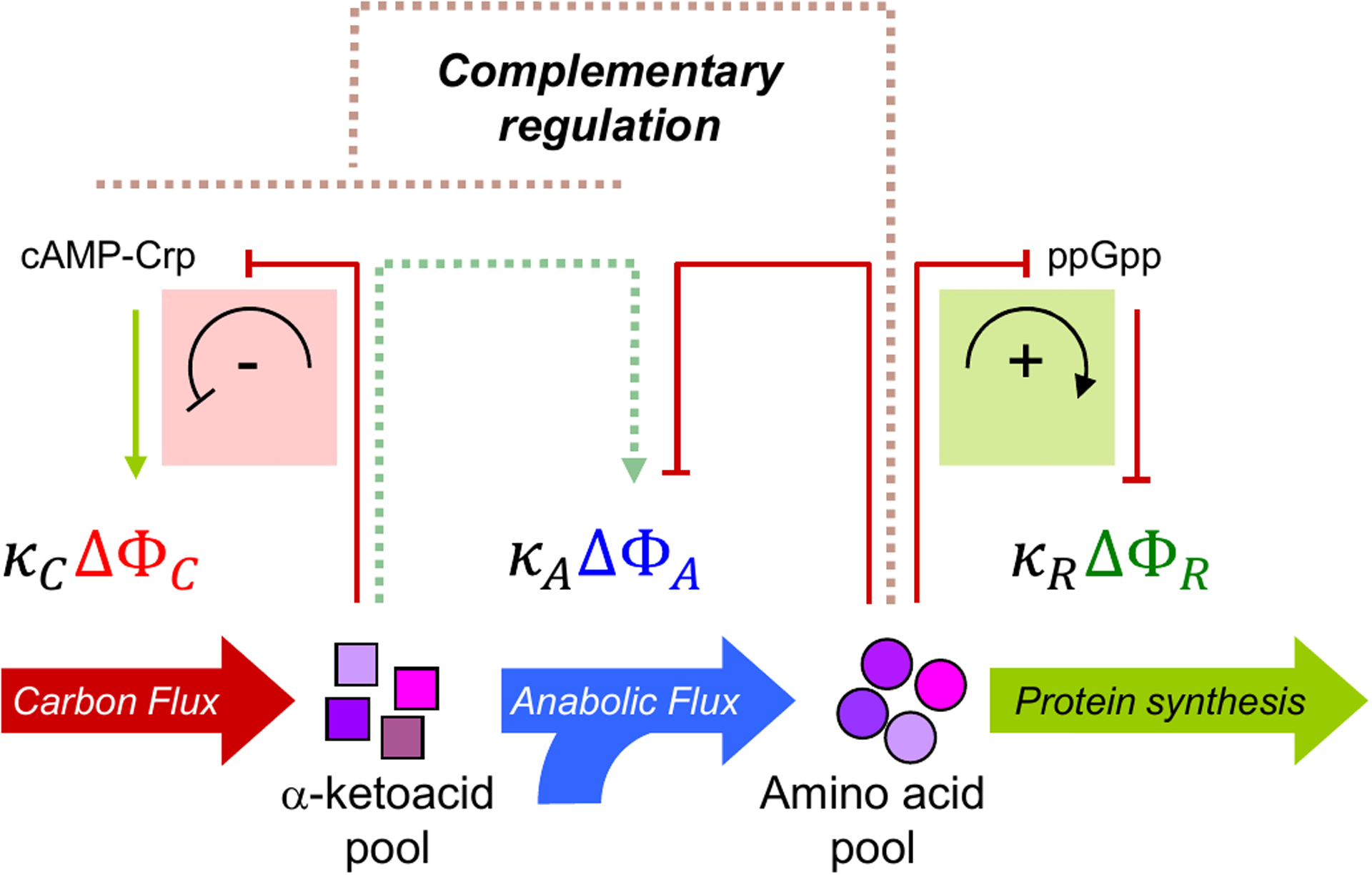
Two notable features of the growth dependence in the various protein fractions in Figs. 3b–d are the near-linear response and the strong anti-correlation. The linearity can be rationalized by assuming that the flux mediated by each sector is proportional to protein mass⁶¹, where the proportionality constants κ_i are a measure of the catalytic efficiency of each sector. The anti-correlation suggests the existence of complementary regulation to enforce the proteome-allocation constraints. The direct regulatory interactions are well-characterized (solid lines). Accumulation of α-ketoacids results in down-regulation of carbon-catabolic proteins (ΔΦ_C) by decreasing the activity of the global activator cyclic adenosine monophosphate (cAMP)–cAMP receptor protein (Crp) negative feedback loop indicated in the red box)⁶⁵. Accumulation of amino acids leads to upregulation of ribosomal proteins (ΔΦ_R) by decreasing the level of the alarmone ppGpp which represses ribosome biogenesis (positive feedforward loop indicated in the green box)^66,67. The biosynthetic proteins (ΔΦ_A) are directly regulated by end-product inhibition via individual amino acids⁶⁸ (red solid arrow). In addition to these direct mechanisms, proteome-allocation constraints necessitate anti-correlated, complementary regulation (complementary regulation is denoted by the dotted lines).

lux balance between carbon catabolism and biosynthesis is maintained by the regulatory complex cAMP-Crp which activates the expression of carbon-catabolic genes³⁸, whose abundance is denoted by Φ_C in Fig. 4. The readout of a flux-mismatch appears to be the ketoacid pool (e.g. α-ketoglutarate, pyruvate and oxaloacetate), with a build-up of ketoacids attenuating the synthesis of cAMP²⁴. Consequently, an increase in the ketoacid pools produces an effective feedback inhibition of the carbon-catabolic genes via downregulation of the activator cAMP-Crp (Fig. 4, red box). Less is known about the regulation of biosynthesis enzymes, whose abundance is denoted by Φ_A in Fig. 4. The abundance of biosynthetic enzymes is reduced under carbon-limited growth^19,24,27; this could arise from end-product inhibition mediated by the pool of individual amino acids and/or tRNAs⁶⁸ (red line), inhibition due to the lack of carbon precursors^24,65,70 (green dotted arrow), or passive effects of global regulation⁷¹ (red dotted line).

Despite divergent molecular mechanisms for achieving flux balance, there are two key regulatory motifs that allow E. coli to use the concentration of a signaling molecule to sense and control flux (Box 3). A persistent feature of the proteome fractions is the linear growth-rate dependence under various modes of growth limitation. Flux-based regulation provides a mechanism to generate a linear relation between the flux and the enzyme concentration. Consider, for example, the feed-forward scheme illustrated in Box 2, figure part a. If the concentration of an active enzyme Z is directly proportional to the concentration [S] of a signaling molecule S; that is, [Z] = c[S], and if the flux through the enzyme Z has a Michaelis–Menten dependence on the signalling molecule S; that is, ν = k_cat[Z][S]/(K_S + [S]), then a linear relation between flux and the total enzyme concentration is obtained over a range of fluxes (as long as the flux is not too small), with

$$\left[\mathit{\text{Z}}\right]=\mathit{\text{a v}}+\mathit{\text{b}},$$

where $a\approx k_{\text{cat }}^{-1}$ is the slope and b ∝ c K_S is the flux-independent offset. This relation would readily give rise to a linear dependence of the enzyme concentration on the growth rate λ, because many metabolic fluxes are proportional to the growth rate⁷⁸.

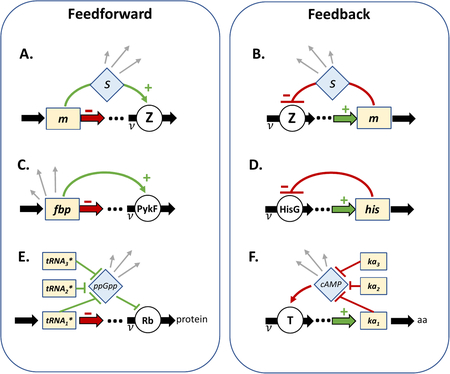
Box 3: Implementation of flux-controlled regulation.

Flux-controlled regulation shares common features (see the figure, parts A and B):

• The abundance of a metabolite pool m is affected by the pathway-flux ν modulated by an enzyme Z.

• The activity of the enzyme Z uniquely determines the pathway-flux ν.

• A signaling molecule s determines the activity of the enzyme Z.

• The concentration of the signalling molecule s responds to the metabolite pool m to provide stable feedback.

Here we describe implementations of the core motifs. (C) Kochanowski et al.⁷² have characterized a glycolytic flux sensor⁷³. The metabolite fbp is an allosteric activator of the downstream enzyme PykF. The flux ν through the pathway consumes, and hence depletes, fbp (thick red arrow), but the activation of PykF by fbp (green regulatory link) ensures flux-balance. End-product inhibition is another common flux-responsive regulatory strategy. In the histidine biosynthesis pathway (D), histidine (his) is an allosteric inhibitor of the upstream enzyme HisG⁷⁴. If the flux of histidine synthesis (thick green arrow) does not balance the incorporation into protein synthesis, negative feedback (red regulatory link) acts to restore the balance. In panels C and D, the metabolite pool acts as its own signalling molecule. If the flux depends upon a spectrum of metabolites, then a signaling metabolite s is necessary to integrate their combined effect on the pathway-flux as is the case in the regulation of protein synthesis (E) and carbon catabolic protein expression (F). Ribosomes convert charged tRNA (tRNA^⋆) to proteins (E, thick red arrow). The regulatory link⁶⁷ from the charged tRNA to ribosome abundance involves a signaling molecule⁷⁵, ppGpp, which detects the shortage of any one of the charged tRNAs by monitoring the ribosome elongation rate⁶⁹. The double-negative regulation results in an overall positive connection between charged tRNA and ribosome abundance (green regulatory links). Ketoacid pools (ka) report on total carbon flux ν (F, thick green arrow), and are supplied by the carbon catabolic enzymes denoted by the transporter T. The ketoacids inhibit the synthesis of cAMP²⁴, which activates the expression of many catabolic enzymes³⁸, resulting in an overall negative connection between ketoacid pools and catabolic enzyme abundance (red regulatory links). Signalling molecules such as ppGpp^76,77 and cAMP^31,41 are global physiological signals that are used to regulate numerous other operons (grey arrows), effectively coupling the expression of many distal genes to the pathway-flux ν, driving coherent global changes observed in proteome dynamics.

The simplest way to realize this regulatory scheme is for the signaling molecule S be the substrate of the enzyme Z, or the substrate of another reaction in the same linear pathway as Z (and hence sharing the same flux). The latter has been demonstrated explicitly for the glycolytic enzyme PykF⁷² (Box 3C), for which the linear dependence between flux and enzyme abundance is expected to hold so long as the enzyme is biased to operate in the regime of excess substrate [S] ≥ K_S (such is the case for many metabolic enzymes^61,79). A more elaborate implementation of this regulatory scheme is known for ribosome biogenesis (Box 2, figure part e). In this case, the charged tRNAs are the substrates of the ribosomes^8,80, and ppGpp is the signal that integrates the different substrates. An effective Michaelis–Menten relation between the substrates and the flux, assumed in past phenomenological studies^8,21,80,81, is shown to be regulated molecularly by ppGpp via its response to translational elongation rate on the one hand and its regulation of rRNA and tRNA on the other⁶⁹.

Under conditions of severe growth-limitation, the linear relation generated by the simple scheme above would break down; however, the relation between the ribosome concentration and growth rate in E. coli is still found to be approximately linear when grown in very poor carbon sources²¹ or carbon-limited chemostat⁸². The maintenance of this linear relation has recently been suggested⁶⁹ to involve the additional regulation of the translational activity of the ribosome, by employing ribosome hibernating factors to make the majority of ribosomes inactive at very slow growth⁸³. In nitrogen-limited growth⁸², by contrast, it appears that tRNA charging (primarily glutamine) becomes rate-limiting, whereas in phosphate-limited growth⁸², the decreased synthesis of nucleic acid itself reduces ribosome abundance. How N- and P- limitations lead to their corresponding ribosome abundances is not understood at the same quantitative level as carbon limitation.

The right column of Box 3 shows a similar regulatory motif implemented by a feedback circuit (Box 3B). Qualitatively this regulatory motif is established for a broad range of metabolic systems including amino acid biosynthesis (Box 3D) and catabolite repression (Box 3F), although the details of how the catabolite repression circuit senses flux and leads to the C-line (Fig. 3B) have yet to be quantitatively established.

Growth on multiple carbon sources

Microbes exhibit preferential utilization when presented with several substitutable carbon sources³³. While this was demonstrated by Monod in the context of kinetic growth transitions⁸⁴, the phenomenon of preferential nutrient usage can be elucidated quantitatively in steady-state growth^85,86. For E. coli, it was observed that most pairs of glycolytic carbon sources are hierarchically utilized, whereas pairs of gluconeogenic carbon sources are simultaneously utilized, as are combinations of the two types⁸⁵. The observed substrate utilization pattern has been rationalized in terms of the proteome cost involved in the conversion between glycolytic and gluconeogenic substrates⁸⁷, or more generally in terms of ‘elementary growth modes’⁸⁸; see Okano et al.⁸⁹ for a recent review.

Hierarchically utilized carbon sources:

In a mixture of carbon sources, these are carbon sources that are metabolized one-at-a-time.

Simultaneously utilized carbon sources:

In a mixture of carbon sources, these are carbon sources that are metabolized con-currently.

For those combinations that are simultaneously utilized, the uptake rate of each substrate is generally not equal: it is reduced in the presence of a co-utilized substrate, yet the steady-state growth rates on two substrates exceed that on either substrate alone. The same inverse linear relation between carbon catabolic enzyme expression and growth rate (‘C-line’) is observed for growth on various combinations of co-utilized carbon substrates, with the same intercept, λ_C=1.2 h-1 (Fig. 3B)⁸⁵. The common intercept λ_C implies that although the growth rate on multiple substrates increases with respect to a single substrate, there is a ‘speed limit’ imposed at λ_C. The co-utilization phenomenon can be accounted for quantitatively using the same flux-matching scheme as in the single-carbon case (now allowing for carbon influx from multiple sources). The resulting model can predict, using only carbon-limited speed limit λ_C, the growth rate on multiple substrates based on growth rates on individual substrates⁸⁵.

For the combinations of substrates that give rise to hierarchical usage, the preferred substrate is usually the one with a higher single-substrate growth rate. This preferred utilization can be converted to simultaneous utilization if the uptake rate of the preferred substrate is reduced below the uptake rate of the other substrate⁸⁶, indicating that the onset of preferred utilization is again controlled by a flux-controlled regulation scheme. Detailed analysis⁸⁶ identified the involvement of cAMP-Crp together with another substrate-specific regulator.

Growth transition kinetics

For controlling the kinetics of growth transitions, the cell needs to monitor its own state of growth which involves thousands of reactions. Which molecular species should the cell monitor to diagnose its own state of protein synthesis? A useful strategy, both for the scientists studying bacterial response and for the bacterium managing its own growth, is to capture key kinetic variables that reflect the coarse-grained dynamics of the cell^69,90.

The feedback/feedforward control schemes mediated by cAMP-Crp and ppGpp outlined in the previous sections (and shown schematically in Fig. 4) exhibit a common flux-controlled regulatory motif (Box 3). In both cases, flux-mismatch is measured by the accumulation of signaling molecules (α-ketoacids in the case of CCR, and amino acids in the case of ribosome biogenesis). The result of accumulation of the signaling molecule is a reduction of the supply flux along with a simultaneous increase of the consumption flux. A transformative effect of the cAMP and ppGpp signaling pathways is for the cell to condense, or coarse-grain, the large variety of individual metabolites (e.g., the different species of ketoacids for cAMP signaling²⁴ and the different amino acid/tRNA species for ppGpp signaling⁶⁹) onto the concentrations of just two molecular species, cAMP and ppGpp (Box 3E,F). In this way, the metabolites no longer participate directly in downstream regulation, but rather participate through their signaling molecules.

This qualitative coarse-graining picture does not, however, lend itself immediately to quantitative prediction because it remains largely unknown how cAMP and ppGpp synthesis/turnover respond to changes in the large number of metabolites they monitor. In the work of Erickson et al.⁶⁰, a simple coarse-grained framework was developed so that quantitative predictions of kinetic transitions (e.g., variations of the classic diauxic shift) can be made based on the gross topology of cAMP/ppGpp signaling (Box 3EF) and their effect on proteome allocation in the steady state (i.e., the C-line and the R-line in Fig. 3B and D), without the need to know any details of the signaling pathways. Instead of describing the complex regulatory interactions that link the concentrations of ketoacids and amino acids to cAMP and ppGpp signaling which control the expression of carbon-catabolic and ribosomal protein mass (Fig. 5, M_C and M_R), the authors postulated⁶⁰ that the flux-controlled regulation is driven by the translational activity σ, defined as the ratio between the protein synthesis flux, J_R, and the ribosomal protein mass, M_R. Growth kinetics are then determined by a simple dynamic loop involving the effect of the present allocation of the proteome (M_C and M_R) on translational activity, and the effect of translational activity on future allocation of M_C and M_R, via the regulatory functions χ_C and χ_R (Fig. 5). The form of the regulation functions, which are implemented by the signaling molecules cAMP and ppGpp and not known quantitatively, was bypassed in their treatment by using the relation between the regulatory functions χ_C,R and the translational activity σ in the steady state (easily obtained via empirical steady state correlations), and by assuming that the same relation determines the regulation function in the kinetic regime, where translational activity itself changes in time⁶⁰.

Figure 5: Flux-controlled regulation and proteome remodeling during growth transitions.

a. The steady-state growth-dependence of the various protein fractions enables quantitative characterization of the kinetics of growth transitions. The schematic network shown in Fig. 4 can be further simplified to emphasize the main (direct) regulatory loops. The α-ketoacids and amino acids are collected into a pool of ‘precursors’ that affect the magnitude of a single coarse-grained variable, the ribosome’s translational activity σ. The carbon uptake flux J_C is proportional to the carbon-catabolic protein mass M_C. It is matched to the protein synthesis flux J_R, which is proportional to the ribosomal protein mass M_R. The ratio of the flux J_R and the mass M_R defines the translational activity σ = J_R/M_R, which is the central dynamical variable regulating the expression of carbon-catabolic proteins (M_C, via cyclic adenosine monophosphate (cAMP)–cAMP receptor protein (Crp)), and ribosomal proteins (M_R, via guanosine tetraphosphate (ppGpp))⁶⁰. These direct regulatory effects are implemented through two regulatory functions, χ_C(σ), the fraction of ribosomes actively translating carbon-catabolic proteins, and χ_R(σ), the fraction of ribosomes actively translating ribosomal proteins. The quantitative form of the regulatory functions χ_C and χ_C are determined by the observed steady-state correlations of these quantities. In this way, the dynamic response of a bacterial culture to a shift in carbon substrate can be fully predicted by solving a single differential equation for the translational activity σ(t). From the solution, the dynamic remodeling of the proteome; that is, changes in the cellular mass of proteins for ribosomes (M_R(t)), carbon catabolism (M_C(t)), and anabolism (M_A(t)); can be obtained by integrating the regulatory functions χ_C(σ(t)) and χ_C(σ(t)), with the anabolic protein mass M_A(t) obtained from the constraint on total protein synthesis. For transitions between simultaneously-utilized carbon sources, the time course of growth kinetics and proteome remodeling can be predicted for both up-shifts and down-shifts, using only the above mentioned information on steady-state growth in the pre-shift and post-shift medium; see b and c for the relaxation of the instantaneous growth rate λ = d(lnM)/dt during two exemplary shifts (circles are data, solid black lines are predictions with no fitting parameters). Small modification of the same approach can also be used to capture the growth kinetics for shift between hierarchically utilized carbon sources. d Shown are the result of the classic diauxie between glucose and lactose, whereby a single fitting parameter is introduced to set the time point of the lac operon activation after glucose depletion. Dashed lines denote the final growth rate on the second substrate. Data from Figs. 1B, 1G and 3B of Erickson et al.⁶⁰.

The mechanistic justification of Erickson et al.’s treatment of using translational activity to drive the regulation of ribosome biogenesis χ_R has since been substantiated through the discovery that the ppGpp pool responds directly to the peptide elongation rate⁶⁹: Because the translational activity σ so-defined is a product of the peptide elongation rate and the fraction of active ribosomes. and the ppGpp pool regulates the active ribosome fraction^67,69, it follows that the translational activity σ is uniquely dependent on the ppGpp pool and acts as its proxy. In light of the relation between ppGpp and translational activity, we can understand the tremendous degree of ‘dimensional reduction’ performed in Erickson et al.’s work, where the kinetics of bacterial growth transitions are determined by a few parameters despite the formal involvement of a large number of variables and parameters (metabolite concentrations and kinetic constants characterizing each reaction), as a consequence of coarse-graining by the cell itself, where ppGpp senses the availability of all the amino acids and tRNAs by simply sensing the rate of peptide elongation^69,90.

We note that a similar understanding of the connection between translational activity and the regulation of catabolic protein synthesis assumed in Erickson et al. is currently still lacking. It does not mean mechanistically that ppGpp activates the catabolic sector. The catabolic sector is clearly regulated via cAMP-Crp, and cAMP synthesis is affected by the ketoacid pools²⁴. We hypothesize that a coarse-graining scheme similar to that which relates the amino acids to ppGpp (via the peptide elongation rate⁶⁹) relates the ketoacids to cAMP. However, because the ketoacids and amino acids are reversibly connected through trans-amination^70,91, a relation exists between the cAMP and ppGpp pools when growth is limited by carbon influx (as during diauxic shifts), leading to a connection between catabolic allocation χ_C and translational activity σ exploited by Erickson et al.

Under these key assumptions, the dynamics of a nutrient-shift are fully specified with the only additional information being the steady-state growth rate in the pre- and post-shift medium (λ_i and λ_f, respectively). Furthermore, both nutrient down-shifts and nutrient up-shifts are accommodated within the same framework (distinguished only by whether λ_i is larger or smaller than λ_f).

The simplest nutrient shift is achieved by exhausting one of the simultaneously utilized carbon sources. In that case, all requisite enzymes and transporters are present throughout, and their cellular mass abundances are known from the pre-shift steady-state. Figs. 5B, 5C show the predictability of this flux-controlled kinetic model on the adaptation dynamics of the instantaneous growth rate for an exemplary up- and down-shift; similar predictability is observed in the dynamics of proteome remodeling⁶⁰. An unexpected feature of the growth-shift kinetics for simultaneously utilized carbon sources is that, despite the expression of all the required processing enzymes and cognate transporters prior to the shift, it takes several hours to reach the post-shift steady-state. The success of the theoretical framework (Figs. 5B, 5C, solid lines) suggests several contributions of the proteome-allocation constraints on the prolonged adaptation timescale. First, flux-controlled regulation leads to coordinated response of large sectors of the proteome. Induction of a single operon is very rapid but remodelling the proteome following a nutrient shift requires altering the degree of expression of hundreds of genes (e.g., carbon-catabolic genes that comprise up to 30% of the proteome for a switch to poor-carbon conditions) and greatly extends the adaptation time. Second, beyond adjusting synthesis rates, the cell must remove proteins that are ‘over-expressed’ with respect to the post-shift growth condition. The inherent stability of most bacterial proteins means that a decrease in mass fraction must be achieved by dilution through cell doubling. For a down-shift, this involves replacing a fraction of the ribosomal protein and anabolic proteins by carbon-catabolic proteins, and vice versa for an up-shift. Depending upon the nature of shifts, additional internal metabolic bottlenecks may further lengthen the adaptation time^92,93.

The model of flux-controlled regulation described for shifts between simultaneously-utilized substrates can be readily adapted to describe diauxic growth between hierarchically utilized substrates. Fig. 5D is an example of hierarchical utilization between glucose and lactose. In this case, glucose and lactose support almost identical steady-state growth rates; yet glucose in the medium results in a near-complete repression of the lactose catabolic genes. Although hierarchical utilization requires additional regulatory mechanisms (in this case, ‘inducer exclusion’^94,95), it appears that cAMP-Crp continues to be the primary flux-sensor⁸⁶. The kinetics of hierarchical utilization of glucose and lactose can be accurately described by invoking a single fitting parameter that specifies the time at which the lac operon is de-repressed, reflecting a threshold in glucose influx below which lactose starts to be taken up⁸⁶. Thereafter, as with the simple nutrient shifts, the kinetics of hierarchical utilization conform to what is predicted from the coarse-grained model (Fig. 5D). Much faster transition times can be attained if the synthesis of growth-limiting enzymes are prioritized^93,96. In the canonical shift from glucose to lactose (both of which support doubling times of about 40 minutes), at full-induction the lac proteins occupy approximately 1–2% of the protein content of the cell. A targeted response to the shift would be expected to take less than a minute (1–2% of 40 minutes), and empirically can be achieved in less than two minutes⁹⁷. Instead, it appears that E. coli adopts the versatile, generalist strategy of flux-controlled regulation which, though independent of the details of how metabolic flux is generated, nevertheless carries with it the burden of global proteome remodelling, extending the adaptation time. Instead of upregulating the required 1–2% of the catabolic proteins needed to respond to a carbon downshift, the cell upregulates the entire sector of catabolic proteins, most of which carry no flux^19,93. This surprising behavior possibly reflects the lack of dedicated sensors/regulators to detect the instantaneous nutrient landscape and ‘compute’ the optimal cause of action⁹⁸. It is also possible that in natural environment, the remaining nutrients is distributed across a variety of different types, rather than in one type as usually done in diauxic shift studies⁸⁴.

Diauxic growth:

Multiple stages of exponential growth as carbon sources are preferentially utilized. The time to switch between carbon sources can take several hours.

Concluding remarks

The bacterial cell can be viewed in (at least) two different ways: as a membrane-enclosed auto-catalytic loop of ribosomes synthesizing ribosomes (along with the necessary metabolic enzymes fueling the substrates needed for the ribosomes to do their work), or, alternatively, as a finely-tuned collection of metabolic enzymes orchestrated by a chemical soup of signaling molecules designed to transform external nutrients into a replicating cell. Although both views are simultaneously accurate and useful, they constrain one another²², and irrespective of whether the object of focus is protein synthesis or metabolism, the physiological constraints operating in the background unavoidably sculpts the gene expression landscape and consequently shape the behavior of the system.

In this review, we focused on the correlation between ribosomal protein abundance and growth rate (R-line, Figs. 2A, 3D) which imposes complementary regulation on the expression of all other non-ribosomal proteins. Among these, the expression of carbon catabolic proteins exhibits further strong correlation with growth rate (C-line, Box 1 and Fig. 3B), a phenomenon synonymous with carbon catabolite repression. Together, these proteome-allocation constraints were captured by a phenomenological model of bacterial growth that quantitatively predicts the dynamics of growth transitions among carbon sources without adjustable parameters.

Underlying the growth-dependent proteome-allocation constraints are nested loops of flux-controlled regulation responsible for coordinating the flux through large sectors of the proteome (Fig. 4 and Box 3). Flux-sensing regulatory motifs are particularly useful in mediating the interface between large networks because they are not sensitive to the details of how the flux is generated, providing a generalized strategy that can accommodate metabolic innovation without adjudicating on a case-by-case basis. The plug-and-play functionality of flux-controlled regulation has the benefit of not being tailored to any single growth environment, but of course this generality may suffer from occasional non-optimal response under exotic growth conditions^98,99. Nevertheless, the success of the phenomenological approach in the study of carbon catabolite repression points to the importance of proteome allocation constraints and flux-controlled regulation in studies of gene expression.

A number of recent theoretical studies^100–102 have suggested that existing observations on bacterial proteome allocation (including the R-line and C-line), support the notion that the proteome is optimally allocated to maximize the growth rate. Closer quantitative inspection of the existing data necessitates a broader definition of optimality that can accommodate the substantial non-flux-carrying protein sectors (both the growth-rate independent proteome sector⁶¹, and the growth-dependent catabolic proteins that carry no flux^19,93).

Future outlook

Although the proteome allocation constraints discussed in this review provide a quantitative framework for predicting the interdependence between the growth rate and gene expression, many open questions remain and the applicability of this approach beyond Escherichia coli is largely unexplored.

To coordinate ribosome allocation and proteome allocation constraints with growth rate change requires a mechanism to sense the growth rate. In E. coli, ppGpp plays that role^69,103. The alarmone ppGpp exerts its regulatory effect primarily through modulation of transcription^64,77. In other species, what are the molecular signals that sense growth-rate change, and transform this information into the appropriate proteome allocation? The best-characterized physiological constraints have come from nutrient-limited growth – either balanced exponential growth, or transitions between balanced growth states. What about growth under stress, where the growth-limiting factor is not any nutrient component, but other environmental parameters such as temperature, pH, osmolarity, etc.? Quite a lot of information is available on regulatory factors operating under these conditions^104–106. However, little is known at the quantitative level regarding the physiological constraints imposed by these environmental factors, nor about their effects on growth reduction. Our focus on proteome allocation constraints has not touched upon changes in cell size. The broader question of how cell size homeostasis and DNA replication¹⁰⁷ is coordinated with proteome partitioning and protein-synthesis constraints remains unknown. Current ideas are centered around the accumulation of some protein(s) for initiating cell division^12,107–109.

What about non-growing or stationary conditions? Is it similar to a very slowly growing state¹¹⁰, or fundamentally different? How do physiological constraints affect gene expression by cells in stationary phase¹¹¹? What about survival through the stationary phase¹¹²? Recent work on the effect of pre-shift growth conditions on survival¹¹³ provides a rare example of physiological study of stationary cells but much work is left to be done.

The coordination of ribosome abundance with growth rate⁶⁴, and carbon catabolic repression^33,34 are ubiquitous responses in bacteria. Are the protein-synthesis constraints active in other organisms the same as those found in E. coli, and if so, are these constraints responding to similar flux-matching signals? Certainly the molecular details are different among distant species. In the model firmicute Bacillus subtilis, for example, guanosine (penta)tetraphosphate ((p)ppGpp) appears to modulate ribosomal RNA operon activity indirectly, by lowering the concentration of GTP rather than by direct binding to the RNA polymerase as in E. coli¹¹⁴. Furthermore, carbon catabolite repression in B. subtilis is achieved by transcriptional repression, rather than via cAMP-Crp activation of the catabolic promoters^33,34. Despite these differences in implementation, are the resulting control structures responding to similar cues to generate a similar flux-balance among proteome sectors?

B. subtilis and E. coli are both capable of rapid growth – are similar proteome-allocation constraints operating in slowly-growing bacteria? Are proteome allocation constraints relevant in slow-growing species, or is the protein synthesis machinery no longer a growth-limiting resource under these conditions¹¹⁵? Although the proteins responsible for (p)ppGpp signaling and the regulation of ribosome biogenesis are largely conserved among bacteria¹¹⁶, there are varied molecular implementations depending upon whether the bacteria are copiotrophic or oligotrophic. Bacteria adapted to nutrient-rich environments (copiotrophs) tend to synthesize ppGpp in response to a number of individual starvation cues, exhibiting OR-logic combinatorial control; whereas bacteria adapted to chronic starvation (oligotrophs) tend to synthesize ppGpp in response to a combination of cues, typically in addition to amino acid starvation, exhibiting AND-logic combinatorial control¹¹⁷. Are proteome-allocation constraints (and other physiological constraints) likewise shaped by the bacterial lifestyle? Are they found in extremophiles and archaea? Quantifying physiological constraints in photosynthetic organisms is complicated by the additional degrees of freedom afforded to growth modulation via light intensity and duration. Nevertheless, it appears that simple empirical relationships exist, e.g. linking cellular glycogen to growth rate in cyanobacteria¹¹⁸.

Microorganisms continue to be an important vector for biomanufacturing and synthetic circuits design. Proteome allocation constraints impose a hard upper-limit on the mass fraction that can be occupied by heterologous protein^12,22, irrespective of whether the protein is produced endogenously or via an orthogonal synthesis pathway¹¹⁹. Is it possible to engineer the host¹²⁰ or the growth medium to increase the heterologous protein limit? Or, alternatively, are there suitable microorganisms that have a larger propensity for heterologous production? The implementation of synthetic genetic circuits is limited by a lack of predictability, largely due to unaccounted crosstalk between the host and the synthetic construct^121,122 (or among different modules of the construct¹²³). Including physiological constraints in mechanistic models of gene expression improves predictability^122,124,125, particularly when the growth rate changes. Designing flux-controlled regulation that couples the synthetic circuit to the host physiology could improve performance by ensuring flux-matching among modules.

Beyond bacteria and archaea, unicellular eukaryotes are subjected to far more complex protein-expression regulation and compartmentalization. Yet they exhibit apparent catabolite repression¹²⁶ and other metabolic transitions such as overflow metabolism¹²⁷ that are also manifested in bacteria. Work has been done quantifying some physiological constraints in Saccharomyces cerevisiae^128–131, fungi^132,133 and mammalian cell lines¹³⁴, but for the most part, eukaryotic organisms, particularly higher eukaryotes, remain under-investigated. Generally, much less is known quantitatively about issues specific to eukaryotes, e.g., the role of protein turnover and secretion on proteome allocation^135,136. The existence of a constraint on biomass density and hence protein concentration is another unknown. Indeed, even defining the intracellular protein concentration is nontrivial in eukaryotes due to the existence of many intracellular compartments, in particular, vacuoles which can take up substantial intracellular volume but do not directly affect the cytosolic protein concentration^135,137.

Turning to communities of interacting microorganisms, can we define meta-physiological constraints? These may be particularly straightforward to define in model ecosystems comprised of a few species^138–140. As a simple example, in a two species Lotka-Volterra-type system where both the densities of the predator and prey oscillate, the ribosome abundance in the predator is expected to oscillate with the predator growth rate, whereas in the prey, the ribosome abundance is expected to exhibit no time dependence (since the density change of the prey is due to changes in predation, not growth). Can empirical correlations of this kind be used to trace putative predator-prey interactions in environmental samples?

Finally, the proteome-allocation constraints we have focused on in this review operate on the scale of days; how do the characterizations of these constraints change over evolutionary timescales? One of the outstanding mysteries surrounding physiological constraints in E. coli is the significant allocation of the proteome to non-flux carrying genes^19,93. Does this strategy arise from a tradeoff between optimizing current need against a contingency for future uncertainty? If so, then how is the magnitude of the non-flux carrying proteome determined? Recent work predicting the emergence of antibiotic resistance¹⁴¹ suggests that physiological constraints persist over short adaptation periods. Is it possible to use coarse-grained phenomenological parameters to infer underlying physiological changes during other evolutionary adaptation scenarios? Will this provide a wider outlook than a regulator-centric view? Although simple to state, and often simple to quantify, proteome allocation constraints have far-ranging implications for how we understand gene regulation in microorganisms.