Segmentation by Test-Time Optimization (TTO) for CBCT-based Adaptive Radiation Therapy

Abstract

Online adaptive radiotherapy (ART) requires accurate and efficient auto-segmentation of the target volumes and organa-at-risk (OARs) in, most times, cone-beam computed tomography (CBCT) images, which often have severe artifacts and lack soft tissue contrast, making the direct segmentation very challenging. Propagating expert-drawn contours from the pre-treatment planning CT (pCT) through traditional or deep-learning (DL) based deformable image registration (DIR) can achieve improved results in many situations. Typical DL-based DIR models are population based, i.e., trained with a dataset for a population of patients, which may suffer from the generalizability problem. In this paper, we propose a method called test-time optimization (TTO) to refine a DL-based DIR model, pre-trained on a population of patients, for each individual test patient and then progressively for each fraction of online ART treatment. Our proposed method is less susceptible to generalizability problem, and thus can improve overall performance of different DL-based DIR models by improving model accuracy especially for outliers. 239 patients with head and neck squamous cell carcinoma were used in our experiments to test the proposed method. Firstly, we trained a population model with 200 patients, and then applied TTO to the rest 39 test patients by refining the trained population model to get 39 individualized models. We compared each of the individualized models with the population model in terms of segmentation accuracy. We also evaluated the efficiency gain of deriving the individualized models from the pre-trained population model versus from an un-trained model. The average improvement of Dice Similarity Coefficient (DSC) and 95% Hausdorff Distance (HD95) of the segmentation can be up to 0.04 (5%) and 0.98 mm (25%), respectively, with the individualized models compared to the population model over 17 selected OARs and target of 39 patients. While the average improvement may seem mild, we found that the improvement for outlier patients is significant. The number of patients with at least 0.05 DSC improvement or 2 mm HD95 improvement by TTO averaged over the 17 selected structures for the state-of-the-art architecture Voxelmorph is 10 out of 39 test patients. The average time for deriving the individualized model using TTO from the pre-trained population model is approximately 4 minutes, which is about 150 times faster than that required to derive the individualized model from an un-trained model. We also generated the adapted fractional models for each of the 39 test patients by progressively refining the individualized models using TTO to CBCT images acquired at the later fractions of online ART treatment. When adapting the individualized model to a later fraction of the same patient, the average time is reduced to about 1 minute and the accuracy is slightly improved. The proposed TTO method can boost the segmentation accuracy for DL-based DIR models, especially for outlier patients where the pre-trained models fail, and is well suited for online ART.

1. Introduction

Online adaptive radiotherapy (ART) is an advanced radiotherapy technology where, during the treatment course and before the delivery of the daily treatment, the treatment plan is adapted to patient’s changing anatomy (e.g., shrinking tumor), typically using cone beam computed tomography (CBCT) images. The online nature of the treatment demands high efficiency since the patient is immobilized to the treatment position waiting for the treatment to start. The time-consuming process of segmenting the tumor volumes and organs at risk (OARs) has become a major bottleneck for the widespread use of online ART. Accurate auto-segmentation tools are urgently needed¹.

Auto-segmentation in CBCT images is a very challenging task, mainly due to severe artifacts, low soft-tissue contrast, and image truncations¹. Currently there are two main categories of CBCT auto-segmentation methods for online ART: deformable image registration (DIR) based and deep learning (DL) based². The DIR-based auto-segmentation is widely used in clinical ART workflow^1,3,4. It deforms the pre-treatment planning CT (pCT) image, in which the target and OAR contours have been determined by experts, to the CBCT image, based on which the treatment plan is adapted to the new anatomy. The resulted deformation vector field (DVF) is then used to propagate the contours from pCT to CBCT. Evaluation of different DIR algorithms for contour propagation between pCT and CBCT in head & neck (H&N) ART suggests that careful examinations and modifications are still required⁵. DL-based auto-segmentation has achieved clinically acceptable performance in many image modalities², such as CT. DL-based direct segmentation in CBCT images is still very challenging due to the poor image quality. A hybrid auto-segmentation approach for CBCT-based online ART has been implemented in clinical practice⁸. It uses a DL-based model to direct segment easier OARs in CBCT images and then uses the segmentation results to constraint the DIR between pCT and CBCT, which propagates the target and rest of OARs from pCT and CBCT. Although working for some OARs and targets, manual editing of challenging OARs and target volumes is still required and time consuming.

Popular traditional DIR methods include extensively studied B-spline algorithms, represented by ELASTIX⁹ and 3DSlicer B-spline registration¹⁰, and Demons algorithms^11,12. Recently, DL-based DIR methods have shown the state-of-the-art performance in many applications. Jaderberg et al in 2015 proposed a spatial transformer network (STN), which allows for spatial transformations on the input image inside a neural network, is differentiable, and can be added to any other existing architectures¹³. STN network has inspired lots of unsupervised DIR methods. A typical unsupervised DIR model can be divided into two parts: DVF prediction and spatial transformation. In DVF prediction, a neural network takes a pair of fixed and moving image as input and outputs a DVF. Then in spatial transformation, the STN network warps the moving image according to the predicted DVF to get the moved image. The loss function for model training is usually composed of image similarity loss between the fixed and moved images and a regularization term on DVF. Voxelmorph proposed by Dalca et al combined a probabilistic generative model and a DL model for diffeomorphic registration¹⁴. They used a U-Net architecture to predict velocity field and diffeomorphic integration layers to sample DVF from the predicted velocity field. Then a STN network is followed to warp the moving images. Image similarity and Kullback-Leibler divergence constraint were used in the loss function. A similar work, FAIM, used a U-Net architecture to predict DVF directly and a STN network to warp images¹⁵. The loss function of FAIM is also composed of image similarity and regularization terms to constrain DVF smoothness. To further improve the performance of unsupervised DL methods, Zhao et al built recursive cascaded networks¹⁶ on top of a base network including VTN¹⁷ and Voxelmorph¹⁸. The cascade procedure is done by recursively performing registration on warped images. The final DVF is a composition of all predicted DVFs. The results showed that recursive cascaded networks outperform the base network with significant gains.

These DL models for DIR are all population based, e.g., trained on a dataset representing a population of patients. Generalizability problem may exist in these models when deployed to patients where the joint distribution of inputs and outputs differs from that of the training dataset. In the targeted clinical applications of this work, many factors could cause such a problem, including different anatomical sites, scanning machines, and scanning protocols. Therefore, the model generalizability problem needs to be carefully addressed.

To solve this problem, inspired by the work of Chen et al²² and Fechter et al²³, where one shot learning is used for DIR to generate anthropomorphic phantoms and to track periodic motion with DL models, respectively, we propose a method called test-time optimization (TTO) to individualize a pre-trained population DL model for one pair of fixed and moving image, by iteratively refining the weights of the DL model in a traditional optimization matter. The predicted DVF is then used to warp the moving image to match the fixed image. Essentially, TTO overfits the DL model to a specific pair of moving and fixed images, promising a better performance than the direct use of the population DL model and the avoidance of potential generalization problem of the population DL model. When TTO is applied to a pre-trained DL model, versus to an untrained model as in the work of Chen et al²² and Fechter et al²³, much improved efficiency is also expected, which is critical for online applications. For CBCT-based online ART, TTO can be used to refine a pre-trained DL model to a new patient (inter-patient TTO) to get an individualized model and also to further refine the individualized model to a new treatment fraction for the same patient (intra-patient TTO) to get a fractional model.

In the following content, we first introduce the common architecture used in unsupervised DL-based DIR algorithms in Section 2.1. Then we introduce the concept of inter-patient TTO and intra-patient TTO methods that can be applied to the unsupervised DIR algorithms in Section 2.2. Lastly, we describe the data used in the experiments and the experiment design in Section 2.3 and Section 2.4. Three main experiments have been performed in this study. First, we compared the performance of the individualized TTO model with the population model for different DL architectures. Second, we compared the efficiency of inter-patient TTO starting from a pre-trained population model and an untrained model with random weights for two best DL architectures. Third, we further refined the individualized model to a later treatment fraction of the same patient to obtain a fractional model to illustrate intra-patient TTO application in CBCT-based online ART workflow. We present the results of the three experiments in Section 3 and the conclusions and discussion in Section 4.

Our main contributions are:

1. We proposed a TTO method that can refine a pre-trained DL-based population DIR model for each individual test patient and then progressively for each fraction of online ART treatment, to mitigate the model generalizability problem.

2. We did extensive experiments for multiple state-of-the-art DL architectures to show that TTO can significantly improve a population model’s performance especially when the population model doesn’t work well for a particular patient.

3. We showed that TTO models are less susceptible to the generalizability problem which appears quite common for the population models in the targeted clinical applications.

4. The individualized models from TTO outperform the population DL models and traditional DIR models.

5. We showed that the inter-patient TTO and intra-patient TTO can be accomplished in a few minutes.

6. Inter- and intra-patient TTO can be applied to DIR in online ART workflow for auto-segmentation effectively and efficiently, by adapting a population model to a new patient or adapting an individualized model to a new treatment fraction of the same patient.

2. Materials and methods

2.1. Unsupervised DL-based DIR algorithms

Let’s set two pair of images be the moving images I_m(x′), and the fixed images I_f(x); we assume that they are pre-rigid aligned. DIR tries to find the best DVF u(x′), that can minimize the difference between the fixed and moved images. Thus, an ideal DIR between I_m and I_f can be expressed as:

$$I_f\left(x\right)=I_m\circ u=I_m\left(x^{\prime }+u\left(x^{\prime }\right)\right).$$

Typical unsupervised DL-based DIR algorithm is shown in Figure 1. A transformation neural network is used predict DVF from a pair of moving and fix images and then a STN is used to warp the moving image based on predicted DVF to obtain deformed moving image. The transformation model can be any neural networks, from very simple one like convolutional neural network (CNN) to state-of-the-art architectures like Voxelmorph^{14, 18} and cascaded VTN¹⁶. The loss function can be described as:

$$ℒ={ℒ}_{sim}\left(I_f,I_m\circ u\right)+\lambda R\left(u\right)={ℒ}_{sim}\left(I_f,I_m\circ f\left(I_m,I_f\right)\right)+\lambda R\left(f\left(I_m,I_f\right)\right),$$

where ℒ_sim is the image similarity measures between fixed and deformed moving images, R is regularization terms of u, and λ is a weighting factor. In our study,I_m is pCT and I_f is CBCT. And the DL model is optimized to minimize the gradients of loss function. A population model is trained on large dataset. After training, during inference phase, DVF can be predicted by the population model from a pair of pCT and CBCT images. Then STN can be used to warp the contours on pCT to get auto-segmentations on CBCT with the predicted DVF.

Figure 1.

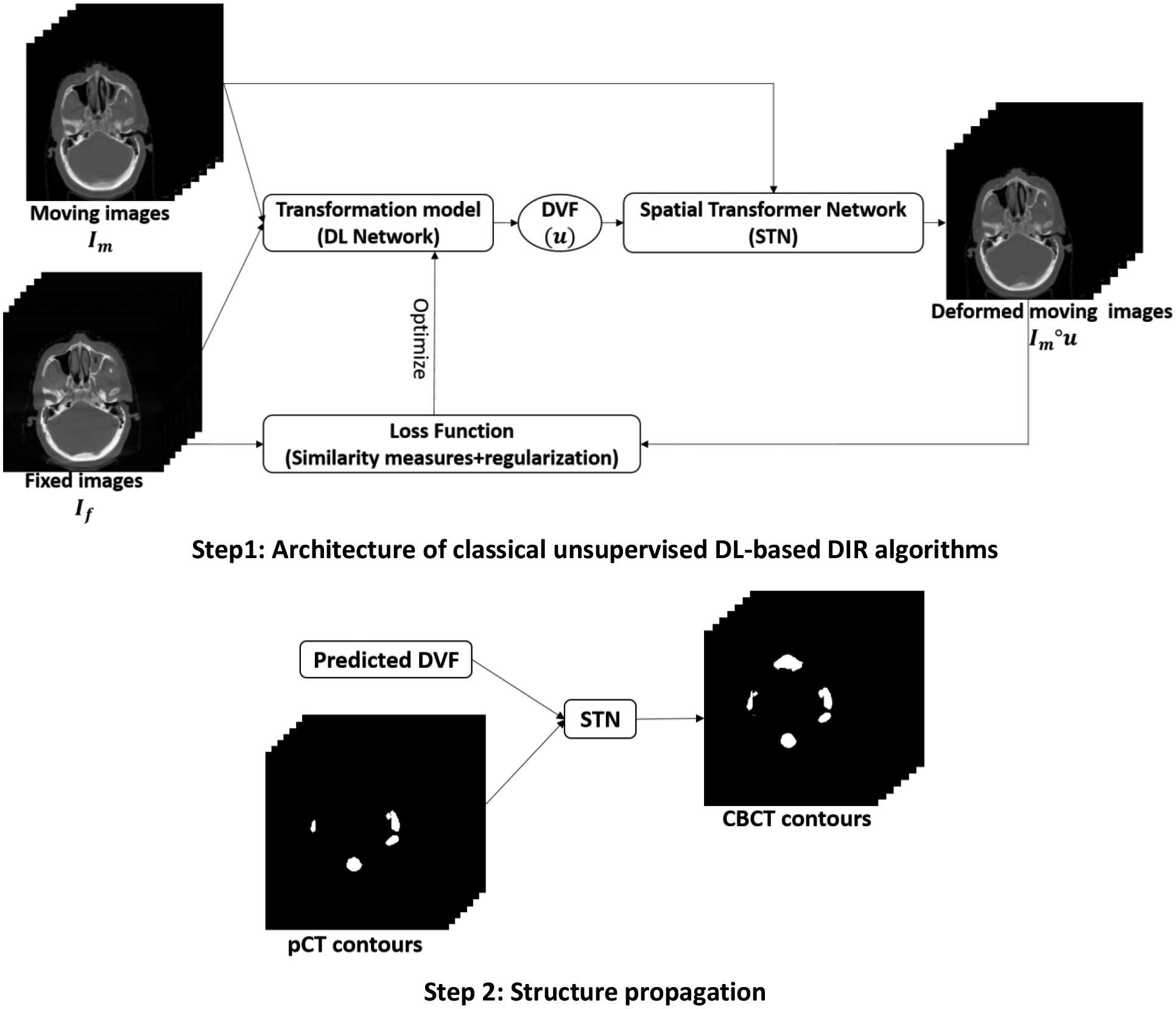
Step 1 shows a classical training architecture of unsupervised DL-based DIR algorithms. During training, the transformation model is optimized by backpropagating the gradients of loss function. Step 2 shows the inference phase, where predicted DVF can be used to warp pTV contours through STN to obtain contours on CBCT.

2.2. Inter-patient TTO and intra-patient TTO

A feedforward network with a single layer is sufficient to represent any function, but the layer may be infeasibly large and may fail to learn and generalize correctly²⁴. In the mathematical theory of artificial neural networks, universal approximation theorems are results²⁵ that establish the density of an algorithmically generated class of functions within a given function space of interest. There are variety of results between non-Euclidean spaces and other commonly used architectures and, more generally, algorithmically generated sets of functions, such as the CNN architecture^26,27, radial-basis-function networks²⁸, or invariant/equivariant network²⁹. Universal approximation theorems imply that neural networks can approximate any functions with appropriate capacities. Thus according to universal approximation theorems, a DL neural network can approximate a transformation function in DIR with only a moving and a fixed image.

Unlike common DL training strategy where a DL model is trained on large dataset to get a population model and tested on unseen dataset, TTO doesn’t need pre-training on lots of data. Instead, only one pair of moving and fix image is enough for DL network to generate a transformation function for that image pair according to universal approximation theorems. In our application, the biggest advantage of TTO is that patient-specific transformation model can be generated for each patient rather than a population model applied for all patients. Therefore, the common generalizability problem or overfitting problem in machine learning can be avoided by the TTO strategy. However, like the other optimization methods, TTO may also suffer from computation time cost. This issue can be greatlyt mitigated by starting TTO from a pre-trained population model rather than starting from scratch to reduce the number of iterations needed. Lots of studies have shown that the amount of time or iterations needed to learn an accurate neural network model can be significantly reduced by transfer learning over learning from scratch^30–32. Therefore, the model parameters from a population model that have been trained on large datasets can be utilized in TTO to start the optimization process.

Figure 2 illustrates the concept of inter-patient TTO and intra-patient TTO in our application. First step is to get a population model by training a DL network on large dataset. If a new patient’s anatomy is very different from the training data, the population model might fail. However, TTO can adjust the population model parameters to the new patient to obtain the individualized model. That means we can apply TTO to a DL model starting from the population model parameters rather than starting from the scratch on a new patient’s data in order to achieve the best performance for that specific patient. Therefore, TTO will not only improve DIR accuracy compared to population model, it will also decrease the number of iterations and optimization time by starting TTO from a warm-start. Thus the second step is to get an individualized model by finetuning the population model to a new patient.

Figure 2. Concept of the population model, individualized model (inter-patient TTO), and fraction model (intra-patient TTO).

Population model is obtained by typical training strategy, which trains a DL model on a large dataset. Inter-patient TTO: an individualized model for a new patient can be obtained by adapting the population model to the new patient’s data. Intra-patient TTO: a fractional model for the same patient can be obtained by adapting the individualized model to the new fraction’s data.

In CBCT-based ART workflow, CBCT images are frequently taken during radiation courses to monitor anatomical changes. Assuming a new patient has a CBCT image for each treatment fraction and already has an individualized model refined to the CBCT image from the first fraction. In this case, TTO can be applied to the individualized model on the image pair of the next fraction to obtain the fractional model, and so forth. Therefore, each fraction will have a fractional model that has the best fit for that fraction by TTO. Then the third step is to get a fractional model by fine-tuning the individualized model to a new treatment fraction of the same patient.

2.3. Data

We retrospectively collected data from 239 patients with head and neck squamous cell carcinoma treated with external beam radiotherapy with radiation dose around 70Gy. Each patient includes a 3D pCT volume acquired before the treatment course, OARs and target segmentations delineated by physicians on the pCT, and two sets of 3D CBCT volume acquired at fraction 20 and fraction 21 during treatment course. The pCT volumes were acquired by a Philips CT scanner with 1.17 × 1.17 × 3.00 mm³ voxel spacing. The CBCT volumes were acquired by Varian On-Board Imagers with 0.51 × 0.51 × 1.99 mm³ voxel spacing and 512 × 512 × 93 dimensions. The pCT is rigid registered to CBCT through Velocity (Varian Inc., Palo Alto, USA). Therefore the rigid-registered pCT has the same voxel spacing and dimensions as CBCT. Synthetic CT (sCT) images with less artifacts and CT-like Hounsfield units were generated from CBCT using an in-house DL model developed previously³³. In this paper, sCT replaced CBCT in all the following DIR experiments since better image quality would lead to more accurate DIR. The dimensions of pCT and sCT volumes were both down-sampled to 256 × 256 × 93 from 512 × 512 × 93, and then cropped to 224 × 224 × 64. We randomly picked 39 out of 239 patients for testing. We selected 17 structures that either are critical OARs or have large anatomical changes during radiotherapy courses. They are left brachial plexus (L_BP), right brachial plexus (R_BP), brainstem, oral cavity, constrictor, esophagus, nodal gross tumor volume (nGTV), larynx, mandible, left masseter (L_Masseter), right masseter (R_Masseter), inferior pharyngeal constrictor (PACS), left parotid gland (L_PG), right parotid gland (R_PG), left submandibular gland (L_SMG), right submandibular gland (R_SMG), spinal cord. The contours of these 17 structures were first propagated from pCT to CBCT of fraction 21 using rigid and deformable image registration in Velocity, and then modified and approved by an radiation oncology expert as ground truth contours on CBCT of fraction 21 for test.

2.4. Experiments design

We did extensive experiments to answer the following questions: does the TTO method have any advantage over typical training strategy and how to use TTO in an efficient way for CBCT-based online ART? The experiment design is shown in Figure 3.

Figure 3.

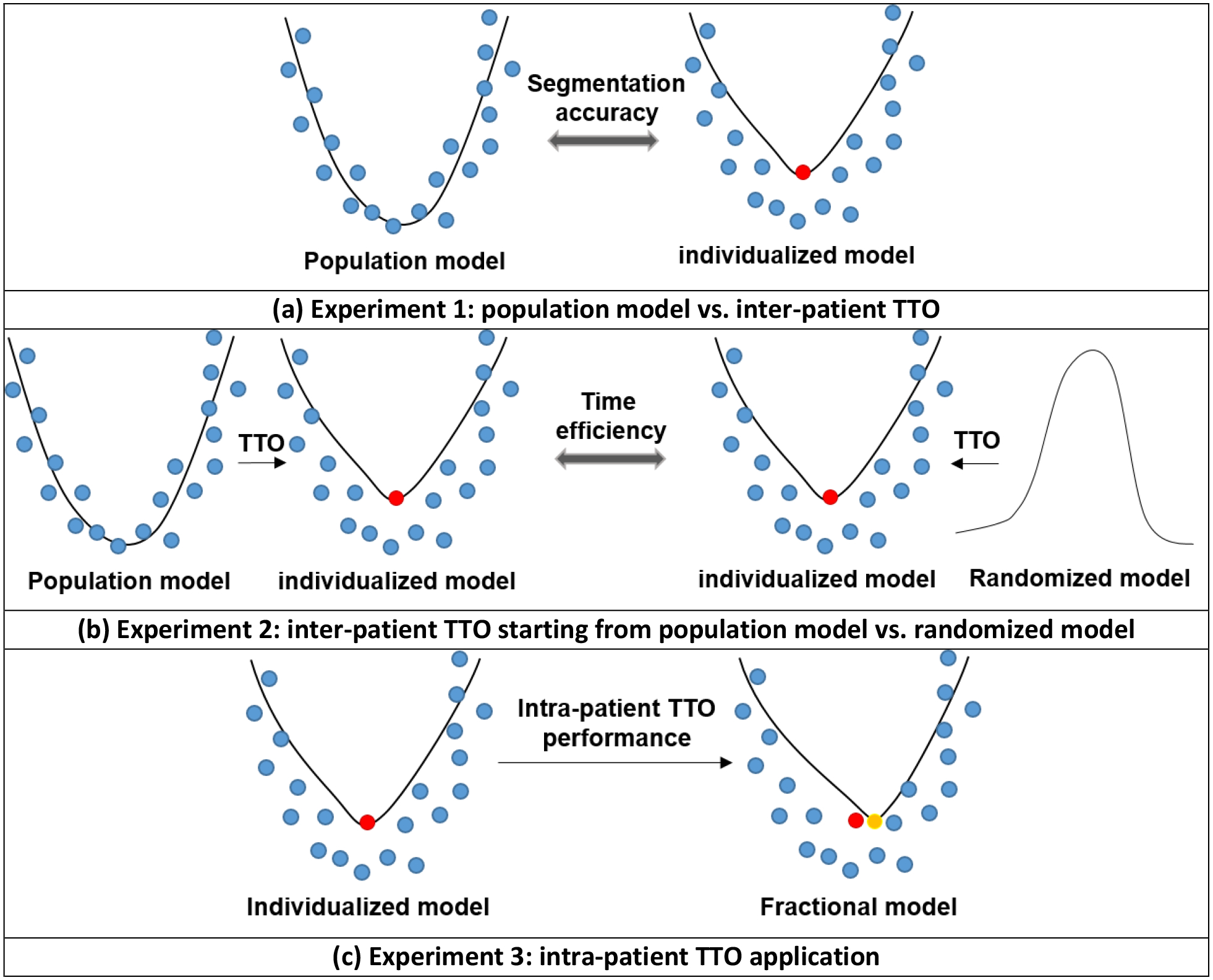
Experiment design. (a) Experiment 1: we compare the population model and the individualized model in terms of segmentation accuracy. (b) Experiment 2: we compare the individualized model refined from the population model with the individualized model refined from the randomized model in terms of efficiency. (c) Experiment 3: intra-patient TTO was applied to refine the first individualized model to a later fraction for performance evaluation.

In experiment 1 shown in Figure 3(a), population model was trained on pCT and CBCT fraction 21 pairs from 200 training patients and then tested on pCT and CBCT fraction 21 pairs from the 39 test patients. Individualized models are obtained by applying inter-patient TTO to the 39 test patients starting from the trained population model. TTO process stops when the loss curve converges. In this and all the following experiments, an absolute change of less than 0.005 in the loss function is counted as no decrease and the loss function stops to decrease in 50 iterations is defined as convergence. We compared the segmentation accuracy of individualized TTO models and population model with different DL networks from very simple one to the-state-of-art neural networks including CNN, FIAM¹⁵, Voxelmorph¹⁴, 5-cascaded Voxelmorph, VTN¹⁷, and 10-cascaded VTN¹⁶. CNN is a simple network that only has 10 convolutional layers without any downsampling or upsampling layer. Each convolutional layer has 16 filters and are followed by LeakyReLU activation layer. We added CNN architecture to our experiments to illustrate the generalizability of TTO to different types of architectures. Traditional methods including Elastix, 3DSlicer B-spline deformable registration, and 3DSlicer demon deformable registration were also performed for comparison. Since sCT and CT are considered as the same image modality and used as fixed and moving images in our experiments, the loss function of all the algorithms in this study are based on intensity based similarity metrics. We add regularization terms weighted by λ in the loss function for stabilization purpose. Weighting factor λ in the loss function are set to the default values used in the originally published papers. Adam optimization with learning rate of 0.0002 and batch size of 1 was used for all the TTO and population models.

Since individualized models can also be obtained by TTO starting from a randomized DL model on a new patient data directly (one shot learning), time efficiency was studied between inter-patient TTO starting from population model versus starting from scratch in experiment 2, shown in Figure 3(b). The 39 test patients with pCT and CBCT fraction 21 pairs were used in this experiment. TTO process stops when the loss curve converges for each case during optimization. We picked the best two DL architectures for this experiment: 5-cascaded Voxelmorph and 10-casccaded VTN, since only these two can compete with traditional DIR methods.

In the last experiment, performance of intra-patient TTO application was studied. An individualized model was obtained by applying TTO to pCT and CBCT fraction 20 of a test patient starting from the population model. Then a fractional model was obtained by applying TTO to pCT and CBCT fraction 21 of the same test patient starting from the individualized model. We repeat this process for the 39 test patients. Similar to the previous experiment, the performance gain and the optimization time for intra-patient TTO models to converge for the test patients were studied. The best two DL architectures including 5-cascaded Voxelmorph and 10-casccaded VTN were selected for this experiment.

2.4. Evaluation metrics

To quantitatively evaluate segmentation accuracy, dice similarity coefficient (DSC) and 95% Hausdorff distantace (HD95) were calculated between predicted and manual segmentations. DSC is intended to gauge the similarity of the prediction and ground truth by measuring volumetric overlap between them. It is defined as

$$DSC=\frac{2\left|X\cap Y\right|}{\left|X\right|+\left|Y\right|}$$ (17)

where X is the prediction, and Y is the ground truth.

HD is the maximum distance from a set to the nearest point in another set. It can be defined as

$$HD\left(X,Y\right)=\text{max}\left(d_{XY},d_{YX}\right)=\text{max}\left\{{\text{max}}_{x\in X}{\text{min}}_{y\in Y}d\left(x,y\right),{\text{max}}_{y\in Y}{\text{min}}_{x\in X}d\left(x,y\right)\right\}.$$ (18)

HD95 is based on the 95^th percentile of the distances between boundary points in X and Y. The purpose of this metric is to avoid the impact of a small subset of the outliers.

3. Results

3.1. Population vs. inter-patient TTO

We compared the segmentation accuracy of individualized models and population model for different architectures from very simple one like CNN to the-state-of-art architecture like Voxelmorph and cascaded VTN. The individualized model is obtained by applying inter-patient TTO from a population model. The average dice coefficients and HD95 of the 17 selected organs and target from 39 test patients using population models and individualized models with different architectures including CNN, FAIM, Voxelmorph, VTN, 5-cascaded Voxelmorph, and 10-cascaded VTN are shown in Table 1. The performance of each 17 structures compared between population models and individualized models with all the tested architectures are shown in Supplementary figures 1–6. From Table 1, we can see that individualized models all have improvement from the corresponding population models for all the architecture tested in dice coefficient and HD95. The absolute improvement from the population models to the individualized models are 0.03, 0.03,0.03,0.04, 0.01, and 0.02 in dice coefficient, and 0.35 mm, 0.27 mm, 0.98 mm, 0.32 mm, 0.07 mm, and 0.06 mm in HD95 for CNN, FAIM, Voxelmorph, VTN, 5-cascaded Voxelmorph, and 10-cascaded VTN respectively. For visual comparison, examples of autosegmentation by 10-cascaded population model and individualized model were plotted in Figure 4. Overall, the architectures which have bad population model performance tend to have large performance gain through TTO method. On the contrary, architectures with good population model performance tend to have small performance gain through TTO method.

Table 1. The average DSC and HD95 of the 13 selected structures from the 39 test patients for different DL architectures with population models and individualized models.

Individualized models are obtained by applying inter-patient TTO from a population model. The green numbers are the absolute improvements from the population model to the individualized model.

DL Architecture	DSC			HD95 (mm)
	Population model	Individualized model	Improvement	Population model	Individualized model	Improvement
CNN	0.78	0.81	+0.03	3.18	2.83	−0.35
FAIM	0.80	0.83	+0.03	2.88	2.61	−0.27
Voxelmorph	0.79	0.82	+0.03	3.87	2.89	−0.98
VTN	0.81	0.85	+0.04	2.82	2.50	−0.32
5-cascaded Voxelmorph	0.83	0.84	+0.01	2.53	2.46	−0.07
10-cascaded VTN	0.83	0.85	+0.02	2.39	2.33	−0.06

Figure 4. Contours of test patients from axial view.

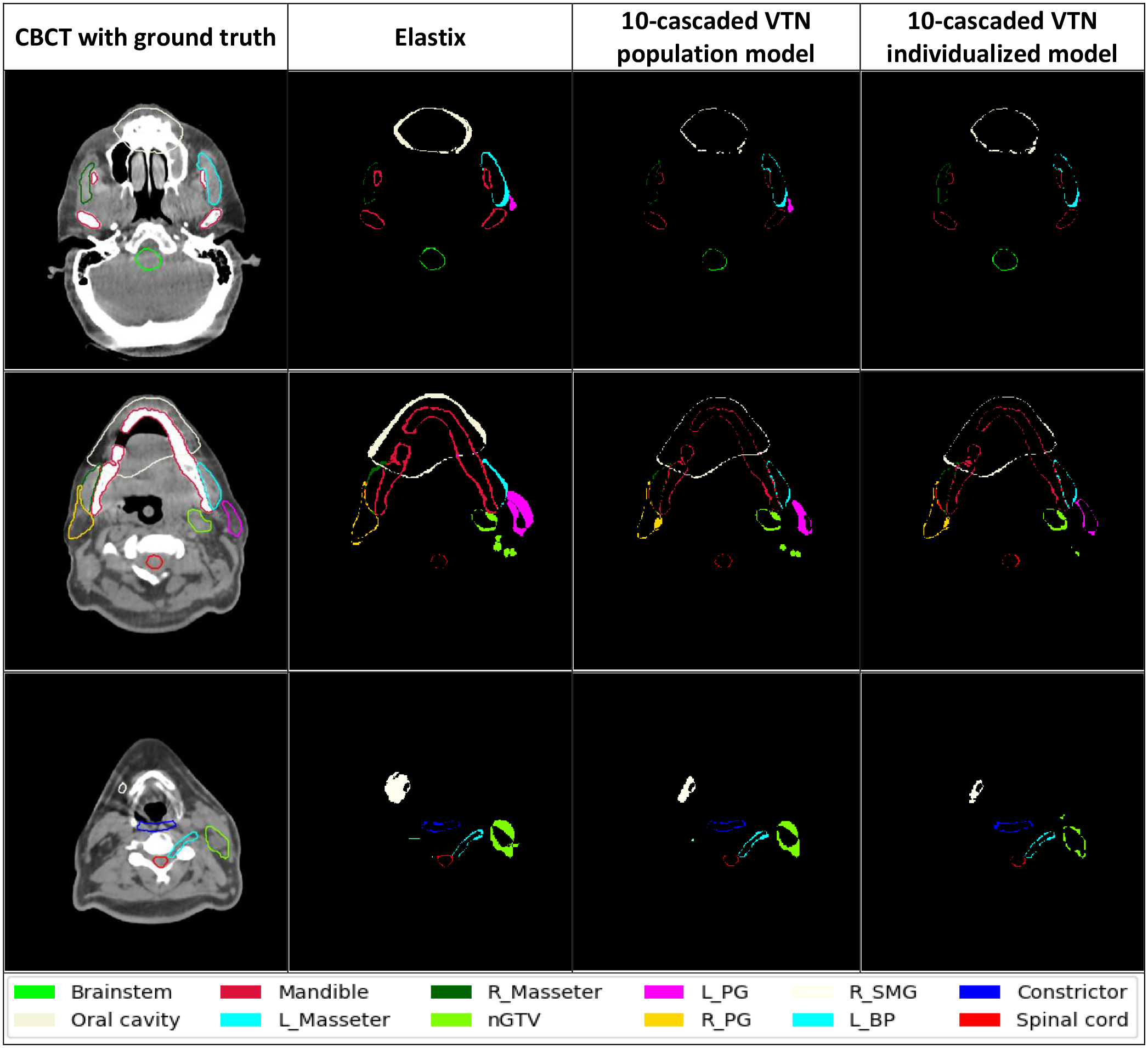
The images from left to right are CBCT with manual ground truth contours on it, the discrepancy between Elastix contours and ground truth contours, the discrepancy between 10-cascaded VTN population model contours and ground truth contours, and the discrepancy between 10-cascaded VTN individualized model contours and ground truth contours respectively.

When comparing the performance of individualized models among all the tested architectures shown in Supplementary figure 7, CNN individualized model has the worst performance among all, even though it has big improvement gain from population model. While 5-cascaded Voxelmorph and 10-cascaded VTN individualized models only have little improvement from population models, but they still have the best performance among all the individualized models. We can see from Supplementary figure 7 that a better architecture has better performance not only in typical training strategy, but also in TTO mode. Apparently the performance of individualized model is architecture related, and better architecture will surely lead to better performance with TTO method.

For the state-of-the-art architectures, like 5-cascaded Voxelmorph and 10-cascaded VTN, even though the improvement from population models by TTO are small when averaged over all the testing patients, significant performance gain can be observed for outlier patients where population models failed. From figure 5, we can see that there is 1 patient having 0.12 DSC gain for 5-cascaded Voxelmorph and 0.11 DSC gain for 10-cascaded VTN by TTO method. The number of patients which have at least 0.05 DSC improvement or 2 mm HD95 improvement by inter-patient TTO for CNN, FAIM, Voxelmorph, VTN, 5-cascaded Voxelmorph, and 10-cascaded VTN architectures are 5, 6, 10, 9, 2 and 2 out of 39 test patients, respectively. Thus models generated by TTO method are less vulnerable to generalizability problem.

Figure 5. Distribution of DSC and HD95 change from a population model to an individualized model for 39 test patient.

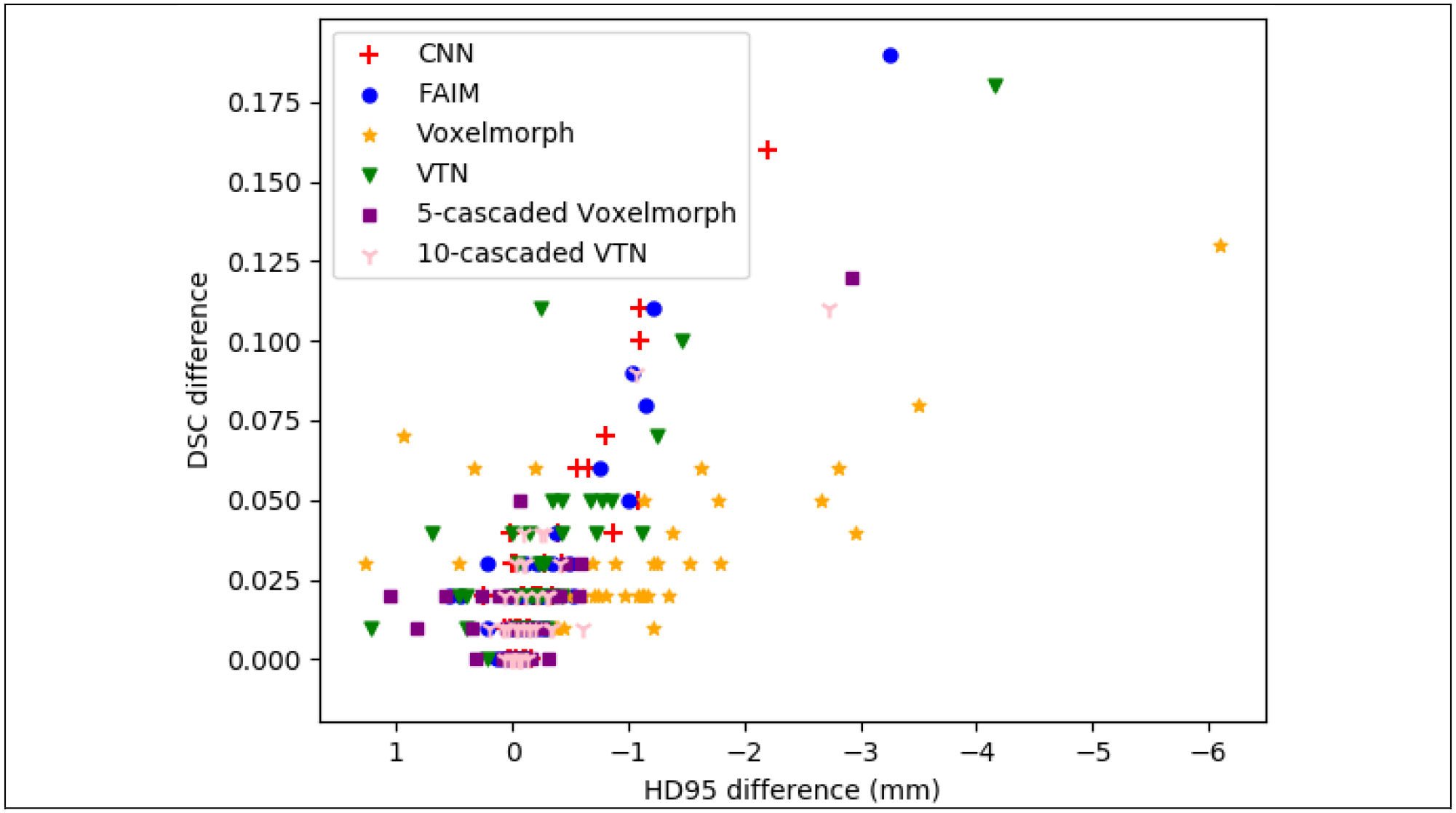
X axis and Y axis are the average HD95 difference and average DSC difference of 17 structures between a population model and an individualized model for a patient.

We also compared individualized models to traditional DIR methods including 3DSlicer B-spline deformable registration, 3DSlicer Demon deformable registration, and Elastix, shown in Table 2. We only picked the best 2 architectures for comparison: 5-cascaded Voxelmorph and 10-casscaded VTN, since only these two architectures can compete with traditional methods. 5-cascaded Voxelmorph individualized model and 10-cascaded VTN individualized model have higher average dice coefficients and lower HD95 values than traditional DIR methods over all 17 structures from 39 test patients. Since Elastix has the best performance among traditional methods, only Elastix is plotted in Supplementary figure 7 for comparison with individualized models in each structure. The autosegmentation generated by Elastix and 10-cascaded VTN individualized models from some test patients are shown in Figure 4 for visual evaluation. It is clear to see that the discrepancy between contours generated by individualized models and ground truth contours are much less than the discrepancy between contours generated by Elastix and ground truth. Overall, 5-cascaded Voxelmorph and 10-cascaded VTN using our proposed TTO method can outperform traditional methods.

Table 2. Comparison between traditional DIR methods and individualized models with state-of-the-art DL architectures.

Numbers in this table were calculated by the average DSC and HD95 of the 13 selected structures from the 39 test patients.

	3DSlicer Demon	3DSlicer B-spline	Elastix	5-cascaded Voxelmorph individualized model	10-cascaded VTN individualized model
DSC	0.78	0.82	0.83	0.84	0.85
HD95 (mm)	3.55	2.82	2.83	2.46	2.33

3.2. Inter-patient TTO: starting from population model vs. starting from randomized model

In inter-patient TTO application, we refine a population model to a new patient instead of starting TTO from scratch for efficiency gain. The time cost for inter-patient TTO starting from a randomized model and a population model is plotted in Figure 6. The average time cost for inter-patient TTO starting from a randomized model is 10.25 hours for 5-cascaded Voxelmorph and 9.44 hours for 10-cascaded VTN. However, the convergence time are dramatically decreased to 3.78 minutes and 3.60 minutes respectively by starting from a population model. Majority test patients can have personalized model ready in 4 minutes, and the maximum time cost is no more than 10 minutes. Figure 7 shows an example of how the autosegmentation improves with time during inter-patient TTO. Sharp improvement happened at approximately 3 minutes, while after that, the improvement starts to slow down and finally becomes visually unobvious. Therefore the time needed by inter-patient TTO for model performance gain is clinically acceptable.

Figure 6. The time cost for inter-patient TTO.

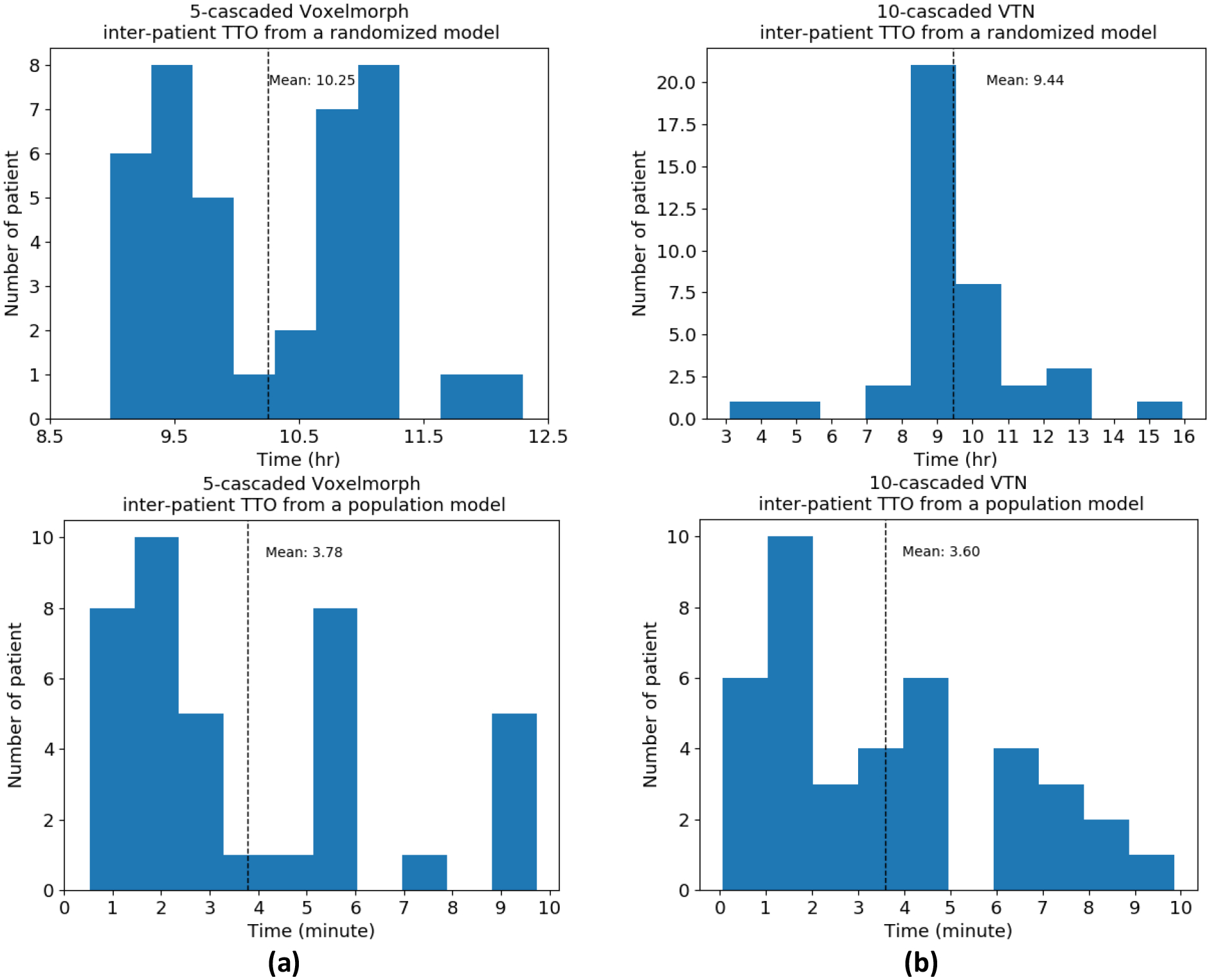
Two architectures were tested: (a) 5-cascaded Voxelmorph and (b) 10-cascaded VTN.

Figure 7. One example of autosegmentation performance change with inter-patient TTO starting from a population moel.

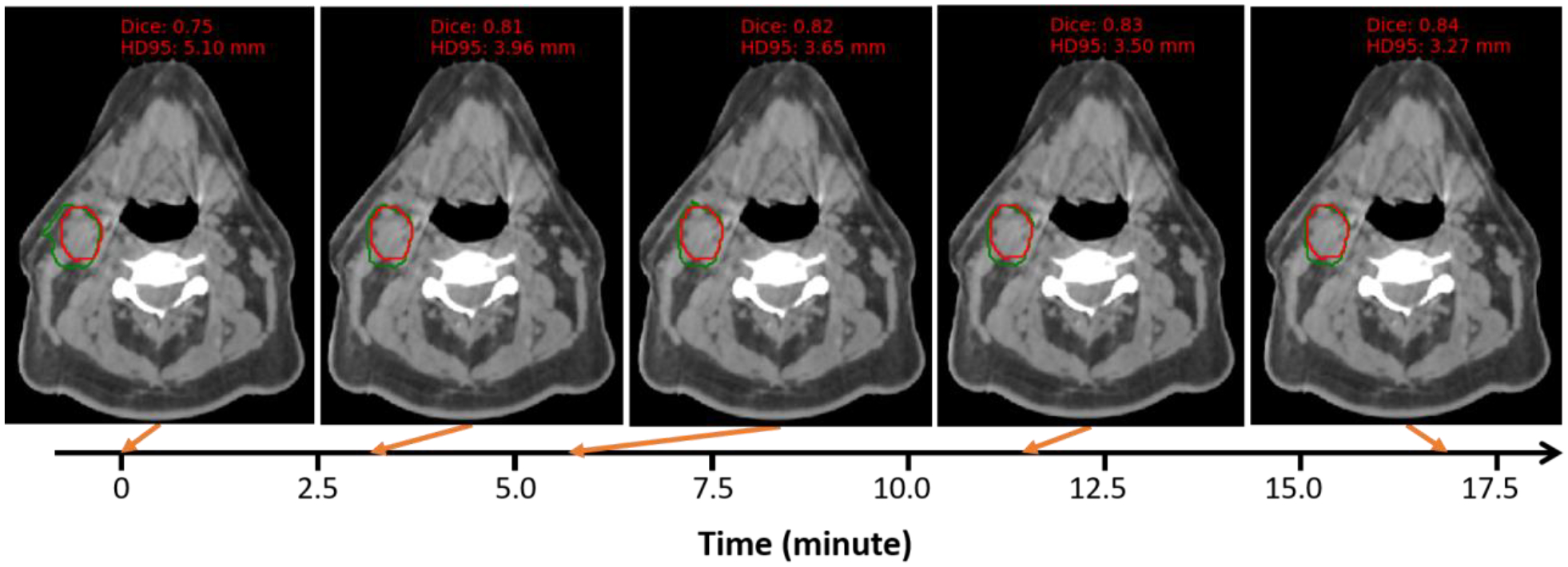
The architecture used here is 10-cascaded VTN. Background image is CBCT and the structure contoured is nGTV. Red is the ground truth contour and green is the TTO contour.

3.3. Intra-patient TTO

In intra-patient TTO application, the time cost for intra-patient TTO model to converge starting from an individualized model is plotted in Figure 8. The average intra-patient TTO time for 39 test patients is 1.06 minutes for 5-cascaded Voxelmorph architecture and 1.24 minutes for 10-cascaded VTN architecture. Majority test patients can have personalized model ready in 1 minute, and the maximum time cost is no more than 6 minutes. The segmentation performance gain through intra-patient TTO is not obvious, shown in Table 3. Figure 9 shows an example of how the autosegmentation improves with time during intra-patient TTO. Sharp improvement happened at approximately 1.5 minutes, while after that, the improvement is negligible. The individualized model that has been optimized on a pair of images from only one fraction from a specific patient can work pretty well on another pair of images from the next fraction. That means very few number or no iterations may be needed between fraction and fraction within a patient.

Figure 8. The time cost for intra-patient TTO starting from an individualized model.

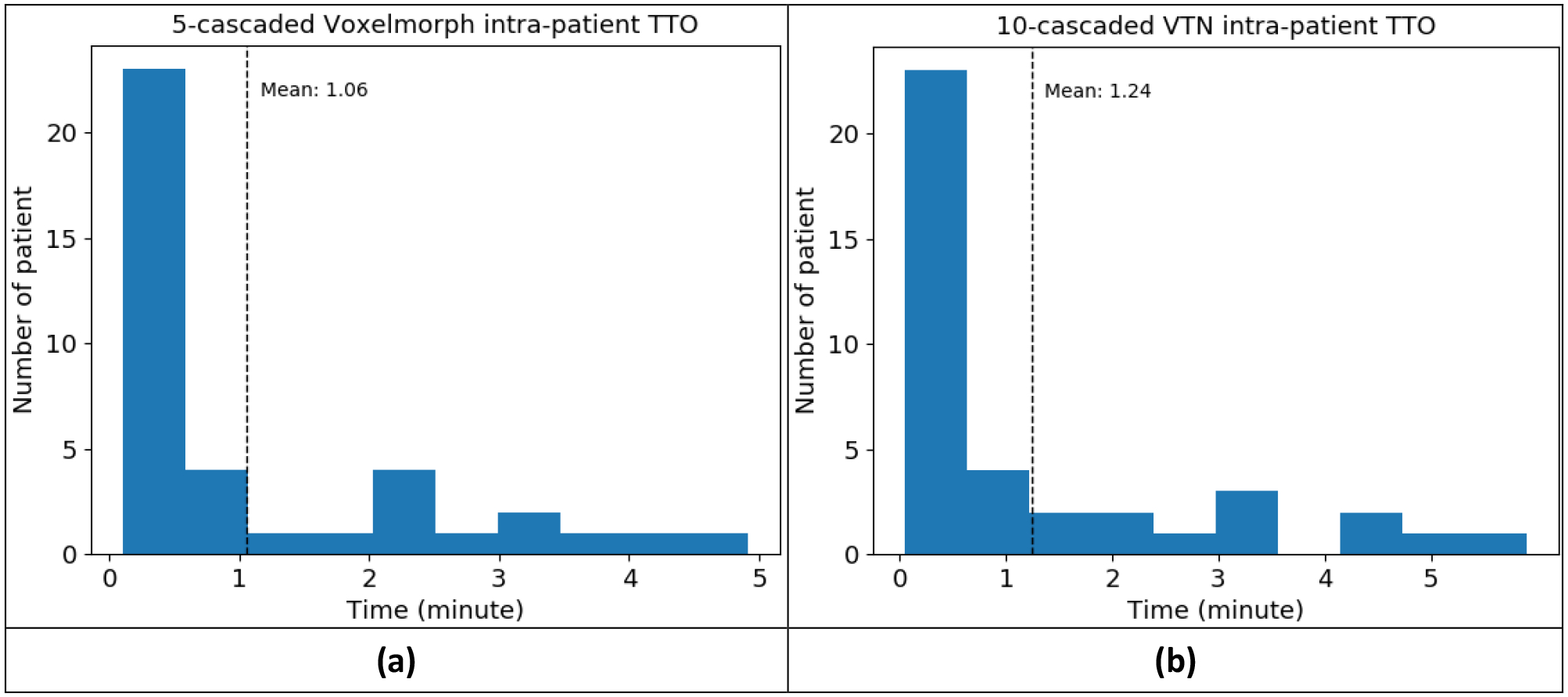
Two architectures were tested: (a) 5-cascaded Voxelmorph and (b) 10-cascaded VTN.

Table 3.

Average DSC of 39 test patients with 13 selected structures before and after intra-patient TTO

	Before intra-patient TTO	After intra-patient TTO
5-cascaded Voxelmorph	0.839	0.842
10-cascaded VTN	0.841	0.842

Figure 9. One example of auto-segmentation performance change with intra-patient TTO.

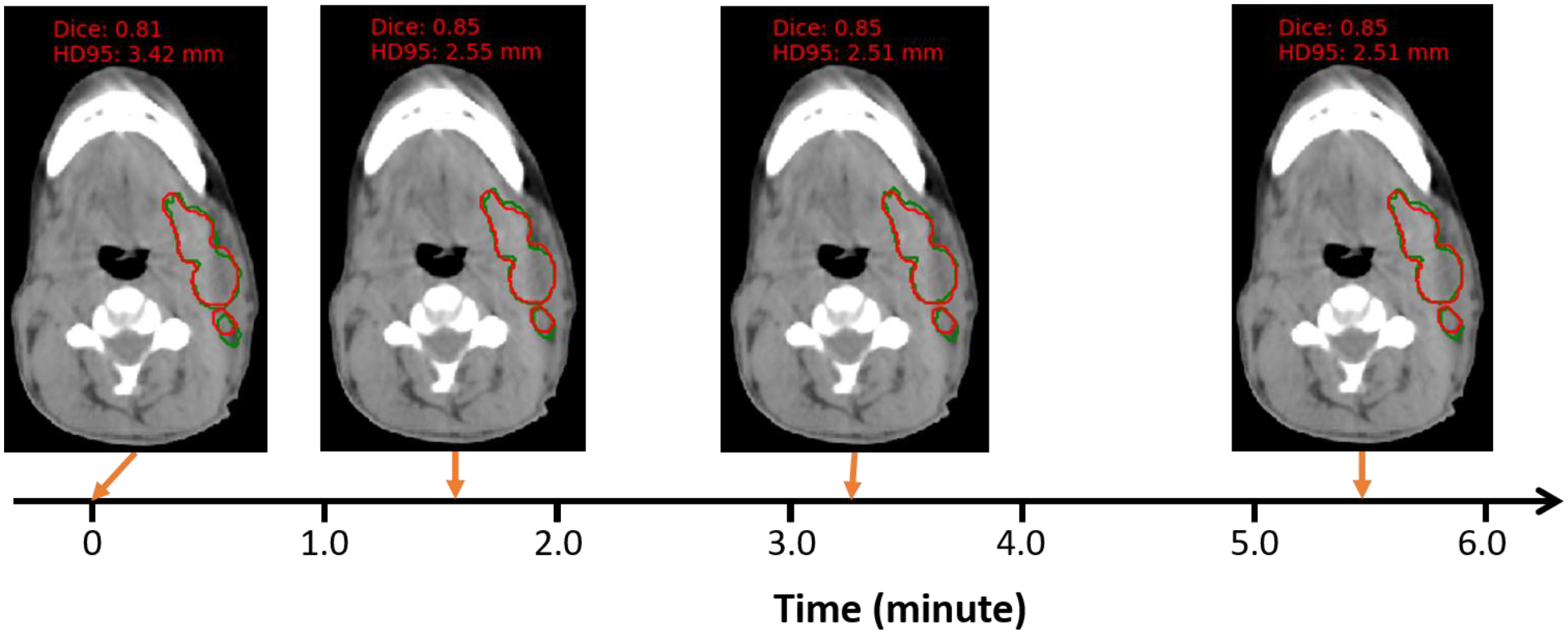
The architecture used here is 10-cascaded VTN. Background image is CBCT and the structure contoured is nGTV. Red is the ground truth contour and green is the TTO contour.

4. Discussion and Conclusion

We conducted extensive experiments by applying the proposed TTO method to different DL architectures from simple ones to the-state-of-art ones. We also compared the TTO method to some traditional methods. We found that the TTO method can improve performance of the population models for all the architectures tested. Worse performance of the population model, more improvement we can observe by the TTO method. The performance of the TTO method is DL architecture related. A better DL architecture will have better performance through the TTO method. A good DL architecture using the TTO method can outperform the traditional DIR methods in terms of accuracy and robustness.

The efficiency of the TTO method was also studied in inter-patient and intra-patient applications, taking CBCT-based ART as an example. It takes about 3 minutes for a model to converge starting from a pre-trained population model in the inter-patient application, and about 1 minute for a model to converge starting from a pre-trained individualized model in intra-patient application. Compared to one shot DIR learning, which starts to train a model from scratch using only a pair of moving and fixed image, TTO can dramatically decrease the time cost and make it feasible for online applications such as CBCT-based online ART.

One advantage of the TTO method is its flexibility. It can be applied to any unsupervised DIR neural networks. The TTO optimization process is also very easy. The hyper-parameters used in the deep neural networks can be fixed for all the cases. So it avoids the parameter tuning process in traditional DIR methods.

Another main advantage of the TTO method is its ability to improve model generalizability. A population model can be adapted to each individual patient by TTO rather than a same population model applied to all patients. Each individualized model can further be adapted from fraction to fraction through the ART course. In the case when population model fails, TTO adapted models can boost model performance significantly. We showed a patient case in Supplementary Figure 8(d) and (e) where the population model totally failed in delineating constrictor and larynx at the border slices, whereas the TTO model can avoid these failure. In the other figures in Supplementary Figure 8, TTO model significantly improves segmentation accuracy compared to population model.

All experiments in this work were done by one NVIDIA V100 GPU with 32 GB RAM. The time cost per iteration during TTO was around 3 seconds for 5-cascaded Voxelmorph and 10-cascaded VTN architecture. Since the number of iterations needed for a population model to converge on a specific patient data to get individualized model is so low, inter-patient TTO can be completed online. The anatomy difference between two consecutive fractions for the same patient is so small, intra-patient TTO can be accomplished in real time.

In conclusion, we designed a novel TTO strategy to achieve patient and treatment fraction specific models for image registration and structure propagation to facilitate CBCT-based online ART workflow.

Data availability

All datasets were collected from one institution and are non-public. According to HIPAA policy, access to the dataset will be granted on a case-by-case basis upon the submission of a request to the corresponding authors and the institution.