Waves in embryonic development

Abstract

Embryonic development hinges on effective coordination of molecular events across space and time. Waves have recently emerged as an ubiquitous mechanism that ensure rapid spreading of regulatory signals across embryos, as well as reliable control of their patterning, namely for the emergence of body plan structures. Here, we review a selection of recent quantitative work on signaling waves, and present an overview of theory of waves. Our aim is to provide a succinct, yet comprehensive guiding reference for the theoretical frameworks by which signaling waves can arise in embryos. We start then from reaction-diffusion systems, both static and time-dependent, move to excitable dynamics and conclude with systems of coupled oscillators. We link these theoretical models to molecular mechanisms recently elucidated for the control of mitotic waves in early embryos, patterning of the vertebrate body axis, micropattern cultures and bone regeneration. Our goal is to inspire experimental work that will advance theory in development and bridge its predictions to quantitative biological observations.

1. Introduction

Timely and precise coordination of biochemical signals across a wide range of spatial and temporal scales is required for proper development [117, 91, 172, 147]. At the basis of this coordination are molecular and physical mechanisms ensuring that cells act collectively. This coordination is observed across hundreds of microns and cells, and a wide range of timescales (minutes to days). Both inter- and intra-cellular mechanisms of communication contribute to the collective dynamics observed during embryogenesis. Quantitative imaging methodologies allow us to probe the dynamics behind the collective regulation of embryogenesis. Signaling waves have emerged as a new principle of regulation of cellular dynamics [51, 25, 129]. Waves can help synchronize signals across large spatial scales (hundreds of microns for typical cases in embryonic development), as well as organize signaling dynamics to ensure proper patterning of repeated structures. It is therefore timely to recapitulate the state of the art and provide a summary of theoretical ideas and methods that are relevant for the understanding of wave dynamics. These two goals constitute the motivation for our review and define its scope. We shall start by a brief overview of the phenomenology observed in a selection of developmental examples, which is followed by theoretical material on wave dynamics in various systems, bistable, excitable, and oscillatory. The main text provides a compendium that is integrated by more extended discussions and technical details in the appendices. Biological examples are then revisited to discuss their current understanding, and we conclude by highlighting open issues and future challenges.

2. Selected examples of waves in embryonic development

Our first example is provided by mitotic waves of early embryogenesis. In most metazoans, early embryogenesis unfolds outside of the mother, which puts a strong evolutionary pressure for embryos to be large (to store nutrients and genetic material) and develop quickly (to avoid predation) [121]. Consistent with this idea, embryos of many species undergo very rapid and synchronous cleavage divisions at the beginning of development [122]. Drosophila embryos are (approximate) ellipsoids of about $500\mu m$ in length and $200\mu m$ in the perpendicular directions. In the early stages, embryos develop as a syncytium, that is a large multinucleated cell that allows for cytoplasmic diffusion. All nuclei in the embryo divide within two minutes from each other and mitosis proceeds in wave-like patterns [43, 68, 26], as shown in Fig. 1. Similar waves are observed in Xenopus embryos [130]. The importance of these repeated waves is likely to ensure that all nuclei reach at about the same time gastrulation, which requires spatiotemporal coordination to ensure the proper setting of the body plan [88, 98]. Drosophila embryos consistently undergo 13 nuclear divisions before a long pause in cell division at the maternal-to-zygotic transition (MZT) [37]. This transition coincides with the time when the embryo switches from predominantly maternal control to zygotic contributions to development [37, 12, 87]. Thus, mitotic waves contribute significantly to the control of a crucial developmental transition. Moreover, waves do not have fixed dynamic properties but undergo changes that coincide with the developmental reprogramming of nuclear cycles. A slowdown of about 3-fold in the speed of mitotic waves is observed as cell cycle lengthens with the approach to the MZT [68]. The slowdown is controlled by activation of the DNA replication checkpoint [26] and mediated by the activity of Chk1 [37, 146, 145, 153, 103, 154, 38]. In summary, the early Drosophila embryo is a unique system for experiments and theory aimed at elucidating mechanisms and function of mitotic waves.

Figure 1: Mitotic waves in Drosophila embryos.

A) Cartoon illustrating coordinated nuclear divisions that spread as traveling waves across the embryo. Two waves are shown: one starts from the prospective head (left) and the other from the prospective tail (right), respectively. Both of them spread along the antero-posterior axis toward the center of the embryo. B) Confocal images of embryos expressing HisAv-mRFP to visualize nuclei. Note the two waves spreading from the poles toward the interior. C) Heatmap of Cdk1 activity as a function of time and space along the anterior-posterior axis from nuclear cycle 10 to 13. The dotted/full line in cycle 13 indicate the time of mitotic entry/exit at each position. D) Cdk1 activity as function of time in different regions of the embryo. The slight shifts among the various curves allow to visualize direction and speed of traveling waves of Cdk1 activity.

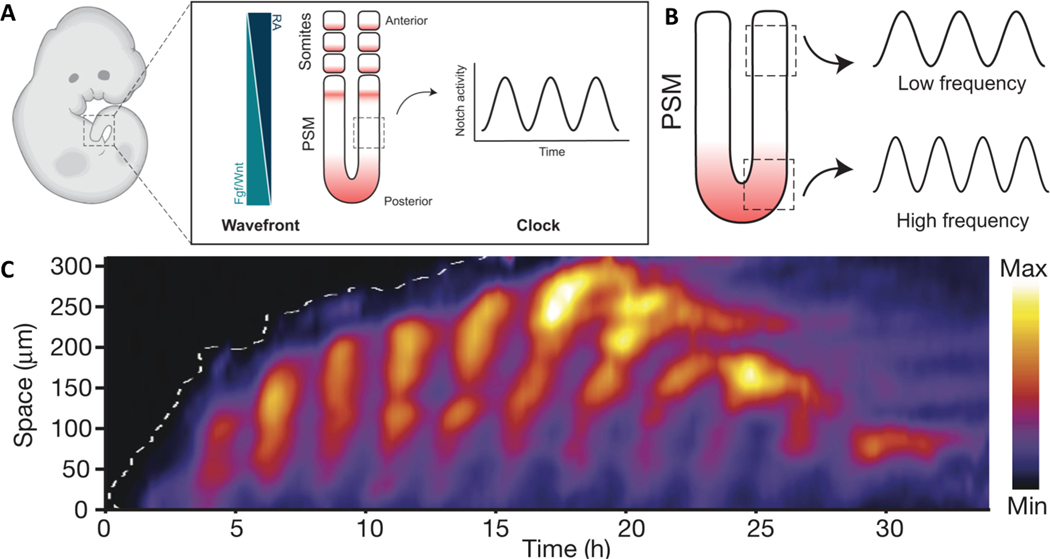
Another developmental system where signaling waves are important and much quantitative work is being conducted is somitogenesis, which is crucial for laying the body plan of vertebrate animals. Somites are specified in the presomitic mesoderm (PSM) in a recurring, sequential manner, resulting in a segmented pattern [120, 66], see Fig. 2. At the core of this process is a sequence of signaling waves, which repetitively travel across the tissue [120, 66, 53, 100, 7, 85, 149, 143]. Specifically, the activity of the major signaling pathway Notch propagates as a wave across the tissue, and induces the differentiation of a new segment into a somite, once the wave reaches the boundary defined by the last somite formed. The process repeats until the entire tissue is patterned. A similar phenomenology for the formation of periodic structures is observed in the patterning of short germ-band insects [139, 33]. Thus, repeated waves represent a general mechanism for the morphogenesis of periodic spatial structures. Repeated traveling waves of Erk activity were also recently discovered in zebrafish bone regeneration, where they regulate tissue growth [24], and in the mouse inner ear, where they control collective cell migration [69].

Figure 2: Traveling waves in somitogenesis.

A) A cartoon representing the position of the pre-somitic mesoderm (PSM) in a mouse embryo (left). Gradients of Fgf/Wnt and Retinoic Acid in the tissue, its geometric organization, showing PSM and the somites already specified, and the activity of Notch in a given region of the tissue (right). The size of the PSM varies over the stages of development in a range that goes from a minimum ~ 0.5 mm to a maximum ~ 1.4 mm [155]. B) Frequency gradient of Notch oscillations: the posterior oscillates at higher frequency than the anterior. C) Kymograph of a Notch activity reporter (LuVeLu) across an ex-vivo PSM culture. Adapted with permission from [85].

In other systems, morphogenesis is driven by an individual wave traversing the tissue. For example, in the formation of bird feathers and Drosophila ommatidia, periodic spatial structures are specified following a traveling wavefront of gene expression that traverses the entire tissue [63, 9, 135]. In micropatterned cultures of human embryonic stem cells that mimic the formation of the primitive streak, a wave of Wnt signaling has been shown to control the Epithelial-to-Mesenchymal Transition (EMT) [99]. Specifically, following addition of a Wnt ligand, cells in the culture undergo a E-cadherin dependent EMT, which is controlled by wave-like expression of the Wnt inhibitor Dkk1 [99]. During Drosophila gastrulation, the invagination of the endoderm has been shown to be initiated by spatially restricted transcription of an activator of cell contractility, and propagated by a mechanical wave arising from a feedback mechanism that requires the activity of myosin motors [8]. Similarly, the morphogenetic wave traveling across the Drosophila eye imaginal disc might integrate biochemical and mechanical inputs [48].

Collectively, the above biological examples highlight the role of traveling waves as a general principle for the spatiotemporal organization of multicellular systems. Our goal here is to provide the reader with a short, yet rather complete, presentation of theories for waves, and a grasp of how the interplay of theory and experiments is advancing our comprehension of mechanisms and function of developmental traveling waves.

3. Waves in bistable reaction-diffusion systems

Motivated by previous experimental observations, we start here our overview of theoretical methods and ideas. We first consider bistable systems, static and time-dependent, and move then to excitable and oscillatory systems in the following two Sections. As it will be explained below and in Section 6.1, the dynamics of bistable systems is particularly relevant to the understanding of mitotic traveling waves illustrated in Fig. 1, viz. the nature of the observed waves, their speed and profile, as well as their dependence on parameters such as the speed of the cell cycle, temperature, Cdk1 diffusivity, level of biochemical noise, etc.

3.1. Time-independent bistable systems and trigger waves

A static bistable dynamical system has two stable equilibrium states where it can rest (see Fig. 3). While both of them are locally stable, one of the two is generically globally stable and the other one just metastable. For spatially extended systems in the presence of diffusion, it is then possible to generate waves where regions at the stable level invade those at the metastable level, as we discuss hereafter. These bistable waves are distinct from Fisher-Kolmogorov waves, see [112], where a stable state invades an unstable one.

Figure 3: Static bistable systems and trigger waves.

A) A typical force profile $f(\varphi )$ for a bistable system. The black/open dots indicate stable/unstable fixed points (zeros of $f$). B) The corresponding potential $V(\varphi )$ defined by $f=-\frac{\partial V}{\partial \varphi }$. Out of the two stable points, the rightmost is globally stable while the leftmost is metastable. C) The mechanical analogy presented in the text shows that the speed of the traveling wavefront shown in (D) is given by the friction coefficient needed for a ball rolling down from the highest peak of the inverse potential $-V(\varphi )$ to land exactly on the lowest peak. D) Traveling wavefront connecting the stable and the metastable points.

The model equation considered here is the reaction-diffusion equation

$$\frac{\partial \varphi (\mathit{x},t)}{\partial t}=D\text{Δ}\varphi (\mathit{x},t)+F_{0}f(\varphi ),$$ (1)

where $\varphi (\mathit{x},t)$ is the scalar field (rescaled to be dimensionless) which features waves, e.g., the activity of the cell-cycle regulator Cdk1 for Drosophila early embryogenesis. The Laplacian $\text{Δ}={\sum }_{i=1}^d\frac{{\partial }^2}{\partial x_i^2}$ accounts for diffusive effects and $D$ is the diffusivity. Reaction terms depend on the (typically nonlinear) non-dimensional function $f$ and the amplitude coefficient $F_0$ (which has dimensions of inverse of time). The dimension of space is $d$ yet we shall mostly consider one-dimensional fronts, with variations in a single direction $x$. The coefficients $D$ and $F_0$ in Eq. (1) are set to unity rescaling time and space by $1/F_0$ and $\sqrt{D/F_0}$. The role of additional noise terms in Eq. (1) is discussed at the end of Section 3.1.2.

Bistability is embodied in the reaction term which has three fixed points, i.e., zeros of $f$, and the generic shape shown in Fig. 3A. The corresponding potential $V$, defined by $f=-\frac{\partial V}{\partial \varphi }$, is shown in Fig. 3B. By a shift and rescaling of the field $\varphi$, we can have the two minima of $V$ at $x=0$ and $x=1$ (locally stable fixed points). The third zero of the force $f$ corresponds to a maximum of the potential $V$, that is an unstable fixed point. Note that the force $f(\varphi )$ is static, contrary to Section 3.2 where time-dependent effects are considered.

3.1.1. Trigger waves

The spreading a wave corresponds to the existence of solutions $\varphi (x,t)=\phi (\xi )$, which is non-trivial as dependencies on $x$ and $t$ are reduced to a single variable $\xi \equiv x-ct$, where $c$ is the wave speed coefficient (the speed in dimensional units is $c\sqrt{F_{0}D}$). The ansatz reduces Eq. (1) to the ordinary differential equation (ODE):

$$\frac{d^2\phi }{d{\xi }^2}=-c\frac{d\phi }{d\xi }-f(\phi ).$$ (2)

A major property of bistable reaction-diffusion systems is that they do support waves, which is reflected in Eq. (2) admitting solutions, as shown by the following mechanical analogy.

Interpreting $\xi$ as “time”, Eq. (2) is recognized as Newton’s equation for a particle of unit mass, subject to friction with coefficient $c$, and to a force $-f$, i.e., moving into a potential $-V$ as shown in Fig. 3C. A wavefront profile as in Fig. 3D corresponds to a solution starting from the top of the hill at $\phi =1$ (as $\xi \to -\infty$) and landing on top of the hill at $\phi =0$ (as $\xi \to +\infty$). Stopping exactly on the top of the hill requires a particular value of the “friction coefficient” $c$, which dissipates the right amount to avoid rolling back or over the top. This entails that the wave profile and velocity are unique. In fact, further reducing the friction coefficient might allow to land again on top of the hill after some oscillations on the left of the origin. However, Appendix A shows that those non-monotonic solutions are linearly unstable [158]. For global results on basins of attraction of traveling wavefronts, see Appendix B.

The above mechanical analogy also shows that the sign of the velocity $c$ is determined by the depth of the minima of $V$, viz. the deeper (stable) state invades the (metastable) higher one. That is confirmed algebraically, multiplying Eq. (2) by ${\phi }^{\prime }=d\phi /d\xi$, integrating and using that derivatives vanish at infinity, to finally obtain:

$$c=\frac{{\int }_0^{1}f(\phi )d\phi }{{\int }_{-\infty }^{\infty }{\phi }^{\prime 2}d\xi }=\frac{V(\phi =0)-V(\phi =1)}{{\int }_{-\infty }^{\infty }{\phi }^{\prime 2}d\xi }.$$ (3)

Alternative arguments in Appendix C reach the same above conclusions by using dynamical-systems theory [151] to demonstrate that a heteroclinic trajectory connects the two saddle points $\phi =0$ and $\phi =1$ of Eq. (2).

3.1.2. Determining the velocity and profile of fronts

Eq. (2) has reduced the calculation of the velocity $c$ and the wavefront to the integration of an ODE, yet the equation is still nonlinear and has two-point boundary conditions, which generally requires numerical methods. Two notable exceptions are piecewise linear and cubic forces, which are both analytically solvable [75] (see Appendix D). The wavefront profile for the cubic case has the simple expression: $2\phi (\xi )=1-\tanh (\xi /\ell )$, with the width of the transition region $\ell =2\sqrt{2}$ multiplied by $\sqrt{D/F_0}$ in the original units.

In general, the velocity and the profile can be determined by integrating numerically Eq. (2) with a large initial friction, which leads to landing in the intermediate minimum of the inverted potential $-V$ (see Fig. 3C). Friction is then reduced until the particle reaches the top of the hill at $\phi =0$. The corresponding value $c=c^{\ast }$ yields the velocity of the wave in dimensional units as $c^{\ast }\sqrt{F_{0}D}$. The expression with $c^{\ast }=2$ is commonly known as Luther’s formula [94]. The profile of the front is read from the “time” course of the corresponding trajectory at $c^{\ast }$. Corrections in discrete systems are discussed in Section 6.2.3 of [75].

A final remark on noise, which is widespread in spatially extended systems [49]. Indeed, reaction terms in Eq. (1) often involve noisy processes, e.g., biochemical reactions. The resulting additional noise terms do play a major role in the nucleation of the “bumps” that will then spread as fronts [49], and for time-dependent situations, as discussed in Section 3.2. Our rationale for not including noise in this Section was that corrections to the velocity and the profile of a bistable front are relatively weak, as shown in Appendix E.

3.2. Time-dependent bistable systems and sweep waves

Motivated by the phenomenology in Section 2 of Drosophila mitotic waves that take place on timescales comparable to variations associated to the cell cycle, we now consider the time-dependent version of Eq. (1):

$$\frac{\partial \varphi (\mathit{x},t)}{\partial t}=D\text{Δ}\varphi (\mathit{x},t)+f(\varphi ,t)+\sqrt{2\nu }\eta (x,t),$$ (4)

where the (white) noise $\eta$ is now included for the reasons elucidated below, and the reaction term $f$ depends on time as sketched in Fig. 4A. While the phenomenology described hereafter has general validity, it is convenient to consider the specific case

$$f(\varphi ,t)=-F_0\varphi \left(\varphi -\frac{1}{2}\right)(\varphi -1)+\beta t\equiv -F_0\left(\varphi -{\varphi }_0(t)\right)(\varphi -a(t))\left(\varphi -{\varphi }_1(t)\right),$$ (5)

with ${\varphi }_0\le a<{\varphi }_1$. Initially, the unstable point $a(0)=1/2$ so that the potential minima (see Fig. 3B) at ${\varphi }_0(0)=0$ and ${\varphi }_1(0)=1$ have the same depth. As time progresses, the time-dependent constant $\beta t$ raises the force field, i.e., tilts the potential by $-\beta t\varphi$, which shifts the zeros of $f$ and favors the stability of ${\varphi }_1(t)$ vs. ${\varphi }_0(t)$ (see Fig. 4A). Bistability is eventually lost at the time $t^{\ast }$ when ${\varphi }_0\left(t^{\ast }\right)$ and $a\left(t^{\ast }\right)$ merge and then turn complex conjugate by a saddle-node bifurcation. Two dynamical phases can schematically be distinguished, as shown in Fig. 4.

Figure 4: Transient bistability and sweep waves.

A) A typical force field $f(\varphi ,t)$ that transitions from bistability at early times (blue) to monostability at late times (highest curve in red). As shown in Fig. 3, fixed points are the crossings of $f$ with zero (indicated here by the black line). The three zeros in the bistable regime are denoted in the text as ${\varphi }_0(t)$, $a(t)$ and ${\varphi }_1(t)$, from left to right. Profiles around the saddle-node bifurcation that leads to loss of bistability are shown in red. The inset zooms the blue curves around ${\varphi }_0$ to illustrate the progressive reduction of the corresponding slope. B) Ref. [160] shows that trigger waves (as in Section 3.1) are observed for slow transitions from bistability to monostability, whilst faster sweep waves are observed when the transition is rapid. Specific conditions for “rapid” and “slow” are discussed in the text and Appendix F. The panels show that the space-time profiles of the fields are markedly different in the two cases. C) The simple geometric argument showing that the speed of phase waves, such as sweep waves of Cdk1 in panel (B), have an inverse dependence on the phase gradient [79, 168]. D) A kymograph illustrating the $1/g$ dependence for the idealized case in panel (C). E) Experimental data [160] demonstrating the $1/g$ dependence for Drosophila Cdk1 sweep waves.

• Phase I: adiabatic evolution.

At early times, a system starting from $\varphi (x,0)\sim 0$ will follow ${\varphi }_0(t)$ (adiabatic evolution). Indeed, as shown in the inset of Fig. 4A, the zero ${\varphi }_0(t)$ has a steep negative slope, i.e.,

$$f(\varphi )\simeq -\frac{1}{\tau }\left(\varphi -{\varphi }_0(t)\right)\text{with}{\tau }^{-1}(t)=\left|f^{\prime }\left({\varphi }_0(t)\right)\right|.$$ (6)

The reaction term acts then as a spring with equilibrium length ${\varphi }_0(t)$ and stiffness ${\tau }^{-1}$. Appendix F shows that its effect is to keep an average level $\langle \varphi \rangle \sim {\varphi }_0(t)$ and tame fluctuations induced by the noise in Eq. (4) at a typical level $\sqrt{\nu }$. Correlations decay exponentially in space with a correlation length $\lambda (t)=\sqrt{D\tau (t)}$ that grows with time due to the flattening of $f$ at ${\varphi }_0$ (inset of Fig. 4A). The expression of $\lambda (t)$, which differs from the diffusive length $\sqrt{Dt}$, reflects the combined role of diffusive and reactive terms. In sum, during the early adiabatic phase, the $\varphi$ field grows as ${\varphi }_0(t)$ and establishes correlations on longer and longer spatial scales $\lambda (t)$. Section 6.1 will present supporting experimental evidence in Drosophila development.

• Phase II: non-adiabatic dynamics around the bifurcation point.

Phase I ends when the relaxation time $\tau (t)$ becomes comparable to the time of variation of ${\varphi }_0(t)$ (Appendix F). The smaller is $\beta$, the later is the transition, yet it will eventually happen since $\tau$ diverges at the saddle-node bifurcation. If noise drives an extended region above the unstable point $a\left(t\right)$ before phase II sets in, then the trigger waves scenario (see Fig. 4B) of Section 3.1.1 applies; this regime holds for small $\beta$ (see Appendix F for details). Conversely, for larger $\beta$’s the field $\varphi$ is driven to values around the minimum of $f$ at times comparable to the time of the saddle-node bifurcation (see red curves in Fig. 4A). Around the bifurcation, the dynamics is mainly driven by the time-dependent component $\beta \left(t-t^{\ast }\right)$ as the remainder of $f$ in Eq. 5 is small (the so-called saddle-node ghost [151]). Being $\varphi$-independent, $\beta \left(t-t^{\ast }\right)$ raises the level of $\varphi$ without distorting it. Furthermore, diffusive effects may be neglected if $\lambda (t)$ has grown enough. It is concluded (see Appendix F) that the profiles and the gradients created during phase I are swept up undistorted during phase II, as shown in Fig. 4B.

Gradients formed in phase I and swept up in phase II lead to the appearance of a phase wave (called “sweep” in [160]). Indeed, local maxima of $\varphi$ reach a threshold level first, then neighbors a little later, and so on along the gradients. The hallmark of a phase wave is that its velocity $\propto 1/g$, where $g$ is the local gradient [79, 168]. The other factor that determines the wave speed $U_{sweep}$ is the rate at which the field $\varphi$ is swept up (see Fig. 4C-D). Analyzing the dynamics of these two factors (see Appendix (F)), one finally arrives at the scaling law [160]:

$$U_{sweep}=\frac{d\varphi /dt}{g}\propto \frac{{\beta }^{7/12}{D}^{3/4}}{{\nu }^{1/2}{F}_0^{5/12}}.$$ (7)

The inverse dependency on $F_0$ and the $D^{3/4}$ contrast with the square-root for trigger waves in Section 3.1.2. Similarly, the ${\nu }^{-1/2}$ scaling, which traces back to $U_{sweep}\propto 1/g$, contrasts with the weak dependency on noise found in Appendix E. In conclusion, sweep waves in time-dependent bistable systems have a different nature than trigger waves in static cases. This fundamental difference reflects in their dependence on dynamical parameters and their speed, which typically overcomes the maximum speed that a trigger wave can reach [160].

3.3. Phase vs. trigger waves

Phase waves are like the lights on a marquee or the chain of flashing strobe lamps at an airport runway: they reflect delays among spatial locations, and their spreading does not involve mutual interactions. That contrasts with trigger waves in Section 3.1.1. The speed of phase waves $\propto 1/g$ can become arbitrarily large for shallow gradients [79, 168] (see Fig. 4C-D). All that explains why phase waves are sometimes dismissed as “pseudo waves” [168]. While the absence of interactions is a fact, we would like to tame this stand. Indeed, gradients of delays in natural phenomena are not the action of an external watchmaker, but they are generated by some dynamical process that does couple the various spatial locations. It is then to be explained how gradients are generated, and why interactions matter during gradients’ formation and not during the spreading of the phase wave. The example above of a transiently bistable system illustrates all of these points; consequences for barrier experiments and discrimination of phase vs. trigger waves are addressed in Section 6.2. Note finally that within the same dynamical system, and even the same wave, one can have a mixture of trigger and phase waves. For instance, traveling pulses in excitable systems can feature a trigger wave front and a phase wave back, as discussed in Section 4.3.

4. Waves in excitable systems

Contrary to bistable systems in Section 3, excitable systems have a single fixed point yet they are close to a bifurcation, which causes wild excursions that are the origin of their name [75]. Indeed, while small perturbations (subthreshold) to the fixed points are dampened rapidly, perturbations of sufficient amplitude generate wide excursions before decaying, see Fig. 5A. Depending on the type of bifurcation that the fixed point is undergoing, different subthreshold relaxation processes and bursting are observed [70]. Proximity to a bifurcation also accounts for the importance of noise, which can lead to a variety of effects, such as noise-induced oscillations, stochastic resonance and synchronization, reviewed in [92].

Figure 5: Dynamics of FitzHugh-Nagumo (FHN) model.

A) Nullclines for the FHN model in the excitable regime. The fixed point is stable. In response to a perturbation below/above threshold (red open dot) the system relaxes to the stable state after a small/long excursion (blue/black arrows). B) In the range $W_{min}<w<W_{max}$ the nullcline $f=0$ has three intercepts with a horizontal line: $V_r(w)\le V_u(w)\le V_e(w)$, where the indices refer to “recovery”, “unstable” and “excitatory”, respectively. C) Nullclines for the FHN model in the oscillatory regime, characterized by the existence of a limit cycle. D) & E) The geometry of excitable FHN traveling waves. The purple and red arrows indicate the fast processes that generate the front and the back of the wave pulse shown in (F). Panels (D) and (E) refer to the two cases discussed in the text: the speed of the wavefront is respectively smaller or larger than the maximal possible speed of the backfront, which is attained at $W_{max}$. As discussed in the text, phase waves of the Fisher-Kolmogorov type are observed for the situation of panel (E).

Excursions in excitable systems are exemplified by action potentials analyzed in the pioneering Hodgkin-Huxley model [64]. A great deal of activity has therefore concentrated on neuroscience [70]. Since then, excitable systems have spread to other textbook situations, see [75], which include cardiac dynamics [23, 19, 73, 115] and Dictyostelium discoideum developmental processes [89, 77]. Section 6.3 will discuss the relevance of excitable systems for somitogenesis shown in Fig. 2, and Section 6.4 will discuss ongoing work based on excitable models for Erk waves. Following our goals, we focus on the analysis of waves and the paradigmatic example of the FitzHugh-Nagumo model [42, 114], which lends to a synthetic presentation of the essence of excitability.

4.1. The FitzHugh-Nagumo (FHN) model

The FHN model in its general form is defined by the following systems of equations:

$$\frac{\partial v(x,t)}{\partial t}=D{\partial }_x^{2}v+\frac{1}{{\tau }_v}f(v,w);\frac{\partial w(x,t)}{\partial t}=\frac{1}{{\tau }_w}g(v,w),$$ (8)

where $v$ and $w$ are the excitatory/recovery variables, or propagator/controller in [40]. The reaction function $f$ typically embodies positive nonlinear feedbacks, e.g., related to the opening of ion channels for neurons. Conversely, the function $g$ models negative feedback effects that lead to relaxation after an excitatory event, e.g., the closing of ion channels for neurons. The ratio $r={\tau }_v/{\tau }_w$ controls the separation in timescales between excitation and relaxation processes. Here, we shall suppose $r$ small, and that the excitatory variable $v$ spreads globally via diffusion while the recovery variable $w$ is local.

Nullclines $f=0$ and $g=0$ intercept at a single stable point $S=\left(v_s,w_s\right)$, see Fig. 5. The nullcline $f=0$ has a “cubic-like” shape and, in the range $W_{min}<w<W_{max}$, three intercepts with a horizontal line: $V_r(w)\le V_u(w)\le V_e(w)$, where the indices refer to “recovery”, “unstable” and “excitatory”, respectively (see Fig. 5B). The inhibitory effect of $w$ on the growth of $v$ and the increase of $w$ as $v$ increases are reflected by the requirements $\partial f/\partial w<0$ and $\partial g/\partial v>0$. Finally, $\partial g/\partial w<0$ keeps in check recovery effects. The specific model in the works by FitzHugh [42] and Nagumo et al. [114] has $f(v,w)=\tilde{f}(v)-w$ and $g=bv-b^{\prime }w$, with $\tilde{f}$ cubic-like, and $b$ and $b^{\prime }$ parameters.

4.2. Excitatory dynamics in the FHN model

To build up understanding of wave propagation, let us start by considering the dynamical behavior of an individual local element in Eq. (8), i.e., $D\equiv 0$. The appeal of the FHN model is that its two-dimensional nature lends to phase-plane techniques [151]. Fig. 5A illustrates the local stability of the fixed point $S$ when it is on the left recovery branch (see Appendix G). Vice versa, when the fixed point is on the middle branch, the action of $f$ on $v$ tends to destabilize the system. That leads to a Hopf bifurcation (see Appendix G) and to trajectories flowing toward a limit cycle (see Fig. 5C). The bifurcation can be driven by applying a stimulus $F_{app}$, which moves up or down the profile of $f$. A notable developmental example is provided by the Erk waves in zebrafish scales [24, 59] discussed in Section 6.4.

Consequences of the proximity to a bifurcation point are shown in Fig. 5A: small fluctuations decay rapidly whilst large-amplitude fluctuations take a long detour before relaxing to the stable fixed point. Wide excursions are conveniently described in the limit $r={\tau }_v/{\tau }_w\ll 1$. The trajectory will then stick close to the nullcline $f=0$ on the recovering/excitatory branches, where it will vary on slow timescales as $dw/dt=g\left(V_{r/e}(w),w\right)\equiv G_{r/e}(w)$, respectively. Paths connecting the two branches cannot satisfy $f=0$ and will be completed very rapidly, on timescales $\sim r$. The separation in timescales between $v$ and $w$ ensures that the corresponding variation of $w$ is minor and the connecting paths are roughly horizontal lines. Most of the time for completing a cycle is taken by the slow motion along the nullclines, $T_e={\int }_{w_s}^{W_{max}}\frac{du}{G_e(u)}$ and $T_r=-{\int }_{w_s}^{W_{max}}\frac{du}{G_r(u)}$, where $w_s$ is the fixed-point value of $w$.

4.3. Wave propagation in the FHN model

Reasoning in Section 4.2 also allows one to grasp wave propagation and establish the connection with bistable waves of Section 3.1.1. Let us indeed consider an initial state with the system at rest $\left(v=v_s,w=w_s\right)$ for $x>0$ and the variable $v$ on the excitatory branch $\left(v=V_e\left(w_s\right)\right)$ for $x<0$. Diffusion will smooth out the discontinuity at the origin into an up-front. To analyze its space-time profile, we introduce the wave variable $\xi \equiv x/\sqrt{D{\tau }_v}-ct/{\tau }_v$, analogous to that used for Eq. (2). Inserting into Eq. (8), we obtain

$$v^{″}+c{v}^{\prime }+f(v,w)=0,-c{w}^{\prime }=rg(v,w),$$ (9)

where the prime indicates $\xi$-derivatives. The second equation states that $w$ does not change over the profile, whence its name “controller” [40]. For fixed $w$’s, the first equation is identical to Eq. (2), i.e., it describes the velocity and profile of a wavefront that connects the two branches $v\to V_{r,e}(w)$ as $\xi \to \pm \infty$. Eq. (3) for the velocity $c$ shows that the profile moves with velocity $c(w)\propto {\int }_{V_r(w)}^{V_e(w)}f(v,w)dv$. Varying $w$ in the “bistable” range $W_{min}<w<W_{max}$ shown in Fig. 5B, we go from a maximum $c_{max}>0$ for $w=W_{min}$ to a minimum $c_{min}<0$ for $w=W_{max}$. Fig. 5D has $c\left(w_s\right)>0$, i.e., the up-front moves to the right for $w=w_s$.

So far, the dynamics is the same as for bistable systems. Differences stem from the recovery process in the back of the wave, which modifies the front of Fig. 3D into the pulse of Fig. 5F. Indeed, in the back of the up-front, $w$ evolves according to Eq. (9) with $v=V_e(w)$. The recovery variable $w$ will then increase (and $v$ decrease) until the upper knee in Fig. 5A is reached: the system cannot stick to the nullcline $f=0$ any longer, and a second front develops, which jumps down from $V_e\left(W^{\ast }\right)$ to $V_r\left(W^{\ast }\right)$. In the back of the down-front, the recovery variable $w$ evolves along $v=V_r(w)$, which drives the system to the steady-state $S$ and completes the formation of the pulse. Analogously to the up-front, the down-front is governed by Eqs. (9), yet boundary conditions are reversed ($v\to V_{e,r}\left(W_{max}\right)$ as $\xi \to \pm \infty$), so that its speed is initially $\left|c_{min}\right|$ and it moves to the right. Two cases are possible (see Fig. 5D-E):

• For $c\left(w_s\right)\le \left|c_{min}\right|$, the speed of the down-front either matches or is faster than the up-front. In the latter case, the down-front tends to catch up the up-front and thereby moves towards lower values of $w$. During this process, the front progressively deforms and slows down until it reaches the value $\overline{w}$ such that $c(\overline{w})=c\left(w_s\right)$, which finally yields the stationary shape of the down-front and the whole pulse. Similar reasoning is used in Appendix H to analyze dispersion relations for periodic wave trains.

• For $c\left(w_s\right)>\left|c_{\mathit{min}}\right|$, the knee is reached, which is a locally unstable (and not metastable) point. This leads to Fisher-Kolmogorov waves with a continuous spectrum of velocities [112]. The upshot of the analysis in Appendix I is that the (phase) wave that moves with the speed $c\left(w_s\right)$ matching the up-front is eventually selected.

We conclude by a short comment about the effects of curvature onto the propagation of waves in excitable (or bistable) systems. The basic mechanism of wave spreading is that if a region is locally driven beyond threshold, then diffusion will drag neighboring regions across threshold, and reaction effects will drive them to the excitatory branch (or to the stable fixed point for bistable systems). Consider then cases in Fig. 6: in the middle one, the region before the wavefront is excited more rapidly than if the wavefront were planar, and the wave speed will then be greater; vice versa, it will be reduced (see Appendix J for details and equations).

Figure 6: Effect of curvature on wave speed.

A sketch of a planar and two curved wavefronts where the velocity increases (mid panel) or decreases (right panel) with respect to regions of no curvature.

5. Waves in coupled oscillators

A common situation for an excitable system is its being close to a Hopf bifurcation: two conjugate imaginary eigenvalues cross the imaginary axis while all the others remain on the left half-plane, i.e., have their real parts negative [151]. Stability is then lost and an oscillatory behavior sets in. Oscillators are ubiquitous in biology and the coupling of cellular oscillators can lead to interesting patterns in development. A notable example relevant to this review is somitogenesis shown in Fig. 2, which will be further discussed in Section 6.3. The role for the embryonic segmentation clock of the phase response curve and entrainment phenomena discussed below has recently been highlighted in [136].

An instance of Hopf bifurcation is the FHN model when the intercept of the two nullclines switches from the left to the middle branch, see Fig. 5 and Appendix G. The amplitude of the limit cycle close to a Hopf bifurcation can be small (supercritical bifurcation) or have a finite amplitude (subcritical bifurcation). Coupling of oscillatory units by diffusion leads to a system of coupled nonlinear oscillators that can support the propagation of waves, as we discuss in this Section. We start by waves close to a supercritical bifurcation, and move then to subcritical cases or oscillations far from a critical point.

5.1. Waves for coupled oscillators close to a supercritical Hopf bifurcation

Close to bifurcations, one can reduce a generic nonlinear dynamical system to its normal form, that is a simplified form that preserves the essential features of the dynamics [151, 70]. For a Hopf bifurcation, the normal form is the Stuart-Landau equation for the complex amplitude $z$ of perturbations (see [58, 65, 82, 125, 126] and Appendix K for details):

$$\frac{dz}{dt}=z\left[(a+ib)-(p+iq)|z{|}^2\right].$$ (10)

The coefficient $a$ becomes positive beyond the critical point, which drives instability and growth of perturbations. If $p>0$ (supercritical case), then the nonlinear term blocks the growth at an amplitude $|z|=\sqrt{a/p}$ and the other terms drive an oscillatory behavior $z(t)=\sqrt{a/p}{e}^{i{\omega }_{0}t}$ with frequency ${\omega }_0=b-aq/p$. The solution is stable and (10) is recognized as a particular case of the $\lambda -\omega$ model [80] (see Appendix L). Since the coefficient $a$ is small close to the bifurcation, the amplitude is also small (square-root of the deviation to the critical point), which is key to analytical progress. Conversely, if $p<0$ (subcritical case), then higher-order nonlinear terms are involved in the saturation of the amplitude, which is generally not small. The sign of $p$ is determined by the expression at page 156 of [58].

Waves appear when a field of the above Hopf oscillators are coupled, viz. by diffusion. The resulting Ginzburg-Landau equation (see [82] and Appendix K) reads:

$$\frac{\partial z(\mathit{x},t)}{\partial t}=z\left[1-(1+ic)|z{|}^2\right]+(1+id)\text{Δ}z,$$ (11)

which is encountered in a variety of natural situations [5]. The parameters $a$, $p$ and the diffusivity are set to unity by rescaling space, time and amplitude, while the $b$ term is eliminated from Eq. (10) by considering $z{e}^{-ibt}$. Eq. (11) indeed admits plane waves solutions:

$$z(x,t)=A(k)e^{i(\mathit{k}\cdot \mathit{x}-\omega (k)t)},$$ (12)

with magnitude $A(k)=\sqrt{1-k^2}$ and dispersion relation $\omega (k)=c\left(1-k^2\right)+d{k}^2$. Stability of the waves is governed by the Benjamin-Feir-Newell criterion discussed in Appendix M. Their nonlinear nature is witnessed by the fact that when two waves collide they almost do not interpenetrate and create shocks, contrary to linear waves [5]. For other one-dimensional coherent structures, which include fronts and pulses, see [159]. For two-dimensional spiral waves and three-dimensional coherent structures, see the review [5].

The generality of traveling wave solutions for reaction-diffusion systems close to a Hopf bifurcation was addressed in Ref. [80]. The paper considers the equation

$$\frac{\partial \mathit{X}(\mathit{x},t)}{\partial t}=\mathit{F}(\mathit{X})+K\text{Δ}\mathit{X},$$ (13)

and establishes the existence of small-amplitude plane waves when the diffusivity matrix $K$ does not deviate much (see Appendix N for precise statements) from a scalar matrix. In plain words, cross-diffusivities should be relatively small and self-diffusivities close to one another. Eq. (13) admits a solution $\mathit{X}=\mathit{h}(\mathit{k}\cdot \mathit{x}-\omega t)$ periodic in its argument. The idea of the proof (see Appendix N) is to exploit the Hopf structure of the Jacobian $J_{ij}=\partial F_i/\partial X_j$ to control the spectrum of the linear dynamics of Eq. (13) (which is related to $J-k^{2}K$) and apply the Hopf bifurcation theorem [58] to establish the existence of a periodic solution.

5.2. Weakly perturbed nonlinear oscillators

We now consider oscillations with arbitrary amplitude yet weakly perturbed, e.g., by an external forcing or interactions with other oscillators. Let us consider an $m$-dimensional dynamical system having a stable periodic orbit $\text{Γ}$ with period $T_0$. In the $m$-dimensional phase space $\mathit{X}=\left(X_1,\dots ,X_m\right)$, $\text{Γ}$ defines an isolated attractive closed orbit, as shown in Fig. 7A. Stability implies that there is a neighborhood of the orbit such that all trajectories starting in that neighborhood asymptotically converge to $\text{Γ}$. The position along the limit cycle can be characterized by a phase $\text{Θ}(\mathit{X})$ that generalizes the azimuthal coordinate in a circumference. The phase $\text{Θ}$ steadily increases by $2\pi$ while $\text{Γ}$ is described, that is

$$\frac{d\text{Θ}}{dt}={\omega }_0,$$ (14)

where ${\omega }_0=2\pi /T_0$. The zero of the phase is arbitrary and defined conventionally, e.g., the firing for a tonic neuron [35]. Any $2\pi$-periodic angular variable $\theta (t)$ is converted into the (uniformly increasing) phase by $\text{Θ}={\omega }_0{\int }_0^{\theta }dt/\dot{\theta }$.

Figure 7: Phases and isochrones for nonlinear oscillators.

A) A limit cycle (bold curve), here for a two-dimensional dynamical system. The limit cycle $\text{Γ}$ is stable as shown by neighboring trajectories attracted to the cycle. B) The phase for a point in the basin of attraction is defined by following its trajectory (red) and determining which trajectory on $\text{Γ}$ (black) it will asymptotically match. C) The contour lines of the phases for the Stuart-Landau Eq. (10), a (rare) case where an explicit (spiral) form for the isochrones is known analytically, see Appendix O.

Phases and Eq. (14), defined so far on $\text{Γ}$ only, can be extended to the entire basin of attraction. For that, one uses that a point in the basin will eventually converge to $\text{Γ}$ and defines its phase as the value $\text{Θ}$ on $\text{Γ}$ that its trajectory will asymptotically match, see Fig. 7B. Surfaces of equal phase are called “isochrones” [164] and were systematically investigated in [57]. Their shape for the Stuart-Landau Eq. (10) is calculated in Appendix O and shown in Fig. 7C. Isochrones have the important property (see Appendix O) that their phases progress at the same rate as on $\text{Γ}$, that is Eq. (14) is generally valid. The equation shows that, contrary to the other $m-1$ degrees of freedom that decay exponentially, a phase perturbation will not relax. If the system is at $\mathit{X}$ on $\text{Γ}$, the phase shift $\delta \text{Θ}$ in response to a small perturbation $\delta \mathit{X}$ is

$$\delta \text{Θ}=\frac{\partial \text{Θ}}{\partial \mathit{X}}\cdot \delta \mathit{X}\equiv \mathit{Z}(\text{Θ})\cdot \mathit{\delta }\mathit{X},$$ (15)

where the vector function $\mathit{Z}(\text{Θ})$ is the linear response or sensitivity function [82]. The direction of $\mathit{Z}$ is normal to the isochrone of $\mathit{X}$ and its length is determined by Eq. (14), which states (by the chain rule) that $\mathit{Z}\cdot \frac{d\mathit{X}}{dt}={\omega }_0$. We refer to Appendix P for more properties of $\mathit{Z}$, and its relation to the phase resetting curve (PRC) popularized in [165].

5.2.1. Phase dynamics

Phases, being a single variable, are more parsimonious than the original $m$ degrees of freedom but do not fully describe the dynamical system. A concise description can still be achieved when limit cycles are perturbed weakly, as we discuss here. The simplest case of a limit cycle perturbed by a periodic forcing is considered in Appendix Q. We consider here the dynamics of $n$ coupled oscillators

$$\frac{d{\mathit{X}}_i}{dt}={\mathit{F}}_i(\mathit{X})+\epsilon \sum _{j=1}^n{\mathit{g}}_{ij}\left({\mathit{X}}_i,{\mathit{X}}_j\right),i=1,\dots ,n,$$ (16)

where each ${\mathit{X}}_i$ is an $m$-dimensional vector. Each one of the uncoupled $(\epsilon =0)$ systems has a limit cycle described by a phase ${\text{Θ}}_i$ satisfying Eq. (14) with angular frequency ${\left({\omega }_0\right)}_i$. Taking the time-derivative of ${\text{Θ}}_i\left({\mathit{X}}_1,\dots ,{\mathit{X}}_n\right)$, we obtain:

$$\frac{d{\text{Θ}}_i}{dt}\simeq {\left({\omega }_0\right)}_i+\epsilon \sum _{j=1}^n{\mathit{Z}}^{(i)}\left({\text{Θ}}_i\right)\cdot {\mathit{g}}_{ij}\left({\mathit{X}}_i\left({\text{Θ}}_i\right),{\mathit{X}}_j\left({\text{Θ}}_j\right)\right)\equiv {\left({\omega }_0\right)}_i+\epsilon \sum _{j=1}^n{Q}_{ij}\left({\text{Θ}}_i,{\text{Θ}}_j\right).$$ (17)

For the first step, we used ${\mathit{Z}}^{(i)}\cdot {\mathit{F}}_i={\left({\omega }_0\right)}_i$ and the key approximation of weak-coupling: since the coupling $\epsilon$ is small, derivatives $\frac{\partial {\text{Θ}}_i}{\partial {\mathit{X}}_j}$ are estimated on the unperturbed limit cycles and therefore depend on the phases only, which allows to close the equations.

As in swings and other resonant phenomena [151], the effect of couplings in Eq. (17) depends on the existence of resonances $k_1{\left({\omega }_0\right)}_1+\dots k_n{\left({\omega }_0\right)}_n\simeq 0$ for some appropriate set of integers $k_1,\dots k_n$. Resonances ensure that perturbations, in spite of their being weak, have a sizeable effect. The simplest instance is when the ${\mathit{F}}_i$’s are identical and frequency differences among the oscillators produced by the self-couplings ${\mathit{g}}_{ii}$ are then of order $\epsilon$. For general resonances, see [65] and Appendix Q. Introducing ${\theta }_i\equiv {\text{Θ}}_i-{\omega }_{0}t$, we obtain $\frac{d{\theta }_i}{dt}=\epsilon \sum _{j=1}^n{Q}_{ij}\left({\theta }_i+{\omega }_{0}t,{\theta }_j+{\omega }_{0}t\right)$, which shows that $\theta$ variables vary slowly, on timescales of the order $O(1/\epsilon )$. It is intuitively clear – and it can be demonstrated systematically [58, 65, 138] – that fast oscillations with the original period $T_0$ do not matter for the long-time behavior and can be averaged out. In other words, one can replace the coupling terms by their averages over $T_0$. We finally conclude that the long-term evolution is governed by

$$\frac{d{\theta }_i}{\epsilon dt}\simeq {\omega }_i+\sum _{j\ne i}{q}_{ij}\left({\theta }_j-{\theta }_i\right).$$ (18)

where $q_{ij}\equiv \frac{1}{T_0}{\int }_0^{T_0}{Q}_{ij}\left({\theta }_i+{\omega }_{0}t,{\theta }_j+{\omega }_{0}t\right)dt$ and the frequency shifts ${\omega }_i\equiv Q_{ii}(0)$.

For two coupled oscillators, Eq. (18) yields for the phase difference $\psi \equiv {\theta }_2-{\theta }_1$:

$$\dot{\psi }=-\text{Δ}\omega +q(\psi ),$$ (19)

where the dot denotes derivative with respect to the slow time $\epsilon t$, the frequency mismatch $\text{Δ}\omega \equiv {\omega }_1-{\omega }_2$ and the coupling $q(\psi )=q_{21}(-\psi )-q_{12}(\psi )$. For two identical oscillators, the coupling $q$ is odd and $\text{Δ}\omega =0$, so that $\psi =0$ is always an equilibrium (possibly unstable). Eq. (19) has the same structure as for the entrainment by a periodic forcing (see Appendix Q). If $\min (q)<|\text{Δ}\omega |<\max (q)$, then Eq. (19) has stationary solutions ${\psi }^{\ast }=q^{-1}(\text{Δ}\omega )$, which are stable or unstable depending on the derivative $q^{\prime }\left({\psi }^{\ast }\right)$ being negative or positive. If a stable solution exists, then the two oscillators vary at the same frequency and keep a fixed phase difference ${\psi }^{\ast }$, which is an instance of the general phenomenon of synchronization [152] that underlies wave propagation discussed next. When the mismatch $|\text{Δ}\omega |$ is too strong, then the oscillators vary at different frequencies and phases drift apart [126].

5.3. Waves in chains of coupled oscillators

We consider a chain of $n$ oscillators with nearest-neighbor couplings. Eq. (18) reads

$$\{\begin{array}{l}{\dot{\theta }}_1={\omega }_1+q^{+}\left({\theta }_2-{\theta }_1\right);{\dot{\theta }}_n={\omega }_n+q^{-}\left({\theta }_{n-1}-{\theta }_n\right);\hfill \\ {\dot{\theta }}_i={\omega }_i+q^{+}\left({\theta }_{i+1}-{\theta }_i\right)+q^{-}\left({\theta }_{i-1}-{\theta }_i\right)\text{for}i=2,\dots n-1.\hfill \end{array}$$ (20)

where $q^{\pm }$ account for the coupling with the nearest oscillator on the right/left.

A traveling wave solution of Eq. (20): ${\theta }_i=\omega t-k{x}_i$, has the oscillators varying at a common frequency $\omega$ and their relative phases ${\varphi }_i={\theta }_i-\omega t$ locked at values that monotonically vary along the chain by a fixed amount $\text{Δ}\varphi \propto -k$. The wavefront will travel with velocity $v\propto \omega /k$. The conditions for the existence of such traveling waves are most conveniently found by subtracting each equation from the second

$${\omega }_2+q^{-}(-\text{Δ}\varphi )={\omega }_1;{\omega }_2={\omega }_i;{\omega }_2+q^{+}(\text{Δ}\varphi )={\omega }_n,$$ (21)

and subtracting the second from the sum of the first and the $n$-th equation: $\omega ={\omega }_1+{\omega }_n-{\omega }_2$. Let us assume that couplings tend to pull neighboring oscillators into phase with one another, i.e., that $q^{\pm }$ are positive/negative for positive/negative arguments. A positive $\text{Δ}\varphi$ will then entail $k$ and $v$ negative, and the frequencies ${\omega }_1<{\omega }_2=\dots ={\omega }_{n-1}<{\omega }_n$, i.e., the wavefront travels from the fastest ${\omega }_n$ to the slowest ${\omega }_1$. The common frequency $\omega$ is intermediate between ${\omega }_1$ and ${\omega }_n$ and equals ${\omega }_2$ if $q^{-}(-\text{Δ}\varphi )+q^{+}(\text{Δ}\varphi )=0$. Eqs. (21) were presented in [70] but the stability of their solutions was not addressed, which we do in Appendix R by solving analytically the corresponding tridiagonal matrix problem.

5.4. Waves and twisted states in rings of coupled oscillators

To illustrate the role of boundary conditions, we now consider waves in a ring of coupled oscillators. Ref. [162] considers the following form of Eq. (18) for the phases $\varphi (x)=\theta (x)-{\omega }_{0}t$ in the frame of reference rotating with the natural frequency ${\omega }_0$ of the oscillators:

$$\dot{\varphi }={\int }_{-\pi }^{+\pi }G(x-y)\sin [\varphi (y,t)-\varphi (x,t)]dy.$$ (22)

The coupling $G(s)$ are non-negative, symmetric about $s=0$ and decrease as $s$ increases up to its maximum value on the ring. It is immediate to check that Eq. (22) is a gradient system with the potential $V=-\frac{1}{2}\iint G(|x-y|)\cos (\varphi (y)-\varphi (x))$, so that the asymptotic behavior cannot feature limit cycles or more complicated behaviors [151]. Waves correspond to fixed points with a constant phase difference $\varphi (x,t)=qx$, where $q$ must be an integer to match periodic boundary conditions on the ring. Those solutions do exist for any $q$, as it follows from $G$ and the sine functions being even and odd, respectively. Wave solutions (in the original $\theta$ variables) are also called $q$-twisted state, as $q$ counts the number of full twists of the phase $\varphi$ around the ring. Nontrivial aspects appear when the stability of the twisted states is considered as a function of the coupling range. The function $G(x)$ is cut to zero beyond a distance $|x|>r\pi$, i.e., each oscillator interacts with fixed strength $1/2\pi r$ with the closest fraction $r$ of the ring and not with the rest. The important result proved in [162] is that the stability of twisted states requires a short range $r$ and reduces as the number of twists increases, viz. the $q$-twisted state is stable if $|q|r<\mu \simeq 0.6626$. For the critical first mode $q=1$, the threshold is $r_c(q=1)\simeq 0.6809$. For $r>r_c$ (1) numerical evidence suggests that the only possible attractor is the fully synchronized state where all phases are locked as in Kuramoto’s fully-coupled case [82]. Breaking the gradient nature of the system can induce more complicated dynamics. Namely, chimera states, a mixture of synchronized and drifting spatial regions, are observed when the coupling is modified into $\sin \left({\theta }_j-{\theta }_i+\alpha \right)$ and oscillators are non-locally coupled [83, 1].

6. Toward bridging experiments and theory

6.1. Mitotic waves

The existence of a bistable switch at the core of mitotic entry [108, 127, 140] suggests that mitotic waves in Fig. 1 might be driven by trigger waves of activity of the cell cycle master regulator, the Cyclin-dependent kinase 1 (Cdk1). This idea was first proposed to explain mitotic waves observed in the slime mold Physarum Polycephalum [119]. Mitotic waves were later observed experimentally using Xenopus extracts enclosed in long tubes. Results were interpreted as trigger waves of Cdk1 activity based on desynchronization observed when the tube was cut in half (see Section 6.2), and on pharmacological perturbations of Cdk1 inhibitors [18]. A limitation of these early experiments was the lack of direct measurements of Cdk1 activity. This limitation was recently overcome with the use of a FRET biosensor [50], which probes the activity of Cdk1 in embryos [26].

Direct observations in Drosophila embryos demonstrated that the spatial propagation of Cdk1 activity lacks the hallmark of trigger waves discussed in Section 3.1, i.e., a traveling wavefront as in Fig. 3D. Instead, spatially smooth profiles of Cdk1 activity formed during early-mid interphase were experimentally seen (Fig. 1 in [160] and Fig. 8) to be swept up over time, much like in Fig. 4B. The resulting wave-like profiles of mitotic entry inspired the discovery of sweep waves discussed in Section 3.2. A series of theoretical predictions was successfully tested in [160]. In particular, the speed of Cdk1 and mitotic waves was measured when the synthesis of cyclins was altered. Cyclins [108, 111], an obligate partner for Cdk1 to be active, accumulate during the cell cycle and drive up Cdk1 activity analogously to the parameter $\beta$ in Section 3.2. While the speed of trigger waves should have a weak dependency on the rate of accumulation of cyclins (see Eq. 50 in Appendix F), sweep waves should significantly depend on $\beta$, as predicted by Eq. (7). Experimental data were found to be consistent with the latter and not the former. Moreover, the hallmark of a phase wave, the inverse dependence of speed on the local gradient (see section 3.2), was directly verified (see Fig. 7 in [160] and Fig. 4E). Gradients of Cdk1 activity similar to those predicted by sweep waves, have been proposed to organize also cortical actomyosin in early starfish embryos [11, 161].

Figure 8: Timed barrier experiments in early Drosophila embryos.

Upper panels: A physical barrier desynchronizes the two halves of the embryo when inserted in early to mid-interphase (left), while insertion in late interphase is unable to block mitotic waves (right). This phenomenology is explained in Section 3.2 and summarized in the lower panels. During phase I, Cdk1 gradients are formed with growing correlation length (the left panel shows the two-point correlation function from experimental data). Introducing a barrier at this stage disrupts gradients’ formation and results in the asynchrony of the upper panel. During the later phase II, Cdk1 profiles are swept up across the embryo (the right panel shows Cdk1 activity experimental data). Since the sweeping is essentially independent of diffusion, no disruption is expected, consistently with the upper panel.

Elucidating the dynamics of Cdk1 activity also allowed to clarify the nature of waves of mitotic exit and division, as shown in Fig. 1. Waves of mitotic exit were observed experimentally to follow waves of Cdk1 activity with a fixed delay [26]. This is theoretically understood as witnessing the time-autonomous and space-uncoupled growth of Cdk1 activity during mitosis, which preserves delays determined by Cdk1 waves (see Appendix F, phase III). The relationship between entry and exit waves was preserved [26] even when embryos were mechanically ligated (see Section 6.2), thus supporting that mitotic exit waves are phase waves that simply follow the temporal delays imposed by Cdk1 sweep waves.

Transiently bistable systems are predicted to feature trigger or sweep waves depending on the speed at which the system is driven (the $\beta$ parameter in Section 3.2). In Drosophila embryos, sweep waves are observed in cycles of the wild type but trigger waves can be induced in the mutant $tw{e}^{3A}wee{1}^{9A}$ [160]. In other systems, namely Xenopus extracts, a transition from sweep to trigger waves might be observed in successive cycles, which is consistent with recent experimental observations [118, 3]. Indeed, the cell cycle duration in Xenopus extracts substantially lengthens over time. Remarkably, mitotic waves are fast in the first rapid cycles, and their speed shows a clear dependency on cell cycle duration. Following these early cycles, the speed of mitotic waves becomes essentially independent of the period of the cell cycle. This observation suggests that the extract might have transitioned from sweep to trigger waves [118], as predicted by the theory in Section 3.2. In the future, the use of biosensors in the extract system will be crucial to test this hypothesis.

6.2. Barrier experiments are not a smoking gun for phase vs. trigger waves

Physical barriers have been proposed as a mechanism to discriminate between phase and trigger waves. As discussed in Section 3.3, inserting a physical barrier is indeed discriminatory but only if properly timed, that is after the establishment of the gradients. While this is simple to do in controlled situations, mechanisms and timings of gradients in natural biological system are often hard to control. Thus, barrier experiments ought to be interpreted carefully and cannot be used blindly as the litmus test for trigger vs. phase waves.

A clear example in case is Drosophila. Embryos are mechanically ligated using razor blades attached to a micromanipulator [137, 32]. If the embryo is ligated naïvely, i.e., without precautions on the timing, the two halves of the embryo eventually desynchronize, suggesting a trigger wave. However, a modified macromanipulator that allows for precisely timed ligations reveals the actual nature of the process [26]. A physical barrier desynchronizes the two halves of the embryo (Fig. 8) when inserted in early to mid-interphase, i.e., when Cdk1 gradients are being formed (phase I in Section 3.2). Conversely, insertion in late interphase (phase II in Section 3.2) is unable to block mitotic waves. These timed experiments show that the barrier blocks the formation of the gradients, which does require physical coupling, and not the Cdk1 waves, which are phase waves. To conclude, barrier experiments are a valuable method to pinpoint physical couplings and discriminate the nature of waves, but identifying the steps actually involved requires well-controlled timing.

6.3. Somitogenesis

Experiments with cells isolated from the PSM tissue showed that they are oscillatory [100]. Oscillations are preserved in isolated tissue pieces, as shown in Fig. 2, which exhibit oscillatory activity with the correct period of oscillations [97, 85]. While isolated cells from the chick PSM likely have less regular oscillations [100], recent data in zebrafish argue that much of the tissue dynamics might be recapitulated by single cells in isolation [134]. Analysis of the oscillations across the PSM shows both frequency and phase gradients [53, 120, 156, 149, 143, 142]. While the mechanisms that establish these gradients remain to be elucidated, it is likely that they are linked to signaling gradients (Fgf, Wnt and Retinoic Acid) that span across the entire tissue along the Anterior-Posterior direction [66].

The collection of the above observations has led to the widespread sense that waves observed in Fig. 2C are related to coupled oscillators dynamics as discussed in Section 5. Since the clock and wavefront model in [21], theoretical ideas have indeed revolved around the rhythmic nature of somitogenesis. Approaches in the literature [116, 71, 90, 96, 144, 113] consider models of individual oscillators coupled by signaling communication between neighboring oscillators. For instance, mutual adjustment of frequencies can result from processes like activation of Notch receptors in a presomitic mesoderm cell by Delta from neighboring cells, which then affects the dynamics of Notch pathway components in the target cell. In particular, references [71, 136] discuss the effects exerted by the type of bifurcation that leads to oscillatory behavior upon features of metazoan segmentation, with a direct and concrete comparison presented for Hopf vs SNIC (saddle node on invariant cycle) [151] bifurcations. Important support to the coupled oscillators paradigm has emerged by investigating the ability of pre-somitic cells to self-organize into structures able to sustain waves [156]. In a remarkable set of experiments, it was shown that cells isolated from the mouse PSM, dissociated and reassociated were able to self-organize into structures whose spatiotemporal signaling dynamics closely resembles that observed in vivo [156]. Mixing cells of different phases and/or periods gave rise again to structures able to generate waves resembling those observed in vitro. Interestingly, the system not only reconstituted the oscillatory pattern but also the Fgf/Wnt signaling gradients. Thus, current evidence is that the PSM is a tissue able to fully self-organize into dynamic entities that can support traveling waves. Precise temporal measurements also revealed that the oscillatory activities of the Notch and Wnt display phase shifts that are key for patterning, as demonstrated by microfluidic entrainment experiments [148].

While cells isolated from the PSM tissue are oscillatory [100], a transition to non-oscillatory dynamics was observed in in vitro experiments altering the property of the substrates on which cells were plated or the mechanotransduction pathway Yap [67]. This suggests that oscillators underlying somitogenesis might be relatively close to a bifurcation qualitatively similar to that in Figs. 5A and C. The actin cytoskeleton and Yap signaling might be two knobs that shift the nullclines and drive a bifurcation from excitable to oscillatory and vice versa. While quantitative aspects and functional implications remain largely open, the ability to induce human embryonic stem cells to differentiate into PSM cells has started to unveil how those processes might be controlled in human embryos [102, 101, 28, 20].

6.4. Erk waves

The Erk signaling pathway sustains traveling waves in multiple contexts. Erk is downstream of the MAPK/Ras signaling pathway and can be activated by multiple growth factor ligands [86, 124]. In wound healing assays, both in epithelial in vitro culture and in the epidermis of living mouse, Erk waves travel in the direction opposite of cell movement, playing a key role in driving collective cell migration [4, 62]. Similar waves controlling cell migration are observed in the development of the mouse cochlear duct and might involve a different ligand family, i.e., Fgf instead of Egf [69]. EGFR-Erk waves have also been shown to control epithelial invagination in Drosophila tracheal placodes [123] and the response of cells to apoptosis [47, 157]. Finally, Erk waves are observed in the regulation of zebrafish scale regeneration, where they control cell and tissue growth [24]. Specifically, repeated waves emerge from a common source and travel across the entire tissue. Current evidence is that those waves are associated to an excitable dynamics of the type discussed in Section 4. In particular, modeling in [24, 59] has the system behave like a FHN model discussed in Section 4.1. The source region is driven by the localized production of ligands in the oscillatory regime of the FHN dynamics (see Fig. 5C). Conversely, the rest of the tissue is in an excitable state (see Fig. 5A). As a consequence, as the source periodically passes the threshold of excitability of the neighboring tissue, a wave is originated that is able to travel across the entire tissue. The function of these waves is to instruct cell growth and likely to favor tissue growth by preventing the accumulation of mechanical stress in the tissue [24]. While the model for Erk waves in scales is purely chemical, mechanical inputs have been implicated in the context of collective cell migration. Erk waves arise then from a mechanochemical coupling, where cell deformation causes activation of Erk via EGFR which feeds back upon cell deformation [4, 61, 13]. A future challenge is to combine quantitative imaging experiments and theory to provide further insight on the mechanisms of Erk waves and the integration of biochemical and mechanical signals in different biological settings.

7. Future perspectives

Open challenges for each one of the developmental examples selected here have been presented in each of the Sections 6. While previous examples stressed the importance of the presence of waves, many developmental instances require to suppress waves to keep signals localized. A clear example is the formation of morphogen gradients which drive cell fate specification in a dose-dependent manner [14, 169]. While simple diffusion and ligand/receptor interactions are in principle sufficient to establish gradients, additional feedback mechanisms are found ubiquitously in signaling pathways [56, 110, 150]. A mechanism that suppresses wave spreading was recently shown in Nodal signaling in zebrafish embryos [93]. Nodal establishes a gradient that can be well-recapitulated by simple diffusion and ligand/receptor interactions. However, removal of a coreceptor caused signaling to spread as a wave rather than remaining localized as a gradient [93]. Thus, in this system a mechanism suppresses wave spreading to help maintaining the signal localized. The early Drosophila embryo provides another example where localized signals and waves coexist. The latter have been discussed in Section 6.1 for blastoderm embryos. Conversely, in the early cycles, when nuclei occupy a small region of the embryo, oscillations of the cell cycle are observed only in the region of cytoplasm surrounding the nuclei [27]. Control by mitotic phosphatases that counteract Cdk1 activity [27, 72, 131, 107, 106, 60, 170] is crucial to keep the activity localized and drive proper cytoplasmic flows that uniformly position nuclei across the embryo [27]. Thus, embryonic systems have evolved mechanisms to both facilitate and tame the spreading of signaling waves. Understanding how systems utilize and switch between these modes of regulation will also reveal new principles of control of embryogenesis.

In conclusion, we described several examples from developmental biology where signaling waves play a major role, and we provided an excerpt of the theory of waves in various settings relevant for development. Our goal is to inspire future research connecting experiments with theory. Specifically, our analysis shows that theoretical arguments allow one to make quantitative predictions on traveling waves, e.g., their speed and the geometry of traveling wavefronts. Developing the experimental tools needed to measure these quantities offers unique opportunities to elucidate the underlying molecular mechanisms. This is exemplified by the sweep waves in the control of mitosis in the early Drosophila embryo [160]. Their recognition could be made because the use of a new biosensor for Cdk1 activity [26] revealed that Cdk1 waves are not characterized by a traveling wavefront but rather by sweeping Cdk1 gradients [160]. We expect that the combination of biosensors to monitor signaling dynamics [132, 54], fluorescence methods to follow gene expression products (mRNA and proteins) [55, 30] and biophysical measurements to probe diffusion [171, 109] and directed motion of molecules [27, 105, 141] will play similar roles and raise novel challenges. The combination of those methods with recent optogenetic techniques to manipulate protein localization and signaling will provide unique opportunities to further strengthen the ongoing emergence of theory in development [36, 81, 133].

A. Linear stability of bistable wavefront profiles

The goal of this Appendix is to demonstrate that monotonic profiles of bistable wavefronts are stable (and non-monotonic ones are unstable). We consider the original equation (1) (in rescaled units to have $D=F_0=1$) and the evolution of perturbations $\eta (\xi ,t)$ to a wavefront $\phi (\xi )$, i.e., $\varphi (x,t)=\phi (\xi )+\eta (\xi ,t)$, where $\xi \equiv x-ct$ and $\phi (\xi )$ solves Eq. (2). The resulting equation for $\eta$ reads:

$$\frac{\partial \eta (\xi ,t)}{\partial t}={\partial }_{\xi }^2\eta +c{\partial }_{\xi }\eta +f^{\prime }(\phi (\xi ))\eta ,$$ (23)

where we have considered $\eta$ small so that $f(\phi +\eta )\simeq f(\phi )+\eta f^{\prime }(\phi )$. The invariance to time translations of the original equation for $\varphi (x,t)$ implies that any solution $\phi (\xi )$ can be translated and will still solve Eq. (2). From the expansion of the translated solution $\phi (\xi +ϵ)\simeq \phi (\xi )+ϵ{\phi }^{\prime }(\xi )$, it follows that $\eta (\xi )={\phi }^{\prime }(\xi )$ is a stationary solution of Eq. (23). This is verified directly noting that the right-hand side of Eq. (23) coincides then with the derivative of Eq. (2), which is solved by $\phi (\xi )$.

The linearity of the equation in $\eta$ allows to decompose the solution as a superposition of eigenmodes of the form $e^{-Et}\chi (\xi )$. Stability amounts then to the energy of eigenmodes, with negative energies $E<0$ corresponding to unstable modes. The issue is best addressed by recasting the equation for $\chi (\xi )$ into a Schrödinger form. To eliminate the first-derivative term, we write $\chi (\xi )=e^{-c\xi /2}\psi (\xi )$ and obtain for $\psi$:

$$E\psi =-\frac{d^2\psi }{d{\xi }^2}+\left[\frac{c^2}{4}-f^{\prime }(\phi (\xi ))\right]\psi .$$ (24)

The original question of stability is thus reduced to the question of whether or not the potential $\frac{c^2}{4}-f^{\prime }(\phi (\xi ))$ admit bound states $(E<0)$. A generic potential not being integrable, the full spectrum is not computable, yet we can still conclude on the existence of bound states by using the translation invariance of the original Eq. (2) that was mentioned above. The fact that $\eta (\xi )={\phi }^{\prime }(\xi )$ is a zero mode, i.e., solves Eq. (24) with $E=0$, is used in combination with the result, well-known from quantum mechanics and Sturm-Liouville theory [84, 22], that ground states have no nodes (zeros) and excited states have an increasing number thereof. It follows that if ${\phi }^{\prime }$ has no zeros, i.e., $\phi$ is monotonic, then ${\phi }^{\prime }$ is the ground state and therefore there is no eigenstate with energy $E<0$. Vice versa, if ${\phi }^{\prime }$ has one or multiple zeros, then it is an excited state. Since $E=0$ is not the lowest energy state, there is a lower ground state (at least) with negative energy, and therefore an unstable mode.

B. Basins of attraction and threshold property in bistable systems

While results in Appendix A show that wavefront solutions exist and are linearly stable, it is also important to assess their global basin of attraction. Results in [41, 39] ensure that broad classes of initial conditions do converge to a wavefront profile that solves Eq. (2). For concreteness, we shall state results for the case where the two stable points are at $\phi =0$ and $\phi =1$. Generalizations are obvious.

A first convergence result states that smooth initial conditions “close” to unity at $-\infty$, “close” to zero at $\infty$ and taking values in (0, 1), will exponentially converge to the above wavefront (with a shift determined by the initial condition). “Close” means that the limits ${\phi }_{\mp }$ at $\mp \infty$ should be such that $f\left({\phi }_{-}\right)>0$ and $f\left({\phi }_{+}\right)<0$, i.e., ${\phi }_{-}>a$ and $\phi +<a$, $a$ being the point where $f$ changes sign (see Fig. 3A). If the initial condition is reversed and tends to ${\phi }_{\mp }$ at $\pm \infty$, then the solution converges to a wavefront traveling from right to left.

An additional convergence result states that, if the initial condition asymptotically vanishes on both sides but contains a “bump” of sufficient height and width, then two diverging wavefronts will ensue, with the profile and the speed determined above. That reflects that the state $\phi (x)=0$ is not globally stable, even with respect to perturbations of bounded support, in spite of its being locally stable, i.e., decaying if the perturbation is weak. The latter property is demonstrated using the maximum principle [6] hereafter.

The maximum principle states [6] that two solutions ${\phi }_1$ and ${\phi }_2$ that are initially reciprocally bounded ${\phi }_1(x,0)\le {\phi }_2(x,0)$ will preserve their order throughout their evolution under Eq. (1). Indeed, the equation for their difference $\delta \phi ={\phi }_2-{\phi }_1$ is

$$\frac{\partial (\delta \phi )}{\partial t}-\frac{{\partial }^2(\delta \phi )}{\partial x^2}=f\left({\phi }_2\right)-f\left({\phi }_1\right)=\delta \phi \times f^{\prime }\left({\phi }_1+\theta (\delta \phi )\right)\ge \delta \phi \times m.$$ (25)

Here, $0<\theta <1$, we have used the theorem of the mean for the second step, and the minimum of the derivative $f^{\prime }(\phi )$ is denoted $m$. The conservation of the order follows then from the maximum principle for linear parabolic inequalities [128]. Its non-rigorous version is that the minimum of $\delta \phi$, which is initially non-negative, cannot become negative because the time-derivative at the minimum is $\ge m\times \delta \phi +\frac{{\partial }^2(\delta \phi )}{\partial x^2}$. Since the first term may be negative but vanishes with $\delta \phi$, and the second term is non-negative because of the minimum condition, the time derivative is non-negative and crossing of the line $\delta \phi =0$ is therefore not allowed.

The result on local stability of the state $\phi \equiv 0$ that we announced above can now be proved by comparing an initial condition ${\phi }_1(x,0)\le \gamma <a$ to the evolution of a uniform initial condition ${\phi }_2=\gamma$. The latter will remain uniform and decay to zero as $\frac{d{\phi }_2}{dt}=f\left({\phi }_2\right)<0$, which implies that ${\phi }_1(x,t)$ will also asymptotically vanish.

Initial conditions that decay to zero are not constrained to stay below $a$. Theorems 3.2 in [6] and [41], respectively, give conditions ensuring the decay or the spreading of waves that will eventually bring the system to the fixed point $\phi =1$. The latter situations explicitly show that the state $\phi \equiv 0$ is not globally stable. The combination of those results and the maximum principle illustrate the threshold property of bistable reaction-diffusion systems: bounded-support perturbations of $\phi =0$ that are strong enough on a sufficiently wide spatial interval grow to one, while all perturbations below a threshold die out.

C. Dynamical-systems arguments for wave propagation in static bistable systems

In alternative to the mechanical analogy discussed in Section 3.1.1, the propagation of waves for a bistable reaction-diffusion system can be demonstrated by dynamical-systems arguments based on heteroclinic orbits [151]. The possibility of spreading a wave corresponds indeed to the existence of an (heteroclinic) orbit connecting the metastable fixed point at $\phi =0$ and the stable fixed point at $\phi =1$, see Fig. 9. The second-order Eq. (2) is reformulated as a first-order system:

$$\frac{d\phi }{d\xi }=w;\frac{dw}{d\xi }=-cw-f(\phi ).$$ (26)

Its local stability analysis [151] shows then that both $\phi =0$ and $\phi =1$ are saddle-points, with one positive and one negative eigenvalue:

$${\lambda }_{\pm }=\frac{-c\pm \sqrt{c^2+4\left|f^{\prime }\right|}}{2},$$ (27)

where we have recast the expression in a form which stresses that the derivative of $f$ at $\phi =0$ and $\phi =1$ is negative. The corresponding eigenvectors have components $\left(e_{\phi },e_w\right)$ with ratio $e_w/e_{\phi }=\lambda$. The heteroclinic orbit corresponding to the wavefront in Fig. 3D in the main text should emerge from $\phi =1$ along its unstable direction $e_w/e_{\phi }={\lambda }_{+}(\phi =1)$, and land at $\phi =0$ along its stable eigenvector $e_w/e_{\phi }={\lambda }_{-}(\phi =0)$. Equivalently, we can look at trajectories flowing backward in “time” from $\phi =0$ to $\phi =1$, as shown in Fig. 9. The existence of a heteroclinic orbit is generally demonstrated by showing that the solution for $c=0$ undershoots, and that solutions for large $c$ overshoot the target point ($\phi =1$, $w=0$). By using the smooth dependence and monotonicity of solutions on $c$, it is then concluded that there is an intermediate value of $c$ that will hit $\phi =1$.

The first statement is a simple consequence of the identity (3) between the velocity of the wave and the potential $V$ defined by the equality $f=-\partial V/\partial \phi$. It follows from (3) that if $V(\phi =0)-V(\phi =1)\ne 0$, then $c$ cannot vanish. Furthermore, it is clear from the second equation in (26) that (going backward in time) $w$ is initially pushed down by the negative part of the force $f$ but then its positive component starts pushing $w$ up. For $V(\phi =0)-V(\phi =1)>0$, the latter is stronger than the former and the trajectory will then cross the $w=0$ axis before reaching the target point $\phi =1$ (see Fig. 9).

The second statement follows by showing that the trajectory emerging (backward in time) from the origin stays below a line $w=-b\phi$ for large enough $c$. The choice of the positive constant $b$ is discussed hereafter. Indeed: (i) the slope at the origin $\left|{\lambda }_{-}\right|>c$, which can be made $>b$ by choosing $c>b$. The trajectory starts then below the line $w=-b\phi$; (ii) the trajectory can be made to remain below the line, because for $w+b\phi =0$:

$$\frac{d(w+b\phi )}{d\xi }=-cw-f+bw\ge \phi \left[bc-b^2-K\right],$$ (28)

where $\max \left(\frac{f(\phi )}{\phi }\right)\le K$ is finite for bounded smooth potentials. The bound is tightest for $b=c/2$, which respects the condition in (i) and yields that the derivative is positive (negative backward in time) for $c>2\sqrt{K}$. It follows that the trajectory (moving backward in time) cannot cross the line $w=-b\phi$ and therefore remains below the target point ($\phi =1$, $w=0$).

Figure 9: Wave speed of bistable trigger waves and heteroclinic orbits.

The curves show typical graphs of solutions to Eqs. (26) flowing backward in “time” from $\phi =0$. The value $c^{\ast }$ indicates the speed of the bistable trigger wave. For $c<c^{\ast }$, solutions “undershoot” and curve back before reaching the target $(\phi =1,w=0)$. At $c=0$, the trajectory describes a homoclinic trajectory that asymptotically goes back to the origin (energy is conserved for $c=0$). Vice versa, for $c>c^{\ast }$, solutions overshoot the target. The value $c^{\ast }$ is the special value for which the solution connects the two stable points $\phi =0$ and $\phi =1$ (heteroclinic orbit). The wavefront profile is obtained from the “time”-course of the heteroclinic orbit.

Finally, monotonicity in $c$ is proved by analyzing the dependence on $c$ for $w(\phi )$. Let us consider the equation for the difference $\delta w(\phi )=w_2-w_1$ of the functions $w_1$ and $w_2$ for two velocities $c_1$ and $c_2$:

$$\frac{d(\delta w)}{d\phi }-\frac{f(\phi )}{w_1{w}_2}(\delta w)=-\left(c_2-c_1\right),$$ (29)

which is reduced to

$$\frac{d\chi (\phi )}{d\phi }=-\left(c_2-c_1\right)e^{-{\int }_a^{\phi }\frac{f(u)}{w_1{w}_2}du};\chi \equiv \delta w{e}^{-{\int }_a^{\phi }\frac{f(u)}{w_1{w}_2}du},$$ (30)

by introducing the proper integrating factor. Here, $a$ is the position of the (unstable) middle fixed point, so that $f\le 0$ for $0\le \phi \le a$. It follows from Eq. (30) that its right-hand side is negative for $c_2>c_1$, that is $\chi$ is monotonically decreasing in $\phi$. Furthermore, $\chi$ vanishes at the origin, as verified noting that: (i) the argument ${\int }_{\phi }^a\frac{f(u)}{w_1(u)w_2(u)}du$ of the exponential is negative; (ii) as $\phi \to 0$, the argument of the exponential diverges ($f$ vanishes linearly but both $w_1$ and $w_2$ vanish linearly as well). We conclude that $\chi (\phi )\le 0$ and therefore $w_2\le w_1$.

D. Two solvable cases of bistable trigger waves

We consider Eq. (2)

$$\frac{d^2\phi }{d{\xi }^2}=-c\frac{d\phi }{d\xi }-f(\phi ),$$ (31)

for piecewise linear and cubic forces:

$$f(\phi )=\left({\phi }_0-\phi \right)+\left({\phi }_1-{\phi }_0\right)H(\phi -a);f(\phi )=-\left(\phi -{\phi }_0\right)(\phi -a)\left(\phi -{\phi }_1\right),$$ (32)

with ${\phi }_0<a<{\phi }_1$. Here, $H$ denotes the Heaviside step function.

D.1. Piecewise linear

Equation (31)

$${\phi }^{″}+c{\phi }^{\prime }+{\phi }_0-\phi =0\text{for}\phi <a;{\phi }^{″}+c{\phi }^{\prime }+{\phi }_1-\phi =0\text{for}\phi >a,$$ (33)

has solutions

$$\phi ={\phi }_0+A{e}^{{\lambda }_{+}\xi }\text{for}\xi <{\xi }^{\ast };\phi ={\phi }_1+B{e}^{{\lambda }_{-}\xi }\text{for}\xi >{\xi }^{\ast };{\lambda }_{\pm }=\frac{-c\pm \sqrt{c^2+4}}{2},$$ (34)

where ${\xi }^{\ast }$ is the (yet unknown) point where the two branches reach the common discontinuity level $a$. By imposing this condition, as well as continuity of first derivatives, we have

$${\phi }_0+A{e}^{{\lambda }_{+}{\xi }^{\ast }}=a;{\phi }_1+B{e}^{{\lambda }_{-}{\xi }^{\ast }}=a;{\lambda }_{+}\left(a-{\phi }_0\right)={\lambda }_{-}\left(a-{\phi }_1\right).$$ (35)

Elementary algebra on the last equation yields the final result

$$c=\frac{{\phi }_1+{\phi }_0-2a}{\sqrt{a\left({\phi }_0+{\phi }_1\right)-{\phi }_0{\phi }_1-a^2}}.$$ (36)

D.2. Cubic force

Equation (31) for the cubic force in (32) admits the solution

$$\phi (\xi )=\frac{1}{2}\left[{\phi }_1+{\phi }_0-\left({\phi }_1-{\phi }_0\right)\tanh \left(\frac{\xi }{\ell }\right)\right],$$ (37)

where $\ell$ controls the width of the transition region between the asymptotic values ${\phi }_1$ at $\xi \to -\infty$ and ${\phi }_0$ at $\xi \to \infty$. Indeed, when (37) is inserted into (31), the special cubic structure makes that the nonlinear force generates terms that have the same exact structure as the linear ones. Eq. (31) reduces then to:

$$\frac{\sinh \left(\frac{\xi }{\ell }\right)}{{\cosh }^3\left(\frac{\xi }{\ell }\right)}\left[-\frac{1}{{\ell }^2}+\frac{{\left({\phi }_1-{\phi }_0\right)}^2}{8}\right]+\frac{1}{{\cosh }^2\left(\frac{\xi }{\ell }\right)}\left[\frac{c}{2\ell }-\frac{\left({\phi }_1-{\phi }_0\right)\left({\phi }_1+{\phi }_0-2a\right)}{8}\right]=0.$$ (38)

It follows that

$$\ell =\frac{2\sqrt{2}}{{\phi }_1-{\phi }_0};c=\frac{{\phi }_1+{\phi }_0-2a}{\sqrt{2}}.$$ (39)

E. Effects of noise on the velocity of bistable trigger waves

The aim of this Appendix is to give a short adaptation to the case of bistable fronts of the arguments developed in [15, 16] for the (more difficult) case of the Fisher-Kolmogorov equation, where a stable state invades an unstable one [112]. The intuitive idea put forward in [15, 16] is that noise will be mostly important in the region where the field $\varphi$ is small, and one can grasp its effects by cutting off the reaction term $f(\varphi )$ when the field $\varphi$ reaches small values $\simeq ϵ$. The presence of a cutoff physically accounts for discretization effects due to few individuals left in the population for the Fisher-Kolmogorov case or due to few reacting molecules in chemical reactions. In both cases, noise results, which induces stochastic effects, like for instance genetic drift, that can be substantial [78, 52]. The simple physical picture of a cutoff on $f$ allows to draw important conclusions on the effects of noise, as shown hereafter.

The dynamical-systems analysis of Appendix C shows that the asymptotic behavior at infinity of the front $\phi$ (in the absence of cut-off) is

$$\phi (\xi )\simeq A{e}^{{\lambda }_{-}\xi }+0\times e^{{\lambda }_{+}\xi },$$ (40)

where the positive eigenvector must vanish in the absence of a cutoff because it would grow at infinity, $A>0$ and it is understood that Eq. (27) for ${\lambda }_{\pm }$ is calculated at the point $\phi =0$. The corresponding velocity is denoted $c_0$. The presence of a cutoff will slightly modify the velocity into $c_n$ and allow for the coefficient of the growing exponential not to vanish as the solution is cut off at finite distances. The resulting behavior will then be

$${\phi }_n(\xi )\simeq A{e}^{{\lambda }_{-}\xi }+B\left(c_n-c_0\right)e^{{\lambda }_{+}\xi },$$ (41)

where the perturbative nature of the second term is brought by the small factor $\left(c_0-c_n\right)$. By imposing that both terms are of the order of the threshold $ϵ$ at the cutoff distance ${\xi }_c$:

$$A{e}^{{\lambda }_{-}{\xi }_c}\simeq B\left(c_n-c_0\right)e^{{\lambda }_{+}{\xi }_c}\simeq ϵ\text{,}$$ (42)

we conclude that ${\xi }_c\simeq -\log (ϵ/A)/\left|{\lambda }_{-}\right|$ and the correction to the velocity

$$c_n\sim c_0+\frac{{ϵ}^{1+\frac{{\lambda }_{+}}{\left|{\lambda }_{-}\right|}}}{B{A}^{\frac{{\lambda }_{+}}{\left|{\lambda }_{-}\right|}}}.$$ (43)

The important aspect to notice is that the amplitude of the correction features a power of $ϵ$ larger than unity. That implies that corrections will be relatively small as compared to the substantial ones $\propto 1/{\log }^2(ϵ)$ of the Fisher-Kolmogorov case [15, 16]. Similar arguments can be developed to investigate the diffusion of the traveling front’s position [15, 16].

F. Time-dependent bistable systems

The goal of this Appendix is to provide more information on the dynamics of transiently bistable systems as in Fig. 4, and the associated sweep waves. For full details, we refer to Ref. [160]. We consider Eq. (4):

$$\frac{\partial \varphi (\mathit{x},t)}{\partial t}=D\text{Δ}\varphi (\mathit{x},t)+f(\varphi ,t)+\sqrt{2\nu }\eta (x,t).$$ (44)

Here, $\nu$ controls the amplitude of the noise and $\eta$ is $\delta$-correlated in space and time $\langle \eta (x,t)\eta \left(x^{\prime },t^{\prime }\right)\rangle =\delta \left(x-x^{\prime }\right)\delta \left(t-t^{\prime }\right)$. The reaction term $f$ depends on time as sketched in Fig. 4A, i.e., it is transiently bistable. For the sake of concreteness, we consider the specific case

$$f(\varphi ,t)=-F_0\varphi \left(\varphi -\frac{1}{2}\right)(\varphi -1)+\beta t\equiv -F_0\left(\varphi -{\varphi }_0(t)\right)(\varphi -a(t))\left(\varphi -{\varphi }_1(t)\right),$$ (45)

with ${\varphi }_0(t)\le a(t)<{\varphi }_1(t)$, as shown in Fig. 4. The advantage of this form is that its static version $\beta =0$ has an analytical solution (see Appendix D) and the $\beta t$ has a direct connection to the growth of cyclins during the cell cycle in Drosophila mitotic waves, as explained in the main text. Initially, the unstable point $a(0)=1/2$ so that the potential defined by $-\partial V/\partial \varphi =f$ has the same depth at the two stable zeros ${\varphi }_0(0)=0$ and ${\varphi }_1(0)=1$. As time progresses, the time-dependent constant $\beta t$ progressively raises the force field, i.e., tilts the potential by a term $-\beta t\varphi$, which shifts the zeros of $f$ and favors the stability of ${\varphi }_1(t)$ vs. ${\varphi }_0(t)$. Bistability is eventually lost for $\beta t^{\ast }=F^{\ast }=F_0\sqrt{3}/36$ when ${\varphi }_0\left(t^{\ast }\right)$ and $a\left(t^{\ast }\right)$ coincide at the value ${\varphi }^{\ast }=0.5-\sqrt{3}/6$ where the cubic in $f$ has its minimum, and then they turn complex conjugate by a saddle-node bifurcation. The derivative of $f$ at ${\varphi }_0(t)$ reads $-f^{\prime }\left({\varphi }_0(t)\right)\equiv \frac{1}{\tau }=F_0\left(a-{\varphi }_0\right)\left({\varphi }_1-{\varphi }_0\right)$. Close to the saddle-node bifurcation, $f$ is well approximated by its quadratic expansion around its minimum, which yields

$$\left(a(t)-{\varphi }_0(t)\right)\propto \sqrt{\frac{F^{\ast }-\beta t}{F_0}};\tau \simeq {\left[F_0\left(F^{\ast }-\beta t\right)\right]}^{-1/2}.$$ (46)

It is convenient to distinguish three dynamic phases that we will discuss sequentially hereafter: the early adiabatic phase I, the middle phase II close to the critical bifurcation, and the late phase III when the system is monostable (see Fig. 4 in the main text).

Phase I: quasi-adiabatic dynamics and trigger waves at slow drives.

We consider an initial condition starting at low values of $\varphi$ and its dynamics at early times, smaller than the saddle-node bifurcation time $t^{\ast }$. The force $f$ crosses the axis at ${\varphi }_0(t)$ with a slope $-1/\tau$. As long as $\tau \ll \frac{{\varphi }_0(t)}{d{\varphi }_0/dt}$, i.e., relaxation is rapid as compared to the typical time of variation of ${\varphi }_0(t)$, the system will evolve quasi-adiabatically and follow the evolution of ${\varphi }_0(t)$. Specifically, at each time $t$ its state will approximately correspond to the stationary state of the linearized equation

$$\frac{\partial \varphi (\mathit{x},t)}{\partial t}=D\text{Δ}\varphi (\mathit{x},t)-\frac{\varphi -{\varphi }_0(t)}{\tau }+\sqrt{2\nu }\eta (x,t).$$ (47)

Gaussianity of the noise and linearity of Eq. (47) imply that $\varphi$ is Gaussian, i.e., its single-time statistics is fully characterized by its average, which is ${\varphi }_0(t)$, and its covariance $C_t\left(x,x^{\prime }\right)=\langle \left(\varphi (x,t)-{\varphi }_0(t)\right)\left(\varphi \left(x^{\prime },t\right)-{\varphi }_0(t)\right)$, which is (see SI in [160] for details):

$$C_t\left(x,x^{\prime }\right)=C(0)e^{-\frac{\left|x-x^{\prime }\right|}{\lambda }};C(0)=\frac{\nu }{2}\sqrt{\frac{\tau }{D}};\lambda =\sqrt{D\tau }.$$ (48)

Note that both the amplitude $C(0)$ and the correlation length $\lambda$ depend on time via $\tau (t)$. The expression of $\lambda$ differs from the diffusive length $\sqrt{Dt}$ and illustrates the combined role of diffusion and reactions. It follows from Eq. (48) that at any given time, $\varphi (x,t)$ is a Uhlenbeck-Ornstein process in space, with an exponential decay of correlations. The estimate of the typical amplitude of the gradients

$$g\sim \frac{\sqrt{C(0)}}{\lambda }\sim \frac{{\nu }^{1/2}}{D^{3/4}}{\tau }^{-1/4},$$ (49)

is the typical amplitude of the fluctuations divided by their characteristic length scale.

Let us first consider the regime of slow drives, i.e., small $\beta$. The height of the metastable barrier reduces as the distance $\left(a(t)-{\varphi }_0(t)\right)$ shrinks with time (see Eq. (46)). Conversely, the amplitude of fluctuations, $\sqrt{C(0)}$ increases as time progresses (see Eq. 48). Eventually, these trends will lead to a jump above the metastable barrier and the nucleation of a seed that will spread as a trigger wave, as discussed in Section 3.1. Since $f$ changes with time, the typical speed $U_{trigger}$ of the trigger waves will change accordingly. Its dependence on $D$ and $F_0$ is the usual square-root (see Section 3.1.1) for trigger waves. Its dependence on $\beta$ is determined as follows.

Jumps occur at a typical time such that the rate of transition across the metastable barrier multiplied by the time spent quasi-adiabatically in that state is of order unity. The latter is clearly $\propto 1/\beta$. As for the former, a jump requires that the maximum of the field $\varphi (x,t)$ passes the threshold imposed by the metastable barrier. The calculation of the statistics of strong excursions for the Uhlenbeck–Ornstein process in Eq. (48) is detailed in [160]. The upshot is that the exponentially dominant term (apart from dimensional prefactors) for the rate of transition above the metastable barrier is $\sim \exp \left[-\frac{{\left(a-{\varphi }_0\right)}^2}{2C(0)}\right]$. We can then use $C(0)$ in Eq. (48) and Eq. (46) to conclude that the factor at the exponential $\propto {\left(F^{\ast }-\beta t\right)}^{5/4}$ and therefore $F^{\ast }-\beta t\sim {(-\log \beta )}^{4/5}$. The speed of a trigger wave close to the bifurcation point is $U^{\ast }-U_{trig}\propto a(t)-{\varphi }_0(t)\propto \sqrt{F^{\ast }-\beta t}$, where $U^{\ast }$ is the maximal speed that is attained at the bifurcation itself (see, for instance, the analytical formula Eq. (39)). We conclude that

$$U^{\ast }-U_{trigger}\propto {(-\log \beta )}^{2/5},$$ (50)

which was confirmed by numerical simulations in [160].

Phase II: critical dynamics and sweeep phase waves at fast drives.

For fast drives, the adiabatic condition for the validity of phase I is violated before a wave is triggered and a different regime sets in. It is intuitive that as ${\varphi }_0(t)$ moves at speeds comparable to the relaxation time $\tau$, typical values of $\varphi$ will lag and the difference $\langle \varphi (x,t)\rangle -{\varphi }_0(t)$ will be negative (see [160] for an explicit expression). The actual time $t_{min}$ to reach the level ${\varphi }^{\ast }$ where $f$ has its minimum will then be longer than $t^{\ast }=F^{\ast }/\beta$. Close to its minimum ${\varphi }^{\ast }$, the force in Eq. 45 is well approximated by its quadratic expansion $\beta t-F^{\ast }+F_0\gamma {\left(\varphi -{\varphi }_{\ast }\right)}^2$, where $\gamma =\sqrt{3}/2$. Neglecting diffusion, the growth of $\text{Φ}\equiv \varphi -{\varphi }^{\ast }$ is then given by

$$\beta \frac{d\text{Φ}}{dz}=F_0\gamma {\text{Φ}}^2+z+\delta ,$$ (51)

where we have defined $z\equiv \beta \left(t-t_{min}\right)$ and $\delta$ is the delay $\beta \left(t_{min}-t^{\ast }\right)$ due to non-adiabatic effects. It is checked that the equation is scale invariant if ${\text{Φ}}^2$, $z$ and $\delta$ are all scaled by ${\beta }^{2/3}$. More precisely, since $\beta$ has dimensions ${\mathit{time}}^{-2}$ and $F_0$ has dimensions ${\mathit{time}}^{-2}$, the scalings are ${\left(\beta /F_0^2\right)}^{2/3}$ for ${\text{Φ}}^2$ and $F_0{\left(\beta /F_0^2\right)}^{2/3}$ for $z$ and $\delta$. For those times and amplitudes, all terms in Eq. (51) are balanced and comparable. For smaller values of $\text{Φ}$, quadratic terms are negligible, which leads to the behavior $\beta \text{Φ}\sim z^2/2+z\delta$. As noted in the main text, during this phase the profiles are swept up without any distortion, i.e., spatial gradients are preserved, which leads to a phase wave with speed

$$U_{sweep}=\frac{d\text{Φ}/dt}{g}.$$ (52)

The expression involves the factor $1/g$ typical of phase waves [79, 168] and the numerator is the rate at which the field is swept up.

Eq. (7) for the speed in the main text is obtained as follows. The numerator is estimated at the upper limit of phase II as $d\text{Φ}/dt=z+\delta \sim F_0{\left(\beta /F_0^2\right)}^{2/3}$. The denominator is estimated at the lower limit of phase II, when phase I is transitioning to phase II. Then, the gradients have been formed and are getting frozen. The expressions (49) and (46), together with the scalings of $z$ and $\delta$, yield $\tau \sim {\left(\beta F_0\right)}^{-1/3}$ and therefore $g\sim {\nu }^{1/2}{D}^{-3/4}{\left(\beta F_0\right)}^{1/12}$. By combining numerator and denominator, we finally obtain Eq. (7):

$$U_{sweep}\propto \frac{{\beta }^{7/12}{D}^{3/4}}{{\nu }^{1/2}{F}_0^{5/12}}.$$ (53)

We refer to the original Ref. [160] for experimental and numerical tests.

Phase III: conservation of temporal delays.

Phase III, corresponds to the late period when the system is monostable and typical values of the field $\varphi (x,t)$ are well above zero but have not reached yet the unique fixed point left. The time-independent component of the force (cubic in Eq. (45)) is then strong and dominates over $\beta t$. Diffusion was already neglected in phase II, and will then be even more negligible as compared to the stronger forcing of phase III. It follows that spatial regions of the field $\varphi$ grow by and large independently of each other, and their rate of growth is roughly time-independent (autonomous growth).

The major consequence of autonomous growth taking place in phase III is that delays among different spatial points are conserved. Indeed, let us consider the autonomous equation $d\varphi /dt=f(\varphi )$, where $f$ is the force profile at a fixed typical time during phase III, and integrate it as $\int \frac{d\varphi }{f(\varphi )}=\int dt$ between two levels: ${\varphi }_1$ and a higher level ${\varphi }_2$. We see then that the time needed for that growth is fixed, i.e., does not depend on the time at which ${\varphi }_1$ was reached. In the presence of noise, the above argument remains valid on average. We conclude that the delays set during phase II among the spatial points of the field $\varphi$ are conserved on average during phase III, and they do not depend on the threshold.

In sum, the passages of a threshold level by different spatial points are temporally ordered during phase III as at the end of phase II (when sweep waves set the delays). The connection with mitotic waves in Drosophila development is that phase II corresponds to the middle/end of the S phase, and phase III spans the various phases of mitosis. The conservation of delays during phase III rationalizes the experimental observation that the waves at the entry into (and exit out of) mitosis are strongly correlated with the speed of the chemical Cdk1 wave generated during the S phase of the cell cycle [26, 160].

G. FHN stability analysis

The Jacobian stability matrix for the FHN model (see Eq. 8 in 4.1 with $D=0$) is proportional to:

$$J=\left(\begin{array}{cc}{f}_v/r& f_w/r\\ g_v& g_w\end{array}\right),$$ (54)

where all the partial derivatives are evaluated at the fixed point and $r={\tau }_v/{\tau }_w$ is the ratio of the timescales defined in Section 4.1. Most terms in the trace and the determinant

$${\text{Tr}}_J\propto f_v+r{g}_w;{\text{Δ}}_J\propto f_v{g}_w-f_w{g}_v$$ (55)

have a fixed sign by the definition of the FHN model (see Section 4.1): $g_w<0$, $f_w<0$ and $g_v>0$. Conversely, the sign of $f_v$ depends on the location of the fixed point (see Fig. 5): (I) if the fixed point is on the recovery or the excitatory branch, then $f_v<0$; (II) if the fixed point is on the middle, unstable branch, then $f_v<0$. In case (I), it follows then that $T{r}_J<0$ and ${\text{Δ}}_J>0$, which implies that the fixed point is stable (see Fig. 5.2.8 in [151]). For case (II), the signs of both trace and determinant can change. However, for $r$ small, it will generally happen that the first to change sign will be the trace while ${\text{Δ}}_J$ is still positive. This is the condition for the two complex eigenvalues to cross the imaginary axis, that is a Hopf bifurcation [151]. That leads to loss of stability of the fixed point and flow of the orbits towards a limit cycle.

H. Wave trains in excitable systems

The framework that we have used to investigate the propagation of a single pulse in excitable systems can also be used to understand how periodic wave trains are supported and how their dispersion relation is shaped in excitable systems. Let us consider again a pulse as in Section 4.3, traveling with velocity $c\left(w_s\right)$. After a time $T$, we deliver a second stimulation at the origin, which we repeat periodically, by giving a strong kick to the excitatory variable $v$ and keeping $w$ fixed. Pulses following the first one are triggered before the system has fully recovered and the level of their controller variable $w$ will then be greater than $w_s$. That leads to a (generally slower) velocity, which will itself affect the controller level in the back of the up-front as we have described in Section 4.3. Over time, the controller levels at the front and the back of individual pulses will stabilize to constant levels, denoted by $w_f$ and $w_b$, respectively. Their values are determined by imposing the two conditions that the various pulses travel at the same speed and that the time to complete the cycle is the stimulation time $T$:

$$c\left(w_f\right)=\left|c\left(w_b\right)\right|;T=T_e+T_r\simeq {\int }_{w_f}^{w_b}\frac{du}{G_e(u)}+{\int }_{w_b}^{w_f}\frac{du}{G_r(u)},$$ (56)

where $G_{r/e}(w)\equiv g\left(V_{r/e}(w),w\right)$ and we neglected the short duration of the phases of crossing between the excitatory and recovery branches because $r\ll 1$. The dispersion relation $c(T)$ resulting from Eqs. (56) typically features a minimal period and multiple branches with different stability properties. For more information, we refer to the original publications [29, 95].

I. Fisher-Kolmogorov waves for a quadratically unstable potential

As in Appendix C, we consider the system of equations (26) but, contrary to the metastable case considered there, the function $f$ at the origin is not locally stable. The standard Fisher-Kolmogorov case has $f^{\prime }(0)>0$ [112], while here we need to consider the case where $f(\phi )\sim {\phi }^2$ near the origin.

This problem is motivated by the case of excitable waves when the speed of the upfront, say $c\left(w_s\right)$ for a front at the controller level $w_s$ of the fixed point, exceeds the maximal speed of the downfront $\left|c_{min}\right|$. As discussed in the main text, the knee of the $f$ nullcline is reached and it is unclear how up- and downfronts can match. We want to show that, as for the standard Fisher-Kolmogorov case, there is a continuum of possible speeds, starting from $\left|c_{min}\right|$ and going up to arbitrarily fast ones. Solutions are normally selected by the spatial decay of the initial condition [158]: rapidly decaying ones propagate with the minimum velocity (which corresponds to the fastest decay), and higher and higher speeds are selected as initial conditions decay more and more slowly. In the case of excitable waves, the “initial condition” for the down-front is determined by the back of the up-front, which progressively selects the mode that moves with speed $c\left(w_s\right)$.

For concreteness, we consider the case of a front that converges to 0 and 1 as $\xi \to \pm \infty$, respectively. As shown in Appendix C, the point $\phi =1$ is a saddle point, eigenvalues are given by Eq. (27) and the slope along the unstable direction is $e_w/e_{\phi }={\lambda }_{+}$, which is a decreasing function of $c$. This result, together with the fact that $\frac{dw}{d\xi }$ increases with $c$ (see Eq. (26) and we remind that $w<0$), show that the trajectory ${\phi }_1$ for $c_1>c_2$ is above ${\phi }_2$. The difference with the metastable case is that $f$ is positive in $(0,1)$, which implies that the trajectory cannot cross the axis $w=0$ (see the Eq. (26) for $dw/d\xi$: on the axis $w=0$, the derivative $dw/d\xi =-f\le 0$). We conclude that, if there is a heteroclinic trajectory for $\overline{c}$, then all $c>\overline{c}$ will have a heteroclinic trajectory (because they are trapped between the axis $w=0$ and the trajectory ${\varphi }_{\overline{c}}$).

It remains to prove that there is indeed a heteroclinic trajectory for a proper choice $c=\overline{c}$. This is shown exactly as in Appendix C. The trajectory at ($\phi =1$, $w=0$) is indeed above the line $w+b\phi =0$ and Eq. (28) shows that for $c\ge 2\sqrt{K}$ the trajectory cannot cross the line. Since the trajectory cannot cross the axis $w=0$ either (because $f\ge 0$), it follows that the trajectory is trapped in a triangle and, since $d\phi /d\xi =w<0$, it must asymptotically land at $(0,0)$.

Finally, we remark that the condition $c\ge 2\sqrt{K}$ is sufficient but not necessary, as shown by the explicit example of the force $f={\phi }^2(1-\phi )$, which can be solved analytically. Indeed, taking the limit $a\to {\phi }_0=0$ and ${\phi }_1=1$ in the general solution (39), we obtain a minimum speed $c=1/\sqrt{2}$, which is below the bound $2\sqrt{K}=2\sqrt{\max \left(\frac{f(\phi )}{\phi }\right)}$.

J. Curvature effects in multi-dimensional fronts

Effects of curvature were first discussed by Zykov [173, 174], later re-derived in [76, 74] and experimentally tested in [44]. Here, we shall give a brief introduction to those effects and then present the methodology in [76, 74], which builds on the eikonal-type equations that were also exploited for flame fronts [45, 46].

The intuition is conveyed visually by Figure 6 in the main text and confirmed by the following formula. Given the general Eq. (1), the expression for the speed $U_{\kappa }$ of a curved front reads (see below for a derivation):

$$U_{\kappa }=c\sqrt{D{F}_0}-D(\mathbf{\nabla }\cdot \widehat{\mathit{n}}),$$ (57)

where $c$ is the speed of a planar front in non-dimensional units (which may for instance be obtained by solving Eq. (2) as discussed previously). The factor $-(\mathbf{\nabla }\cdot \widehat{\mathit{n}})$ involves the divergence of the normal to the front in the sense of its progression. That is shown (see below) to be the mean curvature of the wavefront in two dimensions, and twice the mean curvature in three dimensions. Its sign is positive if the front curves “toward” the normal and negative in the opposite case (see Fig. 6 in the main text).

Two remarks are in order. First, the expression (57) illustrates the physical need of a sufficiently large excited area for a wavefront to propagate away from a center. Indeed, the wavefront will fail to spread outward $\left(U_{\kappa }\le 0\right)$ if the initial radius $R\lesssim \sqrt{D/F_0}$. Second, the net effect of the correction term is to stabilize planar fronts: a protruding bulge on a planar front will indeed slow down and be caught up by the rest of the front, whilst an intruding cavity is sped up and will catch up with the rest of the front. These effects of course do not prevent the formation and propagation of curved fronts in the presence of spatial non-homogeneities and/or proper stimulation. That is the case of spiral waves in two dimensions, which are relevant for the aggregation of Dictyostelium discoideum colonies [89, 77], and scroll waves in three dimensions, which are relevant for excitable cardiac tissues [23, 19, 73, 115]. A detailed discussion of scroll and spiral waves is beyond the scope of our review, and we refer to Winfree’s pioneering publications [167, 166], the review [104] and references therein.

J.1. Eikonal-type equations

We introduce coordinates $\mathit{\xi }$ attached to the front, with the original coordinate $\mathit{x}=\mathit{X}(\mathit{\xi },\tau )$ and $\tau =t$ introduced just to keep notation clear. It follows that ${\partial }_{{\xi }_i}=\frac{\partial x_j}{\partial {\xi }_i}{\partial }_{x_j}$ and ${\partial }_{\tau }={\partial }_t+\frac{\partial x_j}{\partial \tau }{\partial }_{x_j}$ and therefore

$$\frac{\partial }{\partial x_i}=T_{ij}\frac{\partial }{\partial {\xi }_j};\frac{\partial }{\partial t}=\frac{\partial }{\partial \tau }-\frac{\partial x_i}{\partial \tau }{T}_{ij}\frac{\partial }{\partial {\xi }_j},$$ (58)

where the matrix $T$ is the inverse of the matrix $\frac{\partial x_j}{\partial {\xi }_i}$. Using (58), we transform the original reaction-diffusion equation (1) into

$$\frac{\partial \varphi }{\partial \tau }-T_{ij}\frac{\partial x_i}{\partial \tau }\frac{\partial \varphi }{\partial {\xi }_j}=D{T}_{ij}{T}_{ik}\frac{{\partial }^2\varphi }{\partial {\xi }_j\partial {\xi }_k}+D\frac{\partial T_{ij}}{\partial x_i}\frac{\partial \varphi }{\partial {\xi }_j}+F_{0}f(\varphi ).$$ (59)

As in geometric optics, the eikonal equation aims at describing the phase fronts of waves. It is assumed that the field $\varphi$ changes most rapidly along one direction (the normal to the front), which we identify as the ${\xi }_1$ coordinate. The other coordinates (one in 2D and two in 3D) are transverse to the front, i.e., change along it. Derivatives of $\varphi$ with respect to transverse coordinates are negligible, as well as variations in time in the frame attached to the front. It follows that (59) reduces to

$$D|\mathit{s}{|}^2{\varphi }^{″}+{\varphi }^{\prime }\left[D(\mathbf{\nabla }\cdot \mathit{s})+\mathit{s}\cdot \frac{\partial \mathit{X}}{\partial \tau }\right]+F_{0}f(\varphi )=0,$$ (60)

with the components of the vector $\mathit{s}$ defined as $s_i\equiv T_{i1}$, ${\nabla }_j\equiv {\partial }_{x_j}$ and primes indicate derivates with respect to ${\xi }_1$.

Eq. (60) is recognized to be of the form (2) in Section 3.1.1, provided

$$D|\mathit{s}{|}^2=F_0;D(\mathbf{\nabla }\cdot \mathit{s})+\mathit{s}\cdot \frac{\partial \mathit{X}}{\partial \tau }=c{F}_0.$$ (61)

We will show momentarily that $\mathit{s}$ is along the normal ${\widehat{\mathit{n}}}_1$ to the front in its direction of propagation. Furthermore, the first equation shows that $|\mathit{s}|=\sqrt{F_0/D}$. From the second equation, we conclude then that the velocity of the front $U_{\kappa }$ is

$$U_{\kappa }={\widehat{\mathit{n}}}_1\cdot \frac{\partial \mathit{X}}{\partial \tau }=c\sqrt{F_{0}D}-D\left(\mathbf{\nabla }\cdot {\widehat{\mathit{n}}}_1\right),$$ (62)

which is the formula (57) announced above.

The fact that the factor $-\left(\mathbf{\nabla }\cdot {\widehat{\mathit{n}}}_1\right)$ is indeed proportional to the mean curvature in 2D or twice it in 3D can either be read in books on differential geometry (see, e.g., [17]) or verified directly. The local structure of the contour levels for a 3D situation will indeed be $\varphi =x+a{y}^2+2byz+c{z}^2=\text{const.}$, where $x$ is the coordinate normal to the front and the two other coordinates are transverse. It follows that the normal

$${\widehat{\mathit{n}}}_1=\frac{(1,2(ay+bz),2(by+cz))}{\sqrt{1+4{(ay+bz)}^2+4{(by+cz)}^2}}.$$ (63)

Taking the divergence of the vector at the origin yields $-\left(\mathbf{\nabla }\cdot {\widehat{\mathit{n}}}_1\right)=-2(a+c)$, which is indeed twice the mean curvature. In 2D, there is no $z$ coordinate and the expression reduces indeed to the second derivative $-2a$, which gives the curvature. Finally, the sign is positive/negative for the two situations sketched in Figure 6.

It remains to show that $\mathit{s}\parallel {\widehat{\mathit{n}}}_1$, where $s_i\equiv T_{i1}$. The starting point is $T_{ij}^{-1}=\frac{\partial x_j}{\partial {\xi }_i}$, which stems from Eq. (58). We define the $i$-th tangent vector ${\mathit{t}}_i=\frac{\partial \mathit{x}}{\partial {\xi }_i}$; its $j$-th component is the matrix element $T_{ij}^{-1}$. For the inversion of the matrix, it is convenient to introduce normal vectors. In 2D, we introduce ${\mathit{n}}_1={\mathit{t}}_2\times \widehat{z}$ and ${\mathit{n}}_2=\widehat{z}\times {\mathit{t}}_1$. By orienting ${\mathit{t}}_1$ normal to the front and in the direction of motion, and the other two axes to form a right-handed system, simple algebra yields that the determinant $\left|T^{-1}\right|={\mathit{t}}_1\cdot {\mathit{n}}_1={\mathit{t}}_2\cdot {\mathit{n}}_2$ and $T_{ij}\propto {\left({\mathit{n}}_j\right)}_i$, which is what we meant to obtain. In 3D, we similarly introduce ${\mathit{n}}_1={\mathit{t}}_2\times {\mathit{t}}_3$, ${\mathit{n}}_2={\mathit{t}}_3\times {\mathit{t}}_1$ and ${\mathit{n}}_3={\mathit{t}}_1\times {\mathit{t}}_2$. We orient again ${\mathit{t}}_1$ normal to the front and in the direction of motion, and the other two axes to form a right-handed system. Algebra yields again that the determinant $\left|T^{-1}\right|={\mathit{t}}_1\cdot {\mathit{n}}_1={\mathit{t}}_2\cdot {\mathit{n}}_2={\mathit{t}}_3\cdot {\mathit{n}}_3$ and $T_{ij}\propto {\left({\mathit{n}}_j\right)}_i$, as anticipated.

K. The dynamics close to a Hopf bifurcation

This appendix will detail the derivation of the Stuart-Landau equation, for which we shall be following the procedure outlined in Kuramoto’s book [82]. The starting point is the rewriting of the generic dynamical-system equation $d\mathit{X}/dt=F(\mathit{X})$ as

$$\frac{d\mathit{u}}{dt}=J\mathit{u}+M\mathit{u}\mathit{u}+N\mathit{u}\mathit{u}\mathit{u}+\dots \dots ,$$ (64)

where $\mathit{u}=\mathit{X}-{\mathit{X}}_0$ is the deviation to the steady-state solution, which is supposed to be stable for negative value of the control parameter $\mu$ and lose stability at $\mu =0$. The Jacobian matrix has elements $J_{ij}=\partial F_i/\partial X_j$ with derivatives calculated at the critical point. The matrix has all its eigenvalues in the left half-plane except two, which are complex conjugate and cross the imaginary axis at $\mu =0$. Their values are $\pm i{\omega }_0$. Additional terms in (64) stand for higher-order terms in the Taylor expansion of $F$, e.g., $M\mathit{u}\mathit{u}=\frac{1}{2}\frac{{\partial }^2{F}_i}{\partial X_j\partial X_k}{u}_j{u}_k$, etc.. Note that $M$ is symmetric in the indices $j$ and $k$, and a similar property holds for $N$.

The amplitude of the oscillations on the unstable side is expected to be $\propto \sqrt{\mu }$. We define then $ϵ\equiv \sqrt{|\mu |}$ and expand

$$\mathit{u}=ϵ{\mathit{u}}_1+{ϵ}^2{\mathit{u}}_2+\dots$$ (65)

The matrices $J$, $M$ and $N$ are expected to be expandable in the control parameter $\mu$, i.e.,

$$J=J_0+{ϵ}^2\chi J_1+{ϵ}^4{J}_2+\dots ;M=M_0+{ϵ}^2\chi M_1+\dots \dots ;\text{etc}..$$ (66)

where $\mu ={ϵ}^2\mathrm{sgn}(\mu )\equiv {ϵ}^2\chi$. Finally, the growth of the amplitude is expected to occur on long timescales of the order $1/\mu$, which suggests to introduce a slow-time $\tau ={ϵ}^{2}t$. Following the multiple timescale methods [10], $\tau$ is treated as independent of $t$ so as to remove secular terms which would spoil the naïf perturbation scheme. Inserting all these expansions, reorganizing the terms and grouping them by their order in $ϵ$, we obtain a system of equations of the form

$${𝓛}_0{\mathit{u}}_{\nu }\equiv \left(\frac{\partial }{\partial t}-J_0\right){\mathit{u}}_{\nu }={\mathit{B}}_{\nu }(t),$$ (67)

where

$${\mathit{B}}_1=0;{\mathit{B}}_2=M_0{\mathit{u}}_1{\mathit{u}}_1;B_3=2M_0{\mathit{u}}_1{\mathit{u}}_2+N_0{\mathit{u}}_1{\mathit{u}}_1{\mathit{u}}_1-{\partial }_{\tau }{\mathit{u}}_1+\chi J_1{\mathit{u}}_1.$$ (68)

Because of the structure of $J$, the solution of the basic equation ${𝓛}_0{\mathit{u}}_1=0$ is

$${\mathit{u}}_1=\mathit{U}{e}^{i{\omega }_{0}t}W(\tau )+c.c.$$ (69)

where $c.c.$ stands for complex conjugate, and $\mathit{U}$ is the right eigenvector of $J_0$. All the other components relax rapidly to zero because the non-critical eigenvalues of $J$ are in the left half-plane. The left eigenvector of $J_0$ corresponding to the eigenvalue $i{\omega }_0$ is denoted by $\mathit{V}$, that is $\mathit{V}{J}_0=i{\omega }_0\mathit{V}$. Left and right eigenvectors being orthogonal, it holds ${\mathit{V}}^{\ast }\cdot \mathit{U}=0$ with the star denoting complex conjugation.

The Fredholm alternative theorem states that linear non-homogeneous equations of the type Eq. (67) admit a solution only if their right-hand side is orthogonal to the zero modes of the adjoint operator [22]. In our case, the operator adjoint to ${𝓛}_0$ is ${𝓛}_0^{†}=-{\partial }_t-J_0^{†}$, where $J_0^{†}$ is the matrix transposed and complex conjugated. Since ${\mathit{V}}^{\ast }{J}_0^{\ast }=J_0^{†}{\mathit{V}}^{\ast }=-i{\omega }_0{\mathit{V}}^{\ast }$, it follows that the solutions of ${𝓛}_0^{†}\mathit{Z}=0$ are ${\mathit{V}}^{\ast }{e}^{i{\omega }_{0}t}$ and its complex conjugate. We conclude that the solvability condition for Eqs. (67) reads:

$${\int }_0^{2\pi /{\omega }_0}\mathit{V}\cdot {\mathit{B}}_{\nu }{e}^{-i{\omega }_{0}t}dt=0.$$ (70)

The complex conjugate orthogonality condition does not bring any additional constraint for real ${\mathit{B}}_{\nu }$’s. Notice that the only components of ${\mathit{B}}_{\nu }$ which yield a non-trivial solvability condition are those $\propto e^{+i{\omega }_{0}t}$.

The right-hand side ${\mathit{B}}_2$ contains the square of ${\mathit{u}}_1$ and therefore no component $\propto e^{+i{\omega }_{0}t}$, i.e., the solvability condition is automatically satisfied. The solution at the second order is then

$${\mathit{u}}_2=\left[\left({\mathit{A}}_{+}{e}^{2i{\omega }_{o}t}{W}^2(\tau )+c.c.\right)+{\mathit{A}}_0|W(\tau ){|}^2\right]+\left(\mathit{U}{e}^{i{\omega }_{0}t}{W}_2(\tau )+c.c.\right),$$ (71)

where the terms in square/round brackets are the non-homogeneous/homogenous parts of the solution. The vectors ${\mathit{A}}_{+}=-{\left(J_0-2i{\omega }_0\right)}^{-1}{M}_0\mathit{U}\mathit{U}$ and ${\mathit{A}}_0=-2J_0^{-1}{M}_0\mathit{U}{\mathit{U}}^{\ast }$. The (last) homogeneous term of the solution will not play any role in the sequel.

At the third order, we finally obtain the first non-trivial solvability condition, which yields the long-term evolution of the amplitude $W(\tau )$. Identifying the terms $\propto e^{i{\omega }_{0}t}$ of ${\mathit{B}}_3$ in Eq. (68), we obtain

$${\partial }_{\tau }W(\tau )=\chi {\lambda }_{1}W(\tau )-g\left|W^2\right|W,$$ (72)

where $g\equiv -2\mathit{V}{M}_0\mathit{U}{\mathit{A}}_0-2\mathit{V}{M}_0{\mathit{U}}^{\ast }{\mathit{A}}_{+}-3\mathit{V}{N}_0\mathit{U}\mathit{U}{\mathit{U}}^{\ast }$. We have normalized for convenience the eigenvectors to have $\mathit{V}\cdot \mathit{U}=1$. The coefficient ${\lambda }_1=\mathit{V}{J}_1\mathit{U}$ is the first-order eigenvalue of the Jacobian. Indeed, using $\left(J_0+\mu J_1\right)\left(\mathit{U}+\mu {\mathit{U}}_1\right)=\left(i{\omega }_0+\mu {\lambda }_1\right)\left(\mathit{U}+\mu {\mathit{U}}_1\right)$, multiplying by $\mathit{V}$ on the left, and using $\mathit{V}{J}_0{\mathit{U}}_1=i{\omega }_0\mathit{V}\cdot {\mathit{U}}_1$, we obtain the above equality.

Eq. (72) is the Stuart-Landau equation discussed in the main text, with the standard replacement of the slow time-derivative by the original one, so that the derivative is taken with respect to the original time $t$, although the amplitude $W$ changes only slowly. Similar methods are used to obtain the Ginzburg-Landau Eq. 11 for extended systems, see [82].

L. The $\lambda -\omega$ model

The $\lambda -\omega$ is a class of two-dimensional non-linear oscillators that is particularly useful as it admits analytical solutions [80]. The model is defined as

$$\frac{dx}{dt}=\lambda (r)x-\omega (r)y;\frac{dy}{dt}=\omega (r)x+\lambda (r)y.$$ (73)

In radial coordinates $(r,\varphi )$, the equations reads

$$\frac{dr}{dt}=r\lambda (r);\frac{d\varphi }{dt}=\omega (r).$$ (74)

The equation for the radial coordinate lends then to quadrature. In particular, if $\lambda (r)$ has at least one zero $r=r^{\ast }$ with a negative derivative $d\lambda /dr<0$ at $r=r^{\ast }$, then the system has a limit cycle with $r=r^{\ast }$ and the azimuthal coordinate rotating with the constant speed $\omega \left(r^{\ast }\right)$. The phase on the limit cycle coincides then with the azimuthal coordinate $\varphi$.

To determine the phase $\text{Θ}$ outside of the limit cycle, it is convenient to specify the form of the two functions as $\lambda (r)=1-r^2$ and $\omega (r)=\alpha -\beta r^2$. Eq. (74) reduces then to the radial form of the Stuart-Landau equation (with proper rescalings) discussed in the main text:

$$\frac{dr}{dt}=r\left[1-r^2\right];\frac{d\varphi }{dt}=\left[\alpha -\beta r^2\right].$$ (75)

Other choices for $\lambda$ and $\omega$ can be treated similarly. The limit cycle at $r^{\ast }=1$ has uniform angular speed $\alpha -\beta$, and its basin of attraction is the whole plane except the origin. The radial equation is readily integrated by partial fraction decomposition to give

$$r(t)={\left(1+\frac{1-r_0^2}{r_0^2}{e}^{-2t}\right)}^{-1/2}.$$ (76)

Note that $d\log r=\lambda (r)dt=\left(1-r^2\right)dt$. The equation for $\varphi$ reads then

$$\frac{d\varphi }{dt}=\alpha -\beta +\beta \left(1-r^2\right)=\alpha -\beta +\beta \frac{d\log r}{dt}.$$ (77)

This relation will be used in Appendix O to determine the expression of the isochrones shown in Fig. 7C of the main text.

The addition of diffusion to Eq. (73) permits the spreading of traveling waves. Indeed, Eq. (73) in radial coordinates becomes then

$$\frac{\partial r}{\partial t}=r\lambda (r)+r_{\xi \xi }-r{\left(\frac{\partial \varphi }{\partial \xi }\right)}^2;\frac{\partial \varphi }{\partial t}=\omega (r)+\frac{1}{r^2}\frac{\partial }{\partial \xi }\left(r^2\frac{\partial \varphi }{\partial \xi }\right),$$ (78)

where we have taken the wave to spread in a generic spatial $\xi$-direction. Let us consider for simplicity the case of the Stuart-Landau equation with $\beta =0$. Eqs. (78) admit then the solution $r=r_0<1$ and $\varphi =\omega t-k\xi$, where $k^2=1-r_0^2$ and $\omega =\alpha$. We refer to [34] for more details and results on the stability of these traveling waves.

M. Stability of plane waves in the Ginzburg-Landau equation

The goal of this Appendix is to detail the derivation of the Benjamin-Feir-Newell criterion that governs the stability of plane waves solutions Eq. (12) to the Ginzburg-Landau (GL) equation that were discussed in the main text. Let us consider a small perturbation $a(\mathit{x},t)$ of the wave solution and study its evolution:

$$z(\mathit{x},t)=\sqrt{1-k^2}[1+a(\mathit{x},t)]e^{i\mathit{k}\cdot \mathit{x}-\omega (k)t}.$$ (79)

Inserting into the GL Eq. (11), linearizing and after some algebra, we obtain for $a$:

$${\partial }_{t}a=-\left(a+a^{\ast }\right)\left(1-k^2\right)(1+ic)+(1+id)(\text{Δ}a+2i\mathit{k}\cdot \mathbf{\nabla }a).$$ (80)

The presence of $a^{\ast }$ at the right-hand side makes that each Fourier mode $e^{i\mathit{q}\cdot \mathit{x}}$ will be coupled to its complex conjugate and vice versa. We can then search for a solution in the form

$$a(\mathit{x},t)=R(t)e^{i\mathit{q}\cdot \mathit{x}}+S^{\ast }(t)e^{-i\mathit{q}\cdot \mathit{x}},$$ (81)

where the complex conjugate on $S$ is just a matter of convenience. Insertion of (81) into (80) yields the equations for $R$ and $S$:

$$\{\begin{array}{l}{\partial }_{t}R=\left[-\left(1-k^2\right)(1+ic)-q^2(1+id)-2(1+id)\mathit{k}\cdot \mathit{q}\right]R-\left(1-k^2\right)(1+ic)S,\hfill \\ {\partial }_{t}S=\left[-\left(1-k^2\right)(1-ic)-q^2(1-id)+2(1-id)\mathit{k}\cdot \mathit{q}\right]S-\left(1-k^2\right)(1-ic)R.\hfill \end{array}$$ (82)

Note that Eq. (82) has a zero-mode for $q=0$, i.e., $S=-R$ is a stationary solution. For $\mathit{q}\ne 0$ this marginal mode can become stable or unstable as we proceed to discuss.

The equation for the eigenvalues $e^{\lambda t}$ of Eq. (82) is:

$$\begin{array}{r}0={\lambda }^2+2\lambda \left[1-k^2+q^2+2id\mathit{k}\cdot \mathit{q}\right]+2q^2\left(1-k^2\right)(1+cd)\\ +q^4\left(1+d^2\right)+4i\mathit{k}\cdot \mathit{q}\left(1-k^2\right)(d-c)-4\left(1+d^2\right){(\mathit{k}\cdot \mathit{q})}^2.\end{array}$$ (83)

By expanding this equation for small $q$, we find for the marginal mode:

$$\lambda \simeq -2i(\mathit{k}\cdot \mathit{q})(d-c)-q^2\left[(1+cd)-2\frac{{(\mathit{k}\cdot \mathit{q})}^2}{q^2\left(1-k^2\right)}\left(1+c^2\right)\right]+O\left(q^3\right).$$ (84)

The expression (84) finally yields the Benjamin-Feir-Newell criterion for stability: If $1+cd>0$, then the range of modes $k^2<\frac{1+cd}{3+cd+2c^2}$ is stable. The modes that destabilize first are longitudinal, i.e., maximizing ${(\mathit{k}\cdot \mathit{q})}^2$. For $c=d$, the Benjamin-Feir-Newell expression reduces to the classical Eckhaus criterion $k^2<1/3$ [31]. For the evolution of unstable modes beyond their threshold of instability, we refer again to the classical review [5] and references therein.

N. Plane waves in reaction-diffusion equations close to a Hopf bifurcation

The goal of this Appendix is to provide a description of the arguments in [80] that show the generic presence of waves for reaction-diffusion equations close to a Hopf bifurcation. The starting point is the general reaction-diffusion form

$$\frac{\partial \mathit{X}(x,t)}{\partial t}=\mathit{F}(\mathit{X})+K\text{Δ}\mathit{X},$$ (85)

where $K$ is the positive-definite and symmetric diffusivity matrix and the Jacobian matrix $J_{ij}=\partial F_i/\partial X_j$ is assumed to have the Hopf structure, i.e., two conjugate eigenvalues cross the imaginary axis and all the others are in the left half plane. The goal is to prove the existence of small-amplitude periodic solutions $\mathit{X}=\mathit{h}(\mathit{k}\cdot \mathit{x}-\omega t)$ to Eq. (13). To adapt to the notation in [80], we shall use the equivalent variable $\xi \equiv t-\frac{\widehat{\mathit{n}}\cdot \mathit{x}}{v}$, where $v$ is the phase velocity. Inserting this ansatz into Eq. (13), the problem is rephrased into the existence of a periodic solution for

$${\mathit{h}}^{\prime }=J\mathit{h}+\beta K{\mathit{h}}^{″},$$ (86)

where the prime denotes the derivative with respect to $\xi$. If a solution of period $T$ is found for some $\beta >0$, then $\omega =2\pi /T$, the phase velocity of the wave $v=1/\sqrt{\beta }$ and its wavenumber $k=\omega \sqrt{\beta }$. We shall restrict here for simplicity to the case of a two-dimensional system: $\mathit{X}=\left(X_1,X_2\right)$, and refer to [80] for the general case.

The $2\times 2$ Jacobian matrix $J$ has eigenvalues ${\lambda }_0\pm i{\omega }_0$, with ${\lambda }_0,{\omega }_0>0$. The matrices $J$ and $K$ are rewritten as

$$J=\frac{\text{Tr}J}{2}(I+\tilde{J})={\lambda }_0(I+\tilde{J});K=\frac{\text{Tr}K}{2}(I+\kappa \tilde{K}),$$ (87)

where the traces $\text{Tr}\tilde{J}=0$, $\text{Tr}\tilde{K}=0$, the matrix $\tilde{K}$ has eigenvalues $\pm 1$. The parameter $\kappa \ge 0$ is a measure of the deviation of $K$ from a scalar matrix $\propto I$. Indeed, its expression in terms of $K$ matrix elements reads: $\kappa \propto \sqrt{4K_{12}^2+{\left(K_{11}-K_{22}\right)}^2}$, vanishing if $K\propto I$. The statement in [80] is that there is a one-parameter family of periodic solutions to Eq. (86) if

$$2\kappa <\text{Tr}(\tilde{J}\tilde{K})+\sqrt{{[\text{Tr}(\tilde{J}\tilde{K})]}^2+4{\left(\frac{{\omega }_0}{{\lambda }_0}\right)}^2}.$$ (88)

In plain words, a solution exists generically for systems where the diffusivity matrix is not far from the identity.

N.1. The steps of the proof

The basic tool of the proof is the Hopf bifurcation theorem [58, 151] applied to the $4\times 4$ matrix

$$M=\left(\begin{array}{cc}0& I\\ -\frac{1}{\beta }{K}^{-1}J& \frac{1}{\beta }{K}^{-1}\end{array}\right),$$ (89)

which governs the linearized dynamics of the second-order equation (86) reformulated as a system of first-order equations:

$$\left(\begin{array}{l}{\mathit{h}}^{\prime }\hfill \\ {\mathit{g}}^{\prime }\hfill \end{array}\right)=M\left(\begin{array}{l}\mathit{h}\hfill \\ \mathit{g}\hfill \end{array}\right)$$ (90)

The proof proceeds in three steps:

1. The eigenvalues of $M$ are the roots $\lambda (\beta )$ of the polynomial $\zeta \left(-\beta {\lambda }^2,\lambda \right)$, where $\zeta$ is the characteristic polynomial of the matrix $J-{\alpha }^{2}K$:

   $$\zeta \left({\alpha }^2,\mu \right)\equiv \text{Det}\left(J-{\alpha }^{2}K-\mu I\right)=0.$$ (91)

   This is an immediate consequence of the fact that a solution $\mathit{U}{e}^{\lambda \xi }$ to Eq. (86) is equivalent to $\left(J+\beta {\lambda }^{2}K-\lambda I\right)\mathit{U}=0$, i.e., Eq. (91). The key consequence is that the existence of a pair of conjugate eigenvalues is transferred from the $4\times 4$ matrix $M$ to the $2\times 2$ matrix $J-{\alpha }^{2}K$. Namely, if the latter has a pair of imaginary values $\pm i\sigma$ at ${\alpha }^2={\alpha }_c^2$, i.e., $\text{Det}\left(J-{\alpha }_c^{2}K\pm i\sigma I\right)=0$, then $M$ will have the same pair for $\beta ={\beta }_c={\alpha }_c^2/{\sigma }^2$.

2. The condition (88) ensures that there is a (single) value ${\alpha }^2={\alpha }_c^2$ for which the matrix $J-{\alpha }^{2}K$ has a pair of conjugate pure eigenvalues $\mu \left({\alpha }^2\right)$. The eigenvalues satisfy the transversality condition $\text{Re}\left(d\mu /d{\alpha }^2\right)<0$ at ${\alpha }_c^2$. Combined with 1. above, these properties demonstrate that $M$ has a pair of conjugate imaginary eigenvalues $\lambda (\beta )$ for a single value ${\beta }_c$.

3. The imaginary eigenvalues $\lambda \left({\beta }_c\right)$ of $M$ are simple and inherit from $\mu \left({\alpha }^2\right)$ the transversality condition $\text{Re}(d\lambda /d\beta )<0$.

Properties 2. and 3. involve some straightforward but lengthy algebra, for which we refer to the original work [80]. Explicit expressions for the waves obtained in [80] for the $\lambda -\omega$ model are discussed in Appendix L.

O. Phases and isochrones

The goal of this Section is to provide more details on the definition of the phase outside of the limit cycle $\text{Γ}$ of an oscillatory dynamical system.

Phases $\text{Θ}$ for points ${\mathit{X}}_0$ on the cycle are simply defined by Eq. (14). If ${\mathit{Y}}_0$ is now a point in the basin of attraction and ${\mathit{X}}_0$ is the point on the limit cycle such that the distance $\Vert \mathit{X}\left({\mathit{Y}}_0,t\right)-\mathit{X}\left({\mathit{X}}_0,t\right)\Vert \to 0$ as $t\to \infty$, then $\text{Θ}\left({\mathit{Y}}_0\right)\equiv \text{Θ}\left({\mathit{X}}_0\right)$. For each point ${\mathit{X}}_0$ on the limit cycle, the previous equality defines the $(m-1)$-dimensional surface of points with its same phase – dubbed “isochrone” in [164] and systematically analyzed in [57]. A (rare) case where isochrones can be calculated analytically is the $\lambda -\omega$ model [80] presented in Appendix L. Indeed, by using the relation (77), we conclude that the phase $\text{Θ}=\varphi -\beta \log (r)$, rotates as the constant speed $\alpha -\beta$. The isochrones are then the spirals $\varphi -\beta \log (r)=constant$, some of which were shown in Fig. 7C. For $\beta =0$, the isochrones reduce to simple radii $\varphi =constant$, as shown in Fig. 10.

By its very definition, the phase on $\text{Γ}$ has period $T_0$. Let us now consider a point ${\mathit{Y}}_0$ on the isochrone of the point ${\mathit{X}}_0$ on $\text{Γ}$, and its mapping $\mathit{X}\left({\mathit{Y}}_0,T_0\right)$ under the stroboscopic mapping of ${\mathit{Y}}_0$ with period $T_0$. The latter point has the important property that it belongs to the same isochrone as ${\mathit{Y}}_0$, i.e., an isochrone is mapped onto itself under the Poincaré mapping with the basic period $T_0$. Indeed, by breaking the (asymptotically long) duration $t$ in the two chunks $T_0$ and $t-T_0$, we recognize that $\Vert \mathit{X}\left({\mathit{Y}}_0,t\right)-\mathit{X}\left({\mathit{X}}_0,t\right)\Vert$ (vanishing as $t\to \infty$) has the same limit as $\Vert \mathit{X}\left(\mathit{X}\left({\mathit{Y}}_0,T_0\right),t-T_0\right)-\mathit{X}\left(\mathit{X}\left({\mathit{X}}_0,T_0\right),t-T_0\right)\Vert$, which yields the sought result since the phase of $\mathit{X}\left({\mathit{X}}_0,T_0\right)$ is the same as for ${\mathit{X}}_0$. More generally, we can replace the period $T_0$ by a generic time, and thereby conclude that the phase progresses on the isochrones at the same rate as on the limit cycle, that is Eq. (14) is generally valid (and not just on $\text{Γ}$).

P. The phase sensitivity function and phase resetting curve

The vector function ${\mathit{Z}}_i(\text{Θ})\equiv \frac{\partial \text{Θ}}{\partial X_i}$ appeared in the main text to account for the variation of the phase due to a small stimulus. Here, we want to provide some more information on its properties and its relation to the phase resetting curve popularized in [165]. We refer to [164, 82, 35] for full details.

Suppose a perturbation (with components along the $m$ possible directions) is applied to a dynamical system while it is running along its limit cycle. The initial phase is $\text{Θ}$. The perturbation will move the system to another point within the basin of attraction, which will be on an isochrone with phase ${\text{Θ}}^{\prime }$. The new phase is a function of $\text{Θ}$ and the type of perturbation applied. The function ${\text{Θ}}^{\prime }(\text{Θ})$ (for a prescribed perturbation protocol) is called phase transition curve (PTC). The difference $D(\text{Θ})={\text{Θ}}^{\prime }-\text{Θ}$ is known as phase resetting curve (PRC). In the limit when the perturbation is weak:

$$D(\text{Θ})\equiv {\text{Θ}}^{\prime }-\text{Θ}=\frac{\partial \text{Θ}}{\partial X_i}\delta X_i=\mathit{Z}(\text{Θ})\cdot \delta \mathit{X},$$ (92)

which is the reason why the sensitivity function $\mathit{Z}$ is also called infinitesimal PRC.

P.1. The sensitivity function solves the adjoint equation

Let us consider the linearization of the original equation $\frac{d\mathit{X}}{dt}=\mathit{F}(\mathit{X})$ around its limit cycle $\text{Γ}$ with period $T_0$. The corresponding periodic trajectory is denoted $X_0(t)$. The $m\times m$ matrix $J_{ij}(t)=\frac{\partial F_i}{\partial X_j}\left(X_0(t)\right)$ described the dynamics of perturbations $\delta \mathit{X}$ around the limit cycle:

$$\frac{d\delta \mathit{X}}{dt}-J(t)\delta \mathit{X}(t)\equiv L\delta \mathit{X}=0.$$ (93)

The operator $L^{†}$ adjoint to $L$ is defined as

$$L^{†}\delta \mathit{X}\equiv -\frac{d\delta \mathit{X}}{dt}-J^{†}(t)\delta \mathit{X}(t),$$ (94)

which follows the standard definition of adjoint operators [22], with the scalar product between two $T_0$-periodic vector functions $\mathit{u}(t)$ and $\mathit{v}(t)$ defined as $\langle \mathit{u},\mathit{v}\rangle \equiv {\int }_0^{T_0}\mathit{u}(t)\cdot \mathit{v}(t)dt$. The matrix $J^{†}$ in Eq. (94) is the transposed of $J$.

The goal of this subsection is to show that the sensitivity function $\mathit{Z}$ satisfies

$$L^{†}\mathit{Z}(t)=0;\mathit{Z}(\text{Θ})\cdot \frac{d{\mathit{X}}_0}{d\text{Θ}}=1.$$ (95)

Indeed, let us consider Eq. (14) that defines the phase. By applying a perturbation $\delta \mathit{X}$ to both sides, we obtain that $\frac{d}{dt}[\mathit{Z}\cdot \delta \mathit{X}]=0$. By using Eq. (93), we obtain then

$$\frac{d\mathit{Z}}{dt}\cdot \delta \mathit{X}+\mathit{Z}\cdot J\cdot \delta \mathit{X}=\left[\frac{d\mathit{Z}}{dt}+J^{†}\mathit{Z}\right]\cdot \delta \mathit{X}=0.$$ (96)

Since $\delta \mathit{X}$ is arbitrary, we conclude that the left-hand side of Eq. (95) holds. Since the equation is homogeneous, a normalization condition is required to determine the amplitude. That is provided by the right-hand side of Eq. (95), obtained by taking the derivative with respect to $\text{Θ}$ of the identity $\text{Θ}(\mathit{X}(\text{Θ}))=\text{Θ}$ for points ${\mathit{X}}_0$ on the limit cycle.

A (rare) example where the sensitivity function can be calculated analytically is the $\lambda -\omega$ model discussed in Appendix L. If $\lambda (1)=0$ and ${\lambda }^{\prime }(1)<0$ then a limit cycle exists with radius $r^{\ast }=1$ and angular velocity $\omega (1)$, which can be taken to be unity. The limit cycle is then ${\mathit{X}}_0(t)=(\cos t,\sin t)$. Differentiating Eq. (73), we find that the transposed of the perturbation matrix $J$ reads:

$$J^{†}=\left(\begin{array}{cc}{\lambda }^{\prime }(1){\cos }^{2}t-{\omega }^{\prime }(1)\sin t\cos t& {\lambda }^{\prime }(1)\sin t\cos t+{\omega }^{\prime }(1){\cos }^{2}t+1\\ {\lambda }^{\prime }(1)\sin t\cos t-{\omega }^{\prime }(1){\sin }^{2}t-1& {\lambda }^{\prime }(1){\sin }^{2}t+{\omega }^{\prime }(1)\sin t\cos t\end{array}\right).$$ (97)

Some algebra shows then that the two combinations $𝓓=Z_1\sin t-Z_2\cos t$ and $𝓢=Z_1\cos t+Z_2\sin t$ satisfy $\frac{d𝓓}{dt}=0$ and $\frac{d𝓢}{dt}=-{\lambda }^{\prime }(1)𝓢+{\omega }^{\prime }(1)𝓓$. The first equation reflects the normalization condition in Eq. (95), which yields $𝓓=-1$ Since ${\lambda }^{\prime }(1)<0$, the homogeneous part of $𝓢$ ought to vanish and $𝓢=\frac{{\omega }^{\prime }(1)}{{\lambda }^{\prime }(1)}𝓓\equiv a$. We conclude that

$$Z(t)=(a\cos t-\sin t,a\sin t+\cos t),$$ (98)

which is the solution reported in [35].

Apart from a few other cases where an analytical solution can be obtained (see Chapter 8 in [35]), the $Z$ function ought to be computed numerically or estimated from data. Numerically, Eq. (95) can be integrated backward in time. Since the limit cycle is stable and the sign of the time derivative is reversed between $L$ and $L^{†}$, backward integration will relax all the modes but the periodic one, which yields the sought periodic solution. Its overall amplitude can finally be rescaled so as to match the normalization condition. For the experimental determination and a useful example of MATLAB script to process the data (neuronal but the underlying methods are general) we refer to Chapter 10 of [70], available online at www.izhikevich.com.

P.2. Two types of phase transition curves

For the experimental determination of the sensitivity function, a perturbation is applied to the system during its oscillatory limit cycle. While its amplitude should a priori be infinitesimal, in practice it must be strong enough to generate appreciable effects and to overcome noise. It is therefore important to be aware that, when the amplitude increases, a sharp change of regime may occur. Its underlying reason is intuited by Fig. 10, which illustrates the shift in the phase for the radial $\lambda -\omega$ model ($\beta =0$, see Appendix L) under overall shifts along the abscissae. The crossing of the origin clearly discriminates between two drastically different shapes of the transition curves. The two shapes were classified in [165] as type-1 (weak) or type-0 (strong) based on the linking number of the curve when plotted on a torus [65]. Even though the example shown here is deliberately as simple as possible, the existence of such a transition is quite general; its topological nature reflects the inevitable existence of singular points (as the origin in the plots of Fig. 10 or 7C in the main text) where the phase is undefined. Similar differences are present for the phase resetting curve. We refer to [165] for a fascinating discussion of this subject and singular points in natural examples, namely the circadian rhythm.

Figure 10: An illustration of the two possible types of phase transition curves.

The limit cycle and the radial isochrones are shown for the Stuart-Landau model Eq. (75) discussed in the Appendix L on the $\lambda -\omega$ model. The applied perturbation is a global rightward shift along the $x$-axis. The origin is a singular point where the phase is undefined. When the shift is small enough not to cross the origin, then the new phase has a monotonic dependence on the old one and span the entire range $(0,2\pi )$. This is known as type 1 or weak resetting. Vice versa, if the origin is crossed, then a limited range of new phases and a non-monotonic curve are obtained. This is known as type 0 or strong resetting.

Q. Frequency entrainment and phase locking

The simplest example of phase dynamics is obtained by perturbing the limit cycle $\text{Γ}$ (period $T_0$) of an $m$-dimensional dynamical system $\frac{d\mathit{X}}{dt}=\mathit{F}(\mathit{X})$, by adding a small-amplitude force $\epsilon \mathit{f}(\mathit{X},t)$ periodic in time with angular frequency $\omega$. Phases, isochrones and the sensitivity function $\mathit{Z}$ are defined as discussed in Appendices O and P. Taking the time-derivative of the phase $\text{Θ}(\mathit{X})$, we obtain:

$$\frac{d\text{Θ}}{dt}=\frac{\partial \text{Θ}}{\partial X_i}\left[{\mathit{F}}_i+\epsilon {\mathit{f}}_i\right]={\omega }_0+\epsilon \frac{\partial \text{Θ}}{\partial X_i}{\mathit{f}}_i(\mathit{X},t)\simeq {\omega }_0+\epsilon \frac{\partial \text{Θ}}{\partial X_i}{\mathit{f}}_i(\mathit{X}(\text{Θ}),t)\equiv {\omega }_0+\epsilon Q(\text{Θ},\omega t).$$ (99)

For the first two equalities, we used the chain rule and the normalization property of the sensitivity function $\mathit{Z}(\text{Θ})\cdot \mathit{F}={\omega }_0$. The key step in Eq. (99) is the third approximation of weak-coupling: since the perturbation is small and the amplitude modes relax rapidly (while the phase does not), the long-term evolution of the trajectory can be reduced to the phase only. This approximation allows us to close the equation in terms of the phase, and obtain a one-dimensional equation rather than the $m$-dimensional original one. Note that the function $Q$ is $2\pi$-periodic in both variables.

Defining $\theta \equiv \text{Θ}-{\omega }_{0}t$, we obtain $\frac{d\theta }{dt}=\epsilon Q\left(\theta +{\omega }_{0}t,\omega t\right)$, which shows that the variable $\theta$ varies slowly, on timescales of the order $O(1/\epsilon )$. Averaging methods ensure [58, 138, 65] that the long-term evolution $d\theta /\epsilon dt$ is determined by the time average of $Q\left(\theta +{\omega }_{0}t,\omega t\right)$. By Fourier decomposing the $2\pi$-periodic function $Q={\sum }_{k,l}{a}_{k,l}{e}^{ik\theta +i\left(k{\omega }_0+\ell \omega \right)t}$. we see that the only terms contributing to the average must satisfy the resonance condition $k{\omega }_0+\ell \omega \simeq 0$. The simplest resonance is for $\omega \simeq {\omega }_0$ and leaves $\ell =-k$. That reduces the sum to a function $q\left(\theta +\left({\omega }_0-\omega \right)t\right)=q(\text{Θ}-\omega t)$. Defining $\psi \equiv \text{Θ}-\omega t$, we finally obtain

$$\frac{d\psi }{dt}=-\text{Δ}\omega +\epsilon q(\psi ),$$ (100)

where $\text{Δ}\omega \equiv \omega -{\omega }_0$ is the frequency mismatch (supposed to be order $O(\epsilon )$). For higher-order resonances where $\omega \simeq {\omega }_{0}k/\ell$, we similarly have that the average of the Fourier decomposition of the $Q$-function reduces to $Q\simeq {\sum }_j{a}_{jk,-j\ell }{e}^{ijk\theta +ij\left(k{\omega }_0-\ell \omega \right)t}$, that is a function of the argument $k\text{Θ}-\ell \omega t$. Defining $\psi \equiv k\text{Θ}-\ell \omega t$ and the frequency mismatch $\text{Δ}\omega \equiv \ell \omega -k{\omega }_0$, we obtain again the same structure as in Eq. (100). The points $k{\omega }_0=\ell \omega$ define the tips of the regions where synchronization takes place, the so-called Arnold tongues because of their typical characteristic shape [126]. In the main text, we have shown that Eq. (100) also emerges as the equation governing the dynamics of the phase difference between two weakly coupled oscillators. In that case, $\psi$ is the phase difference between the two oscillators and $\text{Δ}\omega$ is their frequency mismatch.

Since the scope of this review is about waves, we defer to textbooks, see, e.g., [82, 126], for a full-fledged treatment of synchronization and restrict here to the analysis of Eq. (100) in the simplest case where the function $q$ contains only its first harmonic: $q(\psi )\propto \sin \psi$. While its analysis is technically simplified, the corresponding Adler’s equation (Eq. [2] in the main text):

$$\frac{d\psi }{dt}=-\text{Δ}\omega +K\sin (\psi ),$$ (101)

qualitatively conveys the main general features of synchronization [82]. When the positive amplitude of the forcing $K\ge |\text{Δ}\omega |$, the system synchronizes (the frequency of oscillation coincides with that of the forcing $\omega$) and the phase sets to the constant shift ${\psi }_{lock}=\arcsin \left(\frac{\text{Δ}\omega }{K}\right)$ (phase locking). We remind that entrainment can take place for various resonances, namely entrainment taking place around the region $\ell \omega =k{\omega }_0$ is known as synchronization of order $\ell :k$. The shape of the synchronization region (Arnold tongue) in the regime of weak amplitudes is a triangle, i.e., as the amplitude of the forcing $K$ increases, the range of synchronized frequencies $|\text{Δ}\omega |$ widens $\propto K$. The shape of the tongues is deformed in the regime of moderate amplitudes, and the dynamics can transition to chaos for strong enough amplitudes [126].

Outside of the synchronized regions, the phase drifts. Its time evolution can be obtained analytically for the simple form of the Adler’s equation by using the indefinite integral

$$\stackrel{X}{\int }\frac{dx}{a-b\sin x}=\frac{2\arctan \left[\frac{a\tan \frac{X}{2}-b}{\sqrt{a^2-b^2}}\right]}{\sqrt{a^2-b^2}}.$$ (102)

We obtain then the time-evolution of the phase as

$$t=-\frac{2\arctan \left[\frac{\text{Δ}\omega \tan \frac{\psi }{2}-K}{\sqrt{\text{Δ}{\omega }^2-K^2}}\right]}{\sqrt{\text{Δ}{\omega }^2-K^2}}.$$ (103)

The period $T$ is the time taken to complete a full cycle, which yields

$$T=\frac{2\pi }{\sqrt{\text{Δ}{\omega }^2-K^2}}.$$ (104)

Close to the critical point $\text{Δ}\omega =\pm K$, the period diverges as $T\propto 1/\sqrt{|\text{Δ}\omega -K|}$, which is the general behavior that takes place close to the desynchronization transition. Indeed, the square-root witnesses the critical slowdown associated to the saddle-node bifurcation [151] occurring at $\text{Δ}\omega =\pm K$ for the Adler’s equation.

R. Stability of waves in chains of coupled oscillators

To investigate the stability of the waves identified in Section 5.3, we consider small perturbations: ${\theta }_j(t)=\omega t+j\text{Δ}\varphi +{\eta }_j(t)$, and study their equations of motion:

$$\{\begin{array}{l}{\dot{\eta }}_1={\left(q^{+}\right)}^{\prime }\left({\eta }_2-{\eta }_1\right);{\dot{\eta }}_n={\left(q^{-}\right)}^{\prime }\left({\eta }_{n-1}-{\eta }_n\right);\hfill \\ {\dot{\eta }}_i={\left(q^{+}\right)}^{\prime }\left({\eta }_{i+1}-{\eta }_i\right)+{\left(q^{-}\right)}^{\prime }\left({\eta }_{i-1}-{\eta }_i\right)\text{for}i=2,\dots n-1.\hfill \end{array}$$ (105)

The tridiagonal matrix that controls the stability of Eq. (105) is then (see below for reasons of notation)

$$M=\left(\begin{array}{cccccc}b-\alpha & c& 0& \dots & 0& 0\\ a& b& c& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \dots & a& b-\beta \end{array}\right),$$ (106)

where $b\equiv -\left({\left(q^{+}\right)}^{\prime }+{\left(q^{-}\right)}^{\prime }\right)$, $a\equiv {\left(q^{-}\right)}^{\prime }$, $c\equiv {\left(q^{+}\right)}^{\prime }$, $\alpha \equiv -{\left(q^{-}\right)}^{\prime }$ and $\beta \equiv -{\left(q^{+}\right)}^{\prime }$. The primes indicate derivatives, which are calculated at $\pm \text{Δ}\varphi$ for $q^{\pm }$, respectively. Stability of the wave solution is reduced to the sign of the real part of the $M$ matrix eigenvalues.

The notation in Eq. (106) was chosen to match that of Ref. [163], where the spectrum of some tridiagonal matrices was worked out analytically. Our matrix (106) has the property that $d^2\equiv ac=\alpha \beta$, which is in the list of those that admit an explicit solution [163]. Specifically, the spectrum of eigenvalues ${\lambda }_1,\dots {\lambda }_n$ are given by formula (40) in [163]:

$${\lambda }_m=b+2d\cos \left(\frac{\pi m}{n}\right)\text{for}m=1,\dots ,n-1;{\lambda }_n=b-(\alpha +\beta ).$$ (107)

In our case, the last eigenvalue ${\lambda }_n=0$. The corresponding eigenvector is verified to be $(1,\dots ,1)$, which adds a constant phase to all the oscillators and has then a zero eigenvalue because it just amounts to a phase redefinition. As for the other $n-1$ eigenvalues, we have

$${\lambda }_m=-\left({\left(q^{+}\right)}^{\prime }+{\left(q^{-}\right)}^{\prime }\right)+2\sqrt{{\left(q^{-}\right)}^{\prime }{\left(q^{+}\right)}^{\prime }}\cos \left(\frac{\pi m}{n}\right)\text{for}m=1,\dots ,n-1.$$ (108)

If both derivatives are positive, then all the $n-1$ non-trivial eigenvalues are negative and the wave solution is linearly stable. Vice versa, if both derivatives are negative then the solution is unstable. For $q$ functions of the type shown in Fig. 11, this criterion selects the branch of the solutions of Eqs. (21). For instance, in the simplest case $q^{+}=q^{-}=\sin (\text{Δ}\varphi )$, stability limits $\text{Δ}\varphi$ in the range $(-\pi /2,\pi /2)$. For functions like the red one in Fig. 11A, which are still odd but more structured, multiple wave solutions (or no wave) are possible. The frequency of oscillation $\omega$ is the same for all of those solutions but the phase gradient $\text{Δ}\varphi$ will differ (see Fig. 11C). Convergence to the various solutions is determined by the initial conditions. In the simplest cases, $\text{Δ}\varphi$ is the same at all locations and a gradients ensues (see blue and purple curves in Fig. 11C). In the general case, the phase difference is not the same at all locations and no gradient is then observed (see red curve in Fig. 11C and Fig. 11D). Finally, in the general case where the functions are different and/or not odd, it is possible to have solutions where derivatives have different signs. The eigenvalues will then have an imaginary component but oscillatory fluctuations will still decay provided the sum ${\left(q^{+}\right)}^{\prime }+{\left(q^{-}\right)}^{\prime }>0$.

Figure 11: Chains of coupled oscillators.

A) Two types of coupling function $q(\varphi )$ that appear in Eq. (105) and Section 5.3. The blue curve is simply the first harmonic $\sin (\varphi )$, which has two intercepts with a horizontal line, one with positive and the other with negative slope. The red curve shows the combination $\sin (\varphi )-0.55\sin (2\varphi )+0.55\sin (3\varphi )$ of the first three harmonics with coefficients that produce multiple (two) intercepts with positive slopes (full dots). Open dots indicate intercepts with negative slopes, which are unstable. B) The curve ${\varphi }_j(t)$ vs $t$ for three different positions in the chain. The frequencies are ${\omega }_2=1$, ${\omega }_1=1-0.4$ and ${\omega }_n=1+0.4$, the couplings $q^{+}=q^{-}$ and their profile is the red one of panel A). The predicted $\omega ={\omega }_1+{\omega }_n-{\omega }_2=1$ is well observed in simulations, with phase shifts among the spatial positions that are considered in the following panels. C) For initial conditions such as ${\varphi }_j=0$ (purple curve), the selected solution of Eq. (21) $q(\text{Δ}\varphi )=0.4$ for the spatial phase shift $\text{Δ}\varphi ={\varphi }_j-{\varphi }_{j-1}$ is ${\text{Φ}}_1$ in panel A). We remind that the local wave velocity is $\propto -\omega /\text{Δ}\varphi$. For initial conditions such as ${\varphi }_j=2j$ (blue curve), the selected solution is $\text{Δ}\varphi ={\text{Φ}}_2$. Finally, for an initial condition such as ${\varphi }_j=j$ (the unit slope being close to the middle unstable solution in panel A), we obtain a curve (red) that regularly alternates between the two solutions $\text{Δ}\varphi ={\text{Φ}}_1$ and $\text{Δ}\varphi ={\text{Φ}}_2$, which yields an effective slope $\left({\text{Φ}}_1+{\text{Φ}}_2\right)/2$. D) For noisy initial conditions (shown in the inset), the profile ${\varphi }_j$ vs. $j$ settles on a combination of solutions of $q(\text{Δ}\varphi )=0.4$, including ${\text{Φ}}_1+2\pi$ at locations where the initial gradients are very steep. No constant-gradient (wave) solution is then observed.

The above analysis also applies to the case of waves where frequencies are equal (${\omega }_i={\omega }_0$ for $i=1,\dots ,n$), which requires some special forms of the couplings. Indeed, Eqs. (20) yield:

$$\omega ={\omega }_0+q^{+}(\text{Δ}\varphi );\omega ={\omega }_0+q^{-}(-\text{Δ}\varphi );\omega ={\omega }_0+q^{+}(\text{Δ}\varphi )+q^{-}(-\text{Δ}\varphi )$$ (109)

The equalities are equivalent to having $q^{+}(\text{Δ}\varphi )=q^{-}(-\text{Δ}\varphi )=0$ and $\omega ={\omega }_0$. In other words, the two functions $q^{\pm }(\pm \text{Δ}\varphi )$ should have a joint zero at non-trivial values of the phase difference and derivatives at those zeros should satisfy the stability conditions (108).